Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatial-confinement induced electroreduction of CO and CO2 to diols on densely-arrayed Cu nanopyramids†
Ling
Chen
 ,
Cheng
Tang
,
Cheng
Tang
 ,
Kenneth
Davey
,
Kenneth
Davey
 ,
Yao
Zheng
,
Yao
Zheng
 ,
Yan
Jiao
,
Yan
Jiao
 * and
Shi-Zhang
Qiao
* and
Shi-Zhang
Qiao
 *
*
School of Chemical Engineering and Advanced Materials, The University of Adelaide, South Australia 5005, Australia. E-mail: yan.jiao@adelaide.edu.au; s.qiao@adelaide.edu.au
First published on 7th May 2021
Abstract
The electroreduction of carbon dioxide (CO2) and carbon monoxide (CO) to liquid alcohol is of significant research interest. This is because of a high mass-energy density, readiness for transportation and established utilization infrastructure. Current success is mainly around monohydric alcohols, such as methanol and ethanol. There exist few reports on converting CO2 or CO to higher-valued diols such as ethylene glycol (EG; (CH2OH)2). The challenge to producing diols lies in the requirement to retain two oxygen atoms in the compound. Here for the first time, we demonstrate that densely-arrayed Cu nanopyramids (Cu-DAN) are able to retain two oxygen atoms for hydroxyl formation. This results in selective electroreduction of CO2 or CO to diols. Density Functional Theory (DFT) computations highlight that the unique spatial-confinement induced by Cu-DAN is crucial to selectively generating EG through a new reaction pathway. This structure promotes C–C coupling with a decreased reaction barrier. Following C–C coupling the structure facilitates EG production by (1) retaining oxygen and promoting the *COH–CHO pathway, which is a newly identified pathway toward ethylene glycol production; and, (2) suppressing the carbon–oxygen bond breaking in intermediate *CH2OH–CH2O and boosting hydrogenation to EG. Our findings will be of immediate interest to researchers in the design of highly active and selective CO2 and CO electroreduction to diols.
Introduction
Electrocatalytic conversion of carbon dioxide (CO2) and carbon monoxide (CO) to value-added chemicals and fuels provides a sustainable and carbon-neutral route for storage of renewable energy.1 Electrocatalytic reduction of CO2 to C1 chemicals, including CO and formate (HCOO−), has been reported with relatively high efficiencies and reaction rates.2,3 Additionally, production activities and efficiencies toward particular C2 chemicals, including ethylene and ethanol, are improving.4,5 However, the selective production of higher-value C2 chemicals by electrochemical methods, such as diols, has not been demonstrated.Diols are critical intermediates in synthetic chemistry and essential building blocks in organic chemistry. It is both practically important and fundamentally significant to discover new electrochemical production routes toward diols.6,7 For example, ethylene glycol ((CH2OH)2, EG) is the most common industrial diol.8 However, current mainstream technology for large-scale production of ethylene glycol relies on a multi-staged process that is energy and cost intensive, and is not economically sustainable.8–12 Alternatively, EG production from CO/CO2via electrochemical methods, especially when combining with renewable energy input, could offer an alternative route that is clean and sustainable.
A bottleneck for realizing conversion to diols is the development of necessary highly selective and active catalyst materials. This is practically challenging given that electrochemical reduction of CO2 or CO to alcohols has lower Faraday efficiency compared with hydrocarbon products, mainly because of the difficulty to retain oxygen for hydroxyl group formation.13–15 Several strategies have been proposed to improve selectivity of catalyst materials toward alcohol products. These strategies include morphology control,16,17 crystal phase engineering,18 bimetallic catalysts,19 molecule modification,20 vacancy engineering21 and compressive strain.22 In addition to these catalyst design strategies we have proposed a new strategy that could improve multi-carbon products selectivity, namely, formation of copper nanopyramids.23
These copper nanopyramids showed improved electrocatalytic activity that is attributed to a pyramidal effect that promotes C2 selectivity from three aspects: (1) improved *CO adsorption; (2) geometrically preferable sites for C–C coupling; and, (3) boosted surface electron transfer.23 In addition, we observed a unique feature which is the confined space between adjacent nanopyramids. We concluded that this might provide opportunities for C–C coupling and retaining of oxygen through O–Cu bond formation between the oxygen in the intermediates and copper on adjacent nanopyramids. Therefore we proposed nanopyramid-based structures to improve selectivity toward diols.
Given that reduction of CO2 to CO is close to 100% Faraday efficiency2,4 and that *CO is the most important intermediate in CORR and CO2RR,6 investigation of CO2 reduction to ethylene glycol can be readily combined with CO reduction. Following two *CO adsorption being formed on the surface, two post-C–C coupling pathways exist on a conventional copper surface following formation of *COH–CO as is outlined in Scheme S1.†24–26 Following dehydroxylation at different stages, both pathways lead to the formation of *CH–COH where the pathway bifurcates into two sub-routes toward hydrocarbons (i.e. ethylene) formation or oxygenates (i.e. ethanol) formation. The ratio of produced ethylene and ethanol is about 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, together with negligible diol such as ethylene glycol.24,27,28 The fundamental reason for a low selectivity for ethylene glycol lies in the dehydroxylation at early stage in conventional pathways: intermediates *COH–CO and *COH–COH are dehydroxylated to *C–CO and *C–COH, respectively, which make the pathway to diols blocked.24,27 Therefore existing catalysts that follow conventional reaction pathways are unable to retain the oxygen atoms in the key reaction intermediates for diol production.
1, together with negligible diol such as ethylene glycol.24,27,28 The fundamental reason for a low selectivity for ethylene glycol lies in the dehydroxylation at early stage in conventional pathways: intermediates *COH–CO and *COH–COH are dehydroxylated to *C–CO and *C–COH, respectively, which make the pathway to diols blocked.24,27 Therefore existing catalysts that follow conventional reaction pathways are unable to retain the oxygen atoms in the key reaction intermediates for diol production.
The challenge could be addressed by enabling an alternative pathway by altering the coordination environment and confined-space, as such an environment could facilitate carbon–oxygen bond retention. Therefore we proposed that Cu nanopyramids with confined space could enable this new pathway for diol production.
The nanomorphology of a confined space boosts the adsorption of particular intermediates to drive selectivity along a desired reaction pathway. This is well-established and widely applied in catalyst design to regulate product selectivity. For example, Yang et al. used spatial confinement to explain a selectivity shift from C1 to C2 (ref. 29) and, Zhuang et al. applied it to boost C3 production through extending the retention of C2 species within copper nanocavity structures.30
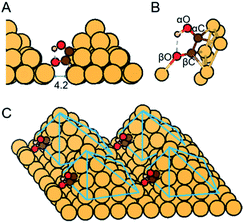
Here we report assessment of alternative pathways for the direct electroreduction of CO/CO2 to ethylene glycol on densely arrayed Cu nanopyramids (Cu-DAN) using density functional theory (DFT) computations. Our results show that a unique spatial-atomistic arrangement on Cu-DAN promotes C–C coupling and accelerates the formation of favorable intermediates following C–C coupling. Because of the confined space there is an extra bond between the adsorbed *COH–CO and the adjacent Cu nanopyramid as is shown in Fig. 1. This Cu–O interaction keeps the C–O bond intact against dehydroxylation, alters the objective and priority of hydrogenation to form intermediates with comparatively lower kinetic formation energy, and increases the kinetic barriers for competing pathways. This facilitates an alternative *COH–CHO reaction pathway that leads to direct electrosynthesis of ethylene glycol from CO.
Methods and models
Models
We examined three surfaces and compared the relevant ethylene glycol production pathways. The three structures include Cu-DAN, sparsely arrayed Cu nanopyramid (Cu-SAN), and planar Cu(100). These latter two are included for comparison. The lattice constant for Cu was optimized to be 3.64 Å in its fcc crystal structure. As is displayed in Fig. S1† four [111] diamond nanopyramids23 were proposed based on a 10 × 10 × 1 Cu surface with 4.2 Å distance in between to represent the dense-array, and on a 12 × 12 × 1 Cu surface with 5.8 Å distance to represent the sparse-array. The base layers were fixed whilst nanopyramids and adsorbates were permitted to fully relax in all configurations. Planar Cu(100) was modeled with a periodic 4 × 3 × 3 model with two bottom layers fixed and top layer relaxed. The vertical separation between periodically repeated images was set at least 10 Å in all cases to ensure no interaction between images. Moreover, the proposed Cu-DAN models show electrochemical stability as analyzed in ESI Fig. S2 and Note 1.†Computational methods
DFT computations were performed with the Vienna Ab Initio Simulation Package (VASP) code.31 The Perdew–Burke–Ernzerhof (PBE) functional was employed to compute the electron exchange–correlation energy.32 Projector Augmented Wave (PAW) potentials were used to describe the ionic cores.33 The atomic relaxations were carried out with the quasi-Newton minimization scheme, until the maximum force on any atom was less than 0.02 eV Å−1. Geometry optimizations were performed with a plane-wave cutoff of 400 eV. An irreducible 3 × 3 × 1 Monkhorst–Pack k-point grid was used34 with the center shifted to the gamma point. The Fermi level was smeared with the Methfessel–Paxton approach with a smearing of 0.1 eV. Dipole corrections were included in all computations to minimize inaccuracies in the total energy because of simulated slab interactions. The dipole moment was computed parallel to the z-direction.A general electroreduction reaction is described by the following eqn (1):
| *A + H+ + e− = *AH | (1) |
| ΔG = G*AH − G*A − [GH2/2 − eU] | (2) |
Kinetic barrier is essential to determine the product selectivity and dominant reaction pathway. This was computed using the nudged elastic band (NEB) method.37 The total energy and force thresholds for geometry optimizations were 1 × 10−5 eV and 0.05 eV Å−1, respectively. The minimum energy pathway (MEP) was examined using six images during the transition state search.
We identified in total 10 relevant elementary reaction steps, and correspondingly calculated 13 possible pathways on three surfaces, as is summarized in Table S2.† Both H-shuttling and surface *H transfer mechanism were considered for these reactions. Solvation effects were considered under H-shuttling model by including one explicit water molecule in the computations.36,38 Such consideration for solvation effect was used previously to study facet dependence of CO2 reduction pathways on Cu surface.39 The MEP for these 13 pathways are presented in ESI Fig. S3–S12,† with the atomic coordinate of initial, transition and final state summarized in Tables S3–S15.† Each transition state was confirmed to have a single imaginary vibrational frequency along the reaction coordinate. The kinetic barriers ΔG‡ under potential U were then deduced from MEP obtained ΔG‡(U0) as is described in eqn (3).39
| ΔG‡(U) = ΔG‡(U0) + eβ′(U − U0) | (3) |
In computing relative onset potential we assumed that 0.75 eV is the threshold barrier (Ethresholda) that can be overcome to give acceptable production rates at room temperature.40 For key reaction steps identified in the alternative pathway, a lower Ethresholda of 0.40 eV was adopted.41 The onset potential Uonset was computed via solving the expression of potential-determining step (PDS), eqn (4).
| Ethresholda = ΔG‡(U0) + eβ′(Uonset − U0) | (4) |
Results and discussion
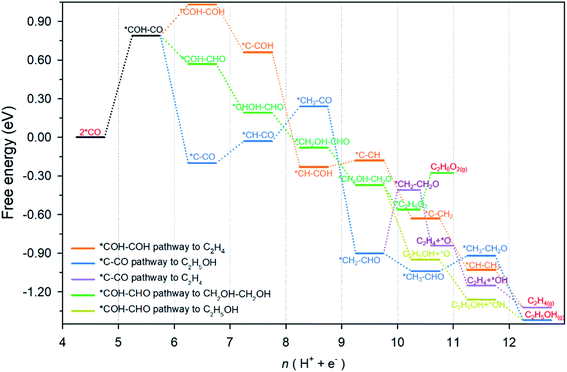
An overview of possible reaction pathways and related free energy values identified in this research is given in Fig. 2. Pathways demonstrated in the figure begin with 2 *CO on Cu-DAN. Further reduction of 2 *CO to C2 products proceeds in three major pathways, namely, (1) *COH–COH pathway (in orange color) – a conventional pathway toward ethylene (C2H4) formation;24 (2) *C–CO pathway which bifurcates from *CH2–CHO to ethylene (in purple) and ethanol (C2H5OH, blue);25,26 and, (3) *COH–CHO pathway for CH2OH–CH2OH formation (green) with a bifurcation to C2H5OH (brown) from *CH2OH–CH2O. Fig. S13† illustrates the chemical structure of all intermediates in the overall reaction network. The competing hydrogen evolution reaction (HER) is significantly inhibited on the structure, as is shown in ESI Fig. S14 and Note 2.† In the following we explore the reduction of *CO moieties on Cu-DAN surface in the major pathways, and provide quantitative insight into how the morphology drives selectivity for ethylene glycol over alternative C2 products, including ethylene/ethanol.CO–CO coupling to *COH–CO
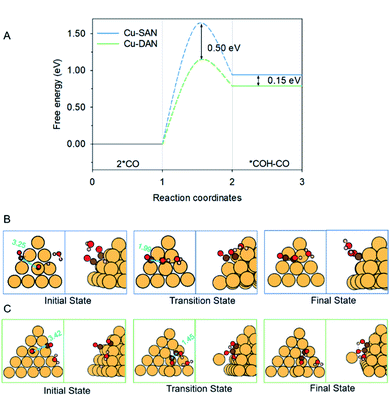
The coupling of two *CO, and subsequent proton-coupled electron transfer (PCET, 2 *CO + H+ + e− → *COH–CO), occur concomitantly. This was identified as the rate-determining step (RDS) for the onset potential.22 We referenced published data as the benchmark to decide whether C–C coupling was kinetically facile. Luo et al. for example, adopted this same computational model to determine the reaction barrier for C–C coupling on planar Cu(100) as equal to 1.52 eV.39 In consequence for a reaction barrier value less than 1.52 eV we reasonably assumed the C–C coupling is kinetically facile. This is because the coupling performance is better than planar Cu(100) surface known to favor C2 production, and vice versa. We calculated the C–C coupling steps from two models, namely the Cu-SAN and Cu-DAN, to reveal the coupling promotion supplied by confined-space. Additionally, *CO coverage has some impact on C–C coupling. This is analyzed in ESI Fig. S15, S16 and Note 3.†The reaction pathways and different transition state structures for *COH–CO formation on Cu-SAN and Cu-DAN are displayed as Fig. 3. As is shown in Fig. 3A *COH–CO formed on Cu-DAN establishes an extra O–Cu bond with the adjacent Cu nanopyramid. This state is more stable by 0.15 eV compared with that for Cu-SAN. The coupling barrier on Cu-DAN of 1.13 eV is significantly less than that of the adopted benchmark of 1.52 eV. This barrier value on Cu-DAN is 0.50 eV less than that on Cu-SAN of 1.63 eV. The lowered barrier significantly decreases the onset potential from −1.78 to −0.77 V vs. RHE, which means that the C–C coupling on Cu-DAN is significantly promoted. We conclude that this finding is a result of the combined effect of the breaking of scaling relation between key intermediates, together with more active C–C bond formation facilitated by spatial-confinement.
 | ||
| Fig. 3 (A) Reaction energetics involved in 2 *CO dimerization and reduction to *COH–CO at 0 V vs. RHE. Structures of the initial, transition and final states in CO–CO coupling on (B) Cu-SAN and (C) Cu-DAN, respectively. Minimum energy path for reaction barriers in panel A is found in Fig. S3.† Color code: Cu, orange; C, brown; O, red; H, pink. Distances are in Å. | ||
Spatial-confinement facilitated *COH–CO formation
The binding energies of reaction intermediates on catalysts are dependent on each other, as is decided by scaling relationships.42,43 This is because adsorptions of different intermediates with the same pattern, e.g. C containing intermediates are correlated.44,45 Although this intrinsic relationship facilitates activity prediction of heterogeneous catalysts, it always imposes limitations to improve catalytic performance as optimizing for one adsorbed species will reduce other steps from optimal value. This underscores that establishing effective strategies to break the scaling relationships for optimized CRR performance is a present significant research theme.46,47As is displayed in Fig. S17,† the adsorption energy of 2 *CO on Cu-SAN is linearly-correlated to the formation energy of *COH–CO with a slope of −0.37. However the formation energy of *COH–CO on Cu-DAN is significantly shifted away from the scaling relation, with the value reduced from 0.51 eV (the trend fitted level) to 0.18 eV. This finding indicates that the extra O–Cu bond formed between βO of *COH–CO and Cu atom of the adjacent nanopyramid breaks the scaling relation between carbonaceous intermediates, *CO and *COH–CO. The reason is that the new adsorption pattern (via O adsorption) introduced by forming extra O–Cu bond independently boosts the adsorption of *COH–CO, whilst the adsorption of 2 *CO in the previous step is almost unaffected because the electronic properties of surface Cu is unchanged. In consequence *CO dimerization is promoted on the densely-arrayed nanopyramids. This is in contrast to other approaches such as elemental alloying48 and vacancy engineering.21
We attribute the underlying reason for the breaking of scaling relationship to the spatial-confinement effect on Cu-DAN. As is shown in Fig. 3B, on Cu-SAN the distance between two *CO moieties in the initial state is 3.25 Å. In the transition state these two C atoms have not coupled, although the distance is decreased to 1.99 Å. The reaction barrier for this step of 1.63 eV at 0 V vs. RHE is greater than that of the benchmark. This means C–C coupling is not facile on this surface. As is shown schematically in Fig. 3C on Cu-DAN, the distance between two *CO moieties is significantly shortened from 3.42 Å in the initial state to 1.45 Å – this being a typical C–C single bond length – in the transition state, with a lowered reaction barrier of 1.13 eV. Both O–Cu and C–C bond formation complete in the transition state on Cu-DAN. This confirms that this structure with an extra O–Cu bond provides a more active C–C coupling site via reducing the energy of the transition state. Because of the difficulty of C–C coupling on Cu-SAN, this structure was not further investigated.
*COH–COH pathway
Following the formation of *COH–CO, the pathway trifurcates to *COH–COH, *C–CO and *COH–CHO. The reaction barrier and formation energy of the three key intermediates on all investigated surfaces are summarized in Fig. 4, together with the formation scheme on Cu(100) and Cu-DAN.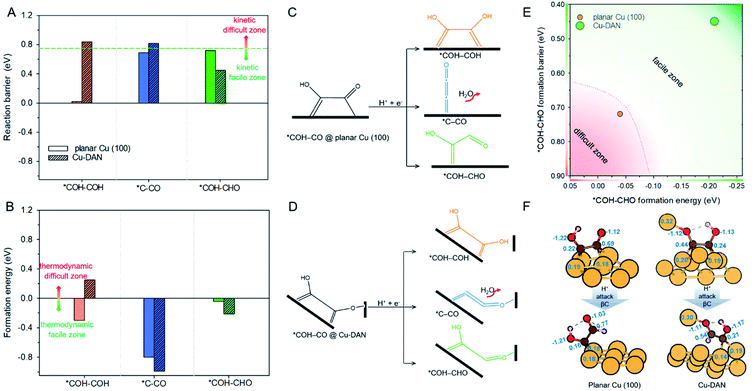 | ||
| Fig. 4 (A) Reaction barrier, (B) formation energy of key intermediates *COH–COH, *C–CO and *COH–CHO, and reaction schemes toward formation of intermediates on (C) planar Cu(100) surface, and (D) Cu-DAN. The reaction barriers for *COH–COH and *C–CO on planar Cu(100) surface were obtained from Cheng et al.24 The energy bars for *COH–COH, *C–CO and *COH–CHO are displayed in, respectively, orange color, blue and green, to coordinate with the code in Fig. 2. (E) Reaction energetics involved in *COH–CO reduction to *COH–CHO on planar Cu(100) surface and Cu-DAN with extra O–Cu bond. (F) Adsorption geometries of *COH–CO and *COH–CHO on, respectively, planar Cu(100) and Cu-DAN. The Bader charges (|e−|) on *COH–CO and *CHO–COH are marked on intermediates and copper atoms as active center. Color code: Cu, orange; C, brown; O, red; H, pink. | ||
On Cu-DAN, the *COH–COH pathway starts with cleavage of strong O–Cu bond (2.63 eV, Fig. S18†) and successive protonation of O (MEP in Fig. S4†). This bond breaking imposes a higher barrier toward *COH–COH formation on Cu-DAN. This is 0.84 eV at 0 V vs. RHE, in comparison with 0.02 eV at 0 V vs. RHE on the Cu(100) surface.24 In addition, this process on Cu-DAN is endergonic with an uphill free energy change of 0.25 eV. Therefore the pathway is both thermodynamically and kinetically unfavored on Cu-DAN, compared with other competitive pathways.
*C–CO pathway
On both Cu(100) surface and Cu-DAN, *C–CO formation is thermodynamically advantageous whilst kinetically disadvantageous (Fig. 4A and B).24 The barrier value for *COH–CO reduction to *C–CO on planar Cu(100) is high (ΔG‡ = 0.69 eV),24 and is attributed to the significant atomic configurations transformation from a parallel adsorption pattern with two C atoms binding to surface in the initial state, to a vertical adsorption pattern with only one bond formed between copper and carbon atom in the final state (Fig. 4C).26 With Cu-DAN, *COH–CO is dehydrated to *C–CO with a downhill ΔG = −0.99 eV and reaction barrier ΔG‡ = 0.82 eV (MEP in Fig. S5A†). This increased reaction barrier on Cu-DAN surface is attributed to the spatial-confinement effect (Fig. 4D and S19†). In the final state, three atoms in the *C–CO adsorbate align linearly, as is the same as that on Cu(100). However, the O–Cu bond between βO and Cu atom of the adjacent nanopyramid limits the stretching of βO atom, and therefore a higher reaction barrier. It is concluded therefore that on Cu-DAN surface the *C–CO pathway is less probable.*COH–CHO pathway
In this pathway, βC on *COH–CO is protonated to form *COH–CHO. The free energy change ΔG is −0.21 eV for *COH–CHO formation with a low energy barrier ΔG‡ = 0.45 eV (Fig. S6A†). This barrier value is lower than that on Cu(100) (Fig. S6B†), and is contributed to two factors: (1) the extra βO–Cu bond impedes cleavage of O–Cu bond and the subsequent H atom shift from βC to βO toward *COH–COH (Scheme 1A). This significantly facilitates and stabilizes formation of *COH–CHO which is thermodynamically more stable than *COH–COH by 0.45 eV, and; (2) the (100) and (111) facets possessed by Cu-DAN facilitate *CHO and *COH adsorption, and correspondingly therefore promote coupling between *COH and *CHO.37 Consequently the formation of *COH–CHO has significantly lower formation energy and reaction barrier in comparison with planar Cu(100) surface. This is shown in Fig. 4E.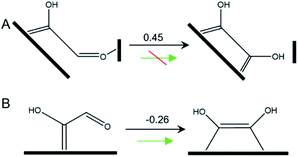 | ||
| Scheme 1 Tautomerization of *COH–CHO on (A) Cu-DAN surface and (B) planar Cu(100). The values shown above arrows are ΔG (eV) at 0 V vs. RHE. | ||
On Cu(100) such a pathway is unfavored due to the high energy barrier. In addition *COH–CHO can undergo a facile tautomerization to *COH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COH (Scheme 1B and ESI Note 4†). Therefore this new pathway is considered as exclusive to Cu-DAN.
COH (Scheme 1B and ESI Note 4†). Therefore this new pathway is considered as exclusive to Cu-DAN.
Origin of *COH–CHO formation on Cu-DAN
We performed further analyses to reveal how the extra O–Cu bond on Cu-DAN facilitates formation of *COH–CHO. Fig. 4F shows the adsorption geometries of the reactant and product regarding *COH–CHO formation (*COH–CO + H+ + e− → *COH–CHO) on planar Cu(100) and Cu-DAN and corresponding Bader charge analysis of the surface atoms.49On planar Cu(100) surface the *COH–CO binds through two C atoms to four surface Cu atoms. The number of electrons provided by Cu bonded to C atoms is around 0.20 e−. On Cu-DAN surface the *COH–CO binds through both C and βO atoms to five surface Cu atoms. The number of electrons provided by Cu to C atoms is similar to that on planar Cu(100). However the electron provided by Cu bonded to βO is greater (0.32 e−). This finding suggests that some electron are transferred to adsorbate via the extra Cu–O bond. The electrons on βO are similar on both planar Cu(100) and Cu-DAN surfaces (1.12 e−). Therefore the extra electron transfer to βO from the adjacent nanopyramid on Cu-DAN indicates that βC provides less electron charge to βO. This results in more electrons kept on the βC atom than on planar Cu(100) (0.25 e− more).
The βC atom is a type of Lewis base with a lone electron pair, whilst H+ is a naked proton with an unoccupied molecular orbital. The protonation of βC is the process where βC utilizes the highest occupied molecular orbital (HOMO) to interact with the lowest unoccupied molecular orbital (LUMO) of H+.50 A more negatively charged βC means a stronger Lewis base with a higher nucleophilicity, which facilitates protonation.
Post *COH–CHO pathways on Cu-DAN and role of spatial-confinement
Following the formation of *COH–CHO, reaction steps thereafter exhibit a preference toward hydrogenation of C atoms to produce *CHOH–CHO, rather than dehydroxylation to *C–CHO. This is because both the reaction barrier and free energy change for *CHOH–CHO (0.56 eV and −0.38 eV, Fig. S7†) are lower than those for *C–CHO (1.07 eV and 0.04 eV, Fig. S8†). *CHOH–CHO is then reduced successively to *CH2OH–CHO with ΔG‡ = 0.23 eV and ΔG = −0.27 eV (Fig. S9†), and *CH2OH–CH2O with ΔG‡ = 0.43 eV and ΔG = −0.29 eV (Fig. S10†). Notably, all reaction barriers are readily surmountable at room temperature. Amongst these reduction steps, spatial-confinement shows a pivotal role to preferential hydrogenation of C atoms, whilst keeping both O atoms intact. This is the key requirement to produce diols. How spatial-confinement drives selectivity toward oxygenates through concomitantly protecting both O atoms against dehydroxylation is explained in the following.Further hydrogenation of key intermediate *COH–CHO on the COH moiety has two options as is illustrated in Scheme S2:† (1) protonation of αO and subsequent dehydroxylation to *C–CHO, and; (2) direct protonation of αC to *CHOH–CHO. *C–CHO transformation is not facile to process on Cu-DAN. This is because of spatial-confinement induced relocation of adsorption site. With the cleavage of αC–OH bond as a consequence, αC forms a stronger bond with surface Cu with shorter bond length so as to conform to the octet rule (namely, that every carbon atom must form four covalent bonds to achieve a stable structure with eight electrons in the valence shell).51 The *C–CHO transformation is not facile to proceed on Cu-DAN because the spatial confinement restricts both sides of the intermediate from stretching, and consequently relocates αC to hexagonal close packed (HCP) site (Fig. S20†). In contrast the formation of *CHOH–CHO is more facile. This is because of less restriction from spatial-confinement, and results in a significantly lower formation barrier. Therefore the spatial-confinement promotes selective hydrogenation on αC to leave αO reserved in the hydroxyl group.
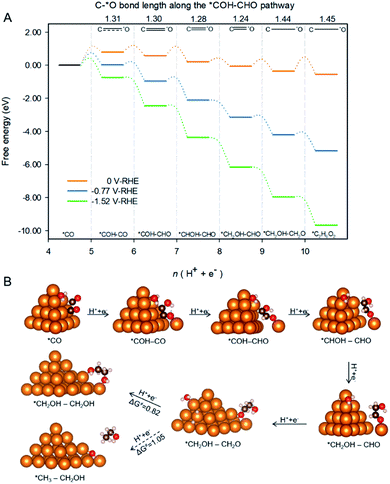
Spatial-confinement also protects βO by maintaining the double bond between βC and βO until formation of *CH2OH–CH2O as is shown in Fig. 5A. The figure depicts the pathway and associated reaction energetics for ethylene glycol production starting with 2 *CO on Cu-DAN at 0 V, −0.77 V (the onset potential with 0.75 eV barrier threshold), and −1.52 V vs. RHE (the onset potential corresponding to 0.40 eV barrier threshold). The atomic structures of intermediates in the pathway are shown schematically in Fig. 5B where the βC–O bond length is used to estimate bond strength in the intermediates along the pathway.26 The βC–O bonds in the first three post *COH–CO intermediates along the pathway i.e. *COH–CHO, *CHOH–CHO and *CH2OH–CHO, can be classified as strong bonds with a bond length shorter than 1.30 Å, a typical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond. A strong C
O double bond. A strong C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond hinders protonation of βO and subsequent dehydroxylation. It therefore reserves βO atoms in these intermediates.
O double bond hinders protonation of βO and subsequent dehydroxylation. It therefore reserves βO atoms in these intermediates.
Additionally, as a result of kinetic selectivity derived from spatial-confinement the hydrogenation preferentially happens to αC instead of αO, until the second-last step where αC is completely disconnected from original nanopyramid, Fig. 5B. Without the restriction of confined-space the βC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond is facilely stretched, and turns into a single bond with a bond length longer than 1.44 Å. This facilitates hydrogenation of βO to yield the final product – ethylene glycol – with downhill ΔG = −0.19 eV.
O double bond is facilely stretched, and turns into a single bond with a bond length longer than 1.44 Å. This facilitates hydrogenation of βO to yield the final product – ethylene glycol – with downhill ΔG = −0.19 eV.
Post *CH2OH–CH2O to ethylene glycol due to spatial-confinement
The final step toward formation of ethylene glycol has a competing pathway which is the formation of CH3–CH2OH via an exothermal protonation of βC (ΔG = −0.58 eV at 0 V vs. RHE). However, the reaction barrier for the step (1.05 eV, Fig. S11†) is greater than that for ethylene glycol (0.82 eV, Fig. S12†), indicating that the production of ethanol is kinetically less favorable. Moreover the reaction barrier for the final step toward ethylene glycol is further reduced to 0.44 eV under potential of −0.77 V applied to facilitate the previous C–C coupling step. This is below the 0.75 eV threshold, and can therefore be overcome to give appreciable production rates at room temperature.40In the pathway toward ethylene glycol, the two oxygen atoms have substantial binding with copper (O–Cu distance of ∼2.0 Å, as is shown schematically in Fig. S12†). This finding reveals that the hydrogenation of βO does not break the O–Cu bond. In contrast the hydrogenation of βC results in the breaking of O–C bond and the adsorbate i.e. ethanol is driven further away from the surface as a result of the adverse alignment of OH group dipole moment with charged surface (Fig. S11†).28 Therefore it is more kinetically facile to form the surface bound ethylene glycol because the process does not involve bond breaking. Additionally the desorption of ethylene glycol from nanopyramid surface is slightly endothermic at 0.28 eV, and can be readily overcome.
Overall, the extra binding between O and Cu that occurs because of the confined-space amongst adjacent nanopyramids promotes selectivity toward ethylene glycol by facilitating an alternative pathway of three parts: (1) the atomic arrangement with an extra O–Cu bond kinetically suppresses the other two competing pathways by increasing relevant reaction barriers; (2) greater electron transfer via O–Cu bond and consequent greater nucleophilicity on βC lowers the formation barrier of key intermediate *COH–CHO. This is the foundation for the new pathway, and; (3) spatial-confinement facilitates the extra O–Cu binding that preserves both O atoms against dehydroxylation through geometrically selecting hydrogenation toward formation of ethylene glycol.
Conclusions
New reaction mechanisms and alternative pathways based on DFT computations for the electroreduction of CO2 to ethylene glycol on densely-arrayed Cu nanopyramids (Cu-DAN) show that there exists an alternative pathway that facilitates the direct electrosynthesis of ethylene glycol. This pathway is not favorable on planar Cu(100) surface and sparsely-arrayed nanopyramids without an extra binding between O atom and surface Cu atom from the adjacent nanopyramid. It is concluded that the extra O–Cu bond: (1) promotes C–C coupling; (2) reserves both O atoms against dehydroxylation through spatial-confinement; (3) disadvantages both two conventional electroreduction pathways; and, (4) facilitates an alternative pathway to directly synthesize ethylene glycol. Findings highlight the importance of forming Cu nanopyramids with desired morphologies that are carefully tuned to modify the activity and selectivity of electrocatalytic CO2 reduction reactions. These will aid practical efforts to increase selectivity toward poly-hydroxyl oxygenates, and be of immediate benefit in the design of highly active and selective electrocatalysts for CO2 electroreduction via morphology control.Author contributions
L. C. carried out the theoretical simulation and data analysis. C. T. carried out part of the simulation. K. D. and Y. Z. carried out part of the data analysis. Y. J. and S. Z. Q. conceived and supervised the research. Y. J. designed the theoretical simulation, and directed the manuscript writing and revision. All co-authors assisted in writing and revising the manuscript. All co-authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support by the Australian Research Council (FT190100636, FL170100154 and DP190103472). DFT computations were supported by computational resources provided by the Australian Government through NCI under the National Computational Merit Allocation Scheme, and the Phoenix High Performance Compute (HPC) Service at The University of Adelaide.References
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC
.
- C. M. Gabardo, A. Seifitokaldani, J. O. Edwards, C.-T. Dinh, T. Burdyny, M. G. Kibria, C. P. O'Brien, E. H. Sargent and D. Sinton, Energy Environ. Sci., 2018, 11, 2531–2539 RSC
.
- X. Zheng, P. D. Luan, F. P. G. de Arquer, B. Zhang, N. Becknell, M. B. Ross, Y. Li, M. N. Banis, Y. Li, M. Liu, O. Voznyy, C. T. Dinh, T. Zhuang, P. Stadler, Y. Cui, X. Du, P. Yang and E. H. Sargent, Joule, 2017, 1, 794–805 CrossRef CAS
.
- Y. C. Li, Z. Wang, T. Yuan, D.-H. Nam, M. Luo, J. Wicks, B. Chen, J. Li, F. Li, P. G. de Arquer, Y. Wang, C.-T. Dinh, O. Voznyy, D. Sinton and E. H. Sargent, J. Am. Chem. Soc., 2019, 141(21), 8584–8591 CrossRef CAS PubMed
.
- N.-T. Suen, Z.-R. Kong, C.-S. Hsu, H.-C. Chen, C.-W. Tung, Y.-R. Lu, C.-L. Dong, C.-C. Shen, J.-C. Chung and H. M. Chen, ACS Catal., 2019, 9(6), 5217–5222 CrossRef CAS
.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Y. Liu, A. K. Engstfeld, S. Horch, B. Seger, E. L. Stehens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed
.
- H. Yue, Y. Zhao, X. Ma and J. Gong, Chem. Soc. Rev., 2012, 41, 4218–4244 RSC
.
- K. Dong, S. Elangovan, R. Sang, A. Spannenberg, R. Jackstell, K. Junge and Y. Li, Nat. Commun., 2016, 7, 12075 CrossRef PubMed
.
- Y. Lum, J. E. Huang, Z. Wang, M. Luo, D.-H. Nam, W. R. Leow, B. Chen, J. Wicks, Y. C. Li, Y. Wang, C.-t. Dinh, J. Li, T.-T. Zhuang, F. Li, T.-K. Sham, D. Sinton and E. H. Sargent, Nat. Catal., 2020, 3, 14–22 CrossRef CAS
.
- F. E. Celik, T.-j. Kim and A. T. Bell, Angew. Chem., Int. Ed., 2009, 48, 4813–4815 CrossRef CAS PubMed
.
- F. E. Celik, H. Lawrnce and A. T. Bell, J. Mol. Catal., 2008, 288, 87–96 CrossRef CAS
.
- R. F. Dye, Korean J. Chem. Eng., 2001, 18, 571–579 CrossRef CAS
.
- M. Luo, Z. Wang, Y. C. Li, F. Li, Y. Lum, D.-H. Nan, B. Chen, J. Wicks, A. Xu, T. Zhuang, W. R. Leow, Z. Wang, X.-T. Dinh, Y. Wang, Y. Wang, D. Sinton and E. H. Sargent, Nat. Commun., 2019, 10, 5814 CrossRef CAS PubMed
.
- D. Gao, I. Sinev, F. Scholten, O. R. Aran-Ais, J. A. Divins, K. Kvashnina, J. Timoshenko and B. R. Cuenya, Angew. Chem., Int. Ed., 2019, 58, 17047–17053 CrossRef CAS PubMed
.
- H. Li, X. Qin, J. T. iang, X.-Y. Ma, K. Jiang and W.-B. Cai, ChemCatChem, 2019, 11, 6139–6146 CrossRef CAS
.
- A. Vasileff, C. Xu, Y. Jiao, Y. Zheng and S. Qiao, Chem, 2018, 4, 1809–1831 CAS
.
- P. Chen, Y. Jiao, Y. Zhu, S. Chen, L. Song, M. Jaroniec, Y. Zheng and S. Qiao, J. Mater. Chem. A, 2019, 7, 7675–7682 RSC
.
- Y. Chen, Z. Fan, J. Wang, C. Ling, W. Nie, Z. Huang, G. Liu, B. Chen, Z. Lai, X. Liu, B. Li, Y. Zong, L. Gu, J. Wang, X. Wang and H. Zhang, J. Am. Chem. Soc., 2020, 142(29), 12760–12766 CrossRef CAS PubMed
.
- D. Ren, B. S.-H. Ang and B. S. Yao, ACS Catal., 2016, 6(12), 8239–8247 CrossRef CAS
.
- C. G. Morales-Guio, E. R. Cave, S. A. Nitopi, J. T. Feaster, L. Wang, K. P. Kuhl, A. Jackson, N. C. Johnson, D. N. Abram, T. Hatsukade, C. Hahn and T. F. Jaramillo, Nat. Catal., 2018, 1(10), 764–771 CrossRef CAS
.
- T.-T. Zhang, Z.-Q. Liang, A. Seifitokaldani, P. De Luna, T. Burdyny, F. Che, F. Meng, Y. Min, R. Quintero-Bermudez, C. T. Dinh, Y. Pang, M. Zhong, B. Zhang, J. Li, P.-N. Chen, X.-L. Zheng, H. Liang, W.-N. Ge, B.-J. Ye, D. Sinton, S.-H. Yu and E. H. Sargent, Nat. Catal., 2018, 1(6), 421–428 CrossRef
.
- E. L. Clark, C. Hahn, T. F. Jaramillo and A. T. Bell, J. Am. Chem. Soc., 2017, 139(44), 15848–15857 CrossRef CAS PubMed
.
- L. Chen, C. Tang, Y. Jiao and S. Z. Qiao, ChemSusChem, 2021, 14, 671–678 CrossRef CAS PubMed
.
- T. Cheng, H. Xiao and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(8), 1795–1800 CrossRef CAS PubMed
.
- Y. Lum, T. Cheng, W. A. Goddard III and J. W. Ager, J. Am. Chem. Soc., 2018, 140, 9337–9340 CrossRef CAS PubMed
.
- F. Calle-Vallejo and M. T. M. Koper, Angew. Chem., Int. Ed., 2013, 52(28), 7282–7285 CrossRef CAS PubMed
.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5(5), 7050–7059 RSC
.
- J. A. Garza, T. A. Bell and M. Head-Gardon, ACS Catal., 2018, 8, 1490–1499 CrossRef
.
- K. D. Yang, W. R. Ko, J. H. Lee, S. J. Kim, H. Lee, M. H. Lee and K. T. Nam, Angew. Chem., Int. Ed., 2017, 56, 796–800 CrossRef CAS PubMed
.
- T. T. Zhuang, Y. Pang, Z.-Q. Liang, Z. Wany, Y. Li, C.-S. Tan, J. Li, C. T. Dinh, P. De Luna, P. L. Hsieh, T. Burdyny, H.-H. Li, M. Liu, Y. Wang, F. Li, A. Proppe, A. Johnston, D.-H. Nam, Z.-Y. Wu, Y.-R. Zheng, H. A. Ip, H. Tan, L.-J. Chen, S.-H. Yu, S. O. Kelly, D. Sinton and E. H. Sargent, Nat. Catal., 2018, 1, 946–951 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pace, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem., 2004, 108, 17886–17892 CrossRef
.
- X. Nie, M. R. Esopi, M. J. Janik and A. Asthagiri, Angew. Chem., Int. Ed., 2013, 52, 2459–2462 CrossRef CAS PubMed
.
- G. Henkelman and H. J. Jónsson, Chem. Phys., 2000, 113, 9978–9985 CAS
.
- X. Nie, W. Luo, M. J. Janik and A. Asthagiri, J. Catal., 2014, 312, 108–122 CrossRef CAS
.
- W. Luo, X. Nie, M. J. Janik and A. Asthagiri, ACS Catal., 2016, 6, 219–229 CrossRef CAS
.
- J. H. Montoya, C. Shi, K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2032–2037 CrossRef CAS PubMed
.
- W. L. Yim and J. K. Johnson, J. Phys. Chem. C, 2009, 113, 17636–17642 CrossRef CAS
.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed
.
- M. Anand and J. K. Nørskov, ACS Catal., 2020, 10(1), 336–345 CrossRef CAS
.
- A. Vojvodic and J. K. Nørskov, Natl. Sci. Rev., 2015, 2, 140–143 CrossRef CAS
.
- A. Peterson and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS
.
- Y. Li and Q. Sun, Adv. Energy Mater., 2016, 6, 1600463 CrossRef
.
- J. Perez-Ramirez and N. Lopez, Nat. Catal., 2019, 2, 971–976 CrossRef
.
- D. Kim, J. Resasco, Y. Yu, A. Asiri and P. Yang, Nat. Commun., 2014, 5, 4948 CrossRef CAS
.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed
.
- X. P. Chen, J. K. Jiang, Q. H. Liang, N. Yang, H. Y. Ye, M. Cai, L. Shen, D. G. Yang and T. L. Ren, Sci. Rep., 2015, 5, 16907 CrossRef CAS PubMed
.
- G. D. P. Gomes, A. Wimmer, J. M. Smith, B. Konig and I. V. Alabugin, J. Org. Chem., 2019, 84, 6232–6243 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01694f |
| This journal is © The Royal Society of Chemistry 2021 |