Open Access Article
Open Access ArticleManipulating valence and core electronic excitations of a transition-metal complex using UV/Vis and X-ray cavities†
Bing
Gu
 a,
Stefano M.
Cavaletto
a,
Stefano M.
Cavaletto
 a,
Daniel R.
Nascimento‡
b,
Munira
Khalil
c,
Niranjan
Govind
a,
Daniel R.
Nascimento‡
b,
Munira
Khalil
c,
Niranjan
Govind
 b and
Shaul
Mukamel
b and
Shaul
Mukamel
 *a
*a
aDepartment of Chemistry and Department of Physics & Astronomy, University of California, Irvine, CA 92697, USA. E-mail: smukamel@uci.edu
bPhysical and Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland, WA 99352, USA
cDepartment of Chemistry, University of Washington, Seattle, WA, USA
First published on 6th May 2021
Abstract
We demonstrate how optical cavities can be exploited to control both valence- and core-excitations in a prototypical model transition metal complex, ferricyanide ([Fe(III)(CN)6]3−), in an aqueous environment. The spectroscopic signatures of hybrid light-matter polariton states are revealed in UV/Vis and X-ray absorption, and stimulated X-ray Raman signals. In an UV/Vis cavity, the absorption spectrum exhibits the single-polariton states arising from the cavity photon mode coupling to both resonant and off-resonant valence-excited states. We further show that nonlinear stimulated X-ray Raman signals can selectively probe the bipolariton states via cavity-modified Fe core-excited states. This unveils the correlation between valence polaritons and dressed core-excitations. In an X-ray cavity, core-polaritons are generated and their correlations with the bare valence-excitations appear in the linear and nonlinear X-ray spectra.
1 Introduction
Hybrid light-matter states termed polaritons emerge when the coupling strength between material transition and a confined optical cavity photon mode is stronger than the decay rates of both matter and light. Optical cavities can be made with, e.g., Fabry–Perot setup, photonic crystals, and plasmonics.1–3 The effective light-matter coupling strength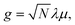 where
where 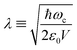 measures the vacuum electric field fluctuations, can be enhanced by reducing the cavity mode volume V and increasing the number of molecules N. Here, μ is the transition dipole moment, ε0 is the vacuum permittivity, and ωc is the cavity frequency. Vibrational and electronic polaritons have been demonstrated experimentally to alter chemical processes2,4 such as modifying photoisomerization reaction rates,5 reversing the selectivity of a ground-state chemical reaction,6 enhancing optical nonlinearities,7 and enabling long-range energy transfer.8 These experiments have triggered extensive theoretical studies elucidating the underlying mechanisms and proposing new strategies to employ polaritons to control chemical processes (i.e. to manipulate molecular processes by tuning the cavity).9–21 While current polariton chemistry focuses on cavity resonances in the infrared and visible regime, X-ray cavities are receiving interest for applications in X-ray quantum optics and control,22–26 and for probing and manipulating electronic interactions at X-ray frequencies.26 X-ray cavities can be made in a planar geometry with alternating nanometer layers of materials with different indices of refraction.23 We recently demonstrated that novel core-excitations, core-polaritons, can be created by placing molecules with nonequivalent core orbitals in an X-ray cavity.27 Localized core-excitations involving different core-orbitals can be coherently coupled by exchanging cavity photons. Core-excitations are fundamental for photochemical processes, as they allow probing transient electronic coherence during the passage through a conical intersection28 and creating broader electronic wavepackets than through ultraviolet/visible (UV/Vis) pulses.29
measures the vacuum electric field fluctuations, can be enhanced by reducing the cavity mode volume V and increasing the number of molecules N. Here, μ is the transition dipole moment, ε0 is the vacuum permittivity, and ωc is the cavity frequency. Vibrational and electronic polaritons have been demonstrated experimentally to alter chemical processes2,4 such as modifying photoisomerization reaction rates,5 reversing the selectivity of a ground-state chemical reaction,6 enhancing optical nonlinearities,7 and enabling long-range energy transfer.8 These experiments have triggered extensive theoretical studies elucidating the underlying mechanisms and proposing new strategies to employ polaritons to control chemical processes (i.e. to manipulate molecular processes by tuning the cavity).9–21 While current polariton chemistry focuses on cavity resonances in the infrared and visible regime, X-ray cavities are receiving interest for applications in X-ray quantum optics and control,22–26 and for probing and manipulating electronic interactions at X-ray frequencies.26 X-ray cavities can be made in a planar geometry with alternating nanometer layers of materials with different indices of refraction.23 We recently demonstrated that novel core-excitations, core-polaritons, can be created by placing molecules with nonequivalent core orbitals in an X-ray cavity.27 Localized core-excitations involving different core-orbitals can be coherently coupled by exchanging cavity photons. Core-excitations are fundamental for photochemical processes, as they allow probing transient electronic coherence during the passage through a conical intersection28 and creating broader electronic wavepackets than through ultraviolet/visible (UV/Vis) pulses.29
Coherent spectroscopic measurements can be used to track the complex polariton dynamics in time, as experimentally demonstrated by transient absorption and multidimensional infrared spectroscopies.30–32 Ultrafast X-ray spectroscopic techniques, enabled by recently developed free-electron lasers,33 can probe the local electronic structure of a specific atom, in contrast to UV/Vis spectroscopy which typically probes transitions between delocalized electronic states. This element specificity can be used to selectively excite polaritonic states that are only accessible via the core orbitals, and their electron dynamics can be monitored on the attosecond timescale via time-resolved X-ray spectroscopy.13,28,34–36
Here, we demonstrate how UV/Vis and X-ray cavities offer rich opportunities to manipulate electronic excitations in a transition metal complex, which are revealed by nonlinear X-ray signals. Transition metal complexes serve as catalysts for many important organic, inorganic, and biological reactions.37 Their functionality is rooted in the nature of their electronic excitations. Optical cavities provide a novel means to manipulate the electronic structure of transition metal complexes without chemical modifications. We investigate the ferricyanide complex in water, which serves as a prototypical model system for the structure and spectroscopy of Fe(III) octahedral transition metal complexes.38–40 We consider cavities with resonance frequencies in the UV/Vis and X-ray regimes and develop the formalism for signals involving non-Hermitian polariton Hamiltonians, which include cavity dissipation and exciton decay.
For an UV/Vis cavity mode, we observe valence-polariton states in the absorption spectrum only to the red of the cavity frequency, in contrast to a pair of polariton states as in the quantum Rabi model. This is because the cavity is weakly coupled to several resonant valence states and strongly coupled to off-resonant states at the same time. This rich combination of couplings leads only to lower-energy polaritons, and to a redistribution of oscillator strengths to a few polariton states.
We further predict stimulated X-ray Raman spectroscopy (SXRS) of the polaritonic system, and reveal signatures of higher-lying valence-polaritons in two-dimensional (2D) spectra. The appearance of bipolariton states in the SXRS signal stems from cavity-induced modifications to the core-excitations. The hybrid light-matter core-excitations cannot be clearly distinguished in the X-ray absorption near edge structure (XANES) spectrum, but are indirectly revealed by the SXRS signal. We further investigate X-ray cavities, which create core-polariton states with clear signatures in the XANES spectrum. Correlations between these core-polaritons and the bare valence-excited states are apparent in the 2D SXRS spectrum.
2 Model and computation
The polariton Hamiltonian describes N molecules coupled to a single cavity mode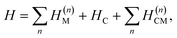 as schematically shown in Fig. 1a. The Hamiltonian for the nth molecule reads
as schematically shown in Fig. 1a. The Hamiltonian for the nth molecule reads 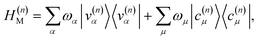 where |v(n)α〉 and |c(n)μ〉 denote the valence-excited many-body states and core-excited states at the Fe K-edge. We use atomic units ℏ = 1 throughout. The cavity Hamiltonian is HC = ωca†a, where a and a† are respectively the cavity-mode annihilation and creation operators satisfying [a, a†] = 1. The cavity-molecule coupling is given by the electric-dipole approximation
where |v(n)α〉 and |c(n)μ〉 denote the valence-excited many-body states and core-excited states at the Fe K-edge. We use atomic units ℏ = 1 throughout. The cavity Hamiltonian is HC = ωca†a, where a and a† are respectively the cavity-mode annihilation and creation operators satisfying [a, a†] = 1. The cavity-molecule coupling is given by the electric-dipole approximation 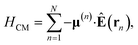 where Ê(rn) = iλ(aeik·rn − a†e−ik·rn)ec is the electric field operator of the cavity mode, which can be tuned either to the valence or core states in the molecule, and ec is the field polarization. When the molecular separations are small compared to the wavelength of the cavity mode, the long-wavelength approximation applies, E(rn) ≈ E(rM) where rM is the center of mass of all molecules. The cavity-molecule coupling is then given by
where Ê(rn) = iλ(aeik·rn − a†e−ik·rn)ec is the electric field operator of the cavity mode, which can be tuned either to the valence or core states in the molecule, and ec is the field polarization. When the molecular separations are small compared to the wavelength of the cavity mode, the long-wavelength approximation applies, E(rn) ≈ E(rM) where rM is the center of mass of all molecules. The cavity-molecule coupling is then given by 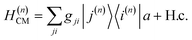 with gji = iλ〈j|μ⋅ec|i〉 and i, j run over all molecular states. For an assembly of molecules N > 1, it is convenient to introduce the delocalized exciton states
with gji = iλ〈j|μ⋅ec|i〉 and i, j run over all molecular states. For an assembly of molecules N > 1, it is convenient to introduce the delocalized exciton states 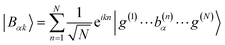 where |g(n)〉 is the ground state of the nth molecule, k = 2πj/N, j = 0,…, N − 1, b = {c, v} and, correspondingly, B = {C, V}. The k = 0 states |Bα0〉 are optically bright while k ≠ 0 are dark. Thus, in the single-excitation subspace, the relevant states in linear spectroscopy are the bright k = 0 states involving {|Vα0〉, |Cμ0〉}, and the absorption signal for N identical molecules with single-molecule coupling g is equivalent to the single-molecule case with coupling enhanced by
where |g(n)〉 is the ground state of the nth molecule, k = 2πj/N, j = 0,…, N − 1, b = {c, v} and, correspondingly, B = {C, V}. The k = 0 states |Bα0〉 are optically bright while k ≠ 0 are dark. Thus, in the single-excitation subspace, the relevant states in linear spectroscopy are the bright k = 0 states involving {|Vα0〉, |Cμ0〉}, and the absorption signal for N identical molecules with single-molecule coupling g is equivalent to the single-molecule case with coupling enhanced by 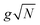 . However, the higher-lying polariton states and collective dark states, required for nonlinear time-resolved spectroscopy, cannot simply be described by
. However, the higher-lying polariton states and collective dark states, required for nonlinear time-resolved spectroscopy, cannot simply be described by 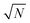 factor.10,11
factor.10,11
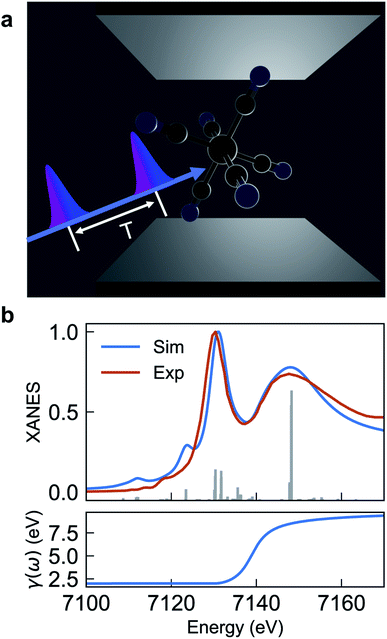 | ||
| Fig. 1 (a) Schematic of [Fe(III)(CN)6]3− molecules embedded in an optical cavity and pulse sequence used in the SXRS signal. The cavity length is in the μm scale for UV/Vis cavities, and nm scale for X-ray cavities. (b) Comparison of experimental and simulated XANES spectrum eqn (2) (upper panel) and frequency-dependent broadening function (lower panel). The simulated spectrum is blueshifted by 142 eV to fit experiment. | ||
The cavity-molecule coupling can be intuitively understood in terms of the molecular orbitals. The valence excitations promote valence electrons from occupied molecular orbitals {i} to unoccupied orbitals {a}. Such excitations are mixed with the cavity photon mode through
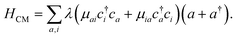 | (1) |
The resulting polariton states, eigenstates of H, are given by a linear combination of valence and photon excitations 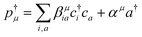 where β, α are the mixing coefficients. For a single electronic configuration, only one i → a transition is involved for each valence excitation. For valence excitations involving multiple electronic configurations, many molecular orbitals contribute. Eqn (1) also applies in the presence of a hole in the core orbital, which is responsible for cavity-modifications to the core-excitations. For an X-ray cavity mode coupled to the core-excitations, i refers to the Fe 1s orbital. Hereafter we use |eβ〉 to denote valence/valence-polariton states, and |fν〉 to denote core/core-polariton states.
where β, α are the mixing coefficients. For a single electronic configuration, only one i → a transition is involved for each valence excitation. For valence excitations involving multiple electronic configurations, many molecular orbitals contribute. Eqn (1) also applies in the presence of a hole in the core orbital, which is responsible for cavity-modifications to the core-excitations. For an X-ray cavity mode coupled to the core-excitations, i refers to the Fe 1s orbital. Hereafter we use |eβ〉 to denote valence/valence-polariton states, and |fν〉 to denote core/core-polariton states.
The valence- and core-excitation energies are computed with time-dependent density functional theory (TDDFT), and the transition dipole moments between many-electron states are computed by employing the pseudo-wavefunction approach also within TDDFT, as reported in ref. 41 and implemented in a development version of the NWChem program.42–45
The valence-polaritons in an UV/Vis cavity were computed by diagonalizing the polaritonic Hamiltonian using the direct product basis set |αn〉 ≡ |vα〉 ⊗ |n〉c, i.e., 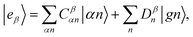 where |n〉c is the number state in the cavity mode. We use the non-Hermitian Hamiltonian
where |n〉c is the number state in the cavity mode. We use the non-Hermitian Hamiltonian 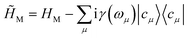 where the imaginary part represents the lifetime broadening of core-states, and
where the imaginary part represents the lifetime broadening of core-states, and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) C =
C = ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ca†a for the cavity, where
ca†a for the cavity, where ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) c = ωc − iκ and κ−1 is the cavity photon lifetime. The resulting polariton Hamiltonian
c = ωc − iκ and κ−1 is the cavity photon lifetime. The resulting polariton Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) =
= ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) M +
M + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) + HCM is thus non-Hermitian. The right eigenstates of
+ HCM is thus non-Hermitian. The right eigenstates of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) and
and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) † are biorthogonal polariton states, |eβ〉 and |ẽβ〉, respectively, with complex eigenvalues
† are biorthogonal polariton states, |eβ〉 and |ẽβ〉, respectively, with complex eigenvalues ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) β and
β and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) β*, and with 〈ẽβ|eβ′〉 = δββ′. These states will be used to compute the absorption and SXRS signals. The electric-dipole coupling between the molecules and the external laser pulses used in the spectroscopic measurements is given by HLM(t) = −μ·Eext(t). A single pulse is used in absorption measurements for both UV/Vis and X-ray frequencies, whereas two X-ray pulses are employed in SXRS, schematically shown in Fig. 1a. The electric quadrupole coupling
β*, and with 〈ẽβ|eβ′〉 = δββ′. These states will be used to compute the absorption and SXRS signals. The electric-dipole coupling between the molecules and the external laser pulses used in the spectroscopic measurements is given by HLM(t) = −μ·Eext(t). A single pulse is used in absorption measurements for both UV/Vis and X-ray frequencies, whereas two X-ray pulses are employed in SXRS, schematically shown in Fig. 1a. The electric quadrupole coupling 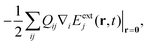 where Qij = −erirj, i, j ∈{x, y, z}, is only included in Fig. 1b to capture the pre-edge transitions at the Fe K-edge, which are not included in the polariton simulations due to their relatively weak strength. We shall compute the SXRS for a single molecule, thus excluding the two-exciton states from different molecules in the double-excitation manifold.
where Qij = −erirj, i, j ∈{x, y, z}, is only included in Fig. 1b to capture the pre-edge transitions at the Fe K-edge, which are not included in the polariton simulations due to their relatively weak strength. We shall compute the SXRS for a single molecule, thus excluding the two-exciton states from different molecules in the double-excitation manifold.
3 Results and discussion
Fig. 1a depicts the equilibrium geometry of [Fe(III)(CN)6]3−. The geometry was optimized using density functional theory (DFT) with the PBE0 exchange–correlation functional.46 For the geometry optimization, we used the Stuttgart-RSC-1997 ECP47 and the corresponding basis set for the Fe atom, while the C and N atoms were represented with the 6-311G**48 all-electron basis set. For the TDDFT-based valence- and core-excitations, the effective core potential was replaced with the all-electron Sapporo TZP-2012 basis set49 for the Fe atom. The effects of the solvent (water) were included implicitly via the Conductor-like Screening Model (COSMO).50,51 By representing the solvent implicitly, we acknowledge that the explicit influence of the cavity on the solvent states have been ignored. These calculations were performed with the NWChem program.42,43The bare-molecule simulated XANES spectrum at the Fe K-edge in [Fe(III)(CN)6]3− is shown in the upper panel of Fig. 1b. The spectrum is computed using the sum-over-states expression
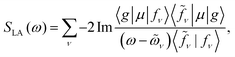 | (2) |
The complex eigenvalues ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ν = ων − iγν account for both the transition frequency ων and the decay rate γν of state |fν〉. To fit the calculated XANES spectra with experiment we have used the frequency-dependent broadening, shown in the lower panel of Fig. 1b:
ν = ων − iγν account for both the transition frequency ων and the decay rate γν of state |fν〉. To fit the calculated XANES spectra with experiment we have used the frequency-dependent broadening, shown in the lower panel of Fig. 1b:
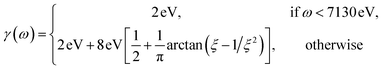 | (3) |
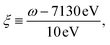 and added a background contribution from the continuum 0.16 × (1 + tanh(10(ω/eV − 7140))). The linewidth should contain all decay channels for the XANES signal including photoionization and Auger effects. The weak peaks in the XANES spectrum around 7120 eV are due to electric quadrupole transitions 1s → 3d,38 whereas strong 7130 eV and 7150 eV features correspond to dipole-allowed s → np transitions and shape resonances.38,52
and added a background contribution from the continuum 0.16 × (1 + tanh(10(ω/eV − 7140))). The linewidth should contain all decay channels for the XANES signal including photoionization and Auger effects. The weak peaks in the XANES spectrum around 7120 eV are due to electric quadrupole transitions 1s → 3d,38 whereas strong 7130 eV and 7150 eV features correspond to dipole-allowed s → np transitions and shape resonances.38,52
3.1 UV/Vis cavity
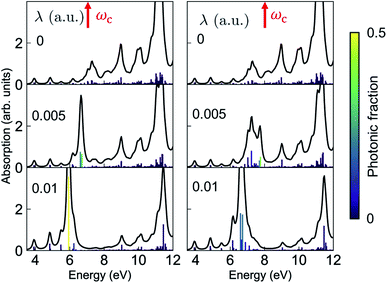
The absorption spectra of the valence-polaritons are shown in Fig. 2 for various cavity-molecule coupling strengths and for cavities frequencies ωc = 7 eV and 8 eV. The spectrum is computed using eqn (2) with the valence-polariton states replacing the core-excited states. The mixing of valence-excitations with the cavity mode is depicted by the color of the vertical lines, which also mark the relative transition dipole moment strength. We observe a cavity-induced redistribution of oscillator strengths to a few polariton states, and a redshift of the polariton states which increases with the coupling strength. These observations arise from the complex electronic structure of this transition metal complex and can be understood as follows: a redistribution of the oscillator strength can be explained by considering a single cavity mode coupled to many resonant electronic transitions {ωj = ωc} with strength {gj}. This model can be reduced to the cavity mode coupled to a single collective molecular transition with coupling strength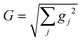 while all other collective states are dark.53 Thus, in the absorption spectrum, the many bright molecular transitions reduce to two polariton peaks with strong transition dipole moments. The redshifts of the polariton states and the fact that we only observe them in the red side of the cavity frequency are due to coupling to the higher-energy states at ∼11.5 eV. Even though these electronic transitions have large detunings from the cavity frequency, the coupling strengths are much larger than those nearby, as seen from the bare absorption spectrum (λ = 0) in Fig. 2. The polariton states are redshifted with increasing coupling strength, leaving a transparency window around the cavity frequency. These observations suggest that higher-lying molecular states may be important for molecules with dense manifolds of electronic states under strong light-matter coupling. If we exclude the higher-energy states with ω > 9 eV in the simulations, the absorption spectra (Fig. S1†) show both upper and lower polaritons, which deviates significantly from Fig. 2.
while all other collective states are dark.53 Thus, in the absorption spectrum, the many bright molecular transitions reduce to two polariton peaks with strong transition dipole moments. The redshifts of the polariton states and the fact that we only observe them in the red side of the cavity frequency are due to coupling to the higher-energy states at ∼11.5 eV. Even though these electronic transitions have large detunings from the cavity frequency, the coupling strengths are much larger than those nearby, as seen from the bare absorption spectrum (λ = 0) in Fig. 2. The polariton states are redshifted with increasing coupling strength, leaving a transparency window around the cavity frequency. These observations suggest that higher-lying molecular states may be important for molecules with dense manifolds of electronic states under strong light-matter coupling. If we exclude the higher-energy states with ω > 9 eV in the simulations, the absorption spectra (Fig. S1†) show both upper and lower polaritons, which deviates significantly from Fig. 2.
 | ||
| Fig. 2 Absorption spectrum of the valence-polaritons [eqn (2)] for ωc = 7 eV (left) and 8 eV (right), varying the coupling strengths as indicated. The color of the vertical lines encodes the magnitude of the cavity-photon component 〈eβ|a†a|eβ〉 for each valence-polariton state. 1 a.u. = 0.514 V Å−1. | ||
Resonant X-ray signals offer atom-specific selectivity and may be used to probe the couplings between the valence- and core-excited state.54–57 Resonant X-ray Raman scattering was demonstrated in Neon58,59 and, more recently, for the impulsive excitation of nitric oxide.60 Here, we use SXRS to monitor the cavity-induced modifications of valence- and core-polaritons and their couplings. SXRS is a pump–probe technique that employs two attosecond X-ray pulses, described by the external electric field Eext(t) = Epu(t) + Epr(t − T). The pump pulse Epu(t) induces a resonant Raman process via the core-excited states, thereby creating a superposition of valence-polaritons. Their time evolution is monitored by a probe pulse Epr(t − T), delayed by T, via a second resonant Raman process. The frequency- and time-resolved signal S(ωs, T) is obtained by measuring the absorption spectrum of the transmitted probe pulse at varying interpulse delays T. The 2D SXRS signal,55 including the non-Hermitian nature of the core-excitations, is given by
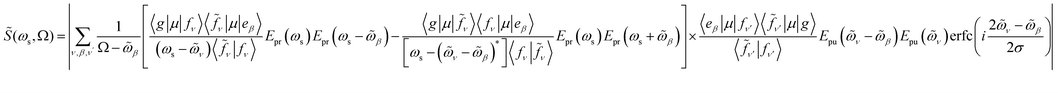 | (4) |
![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (ωs, Ω) = |S(ωs, T)eiΩTdT| is the Fourier transform of the SXRS signal with respect to T, ωs is the detected frequency, Ω is the conjugate variable to time delay T, erfc(z) is the complementary error function, and
(ωs, Ω) = |S(ωs, T)eiΩTdT| is the Fourier transform of the SXRS signal with respect to T, ωs is the detected frequency, Ω is the conjugate variable to time delay T, erfc(z) is the complementary error function, and  .
.
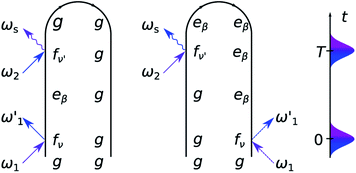
As can be seen from the two loop diagrams for the SXRS signal, shown in Fig. 3, the spectrum exhibits pairs of peaks at the signal frequency ωs, centered at the transition frequencies between the core-excited states and the ground state |g〉 or the valence-polaritons |eβ〉. The 2D spectrum ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) (ωs, Ω) shows valence-polariton peaks along the conjugated frequency Ω, thereby revealing which valence-polaritons are generated by the Raman excitation as well as their couplings to the core-excitations. Different regions of the molecule can be monitored by tuning the X-ray pump and probe pulses to different element-specific K-edges.54
(ωs, Ω) shows valence-polariton peaks along the conjugated frequency Ω, thereby revealing which valence-polaritons are generated by the Raman excitation as well as their couplings to the core-excitations. Different regions of the molecule can be monitored by tuning the X-ray pump and probe pulses to different element-specific K-edges.54
The 2D SXRS spectra for an UV/Vis cavity are shown in Fig. 4. For λ = 0, the signal reveals bare valence states due to resonant excitation of the core states appearing along ωs. By turning the cavity-molecule coupling on, new peaks emerge at energies ∼14 eV, which are absent in the bare spectrum. The strengths and positions of the lines at Ω < 10 eV are only weakly affected by the cavity-molecule coupling strength since the transitions from the core-excited states to single-polaritons are forbidden. This is because the single-polariton states are a linear combination of bright valence states |vb〉 and cavity photon mode |g1〉 whereas the core-excitations are the mixtures of |cb0〉, |cd1〉 and even higher-energy states like |cb2〉. The subscripts b, d indicate bright and dark states, respectively. In stark contrast, the new peaks at ∼14 eV significantly grow with λ, and their positions exhibit a redshift. These peaks can be attributed to the bipolariton states as discussed below.
To analyze these 2D spectra, we group the valence- and core-excited states into dark (|vd〉, |cd〉) and bright states (|vb〉, |cb〉), as shown in Fig. 5. The molecule contains an inversion center and the eigenstates have a definite parity. Bright and dark states are thus a consequence of the Laporte rule, which forbids transitions between states with the same parity. In the bare molecule, SXRS proceeds via the pathway |g〉 → |cb〉 → |vd〉, while the absorption spectrum involves the |g〉 → |vb〉 transition. The two techniques thus selectively access different dark or bright valence states.
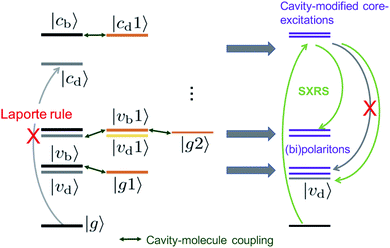 | ||
| Fig. 5 Energy level scheme illustrating how an optical cavity photon mode affects the valence- and core-excitations. The subscripts b, d indicate the bright and dark states, respectively. | ||
The cavity-molecule coupling produces valence-polaritons which couple the bright |vb0〉 and one-photon state |g1〉. These are accessible by absorption, but not via SXRS. As a result, the Ω < 10 eV region of the spectrum is hardly affected by the cavity. Nevertheless, higher-lying bipolariton states are generated due to the coupling among bare valence states |vd0〉 with energies around 2ωc, single-photon valence states |vb1〉 and two-photon state |g2〉. These bipolaritons are clearly observed in the SXRS spectra in Fig. 4. The cavity also induces a blueshift of all excitation frequencies. Hybridized core states are needed to reach these bipolariton states by resonant Raman excitation. Had the cavity not modified the core states, the bipolariton states would have been absent in the SXRS spectrum. This is because the pathway |g0〉 → |cb0〉 → |vb1〉 is forbidden due to Laporte rule and |g0〉 → |cb0〉 → |g2〉 is neither allowed due to photon mismatch. SXRS thus provides direct evidence of cavity-modified core-excitations, emerging when the transitions |cμ〉 ↔ |cμ′〉 mix with the photon mode, as shown in Fig. 5. These cavity-induced modifications of the core states are not clearly observed in the XANES spectrum, because their broadenings are significantly larger than the coupling strengths. This is visible in the top panels of Fig. 4. By showing the coupling between bipolariton and hybridized core states, 2D SXRS reveals the modifications of both valence and core electronic excitations by the optical cavity.
3.2 X-ray cavity
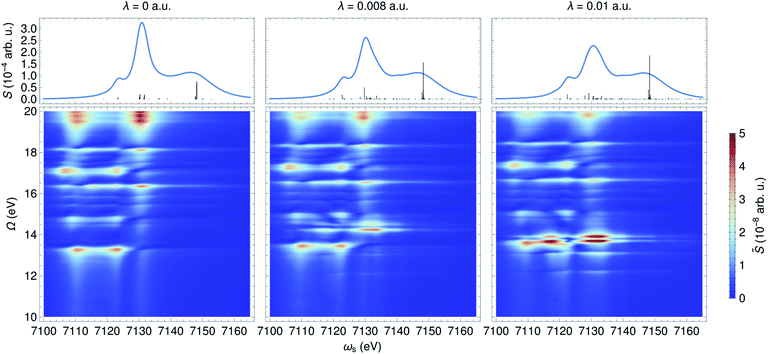
In contrast to an UV/Vis cavity, X-ray cavities do not modify the valence excitations due to frequency mismatch. The X-ray cavity photon directly couples to the core-level transitions |g〉 → |cα〉 in a molecule, where |cα〉 runs over the bright core-excited states. This is different from how an UV/Vis cavity modifies the core excitations. Fig. 6 depicts the XANES and time-resolved SXRS when the molecule is placed in an X-ray cavity with ωc = 7132 eV and various coupling strengths. Since the cavity frequency is close to the core-excitations at ∼7130 eV, we observe clearly a splitting of core-polariton states in the XANES spectrum. This is the X-ray analog of the Rabi splitting in the Jaynes–Cummings model, and is determined by many core-transitions close to the cavity frequency. This splitting is monitored by both the XANES and SXRS spectra, which probe the same core-polariton states given by linear combinations of |cb0〉 and |g1〉, while the dark core-excitations do not contribute to the signal. In addition, the SXRS spectra show the correlations between core-polaritons and the bare valence excitations that are not modified by the X-ray cavity. As a result, the peak positions along the Ω axis are not affected by the cavity, whereas the peaks along the ωs axis are.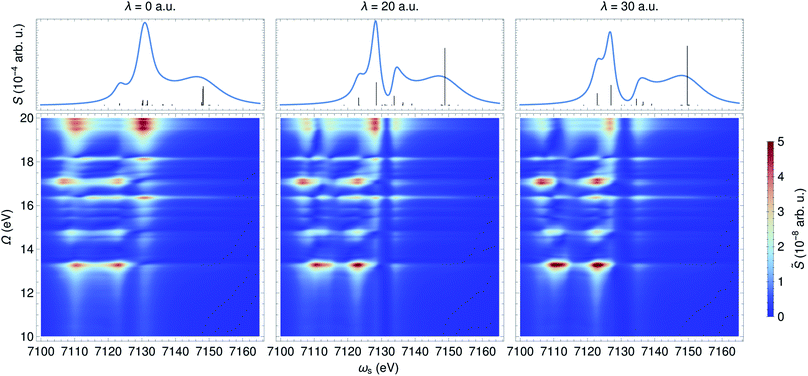 | ||
| Fig. 6 XANES (top) and SXRS (bottom) of ferricyanide embedded in an X-ray cavity of frequency ωc = 7132 eV and varying coupling strengths λ, as indicated. | ||
4 Conclusions
We have investigated how an optical cavity can be utilized to control the electronic excitations in ferricyanide, and predicted the polaritonic signatures in absorption and 2D SXRS signals. For an UV/Vis cavity, we found that the observed polariton states arise from a combined effect of valence excitations close to and far detuned from the cavity resonance. The SXRS signal selectively probes the bipolariton states emerging from the coupling between dark and bright valence states with different photonic excitations. In addition, it uncovers the modifications imprinted by the UV/Vis cavity to the core-excitations, despite the fact that the lifetime broadening is much larger than the coupling strength. Correlations between cavity-modified core-excitations and bipolariton states are clearly observed. In contrast, an X-ray cavity directly modifies the core-excitations leading to hybrid core-polaritons. The SXRS signal then shows the correlation between the unperturbed valence-excitations and these core-polariton states. Our results demonstrate the power of optical cavities to manipulate electronic excitations in transition metal complexes with dense electronic states. Nonlinear X-ray signals unveil the complex correlations among the dressed valence- and core-states generated in the cavity. Further extensions of our work may include using the minimal coupling Hamiltonian to account for all multipoles in the light-matter coupling between molecules and X-ray cavity modes and pulses.Author contributions
S. M. conceived the project. B. G. and S. M. C. carried out the polariton and spectroscopy simulations. D. N. R. and N. G. performed the electronic structure simulations. M. K. provided the experimental data. All authors contributed to the analysis and interpretation of the results, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. M. is a Fellow of the Hagler Institute for Advanced Study at Texas A&M University. The support of the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Award no. DE-FG02-04ER15571 (S. M. C. partial support), KC-030103172684 (D. R. N., N. G.), DE-SC0019277 (M. K.), and of the National Science Foundation grant CHE-1953045 (B. G., S. M.) are gratefully acknowledged. S. M. C. also acknowledges the support of the Alexander von Humboldt foundation through the Feodor Lynen program. A portion of the computational work was performed at EMSL, a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research and located at PNNL. PNNL is operated by Battelle Memorial Institute for the United States Department of Energy under DOE Contract no. DE-AC05-76RL1830.Notes and references
- R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Nature, 2016, 535, 127–130 CrossRef CAS PubMed.
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403–2412 CrossRef CAS PubMed.
- Y. Sato, Y. Tanaka, J. Upham, Y. Takahashi, T. Asano and S. Noda, Nat. Photonics, 2012, 6, 56–61 CrossRef CAS.
- F. Herrera and J. Owrutsky, J. Chem. Phys., 2020, 152, 100902 CrossRef CAS PubMed.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef CAS PubMed.
- A. Thomas, L. Lethuillier-Karl, K. Nagarajan, R. M. A. Vergauwe, J. George, T. Chervy, A. Shalabney, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Science, 2019, 363, 615–619 CrossRef CAS PubMed.
- A. Shalabney, J. George, J. Hutchison, G. Pupillo, C. Genet and T. W. Ebbesen, Nat. Commun., 2015, 6, 5981 CrossRef CAS PubMed.
- X. Zhong, T. Chervy, S. Wang, J. George, A. Thomas, J. A. Hutchison, E. Devaux, C. Genet and T. W. Ebbesen, Angew. Chem., 2016, 128, 6310–6314 CrossRef.
- B. Gu and S. Mukamel, Chem. Sci., 2020, 11, 1290–1298 RSC.
- B. Gu and S. Mukamel, J. Phys. Chem. Lett., 2020, 11, 5555–5562 CrossRef CAS PubMed.
- B. Gu and S. Mukamel, J. Phys. Chem. Lett., 2020, 11, 8177–8182 CrossRef CAS PubMed.
- K. Bennett, M. Kowalewski and S. Mukamel, Faraday Discuss., 2016, 194, 259–282 RSC.
- M. Kowalewski, K. Bennett, J. R. Rouxel and S. Mukamel, Phys. Rev. Lett., 2016, 117, 043201 CrossRef PubMed.
- D. R. Nascimento and A. E. DePrince, J. Chem. Phys., 2015, 143, 214104 CrossRef PubMed.
- X. Li, A. Mandal and P. Huo, Nat. Commun., 2021, 12, 1315 CrossRef CAS PubMed.
- M. Du, L. A. Martínez-Martínez, R. F. Ribeiro, Z. Hu, V. M. Menon and J. Yuen-Zhou, Chem. Sci., 2018, 9, 6659–6669 RSC.
- R. F. Ribeiro, L. A. Martínez-Martínez, M. Du, J. Campos-Gonzalez-Angulo and J. Yuen-Zhou, Chem. Sci., 2018, 9, 6325–6339 RSC.
- J. B. Pérez-Sánchez and J. Yuen-Zhou, J. Phys. Chem. Lett., 2020, 11, 152–159 CrossRef PubMed.
- Z. Zhang, K. Wang, Z. Yi, M. S. Zubairy, M. O. Scully and S. Mukamel, J. Phys. Chem. Lett., 2019, 10(15), 4448–4454 CrossRef CAS PubMed.
- F. Herrera and F. C. Spano, Phys. Rev. Lett., 2017, 118, 223601 CrossRef PubMed.
- B. Gu and S. Mukamel, J. Phys. Chem. Lett., 2021, 12, 2052–2056 CrossRef CAS PubMed.
- R. Röhlsberger, K. Schlage, B. Sahoo, S. Couet and R. Ruffer, Science, 2010, 328, 1248–1251 CrossRef PubMed.
- R. Röhlsberger, J. Evers and S. Shwartz, Synchrotron Light Sources and Free-Electron Lasers, Springer International Publishing, Cham, 2020, pp. 1399–1431 Search PubMed.
- B. W. Adams, C. Buth, S. M. Cavaletto, J. Evers, Z. Harman, C. H. Keitel, A. Pálffy, A. Picón, R. Röhlsberger, Y. Rostovtsev and K. Tamasaku, J. Mod. Opt., 2013, 60, 2–21 CrossRef.
- K. P. Heeg, A. Kaldun, C. Strohm, C. Ott, R. Subramanian, D. Lentrodt, J. Haber, H.-C. Wille, S. Goerttler, R. Rüffer, C. H. Keitel, R. Röhlsberger, T. Pfeifer and J. Evers, Nature, 2021, 590, 401–404 CrossRef CAS PubMed.
- J. Haber, J. Gollwitzer, S. Francoual, M. Tolkiehn, J. Strempfer and R. Röhlsberger, Phys. Rev. Lett., 2019, 122, 123608 CrossRef CAS PubMed.
- B. Gu, A. Nenov, F. Segatta, M. Garavelli and S. Mukamel, Phys. Rev. Lett., 2021, 126, 053201 CrossRef CAS PubMed.
- M. Kowalewski, K. Bennett, K. E. Dorfman and S. Mukamel, Phys. Rev. Lett., 2015, 115, 193003 CrossRef PubMed.
- K. Bennett, Phys. Scr., T, 2016, 16 Search PubMed.
- A. D. Dunkelberger, B. T. Spann, K. P. Fears, B. S. Simpkins and J. C. Owrutsky, Nat. Commun., 2016, 7, 13504 CrossRef CAS PubMed.
- C. A. DelPo, B. Kudisch, K. H. Park, S.-U.-Z. Khan, F. Fassioli, D. Fausti, B. P. Rand and G. D. Scholes, J. Phys. Chem. Lett., 2020, 11, 2667–2674 CrossRef CAS PubMed.
- B. Xiang, R. F. Ribeiro, A. D. Dunkelberger, J. Wang, Y. Li, B. S. Simpkins, J. C. Owrutsky, J. Yuen-Zhou and W. Xiong, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 4845–4850 CrossRef CAS PubMed.
- C. Pellegrini, A. Marinelli and S. Reiche, Rev. Mod. Phys., 2016, 88, 015006 CrossRef.
- F. Lépine, M. Y. Ivanov and M. J. J. Vrakking, Nat. Photonics, 2014, 8, 195–204 CrossRef.
- I. V. Schweigert and S. Mukamel, Phys. Rev. A, 2008, 78, 052509 CrossRef.
- S. Mukamel, D. Healion, Y. Zhang and J. D. Biggs, Annu. Rev. Phys. Chem., 2013, 64, 101–127 CrossRef CAS PubMed.
- H. Lu and X. Peter Zhang, Chem. Soc. Rev., 2011, 40, 1899–1909 RSC.
- M. Ross, A. Andersen, Z. W. Fox, Y. Zhang, K. Hong, J.-H. Lee, A. Cordones, A. M. March, G. Doumy, S. H. Southworth, M. A. Marcus, R. W. Schoenlein, S. Mukamel, N. Govind and M. Khalil, J. Phys. Chem. B, 2018, 122, 5075–5086 CrossRef CAS PubMed.
- A. M. March, G. Doumy, A. Andersen, A. Al Haddad, Y. Kumagai, M.-F. Tu, J. Bang, C. Bostedt, J. Uhlig, D. R. Nascimento, T. A. Assefa, Z. Németh, G. Vankó, W. Gawelda, N. Govind and L. Young, J. Chem. Phys., 2019, 151, 144306 CrossRef PubMed.
- M. Chergui, Coord. Chem. Rev., 2018, 372, 52–65 CrossRef CAS.
- D. R. Nascimento, E. Biasin, B. Poulter, M. Khalil, D. Sokaras and N. Govind, J. Chem. Theory Comput., 2021 DOI:10.1021/acs.jctc.1c00144.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. Van Dam, D. Wang, J. Nieplocha, E. Apra and T. L. Windus, et al. , Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, A. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- Y. Zhang, J. D. Biggs, D. Healion, N. Govind and S. Mukamel, J. Chem. Phys., 2012, 137, 194306 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124 Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- D. M. York and M. Karplus, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS.
- A. Bianconi, M. Dell'Ariccia, P. J. Durham and J. B. Pendry, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 6502–6508 CrossRef CAS.
- S. M. Dutra and K. Furuya, Phys. Rev. A, 1997, 55, 3832–3841 CrossRef CAS.
- D. Healion, Y. Zhang, J. D. Biggs, N. Govind and S. Mukamel, J. Phys. Chem. Lett., 2012, 3, 2326–2331 CrossRef CAS PubMed.
- J. D. Biggs, Y. Zhang, D. Healion and S. Mukamel, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15597–15601 CrossRef CAS PubMed.
- Y. Zhang, J. D. Biggs, N. Govind and S. Mukamel, J. Phys. Chem. Lett., 2014, 5, 3656–3661 CrossRef CAS PubMed.
- K. Bennett, Y. Zhang, M. Kowalewski, W. Hua and S. Mukamel, Phys. Scr., T, 2016, 169, 014002 CrossRef.
- C. Weninger, M. Purvis, D. Ryan, R. A. London, J. D. Bozek, C. Bostedt, A. Graf, G. Brown, J. J. Rocca and N. Rohringer, Phys. Rev. Lett., 2013, 111, 233902 CrossRef PubMed.
- N. Rohringer, Philos. Trans. R. Soc., A, 2019, 377, 20170471 CrossRef CAS PubMed.
- J. T. O'Neal, E. G. Champenois, S. Oberli, R. Obaid, A. Al-Haddad, J. Barnard, N. Berrah, R. Coffee, J. Duris and G. Galinis, et al. , Phys. Rev. Lett., 2020, 125, 073203 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational details of valence- and core-polariton states; derivation of eqn (3). See DOI: 10.1039/d1sc01774h |
| ‡ Present address: Department of Chemistry, University of Memphis, Memphis, TN 38152, USA. |
| This journal is © The Royal Society of Chemistry 2021 |