Sub-micron moulding topological mass transport regimes in angled vortex fluidic flow

Abstract

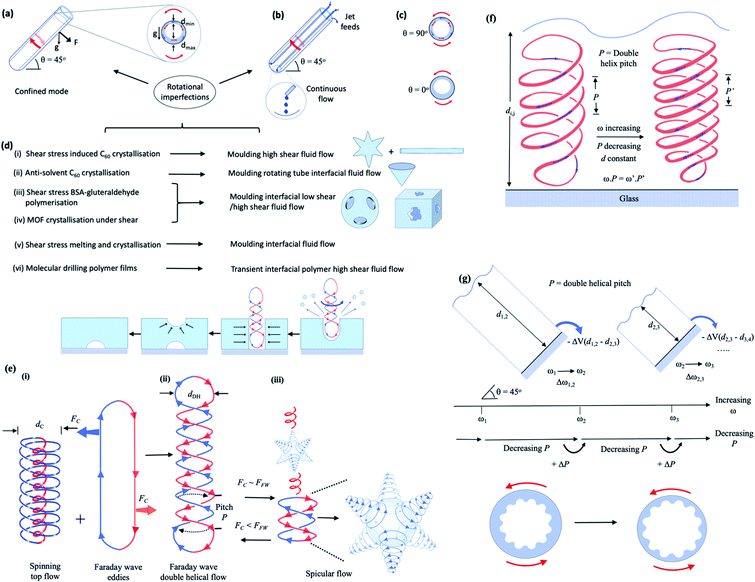
Shear stress in dynamic thin films, as in vortex fluidics, can be harnessed for generating non-equilibrium conditions, but the nature of the fluid flow is not understood. A rapidly rotating inclined tube in the vortex fluidic device (VFD) imparts shear stress (mechanical energy) into a thin film of liquid, depending on the physical characteristics of the liquid and rotational speed, ω, tilt angle, θ, and diameter of the tube. Through understanding that the fluid exhibits resonance behaviours from the confining boundaries of the glass surface and the meniscus that determines the liquid film thickness, we have established specific topological mass transport regimes. These topologies have been established through materials processing, as spinning top flow normal to the surface of the tube, double-helical flow across the thin film, and spicular flow, a transitional region where both effects contribute. The manifestation of mass transport patterns within the film have been observed by monitoring the mixing time, temperature profile, and film thickness against increasing rotational speed, ω. In addition, these flow patterns have unique signatures that enable the morphology of nanomaterials processed in the VFD to be predicted, for example in reversible scrolling and crumbling graphene oxide sheets. Shear-stress induced recrystallisation, crystallisation and polymerisation, at different rotational speeds, provide moulds of high-shear topologies, as ‘positive’ and ‘negative’ spicular flow behaviour. ‘Molecular drilling’ of holes in a thin film of polysulfone demonstrate spatial arrangement of double-helices. The grand sum of the different behavioural regimes is a general fluid flow model that accounts for all processing in the VFD at an optimal tilt angle of 45°, and provides a new concept in the fabrication of novel nanomaterials and controlling the organisation of matter.

---

Introduction

Controlling organisation and forces in liquids under non-equilibrium conditions is fundamental for building complex systems and the function of living cells.¹ Shear stress in thin film vortex microfluidics can generate non-equilibrium conditions^2–7 but the nature of the fluid flow is not understood. In general, understanding fluid flow is important in microfluidics where processing has primarily focused on manipulating liquids through channels.⁸ A less developed area of microfluidics involves films of liquid ≤ 500 μm thick which are centrifugally generated by passing liquids over rotating surfaces, as in spinning disc processors (reactors),^9,10 horizontally aligned rotating tube processors,^10,11 and in the vortex fluidic device (VFD),^2–7Fig. 1(a–c). The latter is a variant of the rotating tube processor but where the orientation of the tube, θ, can be varied^2–7 and is distinctly different to Couette flows where liquids are periodically forced between two surfaces.¹² These processors are also distinctly different to conventional microfluidics and do not suffer from clogging. They are effective in controlling chemical reactions, probing the structure of self-organised systems, and in the top down and bottom up synthesis of nanomaterials.^2,9,10 Control of the flow environment in the VFD itself has been shown effective in a variety of applications for which conventional batch processing is not possible or is of limited practicability, and low in green chemistry metrics. Such applications include accelerating enzymatic reactions,³ folding proteins,⁴ slicing carbon nanotubes,⁵ exfoliating graphene,⁶ and wrapping bacteria in graphene oxide.⁷ For the standard 20 mm outside diameter (OD) (internal dimeter (ID) 17.5 mm) quartz or glass tube in the VFD, changing the fluid flow behaviour with the rotational speed (ω) over the range of 3k to 9k rpm has revealed benefits of the device most effectively at a θ = 45° tilt angle;² 9k rpm rotational speed is the upper limit of the VFD housing a 20 mm (or 10 mm) OD tube.

Fig. 1 Characteristics of the vortex fluidic device (VFD) and moulded fluid flow. (a) Confined mode of operation of the VFD with the expected oscillation in film thickness which also prevails in (b) the continuous flow mode where liquids are injected as droplets into the rapidly rotating tube. (c) Expected fluid flow and film thickness at 90° and 0° degree tilt angles (θ). (d) (i) Shear stress induced fullerene C₆₀ crystallisation resulting in spicules or rods, (ii) anti-solvent crystallisation at the glass–liquid interface, leading to cones, (iii) BSA and glutaraldehyde polymerization in moulding high shear and low shear flow, (iv) as for (iii) for the nucleation and growth of a metal organic framework (MOF5), (v) shear stress melting elemental bismuth, and (vi) shear stress ‘molecular drilling’ of holes on polysulfone with their signature retained at the glass–polymer interface post positional shift of the double-helical fluid flow. (e) Possible representation of the fluid flow behaviour for the spinning top and double-helical flow from Faraday waves into spicular flow. (f) Double-helical fluid flow with a reduction in helical pitch (P) for increasing rotational speed, ω, for the same thickness of the film, d_i,j, with preservation of ωP. (g) Diagrammatic representation of change in film thickness in a type γ liquid which is dominated by double-helical flow across the rotational landscape, and the reduction in film thickness and associated Faraday waves driving the formation of linear arrays of double-helical flows orientated parallel to the rotation axis of the tube.

Establishing the nature of the complex fluid dynamics within the VFD for utility in chemical processing has proved challenging. A general model for determining the film thickness and the distance it extends up the tube, depending on θ and ω, has been established,¹³ but there is the realisation that other factors must be involved, beyond vibrations within the system.^14,15 For the accessible range of rotational speeds and possible solvent substrates, Reynolds numbers (Re) in the range 500 to 10 000 are readily achievable during flow that exhibits partial turbulence. Experimental attempts to observe the fluid flow in the VFD have been hampered by unavoidable distortions, estimated to be <100 μm. Direct measurement of fluid flow at the dimensionality of processing materials (∼1 to 5 μm), for example, in scrolling graphene oxide (GO)¹⁶ and generating cones of assembled fullerene C₆₀,¹⁷ is a longstanding issue. Interestingly, it has been demonstrated that standing waves on the surface of a liquid provide templates for microscale materials to assemble into ordered structures, which take on the shape defined by the standing wave.¹⁸ We hypothesised that this relationship could be inverted to provide insight into the spatial arrangement of mass transport patterns within the VFD at micron and sub-micron dimensions, depending on the experimental conditions, as moulding or templating materials processing outcomes, Fig. 1(d). The range of structures that have been captured in Fig. 1(d) can be explained by identifying which fluid flow phenomena dominate in the VFD at an inclination angle of θ = 45°, which is the optimal angle for applications of the VFD.^2–7 The fluid flow phenomena include rotational speed dependent Coriolis driven spinning top flow; double-helical topological flow associated with the onset of Faraday waves, previously reported as a mechanical response from vibrations,¹⁴ that couple with the Coriolis driven spinning top; and the combined interplay of these giving spicular flow. The latter is a sub-micro scale tornado type flow along the needle-like or horn-like shaped surface. The key outcomes are presented in Fig. 1(d–g), and the experiments leading to these findings are described in Fig. 2–5.

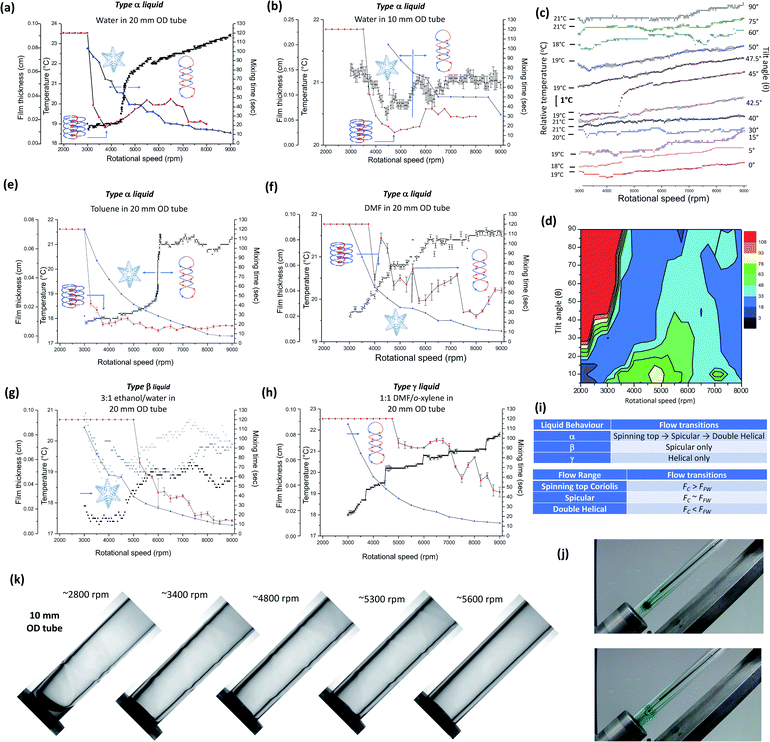Fig. 2 Mixing and thermal response, and film thickness. (a) and (b) Thermal response and mixing times, and change in average film thickness versus ω for water in a 20 mm OD quartz tube (17.5 mm ID) and 10 mm tube (8.5 mm ID) respectively, with all data points measured in triplicates. Mixing time (red) corresponds to the time taken for a drop of water containing a small amount of dye added at the bottom of the tube rotating at a specific speed to uniformly mix in half way up the preformed film generated from 2 mL of water. The temperature (black) was measured midway along the tube using an IR camera, for residual water present in the tube, being equivalent to the continuous flow mode of operation of the VFD (water along the complete length of the tube), with the average film thickness (blue) determined at θ = 45° for a specific speed from the mass of residual water also equivalent to the continuous flow mode of operation of the VFD, converted to a volume of liquid spread uniformly on the inner wall of the tube. (c) Thermal response for water in the tube, retaining the maximum amount of water at each speed, for varying tilt angles, θ, using a 20 mm OD tube. (d) Mixing time (s) for 2 mL of liquid in the 20 mm OD tube for change in θ and ω. (e–h) Thermal response (black), mixing times (red) and film thickness (blue) versus ω for toluene (small film thickness at high speed arises from solvent evaporation under high shear in the liquid), DMF, a 3 : 1 mixture of ethanol and water, and a 1 : 1 mixture of DMF and o-xylene in 20 mm OD tubes, respectively. Temperatures were recorded at the mid-point along the tube to minimise any heating from the bearings. Recording change in temperature starts at high ω relative to ω for recording mixing times, a consequence of requiring extra liquid in the tube when mimicking continuous flow processing, and this requires higher ω to generate a vortex to the bottom of the tube. Three separate thermal response plots are provided for (g) because of fluctuations from one temperature run to another, whereas for all other plots (a–f and h), a single plot of the average of three runs are provided. (i) Summary of the different fluid flows, and flow regimes characterised by the relative contributions from the spinning top Coriolis (F_C) and Faraday wave (F_FW) induced flows, supported by computational fluid dynamics (CFD) simulations conducted using OpenFoam v1806, as detailed in the ESI Section 11.† (j) Images of water in a 10 mm tube at different rotational speeds, captured from 5k frames per s (Movie S2†). (k) Photographs of partitioned mixing of an aqueous dye in water into 2 mL of water in a 10 mm OD tube rotating at 2k rpm where the vortex is not developed to the bottom of the tube (Movie S1†). Additional information is provided in the ESI file†).

Fig. 3 Manipulating graphene oxide. Processing GO in a 20 mm OD tube (17.5 cm ID) at θ 45°, 0.2 mg mL⁻¹ in DMF, flow rate 0.45 mL min⁻¹, result in (i) scrolls at 4k rpm, (ii) crumbling into globular particles at 5k rpm, and (iii) no perturbation at 8k rpm, with the ability to cycle between the three forms of GO by changing the rotational speed akin to another form, with transformation of the GO into ca. 100 nm spheroidal particles at 5.5k rpm (transition from spicular to double-helical flow at the dynamic equilibrium).

Fig. 4 Moulding nano-carbon and polymer material. (a) Shear stress induced crystallisation and self-assembly of C₆₀ in toluene (0.1 mg mL⁻¹, θ 45°), affording (i) spicules (flow rate 0.1 mL min⁻¹) and (ii) rods (flow rate 1.0 mL min⁻¹), and (iii) mixtures of spicules and rods (flow rate 0.5 mL min⁻¹), at 4, 7, and 6k rpm, corresponding to spicular flow, transitioning from spicular to double-helical flow and helical flow respectively. (b) Micromixing a 1 : 1 solution of o-xylene solution of C₆₀ (0.1 mg mL⁻¹, flow rate 0.1 mL min⁻¹) and DMF (0.1 mL min⁻¹) in a VFD, θ 45°, 20 mm OD tube, affording (i) regular and (ii) irregular cones in a 20 mm OD tube, and (iii) and (iv) sharper pitch cones with extended arms in a 10 mm OD tube. (v) Cones attached to the wall of the glass tube in the VFD, post VFD processing in a 10 mm OD tube. (c) (i and ii) Signature of the pattern of the double-helical flows formed at the interface of the glass tube and a thin film of polysulfone (ca. 5 μm) formed in toluene at 20 °C, θ = 45°, 7k rpm rotational speed, along the length of the tube, with the arrow representing the rotational direction of the axis of the tube.

Fig. 5 Moulding elemental bismuth. (a) SEM image of an as received particle of elemental bismuth, with (b–f) as SEM images of material formed after confined mode processing of the material in (a) in 1 mL isopropyl alcohol (IPA) with the 20 mm diameter quartz tube tilted at θ = 45° and spun at 8k rpm for 20 min under nitrogen, at room temperature; the image in (f) appears to be the reverse side of the crater (that was attached to the surface of the tube), and shows rods mattered together. (g) One possible mechanism for the formation of the resulting craters and rods.

Faraday waves^19,20 are characterised by pressure fluctuations that induce eddies, much like the pressure system and wind patterns exhibited in the Earth's atmosphere, but around the inside surface of a curved cylindrical surface, rather than the outside of a spherical one. In this situation, the Faraday wave ‘eddies’ are aligned vertically within the thickness of the film, Fig. 1(e). As the tube rotates in the VFD, any oscillation in film thickness at θ < 90°, Fig. 1(a and b), which could also arise from distortions in the tube, has potential to drive the formation of Faraday waves. Their presence and other fluid dynamic behaviour in the VFD will impact on the movement of the liquid (mixing), and consequently, the resultant heat and mass transfer. Variation in the relative strengths of these competing processes results in overall fluid behaviours that create regimes of unique processing conditions within the VFD, with each process introducing a moulding or fabrication capability for their own unique nanostructures. These findings also reveal that there are domains of fluid flow in the VFD where any outcome of processing is not limited by conventional bulk diffusion control, but rather this is compounded by orientation effects associated with diffusion or mass transport that appears within the different topological flow regimes. As will be presented herein, the shear stress in the thin film of liquid in the VFD is not uniform but rather it can be uniformly localised. Shear stress induced aggregation of colloids,²¹ colloidal breakup,²² and nucleation and crystallisation of colloids²³ are understood on theoretical grounds, accounting for flow mediated transport of molecules.

Results and discussion

In leading up to the experiments that establish the presence of spinning top, spicular and double-helical flow, the processing options for the VFD are highlighted. The confined mode of operation of the VFD is where a finite volume of liquid is spun in the tube, whereas the continuous flow mode has liquid constantly fed into the base of the tube or at positions along the tube, with the liquid centrifugally driven out of the top of the tube against gravity, Fig. 1(a and b).² Continuous flow processing in the VFD addresses scalability of the experimental processing up front, and the effect is essentially the sum of the confined mode in between drops of liquid entering the tube.^2,14 This finding is understood herein by the reestablishment of the process specific fluid flow topologies, Fig. 1(e and f), between each drop. Importantly, for any processing in the VFD, the bulk vortex rising up the tube has to be maintained to expose the base of the tube, otherwise the fluid behaviour is even more complex with partitioning of fluid flow, Fig. 2(k) (ESI Section 2 and Movie S1†).¹⁵

Mixing experiments, whereby the time taken for a drop of dye added to a finite volume of liquid in the tube to visibly form a uniformly mixed solution half way up the film, were performed across a range of rotational speed ω values at θ = 45°, along with changes in temperature and film thickness at this unique tilt angle. Collectively, these data provide a signature for each liquid, as depicted for water at ∼20 °C in a 20 mm and 10 mm OD tube (17.5 mm and 8.5 mm ID, respectively), Fig. 2(a and b), for use in predicting rotational speed processing outcomes. The temperature of the tube was also measured mid-way along its length using an IR thermal imaging camera, for a range of values of ω and θ, for a 20 mm OD tube, revealing a significant rise in temperature at 4.5k rpm for water, approximately 2 °C, around a tilt angle of 45°, Fig. 2(c). The general trend in change in film thickness and its shape for increasing ω follows a mathematical model,¹³ but it does not account for regimes of near constant film thickness. The mixing profiles across different tilt angles for 20 mm and 10 mm diameter tubes have also been determined, Fig. 2(d) and ESI Section 3,† respectively. While mixing times vary dramatically, at θ = 45°, they provide insight into the fluid structure and resultant behaviour within the VFD.

Mixing time profiles, change in temperatures at θ = 45° and change in film thickness are unique for each liquid, highlighted for toluene, DMF, a 3 : 1 ethanol/water, and 1 : 1 o-xylene/DMF mixtures, Fig. 2(e–h). This behaviour describes how the physical properties of a liquid (such as viscosity, density, surface tension) drive the signature flow characteristics for the liquid within the VFD environment. For water, as the speed increases, the time for mixing dramatically drops at 3k rpm, where spinning top flow prevails (see below regarding scrolling of graphene oxide, GO), then increases above ∼3.8k rpm as spicular flow dominates (see below regarding shear stress induced crystallisation of fullerene C₆₀). We propose that this flow arises from the interplay of Faraday wave double-helical flow and spinning top flow, Fig. 1(e), which arises from the Coriolis from the hemispherical base of the tube. At speeds above 4.5k rpm, the spinning top component of flow diminishes and only the double-helical flow remains. For water at 4.5k rpm, there is a sharp rise in temperature, Fig. 2(a), which we ascribe as a transition from spicular to double-helical flow (see below regarding shear stress induced crystallisation of C₆₀ within the confines of the double-helical flow), and is associated with a reduction in average film thickness. The large change in film thickness (determined from ∼50% volume changes at this speed) indicate that this is along the length of the film rather than being localised to specific places along the tube. To simplify the description of the three distinct flow regimes studied, we define this first type of signature as corresponding to an α-liquid. Toluene behaves in a similar manner with the onset of rapid mixing above 3k rpm, now with a rapid change in temperature at 6k rpm, Fig. 2(e), and is likewise classified as an α-liquid, as is the classification of the fluid response, Fig. 2(f). A mixture of ethanol and water (3 : 1) has distinctly different mixing and temperature profiles, as shown in Fig. 2(g), and is classified as a β-liquid, having spicular flow for increasing rotational speed ω values, which matches the moulding of high shear regimes in forming BSA-glutaraldehyde porous spheres (see below).

A sudden increase in temperature is observed as conditions transition from (i) spicular to double-helical flow (i.e. decoupling of spinning top and double-helical flow) with a reduction in film thickness, or (ii) from double-helical flow to a smaller pitch double-helical flow (i.e. where opposing up and down directional transport in the double-helical flow are too close to be maintained), Fig. 1(f and g). The presence of double helices in the film is illustrated below for the case of ‘drilling holes’ in thin film of polymers attached to the inside of the tube, where preferential etching occurs due to increased localised mass transport regimes, and amplified where the film thickness change is dramatic and readily measurable.

The 1 : 1 mixture of DMF and o-xylene has a distinct series of step increases in temperature, with double-helical flow across the rotational landscape, Fig. 2(h), and this liquid is classified a γ-liquid. An alternative explanation of concentric double helices being formed, with the flow down and up the thin film, of opposite chirality as in the spinning top topological fluid flow, is expected to give cylinders of self-assembled fullerene C₆₀ rather than the observed rods (see above). Any sudden increase in temperature (ΔT) with increasing ω does not arise from vibrations induced from the motor or the two bearings at either end of the tube. This conclusion is based on the notion that different rotational speeds are needed for a sudden increase in temperature for a number of liquids, and for different diameters of the tube (20 versus 10 mm OD), along with the phenomenon being associated with a tilt angle of 45° and that this is independent on the choice of motor driving the rotation of the tube. If it were simply an artefact of the drive system, the behaviour would always appear for every liquid at some fixed rotational speed. Moreover, the position for rapid change in temperature of the liquid is independent of the volume of liquid in the tube, and with minimal change from one tube to another of the same diameter (ESI Section 2†). These results rule out instrumental contributions being responsible for generating the observed effect. The volume independence of the position of ΔT suggests a characteristic film profile for a particular rotational speed, for all volumes up to the equivalence of continuous flow (liquid at the maximum height up the tube). Less than this will have fingering instability of the liquid beyond the edge where the film thickness is constant.¹⁵ Identifying positions of ΔT and change in volume/film thickness at θ = 45° provides a powerful method to rapidly establish the rotational speed for transitioning from spicular-like fluid flow to double-helical flow, and for double-helical flow of one diameter to a double-helical flow of a smaller diameter tube, as in a 1 : 1 mixture of DMF and o-xylene, for any liquid, without the need for prior knowledge of the properties of the liquid. High speed photography of water in a 10 mm OD tube reveals that as the speed increases, helical waves appear along the tube (distinctly different to the above double-helical flow) (ESI Section 4 and Movie S2†). However, they disappear at ∼5.6k rpm, where beyond this speed there is a plateau region of constant average film thickness, Fig. 2(k). This approximates to ω for a sudden drop in volume of liquid in the film (and drop in film thickness), Fig. 2(a) (and ESI Section 5†). A constant thickness for increasing rotational speed is consistent with double-helical flow being maintained but with a reduction in pitch of the double-helix as the rotational speed increases, Fig. 1(f), presumably preserving ωP (P = pitch of the double-helix in the fluid flow). As the pitch decreases for increasing speed, a threshold will be reached where the distance between opposite flow up and down the helix cannot be maintained, where the length scales of the Faraday wave and spinning top Coriolis flows are comparable, F_FW ∼ F_C, Fig. 1(e), creating a dynamic equilibrium state through the combination of the two flow patterns. Increasing ω further results in a thinner film and double-helical flow starting with a larger pitch prevailing over the spinning top flow (F_FW > F_C), Fig. 1(g), with moulding experiments consistent with a reduction in effective diameter of the double helix, in accordance with reduction in the diameter of self-assembled cones of C₆₀.¹⁷

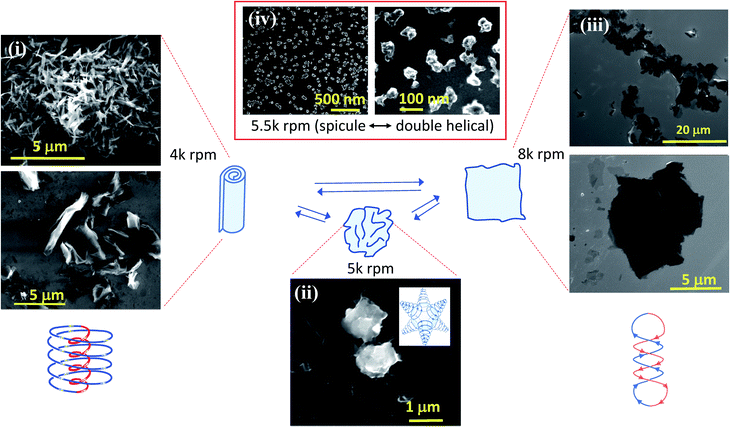
To further understand the fluid dynamic response in the VFD, we subjected single graphene oxide (GO) sheets (that have been dispersed in DMF) to different rotational speeds, Fig. 3 (and ESI Section 7†). At speeds aligned with a minimum mixing time in this solvent (4k rpm, Fig. 2(f)), GO is forced into a morphology of scrolls, Fig. 3(i), corresponding to spinning top flow, whereas at 5k rpm the GO sheets collapse into globular shapes that are approximately 1–2 μm in diameter, Fig. 3(ii), corresponding to spicular flow, and at 8k rpm (the shortest mixing times), the GO sheets appear to be unaffected. However, at this speed preformed GO scrolls become disrupted and unravel if they are introduced or in the starting fluid, Fig. 3(iii), and preformed globular GO sheets unravel into flat sheets. In the same way, preformed globular GO at 4k rpm alter their morphology into scrolls. These results are consistent with GO being confined during the processing in DMF in a spheroidal environment at 5k rpm, as in spicular topological fluid flow, and experiencing a spinning top Coriolis flow dominated regime at 4k rpm. At 5.5k rpm, the rapid interconversion between the proposed spicular and double-helical flow results in shredding of the GO sheets into ca. 100 nm particles, Fig. 3(iv).

Un-scrolling GO requires another force at play with smaller dimensionality to the diameter of the scrolls, and this is ascribed as coming from the resonant vibrational eddy currents associated with Faraday waves taking on a double-helix arrangement, Fig. 1(e and f). We have previously established the ability to wrap bacteria with GO in water within a 10 mm diameter tube at 5k and 8k rpm,⁷ and this is now explained as coming from spinning top flow. We found that recording changes in temperature in the smaller diameter 10 mm tube are unreliable (Fig. 2(b)), presumably because of more rapid heat flow from a thinner film and thinner glass wall of the tube. The change in film thickness can be used instead to identify the threshold rotational speed ω where different topological mass transfer patterns prevail as ω increases. The Coriolis forces arise from inertial forces and will therefore be more pronounced for the smaller diameter tubes, which is demonstrated herein, with ca. 30% reduction in the dimensionality of the topological flow for a 10 mm dimeter tube relative to a 20 mm diameter tube (see below regarding the formation of C₆₀ cones). The order of the type of fluid flow in the tube for increasing ω is spinning top flow followed by spicular flow, then double-helical flow, for the 9k rpm rotational speed limit of the VFD housing a 20 mm (or 10 mm) OD tube, as an archetypal α-liquid.

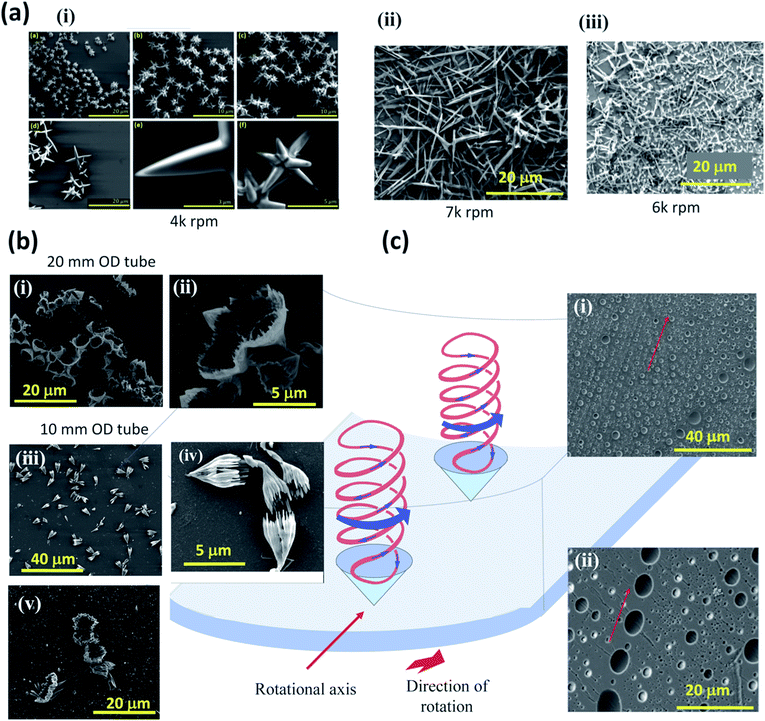
The mixing of a toluene solution of fullerene C₆₀ with water in the VFD results in the crystallisation of tubules.²⁴ We have now established that subjecting a toluene solution of the fullerene (≪saturation level) to shear stress in the VFD, in the absence of water, results in the formation of self-assembled fullerene particles as a new form of crystallisation, adding to the limited number of ways of inducing crystallisation, namely sublimation, cooling, evaporating, and heating to strip away surfactants.¹⁵ Fullerene C₆₀ only slowly dissolves in toluene, so that any particles generated by the induced shear stress do not rapidly dissolve, with ample time for collecting them by centrifugation and washing post VFD processing, before dissolution in reaching the thermodynamically controlled state. At ω values below 6k rpm, spicules are generated uniformly in size and number of spicules, Fig. 4(a(i)). These are comprised of ∼6.5 nm particles of self-assembled C₆₀ (ESI Section 7†). Spicules and the rods formed at rotational speeds above 6k rpm, Fig. 4(a(ii)) and S7f(c),† can only form and grow under conditions of high mass transfer in the liquid, otherwise they would re-dissolve under thermodynamic control. Thus, spicules are a mould of the fluid flow corresponding to a combination of spinning top flow and double-helical flow, Fig. 1(e and f), with the edges of the spicules slightly curved, Fig. 4(a(i)). Close inspection of the rods also reveals slightly curved surfaces, Fig. 4(a(ii)), and this is consistent with them being formed under shear within the double-helical liquid flow, rather than the formation of well-defined crystallographic controlled facets. Outside of these conditions they would re-dissolve, noting that the spinning top flow from Coriolis forces no longer dominates the flow behaviour at high rotational speeds (ca. >6000 rpm) when the film gets thinner. In addition, the diameter of the rods (∼0.5 μm) is consistent with the overall diameter of the double-helix (see below). At the transitioning speed for toluene, 6k rpm (Fig. 2(e), a mixture of spicules and rods are formed, Fig. 4(a(iii)). An alternative strategy for fluid flow moulding is the crystallisation of C₆₀ using an anti-solvent approach. Delivering a solution of C₆₀ in o-xylene into the base of the rotating tube in the VFD with another jet feed simultaneously delivering DMF within which the fullerene is only sparingly soluble (as periodic drops), results in the formation of cones ∼0.5–2.5 μm in diameter which are comprised of ∼6.5 nm particles of fcc fullerene C₆₀, Fig. 4(b(i and ii)).²⁵ Cones formed in the 20 mm OD tube have small whiskers running parallel to the symmetry axis of the cones, and these are more pronounced for cones generated in the 10 mm OD tube, with the diameter of the cones reduced by ca. 30% relative to those generated in the 20 mm OD tube, Fig. 4(b(iii and iv)). The formation of cones is consistent with the small first formed ca. 6.5 nm particles of C₆₀ assembling at points of high mass transfer on the surface of the tube, where the double-helical flow strikes the surface of the tube. Thermal imaging reveals increasing temperatures for a 1 : 1 mixture of the two solvents as ω increases, Fig. 2(h), which correspond to ongoing fluctuations in pitch (decreasing then increasing), Fig. 1(e and g), and consequential change in film thickness, Fig. 2(h). In the absence of shear on mixing the two liquids (no VFD), the small nano-particles of the fullerene aggregate randomly,²⁵ whereas in the VFD the ca. 6.5 nm particles assemble only at the interface of high mass transfer in the liquid and the surface of the tube, effectively ‘writing’ cones at the end of the double-helix which itself is likely to be rotating along the axis of the helix, with all the cavities facing in the same direction. Given that the cones are formed under continuous flow whereby the product primarily exits the top of the VFD tube, any attachment to the tube through their apex must be weak and at the nm dimensions. Indeed, breaking a tube post-VFD processing revealed some cones attached to the surface of the tube through their apical positions, Fig. 4(b(v)) (and ESI Section 7†). Clearly the residence time of such structures near the surface of the tube is maximised and sufficient for them to adhere. Within the liquid, the combination of Faraday waves, Coriolis flow and resonant eddy currents, each of which tends to dominate in each of the operating regimes, could have transition points of ‘dynamic equilibrium’ within the liquid where they effectively oppose each other as the operating conditions transition between the different regimes of dominant flow. In such places, mass transport of larger structures will be relatively slower than at other places within the liquid, and residence times for interaction with other smaller species will be longer.

Given the frailty of the point of attachment of the cones to the surface of the tube through their apex, the formation of cones does not provide information on the spatial arrangement of the associated double-helical flow. For this, we explored the possibility of double-helical flow generating holes in a thin layer of polymer attached to the inner surface of the tube, with polysulfone as the polymer of choice. Surprisingly the arrangement of holes that potentially arise from double-helices was determined from the surface of the polymer attached to the glass tube rather than the surface in contact with the liquid. Peeling the polymer from the glass surface revealed lines of regularly arranged holes several μm in diameter, Fig. 4(c) (and ESI Section 8†), which have the dimensionality of the moulding of the cones, although the solvent here was toluene with the tube rotating at 7k rpm, where double-helical flow prevails, Fig. 2(e). The holes are arranged in lines co-parallel to the rotational axis of the glass tube. This arrangement demonstrates points of localisation where the diffusion of material is highest, and can explain the ability of double-helical flow to exfoliate graphene from graphite⁶ and the unscrolling of GO into flat sheets, Fig. 3, between rows of vertically arranged double-helices that are the liquid analogy of adjacent rollers used to produce flat sheet products. The original proposed mechanism involved exfoliation at the interface of the graphite flakes and the surface of the tube, and/or at the interface of the liquid and graphite held parallel to the surface of the tube.⁶ The mechanism of formation of these holes, Fig. 1(d), is potentially understood by the notion of double-helical ‘molecular drills’ piercing the polymer film, and when they move to other locations, the centrifugal force results in collapse of the holes, trapping liquid at the base, with smoothing of the upper surface. The ability for the fluid flow to pierce the polymer layer is consistent with the friction associated with the double-helical flow striking the surface of the tube thereby increasing the temperature of the liquid, and the melting the polymer which has an onset of glass transition >120 °C.²⁶ In addition, the pattern of holes is commensurate with the presence of arrays of Faraday waves on larger length scales.

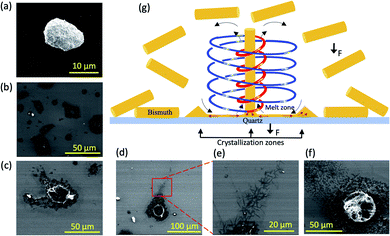
Determining the spinning top topological flow as a Coriolis from the hemispherical base of the tube involved melting and crystallising elemental bismuth (mp 271.4 °C). As received bismuth particles, typically 10–20 μm in diameter, Fig. 5(a), were dispersed in isopropyl alcohol (IPA) in a 20 mm OD quart tube rotating at 8k rpm for 20 min with θ = 45°, at room temperature and under a nitrogen atmosphere to avoid any oxidation. This afforded crater shaped bismuth metal, Fig. 5(b–e) with the SEM image in Fig. 5(f) appearing to be the back of a crater that was attached to the surface of the tube. Thus the metal has undergone in situ melting followed by rapid crystallisation with the diameter of the craters ca. 10 to 30 μm, which represents the outside diameter of the spinning top topological fluid flow, Fig. 5(g). We note that the proposed flow model represents one possible flow pattern for the spinning top flow, with an alternative model being similar to that in Fig. 5(g) with the flow direction being reversed, with the central helical flow of the spinning top directed onto the surface of the tube. The exfoliation of graphene in a mixture of toluene and water results in the spinning of long fibres of graphene scrolls.²⁷ They arise from multiple sheets being sequentially exfoliated from a single block of graphite held centrifugally against the surface of the tube and this is also possible for either direction of flow.

The heat generated as the solvent molecules strike the bismuth when held to the internal tube surface is sufficient to melt bismuth, which then rapidly crystallises outside the craters. Beyond the edge of the craters, rods ca. 10 μm in length and ca. 200 nm in diameter are present. The origin of these rods is from the liquid metal being drawn up into the helical flow of the spinning top which then crystallises under high heat transfer, with the rods exiting the spinning top and collecting under centrifugal force on the outside of the crater. The rods close to the crater are mattered together, ruling out a self-assembly of the rods associated with drop casting in preparing the sample for SEM. This implies that there is a flow pattern near the centre of the spinning top which provides sufficient updraft to extract material from the bismuth metal (density at its melt point 10.022 g cm⁻³) as the bulk material is being centrifugally held against the surface of the tube. This lift coupled with torsional shear stress accounts for the ability of the VFD to readily exfoliate 2D materials such as graphite and boron nitride.⁶ Also important here is that the localised heating of the surface of a 2D starting material is likely to create a lattice mismatch relative to the cooler layers below, further facilitating the exfoliation process. We note though that the signature of IPA is not informative for predicting the optimal rotational speed for the spinning top Coriolis flow, Fig. S1,† unlike many of the other solvents studied herein.

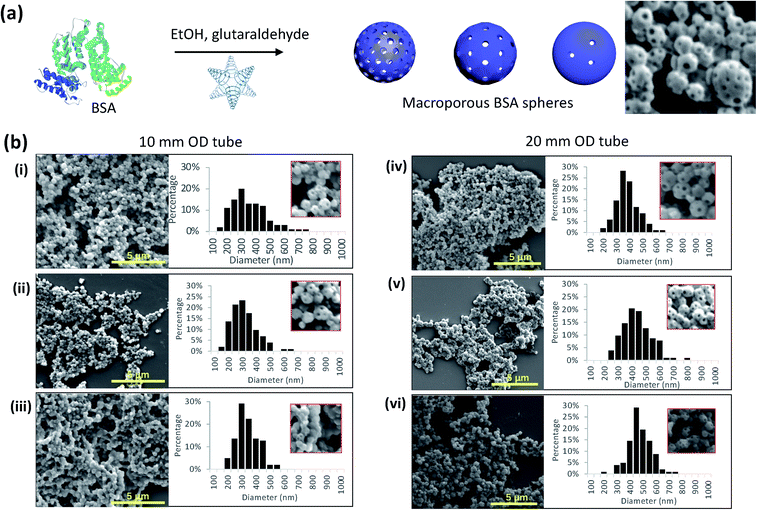
The reaction of BSA with glutaraldehyde in the VFD in a 3 : 1 mixture of ethanol and water as PBS, a β-liquid with spicular flow, Fig. 2(g), results in the formation of porous polymeric hollow spheres with other ratios of the two solvents ineffective in forming uniform sized hollow spheres,²⁸ and having different signatures (ESI Section 2†). Higher rates of polymerisation are expected where there is high mass transfer,²i.e. within the spicules, with the polymer then building up at the closest proximity with low shear, on the surface of a sphere with holes representing where the spicules protruded, Fig. 6(a and b). The formation of the holes on the surface of the spheres is also likely to depend on the ability to organise anisotropic shaped BSA into 3D structures. This material then represents a ‘negative’ mould of spicular flow, with the formation of the C₆₀ spicules as the ‘positive’ mould. The size of the porous spheres is ca. 10–38% smaller for the 10 mm tube relative to the 20 mm tube, Fig. 6(b) (and ESI Section 9†), as for the formation of C₆₀ cones in the smaller tube. The number of holes in each sphere (=number of spicules of fluid flow) varies for each sample preparation for different operational parameters of the VFD, as is the case for the formation of spicules of C₆₀, Fig. 4(a).

Fig. 6 Moulding polymer growth. (a) Schematic of the formation of porous spheroidal particles of cross linked BSA with glutaraldehyde formed in the VFD under confined mode BSA in aqueous 10 mM PBS of pH 7.4 (1 mg mL⁻¹) to ethanol ratio 1 : 3 (300 : 900 μL) and 15 μL of glutaraldehyde, using (b) 0.5 mL of combined solution in a 10 mm OD tube for 1 min at 3k, 5k and 7k rpm (i–iii) respectively, and 1 mL of combined solution for a 20 mm OD tube, for 1 min at 3k, 5k and 7k rpm (iv–vi) respectively, reporting SEM images and derived particle size distributions from 100 randomly chosen spheres.

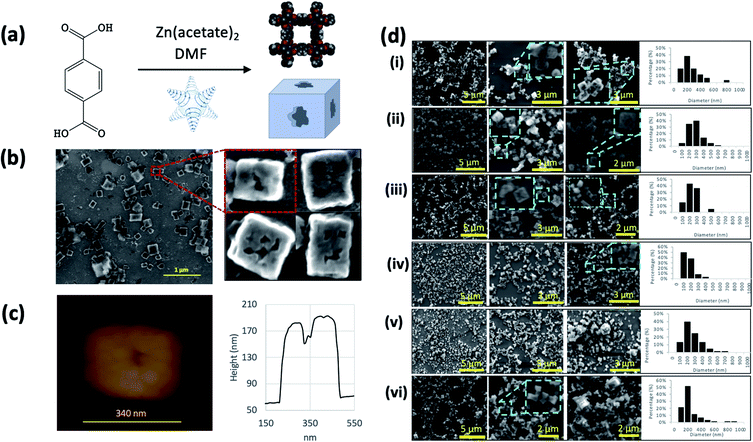
Terephthalate/Zn MOF5 formed using batch processing,²⁹ as cuboid particles varying from sub-micron to micron dimensions, is commonly synthesised in coordinating solvent such as DMF. Confined mode synthesis in DMF in the VFD at 110 °C also produces cuboids of the same structure (Fig. 7 (a–d)) (and ESI Section 10†), except for processing below 5.5k rpm, where spicular flow prevails, Fig. 2(f), which generates cuboids with irregular shaped cavities on each face. The cavities are then the ‘negative’ moulds of high shear at the spicules, with any crystallisation in the cavities likely to lead to shear stress dissolution, and regrowth on the faces, away from the high shear. Thus, nucleation and growth of MOF5 provides a partial mould of spicular flow, with the position of spicular flow in DMF at 110 °C at ca. 4k rpm, which is 1.5k rpm lower than such flow at room temperature, Fig. 2(f).

Fig. 7 Moulding metal organic frameworks. (a) Schematic of the synthesis of MOF5 where terephthalic acid (63.3 mg) and triethylamine (106.3 μL) were dissolved in 4.9 mL of DMF and Zn(OAc)₂·2H₂O (169.9 mg) was dissolved in 5 mL of DMF. For a typical VFD experiment, 556 μL of zinc solution was added to 444 μL terephthalic acid solution followed by 20 mm VFD processing for 30 min at 110 °C. (b and c) SEM and AFM images respectively for MOF5 formed at 110 °C for 30 min at 4k rpm. (d) Variation in morphology of the particles formed under the same processing as a function of rotational speed (i–vi), 3k, 4k, 5k, 5.5k, 6k and 7k rpm, respectively, for the confined mode of operation of the VFD for 30 min, showing SEM images and particle size plots, determined by randomly counting 100 particles.

The above results provide a model of fluid flow within the VFD that can empirically describe the behaviour that is thought to occur to produce the very real nanostructures observed. At the minimum mixing time, the high shear spinning top flow, at most a few μm in diameter, is thought to prevail. Beyond this rotational speed, the model considers Faraday waves combining with Coriolis spinning top flow, with the lines of high shear fluid flow on the surface of a spicule. At greater rotational speeds as the mixing times peak, Faraday waves dominate, where double-helical eddies associated with them are normal to the thin film. For other liquids, double-helical flow dominates across values of rotational speed. Eddies associated with Faraday waves are twisted into double-helices by the spinning top flow, with flow up one strand of each helix, and down the other. Superimposing the associated vectors of flow with those of the spinning top flow, the length scales of the flows are comparable (FC ∼ F_FW), which necessarily creates a flow of liquid around a sphere. Here a full turn of the double-helix being the diameter of the double-helical Faraday waves eddies corresponds to the diameter of the spinning top flow, Fig. 1(e). The spicular flow sphere of influence is approximately 1–2 μm for the 20 mm diameter tube, and ca. 30% smaller for the 10 mm OD tube. For spicular flow, the diameter of the double-helix is defined by the diameter of the fullerene C₆₀ spicules, and thus the diameter of the associated double-helix, d_DH, Fig. 1(e). For d_DHca. 2 μm, and assuming that for one rotation of the VFD tube, that eddies complete a full turn of the double-helix, ca. 5 μm, then at 6k rpm (100 Hz), the velocity of the molecules in the double-helical flow is ca. 0.5 mm s⁻¹. This is consistent with the shear stress in the VFD increasing the average velocity of the molecules, without external heating, and that the system has regimes which are not limited to diffusion control processes. Moreover, for increasing rotational speeds, with Faraday wave dominated flow patterns (F_FW > F_C), the path length of fluid flow induced by each rotation of the tube will decrease, and this explains why the enhancement effects of the VFD diminish above ca. 8k rpm in a 20 mm OD tube.² Overall, the established fluid flow model, while speculative, explains all of the processing that has been observed in the VFD, including protein folding and enzymatic rate enhancements, with double-helical flow and associated pressure fluctuations from the Faraday waves themselves effective in accelerating enzymatic reactions.³ It also accounts for the unique rotational dependence for an enzyme, which relates to their different sizes and shapes.³

Conclusions

We have established the topological features of high shear fluid flow in the vortex fluidic device (VFD) at sub-micron dimensions, at a tilt angle of 45°, which corresponds to the optimal angle for a myriad of applications of the device.^2–7 The rotational speeds for high shear spinning top flow (F_C > F_FW), spicular flow (F_C ∼ F_FW) and double-helical flow (F_C < F_FW) can be determined by measuring changes in temperature and mixing times, and average film thickness as a unique signature for any liquid. Sudden increases in temperature of the liquid correspond to discontinuities in fluid flow, with a sudden reduction in film thickness for increasing rotational speed rather than continuously changing film thickness, as a new phenomenon in thin films. The proposed flow patterns in the VFD provide insights that allow us to predict and control the formation of nanostructures in the VFD, but these models still require real-time tracking of fluids at sub-micron dimensions for verification. The flow patterns also provide an understanding of the advantages of VFD processing relative to using other methods, and indeed where the VFD processing is without precedent. Also noteworthy is that the unique signature for a liquid in the VFD provides insight into how increasing the concentration of reagents in precursor solutions, which can potential alter such a signature, can result in different processing outcomes.^16,17

The present work also established that the VFD is effective in creating systems in non-equilibrium states, in establishing a new form of crystallization induced by shear stress, adding to the ubiquitous methods of sublimation, cooling and evaporating, and also stripping away surfactants.²⁵ Also of note is the ability to create novel spicule structures which map out the high mass topologies in a liquid, or the ‘negative’ of these structures where material formed in the spicular fluid flow under high shear assemble at the closest points of low shears, in between the spicules.

With the VFD and an understanding of its operating regimes, structures are moulded with predictable shapes by the mechanical force of fluid flow and diffusion of species within the liquid. Fundamentally, the vast differences in the morphology of the resultant structures between the three topological fluid flow regimes must result from unique diffusion behaviour within the liquid. Thus, the VFD demonstrates the ability to mediate or control both the forces exerted by the liquid on nanostructures and the diffusion of species supplied to their surface. The findings also have implications on using shear stress driven boundary mediated control of fluid flow for controlling self-assembly and chemical reactions under non-equilibrium conditions, and manipulating cells under tuneable stress regimes, which are areas we are currently investigating.

As an example of the ability now to predict the processing requirements and application of the VFD, we recently established that spicules of fullerene C₆₀ can be generated on the surface of polystyrene beads.³⁰ This is for beads of a specific diameter suspended in a non-saturated toluene solution of C₆₀, using a quartz tube of a specific diameter spun at the rotational speed corresponding to spicular flow present at the ubiquitous tilt angle of 45°. Such coating of polystyrene beads is not possible using conventional batch processing. In the same way we envisage the ability to access other composite nanomaterials using the VFD, along with the ability to control their size, shape and morphology, as well as crystallinity.

Author contributions

T. M. D. A. carried out graphene oxide experiments, T. M. D. A. and I. K. A. carried out the fullerene nano-cone experiments, B. S. A. H. and T. M. D. A. carried out the shear stress induced crystallisation of fullerene spicules and rods, A. I. carried out the polymer moulding experiments, F. A. J. A. carried out bismuth moulding experiments, X. L. carried out the BSA and MOF experiments, M. J. and K. V. carried out thermal imaging and mixing experiments, M. J. and X. L. determined film thickness, X. C. carried out the imaging experiments, K. A. S., J. M. C., W. Z. and R. A. B. contributed to the development of the experiments, J. S. Q. developed an understanding the dynamic equilibrium, D. B. J. developed an understanding of the forces in the thin films, and C. L. R. designed the VFD microfluidic platform, coordinated the research and developed the model for the fluid behaviour. All authors contributed to writing and editing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support of this work by the Australian Research Council (DP200101105 and DP200101106), the Australian Nuclear Science and Technology Organisation, and the Government of South Australia is greatly acknowledged. The authors also acknowledge helpful discussion with Stuart B. Dalziel (University of Cambridge) and the expertise, equipment and support provided by Microscopy Australia through Flinders Microscopy and Microanalysis.

Notes and references

1. T. D. Ross, et al., Controlling organization and forces in active matter through optically defined boundaries, Nature, 2019, 572, 224–229.
2. J. Britton, K. A. Stubbs, G. A. Weiss and C. L. Raston, Vortex fluidic chemical transformations, Chem.–Eur. J., 2017, 23, 13270–13278.
3. J. Britton, L. Meneghini, M. C. L. Raston and G. A. Weiss, Accelerating enzymatic catalysis using vortex fluidics, Angew. Chem., Int. Ed., 2016, 55, 11387–11391.
4. T. Z. Yuan, et al., Shear-stress-mediated refolding of proteins from aggregates and inclusion bodies, ChemBioChem, 2015, 16, 393–396.
5. T. M. D. Alharbi, K. Vimalanathan, W. D. Lawrance and C. L. Raston, Controlled slicing of single walled carbon nanotubes under continuous flow, Carbon, 2018, 140, 428–432.
6. X. Chen, J. F. Dobson and C. L. Raston, Vortex fluidic exfoliation of graphite and boron nitride, Chem. Commun., 2012, 48, 3703–3705.
7. M. H. Wahid, et al., Microencapsulation of bacterial strains in graphene oxide nano-sheets using vortex fluidics, RSC Adv., 2015, 5, 37424–37430.
8. G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442, 368–373.
9. C. Brechtelsbauer, N. Lewis, P. Oxley, F. Ricard and C. Ramshaw, Evaluation of a spinning disc reactor for continuous processing, Org. Process Res. Dev., 2001, 5, 65–68.
10. X. Chen, N. M. Smith, K. S. Iyer and C. L. Raston, Controlling nanomaterial synthesis, chemical reactions and self-assembly in dynamic thin films, Chem. Soc. Rev., 2014, 43, 1387–1399.
11. H. Lodha, R. Jachuck and S. S. Singaram, Intensified biodiesel production using a rotating tube reactor, Energy Fuels, 2012, 26, 7037–7040.
12. E. K. Sitepu, et al., Continuous flow biodiesel production from wet microalgae using a hybrid thin film microfluidic platform, Chem. Commun., 2018, 54, 12085–12088.
13. T. E. Solheim, F. Salvemini, S. B. Dalziel and C. L. Raston, Neutron imaging and modelling inclined vortex driven thin films, Sci. Rep., 2019, 9, 2817.
14. J. Britton, S. B. Dalziel and C. L. Raston, Continuous flow Fischer esterifications harnessing vibrational-coupled thin film fluidics, RSC Adv., 2015, 5, 1655–1660.
15. J. Britton, S. B. Dalziel and C. L. Raston, The synthesis of di-carboxylate esters using continuous flow vortex fluidics, Green Chem., 2016, 18, 2193–2200.
16. T. M. D. Alharbi, et al., Shear stress mediated scrolling of graphene oxide, Carbon, 2018, 137, 419–424.
17. I. K. Alsulami, T. M. D. Alharbi, D. P. Harvey, C. T. Gibson and C. L. Raston, Controlling the growth of fullerene C₆₀ cones under continuous flow, Chem. Commun., 2018, 54, 7896–7899.
18. P. Chen, et al., Microscale Assembly Directed by Liquid-based Template, Adv. Mater., 2014, 26, 5936–5941.
19. N. Périnet, P. Gutiérrez, H. Urra, N. Mujica and L. Gordillo, Streaming patterns in Faraday waves, J. Fluid Mech., 2017, 819, 285–310.
20. K. Kumar, Linear theory of Faraday instability in viscous liquids, Proc. R. Soc. London, Ser. A, 1996, 452, 1113–1126.
21. A. Zaccone, et al., Theory of activated-rate processes under shear with application to shear-induced aggregation of colloids, Phys. Rev. E, 2009, 80, 052404.
22. B. O Conchuir and A. Zaccone, Mechanism of flow-induced biomolecular and colloidal aggregate breakup, Phys. Rev. E, 2013, 87, 032310.
23. F. Mura and A. Zaccone, Effects of shear flow on phase nucleation and crystallization, Phys. Rev. E, 2016, 93, 032310.
24. K. Vimalanathan, et al., Surfactant-free fabrication of fullerene C₆₀ nanotubules under shear, Angew. Chem., Int. Ed., 2017, 56, 8398–8401.
25. L. Wu, J. J. Willis, I. S. McKay, B. T. Diroll, J. Qin J., M. Cargnello and C. J. Tassone, High-temperature crystallization of nanocrystals into three-dimensional superlattices, Nature, 2017, 548, 197–201.
26. G. V. Malysheva, E. Sh. Akhmetova and A. N. Marycheva, Estimation of glass transition temperature of polysulfone modified epoxy binders, Glass Phys. Chem., 2014, 40, 543–548.
27. K. Vimalanathan, I. Suarez-Martinez, M. C. R. Peiris, J. Antonio, C. de Tomas, Y. Zou, J. Zou, X. Duan, R. N. Lamb, D. P. Harvey, Th. M. D. Alharbi, C. T. Gibson, N. A. Marks, N. Darwish and C. L. Raston, Vortex fluidic mediated transformation of graphite into highly conducting graphene scrolls, Nanoscale Adv., 2019, 1, 2495–2501.
28. X. Luo, et al., Vortex fluidic mediated synthesis of macroporous bovine serum albumin-based microspheres, ACS Appl. Mater. Interfaces, 2018, 10, 27224–27232.
29. N. L. Rosi, et al., Hydrogen storage in microporous metal-organic frameworks, Science, 2003, 300, 1127–1129.
30. M. Jellicoe, et al., High shear spheroidal topological fluid flow induced coating of polystyrene beads with C₆₀ spicules, Chem. Commun., 2021 10.1039/d0cc07165j.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00195g

‡ Authors contributed equally to this work.

---