Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Robust, flexible, freestanding and high surface area activated carbon and multi-walled carbon nanotubes composite material with outstanding electrode properties for aqueous-based supercapacitors†
Bruno
Freitas
 a,
Willian G.
Nunes
a,
Willian G.
Nunes
 a,
Davi Marcelo
Soares
a,
Davi Marcelo
Soares
 a,
Fernando C.
Rufino
a,
Fernando C.
Rufino
 a,
Cássio Murilo
Moreira
b,
Leonardo Morais
Da Silva
*b and
Hudson
Zanin
a,
Cássio Murilo
Moreira
b,
Leonardo Morais
Da Silva
*b and
Hudson
Zanin
 *a
*a
aAdvanced Energy Storage Division, Center for Innovation on New Energies, Carbon Sci-Tech Labs and Manufacturing Group, School of Electrical and Computer Engineering, University of Campinas, Av. Albert Einstein 400, Campinas, SP 13083-852, Brazil. E-mail: hzanin@unicamp.br
bDepartment of Chemistry, Laboratory of Fundamental and Applied Electrochemistry, Federal University of Jequitinhonha e Mucuri's Valley, Rodovia MGT 367, km 583, 5000, Alto da Jacuba, 39100-000, Diamantina – MG, Brazil. E-mail: lsilvamorais@hotmail.com
First published on 30th March 2021
Abstract
We report on multi-walled carbon nanotubes (MWCNTs) and an activated carbon (AC) composite material as an electrode for electrical double-layer capacitors (EDLCs). Material flexibility, robustness, and electrical conductivity are features that come from the MWCNTs, while a high specific surface area is an AC's intrinsic property. We prepared different MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC ratios in solutions, which were filtered to form a buckypaper. We investigated the specific capacitance, equivalent series resistance, working voltage window (WVW), and the specific energy and power. The best electrochemical findings were obtained for the MWCNT
AC ratios in solutions, which were filtered to form a buckypaper. We investigated the specific capacitance, equivalent series resistance, working voltage window (WVW), and the specific energy and power. The best electrochemical findings were obtained for the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC ratio of 1
AC ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 with a specific capacitance reaching the theoretical limit. A high working voltage window of 1.4 V was verified in aqueous solution. Simultaneously, the symmetric cells were able to cycle for more than one million cycles in fast charge–discharge galvanostatic tests with 93% capacitance retention. Finally, the main criticism regarding the self-supported electrode materials is the difficulty of welding. In this sense, we presented a particular welding process as proof of concept for electrode scalability. Overall, this novel electrode material exhibits a set of exciting properties, which we now tested in EDLCs.
3 with a specific capacitance reaching the theoretical limit. A high working voltage window of 1.4 V was verified in aqueous solution. Simultaneously, the symmetric cells were able to cycle for more than one million cycles in fast charge–discharge galvanostatic tests with 93% capacitance retention. Finally, the main criticism regarding the self-supported electrode materials is the difficulty of welding. In this sense, we presented a particular welding process as proof of concept for electrode scalability. Overall, this novel electrode material exhibits a set of exciting properties, which we now tested in EDLCs.
1. Introduction
The low molecular mass of the active electrode component, feasible cost, chemical stability, and high capability to store charge for thousands of cycles are aspects of interest for materials that are used in energy storage devices called electrochemical capacitors or supercapacitors.1 Thus, fulfilling these requirements, some carbon allotrope materials have gained attention due to their high specific surface area, which has implications in the specific capacitance, energy, and power characteristics. Electrical double-layer capacitors (EDLCs) based on the physical charge separation process are intrinsically different from the pseudocapacitors (PCs), where intercalation and/or surface faradaic reactions significantly contribute to the overall charge-storage mechanism. In the former case, arising from the formation of an electrical double-layer (EDL) at the electrode/electrolyte interface, the charge storage process on carbon materials occurs through ionic adsorption (e.g., the generation of a surface ionic excess) at the walls of the accessible pores as a function of the applied electric potential or voltage.2 Because the energy is practically stored due to the electrostatic phenomenon involving finite-sized ionic species and electrons at both sides of the interface, EDLC devices do not present an expansion in the crystalline materials or pronounced redox reactions during the charge–discharge processes. Only minor contributions from the solid-state faradaic reactions occur in EDLCs due to the almost reversible redox activity involving the oxygenated surface groups. As a result, EDLCs are highly stable, thus allowing them to perform up to a million cycles during its service life.3According to the theoretical capacitance equation presented by Helmholtz et al.,4 the higher the surface area, the higher the capacitance. However, experimental results have shown that although the surface area is relevant, the predicted linear relationship does not always apply.5 This is, in part, because the finite-sized solvated ionic species from the electrolyte may not access some porous regions of the electrode material that contain narrow micropores (0.2–2 nm). An exception is some carbide-derived carbons (CDCs), where a deep insertion of the bare ionic species into the micropores can be verified.6
Deemed to be the best commercial material for EDLCs due to its cost-effective characteristics, activated carbons (ACs) are 3D porous materials with sp2 hybridization, and are commonly synthesized from physical and chemical activation processes from different organic precursors.7,8 ACs can have a very high surface area (e.g., ∼1000–3000 m2 g−1), and they exhibit low-moderate electronic conductivity. In this sense, at least in principle, combining AC structures with metallic conductive additives, such as black carbon (BC) or multi-walled carbon nanotubes (MWCNTs), is an excellent strategy to overcome some drawbacks exhibited by ACs. As a result, the charge-storage process can be accomplished without significant ohmic losses during the electron flow across the hierarchically interconnected pore walls, improving the overall EDLC characteristics. The traditional recipe found in the literature typically involves a mix of AC (80%) with additives (10%) and a binder (10% of PVDF or PTFE). This mixture forms a slurry that can be conveniently deposited onto a thin foil aluminum current-collector, mainly when organic electrolytes are used. Although necessary, the binder species result in very poorly conducting media, thus significantly contributing to the equivalent series resistance (ESR). Moreover, binder substances adequate for EDLCs are costly and may require the use of unfriendly solvents (e.g., N-methyl-2-pyrrolidone (NMP)) which have carcinogenic properties.9
As another relevant parameter of supercapacitors (SCs), electrolytes play an essential role in the overall electrochemical performance of these devices. Therefore, companies are intensely interested in increasing the working voltage window (WVW) of different electrolyte solutions that are less harmful and not flammable to boost the specific energy density, i.e., E = 0.5CV2, where C is the specific capacitance, and V is the WVW.10 Electrolytes also influence the ESR, operating temperature, distributed capacitance, self-discharge, toxicity, and fabrication costs.10,11
Table 1 gathers some properties of carbon-based electrodes using different electrolytes. For instance, Li et al.12 developed a freestanding composite material made of carbonized cellulose and AC using an ionic liquid (IL) as the electrolyte. This material housed in a two-electrode system yielded a WVW of 3 V and a specific capacitance of 85 F g−1 (0.1 A g−1 and BMPY/TFSI). In principle, ILs are considered promising candidates for conventional organic electrolytes since they exhibit high thermal stability and good ionic conductivity. Besides, their solvent-free characteristics permit them to obtain very high WVWs (e.g., 3.5–4.0 V). However, a significant drawback involving ILs is their high cost compared with the organic electrolytes used in practical devices.13,14
| Electrode material | SSA(m2 g−1) | Electrolyte (mol l−1) | C g (F g−1), Ca (mFcm−2), Cv (F cm−3) | Mass loading (μg cm−2) | Electrode thickness (μm) | Voltage window (V) | Test conditions | Ref. |
|---|---|---|---|---|---|---|---|---|
| Graphene–CNT composite | — | 1 M TEABF4/PC | 110 (g), 78 (g) | — | — | 3 | 0.5 Ag−1, 5 A g−1 | 15 |
| Kuraray AC | 1600 | 1 M TEABF4/HFIP | 110 (g) | — | 200 | — | 1 mV s−1 (3el) | 16 |
| Graphene/MnO2/graphene | Na2SO4 (1) | 31 (g) | 2 | 500 mA g−1 (2el) | 17 | |||
| MWCNT | 200 | TEABF4 (1.5) | 18 (g) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | 2.3 | 5 mA cm−2 (2el) | 18 |
| SWCNT/PANI | H2SO4 (1) | 55 (g) | — | 0.120 | 0.8 | 2.6 A g−1 | 19 | |
| PANI@CNT | H2SO4/PVA gel | 346.6 (g) | — | — | 0.8 | 10 mV s−1 | 20 | |
| Graphene/CNT | — | H2SO4 (1) | 120 (g) | — | — | 0.6 | CV | 21 |
| CNT, activated CNT, NMCNT | 218, 778, 200 | H2SO4 (1) | 48.4, 151.7, 190.8 | — | — | 1 | 5 mV s−1 | 22 |
| SWCNT | — | H2SO4 (1), PVA/H3PO4 | 120 (g), 110 (g) | — | 20–40 | 1 | 1 mA mg−1 | 23 |
| rGO–CNT | 240 | KOH (6) | 250 (v) | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | 1.2 | 1 A g−1 | 24 |
| AC/CNT/rGO | 913.4 | LiClO4 (1) | 101 (g) | 0.453 | — | 3 | 0.2 A g−1 | 25 |
| Bacterial cellulose-rGO/CNF | 137 | KOH (6) | 216 (g) | Mass – 0.95 mg | 1200 | 1 | 1 A g−1 | 26 |
| Submicron CFs | 1005 | Na2SO4 (1) | 47 (g) | — | — | 1.3 | 1 A g−1 | 27 |
| Submicron activated CFs | — | KOH (6) | 344 (g) | 1800 | 1 | 10 mV s−1 | 28 | |
| Carbon monolith | 770 | EMITFSI | 75 (g) | — | — | 2.5 | 10 mV s−1 | 29 |
| Lithographically AC | 1636 | H2SO4 (1) | 325 | — | ∼1.5 | 0.6 | 45 A g−1 | 30 |
| AC/graphene | 2070 | H2SO4 (1) | 186 (g) | — | — | 1.1 | 0.5 A g−1 (3el) | 31 |
| AC | 1137 | LiOH (1) | 204 (g) | — | 600 | 0.8 | 1 A g−1 | 32 |
| CNT/holey graphene | — | H2SO4 (0.5) | 268 (g) | 1000 | — | 0.7 | 0.25 A g−1 (3el) | 33 |
| AC | 2562 | Na2SO4 (1) | 294.3 (g) | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | 1.79 | 0. 5 A g−1 (2el) | 34 |
| CNT fiber | — | H2SO4–PVA | 4.28 (a) | — | — | 0.8 | 50 mV s−1 | 35 |
| Self-stacked solvated graphene film | — | H2SO4 (1) | 215 (g) | 45 | — | 1 | 0.1 A g−1 (2el) | 36 |
| Flower-like hierarchical porous carbon | 761.5 | Na2SO4 (1) | 35.6 (v) | — | — | 1.8 | — | 37 |
| Laser-scribed graphene | 1520 | NEt4–BF4 in ACN (1) | 265 (g), 4.82 (a) | — | <100 | 3 | — | 38 |
| EMIMBF4 | 276 (g), 5.02 (a) | 4 |
Organic electrolytes may also present a WVW in the range of 2.5–2.8 V, resulting in high specific energies.10 As a consequence, they have been traditionally used in several commercial devices. Gogotsi et al.18 reported MWCNTs (200 m2 g−1, 15 mg cm−2, and 1.5 M TEABF4) with a low specific capacitance of 18 F g−1 and a WVW of 2.3 V. These authors claimed that the low capacitance is mainly due to the low specific surface area. In the study conducted by Jung et al.,15 using CNTs and reduced graphene oxide (rGO) as a freestanding composite film and 1.0 M TEABF4 + PC, the authors reported a moderate capacitance value of 110 F g−1 at 0.5 A g−1. These authors emphasized the high-surface-area of graphene of 2630 m2 g−1, which, in principle, might result in a theoretical capacitance of ca. 550 F g−1.
Therefore, the practical electrochemical response of nanostructured carbon materials is still far from the expected theoretical values.39,40 In this sense, graphene still poses several practical difficulties related to scalability, cost-effectiveness, the synthesis process, and the re-stacking process caused by π–π interactions, etc. These drawbacks severely restrict the practical use of some nanostructured electrode materials.41–43
For example, using a conventional carbon material, Francke et al.16 reported a detailed study using commercial AC from Kuraray Chemicals Co. (Japan) with a specific surface area of 1600 m2 g−1. Using 1,1,1,3,3,3-hexafluoroisopropan-2-ol (HFIP) as the electrolyte, whose conductivity is higher than the propylene carbonate (PC) + 1 M TEABF4 mixture, these authors found a specific capacitance for the individual electrodes of 110 F g−1.
To summarize, besides presenting a wider WVW, the use of organic electrolytes is favored due to the practical absence of corrosion processes involving the aluminum current collector materials. Nonetheless, issues related to high cost, toxicity, flammability, volatility, and safety concerns remain. Moreover, a complex purification process is necessary for removing impurities, such as water, which, besides safety concerns, may lead to fast electrolyte degradation and accelerated self-discharge processes.10,44,45 For these reasons, since 1997, the study of aqueous-based electrolytes has become very exciting to obtain friendlier conditions for the use and fabrication of SCs.
A significant issue regarding aqueous electrolytes is the low WVW of ca. 1.0 V. Due to thermodynamic and kinetic factors, the water-splitting reaction commonly occurs at low cell voltages. Therefore, the great challenge involving these electrolytes is to increase the WVW to improve the overall device performance characteristics. Different aspects regarding water-based electrolytes have been discussed by Beguin et al.,46 who showed that for neutral solutions (e.g., Li2SO4 and Na2SO4), the WVW is higher compared with H2SO4 and KOH solutions. However, H2SO4 solutions are widely used in the literature reports.42 Zhong et al.10 reported that H2SO4 solutions are exciting due to their higher ionic conductivity, leading to low ESR values. For instance, Deng et al.33 developed a CNT/holey graphene binder-free electrode (1.0 mg), which in 0.5 M H2SO4 presented a specific capacitance for the individual electrodes of 268 F g−1 at 0.25 A g−1. Kaempgen et al.23 developed a single-walled CNT printed thin-film supercapacitor and presented a comparative study involving several electrolyte species. Using a 1.0 M H2SO4 solution, these authors reported a high capacitance of 120 F g−1 at 1.0 A g−1. This value corresponded to an areal capacitance of 0.25 F cm−2. In the case of alkaline solutions, Chang et al.,26 using a biomass-derived carbon composite containing rGO (137 m2 g−1 and 0.95 mg), reported a specific capacitance for the individual electrodes of 216 F g−1 at 0.1 A g−1 (6.0 M KOH).
It is crucial to emphasize that the electrode active mass strongly influences the capacitance values.47 The former should be higher than 10 mg with a lower capacitance limit of 0.25 F. Likewise, as Gogotski and Simon48 stated, commercial electrodes traditionally possess a thickness of 100–200 μm, corresponding to a mass loading of ∼10 mg cm−2. It is important to note that the possibility to extrapolate the electrode performance considering a low thickness of ∼1 μm for practical applications is meaningless. In this sense, Peng et al.7,49 presented a carbon-based material derived from the biomass-derived carbon obtained from tea leaves. For a high specific surface area of 2841 m2 g−1 and an electrode mass of 8 mg, these authors found a high value of 330 F g−1 in 2.0 M KOH for the individual electrode capacitance. However, it is worth mentioning that real symmetric devices commonly exhibit 1/4 of the specific capacitance verified for individual electrodes measured in three-electrode cells.
From the above considerations, we report in this work binder-free and self-supported MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC buckypaper electrodes in an aqueous electrolyte where no metallic current collector was used to avoid corrosion issues. In this sense, we also presented an innovative, robust welding technology capable of delivering secure and facile fastening of metallic connectors to the freestanding electrode whilst guaranteeing high electronic contact. The buckypaper was synthesized using several MWCNT
AC buckypaper electrodes in an aqueous electrolyte where no metallic current collector was used to avoid corrosion issues. In this sense, we also presented an innovative, robust welding technology capable of delivering secure and facile fastening of metallic connectors to the freestanding electrode whilst guaranteeing high electronic contact. The buckypaper was synthesized using several MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC ratios aiming to provide the best electrode mass-loading conditions that resemble commercial devices. Since the porous buckypaper material has several voids between the carbon particles, we applied a hot-pressing treatment to improve the composite's overall conductivity. A rigorous experimental procedure was reported to correctly identify the capacitive voltage range in the absence of water-splitting.
AC ratios aiming to provide the best electrode mass-loading conditions that resemble commercial devices. Since the porous buckypaper material has several voids between the carbon particles, we applied a hot-pressing treatment to improve the composite's overall conductivity. A rigorous experimental procedure was reported to correctly identify the capacitive voltage range in the absence of water-splitting.
2. Experimental section
2.1. Materials and chemicals
Model Ctube-120 MWCNTs (95% purity, diameter 10–40 nm, and length 1–40 μm) were purchased from CNT Co. Ltd (Korea) while model YP-50F AC (1692 m2 g−1 and 0.3 g mL−1) was purchased from Kuraray Co. Ltd (Japan). The other “purum” p.a. chemicals were provided by Synth® (Brazil) and used without further purifications.2.2. Preparation of the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) AC buckypaper electrodes
AC buckypaper electrodes
Buckypaper electrodes were synthesized using the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC mass ratios of 1
AC mass ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 1
2, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, henceforth referred to as b1
3, henceforth referred to as b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, b1
0, b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, b1
1, b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and b1
2, and b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, respectively. Mass values are specified in Table 2.
3, respectively. Mass values are specified in Table 2.
| Sample | MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC ratio AC ratio |
MWCNT (wt%) | AC (wt%) | Electrode mass (mg) |
|---|---|---|---|---|
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
100.0 | 0.0 | 33.3 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
50.0 | 50.0 | 29.1 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
33.3 | 66.7 | 27.5 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
25.0 | 75.0 | 29.3 |
The materials were dispersed in deionized water for each sample using a 0.5 wt% sodium dodecyl sulfate (SDS) solution. The SDS was added to increase the interaction of the MWCNTs with water. MWCNTs are hydrophobic, making buckypaper with them difficult and inefficient in the production in aqueous media (water is the cheapest, low toxic and easy-to-handle solvent). We added SDS, because it has polar and nonpolar parts, which means that the hydrophilic and hydrophobic parts in its molecule bind to water and MWCNT to make them join together. Afterward, the suspension was sonicated using an ultrasound tip probe from Ultronique® (80 W and 30 min) to obtain a homogenous dispersion of carbon. Each dispersion was then filtered under a vacuum using a 0.22 μm PTFE porous membrane (Millipore®) over ∼2 h. The residue of SDS was removed after a copious washing process using deionized water. The carbon-based layers that were formed after filtration were peeled off from the PTFE membrane. After the preparation of buckypaper, it was washed carefully many times and dried at room temperature overnight. A hot-pressing method was applied to improve the physical/electrical contact between the carbon material particles. This treatment was accomplished at 100 °C and 10 rpm using a hot-rolling press (TOB-DR-H150). For each sample, the procedure was repeated twice. Lastly, electrodes with an appropriate diameter to fit the model CR2032 coin cell were punched out of the buckypaper for the cell assembly process.50,51
2.3. Materials characterization
Surface morphologies were examined by scanning electron microscopy (SEM) using model S-3400N equipment from Hitachi. Structural micrographs were performed using a JEOL JEM 2100 LaB6 instrument. X-ray diffraction was performed using a Philips Analytical X-Ray diffractometer with Cu-Kα radiation (λ = 1.5418 Å) in a Bragg–Brentano θ/θ configuration (Goniometer PW3050/10) for investigation of the crystalline nature of the nanoparticles. The diffraction patterns were collected with steps of 0.01° and an accumulation time of 0.6 s per step within the range of 10°–60° (2θ). Raman spectra were obtained using a Renishaw inVia spectrometer with a 633 nm excitation wavelength (50% laser intensity, 10 accumulations, and a 5× objective lens). Notably, the authors compared the first and last intensity ratios (ID/IG) of the Raman bands to ensure that the incoming laser radiation did not damage the samples. BET and BJH analyses comprising the specific surface area and pore size distribution, respectively, of the carbon materials were accomplished via the physical adsorption technique using N2 at 77 K with a model ASAP 2010 equipment from Micromeritics®. Firstly, the samples were preconditioned in a dry oven at 70 °C utilizing a vacuum for 12 h. Afterward, the samples were heated to 120 °C for 6 h until the desired isobaric condition (P = 2 μm Hg) was reached.2.4. Electrochemical characterization using a symmetric coin cell
For the electrochemical tests, the buckypaper electrodes and the porous separator (cellulosic membrane) housed in the symmetric CR2032 coin cell were soaked with 60 μL of a 1.0 M Li2SO4 solution (aqueous electrolyte).An experimental approach to correctly identify the capacitive voltage window in the SCs: A significant issue regarding SCs is concerned with the apparent (incorrect) evaluation of the capacitive voltage window due to the contribution to the overall current of a small faradaic current due to solvent decomposition (e.g., water-splitting). The situation is more dramatic for techniques involving the rapid application of the voltage or current increments, as in the CV and GCD techniques. Therefore, these techniques must be carefully applied to identify the capacitive voltage interval correctly. In this sense, the capacitive voltage window was determined in the present work by combining CV and single-step chronoamperometry (SSC) experiments. Firstly, cyclic voltammograms were recorded at a low scan rate of 5 mV s−1 since this condition allows identifying the presence of an irreversible faradaic process close to the vertex voltages. The cell voltage was progressively increased from the OCP in steps of 0.1 V until a voltammetric ‘current tail’ was detected. Afterward, an SSC experiment was carried out for that voltage to verify whether or not the transient current becomes negligible after a brief interval of ca. 150 s. If an almost stationary (faradaic) current is confirmed, the voltage window is reduced in small voltage steps until a negligible background current is obtained. In addition, the impedance spectra were recorded at different d.c. voltages and were used to discriminate the correct capacitive voltage window in the absence of water-splitting, i.e., the almost-vertical straight line verified in the complex-plane plot at low frequencies for pure capacitive behavior becomes a poorly developed semicircle in the presence of water electrolysis due to the charge-transfer resistance occurring in parallel to the electrical double-layer capacitance.
Cyclic voltammetry (CV), galvanostatic charge–discharge (GCD), single-step chronoamperometry (SSC), and electrochemical impedance spectroscopy (EIS) experiments were accomplished using a model BCS-810 cycler instrument from Bio-logic Science Instruments®. For the different fixed (d.c.) voltages, the EIS findings were registered for the frequency range of 10 kHz to 10 mHz by applying a small sinusoidal signal of 10 mV (peak-to-peak) to ensure linearity on the impedance response.
After the correct determination of the WVW as mentioned above, CV and GCD experiments were performed at more realistic dynamic conditions of 100 mV s−1 and 1.0 A g−1, respectively, to evaluate the carbon-based symmetric coin cell's overall performance. Cyclability tests were performed in the best samples for 1 million cycles at 2 A g−1.
3. Results and discussion
3.1. Materials characterization
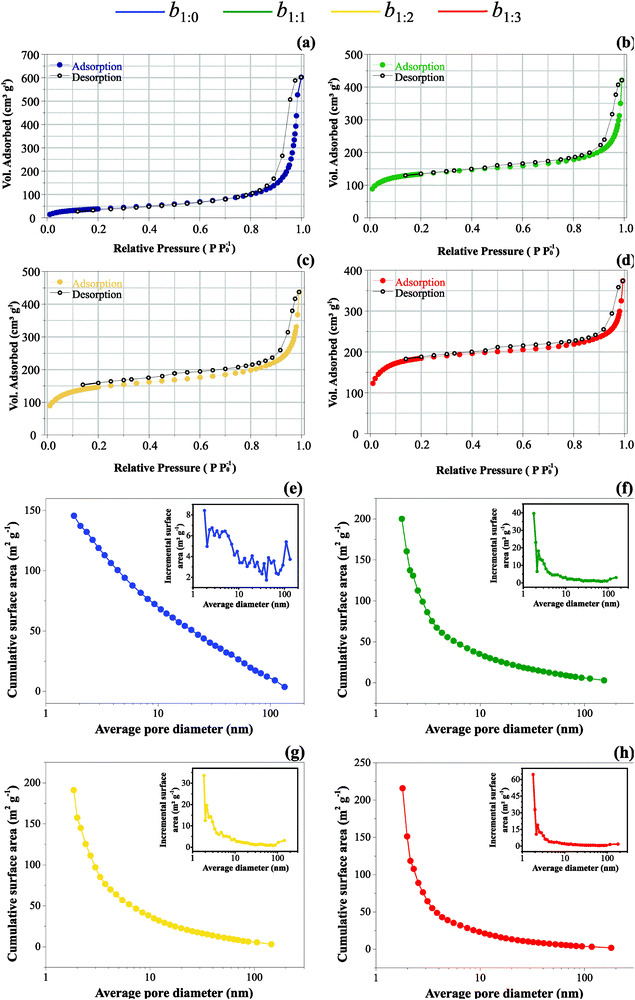
Fig. 1 shows the SEM micrographs of the buckypaper samples. According to Fig. 1(a), one can see the alteration of the material's morphology upon increasing the AC mass ratio. As a template, Fig. 1(a–d) depicts the buckypaper synthesized using only MWCNT (b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). The illustrated morphology of the b1
0). The illustrated morphology of the b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sample conveys the advantage of the MWCNTs entangled a spaghetti-like distribution, which provides a freestanding, mechanically robust, and flexible carbon sheet. MWCNTs presented diameters ranging from 20 to 40 nm and an average length of 40 μm in the SEM micrographs (Fig. 1(d)). Analogously, by increasing the AC mass ratio, a morphology with more flakes is evident, as shown in Fig. 1(e–p). It is worth noting that the sample with the highest AC mass ratio (b1
0 sample conveys the advantage of the MWCNTs entangled a spaghetti-like distribution, which provides a freestanding, mechanically robust, and flexible carbon sheet. MWCNTs presented diameters ranging from 20 to 40 nm and an average length of 40 μm in the SEM micrographs (Fig. 1(d)). Analogously, by increasing the AC mass ratio, a morphology with more flakes is evident, as shown in Fig. 1(e–p). It is worth noting that the sample with the highest AC mass ratio (b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) corresponds to the freestanding material that still has remarkable mechanical properties. According to Fig. 1(m–p), in the case of the b1
3) corresponds to the freestanding material that still has remarkable mechanical properties. According to Fig. 1(m–p), in the case of the b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 sample, one can observe that AC is homogeneously dispersed throughout the sample. In contrast, the MWCNT is in contact with the AC flakes, thus creating a highly conducting network. As a result, this material sample is expected to provide good electron transport during the rapid charge–discharge processes (please see further discussion).
3 sample, one can observe that AC is homogeneously dispersed throughout the sample. In contrast, the MWCNT is in contact with the AC flakes, thus creating a highly conducting network. As a result, this material sample is expected to provide good electron transport during the rapid charge–discharge processes (please see further discussion).
 | ||
Fig. 1 SEM micrographs of the different buckypaper samples: (a–d) b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, (e–h) b1 0, (e–h) b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (i–l) b1 1, (i–l) b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and (m–p), b1 2, and (m–p), b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. 3. | ||
Fig. 2(a and b) shows structural micrographs of the MWCNT and AC samples, respectively. TEM confirms that MWCNTs have diameters ranging from 20 to 30 nm with turbostratic structure and negligible internal pores i.e., close caps (Please see detail in hand left size of tube Fig. 2(a) or Fig. 2(h) in ref. 50 for instance). At the same time, according to the different contrasts in the images, the AC sample showed a not well crystalline material with macro- (>50 nm), meso- (2–50 nm), and micro-pores (<2 nm) indicated with green, yellow and blue colors respectively.
 | ||
| Fig. 2 TEM images obtained from the (a) MWCNT and (b) AC carbon materials. We highlighted an example of the AC macropore in green, mesopores in yellow and micropores in blue. | ||
Raman spectroscopy was used to investigate the chemical and structural properties of the carbon-based samples. The findings are shown in Fig. 3(a–d). Based on signal deconvolution of the MWCNT spectrum presented in Fig. 3(b), the findings showed the prominent D, G, D′, and 2D bands at 1326 cm−1, 1580 cm−1, 1612 cm−1, and 2649 cm−1, respectively. Besides, two less intense peaks at ∼1139 cm−1 (D*) and ∼1477 cm−1 (D#) were also observed. The AC Raman spectrum that is presented in Fig. 3(c) showed two main D and G peaks at 1321 cm−1 and 1600 cm−1, respectively. Three less intense peaks denoted as D* (1171 cm−1), D# (1506 cm−1), and 2D (2649 cm−1) were also verified for the AC sample. Please note that G ranges from 1580 to 1600 cm−1, D* ranges from 1139 to 1171 cm−1 and D# ranges from 1477 to 1506 cm−1 for the different carbon forms. All this discrepancy of band position is related to the crystallinity of the materials. Our analysis revealed that the Raman spectrum of the composite samples containing MWCNTs and AC is comprised of the materials’ individual responses.
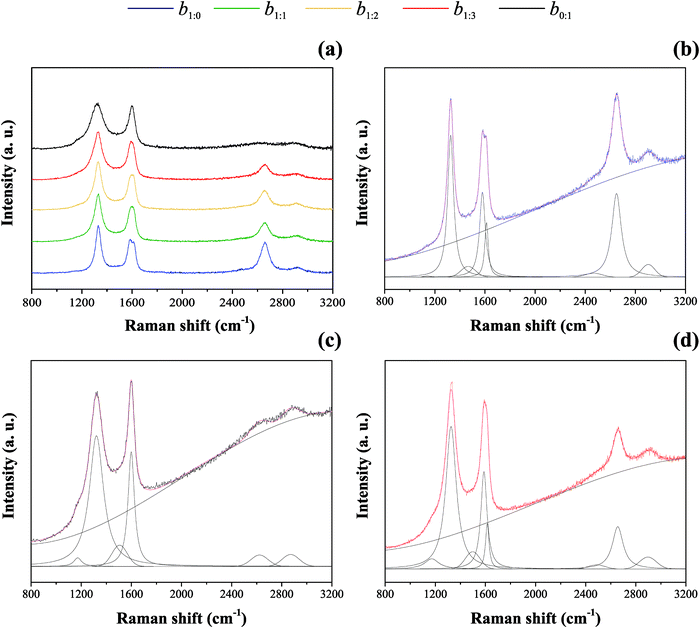 | ||
Fig. 3 Raman spectra of the carbon-based composites (a) and the individual components ((b) MWCNT and (c) AC). The b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 composite is also shown in (d). 3 composite is also shown in (d). | ||
The G-band, also reported as E2g, is centered in 1582–1600 cm−1. This band is originated by the double degenerate vibrational modes of the iLO and iTO phonon branches, crossing at the Γ point in the first Brillouin zone, according to the theoretical band model proposed for graphene materials.52–54 On the other hand, the D-band corresponds to the high-frequency E2g phonon at the Γ point. In this case, the band appearance requires a defect for its activation to account for the breathing modes of the six-atom rings exhibited by the graphene layers.55 These structural defects are generally concentrated at the crystallite edges or boundaries.56,57 Again, the D-band appears when the lattice vibration (Raman-inactive modes) presents a symmetry-breaking defect, affecting the selection rules (q = 0). The D-band is from double resonant LO phonons.55 It is dispersive with excitation wavelength due to the Kohn anomaly around the K point, i.e., its position depends on the laser excitation wavelength. The D* band is related to amorphous-like carbons (e.g., defect-rich short carbon layers). The D# band is assigned to oxygen functional groups on the carbon surface such as C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and COO− as reported by us elsewhere.58–62 Therefore, we refer to D# as the carbon with functional oxygen group band, CfO. The 2D-band is a harmonic of the D signal, but it does not need a defect to be active, which means that a phonon is not scattered during the double resonance process.63
O, and COO− as reported by us elsewhere.58–62 Therefore, we refer to D# as the carbon with functional oxygen group band, CfO. The 2D-band is a harmonic of the D signal, but it does not need a defect to be active, which means that a phonon is not scattered during the double resonance process.63
Table 3 gathers the dependence of the relative intensities of the Raman bands as a function of the AC mass ratio used in the buckypaper samples.
| Sample | Relative intensity of Raman bands | ||||
|---|---|---|---|---|---|
| (IG/ID) | (ID′/ID) | (I2D/ID) | (ICfO/IG) | (ICfO)/ID | |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
0.63 | 0.44 | 0.64 | 0.12 | 0.07 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.61 | 0.43 | 0.4 | 0.20 | 0.12 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
0.6 | 0.42 | 0.39 | 0.17 | 0.10 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
0.45 | 0.32 | 0.3 | 0.18 | 0.12 |
Table 3 shows IG/ID, ID′/ID, I2D/ID, ICfO/IG, and ICfO/ID intensity ratios. With AC incorporation, the IG/ID and I2D/ID values decrease, suggesting that the carbon composite loses crystallinity, which agrees with the TEM data. To support this claim, Fig. S1 (ESI†) shows the X-ray diffraction pattern of carbon materials. The set of peaks correspond to the crystalline phases of carbon, the well-organized graphene hexagonal structuring of the space group P63/mmc (PDF# 01-089-7213);64 the two peaks can be indexed as the lattice planes (002) and (101) in 26.5° and 44.5° as 2θ, respectively. It is evident that with AC incorporation, those peaks broaden like a band. We also observe that the ICfO and ID or IG ratio intensity increases by adding AC, suggesting that oxygen functional groups are essential to improve the wettability of the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC electrode at first cycles. The introduction of AC also promotes improvement regarding the specific surface area due to its highly porous characteristics. Therefore, an excellent experimental strategy involves the right balance between the intrinsic properties of the individual carbon materials used in the composite samples. From these considerations, BET analyses were carried out for the different samples. The isotherms are presented in Fig. 4, while Table 4 gathers the specific surface area values.
AC electrode at first cycles. The introduction of AC also promotes improvement regarding the specific surface area due to its highly porous characteristics. Therefore, an excellent experimental strategy involves the right balance between the intrinsic properties of the individual carbon materials used in the composite samples. From these considerations, BET analyses were carried out for the different samples. The isotherms are presented in Fig. 4, while Table 4 gathers the specific surface area values.
| Sample | b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
b0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|---|---|---|---|---|---|
| SSA/m2 g−1 | 147 | 718 | 988 | 1117 | 1692 |
Fig. 4(a–d) presents the isotherms of the adsorbed volume of N2 as a function of the relative pressure (P P0−1). The large adsorbed volumes are typical of meso- and micro-pore materials. As can be seen, the data in Table 4 indicate that SSA is scaled to the high AC mass ratio due to the influence of the micropores. This proposal is sustained by the pronounced slope verified in the BET plots at low relative pressures (please see point B of Fig. 2(II) in ref. 65).
As one may see in Fig. 4(e and f), the MWCNT buckypaper has mesopores predominantly with an almost homogeneous distribution from 1 nm to 100 nm, i.e., the accumulative surface area with pore distribution is almost a straight-line (please see Fig. 4(e)). Fig. 4(f–h) shows that the incorporation of activated carbon in the buckypaper changes the uniform pores-size distribution scenario, and one may observe an exponential decay of the pores size contribution concerning the accumulative surface area. The main reason is that activated carbon has mainly micropores which make a higher contribution to the surface area i.e., micropores and smaller size mesopores contribute more to the accumulative surface area, and with AC incorporation, they are more present in these samples.
3.2. Electrochemical characterization of the composite buckypaper electrodes
Fig. 5(a–f) presents the effect of the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
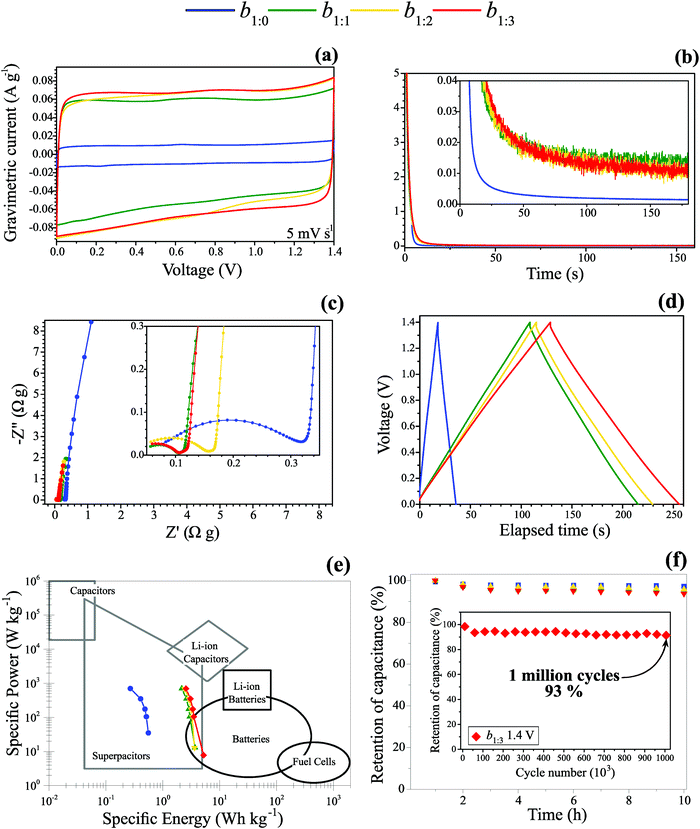
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC mass ratio on the electrochemical behavior of the buckypaper electrodes. The electrochemical findings were obtained using a symmetric coin cell filled with 1.0 mol dm−3 Li2SO4 aqueous solutions. Fig. 5(a) reveals the value of 1.4 V for the working voltage window (WVW) determined using a low scan rate of 5 mV s−1 to ensure the absence of the parasitic water-splitting reaction during the capacitive process (please see the data in Table S1, ESI†). We performed additional experiments using the SSC technique to hold the maximum cell voltage referring to the WVW while the corresponding current transient was measured. This procedure allowed us to discriminate the physicochemical origin of the background/residual current. While a capacitive current must fade away after a brief time interval, the presence of a faradaic current due to water-splitting results in a current plateau according to Faraday's law of electrolysis. It is worth noting that the use of high scan rates (e.g., ∼50–100 mV s−1) is not appropriate for WVW determination since, due to its irreversible kinetics, the water decomposition reaction can be not clearly identified by a ‘current tail’ in the CV profiles, thus leading to unsatisfactory results. Therefore, low scan rates are mandatory for the correct determination of the capacitive voltage range in the SCs. Unfortunately, these precautions are not considered in several literature reports, resulting in very high (incorrect) WVW values.
AC mass ratio on the electrochemical behavior of the buckypaper electrodes. The electrochemical findings were obtained using a symmetric coin cell filled with 1.0 mol dm−3 Li2SO4 aqueous solutions. Fig. 5(a) reveals the value of 1.4 V for the working voltage window (WVW) determined using a low scan rate of 5 mV s−1 to ensure the absence of the parasitic water-splitting reaction during the capacitive process (please see the data in Table S1, ESI†). We performed additional experiments using the SSC technique to hold the maximum cell voltage referring to the WVW while the corresponding current transient was measured. This procedure allowed us to discriminate the physicochemical origin of the background/residual current. While a capacitive current must fade away after a brief time interval, the presence of a faradaic current due to water-splitting results in a current plateau according to Faraday's law of electrolysis. It is worth noting that the use of high scan rates (e.g., ∼50–100 mV s−1) is not appropriate for WVW determination since, due to its irreversible kinetics, the water decomposition reaction can be not clearly identified by a ‘current tail’ in the CV profiles, thus leading to unsatisfactory results. Therefore, low scan rates are mandatory for the correct determination of the capacitive voltage range in the SCs. Unfortunately, these precautions are not considered in several literature reports, resulting in very high (incorrect) WVW values.
From these considerations, we adopted in the present work a set of experiments using the CV, SSC, and EIS techniques to determine the WVW (please see the Experimental section). Almost the same residual (background) current after 25 s was generally verified for the range of voltages applied using the SSC technique (please see Fig. 5b and Fig. S2–S6, ESI†). From the theoretical viewpoint, after applying a step-voltage function, the transient (capacitive) current must obey the relationship I = I0 × exp(−t/τ), where I0 is the initial current at t = 0 and τ is the system's time constant. Thus, when the I/I0 ratio is inferior to 0.01, representing a 99% decrease in the measured current, one can assert that the capacitive current is practically negligible for the corresponding time interval. Therefore, the resulting ‘almost stationary’ current measured for the interval (e.g., t ≥ 25 s, depending on the intrinsic capacitance and resistance) in the SSC experiment is only due to the parasitic water-splitting reaction. In this sense, the behavior of the transient response forms a rigorous criterion for the correct identification of the capacitive voltage window in SCs.
The SSC experimental findings showed in Fig. 5b corroborate the nearly perfect rectangular mirror-like voltammetric profiles expected for EDLCs (please see Fig. 5a). The almost vertical straight lines verified in the low-frequency range of the complex-plane plots (see Fig. 5c) and the almost perfect triangular GCD profiles comprise the behavior theoretically predicted for real EDLCs (see Fig. 5d). GCD data at different current densities were also performed and the corresponding findings are presented in Fig. S2 (ESI†).
Regarding the EIS findings, it is worth mentioning that a small semicircle in the high-frequency range is due to the ‘distributed capacitance’ phenomenon originating from the electrochemically active narrow pores. Unfortunately, this well-known porous impedance behavior is commonly misinterpreted as being caused by false mass-transport limitations and unrealistic ohmic contacts between the electrode/current collector solid interface. According to the robust theoretical EIS model proposed by Bisquert et al.,66 the impedance behavior verified in Fig. 5c indicates an anomalous charge transport in the solid and liquid phases in intimate contact caused by the porous nature of the electrode material. In these cases, the central information for SCs can be extracted from the low-frequency response that yields the electrical double-layer capacitance (Cedl) and the high-frequency limit (e.g., 10 kHz) where the ESR value is accurately determined.
It was verified that the substitution of MWCNTs by the AC particles does not affect the WVW of 1.4 V observed for the buckypaper electrodes. Since this value is higher than the 1.23 V, i.e., the theoretical prediction according to thermodynamics under ‘standard conditions’ (e.g., p(O2) and p(H2) partial pressures of 1.0 bar), we can assert from the kinetic viewpoint that the carbon materials used in the buckypaper electrodes exhibited high overpotentials (e.g., electrochemical activation energies) for the water-splitting reaction. We also observed that the incorporation of AC particles in the buckypaper electrodes increases the specific capacitance (please see Table 5). This was verified by large increases of ∼50% and 75% for the b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and b1
1 and b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 electrodes, respectively. Importantly, for AC loadings higher than 75%, the buckypaper neither forms nor maintains its good mechanical characteristics such as freestanding and flexible properties.
3 electrodes, respectively. Importantly, for AC loadings higher than 75%, the buckypaper neither forms nor maintains its good mechanical characteristics such as freestanding and flexible properties.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC mass ratio on the specific capacitance (SC) of the buckypaper electrodes
AC mass ratio on the specific capacitance (SC) of the buckypaper electrodes
| Sample | SC (F g−1) |
|---|---|
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
7.6 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
44.0 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
48.2 |
b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
51.7 |
Considering that the b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 electrode has the highest specific capacitance and the maximum specific surface area (SSA) (please see Fig. 4 and Table 4), we can propose that the charge-storage process roughly scales with the SSA. In this sense, considering as a benchmark for common carbon-based electrodes an areal capacitance of 5 μF cm−2 (or 0.05 F m−2),67 we found for our data a corresponding specific capacitance of ∼50 F g−1 for the b1
3 electrode has the highest specific capacitance and the maximum specific surface area (SSA) (please see Fig. 4 and Table 4), we can propose that the charge-storage process roughly scales with the SSA. In this sense, considering as a benchmark for common carbon-based electrodes an areal capacitance of 5 μF cm−2 (or 0.05 F m−2),67 we found for our data a corresponding specific capacitance of ∼50 F g−1 for the b1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 electrode. After normalizing the pertinent quantity (e.g., 50 F g−1/0.05 F m−2), one obtains an SSA value of 1000 m2 g−1. Supported by the BET analysis (SSA measurements), this calculation indicates that almost the entire specific surface area of 1117 m2 g−1 of the porous carbon-based electrode is electrochemically active charge-storage process. From the theoretical viewpoint, these findings support the presence of accessible narrow pores interconnected with the meso- and macro-pores that provide the ionic species for the rapid charge–discharge processes.
3 electrode. After normalizing the pertinent quantity (e.g., 50 F g−1/0.05 F m−2), one obtains an SSA value of 1000 m2 g−1. Supported by the BET analysis (SSA measurements), this calculation indicates that almost the entire specific surface area of 1117 m2 g−1 of the porous carbon-based electrode is electrochemically active charge-storage process. From the theoretical viewpoint, these findings support the presence of accessible narrow pores interconnected with the meso- and macro-pores that provide the ionic species for the rapid charge–discharge processes.
Table 5 gathers the specific capacitance determined from the GCD data. The ESR values for the different samples remained in the range of 140 ± 40 mΩ g. In all cases, the capacitance data correspond to an applied specific current of 0.15 A g−1.
The Ragone plot is presented in Fig. 5(e), showing that the incorporation of activated carbon into MWCNT buckypaper electrodes improves the energy density of the devices considerably. Also, it is essential to check the capacitance retention after several cycles. To exclude any doubt from the scientific community and our curiosity, we check the capacitance retention after 1 million cycles with a GCD technique at 2.0 A g−1 for our best composite (other samples were not tested because the test took 100 days to be completed) at a working voltage window of 1.4 V. Fig. 5(f) shows that the high coulombic efficiency of about 93% is incredibly good, evidence that the energy storage process here is mainly electrostatic.
In spite of everything, there is a significant concern regarding the use of self-supported electrode materials, which are great for fundamental science but useless in terms of scalability. The main issue concerns welding freestanding carbon materials, making it difficult to associate them in series or parallel. In this sense, we developed a particular welding process to overcome these constraints and that is presented in Fig. 6. First, we separated several buckypaper strips and aligned them face-to-face. A Ni tab is on both the bottom and top sides of one tip of the buckypaper strips, and with a spot welder, we welded the robust material several times i.e., dots at the Ni tabs. The electric contact between the tabs and buckypaper is excellent, showing metallic continuity i.e., 0 Ω.
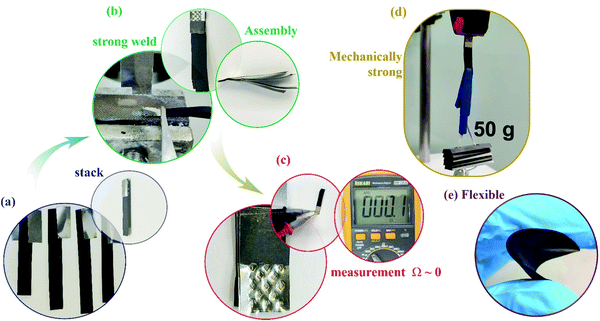 | ||
| Fig. 6 Four steps for welding buckypapers: (a) stacking, (b) welding, (c) measuring the electric contact, and (d) evaluation of the mechanical robustness, showing (e) the flexible material. | ||
4. Conclusions
We reported the synthesis of binder-free, self-supported, and flexible high-surface-area buckypaper electrodes composed of mixtures containing activated carbon (AC) and multi-walled carbon nanotubes (MWCNTs). Our innovative electrode synthesis avoided corrosion issues regarding the current collector. We carried out a robust welding technology capable of providing secure and facile fastening of metallic connectors to the freestanding electrode with very high electronic contact. The Raman study revealed that the chemical properties of the MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC composite is due to both species, confirming a reduction of crystallinity and insertion of oxygen functional groups. The AC particles provided a large specific surface area while the MWCNTs introduced several alternative electron transport pathways. The porous electrode structure was composed of homogeneously dispersed AC particles where the MWCNT is entangled with the AC flake-like structures. The use of self-supported electrodes permitted an increase of the capacitance from 7.6 to 51.7 F g−1, which is very close to the carbon material's theoretical limit considering 5 μF cm−2 of several carbon materials. The buckypaper electrode containing an MWCNT
AC composite is due to both species, confirming a reduction of crystallinity and insertion of oxygen functional groups. The AC particles provided a large specific surface area while the MWCNTs introduced several alternative electron transport pathways. The porous electrode structure was composed of homogeneously dispersed AC particles where the MWCNT is entangled with the AC flake-like structures. The use of self-supported electrodes permitted an increase of the capacitance from 7.6 to 51.7 F g−1, which is very close to the carbon material's theoretical limit considering 5 μF cm−2 of several carbon materials. The buckypaper electrode containing an MWCNT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AC ratio of 1
AC ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 exhibited the best conditions for the charge-storage process, due to its higher surface area. A high working voltage window (WVW) of 1.4 V was obtained in an aqueous electrolyte in the total absence of the water-splitting reaction. The complementary use of chronoamperometry and impedance techniques in addition to cyclic voltammetry seems to be mandatory for the correct identification of the WVW.
3 exhibited the best conditions for the charge-storage process, due to its higher surface area. A high working voltage window (WVW) of 1.4 V was obtained in an aqueous electrolyte in the total absence of the water-splitting reaction. The complementary use of chronoamperometry and impedance techniques in addition to cyclic voltammetry seems to be mandatory for the correct identification of the WVW.
It was verified that for AC loadings higher than 75%, the buckypaper neither forms nor maintains its good mechanical characteristics (e.g., freestanding and flexible properties). The theoretical analysis indicated that almost the entire specific surface area of the buckypaper electrode is electrochemically active during the charge-storage process, which is one great advantage of binder-free systems. The very high electrode stability was verified with 93% capacitance retention after one million charge–discharge cycles. In general, the composite buckypaper electrode material reported in this work is a promising candidate for several different technological applications involving aqueous-based supercapacitors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very grateful to LNNano/CNPEM for support with the SEM analysis and to the financial support from the Brazilian funding agencies CNPq(301486/2016-6) and FAPESP (2014/02163-7, 2017/11958-1, 2018/20756-6). LM Da Silva wishes to thank FAPEMIG (Financial support for the LMMA/UFVJM Laboratory) and CNPq (PQ-2 grant: Process 301095/2018-3). The authors gratefully acknowledge the support from Shell and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas, and Biofuels Agency) through the R&D levy regulation.References
- C. Merlet, B. Rotenberg, P. A. Madden, P. L. Taberna, P. Simon and Y. Gogotsi, et al., On the molecular origin of supercapacitance in nanoporous carbon electrodes, Nat. Mater., 2012, 11(4), 306–310 Search PubMed.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P. L. Taberna and C. P. Grey, et al., Efficient storage mechanisms for building better supercapacitors, Nat. Energy, 2016, 1(6), 16070 Search PubMed.
- P. Simon and Y. Gogotsi, Materials for electrochemical capacitors, Nat. Mater., 2008, 7(11), 845–854 Search PubMed.
- H. Helmholtz, Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern, mit Anwendung auf die thierisch-elektrischen Versuche (Schluss.), Ann. Phys., 1853, 165(7), 353–377 Search PubMed.
- B. Lobato, L. Suárez, L. Guardia and T. A. Centeno, Capacitance and surface of carbons in supercapacitors, Carbon, 2017, 122, 434–445 Search PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Anomalous increase in Carbon at pore sizes less than 1 nanometer, Science, 2006, 313(5794), 1760–1763 Search PubMed.
- H. Shao, Y.-C. Wu, Z. Lin, P.-L. Taberna and P. Simon, Nanoporous carbon for electrochemical capacitive energy storage, Chem. Soc. Rev., 2020, 3005–3039 Search PubMed.
- L. L. Zhang and X. S. Zhao, Carbon-based materials as supercapacitor electrodes, Chem. Soc. Rev., 2009, 38(9), 2520–2531 Search PubMed.
- L. A. Malley, G. L. Kennedy, G. S. Elliott, T. W. Slone, W. Mellert and K. Deckardt, et al., Chronic Toxicity and Oncogenicity of N-Methylpyrrolidone (Nmp) in Rats and Mice by Dietary Administration, Drug Chem. Toxicol., 2001, 24(4), 315–338 Search PubMed.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, A review of electrolyte materials and compositions for electrochemical supercapacitors, Chem. Soc. Rev., 2015, 44(21), 7484–7539 Search PubMed.
- C. Arbizzani, S. Beninati, M. Lazzari, F. Soavi and M. Mastragostino, Electrode materials for ionic liquid-based supercapacitors, 13th Int. Meet Lithium Batter, 2007, 174(2), 648–652 Search PubMed.
- Z. Li, J. Liu, K. Jiang and T. Thundat, Carbonized nanocellulose sustainably boosts the performance of activated Carbon in ionic liquid supercapacitors, Nano Energy, 2016, 25, 161–169 Search PubMed.
- K. L. Van Aken, M. Beidaghi and Y. Gogotsi, Formulation of Ionic-Liquid Electrolyte To Expand the Voltage Window of Supercapacitors, Angew. Chem., Int. Ed., 2015, 54(16), 4806–4809 Search PubMed.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Carbons and Electrolytes for Advanced Supercapacitors, Adv. Mater., 2014, 26(14), 2219–2251 Search PubMed.
- N. Jung, S. Kwon, D. Lee, D.-M. Yoon, Y. M. Park and A. Benayad, et al., Synthesis of Chemically Bonded Graphene/Carbon Nanotube Composites and their Application in Large Volumetric Capacitance Supercapacitors, Adv. Mater., 2013, 25(47), 6854–6858 Search PubMed.
- R. Francke, D. Cericola, R. Kötz, D. Weingarth and S. R. Waldvogel, Novel electrolytes for electrochemical double layer capacitors based on 1,1,1,3,3,3-hexafluoropropan-2-ol, Electrochim. Acta, 2012, 62, 372–380 Search PubMed.
- Z.-S. Wu, W. Ren, D.-W. Wang, F. Li, B. Liu and H.-M. Cheng, High-Energy MnO2 Nanowire/Graphene and Graphene Asymmetric Electrochemical Capacitors, ACS Nano, 2010, 4(10), 5835–5842 Search PubMed.
- C. Portet, G. Yushin and Y. Gogotsi, Electrochemical performance of carbon onions, nanodiamonds, carbon black and multi-walled nanotubes in electrical double layer capacitors, Carbon, 2007, 45(13), 2511–2518 Search PubMed.
- J. Ge, G. Cheng and L. Chen, Transparent and flexible electrodes and supercapacitors using polyaniline/single-walled carbon nanotube composite thin films, Nanoscale, 2011, 3(8), 3084–3088 Search PubMed.
- J. Yu, W. Lu, S. Pei, K. Gong, L. Wang and L. Meng, et al., Omnidirectionally Stretchable High-Performance Supercapacitor Based on Isotropic Buckled Carbon Nanotube Films, ACS Nano, 2016, 10(5), 5204–5211 Search PubMed.
- D. Yu and L. Dai, Self-Assembled Graphene/Carbon Nanotube Hybrid Films for Supercapacitors, J. Phys. Chem. Lett., 2010, 1(2), 467–470 Search PubMed.
- Y. S. Yun, H. H. Park and H.-J. Jin, Pseudocapacitive effects of N-doped carbon nanotube electrodes in supercapacitors, Materials, 2012, 5(7), 1258–1266 Search PubMed.
- M. Kaempgen, C. K. Chan, J. Ma, Y. Cui and G. Gruner, Printable Thin Film Supercapacitors Using Single-Walled Carbon Nanotubes, Nano Lett., 2009, 9(5), 1872–1876 Search PubMed.
- N. Díez, C. Botas, R. Mysyk, E. Goikolea, T. Rojo and D. Carriazo, Highly packed graphene–CNT films as electrodes for aqueous supercapacitors with high volumetric performance, J. Mater. Chem. A, 2018, 6(8), 3667–3673 Search PubMed.
- X. Li, Y. Tang, J. Song, W. Yang, M. Wang and C. Zhu, et al., Self-supporting activated carbon/carbon nanotube/reduced graphene oxide flexible electrode for high performance supercapacitor, Carbon, 2018, 129, 236–244 Search PubMed.
- Y. Chang, L. Zhou, Z. Xiao, J. Liang, D. Kong and Z. Li, et al., Embedding Reduced Graphene Oxide in Bacterial Cellulose-Derived Carbon Nanofibril Networks for Supercapacitors, ChemElectroChem, 2017, 4(10), 2448–2452 Search PubMed.
- R. Berenguer, F. J. García-Mateos, R. Ruiz-Rosas, D. Cazorla-Amorós, E. Morallón and J. Rodríguez-Mirasol, et al., Biomass-derived binderless fibrous carbon electrodes for ultrafast energy storage, Green Chem., 2016, 18(6), 1506–1515 Search PubMed.
- S. Hu, S. Zhang, N. Pan and Y.-L. Hsieh, High energy density supercapacitors from lignin derived submicron activated carbon fibers in aqueous electrolytes, J. Power Sources, 2014, 270, 106–112 Search PubMed.
- S. Zhu, P.-L. Taberna, N. Zhao and P. Simon, Salt-template synthesis of mesoporous carbon monolith for ionogel-based supercapacitors, Electrochem. Commun., 2018, 96, 6–10 Search PubMed.
- L. Wei, N. Nitta and G. Yushin, Lithographically Patterned Thin Activated Carbon Films as a New Technology Platform for On-Chip Devices, ACS Nano, 2013, 7(8), 6498–6506 Search PubMed.
- T. Purkait, G. Singh, M. Singh, D. Kumar and R. S. Dey, Large area few-layer graphene with scalable preparation from waste biomass for high-performance supercapacitor, Sci. Rep., 2017, 7(1), 15239 Search PubMed.
- Y. Li, Q. Zhang, J. Zhang, L. Jin, X. Zhao and T. Xu, A top-down approach for fabricating freestanding bio-carbon supercapacitor electrodes with a hierarchical structure, Sci. Rep., 2015, 5(1), 14155 Search PubMed.
- L. Deng, Y. Gu, Y. Gao, Z. Ma and G. Fan, Carbon nanotubes/holey graphene hybrid film as binder-free electrode for flexible supercapacitors, J. Colloid Interface Sci., 2017, 494, 355–362 Search PubMed.
- Y. Zhang, H. Gao, X. Song, X. Kong and H. Xu, Preparation of Hierarchical Porous Carbon from Wheat Bran for Free-Standing Electrode of High Areal Capacitance Supercapacitor, ChemElectroChem, 2019, 6(21), 5486–5491 Search PubMed.
- P. Xu, T. Gu, Z. Cao, B. Wei, J. Yu and F. Li, et al., Carbon Nanotube Fiber Based Stretchable Wire-Shaped Supercapacitors, Adv. Energy Mater., 2014, 4(3), 1300759 Search PubMed.
- X. Yang, J. Zhu, L. Qiu and D. Li, Bioinspired Effective Prevention of Restacking in Multilayered Graphene Films: Towards the Next Generation of High-Performance Supercapacitors, Adv. Mater., 2011, 23(25), 2833–2838 Search PubMed.
- Q. Wang, J. Yan, Y. Wang, T. Wei, M. Zhang and X. Jing, et al., Three-dimensional flower-like and hierarchical porous carbon materials as high-rate performance electrodes for supercapacitors, Carbon, 2014, 67, 119–127 Search PubMed.
- M. F. El-Kady, V. Strong, S. Dubin and R. B. Kaner, Laser Scribing of High-Performance and Flexible Graphene-Based Electrochemical Capacitors, Science, 2012, 335(6074), 1326 Search PubMed.
- M. F. El-Kady, Y. Shao and R. B. Kaner, Graphene for batteries, supercapacitors and beyond, Nat. Rev. Mater., 2016, 1(7), 16033 Search PubMed.
- D. Li, M. B. Müller, S. Gilje, R. B. Kaner and G. G. Wallace, Processable aqueous dispersions of graphene nanosheets, Nat. Nanotechnol., 2008, 3(2), 101–105 Search PubMed.
- H. Sun, J. Zhu, D. Baumann, L. Peng, Y. Xu and I. Shakir, et al., Hierarchical 3D electrodes for electrochemical energy storage, Nat. Rev. Mater., 2019, 4(1), 45–60 Search PubMed.
- Z. Yang, J. Tian, Z. Yin, C. Cui, W. Qian and F. Wei, Carbon nanotube- and graphene-based nanomaterials and applications in high-voltage supercapacitor: A review, Carbon, 2019, 141, 467–480 Search PubMed.
- E. D. Walsh, X. Han, S. D. Lacey, J.-W. Kim, J. W. Connell and L. Hu, et al., Dry-Processed, Binder-Free Holey Graphene Electrodes for Supercapacitors with Ultrahigh Areal Loadings, ACS Appl. Mater. Interfaces, 2016, 8(43), 29478–29485 Search PubMed.
- B. E. Conway Electrochemical supercapacitors: scientific fundamentals and technological applications, Springer Science & Business Media, 2013 Search PubMed.
- M. J. Loveridge, G. Remy, N. Kourra, R. Genieser, A. Barai and M. J. Lain, et al., Looking deeper into the Galaxy (Note 7), Batteries, 2018, 4(1), 3 Search PubMed.
- L. Demarconnay, E. Raymundo-Piñero and F. Béguin, A symmetric carbon/carbon supercapacitor operating at 1.6V by using a neutral aqueous solution, Electrochem. Commun., 2010, 12(10), 1275–1278 Search PubMed.
- M. D. Stoller and R. S. Ruoff, Best practice methods for determining an electrode material's performance for ultracapacitors, Energy Environ. Sci., 2010, 3(9), 1294–1301 Search PubMed.
- Y. Gogotsi and P. Simon, True Performance Metrics in Electrochemical Energy Storage, Science, 2011, 334(6058), 917 Search PubMed.
- C. Peng, X. Yan, R. Wang, J. Lang, Y. Ou and Q. Xue, Promising activated carbons derived from waste tea-leaves and their application in high performance supercapacitors electrodes, Electrochim. Acta, 2013, 87, 401–408 Search PubMed.
- R. Vicentini, D. M. Soares, W. Nunes, B. Freitas, L. Costa and L. M. Da Silva, et al., Core-niobium pentoxide carbon-shell nanoparticles decorating multi-walled carbon nanotubes as electrode for electrochemical capacitors, J. Power Sources, 2019, 434 Search PubMed.
- W. G. Nunes, B. M. Pires, F. E. De Oliveira, A. M. de Marque, L. F. Cremasco and R. Vicentini, et al., Study of the aging process of nanostructured porous carbon-based electrodes in electrochemical capacitors filled with aqueous or organic electrolytes, J. Energy Storage, 2020, 28(December 2019), 101249 Search PubMed.
- L. M. Aleixo, Voltametria: conceitos e técnicas, Rev. Chemkeys, 2018, 3, 1–21 Search PubMed.
- S. Reich and C. Thomsen, Raman spectroscopy of graphite, Philos. Trans. R. Soc., A, 2004, 362(1824), 2271–2288 Search PubMed.
- R. Vicentini, L. M. Da Silva, D. V. Franco, W. Nunes, J. Fiates and G. Doubek, et al., Raman probing carbon & aqueous electrolytes interfaces and molecular dynamics simulations towards understanding electrochemical properties under polarization conditions in supercapacitors, J. Energy Chem., 2021, 60, 279–292 Search PubMed.
- A. C. Ferrari and D. M. Basko, Raman spectroscopy as a versatile tool for studying the properties of graphene, Nat. Nanotechnol., 2013, 8(4), 235–246 Search PubMed.
- A. C. Ferrari, Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects, Solid State Commun., 2007, 143(1–2), 47–57 Search PubMed.
- K. N. Kudin, B. Ozbas, H. C. Schniepp, R. K. Prud’homme, I. A. Aksay and R. Car, Raman spectra of graphite oxide and functionalized graphene sheets, Nano Lett., 2008, 8(1), 36–41 Search PubMed.
- T. A. Silva, H. Zanin, E. Saito, R. A. Medeiros, F. C. Vicentini and E. J. Corat, et al., Electrochemical behaviour of vertically aligned carbon nanotubes and graphene oxide nanocomposite as electrode material, Electrochim. Acta, 2014, 119, 114–119 Search PubMed.
- A. O. Lobo, S. C. Ramos, E. F. Antunes, F. R. Marciano, V. J. Trava-Airoldi and E. J. Corat, Fast functionalization of vertically aligned multi-walled carbon nanotubes using oxygen plasma, Mater. Lett., 2012, 70, 89–93 Search PubMed.
- H. Zanin, C. M. R. Rosa, N. Eliaz, P. W. May, F. R. Marciano and A. O. Lobo, Assisted deposition of nano-hydroxyapatite onto exfoliated carbon nanotube oxide scaffolds, Nanoscale, 2015, 7(22), 10218–10232 Search PubMed.
- M. A. V. M. Grinet, H. Zanin, A. E. Campos Granato, M. Porcionatto, F. R. Marciano and A. O. Lobo, Fast preparation of freestanding nanohydroxyapatite-vertically aligned carbon nanotube scaffolds, J. Mater. Chem. B, 2014, 2(9), 1196–1204 Search PubMed.
- E. Saito, E. F. Antunes, H. Zanin, F. R. Marciano, A. O. Lobo and V. J. Trava-Airoldi, et al., Oxygen Plasma Exfoliated Vertically-Aligned Carbon Nanotubes as Electrodes for Ultrasensitive Stripping Detection of Pb2+, J. Electrochem. Soc., 2014, 161(5), H321–H325 Search PubMed.
- M. Pawlyta, J. N. Rouzaud and S. Duber, Raman microspectroscopy characterization of carbon blacks: Spectral analysis and structural information, Carbon, 2015, 84(1), 479–490 Search PubMed.
- P. Trucano and R. Chen, Structure of graphite by neutron diffraction, Nature, 1975, 258(5531), 136–137 Search PubMed.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso and J. Rouquerol, et al., Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report), Pure Appl. Chem., 2015, 87(9–10), 1051–1069 Search PubMed.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago and A. Compte, Anomalous transport effects in the impedance of porous film electrodes, Electrochem. Commun., 1999, 1(9), 429–435 Search PubMed.
- T. A. Centeno, O. Sereda and F. Stoeckli, Capacitance in carbon pores of 0.7 to 15 nm: A regular pattern, Phys. Chem. Chem. Phys., 2011, 13(27), 12403–12406 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00783h |
| This journal is © The Royal Society of Chemistry 2021 |