Open Access Article
Open Access ArticleDielectric metasurface based high-efficiency polarization splitters
Zhongyi Guo *a,
Lie Zhua,
Fei Shena,
Hongping Zhoua and
Rongke Gao
*a,
Lie Zhua,
Fei Shena,
Hongping Zhoua and
Rongke Gao *b
*b
aSchool of Computer and Information, Hefei University of Technology, Hefei, 230009, China. E-mail: guozhongyi@hfut.edu.cn
bSchool of Instrument Science and Opto-electronics Engineering, Hefei University of Technology, Hefei, 230009, China. E-mail: rkgao@hfut.edu.cn
First published on 3rd February 2017
Abstract
In this paper, a novel polarization splitter has been designed at the telecommunication wavelength of 1500 nm successfully based on the dielectric metasurface consisting of a silicon nanobrick array, which can generate two different wavefronts for two orthogonal input polarizations with well over 90% transmitted efficiency by exactly selecting the sizes of the used nanobricks. The splitting mechanism is attributed to the fact that the used nanobricks can supply two different incremental transmission phases for the X-linear-polarization (XLP) incidence and Y-linear-polarization (YLP) incidence respectively. A polarization-dependent beam splitter which can effectively deflect the X- and Y-linear-polarization incidences in the opposite direction with 90% transmitted efficiency have been realized based on the same metasurface, where the refracted angle of the co-polarized refracted light can be arbitrarily controlled by changing the lattice constant of the nanobricks. In addition, a polarization-independent beam deflector which can make the linear-polarization (XLP and YLP) incident lights refract in the same direction has also been designed and presented. However, it is very difficult to obtain concrete XLP and YLP compositions in the transmitted fields in real experiments. Thus we have designed a novel metalens to focus the two orthogonal polarization compositions in different positions. The capacities to completely manipulate the phase and wavefronts demonstrate the potential of the designed metasurfaces in realizing most free-space transmissive optical devices such as phase plates, polarizers, as well as vector beam generators and so on.
1. Introduction
Recently, full manipulation of light propagation on the nanoscale has attracted lots of attention due to its great functionalities. Compared to conventional optical devices that are restricted by the permittivity for natural materials and mostly optical thickness, metasurfaces can possess arbitrary values of permittivity and thus manipulate the wavefront of light with extreme freedom. Moreover, metasurfaces are the two-dimensional counterpart, which makes them suitable for integration on a photonic chip and mass production. Generally, metasurfaces are composed of an array of resonators with subwavelength spatial resolution, utilizing asymmetric electric dipole resonances to allow for an abrupt change in the amplitude and phase of the impinging light by manipulating the size and shape of the resonators.1 Based on metasurfaces, recently, plenty of planar optical components have been designed and realized successfully, including optical vortex beam generators,2,3 gratings,4 lenses,5–9 holographic masks,10,11 waveplates,12,13 and so forth.By far, a majority of studies have been focused on metallic resonators and their plasmonic properties, however, the metallic metasurfaces possess relatively low transmission efficiency due to the inherent nonradiative ohmic losses at optical frequencies.14–18 There are several methods commonly used to improve the transmission efficiency, which include the reflective metasurfaces,19 Huygens' metasurfaces20 and all-dielectric metasurfaces.21,22 However, the reflective metasurfaces only operate in reflection mode with a metal ground plane and can not be applied to the mainstream transmission devices. And the Huygens' metasurfaces are fabricated by three-dimensional structures, which has been hindered in the real fabrications. Dielectric metasurfaces offer one potential solution to control lightwaves at the nanoscale with extremely high transmission efficiency, which originate from that the dielectric nanostructures can be optimized to simultaneously possess both electric and magnetic dipole resonances. Thus, the dielectric metasurfaces can enable high transmission efficiency with a full 2π phase control. Furthermore, the nanometer silicon can be easily obtained by mature technology of semiconductor with low manufacture cost, which makes silicon an ideal platform for high-efficiency metasurfaces. However, most researches about the dielectric metasurfaces have focused on the reflective modes23–25 and the major spectral bands of recent researches are the visible regime and near-infrared frequencies.26,27 Although several types of transmissive dielectric metasurfaces have been realized, these metasurfaces can hardly control two different input polarization simultaneously.2,28,29 The ability to simultaneously control the transmitted phase for different incident polarizations was first introduced in recent papers at the wavelength of 915 nm.30 The metasurfaces we propose here can realize a polarization splitter that can generate two arbitrary wavefronts for two orthogonal input polarizations at a distinct wavelength of 1500 nm with high transmission efficiency.
In this letter, we have demonstrated a dielectric metasurface based polarization splitter with high transmission efficiency. The designed polarization-dependent beam splitter can separate the XLP and YLP incident lights to ±16.7° by utilizing structured silicon (Si) nanobricks atop a low index silicon dioxide (SiO2) ground plane with the transmission efficiency larger than 90%. Particularly, the deflected angles of 30° and 60° with high transmission efficiency have also been obtained based on the arrayed nanobricks, where the designed metasurface can arbitrarily separate the incident lights to any desired directions. Furthermore, gradient metasurfaces are designed at the wavelength of 1500 nm, functioning as a polarization-independent beam deflector to redirect the incident lights to an identical refraction angle regardless of the incident polarization states. To obtain the concrete XLP and YLP compositions of the transmitted fields in experiments easily, we have also proposed an optical device with polarization dependence, which can separate the x- and y-polarized lights to two opposite directions and then focus them to different positions successfully.
2. Model, results and discussions
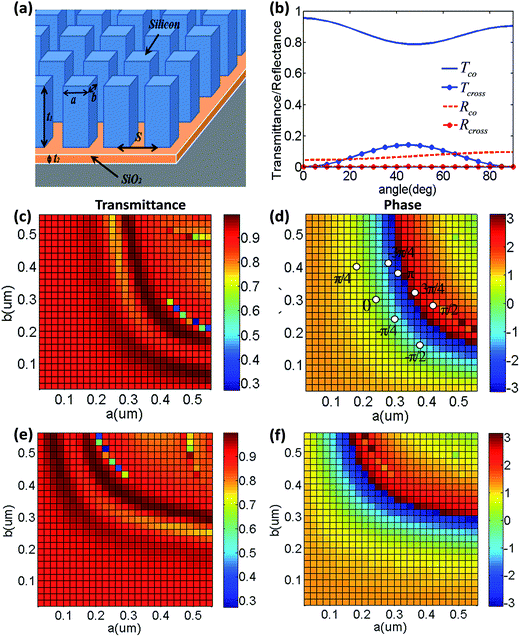
The schematic of the designed nanobricks standing on a glass substrate is depicted in Fig. 1(a). The refractive index of the 900 nm thick silicon nanobrick and 200 nm thick SiO2 are 3.48 and 1.48, respectively. The method of finite-difference time-domain with periodic boundary conditions is used to perform the numerical simulations. Incident plane wave at a fixed wavelength of 1500 nm illuminates to the metasurfaces normally with the linear polarization along the x-axis. Fig. 1(b) clearly shows the corresponding transmission efficiency (T) and reflection efficiency (R) under XLP incidence, as the functions of θ which is the angle between the long axes of the silicon nanobrick and X-axis. The blue solid curves and the blue circular curves represent the transmitted efficiencies of the cross-polarization state (|Tcross|2) and the co-polarization state (|Tco|2) respectively. The red dashed lines and the red circular lines represent the reflected efficiencies of the cross-polarization state (|Rcross|2) and the co-polarization state (|Rco|2) respectively. As depicted in Fig. 1(b), the cross-polarization transmission reaches the maximum when the slant angle of the nanobrick is 45°, nevertheless, the concrete value is still lower than 15%. And the co-polarized transmission remains above 79%, which indicates that there is little polarization conversion, especially at the angle of 0°. In addition, the co-polarized and cross-polarized reflection efficiency remain particularly smaller than 10% and nearly 0%, respectively. Thus the reflection can be ignored in the following simulations. Obviously, the absorption efficiency can be calculated by subtracting both the transmission and reflection efficiency from 100%, which is equal to 0 nearly. According to the theory, the imaginary parts of refractive index of both Si and SiO2 are zero at the wavelength of 1500 nm,31 therefore, there is no absorption, and it agrees well with the simulation results, which promise the extremely high transmission efficiency of our designed metasurfaces. To ensure the lower reflectance, the slant angle is set as 0° in the following numerical simulations for LP incidences and thus only the co-polarized transmission is considered.Fig. 1(c) and (e) shows the calculated intensity transmission efficiencies as the functions of the nanobrick dimensions along X- and Y-directions, a and b, with the range from 20 nm to 560 nm, under the XLP and YLP incidences respectively. The corresponding phase variations as the functions of a and b, under the XLP and YLP incidences, are shown in Fig. 1(d) and (f) respectively. As can be seen from numerical simulations results, the metasurfaces can achieve a full 0 to 2π phase variation, and meanwhile the transmission efficiencies can reach to as high as 90%. The higher co-polarization transmission is originating from the lower reflection, nearly no absorption of the silicon nanobricks at the telecommunication wavelength, and the lower polarization conversion. Thus, any desired phase as well as extremely high transmission can be obtained by properly choosing the parameters. Moreover, it is evident from Fig. 1(d) that under the XLP incidence, with the preconditions of keeping the dimension in y-direction unchanged and higher than 200 nm, we can achieve 0 to 2π phase variation by only changing the dimension of nanobrick along X-direction. Analogously, as shown in Fig. 1(f), under the YLP incidence, due to the symmetry of the nanobricks, we can also achieve complete phase control by only changing the brick diameters along Y-direction. The results means that the phases of XLP refraction light (φx) and YLP refraction light (φy) can be controlled fully by changing the dimensions of nanobrick in x-direction and y-direction, respectively. Thus, any combination of φx and φy can be simultaneously obtained by appropriately choosing two nanobrick parameters of a and b.
The refraction angle of incident light can be calculated by the generalized Snell's law, which is related to the phase gradient along the interface and can be expressed as follow32,33
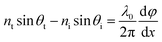 | (1) |
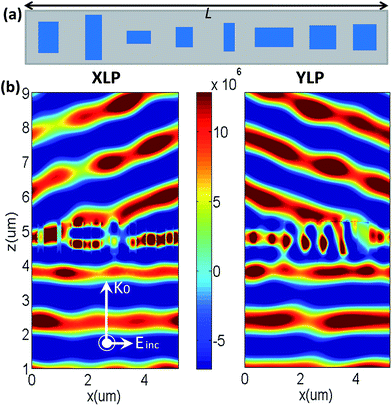
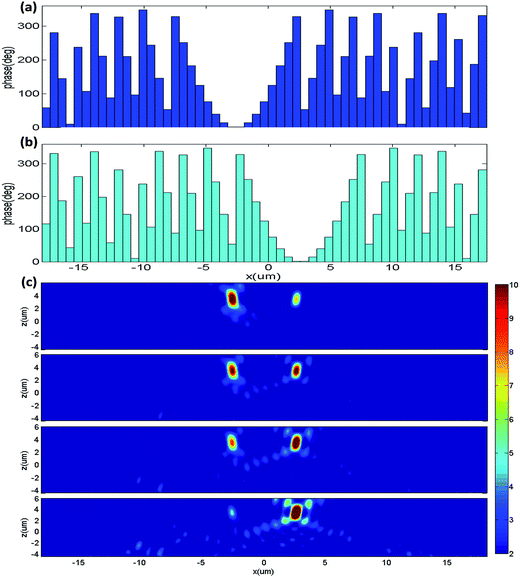
In order to validate the performance of the phase-gradient metasurfaces, a polarization splitter is proposed for generating two different wavefronts with two orthogonal polarizations (XLP and YLP) light at the normal incidences. Here, 8 nanobricks have been chosen in a supercell with a phase increment of φ = π/4, in which there will be a phase variation of 0 to 2π for the XLP incidence, but a phase variation of 2π to 0 for the YLP incidence. Therefore, the refractive beams can be deflected into different directions and formed two different wavefronts for the XLP and YLP incidences. From Fig. 1(d) and (f), the proper dimensions of 1–8 resonators as shown in Fig. 2(a), can be selected respectively as: (1) a = 292 nm, b = 385 nm; (2) a = 240 nm, b = 555 nm; (3) a = 350 nm, b = 160 nm; (4) a = 248 nm, b = 248 nm; (5) a = 160 nm, b = 350 nm; (6) a = 555 nm, b = 240 nm; (7) a = 385 nm, b = 292 nm; (8) a = 340 nm, b = 320 nm.
When a LP wave with the polarized angle of 45° is incident to the designed metasurfaces, the LP wave can be decomposed as the XLP and YLP incidences, and then the whole transmitted fields can be regarded as the superposition of the corresponding transmitted XLP and YLP lights. As depicted in Fig. 2(b), under the 45° LP incidence, the concrete XLP and YLP transmitted electric field distributions can be extracted from the whole transmitted fields, which demonstrate that the designed device can serve as a polarization beam splitter with a proper successive treatment. It is clear that there exist a well-defined phase front with the refracted angles of −17° and 17° for transmitted XLP and YLP lights respectively, which agree well with the theoretical expectation on the refracted angles of ±16.7° based on the eqn (1). As can also be seen from Fig. 2(b), both XLP and YLP wavefronts can transmit from the designed metasurface without being affected by the metasurface, which can further verify that the incident wavefront can transmit from the metasurfaces without reflection.
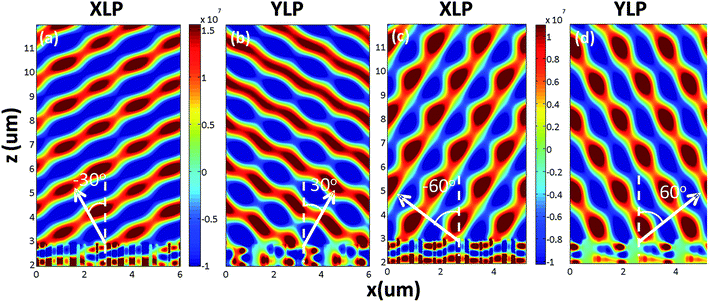
To further verify the effectiveness of the designed metasurfaces, we have also shown that the refracted angles can be arbitrarily controlled to satisfy our needs by changing the periodical length L of supercell. The periodical length of supercell can be expressed as L = sN, where s is the length of the unit cell and N is the number of the used unit cells in one supercell. The desired refracted angles can be modulated by adjusting the length of the unit cell of s and the number of the used unit cells of N when the wavelength is a constant.
Fig. 3(a–d) shows the situation that under the normal LP incidence with the polarized angle of 45° to the designed metasurfaces, the deflected angles are 30° and 60°, respectively, which indirectly verify the validity that the designed metasurface can separate the XLP and YLP incidences and deflect the transmitted light to an arbitrary angle. To achieve refractive angle of 30°, the lattice constant s has been reduced to 500 nm and changing the number of the nanobricks N into six. Similarly, when s has been reduced to 433 nm and N changed into 4, the refractive angle of 60° can be obtained. It should be noted here that the relation between the nanobrick dimensions and the phases should be recalculated and reselected correctly to avoid the occurrence of phase errors. As depicted in Fig. 3(a) and (c), the deflected angles of −30° and −60° match well with the theoretical expectations, although the coupling effect between adjacent resonators has been enhanced due to the decreasing lattice constant. In consequence, the designed metasurface can separate the XLP and YLP lights to arbitrary directions with extremely high transmission efficiency, which can be applied as a polarizing beam splitter.
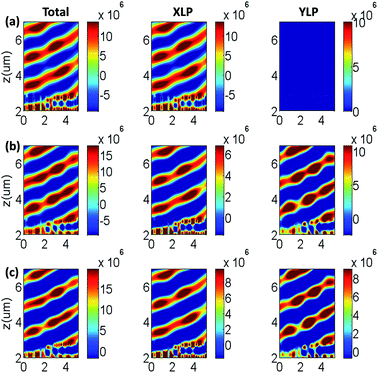
All of the above simulations are polarization-dependent, in which different polarization incidences will be refracted into different directions. In order to further verify the manipulating capability of the designed metasurfaces, here, we will propose a special polarization-independent device that can deflect XLP and YLP incidences to the same direction. Similar as the above, we can find a series of unit cells with a proper dimensions, which possess the same phase variations for the XLP and YLP incidences respectively. By numerical simulations, the 8 unit cells with the phase variations ranging from 0 to 2π with an increment of φ = π/4 for the XLP and YLP incidences simultaneously can be found from Fig. 1(d) and (f). Under the normal incidence of XLP light, the extracted transmitted XLP and YLP compositions have been shown in Fig. 4(a). The total transmitted electric field distributions of the metasurface are the same as the transmitted XLP electric field distributions and there is no transmitted YLP electric field due to the zero cross-polarized conversion. Fig. 4(b) and (c) show the transmitted electric field distributions with normal incidences of 30° LP light and 45° LP light, respectively. Because the two different polarizations have the same phase discontinuity of dφ/dx, the XLP and YLP compositions of the incident beam will be refracted to the same angle of 17° as the same as the above result. Furthermore, it is observed that with increasing the incident polarization-angle, the transmitted XLP electric field clearly increases while the transmitted YLP electric field decreases accordingly. Similarly, an arbitrary refraction angles can be obtained by changing the lattice constants and number of the nanobricks. As shown in Fig. 4, the total transmitted electric field distributions with normal incidences of the XLP light, 30° LP light and 45° LP light are nearly identical and these three different polarization incidences have the same deflection angle of 17°, which verify that the designed device can serve as a beam deflector to redirect the incident lights to the same angle regardless of the incident angle of polarization.
Although we can extract the concrete XLP and YLP compositions of the transmitted fields in theory, it is very difficult to obtain them in experiments if there is no any further treatments. Therefore, here, we will try to design a novel metalens to focus the XLP and YLP compositions in different positions, which can separate the XLP and YLP compositions in the transmitted fields effectively. The metalens with the focusing point in the XOZ plane can be designed by controlling the transmitted phase which follow the hyperboloidal profile5,6,35
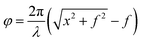 | (2) |
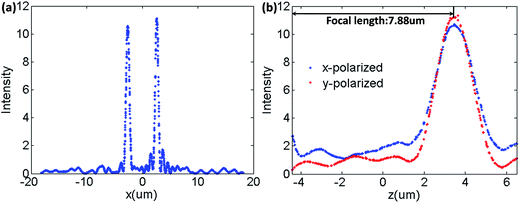
Here, we set the focal length of the metalens as 8 μm, and the focusing points for XLP and YLP components lies in the both sides of Z axis in the XOZ plane, which means the position of the focusing points for XLP and YLP components are set as (−2.6 μm, 0, 4 μm) and (2.6 μm, 0, 4 μm). The concrete calculated phase distributions of the designed metalens for XLP and YLP components have been shown in Fig. 5(a) and (b) respectively. Thus, based on Fig. 1(d) and (f), the length and width of nanobricks corresponding to the desired phases in different position can be obtained to design the metalens. The two desired phases are symmetry about the focusing positions and independent of each other for two orthogonal input polarizations. The focal length defined as the distance between the metalens and the focusing spot is 8 μm at the wavelength of 1.5 μm. As depicted in Fig. 5(c), the designed metalens can focus the XLP and YLP incidences into the upper-left and upper-right spots of the refractive field, respectively. The intensity maps for different polarization angle of 30°, 38°, 45° and 60° are given in Fig. 5(c) respectively. It can be clearly observed that the focusing intensities of the XLP component are getting smaller with increasing the incident polarization-angle. Because the incident intensity component along x-axis is getting smaller when the incident polarization-angle is getting larger, especially the focusing intensities of two different polarization states are nearly the same when the incident angle is 38°. It should be noted that the incident energy components along x- and y-axis are the same for the incident polarization-angle of 45°. Nevertheless, the focusing intensity for y-polarization component is stronger, which is due to the transmission efficiency for x-polarization component is slightly smaller than that for y-polarized component.
For quantitatively analyzing the focusing effect of the designed metalens, the co-polarized electric field intensity along the x-axis and the z-axis at the focal plane for the designed metalens are presented in Fig. 6(a) and (b) respectively. The simulated focal length is slightly smaller than the theoretical prediction, which may be due to the weak coupling between the nearby nanobricks in the simulations. Furthermore, the corresponding FWHMs along the x-direction at the focal plane for the two orthogonal input polarizations are 720 nm and 647.5 nm, which indicate that the designed metalens work in relatively high qualities. The depths of focus (FWHM along the z-direction) are 2.38 μm and 2.12 μm, respectively. And the numerical aperture is about 0.9 (the focusing spots are quite small), which is larger than most of the previous works36 and verifies the better focusing efficiency of our designed metalens. Furthermore, the focusing position can be arbitrary controlled in the focusing plane by changing the phases.
3. Conclusion
In summary, we have demonstrated dielectric gradient metasurfaces consist of periodic arrangement of differently sized silicon nanobricks, which can refract the input light with full 0 to 2π phase control and extremely high efficiency (over 90%) at telecommunication wavelength. The designed metasurfaces can simultaneously achieve two different wavefronts for different incident LP light by exactly selecting the long axis and short axis of the nanobricks. Thus, a novel polarization splitter that separates two orthogonal input polarizations to arbitrary different directions and a beam deflector with polarization independence based on the designed dielectric metasurfaces have been demonstrated. Our demonstrated optical metalens with polarization selectivity can be helpful to obtain the concrete XLP and YLP compositions of the transmitted fields in experiments. Our designs will find a large amount of practical applications with high efficiency, such as antireflection coatings, phase modulators, the vortex converter, and so forth.Acknowledgements
The authors gratefully acknowledge the financial supports for this work from the National Natural Science Foundation of China under Grant No. 61575060 and 61601165, and the Fundamental Research Funds for the Central Universities (2015HGCH0010).References
- Y. Yang, W. Wang, P. Moitra, I. I. Kravchenko, D. P. Briggs and J. Valentine, Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation, Nano Lett., 2014, 14(3), 1394–1399 CrossRef CAS PubMed.
- M. I. Shalaev, J. Sun, A. Tsukernik, A. Pandey, K. Nikolskiy and N. M. Litchinitser, High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode, Nano Lett., 2015, 15, 6261–6266 CrossRef CAS PubMed.
- W. Wang, Z. Y. Guo, Y. X. Sun, F. Shen, Y. Li, Y. Liu, X. S. Wang and S. L. Qu, Ultra-thin optical vortex phase plate based on the L-shaped nanoantenna for both linear and circular polarized incidences, Opt. Commun., 2015, 355, 321–325 CrossRef CAS.
- S. Sun, K.-Y. Yang, C.-M. Wang, T.-K. Juan, W. T. Chen, C. Y. Liao, Q. He, S. Xiao, W.-T. Kung, G.-Y. Guo, L. Zhou and D. P. Tsai, High efficiency broadband anomalous reflection by gradient meta-surfaces, Nano Lett., 2012, 12, 6223–6229 CrossRef CAS PubMed.
- W. Wang, Z. Y. Guo, K. Y. Zhou, Y. X. Sun, F. Shen, Y. Li, S. L. Qu and S. T. Liu, Polarization-independent longitudinal multi-focusing metalens, Opt. Express, 2015, 23(23), 29855–29866 CrossRef PubMed.
- W. Wang, Z. Y. Guo, R. Z. Li, J. R. Zhang, Y. Li, X. S. Wang and S. L. Qu, Plasmonics metalens independent from the incident polarizations, Opt. Express, 2015, 23(13), 16782–16791 CrossRef PubMed.
- F. Aieta, P. Genevet, M. A. Kats, N. Yu, R. Blanchard, Z. Gaburro and F. Capasso, Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces, Nano Lett., 2012, 12(9), 4932–4936 CrossRef CAS PubMed.
- R. Z. Li, Z. Y. Guo, W. Wang, J. R. Zhang, A. J. Zhang, J. L. Liu, S. L. Qu and J. Gao, Arbitrary focusing lens by holographic metasurface, Photonics Res., 2015, 3(5), 252–255 CrossRef.
- W. Wang, Z. Y. Guo, R. Z. Li, J. R. Zhang, Y. Li, X. S. Wang and S. L. Qu, Ultra-thin, planar, broadband, dual-polarity plasmonic metalens, Photonics Res., 2015, 3(3), 68–71 CrossRef CAS.
- G. Zheng, H. Mühlenbernd, M. Kenney, G. Li, T. Zentgraf and S. Zhang, Metasurface Holograms Reaching 80% Efficiency, Nat. Nanotechnol., 2015, 10, 308–312 CrossRef CAS PubMed.
- X. Ni, A. V. Kildishev and V. M. Shalaev, Metasurface holograms for visible light, Nat. Commun., 2013, 4(4), 2807 Search PubMed.
- A. Roberts and L. Lin, Plasmonic quarter-wave plate, Opt. Lett., 2012, 37, 1820–1822 CrossRef CAS PubMed.
- N. K. Grady, J. E. Heyes, D. R. Chowdhury, Y. Zeng, M. T. Reiten, A. K. Azad, A. J. Taylor, D. A. R. Dalvit and H. T. Chen, Terahertz Metamaterials for Linear Polarization Conversion and Anomalous Refraction, Science, 2013, 340(6138), 1304–1307 CrossRef CAS PubMed.
- J. Hao, C. Qu, S. Ma and M. Qiu, Plasmonic metasurfaces: From perfect absorption to phase modulation, 40th International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), IEEE, 2015 Search PubMed.
- M. Farmahini-Farahani, J. Cheng and H. Mosallaei, Metasurfaces nanoantennas for light processing, J. Opt. Soc. Am. B, 2013, 30(9), 2365–2370 CrossRef CAS.
- A. Pors, M. G. Nielsen and S. I. Bozhevolnyi, Analog computing using reflective plasmonic metasurfaces, Nano Lett., 2014, 15(1), 791–797 CrossRef PubMed.
- L. Liu, X. Zhang, M. Kenney, X. Su, N. Xu, C. Ouyang, Y. Shi, J. Han, W. Zhang and S. Zhang, Broadband metasurfaces with simultaneous control of phase and amplitude, Adv. Mater., 2014, 26(29), 5031–5036 CrossRef CAS PubMed.
- A. Pors, M. G. Nielsen, R. L. Eriksen and S. I. Bozhevolnyi, Broadband focusing flat mirrors based on plasmonic gradient metasurfaces, Nano Lett., 2013, 13(2), 829–834 CrossRef CAS PubMed.
- R. Z. Li, F. Shen, Y. X. Sun, W. Wang, L. Zhu and Z. Y. Guo, Broadband, high-efficiency, arbitrary focusing lens by a holographic dielectric meta-reflectarray, J. Phys. D: Appl. Phys., 2016, 49(14), 145101 CrossRef.
- M. Decker, I. Staude, M. Falkner, J. Dominguez, D. N. Neshev, I. Brener, T. Pertsch and Y. S. Kivshar, High-efficiency dielectric Huygens' surfaces, Adv. Opt. Mater., 2015, 3(6), 813–820 CrossRef CAS.
- J. Van de Groep and A. Polman, Designing dielectric resonators on substrates: Combining magnetic and electric resonances, Opt. Express, 2013, 21(22), 26285–26302 CrossRef CAS PubMed.
- L. Zou, C. M. Shah, M. Klemm, S. Sriram and C. Fumeaux, Efficiency and scalability of dielectric resonator antennas at optical frequencies, IEEE Photonics J., 2014, 6(4), 1–10 CrossRef.
- P. Moitra, B. A. Slovick, W. Li, I. I. Kravchencko, D. P. Briggs, S. Krishnamurthy and J. Valentine, Large-scale all-dielectric metamaterial perfect reflectors, ACS Photonics, 2015, 2(6), 692–698 CrossRef CAS.
- Z. Ma, S. M. Hanham, P. Albella, B. Ng, H. T. Lu, Y. Gong, S. A. Maier and M. Hong, Terahertz All-Dielectric Magnetic Mirror Metasurfaces, ACS Photonics, 2016, 3(6), 1010–1018 CrossRef CAS.
- Y. Yang, W. Wang, P. Moitra, I. I. Kravchenko, D. P. Briggs and J. Valentine, Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation, Nano Lett., 2014, 14(3), 1394–1399 CrossRef CAS PubMed.
- A. Zhan, S. Colburn, R. Trivedi, C. Dodson and A. Majumdar, Low contrast dielectric metasurface optics, ACS Photonics, 2016, 3(2), 209–214 CrossRef CAS.
- S. M. Kamali, E. Arbabi, A. Arbabi, Y. Horie and A. Faraon. Highly tunable elastic dielectric metasurface lenses, arXiv preprint arXiv:1604.03597, 2016.
- J. Cheng, D. Ansari-Oghol-Beig and H. Mosallaei, Wave manipulation with designer dielectric metasurfaces, Opt. Lett., 2014, 39(21), 6285–6288 CrossRef PubMed.
- K. E. Chong, I. Staude, A. James, J. Dominguez, S. Liu, S. Campione, S. S. Ganapathi, S. L. Ting, D. Manuel, N. N. Dragomir, B. Igal and Y. S. Kivshar, Polarization-independent silicon metadevices for efficient optical wavefront control, Nano Lett., 2015, 15(8), 5369–5374 CrossRef CAS PubMed.
- A. Arbabi, Y. Horie, M. Bagheri and A. Faraon, Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission, Nat. Nanotechnol., 2015, 10(11), 937–943 CrossRef CAS PubMed.
- J. Kischkat, S. Peters, B. Gruska, M. Semtsiv, M. Chashnikova, M. Klinkmüller, O. Fedosenko, S. Machulik, A. Aleksandrova, G. Monastyrskyi, Y. Flores and W. T. Masselink, Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride, Appl. Opt., 2012, 51(28), 6789–6798 CrossRef CAS PubMed.
- N. Yu, P. Genevet, M. A. Kats, F. Aieta, J. P. Tetienne, F. Capasso and Z. Gaburro, Light propagation with phase discontinuities: generalized laws of reflection and refraction, Science, 2011, 334(333), 333–337 CrossRef CAS PubMed.
- Z. Wang, Y. Sun, L. Han and D. Liu, General laws of reflection and refraction for subwavelength phase grating, arXiv preprint arXiv, 2013, 1312–3855.
- R. Z. Li, Z. Y. Guo, W. Wang, J. R. Zhang, A. J. Zhang, J. L. Liu, S. L. Qu and J. Gao, Ultra-thin circular polarization analyzer based on the metal rectangular split-ring resonators, Opt. Express, 2014, 22(23), 27968–27975 CrossRef PubMed.
- F. Aieta, P. Genevet, M. A. Kats, N. Yu, R. Blanschard, Z. Gaburro and F. Capasso, Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces, Nano Lett., 2012, 12(9), 4932–4936 CrossRef CAS PubMed.
- M. MKhorasaninejad, W. T. Chen, R. C. Devlin, J. Oh, A. Y. Zhu and F. Capasso, Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging, Science, 2016, 352(6290), 1190–1194 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |