Active binary mixtures of fast and slow hard spheres†
Abstract
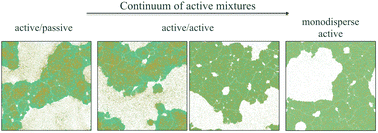
We computationally studied the phase behavior and dynamics of binary mixtures of active particles, where each species had distinct activities leading to distinct velocities, fast and slow. We obtained phase diagrams demonstrating motility-induced phase separation (MIPS) upon varying the activity and concentration of each species, and extended current kinetic theory of active/passive mixtures to active/active mixtures. We discovered two regimes of behavior quantified through the participation of each species in the dense phase compared to their monodisperse counterparts. In regime I (active/passive and active/weakly-active), we found that the dense phase was segregated by particle type into domains of fast and slow particles. Moreover, fast particles were suppressed from entering the dense phase while slow particles were enhanced entering the dense phase, compared to monodisperse systems of all-fast or all-slow particles. These effects decayed asymptotically as the activity of the slow species increased, approaching the activity of the fast species until they were negligible (regime II). In regime II, the dense phase was homogeneously mixed and each species participated in the dense phase as if it were it a monodisperse system (i.e. not mixed at all). Finally, we showed that a weighted average of constituent particle activities, which we term the net activity, defines a binodal for the MIPS transition in active/active binary mixtures. We examined the critical point of the transition and found a critical exponent (β = 0.45) in agreement with similar studies on monodisperse systems, and distinct from equilibrium systems.


 Please wait while we load your content...
Please wait while we load your content...