Impact of metal and active site configurations in hydrogenation reactions with N-doped graphene single atom catalysts

Abstract

Hydrogenation reactions are well-established transformations in both homogeneous and heterogeneous catalysis and are increasingly explored using single-atom catalysts (SACs). Despite this progress, a comprehensive understanding of the underlying reaction mechanisms remains limited, often restricted to specific systems. Moreover, the precise nature of the active sites is elusive, and their reactivity may be influenced by varying coordination numbers, hetero-atom doping, and other factors. To gain insight into hydrogenation reactions in nitrogen-doped graphene-based SACs, we conducted a thorough investigation into hydrogen transfer across Fe, Co, Mn, and Ru systems, considering different charges, spin states, pyrrolic and pyridinic sites. Our findings reveal substantial deviation from conventional homogeneous and heterogeneous systems, with SACs being strongly influenced by the nature of the active site. Analyses using Natural Bond Orbitals (NBO), natural charge, and natural decomposition analysis (NEDA) highlighted differences in nitrogen-metal interactions as a key factor driving the observed reactivity variations between Pyrr and Py systems, as well as between Ru and 1st-row metals.

---

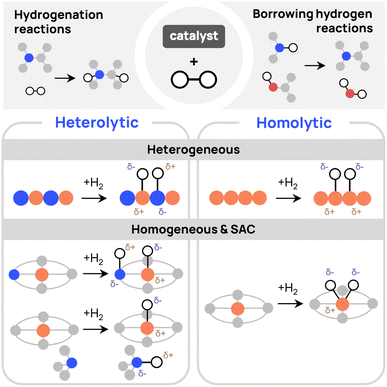
Since the beginning of the last century, catalytic hydrogenation has been a dynamic field, continually expanding with the development of new catalysts,¹ propelled by computational studies and machine learning.^2,3 These research efforts reflect the essential role of hydrogenation reactions in the synthesis of diverse fine chemicals, spanning from agrochemicals to drugs.^4,5 Among the various approaches to reduce unsaturated C–X (X = C, O, N) bonds by hydrogenation, two primary methods stand out: (i) direct hydrogenation (DH), using dihydrogen (H₂) as a reactant, and (ii) transfer hydrogenation (TH) or borrowing hydrogen (BH), using alternative hydrogen sources.^6–8 Typically, both approaches initiate with the transfer of hydrogen atoms to the catalyst (Fig. 1). In DH, this transfer can occur through the homolytic dissociation of H₂ over the metal center, forming hydrides,^9,10 or, alternatively, through the heterolytic cleavage of H₂, involving a base that takes one H as a proton, whereas the other H is transferred to the metal as a hydride.¹¹ In TH and BH, the transfer from the hydrogen donor to the catalyst is more complex as it produces a byproduct, though the catalyst intermediates are similar to those observed in DH.¹² The fundamental understanding of these mechanisms is crucial for the design of new hydrogenation catalysts. For example, leveraging heterolytic dissociation of H₂ has led to the development of bifunctional catalysts that integrate the base as a ligand, enhancing catalytic efficiency.¹³

Fig. 1 Comparison of heterolytic and homolytic dihydrogen addition pathways in hydrogenation and borrowing hydrogen reactions across heterogeneous, homogeneous catalysts and SAC. Spheres in orange, blue, white, red and grey represent metal, nitrogen, hydrogen, oxygen, and carbon atoms, respectively.

Homogeneous and heterogeneous catalysts have been extensively developed for hydrogenation reactions, yet both approaches have inherent limitations.¹⁴ Homogeneous catalysis often faces challenges related to the separation of the catalyst, while heterogeneous catalysis has issues such as low selectivity and atom efficiency. Single-atom catalysts (SACs) are a promising alternative, consisting in dispersing metal atoms over supporting surfaces to combine the benefits of both systems.^15–17 N-doped graphene-based SACs have proven to be highly effective in catalyzing hydrogenation reactions.^18,19 However, the precise picture of the underlying reaction mechanisms remains elusive, as it may involve either homolytic or heterolytic pathways, with a manifold of potential active sites.²⁰

While pyridinic MN₄ sites (M = metal) are frequently studied due to their better anchoring abilities,^21–23 it has been argued that MN₃ sites exhibit greater reactivity.^24–26 This hypothesis is supported by the out-of-plane configuration and co-adsorption of reactants that can facilitate hydrogenation reactions in MN₃ sites. In addition, the homolytic and heterolytic dissociation of H₂ on MN₄ sites was found to be largely endothermic for several metals, suggesting these sites may not be those promoting catalysis.²⁷ Other investigations suggested that frustrated Lewis pairs and vacancies within the graphene lattice may also play a crucial role.^18,28,29 In these systems, the co-existence of acid and basic sites promotes the heterolytic cleavage of H₂. Additional doping with sulfur or phosphorus is also an efficient approach to promoting this reaction in SACs.^30–32

Among the alternative active sites for improved reactivity, pyrrolic MN₄ sites remain underexplored. An et al. report exceptional reactivity for Fe-based pyrrolic SACs, with performance for transfer hydrogenation being four orders of magnitude higher than other Fe catalysts.³³ Similarly, Zhang et al. suggest that pyrrolic sites offer superior support compared to pyridinic sites due to their increased electron density, which facilitates hydrogenation reactions with quinoline in CuN₆ SACs.³⁴ In a previous study, we also found that pyrrolic NiN₄ sites are much more active than the pyridinic counterparts for BH reactions. In the same study, the reaction pathway was found to be different from the conventional homolytic and heterolytic mechanisms.³⁵ The previous findings suggest that pyrrolic sites should hold significant potential to enhance a unique catalytic activity in SACs. Further, comparative studies between pyrrolic and pyridinic sites may reveal additional insights into how these different N-doped configurations influence the activity, robustness, and selectivity of these catalysts.

In the present study, we used computational methods to investigate the DH and TH mechanisms in N-doped graphene SACs of Mn, Fe, Co, and Ru, considering both pyridinic (Py) and pyrrolic (Pyrr) active sites. On top of the coordinating environment and the different metals, the configuration of the binding site (charge and spin multiplicity) can have a strong impact on the stability and reactivity of SAC systems, as shown in the recent study of Zaoralová et al.³⁶ Therefore, here, we systematically explored the influence of charge ([0], [+2]) and spin states (low, intermediate, and high) across four distinct transfer modes, revealing a broad range of reactivities. The results indicate that pyrrolic sites demonstrate heightened activity compared to pyridinic systems, and significant variation is observed between 1st-row metals and Ru, all of which are driven by differences in nitrogen–metal interactions. Interestingly, Ru systems are the most aligned with the homogeneous mechanisms, yielding the most favourable hydrogenation thermodynamics, while 1st-row metals exhibit a unique but similar reactivity. This study shows the critical role played by charge and spin states, the higher activity of the pyrrolic sites, and the contrasting behaviour between Ru and the first-row transition metals.

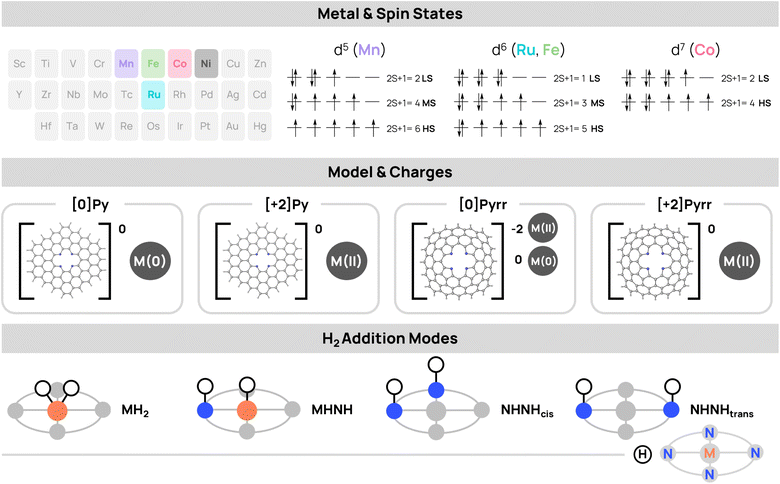
Computational methods

The SAC metals Mn, Fe, Co, and Ru were selected based on two principal criteria: (i) their previous use in doped graphene SACs for hydrogenation-related reactions,^37–44 and (ii) their various d-electron configurations. We investigated two distinct reactive sites in which the metals are coordinated to either four pyridine (Py) or four pyrrole (Pyrr) rings integrated onto N-doped graphene (Fig. 2). The choice of model is crucial for accurately describing such systems. While both periodic and cluster models are possible,⁴⁵ SACs were considered as hydrogen-atom-terminated graphene flakes for a deeper analysis of the electronic structure with a more accurate method. The flake size was defined as two supramolecular rings of fused benzenes around the metal, as this model was found to balance accuracy and computational cost in a previous work.³⁵ The Pyrr systems can be modeled either by incorporating holes in the structure to keep the surface flat or by keeping the graphene conjugation, in which a curvature is observed. In this study, the latter was selected, as systems with a high degree of curvature are experimentally relevant.^46,47 All four metals were examined in the low oxidation states (II) and (0). Given that the Py site is neutral, while the Pyrr can be either neutral or dianionic, we analyzed all systems in the charge [Q], where Q, the total charge of the system, is equal to either 0 (neutral Py or Pyrr with metal(0) oxidation state, or dianionic Pyrr with metal(II) oxidation state) or +2 (neutral Py or Pyrr with metal(II) oxidation state). Further, three different spin states were studied: (1) low-spin (LS), which is singlet for Fe and Ru and doublet for Mn and Co, and singlet for Fe and Ru; (2) intermediate-spin (IS), which is triplet for Fe and Ru, and quartet for Mn; and (3) high-spin (HS), which is quartet for Co, quintet for Fe and Ru, and sextet for Mn. The feasibility of the hydrogenation reactions was investigated by assessing the thermodynamics (free energy, ΔG at 298 K and 1 atm) of the addition of H₂ to the catalysts (cat + H₂ → cat(H)₂), as it was shown to be a good indicator for BH feasibility in a previous study, including reaction kinetics.³⁵

Fig. 2 Metals (Mn, Ru, Fe, Co), spin states (singlet, doublet, triplet, quartet, quintet, sextet), models (pyridinic: Py, and pyrrolic: Pyrr), charges ([0] or [+2]) for the studied model of N-doped graphene-based SACs, and the H₂ addition modes considered (MH₂, MHNH, NHNH_trans, NHNH_cis). For the H₂ addition modes, spheres in orange, blue, white, and grey represent metal, nitrogen, hydrogen, and carbon atoms, respectively.

The ΔGs were systematically calculated for all metal-charge-spin configurations of the SAC sites. The ΔGs were evaluated with the cat in its ground-state spin multiplicity. Only in a few systems, the lowest-energy spin multiplicity of the hydrogenated intermediate differs from that of the naked catalyst ground state (see SI). Reactivity was also modeled by considering three distinct hydrogenation modes: (1) both H atoms transferred to the metal, yielding a metal dihydride MH₂ intermediate (H–H bond homolytic cleavage); (2) one H atom transfers to the metal and the other to the N of the doped graphene support, yielding an MHNH intermediate (H–H bond heterolytic cleavage); (3) both H atoms are transferred to the support, yielding either cis (NHNH_cis) or trans (NHNH_trans) intermediates.

Calculations were performed using density functional theory (DFT) with the Gaussian 16 software.⁴⁸ The hybrid functional PBE0-D3BJ and the polarized double-ζ basis set def2-SVP were used for all calculations.^49–52 Frequency calculations were carried out at the same level to verify the nature of the stationary points.

In our previous study, for a Nickel system, we observed that changing the functional does not affect the results and trends for key transition states detrimentally.³⁵ In addition, the def2-SVP basis set was used to reduce the computational cost. To evaluate the influence of the basis set, we recomputed the energy for a selection of systems using the triple-ζ def2-TZVP basis set. While in some cases we observed significant differences between double-ζ and triple-ζ energies, the trends remained the same (Fig. S10).

For SAC systems, particularly those with significant charge separation, the use of a solvation model can have a massive effect on energy values and trends.³⁶ To account for the solvent effects of benzyl alcohol (experimentally used as reactant in excess), an implicit continuum model based on the SMD method was employed.^12,53

Natural bond orbital (NBO) calculations were conducted using the NBO7 program to obtain natural atomic charges and to determine the stabilization energies (E⁽²⁾) of donor–acceptor interactions.⁵⁴ The same program was used to perform natural energy decomposition analysis (NEDA), which breaks down the interaction energies into five components: electrostatic (ES), polarization (POL), exchange (X), charge transfer (CT), and deformation (DEF). For the NEDA analysis, the interacting fragments were defined as the SAC flake and the metal atom for the 16 catalysts. All energies reported in the text are in kcal mol⁻¹.

Results and discussion

H₂ addition

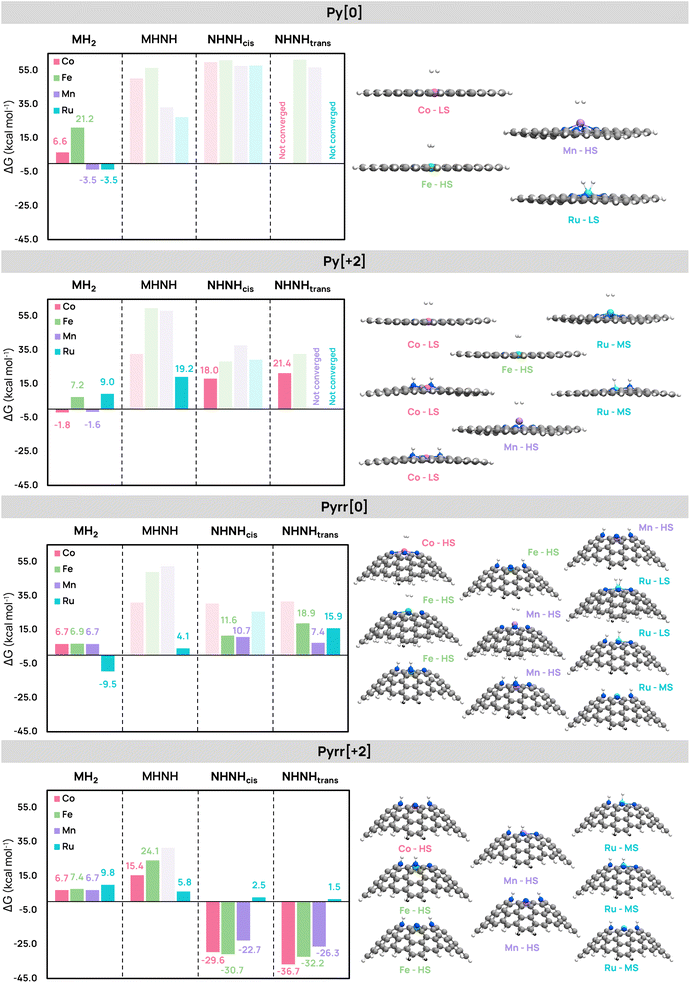
We investigated the hydrogenation thermodynamics of the pyrrolic (Pyrr) and pyridinic (Py) models with Co, Fe, Mn, and Ru using global charges of [0] and [+2]. All feasible spin multiplicities and hydrogenation modes (MH₂, MHNH, NHNH_cis, NHNH_trans) were considered and most of them could be optimized, leading to a total of 60 structures. From them, only the structures with energies within 5 kcal mol⁻¹ of the lowest and providing hydrogenation free energies lower than 25 kcal mol⁻¹ are discussed in this section (darker color bars in Fig. 3). To evaluate the impact of the model and the charge in the energies, the results were organized over the four categories defined by the model and the charge: [0]Py, [+2]Py, [0]Pyrr, and [+2]Pyrr.

Fig. 3 Free energy changes (ΔG, kcal mol⁻¹) for H₂ addition (MH₂, MHNH, NHNH_cis, NHNH_trans) to the different surfaces ([0]Py, [+2]Py, [0]Pyrr, [+2]Pyrr) for Co (pink bars), Fe (green bars), Mn (purple bars), and Ru systems (blue bars). Faded colors indicate ΔG values superior to 25 kcal mol⁻¹. Structures of the hydrogenated SACs are shown for the systems with ΔG lower than 25 kcal mol⁻¹, except for [+2]Pyrr MH₂ modes (omitted for clarity).

In the [0]Py systems, the most stable hydrogenated species for Fe, Co, and Mn do not involve complete H₂ bond cleavage, only a weak elongation of the dihydrogen bond by 0.02–0.03 Å. For Co and Fe, the adsorption of the H₂ molecule to the metal is an endergonic process. Contrary to other metals, the Mn atom shifts out of the plane in its most stable spin state (sextet) and lowest energy intermediate (MH₂). Only the Ru system achieves H₂ bond cleavage, with the two hydrogen atoms separated by 1.4 Å and bound to Ru at a distance of 1.55 Å. This reaction shows a slight exergonic character, making this system promising for hydrogen transfer reactions.

In [+2]Py, all hydrogenation reactions are more favorable than with the neutral systems, except for Ru. Additionally, hydrogenation modes, other than MH₂, become energetically accessible: the MHNH mode for Ru is at 19.2 kcal mol⁻¹, and both cis and trans NHNH modes for Co are slightly below 25 kcal mol⁻¹. For all metals, the MH₂ structures show a weakly adsorbed and activated H₂, with these average interatomic distances: d(M–H) = 2.57 Å and d(H–H) = 0.77 Å (0.74 Å in free H₂). Similar to the [0]Py-Mn model, both Mn and Ru appear slightly elevated above the graphene plane.

Switching to the [0]Pyrr model, the hydrogenation energies continued to drop, with the MHNH and NHNH products yielding hydrogenation energies smaller than 25 kcal mol⁻¹ for all metals except Co. However, the complete cleavage of H₂ in the MH₂ product is endergonic for all metals except Ru. The NHNH mode exhibits reasonable energies (7–11 kcal mol⁻¹) in cis for Fe and both cis and trans for Mn. In contrast, all attempts to cleave the H₂ bond with Co yielded large hydrogenation energies above the 25 kcal mol⁻¹ threshold. The behavior of Ru with the [0]Pyrr model resembles the [0]Py system if we look at the MH₂ mode, which has an elongated, yet to a lesser extent, dihydrogen bond (d(H–H) = 1.0 Å) and is the result of an exergonic reaction. However, in this case, both MHNH and NHNH_trans modes are accessible with energies of 4.1 and 15.9 kcal mol⁻¹, respectively.

The most exergonic hydrogenation values are found with the [+2]Pyrr model. It was only in this model that the Co systems yielded favorable H₂ cleavage, resulting in the most exergonic value among all systems at −36.7 kcal mol⁻¹ (NHNH_trans product). Similarly, Fe and Mn exhibit highly exergonic energies for both the NHNH_trans and NHNH_cis products. In contrast, Ru displays endergonic energies similar to those in the [+2]Py model. Among the Ru species, NHNH_trans, NHNH_cis, and MHNH have comparable energies, all close to thermo-neutrality and ranging from 1.5 to 5.8 kcal mol⁻¹, with NHNH_trans being the most favorable product.

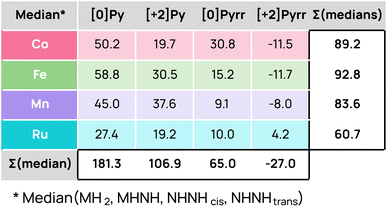
By calculating the median ΔG across all hydrogenation modes (MH₂, MHNH, NHNH_cis, NHNH_trans) for each metal (Co, Fe, Mn, Ru) and model system ([0]Py, [+2]Py, [0]Pyrr, [+2]Pyrr), and then summing these values, Fig. 4 clearly illustrates that the charge and graphene model both have a greater impact on reactivity than the choice of metal itself. These results align with recent findings in the field, highlighting the importance of investigating various electronic and geometric configurations of the active sites.³⁶

Fig. 4 Table of median ΔG values (kcal mol⁻¹) for MH₂, MHNH, NHNH_cis, and NHNH_trans addition modes across Co, Fe, Mn, and Ru systems and all models and charge systems ([0]Py, [+2]Py, [0]Pyrr, [+2]Pyrr). The sum of medians (∑(medians)) is reported per metal (last column) and per model and charge system (last row).

The sums of the medians (∑(medians)) for Co, Fe, and Mn systems range between 83 and 93 kcal mol⁻¹, indicating moderate differences among the 1st-row systems, whereas Ru is at 60.7 kcal mol⁻¹, showing distinct behavior and trends. Except for this metal, hydrogenation was unfeasible in the [0]Py model. The H₂ molecule only lies on the surface with negligible activation. In both the [0]Py and [+2]Py pyridinic models, hydrogen adsorption required the metal to move out of the SAC plane (more information in the SI), a scenario not desirable, as it favors metal leaching and the formation of NPs.^55,56

In contrast, Pyrr models exhibit greater reactivity. The [0]Pyrr system yielded reasonable endergonic energies for Mn and Fe (7–19 kcal mol⁻¹) and favorable H₂ bond cleavage for Ru. The [+2]Pyrr form provided highly exergonic energies (∑(medians) is by far the lowest in this mode at −27.0 kcal mol⁻¹), potentially trapping hydrogen on the surface for 1st-row transition metals, while Ru uniquely displays moderately endergonic energies. While we observed similar reactivity for the 1st-row transition metals, Co yielded the most exergonic or endergonic hydrogenation energies, depending on the charge and graphene model. Only Ru showed a preference for activating hydrogen in neutral and pyridinic systems over dicationic and pyrrolic ones, with nearly thermoneutral reactions. This property is usually beneficial for catalytic hydrogenation reactions in which the H atoms transferred in the process should not be over-stabilized by the catalyst. In line with this, recent studies have proposed pyridinic Ru SACs as promising candidates for the catalytic hydrogenation of various organic substrates.^27,57

The computed hydrogenation thermodynamics indicated that the most exergonic reactions are those involving the addition of H₂ to the nitrogen atoms in either cis or trans. From a homogeneous catalysis perspective, this behavior may appear as unexpected since heterolytic cleavage in bifunctional moieties, where a base takes one H atom as a proton and a metal takes the other as a hydride, is the most common H₂ activation mechanism, hereby prompting the question of what is the actual role of the metal in these SAC systems. Our calculations suggest that the hydrogen activation reaction might be even more exergonic without any metal, potentially leading to surface poisoning by hydrogen immobilization (Fig. S11). Feng et al. give a similar explanation to rationalize the hydrogen transfer in their NiN₄ Py-SAC study, with hydrogens easily adsorbed on the metal-free system but difficult to desorb.⁵⁸ However, it should be noted that the metal also plays the role of stabilizing the N-doped sites that disrupt the otherwise pristine structure of graphene.

Origin of Py and Pyrr model reactivity differences

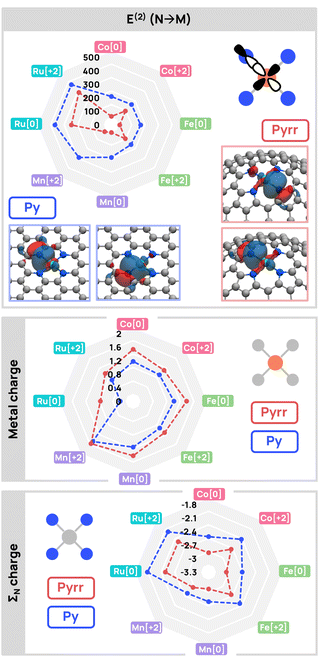
To understand the origin of the reactivity differences, we carried out an NBO analysis of the non-hydrogenated catalysts in their ground spin state (Fig. 5). Charge distribution and donor–acceptor interactions were analysed on the basis of natural charges and stabilisation energies (E⁽²⁾), respectively. In the top panel of Fig. 5, we can see that, for all metals, the Py model systems consistently exhibit higher donation from the nitrogen sp orbitals to the in-plane, and in-phase, d orbital of the metal (E⁽²⁾∑(N → M) ∼200–400 kcal mol⁻¹) compared to Pyrr systems (E⁽²⁾∑(N → M) ∼50–140 kcal mol⁻¹), probably due to the flat surface of the Py model increasing orbital overlap. The weaker donation in the Pyrr systems is reflected in the charge distributions, where the total charge of the metal-bound nitrogen atoms (∑N) is, on average, 0.3e units more negative, with the metal centres being more oxidised by a similar amount, that is, ∼0.3e units more positive. The stronger basicity of the Pyrr nitrogen atoms is consistent with the higher stability of the NHNH hydrogenation products.

Fig. 5 Stabilization energies (E⁽²⁾) from nitrogen-to-metal orbital donor–acceptor interaction (top), natural charges of the metal center (middle), and total nitrogen natural charges (∑N, bottom) across all metal and charge states. Blue points represent Py systems, red points represent Pyrr systems.

Akin to the hydrogenation thermodynamics, the 1st-row transition metal systems exhibit similar behavior, while Ru deviates from the trend. Ru systems yield substantially greater nitrogen-to-metal donation in Py and Pyrr systems (E⁽²⁾∑(N → M) ∼250–400 kcal mol⁻¹) compared to Co, Fe, Mn systems (E⁽²⁾∑(N → M) ∼50–200 kcal mol⁻¹). Consequently, the charge of Ru is the least cationic among the metals, and the nitrogens in these systems are less negatively charged. This charge transfer during complexation from the nitrogens of the surface to the metal atom is highlighted in the NEDA analysis, which shows a larger CT component in Ru systems compared to 1st-row metals. Furthermore, the value for the XC component of the interaction energy is notably lower for Ru by 50 to 100 kcal mol⁻¹, indicating enhanced delocalization and covalent interactions (Fig. S12). In contrast, 1st-row metal systems with a dominant electrical interaction, primarily arising from polarization, lead to more accessible nitrogen orbitals with increased negative charges.

Combining donor–acceptor interactions, charge analysis, and NEDA analysis reveals that 1st-row and Pyrr systems achieve superior charge separation, making nitrogens more reactive. In contrast, Ru and Py systems have stronger interactions between the nitrogens and the metal, resulting in a redistribution of electronic density. The distinction between neutral and dicationic states emerges mainly in NEDA results, where [+2] systems display consistently higher POL components compared to [0] systems. In terms of addition mode, the accessible nitrogen orbitals in 1st-row and Pyrr systems support the NHNH reactivity, facilitated by ionic interactions and further enhanced by dicationic charges. Ru systems show a distinct behavior where nitrogen does not facilitate hydrogen transfer. Instead, the interaction between the SAC surface and the metal atom predominantly promotes MH₂ addition. Unexpectedly, the hydrogens in MH₂ Ru systems are not hydridic. In fact, for both Py and Pyrr systems and for all hydrogenation modes, the NBO charges indicate that the transferred hydrogens have a protonic character while the graphene surface (nitrogen and carbon, i.e., ∑N, ∑C) gains electrons (Fig. S13 and S14). The metal charge is also impacted, by +0.4e in most cases, and, in the few cases where it is not reduced, the electron charge is largely absorbed by the metal-bound nitrogen atoms (Fig. S15). The transfer of electrons from the hydrogens to the catalysts resembles the proton-coupled electron transfer (PCET), described in electrochemical reactions, with the protons and electrons transferred simultaneously but to different parts of the system. This type of mechanism is well represented in porphyrinic systems, which are structurally similar to the Pyrr systems.^59–62 The numerous examples of SAC in electrocatalysis, where PCET can take place, also reflects the potential of the graphene support to facilitate electron transfer and, therefore, this type of mechanism.^63–66

Ultimately, SACs seem to react as electrocatalysts rather than thermocatalysts. The homolytic or heterolytic H₂ cleavage was not observed in any 1st-row systems. Enhancing ionic interactions via pyrrolic and dicationic environments is crucial for activating Co, Fe, and Mn systems, wherein hydrogen transfer occurs through the NHNH addition mode. The curvature of these systems may contribute significantly to their high reactivity,⁴⁶ and further research on this criterion is recommended. While Ru-SACs can also capitalize on pyrrolic environments and, to a lesser extent, on dicationic configurations, they display unique reactivity through the MH₂ addition mode due to enhanced interactions between the support and the metal atom. Graphene-based SACs, therefore, offer the potential to unlock novel reactivity for processes such as hydrogenation, for which alternative paths are often overlooked or lack thorough exploration.

Conclusions

In conclusion, this study highlights the distinct reactivity profiles of N-doped graphene-based SACs during hydrogenation processes. By examining the thermodynamics of dihydrogen addition, we identified the active sites for hydrogenation, revealing two main reactivity patterns that differ from traditional homogeneous catalysis. Hydrogen atoms are either transferred to two nitrogens or directly to the metal atom. The transferred hydrogens adopt a protonic character while the remaining electron gets transferred to the surface, a mechanism favored by the conductivity properties of graphene. Pyrrolic systems exhibited greater activity, with energies often below 25 kcal mol⁻¹, while pyridinic systems remained mostly inactive, with the exception of Ru. Ru systems are also different in their addition mode, favoring MH₂, while Co, Fe, and Mn systems displayed similar behavior, preferring NHNH modes.

NBO, natural charge, and NEDA analyses revealed electronic structural differences driving these reactivity variations. Pyrr systems showed lower donation from nitrogen orbitals to the metal ones compared to Py systems, leading to enhanced charge separation, accessible N orbitals, and increased nitrogen basicity, favoring NHNH addition mode. Fe, Co, and Mn leverage these characteristics with higher POL components in interaction energies compared to Ru, furthering the preferences of Pyrr systems and NHNH mode. Dicationic systems amplify this trait, making [+2]Pyrr configurations the most reactive sites. In contrast, Py systems are characterized by dominant CT and X interactions, with substantial nitrogen orbital donation, more covalent N–M bonds, and reduced nitrogen accessibility. These characteristics are heightened for Ru, where MH₂ is readily accessible across all sites.

Ultimately, strong reactivity differences could be observed between Ru and 1st-row metals and Py and Pyrr systems, arising from different electronic structures. These differences must be acknowledged when designing SACs and further investigated both computationally and experimentally.

Author contributions

A. E. F. D. was responsible for performing all calculations and producing the initial draft of the manuscript (text, tables, and figures), which was later revised by A. N. and D. B. All authors played a significant role in the conception and development of the project, with A. N. and D. B. being the main contributors in the research project design and supervision.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: structures, including an xyz file; energies obtained without the metal and with different basis sets; and details on natural charges, spin states and NEDA analysis. See DOI: https://doi.org/10.1039/d5ta08094k.

Acknowledgements

Research Council of Norway (RCN) FRIPRO program supporting the CO2pCat project, with number 314321 (A. N.). RCN FRIPRO program supporting the catLEGOS project, with number 325003 (A. E. F. D. and D. B.). RCN support through the Centers of Excellence program, including the Hylleraas Centre, with project number 262695, and the Sigma2 National Infrastructure for High-Performance Computing and Data Storage in Norway, with grant numbers NN4654K and NS4654K (A. E. F. D., A. N., and D. B.).

Notes and references

1. V. G. Chandrashekhar, W. Baumann, M. Beller and R. V. Jagadeesh, Science, 2022, 376, 1433–1441.
2. P. Ferrin, S. Kandoi, A. U. Nilekar and M. Mavrikakis, Surf. Sci., 2012, 606, 679–689.
3. S. Das, R. Laplaza, J. T. Blaskovits and C. Corminboeuf, J. Am. Chem. Soc., 2024, 146, 15806–15814.
4. F. Meemken and A. Baiker, Chem. Rev., 2017, 117, 11522–11569.
5. H. Blaser, C. Malan, B. Pugin, F. Spindler, H. Steiner and M. Studer, Adv. Synth. Catal., 2003, 345, 103–151.
6. S. E. Clapham, A. Hadzovic and R. H. Morris, Coord. Chem. Rev., 2004, 248, 2201–2237.
7. D. Wang and D. Astruc, Chem. Rev., 2015, 115, 6621–6686.
8. A. Corma, J. Navas and M. J. Sabater, Chem. Rev., 2018, 118, 1410–1459.
9. G. J. Kubas, Science, 2006, 314, 1096–1097.
10. K. Christmann, Surf. Sci. Rep., 1988, 9, 1–163.
11. D. R. Aireddy and K. Ding, ACS Catal., 2022, 12, 4707–4723.
12. E. Podyacheva, O. I. Afanasyev, D. V. Vasilyev and D. Chusov, ACS Catal., 2022, 12, 7142–7198.
13. B. Ramasamy and P. Ghosh, Eur. J. Inorg. Chem., 2016, 2016, 1448–1465.
14. X. Cui, W. Li, P. Ryabchuk, K. Junge and M. Beller, Nat. Catal., 2018, 1, 385–397.
15. W. Zhang, Q. Fu, Q. Luo, L. Sheng and J. Yang, JACS Au, 2021, 1, 2130–2145.
16. S. K. Kaiser, Z. Chen, D. Faust Akl, S. Mitchell and J. Pérez-Ramírez, Chem. Rev., 2020, 120, 11703–11809.
17. H. Hu and J. Xi, Chin. Chem. Lett., 2023, 34, 107959.
18. C. Lv and D. Chen, ChemCatChem, 2024, 16, e202401084.
19. Z. Wei, D. Guo, Y. Hou, H. Xu and Y. Liu, J. Taiwan Inst. Chem. Eng., 2016, 67, 126–139.
20. X. Deng, J. Wang, N. Guan and L. Li, Cell Rep. Phys. Sci., 2022, 3, 101017.
21. A. Baby, L. Trovato and C. Di Valentin, Carbon, 2021, 174, 772–788.
22. W. Yang, S. Xu, K. Ma, C. Wu, I. D. Gates, X. Ding, W. Meng and Z. Gao, Nano Mater. Sci., 2020, 2, 120–131.
23. H. Fei, J. Dong, Y. Feng, C. S. Allen, C. Wan, B. Volosskiy, M. Li, Z. Zhao, Y. Wang, H. Sun, P. An, W. Chen, Z. Guo, C. Lee, D. Chen, I. Shakir, M. Liu, T. Hu, Y. Li, A. I. Kirkland, X. Duan and Y. Huang, Nat. Catal., 2018, 1, 63–72.
24. M. D. Esrafili and B. Nejadebrahimi, Appl. Surf. Sci., 2019, 475, 363–371.
25. F.-F. Wang, R. Guo, C. Jian, W. Zhang, R. Xue, D.-L. Chen, F. Zhang and W. Zhu, Inorg. Chem., 2022, 61, 9138–9146.
26. J. Chen, Y. Xia, Y. Ling, X. Liu, S. Li, X. Yin, L. Zhang, M. Liang, Y.-M. Yan, Q. Zheng, W. Chen, Y.-J. Guo, E.-H. Yuan, G. Hu, X. Zhou and L. Wang, Nano Lett., 2024, 24, 5197–5205.
27. H. Wang, F. Shi, M. Pu and M. Lei, ACS Catal., 2022, 12, 11518–11529.
28. J. Zhang, C. Jian, F. Wang, W. Zhang, Z. Tian and D. Chen, ChemPhysChem, 2024, 26, e202400628.
29. H. Huang, C. Jian, Y. Zhu, R. Guo, X. Chen, F.-F. Wang, D.-L. Chen, F. Zhang and W. Zhu, Phys. Chem. Chem. Phys., 2021, 23, 25761–25768.
30. H. Jin, P. Li, P. Cui, J. Shi, W. Zhou, X. Yu, W. Song and C. Cao, Nat. Commun., 2022, 13, 723.
31. J. Kuang, M. Gong, G. Chen, L. Peng, C. Zou, Z. Peng, W. Chen, Y. Li, Y. Zhang, T. Xue, C. Li, Y. Dong, J. Wu, I. Akpinar, L. Lin, X. Zeng, X. Tang, Y. Sun, J.-C. Dong, L. Sun, W. Chen, P. Lyu, S. Yang, C. Cao, W. Song and J.-F. Li, Chem. Eng. J., 2024, 490, 151678.
32. G. Zhang, F. Tang, X. Wang, L. Wang and Y.-N. Liu, ACS Catal., 2022, 12, 5786–5794.
33. Z. An, P. Yang, D. Duan, J. Li, T. Wan, Y. Kong, S. Caratzoulas, S. Xiang, J. Liu, L. Huang, A. I. Frenkel, Y.-Y. Jiang, R. Long, Z. Li and D. G. Vlachos, Nat. Commun., 2023, 14, 6666.
34. J. Zhang, C. Zheng, M. Zhang, Y. Qiu, Q. Xu, W.-C. Cheong, W. Chen, L. Zheng, L. Gu, Z. Hu, D. Wang and Y. Li, Nano Res., 2020, 13, 3082–3087.
35. A. E. F. Denjean, A. Nova and D. Balcells, ACS Catal., 2024, 14, 11332–11342.
36. D. Zaoralová, R. Langer and M. Otyepka, ACS Sustain. Chem. Eng., 2025, 13, 8319–8330.
37. X. Sun, A. I. Olivos-Suarez, D. Osadchii, M. J. V. Romero, F. Kapteijn and J. Gascon, J. Catal., 2018, 357, 20–28.
38. Y. Han, Z. Wang, R. Xu, W. Zhang, W. Chen, L. Zheng, J. Zhang, J. Luo, K. Wu, Y. Zhu, C. Chen, Q. Peng, Q. Liu, P. Hu, D. Wang and Y. Li, Angew. Chem., Int. Ed., 2018, 57, 11262–11266.
39. M. Li, C. Zhang, Y. Tang, Q. Chen, W. Li, Z. Han, S. Chen, C. Lv, Y. Yan, Y. Zhang, W. Zheng, P. Wang, X. Guo and W. Ding, ACS Catal., 2022, 12, 11960–11973.
40. G.-P. Lu, H. Shan, Y. Lin, K. Zhang, B. Zhou, Q. Zhong and P. Wang, J. Mater. Chem. A, 2021, 9, 25128–25135.
41. M. S. Ahmad, Y. Inomata and T. Kida, Mol. Catal., 2022, 526, 112390.
42. M. Subaramanian, P. M. Ramar, G. Sivakumar, R. G. Kadam, M. Petr, R. Zboril, M. B. Gawande and E. Balaraman, ChemCatChem, 2021, 13, 4334–4341.
43. H. Fan, F. Qin, Q. Yuan, Z. Sun, H. Gu, W. Xu, H. Tang, S. Liu, Y. Wang, W. Chen, J. Li and H. Zhai, J. Mater. Chem. A, 2023, 11, 17560–17569.
44. H. Qi, J. Yang, F. Liu, L. Zhang, J. Yang, X. Liu, L. Li, Y. Su, Y. Liu, R. Hao, A. Wang and T. Zhang, Nat. Commun., 2021, 12, 3295.
45. M. Urso, X. Ju, R. Nittoor-Veedu, H. Lee, D. Zaoralová, M. Otyepka and M. Pumera, ACS Catal., 2025, 15, 11617–11663.
46. Y. Liu, Z. Wu, C. Gu, J. Chen, Y. Zhu and L. Wang, Small, 2024, 20, e2404758.
47. M. Xu, Y. Yu, G. Shi, P. Jian, X. Hou and E. Yuan, ACS Appl. Nano Mater., 2024, 7, 11952–11964.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc. Wallingford CT, 2016.
49. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
50. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
51. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
52. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
53. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
54. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2018, http://nbo7.chem.wisc.edu/.
55. L. Liu, T. Chen and Z. Chen, Adv. Sci., 2024, 11, 2308046.
56. F. Mo, C. Song, Q. Zhou, W. Xue, S. Ouyang, Q. Wang, Z. Hou, S. Wang and J. Wang, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2300281120.
57. L. Huai, J. Zhang and W. A. Goddard, J. Am. Chem. Soc., 2024, 146, 31251–31263.
58. Y. Feng, S. Long, B. Chen, W. Jia, S. Xie, Y. Sun, X. Tang, S. Yang, X. Zeng and L. Lin, ACS Catal., 2021, 11, 6398–6405.
59. P. Hutchison, A. V. Soudackov and S. Hammes-Schiffer, ACS Catal., 2024, 14, 14363–14372.
60. J. J. Warren and J. M. Mayer, J. Am. Chem. Soc., 2011, 133, 8544–8551.
61. S. Y. Reece, J. M. Hodgkiss, J. Stubbe and D. G. Nocera, Philos. Trans. R. Soc., B, 2006, 361, 1351–1364.
62. J. Thomas, T. Mokkawes, L. Senft, A. Dey, J. B. Gordon, I. Ivanovic-Burmazovic, S. P. de Visser and D. P. Goldberg, J. Am. Chem. Soc., 2024, 146, 12338–12354.
63. Q. Zhang, H. J. Tsai, F. Li, Z. Wei, Q. He, J. Ding, Y. Liu, Z. Lin, X. Yang, Z. Chen, F. Hu, X. Yang, Q. Tang, H. B. Yang, S. Hung and Y. Zhai, Angew. Chem., Int. Ed., 2023, 62, e202311550.
64. N. Heppe, C. Gallenkamp, R. Z. Snitkoff-Sol, S. D. Paul, N. Segura-Salas, H. Haak, D. C. Moritz, B. Kaiser, W. Jaegermann, V. Potapkin, A. Jafari, V. Schünemann, O. Leupold, L. Elbaz, V. Krewald and U. I. Kramm, J. Am. Chem. Soc., 2024, 146, 12496–12510.
65. C. Gao, S. Chen, Y. Wang, J. Wang, X. Zheng, J. Zhu, L. Song, W. Zhang and Y. Xiong, Adv. Mater., 2018, 30, 1704624.
66. H. Fei, J. Dong, D. Chen, T. Hu, X. Duan, I. Shakir, Y. Huang and X. Duan, Chem. Soc. Rev., 2019, 48, 5207–5241.

---