Combining chemical, geometric, and novel topological features to develop generalizable machine learning models for predicting mechanically stable MOFs

Abstract

Metal–organic frameworks (MOFs) are promising functional materials, but poor mechanical stability leading to loss of porosity and degraded performance under external pressure limits their commercial use. The diversity of MOF building blocks makes exhaustive experimental or simulation-based screening for high mechanical stability impractical. While some prior work has used machine learning (ML) to accelerate discovery, ML models typically lack the ability to generalize across diverse MOF topologies. Starting from a dataset with around an order of magnitude more secondary building units and topology types than previously studied, we develop a generalizable and interpretable ML framework to predict MOF mechanical stability (i.e., by predicting the bulk modulus). Our ML models incorporate novel and interpretable topological features developed based on principles of net theory and chemical features that are applicable across a broad range of MOF chemistries and topologies. We employ our models in a virtual high-throughput screening of over ∼435k MOFs from existing hypothetical and experimental databases to identify the most mechanically stable candidates with potential industrial applications.

---

1. Introduction

Metal–organic frameworks¹ (MOFs) represent a prominent class of porous, crystalline materials assembled from inorganic secondary building units (SBUs) and organic linkers. Their exceptional chemical tunability^2,3 and high porosity⁴ make them promising candidates for a wide range of applications, including gas separation and storage,^5,6 catalysis,^7,8 atmospheric water harvesting,^9–12 and desalination.^13–15 The modular nature of MOF construction allows for a vast combinatorial space, offering extensive possibilities for designing materials with tailored properties. Despite their potential, a significant barrier to the widespread, real-world implementation of MOFs is their typically limited mechanical stability. Under external stress, many MOFs undergo deleterious phase transitions that can lead to a loss of crystallinity, reduced pore volume, and eventual structural collapse.^16–19 This mechanical fragility curtails their utility in large-scale applications where structural integrity is paramount.^20–22 Consequently, identifying exceptionally stable MOFs and establishing clear design principles to enhance their mechanical robustness are critical steps toward realizing the industrial potential of this material class.

The extensive combinatorial space of MOF SBUs, linkers, and nets corresponds to millions of potential structures,²³ making experimental discovery of a MOF with the optimal properties for a desired application a formidable challenge. Experimentally validated MOFs have been compiled from the Cambridge Structural Database²⁴ by refining single-crystal structures, with around 9–10 000 MOFs total from either the CoRE MOF 2019 ASR²⁵ or the revised CoRE MOF DB 2025 v2.0 ASR²⁶ databases. Hypothetical MOFs have been systematically enumerated by combining different building blocks. Earlier hypothetical databases include hMOF²⁷ (∼130 000 structures), BW-DB²⁸ (∼300 000 structures), and ToBaCCo²⁹ (∼13 000 structures). Motivated by the observation of a lack of diversity³⁰ and stability³¹ in these hypothetical MOFs compared to experimental MOFs, USMOF³¹ (∼54 000 structures) was developed with more topological and metal diversity. Systematically synthesizing and testing this vast array of either experimental or hypothetical candidates for mechanical stability is both resource-intensive and prohibitively time-consuming. As a result, virtual high-throughput screening (VHTS) powered by computer simulations has emerged as an indispensable tool for efficiently navigating this expansive chemical space to identify promising new materials.^26–28

A key indicator of the mechanical failure point of a MOF is the pressure at which it loses crystallinity, as determined from its stress–strain curve.^32,33 However, computing the entire stress–strain curve for thousands of structures is computationally intractable for VHTS. The bulk modulus, a measure of a material's resistance to compression calculated within its elastic regime, has been established as a reliable and computationally efficient proxy for mechanical stability³⁴ suitable for VHTS.³⁵ Bulk moduli can most accurately be obtained from DFT and ab initio molecular dynamics,^36,37 but classical force fields offer a faster alternative with reasonable accuracy.^35,38 Nevertheless, for truly large-scale screening on the order of 500k experimental and hypothetical MOFs, even faster alternatives are needed.

To mitigate the cost of VHTS, machine learning (ML) has proven to be a powerful accelerator. By establishing quantitative structure–property relationships (QSPRs), ML models can rapidly predict the properties of unseen MOFs, bypassing the need for expensive simulations.^39–42 In recent years, ML has been successfully applied to predict MOF performance in various applications like separation^43–48 and storage,^49–51 along with their stability^52–58 under varying conditions. However, previous applications of ML to mechanical stability have faced several key limitations. QSPRs for the bulk modulus have often been constrained by datasets with limited diversity in MOF building blocks and topologies. For instance, an early ML model trained on 3385 ToBaCCo²⁹ MOFs highlighted the influence of pore geometry on stability but lacked the chemical and topological breadth needed for broad generalizability. Another effort using 20 342 QMOFs⁵⁹ addressed the building block limitations of the ToBaCCo set but failed to address the question of topological diversity.⁵³ Furthermore, a critical gap in many of these studies has been the absence of robust featurization methods capable of encoding the global topology of the framework,^53–55 which is crucial for establishing clear QSPRs linking a MOF's topology to its stability. As a result, a systematic understanding of which building blocks are most or least critical for mechanical integrity remains largely unexplored, and a unified ML-driven workflow for discovering exceptionally stable MOFs across all major databases has been missing.

In this work, we address these limitations to build the most comprehensive and generalizable QSPR model for MOF mechanical stability to date. We previously curated³¹ a bulk modulus dataset for 7330 thermally and activation stable USMOFs, which offers an order of magnitude greater diversity in its building blocks and topologies compared to the preceding ToBaCCo set. Nevertheless, no QSPRs were established on that dataset, which we address in the present study. First, we use this dataset to systematically quantify the hierarchical influence of different MOF building blocks on the bulk modulus, identifying the structural components most critical for enhancing stability. Next, we introduce a set of novel and interpretable topological features derived from net theory to overcome the representation challenges of previous models. We demonstrate that combining these topological features with established geometric and chemical descriptors leads to ML models with good generalizability. Finally, we leverage our predictive models to perform a massive VHTS campaign across both hypothetical and experimental MOF databases, identifying over 22 000 candidates with exceptionally mechanical stability. We validate our high-throughput screening results by performing direct MD simulations on the top-performing structures, confirming the efficacy of our ML-guided discovery pipeline.

2. Computational details

2.1 Data set

We employed 7330 hypothetical “ultrastable” MOFs (i.e., with respect to thermal stability and activation stability) in the ultrastable MOF database (USMOF DB) and their Voigt–Reuss–Hill bulk modulus (K_VRH) computed in prior work.³¹ As in the original study, we categorized the building blocks of USMOFs as nodes (any organic or inorganic component containing more than two connection points) and edges (organic building blocks with two connection points) rather than using the terms “linker” and “SBU,” enabling an unambiguous decomposition of a MOF structure into distinct building blocks.³¹ As per the definitions of node and edge, both organic nodes and edges are essentially linkers, while inorganic nodes are SBUs. The 7330 USMOFs used in our study comprise three configurations of inorganic nodes, organic nodes, and organic edges: (1) one inorganic node and one edge (1inor–1edge, totaling 3900 MOFs), (2) one inorganic node, one organic node, and one edge (1inor–1org–1edge, totaling 2395 MOFs), and (3) two inorganic nodes and one edge (2inor–1edge, totaling 1035 MOFs). Another effort using 20 342 QMOFs⁵⁹ addressed the building block limitations of the ToBaCCo set, but we do not use bulk moduli calculated in that study because differences in calculation protocol make it hard to combine both datasets for the ML prediction task.

2.2 MOF featurization

In this work, we used both numerical and text-based MOF features to train and fine-tune different machine-learning models. We used three classes of numerical descriptors: (1) 176 revised autocorrelations⁶⁰ (RACs) obtained using molSimplify v1.7.3,⁶¹ (2) 14 geometric descriptors obtained from Zeo++ v0.3,⁶² and (3) 10 novel topological features that we developed in this work based on the principles of net theory. RACs, initially created as features for transition metal complexes⁶⁰ and subsequently adapted for MOFs,⁶³ identify the chemical features and local topology of MOFs by assessing the products and differences of different atomic properties (Text S1 and Table S1). Out of 176 RACs, we removed 28 that were invariant over USMOF DB, leaving us with 148 RACs as MOF descriptors (Table S2). The geometric descriptors assess the pore geometry of MOFs by measuring pore size, probe accessible and non-accessible volume, surface area, and pore volume (Table S3). To calculate the probe accessible/non-accessible volume, we selected a probe radius of 1.86 Å, which reflects the approximate radius of a nitrogen molecule.

The combined use of RACs and geometric descriptors has allowed ML models to attain outstanding results in forecasting MOF properties in numerous recent studies.^{31,44,46,56,57,64} Still, prior work⁵⁵ has shown a strong correlation between MOF nets and mechanical stability. Hence, in this work, we introduce novel topological features to explore their effect on the performance of our models. The novel topological features are developed based on the short symbol⁶⁵ representation of periodic nets. They contain the normalized frequency of different cycle lengths, starting from the minimum cycle length of three up to the maximum cycle length of twelve found amongst 495 distinct nets in the USMOF database (Text S2 and Table S5). A net with a higher frequency of smaller cycle lengths (e.g., 3, 4, and 5) corresponds to a higher average metal coordination number (MCN) and a more rigid pore network, thereby resulting in greater mechanical stability (Text S2 and Table S4). We also use two combinations of the numerical features to train our ML models: (1) RACs and Zeo++ features and (2) RACs, Zeo++, along with topological features, which allows us to investigate the explicit effect of topological features on the performance of our ML models (Fig. S1). For text-based representation of MOFs, we used the previously developed MOFid,⁶⁶ which is a structure-agnostic representation of MOFs containing symbols of metals present in the SBU, SMILES⁶⁷ strings of MOF linkers, and the Reticular Chemistry Structural Resource⁶⁸ (RCSR) symbol of MOF nets (Fig. S2).

2.3 Development of ML models and MOF screening

We used scikit-learn⁶⁹ v1.3.0 to train ML models with four different architectures: random forest regressor (RFR), gradient boosting regressor (GBR), and kernel-ridge regressor (KRR) with Laplacian or radial basis function kernel. We also used PyTorch⁷⁰ v1.10.1 with CUDA Toolkit v11.3.1 support to train artificial neural networks (ANNs) with more complex architectures. Since the USMOF database contains three distinct classes of MOFs based on the number and type of nodes (1inor–1edge, 1inor–1org–1edge, and 2inor–1edge), it is important to know if a model trained on one MOF class can generalize to other classes. For each of the five model architectures, we trained three ML models for each MOF class separately and one model for all the MOFs, resulting in a total of twenty models trained from scratch. All twenty ML models across the five different ML architectures were trained using two combinations of the numerical descriptors (see Section 2.2). Apart from training ML models from scratch, we also implemented a transfer learning approach where we fine-tuned a previously developed transformer model with a self-attention mechanism called MOFormer⁷¹ to predict mechanical stability in MOFs. As we did for the other ML architectures, we fine-tuned four different MOFormer models separately for each MOF class and the entire USMOF DB using MOFid (see Section 2.2) as a text-based representation of MOFs. Before model training and fine-tuning, we created 80/20 train/test splits for our datasets. For numerical features, we Z-normalized both the training and test set features using the mean and standard deviation of the respective training set features. After dataset normalization, we performed recursive feature addition (RFA) for all models except the ANNs (i.e., the RFR, GBR, and KRR models) to avoid overfitting and improve interpretability and generalizability (Tables S6). For RFA, we began with the five most important features and incrementally added additional features until model performance no longer improved. We performed extensive hyperparameter optimization either using grid search for RFR, GBR, and KRR models or using hyperopt v0.2.7 (ref. 72) for the ANN models, along with five-fold cross-validation (Table S7). Due to the large computational cost associated with fine-tuning the MOFormer model, we carried out a less extensive hyperparameter optimization with three-fold cross-validation for that model (Table S7). After training and fine-tuning, we assessed the performance of all the models on the set-aside test set and performed Shapley additive explanation (SHAP)⁷³ analysis of the best-performing models to understand the structure–property relationships in mechanical stability. We also computed the latent space distance (LSD) scaled by the maximum latent space distance to any point in the test set and averaged over ten nearest neighbors⁷⁴ to use as an uncertainty quantification metric. Before screening for novel MOFs with exceptional stability using our ANN model, we implemented the uniform manifold approximation and projection⁷⁵ (UMAP) algorithm to reduce the dimensionality of the 512-dimensional latent space of the model into two dimensions, which illustrates the coverage of the training USMOFs in the space of hypothetical and experimental MOFs. To determine if these datasets contained duplicate MOFs, we identified them using the Weisfeiler-Lehman graph hash⁷⁶ method implemented in NetworkX⁷⁷ v3.0.

2.4 Molecular simulation for K_VRH estimation

We calculated MOF K_VRH for MOFs not previously assessed following the same methodology as in our earlier work.³¹ We employed the LAMMPS v29Sep2021 (ref. 78) package and the UFF4MOF^79,80 force field to describe the MOFs. The K_VRH values were obtained from the 6 × 6 stiffness matrix.⁸¹ This tensor encompasses all the information regarding the mechanical behavior of a MOF in the elastic region of the stress–strain curve. To compute the stiffness matrix, we imposed a maximum strain of 1% and assessed the relative energy variation between the deformed and the original structure. Conjugate gradient minimization was employed for geometry optimization prior to stiffness calculation.

3. Results and discussion

3.1 Trends among K_VRH and MOF properties

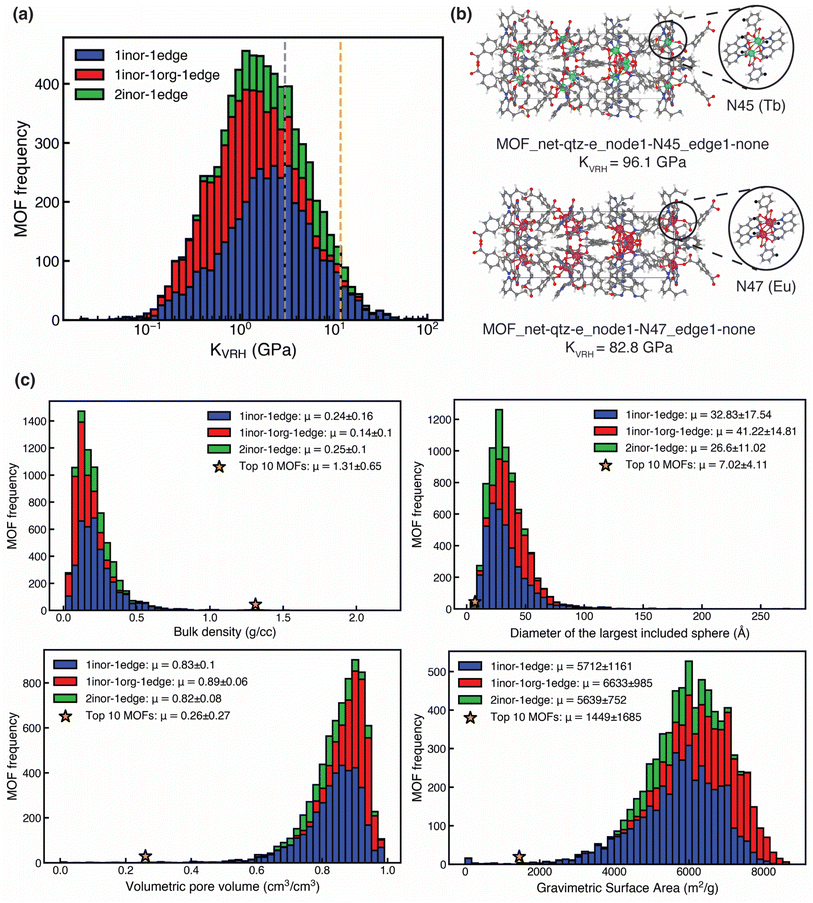
We first explored the distribution of K_VRH previously calculated in the USMOF dataset.³¹ We observed a wide range (0.02–96.0 GPa) of mechanical strengths in our dataset with moderate average values (3.02 GPa) and a long-tailed distribution (Fig. 1a). We identified a set of 270 (3.7% of 7330) exceptionally mechanically stable MOFs, which we define as those with mechanical stability at least two standard deviations above average (i.e., all MOFs with K_VRH > 11.86 GPa). Of the connectivity classes, we found most exceptionally stable MOFs were 1inor–1edge MOFs (200 MOFs, 74.1%), and the fewest were 1inor–1org–1edge MOFs (23 MOFs, 8.5%). When we compared this distribution of MOFs with that of the original set, we found enrichment of 1inor–1edge MOFs (53.2% MOFs in the original set) and significant depletion of 1inor–1org–1edge MOFs (32.7% MOFs in the original set) in the exceptionally stable subset. Focusing on the ten most mechanically stable MOFs, we found all the MOFs with outstanding mechanical stability (K_VRH > 39 GPa) to be from the 1inor–1edge class. The two most mechanically stable are characterized by lanthanide-based (Tb or Eu) dinuclear nodes with carboxylate and bipyridine linkers that lead to exceptionally high mechanical stability (Fig. 1b and Table S8).⁸²

Fig. 1 (a) Stacked bar plots showing the distribution of K_VRH for 1inor–1edge MOFs (blue bars), 1inor–1org–1edge MOFs (red bars), and 2inor–1edge MOFs (green bars). The vertical dashed lines denote the following: gray for overall mean K_VRH and orange for two standard deviations above the overall mean K_VRH. (b) Structures of the two MOFs with the highest K_VRH in our dataset. The inorganic nodes in both the MOFs are shown in the inset, with the node identities and metals present in the nodes. The K_VRH values are reported for these examples. In the structures, the atoms are colored as follows: white for hydrogen, gray for carbon, blue for nitrogen, red for oxygen, magenta for europium, and turquoise for terbium. (c) Stacked bar plots representing the distribution of bulk density (top left), diameter of the largest included sphere (top right), volumetric pore volume (bottom left), and gravimetric surface area (bottom right) of 1inor–1edge MOFs (blue bars), 1inor–1org–1edge MOFs (red bars), and 2inor–1edge MOFs (green bars). In each plot, the orange star denotes the mean geometric property of the top ten exceptionally stable MOFs (Table S8). The mean geometric properties of all three classes of MOFs and the top ten MOFs are reported in the insets.

We next investigated the geometric properties of the ten most mechanically stable MOFs in our dataset. MOF geometry has been found to be significantly relevant for mechanical stability.^53,55 We computed and compared the distribution of four geometric properties (see Section 2.2): bulk density (ρ), diameter of largest included sphere (D_i, also known as the largest cavity diameter), fractional volumetric pore volume (VPOV), and gravimetric surface area (GSA). We found the mean D_i, VPOV, and VSA of the top ten MOFs to be at least three times lower than the rest of the MOF set, and we found the mean ρ of the top ten MOFs to be over six times higher than the mean ρ of the remaining MOFs (Fig. 1c and Table S9). Thus, the top ten MOFs are characterized by lower porosity and higher bulk density, as might be expected.^53,55 Our observation is further confirmed by the negative correlation between pore dimensions (D_i, VPOV, and VSA) and K_VRH (Spearman's r ≤ −0.41) and a positive correlation between ρ and K_VRH (Spearman's r ≥ 0.53) for all three classes of MOFs present in our dataset (Fig. S3). This explains why MOFs in the class that contains organic nodes lack exceptional mechanical stability, as they have consistently higher pore dimensions (D_i, VPOV, and VSA) and lower density (Fig. 1c). While mechanically stable MOFs with lower porosity are expected, we investigated if there are MOFs that have high mechanical stability despite having high porosity, since such MOFs are likely targets for gas storage applications. We identified one such Mg-based 1inor–1edge MOF with carboxylate linkers that both belongs to the exceptionally stable subset (K_VRH = 19.30 GPa) and possesses above average (i.e., by one std. dev.) porosity as judged by the largest included sphere (D_i = 64.5 Å, Fig. S4).

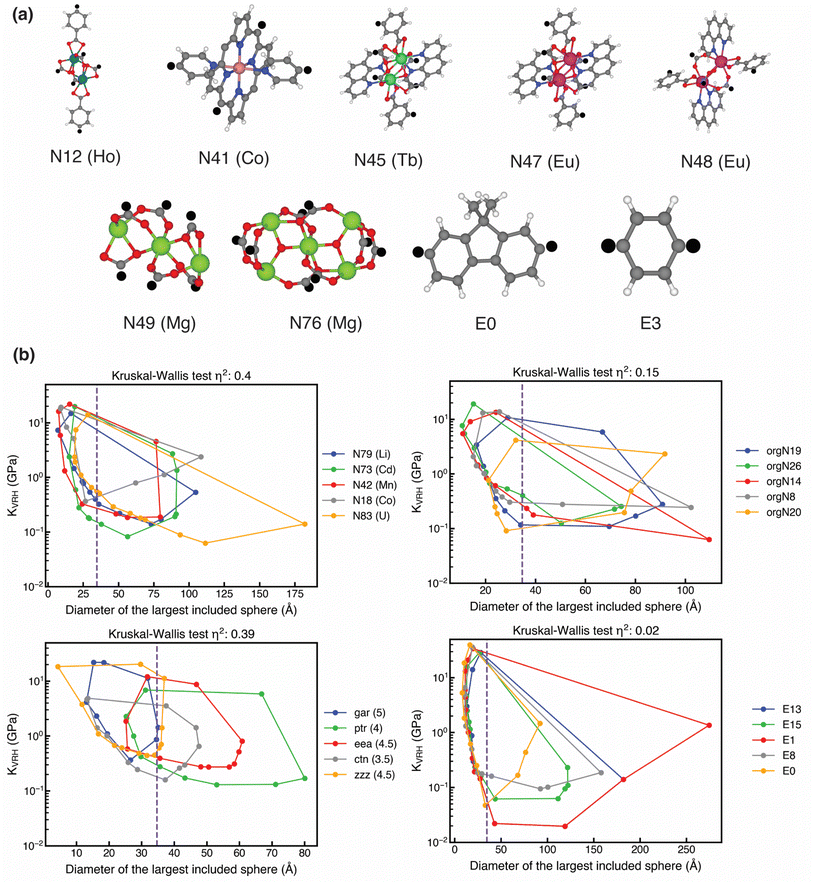
We next investigated the building blocks in the most mechanically stable MOFs. We first explored the linker chemistry that was common across the distinct inorganic nodes (N12, N41, N45, N47, N48, N49, and N76) present in the ten most stable MOFs (Fig. 2a). We observed three distinct linker chemistries with similar frequency: carboxylate linkers (4 MOFs, nodes N12, N49, and N76), porphyrin linkers (3 MOFs, node N41), and combined carboxylate/bipyridine linkers (3 MOFs, nodes N45, N47, and N48) (Fig. 2a). Upon investigating only the linker chemistries that are enriched in mechanically stable MOFs compared to the entire set, we discovered significant enrichment of both porphyrin and combined carboxylate/bipyridine linkers, with nearly eight times enrichment of porphyrin linkers and two times enrichment of combined carboxylate/bipyridine linkers (Table S10). To isolate our focus to the portion of the linker that does not coordinate the metal, we evaluated edge frequency. As per the definition of node and edge, MOFs in our dataset can occasionally only be comprised of nodes and lack edges (see Section 2),³¹ and, indeed, most of the highest-stability MOFs (8 of 10) lack edges (Table S8).^55,83,84 In the remaining two MOFs, we found two edges (E0 and E3) with short lengths (Fig. 2a and S5).³¹

Fig. 2 (a) Structures of the seven distinct inorganic nodes (N12, N41, N45, N47, N48, N49, and N76) and two distinct organic edges (E0 and E3) present in the ten most mechanically stable MOFs. The metals present in the inorganic nodes are reported in the labels below each node. In the structures, the atoms are colored as follows: white for hydrogen, gray for carbon, blue for nitrogen, red for oxygen, yellow-green for magnesium, light pink for cobalt, magenta for europium, turquoise for terbium, and teal for holmium. The black circles denote the atoms present in the inorganic nodes and edges that serve as connection points with other building blocks. (b) 2D convex hull of K_VRH vs. diameter of the largest included sphere for MOFs containing any of the five most frequent inorganic nodes (top left), organic nodes (top right), nets (bottom left), and edges (bottom right) in our entire dataset (more results shown in Fig. S6). In each panel, the purple vertical dashed line corresponds to the average diameter of the largest included sphere (34.7 Å) of all MOFs in our dataset. The metals present in the inorganic nodes are shown in the legend, the average metal coordination number of the nets is shown in the legend, and the η² values from the Kruskal–Wallis tests are reported above each pane.

Turning to SBU chemistry, there are five unique metals present across seven distinct inorganic nodes, out of which three are lanthanides (Tb, Eu, and Ho) and two are lighter elements (Co, Mg, Fig. 2a). All five metals were enriched in the most stable MOFs over the original set, with the highest enrichment of Ho (10% of the top ten MOFs vs. 0.7% of 7330 MOFs, Table S11 and Fig. S7). Although the presence of Co, specifically in porphyrinic nodes, and lanthanides has been shown to enhance the mechanical stability of MOFs,⁵³ the observation Mg MOFs having high mechanical stability had not been reported.

We also investigated the most frequent nets in the top ten mechanically stable MOFs. Despite the highest presence of gar and ptr nets over our entire dataset (7.1% and 6.8% respectively), we discovered the qtz-e net to be the net for the three most stable MOFs and, therefore, the most frequent among the top ten (Fig. S8 and Table S8). This is a significant enrichment of this net from its presence in the original set (0.16% of 7330 MOFs). We further probed the average metal coordination number (MCN) of the nets. Consistent with prior work,⁵⁵ we found enrichment of higher MCNs of six (6 top-ten MOFs vs. 16.5% of all MOFs) and eight (1 top-ten MOF vs. 1.1% of all MOFs) in comparison to the predominant MCN of 4 in the overall set (38.9% of all MOFs, Fig. S9). The fact that the qtz-e net has an MCN of six potentially contributes to its abundance among the ten most stable MOFs.

To uncover the influence of the MOF building blocks and nets on K_VRH, we performed non-parametric Kruskal–Wallis tests,⁸⁵ which can quantify the extent of variations in K_VRH with different MOF building blocks and nets using a η² metric (i.e., higher values indicate larger variations). For the five most frequent building blocks and nets across all MOFs in our dataset, we found the most significant variations in K_VRH for inorganic nodes and nets (η² of 0.40 and 0.39 for inorganic nodes and nets, Fig. 2b, S6 and Text S3). Although both organic nodes and edges are analogous to MOF linkers, we discovered significantly lower variation in K_VRH with edges than with organic nodes (η² of 0.02 vs. 0.15), which can be explained by the substantially greater influence of organic nodes on MOF pore size than edges (Fig. 2b and S10). Our finding that the identity of the inorganic node has the highest influence on MOF mechanical stability was consistent across all three classes of MOFs, at odds with prior work that identified MOF net to be the dominant factor for predicting mechanical stability (Fig. S11–S13).⁵⁵

3.2 ML models for mechanical stability prediction

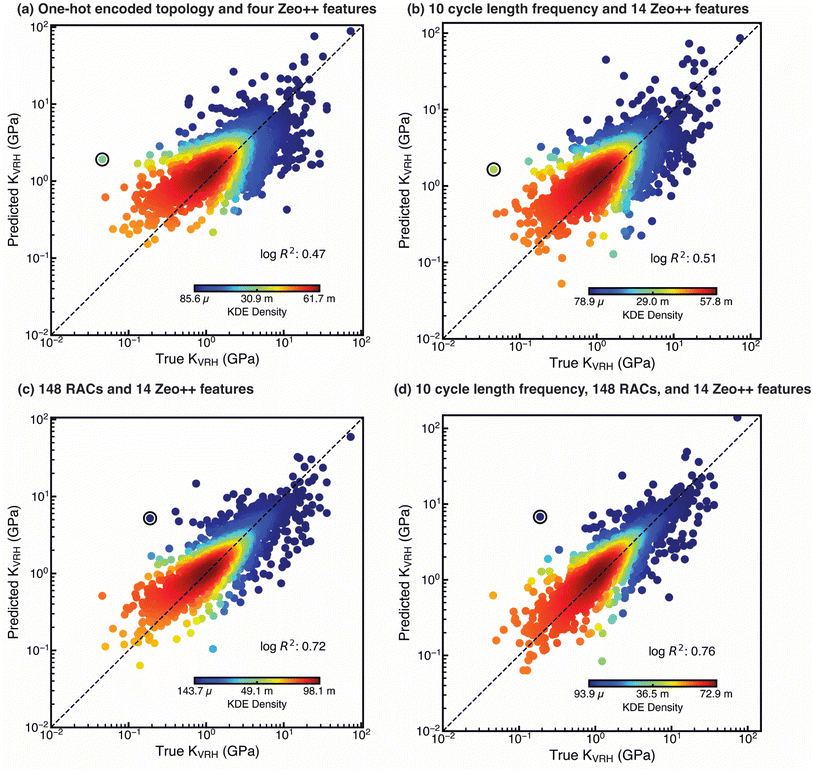
To capture complex structure–property relationships between mechanical stability and MOF building blocks, topology, and pore geometry, we trained interpretable ML models. We considered several strategies for featurizing our MOFs. We introduced a new type of topological feature that encodes the frequency of different cycle lengths (i.e., connected rings in the structure of the MOF). We also featurized MOFs using graph-based RACs^30,86 that encode atom-wise chemistry and local connectivity, and we included Zeo++ features⁶² that encode MOF pore geometry (Texts S1, S2 and Tables S1–S3). We also trained models over each of the three individual classes of MOFs (1inor–1edge, 1inor–1org–1edge, and 2inor–1edge) to investigate possible variability in the structure–property relationships between the three MOF classes.

Inspired by previous work on ML for MOF mechanical stability,⁵⁵ we first trained an ANN using only four geometric features (ρ, D_i, VPOV, and GSA) obtained using Zeo++ in combination with one-hot encoded net features to evaluate if this set of features alone is sufficient to develop generalizable ML models for K_VRH prediction across our dataset. Due to the heavily skewed distribution of K_VRH towards lower values, we selected the log R² (i.e., the log transform was applied prior to computing R²) as a more appropriate performance evaluation metric for our models instead of R², since achieving high R² in significantly skewed data is challenging.⁵³ Unlike in prior work, we observed extremely poor performance for the ANN model trained over the entire dataset (test set log R² = 0.47, Fig. 3a). Similar unsatisfactory performance by the ANN models was observed when training on individual classes of MOFs, with the best performance for 1inor–1org–1edge MOFs and the worst performance for 2inor–1edge MOFs (test set log R² = 0.51 vs. 0.42, Table S12). Overall, the poor performance of the models is likely due to the greater chemical and topological diversity in our USMOF dataset than in the subset of ToBaCCo MOFs used in the previous work.^29,55

Fig. 3 Test set parity plots of predicted vs. true K_VRH for the ANN models trained on the entire USMOF dataset containing all three classes (1inor–1edge, 1inor–1org–1edge, and 2inor–1edge) of MOFs using (a) one-hot encoded topology and four Zeo++ features, (b) 10 cycle length frequency and 14 Zeo++ features, (c) 148 RAC and 14 Zeo++ features, and (d) 10 cycle length frequency, 148 RAC, and 14 Zeo++ topological features. The data points are colored by kernel density estimation (KDE) density values as shown by inset color bars, and black dashed lines indicate the parity lines. For each model, the datapoint corresponding to the most extreme outlier MOF is denoted by the black circle, and the structures of those MOFs are shown in Fig. S14. The values of log R² are reported in the insets.

While investigating the most extreme outlier MOF (id: MOF_net-sod-g_node1-N66_edge1-E7) during our prediction task over the entire set, we found the MOF to be highly porous (ρ = 0.048 g cm⁻³, D_i = 92.3 Å, and VPOV = 0.96 cm³ cm⁻³) with a bulk density less than 25% of the average for MOFs in our dataset (Fig. S14 and Table S9). This motivated us to explore alternativ featurization. To investigate whether adding other geometric features (e.g., the diameter of the largest free sphere) could improve the performance of the ANN models, we retrained our models with ten additional geometric features obtained using Zeo++, but we did not observe any improvement in model performance (Tables S3 and S12).

Motivated by the overriding effect that topology had in earlier estimations of mechanical stability, we next investigated whether we could introduce customized topological features to improve ANN model performance over one-hot encoded features. One disadvantage of one-hot encoded features in our USMOF set is that this approach does not encode any measure of similarity among different nets. Using a feature set based on the properties, rather than the identities, of the nets allows similarity to be leveraged by the model. We developed topological features based on the short symbol⁶⁵ representation of periodic nets. Specifically, these features contain the normalized frequency of different cycle lengths (Text S2). Our models trained only with these new topological features and all fourteen Zeo++ features showed somewhat enhanced performance over the entire dataset (test set log R² = 0.51 vs. 0.47) in comparison to the one-hot encoding and Zeo++ feature set (Fig. 3b). Still, our model performance was only somewhat improved with the topological features, which we attribute to the absence of MOF chemical information from the feature set.

With the aim of improving upon the geometry/topology-only model in mind, we encoded the chemistry of the MOFs through a combination of RAC and Zeo++ features used extensively in our previous work on MOFs, but we omitted information about the global topology.^{30,31,44,46,49,56,57,64} Although global topology is not explicitly present in this new feature set, this information is partially encoded in the MOF graph captured by RACs as the local connectivity between atoms. Using RAC and Zeo++ features, we found significant improvement in the performance of the models over the geometry/topology-only models for the entire set (test set log R² = 0.72 vs. 0.51, MAE = 1.19 GPa, Fig. 3c). We again observed the best performance for the model trained on 1inor–1org–1edge MOFs and the worst for the model trained on 2inor–1edge MOFs (test set log R² = 0.72 vs. 0.66, Table S12).

We next investigated whether we could further improve the performance of the models by adding information about the global topology missing in RACs. We first added the one-hot encoded topology to the set of RAC and Zeo++ features, but the ANNs trained with this new feature set performed similarly to the models trained with RAC and Zeo++ features alone (Table S12). When we instead added our novel topological features instead of one-hot encoded topology features, we observed further improvement in model predictions beyond the performance of models trained with only RAC and Zeo++ features (test set log R² = 0.76 vs. 0.72 when training and evaluating over the entire set, MAE = 1.13 GPa, Fig. 3d). However, out of the three individual MOF classes, we only found appreciable model performance improvement for the model trained on 1inor–1edge MOFs when using this feature set (test set log R² = 0.74 vs. 0.72, Table S12). The negligible influence of our novel topological features on the model performance for 1inor–1org–1edge MOFs is possibly due to a lower influence of topology on K_VRH for those MOFs, as hypothesized earlier. However, a low effect for 2inor–1edge MOFs is probably due to the similarity of topologies present in those MOFs, with most of them having an average MCN of 5 (78% of MOFs, Fig. S9). For all feature sets considered (i.e., after adding RACs), the most extreme outlier is the same for all models (id: MOF_net-ske_node1-N17_edge1-E13, Fig. S14). Despite the building blocks of the outlier MOF appearing during training, the inability to correctly predict K_VRH for this MOF is likely due to a more complex synergistic effect between building blocks that is not represented elsewhere in the training data.

We next investigated if we could further improve the performance of our best-performing ANN models trained with RAC, Zeo++, and the novel topological features by employing more interpretable model architectures and feature engineering. Such models have previously demonstrated comparable performance to ANNs.^49,57 To test this, we used four distinct simpler model architectures: a random forest regressor (RFR), a gradient boosting regressor (GBR), and a kernel ridge regressor (KRR) utilizing either a Laplacian kernel (KRR-Laplacian) or a radial basis function kernel (KRR-RBF). The KRR kernels encode similarity relationships, unlike ANNs which encode complex non-linear relationships. To prevent overfitting and to reduce the impact of uninformative features in these models, we employed recursive feature addition (RFA) (Table S6). All four RFA-trained model architectures modestly outperform our best-performing ANN models, both when evaluating over the entire set and also when restricting scope to each of the three individual MOF classes (Table S13 and Fig. S15). Of the four models, we found the KRR-Laplacian model to perform best across the entire set (test set log R² = 0.79 vs. 0.76 for the best-performing ANN model, MAE = 1 GPa) and also when trained on individual MOF classes.

To compare against an alternative approach to the K_VRH prediction task, we implemented a transfer learning approach where we fine-tuned a previously developed transformer model with a self-attention mechanism called MOFormer.⁷¹ MOFormer, which was pretrained on > 400k MOF structures, has demonstrated excellent performance when fine-tuned on relatively small datasets (∼14k to ∼137k) in predicting band gap and gas adsorption.⁷¹ For the USMOFs in our dataset, we first obtained the structure-agnostic text-based representation of MOFs used by MOFormer, called the “MOFid,” which encodes MOF chemistry and topology (Fig. S2).⁶⁶ We fine-tuned MOFormer on individual USMOF classes and also over the entire USMOF DB. Surprisingly, we found poor performance of the MOFormer model in all the prediction tasks when compared to our best-performing KRR-Laplacian model (test set log R² over the entire set = 0.65 for MOFormer vs. 0.79 for the KRR-Laplacian model, Fig. S16 and Table S14). When we compared the performance of the MOFormer model with the ANNs trained earlier, we found that the fine-tuned MOFormer performed better than all the geometry/topology-only models, but it always performed worse than an ANN when RACs were included in the ANN feature set. This can most likely be attributed to the smaller training dataset size compared to past prediction tasks and missing information about MOF 3D structure in MOFid that is extremely relevant for MOF mechanical stability. Thus, out of all the models considered, we identified the KRR-Laplacian model with RACs, Zeo++, and topological features to be the best-performing model across our data, with mean absolute errors of 1 GPa over all test MOFs and 8.24 GPa over exceptionally stable test MOFs (Tables S13 and S15).

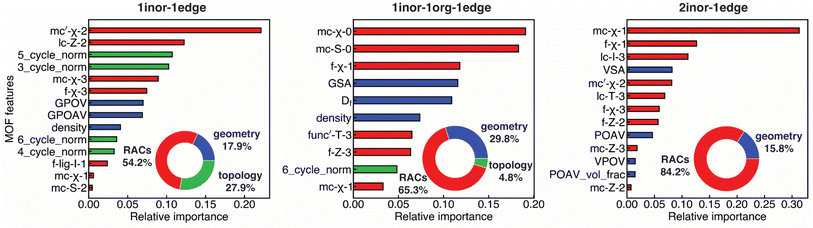
We next identified the most influential MOF features and quantified their contribution to predicting K_VRH with our best-performing KRR-Laplacian model for the three MOF classes (1inor–1edge, 1inor–1org–1edge, and 2inor–1edge) using feature importance analysis (see Section 2).⁷³ This analysis assigned importance values to each feature, which we then normalized to show relative importance (Fig. 4). Consistent with observations on model performance depending strongly on the addition of RACs, our analysis revealed the paramount importance of RACs for all the MOF classes, with RACs having the highest importance for 2inor–1edge MOFs (84.2% of collective importance, Fig. 4). Specifically, we found the electronegativity of the metal and around the metal center (mc-χ-0, mc-χ-1, and mc′-χ-2, where ′ indicates a difference RAC) to be the most important out of all the RACs (e.g., mc-χ-1 contributes 31% for 2inor–1edge MOFs, Fig. 4 and Table S1). The key importance of metal electronegativity can be attributed to hard–soft acid–base (HSAB) theory, where metals with low electronegativity form exceptionally strong bonds with hard bases like O and N common to MOF linkers. This feature importance result is consistent with the prevalence of lanthanides and Mg in the ten most stable MOFs, since such metals are harder acids than more abundant 3d transition metals like Cd and Zn present in USMOFs (Fig. 2, S7 and Table S11).³¹

Fig. 4 SHAP feature importance analysis for the best-performing KRR-Laplacian models individually trained on the K_VRH dataset containing 1inor–1edge MOFs (left), 1inor–1org–1edge MOFs (center), and 2inor–1edge MOFs (right). The relative importance of all the features is shown in the bar plots. The bars are color-coded based on the feature class to which each feature belongs: blue for geometric features, green for topological features, and red for RACs. The percentage of importance of the geometric features, topological features, and RACs is shown in the inset pie charts. See Tables S1–S3, Texts S1 and S2 for explanation of feature nomenclature.

We next investigated the most important geometric and topological features. Out of all the geometric features, we found MOF surface area and pore volume to be the most important, which is consistent with the strong negative correlation between those features and K_VRH (Fig. S3). When comparing the three MOF types, geometric features had the most significant effect for 1inor–1org–1edge MOFs out of the three MOF classes (29.8% of total importance), emphasizing our hypothesis that geometry is more important for these MOFs because they sample a larger range of high porosities. With respect to topological features, we found these to be most important for 1inor–1edge MOFs (27.9%), with the normalized frequencies of three to six cycle lengths being the most important topological features. The maximum cycle length in our set is twelve, and thus emphasizing smaller cycle lengths suggests the importance of higher connectivity (i.e., higher average MCN) for mechanical stability. For the other MOFs, we expected higher influence of geometric features for 1inor–1org–1edge MOFs, and we attribute the lack of topological diversity for 2inor–1edge MOFs as the reason why those features are not selected (Fig. 4). For example, 78% of 2inor–1edge MOFs have an average MCN of 5 (Fig. S9). Overall, our feature importance analysis consistently demonstrated the strongest influence of metal chemistry on mechanical stability for all classes of MOFs in comparison to geometry or topology.

3.3 Identifying mechanically stable MOFs in databases

To identify MOFs with exceptional mechanical stability in databases of hypothetical and experimental MOFs, we next used our ML models to screen these MOFs. For experimental MOFs, we selected the all-solvent-removed (ASR) MOFs from the CoRE MOF DB 2025 v2.0 ASR (ref. 26) database, whereas the hypothetical MOFs were selected from three databases: (1) BW-DB,²⁸ (2) hMOF,²⁷ and (3) ToBaCCo.²⁹ Despite the best performance of the KRR-Laplacian model across our USMOF DB, we chose the second-best model, which is an ANN, for the screening task because ANNs perform well in their application to unseen materials (Table S12). We selected the ANN model trained with RACs, Zeo++, and novel topological features trained over the entire USMOF DB, which showed the best performance out of all the ANN models in our work (see Fig. 3). Because the topological features are essential for the screening task, we only screened MOFs that (1) do not have any ambiguities associated with their topology and (2) their topologies have valid short symbol representations to enable the determination of their topological features. Starting from 475 891 hypothetical and 8854 experimental MOFs, this filtering step reduced our MOFs to a total of 433 550 hypothetical and 3157 experimental MOFs. We further removed 949 duplicate experimental MOFs (see Section 2), resulting in a final pool of 2208 experimental MOFs (Table S16). Overall, we observed a significantly higher attrition rate of experimental MOFs than hypothetical MOFs in obtaining our final MOF pool, which is expected since a vast majority of experimental MOFs (35% MOFs) contain topologies that cannot be assigned RCSR symbols.

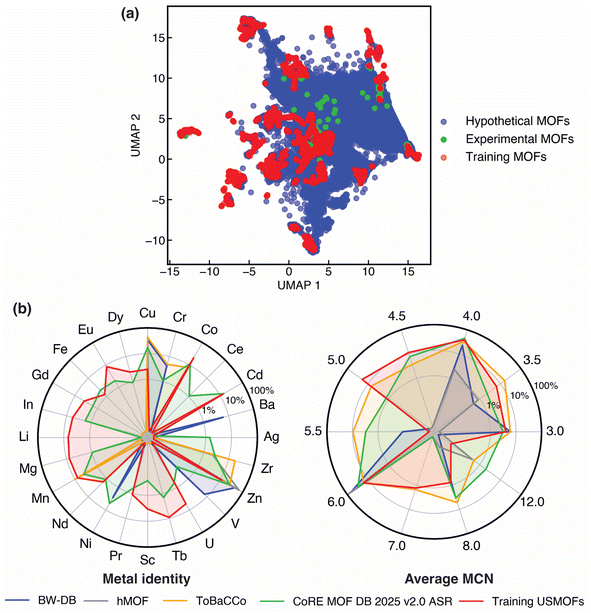
To first assess the suitability of applying the ANN model to unseen experimental and hypothetical MOFs, we compared the distribution of hypothetical and experimental MOFs with the training set USMOFs in the latent space of the model. We employed dimensionality reduction to visualize the coverage of training MOFs in the space of hypothetical and experimental MOFs (Fig. 5). While we observed overall good overlap of the training MOFs with the broader hypothetical and experimental MOF space, some regions of space were more well populated than others. Although, by design,³¹ the USMOFs have similar metal diversity to experimental MOFs, Cu and Zr metals were less well represented in USMOFs compared to experimental or hypothetical MOFs. In terms of geometric properties, all hypothetical and experimental MOFs are significantly less porous than the training set USMOFs, with an average bulk density 4–6× that of the training set USMOFs (Table S17). The connectivity (i.e., the MCN), all three sets of MOFs were quite similar (Fig. 5b). Overall, good coverage in properties is observed between the training set of USMOFs and the sets we would like to predict properties on, but we might expect relatively high model uncertainty for model predictions due to differences in the porosity and metal frequency between the USMOFs and the other datasets.

Fig. 5 (a) Uniform manifold approximation and projection (UMAP) dimensionality reduction on the latent space of the ANN model trained with RACs, Zeo++, and novel topological features over the entire USMOF DB to visualize the coverage of training set USMOFs (red points) across the space of hypothetical (blue points) and experimental (green points) MOFs. (b) Radar plots showing the distribution of metal identities (left) and average metal coordination number (MCN, right) for training set USMOFs and the set of MOFs present in three hypothetical databases (BW-DB, hMOF, and ToBaCCo) and the experimental CoRE MOF DB 2025 v2.0 ASR database that were used to screen exceptionally mechanically stable MOFs. The distributions are shown on a logarithmic scale. For metal identity, the sum of the MOF percentages for all the metals may exceed one since a MOF can have more than one metal type. The average MCN is computed by averaging over the MCNs of all distinct types of nodes present in a MOF, which can make the average MCN fractional (e.g., average MCN of 3.5 for a MOF with nodes having MCNs 3 and 4).

To overcome potential limitations in coverage of hypothetical and experimental MOF space by the USMOF DB training data, we incorporated uncertainty quantification (UQ) prior to making predictions. The distance to training data (i.e., LSD) in the last layer of the model provides an estimate of model uncertainty.⁷⁴ We scaled the LSD with respect to training data and confirmed that the threshold value of this quantity can be adjusted to systematically reduce test set error (Fig. S17). For screening unseen MOFs, we selected the LSD threshold (0.37) that produced a 1 GPa mean absolute error on the retained test set MOFs. Using this threshold, we estimated K_VRH for 35% of hypothetical MOFs (152 805 out of 433 550 MOFs) with the highest percentage for ToBaCCo MOFs (46.4%) and the lowest percentage for hMOFs (23.4%), which can be attributed to their relative similarity to USMOF MOFs in terms of their average geometric properties (Tables S17 and S18). Unlike hypothetical MOFs, we were only able to make uncertainty-controlled estimates of K_VRH for 6.9% of experimental MOFs (152 out of 2208 MOFs), which can be explained by the low porosity of experimental MOFs that makes their geometric properties most dissimilar to those of training set USMOFs (Tables S17, S18 and Fig. S18).

In total, we estimated K_VRH of 152 957 MOFs. From this subset, we identified 22 609 exceptionally stable MOFs (22 583 hypothetical and 26 experimental) that have two standard deviations higher K_VRH than the mean K_VRH of USMOFs (K_VRH > 11.86 GPa). Out of the 22 583 hypothetical MOFs with exceptional stability, we found the vast majority to be BW-DB MOFs (18 883 MOFs) with the lowest representation of ToBaCCo MOFs (only 43 MOFs, Table S18). When we investigated the percentage of MOFs with estimated K_VRH that have exceptional stability, we observed significantly higher percentages for both BW-DB and hMOFs (15.1% and 15.6%) over ToBaCCo MOFs (1.1%), which can be explained by the lower porosities of BW-DB and hMOFs compared to ToBaCCo MOFs (Tables S17 and S18). We observed the percentage of exceptionally stable MOFs to be even higher for experimental MOFs (17.1%), which can similarly be explained by the lowest porosity of experimental MOFs out of all the MOF databases (Tables S17 and S18). A comprehensive list of all exceptionally stable MOFs is provided in the Zenodo repository.⁸⁷

For our predicted top-performing MOFs, we next validated our ANN-predicted K_VRH values with molecular simulation. Out of eight MOFs corresponding to the top two from each of the four experimental/hypothetical databases, six were found to be exceptionally stable (K_VRH > 11.86 GPa) based on their simulated K_VRH values (Table S19). The ANN-predicted K_VRH values on hypothetical MOFs showed considerable deviations from simulated values, with errors as high as 295%. For the experimental MOFs, this error generally corresponded to an underprediction, while for hypothetical MOFs it often corresponded to an overprediction. For top experimental MOFs, the underprediction by our model is likely due to the limitation of the model in extrapolating to MOFs with K_VRH higher than the mean K_VRH of top experimental MOFs (K_VRH > 30.8 GPa), since our training set of USMOFs contains only 0.4% of such MOFs. Nevertheless, the 75% successful validation rate of the ANN model demonstrates its potential in uncovering novel and exceptionally stable MOFs. A broader analysis of 100 randomly sampled MOFs from the set of exceptionally stable screened MOFs achieved a 70% success rate in classifying MOFs (Text S4 and Fig. S19). Our analysis has also identified that the instances of limited generalization by our models arise due to significant mismatches between the geometric features of training USMOFs and the screened MOFs.

We further examined the characteristics of the six (i.e., exceptionally stable) highest-performing screened MOFs that were predicted by our ML model and validated by simulation. We found that they all contained common metals (Zn, Cu) and linker chemistry (i.e., N or O coordination), consistent with the prevalence of these features in the overall MOF sets (Fig. 6 and S20). Surprisingly, we did not find any lanthanide MOFs in our top MOFs even though we found those MOFs to be the most stable in USMOFs, which can be explained by the absence of lanthanides in the hypothetical MOFs and limited presence of such MOFs in the prediction set of experimental MOFs (8.6% of MOFs in the experimental prediction set vs. 23.8% of USMOFs). In terms of overall topology, we observed that four out of six MOFs have the pcu net with an MCN of 6 (Fig. 6). This is again likely due to the higher frequency of the pcu net in both the experimental and combined hypothetical prediction set (i.e., 26% of experimental MOFs and 64% of combined hypothetical MOFs) and the fact that an MCN of 6 is the highest possible value in all sets excluding ToBaCCo (Fig. S21). Finally, we assessed four key geometric properties (D_i, ρ, VPOV, and GSA) for all the top six stable MOFs. We observed that four out of the six exceptionally stable MOFs were less porous than the average MOF in the respective prediction set, with as much as 3.7× lower GSA than an average MOF in the prediction set (for the top stable ToBaCCo MOF, Tables S20 and S21).⁸⁸ Overall, our results indicate that a preference for the topology with the highest available MCN and lower porosity than the original training set is a common feature of highly mechanically stable MOFs. However, based on the feature analysis on our models, further significant improvement in the mechanical stability can be achieved by judicious metal substitution in SBUs based on the chemistry of the linker connecting atoms. Specifically, hard acid metals like lanthanides and magnesium substitution are highly recommended in MOFs with oxygen or nitrogen as linker connecting atoms.

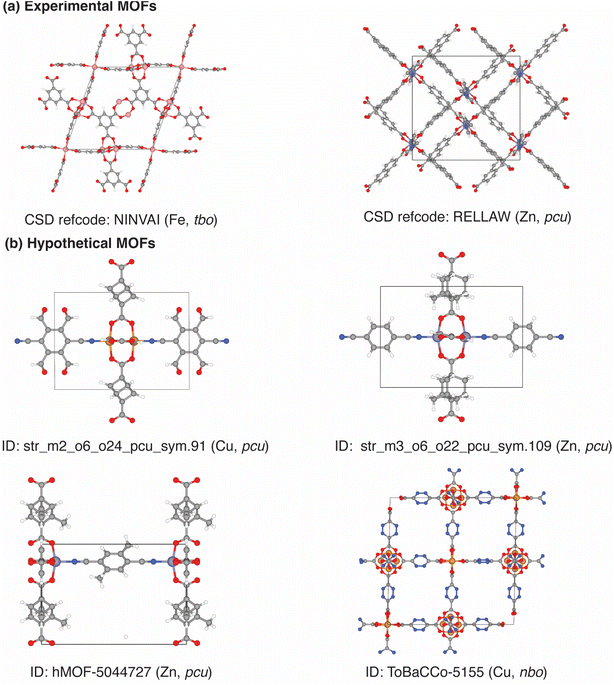Fig. 6 Structures of the top simulation-validated, exceptionally stable (K_VRH > 11.86 GPa) (a) experimental and (b) hypothetical MOFs derived after screening MOFs in the experimental MOF (CoRE MOF DB 2025 v2.0 ASR) database and three hypothetical MOF databases (BW-DB, hMOF, and ToBaCCo). The experimental CoRE MOFs and hypothetical MOFs are denoted using their Cambridge Structural Database²⁴ (CSD) reference code and their database ID, respectively. Each MOF is noted with its metal identity and the Reticular Chemistry Structure Resource⁶⁸ (RCSR) topology symbols (in parentheses). In the structures, the atoms of MOFs are color-coded as follows: white for hydrogen, gray for carbon, blue for nitrogen, red for oxygen, pink for iron, yellow for copper, and gray blue for zinc. The geometric properties of the MOFs and their ANN-predicted and molecular simulation-calculated K_VRH values are provided in Table S19.

We finally investigated the chemical realizability of 22 583 exceptionally stable hypothetical MOFs. The building blocks of these MOFs were originally obtained from experimental MOFs in previous databases (e.g., CoRE 2014 (ref. 89) and CoRE 2019 (ref. 25)), which contained several structural errors, including overlapping atoms, invalid atom connectivity, and incorrect metal oxidation states.^90–92 By employing a recently developed positive-unlabeled crystal graph convolutional network, MOFClassifier,⁹³ we have identified 6863 exceptionally stable hypothetical MOFs with valid structures, suggesting their potential synthetic feasibility. In total, our VHTS approach has enabled the identification of 6889 exceptionally stable MOFs (6863 hypothetical and 26 experimental) with chemically valid structures. The list of stable hypothetical MOFs with valid structures is provided in our Zenodo repository.⁸⁷

4. Conclusions

In this work, we have advanced the search for mechanically stable MOFs by developing generalizable ML models trained with novel topological features and chemical descriptors (i.e., RACs). We started with a dataset of 7330 hypothetical ultrastable MOFs (USMOFs) with over six times the inorganic node diversity and ten times the topological diversity of prior work. While we found a dominant presence of hard acid metals like lanthanides and magnesium in the most mechanically stable MOFs, we also discovered the frequent appearance of topologies with high average metal coordination numbers in the most stable MOFs. Using non-parametric Kruskal–Wallis tests, we uncovered the most significant dependence of K_VRH on inorganic node identity, followed by topology, organic nodes, and edges.

We next constructed ML models with different architectures and MOF features to identiy structure–stability relationships. Contrary to prior work, we demonstrated the significant limitations of only geometric and categorically encoded topological features in developing generalizable models across broad MOF chemistry. We showed improvement in the performance of our models after incorporating RACs encoding MOF chemistry and local connectivity as well as through novel topological features based on the short symbol representation of periodic nets. Feature importance analysis on our models revealed the most significant contribution to dictating MOF mechanical stability to be metal chemistry rather than MOF geometry or topology.

Finally, we screened around 433k hypothetical and 2.2k experimental MOFs to identify exceptionally stable MOFs. Using our best-performing ANN model, we confidently identified K_VRH of 152 957 MOFs (152 805 hypothetical and 152 experimental) with a 75% successful validation rate of our model identifying MOFs with exceptional stability in a set of eight highly stable MOFs. Further improvement of the models in this work, especially in identifying stable experimental MOFs, could be achieved by enlarging training datasets to capture more MOFs with lower porosity that are representative of the geometric properties of experimental MOFs. Additionally, the accuracy of predicted K_VRH could be further enhanced by developing integrated ML-based workflows with judicious DFT screening or employing emergent machine-learned interatomic potentials that can achieve DFT-level accuracy with significantly lower computation cost than DFT. Overall, we expect that hard acid metal substitution will be a successful strategy to enhance mechanical stability in porous MOFs and that the developed topological features could be useful in other materials such as covalent organic frameworks and polymer networks.

Conflicts of interest

The authors declare no competing financial interest.

Data availability

The data supporting this article has been included as part of the supplementary information (SI) or in a Zenodo repository described below.

Zenodo repository: the features and K_VRH of our USMOF dataset, features of hypothetical and experimental MOFs, Python scripts to train machine learning models, a Jupyter notebook for MOF screening, K_VRH of screened MOFs, a Jupyter notebook and associated files to construct USMOFs from their building blocks, and LAMMPS scripts to determine MOF K_VRH are available at an online Zenodo repository (https://doi.org/10.5281/zenodo.17088767).

Supplementary information: details of revised autocorrelations (RACs); list of different types and number of RACs; list of invariant RACs; list of geometric features; details of topological features developed using net theory; list of MOF nets with missing topological features; details of MOFid representation; list of recursive feature addition selected features; details of ML hyperparameter optimization; list of top ten mechanically stable USMOFs; list of mean geometric properties of top ten USMOFs; correlation between K_VRH and geometric properties; structures of the exceptionally stable USMOFs with high porosity; linkers and metals present in the top ten stable MOFs; metals and nets, average metal coordination number (MCN) distribution in USMOFs; length of edges present in USMOFs; details of Kruskal–Wallis test; list of most frequent building blocks in USMOFs; convex hull of pore volume vs. diameter of the largest included sphere; convex hull of K_VRH vs. cavity diameter for 1inor–1edge, 1inor–1org–1edge, and 2inor–1edge MOFs; test set performance of ML models; structures of the most extreme outlier MOF; test set ML parity plots; number of MOFs in hypothetical and experimental databases; mean geometric properties of MOFs that were screened; details of uncertainty quantification; summary of MOF screening results; K_VRH and geometric properties of top screened MOFs; metal, MCN, and geometric properties of hypothetical and experimental MOFs within ANN uncertainty. See DOI: https://doi.org/10.1039/d5ta08080k.

Acknowledgements

This work was supported by the Defense Threat Reduction Agency under grant number HDTRA12510008. A. K. B. was partially supported by a Massachusetts Institute of Technology School of Engineering MathWorks Fellowship. H. J. K. acknowledges support in the form of an Alfred P. Sloan Foundation Fellowship in Chemistry and the Simon Family Faculty Research Innovation Fund. The authors acknowledge the MIT SuperCloud and Lincoln Laboratory for providing HPC resources that have contributed to developing the ML models reported within this article. The authors thank Adam H. Steeves for providing a critical reading of the manuscript.

References

1. H.-C. Zhou, J. R. Long and O. M. Yaghi, Introduction to Metal–Organic Frameworks, Chem. Rev., 2012, 112, 673–674.
2. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, The Chemistry and Applications of Metal-Organic Frameworks, Science, 2013, 341, 1230444.
3. R. Wei, C. A. Gaggioli, G. Li, T. Islamoglu, Z. Zhang, P. Yu, O. K. Farha, C. J. Cramer, L. Gagliardi, D. Yang and B. C. Gates, Tuning the Properties of Zr₆O₈ Nodes in the Metal Organic Framework UiO-66 by Selection of Node-Bound Ligands and Linkers, Chem. Mater., 2019, 31, 1655–1663.
4. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Ultrahigh porosity in metal-organic frameworks, Science, 2010, 329, 424–428.
5. O. I.-F. Chen, C.-H. Liu, K. Wang, E. Borrego-Marin, H. Li, A. H. Alawadhi, J. A. R. Navarro and O. M. Yaghi, Water-Enhanced Direct Air Capture of Carbon Dioxide in Metal–Organic Frameworks, J. Am. Chem. Soc., 2024, 146, 2835–2844.
6. M. M. Sadiq, M. P. Batten, X. Mulet, C. Freeman, K. Konstas, J. I. Mardel, J. Tanner, D. Ng, X. Wang, S. Howard, M. R. Hill and A. W. Thornton, A Pilot-Scale Demonstration of Mobile Direct Air Capture Using Metal-Organic Frameworks, Adv. Sustainable Syst., 2020, 4, 2000101.
7. L. Alaerts, E. Séguin, H. Poelman, F. Thibault-Starzyk, P. A. Jacobs and D. E. De Vos, Probing the Lewis Acidity and Catalytic Activity of the Metal–Organic Framework [Cu₃(btc)₂] (BTC=Benzene-1,3,5-tricarboxylate), Chem.–Eur. J., 2006, 12, 7353–7363.
8. M. Fujita, Y. J. Kwon, S. Washizu and K. Ogura, Preparation, Clathration Ability, and Catalysis of a Two-Dimensional Square Network Material Composed of Cadmium(II) and 4,4'-Bipyridine, J. Am. Chem. Soc., 2002, 116, 1151–1152.
9. H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Water harvesting from air with metal-organic frameworks powered by natural sunlight, Science, 2017, 356, 430–434.
10. W. Xu and O. M. Yaghi, Metal–Organic Frameworks for Water Harvesting from Air, Anywhere, Anytime, ACS Cent. Sci., 2020, 6, 1348–1354.
11. M. J. Kalmutzki, C. S. Diercks and O. M. Yaghi, Metal–Organic Frameworks for Water Harvesting from Air, Adv. Mater., 2018, 30, 1704304.
12. M. W. Logan, S. Langevin and Z. Xia, Reversible Atmospheric Water Harvesting Using Metal-Organic Frameworks, Sci. Rep., 2020, 10, 1492.
13. N. Abdullah, N. Yusof, A. F. Ismail and W. J. Lau, Insights into metal-organic frameworks-integrated membranes for desalination process: A review, Desalination, 2021, 500, 114867.
14. R. Ou, H. Zhang, V. X. Truong, L. Zhang, H. M. Hegab, L. Han, J. Hou, X. Zhang, A. Deletic, L. Jiang, G. P. Simon and H. Wang, A sunlight-responsive metal–organic framework system for sustainable water desalination, Nat Sustainability, 2020, 3, 1052–1058.
15. Z. Cao, V. Liu and A. Barati Farimani, Water Desalination with Two-Dimensional Metal–Organic Framework Membranes, Nano Lett., 2019, 19, 8638–8643.
16. S. H. Lapidus, G. J. Halder, P. J. Chupas and K. W. Chapman, Exploiting High Pressures to Generate Porosity, Polymorphism, And Lattice Expansion in the Nonporous Molecular Framework Zn(CN)₂, J. Am. Chem. Soc., 2013, 135, 7621–7628.
17. S. A. Moggach, T. D. Bennett and A. K. Cheetham, The Effect of Pressure on ZIF-8: Increasing Pore Size with Pressure and the Formation of a High-Pressure Phase at 1.47 GPa, Angew. Chem., Int. Ed., 2009, 48, 7087–7089.
18. P. Ramaswamy, J. Wieme, E. Alvarez, L. Vanduyfhuys, J.-P. Itié, P. Fabry, V. Van Speybroeck, C. Serre, P. G. Yot and G. Maurin, Mechanical properties of a gallium fumarate metal–organic framework: a joint experimental-modelling exploration, J. Mater. Chem. A, 2017, 5, 11047–11054.
19. P. G. Yot, K. Yang, V. Guillerm, F. Ragon, V. Dmitriev, P. Parisiades, E. Elkaïm, T. Devic, P. Horcajada, C. Serre, N. Stock, J. P. S. Mowat, P. A. Wright, G. Férey and G. Maurin, Impact of the Metal Centre and Functionalization on the Mechanical Behaviour of MIL-53 Metal–Organic Frameworks, Eur. J. Inorg. Chem., 2016, 2016, 4424–4429.
20. R. Adams, C. Carson, J. Ward, R. Tannenbaum and W. Koros, Metal organic framework mixed matrix membranes for gas separations, Microporous Mesoporous Mater., 2010, 131, 13–20.
21. G. W. Peterson, J. B. DeCoste, T. G. Glover, Y. Huang, H. Jasuja and K. S. Walton, Effects of pelletization pressure on the physical and chemical properties of the metal–organic frameworks Cu₃(BTC)₂ and UiO-66, Microporous Mesoporous Mater., 2013, 179, 48–53.
22. B. Zornoza, C. Tellez, J. Coronas, J. Gascon and F. Kapteijn, Metal organic framework based mixed matrix membranes: An increasingly important field of research with a large application potential, Microporous Mesoporous Mater., 2013, 166, 67–78.
23. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 1–10.
24. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
25. Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64, 5985–5998.
26. G. Zhao, L. M. Brabson, S. Chheda, J. Huang, H. Kim, K. Liu, K. Mochida, T. D. Pham, Prerna, G. G. Terrones, S. Yoon, L. Zoubritzky, F.-X. Coudert, M. Haranczyk, H. J. Kulik, S. M. Moosavi, D. S. Sholl, J. I. Siepmann, R. Q. Snurr and Y. G. Chung, CoRE MOF DB: A curated experimental metal-organic framework database with machine-learned properties for integrated material-process screening, Matter, 2025, 8, 102140.
27. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-scale screening of hypothetical metal–organic frameworks, Nat. Chem., 2011, 4, 83–89.
28. P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Data-driven design of metal–organic frameworks for wet flue gas CO2 capture, Nature, 2019, 576, 253–256.
29. Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Topologically Guided, Automated Construction of Metal–Organic Frameworks and Their Evaluation for Energy-Related Applications, Cryst. Growth Des., 2017, 17, 5801–5810.
30. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068.
31. A. Nandy, S. Yue, C. Oh, C. Duan, G. G. Terrones, Y. G. Chung and H. J. Kulik, A database of ultrastable MOFs reassembled from stable fragments with machine learning models, Matter, 2023, 6, 1585–1603.
32. K. W. Chapman, G. J. Halder and P. J. Chupas, Pressure-Induced Amorphization and Porosity Modification in a Metal−Organic Framework, J. Am. Chem. Soc., 2009, 131, 17546–17547.
33. P. G. Yot, K. Yang, F. Ragon, V. Dmitriev, T. Devic, P. Horcajada, C. Serre and G. Maurin, Exploration of the mechanical behavior of metal organic frameworks UiO-66(Zr) and MIL-125(Ti) and their NH₂ functionalized versions, Dalton Trans., 2016, 45, 4283–4288.
34. S. M. J. Rogge, J. Wieme, L. Vanduyfhuys, S. Vandenbrande, G. Maurin, T. Verstraelen, M. Waroquier and V. Van Speybroeck, Thermodynamic Insight in the High-Pressure Behavior of UiO-66: Effect of Linker Defects and Linker Expansion, Chem. Mater., 2016, 28, 5721–5732.
35. S. M. Moosavi, P. G. Boyd, L. Sarkisov and B. Smit, Improving the Mechanical Stability of Metal–Organic Frameworks Using Chemical Caryatids, ACS Cent. Sci., 2018, 4, 832–839.
36. J.-C. Tan, B. Civalleri, C.-C. Lin, L. Valenzano, R. Galvelis, P.-F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Exceptionally Low Shear Modulus in a Prototypical Imidazole-Based Metal-Organic Framework, Phys. Rev. Lett., 2012, 108, 095502.
37. J.-C. Tan, B. Civalleri, A. Erba and E. Albanese, Quantum mechanical predictions to elucidate the anisotropic elastic properties of zeolitic imidazolate frameworks: ZIF-4 vs. ZIF-zni, CrystEngComm, 2015, 17, 375–382.
38. N. Castel and F.-X. Coudert, Computation of Finite Temperature Mechanical Properties of Zeolitic Imidazolate Framework Glasses by Molecular Dynamics, Chem. Mater., 2023, 35, 4038–4047.
39. M. L. Barsoum, K. M. Fahy, W. Morris, V. P. Dravid, B. Hernandez and O. K. Farha, The Road Ahead for Metal–Organic Frameworks: Current Landscape, Challenges and Future Prospects, ACS Nano, 2025, 19, 13–20.
40. H. Demir, H. Daglar, H. C. Gulbalkan, G. O. Aksu and S. Keskin, Recent advances in computational modeling of MOFs: From molecular simulations to machine learning, Coord. Chem. Rev., 2023, 484, 215112.
41. M. Fernandez, T. K. Woo, C. E. Wilmer and R. Q. Snurr, Large-Scale Quantitative Structure–Property Relationship (QSPR) Analysis of Methane Storage in Metal–Organic Frameworks, J. Phys. Chem. C, 2013, 117, 7681–7689.
42. Y. Liu, Y. Dong and H. Wu, Comprehensive overview of machine learning applications in MOFs: from modeling processes to latest applications and design classifications, J. Mater. Chem. A, 2025, 13, 2403–2440.
43. X. Bai, Z. Shi, H. Xia, S. Li, Z. Liu, H. Liang, Z. Liu, B. Wang and Z. Qiao, Machine-Learning-Assisted High-Throughput computational screening of Metal–Organic framework membranes for hydrogen separation, Chem. Eng. J., 2022, 446, 136783.
44. C. Oh, A. Nandy, S. Yue and H. J. Kulik, MOFs with the Stability for Practical Gas Adsorption Applications Require New Design Rules, ACS Appl. Mater. Interfaces, 2024, 16, 55541–55554.
45. Z. Qiao, Y. Yan, Y. Tang, H. Liang and J. Jiang, Metal–Organic Frameworks for Xylene Separation: From Computational Screening to Machine Learning, J. Phys. Chem. C, 2021, 125, 7839–7848.
46. M. P. Rivera, G. G. Terrones, T. H. Lee, Z. P. Smith and H. J. Kulik, Data-Driven Screening and Discovery of Metal–Organic Frameworks as C₂ Adsorbents from over 900 Experimental Isotherms, ACS Appl. Mater. Interfaces, 2024, 16, 64759–64773.
47. X. Xue, M. Cheng, S. Wang, S. Chen, L. Zhou, C. Liu and X. Ji, High-Throughput Screening of Metal–Organic Frameworks Assisted by Machine Learning: Propane/Propylene Separation, Ind. Eng. Chem. Res., 2023, 62, 1073–1084.
48. L. Yuan, M. Xu, Y. Zhang, Z. Gao, L. Zhang, C. Cheng, C. Ji, M. Hua, L. Lv and W. Zhang, Machine learning-assisted screening of metal-organic frameworks (MOFs) for the removal of heavy metals in aqueous solution, Sep. Purif. Technol., 2024, 339, 126732.
49. A. K. Ball, G. G. Terrones, S. Yue and H. J. Kulik, Data-Driven Discovery of Water-Stable Metal–Organic Frameworks with High Water Uptake Capacity, ACS Appl. Mater. Interfaces, 2025, 17, 35971–35985.
50. N. S. Bobbitt and R. Q. Snurr, Molecular modelling and machine learning for high-throughput screening of metal-organic frameworks for hydrogen storage, Mol. Simul., 2019, 45, 1069–1081.
51. R. Wang, Y. Zhong, L. Bi, M. Yang and D. Xu, Accelerating Discovery of Metal–Organic Frameworks for Methane Adsorption with Hierarchical Screening and Deep Learning, ACS Appl. Mater. Interfaces, 2020, 12, 52797–52807.
52. R. Batra, C. Chen, T. G. Evans, K. S. Walton and R. Ramprasad, Prediction of water stability of metal–organic frameworks using machine learning, Nat. Mach. Intell., 2020, 2, 704–710.
53. I. Lee, J. Lee, M. Kim, J. Park, H. Kim, S. Lee and K. Min, Uncovering the Relationship between Metal Elements and Mechanical Stability for Metal–Organic Frameworks, ACS Appl. Mater. Interfaces, 2024, 16, 52162–52178.
54. J. Lee, I. Lee, J. Park, H. Kim, M. Kim, K. Min and S. Lee, Optimal Surrogate Models for Predicting the Elastic Moduli of Metal–Organic Frameworks via Multiscale Features, Chem. Mater., 2023, 35, 10457–10475.
55. P. Z. Moghadam, S. M. J. Rogge, A. Li, C.-M. Chow, J. Wieme, N. Moharrami, M. Aragones-Anglada, G. Conduit, D. A. Gomez-Gualdron, V. Van Speybroeck and D. Fairen-Jimenez, Structure-Mechanical Stability Relations of Metal-Organic Frameworks via Machine Learning, Matter, 2019, 1, 219–234.
56. A. Nandy, C. Duan and H. J. Kulik, Using Machine Learning and Data Mining to Leverage Community Knowledge for the Engineering of Stable Metal–Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 17535–17547.
57. G. G. Terrones, S.-P. Huang, M. P. Rivera, S. Yue, A. Hernandez and H. J. Kulik, Metal–Organic Framework Stability in Water and Harsh Environments from Data-Driven Models Trained on the Diverse WS24 Data Set, J. Am. Chem. Soc., 2024, 146, 20333–20348.
58. Z. Zhang, F. Pan, S. A. Mohamed, C. Ji, K. Zhang, J. Jiang and Z. Jiang, Accelerating Discovery of Water Stable Metal−Organic Frameworks by Machine Learning, Small, 2024, 20, 2405087.
59. A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4, 1578–1597.
60. J. P. Janet and H. J. Kulik, Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure-Property Relationships, J. Phys. Chem. A, 2017, 121, 8939–8954.
61. E. I. Ioannidis, T. Z. Gani and H. J. Kulik, molSimplify: A toolkit for automating discovery in inorganic chemistry, J. Comput. Chem., 2016, 37, 2106–2117.
62. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials, Microporous Mesoporous Mater., 2012, 149, 134–141.
63. S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11, 4068.
64. H. Adamji, A. Nandy, I. Kevlishvili, Y. Román-Leshkov and H. J. Kulik, Computational Discovery of Stable Metal–Organic Frameworks for Methane-to-Methanol Catalysis, J. Am. Chem. Soc., 2023, 145, 14365–14378.
65. A. F. Wells, Three-Dimensional Nets and Polyhedra (Pure and Applied Mathematics), John Wiley & Sons, 1977.
66. B. J. Bucior, A. S. Rosen, M. Haranczyk, Z. Yao, M. E. Ziebel, O. K. Farha, J. T. Hupp, J. I. Siepmann, A. Aspuru-Guzik and R. Q. Snurr, Identification Schemes for Metal–Organic Frameworks To Enable Rapid Search and Cheminformatics Analysis, Cryst. Growth Des., 2019, 19, 6682–6697.
67. D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 2002, 28, 31–36.
68. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets, Acc. Chem. Res., 2008, 41, 1782–1789.
69. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
70. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, Pytorch: an Imperative Style, High-Performance Deep Learning Library, Curran Associates, Inc., 2019.
71. Z. Cao, R. Magar, Y. Wang and A. B. Farimani, MOFormer: Self-Supervised Transformer Model for Metal–Organic Framework Property Prediction, J. Am. Chem. Soc., 2023, 145, 2958–2967.
72. J. Bergstra, D. Yamins and D. D. Cox, Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms, SciPy, 2013, vol. 13, p. 20.
73. S. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, Curran Associates, Inc., 2017.
74. J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci., 2019, 10, 7913–7922.
75. L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv, 2018, preprint, arXiv:1802.03426,  DOI:10.48550/arXiv.1802.03426.
76. N. Shervashidze, P. Schweitzer, E. J. Van Leeuwen, K. Mehlhorn and K. M. Borgwardt, Weisfeiler-lehman graph kernels, J. Mach. Learn. Res., 2011, 12, 2539–2561.
77. A. Hagberg, P. J. Swart and D. A. Schult, Exploring network structure, dynamics, and function using NetworkX, Los Alamos, NM (United States), 2008.
78. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
79. D. E. Coupry, M. A. Addicoat and T. Heine, Extension of the Universal Force Field for Metal–Organic Frameworks, J. Chem. Theory Comput., 2016, 12, 5215–5225.
80. M. A. Addicoat, N. Vankova, I. F. Akter and T. Heine, Extension of the Universal Force Field to Metal–Organic Frameworks, J. Chem. Theory Comput., 2014, 10, 880–891.
81. F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
82. S. Zou, Q. Li and S. Du, Efficient and tunable multi-color and white light Ln-MOFs with high luminescence quantum yields, RSC Adv., 2015, 5, 34936–34941.
83. A. Kuc, A. Enyashin and G. Seifert, Metal−Organic Frameworks: Structural, Energetic, Electronic, and Mechanical Properties, J. Phys. Chem. B, 2007, 111, 8179–8186.
84. H. Wu, T. Yildirim and W. Zhou, Exceptional Mechanical Stability of Highly Porous Zirconium Metal–Organic Framework UiO-66 and Its Important Implications, J. Phys. Chem. Lett., 2013, 4, 925–930.
85. W. H. Kruskal and W. A. Wallis, Use of Ranks in One-Criterion Variance Analysis, J. Am. Stat. Assoc., 1952, 47, 583–621.
86. J. P. Janet and H. J. Kulik, Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure–Property Relationships, J. Phys. Chem. A, 2017, 121, 8939–8954.
87. A. K. Ball, C. Oh, G. Dovranova and H. J. Kulik, Combining Chemical, Geometric, and Novel Topological Features to Develop Generalizable Machine Learning Models for Predicting Mechanically Stable MOFs, Zenodo, 2025,  DOI:10.5281/zenodo.17850321.
88. H. B. Mann and D. R. Whitney, On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other, Ann. Math. Stat., 1947, 18, 50–60.
89. Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Computation-Ready, Experimental Metal–Organic Frameworks: A Tool To Enable High-Throughput Screening of Nanoporous Crystals, Chem. Mater., 2014, 26, 6185–6192.
90. T. Chen and T. A. Manz, Identifying misbonded atoms in the 2019 CoRE metal–organic framework database, RSC Adv., 2020, 10, 26944–26951.
91. X. Jin, K. M. Jablonka, E. Moubarak, Y. Li and B. Smit, MOFChecker: a package for validating and correcting metal–organic framework (MOF) structures, Digital Discovery, 2025, 4, 1560–1569.
92. A. J. White, M. Gibaldi, J. Burner, R. A. Mayo and T. K. Woo, High Structural Error Rates in “Computation-Ready” MOF Databases Discovered by Checking Metal Oxidation States, J. Am. Chem. Soc., 2025, 147, 17579–17583.
93. G. Zhao, P. Zhao and Y. G. Chung, MOFClassifier: A Machine Learning Approach for Validating Computation-Ready Metal–Organic Frameworks, J. Am. Chem. Soc., 2025, 147, 33343–33349.

---