Gradient-multiscale-interconnected architectures enable waterborne superomniphobic surfaces to resist the high-strength impact of solids and fluids

Abstract

A bottom-up waterborne emulsion system is developed to construct gradient-multiscale-interconnected (GMI) architectured superomniphobic surfaces (SOSs). The GMI architectures are verified to be of both high mechanical flexibility and trapped-air stability, making SOSs resistant to high-strength impact of solids and fluids and thus competent for for real-world dynamic long-term applications.

---

Introduction

The typical combination of micro- and nano-scale topography and low surface-energy chemistry makes surfaces superomniphobic, rendering them repellent to common liquids with contact angles ≥150° and roll-off angles of ≤10° at solid–gas interfaces.^1,2 Such a surface can find a large number of static applications, such as self-cleaning,^3,4 anti-bacterial,^5,6 corrosion protection,^7,8 energy-efficient fluid transport,^9,10 and water–oil separation.^11,12 However, the micro- and nano-scale topography of superomniphobic surfaces (SOSs) constructed using conventional strategies is intrinsically fragile and thus highly susceptible to impacts from solids (e.g., abrasion) and fluids (e.g., heavy rain), thereby increasing the effective contact area between solids and liquids.¹³ Moreover, trapped air in even undamaged micro- and nano-scale topography is unstable and particularly prone to escaping from surfaces exposed to impact, which brings about negative pressure.¹⁴ Both the increased effective contact radius and extra negative pressure lower the capillary pressure (P_c, eqn (S1)), and consequently lead SOSs to transform from the Cassie–Baxter state to the Wenzel state.¹⁵ The impact of solids and fluids pervades the dynamic applications, including but not limited to anti-fouling and anti-icing for land-marine-air vehicles, exterior walls of buildings, radar radomes, transmission towers, public infrastructures, and even friction components of implants, and hence the SOSs with Wenzel state are inefficient for dynamic applications.^3,16

With rising concerns about the fragility of micro/nano-scale topography and the instability of trapped air, top-down strategies have emerged as a solution for creating robust superhydrophobic surfaces (SHSs) over the past few decades. For example, microscale inverted-pyramidal cavities are formed on silicon, ceramic, metal, and glass substrates by photolithography and hot/cold-pressing, and SHSs with resistance to high-speed water-jet impingement and violent abrasion are achieved by depositing hydrophobic silica nanoparticles (SiNPs).¹³ Besides, various lasers,^17,18 reactive-ion etching,^19,20 and templated imprinting²¹ techniques are introduced to create micro/nano-scale topography or re-entrant structures on surfaces of metal substrates, and a mechanically durable SHS is produced with the assistance of some supplementary processes (such as chemical oxidation). Notably, these top-down methods require extensive processing and apply only to hard substrates for robust freestanding SHSs, rendering them impractical for large-scale use. From an engineering perspective, considerable effort has been devoted to developing robust SHSs based on bottom-up strategies, including longitudinal self-similar structures,^3,16 rigid microshell structures,²² all-organic fluoride structures,²³ inorganic adhesive-enhanced structures,²⁴ and organic adhesive-based hierarchical structures.²⁵ However, these bottom-up methods may pose health risks, such as the inevitable use of environmentally unfriendly chemicals, or the resulting robust SHSs may be incapable of repelling low-surface-tension liquids (i.e., only hydrophobic, not amphiphobic). Further, the high stability of trapped air remains a significant challenge for SHSs, and they cannot withstand high-impact loads (e.g., moving cars or wind turbine blades are exposed to high-speed sand grains, and water drops with a Weber number (W_e) ≥10 000). Given the high-strength impact of solids and fluids (not merely water) in real-world dynamic long-term applications, the development of an SOS with high mechanical robustness of micro/nano-scale topography and high stability of trapped air via a bottom-up waterborne system is highly necessary.

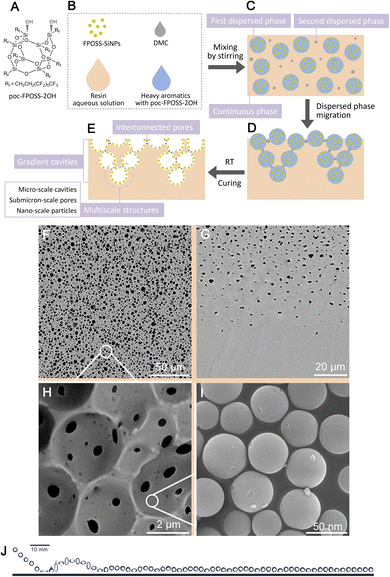
In nature, chemically and physically gradient structures are ubiquitous in animal and plant tissues, having evolved over billions of years and proving extremely efficient at resisting external impacts by reducing concentrated stress and progressively dispersing it, as seen in human skin/bone and in bamboo poles.^25,26 Considering repellence to widespread liquids and the desired maximum capacity of trapped air, the multiscale and interconnected characteristics are combined into bio-inspired gradient structures, and we propose exploiting a SOS with gradient-multiscale-interconnected (GMI) architectures via a bottom-up waterborne system. The system is an aqueous emulsion comprising heavy aromatics (HA), partially open cage fluorinated polyhedral oligomeric silsesquioxane bearing a pair of –OH (poc-FPOSS–2OH) and FPOSS–SiNPs as first dispersed phases, dimethyl carbonate (DMC) as second dispersed phases, and resin (the common polymers for industrial use) aqueous solution as continuous phases. It is air-dried to form a SOS at room temperature on spray-coated common substrates. The GMI architectures are expected to exhibit high mechanical robustness and trapped-air stability, thereby imparting the SOSs with resistance to the high-strength impacts from solids and fluids. Through anti-icing tests under dynamic conditions, the GMI-SOSs have been demonstrated to be practical and reliable in real-world dynamic long-term applications.

Results and discussion

First, as reported in our previous works,^7,27,28 the synthesized poc-FPOSS–2OH, consisting of a silicon–oxygen (Si–O) inorganic core with partially open-cage-liked structure and a fluoroalkyl (with a controlled –CF₃/–CF₂ chain length, –C₆F₁₃ in this work) organic periphery, is an incompletely condensed fluoroalkyl silsesquioxane compound and of extremely low surface energy (Fig. 1A and S1). Second, the poc-FPOSS–2OH is utilized to produce FPOSS–SiNPs with a size of ∼45 nm based on acid-triggered protonation of poc-FPOSS–2OH and poc-FPOSS–2OH wrapping SiNPs (Fig. S2).²⁷ Further, in view of the immiscibility of DMC and HA mixing with poc-FPOSS–2OH, a waterborne emulsion is prepared by fierce dispersion of FPOSS–SiNPs, DMC, HA/poc-FPOSS–2OH, and resin aqueous solution (waterborne air-drying polyurethane (PU) if not otherwise specified) (Fig. 1B and C). It is important to note that both HA and DMC are environmentally benign chemicals and are widely used in industrial applications. This white emulsion system is thermodynamically stable, which consists of first dispersed phases (i.e., FPOSS–SiNPs and HA/poc-FPOSS–2OH), second dispersed phases (i.e., DMC), and continuous phases (i.e., resin aqueous solution) (Fig. S3A). The Zetasizer reports sizes of 4 µm and 380 nm for the first and second dispersed phases, respectively (Fig. S3B). Because the FPOSS–SiNPs are exclusively distributed in dispersed phases rather than continuous phases, their size distribution peak is absent. By simple spraying, waterborne emulsion can coat widespread substrates (glass plate if not otherwise specified). After air-drying for 8 h at room temperature, the waterborne emulsion with a thickness of 300 µm is fully cured, and a coating with a GMI-SOS is formed. Herein, we raise a hypothetical insight into the formation of GMI architectures. Although the HA is of lower density (0.879 g cm⁻³) than water or continuous phases, the presence of poc-FPOSS–2OH and FPOSS–SiNPs makes the density of the first dispersed phases very close to the continuous phases. In addition, DMC has a density similar to that of water or of the continuous phase. Therefore, the two dispersed phases are in a suspension state in this waterborne emulsion. As water evaporates much faster than HA and DMC, the continuous phase becomes progressively denser once the waterborne emulsion coats the substrates and is exposed to air. At a specific point in time, the two dispersed phases become lighter than the continuous phase and are allowed to migrate toward the liquid–air interface. In this way, the dispersed phases aggregate and appear as a longitudinal direction gradient of distribution density (Fig. 1D). Owing to their much smaller size, the second dispersed phases are stuck between the first dispersed phases. During air-drying, the cured resin creates a confined space for the two dispersed phases. When HA and DMC completely evaporate, unique porous structures composed of microscale pores from the first dispersed phases and submicro-scale pores from the second dispersed phases are shaped. These porous structures with gradient distribution density are interconnected (microscale pores are interconnected with submicro-scale pores) and multiscale (microscale pores, submicro-scale pores, and nano-scale particles), that is, the GMI architectures (Fig. 1E). In more detail, the porous coating surfaces are defect-free (Fig. 1F). The whole gradient depth exceeds 50 µm (Fig. 1G). The microscale pores (∼3 µm) are interconnected with numerous submicro-scale pores (∼350 nm) (Fig. 1H and S4). The sizes of both microscale and submicro-scale pores agree well with Zetasizer values for the waterborne emulsion (Fig. S3B; first dispersed phase: 4 µm; the second dispersed phase: 380 nm). Numerous FPOSS–SiNPs embedded inside microscale pores can be observed (Fig. 1I). When an 8 µL dodecane droplet (with 2.5 mm in diameter) is released at a height of 1 cm, it continuously bounces 11 times before residing on a horizontally placed GMI-SOS (Fig. 1J). The GMI-SOSs have a virtually double bouncing number as conventional SOSs,²⁵ thus manifesting their unmatched repellency to liquids.

Fig. 1 (A) Chemical structure of poc-FPOSS–2OH. (B–E) Schematic illustration of the formation of both waterborne emulsions and GMI-SOSs. (F) Field emission scanning electron microscopy (FE-SEM) image of GMI-SOSs from the top view. (G) FE-SEM image of GMI-SOSs from the cross-sectional view. (H) FE-SEM image of interconnected porous structure at the selected area in (F). (I) FE-SEM image of FPOSS–SiNPs at the selected area in (H). (J) Snapshot images of the contacting/bouncing process of a dynamic dodecane droplet (release height: 10 mm) on a horizontally placed GMI-SOS.

According to the hypothetical insight above, the gradient in distribution density is directly associated with dispersed phase migration, as evidenced by changes in optical transmittance across various regions of the waterborne emulsion (Fig. S5A). As the visible light transmittance of a waterborne emulsion is inversely proportional to the amount of dispersed phase, it reflects the real-time in situ density of the dispersed phase. In open space (Fig. S5B), the whole waterborne emulsion has unaltered transmittance prior to 330 min (standing time). An increase in transmittance at the bottom site and a decrease at the top site are detected after 330 min, which remain steady until 390 min. Unlike in open space, no fluctuation in transmittance occurs at either the top or the bottom sites during 480 min in an enclosed space (Fig. S5C). These results account for the fact: at the beginning (t₀), the density of dispersed phases (ρ_dp) and continuous phases (ρ_cp) approaches each other, i.e., ρ_dp ≈ ρ_cp; with water evaporation for a specific period of time (from t₁ to t₂) in open space, the continuous phases get obviously concentrated, i.e., ρ_dp < ρ_cp, the dispersed phases are prone to upward migration and assembly; the closer to liquid–air interfaces, the more dispersed phases are present, and finally their distribution density gradient is established (t₃, Fig. S5D); as no water evaporation occurs in enclosed space, the ρ_dp ≈ ρ_cp prevents migration of dispersed phases, and the dispersed phases are always evenly distributed in waterborne emulsion (Fig. S5E).

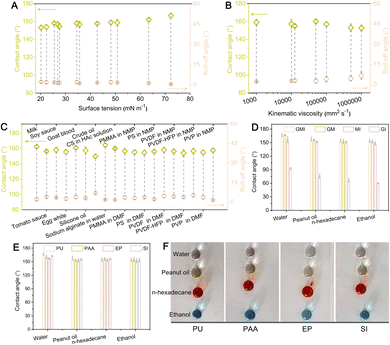
The superomniphobic properties of coatings with GMI architectures are discussed in terms of liquid surface tension and viscosity, as well as different non-Newtonian liquids. First, it is made clear that the coating surfaces display superomniphobicity (with contact angles of >150° and roll-off angles of <10°) to diverse liquids with surface tension ranging from 72.3 mN m⁻¹ (water) to 20.1 mN m⁻¹ (n-heptane) (Fig. 2A). Generally, with increase in surface tension of liquids, their contact angles follow a rising trend, while their roll-off angles are in a declining trend. Second, dimethyl silicon oil (with a surface tension of ∼21 mN m⁻¹), with kinematic viscosity roughly varying from 1000 to 1 000 000 mm² s⁻¹, is not allowed to wet and consequently roll off the surfaces with ease (Fig. 2B). Third, in addition to Newtonian liquids (Fig. 2A), non-Newtonian liquids as omnipresent matter in our daily life (e.g., milk, tomato sauce and egg white), industrial (e.g., crude oil) and medical (e.g., blood) fields, whose viscosities depend on shear rate (i.e., cannot be described with Newton's law of viscosity that defines the relationship between the shear stress and shear rate of a fluid subjected to a mechanical stress), are applied to the GMI-SOSs (Fig. 2C). It is shown that almost all these experimental non-Newtonian liquids (some of these are self-made specimens, SI Experimental section gives more details) seem to permit a motion with minimal resistance on slightly sloping surfaces. Additionally, the coatings exhibit superomniphobic properties independent of their area, indicating good scalability (Fig. S6). When coatings are formed on non-flat, rough, or soft substrates, no significant discrepancy in superomniphobicity is observed compared with glass plates (Fig. S7). Through some specific regulations based on the above-proposed hypothetical insight, the other three architectures of the coating surfaces were prepared for comparison with GMI-SOSs (Fig. S8, SI Experimental section provides the preparation detail). These include: (i) gradient-multiscale (GM) architectured SOSs without interconnected structures, achieved by removing second dispersed phases to prevent interconnected pore formation; (ii) multiscale-interconnected (MI) architectured SOSs without gradient structures, prepared by immediate 150 °C for 5 min after spray-coating for inhibition against dispersed phase migration; (iii) gradient-interconnected (GI) architectured SOSs without multiscale structures, obtained by removing FPOSS–SiNPs to eliminate low-surface-energy nano-scale features. Despite the absence of interconnected or gradient structures, coatings with GM or MI architectures still exhibit superomniphobicity. At the same time, the GMI-SOSs possess relatively higher contact angles of water, peanut oil, n-hexadecane, and ethanol (Fig. 2D). As to the coatings with GI architectures, nevertheless, they lose repellency to liquids (even for water), indicating the indispensability of low-surface-energy nano-scale topography (i.e., the FPOSS–SiNPs). This emulsion system can also be prepared using other waterborne air-drying polymers as resin matrices, such as polyacrylate (PAA), epoxy (EP), and silicone (SI). Using these alternative polymers, the resulting coatings exhibit nearly identical superomniphobic properties (Fig. 2E and F), as their surface layers bear a structural resemblance to GMI architectures.

Fig. 2 Plots the contact/roll-off angle of the liquids on GMI-SOSs versus (A) surface tension of liquids, (B) kinematic viscosity of liquids, and (C) a variety of non-Newtonian liquids. (D) Plot of the contact angle of 4 kinds of liquids on coatings with different surface architectures. (E) Plot of contact angle of 4 kinds of liquids on GMI-SOSs based on different resins. (F) Photographs of 4 kinds of liquids beading up on GMI-SOSs in (E).

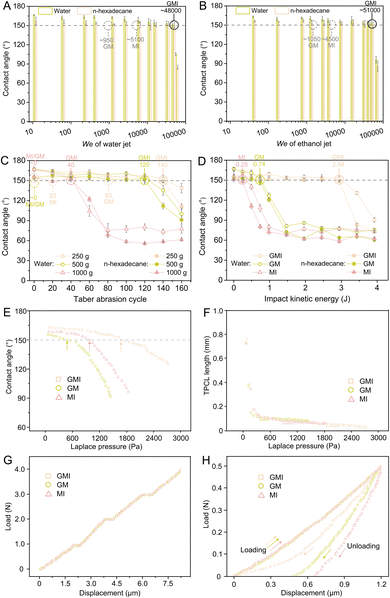
To assess the mechanical robustness and trapped-air stability of GMI architectures, GMI-SOSs are subjected to impacts from solids and fluids, with GM-SOSs and MI-SOSs as comparisons. The liquid jets with a known speed and diameter correspond to a dimensionless W_e (eqn (S2)), which is often invoked to quantify their impact strength. Using a high-pressure nozzle, the water and ethanol jets are applied in a series of W_e to impinge the SOSs. As expected, the GMI-SOSs remain super-repellent to water and n-hexadecane after 100 s-impact of water jets with W_e up to ∼48 000 (Fig. 3A) and ethanol jets with W_e up to ∼51 000 (Fig. 3B), which is the highest liquid impact resistance so far in comparison with state-of-the-art SHSs and SOSs fabricated by bottom-up strategies,²³ and in some degree comparable with the SHSs fabricated by top-down strategies^17,29 (more comparisons are listed in Table S1). As shown in Fig. 3A and B, the MI-SOSs afford relatively low W_e for water and ethanol jet impacts. When gradient structures are absent in GMI architectures, the forming GM-SOSs can withstand only the impact of water jets with W_e ∼950 and ethanol jets with W_e ∼1050. The solid impact tests are conducted using the Taber abrasion and hammer impact methods. The GMI-SOSs can tolerate the Taber abrasion for 140 cycles with 250 g load, 120 cycles with 500 g load, or 40 cycles with 1000 g load (Fig. 3C). As labelled in Fig. 3C, the GM-SOSs and MI-SOSs are still incapable of holding their superomniphobic properties after Taber abrasion with 250 g load for 80 and 20 cycles, respectively, but both collapse at the first blow once the loads are increased to 500 and 1000 g. The metal hammer is released from a predetermined height and is allowed to freely fall, imparting a certain kinetic energy to the coatings. The GMI-SOSs can withstand an impact with a kinetic energy of 2.94 J, which undoubtedly is much higher than GM-SOSs (0.74 J) and MI-SOSs (0.25 J). Among the three types of SOSs, it seems that the GM-SOSs without interconnected structures exhibit the weakest tolerance against fluid impact, and the MI-SOSs without gradient structures show the weakest tolerance against solid impact. In other words, only the SOSs with GMI architectures are qualified to withstand the high-strength impact of both solids and fluids. Herein, Cassie–Baxter state stability is adopted to assess the trapped-air stability of these SOSs with different architectures. The Cassie–Baxter state stability of the three types of SOSs is quantified by critical Laplace pressures (P_cl), which indicate the threshold for a surface to lose its Cassie–Baxter state during the evaporation of a water droplet (see Laplace pressure P_l in Fig. S9 and eqn (S3)). A relatively small value decides the P_cl between P_clc and P_clt (the adopted criteria or correlation is referred to ref. 30), where P_clc is the critical Laplace pressure for contact angle turning into <150° (i.e., not a super-repellent state any more) and P_clt is the critical Laplace pressure for triple-phase contact line (TPCL) length at the onset of its first asymptotic direction (i.e., TPCL length remains unchanged with Laplace pressure in a certain range for the first time). The GMI-SOSs, GM-SOSs, and MI-SOSs have corresponding P_clc around 1660, 470, and 975 Pa (Fig. 3E), as well as P_clt about 1820, 400, and 890 Pa (Fig. 3F). That is to say, the GMI-SOSs express a P_cl of 1660 Pa higher than the other SOSs. Both GM-SOSs and MI-SOSs show P_clc > P_clt and so indicate that losing Cassie–Baxter state occurs at the moment of P_clt, and the transition from Cassie–Baxter state to Wenzel state is finished before contact angle <150°. By contrast, P_clc < P_clt for GMI-SOSs indicates that the Cassie–Baxter state is lost at the instant of P_clc, and the Wenzel state will not occur. Given this, GMI-SOSs exhibit a highly stable Cassie–Baxter state, possibly related to the interconnected structures in GMI architectures. The interconnected structures allow greater access to air and improved air circulation within GMI architectures after liquid impact, and it appears that trapped air is more stable. Therefore, it makes sense that GMI-SOSs can resist high-strength liquid impact due to their very stable trapped air, and, as with conventional SHSs or SOSs, GM-SOSs are much more sensitive to fluid impact due to the absence of interconnected structures. It should be noted that the P_cl of 1660 Pa is the highest among those of state-of-the-art SHSs or SOSs. Furthermore, the mechanical robustness of the three types of SOSs is assessed using nanoindentation. All the load-displacement curves of the three types of SOSs exhibit breakpoints at three stages (Fig. 3G), which are due to saltation during loading and rapid displacement caused by microstructural fractures. Clearly, the breakpoints of GMI-SOSs correspond to loading forces similar to those of both GM-SOSs and MI-SOSs, despite their different surface architectures, indicating no apparent discrepancy in mechanical strength among these SOSs. Before the appearance of the first breakpoints at 1.90 µm/0.95 N, the residual depths of GM-SOSs and MI-SOSs upon unloading are 0.47 and 0.65 µm, respectively, but GMI-SOSs have no residual depth (Fig. 3H). This means that the GMI architectures are more mechanically flexible or elastic than both GM and MI architectures, even though they differ only slightly in mechanical strength. The greater mechanical flexibility is estimated to be closely correlated with gradient structures in the GMI architectures. The gradient structures are prone to reducing concentrated stress and progressively dispersing stress once the coatings encounter solid impact.²⁶ Specifically, just as human skin with gradient structures comprising epidermis, dermis, and hypodermis, or a bamboo pole transect with gradient distribution of fasciculus,^25,26 outer regions of gradient structures of GMI-SOSs show high porosity (i.e., high pore distribution density) and have a low modulus, which facilitates absorption of impact energy through structural deformation. Then, impact energy is progressively absorbed and even dissipated across transitional regions. Deeper regions of gradient structures show low-porosity (i.e., low pore distribution density) and serve as a supporting framework to prevent crack initiation and propagation and maintain structural integrity, which is a mechanical prerequisite for the reversibility of deformation. As a result, the GMI architectures exhibit deformation recovery in response to high-strength impacts, whereas the superomniphobic properties of MI-SOSs are much more susceptible to solid impacts due to the lack of gradient structures. With the adjustment of the dispersed phase amount in the waterborne emulsion system, the gradient depths of GMI-SOSs can be turned from ∼25 to 80 µm (Fig. S10). 51–56 µm is certified as an optimized gradient depth (also the gradient depth in Fig. 1G) that makes GMI-SOSs resistant to hammer impact with a maximum kinetic energy (2.94 J), possibly because it delivers the highest efficiency in reducing concentrated stress and progressively dispersing it. In brief, GMI architectures endow the SOSs with both high mechanical flexibility and trapped-air stability, thereby enabling the coatings to withstand the high-impact forces of solids and fluids. In addition, the GMI-SOSs are proven to exhibit comprehensive robustness, including sonication, UV radiation, exposure to air at different humidities, hot/cold cycles (100/−40 °C), and immersion in acids, bases, and organic solvents (Fig. S11 and S12).

Fig. 3 Plots of the contact angle of water and n-hexadecane on GMI-SOS after 100 s of (A) water and (B) ethanol jet impinging versus W_e of liquid jet. (C) Plots of the contact angle of water and n-hexadecane on GMI-SOS versus Taber abrasion cycles applied to the GMI-SOS under three loads. (D) Plots of the contact angle of water and n-hexadecane on GMI-SOS, GM-SOS, and MI-SOS versus kinetic energy (hammer impact) applied to these surfaces. Dependence of (E) contact angle and (F) TPCL diameter versus Laplace pressure during droplet evaporation on GMI-SOS, GM-SOS, and MI-SOS. (G) Load-displacement curves of GMI-SOS, GM-SOS, and MI-SOS recorded with a loading rate of 200 mN min⁻¹ and reaching a load of 4 N. (H) Load-displacement curves of GMI-SOS, GM-SOS, and MI-SOS recorded with a loading/unloading rate of 200 mN min⁻¹ and reaching a load of 0.5 N.

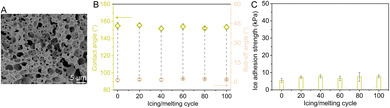
Given the GMI-SOS merit for high solid and fluid impact resistance, tests for anti-icing in a dynamic environment are being designed. To mimic the rugged environment in real-world dynamic long-term applications, the GMI-SOSs first undergo 30 s-impact of a water jet with W_e ∼34 000, 30 s-impact of an ethanol jet with W_e ∼32 000, and 30 cycles of Tabler abrasion with 500 g load and ∼1.5 J of kinetic energy of hammer impact in sequence. Despite the high-strength solid and fluid impacts, the GMI architectures of SOSs exhibit only slight wear and maintain complete skeleton structures (Fig. 4A). Subsequently, the GMI-SOSs undergo a cyclic icing/melting trial. After 100 icing/melting cycles, the contact and roll-off angles of n-hexadecane remain steady at >150 and <4° after 100 cycles, respectively (Fig. 4B). Naturally, the ice adhesion is undoubtedly intimately correlated with the wetting states of solid surfaces. The ice adhesion strength shows slight fluctuations and is <8 kPa after 100 cycles (Fig. 4C). This suggests that GMI-SOSs expose only a very small solid–liquid contact area to water and ice, accounting for their robust superomniphobic properties after multiple impacts. The small solid–liquid contact areas lead to weaker adhesion of the ice cylinder. These demonstrate that the GMI-SOSs from the bottom-up waterborne system are competent for real-world dynamic long-term applications due to their satisfactory practicality and reliability.

Fig. 4 (A) FE-SEM image of the GMI-SOS after impact of fluids and solids. Plots of (B) contact and roll-off angle of n-hexadecane droplet on GMI-SOS and (C) ice adhesion strength of GMI-SOS versus icing/melting cycle.

Conclusions

In summary, facing the great challenge posed by the fragility of micro/nano-scale topography and the instability of trapped air, which hinder the dynamic applications of SOSs, a bottom-up waterborne emulsion system is proposed. This system comprises HA, synthesized poc-FPOSS–2OH (a hybrid molecule with extremely low surface energy) and FPOSS–SiNPs as the first dispersed phases (4 µm in size), DMC as the second dispersed phase (380 nm in size), and a resin aqueous solution as the continuous phase. During waterborne emulsion coating on substrates, two dispersed phases migrate toward liquid–air interfaces, and SOSs with bio-inspired GMI architectures form upon air-drying at room temperature. The GMI-SOSs exhibit excellent repellency to a wide range of liquids (including those with surface tensions as low as 20.1 mN m⁻¹ and viscosities up to 1 000 000 mm² s⁻¹, as well as a series of non-Newtonian liquids). The GMI-SOSs can endure not only the impact of water jets with W_e ∼48 000 and ethanol jets with W_e ∼51 000 but also the Taber abrasion for 140 cycles with 250 g load, 120 cycles with 500 g load, or 40 cycles with 1000 g load and hammer impact with kinetic energy of 2.94 J. It seems that GMI-SOSs have the highest liquid impact resistance so far in comparison with state-of-the-art bottom-up SHSs and SOSs, and, to some degree, can rival the top-down SHSs. Notably, they are fabricated in an eco-friendly manner (waterborne attribute; HA and DMC as environmentally benign chemicals), using a facile spray-coating process, with energy-efficient air-drying at room temperature. Moreover, this method is universal (common industrial resin; applicable to a majority of substrates). In fact, the interconnected structures contribute high trapped-air stability by absorbing more air and allowing air circulation when the liquid impacts; the gradient structures offer high mechanical flexibility, as they are prone to reducing concentrated stress and progressively dispersing it when the coatings encounter solid impact. Through anti-icing tests in combination with multiple high-strength impacts from solids and fluids, the GMI-SOSs are demonstrated to be practical and reliable in real-world dynamic long-term applications. This work opens a new avenue for the environmentally benign design of SOSs with superior impact resistance against both solids and fluids. It promotes their practical use in dynamic and complex environments.

Author contributions

J. Liao, J. Zhong, Y. Zhai, and X. Yan conceptualized the study. J. Liao and F. Suo wrote the initial draft. F. Suo, B. Chen and Z. Lin conducted the experimental work. J. Liao, J. Zhong, and X. Yan acquired project funding. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article are included in the supplementary information (SI). Supplementary information: experimental section; equations about P_c, W_e and P_l synthesis illustration of poc-FPOSS–2OH and FPOSS-SiNPs; particle size distribution of waterborne emulsion; FE-SEM images of GMI-SOSs from cross-sectional view; transmittance of waterborne emulsion versus standing time and schematic illustration of migration behaviors of dispersed phases; contact angle of various liquids on GMI-SOSs versus coating area; contact angle of various liquids on GMI-SOSs formed on different substrates; schematic illustration and FE-SEM images of SOSs with different architectures; comparision of W_e of SOS and SHS obtained by different strategies; schematic illustration of P_l calculation; the comprehensive robustness tests of GMI-SOSs; photograph of device for ice adhesion measurements. See DOI: https://doi.org/10.1039/d5ta08033a.

Acknowledgements

The authors acknowledge the financial support provided by the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2025A1515010974 and 2022A1515010755) and the National Natural Science Foundation of China (Grant No. 51703037).

Notes and references

1. H. Zhou, H. Niu, H. Wang and T. Lin, Chem. Rev., 2023, 123, 663–700.
2. M. Liu, S. Wang and L. Jiang, Nat. Rev. Mater., 2017, 2, 1–17.
3. J. Wei, J. Zhang, X. Cao, J. Huo, X. Huang and J. Zhang, Nat. Commun., 2023, 14, 2862.
4. L. Wang, Z. Tian, X. Luo, C. Chen, G. Jiang, X. Hu, R. Peng, H. Zhang and M. Zhong, Nano Res., 2023, 16, 3267.
5. E. Arzt, H. Quan, R. M. McMeeking and R. Hensel, Prog. Mater. Sci., 2021, 120, 100823.
6. Y. J. Lai, P. C. Oh, T. L. Chew and A. L. Ahmad, ACS Omega, 2025, 10, 5172–5192.
7. B. X. Chen, X. L. Lin, M. J. Yang, Z. L. You, W. F. Liu, H. L. Meng, Y. H. Zhou, H. Yuan and J. W. Liao, J. Mater. Chem. A, 2022, 10, 4944–4951.
8. M. Ezazi, B. Shrestha, N. Klein, D. H. Lee, S. Seo and G. Kwon, ACS Appl. Mater. Interfaces, 2019, 11, 30240.
9. J. Wassgren and A. Hozumi, ACS Nano, 2025, 19, 27075–27115.
10. R. Malinowski, I. P. Parkin and G. Volpe, Chem. Soc. Rev., 2020, 49, 7879–7892.
11. J. K. George and N. Verma, J. Membr. Sci., 2022, 654, 120538.
12. X. Q. Cheng, Y. Jiao, Z. Sun, X. Yang, Z. Cheng, Q. Bai, Y. Zhang, K. Wang and L. Shao, ACS Nano, 2021, 15, 3500–3508.
13. D. H. Wang, Q. Q. Sun, M. J. Hokkanen, C. L. Zhang, F. Y. Lin, Q. Liu, S. P. Zhu, T. F. Zhou, Q. Chang, B. He, Q. Zhou, L. Q. Chen, Z. K. Wang, R. H. A. Ras and X. Deng, Nature, 2020, 582, 55–59.
14. F. Chen, Y. Wang, Y. Tian, D. Zhang, J. Song, C. R. Crick, C. J. Carmalt, I. P. Parkin and Y. Lu, Chem. Soc. Rev., 2022, 51, 8476.
15. S. Wang, K. Liu, X. Yao and L. Jiang, Chem. Rev., 2015, 115, 8230–8293.
16. J. Wei, B. Li, N. Tian, J. Zhang, W. Liang and J. Zhang, Adv. Funct. Mater., 2022, 32, 2206014.
17. D. Li, L. Wang, R. Peng, Z. Song, Z. Liu, Z. Chang, H. Zhang, P. Fan and M. Zhong, Adv. Sci., 2025, e08272.
18. L. Wang, D. Li, G. Jiang, X. Hu, R. Peng, Z. Song, H. Zhang, P. Fan and M. Zhong, ACS Nano, 2024, 18, 12489–12502.
19. Y. Fan, C. Wu, J. Yang, Y. Wang, Y. Zhou, J. Zhou, J. Luo, J. Zhang, S. Huang and X. Tian, Chem. Eng. J., 2022, 448, 137638.
20. T. L. Liu and C.-J. C. Kim, Science, 2014, 346, 1096–1100.
21. K. L. A. Cao, A. M. Rahmatika, Y. Kitamoto, M. T. T. Nguyen and T. Ogi, J. Colloid Interface Sci., 2021, 589, 252–263.
22. W. Gu, W. Li, Y. Zhang, Y. Xia, Q. Wang, W. Wang, P. Liu, X. Yu, H. He, C. Liang, Y. Ban, C. Mi, S. Yang, W. Liu, M. Cui, X. Deng, Z. Wang and Y. Zhang, Nat. Commun., 2023, 14, 5953.
23. C. Peng, Z. Chen and M. K. Tiwari, Nat. Mater., 2018, 17, 355–360.
24. C. Li, H. Lai, Z. J. Cheng, J. J. Yan, L. H. Xiao, L. Jiang and M. Z. An, Chem. Eng. J., 2020, 385, 123924.
25. S. Pan, R. Guo, M. Bjornmalm, J. J. Richardson, L. Li, C. Peng, N. Bertleff-Zieschang, W. Xu, J. Jiang and F. Caruso, Nat. Mater., 2018, 17, 1040–1047.
26. Z. Zhang, Z. Zhao, X. Liu, S. Sheng, J. Han, Z. Liu, C. Yu, R. H. A. Ras, S. Niu, Y. Ning, K. Liu and L. Jiang, Adv. Mater., 2025, e13238.
27. B. Chen, M. Yang, X. Lin, W. Liu, H. Yuan and J. Liao, Chem. Commun., 2022, 58, 4263–4266.
28. J. Liao, X. Lin, B. Chen, M. Yang, W. Liu, Y. Cao, J. Zhou and J. Zhong, Nano Lett., 2024, 24, 187–194.
29. F. Chen, Y. Wang, Y. Tian, D. Zhang, J. Song, C. R. Crick, C. J. Carmalt, I. P. Parkin and Y. Lu, Chem. Soc. Rev., 2022, 51, 8476–8583.
30. R. Pan, M. Cai, W. Liu, X. Luo, C. Chen, H. Zhang and M. Zhong, J. Mater. Chem. A, 2019, 7, 18050–18062.

---