Broadband lightweight metal-mesh-integrated acoustic metaliner
Yujie
Cheng†
a,
Hua
Ding†
a,
Yilong
Yang†
 b,
Nengyin
Wang
a,
Tongwei
Lu
a,
Kai
Zhang
b,
Yabin
Jin
*c and
Yong
Li
b,
Nengyin
Wang
a,
Tongwei
Lu
a,
Kai
Zhang
b,
Yabin
Jin
*c and
Yong
Li
 *a
*a
aInstitute of Acoustics, School of Physics Science and Engineering, Tongji University, Shanghai 200092, China. E-mail: yongli@tongji.edu.cn
bSchool of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China
cInstitute of Computational Mechanics × AI & College of Intelligent Robotics and Advanced Manufacturing, Fudan University, Shanghai, 200433, China. E-mail: yabinjin@fudan.edu.cn
First published on 2nd December 2025
Abstract
Engine nacelle acoustic liners are key components in modern aircraft engine noise control. The high-bypass-ratio turbofan engines possessing outstanding performance impose stringent constraints on the noise reduction design, thereby presenting multifaceted challenges for acoustic liners in terms of sound absorption performance, installation space, and mechanical properties. Consequently, the development of novel acoustic liners with lightweight, broadband sound absorption characteristics and excellent mechanical performance has become a critical research priority. In this study, we present a novel double-layer honeycomb metaliner featuring embedded apertures and surface metal mesh to address these challenges. The embedded aperture configurations with varying lengths enable flexible acoustic impedance manipulation. The comprehensive effects of resistive modulation by the metal mesh and coupling among the sound absorption units suppress the impedance oscillation and further enhance the low-frequency broadband sound absorption efficiency. The experimental and simulation results demonstrate that the proposed liner, with a thickness of 39 mm, achieves an average sound absorption coefficient of 0.912 within the frequency range of 1000 to 5000 Hz. Furthermore, mechanical tests reveal that the honeycomb structure exhibits a superior load-bearing capacity and weight efficiency compared to traditional square structures. This study offers a promising solution for the next generation of aircraft engine noise control, with potential applications in aerospace and other industries that require efficient sound attenuation in complex environments.
Introduction
In recent years, the aviation industry has increasingly focused on engine noise control, with engine nacelle acoustic liners playing a crucial role in aircraft noise reduction.1–7 As aviation technology, including the rise of new aircraft technologies such as electric vertical takeoff and landing (eVTOL) aircraft, develops rapidly, modern aircraft impose higher and more urgent demands on engine noise control.8–12 Acoustic liners not only need to provide effective noise attenuation over a broad frequency range, but also must meet the increasingly stringent spatial constraints of aircraft design, resulting in the requirements of lightweight and compact acoustic liners in aircraft nacelles. Furthermore, noise control technologies must perform optimally under extreme conditions for the complex operating environments of aero-engines, such as high structural loading, high flow speed, high sound intensity, and the coupling interactions of complex flow fields, sound fields, and temperature fields. Nevertheless, prevailing acoustic liners still encounter challenges due to their bulk geometry and bandwidth limitations, and their mechanical properties also remain to be further optimized.Traditional resistive sound-absorbing materials (such as porous foams and fibrous materials) rely on their porous microstructure to generate friction and viscous effects, converting sound energy into heat and achieving sound absorption. These materials typically require geometric dimensions comparable to the working wavelength, making them primarily suitable for high-frequency sound absorption scenarios. Their porous nature compromises stable acoustic performance under extreme conditions like high structural loads or elevated temperatures, rendering them unsuitable for acoustic liner manufacturing.13–22 To address these limitations, conventional acoustic liners employ an innovative design based on resonant sound absorption principles, consisting of three key components: a micro-perforated panel, a rigid backplate, and an intermediate resonant cavity, thereby eliminating reliance on porous materials.23–35 For the resonant cavity design, the honeycomb structure presents a promising alternative due to its superior mechanical performance and lightweight characteristics. Its hollow geometry facilitates significant weight reduction while retaining high stiffness and load-bearing capacity.36–48 However, due to structural simplicity and insufficient degrees of freedom, their broadband noise control performance remains fundamentally constrained by inadequate acoustic impedance modulation bandwidth.
The development of acoustic metamaterials has provided a transformative foundation for designing advanced acoustic liners. These materials, equipped with deep subwavelength structural configurations, can flexibly manipulate sound waves to achieve efficient acoustic energy absorption.49–70 In particular, research on multi-resonator coupled metamaterials, a key enabler for next-generation liners, has progressed significantly, enabling broadband high-efficiency sound absorption at ultra-thin thicknesses. Cummer et al. successfully achieved full sound absorption at 511 Hz with a 33.5 mm-thickness structure by coupling resonators.71 Assouar et al. designed a deep subwavelength metasurface combining labyrinthine channels and coiled cavities, achieving perfect low-frequency absorption at 50 Hz with a 13 mm-thick photosensitive resin structure.72 In the past five years, the discovery of the global coupling design method has led to significant advancements in the development of acoustic liners. This method further compressed the dimensions of sound absorbers by utilizing weak absorption units, enabling more compact and efficient designs.73–75 These exemplary cases underscore the potential of metamaterial-based approaches for pushing the performance boundaries of traditional acoustic liners. Nevertheless, multi-resonator coupled absorption structures require sufficient intrinsic loss to achieve optimal broadband absorption performance.
To further improve the broadband sound absorption performance of resonant coupled absorbers, researchers have introduced metal mesh as a tuning element. As a near-zero-thickness material, the metal mesh demonstrates excellent airflow erosion resistance, superior mechanical properties, and wide operational stability, enabling effective modulation of the overall acoustic impedance characteristics without altering the structural thickness, thereby achieving superior acoustic performance. Studies have established a well-defined correlation between the mesh count and acoustic impedance properties, with the latter being precisely determinable.76,77 Considering these characteristics, the metal mesh plays a pivotal role in acoustic liner design due to its distinctive impedance modulation capabilities.
Here, we address the above challenge of multifunctional acoustic metaliners and propose a novel double-layer metaliner with honeycomb cavities covered by metal mesh. Retaining the superior mechanical properties, this design improves the overall sound absorption bandwidth and efficiency due to the incorporation of embedded apertures and the metal mesh. This work introduces a new paradigm for the development of high-performance acoustic liners. Such innovative design can provide more effective and sustainable solutions for aircraft noise control. The subsequent sections develop the theoretical framework for the proposed acoustic liner, present and discuss its sound absorption characteristics and mechanical properties, summarize the principal findings, and detail the experimental methodology.
Theoretical model
The sound absorption coefficient is a physical quantity that describes the sound absorption ability of materials or structures. It can be determined from the normal acoustic impedance Za, as follows: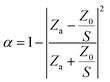 | (1) |
The proposed metaliner unit (as shown in Fig. 1(a)), covered by a layer of metal mesh on the surface, consists of four double-layered honeycomb cavities with embedded apertures. We first calculate the impedance of each individual unit. The internal air domain is divided into 8 regions, which include the tube section, the cavity section, and the cavity between the tube and cavity as shown in Fig. 1(b).
The sound pressure and velocity between the inlet and outlet of each section satisfy the transfer matrix relation:
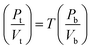 | (2) |
The transfer matrix T can be written as:
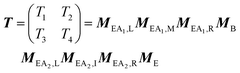 | (3) |
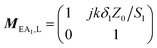 | (4) |
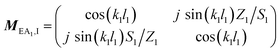 | (5) |
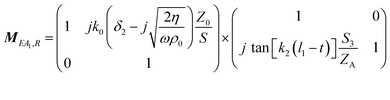 | (6) |
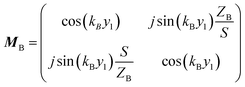 | (7) |
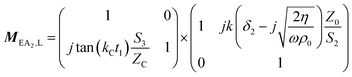 | (8) |
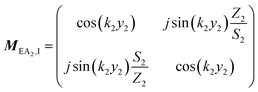 | (9) |
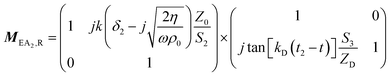 | (10) |
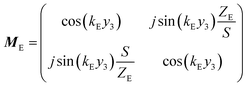 | (11) |
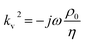 | (12) |
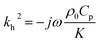 | (13) |
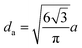 in the calculation, the viscous and thermal effects can be expressed as:
in the calculation, the viscous and thermal effects can be expressed as: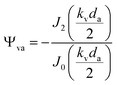 | (14) |
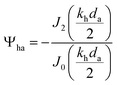 | (15) |
From this, we can calculate the equivalent sound propagation parameters in the interstitial hole as follows:
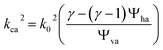 | (16) |
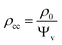 | (17) |
For the hexagonal honeycomb cavity, when calculating the effects of viscosity and thermal conduction, the wide-tube approximation method is used. Its parameters are expressed as:79
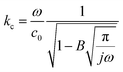 | (18) |
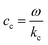 | (19) |
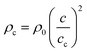 | (20) |
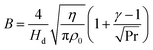 ,
, 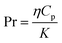 , γ is the specific heat ratio, Hd is the hydraulic diameter of the cavity cross-section, and Pr is the Prandtl number.
, γ is the specific heat ratio, Hd is the hydraulic diameter of the cavity cross-section, and Pr is the Prandtl number.
The transfer matrix of the inlet tube opening can be corrected using the impedance characteristics of the metal mesh added to the surface. The specific expression is as follows:
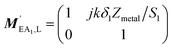 | (21) |
| Zmetal = (0.081062168 + ik·0.000193)Z0 | (22) |
The surface impedance of the final structural unit can be expressed as:
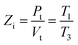 | (23) |
Considering the coupling of multiple units, the overall surface impedance of the system can be expressed as:
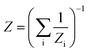 | (24) |
Results and discussion
Sound absorption performance
For the metaliner used in this study, the side length and tube length of the upper and lower hexagonal perforated tubes, including a1, a2, l1, l2, the position of the perforated tube (lu), the vertical length distribution of the lower perforated tube (t1 and t2), and the mesh number (Mn) of the surface metal mesh are all optimizable variables. The structure exhibits a high degree of freedom, allowing for precise control of the acoustic absorption coefficient within the target frequency range by adjusting the overall impedance, thereby achieving efficient sound absorption. The overall optimization of the parallel coupled structure is performed using a genetic algorithm. During the optimization process, the target frequency range was selected to cover 1000–5000 Hz based on practical aeroacoustic engineering needs, a common range for aircraft noise. The acoustic liner's unit cell adopts a hexagonal cavity with a side length of 5.5 mm, chosen based on the widely used aramid paper honeycomb material in current industrial production. The overall structural height of the double-layer configuration is constrained to 39 mm to accommodate the limited space in the short nacelle. Other structural parameters are also defined within specific ranges. The resulting metaliner achieves a theoretical average absorption coefficient of 0.92 within the target frequency range, with the structural parameters shown in the table below (Table 1).| Unit number | a 1 | a 2 | l 1 | l 2 | a | l u | l |
|---|---|---|---|---|---|---|---|
| 1 | 3.1 | 4.3 | 0.8 | 1.7 | 5.5 | 1.9 | 39.0 |
| 2 | 2.9 | 2.2 | 1.8 | 9.3 | 5.5 | 15.3 | 39.0 |
| 3 | 2.7 | 2.8 | 0.8 | 5.2 | 5.5 | 11.3 | 39.0 |
| 4 | 3.3 | 1.1 | 1.0 | 16.7 | 5.5 | 23.6 | 39.0 |
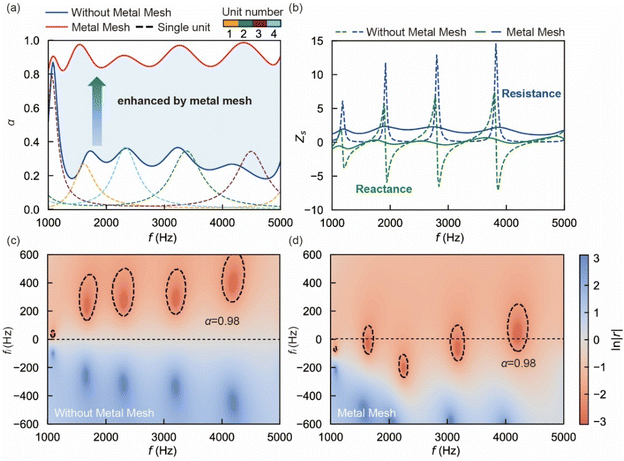
We investigate the impact of incorporating 500-mesh metal mesh on the acoustic absorption effect by integrating it into the four-cavity dual-layer perforated tube-type acoustic liner. Fig. 2(a) illustrates the variation of the sound absorption coefficient α with frequency for the four-cavity structure with and without the mesh. It is clear that the addition of the metal mesh significantly increases the absorption coefficient in the mid-to-high frequency range, particularly between 1500 Hz and 5000 Hz, where the mesh enhances the absorption capacity, approaching the ideal state of perfect sound absorption.
Further acoustic impedance analysis reveals the impact of the metal mesh on sound impedance. The comparison of acoustic impedance in Fig. 2(b) shows that the inclusion of the metal mesh alters the system's acoustic response characteristics. The above results indicate that the extremely thin configurations of resonant honeycomb cavities brought by the imperfect absorption lay the foundation for broadband sound absorption. The coupling among units significantly flattens the acoustic impedance curve oscillations, leading to significant improvement of sound absorption performance. The final sound absorption efficiency is notably enhanced due to the influence of the metal mesh on the overall system loss.
To elucidate the underlying mechanism responsible for the remarkable sound absorption efficacy, we introduce the concept of the complex frequency plane. The imaginary part of frequency, denoted as fi, is incorporated to quantify the supplementary dissipation within the system. It constitutes the complex frequency in conjunction with the system's intrinsic loss frequency component fe:
| f′ = fe − jfi | (25) |
This complex frequency supplants the original real frequency. Within the complex plane, the reflection coefficient r′ = 1 – α transforms into a function dependent on both real and imaginary frequencies. It is illustrated that when the zeros—the locus corresponding to the nadir of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∣r′∣—reside beneath the real axis in the complex frequency plane, the system enters an over-damped state.73,74,81,82 In this state, the absorber is capable of attaining perfect sound absorption with minimal thickness.
∣r′∣—reside beneath the real axis in the complex frequency plane, the system enters an over-damped state.73,74,81,82 In this state, the absorber is capable of attaining perfect sound absorption with minimal thickness.
However, resonant sound absorption is inherently characterized by multiple resonance peaks, which inevitably introduce anti-resonances (absorption dips) between them, resulting in a wavy absorption curve. Our globally coupled design effectively mitigates this issue, ensuring that even the absorption valleys remain above 0.8. Essentially, the metal mesh optimizes the impedance matching and suppresses the dispersive characteristics of the resonators by increasing intrinsic loss. The rational regulation of intrinsic loss enables the metaliner to achieve excellent broadband sound absorption performance by limiting fluctuations in resistance and reactance around the resonant frequency.
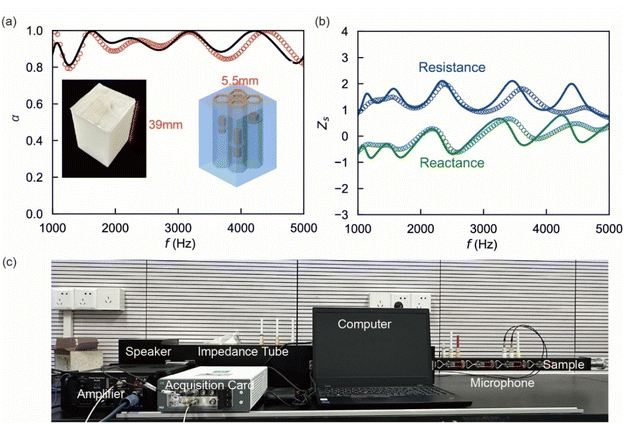
To corroborate the simulation and theoretical findings, experimental specimens were meticulously fabricated utilizing 3D printing technology. Photosensitive resin was selected as the printing material for its high printing precision with an accuracy of 0.1 mm. To maintain the structural fidelity, a rigid boundary was implemented during the printing process to align with the dimensions of the standing wave tube. Subsequently, the printed specimens were inserted into a 30 mm square impedance tube for empirical evaluation.
The experimental setup is shown in Fig. 3(c), where two microphones are used to measure both amplitude and phase data, which are crucial for calculating the sound absorption coefficient and impedance of the specimens. Given that the actual incident area S of the acoustic liner is less extensive than the tube's cross-sectional area S′, a conversion is imperative to ascertain the veritable values of impedance and sound absorption coefficient. In particular, the actual impedance Z correlates with the measured impedance Z′ through the equation: 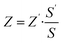 . And the genuine sound absorption coefficient is extrapolated from the actual impedance. The findings illustrated in Fig. 3(a) and (b) reveal that the experimental data are in close concordance with the simulation outcomes, both in terms of the sound absorption coefficient and impedance throughout the intended frequency spectrum. The recorded average absorption coefficient attained a value of 0.912, affirming the acoustic liner's high efficacy within the 1000–5000 Hz bandwidth. Slight discrepancies from the theoretical predictions are likely due to processing variances and manufacturing anomalies.
. And the genuine sound absorption coefficient is extrapolated from the actual impedance. The findings illustrated in Fig. 3(a) and (b) reveal that the experimental data are in close concordance with the simulation outcomes, both in terms of the sound absorption coefficient and impedance throughout the intended frequency spectrum. The recorded average absorption coefficient attained a value of 0.912, affirming the acoustic liner's high efficacy within the 1000–5000 Hz bandwidth. Slight discrepancies from the theoretical predictions are likely due to processing variances and manufacturing anomalies.
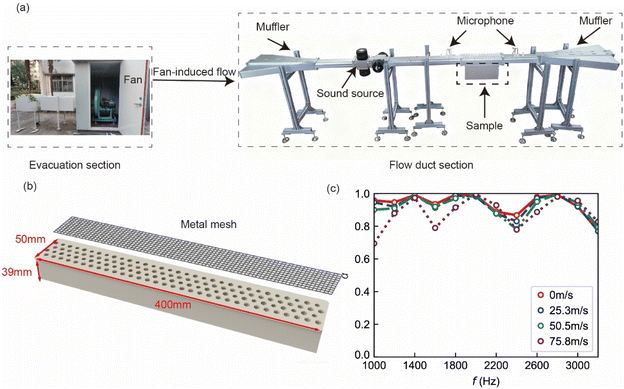
The innovation of this structure lies in the integration of metal mesh within the static design to enable precise control of the overall acoustic impedance. Notably, the metal mesh itself exhibits exceptional flow-field rectification properties. Given that the practical application of the metaliner frequently involves environments with flow impingement, the inclusion of the mesh contributes to maintaining the stability of the metaliner's acoustic performance under such conditions. Building on this consideration, acoustic validation of the proposed metaliner structure was further conducted using a flow duct experimental system.
The unit cell structure designed under static conditions was extended both laterally and longitudinally to fabricate a flow duct test sample with a width of 50 mm, length of 400 mm, and height of 39 mm. The experimental setup is shown in Fig. 4(a), with the detailed sample configuration presented in Fig. 4(b). By measuring the sound absorption coefficients under various flow velocities using the flow duct system, we systematically evaluated the flow velocity's effect on the acoustic performance. Due to limitations of the flow duct system, the test frequency range was 1000–3200 Hz.
The experimental results, shown in Fig. 4(c), demonstrate that the structure exhibits excellent acoustic stability at flow velocities below 50.5 m s−1, with the sound absorption curve remaining largely intact and exhibiting minimal fluctuations. Even at a high flow velocity of 75.8 m s−1, only a slight shift in the absorption peak and a limited decrease in performance were observed, confirming its engineering applicability under real flow conditions. This also highlights the structure's robust performance and long-term acoustic durability. The stabilizing effect of the metal mesh in dynamic flow environments is evident, as it not only provides impedance modulation and additional damping through local resonance effects under static conditions, but also stabilizes the flow field at the apertures in dynamic environments through its rectification effect, mitigating flow-induced acoustic disturbances such as vortex shedding. Thus, the incorporation of the metal mesh offers a dual enhancement of the metaliner's performance under both static and dynamic conditions.
Particularly noteworthy is the structure's ability to preserve the acoustic impedance integrity of the resonant cavity across a wide range of flow velocities, ensuring that the overall structure retains good impedance matching characteristics even under complex flow conditions. This feature holds significant practical value for engineering applications such as aircraft engine intake ducts and silencers in ventilation systems, providing an efficient and streamlined solution for flow-induced noise control.
Mechanical performance
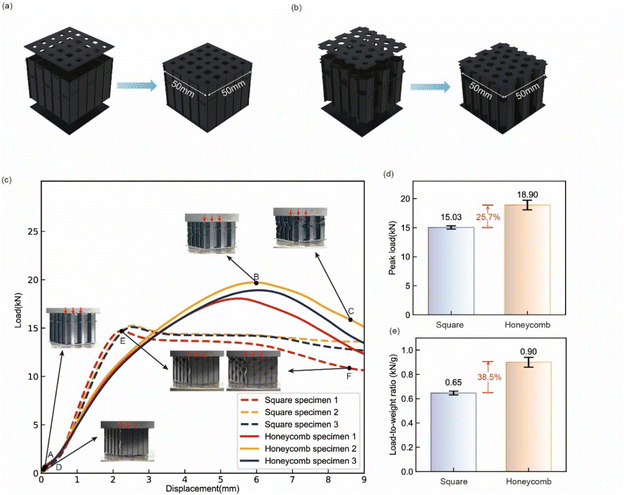
In the realm of sound absorber design, square structures have been extensively adopted in both research and practical applications, owing to their superior utilization of the sound absorption effective area and enhanced flexibility in optimization. Nonetheless, in the context of acoustic liner design, the stringent application environments necessitate the consideration of a multitude of performance factors, including mechanical properties, thereby rendering honeycomb designs more prevalent. To elucidate the mechanical performance disparities between honeycomb and square acoustic liners, a square sound absorber, exhibiting equivalent sound absorption performance to the study structure, was chosen as a control (with congruent cross-sectional areas for each unit cell and perforated tube) for quasi-static compression experiments, with each structure subjected to triplicate testing. To emulate the aramid paper material commonly utilized in aerospace acoustic liners, composite materials were selected for 3D printing. In the experimental setup, the influence of the perforated tube on the results was negligible under positive pressure, hence only the inserts and holes were preserved, and the printed segment was confined to a 50 × 50 mm square region, as shown in Fig. 5(a) and (b). The experimental apparatus employed was a universal testing machine with a load capacity of 100 kN, and the quasi-static compression velocity was calibrated to 1 mm min−1. Photographic documentation was undertaken when structural properties manifested abrupt alterations (points A–F in Fig. 5(c)).Analysis of the load–displacement curves reveals that, within the initial range of minor deformation, both honeycomb and square structures exhibited elastic deformation. As deformation progressed, both structures demonstrated nonlinear load–displacement responses, signifying the onset of the plastic deformation phase. The square structure's curve indicated a more gradual load increase at lesser compressive displacements, accompanied by a relatively subdued peak load. Conversely, the honeycomb structure exhibited a more pronounced load increase during compression, showcasing a higher peak load and a more defined yield phase, as seen in Fig. 5(c). The experimental points denoted by arrows in Fig. 5(c) (A to F) delineate the deformation stages of the two structures across various compression phases: points A and D signify initial compression, points B and E denote the commencement of structural yielding, and points C and F correspond to the advanced stages of structural compression.
Fig. 5(d) and (e) present the comparative results of strength and specific strength (strength-to-weight ratio). The illustrations clearly indicate that the honeycomb structure's strength (18.90 kN) markedly surpasses that of the square structure (15.03 kN), underscoring the honeycomb structure's augmented load-bearing capacity. Moreover, the specific strength of the honeycomb structure (0.90 kN g−1) also exceeds that of the square structure (0.65 kN g−1), highlighting the honeycomb structure's superior weight efficiency while sustaining elevated load-bearing capacity.
The honeycomb structure manifests mechanical advantages, particularly in terms of high load-bearing capacity and lightweight design. Its exceptional performance renders it a pivotal choice in acoustic liner design. In comparison to traditional structures, the honeycomb structure not only furnishes higher strength but also efficaciously diminishes overall weight, a critical factor for applications demanding efficient noise reduction and lightweight materials. With the progression of manufacturing technology, the honeycomb structure harbors significant potential for further advancements in acoustic liner design.
Conclusion
In this study, we developed a double-layered honeycomb metaliner structure, covered with metal mesh and equipped with embedded tubes of varying lengths, which successfully achieved high-efficiency sound absorption in the 1000 Hz to 5000 Hz frequency range. Experimental and simulation results show that this structure exhibits significant acoustic absorption performance, with an average absorption coefficient of 0.912. This design not only achieves effective absorption of broadband noise but also retains the ultra-thin characteristics of the structure, meeting the demands for high-efficiency sound absorption in space-limited environments.Further analysis indicates that the introduction of the metal mesh provides more freedom in the design, allowing for flexible adjustment of the intrinsic losses of the metaliner, thus effectively suppressing the anti-resonance phenomenon and preventing a significant drop in absorption performance between the absorption peaks. Additionally, the metal mesh can optimize the positions of zeros on the complex frequency plane, providing a means for broadly tuning the absorption performance. The impedance changes caused by adjusting the mesh density also help regulate the overall acoustic impedance characteristics of the structure. At the same time, flow duct tests have validated that the metal mesh enhances the stability of the structure under flow conditions, stabilizing the flow field and suppressing flow-induced disturbances such as vortex shedding, which could otherwise negatively impact acoustic performance. Additionally, the sound absorption results of each component and the entire structure contrast and explain the dominant role of the coupling effects in regulating the overall absorption performance. Therefore, the design method of the metaliner proposed in this study takes into account the coupling between components, achieving broadband sound absorption under ultra-thin conditions. Moreover, the introduction of the honeycomb structure significantly enhances the mechanical performance of the metaliner. Compared with traditional square structures, the honeycomb structure, with its unique geometry, increases the structural strength while retaining a lower weight, offering higher peak load capacity and better weight efficiency. This allows the design to provide improved compressive strength and stability in high-intensity and vibration-prone environments.
This study provides additional methods for controlling the resonances, coupling effects, and intrinsic losses of the metaliner, while incorporating mechanical performance considerations into the design of acoustic liners. These innovations potentially inspire the development of reliable and efficient acoustic liners for aircraft engines. Future research can further optimize the structural design and explore different materials and techniques, especially considering tangential flow effects.
Experimental section
Computational prediction and optimization
This study employed the genetic algorithm from the MATLAB R2023b (MathWorks, Inc.) Optimization Toolbox for the parametric optimization design of acoustic metamaterials. The optimization process aimed to maximize the average sound absorption coefficient within the 1000–5000 Hz frequency band, with performance evaluation based on the impedance ratio between the structural acoustic impedance and the characteristic impedance of air. The key geometric parameters subject to optimization included the diameters and lengths of upper/lower embedded tubes in parallel absorption modules, cavity dimensions, overall structural thickness, and the metal mesh count. The algorithm configuration followed standard genetic algorithm procedures: an initial population of 200 randomly generated parameter sets constituted the first generation, with subsequent generations produced through crossover and mutation operations at a probability of 0.3. The evolutionary process continued for a maximum of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generations to ensure convergence to optimal solutions.
000 generations to ensure convergence to optimal solutions.
3D printing
The acoustic models were developed using commercial finite element analysis software and exported as STL files for 3D printing. The acoustic test specimens were fabricated using the C-UV 9400 EF photosensitive resin material produced by Aide Synthetic Material Technology Co., Ltd (Dongguan, China) and printed on a UnionTech Lite800 industrial-grade stereolithography apparatus. This ABS-like resin material demonstrates high printing accuracy and excellent durability. All specimens underwent isopropanol cleaning and UV post-curing treatment before acoustic performance testing. The mechanical test specimens were fabricated using a nylon-based short carbon fiber reinforced nylon matrix composite through fused deposition modeling (FDM) technology to simulate conventional plastic materials in aerospace applications, with all specimens printed on a Mark Two 3D printer (Markforged, USA) at 0.1 mm layer thickness after structural slicing and path planning using Eiger software (Markforged, USA). The high-strength and high-toughness specimens were subsequently post-processed by support removal and desiccator storage before compression testing under identical environmental conditions.Sound absorption tests
The impedance tube experimental setup included a BSWA Tech SW477 series impedance tube (30 mm diameter), GRAS 46BD 1/4″ NVH acoustic sensors, and a LabVIEW data acquisition system. The test specimens were 3D-printed square microstructures with a 30 mm side length, precisely machined to ensure an airtight fit with the impedance tube wall. All sound absorption coefficient results were the arithmetic mean of three repeated measurements.The flow tube experimental setup, on the other hand, utilized a laboratory-developed flow tube system and pipeline, equipped with GRAS 46BD 1/4″ NVH acoustic sensors and a LabVIEW data acquisition system. The test specimens were 3D-printed rectangular structures with dimensions of 400 mm by 50 mm, arranged in periodic units. Flow velocity was measured at the center using a pitot tube, and the sound absorption results were processed using a laboratory-developed program.
Mechanical tests
Quasi-static compression tests were conducted on non-standard square and honeycomb specimens to compare their in-plane and out-of-plane mechanical performance. The tests were performed using a universal testing machine (Tinius Olsen 100ST, USA) with a 100 kN load capacity. A Horizon data acquisition system was employed for data collection. The quasi-static compression speed was set at 1 mm min−1. All test specimens were 3D-printed composite samples with dimensions of 50 × 50 mm. Three samples of each structure were fabricated and tested to ensure repeatability of the compressive properties.Author contributions
Yujie Cheng: writing – original draft, methodology, investigation, validation. Hua Ding: writing – review & editing, methodology, investigation. Yilong Yang: writing – original draft, investigation, validation. Nengyin Wang: methodology, software. Tongwei Lu: investigation, validation. Kai Zhang: methodology, investigation, project administration. Yabin Jin: supervision, writing – review & editing, funding acquisition. Yong Li: conceptualization, supervision, funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
All supporting data for this article, including experimental details, additional characterization results, and supplementary figures, have been included in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ta07233f.Acknowledgements
This work was supported by the National Key R&D Program of China (Grant No.2022YFB4602000), the National Natural Science Foundation of China (No.12272267), the Shanghai Science and Technology Committee (No.22JC1404100), the Shanghai Gaofeng Project for University Academic Program Development, the Shanghai Pilot Program for Basic Research, the Xiaomi Young Talents Program, and the Scientific Research Innovation Capability Support Project for Young Faculty (Grant No. ZYGXQNJSKYCXNLZCXM-D8).Notes and references
- M. G. Jones, F. Simon and R. Roncen, AIAA J., 2022, 60, 2481–2500 CrossRef.
- X. Ma and Z. Su, Sci. China: Technol. Sci., 2020, 63, 2491–2504 CrossRef.
- D. L. Sutliff, D. M. Nark and M. G. Jones, Int. J. Aeroacoustics, 2021, 20, 792–825 CrossRef.
- C. Lahiri and F. Bake, J. Sound Vib., 2017, 400, 564–605 CrossRef.
- Z. Lu, X. Jing, X. Sun and X. Dai, J. Vib. Control, 2016, 22, 2337–2346 CrossRef.
- Y. Zhang, L. Cattafesta, K. Pascioni and M. Choudhari, Prog. Aero. Sci., 2024, 146, 100996 CrossRef.
- A.-G. Totu, G. Cican and D.-E. Crunteanu, Aerospace, 2024, 11, 292 CrossRef.
- D. Casalino and C. Schram, J. Sound Vib., 2025, 596, 118732 CrossRef.
- T. Zhang, G. N. Barakos and A. Filippone, et al. , J. Sound Vib., 2024, 584, 118453 CrossRef.
- S. Xiang, A. Xie, M. Ye, X. Yan, X. Han, H. Niu, Q. Li and H. Huang, Green Energy Intell. Transp., 2024, 3, 100140 CrossRef.
- S. Altouq, C. M. Fong, P. J. Norman and G. M. Burt, IET Electr. Syst. Transp., 2025, 2025, 7218316 CrossRef.
- T. Zhang, G. N. Barakos and M. Foster, et al. , Aerosp. Sci. Technol., 2023, 137, 108307 CrossRef.
- M. El Messiry and Y. Ayman, J. Ind. Text., 2022, 51, 5347S–5369S Search PubMed.
- M. J. Cops, J. G. McDaniel, E. A. Magliula, D. J. Bamford and J. Bliefnick, Appl. Acoust., 2020, 160, 107138 Search PubMed.
- Y. Zhou, D. Li, Y. Li and T. Hao, Appl. Phys. Lett., 2019, 115, 5107439 Search PubMed.
- C. Zhang, H. Li, J. Gong, J. Chen, Z. Li, Q. Li, M. Cheng, X. Li and J. Zhang, Text. Res. J., 2023, 93, 434–449 CrossRef CAS.
- S. Huang, Y. Li, J. Zhu and D. P. Tsai, Phys. Rev. Appl., 2023, 20, 010501 CrossRef CAS.
- X. Sagartzazu, L. Hervella-Nieto and J. Pagalday, Arch. Comput. Methods Eng., 2008, 15, 311–342 CrossRef.
- J. P. Arenas and M. J. Crocker, Sound Vib., 2010, 44, 12–18 Search PubMed.
- L. Peng, B. Song, J. Wang and D. Wang, Adv. Mater. Sci. Eng., 2015, 2015, 274913 Search PubMed.
- L. Egab, X. Wang, M. Fard and I. J. Veh, Noise Vib., 2014, 10, 129–149 CrossRef.
- M. Amran, R. Fediuk, G. Murali, N. Vatin and A. Al-Fakih, Sustainability, 2021, 13, 10712 CrossRef CAS.
- V. L. Jordan, J. Acoust. Soc. Am., 1947, 19, 972–981 CrossRef.
- P. Tang and W. Sirignano, J. Sound Vib., 1973, 26, 247–262 CrossRef.
- M. Jones, B. Howerton and E. Ayle, 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), 2012, p. 2194 Search PubMed.
- M. G. Jones, D. M. Nark, A. Baca and C. R. Smith, 24th AIAA/CEAS Aeroacoustics Conference, 2018, p. 3445 Search PubMed.
- D. L. Sutliff and D. M. Nark and M. G. Jones and N. H. Schiller, 25th AIAA/CEAS Aeroacoustics Conference, 2019, p. 2582 Search PubMed.
- M. G. Jones and D. M. Nark and W. R. Watson and B. M. Howerton, 23rd AIAA/CEAS Aeroacoustics Conference, 2017, p. 3022 Search PubMed.
- T. L. Parrott and M. G. Jones, Noise Control Eng. J., 1995, 43, 183–195 CrossRef.
- B. M. Howerton and M. G. Jones, 21st AIAA/CEAS Aeroacoustics Conference, 2015, p. 2230 Search PubMed.
- C. H. Gerhold and M. Brown and C. Jasinski, 54th AIAA Aerospace Sciences Meeting, 2016, p. 1267 Search PubMed.
- R. H. Thomas and C. L. Burley and C. L. Nickol, 54th AIAA Aerospace Sciences Meeting, 2016, p. 0863 Search PubMed.
- Y. Wang, L. Du, X. Qiu, Y. Lyu, X. Jing, X. Wang, C. Liu and X. Sun, Appl. Acoust., 2025, 228, 110287 CrossRef.
- D. L. Sutliff and D. M. Nark and M. G. Jones, 22nd AIAA/CEAS Aeroacoustics Conference, 2016, p. 3005 Search PubMed.
- M. Jones, INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 2021, pp. 1633–1644 Search PubMed.
- Y. M. Ge, J. Y. Xue, L. P. Liu, H. Wan and Y. Yang, Mater. Today Commun., 2024, 38, 108013 CrossRef CAS.
- Y. He, Z. Bi, T. Wang, L. Wang, G. Lu, Y. Cui and K. M. Tse, Int. J. Mech. Sci., 2024, 270, 109091 CrossRef.
- P. Song, H. Qiu, L. Wang, X. Liu, Y. Zhang, J. Zhang, J. Kong and J. Gu, Sustain. Mater. Technol., 2020, 24, e00153 CAS.
- H. Lv, S. Shi, B. Chen, J. Ma and Z. Sun, Int. J. Mech. Sci., 2023, 246, 108149 CrossRef.
- H. Guo, H. Yuan, J. Zhang and D. Ruan, Thin-Walled Struct., 2024, 196, 111541 CrossRef.
- Z. Li, H. Li, Y. Yang, C. Ren, H. Zhang, H. Wang, J. Zhou, B. Zhou and Z. Guan, Mech. Syst. Signal Process., 2025, 232, 112676 CrossRef.
- J. Ji, Q. Luo and K. Ye, Mech. Syst. Signal Process., 2021, 161, 107945 CrossRef.
- X.-Y. Li, X.-Y.-H. Wang, Q.-Q. Wu, Y. Jin, Z. Lin and L.-Z. Wu, Mech. Syst. Signal Process., 2025, 227, 112364 CrossRef.
- L. Zhang, W. Zhang and F. Xin, Mech. Syst. Signal Process., 2023, 196, 110311 CrossRef.
- M. Hosseini and H. Mazaheri, Int. J. Mech. Sci., 2024, 276, 109223 CrossRef.
- Y. Wu, J. Fang, C. Wu, C. Li, G. Sun and Q. Li, Int. J. Mech. Sci., 2023, 246, 108102 CrossRef.
- E. Wang, R. Yao, Q. Li, X. Hu and G. Sun, Int. J. Mech. Sci., 2024, 270, 108795 CrossRef.
- J. Lu, Q. Li, R. Qin, X. Wang, T. Li, H. Niu and B. Chen, Int. J. Mech. Sci., 2025, 299, 110404 CrossRef.
- Z. Liu, X. Zhang, Y. Mao, Y. Y. Zhu, Z. Yang, C. T. Chan and P. Sheng, Science, 2000, 289, 1734–1736 CrossRef CAS PubMed.
- Y. Li, B. Liang, Z.-m. Gu, X.-y. Zou and J.-c. Cheng, Sci. Rep., 2013, 3, 02546 CrossRef PubMed.
- J. Zhao, B. Li, Z. Chen and C.-W. Qiu, Sci. Rep., 2013, 3, 02537 CrossRef.
- G. Ma, M. Yang, S. Xiao, Z. Yang and P. Sheng, Nat. Mater., 2014, 13, 873–878 CrossRef CAS.
- J. Mei and Y. Wu, New J. Phys., 2014, 16, 123007 CrossRef.
- K. Tang, C. Qiu, M. Ke, J. Lu, Y. Ye and Z. Liu, Sci. Rep., 2014, 4, 6517 CrossRef CAS.
- Y. Xie, W. Wang, H. Chen, A. Konneker, B.-I. Popa and S. A. Cummer, Nat. Commun., 2014, 5, 5553 CrossRef CAS PubMed.
- Y. Cheng, C. Zhou, B. G. Yuan, D. J. Wu, Q. Wei and X. J. Liu, Nat. Mater., 2015, 14, 1013–1019 CrossRef CAS PubMed.
- M. Yang, Y. Li, C. Meng, C. Fu, J. Mei, Z. Yang, P. Sheng and C. R. Mécanique , C. R. Mécanique, 2015, 343, 635–644 CrossRef.
- Y. Li, C. Shen, Y. Xie, J. Li, W. Wang, S. A. Cummer and Y. Jing, Phys. Rev. Lett., 2017, 119, 035501 CrossRef PubMed.
- B. Assouar, B. Liang, Y. Wu, Y. Li, J.-C. Cheng and Y. Jing, Nat. Rev. Mater., 2018, 3, 460–472 CrossRef CAS.
- X. Wang, X. Fang, D. Mao, Y. Jing and Y. Li, Phys. Rev. Lett., 2019, 123, 214302 CrossRef CAS.
- Y.-X. Shen, Y.-G. Peng, F. Cai, K. Huang, D.-G. Zhao, C.-W. Qiu, H. Zheng and X.-F. Zhu, Nat. Commun., 2019, 10, 3411 CrossRef.
- M. Sun, X. Fang, D. Mao, X. Wang and Y. Li, Phys. Rev. Appl., 2020, 13, 044028 CrossRef CAS.
- M.-H. Lu, L. Feng and Y.-F. Chen, Mater. Today, 2009, 12, 34–42 CrossRef CAS.
- N. Fang, D. Xi, J. Xu, M. Ambati, W. Srituravanich, C. Sun and X. Zhang, Nat. Mater., 2006, 5, 452–456 Search PubMed.
- C. Ge, N. Wang, X. Wang and Y. Li, Phys. Rev. Lett., 2025, 134, 237001 CrossRef CAS PubMed.
- Y. Li, X. Jiang, R.-Q. LI, B. Liang, X.-Y. Zou, L.-L. Yin and J.-C. Cheng, Phys. Rev. Appl., 2014, 2, 064002 CrossRef.
- J. Ji, D. Li, Y. Li and Y. Jing, ACE Library.html, 2020, 6, 586249 Search PubMed.
- G. Ma and P. Sheng, Sci. Adv., 2016, 2, e1501595 CrossRef PubMed.
- S. A. Cummer, J. Christensen and A. Alù, Nat. Rev. Mater., 2016, 1, 1–13 Search PubMed.
- T. Lu, C. Liu, N. Wang, C. Shao and Y. Li, Int. J. Mech. Sci., 2025, 293, 110173 CrossRef.
- J. Li, W. Wang, Y. Xie, B.-I. Popa and S. A. Cummer, Appl. Phys. Lett., 2016, 109, 4961671 Search PubMed.
- K. Donda, Y. Zhu, S.-W. Fan, L. Cao, Y. Li and B. Assouar, Appl. Phys. Lett., 2019, 115, 5122704 CrossRef.
- S. Huang, X. Fang, X. Wang, B. Assouar, Q. Cheng and Y. Li, J. Acoust. Soc. Am., 2019, 145, 254–262 CrossRef CAS.
- H. Ding, N. Wang, S. Qiu, S. Huang, Z. Zhou, C. Zhou, B. Jia and Y. Li, Int. J. Mech. Sci., 2022, 232, 107601 CrossRef.
- S. Huang, Z. Zhou, D. Li, T. Liu, X. Wang, J. Zhu and Y. Li, Sci. Bull., 2020, 65, 373–379 CrossRef.
- X. Qiu, L. Du, X. Jing and X. Sun, J. Sound Vib., 2024, 582, 118425 CrossRef.
- N. Wang, S. Huang, Z. Zhou, D. P. Tsai, J. Zhu and Y. Li, Natl. Sci. Rev., 2025, nwaf199 CrossRef.
- M. R. Stinson, J. Acoust. Soc. Am., 1991, 89, 550–558 CrossRef.
- S. Qiu, H. Ding, T. Lu, S. Liu, P. Qian and N. Wang, et al. , Chin. Sci. Bull., 2023, 68, 3482–3490 CrossRef.
- E. Rice, 7th Aeroacoustics Conference, 1981, p. 1999 Search PubMed.
- X. Qiu, X. Jing, L. Du, J. Yang, X. Sun and X. Zhang, AIAA J., 2022, 60, 5521–5532 CrossRef.
- Z. Zhou, S. Huang, D. Li, J. Zhu and Y. Li, Natl. Sci. Rev., 2022, 9, nwab171 CrossRef.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |