Open Access Article
Open Access ArticleA technique to create hydrogels with tethered concentration gradients of molecules in vitro
Thomas C.
O’Shea
a,
Ahmad
Salem
b and
Kelly M.
Schultz
 *a
*a
aPurdue University, Davidson School of Chemical Engineering, 480 Stadium Mall Drive, West Lafayette, IN 47907, USA. E-mail: kmschultz@purdue.edu
bLehigh University, Department of Chemical and Biomolecular Engineering, 124 East Morton Street, Bethlehem, PA 18015, USA
First published on 19th December 2025
Abstract
This work develops a technique to create and quantify tethered molecular concentration gradients in a hydrogel using a flow chamber. This device is designed to enable isotropic scaffold swelling, nutrient diffusion and real-time microrheological measurements. A hydrogel is first photopolymerized in the flow chamber ensuring that the mechanical properties of the hydrogel across samples are the same prior to molecular concentration gradient creation. Then molecules are passively diffused into the scaffold and a second photopolymerization tethers the concentration gradient into the material. This technique creates in vitro mimics of aspects of biological environments, such as the environment around a hydrogel implanted in the body for cell delivery. We use a well-defined synthetic scaffold with a poly(ethylene glycol) (PEG)-norbornene backbone cross-linked with a matrix metalloproteinase (MMP)-degradable peptide, a standard material for cell encapsulation. The method to tether molecular concentration gradients is validated using a fluorescent PEG-thiol (FITC-PEG-SH), an ideal polymer. We first create a calibration curve by measuring the fluorescence intensity of hydrogels with known uniform concentrations of the tethered fluorescent molecule. The calibration curve is used to calculate spatial concentration from measured fluorescence intensity in hydrogels with polymer or protein concentration gradients. FITC-PEG-SH is diffused through our hydrogel in a flow chamber for 6, 24 and 48 hours. We make consistent gradients and quantify the concentration of the fluorescent molecule every 25 µm along the material. Next, we make tethered concentration gradients of tumor necrosis factor-α (TNF-α), a pro-inflammatory cytokine found in the wound environment, after 24 hours of diffusion. These gradients are consistent when normalized by the concentration at the edge of the hydrogel, which varies due to pore clogging. From both molecular concentration gradients, we calculate an effective diffusion coefficient that is the same order of magnitude as the value calculated using the multiscale diffusion model. Significant advances made with this technique include limited confinement of the material, which enables isotropic swelling and facile nutrient diffusion, the ability to image through the device and the same hydrogel rheological properties across samples. This technique can be used in future work to characterize cell-laden hydrogels which present the same physical cues to cells and tethered concentration gradients of chemical cues using microrheology.
1 Introduction
This study details the development and demonstration of a new technique to create and quantify hydrogels with tethered concentration gradients. This device is designed to enable sequential photopolymerization of the material and then the molecular concentration gradient, isotropic swelling of the scaffold, nutrient diffusion into the material and real-time microrheological measurements. Sequential photopolymerization ensures that the hydrogel scaffold has the same rheological properties prior to tethering of the molecular concentration gradient.1 Confinement of the hydrogel in the device is limited, which enables isotropic swelling, maintaining a consistent pore structure, and nutrient diffusion, which will enable measurements of live cells in hydrogels. Finally, the device is designed for fluorescent imaging, enabling microrheological characterization of the hydrogel after tethering of the molecular concentration gradient. This technique is designed to mimic aspects of the in vivo environment in vitro. For example, in the native environment, concentration gradients of cell signaling molecules direct cells to migrate to wounded tissue and specify lineage during differentiation.1–8 Hydrogels are also used for cell delivery where they encapsulate and deliver cells to wounded tissue to enhance healing and tissue regeneration.9–16Fabricating hydrogels with tethered or untethered concentration gradients of molecules is well-established.2,3,5,6,17–19 Previously, collagen mats are made with linear concentration gradients of stromal cell derived factor 1-α (SDF1-α).20 In this work, they measure an increase in directed neural stem cell migration and differentiation in high concentration regions.20 Other work uses gradient makers hooked up to peristaltic pumps to form RGDS or basic fibroblast growth factor (bFGF) concentration gradients in hydrogels.5,6 Both of these techniques use syringe pumps to form concentration gradients in hydrogels during photopolymerization, which could lead to varied hydrogel rheological properties across the scaffold. Another method uses capillary tubes to diffuse different fluorescent proteins through a hydrogel and measures fluorescence with microscopy.21 The μ-slide is a commercially available flow channel (Ibidi) that can be used to create gradients with live cell systems. However, this commercial device constricts the gel in 3D. As a result, after photopolymerization the material will have a non-uniform pore structure after it is swollen. Non-uniform pore structures will introduce another physical cue into an experiment. In this work, we develop a device that allows for future cell–material interaction measurements in a system that has only a chemical gradient using microrheology.
Microrheology has been used to characterize evolving hydrogels and measure spatio-temporal cell–material interactions in the pericellular region around 3D encapsulated cells.22–28 Our device is designed to enable microrheology characterization, specifically multiple particle tracking microrheology (MPT). MPT uses video microscopy to measure the Brownian motion of embedded fluorescently labeled probe particles in a material to characterize dynamically evolving material properties.26,29–46 MPT has fast acquisition times, which allows for the collection of data points in a dynamically evolving material, such as a hydrogel during cell-mediated degradation. However, at this time there is not a device where a hydrogel can be made with a tethered concentration gradient and characterized with microrheology. We will use microrheology in future work to compare the effectiveness of a material with a uniform tethered chemical signal to that of a material with a tethered concentration gradient of the same cue.
To develop this technique we consider our future applications characterizing cell-laden hydrogels and use a well-defined poly(ethylene glycol) (PEG)-based scaffold that has been widely used for in vivo and in vitro experiments.10,11,26,47–55 The scaffold consists of a poly(ethylene glycol) (PEG)-norbornene backbone cross-linked with a matrix metalloproteinase (MMP)-degradable peptide sequence (KCGPQG↓IWGQCK).11 This scaffold uses thiol–ene chemistry.56 The formulation is designed to contain unreacted -ene groups in the final scaffold, which we leverage to tether molecules into the scaffold that are end functionalized with thiols. To create a concentration gradient of chemical cues, we allow passive diffusion of these molecules into the cross-linked scaffold and tether them into the scaffold using a second photopolymerization reaction. We illustrate this technique using fluorescently labeled PEG-thiol or thiolated TNF-α.
In this work, we develop a method to create concentration gradients of molecules and tether them into a hydrogel. A concentration gradient is made using passive diffusion in a flow chamber. This device uses facile fabrication techniques and is designed to enable incubation of the hydrogel in a fluid environment after fabrication. This is done for future applications where cell-laden hydrogels will be created with cytokine concentration gradients requiring incubation in media for cell survival. Before forming these gradients, we make calibration curves to relate measured fluorescence intensity to known concentrations of each fluorescent molecule. This enables spatial molecular concentration to be calculated from measured fluorescence intensity once it is tethered into the hydrogel. As a check of our measurements of tethered concentration gradients, we fit them to a solution of Fick's second law to calculate effective diffusivity for each molecule and compare these values to theoretical predictions from the multiscale diffusion model. We first show proof-of-concept of this technique by tethering a concentration gradient of fluorescent PEG-thiol (FITC-PEG-SH) into our hydrogel scaffold. We show we can consistently make concentration gradients and the measured effective diffusivity of PEG in our network is the same order of magnitude as predicted values. We then show we can create a tethered cytokine concentration gradient in our scaffold. Since the cytokine is similar in size to the pores of the hydrogel we measure pore clogging at the edge of the hydrogel. Data from these concentration gradients are consistent when normalized by the concentration of the cytokine at the edge of the hydrogel. A new workflow and technique is developed using two photopolymerizations to create consistent concentration gradients of tethered molecules in hydrogels with the same rheological properties. Our device enables isotropic swelling, nutrient diffusion and live cell imaging, which are key advances. This device can be used in a wide range of applications including enabling fabrication of materials with changing molecular microenvironments and measurements of cell–material interactions.
2 Materials and methods
2.1 Poly(ethylene glycol)-norbornene scaffold
The hydrogel used in this work is composed of a 4-arm poly(ethylene glycol)-norbornene backbone (PEG-N, Mn = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, 3 mM, f = 4, where f is the functionality of the polymer, JenKem) cross-linked with a matrix metalloproteinase (MMP)-degradable peptide (KCGPQG↓IWGQCK, Mn = 1346 g mol−1, 3.9 mM, f = 2, Bachem). The precursor solution contains lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP, Mn = 294 g mol−1, 1 mM, Sigma-Aldrich).11,26 LAP is a photoinitiator and begins step-growth polymerization when the precursor solution is exposed to ultraviolet (UV) light (5 mW cm−2, 365 nm, UVP, LLC) for 3 minutes. The material is uniformly cured and fully cross-linked before 3 minutes of UV light exposure is complete.48,53,57 LAP is chosen for its inert reactivity when encapsulating proteins in gels.58 All components are diluted in phosphate buffered saline (1× PBS, Gibco) and hydrogels are formed at the concentrations described above with 51 vol% PBS. The scaffold is cross-linked at a thiol
000 g mol−1, 3 mM, f = 4, where f is the functionality of the polymer, JenKem) cross-linked with a matrix metalloproteinase (MMP)-degradable peptide (KCGPQG↓IWGQCK, Mn = 1346 g mol−1, 3.9 mM, f = 2, Bachem). The precursor solution contains lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP, Mn = 294 g mol−1, 1 mM, Sigma-Aldrich).11,26 LAP is a photoinitiator and begins step-growth polymerization when the precursor solution is exposed to ultraviolet (UV) light (5 mW cm−2, 365 nm, UVP, LLC) for 3 minutes. The material is uniformly cured and fully cross-linked before 3 minutes of UV light exposure is complete.48,53,57 LAP is chosen for its inert reactivity when encapsulating proteins in gels.58 All components are diluted in phosphate buffered saline (1× PBS, Gibco) and hydrogels are formed at the concentrations described above with 51 vol% PBS. The scaffold is cross-linked at a thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ene ratio of 0.65, a widely used composition with a low cross-link density that enables molecular diffusion through the network.52,56 In addition, the thiol
ene ratio of 0.65, a widely used composition with a low cross-link density that enables molecular diffusion through the network.52,56 In addition, the thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ene ratio creates a material with a storage modulus that mimics the stiffness of soft tissues, such as adipose tissue.26,48 Due to network imperfections, even at a higher thiol
ene ratio creates a material with a storage modulus that mimics the stiffness of soft tissues, such as adipose tissue.26,48 Due to network imperfections, even at a higher thiol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ene ratio, there would be unreacted norbornene molecules present, and additional thiol functionalized molecules could be tethered into the material.
ene ratio, there would be unreacted norbornene molecules present, and additional thiol functionalized molecules could be tethered into the material.
2.2 Flourescein poly(ethylene glycol)-thiol (FITC-PEG-SH)
Flourescein poly(ethylene glycol)-thiol (FITC-PEG-SH, Mn = 1000 g mol−1, 0.1 mM, f = 1, Nanocs) is tethered into the hydrogel scaffold to validate the technique. This molecule is used as received. Calibration curves relating FITC-PEG-SH fluorescence intensity to known concentrations are made by mixing FITC-PEG-SH at varying concentrations into hydrogel precursor solutions described above. Briefly, a stock solution of 1 mM FITC-PEG-SH is made in 1× PBS. Then, this stock solution is diluted to varying final concentrations in each hydrogel precursor solution. The amount of PBS in the final solution is decreased to account for the added FITC-PEG-SH solution.FITC-PEG-SH is also diffused through cross-linked PEG-N hydrogels to make concentration gradients. The concentration of FITC-PEG-SH used to make concentration gradients is 0.05 mM. FITC-PEG-SH is covalently tethered into the scaffold after passive diffusion using thiol–ene chemistry and additional UV light exposure for 30 seconds. FITC-PEG-SH is chosen to show proof-of-concept of the method. The molecule has a single thiol group that can be covalently tethered into the network. Additionally, it is significantly smaller than the pore size of the network.
2.3 Thiolation of tumor necrosis factor-α (TNF-α)
TNF-α (PeproTech) is prepared for long-term storage by re-hydrating lyophilized TNF-α and adding an equal volume of 10 wt% D-(+)-trehalose solution (Sigma-Aldrich) to create a solution with a final concentration of 5 wt% of D-(+)-trehalose to prevent protein degradation. Next, TNF-α is thiolated by adding 20 molar excess of 2-iminothiolane hydrochloride (Traut's regent, Sigma-Aldrich) following previous protocols.54,55,58–60 The reaction is incubated at room temperature for 1 hour. During incubation, additional thiol groups are covalently bound to the surface of TNF-α. The solution is added to a desalting column (7000 Da molecular weight cut-off, zebra spin desalting column, Thermo Fisher Scientific) and centrifuged at 1500 relative centrifugal force (RCF) for 3 minutes. Unreacted thiol will be trapped in the desalting column and thiolated TNF-α will flow through the column. 10 wt% trehalose is again added to maintain the concentration of 5 wt% trehalose to prevent protein degradation. The protein is stored in a −80 °C freezer until use. Uniformly tethering TNF-α does not change the storage modulus or the microstructure of the material.1 Based on our previous analysis, we determine that thiolated TNF-α does not contribute to cross-linking. Thiolated biomolecules have been previously shown to maintain bio-activity in similar hydrogels using the same thiolation reaction.1,54,59,61–632.4 Fluorescently labeling TNF-α
TNF-α is fluorescently labeled to enable spatial measurement of concentration once it is tethered into a hydrogel scaffold following the manufacturer's protocol.64 Before dying thiolated TNF-α the solution is lyophilized (Free Zone 4.5 Liter, Labconco) to remove the solution from the chemically modified protein. Lyophilized thiolated TNF-α is added to a 1.0 M sodium bicarbonate solution (Anhydrous, Sigma-Aldrich). Separately, 10 µL of deionized water is added to Alexa Flour 488 (Microscale labeling kit, ThermoFisher) and is thoroughly mixed. Thiolated TNF-α and dye are combined ensuring there is at least 5 µg of protein and the dye to protein ratio is not less than 1 µg of protein to 1 µL of dye. The solution is incubated at room temperature and protected from light for 20 minutes. After completion of the reaction, the solution is passed through a 7000 Da molecular weight cut-off zebra desalting column (Thermo Fischer Scientific) and centrifuged at 1500 RPM for 2 minutes. Unreacted dye will remain trapped in the desalting column and the product will flow through the column.Fluorescently labeled TNF-α is added to hydrogel scaffolds to make calibration curves as described for FITC-PEG-SH. TNF-α is made at a stock concentration of 28.7 µM and diluted to varying final concentrations in the hydrogel precursor solution prior to UV exposure. TNF-α is also used to make concentration gradients tethered into hydrogel scaffolds. TNF-α is made at a stock concentration of 31.1 nM and contacted with the hydrogel scaffold for passive diffusion in the flow chamber. After diffusion the scaffold is exposed to UV light to tether TNF-α into the material. A post-operative wound has a local concentration of 11.1 ng mL−1 of TNF-α.65 In our work, we use a higher concentration to measure the molecule in the material.
2.5 Modified indirect enzyme-linked immunosorbent assay (ELISA)
A modified indirect ELISA is adapted from published protocols to detect a tethered biomolecule in a hydrogel.55,59–62,66 Experiments use triplicate hydrogel replicates. 3 gels with tethered TNF-α are formed and 3 gels are made without TNF-α. Gels are washed 3× in 3 mL of 1× PBS (Gibco). Next, PBS is decanted and the gels are incubated overnight in 3 mL of mouse-anti-human TNF-α solution (5 µg mL−1, monoclonal antibody, Peprotech) dissolved in ELISA wash. ELISA wash is a mixture of 0.1% bovine serum albumin (BSA, Sigma-Aldrich) and 0.05% Tween-20 (Thermo Fisher Scientific) in PBS. Gels are then rinsed 3× in ELISA wash. Next, gels are incubated in 100 ng mL−1 horseradish peroxidase-conjugated goat-anti-mouse secondary antibody (Jackson ImmunoResearch) for 4 hours. Gels are again rinsed 3× in ELISA wash and incubated overnight. The following morning, gels are rinsed a final time for 1 hour in ELISA wash to remove any unbound secondary antibody. Gels are moved to a sterile 96-well plate. 70 µL of PBS is added to the top of the gels and 100 µL of 3,3′,5,5′-tetramethylbenzidine (TMB, Thermo Fisher Scientific) is added to each well. After 20 minutes, the reaction is quenched with 100 µL of 65% sulfuric acid (Thermo Fisher Scientific). Absorbance is measured using a spectrophotometer at 450 nm (Spectra Max id3, Molecular Devices). Results in Fig. 1 show that there is a statistically significant increase in absorbance of scaffolds with TNF-α compared to scaffolds with no cytokine. This indicates that TNF-α is present in the hydrogel scaffold.2.6 Fluorescence measurements and image analysis for calibration curves
Hydrogels with known concentrations of fluorescent molecules (FITC-PEG-SH or thiolated TNF-α, N = 5 where N is the number of replicates) are imaged using a laser scanner (Cytvia Amersham Typhoon, Cy2) to measure fluorescence intensity. 17 µL gels are formed on a microscope slide, rinsed 3× (with 1× PBS or cell media) and loaded onto the laser scanner stage. Voltage is set to 275 V for the FITC-PEG-SH calibration curve and concentration gradient measurements. For the TNF-α calibration curve and concentration gradient measurements, the voltage is set to 356 V. Data are collected in proprietary file types (.gel) to limit compression and analyzed using ImageJ (NIH).Analysis of hydrogels for calibration curves is done by first tracing an area in the 17 µL gel, shown in Fig. 2 for gels with fluorescent TNF-α. The edge of the gel is excluded due to imaging artifacts. The median fluorescence intensity of the selected area in A.U. is calculated. The calibration curve hydrogels with FITC-PEG-SH have concentrations between 0–0.40 mg mL−1 and corresponding fluorescence intensity between 1210 ± 90 A.U. and 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 150 A.U.
300 ± 150 A.U.
Hydrogels made for the tethered TNF-α calibration curve are swollen overnight in cell media. Cell media contains proteins and is required for cell survival within our hydrogels, which will be needed for future work. Hydrogels are swollen in cell media to ensure the fluorescent cytokine can still be detected in a solution with other proteins. Cell media is made of RoosterNourish Basal-MSC-CC (RoosterBio) and prepared according to the manufacturer's protocol. 50 U mL−1 penicillin/streptomycin (Gibco) and 0.5 µg mL−1 fungizone (Gibco) are added to reduce fungi and bacterial growth. 17 µL hydrogels are loaded on the laser scanner and imaged. The median fluorescence intensity is quantified in ImageJ by outlining an area within the gel. An example is shown in Fig. 2. Again, edges are excluded due to imaging artifacts. Gels have a dyed and thiolated TNF-α concentration range of 0–90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ng mL−1 and corresponding fluorescence intensity between 2430 ± 360 A.U. and 21
000 ng mL−1 and corresponding fluorescence intensity between 2430 ± 360 A.U. and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 ± 2870 A.U.
280 ± 2870 A.U.
To calculate a fluorescence intensity-concentration relationship for FITC-PEG-SH and TNF-α, we fit the experimental data to a power-law,
| B = B0 + ACn | (1) |
2.7 Devices for fabrication of hydrogels with tethered molecular concentration gradients
We have designed a flow chamber that enables the diffusion of a fluorescent molecule in one direction and an inert fluid in the opposite direction. We design this device with the goal of using it in future experiments with cell-laden hydrogels where a cell signaling molecule will diffuse in one direction and there will be counter-diffusion of cell media.This device enables (1) nutrient counter-diffusion, (2) fluorescent imaging and (3) isotropic material swelling. Counter-diffusion of cell media is needed because it provides micro-nutrients for cell survival. Cell viability in the device is shown and quantified in the SI in Fig. S1. Encapsulated cell viability is within error of previous experiments where cells are encapsulated in materials with uniformly tethered TNF-α. Hydrogels made in these devices can also be characterized with microrheology, which requires imaging with a fluorescent microscope. An example of fluorescent imaging of probe particles suitable for microrheology taken in our device is shown in the SI in Fig. S2. Our final consideration during device design is that current commercially available flow chambers constrict material in 3D. The device developed in this work allows for facile photopolymerization of a material that under fills the width of the chamber and does not have a top plate allowing the material to swell after polymerization with a uniform pore size. This is shown in Fig. 3.
Our device is made of five glass parts that form a rectangular microchannel. The bottom of the device is a large microscope slide (l = 75 mm, w = 50 mm, h = 1 mm, Fisher Scientific) with two symmetric rectangular glass skates (l = 55 ± 2 mm, w = 25 ± 0.3 mm, h = 1 mm, Fisher Scientific) and a backstop on each side (l = 26 ± 0.3 mm, w = 14 ± 5.7 mm, h = 1 mm, Fisher Scientific). The skates and backstop have been cut from standard microscope slides. An image of a device is shown in Fig. 3a. The skates and backstops are adhered first to the bottom piece of glass using UV adhesive glue (NOA 81, Norland Optical Adhesive) and exposure to UV light (5 mW cm−2, 365 nm, UVP, LLC) for 5 minutes. This forms the symmetric channel shown in Fig. 3. Each device is exposed to additional UV light for 30 minutes to ensure complete reaction of the UV glue. Devices are then rinsed with 70% ethanol and any excess glue in the channel is removed using a razor blade. Before starting an experiment, each device is measured using a micrometer and the experimental total volume is calculated. The total volume is divided by three, which sets the volume for each component (fluorescent molecule diffusing solution, inert diffusing solution and hydrogel). An additional schematic of the device assembly is shown in the SI in Fig. S3.
2.8 Molecular concentration gradient formation
Gradients are created by polymerizing a hydrogel in the middle of the device by exposing the precursor solution to UV light for 3 minutes, shown in Fig. 3. Once the hydrogel is photopolymerized, an equivalent volume of the fluorescent molecule solution is pipetted on the left side of the hydrogel. Immediately after, the right side of the hydrogel is filled with an equal volume of an inert liquid (PBS for FITC-PEG-SH experiments and cell media for TNF-α experiments). After filling, each device is placed in a humidified incubation chamber to ensure the hydrogel does not dry out while the gradient is formed. The modified incubation environment consists of a bell jar covering a glass Petri dish covered in tin foil to reduce photobleaching of fluorescent molecules. Wet paper towels are placed in the incubation chamber to keep the environment humidified.The flow chamber is left for a specified amount of time, 6, 24 or 48 hours, to allow diffusion of fluorescent molecules into the hydrogel. Once the gradient is formed, the hydrogel is exposed to UV light again for 30 seconds, which tethers the fluorescent molecules into the hydrogel scaffold. To ensure a concentration gradient of fluorescent molecules is tethered into the hydrogel, the scaffold is rinsed 3× either with PBS for FITC-PEG-SH or cell media for TNF-α experiments. An additional schematic of the tethering approach is shown in the SI in Fig. S4. These hydrogels are then loaded onto the laser scanner and imaged at the voltages specified above.
2.9 Image analysis of fluorescent molecule concentration gradient tethered into hydrogel scaffold
Spatial measurements of fluorescence are done using images taken with the laser scanner. These images are analyzed using ImageJ, to confirm that a concentration gradient is successfully tethered into each hydrogel scaffold. An example of this is shown in Fig. 4. The fluorescent region of the image is selected using the rectangular selection tool in ImageJ and the fluorescence intensity profile is plotted and exported. The edges of the material are not selected to avoid imaging artifacts. The plot profile tool does not provide a standard deviation, it only reports a median fluorescence intensity every 25 µm in the gel. The standard deviation is essential to quantify the variation in measured fluorescence. To calculate a standard deviation, the straight line selection tool is used to measure average fluorescence intensity horizontally in 5 sections in a hydrogel along the concentration gradient. From the 5 average horizontal fluorescence intensity measurements, we calculate the standard deviation. This value is only used in the propagation of error and a representative image is provided in the SI in Fig. S5.2.10 Molecular diffusion in hydrogels
The effective diffusion coefficient is calculated from our experimental data. This is done to confirm that the expected molecular diffusion in our hydrogel occurs. We then compare this to theoretical diffusion coefficients for molecular diffusion through a porous medium.We estimate the radius of gyration for FITC-PEG-SH and TNF-α which are 1.95 and 1.71 nm, respectively. An explanation of the calculation of radius of gyration for each molecules is provided in the SI. The Stokes–Einstein–Sutherland equation is used to calculate molecular diffusion in a free volume. This diffusion, D0, is defined as
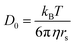 | (2) |
 | (3) |
Mutual diffusivity of a group of identical molecules as they spatially diffuse through a hydrogel can be modeled using a solution of Fick's law, which is
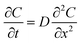 | (4) |
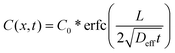 | (5) |
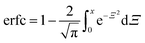 where Ξ is an integration variable. We report an effective diffusion coefficient, Deff, by fitting the entire concentration profile of fluorescent molecules in a gel to eqn (5).
where Ξ is an integration variable. We report an effective diffusion coefficient, Deff, by fitting the entire concentration profile of fluorescent molecules in a gel to eqn (5).
2.11 Statistical analysis
Calibration curves for fluorescent PEG-SH and thiolated TNF-α are created for each system. Each concentration of a fluorescent molecule is measured in 5 hydrogel samples for each concentration. The standard deviation in the measured fluorescence intensity is calculated and reported as the experimental error. Calibration curves are fit to eqn (1) considering the standard deviation.Propagation of error is used to represent the error from the fit of the calibration data and averaging local fluorescence intensity every 25 µm in a gel. To calculate the propagation of error we use
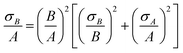 | (6) |
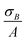 is the sum of the deviation in calculating spatial fluorescence intensity, B is the average fluorescence intensity, σB is the deviation in fluorescence intensity, A is a constant from curve fitting and σA is the error in fitting A. Measured fluorescence intensity is then converted to concentration using the calibration curve. To propagate the error when calculating the concentration of fluorescein poly(ethylene glycol)-thiol we use
is the sum of the deviation in calculating spatial fluorescence intensity, B is the average fluorescence intensity, σB is the deviation in fluorescence intensity, A is a constant from curve fitting and σA is the error in fitting A. Measured fluorescence intensity is then converted to concentration using the calibration curve. To propagate the error when calculating the concentration of fluorescein poly(ethylene glycol)-thiol we use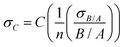 | (7) |
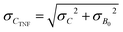 | (8) |
Data and error measurements are calculated and plotted in two ways. Average concentration measurements are plotted with the standard deviation between measurements provided as the shaded region. In addition, we show individual concentration measurements with the propagation of error as the shaded region.
3 Results and discussion
The goal of this work is to develop a method to create a concentration gradient of molecules covalently tethered into a photopolymerized hydrogel scaffold that can be later used for microrheological experiments. Calibration curves are made by measuring the fluorescence intensity of hydrogels with known concentrations of each fluorescent molecule uniformly tethered into the material. The calibration curve enables fluorescence intensity measurements to be used to calculate concentration with respect to distance across a hydrogel with a molecular concentration gradient. We show the validity of the method using a fluorescein poly(ethylene glycol)-thiol, FITC-PEG-SH, which is covalently tethered into the hydrogel. We use our device to enable passive diffusion of FITC-PEG-SH into the scaffold for 6, 24 or 48 hours. After the diffusion time, the scaffold is exposed to UV light to tether the FITC-PEG-SH into the material and the hydrogel is washed. Fluorescence intensity is then measured every 25 µm across the scaffold and concentration is calculated using the established calibration curve. We measure consistent molecular concentration gradients. Next, we use the same method to create and measure tethered cytokine concentration gradients of fluorescent thiolated TNF-α in our hydrogel. This molecule diffuses through the hydrogel for 24 hours and is then tethered into the material with a second UV exposure. We measure consistent molecular concentration gradients when normalized by the concentration at the edge of the hydrogel. We verify the diffusivity of these molecules through the hydrogel by calculating experimental effective diffusion coefficients, which are the same order of magnitude as values calculated with the multiscale diffusion model for both molecules. This is an accessible method to create and tether molecular concentration gradients within a hydrogel scaffold and can be used with a range of hydrogel scaffolds and molecules of interest.3.1 Concentration gradient in a hydrogel made in the flow chamber
The empty device shown in Fig. 5a, uses an equal volume of hydrogel, diffusing molecule and an inert source to create a swollen hydrogel with a molecular concentration gradient. Fig. 5b shows a device where a hydrogel with a chemical gradient is formed over 6 hours. For this image, red food coloring is put on one end of the device and allowed to diffuse through the hydrogel. At the same time, water is added to the other end of the device. The result in Fig. 5b shows a color gradient across the hydrogel scaffold from red to yellow. This process is driven by mutual diffusion or a difference in chemical potential.67 Over time, the driving force will create a concentration gradient in the hydrogel following the diffusion profile described in eqn (5). To quantify concentration using this method a calibration curve is first created.3.2 Tethered FITC-PEG-SH concentration gradients
Fig. 6 is the calibration curve that relates measured fluorescence intensity of FITC-PEG-SH to known concentrations. These scaffolds are rinsed 3× with 1× PBS to ensure any untethered dyed molecules are removed. Hydrogels are placed on a laser scanner and fluorescence intensity is quantified using ImageJ. We make hydrogels with a range of fluorescent polymer, 0–0.4 mg mL−1. Error bars are the standard deviation between measurements of 5 different hydrogels. We fit the data holding the value of B0 constant, which is the measured fluorescence intensity of a hydrogel without FITC-PEG-SH. We hypothesize that fluorescence intensity measurements will plateau at concentrations above 0.4 mg mL−1 FITC-PEG-SH because this value is close to the limit of measurable fluorescence intensity by the laser scanner, Bmax = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 A.U. When creating a calibration curve, it is essential to consider a trade-off between the detection range and precision.
536 A.U. When creating a calibration curve, it is essential to consider a trade-off between the detection range and precision.
Our measurements are precise to six-hundredths of a mg of fluorescent polymer, which is 3610 A.U. detection. This means that the laser scanner can measure a significant difference between a hydrogel with 0 mg mL−1 fluorescent polymer (Bavg = 1210 ± 90 A.U.) and a hydrogel containing 0.006 mg mL−1 (Bavg = 4820 ± 200 A.U.). The data are fit to a non-linear equation, similar to previous work, due to the large concentration range of FITC-PEG-SH.21 For low concentration ranges in Fig. 6, 0 ≤ C ≤ 0.05 mg mL−1, the relationship between concentration and measured fluorescence intensity is linear. A linear equation could be fit to this limited range of data. But due to the wider range of concentrations measured for the calibration curve, our data are fit to the power-law relationship described in eqn (1). A non-linear relationship between measured fluorescence and the concentration of fluorescent molecules at high concentrations has been previously reported and could be caused by three phenomena: static quenching, dynamic quenching or self quenching.21,70 We hypothesize some self quenching is present in our system. During self quenching two fluorophore groups collide, forming a complex that reduces the measured fluorescence signal.70–72Fig. 6 is plotted on a log–log scale and provided in the SI as Fig. S6.
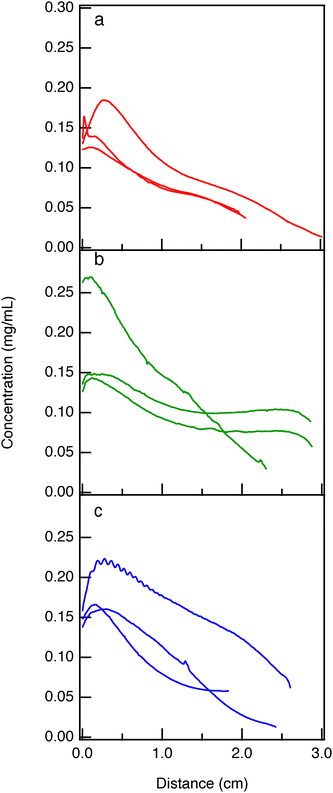
In Fig. 7 hydrogels are formed in devices and passive diffusion is allowed to occur for either 6, 24 or 48 hours. All measured concentration profiles have similar shapes to the profiles described by Fick's second law, eqn (5). The fluorescence intensity of individual hydrogel replicates is measured and concentration is calculated along the scaffold using the calibration curve in Fig. 6. In Fig. 7, concentration is on the y-axis and distance from the edge of the hydrogel is on the x-axis. The propagation of error calculated from the fit in the calibration curve is also plotted as a shaded region behind the solid line. Although the propagation of error is plotted for all measurements, it is small compared to the measurements, so it is not visible in Fig. 7. The starting concentration at the source is 0.05 mg mL−1 of FITC-PEG-SH. At the edge of the gel we measure up to three times that concentration. A difference in chemical potential drives the FITC-PEG-SH molecules from the well into the hydrogel and at the edge of the hydrogel there is slowed molecular diffusion into the porous scaffold, this could cause an increase in concentration. In addition, pores in the scaffold can sometimes become clogged, resulting in a higher concentration at the edge of the gel than in the well. This is supported by the relative size of the scaffold pores to the polymer. The radius of gyration of FITC-PEG-SH, Rg = 1.95 nm, is similar to the mesh size of the hydrogel ∼10 nm.
In Fig. 7a, red lines show the average concentration of FITC-PEG-SH in a hydrogel after diffusing for 6 hours as distance across the length of the hydrogel increases. The length of each hydrogel is slightly different because the total volume of each flow chamber is different. Before starting the experiment each device is measured using a micrometer and the total volume is calculated and the volume of each component is adjusted to ensure they are all equal. The largest deviation in measured concentrations across the width of a single hydrogel is after 6 hours of diffusion, Fig. 7a, compared to diffusion over longer times (24 or 48 hours). The standard deviation between replicates reported in these measurements is shown in the SI in Fig. S7. The source of this error is from averaging the fluorescence intensity every 25 µm. The gel does not have FITC-PEG-SH tethered uniformly across the width of the gel, shown in the SI in Fig. S5. In all three replicates, we measure the highest fluorescence intensity or presence of fluorescent molecules at or near the edge of the gel and lower values in the middle of the channel. We hypothesize that this spatial deviation in concentration is because the difference in chemical potential in the gel and source is the highest at 6 hours. Molecules along the edge of the gel can be stuck to the wall and have slower diffusion due to the no-slip boundary condition and hydrodynamic interactions with the wall.73,74 Due to this slower diffusion, there can be a build up of molecules near the edge of the gel resulting in a higher measured fluorescence intensity. At longer times, 24 and 48 hours, we do not measure this non-uniform distribution of fluorescent molecules across the width of the gel. We hypothesize that there is no significant concentration gradient in the z-axis of the material because it is much smaller compared to the y-axis (width). Also deviations in the y-axis are only measured at 6 hours of diffusion and not at longer times.
Each green line in Fig. 7b shows one of three hydrogel replicates where diffusion occurs for 24 hours. As distance from the source of the flow chamber increases the concentration of FITC-PEG-SH decreases. The three replicates do not have the same concentration at the beginning of the gel. When diffusion occurs for 24 hours, we measure an edge concentration that is on average ∼3.5× higher than the concentration of FITC-PEG-SH in the source. We hypothesize this is because at the edge of the hydrogel there is an increase in concentration due to slowed diffusion into the porous medium and pores may be clogging with FITC-PEG-SH causing a higher concentration at the edge of the gel compared to the concentration added to the well of the flow chamber.
The blue lines in Fig. 7c show three hydrogel replicates where diffusion is allowed to occur for 48 hours. We measure an edge concentration that is on average ∼3× greater than the concentration of FITC-PEG-SH in the source of the device. This is again likely due to slowed diffusion and pore clogging at the entrance of the hydrogel.
To calculate the effective diffusion coefficient of FITC-PEG-SH in our network, we use eqn (5). The results of this calculation are provided in Table 1. When the experiment begins there is 0 mg mL−1 of FITC-PEG-SH in the hydrogel and 0.05 mg mL−1 of FITC-PEG-SH in the source or well. At t = 0 hours, the chemical potential is the highest. The gel and the source are driven to reach chemical equilibrium, which is when the concentration of FITC-PEG-SH is equal in the gel and the source. This will result in a chemical potential equal to zero.67Table 1 shows that as the time of diffusion of the fluorescent molecule into the hydrogel increases, the magnitude of diffusivity decreases because the difference in chemical potential is also decreasing. The theoretical diffusivity of FITC-PEG-SH is 1.19 × 10−10 m2 s−1, calculated using the multiscale diffusion model described by eqn (3). A faster effective diffusion coefficient is measured in the 6 hour experiment compared to the theoretical diffusion coefficient when the chemical potential is the highest. At 24 hours the measured effective diffusivity is the same order of magnitude as the theoretical value. In the 48 hour experiment, we measure an effective diffusivity an order of magnitude slower than predicted by the multiscale diffusion model because chemical potential is the lowest.
| Time (hours) | Diffusion coefficient (m2 s−1) | Error (m2 s−1) |
|---|---|---|
| Theoretical | 1.19 × 10−10 | — |
| 6 | 1.6 × 10−9 | ±3.7 × 10−11 |
| 24 | 3.6 × 10−10 | ±7.3 × 10−12 |
| 48 | 9.1 × 10−11 | ±7.1 × 10−12 |
3.3 Tethered TNF-α concentration gradients
TNF-α is a molecule known to increase stem cell motility and activate human mesenchymal stem cells (hMSCs) during the wound healing process.1,15,75 To design a material that can spatially direct encapsulated cell migration from a hydrogel to a wound, we create hydrogels with tethered concentration gradients of TNF-α. The goal of this work is to show the method previously described and validated with FITC-PEG-SH can be used to create hydrogels with tethered protein gradients. We use the same experimental method and device shown in Fig. 5, but in these experiments the fluorescent molecule diffusing into the hydrogel is the cell signaling molecule TNF-α.Fig. 8 is the calibration curve of measured fluorescence intensity of hydrogels with dyed and thiolated TNF-α. After photopolymerization, gels are triple rinsed to ensure removal of any unbound molecules. Error bars are the standard deviation between fluorescence intensity measurements of different gels. Measurements are fit to the power-law relationship described by eqn (1). In eqn (1), B is the measured fluorescence intensity, B0 is the measured fluorescence intensity of a gel with no dyed TNF-α, A is a constant, C is the concentration of dyed TNF-α in ng mL−1 and n is the power-law exponent. n, A and B0 are fit to experimental measurements. For these measurements, we are measuring a more dilute concentration regime at a higher voltage than FITC-PEG-SH experiments. The smallest amount of dyed TNF-α we can detect is 300 ng mL−1, which is measured at B = 5490 ± 300 A.U. We use such dilute concentrations because cell signaling molecules have been shown to affect cell function at concentrations as low as pg mL−1 and can cause cell death at high concentrations.13,76,77
With the completion of the calibration curve, concentration gradients of TNF-α are formed in samples allowing passive diffusion for 24 hours. 24 hours is chosen because consistent FITC-PEG-SH gradients are formed at this time. Fig. 9 shows individual concentration profiles of fluorescent TNF-α across a hydrogel. Concentration is on the y-axis and distance from the edge of the hydrogel is on the x-axis. The error propagated from the fit to the calibration curve is small compared to the measurements and is not easily seen in Fig. 9. An inset is provided to illustrate this and show one of the replicates more clearly.
The dyed and functionalized TNF-α source concentration is 541 ng mL−1 for all replicates. Fig. 9 shows different starting concentrations for each replicate. We measure similar pore clogging in all experiments. This is more prevalent when concentration gradients are created with tethered TNF-α because it is 17× larger than FITC-PEG-SH. The average concentration profile for all three hydrogels in individual devices is shown in the SI in Fig. S8. To fit experimental data to eqn (5), we hold the initial concentration and time of diffusion constant and calculate an effective diffusivity of 4.94 × 10−10 ± 3.04 × 10−11 m2 s−1. This is shown as the dashed red line in the SI in Fig. S8 and provided in Table 2. To check that expected diffusion is happening in our flow chamber, we use the multiscale diffusion model described by eqn (3) to calculate the theoretical diffusion coefficient. The theoretical value we calculate for TNF-α diffusing through our hydrogel is DMSDM = 1.57 × 10−10 m2 s−1.68 The effective diffusion coefficient calculated from our experimental data is the same order of magnitude but slightly faster compared to the theoretical value. Other work also measures the diffusion of proteins in hydrogels to be the same order of magnitude but faster than predicted by simulations.21 We hypothesize this could be because the multiscale diffusion model neglects the charges of the solute and network.68 Another possibility is that the hydrogel mesh is estimated based on the contour length of PEG-norbornene. A larger network structure would allow TNF-α to move faster through the hydrogel. Larger pores are likely due to the low cross-link density and non-idealities in these network.
| Time (hours) | Diffusion coefficient (m2 s−1) | Error (m2 s−1) |
|---|---|---|
| Theoretical | 1.57 × 10−10 | — |
| 24 | 4.94 × 10−10 | ±3.04 × 10−11 |
Hydrogels with tethered concentration gradients of TNF-α have different concentrations at the edge of the gel. To show this, normalized concentration is plotted against distance in Fig. 10. To normalize the data we use the following equation
 | (9) |
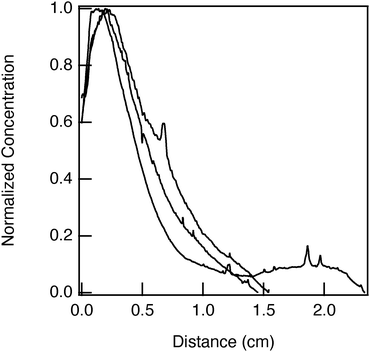 | ||
| Fig. 10 Normalized concentration gradients of TNF-α tethered into hydrogels. Each line is a single gel. | ||
We hypothesize the difference in starting concentrations for each replicate is caused by a difference in initial concentration at the edge of the hydrogel, not by geometric differences. Concentration normalized by the surface area of the gel and by gel volume are shown in the SI in Fig. S9 and S10. Normalization by hydrogel size does not collapse the data set, therefore, the differences in the size of the hydrogel are not causing deviations in our data between samples. The reason for these deviations is the initial concentration at the edge of the gel. This concentration changes because TNF-α is a sequence of 154 amino acids with different local charges, which is undergoing Brownian motion in solution. The radius of gyration of TNF-α is very close to the pore size of the scaffold, as provided in the SI in Table S2. While TNF-α diffuses, it will collide and can possibly aggregate due to local differences in electrostatic charge. An anti-clumping agent is not included in the source of our device. Even at a dilute concentration, it is likely that these molecules can aggregate.78 Due to this, in each replicate, the extent of protein aggregation or pore clogging of the hydrogel is not the same.29 This means the initial concentration at the edge of the hydrogel can vary and leads to differences in gradient formation. A similar phenomenon is shown in FITC-PEG-SH experiments in the SI as Fig. S11. This is a material limitation. The advantage of our technique is we are able to measure the change in the molecular concentration at the edge of the gel due to pore clogging in each replicate and the resulting cytokine concentration gradient.
4 Conclusions
This work develops a device that creates hydrogels with tethered concentration gradients of molecules, allowing for isotropic swelling, facile nutrient diffusion and microscopy. Previous devices restrict scaffold swelling and are not designed to enable collection of microrheology data. This device enables polymerization of a hydrogel, passive diffusion of a molecule through the polymerized scaffold and a second polymerization to tether the molecular concentration gradient into the material. This is done to maintain hydrogel rheological properties and only provide a gradient in chemical cues. Our measurements show that we can covalently tether FITC-SH-PEG or TNF-α into our hydrogels, forming consistent non-linear concentration gradients. This device is suitable for future microrheology experiments to characterize cell–material interactions. The device has the potential to be scaled up or down and only requires standard lab equipment.The results from this work show that higher concentrations can occur at the entrance of the hydrogel due to pore clogging, resulting from the similar size of molecules to the network structure. We first create calibration curves for each molecule used in this work, FITC-PEG-SH and TNF-α. Calibration curves have a non-linear relationship between concentration and fluorescence intensity of fluorescent molecules in hydrogels.
We calculate the effective diffusion coefficients from our measured concentration gradients of FITC-PEG-SH and TNF-α, which are 3.6 × 10−10 ± 7.3 × 10−12 m2 s−1 and 4.94 × 10−10 ± 3.04 × 10−11 m2 s−1, respectively. Our FITC-PEG-SH and TNF-α measurements are the same order of magnitude as values predicted by the multiscale diffusion model. This means that the main mechanism of molecules moving through the hydrogel scaffold to create a concentration gradient is diffusion. The proposed technique can be used to create hydrogels with non-linear concentration gradients of molecules for a wide variety of applications, including biomedical applications.
Author contributions
TCO: data collection, data analysis, investigation, original draft writing; AS: design of experiment; KMS: conceptualization, funding acquisition, project administration, resources, supervision, revision of original manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All the data supporting this article have been included in the manuscript in the form of tables and figures. Additional analysis and data is included as part of the supplementary information (SI). The SI includes parameters used in the multiscale diffusion model; theoretical diffusivities of molecules; cell viability in a device; image offluorescent probes in a device; cartoon of device assembly; cartoon of functionalization chemistry; image of short diffusion of fluorescent molecules in device; calibration curve on log–log plot; average concentration of FITC-PEG-SH measured between replicates; average concentration of TNF-α measured between replicates; normalization of TNF-α gradients by surface area and volume; normalization of FITC-PEG-SH by initial concentration. See DOI: https://doi.org/10.1039/d5sm01194a.Acknowledgements
Research reported in this publication was supported in part by the National Institute of Health under award numbers R15GM119065-02 and 1R35GM147043. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
- T. C. O’Shea, K. J. Croland, A. Salem, R. Urbanski and K. M. Schultz, A rheological study on the effect of tethering pro-and anti-inflammatory cytokines into hydrogels on human mesenchymal stem cell migration, degradation, and morphology, Biomacromolecules, 2024, 25(8), 5127–5137 CrossRef.
- S. Cosson, M. Kobel and M. P. Lutolf, Capturing complex cell–matrix interactions in biomaterials, Adv. Funct. Mater., 2009, 19, 3411–3419 CrossRef CAS.
- J. L. Roam, R. K. Xu, D. L. Nguyen and D. L. Elbert, The formation of spatially patterned hydrogels, Biomaterials, 2010, 31, 8642–8650 CrossRef CAS PubMed.
- S.-Y. Cheng, S. Heilman, M. Wasserman, S. Archer, M. L. Shuler and M. Wu, A hydrogel-based microfluidic device for the studies of directed cell migration, Lab Chip, 2007, 7(6), 763–769 RSC.
- S. A. DeLong, J. J. Moon and J. L. West, Covalently immobilized gradients of bfgf on hydrogel scaffolds for directed cell migration, Biomaterials, 2005, 26(16), 3227–3234 CrossRef CAS PubMed.
- J. A. Burdick, A. Khademhosseini and R. Langer, Fabrication of gradient hydrogels using a microfluidics/photopolymerization process, Langmuir, 2004, 20(13), 5153–5156 CrossRef CAS PubMed.
- I. Batalov, R. R. Stevens and C. A. DeForest, Photopatterned biochemical gradients in hydrogels, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2014194118 CrossRef CAS.
- O. Jeon, E. Alsberg and S. W. Linderman, Biochemical patterning of hydrogels, Adv. Mater., 2013, 25, 6366 CrossRef CAS PubMed.
- B. C. Dash, Z. Xu, L. Lin, A. Koo, S. Ndon, F. Berthiaume, A. Dardik and H. Hsia, Stem cells and engineered scaffolds for regenerative wound healing, Bioengineering, 2018, 5(1), 23 CrossRef PubMed.
- P. Y. Lee, E. Cobain, J. Huard and L. Huang, Thermosensitive hydrogel peg-plga-peg enhances engraftment of muscle-derived stem cells and promotes healing in diabetic wound, Mol. Ther., 2007, 15(6), 1189–1194 Search PubMed.
- M. P. Lutolf, J. L. Lauer-Fields, H. G. Schmoekel, A. T. Metters, F. E. Weber, G. B. Fields and J. A. Hubbell, Synthetic matrix metalloproteinase-sensitive hydrogels for the conduction of tissue regeneration: engineering cell-invasion characteristics, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(9), 5413–5418 CrossRef CAS.
- W. J. Ennis, A. Sui and A. Bartholomew, Stem cells and healing: impact on inflammation, Adv. Wound Care, 2013, 2(7), 369–378 CrossRef PubMed.
- S. Maxson, E. A. Lopez, D. Yoo, A. Danilkovitch-Miagkova and M. A. LeRoux, Concise review: role of mesenchymal stem cells in wound repair, Stem Cells Transl. Med., 2012, 1(2), 142–149 CrossRef CAS.
- S. Yin and Y. Cao, Hydrogels for large-scale expansion of stem cells, Acta Biomater., 2021, 128, 1–20 Search PubMed.
- J. R. García, M. Quirós, W. M. Han, M. N. O'Leary, G. N. Cox, A. Nusrat and A. J. García, Biomaterials, 2019, 220, 119403 CrossRef.
- B. D. Ratner, Biomaterials science: an introduction to materials in medicine, Academic Press, 2004 Search PubMed.
- S. A. Fisher, R. Y. Tam, A. Fokina, M. M. Mahmoodi, M. D. Distefano and M. S. Shoichet, Photochemical approaches to biomaterials design, Biomaterials, 2018, 178, 751–766 Search PubMed.
- Y. Wang, L. Li, Y.-E. Ji, T. Wang, Y. Fu, X. Li, G. Li, T. Zheng and Q. Wu, Silk-based hydrogel materials, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2305704120 Search PubMed.
- R. J. Wade and J. A. Burdick, Engineering ecm signals into biomaterials, Mater. Today, 2012, 15(10), 454–459 Search PubMed.
- X. Li, H. Liang, J. Sun, Y. Zhuang, B. Xu and J. Dai, Electrospun collagen fibers with spatial patterning of sdf1a for the guidance of neural stem cells, Adv. Healthcare Mater., 2015, 4(12), 1869–1876 CrossRef CAS PubMed.
- M. H. Hettiaratchi, A. Schudel, T. Rouse, A. J. Garca, S. N. Thomas, R. E. Guldberg and T. C. McDevitt, A rapid method for determining protein diffusion through hydrogels for regenerative medicine applications, APL Bioeng., 2018, 2, 026110 CrossRef.
- J. A. McGlynn and K. M. Schultz, Measuring human mesenchymal stem cell remodeling in hydrogels with a step-change in elastic modulus, Soft Matter, 2022, 18(34), 6340–6352 Search PubMed.
- M. Daviran, S. M. Longwill, J. F. Casella and K. M. Schultz, Rheological characterization of dynamic remodeling of the pericellular region by human mesenchymal stem cell-secreted enzymes in well-defined synthetic hydrogel scaffolds, Soft Matter, 2018, 14(16), 3078–3089 Search PubMed.
- M. Daviran, J. Catalano and K. M. Schultz, Determining how human mesenchymal stem cells change their degradation strategy in response to microenvironmental stiffness, Biomacromolecules, 2020, 21(8), 3056–3068 CrossRef CAS.
- M. Daviran and K. M. Schultz, Characterizing the dynamic rheology in the pericellular region by human mesenchymal stem cell re-engineering in peg-peptide hydrogel scaffolds, Rheol. Acta, 2019, 58, 421–437 CrossRef CAS PubMed.
- K. M. Schultz, K. A. Kyburz and K. S. Anseth, Measuring dynamic cell-material interactions and remodeling during 3d human mesenchymal stem cell migration in hydrogels, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(29), E3757–E3764 Search PubMed.
- A. Ramirez, B. Merwitz, H. Lee, E. Vaughan and K. Maisel, Multiple particle tracking (mpt) using pegylated nanoparticles reveals heterogeneity within murine lymph nodes and between lymph nodes at different locations, Biomater. Sci., 2022, 10(24), 6992–7003 RSC.
- K. Joyner, S. Yang and G. A. Duncan, Microrheology for biomaterial design, APL Bioeng., 2020, 4, 041508 CrossRef CAS PubMed.
- E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017 Search PubMed.
- M. Ur Rahman, D. F. Fleming, L. Wang, K. P. Rumbaugh, V. D. Gordon and G. F. Christopher, Microrheology of pseudomonas aeruginosa biofilms grown in wound beds, npj Biofilms Microbiomes, 2022, 8(1), 49 Search PubMed.
- S. C. Chew, B. Kundukad, T. Seviour, J. R. C. Van der Maarel, L. Yang, S. A. Rice, P. Doyle and S. Kjelleberg, Dynamic remodeling of microbial biofilms by functionally distinct exopolysaccharides, mBio, 2014, 5(4), 10–1128 Search PubMed.
- M. D. Wehrman, S. Lindberg and K. M. Schultz, Quantifying the dynamic transition of hydrogenated castor oil gels measured via multiple particle tracking microrheology, AIChE J., 2016, 6463–6472 CAS.
- M. T. Valentine, Z. E. Perlman, M. L. Gardel, J. H. Shin, P. Matsudaira, T. J. Mitchison and D. A. Weitz, Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials, Biophys. J., 2004, 86(6), 4004–4014 Search PubMed.
- A. M. Puertas and T. Voigtmann, Microrheology of colloidal systems, J. Phys.: Condens. Matter, 2014, 26(24), 243101 Search PubMed.
- S. He, D. R. Pascucci, M. Caggioni, S. Lindberg and K. M. Schultz, Rheological properties of phase transitions in polydisperse and monodisperse colloidal rod systems, AIChE J., 2021, 67(11), e17401 CrossRef CAS.
- C. R. Nuttelman, Osteogenic poly(ethylene glycol)-based hydrogels for three-dimensional human mesenchymal stem cell culture and bone regeneration, PhD thesis, University of Colorado at Boulder, 2005 Search PubMed.
- H. Zhang, M. D. Wehrman and K. M. Schultz, Structural changes in polymeric gel scaffolds around the overlap concentration, Front. Chem., 2019, 7, 317 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, Methods of digital video microscopy for colloidal studies, J. Colloid Interface Sci., 1996, 179(1), 298–310 CrossRef CAS.
- J. C. Crocker, M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh and D. A. Weitz, Two-point microrheology of inhomogeneous soft materials, Phys. Rev. Lett., 2000, 85(4), 888 CrossRef CAS PubMed.
- L. Masaro and X. X. Zhu, Physical models of diffusion for polymer solutions, gels and solids, Prog. Polym. Sci., 1999, 24(5), 731–775 CrossRef CAS.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Particle tracking microrheology of complex fluids, Phys. Rev. Lett., 1997, 79(17), 3282 CrossRef CAS.
- T. M. Squires and T. G. Mason, Fluid mechanics of microrheology, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- T. H. Larsen and E. M. Furst, Microrheology of the liquid-solid transition during gelation, Phys. Rev. Lett., 2008, 100(14), 146001 Search PubMed.
- T. Larsen, K. Schultz and E. M. Furst, Hydrogel microrheology near the liquid-solid transition, Korea-Australia Rheol. J., 2008, 20(3), 165–173 Search PubMed.
- S. Desai, B. J. Carberry, K. S. Anseth and K. M. Schultz, Characterizing rheological properties and microstructure of thioester networks during degradation, Soft Matter, 2023, 19(38), 7429–7442 RSC.
- J. A. McGlynn, K. J. Druggan, K. J. Croland and K. M. Schultz, Human mesenchymal stem cell-engineered length scale dependent rheology of the pericellular region measured with bi-disperse multiple particle tracking microrheology, Acta Biomater., 2021, 121, 405–417 Search PubMed.
- M. Daviran, H. S. Caram and K. M. Schultz, Role of cell-mediated enzymatic degradation and cytoskeletal tension on dynamic changes in the rheology of the pericellular region prior to human mesenchymal stem cell motility, ACS Biomater. Sci. Eng., 2018, 4(2), 468–472 CrossRef CAS.
- J. A. McGlynn and K. M. Schultz, Characterizing nonuniform hydrogel elastic moduli using autofluorescence, Macromolecules, 2022, 55(11), 4469–4480 Search PubMed.
- B. D. Fairbanks, M. P. Schwartz, C. N. Bowman and K. S. Anseth, Photoinitiated polymerization of peg-diacrylate with lithium phenyl-2, 4, 6-trimethylbenzoylphosphinate: polymerization rate and cytocompatibility, Biomaterials, 2009, 30(35), 6702–6707 CrossRef CAS PubMed.
- M. P. Schwartz, B. D. Fairbanks, R. E. Rogers, R. Rangarajan, M. H. Zaman and K. S. Anseth, A synthetic strategy for mimicking the extracellular matrix provides new insight about tumor cell migration, Integr. Biol., 2010, 2(1), 32–40 CrossRef CAS.
- M. W. Tibbitt and K. S. Anseth, Hydrogels as extracellular matrix mimics for 3d cell culture, Biotechnol. Bioeng., 2009, 103(4), 655–663 Search PubMed.
- K. A. Kyburz and K. S. Anseth, Three-dimensional hmsc motility within peptide-functionalized peg-based hydrogels of varying adhesivity and crosslinking density, Acta Biomater., 2013, 9(5), 6381–6392 CrossRef CAS PubMed.
- A. M. Kloxin, A. M. Kasko, C. N. Salinas and K. S. Anseth, Photodegradable hydrogels for dynamic tuning of physical and chemical properties, Science, 2009, 324(5923), 59–63 CrossRef CAS.
- J. D. McCall and K. S. Anseth, Thiol-ene photopolymerizations provide a facile method to encapsulate proteins and maintain their bioactivity, Biomacromolecules, 2012, 13(8), 2410–2417 Search PubMed.
- P. S. Hume, J. He, K. Haskins and K. S. Anseth, Strategies to reduce dendritic cell activation through functional biomaterial design, Biomaterials, 2012, 33(14), 3615–3625 CrossRef CAS PubMed.
- C. N. Bowman and C. J. Kloxin, Toward an enhanced understanding and implementation of photopolymerization reactions, AIChE J., 2008, 54(11), 2775–2795 CrossRef CAS.
- A. M. Kloxin, M. W. Tibbitt and K. S. Anseth, Synthesis of photodegradable hydrogels, Nat. Protoc., 2010, 5(12), 1867–1887 CrossRef CAS.
- J. D. McCall, C.-C. Lin and K. S. Anseth, Affinity peptides protect transforming growth factor beta during encapsulation in poly(ethylene glycol) hydrogels, Biomacromolecules, 2011, 12(4), 1051–1057 Search PubMed.
- M. C. Schneider, S. Chu, M. A. Randolph and S. J. Bryant, An in vitro and in vivo comparison of cartilage growth in chondrocyte-laden matrix metalloproteinase-sensitive poly (ethylene glycol) hydrogels with localized transforming growth factor β3, Acta Biomater., 2019, 93, 97–110 CrossRef CAS.
- S. A. Schoonraad, M. L. Trombold and S. J. Bryant, The effects of stably tethered bmp-2 on mc3t3-e1 preosteoblasts encapsulated in a peg hydrogel, Biomacromolecules, 2021, 22(3), 1065–1079 Search PubMed.
- S. A. Schoonraad, A. A. Jaimes, A. J. X. Singh, K. J. Croland and S. J. Bryant, Osteogenic effects of covalently tethered rhbmp-2 and rhbmp-9 in an mmp-sensitive peg hydrogel nanocomposite, Acta Biomater., 2023, 170, 53–67 Search PubMed.
- J. D. McCall, J. E. Luoma and K. S. Anseth, Covalently tethered transforming growth factor beta in peg hydrogels promotes chondrogenic differentiation of encapsulated human mesenchymal stem cells, Drug Delivery Transl. Res., 2012, 2, 305–312 CrossRef CAS.
- B. V. Sridhar, N. R. Doyle, M. A. Randolph and K. S. Anseth, Covalently tethered tgf-1 with encapsulated chondrocytes in a peg hydrogel system enhances extracellular matrix production, J. Biomed. Mater. Res., Part A, 2014, 102(12), 4464–4472 CrossRef.
- Invitrogen Corporation, Alexa fluor 488 microscale protein labeling kit, Molecular Probes, 2006.
- R. G. Holzheimer and W. G. Steinmetz, Local and systemic concentrations of pro-and anti-inflammatory cytokines in human wounds, Eur. J. Med. Res., 2000, 5(8), 347–355 Search PubMed.
- B. V. Sridhar, N. R. Doyle, M. A. Randolph and K. S. Anseth, Covalently tethered tgf-β 1 with encapsulated chondrocytes in a peg hydrogel system enhances extracellular matrix production, J. Biomed. Mater. Res., Part A, 2014, 102(12), 4464–4472 CrossRef PubMed.
- P. C. Hiemenz and T. P. Lodge, Polymer chemistry, CRC Press, 2007 Search PubMed.
- E. Axpe, D. Chan, G. S. Offeddu, Y. Chang, D. Merida, H. L. Hernandez and E. A. Appel, A multiscale model for solute diffusion in hydrogels, Macromolecules, 2019, 52(18), 6889–6897 CrossRef CAS PubMed.
- M. D. Greenberg, Advanced engineering mathematics, Pearson Education, India, 1998 Search PubMed.
- F. H. D. S. Rodrigues, G. Delgado, T. S. da Costa and L. Tasic, BBA Adv., 2023, 3, 100091 CrossRef.
- B. P. Cormack, R. H. Valdivia and S. Falkow, Gene, 1996, 173, 33–38 CrossRef CAS PubMed.
- T. J. Lambert, Nat. Methods, 2019, 16, 277–278 CrossRef CAS.
- W. M. Deen. Analysis of Transport Phenomena. Oxford University Press, 2nd edn, 2011 Search PubMed.
- F. A. Morrison, Understanding Rheology, Oxford University Press, Oxford, UK, 2001 Search PubMed.
- C. Ries, V. Egea, M. Karow, H. Kolb, M. Jochum and P. Neth, Mmp-2, mt1-mmp, and timp-2 are essential for the invasive capacity of human mesenchymal stem cells: differential regulation by inflammatory cytokines, Blood, 2007, 109(9), 4055–4063 CrossRef CAS PubMed.
- A. M. Hocking, The role of chemokines in mesenchymal stem cell homing to wounds, Adv. Wound Care, 2015, 4(11), 623–630 Search PubMed.
- R. E. Newman, D. Yoo, M. A. LeRoux and A. Danilkovitch-Miagkova, Treatment of inflammatory diseases with mesenchymal stem cells, Inflammation Allergy:Drug Targets, 2009, 8, 110–123 CrossRef CAS.
- Thermo Fisher Scientific. Reconstitution and storage of gibco and PeproTech recombinant proteins. Thermo Fisher Scientific technical note, 2025. Research Use Only.
| This journal is © The Royal Society of Chemistry 2026 |