 Open Access Article
Open Access ArticlePredicting bio-corona-induced adsorption and uptake of nanoplastics
Wenlin
Zhang
 * and
Anderson D. S.
Duraes
* and
Anderson D. S.
Duraes

Department of Chemistry, Dartmouth College, Hanover, New Hampshire 03755, USA. E-mail: wenlin.zhang@dartmouth.edu
First published on 12th January 2026
Abstract
We employ a theoretical approach to predict bio-corona-induced uptake of nanoplastics (NPLs) across plasma membranes (PMs). A lattice self-consistent field theory (SCFT) is used to model the formation of bio-coronae, which are composed of biopolymers adsorbed on NPLs. As the NPL approaches the PM, we show that weak monomer–PM attractions allow the adsorbed biopolymers to redistribute between the two surfaces. This rearrangement can reduce crowding in the bio-corona and induce an effective attraction between the NPL and the membrane. Using the theory of elasticity for lipid membranes, we show that a weak effective attraction enables NPLs to bind to cell membranes, generating excess stress and increasing elastic free energy in the biological barrier. When the effective NPL–PM interactions are sufficiently strong, nanoplastics can be spontaneously internalized by cells within a short time.
1 Introduction
Microplastics (MPLs) and nanoplastics (NPLs) are either intentionally manufactured small plastic particles1 or formed from discarded plastics through chemical and mechanical degradation.2 These small particles may enter the human body via ingestion, inhalation, or skin contact, posing potential health risks.3–5 For instance, a recent study indicates that exposure to MPLs and NPLs may increase the risk of cardiovascular diseases.6 However, the interactions of MPLs and NPLs with biological systems at the molecular level remain poorly understood. To develop a mechanistic understanding of the fate of NPLs in the human body and assess their potential health impacts, quantifying the interactions between MPLs/NPLs and plasma membranes (PMs), which serve as barriers that prevent small plastic particles from entering cells, is essential.7Experimentally characterizing the interactions between MPLs/NPLs and plasma membranes is challenging. Most previous experimental studies demonstrating the cellular uptake of these particles have relied on model colloidal polystyrene (PS) spheres with surface charges.8 Yet, model PS particles may not capture the wide range of physicochemical properties exhibited by MPLs and NPLs, such as semicrystallinity and hydrophobicity, that may influence particle–membrane interactions. Moreover, characterizing the molecular interactions of MPLs and NPLs with PMs, particularly for small nanoparticles, remains challenging.9,10 Extrapolating results obtained from model colloidal PS particles to smaller NPLs with different molecular structures requires further validation.
The spatiotemporal resolutions of atomistic simulations can provide valuable insights into the NPL–PM interactions. Although such simulations can accurately describe the physicochemical properties of MPLs, NPLs, and PMs, they remain limited in accessible length and time scales.11 Thus, atomistic simulations are only feasible for investigating small NPLs (with diameters on the order of nanometers) in the vicinity of PMs.
To model larger particles, coarse-grained (CG) approaches are required. Popular CG molecular dynamics models, such as the MARTINI,12–14 however, do not always reproduce the physicochemical properties of MPLs and NPLs accurately. Misrepresentations of NPLs/MPLs properties, such as the absence of crystalline order, can introduce artifacts in the effective interactions between plastic particles and PMs.15
Existing CG simulation models also employ resolutions that are not coarse enough to simulate large-scale phenomena, which could be critical for NPLs uptake. In our previous work, we showed that passive diffusion of bare NPLs across lipid membranes requires local bilayer fracture, leading to a high free energy barrier even for the cellular uptake of small NPLs (3–5 nm in size).15 If NPLs exhibit sufficiently strong attraction to PMs, they can adsorb onto the lipid surface, become wrapped by the membrane, and eventually be pinched off into the cell. Such a budding process of adsorbed particles represents a viable cellular uptake mechanism for colloidal particles, including the nucleocapsids of animal viruses.16 Still, this passive uptake pathway remains difficult to simulate using conventional CG approaches.
In this work, we apply a theoretical approach to predict the effective attraction between a nanoplastic and a plasma membrane, induced by biomacromolecules adsorbed on the NPL surface. Indeed, the adsorption of NPLs of commodity plastics could depend on the degree and type of degradation, which may strongly modify the surface chemistry of the particles. Still, bare particles of commodity polymer, such as polyethylene (PE), do not adhere to lipid membranes.15 Nonetheless, organic species, such as humic and fulvic acids, and biopolymers, including proteins and alginate, can adsorb onto NPL surfaces to form the so-called “eco-corona” or “bio-corona”.17,18 This adsorbed layer of organic molecules can induce effective attraction between NPLs and PMs. Together with the theory of elasticity for lipid membranes, we use the theoretical model to show how the bio-corona-induced interactions impact the adsorption of NPLs onto PMs and facilitate their subsequent cellular uptake.
Our paper is organized as follows. (1) In the Methods section, we first introduce a lattice version of self-consistent field theory (SCFT) to describe the adsorption of biopolymers onto NPL surfaces and the formation of the bio-corona. (2) Based on the predicted density profile of the bio-corona, we show how to estimate the effective attraction between an NPL and a lipid membrane. In our model, we consider polymers to experience short-ranged attraction towards the NPL and PM surfaces and exhibit excluded volume interactions in solutions and adsorbed layers. (3) We then describe a theoretical approach, combining the predicted attraction with the elastic free energy of lipid membranes, to estimate NPL adsorption and passive uptake. Readers less interested in the technical details of our approach could refer directly to the Results section. (4) In the Results section, we apply our approach to demonstrate how the molecular properties of polymer layers affect the adsorption and uptake of NPLs in a model NPL–PM system. (5) Finally, in the Discussion section, we outline how our theoretical model can be integrated with atomistic simulations to predict the effects of realistic biomacromolecules on NPL adsorption and uptake.
2 Methods
2.1 Predicting biopolymer adsorption and bio-corona formation
We employ a lattice-based self-consistent field theory (SCFT) to estimate the adsorption of biopolymers, such as intrinsically disordered proteins and polypeptides, onto NPLs. Similar approaches have been used to investigate the self-assembly of block copolymers19–21 and adsorption of telechelic polymers onto colloidal particles.22Considering the biopolymers near the NPLs to be in the marginal regime, the interactions between polymer segments are governed by pairwise, excluded-volume interactions:23
 | (1) |
We compute the distribution of biopolymers near an NPL of radius a by discretizing the space around the particle into a pseudo-one-dimensional lattice {hi} with lattice spacing b (Fig. 1a), such that the radial distance from the particle surface is ΔH = hib. A local chemical potential field W(hi) biases the polymer random walks and is governed by the excluded-volume interactions between Kuhn monomers and a short-ranged surface attraction ε:
| βW(hi) = vc(hi) + ε(hi) | (2) |
 | (3) |
 | ||
| Fig. 1 (a) Discretized lattice used to calculate adsorbed biopolymers around a spherical NPL of radius a. (b) Discretized lattice for adsorbed biopolymers confined between NPL and PM (red) surfaces. | ||
The conditional Boltzmann weight (propagator) for placing the first monomer in a lattice layer is
| q(hi,1) = e−βW(hi) | (4) |
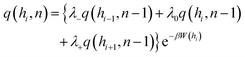 | (5) |
The transition probabilities λ−, λ0, and λ+ correspond to the displacement of the nth Kuhn segment from monomer n − 1 to layer i, originating from layers i − 1, i, and i + 1, respectively.21
When the size of the NPLs is much larger than that of the polymer, the surface can be approximated as a flat wall. In this case, λ−, λ0, and λ+ take the values 1/6, 4/6 and 1/6, respectively, reflecting the fractions of nearest neighbors on the cubic lattice in each of the three layers where the next Kuhn step may reside. For polymers whose sizes are comparable to that of the NPL, we place them on a spherical lattice. In this case, the transition probabilities λ−, λ0, and λ+ depend on the radial distance from the particle center and are given by: (a + hi − b)/(6(a + hi)), 4/6, and (a + hi + b)/(6(a + hi)), respectively. This variation arises because the number of sites differs across lattice layers.
To evolve the propagators, we impose a non-penetration boundary adjacent to the NPL and a reflecting boundary at the outer lattice, such that
| q(h0, n) = 0 and q(hL+1, n) = q(hL, n), | (6) |
The Boltzmann weight for the nth chain segment to occupy the ith layer is
| Q(hi, n) = q(hi, n)q(hi, N − n + 1)eβW(hi) | (7) |
We use the exponential term in eqn (7) to cancel the double-counting of the local chemical potential e−βW(hi) in the two propagators for placing the nth monomer at hi. The single-chain partition function Z is thus the sum of Boltzmann weights for all chain configurations in which the nth monomer occupies any lattice layer:
 | (8) |
 | (9) |
The local concentration profile includes contributions from both adsorbed chains and free polymers. To characterize the bio-corona, we compute the Boltzmann weight distribution Qads(hi, n) for the adsorbed chains, defined as those for which at least one monomer resides in the first lattice layer adjacent to the NPL. To this end, we evolve the propagator qfree(hi, n) of free chains in the known chemical potential field W(hi) after obtaining the self-consistent concentration profile c(hi). The first lattice layer h1 is then treated as an absorbing boundary, while the reflecting boundary is retained at the outer lattice:
| qfree(h1, n) = 0 and qfree(hL+1, n) = qfree(hL, n). | (10) |
The initial condition for the free chain propagator is
| qfree(hi, 1) = e−βW(hi) (i > 1), | (11) |
| Qfree(hi, n) = qfree(hi, n)qfree(hi, N − n + 1)eβW(hi). | (12) |
 | (13) |
| c0ads(hi) = c(hi) − cfree(hi) | (14) |
2.2 Estimating bio-corona-induced NPL–PM attraction
We assume that free chains are washed away when NPLs are transported in biological systems, leaving the adsorbed chains to form the bio-corona. As we demonstrate in the Results section (Section 3), peeling off an adsorbed chain is relatively difficult. To obtain the shape of the unperturbed bio-corona concentration cads, we remove the free chains near the NPL and re-equilibrate the adsorbed chains with a total number of monomers: | (15) |
 | (16) |
 | (17) |
After finding the self-consistent concentration field cads(hi), the free energy per chain for the unperturbed bio-corona is:
 | (18) |
To estimate the effective NPL–PM attraction induced by the bio-corona, we consider an extreme scenario in which a PM is forced to fully wrap around an NPL (Fig. 1b). In this configuration, the bio-corona is confined between the surfaces of the NPL and PM. This confinement, together with a polymer–PM interaction, perturbs the concentration distribution and free energy of the biopolymers. To obtain the new concentration profile, we convert the outer lattice layer, representing the lipid membrane surface, from a reflecting boundary to an adsorbing boundary,
| qads(hL+1, n) = 0. | (19) |
Thus, monomers in the Lth layer now experience a short-range attraction δ2 from the PM:
 | (20) |
We re-equilibrate the biopolymers between the two attractive yet impenetrable surfaces to obtain a new concentration profile and free energy of the bio-corona. This is achieved by evolving the propagator qads(hi, n) from the initial condition in eqn (4)via the recursion relation in eqn (5). From qads(hi, n), the new Boltzmann weight Qads(hi, n) (eqn (7)) can be computed, from which the new partition function (eqn (16)), concentration profile (eqn (17)), and free energy (eqn (18)) of the biopolymers confined between the NPL and PM are obtained. By varying the confinement L, we identify a minimum in ΔF* = Fads − F0ads at L*, induced by the bio-corona, where F0ads is the free energy of a biopolymer chain in the unperturbed bio-corona. The attraction per unit area between the NPL and PM can then be estimated as
 | (21) |
2.3 Free energy of PM wrapping around an NPL
Nanoplastics (NPLs) generated from the degradation of commodity plastic products can exhibit various shapes. To simplify the problem, we model an NPL as a rigid spherical particle with radius a. The formation of a bio-corona makes the particle slightly bulkier, giving it an effective radius a* = a + bL*. Nonetheless, we expect that polymer-coated NPLs do not deform significantly upon contact with the lipid membrane. Therefore, the wrapping process can be treated under cylindrical symmetry,24,25 and we divide the lipid membrane into two regions: an adhesion region, where the NPL interacts with the membrane, and an outer free region, where the membrane bends to accommodate the NPL-induced deformation in the adhesion region (Fig. 2).To describe the adhesion region and quantify the degree of NPL wrapping, we introduce a contact angle α, which defines the point where the lipid membrane begins to detach from the surface of the spherical particle (see Fig. 2). By varying α, we control the degree of wrapping, expressed as
z = (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)/2, α)/2, | (22) |
The free energy of the wrapped region includes the stretching and bending contributions associated with deforming an initially flat membrane. Assuming the PM has an interfacial tension σ and that its relative area change is negligible, we estimate the stretching free energy cost from the excess area pulled toward the wrapping site, ΔAex = 4πa*2z2, as:24
| Fstretch = ΔAexσ = 4πa*2z2σ, | (23) |
The bending free energy cost is governed by the bending modulus κ and the NPL cap area covered by the PM (adhesion region) Aad = 4πa*2z:15,24
 | (24) |
The interactions between the bio-corona and the PM contribute an adhesion energy Fbio:
| Fbio = wAad = 4πwa*2z | (25) |
| F1 = Fstretch + Fbend + Fbio | (26) |
By introducing the dimensionless interfacial tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σa2/κ and the dimensionless adhesion strength
= σa2/κ and the dimensionless adhesion strength ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 2wa2/κ, the dimensionless free energy of the adhesion region can be written as
= 2wa2/κ, the dimensionless free energy of the adhesion region can be written as
 | (27) |
To fully describe the free energy of NPL wrapping, we next solve for the shape profile and the associated elastic energy ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2 (normalized by πκ) of the outer region of the membrane (see Fig. 2). Following the approach of Deserno,24 we write:
2 (normalized by πκ) of the outer region of the membrane (see Fig. 2). Following the approach of Deserno,24 we write:
 | (28) |
 | (29) |
The terms in the curly brackets in eqn (29) represent the bending (quadratic) and stretching free energy, while λr and λh are Lagrange multipliers enforcing the parametrization constraints of the outer membrane shape, as defined in Fig. 2. The term ẋ denotes dx/ds, and the length parameters r, h, and s are normalized by a*.
Minimization of the elastic free energy functional ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2,26
2,26
 | (30) |
![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) , r, λr, λh, yields the following system of ordinary differential equations:
, r, λr, λh, yields the following system of ordinary differential equations: | (31a) |
ṙ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, ψ, | (31b) |
ḣ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, ψ, | (31c) |
 | (31d) |
 | (31e) |
 | (32a) |
 | (32b) |
At s = 0, we impose three boundary conditions that can be identified from Fig. 2 and summarized in eqn (33). Far from the NPL and PM contact, s = S → ∞, the membrane should remain unperturbed and asymptotically flat. By allowing the profile variables r and h to vary freely during minimization, Deserno24 showed that this condition is satisfied by setting ψ(S) = ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) (S) = 0, and by applying eqn (30) for x = ṙ and ḣ at S, which yield
(S) = 0, and by applying eqn (30) for x = ṙ and ḣ at S, which yield
 | (33) |
Applying eqn (30) to the remaining variable x = h and similarly for x = ḣ at the boundary S (as above) implies λh = 0 everywhere.
The system in eqn (31), together with the boundary conditions in eqn (33), defines a boundary value problem that we solve using a collocation algorithm.27 Alternatively, the system in eqn (31) can be solved by converting the boundary value problem into an equivalent initial value problem. Deserno24 employed this approach with the following initial boundary conditions:
 | (34) |
In this approach, the initial boundary condition ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) (0) is unknown and must be iteratively adjusted so that ψ(S) → 0 at a sufficiently large value of S, a procedure known as the shooting method.27
(0) is unknown and must be iteratively adjusted so that ψ(S) → 0 at a sufficiently large value of S, a procedure known as the shooting method.27
For a given ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) and contact angle α (or equivalently, wrapping degree z (eqn (22)), we numerically solve for the shape of the outer membrane region, obtaining ψ, r, h, pψ and pr. The derivative
and contact angle α (or equivalently, wrapping degree z (eqn (22)), we numerically solve for the shape of the outer membrane region, obtaining ψ, r, h, pψ and pr. The derivative ![[small psi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a5.gif) is then extracted from pψ using eqn (32a). With these shape functions, we compute
is then extracted from pψ using eqn (32a). With these shape functions, we compute ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2 in eqn (28) using Simpson's rule.26
2 in eqn (28) using Simpson's rule.26
Combining the elastic free energy of the outer region (eqn (28)) with the adhesion free energy (eqn (27)) yields the total dimensionless free energy,
Δ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) = = ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 1( 1(![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) , , ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , z) + , z) + ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2( 2(![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , z). , z). | (35) |
Because ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2 is independent of
2 is independent of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) , it only needs to be computed once to obtain Δ
, it only needs to be computed once to obtain Δ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) profiles for a fixed
profiles for a fixed ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) and z while varying
and z while varying ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) . To highlight the elastic free energy of PM induced by NPL adsorption, we set
. To highlight the elastic free energy of PM induced by NPL adsorption, we set ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 0 in eqn (35) and write
= 0 in eqn (35) and write
Δ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) el = el = ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 1(0, 1(0, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , z) + , z) + ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) 2( 2(![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , z). , z). | (36) |
3 Results
To demonstrate our computational framework, we consider biopolymers composed of N Kuhn segments of length b = 1 nm adsorbed onto an NPL of radius a = 50 nm. The bulk biopolymer concentration is c0 = 0.1b−3, and the excluded volume parameter is v = 0.1b3. Using the lattice SCFT model, we compute the density distribution of polymer segments around the spherical NPL (Fig. 3a). For the rather large NPL here, we consider the polymer–NPL and polymer–PM interfaces to be flat. Large NPL radius only leads to a negligible difference (less than b/a) between the transition probabilities λ+ and λ− in a spherical lattice for curved interfaces and those in a cubic lattice for flat interfaces. As expected, adsorbed loops and tails accumulate near the NPL surface, depleting the free, non-adsorbed chains in the bio-corona. The adsorption layer becomes thicker with increasing chain length N (Fig. 3b), as longer chains can form more extended loops and tails around the particle. Increasing the polymer–NPL attraction δ1 also produces a denser adsorption layer (Fig. 3c).To obtain the shape of the unperturbed bio-corona, we remove the free chains near the NPL and re-equilibrate the adsorbed chains. The concentration profile of the bio-corona remains largely unchanged (Fig. 4a and b). In a marginal solution, the adsorbed polymer chains behave approximately as ideal random walks, neither swelling nor collapsing when additional solvent enters the corona to replace the free chains. Therefore, we assume the thickness of the bio-corona L* is governed by the polymer molecular weight and scales as L* ≈ N1/2, the characteristic size of Gaussian chains.28
We can assess the stability of the bio-corona by “peeling off” an adsorbed polymer chain. Because the absorbed chains behave as ideal random walks at all length scales in the marginal regime, we assume the peeled chain adopts nearly the same configuration as the adsorbed molecules, except that none of its monomers are in contact with the NPL surface. This configuration corresponds to the maximum free energy of the detached chain, as its monomers no longer experience the attractive interaction with the NPL surface but still experience excluded volume interactions within the crowded bio-corona. Accordingly, we estimate the mean free energy barrier for detaching an adsorbed chain as
| βΔFdetach ≈ −δ14πa2cads(h1)bN/J, | (37) |
 | ||
| Fig. 5 Detachment free energy barrier for an adsorbed chain in a bio-corona βΔFdetachvs. monomer–NPL attraction strength |δ1| (eqn (37)). Bio-coronae formed in solutions with c0 = 0.1b−3. | ||
To estimate the bio-corona-induced attraction between the NPL and PM, we allow the PM to fully wrap the polymer-coated NPL with a varying confinement parameter L (Fig. 1). For each value L between the NPL and PM, the distribution of polymer segments is re-equilibrated. A weak polymer–PM attraction δ2 results in a more uniform polymer density around the NPL across different confinements (Fig. 6a).
Tuning the confinement L varies the interaction between the coated NPL and the PM. For sufficiently large L, the additional polymer–PM attraction allows polymer segments to redistribute and reduce their crowding near the NPL surface, which increases their translational entropy and lowers βFads (Fig. 6b). However, even with this added attraction, decreasing L increases confinement and forces the polymer segments into a more crowded state. This strengthens excluded volume interactions and reduces translational entropy, therefore increasing βFads. As a result, compressing the bio-corona generates repulsive forces between the NPL and PM. We thus assign an effective size a* = a + bN1/2 to a bio-corona-coated NPL. This effective size is then used to calculate the surface attraction w (eqn (21)) that drives NPL uptake.
We calculate the dimensionless surface attraction ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) that drives the NPL adsorption and uptake using eqn (21) and the conversion described in Section 2.3. The value of
that drives the NPL adsorption and uptake using eqn (21) and the conversion described in Section 2.3. The value of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases with the polymer–surface interaction strengths δ1 and δ2 (Fig. 7a). The polymer–NPL interaction δ1 enhances the density of the bio-corona, and together with the polymer–PM attraction δ2, a denser bio-corona leads to a stronger effective attraction between the NPL and PM. Longer chains also lead to a stronger effective attraction
increases with the polymer–surface interaction strengths δ1 and δ2 (Fig. 7a). The polymer–NPL interaction δ1 enhances the density of the bio-corona, and together with the polymer–PM attraction δ2, a denser bio-corona leads to a stronger effective attraction between the NPL and PM. Longer chains also lead to a stronger effective attraction ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) (Fig. 7b).
(Fig. 7b).
Using the predicted ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) , we compute the free energy for a PM wrapping around an NPL (Fig. 8a). We consider a representative biological membrane with an interfacial tension σ = 0.02 dyn per cm and a bending stiffness κ = 20kT24 at room temperature (T = 300 K). By solving the membrane shape equations for a given wrapping degree z (eqn (22)), we obtain the total free energy of the NPL–PM system by summing the elastic free energy of the membrane and the effective attraction induced by the adsorbed biopolymers (eqn (35)). A sufficiently strong NPL–PM attraction (
, we compute the free energy for a PM wrapping around an NPL (Fig. 8a). We consider a representative biological membrane with an interfacial tension σ = 0.02 dyn per cm and a bending stiffness κ = 20kT24 at room temperature (T = 300 K). By solving the membrane shape equations for a given wrapping degree z (eqn (22)), we obtain the total free energy of the NPL–PM system by summing the elastic free energy of the membrane and the effective attraction induced by the adsorbed biopolymers (eqn (35)). A sufficiently strong NPL–PM attraction (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) > 4) is required for the NPL to adhere to the lipid membrane and become partially wrapped. In the partially wrapped state, the bio-corona-induced attraction balances the PM's stretching and bending elastic energies.
> 4) is required for the NPL to adhere to the lipid membrane and become partially wrapped. In the partially wrapped state, the bio-corona-induced attraction balances the PM's stretching and bending elastic energies.
 | ||
Fig. 8 (a) Free energy of a typical PM wrapping around a model NPL vs. bio-corona-induced attraction ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ranging from −4 to −7 (eqn (35)). (b) Elastic free energy of the PM induced by NPL adsorption (eqn (36)), corresponding to the global minimum in (a), vs. polymer-induced adhesion strength | ranging from −4 to −7 (eqn (35)). (b) Elastic free energy of the PM induced by NPL adsorption (eqn (36)), corresponding to the global minimum in (a), vs. polymer-induced adhesion strength |![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) |. (c) Phase diagram for the model NPL and lipid membrane. Effective NPL radius a* = 60 nm. Bio-corona consists of polymers of length N = 100 and a Kuhn length b = 1 nm, formed in a solution with c0 = 0.1b−3. PM has an interfacial tension σ = 0.02 dyn per cm and a bending stiffness κ = 20kT at room temperature (T = 300 K). |. (c) Phase diagram for the model NPL and lipid membrane. Effective NPL radius a* = 60 nm. Bio-corona consists of polymers of length N = 100 and a Kuhn length b = 1 nm, formed in a solution with c0 = 0.1b−3. PM has an interfacial tension σ = 0.02 dyn per cm and a bending stiffness κ = 20kT at room temperature (T = 300 K). | ||
As the bio-corona-induced NPL–PM attraction strengthens, the partial wrapping degree z (eqn (22)) grows, as evidenced by the shift of the global minimum in total free energy (Fig. 8a). For each z corresponding to the global minimum, we compute the PM elastic free energy (eqn (36)) arising from NPL adsorption (Fig. 8b). Greater wrapping leads to larger elastic deformation of the lipid membrane, enhancing local mechanical stress. Such deformation can destabilize the PM, shortening the lifetime of the biological barrier and potentially triggering cellular or tissue inflammation.29
Further strengthening the attraction ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) shifts the global minimum of the free energy to the fully wrapped state (z = 1), ultimately enabling spontaneous NPL uptake. The phase boundary for spontaneous uptake can be determined by finding the critical
shifts the global minimum of the free energy to the fully wrapped state (z = 1), ultimately enabling spontaneous NPL uptake. The phase boundary for spontaneous uptake can be determined by finding the critical ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) at which the fully and partially wrapped states are equally stable (
at which the fully and partially wrapped states are equally stable (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≈ 5.86). By correlating this critical
≈ 5.86). By correlating this critical ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) with the molecular properties of the adsorbed polymers in the bio-corona, specifically the interaction strengths δ1 and δ2 (eqn (20)), we construct a phase diagram describing NPL–PM interactions (Fig. 8c). To facilitate NPL adsorption or uptake, the polymer–PM attraction must be sufficiently strong to overcome the membrane's elastic energy.
with the molecular properties of the adsorbed polymers in the bio-corona, specifically the interaction strengths δ1 and δ2 (eqn (20)), we construct a phase diagram describing NPL–PM interactions (Fig. 8c). To facilitate NPL adsorption or uptake, the polymer–PM attraction must be sufficiently strong to overcome the membrane's elastic energy.
The free energy model also permits the estimation of the characteristic time scale of NPL internalization. To do so, we consider the NPLs and lipid membranes to be immersed in water. We thus write the translational (tt) resistance coefficient of the spherical NPL as ξtt = 6πηa* and the corresponding translational diffusion coefficient as Dtt = kT/ξtt, where η = 0.854 mPa s is the dynamic viscosity of water at T = 300 K.30–32 Using resistance and diffusion coefficients and the free-energy of NPL wrapping (Fig. 8(a)), the mean first-passage time (MFPT) τ for the particle to reach a specific vertical location h = 2a*z satisfies the following boundary value problem,15
 | (38) |
By solving the MFPT equation, we show that a sufficiently large ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) is indeed necessary for the NPL uptake. When the fully and partially wrapped states are equally stable (
is indeed necessary for the NPL uptake. When the fully and partially wrapped states are equally stable (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ≈ 5.86), the uptake barrier (Fig. 8a) prevents internalization as indicated by the diverging MFPT for the system to reach a moderate wrapping degree z. As the attraction
≈ 5.86), the uptake barrier (Fig. 8a) prevents internalization as indicated by the diverging MFPT for the system to reach a moderate wrapping degree z. As the attraction ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) increases, the NPL can be internalized by the cell within hours (
increases, the NPL can be internalized by the cell within hours (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 6.5) or even in less than one millisecond (
= 6.5) or even in less than one millisecond (![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 7) (orange and red symbols in Fig. 9a, respectively). Nevertheless, by computing τ|z=1, we show that the characteristic time of NPL internalization decreases rapidly with increasing bio-corona-induced NPL–PM attractions (Fig. 9b).
= 7) (orange and red symbols in Fig. 9a, respectively). Nevertheless, by computing τ|z=1, we show that the characteristic time of NPL internalization decreases rapidly with increasing bio-corona-induced NPL–PM attractions (Fig. 9b).
 | ||
Fig. 9 (a) Mean first-passage-time for an NPL to reach the wrapping degree z. Different colors correspond to the free energy of wrapping in Fig. 8(a) with ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ranging from −5.86 to −7. (b) Characteristic time of NPL internalization vs. ranging from −5.86 to −7. (b) Characteristic time of NPL internalization vs. ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) . . | ||
4 Discussion
We expect the theoretical model presented here to be particularly useful for studying interactions between moderately sized NPLs and PM. The spatiotemporal resolution required to characterize the cellular uptake of such NPLs often exceeds the capabilities of conventional simulation techniques, including both atomistic and coarse-grained molecular dynamics.The input parameters of our model comprise well-documented elastic properties of the PM, such as interfacial tension and bending stiffness, but also include phenomenological interaction parameters used to estimate the NPL–PM adhesion strength w (eqn (21)). These phenomenological parameters (eqn (20)) play a critical role in the adsorption and uptake of NPLs. Sufficient biopolymer–NPL attraction δ1 is required to form a dense bio-corona around the nanoparticle, while a sufficiently strong biopolymer–PM attraction δ2 is needed to redistribute adsorbed chains between the two surfaces, enhancing their translation entropy and inducing the NPL–PM attraction.
The parameters δ1 and δ2 depend on the molecular structures of biomacromolecules and the compositions of membranes. To quantify their values, we suggest combining atomistic simulations with free energy sampling techniques, such as umbrella sampling and metadynamics.33 Atomistic simulations could accurately capture the properties of various commodity plastics and lipid membranes, including semicrystallinity15,34 and elasticity parameters.35,36 Free energy sampling methods could then be used to compute the binding free energy of a biopolymer on a flat surface, such as a polymer or PM surface. Using metadynamics, Qi and Pfaendtner37 recently demonstrated how to calculate solid-binding energies of peptides from the binding energies of their residues. We expect that a similar approach could provide reliable estimates of δ1 and δ2 for our theoretical model.
Because the lattice SCFT permits the specification of monomer sequences during propagator evolution, the sampled interactions δ1 and δ2 from atomistic simulations can be directly incorporated into our model. Our current model “coarse-grains” polymer chains into random walks of Kuhn segments, which are not equivalent to monomeric units such as amino acids. However, our lattice SCFT for flexible polymers can be readily extended to a lattice of semiflexible worm-like chains, where each monomer represents a chemically well-defined moiety.38 The bending stiffness governing local orientational correlations between adjacent monomers along the semiflexible backbone could then be directly obtained from atomistic simulations. Thus, we expect simulations and free energy calculations based on small systems, such as monomers near NPL and PM surfaces, could provide quantitative input parameters for the lattice model. Investigating how polymer structure and the surface properties of both the NPL and PM influence adsorption and cellular uptake will be an important direction for future work.
Of course, our simple model here only considered excluded volume interactions and short-ranged interactions for biopolymers. However, proteins are often charged and coordinated by nearby water molecules. To accurately model the adsorption behaviors of biopolymers near NPL and PM surfaces, we will need to incorporate the Poisson–Boltzmann equation into the theoretical framework to account for the electrostatic interactions, which are modulated by added salt in the solution. The polymer physics community has developed self-consistent field theories and scaling arguments to model polyelectrolyte adsorption onto different surfaces,39 which can serve as the foundation of further refinement of our current approach. Theoretically modeling water-mediated protein–protein interactions, which are governed by the specific amino acid sequence, is challenging. A possible approach to approximate the water-mediated interactions is to perform osmotic pressure simulations40 of a protein solution. By varying the concentration of proteins in the simulations, one may fit the concentration-dependent osmotic pressure to approximate a two-body effective excluded volume for our model. Testing and validating such an approach are warranted in our future work.
Finally, we would also like to remind the reader that once the NPLs enter the human body, other biological molecules can further modify the surface chemistry of the particles, and in turn, impact their interactions with PMs. For example, the inhaled NPLs and MPLs can be encapsulated by pulmonary surfactants.41 These bio-coronae formed by lung surfactants can induce attraction between NPLs and PMs and cause lung injury.42 Thus, we expect the complex molecular environment in biological systems to result in the formation of complex and heterogeneous bio-coronae around NPLs. Quantitatively modeling such adsorption layers around NPLs remains a challenge and is beyond the scope of this paper.
5 Conclusion
By combining the theory of membrane elasticity with polymer physics, we developed a computational framework to predict how the bio-corona influences the adsorption and uptake of moderately sized nanoplastics (NPLs). A lattice-based self-consistent field theory (SCFT) model enables the prediction of bio-corona formation resulting from the adsorption of biopolymers onto an NPL from bulk solution.Our SCFT model predicts an induced effective attraction between the NPL and PM after re-equilibrating the adsorbed chains between their surfaces. Because bare NPLs composed of commodity plastics such as PE and polypropylene (PP) are repelled by the polar head groups of lipid membranes, this bio-corona-induced attraction is essential for NPLs to adhere to and translocate through the PM.
When the bio-corona induces a sufficiently strong effective attraction, NPLs can adsorb onto PMs and become partially wrapped. The adsorption of NPLs can locally stretch and bend the lipid membrane, potentially generating excess stress and triggering inflammation. Further increasing the effective attraction allows NPLs to be spontaneously internalized by cells, as they become fully wrapped and pinched off. The characteristic time of NPL translocation is strongly affected by the bio-corona-induced NPL–PM interactions and can be estimated using a mean first-passage time analysis (eqn (38)).
Bio-corona-induced attraction depends on polymer properties, including monomer–surface affinity and polymer molecular weight. Although the monomer–NPL and monomer–PM interactions in our current model are phenomenological, we outline how low-cost atomistic simulations and free energy calculations can be used to obtain these input parameters. Indeed, our model here only considers coarse-grained biopolymers as the constituents of bio-coronae. Other molecules in complex biological systems could also adsorb onto NPLs and modify their surface chemistry and interactions with PMs. Still, we expect this work to provide a better understanding of NPL–PM interactions, aiding in the assessment of the potential health impacts of these ubiquitous particles in our environment.
Author contributions
Wenlin Zhang: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, software, resources, supervision, validation, visualization, writing – original draft, and writing – review and editing. Anderson D. S. Duraes: formal analysis, investigation, validation, visualization, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
All numerical data generated using the theoretical tools described in the manuscript are plotted in Fig. 3–9.Acknowledgements
We acknowledge the startup funding from Dartmouth College that supported this research.References
- J. Song, C. Wang and G. Li, ACS ES&T Water, 2024, 4, 2330–2332 Search PubMed.
- N. F. Mendez, V. Sharma, M. Valsecchi, V. Pai, J. K. Lee, L. S. Schadler, A. J. Müller, S. Watson-Sanders, M. Dadmun, G. Kumaraswamy and S. K. Kumar, Nat. Commun., 2025, 16, 3051 Search PubMed.
- A. D. Vethaak and J. Legler, Science, 2021, 371, 672–674 CrossRef CAS PubMed.
- M. B. Paul, V. Stock, J. Cara-Carmona, E. Lisicki, S. Shopova, V. Fessard, A. Braeuning, H. Sieg and L. Böhmert, Nanoscale Adv., 2020, 2, 4350–4367 RSC.
- D. M. Mitrano, P. Wick and B. Nowack, Nat. Nanotechnol., 2021, 16, 491–500 Search PubMed.
- R. Marfella, F. Prattichizzo, C. Sardu, G. Fulgenzi, L. Graciotti, T. Spadoni, N. D’Onofrio, L. Scisciola, R. L. Grotta, C. Frigé, V. Pellegrini, M. Municinò, M. Siniscalchi, F. Spinetti, G. Vigliotti, C. Vecchione, A. Carrizzo, G. Accarino, A. Squillante, G. Spaziano, D. Mirra, R. Esposito, S. Altieri, G. Falco, A. Fenti, S. Galoppo, S. Canzano, F. C. Sasso, G. Matacchione, F. Olivieri, F. Ferraraccio, I. Panarese, P. Paolisso, E. Barbato, C. Lubritto, M. L. Balestrieri, C. Mauro, A. E. Caballero, S. Rajagopalan, A. Ceriello, B. D’Agostino, P. Iovino and G. Paolisso, N. Engl. J. Med., 2024, 390, 900–910 Search PubMed.
- Y. Wei, H. Chen, Y.-X. Li, K. He, K. Yang and H.-B. Pang, ACS Nano, 2022, 16, 5885–5897 Search PubMed.
- A. Khan and Z. Jia, iScience, 2023, 26, 106061 CrossRef CAS.
- N. Qian, X. Gao, X. Lang, H. Deng, T. M. Bratu, Q. Chen, P. Stapleton, B. Yan and W. Min, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2300582121 Search PubMed.
- H. Cai, E. G. Xu, F. Du, R. Li, J. Liu and H. Shi, Chem. Eng. J., 2021, 410, 128208 Search PubMed.
- C. Liu, A. D. S. Duraes, E. L. Jiao and W. Zhang, MRS Adv., 2024, 1–7 Search PubMed.
- O. Hollóczki and S. Gehrke, ChemPhysChem, 2020, 21, 9–12 Search PubMed.
- L. Li, S. Li, Y. Xu, L. Ren, L. Yang, X. Liu, Y. Dai, J. Zhao and T. Yue, Environ. Sci.: Nano, 2022, 10, 440–453 RSC.
- A. Vismara and A. Gautieri, Biophys. Chem., 2024, 308, 107213 CrossRef CAS PubMed.
- A. D. S. Duraes, E. L. Jiao and W. Zhang, J. Phys. Chem. B, 2025, 129, 3385–3395 CrossRef CAS PubMed.
- H. Garoff, R. Hewson and D.-J. E. Opstelten, Microbiol. Mol. Biol. Rev., 1998, 62, 1171–1190 CrossRef CAS PubMed.
- M. Zhu, Z. Zhang, T. Zhang, T. Hofmann and W. Chen, Environ. Sci. Technol., 2023, 57, 331–339 CrossRef CAS.
- S. Liu, M. Junaid, H. Liao, X. Liu, Y. Wu and J. Wang, Sci. Total Environ., 2022, 836, 155703 CrossRef CAS.
- M. D. Lefebvre, M. O. D. L. Cruz and K. R. Shull, Macromolecules, 2004, 37, 1118–1123 CrossRef CAS.
- N. B. Tito, S. T. Milner and J. E. G. Lipson, Macromolecules, 2010, 43, 10612–10620 CrossRef CAS.
- N. B. Tito, S. T. Milner and J. E. G. Lipson, Macromolecules, 2012, 45, 7607–7620 Search PubMed.
- W. Zhang, A. Travitz and R. G. Larson, Macromolecules, 2019, 52, 5357–5365 CrossRef CAS.
- A. N. Semenov, J. Bonet-Avalos, A. Johner and J. F. Joanny, Macromolecules, 1996, 29, 2179–2196 CrossRef CAS.
- M. Deserno, Phys. Rev. E, 2004, 69, 031903 CrossRef PubMed.
- X. Yi, X. Shi and H. Gao, Phys. Rev. Lett., 2011, 107, 098101 CrossRef PubMed.
- K. F. Riley, M. P. Hobson and S. J. Bence, Mathematical Methods for Physics and Engineering, Cambridge University Press, Cambridge, UK, 3rd edn, 2006, pp. 775–802, 984–1040 Search PubMed.
- U. M. Ascher, R. M. M. Mattheij and R. D. Russell, Numerical Solution of Boundary Value Problems for Ordinary Differential Equations, SIAM, Philadelphia, PA, 1995 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003, pp. 309–360 Search PubMed.
- J.-B. Fleury and V. A. Baulin, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104610118 CrossRef CAS.
- E. W. Lemmon, I. H. Bell, M. L. Huber and M. O. McLinden, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. Linstrom and W. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 2025 Search PubMed.
- A. D. S. Duraes and J. D. Gezelter, J. Phys. Chem. B, 2021, 125, 11709–11716 Search PubMed.
- A. D. S. Duraes and J. D. Gezelter, J. Chem. Phys., 2023, 159, 134105 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- L. Zou and W. Zhang, Macromolecules, 2025, 58, 3589–3594 CrossRef CAS.
- K. V. Pinigin, Membranes, 2022, 12, 1149 CrossRef CAS PubMed.
- M. F. Ergüder and M. Deserno, J. Chem. Phys., 2021, 154, 214103 Search PubMed.
- X. Qi and J. Pfaendtner, J. Chem. Theory Comput., 2024, 20, 2959–2968 CrossRef CAS.
- W. Zhang, E. D. Gomez and S. T. Milner, Macromolecules, 2016, 49, 963–971 Search PubMed.
- A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 Search PubMed.
- C. Gillespie and S. T. Milner, Soft Matter, 2020, 16, 9816–9821 Search PubMed.
- L. Li, Y. Xu, S. Li, X. Zhang, H. Feng, Y. Dai, J. Zhao and T. Yue, J. Hazard. Mater., 2022, 427, 127872 Search PubMed.
- X. Xu, R. A. Goros, Z. Dong, X. Meng, G. Li, W. Chen, S. Liu, J. Ma and Y. Y. Zuo, Environ. Sci. Technol., 2023, 57, 21050–21060 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |





