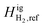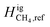Thermal diffusion of hydrogen-containing gas mixtures: applications to underground hydrogen storage
Jimin D.
Zhou
 *a,
Kristian
Jessen
b and
Anthony R.
Kovscek
*a,
Kristian
Jessen
b and
Anthony R.
Kovscek
 a
a
aDepartment of Energy Science & Engineering, Stanford University, Stanford, California, USA. E-mail: jdzhou@stanford.edu
bMork Family Department of Chemical Engineering and Materials Science, University of Southern California, Los Angeles, California, USA
First published on 21st November 2025
Abstract
The modeling of underground hydrogen (H2) storage (UHS) requires understanding the thermodynamics of H2-containing gas mixtures as they approach local equilibrium during storage while subjected to temperature gradients and gravity segregation. Previous investigations using a model based on irreversible thermodynamics have shown the need for experimental measurements of hydrogen thermal diffusion in natural gas to better understand hydrogen composition versus depth during UHS. This work presents thermal diffusion measurements for H2 in methane (CH4) at varying temperatures and compositions. The effect on thermodynamic modeling is discussed, and the effect of other cushion gases such as carbon dioxide (CO2) is also explored. For the H2–CH4 system, it was found that the thermal diffusion factor (αT) increases as a function of composition and temperature, with values ranging from αT = 0.22–0.36 for H2 mole fractions ranging from xH2 = 0.3−0.7. At a fixed composition of 50% H2 and 50% CH4, αT ranged from 0.21 to 0.29 for a median temperature ranging from 250 K to 450 K. Using these values, a reference ideal gas enthalpy of 3.5 kJ mol−1 for CH4 while setting the reference ideal gas enthalpy of H2 to 0 kJ mol−1 is needed to properly match the model with the experimental observations at a constant median temperature. For experiments at varying median temperature, a correlation is needed between the enthalpy of the reference ideal gas of CH4 and the departure of the median temperature from the reference state temperature to match adequately the model with the experimental values. The effect of adding these thermal considerations leads to a more homogeneous mix of H2 with its cushion gas than previously anticipated. Further study of UHS operations could include the effects of shut-in time to determine gas purity during production cycles.
1. Introduction
Underground hydrogen storage (UHS) in porous media is a possible solution for long-term storage of intermittent and seasonal renewable energy. UHS was first introduced as a means of storing energy in porous geological formations in the form of hydrogen (H2) gas. H2 is a versatile energy carrier because it can be created from both renewable and fossil fuel sources.1,2Fig. 1 shows an example of how H2 could be used to address the fluctuating supply of electricity generated by solar power. | ||
| Fig. 1 A schematic showing how underground hydrogen storage can address intermittency challenges for renewable energy sources such as solar power. The image is adapted from Heinemann et al.1 | ||
Excess solar energy can be converted into H2 gas and injected into a storage reservoir.3 During periods of greater energy demand, this stored gas can be produced back to the surface for conversion into electricity. Okoroafor et al.4 performed a case study for northern California, and showed that with current electrolyzer efficiency, the power-to-hydrogen-to-power round trip efficiency was about 36%. H2 recovery was shown to be greater than 75%.
One added complexity of UHS is the use of a cushion gas to maintain pressure during H2 withdrawal stages.5–7 Some of the most common cushion gases are methane (CH4), nitrogen (N2), and carbon dioxide (CO2). In the presence of multiple gases, one must consider the distribution of components along the storage reservoir as the system approaches steady state. Thus, the effects of temperature and gravity on phase behavior must be considered when forecasting UHS operations for injecting and producing H2.
A previous study by Zhou et al.8 showed that the type of cushion gas and the magnitude of the thermal gradient affected H2 distribution along the reservoir. They found that when considering the effects of both gravity and temperature, the distribution of H2 along the depth of the storage reservoir varied from the case where only gravity was considered. The effects of temperature offset some of the component segregation caused by gravitational forces. A sensitivity study showed that an increase in the temperature gradient along the system resulted in an increase in component segregation in the opposite direction to that of a system subject to only gravitational forces, such that more H2 aggregated towards the bottom (warmer) portion of the reservoir. It was also shown that the reference ideal gas specific enthalpy (Higi) for H2 plays a key role in providing an accurate calculation for the compositional grading of a hydrogen-containing mixture.
The presence of a thermal gradient contributes to thermal diffusion, that is a coupled mass and heat transfer process where mixture components segregate under the influence of a temperature gradient.9 This phenomenon was first discovered by Ludwig10 and then further investigated by Soret.11 Thermal diffusion is found in many natural processes, the most relevant of which is the distribution of oil components along a storage reservoir.12
Due to the wide breadth of occurrences, several methods for studying thermal diffusion exist – including but not limited to the classical Soret cell, thermogravitational columns, swing separators, parallel plates and two-chamber thermal diffusion cells.9,13–16 Several theoretical models exist to describe this phenomenon as well, such as those developed by Kempers and Haase.17,18
This paper builds on the work of Zhou et al.8 by contributing experimental measurements of thermal diffusion in the context of UHS, and presenting simulated H2 distributions at steady state in the presence of multiple cushion gases. We present thermal diffusion measurements at specified temperatures, pressures, and compositions pertinent to UHS that have not been clearly reported in the literature. In addition, we provide updated values for thermal diffusion measurements that were performed in the early to mid-20th century. From these thermal diffusion measurements, we are able to tune our model to accurately simulate component distribution under the effects of gravity and a temperature gradient. To date, we know of no comparable analysis for H2 segregation apart from our own that incorporates both of these phenomena using both experimental and computational analyses.
The remainder of the paper is structured as follows. The theory and setup for determining the thermal diffusion factor and subsequently the reference ideal gas specific enthalpy are discussed. The experimental and modeling setups are then introduced. The results are then presented along with a discussion on applications to underground hydrogen storage. Finally, a summary of the work and future considerations conclude the manuscript.
2. Methodology – theory and setup
This section summarizes a computational framework to determine the thermal diffusion factor using irreversible thermodynamics and compositional grading. Afterwards, we present descriptions of the experimental setup and the model developed in COMSOL Multiphysics® to validate the physical results.2.1. Theory
Compositional grading in a non-isothermal system consisting of n components is given by the general equation19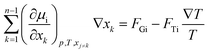 | (1) |
FGi = (Mi − ρ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i)g i)g | (2) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i and Mi are the partial molar volume and molar mass of component i, respectively, ρ is the mass density of the mixture and g is the gravitational constant.
i and Mi are the partial molar volume and molar mass of component i, respectively, ρ is the mass density of the mixture and g is the gravitational constant.
The thermal contributions due to temperature variation are captured in the FTi, or thermal force, term in eqn (1), and expressed through thermal models such as the ones described previously. FTi is associated with a high degree of uncertainty due to the reference ideal gas specific enthalpy (Higi,ref). Previous work by Zhou et al.8 incorporates the Haase model that describes the thermal force contribution as follows:
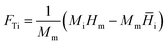 | (3) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) i is the partial molar enthalpy of component i, and Mm and Hm are the molar mass and molar enthalpy of the mixture, respectively. The partial molar enthalpy is calculated from
i is the partial molar enthalpy of component i, and Mm and Hm are the molar mass and molar enthalpy of the mixture, respectively. The partial molar enthalpy is calculated from![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) i = Higi + i = Higi + ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) resi resi | (4) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) resi are the partial ideal gas enthalpy and the residual partial molar enthalpy of component i, respectively.
resi are the partial ideal gas enthalpy and the residual partial molar enthalpy of component i, respectively. ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) resi is evaluated as
resi is evaluated as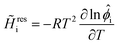 | (5) |
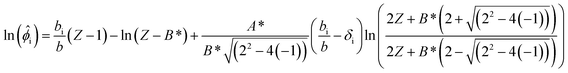 | (6) |
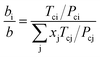 | (7) |
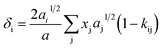 | (8) |
H igi is evaluated as
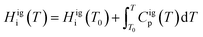 | (9) |
| Cigp(T) = C1i + C2iT + C3iT2 + C4iT3 | (10) |
To better isolate the effects of temperature and Higi,ref, thermal diffusion, or the Ludwig–Soret effect, can be studied. The thermal diffusion factor between two components, αT, is determined as a function of thermal separation q26–28
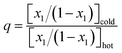 | (11) |
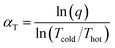 | (12) |
Eqn (1) can be solved to obtain component distributions using numerical integration, but this process can become expensive as the number of components increases. Pedersen and Lindeloff23 presented a simplified solution to this problem as
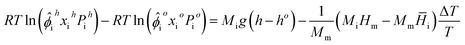 | (13) |
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) i is the fugacity coefficient of component i.
i is the fugacity coefficient of component i.
By solving eqn (13), one can obtain the compositional distribution of gases as a function of distance and temperature. Assuming a linear temperature gradient consistent with the subsurface, the thermal diffusion factor is then calculated using eqn (11) and (12). These calculated thermal diffusion factors are then compared with experimental thermal diffusion factors that have been reported in the literature.15,26,27,29 The reader is referred to the first figure in ref. 8 for an example of matching the reference specific enthalpy of butane based on thermal diffusion factors.
2.2. Model setup
To model compositional grading during UHS, we introduced a model based on the work of Pedersen and Lindeloff23 and applied it to UHS context.8 The model initializes with a reference temperature, pressure, and composition at the midpoint depth of the storage reservoir. It then solves eqn (13) using successive substitution for each depth step above and below the reference depth. Temperature is pre-calculated based on the linear temperature gradient and depth. Solving via successive substitution provides a cost-effective way to obtain multi-component distributions. Zhou et al.8 showed that the results obtained by solving eqn (1)via ODE integration and eqn (13)via successive substitution are comparable.The thermal diffusion factor can then be modeled by setting the gravity term in eqn (13) to 0, and then the problem becomes only a function of temperature.
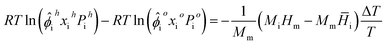 | (14) |
Solving eqn (14) then gives the composition distribution as a function of temperature only, allowing us to then use eqn (11) and (12) to obtain the thermal diffusion factor across the depth of interest.
2.3. Experimental setup
A two-bulb configuration was constructed by connecting two small, stainless steel sample cylinders using stainless steel tubing from Swagelok. The two bulbs were each 50 mL, 304L grade stainless steel DOT sample cylinders (part no. 304L-HDF4-50). The two bulbs were connected by 10 inches of 1/8″ OD 316L grade stainless steel tubing (part no. SS-T2-S-028-20). 316 stainless steel quarter-turn Swagelok valves were placed at the inlets of both cylinders to isolate the ends during sampling, and at the outlets for gas sampling. To prevent any potential leakage within the bulbs, a vacuum leak sealant epoxy was applied to the inlet and outlet fittings of the cylinders.The temperature gradient was controlled using Watlow heat controllers with different set points along the length of the apparatus. The setup was insulated using fiberglass insulation tape and continuously monitored with an Omega DAQ data acquisition system (OMB-DAQ-2408). The pressure was also monitored during the experiment using pressure transducers (Precise Sensors No. 6550-1000-01) attached to each cylinder to ensure that no leaks occurred. Fig. 2 shows the schematic of the experimental setup.
 | ||
| Fig. 2 Experimental setup for thermal diffusion experiments. A linear temperature gradient is maintained across two insulated stainless steel cylinders using Watlow heat controllers. | ||
The gas mixtures used were obtained from Linde. All of the gas mixtures were calibrated prior to testing and were ultra-high-purity mixtures. Table 1 details the gas mixtures. Mixture 1 was used to verify the workflow prior to studying the other listed gas mixtures.
| Mixture no. | Fraction of gas 1 | Fraction of gas 2 |
|---|---|---|
| 1 | 20% H2 | 80% N2 |
| 2 | 50% H2 | 50% CH4 |
| 3 | 30% H2 | 70% CH4 |
| 4 | 70% H2 | 30% CH4 |
| 5 | 50% H2 | 50% CO2 |
The gas mixture was first injected at constant pressure and temperature into the experimental apparatus. For our studies, we selected a constant pressure of 160 psi. While this pressure value is not representative of UHS conditions, we were restricted by the upper limit of the gas cylinder regulator pressure. Additionally, it has been shown that while pressure has a slight effect on thermal diffusion factors, temperature plays a larger role.30,31 This lower pressure also allows us to better compare our measured values with values reported in the literature.
After 24 hours of equilibration, a temperature gradient was imposed on the system by raising the temperature at one end and lowering it at the other by an equal amount. In order to better capture the thermal separation, we augmented the temperature gradient to 27 K across the system to provide better resolution during the subsequent gas sampling and GC analysis. For higher median temperature experiments, we were limited by the upper temperature safety limit set by safety regulations. For lower median temperature experiments, we were limited to ambient temperature, because we did not have ice baths to further reduce the temperature. This temperature gradient was then maintained for five days, after which the samples were taken for measurement. The equilibration time was determined through trial-and-error experiments and simulations using COMSOL Multiphysics® version 6.2. During gas sampling, the two cylinders were isolated and then each cylinder was evacuated into a Mylar sample bag. Once the pressure reading for each cylinder reached atmospheric pressure (0 psig), the Mylar bags were sealed and removed from the cylinders. The H2 mole fraction from each sample was measured immediately using an Agilent GC6890 gas chromatograph. After measuring the H2 mole fractions from both ends, the thermal diffusion factor was calculated using eqn (11) and (12).
2.4. COMSOL model
The experimental setup was replicated in COMSOL Multiphysics® version 6.2. The dimensions of the cylinders and stainless steel tubing were replicated to be as close as possible to those of the physical experimental setup. Fig. 3 shows the experimental setup in COMSOL.Thermal diffusion was simulated using Fick's model within the Transport of Concentrated Species (TCS) physics module. The basic equation for an individual species i is expressed as:
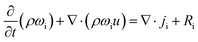 | (15) |
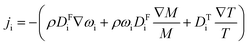 | (16) |
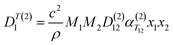 | (17) |
The experimental setup was constructed using a physics-controlled meshing sequence, which examines the physics of the process in question to determine automatically the size attributes and sequences operations needed to create a mesh adapted to the problem. The granularity of the mesh can be set by the user. A sweep of the mesh resolution indicated that the extremely fine mesh could be solved in a reasonable amount of time. Finer meshes did not change the model solution. A sweep of time steps showed that smaller time steps did not yield more accurate results compared to the default time step of 1 hour on the extremely fine mesh. The valves in the actual experimental setup were replaced with stainless steel tubing of equivalent volume. The model parameters for the simulations are summarized in Table 2.
| General | |
|---|---|
| Element size | Extremely fine |
| Timestep (hr) | 1 |
| Initial density (kg m−3) | p, T dependent |
| Sample cylinder | |
|---|---|
| Radius (in.) | 0.56 |
| Length (in.) | 3.38 |
| Endpoint radius (in.) | 0.083 |
| Endpoint length (in.) | 0.5 |
| Tubing | |
|---|---|
| Radius (in.) | 0.0345 |
| Length (in.) | 17.74 |
The simulation followed the same procedure as the physical experiments. The gas mixture was first initialized at constant temperature and pressure throughout the entire model for 24 hours. Then, a temperature gradient was imposed along the model, and the simulation was run for an additional 120 hours. At the end of the simulation period, the mole fractions of gas at both ends of the bulbs were read to calculate the thermal diffusion factor using eqn (11) and (12) to ensure consistency with the experimental measurements.
3. Results & discussion
3.1. Process validation
To verify that the obtained measurements could be used to evaluate binary gas thermal diffusion coefficients, a verification study was performed using Mixture 1 from Table 1. Fig. 4 shows the H2 mole fractions measured by GC after the test. The concentration of H2 is greatest on the warmer side of the apparatus. The error bars show the standard deviation between the multiple measurements taken for each experiment (minimum of five). | ||
| Fig. 4 Measurements of H2 mole fraction for the thermal diffusion tests using Mixture 1 (20% H2–80% N2). | ||
The measured H2 mole fractions were validated against the COMSOL simulation performed on the same mixture ratio under the same test conditions. Fig. 5 shows the H2 mole fraction at selected time steps in the COMSOL simulation. The experimental measurements are shown at the end points of the system. The slight deviations are attributed to a combination of experimental error and some approximations in the diffusion calculations within COMSOL.
 | ||
| Fig. 5 H2 mole fractions at selected times from the COMSOL simulation of Mixture 1 (20% H2–80% N2). A steady profile emerges in about 72 h. | ||
The mole fraction values at the end of the simulation agree with the laboratory measurements. The thermal diffusion factors for each experimental run were then calculated and are shown in Fig. 6. The error bars represent the standard deviation in calculations, which are an extension of the standard deviations shown previously in Fig. 4.
 | ||
| Fig. 6 Calculated αT values from experimental measurements for Mixture 1 (20% H2–80% N2). These values are comparable to the literature value of αT ≈ 0.25.34 | ||
From the literature, the thermal diffusion factor for this mixture is αT ≈ 0.25.34 Thus, the experimental measurements help determine the thermal diffusion factor and tune the reference ideal gas enthalpy values.
3.2. H2–CH4 mixtures
After the process verification step with Mixture 1, Mixture 2 was subjected to the same experimental procedure. For further verification, the calculated αT values were compared with values reported by Drickamer et al.35 for the same gas mixture at different median temperature values. The results are shown in Fig. 7. | ||
| Fig. 7 Comparison of the measured αT values from this work with values reported in ref. 35 using Mixture 2 (50% H2–50% CH4). The average temperature difference across the experiments was 27 K and pressure was constant at P = 160 psig for our measured data points. | ||
The measured data points for Mixture 2 are in good agreement with the values reported by Drickamer et al.35 In the context of UHS, reservoir temperatures are not extremely high, and the issue of composition becomes more prevalent. The following subsections examine first the effects of varying the gas composition at fixed temperature and pressure, and then the effects of varying temperature at a fixed composition and pressure.
Using the experimental results for compositional variation, our model was tuned by adjusting the reference ideal gas enthalpy (Higi,ref). Following the convention by Pedersen and Lindeloff,23 CH4 was maintained as the reference component, and the Higi,ref value for H2 was adjusted accordingly. Fig. 9 shows the comparison of calculated thermal diffusion factors with and without adjusting 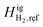 .
.
With CH4 as the reference component, a negative 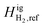 value (−0.5 kJ mol−1) is required to match the experimental observations. While computationally feasible, this is not a physically intuitive value. We propose setting H2 as the reference component so that
value (−0.5 kJ mol−1) is required to match the experimental observations. While computationally feasible, this is not a physically intuitive value. We propose setting H2 as the reference component so that 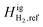 can be set at 0 kJ mol−1. In doing so, we adjust
can be set at 0 kJ mol−1. In doing so, we adjust 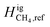 to match the experimental results. Fig. 10 shows the adjustments required to match our model with the experimental results.
to match the experimental results. Fig. 10 shows the adjustments required to match our model with the experimental results.
Using a positive and larger  value of 3.5 kJ mol−1 still allows us to match our model with the experimental results. The larger value could be due to CH4 having a greater mass than H2. Regardless of which component is used as the reference component, it is clear from the simulations that including accurate ideal gas reference enthalpy values is important for calculating component segregation under the influence of temperature.
value of 3.5 kJ mol−1 still allows us to match our model with the experimental results. The larger value could be due to CH4 having a greater mass than H2. Regardless of which component is used as the reference component, it is clear from the simulations that including accurate ideal gas reference enthalpy values is important for calculating component segregation under the influence of temperature.
Further validation was performed by inputting the calculated experimental thermal diffusion factors into the COMSOL simulation to see if the results agreed. Although the COMSOL simulation requires a specified thermal diffusion factor, this additional validation step adds confidence to the results due to the physical sophistication of the COMSOL module. Fig. 11 shows the comparison of the thermal diffusion factor values from the simulation, experimental measurements, and the model calculations.
 | ||
| Fig. 11 Comparison of the calculated thermal diffusion factor from the COMSOL simulations with experimental and simulated values using Mixtures 2, 3 and 4. | ||
The strong agreement between the thermal diffusion factor calculated from the COMSOL simulations and our experimental measurements demonstrates the feasibility of the workflow as well as the importance of including the reference ideal gas enthalpy values in our models. The importance of the reference ideal gas enthalpy in the context of underground hydrogen storage is discussed later.
We then performed individual tuning for each data point to achieve a good match between the simulation and the reported experimental value at the specified temperature. From this exercise, we observed a linear relationship between the reference ideal gas enthalpy and the median temperature of the experiment, as seen in Fig. 12.
Because we calculated the ideal gas portion of the enthalpy with a reference state, we must establish the reference ideal gas enthalpy carefully. So, we propose a correlation between the reference ideal gas enthalpy of CH4 and the deviation between the median temperature, Tm, and the reference state temperature, Tref, as seen in Fig. 13.
 | ||
| Fig. 13 Reference ideal gas enthalpy for CH4 as a function of the deviation from the reference state temperature (Tm–Tref). | ||
Using this linear relationship to express  , we re-computed the thermal diffusion factors and found good agreement between our calculations and the reported measurements, as seen in Fig. 14.
, we re-computed the thermal diffusion factors and found good agreement between our calculations and the reported measurements, as seen in Fig. 14.
 | ||
Fig. 14 Comparison of our calculated thermal diffusion factors with experimental values using 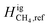 in Fig. 13. in Fig. 13. | ||
Previous studies examining the relationship between temperature and the thermal diffusion factor show that more complex models, such as the Lennard-Jones model, must be employed in order to match experimental results.30,36–38 The thermal diffusion factors for several different gases were calculated using other measurable values, such as viscosity.38,39 Some differences between experimental observations and kinetic theory remain. Mathur and Watson14 presented a semi-theoretical expression for relating the thermal diffusion factor of a H2–He mixture using the Kihara first approximation.40 All of these approximations require utilizing the Lennard-Jones model, which then necessitates more detailed calculations. Future work involves expanding the model to incorporate these molecular interactions and account for physical properties such as the hardness of gas molecules.
3.3. Implications on underground hydrogen storage
| Depth, m | 1005.8 |
| Formation thickness, m | 365.8 |
| Temperature gradient, K m−1 | 0.023 |
| Reference pressure, bar | 120 |
| Reference temperature, K | 320.43 |
| Reference composition, mol% | 30% H2, 70% CH4 |
The equilibrium calculations were performed following the procedure by Pedersen and Lindeloff,23 where the reference ideal gas enthalpy of CH4 is set to 0 J mol−1 and all other components are scaled accordingly. In our previous work, reference ideal gas enthalpy values for both CH4 and H2 were set to 0 kJ mol−1. The reference state temperature that was used for enthalpy calculations was also set to 273.15 K. As previously stated, we now set our reference state temperature to 298.15 K for all equilibrium calculations. By including the tuned reference ideal gas enthalpy value for CH4, and setting 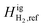 to 0 J mol−1, we observe the change in H2 distribution along the reservoir. Fig. 15 shows a comparison of the Delta salt cavern case study with and without the effects of temperature and the tuned reference ideal gas enthalpy.
to 0 J mol−1, we observe the change in H2 distribution along the reservoir. Fig. 15 shows a comparison of the Delta salt cavern case study with and without the effects of temperature and the tuned reference ideal gas enthalpy.
 | ||
| Fig. 15 Comparison of H2 grading when considering the effects of gravity, temperature, and reference ideal gas enthalpy. | ||
Using a tuned reference ideal gas enthalpy, the H2 distribution lies between the isothermal case and the case without tuned enthalpy values. Similar to the isothermal case, more H2 is expected to settle at the top of the reservoir, but in smaller quantity. This indicates that thermal effects counter the effects of gravity, but not to the extent previously thought. It should be noted that for all cases we see nearly uniform distribution along the storage reservoir.
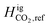 , and the effects on UHS for the same technical specifications as the Delta, Utah case (see Table 3) when using CO2 as the cushion gas.
, and the effects on UHS for the same technical specifications as the Delta, Utah case (see Table 3) when using CO2 as the cushion gas.
 | ||
Fig. 16 (Left): The results of matching  with experimental measurements from Mixture 5 (50% H2–50% CO2) and values obtained from the literature30,31 and (right): the effects of the tuned with experimental measurements from Mixture 5 (50% H2–50% CO2) and values obtained from the literature30,31 and (right): the effects of the tuned 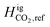 on UHS with CO2 as a cushion gas using the composition ratio specified in Table 3. on UHS with CO2 as a cushion gas using the composition ratio specified in Table 3. | ||
As with the H2–CH4 case, implementing the reference ideal gas enthalpy shows more H2 settling at the top of the storage reservoir. The thermal effects still counteract the effects of gravity, but not as much as in the H2–CH4 case. Compared to the CH4 system, including a non-zero value for 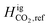 does not lead to a big change in H2 composition distribution. It should be noted, however, that the properties of CO2 vary more significantly with pressure than those of other gases. Becker31 showed an increase in αT values as the pressure increased, suggesting that there could be more component segregation than what is computed here. Additional experiments can be performed to study the thermal diffusion between H2 and CO2 at elevated pressures and varying compositions to obtain more data pertinent to UHS conditions.
does not lead to a big change in H2 composition distribution. It should be noted, however, that the properties of CO2 vary more significantly with pressure than those of other gases. Becker31 showed an increase in αT values as the pressure increased, suggesting that there could be more component segregation than what is computed here. Additional experiments can be performed to study the thermal diffusion between H2 and CO2 at elevated pressures and varying compositions to obtain more data pertinent to UHS conditions.
4. Summary and conclusions
Thermal diffusion measurements were performed for various hydrogen–methane mixtures to measure the thermal diffusion factor (αT), a critical input to understand the compositional grading of H2. A two-bulb experimental setup was introduced, and the process was verified using COMSOL Multiphysics' Transport of Concentrated Species Module. The thermal diffusion factor was used to determine the reference ideal gas enthalpy and thereby reduce a key source of uncertainty in the compositional grading calculations. During this investigation, we propose setting H2 as the reference component (a reference ideal gas enthalpy value of 0 J mol−1), and tuning the reference ideal gas enthalpy of CH4, so that no negative values appear. The effect of temperature on the thermal diffusion factor was also studied, and a temperature-dependent reference ideal gas enthalpy correlation was proposed for the H2–C4 mixture. This correlation provides an approximation that mimics the relationship governed by more sophisticated thermal diffusion models that account for molecular collisions and hardness.The effect of using CO2 as the cushion gas was also briefly examined, with new measurements reported for 50% H2 and 50% CO2 mixtures at temperatures relevant to UHS. The results show that significant mixing also occurs between these two gases during storage, and that pressure will play a larger role when considering CO2 as the cushion gas due to its unique fluid properties. Further experiments at elevated pressures could help determine the true extent of H2–CO2 segregation during UHS operations.
For both CH4 and CO2 as cushion gases, we show that under the effect of only gravity, there is little variation in hydrogen composition along the length of the storage reservoir. When accurate thermal effects such as the reference ideal gas enthalpy are included in the steady-state model, this variation further decreases, leading to an even more homogeneous mixture of H2 and its cushion gas. Further work is suggested to investigate the effects of temperature, storage time and cycling to determine the extent of H2 loss during storage, as well as the expected purity when produced back to the surface.
Author contributions
J. D. Zhou: writing – original draft, writing – review & editing, methodology, investigation, formal analysis. K. Jessen: writing – review & editing, methodology. A. R. Kovscek: writing – review & editing, project administration, funding acquisition, conceptualization.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Abbreviations
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) i
i
| Fugacity coefficient of component i |
| Z | Compressibility factor |
| µ i | Chemical potential of component i |
| F Gi | Gravitational forces acting on component i |
| F Ti | Thermal forces acting on component i |
| g | Gravitational constant |
| R | Universal gas constant |
| x i | Mole fraction of component i |
| M i | Molecular mass of component i |
| M m | Molecular mass of mixture m |
| P ci | Critical pressure of component i |
| T ci | Critical pressure of component i |
| a | Parameter of the cubic equation of state |
| b | Parameter of the cubic equation of state |
| A* | Function of a with respect to temperature and pressure |
| B* | Function of b with respect to temperature and pressure |
| k ij | Function of b with respect to temperature and pressure |
| C igp | Ideal gas heat capacity |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) i
i
| Partial molar enthalpy of component i |
| H m | Molar enthalpy of mixture m |
| ρ | Density |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i
i
| Partial molar volume of component i |
| H igi | Partial ideal gas enthalpy of component i |
| H ig i,ref | Reference ideal gas enthalpy of component i |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) resi
resi
| Residual partial molar enthalpy of component i |
| C igp | Ideal heat capacity |
| D T(2)1 | Binary thermal diffusion coefficient |
| c | Molar concentration |
| D (2)12 | Binary mass diffusion coefficient |
| q | Thermal separation term |
| ω i | Species i |
Data availability
The data supporting this article have been included as part of the appendix. More detailed information on the code is available upon request.Supplementary information is available. See DOI: https://doi.org/10.1039/d5se01192b.
A. Appendix
A.1. EOS validation
To validate our model code, we compared the thermodynamic properties calculated for pure H2, pure CH4, and a 50–50 mixture of H2 and CH4 with values reported in the literature.45,46Fig. 17 and 18 show the comparison of the calculated gas heat capacity values and the density values, respectively, with values obtained from the literature. Pressure was maintained at P = 160 psi for all calculations. | ||
| Fig. 17 Comparison of gas heat capacity values for pure H2, pure CH4, and H2–CH4 mixture from our EOS calculations and data obtained from the literature.45,46 | ||
 | ||
| Fig. 18 Comparison of density values for pure H2, pure CH4, and H2–CH4 mixture from our EOS calculations and data obtained from the literature.45,46 | ||
For the gas heat capacity, we note the deviation from literature values at lower temperatures. In the context of underground hydrogen storage, however, we see good agreement between our calculated values and literature values at temperatures of 330 K and greater. The calculated mixture density is slightly different from the reported mixture density reported by Hassanpouryouzband et al.46
The enthalpy values for the pure components as well as the mixture were checked with calculations from the literature. To properly compare the values, we follow the convention of the GERG-2008 equation of state, that sets the reference temperature and pressure at 298.15 K and 1 atm.47,48 We set the same reference state in REFPROP when obtaining the enthalpy values for the pure components. Fig. 19 shows the comparison of the calculated enthalpy values with the values obtained from the literature.
 | ||
| Fig. 19 Comparison of enthalpy values for pure H2, pure CH4, and H2–CH4 from our EOS calculations and data obtained from the literature.45,46 | ||
The fugacity coefficients for pure components were calculated and compared with the volumetric data obtained from REFPROP.45 From a volume-explicit EOS, the fugacity coefficient is calculated as
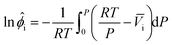 | (A.1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) i is a function of pressure. For a pure gas, eqn (A.1) simplifies to:
i is a function of pressure. For a pure gas, eqn (A.1) simplifies to: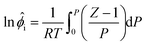 | (A.2) |
Using the calculated Z values, we then calculate and compare our fugacity coefficient values with those obtained from REFPROP. Fig. 22 and 23 show the comparison of the calculated fugacity coefficients from our model with those obtained from REFPROP, and the relative errors, respectively.
 | ||
| Fig. 22 Comparison of our calculated fugacity coefficient values with fugacity coefficients derived from REFPROP data. | ||
 | ||
| Fig. 23 Relative error between our calculated fugacity coefficient values and fugacity coefficients derived from REFPROP data. | ||
Overall, the error between our calculations and the calculations from the REFPROP data is small. To ensure that our enthalpy calculation is accurate, we then evaluate the gradients of Fig. 22 to compute ∂ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) i/∂T, which is needed to calculate the residual molar enthalpy (see eqn (5)). Fig. 24 and 25 show the comparison between the calculated gradient and the gradient calculated from REFPROP, and the absolute errors, respectively.
i/∂T, which is needed to calculate the residual molar enthalpy (see eqn (5)). Fig. 24 and 25 show the comparison between the calculated gradient and the gradient calculated from REFPROP, and the absolute errors, respectively.
 | ||
| Fig. 24 Comparison of the derivatives of the log of the fugacity coefficient with respect to temperature between our calculations and values derived from REFPROP data. | ||
 | ||
| Fig. 25 Absolute error between our calculated gradient and the gradient calculated from REFPROP data. | ||
While there is some deviation at lower temperatures (below 300 K), it should be noted that underground hydrogen storage occurs at higher temperatures (320 K and above) where deviations are much smaller. From these results, we can conclude that there are no issues with our calculations of the partial molar enthalpies from an EOS standpoint.
Acknowledgements
JDZ acknowledges an energy fellowship from Chevron, and thanks Ge (Geo) Zhang for helpful technical discussions. Further support for this work was provided by the SUETRI-A Industrial Affiliates Program.References
- N. Heinemann, J. Alcalde, J. M. Miocic, S. J. T. Hangx, J. Kallmeyer and C. Ostertag-Henning, et al., Enabling large-scale hydrogen storage in porous media – the scientific challenges, Energy Environ. Sci., 2021, 14(2), 853–864 RSC.
- D. Zivar, S. Kumar and J. Foroozesh, Underground hydrogen storage: A comprehensive review, Int. J. Hydrogen Energy, 2021, 46(45), 23436–23462 CrossRef.
- Y. Perez-Claro, A. Kholi, T. W. Kim and A. R. Kovscek, Where is Electricity Curtailment Happening in California? Opportunities for Underground Energy Storage, SPE Western Regional Meeting, 2025 Search PubMed.
- E. R. Okoroafor, N. Nazari, T. W. Kim, H. W. Watkins, S. D. Saltzer and A. R. Kovscek, Assessment of hydrogen storage potential in depleted gas fields and power-to-hydrogen conversion efficiency: A northern California case study, Int. J. Hydrogen Energy, 2024, 71, 982–998 CrossRef.
- M. Kanaani, B. Sedaee and M. Asadian-Pakfar, Role of Cushion Gas on Underground Hydrogen Storage in Depleted Oil Reservoirs, J. Energy Storage, 2022, 45, 103783 CrossRef.
- S. Mao, B. Chen, M. Morales, M. Malki and M. Mehana, Cushion gas effects on hydrogen storage in porous rocks: Insights from reservoir simulation and deep learning, Int. J. Hydrogen Energy, 2024, 68, 1033–1047 CrossRef.
- Q. Zhao, Y. Wang and C. Chen, Numerical simulation of the impact of different cushion gases on underground hydrogen storage in aquifers based on an experimentally-benchmarked equation-of-state, Int. J. Hydrogen Energy, 2024, 50, 495–511 CrossRef.
- J. D. Zhou, K. Jessen and A. R. Kovscek, The role of gravity and temperature on hydrogen-containing mixtures in the subsurface, J. Energy Storage, 2024, 85, 111025 CrossRef.
- S. Srinivasan and M. Z. Saghir, Thermodiffusion in Multicomponent Mixtures: Thermodynamic, Algebraic, and Neuro-Computing Models, Springer, New York, 2013 Search PubMed.
- S. Ludwig, Sitzungsber. Preuss. Akad. Wiss., Phys.-Math. Kl., 1856, 20, 539 Search PubMed.
- C. Soret, On the state of equilibrium that a primitively homogeneous saline solution takes from the point of view of its concentration, two parts of which are brought to temperatures édiffénts, Arch. Sci. Phys. Nat., 1879, 2, 48 Search PubMed.
- A. Vinhal, J. Azeem and K. Pedersen, Modeling of Compositional Grading in Heavy Oil Fields, SPE Annual Technical Conference and Exhibition, 2021 Search PubMed.
- A. Leahy-Dios, L. Zhuo and A. Firoozabadi, New Thermal Diffusion Coefficient Measurements for Hydrocarbon Binary Mixtures: Viscsotiy and Composition Dependency, J. Phys. Chem. B, 2008, 112, 6442–6447 CrossRef CAS PubMed.
- B. P. Mathur and W. W. Watson, Composition and Temperature Dependence of the Thermal Diffusion Factor in H2-He Gas Mixtures, J. Chem. Phys., 1968, 49, 5537–5541 CrossRef CAS.
- W. M. Rutherford and J. G. Roof, Thermal Diffusion in Methane-n-Butane Mixtures in the Critical Region, J. Phys. Chem., 1959, 63(9), 1506–1511 CrossRef CAS.
- I. I. Rhyzhkov and I. V. Stepanova, On thermal diffusion separation in binary mixtures with variable transport coefficients, Int. J. Heat Mass Tran., 2015, 86, 268–276 CrossRef.
- L. J. T. M. Kempers, A comprehensive thermodynamic theory of the soret effect in a multicomponent gas, liquid, or solid, J. Chem. Phys., 2001, 115, 6330–6341 CrossRef CAS.
- R. Haase, Thermodynamics of Irreversible Processes. Addison-Wesley, 1969 Search PubMed.
- L. Høier and C. H. Whitson, Compositional Grading—Theory and Practice, SPE Reservoir Eval. Eng., 2001, 4(6), 525–535 CrossRef.
- D. Y. Peng and D. B. Robinson, A New Two-Constant Equation of State, Ind. Eng. Chem. Fundam., 1976, 15(1), 59–64 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The Properties of Gases and Liquids, McGraw-Hill, 5th edn, 2001 Search PubMed.
- J. W. Qian, J. N. Jaubert and R. Privat, Phase equilibria in hydrogen-containing binary systems modeled with the Peng–Robinson equation of state and temperature-dependent binary interaction parameters calculated through a group-contribution method, J. Supercrit. Fluids, 2013, 75, 58–71 CrossRef CAS.
- K. S. Pedersen and N. Lindeloff, Simulations of Compositional Gradients in Hydrocarbon Reservoirs Under the Influence of a Temperature Gradient, SPE Annual Technical Conference and Exhibition, 2003 Search PubMed.
- K. S. Pedersen and H. P. Hjermstad, Modeling of Compositional Variation with Depth for Five North Sea Reservoirs, SPE Annual Technical Conference and Exhibition, 2015 Search PubMed.
- K. S. Pedersen and H. P. Hjermstad, Modeling of Large Hydrocarbon Compositional Gradient, Abu Dhabi International Petroleum Exhibition and Conference, 2006 Search PubMed.
- P. J. Dunlop, H. L. Robjohns and C. M. Bignell, Diffusion and thermal diffusion in binary mixtures of hydrogen with noble gases, J. Chem. Phys., 1987, 86(5), 2922–2926 CrossRef CAS.
- R. D. Trengrove, K. R. Harris, J. L. Robjohns and P. J. Dunlop, Diffusion and Thermal Diffusion in Some Dilute Binary Gaseous Systems Between 195 and 400 K: Tests of Several Asymmetric Potentials Using Inifinite Order Sudden Approximation, Physica A, 1985, 131(3), 506–519 CrossRef.
- M. Leuenberger and C. Lang, Thermal diffusion: An important aspect in studies of static air columns such as firn air, sand dunes and soil air, 2002 Search PubMed.
- S. K. Deb and A. K. Barua, Thermal diffusion in ternary gas mixtures, Physica, 1967, 34(3), 438–444 CrossRef CAS.
- K. E. Grew and T. L. Ibbs, Thermal Diffusion in Gases, Cambridge University Press, 1952 Search PubMed.
- V. E. W. Becker, Die thermische Entmischung von Gasen bei hohem Druck, Z Naturforschg, 1950, vol. 5a Search PubMed.
- E. R. Okoroafor, L. Sampaio, F. Gasanzade, C. Y. Perez, J. D. Zhou and S. D. Saltzer, et al., Intercomparison of numerical simulation models for hydrogen storage in porous media using different codes, Energy Convers. Manage., 2023, 292, 117409 CrossRef.
- N. Kobayashi and I. Yamamoto, Thermal Diffusion Coefficient in Multi-component Mixture Expressed in Terms of Binary Thermal Diffusion Factors and Binary Diffusion Coefficients, J. Nucl. Sci. Technol., 1995, 32(12), 1236–1242 CrossRef CAS.
- K. Hirota and K. Sasaki, Thermal Diffusion Factor of Hydrogen-Nitrogen Mixture, Bull. Chem. Soc. Jpn., 1954, 27, 27–29 CrossRef CAS.
- H. G. Drickamer, S. L. Downey and N. C. Pierce, Thermal Diffusion in Hydrogen-Hydrocarbon Mixtures, J. Chem. Phys., 1949, 17, 408–410 CrossRef CAS.
- J. E. Lennard-Jones, Cohesion, Proc. Phys. Soc., 1931, 43, 461–482 CrossRef CAS.
- S. Chapman, The characteristics of thermal diffusion, Proc. R. Soc. A., 1940, 177, 38–62 CAS.
- S. C. Saxena, J. G. Kelley and W. W. Watson, Temperature Dependence of the Thermal Diffusion Factor for Helium, Neon, and Argon, Phys. Fluid., 1961, 4(10), 1216–1225 CrossRef CAS.
- J. O. Hirschfelder, R. B. Bird and E. L. Spotz, The Transport Properties for Non-Polar Gases, J. Chem. Phys., 1948, 16, 968–981 CrossRef CAS.
- T. Kihara, Virial Coefficients and Models of Molecules in Gases, Rev. Mod. Phys., 1953, 25, 831–843 CrossRef CAS.
- Utah Division of Oil G, Mining; 2021. Available from: http://ogm.utah.god.
- N. S. Muhammed, B. Haq and D. Al Shehri, CO2 rich cushion gas for hydrogen storage in depleted gas reservoirs: Insight on contact angle and surface tension, Int. J. Hydrogen Energy, 2024, 50, 1281–1301 CrossRef CAS.
- P. Deng, H. Ma, J. Song, X. Peng, S. Zhu and D. Xue, et al., Carbon dioxide as cushion gas for large-scale underground hydrogen storage: Mechanisms and implications, Appl. Energy, 2025, 388, 125622 CrossRef CAS.
- Z. Wang, L. Zhang, W. Lu, H. Guo and Y. Wang, Soret effect on the mixing of H2 and CO2 cushion gas: Implication for underground hydrogen storage, Int. J. Hydrogen Energy, 2024, 83, 1331–1337 CrossRef CAS.
- E. W. Lemmon, I. H. Bell, M. L. Huber and M. O. McLinden, NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology, 2018, available from: https://www.nist.gov/srd/refprop Search PubMed.
- A. Hassanpouryouzband, E. Joonaki, K. Edlmann, N. Heinemann and J. Yang, Thermodynamic and transport properties of hydrogen containing streams, Sci. Data, 2020, 7(1), 222 CrossRef CAS.
- O. Kunz and W. Wagner, The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004, J. Chem. Eng. Data, 2012, 57(11), 3032–3091 CrossRef CAS.
- O. Kunz, R. Klimeck, W. Wagner and M. Jaeschke, The GERG-2004 Wide-Range Equation of State for Natural Gases and Other Mixtures, Verlag des Vereins Deutscher Ingenieure, 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |