Optical spectroscopic determination of photoexcited small-polaron hopping in transition metal oxide photocatalysts

Abstract

Ultrafast small-polaron formation profoundly shapes the electronic and catalytic behaviour of transition metal oxides (TMOs). Despite its significance, spectroscopic investigations of photoexcited polaron hopping in TMOs have been scarcely explored. Here, we present the first optical spectroscopic observation of photoexcited small-polaron hopping across the first-row TMOs, using femtosecond transient absorption spectroscopy. This polaronic feature rises within 500 fs as Drude-type absorption converts to localized, polaronic absorption. Fitting with a small-polaron optical conductivity model yields polaron relaxation energies of 400–650 meV, evidencing substantial energy loss upon self-trapping. Kinetic analysis shows that oxides with open d-shells localize charge most readily: polaron formation activation barriers are low in all TMOs (0–10 meV), whereas hopping barriers remain much higher (200–350 meV). This work establishes key spectroscopic and kinetic insights, highlighting the trade-off between charge localization and mobility, as well as the critical role of polaron formation in TMOs photocatalysts.

---

Introduction

Polaron formation has been widely reported in transition metal oxides (TMOs).^1,2 The significance of polaronic interactions between charge carriers and the lattice has been demonstrated in the electronic,³ magnetic,⁴ and optical^5,6 properties of many TMOs. Polarons are generally classified into large polarons and small polarons, which differ primarily in the strength of the electron–lattice interaction.⁷ For small polarons, the focus of this study, the electron–lattice interaction limits the spatial extent of the polaron distortion to around a lattice constant, and the electrons (or holes) are strongly localized. The localized polaronic charge carriers migrate via hopping, producing a characteristic optical absorption profile that can be well-captured by a theoretical conductivity model derived from the polaron-hopping transport mechanism first proposed by Eagles,⁸ Reik⁹ and later by Bogomolov¹⁰ and Emin.⁶ This small polaron optical conductivity model has been experimentally validated in a range of TMOs^10–15 using steady-state absorption spectroscopy, since polaron optical conductivity is proportional to the small-polaron hopping-induced optical absorption.^9,10,15 This model has more recently been used to describe polaron absorption in superconductors¹⁶ and nonlinear optical crystals.¹⁷ However, application of this small polaron optical conductivity model to photoexcited polarons has been very limited to date, despite the critical role of polaronic semiconductors in solar energy harvesting.

Photoexcited small-polaron hopping-induced absorption (polaron hopping absorption) originates from a light-assisted polaronic electron transfer that occurs following polaron formation. To date, studies of polaron hopping absorption in the literature have primarily focused on polarons in the ground state of chemically doped metal oxides, without involving photoexcitation.¹⁸ To the best of our knowledge, aside from NiO and TiO₂, ground-state polaron-hopping absorption spectra remain unreported for the other five TMOs studied here (BiVO₄, Cr₂O₃, Mn₂O₃, Fe₂O₃, and CuO). Photoexcited polaron hopping absorption spectra have not been demonstrated or analysed for any of the seven TMOs investigated here, including NiO and TiO₂. In the study reported herein, we make the first optical spectroscopic assignment of photoexcited small-polaron hopping for a range of TMOs with different d-shell occupancies, and show these spectra can all be fit remarkably well by the small polaron optical conductivity model. This enables the determination of key descriptors of small polarons across these oxides, including the polaron relaxation energy, phonon frequency and polaron hopping activation energy.

Recently, transient spectroscopies, particularly employing extreme ultraviolet (XUV) and X-ray detection, have been used to evaluated the polaron formation kinetics in typically ranging from tens to hundreds of femtoseconds (fs) in a range of TMOs,^19–32 especially on two TMOs widely employed in PEC devices: TiO₂ ^{21,22,25,29,30} and Fe₂O₃.^{19,20,23,24,28,32} However, a central debate persists regarding whether polaron formation involves an activation barrier: ab initio calculations by Yuan et al. report activation energies as high as 400 meV in oxides,^34,35 while Harris and Yang argue that nuclear tunnelling eliminates any such barrier, making the process effectively barrierless.^36,37 Our study leverages the evolution of the small polaron hopping absorption to directly monitor polaron formation, as photoexcited carriers transition from Drude-like, delocalized absorption to the characteristic localized polaron absorption. Moreover, by conducting temperature-dependent kinetic measurements, we can quantify the polaron formation activation energy, as well as correlate it with the d-shell electron occupation, thereby revealing the propensity for photoexcited charge (de)localization across the first-row TMOs.

Photoexcited small polaron formation in TMOs has significant implications for the photocatalytic (PC) and photoelectrochemical (PEC) function of these photocatalysts. For example, almost all analyses of the energetics of electrons and holes in TMOs to drive surface PC/PEC reactions employ conduction/valence band edge (CBM and VBM) energies, without consideration of the energetic loss resulting from polaronic relaxation.^38,39 Moreover, we have recently proposed that ultrafast polaron formation may be a key driver of charge separation in open d-shell TMOs, mitigating ultrafast band-to-band recombination.⁴⁰ Given the increasing interest in a broad range of TMOs for PC/PEC devices, it is critical to establish the generality of polaron formation and quantify the energetic loss associated with their formation across TMOs,^32,39,40 and thus their impact on PC/PEC solar energy conversion efficiencies.

In this work, we employ femtosecond transient absorption spectroscopy (fs-TAS) to explore photoexcited small polaron formation in seven first-row TMOs (d₀–d₉). In the TMOs studied, we observe an ultrafast evolution of the photoinduced transient absorption from the Drude absorption of initially generated free charges to the small polaron hopping absorption of localized small polarons. Formation of localized charges is further confirmed by the observation of Jahn–Teller splitting of transient optical absorption in Fe₂O₃. Fitting of the photoexcited polaron hopping absorption to the small polaron optical conductivity model allows determination of the key polaron parameters for all the TMOs studied. Furthermore by studying the kinetics of polaron formation, we establish the relationship between the degree of charge localization and d-shell filling in these TMOs, with d₀ and near-d₁₀ oxides tending to delocalize charges, whereas those with partially filled d-shells favour charge localization, consistent with theoretical predictions.^32,33 Moreover, temperature dependent kinetic measurements enable us to quantify the energetic barrier of polaron formation, revealing values that are significantly smaller than the thermal energy at room temperature. Through this work, we highlight the dynamical and energetic significance of understanding the delocalized-to-localized electronic transition in polaronic TMOs for advancing photocatalytic applications.

Results and discussion

In this study, we focused on ultrafast transient absorption (fs-TAS) studies of thin, dense films of seven first-row TMOs with differing d-shell occupancies: d₀_BiVO₄, d₀_TiO₂, d₃_Cr₂O₃, d₄_Mn₂O₃, d₅_Fe₂O₃, d₈_NiO and d₉_CuO. Synthesis and materials characterisation details can be found in the SI. An ultraviolet pump pulse (3.5–4.1 eV) was used to generate electrons and holes in the CB and VB, respectively, and a NIR probe pulse (0.75–1.4 eV) was used to follow the evolution of the absorption of these photoexcited charges. From the steady-state absorption spectra shown in Fig. S5–S11, it is apparent that no significant ground state absorption exists in the NIR range for the TMOs studied, as such, contributions to the photoinduced transient spectra from ground state bleaching are avoided.

Fig. 1a–d show illustrative transient absorption spectra and corresponding kinetics for two representative TMOs BiVO₄ and NiO. Further fs-TAS data for these two TMOs, and for all the other TMOs studied, can be found in Fig. S12–S20. It is apparent from Fig. 1a and b that we can observe distinctly different transient spectra at early time delays, 100–300 fs, and subsequently > 300 fs. In the early time range of 100–300 fs, the absorption spectra monotonically decrease with energy (rise with wavelength). At longer time delays (> circa 300 fs) the absorption spectra transform into broad absorption peaks centred circa 1 eV. A broadly similar spectral evolution was observed for all the TMOs studied, with the notable exception of Fe₂O₃, as discussed below.

Fig. 1 Photoinduced absorption, kinetics, and schematic description of excited charge carriers. (a and b) Averaged fs-TAS spectra from specific time windows for d₀_BiVO₄ and d₈_NiO after excitation at 3.5 eV (355 nm, fluence of 2.5 mJ cm⁻²) and 4.1 eV (305 nm, fluence of 2.1 mJ cm⁻²), respectively. The solid orange lines are fits according to Drude model (blue data points) and small polaron optical conductivity model (brown data points) (see eqn (1)). (c and d) Kinetics of free electrons and small polarons determined for these TMOs using global fitting analyses of fs-TAS spectra as a function of time delay, using the fits to the spectra in a and b as initial inputs. (e) Schematic description of small polaron formation when an electron localizes at a cation (blue circles), illustrated for a face-centred cubic lattice (e.g. NiO, blue circles: cations, and red circles: anions). (f) Illustration of the small-polaron hopping model used to fit the polaron hopping absorption, plotting the electronic energy of a small polaron as function of configurational parameter x; ℏω is the absorbed photon energy; E^non_a is the nonadiabatic hopping activation energy; E^adi_a is the adiabatic hopping activation energy.

The early time absorption spectra (100–300 fs) can be fitted well to the Drude model of free carrier absorption, ΔA ∝ E^−α, where A and E denote the absorbance and photon energy, respectively, as illustrated by the orange fit lines in Fig. 1a and b (with fitted scaling exponents: α = 2.14 ± 0.02 for BiVO₄, α = 1.90 ± 0.03 for TiO₂, α = 1.95 ± 0.03 for NiO, and α = 1.96 ± 0.03 for CuO, see also Fig. S21, S22 and S24–S26; Fig. S23 (Cr₂O₃), which exhibits different behaviour, is discussed below). We note that Mn₂O₃ gave a lower α = 0.93 ± 0.02, possibly caused by mixing with localized absorption. Considering the excellent agreement between the Drude model and the early time transient absorption response, we thus conclude that the initially photoexcited charge carriers are delocalized free carriers.

After 300 fs, the transient spectra evolve into broad peaks in the NIR, as exemplified by the features at 1.1 eV and 0.95 eV in BiVO₄ and NiO respectively (see Fig. 1a and b). Similar spectra were observed in TiO₂, Fe₂O₃, Cr₂O₃, Mn₂O₃, and CuO (see Fig. S27–S34). These broad peaks are all centred at ca. 1 eV, with peak widths (full width at half maximum) of ca. 0.6 eV. For all the TMOs studied, this broad absorption peak was found to be well fitted by the small polaron optical conductivity model given by eqn (1):^6,10

where, α(ω) is the optical absorption coefficient as a function of photon frequency (α(ω) is proportional to optical conductivity in the NIR range^9,10,15), E_p is the polaron relaxation energy, ℏω_op is the energy of the lattice optical phonon coupled with the electron, ℏ is the reduced Planck constant and C is a scaling constant (see details in Section S7). Fits of eqn (1) to the experimental spectra are shown as the orange lines in Fig. 1a and b, and in S27–S34. The two fit parameters determined from these spectra, E_p and ℏω_op, are listed in Table 1.

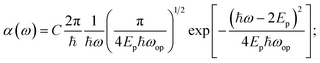Table 1 Fitted parameters from eqn (1)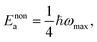, and ref. reported parameters

		Ep (eV)	ℏ op (eV)	E^nona (eV)	Ep (eV)ref^a	ℏωop (eV) ref^b	Ea (eV) ref^c
Note: the literature sources used to compile Metric a are;^10,15,20,28,41–43 for Metric b are;^10,15,27,43,44 and for Metric c are;^2,10,15,45–56 ref. 2 and ref. 10 (TiO2, Ea^adi and Ea^non); ref. 15 (NiO, Ea^non); ref. 45 (Fe2O3, unspecified); ref. 46 (BiVO4, unspecified); ref. 47 (BiVO4, mixed with Ea^adi and Ea^non); ref. 48 (Cr2O3, Ea^adi); ref. 49 (Cr2O3, Ea^non); ref. 50 (Cr2O3, unspecified); ref. 51 (Mn2O3, unspecified); ref. 52 (Fe2O3, Ea^adi); ref. 53–56 (CuO, unspecified), where ‘unspecified refers to reference where the adiabatic/non-adiabatic nature of polaron hopping was not specified); for Metric d is.^44 In ref. 44, a phonon energy of 0.031 eV is suggested. Fitted model parameters are reported as estimate ± standard error.
d0	TiO2	0.42 ± 0.001	0.072 ± 0.003	0.21 ± 0.001	0.40	0.10	0.30; 0.13
d0	BiVO4	0.60 ± 0.001	0.11 ± 0.002	0.30 ± 0.001	0.52	0.102	0.286; 0.268
d3	Cr2O3	0.55 ± 0.003	0.086 ± 0.004	0.28 ± 0.003	—	0.077	0.27–0.32; 0.21–0.30
d4	Mn2O3	0.55 ± 0.001	0.058 ± 0.001	0.28 ± 0.001	—	—	0.30; 0.64
d5	Fe2O3	0.65 ± 0.001	0.033 ± 0.001^d	0.33 ± 0.001	0.48; 0.44	0.082	0.11–0.20
d8	NiO	0.52 ± 0.001	0.084 ± 0.002	0.26 ± 0.001	0.52	0.71–0.80	0.20–0.25
d9	CuO	0.55 ± 0.002	0.097 ± 0.003	0.27 ± 0.002	—	0.077	0.272; 0.13–0.16; 0.22

---

The physical nature of the small polaron optical conductivity model employed in eqn (1) is illustrated in Fig. 1f.² If the lattice of the metal oxide is treated as an array of molecular metal complexes, the nature of small polaron absorption is the photo-assisted electron hopping between two neighbouring ‘molecules’. This hopping process can be pictorially presented by introducing a single configurational coordinate for these two metal centres (see Fig. 1f). The quantity ℏω is the photon energy required to transfer a polaronic electron from one metal centre to the other and is associated with E_p by the relation of 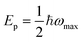(as indicated in eqn (1)). The electronic coupling strength between the two metal centres determines whether the electron hopping mechanism (after polaron formation) is either adiabatic or non-adiabatic, yielding hopping activation energies of E^adi_a or E^non_a respectively. We note in the non-adiabatic limit.²

The broad photoinduced absorption observed at delay time beyond 300 fs is well described by eqn (1), confirming its origin in small-polaron hopping. This interpretation is further supported by its close correspondence to chemically-induced small polaron absorption in doped TiO₂ and NiO.^10,15 Although static small polaron absorption has only been reported for TiO₂ and NiO, for the other oxides studied, indirect evidence from their analogues also supports the polaron absorption spectra we observe. For BiVO₄ and Mn₂O₃, the interpretation is supported by similar polaron bands at ca. 1 eV in V₂O₅ (^47,57, V⁵⁺ as in BiVO₄) and d₃ manganites (⁵⁸, Mn³⁺ as in Mn₂O₃). Likewise, our assignments for Cr₂O₃ and CuO (Fig. S29 and S34) align with previously reported electron-transfer bands at ca. 1 eV,^59–61 considering the electron-transfer nature of polaron hopping absorption. Moreover, the extracted polaron relaxation energies (E_p) and characteristic phonon energies (ℏω_op) agree closely with values from prior chemical-doping or theoretical studies, as demonstrated in Table 1, despite the fundamentally different origin of our photogenerated polarons. With these unambiguous spectroscopic assignments, we can now accurately quantify polaron formation kinetics across the series.

With the assignment of our early time (<300 fs) transient spectra to free charge absorption and later time spectra to polaron hopping absorption, global analyses were performed to estimate the free charge decay and small polaron formation kinetics (see e.g. Fig. 1c and d). For BiVO₄ (Fig. 1c) these analyses yielded a free electron decay half time t_1/2 = 0.5 ps, and polaron rise t_1/2 = 0.31 ps. Similarly for NiO, free charge decay and small polaron formation half-times were t_1/2 = 0.30 ps and t_1/2 = 0.27 ps respectively. These kinetics of free charge decay and polaron formation, on the 200–500 fs timescale, are in the agreement with previous reports on the sub-picosecond kinetics of polaron formation in TMOs.^19,20

To summarize this section, we have assigned the early time (<300 fs) fs-TAS spectra to free charge carriers absorption, and the later time spectra to polaron hopping absorption in BiVO₄, TiO₂, Cr₂O₃, Mn₂O₃, NiO and CuO (we also note the early time spectra for Cr₂O₃ does not fit well to the Drude absorption model, most likely due to electron localization being initiated within our instrument response). Our analysis is based on the clear distinction between the absorption of delocalized free charge carriers versus localizsed small polarons, as previously emphasized by Emin⁶ and Riek.⁶² In particular, we have demonstrated that the later (>300 fs) time delay photoexcited polaron hopping absorption of these TMOs can be well described by the small polaron optical conductivity model. A delocalized-to-localized temporal evolution and the corresponding dynamics were confirmed in metal oxides of BiVO₄, TiO₂, Mn₂O₃, NiO and CuO (see Fig. S20). Key parameters E_p, ℏω_op and E^non_a (listed in Table 1) quantify the physical properties of the photogenerated small polarons. For all the metal oxides, the values of E_p were found to be in the range of 400–650 meV, which indicates a significant energy loss during the delocalized-to-localized transition. In addition, the values of E^non_a determined herein were also found to be generally comparable with reported data, as indicated in Table 1, and indicative of non-adiabatic charge hopping following polaron formation as the dominant mobility mechanism in these TMOs.

Distinct, complementary evidence for ultrafast charge localization in Fe₂O₃ emerges from our fs-TAS data. At 0.4–0.5 ps, Fe₂O₃ displays two absorption bands at 1.03 and 1.24 eV, unlike the single peak seen in other TMOs. Remarkably, these features mirror the 1.03 and 1.31 eV d–d transitions of octahedral [Fe(H₂O)₆]²⁺ complexes (see Fig. 2b), implying that photoexcitation in Fe₂O₃ transiently generates Fe²⁺ sites by polaronic electron localization. We therefore assign the split peaks to internal d–d transitions of photogenerated Fe²⁺, dynamically stabilized by a Jahn–Teller distortion.^63,64 This agreement confirms the ultrafast formation of small electron polarons in Fe₂O₃. Early-time (100–300 fs) spectra deviate from Drude-like behaviour (see Fig. 2a), indicating that electron localization is triggered within our ∼100 fs instrument response.^65,66 Beyond 0.65 ps, a single band at 1.24 eV (see Fig. 2a and S16b) emerges, identical to the Fe³⁺ → Fe²⁺ intervalence transition in Fe-doped sapphires,^67,68 and is thus assigned to polaron hopping absorption. Small polaron optical conductivity model fitting (eqn (1)) yields a relaxation energy, E_p = 0.62 eV, and a non-adiabatic hopping barrier, E_a = 0.31 eV (Table 1), in excellent agreement with ab initio hopping calculations (∼0.34 eV).⁵² The fitted phonon energy of 33 meV differs from the ∼80 meV value generally reported in the literature. Recently, Knowles et al. showed that two phonon modes, at 31 and 81 meV, are involved in small polaron formation in Fe₂O₃, arising from an electron localized on two adjacent Fe atoms and associated with two types of lattice distortion. Our phonon energy of 33 meV agrees very well with the lower mode identified by Knowles et al., suggesting that polaron hopping in Fe₂O₃ is dominated by this lower-mode channel for t > 0.65 ps.⁴⁴

Fig. 2 Optical absorption, kinetics, and theoretical calculations of electron polarons in Fe₂O₃. (a) Representative fs-TAS spectra of d₅_Fe₂O₃ averaged over three time-delay windows. (b) Ground state NIR absorption spectrum of a saturated aqueous FeCl₂ solution. (c) (I). DFT calculations of the pristine crystal structure (top left) of Fe₂O₃ with an electron delocalized in its supercell (bottom left); an electron localized in the Fe₂O₃ supercell to simulate small polaron formation by (II): bond distortion method (middle), and (III): ShakeNBreak distortion method (right). (d) Global fitting of the fs-TAS spectra for d₅_Fe₂O₃ using the three representative spectra in a, labelled as states 1, 2 and 3 based on their sequential time evolution order. The kinetic traces (light blue lines) of states 2 and 3 were fitted with a single exponential model.

To validate our assignment of the 1.24 eV feature to small-polaron hopping in Fe₂O₃, we performed spin-polarized DFT + U simulations (see Section S5 and Table S2). In our calculations, the polaron was modelled as a single-particle excess charge, consistent with the formation of locally excess Fe²⁺ sites upon polaronic electron localization. Excitation-energy-dependent measurements on Fe₂O₃ further indicate that polaron hopping absorption and E_p are independent of the initial electronic state of the hot electrons (see Fig. S31b), thereby supporting the relaxed-state model employed here. Fig. 2c (I) shows the pristine Fe₂O₃ lattice with an extra electron (top left) and the corresponding FeO₆ octahedron (bottom left). Upon polaron formation, localizing the excess electron on one Fe site, both the bond distortion and ShakeNBreak methods yield very similar local structures (Fig. 2c II and III, center) and electron-density maps (right). Crucially, both approaches predict comparable polaron relaxation energies (E_p = 0.64 eV for bond distortion and 0.68 eV for ShakeNBreak), in excellent agreement with our experimental absorption peak at 1.24 eV (where 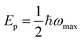), thereby confirming the small polaron origin of this spectral feature.

Comparison of the excited-state kinetics across the full d₀–d₉ series can reveal the impact of d-shell occupancy on charge localization. As shown in Fig. 3a and b, the d₀ oxides (BiVO₄, TiO₂) with empty d-shell exhibit the slowest localization, whereas the nearly filled d₈–d₉ oxides (NiO, CuO) are substantially faster. For Cr₂O₃ (d₃) and Fe₂O₃ (d₅), localization occurs faster than our instrument resolution; we therefore assign an upper limit of 100 fs (see Fig. S23 and 2a). Fig. 3c summarizes these trends: oxides with empty or nearly closed d-shells localize charge carriers more slowly, while those with half-filled to nearly full shells localize most rapidly (t_1/2[d₀] > t_1/2[d₃–d₅] < t_1/2[d₈–d₉]). The root cause of this behaviour is the strength of cation–cation coupling: for metal oxides with empty and nearly closed d-shells, cation–cation interactions are generally larger than oxides with open d-shells, resulting in wider bands and greater charge delocalization. In contrast, metal oxides with open d-shells typically exhibit weaker cation–cation interactions, resulting in narrower bands and promoting electron localization.³³ We have recently proposed that polaron formation is in kinetic competition with ultrafast charge trapping and, for open d-shell metal oxides, ultrafast relaxation through ligand field states.⁴⁰ Here, using a polaron formation perspective, we experimentally demonstrated the relationship between d-shell filling and the propensity for charge (de)localization in TMOs, revealing that those with open d-shells possess a greater propensity for charge localization, in the agreement with our previous work,⁴⁰ as well as the theoretical studies.^32,33

Fig. 3 Comparison of free charge carrier decay and small polaron formation kinetics in first-row TMOs. (a) Free charge carrier decay. (b) Small polaron formation. Both a and b were extracted from global analyses. (c) Summary of the kinetic halftimes for free charge carrier decay and polaron formation. For d₃_Cr₂O₃ and d₅_Fe₂O₃, the instrument response time of ca. 100 fs was used as the upper limit to the kinetic response; the overlaid grey dashed curves were drawn as a guide to the eye.

As a further extension of these kinetic studies, temperature-dependent measurements enable us to address the long-debated question of whether small polaron formation involves an activation energy (E^f_a).^34,35 To quantify E^f_a, we collected fs-TAS data as a function of temperature for TMOs in which the absorption feature of free charge carriers and small polarons can be unambiguously distinguished (see Fig. S35–S88). As shown in Fig. 4, clear but weak Arrhenius temperature dependencies were observed in d₀_TiO₂, d₀_BiVO₄, and d₄_Mn₂O₃, yielding E^f_a values of 2–7 meV for both free charge decay and small polaron formation. In contrast, d₈_NiO and d₉_CuO showed no detectable thermal activation within our experimental uncertainty, indicating barrierless polaron formation (E^f_a ≈ 0; see Fig. 4b). Although theory has predicted the existence of such thermal barriers,^69,70 to our knowledge no direct experimental verification has been reported.^34,35 On the other hand, previous observations of non-Arrhenius temperature dependence (E^f_a in negative value from fitting) were attributed to nuclear tunnelling processes, implying barrierless electron self-trapping.^36,37

Fig. 4 Temperature-dependent kinetics of free charge carrier localization and polaron formation. (a) Arrhenius model fitting of the temperature dependent kinetics of free charge carrier decay (left column) and polaron formation (right column). (b) Table summarizing the corresponding activation energy from the fittings of temperature-dependent carrier localization kinetics. For NiO, we obtained polaron-formation rate constants from decay half-times because single-exponential fitting gave poor fitting.

Herein, we experimentally demonstrate that a small thermal barrier (E^f_a up to 7.01 ± 2.36 meV) is present for small polaron formation at least in d₀ TMOs. The small polaron formation can thus be viewed as a non-equilibrium electron-transfer process, with the observed small barriers arising from coupling to high-frequency, multi-phonon modes, as described by the Bixon–Jortner electron-transfer model⁷¹ (see Fig. 5). Although polaron formation barrier variations across TMOs are subtle, d₀ oxides consistently exhibit higher barriers, reflecting their slower polaron formation kinetics and extended lifetimes (see Fig. 3).⁴⁰

Fig. 5 Electronic potential energy diagram of small polaron formation. Schematic illustration of the electronic potential energy as a function of configurational parameter Y, comparing the ground state surface with those of excited band-like and polaronic states. E^f_a is the polaron formation activation energy, and excited multi-phonon modes are indicated by dashed lines in II: Polaron states. E_g is the optical bandgap, E_func is the functional energy level (E_func = E_g − E_p) corresponding to the enthalpy stored in the photogenerated polarons. While this diagram represents localization of excited electrons, similar energy surfaces can be constructed for small hole polarons.

For PC/PEC applications of semiconducting TMOs, polaron formation fundamentally redefines the functional bandgap, E_func, which sets the enthalpy available in photogenerated carriers to drive interfacial redox reactions. Traditionally, the bandgap is taken from absorption or photoluminescence measurements as the optical gap, E_g, which is assumed to equal, i.e. E_g = E_func.³⁸ However, in every TMO we studied, ultrafast polaron relaxation incurs an energy loss E_p of 400–650 meV, occurring in < 1 ps, faster than almost all interfacial reactions. In n-type semiconductors such as TiO₂, Fe₂O₃ and BiVO₄, this loss is dominated by electron self-trapping, effectively lowering the electronic energy to E_func (E_func = E_g − E_p), i.e. 400–650 meV below the CBM, as illustrated in Fig. 5.

Polaron-formation energy loss has profound implications for the reactivity of photoexcited carriers. The loss we observe (400–650 meV) is comparable to the energy dissipated when electrons trap at defects, such as oxygen vacancies. However, whereas defect-related losses can be mitigated by synthetic control of the vacancy density or via defects passivation afterward, polaron relaxation represents a more intrinsic limit the solar conversion efficiency of TMOs. We note that the impact of polaron formation is not all negative; we have recently argued that polaron localization in TMOs can be a key driver of charge separation, mitigating ultrafast band to band recombination mediated by defect or ligand field states.⁴⁰

Conclusion

In summary, our study establishes an important spectroscopic and kinetic insights into photoexcited small polaron behaviour in TMOs, emphasizing their critical role in PC/PEC applications. This study is based on the first optical spectroscopic observation of photoexcited small-polaron hopping across the series of first-row TMOs. Polaron formation in TMOs is ultrafast (<500 fs), inevitable, and occurs with minimal activation barriers (0–10 meV), dramatically outpacing the timescales of typical interfacial PC/PEC reactions. Consequently, polaronic effects must be explicitly included in mechanistic models. Once formed, polarons undergo thermally activated hopping with large activation energies (200–350 meV), significantly limiting charge transport. The substantial polaron relaxation energy (400–650 meV) reduces the functional electronic bandgap, decreasing the driving force for interfacial electron transfer but also suppressing rapid recombination, thereby prolonging carrier lifetimes. Finally, we highlight that TMOs with d₀ and near-d₁₀ electron configurations exhibit slower polaron formation kinetics, higher energy barriers, and longer lifetimes, indicating that d-shell engineering is a promising strategy to enhance PC/PEC performance.

Author contributions

LT conceived the project. MS was involved in the project discussion all along, prepared the Cr₂O₃, Mn₂O₃, Fe₂O₃ and NiO films, and wrote the global analyses code. LGV did the theoretical calculations of Fe₂O₃. AW supervised the theoretical calculations and made the first suggestion to calculate the small polaron formation activation energy. AK prepared the CuO film and did the XRD pattern fitting and interpretation. VFK prepared the BiVO₄ film and collected XRD raw data of BiVO₄, and IDS made comments for this manuscript. SC contributed to understanding of the underlying concepts and data interpretation. LT did all the rest of the experiments and data analysis. JRD supervised the whole project and proposed the outline of the manuscript framework. LT and JRD wrote this manuscript with input from all other co-authors.

Conflicts of interest

The authors declare no competing interests.

Data availability

The data supporting this article have been included as part of the supplementary information (SI): materials preparation, characterization methods (XRD, UV-vis-NIR absorption, fs-TAS, and temperature dependent fs-TAS), DFT + U calculation, and fitting details (Drude and small polaron absorption model fitting, and E^f_a for polaron formation). See DOI: https://doi.org/10.1039/d5sc08101g.

Acknowledgements

Financial support from the UKRI through the NSF led project HyPT (EP/Y026098/1) is gratefully acknowledged. LT would like to thank VR International Postdoc Fellowship (No. 2020-06511) from the Swedish Research Council, and sincerely thank the supports from his host supervisor Prof. Xiaodong Zou, Stockholm University. VFK and IDS acknowledge support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy-EXC 2089/1-390776260. AK wishes to acknowledge the use of the EPSRC funded Physical Sciences Data-science Service hosted by the University of Southampton and STFC under grant number EP/S020357/1. Lee Tooley, Steve Atkins and Stefanos Karapanagiotidis are thanked for constructing and maintaining the chemical vapour deposition apparatus used herein. LGV and AW thanks the ARCHER2 UK National Supercomputing Service accessed via our membership of the UK's HEC Materials Chemistry Consortium, funded by EPSRC (EP/X035859/1), and the UK Materials and Molecular Modelling Hub for computational resources partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1). We appreciate the constructive suggestions regarding the small activation energy barrier of polaron formation, by considering “multi-phonon modes as in the case of Bixon-Jortner (S–H. Lin, Kuznetsov and Ulstrup) model of Marcus-inverted region”, as noted by a previous reviewer.

References

1. C. Franchini, M. Reticcioli, M. Setvin and U. Diebold, Polarons in materials, Nat. Rev. Mater., 2021, 6, 560–586.
2. I. Austin and N. F. Mott, Polarons in crystalline and non-crystalline materials, Adv. Phys., 1969, 18, 41–102.
3. A. S. Alexandrov and A. B. Krebs, Polarons in high-temperature superconductors, Soviet Physics Uspekhi, 1992, 35, 345.
4. G.-m. Zhao, K. Conder, H. Keller and K. Müller, Giant oxygen isotope shift in the magnetoresistive perovskite La_1–xCa_xMnO_3+y, Nature, 1996, 381, 676–678.
5. P. Calvani, Optical properties of polarons, La Rivista del Nuovo Cimento, 2001, 24, 1–71.
6. D. Emin, Optical properties of large and small polarons and bipolarons, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 13691.
7. K. Miyata, et al., Large polarons in lead halide perovskites, Sci. Adv., 2017, 3, e1701217.
8. D. Eagles, Optical absorption in ionic crystals involving small Polarons, Phys. Rev., 1963, 130, 1381.
9. H. Reik, Optical properties of small polarons in the infrared, Solid State Commun., 1963, 1, 67–71.
10. V. Bogomolov and D. Mirlin, Optical absorption by polarons in rutile (TiO₂) single crystals, Phys. Status Solidi B, 1968, 27, 443–453.
11. H. Reik, Optical effects of small polarons at high frequencies with an application to reduced strontiumtitanate, Z. Phys., 1967, 203, 346–361.
12. P. Gerthsen, R. Groth, K. Hardtl, D. Heese and H. Reik, The small polaron problem and optical effects in barium titanate, Solid State Commun., 1965, 3, 165–168.
13. E. Salje and G. Hoppmann, Small-polaron absorption in W_xMo_1–xO₃, Philos. Mag. B, 1981, 43, 105–114.
14. A. Machida, Y. Moritomo and A. Nakamura, Spectroscopic evidence for formation of small polarons in doped manganites, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, R4281.
15. I. Austin, B. Clay and C. Turner, Optical absorption of small polarons in semiconducting NiO and CoO in the near and far infra-red, J. Phys. C: Solid State Phys., 1968, 1, 1418.
16. S. Mildner, J. Hoffmann, P. E. Blöchl, S. Techert and C. Jooss, Temperature-and doping-dependent optical absorption in the small-polaron system Pr_1−xCa_xMnO₃, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 035145.
17. M. Imlau, H. Badorreck and C. Merschjann, Optical nonlinearities of small polarons in lithium niobate, Appl. Phys. Rev., 2015, 2, 040606.
18. A. Hupfer, L. Vines, E. Monakhov, B. Svensson and F. Herklotz, Photoinduced small polarons bound to hydrogen defects in rutile TiO₂, Phys. Rev. B:Condens. Matter Mater. Phys., 2017, 96, 085203.
19. J. E. Katz, et al., Electron small polarons and their mobility in iron (oxyhydr) oxide nanoparticles, Science, 2012, 337, 1200–1203.
20. L. M. Carneiro, et al., Excitation-wavelength-dependent small polaron trapping of photoexcited carriers in α-Fe₂O₃, Nat. Mater., 2017, 16, 819–825.
21. F. G. Santomauro, et al., Femtosecond X-ray absorption study of electron localization in photoexcited anatase TiO₂, Sci. Rep., 2015, 5, 14834.
22. A. J. Tanner and G. Thornton, TiO₂ polarons in the time domain: implications for photocatalysis, J. Phys. Chem. Lett., 2022, 13, 559–566.
23. S. Bandaranayake, E. Hruska, S. Londo, S. Biswas and L. R. Baker, Small polarons and surface defects in metal oxide photocatalysts studied using XUV reflection–absorption spectroscopy, J. Phys. Chem. C, 2020, 124, 22853–22870.
24. S. Biswas, J. Husek, S. Londo and L. R. Baker, Highly localized charge transfer excitons in metal oxide semiconductors, Nano Lett., 2018, 18, 1228–1233.
25. Y. Zhang, et al., State-selective dynamics of TiO₂ charge-carrier trapping and recombination, J. Phys. Chem. Lett., 2019, 10, 5265–5270.
26. J. S. Pelli Cresi, et al., Ultrafast formation of small polarons and the optical gap in CeO₂, J. Phys. Chem. Lett., 2020, 11, 5686–5691.
27. Y. Fan, Y. Lin, K. H. Zhang and Y. Yang, Recombination of polaronic electron–hole pairs in hematite determined by nuclear quantum tunneling, J. Phys. Chem. Lett., 2021, 12, 4166–4171.
28. E. Pastor, et al., In situ observation of picosecond polaron self-localisation in α-Fe₂O₃ photoelectrochemical cells, Nat. Commun., 2019, 10, 3962.
29. A. J. Tanner, et al., Photoexcitation of bulk polarons in rutile TiO₂, Phys. Rev. B:Condens. Matter Mater. Phys., 2021, 103, L121402.
30. E. Hruska, J. Husek, S. Bandaranayake and L. R. Baker, Visible light absorption and hot carrier trapping in anatase TiO₂: The role of surface oxygen vacancies, J. Phys. Chem. C, 2022, 126, 10752–10761.
31. J. Zhang, J. Shi, Y. Chen, K. H. Zhang and Y. Yang, Bimolecular Self-Trapped Exciton Formation in Bismuth Vanadate, J. Phys. Chem. Lett., 2022, 13, 9815–9821.
32. I. M. Klein, A. Krotz, W. Lee, J. M. Michelsen and S. K. Cushing, Ab Initio calculations of XUV ground and excited states for first-row transition metal oxides, J. Phys. Chem. C, 2023, 127, 1077–1086.
33. J. B. Goodenough, Metallic oxides, Prog. Solid State Chem., 1971, 5, 145–399.
34. N. Mott and A. Stoneham, The lifetime of electrons, holes and excitons before self-trapping, J. Phys. C: Solid State Phys., 1977, 10, 3391.
35. S. Yuan, Z. Wang, M. L. Baron and K. H. Bevan, Ab initio insight into the formation of small polarons: A study across four metal peroxides, Phys. Rev. B:Condens. Matter Mater. Phys., 2019, 100, 205201.
36. N.-H. Ge, C. M. Wong and C. B. Harris, Femtosecond studies of electron dynamics at interfaces, Acc. Chem. Res., 2000, 33, 111–118.
37. Y. Zhang, et al., Barrierless Self-Trapping of Photocarriers in Co₃O₄, J. Phys. Chem. Lett., 2021, 12, 12033–12039.
38. M. Grätzel, Photoelectrochemical cells, Nature, 2001, 414, 338–344.
39. C. Lohaus, A. Klein and W. Jaegermann, Limitation of Fermi level shifts by polaron defect states in hematite photoelectrodes, Nat. Commun., 2018, 9, 4309.
40. M. Sachs, et al., Ligand field states control photocatalytic efficiency of transition metal oxides, Nat. Chem., 2025, 17, 1348–1355.
41. P. M. Weiser, C. Zimmermann, J. Bonkerud, L. Vines and E. V. Monakhov, Donors and polaronic absorption in rutile TiO₂ single crystals, J. Appl. Phys., 2020, 128, 145701.
42. T. W. Kim, Y. Ping, G. A. Galli and K.-S. Choi, Simultaneous enhancements in photon absorption and charge transport of bismuth vanadate photoanodes for solar water splitting, Nat. Commun., 2015, 6, 8769.
43. W. Wang, et al., The role of surface oxygen vacancies in BiVO₄, Chem. Mater., 2020, 32, 2899–2909.
44. J. L. Shelton and K. E. Knowles, Polaronic optical transitions in hematite (α-Fe₂O₃) revealed by first-principles electron–phonon coupling, J. Chem. Phys., 2022, 157, 174703.
45. A. J. Rettie, W. D. Chemelewski, D. Emin and C. B. Mullins, Unravelling small-polaron transport in metal oxide photoelectrodes, J. Phys. Chem. Lett., 2016, 7, 471–479.
46. A. J. Rettie, et al., Combined charge carrier transport and photoelectrochemical characterization of BiVO₄ single crystals: intrinsic behavior of a complex metal oxide, J. Am. Chem. Soc., 2013, 135, 11389–11396.
47. F. Wu and Y. Ping, Combining Landau–Zener theory and kinetic Monte Carlo sampling for small polaron mobility of doped BiVO₄ from first-principles, J. Mater. Chem. A, 2018, 6, 20025–20036.
48. N. Iordanova, M. Dupuis and K. M. Rosso, Theoretical characterization of charge transport in chromia (α-Cr₂O₃), J. Chem. Phys., 2005, 123, 074710.
49. C. S. Cheng, H. Gomi and H. Sakata, Electrical and optical properties of Cr₂O₃ films prepared by chemical vapour deposition, Phys. Status Solidi A, 1996, 155, 417–425.
50. L. Farrell, et al., Conducting mechanism in the epitaxial p-type transparent conducting oxide Cr₂O₃: Mg, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 125202.
51. P. Klose, Electrical properties of manganese dioxide and manganese sesquioxide, J. Electrochem. Soc., 1970, 117, 854.
52. N. Iordanova, M. Dupuis and K. M. Rosso, Charge transport in metal oxides: A theoretical study of hematite α-Fe₂O₃, J. Chem. Phys., 2005, 122, 144305.
53. M. Younas, M. Nadeem, M. Idrees and M. Akhtar, Jahn–Teller assisted polaronic hole hopping as a charge transport mechanism in CuO nanograins, Appl. Phys. Lett., 2012, 100, 152103.
54. J. Wu, B. Yin, F. Wu, Y. Myung and P. Banerjee, Charge transport in single CuO nanowires, Appl. Phys. Lett., 2014, 105, 183506.
55. X. Zheng, et al., Fast suppression of antiferromagnetism in Cu_1−xLi_xO, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 094510.
56. T. J. Smart, A. C. Cardiel, F. Wu, K.-S. Choi and Y. Ping, Mechanistic insights of enhanced spin polaron conduction in CuO through atomic doping, npj Comput. Mater., 2018, 4, 61.
57. A. Talledo, A. Andersson and C. G. Granqvist, Structure and optical absorption of Li_yV₂O₅ thin films, J. Appl. Phys., 1991, 69, 3261–3265.
58. M. Quijada, et al., Optical conductivity of manganites: Crossover from Jahn–Teller small polaron to coherent transport in the ferromagnetic state, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 16093.
59. G. Brunin, G.-M. Rignanese and G. Hautier, High-performance transparent conducting oxides through small-polaron transport, Phys. Rev. Mater., 2019, 3, 064602.
60. W. Ulrici and P. Kleinert, Optical absorption of Cr⁴⁺ in GaAs: Cr, Phys. Status Solidi B, 1985, 129, 339–347.
61. T. Okubo, et al., Intervalence charge-transfer system by 1D assembly of new mixed-valence octanuclear CuI/CuII/CuIII cluster units, Inorg. Chem., 2011, 50, 2708–2710.
62. H. Reik and D. Heese, Frequency dependence of the electrical conductivity of small polarons for high and low temperatures, J. Phys. Chem. Sol., 1967, 28, 581–596.
63. F. Cotton and M. Meyers, Magnetic and spectral properties of the spin-free 3d6 systems iron (II) and cobalt (III) in cobalt (III) hexafluoride ion: probable observation of dynamic Jahn–Teller effects, J. Am. Chem. Soc., 1960, 82, 5023–5026.
64. Y. Fan, Y. Lin, K. Wang, K. H. Zhang and Y. Yang, Intrinsic polaronic photocarrier dynamics in hematite, Phys. Rev. B:Condens. Matter Mater. Phys., 2021, 103, 085206.
65. C. Cheng, Y. Zhu, Z. Zhou, R. Long and W.-H. Fang, Photoinduced small electron polarons generation and recombination in hematite, npj Comput. Mater., 2022, 8, 148.
66. L. Zhang, et al., Dynamics of photoexcited small polarons in transition-metal oxides, J. Phys. Chem. Lett., 2021, 12, 2191–2198.
67. D. Wood and J. Remeika, Optical Transparency of Rare-Earth Iron Garnets, J. Appl. Phys., 1966, 37, 1232–1233.
68. J. Ferguson and P. Fielding, The origins of the colours of natural yellow, blue, and green sapphires, Aust. J. Chem., 1972, 25, 1371–1385.
69. L. D. Landau, Electron motion in crystal lattices, Phys. Z. Sowjetunion, 1933, 3, 664.
70. V. V. Kabanov and O. Y. Mashtakov, Electron localization with and without barrier formation, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 6060.
71. S. R. Rather and G. D. Scholes, From fundamental theories to quantum coherences in electron transfer, J. Am. Chem. Soc., 2018, 141, 708–722.

---