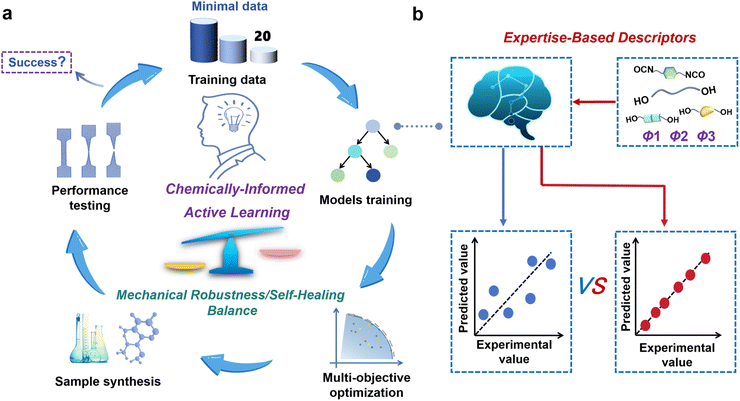
Open Access Article
Open Access ArticleChemically-informed active learning enables data-efficient multi-objective optimization of self-healing polyurethanes
Kang
Liang†
,
Xinke
Qi†
,
Xu
Xiao
,
Li
Wang
 * and
Jinglai
Zhang
* and
Jinglai
Zhang
 *
*
Henan Key Laboratory of Protection and Safety Energy Storage of Light Metal Materials, College of Chemistry and Molecular Sciences, Henan University, Kaifeng 475004, China. E-mail: chemwangl@henu.edu.cn; zhangjinglai@henu.edu.cn
First published on 23rd December 2025
Abstract
Self-healing polyurethanes (PUs) exhibit an inherent trade-off between mechanical strength and self-healing efficiency. Although optimizing the feed ratio can address the above limitations, identifying an appropriate ratio through trial-and-error is not straightforward. Machine learning offers promising approaches for composition-property optimization. However, the multi-property optimization for PUs with specific ingredients remains challenging, especially with minimal samples. A chemically-informed active learning (CIAL) framework is developed that integrates domain knowledge with machine learning to optimize fluorescent self-healing PU with merely 20 experimental datasets. By combining gradient boosting regression with multi-objective optimization, the framework successfully achieves co-optimization of mechanical properties and self-healing efficiency, with the relative error of the comprehensive performance index below 12%. The framework's efficiency is further highlighted to achieve optimal results with only 15 samples when discrete performance data are available. The developed P20B sample serves as an intelligent protective coating for Q235, simultaneously achieving real-time fluorescence visualization of damage sites and long-term anti-corrosion. This work provides an innovative solution for intelligent design of polymer materials using tiny experimental data.
Introduction
Polyurethane (PU) materials have garnered significant attention due to their excellent mechanical properties, tunable chemical structures, and diverse application scenarios.1–3 However, their practical use inevitably suffers from mechanical damage, leading to performance degradation and shortened service life. Self-healing PU materials offer a promising solution to this issue by autonomously repairing damage.4–7 However, the healing process requires time, during which undetected damage progression may exacerbate failures. To mitigate this limitation, fluorescent self-healing PUs have been developed, which can instantaneously visualize damage through optical signals, enabling real-time monitoring and early warning.8–10 By simultaneously incorporating fluorophores (e.g., rhodamine, tetraphenylethylene, and naphthalimide derivatives)11–13 and dynamic reversible bonds (e.g., disulfide bonds, hydrogen bonds)14,15 into the polymer molecular network, dual-functional PUs with customized characteristics can be engineered. Unfortunately, these dynamic reversible bonds are often relatively weak, leading to inferior mechanical strength of the polymer.16 Overall, self-healing efficiency and mechanical strength are trade-off properties for self-healing PUs.17–19Given the inherent trade-off between self-healing capability and mechanical properties, rational adjustment of reactant molar ratios represents a feasible strategy to achieve optimal performance balance.20 However, the conventional trial-and-error approach is inefficient for exploring the complex multidimensional parameter space (e.g., the combinatorial explosion in a four-component system), which fundamentally limits the attainment of desired property equilibrium. Against this backdrop, machine learning has emerged as a revolutionary tool to accelerate material design by exploiting multidimensional relationships between material properties and compositions.21–23 However, its application in PU systems still confronts two key challenges.
Existing literature data not only suffer from limited sample sizes but also exhibit significant heterogeneity, particularly for PU systems with precisely controlled reactants.24,25 Although constructing initial datasets through experiments can improve data quality, conventional approaches require substantial investments of manpower and cost. Taking 50 samples as an example, the entire process from synthesis to performance characterization typically requires 1–5 months for experienced researchers (depending on synthesis complexity). It is of practical significance to minimize data requirements. The second fundamental challenge lies in the predominant focus on optimizing individual performance metrics, while neglecting the inherent trade-off between these parameters. This single-objective optimization paradigm frequently yields materials inadequate for real-world engineering applications that require balanced multi-property performance.26,27 These limitations become particularly pronounced in self-healing PU systems requiring simultaneous optimization of both self-healing and mechanical properties. While Zheng et al.28 successfully employed a reverse design strategy to predict feed ratios for PU elastomers based on merely 25 data points with prediction accuracy (R2) exceeding 0.88, only mechanical properties are optimized in their work. Overall, achieving accurate prediction of feed ratios for self-healing PUs using small-sample data, even less than 25 samples while simultaneously balancing self-healing efficiency and mechanical performance remains a significant challenge. To the best of our knowledge, no relevant studies addressing this specific issue have been reported to date.
In this work, we introduce a chemically-informed active learning (CIAL, Fig. 1) framework for the efficient design of fluorescent self-healing PU, enabling multi-objective optimization with only 20 samples. The distinctive feature of the CIAL framework lies in its deep integration of chemical expertise throughout the entire machine learning pipeline from descriptor construction and data analysis to iterative sample selection, achieving synergistic optimization between human decision-making and optimization algorithm. Taking the self-developed fluorescent self-healing PU (PSSNM) as an example (Fig. S1), merely three iterations with 20 experimental data points successfully established six gradient boosting regression (GBR) models. These models accurately predicted the material's tensile strength (σ), elongation at break (ε), toughness (T), and their corresponding self-healing efficiencies (ησ, ηε, ηT) (with average prediction accuracy R2 > 0.8). Based on these high-precision models, a Pareto front was recommended through Non-dominated Sorting Genetic Algorithm III (NSGA-III) optimization. Experimental validation demonstrated excellent agreement between predicted and measured mechanical properties for optimal sample P20B (with relative errors <12% for comprehensive performance indicators), fully confirming the reliability of the CIAL framework. Furthermore, the property predictions of another self-healing PU system (PBP) using the CIAL framework demonstrated that merely 15 sample sets were sufficient to achieve desirable results. The predicted data showed excellent agreement with experimental measurements, with all comprehensive performance metrics maintaining an average relative error below 13%, which conclusively validated the universality of this framework. Utilizing the optimal P20B sample, an intelligent protective coating was developed for steel that integrates both self-healing functionality and real-time corrosion warning capability. This innovative coating solution provides a promising approach for intelligent protection of critical infrastructure such as oil pipelines. Through the deep integration of chemical intuition and data intelligence, this study establishes a universal machine learning framework that overcomes the “performance trade-off effect” in multifunctional PU materials with tiny data requirements.
Results and discussion
Overview and scope of CIAL framework
The CIAL framework strategically integrates domain knowledge-guided descriptor selection with iterative experimental data through a continuous learning process that systematically incorporates both existing and newly generated experimental data from iterative experiments to explore the optimal feed ratios for PSSNM, ultimately achieving a balance between mechanical properties and self-healing efficiency (Fig. 1). The CIAL framework implements the following systematic five-step strategy: First, the initial dataset was constructed by integrating human knowledge with the design of experiments (DoE) methodology and three key descriptors. Second, the GBR algorithm was employed to establish quantitative composition-property relationship models capable of predicting mechanical properties and self-healing efficiency, respectively. Third, the NSGA-III multi-objective optimization algorithm was applied to identify Pareto-optimal solutions, achieving this balance between mechanical properties and self-healing efficiency. Fourth, a human-guided iterative optimization was performed, where model deficiencies triggered targeted experimental supplementation guided by functional analysis of formulation specificity and rationality. Finally, chemical validation of the optimization results was conducted, forming a complete “prediction-validation-optimization” closed loop system.Foundation model development and evaluation
The PSSNM samples with varying raw material molar ratios were prepared to build the initial dataset. The material architecture employs polytetramethylene ether glycol (PTMEG) containing flexible ether bonds (–O–) as the soft segment to confer flexibility and elasticity,29 while the hard segment comprises three functional components: (i) isophorone diisocyanate (IPDI), whose alicyclic structure confers adequate chain mobility while simultaneously preserving mechanical integrity;29 (ii) bis(2-hydroxyethyl) disulfide (HEDS), which introduces dynamic disulfide bonds that synergize with hydrogen bonds to enable self-healing; and (iii) modified naphthalimide derivatives (4 N-acetylethylenediamine-N-(2-hydroxy-1-hydroxymethylethyl)-1,8-naphthimide, NIAM), whose rigid molecular architecture enhances mechanical strength while its fluorescent moiety provides photoluminescence,13 with additional hydrogen bonding contributions from acetylenediamine groups (the experimental and structural details are shown in Fig. S1).By randomly varying the stoichiometric ratios of four components in PSSNM, nine samples were prepared and their key properties were measured including tensile strength, elongation at break, toughness, and self-healing performance (Table S1). Using the molar ratios of four raw materials as inputs, three models were trained using the GBR algorithm to establish relationships between material composition and three mechanical properties, respectively. Considering that the mechanical property values span 2–3 orders of magnitude, logarithmic transformations were applied. Self-healing performance was determined based on the ratios of tensile strength, elongation at break, and toughness after repair relative to their original values. Accordingly, three additional models were developed to predict the self-healing performance. The models demonstrate excellent fitting performance on the training set (R2 = 0.99, 0.93, 0.99, 0.99, 0.91, and 0.99, respectively), but display inferior predictive accuracy on the testing set (R2 = 0.30, 0.15, 0.40, 0.10, 0.35, and 0.19, respectively). The elevated mean absolute error values (MAE = 0.41, 0.25, 0.37, 0.10, 0.02, and 0.10, respectively) for the testing set (Fig. S2 and S3a) further confirm the presence of severe overfitting. This observation aligns with previous literature reports on machine learning performance with small datasets, where overfitting tends to occur due to limited data availability. Expanding the dataset size is a crucial approach to mitigate this issue. To distinguish the different models, the above six models are designated as MR-9.
To address the issue of data scarcity, the original dataset was expanded from 9 to 12 samples by supplementing three additional experimental specimens and systematically characterizing their performance parameters. The relevant formulations and corresponding performance are listed in Table S2. Based on the enhanced dataset, six predictive models were retrained using the same GBR algorithm (named MR-12). The degree of overfitting is significantly reduced, as evidenced by testing set R2 values of 0.57, 0.17, 0.66, 0.69, 0.66, and 0.52 (Fig. S3b and S4). Correspondingly, the MAE values show notable reductions compared to the original MR-9 models. However, the current model's predictive accuracy remains insufficient to meet the requirements for precise prediction of optimal material compositions. These results suggest that increasing the dataset size can partially alleviate overfitting. However, simply expanding the dataset neither fundamentally enhances model generalization capability nor aligns with our original objective of achieving “accurate prediction with tiny samples”. Therefore, subsequent research will focus on integrating materials science mechanistic analysis with expert knowledge to comprehensively investigate the causes of overfitting.
To reveal the contribution of each descriptor to prediction and investigate the underlying causes of overfitting, feature importance analysis based on GBR algorithm was conducted for the MR-9 and MR-12 models (Fig. S5). The results demonstrate that in the MR-9 model, both IPDI and NIAM variables show zero importance scores for toughness prediction, indicating their negligible contributions to the predictive outcomes. Similarly, these two variables exhibit importance scores below 10% in tensile strength prediction. The MR-12 model also presents inappropriate feature selection with the NIAM variable demonstrating near-zero importance scores for both toughness and corresponding self-healing performance predictions, while maintaining below 10% importance for tensile strength and corresponding self-healing performance predictions. Features with low importance typically contain considerable amounts of irrelevant or redundant information. Such noise is difficult to effectively identify and suppress during model training, leading to overfitting of anomalous patterns in the training data.30 As training progresses, the model's reliance on these noisy features intensifies, further diminishing its adaptability to new (testing) data and significantly compromising its generalization performance and predictive reliability. These findings suggest that models constructed from randomly selected data lack effective learning mechanisms. Therefore, integrating domain expertise to screen critical features and establishing high-quality specialized databases are essential for enhancing model predictive performance and reliability.31
Descriptor optimization and multi-objective optimization
To enhance model reliability, a scientific design of the four-component ratio system plays a decisive role. The DoE methodology provides an effective approach for this optimization. By implementing equal-gradient variations in component concentrations, optimal parameter combinations can be obtained with minimal experimental iterations. In fact, prior to the widespread application of machine learning techniques, DoE served as a fundamental methodology for investigating material composition and process parameters.28,32 However, the rational design of gradient parameters in multi-component systems still constitutes a non-trivial challenge. To overcome this critical limitation, we emphasize the indispensable role of expert knowledge in validating the physical rationality of component gradient configurations.Based on established synthetic protocols for PUs containing dual chain extenders, the most representative stoichiometric formulation follows the molar ratio PTMEG/IPDI/HEDS/NIAM = 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.125
0.125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.125.33 This formulation adheres to the fundamental principle of maintaining a 1
0.125.33 This formulation adheres to the fundamental principle of maintaining a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio between hydroxyl groups and isocyanate groups, theoretically ensuring complete consumption of all functional groups. In this system, PTMEG, HEDS, and NIAM all serve as dihydroxy compounds, and their combined stoichiometry is designed to balance the isocyanate equivalents. Specifically, the 1
1 molar ratio between hydroxyl groups and isocyanate groups, theoretically ensuring complete consumption of all functional groups. In this system, PTMEG, HEDS, and NIAM all serve as dihydroxy compounds, and their combined stoichiometry is designed to balance the isocyanate equivalents. Specifically, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio between PTMEG and IPDI first generates NCO-terminated prepolymers, which subsequently react with the two chain extenders. The disulfide-containing HEDS and NIAM primarily contribute to the self-healing capability and mechanical strength. To achieve an optimal property balance, two distinct extenders are initially incorporated in equimolar proportions.
2 molar ratio between PTMEG and IPDI first generates NCO-terminated prepolymers, which subsequently react with the two chain extenders. The disulfide-containing HEDS and NIAM primarily contribute to the self-healing capability and mechanical strength. To achieve an optimal property balance, two distinct extenders are initially incorporated in equimolar proportions.
According to the above classical molar ratio of four components, at least 27 samples are theoretically required to establish four reactants with equal gradient variations. To minimize the required data, we strategically recombine the four components into three key parameters: reactive group molar ratio (Φ1), chain extender ratio (Φ2), and hard/soft segment ratio (Φ3). They are defined as:
 | (1) |
 | (2) |
 | (3) |
This parametric reconstruction not only retains the regulatory dimensions of the original four-component system but also significantly reduces the experimental scale. Three descriptors (Φ1, Φ2, Φ3) directly encode core chemical knowledge: functional group stoichiometry, the interplay between dynamic covalent bonds and hydrogen bonds, and the hard/soft segment microphase separation principle. Gouveia et al.34 demonstrated that increasing the NCO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OH molar ratio, i.e., Φ1, can enhance the tensile strength of PUs, while adjusting the molar ratio of two chain extenders can effectively regulate hydrogen bonding content, microphase separation degree, self-healing capability and crystallinity.35,36 Most notably, the modulation of hard/soft segment ratio (Φ3) enables not only performance transitions from soft to hard or brittle to tough, but also variations in the material's self-healing properties by regulating molecular chain mobility.37,38 By systematically adjusting these three variables with equal gradient intervals, the minimum required data are successfully reduced from 27 to 9 while still obtaining meaningful patterns in the four-reactant ratio combinations. This refined experimental design achieves a threefold reduction in sample size without compromising the precision of the system.
OH molar ratio, i.e., Φ1, can enhance the tensile strength of PUs, while adjusting the molar ratio of two chain extenders can effectively regulate hydrogen bonding content, microphase separation degree, self-healing capability and crystallinity.35,36 Most notably, the modulation of hard/soft segment ratio (Φ3) enables not only performance transitions from soft to hard or brittle to tough, but also variations in the material's self-healing properties by regulating molecular chain mobility.37,38 By systematically adjusting these three variables with equal gradient intervals, the minimum required data are successfully reduced from 27 to 9 while still obtaining meaningful patterns in the four-reactant ratio combinations. This refined experimental design achieves a threefold reduction in sample size without compromising the precision of the system.
Taking the classical dual-chain-extender formulation (PTMEG/IPDI/HEDS/NIAM = 0.25/0.5/0.125/0.125) as our reference system, Φ1, Φ2, and Φ3 are 1, 0.5, and 0.33, respectively. By setting Φ1, Φ2, and Φ3 gradient intervals at 1/10, 1/4 and 1/3, the dataset containing nine representative formulations was established. Based on this, nine representative material formulations (3 levels) were designed to train the GBR models (detailed composition ratios and corresponding performance are listed in Table S3). With the molar ratios of four raw materials and three key variables as model inputs, predictive models were constructed using the GBR algorithm (MD-9A). As demonstrated in Fig. S6a, the MD-9A models exhibit higher precision than the MR-9 models for most prediction targets, and even outperform some MR-12 models, strongly demonstrating the effectiveness of the refined dataset and the importance of human decision in the optimization process. The utilization of three descriptors (Φ1, Φ2, Φ3) means that the model learns structure–property relationships within a chemically meaningful and constrained framework, which is helpful to enhance the reliability of the GBR models, especially for small datasets. The reliability of MD-9A was validated using the leave-one-out cross-validation (LOO-CV) method (Fig. S7). The following models are also testified by the LOO-CV method. Based on the established single-objective predictive models, the NSGA-III algorithm was further employed for multi-objective optimization. To facilitate the comprehensive evaluation of PSSNM, mechanical property indicators (σ, ε, T) and self-healing capabilities (ησ, ηε, ηT) were transformed into two comprehensive targets, Z1 and Z2, respectively. They are defined as:
 | (4) |
 | (5) |
Subsequently, the Pareto front was recommended and plotted in Fig. S6b and c. It should be noted that the Pareto front in this study is dynamic and iteratively updated, defined as the set of non-dominated solutions within the current dataset. The goal of multi-objective optimization is to identify candidate points with predicted performance that surpasses this current front. After experimental validation, these candidates are incorporated into the dataset to update the front, meaning that breaking through the front represents an iterative and proactive expansion of the performance space. Unlike static Pareto fronts determined after optimization,39 the dynamic front here is updated in real time with new data, enabling efficient discovery of high-performance candidates and adaptive exploration of the evolving chemical space. However, the optimization results do not break through the Pareto front due to constraints imposed by the variable space constructed from the initial nine datasets. While the optimization algorithm can effectively explore existing data space, the inherent limitations of sample space objectively constrain the enhancement of optimization effects, highlighting the necessity to expand datasets or adapt sampling strategies.40
To expand the parameter exploration space, this study refined the experimental design strategy by increasing the Φ1 gradient interval from 0.1 to 0.2, enabling a more comprehensive and systematic search for optimal solutions. Accordingly, nine additional representative material formulations (Table S4) were employed for model training, with the newly designed nine formulations used to retrain the predictive model (MD-9B). The model demonstrates exceptional fitting performance on the training set, with R2 values of 0.99, 0.99, 0.99, 0.43, 0.56, and 0.79 respectively, while maintaining significant predictive accuracy on the testing set, yielding corresponding R2 values of 0.99, 0.76, 0.99, 0.31, 0.36, and 0.64 (Fig. S6d). Compared with MR-9 and MR-12 models, these results further validate that improving data quality is substantially more effective than indiscriminate data expansion for enhancing predictive accuracy, thereby providing empirical evidence for the robustness and effectiveness of integrating DoE with human decision strategies. Unfortunately, the optimization results still fail to completely surpass the Pareto front due to limited quantity of available data (Fig. S6e and f).
Since data scarcity is the critical bottleneck, we integrated data from the above two phases to construct a new dataset containing 15 samples (detailed data are listed in Table S5). The MD-15 models were trained (model accuracy detailed in Fig. S8a) followed by multi-objective optimization. Interestingly, the MD-15 models not only maintain high predictive accuracy but also successfully break the Pareto front (Fig. S8b and c). Two optimal points (denoted as P15A and P15B) were subsequently selected for experimental verification, and the corresponding samples were prepared according to the two recommended formulations outlined in Table S6. The mechanical and self-healing properties of P15A and P15B samples were evaluated by tensile testing (Fig. S8d), and the detailed mechanical property data and corresponding self-healing efficiency are summarized in Fig. S8e, f and Table S7. The tensile strength, elongation at break, and toughness of P15A are 6.06 MPa, 165.04%, and 8.32 MJ m−3, while the corresponding predicted values are 10.65 MPa, 837.94%, and 23.87 MJ m−3. The relative errors between logarithmic values of predicted and measured mechanical properties are 31.3%, 31.8%, and 49.7%, respectively, which are far beyond the acceptable error limitation. P15B exhibited even greater deviations between predicted and experimentally measured values, with relative errors of 116.4%, 122.0%, and 455.8% for tensile strength, elongation at break, and toughness, respectively, suggesting prediction failure.
The Φ2 values consistently approach zero for both P15A and P15B in 15-entry dataset, corresponding to near-zero HEDS molar ratio in these two samples (as shown in Table S6). Notably, this parameter range is absent from the original database. Thus, the inaccurate predictive results may also stem from a significant gap in the parameter space coverage, particularly within the Φ2 value range, besides insufficient data volume. When the multi-objective optimization algorithm recommends samples that are chemically unreasonable or fall outside an existing experimental design space (e.g., for formulations with extremely low Φ2 values, indicating near-absence of the dynamic disulfide bond carrier HEDS), the decision whether to synthesize these samples from high-uncertainty regions should be guided by integrated expertise in chemistry and machine learning. Since disulfide bonds are essential for self-healing performance, the samples without disulfide bonds can fill the specific “chemical gap” in the parameter space, thereby enhancing prediction precision.
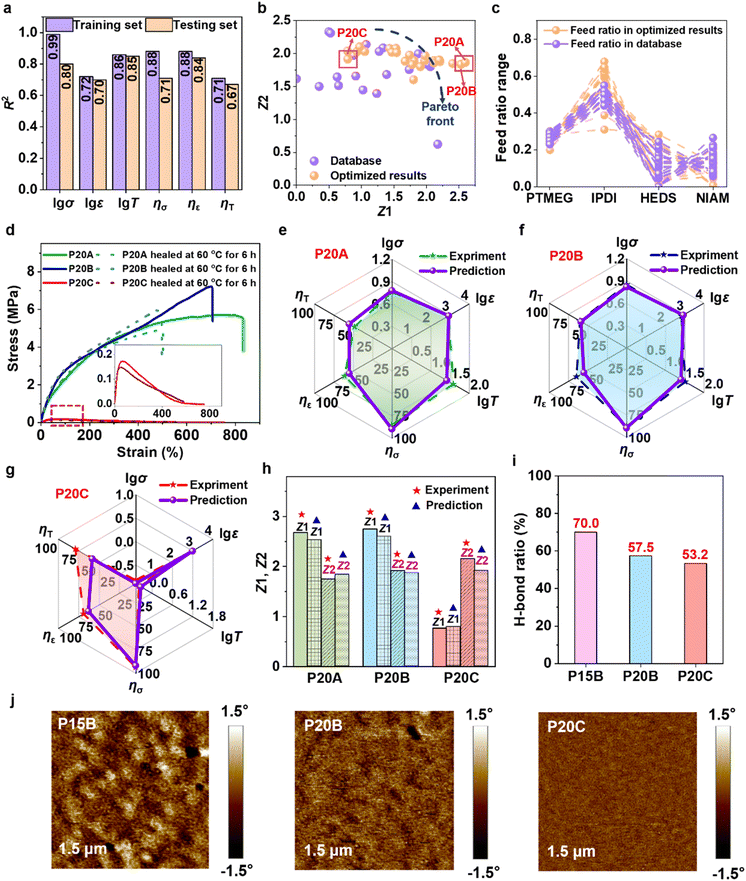
Data expansion and Pareto frontier breakthrough
Based on the preceding analysis, the original dataset was expanded from 15 to 20 entries by incorporating data points where Φ2 equals zero (Table S8), thereby effectively filling the gaps in the parameter space. With this enriched dataset, predictive models were retrained (MD-20), and multi-objective optimization was conducted again. Relative to the MD-15 model, the MD-20 (model accuracy detailed in Fig. 2a) mitigates overfitting and achieves a successful breakthrough of the Pareto front (Fig. 2b and c). During experimental validation, two optimal predicted formulations (P20A and P20B) were selected for sample fabrication, along with a control sample (P20C) that did not surpass the Pareto frontier. The synthesized formulations and their corresponding performance are summarized in Tables S9, S10 and Fig. 2d–g. The measured tensile strength, elongation at break, and toughness of P20A are 5.82 MPa, 846.86%, and 38.70 MJ m−3, respectively, with logarithmic relative errors between experimental values and predicted values (5.98 MPa, 867.77%, and 26.09 MJ m−3) remaining at low levels (relative errors: 0.4–10.8%). For self-healing efficiency, the relative errors between the measured (ησ = 85.6%, ηε = 61.2%, ηT = 48.6%) and predicted values (ησ = 89.8%, ηε = 55.1%, ηT = 55.2%) are also well controlled (relative errors: 5.0–13.6%). P20B exhibits similar performance characteristics to P20A, with prediction errors ranging from 1.8% to 14.7% for all properties. Notably, although the control sample P20C displays superior self-healing performance (ησ = 93.3%, ηε = 67.7%, ηT = 78.0%), its mechanical properties are significantly compromised (tensile strength = 0.15 MPa), which aligns perfectly with the prediction that it does not surpass the Pareto frontier. This finding underscores the critical role of multi-objective optimization in balancing material properties. Analysis of the comprehensive performance indices (Z1 and Z2) further confirms the model's reliability, with relative errors for P20A, P20B and P20C below 12% (Fig. 2h and Table S11).Experimental results demonstrate that P20C sample exhibits optimal self-healing performance, while P20B shows the highest tensile strength. Moreover, P20B achieves the best balance between mechanical features and self-healing performance. The successful synthesis of P20B and P20C was confirmed by fourier transform infrared spectroscopy (FT-IR) and proton nuclear magnetic resonance (1H NMR) spectra (Fig. S9 and S10). FT-IR analysis confirms the formation of urethane linkages and the presence of naphthalene rings in both P20B and P20C, with residual –NCO observed only in P20B due to excess IPDI. 1H NMR spectra further verify the successful incorporation of PTMEG, IPDI, HEDS, and NIAM into the polymer backbones. To investigate the underlying mechanism of these performance differences between P20B and P20C, we systematically analyzed their hydrogen bonding fractions and microphase separation behavior. The P15B was also measured as a baseline control representing high hydrogen-bonding conditions. The absorption region related to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group (1600–1760 cm−1) in the FT-IR spectrum was deconvoluted into three characteristic peaks: free C
O group (1600–1760 cm−1) in the FT-IR spectrum was deconvoluted into three characteristic peaks: free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1718 cm−1, ordered H-bonded C
O at 1718 cm−1, ordered H-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1636 cm−1, and disordered H-bonded C
O at 1636 cm−1, and disordered H-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1687 cm−1 (Fig. S11).41 Quantitative analysis indicates that the total proportion of ordered and disordered H-bonded C
O at 1687 cm−1 (Fig. S11).41 Quantitative analysis indicates that the total proportion of ordered and disordered H-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in P15B reaches 70.0%, significantly higher than that in P20B (57.5%) and P20C (53.2%) (Fig. 2i). This difference in hydrogen bond density directly influences the microphase separation behavior of the materials.42 The microphase separation properties of three aforementioned samples were characterized by means of atomic force microscopy (AFM). As shown in Fig. 2j, AFM results confirm that P15B exhibits the most pronounced microphase separation due to its higher hydrogen bond density and hard segment content, while P20B and P20C show intermediate and weaker microphase separation characteristics, respectively.
O in P15B reaches 70.0%, significantly higher than that in P20B (57.5%) and P20C (53.2%) (Fig. 2i). This difference in hydrogen bond density directly influences the microphase separation behavior of the materials.42 The microphase separation properties of three aforementioned samples were characterized by means of atomic force microscopy (AFM). As shown in Fig. 2j, AFM results confirm that P15B exhibits the most pronounced microphase separation due to its higher hydrogen bond density and hard segment content, while P20B and P20C show intermediate and weaker microphase separation characteristics, respectively.
In-depth structure–property relationship studies reveal that the high hydrogen bond density in P15B originates from its elevated molar ratio of NIAM monomer and higher hard segment content. The synergistic effect between the rigid aromatic rings in NIAM and the dense hydrogen-bonding network in the hard segments forms a highly rigid three-dimensional network structure. This not only severely restricts molecular chain mobility but also eliminates material elasticity, resulting in typical plastic deformation behavior and extremely poor stretchability and self-healing performance. Furthermore, the exceptionally low relative content of dynamic disulfide bonds (HEDS) in P15B further deteriorates its self-healing capability. In contrast, P20C significantly reduces hydrogen bond density by decreasing the NIAM molar ratio and hard segment content. While this modification provides excellent chain mobility and self-healing performance, it comes at the cost of substantially reduced load-bearing capacity. These comparative results clearly demonstrate the inherent trade-off between mechanical properties and self-healing capability in PU materials. The moderate hydrogen bond density, optimal rigid ring amount, well-designed disulfide bond content, and appropriate phase separation degree in P20B ensure mechanical strength while maintaining sufficient self-healing efficiency. This multi-scale structural coordination strategy provides important guidance for designing high-performance self-healing PU materials, fully demonstrating that rational design of molecular composition and structural parameters enables precise control of material properties.
Boundary exploration and generalization validation
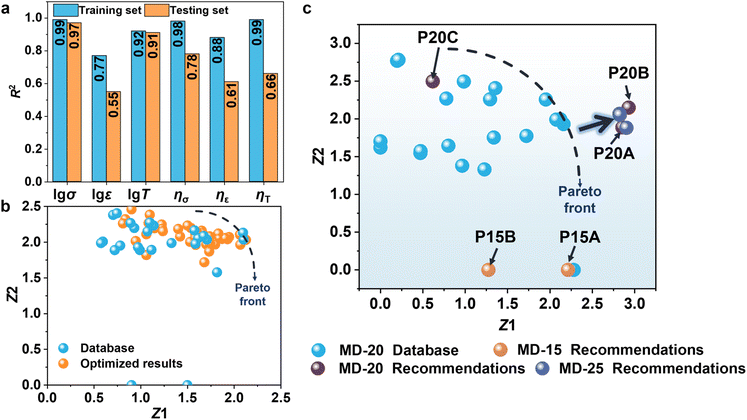
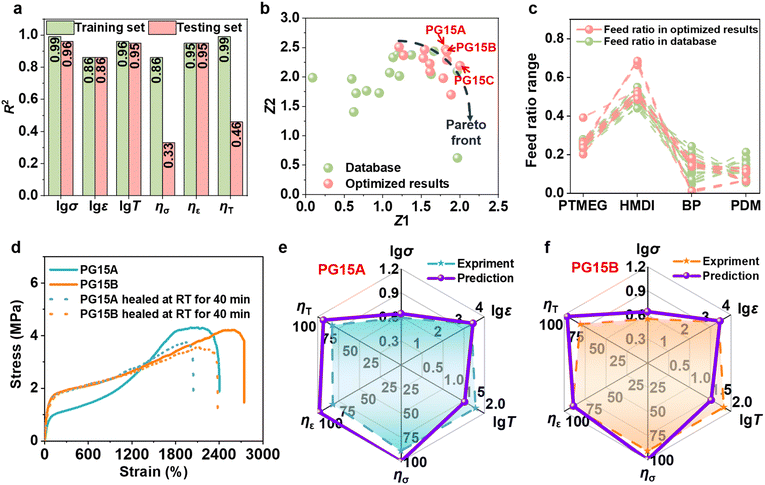
A comprehensive dataset comprising 25 samples was built by supplementing the original 20 samples with five additional specimens (P15A, P15B, P20A, P20B, and P20C) (Table S12). The retrained MD-25 predictive model maintains excellent performance prediction accuracy (Fig. 3a). Multi-objective optimization analysis reveals that the optimization trajectories consistently remain within the original Pareto frontier (Fig. 3b). It demonstrates that the initial 20-sample dataset is sufficient to adequately explore the design space and that the material performance has reached its theoretical limits. Through dynamic tracking of experimental data distribution in the Z1–Z2 plane (Fig. 3c), the evolutionary patterns of the dataset during the active learning optimization process are clearly observed. When the sample size increases to 20, the P20 series samples recommended by the MD-20 model exhibit significant performance improvements. Further expansion to 25 samples and retraining with the MD-25 model still yield optimization results confined within the original Pareto frontier. This series of experimental evidence robustly validates the adequacy and reliability of the gradient-designed 20-sample dataset within the CIAL framework for PU performance prediction.To further validate the generalizability of this model, we prepared 15 new self-healing PU samples (labeled PBP) using the identical gradient design principle (Fig. S12 and Table S13). In PBP, PTMEG as the soft segment was reacted with 4,4′-dicyclohexylmethane diisocyanate (HMDI) to form a prepolymer. Then, 4,4′-biphenol (BP) and 2,6-pyridinedimethanol (PDM) were added step by step as chain extenders to obtain PBP. Using the molar ratios of four new raw materials and three key variables as input parameters, a predictive model designated as MG-15 was developed based on the GBR algorithm. As shown in Fig. 4a, the MG-15 model exhibits excellent fitting performance on the training set and maintains good predictive accuracy on the testing set, demonstrating high overall precision. Furthermore, the robustness of the model is evaluated using LOO-CV, with the results (Fig. S13) indicating that the MG-15 model performs comparably to the reference models MD-15 and MD-20, thereby confirming its strong generalization capability and stability. Building upon the established single-objective predictive models, the NSGA-III was employed for multi-objective optimization. As illustrated in Fig. 4b and c, the optimization process successfully surpasses the Pareto front. Notably, expert chemical judgment was applied to assess the rationality of the recommended formulations. Consequently, two optimized formulations (PG15A and PG15B) were selected for experimental validation. The synthetic formulations with detailed feed ratios are summarized in Table S14, while Fig. 4d–f, S14 and Table S15 present the corresponding properties. The tensile strength, elongation at break, and toughness of PG15A are 3.91 MPa, 2482.09%, and 61.41 MJ m−3. These measurements demonstrate excellent agreement with model predictions (4.33 MPa, 2894.40%, and 33.87 MJ m−3, respectively), as evidenced by logarithmic relative errors of merely 1.9–14.5%. The self-healing efficiencies also demonstrate good agreement between experimental measurements (ησ = 89.0%, ηε = 81.8%, ηT = 82.6%) and model predictions (ησ = 100.0%, ηε = 97.9%, ηT = 93.0%), with relative errors ranging from 12.4% to 14.9%. PG15B exhibits comparable performance to PG15A, with property prediction errors maintained within 1.3–19.5%. The above results testify the scientific validity and practical applicability of the proposed modeling and optimization framework. The Z1 and Z2 values with relative errors for PG15A and PG15B are below 13% (Fig. S15 and Table S16). As to the recommended PG15C sample, the predicted HMDI proportion is excessive leading to a pronounced imbalance in the stoichiometry of –NCO groups. From a fundamental chemical perspective, the PG15C will not exhibit the ideal features. Consequently, the experimental results significantly deviate from predictions (Fig. S14 and Table S15). The incorporation of chemical domain knowledge enables effective pre-screening of predicted formulations, significantly enhancing the reliability of machine learning predictions by eliminating unrealistic candidates. Principal component analysis (PCA) was employed to reduce the dimensionality of the model inputs. As shown in Fig. S16, the recommended formulations from the MD-15 and MD-20 models (e.g., P15A, P20A) and those from the MG-15 model (PG15A, PG15B) are all located within a consistent region defined by PCA1 values between −1 and 0 and PCA2 values between 2 and 4. In contrast, PG15C falls outside this region, exhibiting inferior performance. PCA can serve as a complementary tool for preliminary evaluation of the reliability of recommended formulations following multi-objective optimization.
For the PSSNM system, a larger experimental dataset (20 samples) is required to effectively surpass the Pareto front and achieve successful predictions, whereas only 15 samples are necessary for the PBP system. This difference is mainly attributed to performance distribution in the dataset. The MD-15 dataset exhibits a relatively uniform performance distribution (Fig. S17a–c); nevertheless, the samples recommended by the MD-15 model exhibit much larger tensile strength than those in the original dataset, indicating the considerable potential for further improvement in this performance dimension. Conversely, the optimized values for elongation at break and toughness fall within the original data range, suggesting that these properties may be approaching their theoretical limits within the current material system. The samples (P20A and P20B) recommended by the MD-20 model further support this interpretation, achieving improvements in tensile strength while maintaining high predictive accuracy (Fig. S17d–f). MG-15 contains several extreme outliers and the samples recommended by the MG-15 model show only marginal or no improvements across all three properties (Fig. S17g–i), indicating that the material performance rapidly approaches its theoretical limits under the current optimization cycle. To further investigate the effect of incorporating high-performance samples into the training data, two strategies were explored. In the first strategy, P20A and P20B were used to replace samples P1 and P3 (Entries 1 and 4, Table S5) in the MD-15 dataset. In the second strategy, P20A and P20B were directly added to the MD-15 dataset without removing any existing samples, yielding an expanded training dataset. New models (denoted as MD-15A and MD-15B) were trained based on these datasets and subsequently subjected to multi-objective optimization. As shown in Fig. S18, both MD-15A and MD-15B yield recommended samples exhibiting only marginal or no improvements across all three target properties, consistent with the trends observed for the MG-15 model. In general, the presence of exceptional high-performance data points enables satisfactory prediction outcomes even with remarkably small sample sizes (as few as 15 samples). For data exhibiting concentrated distribution, a targeted expansion to 20 data points can yield comparable predictive performance.
Application as smart anti-corrosion coatings
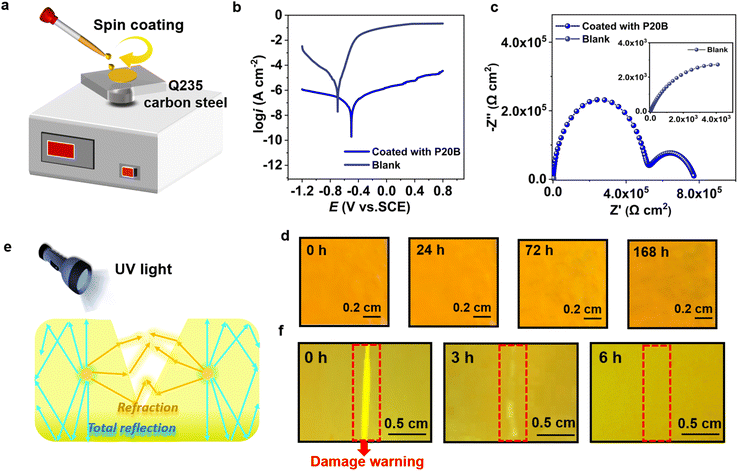
The P20B sample exhibits excellent fluorescence properties, mechanical robustness and self-healing capabilities, showcasing great potential as an intelligent protective coating for carbon steel. Before applying P20B as a smart coating, its long-term stability is evaluated under UV irradiation and in a high-humidity environment (relative humidity of 75 ± 5%). After continuous UV irradiation (120 W, 365 nm) for 168 hours, the tensile strength of P20B is 6.58 MPa along with an elongation at break of 650.26%, reaching 91.9% and 92.2% of the values measured for the fresh sample, respectively. In a high-humidity environment (75 ± 5% RH) for the same time, P20B also maintains excellent mechanical performance with a tensile strength of 5.68 MPa and an elongation at break of 656.52% (Fig. S19). These results confirm the outstanding long-term stability of P20B, underscoring its potential as a protective coating. Then, the P20B coating was prepared on Q235 carbon steel via a spin-coating method (Fig. 5a), and its anti-corrosion performance was systematically evaluated using potentiodynamic polarization (PDP) and electrochemical impedance spectroscopy (EIS). PDP measurements (Fig. 5b) reveal that, compared to the bare substrate, the P20B coating induces a significant positive shift of ∼200 mV in corrosion potential (to −0.50 V) while reducing the corrosion current density by two orders of magnitude. The EIS results (Fig. 5c) further confirm a remarkable increase in the diameter of the capacitive loop for the coated sample, consistent with the PDP data, indicating that the P20B coating effectively suppresses the electrochemical corrosion process of the carbon steel substrate.43 Salt spray tests were conducted to further evaluate the anticorrosion performance. P20B coating maintains its original appearance without any visible corrosive products even after 168 h of exposure, indicating excellent corrosion resistance (Fig. 5d).Notably, the incorporation of the fluorescent NIAM moiety endows the material with unique photoluminescent properties, exhibiting a strong emission peak at 530 nm under 365 nm UV excitation (Fig. S20). When the coating is damaged, the rough fracture surface enhances the refraction and resists the internal reflection, leading to localized fluorescence intensification at the crack sites (Fig. 5e).44,45 As the self-healing process progresses, the surface gradually becomes smooth, accompanied by a corresponding decrease in fluorescence intensity until complete recovery to the initial state. This feature enables real-time visual monitoring of coating damage and precise tracking of the self-repair progress. As shown in Fig. 5f, the scratched region exhibits significantly enhanced fluorescence under UV illumination, whereas the fluorescence signal gradually diminishes to the background level upon healing. Optical microscope images (Fig. S21) confirm the complete disappearance of surface cracks after 6 h of healing at 60 °C, which unequivocally validates the reliability of this fluorescence-based damage warning mechanism. This multifunctional smart coating material, integrating corrosion protection, damage warning, and self-healing capabilities, holds significant scientific and practical value for extending the service life of metallic materials and enhancing the safety of engineering structures.
Conclusions
In this study, a chemistry-informed active learning (CIAL) framework is innovatively developed by deeply integrating domain expertise into the entire machine learning pipeline, including feature engineering, model construction, and sample selection. This approach enables precise design and performance optimization of self-healing PU materials with an extremely small sample size (n = 20). Using the fluorescent self-healing PU system (PSSNM) as a model, the framework successfully determines the optimal molar ratios of four reactants. While maintaining high prediction accuracy (average R2 > 0.8), it overcomes the long-standing challenge of simultaneously optimizing mechanical properties (tensile strength: 7.16 MPa, toughness: 33.43 MJ m−3) and self-healing efficiency (ησ: 88.1%), with a comprehensive performance index relative error below 12%. Remarkably, the framework demonstrates exceptional system universality—for a structurally distinct PU system (PBP), comparable prediction accuracy (comprehensive performance error <13%) is achieved with only 15 training samples. Based on the optimized P20B formulation, a smart protective coating for Q235 carbon steel is prepared that innovatively integrates damage self-healing capability with real-time fluorescence tracking functionality. By establishing this “chemical knowledge-data driven” machine learning framework, this work not only resolves the persistent performance trade-off dilemma in self-healing materials but also significantly shortens material screening cycles, and more importantly develops a universal machine learning framework applicable to the design of multifunctional polymer materials. This provides a standardized technical solution for the targeted development of intelligent materials.Experimental
Synthetic route of PSSNM
The synthesis route of PSSNM is shown in Fig. S1. Firstly, NIAM was obtained via a two-step process, and the synthetic method of NIAM was referred to the ref. 46 Then, PTMEG (1.50 g, 1.50 mmol) was added to a three-necked flask at 110 °C under vacuum for 2 h. Then, IPDI, 10 µL of dibutyltin dilaurate (DBTDL) and 2 mL of anhydrous N,N-dimethylacetamide (DMAc) were poured into the above flask and the reaction mixture was stirred at 80 °C for 3 h under Ar atmosphere to obtain the prepolymer. The pre-weighed HEDS and anhydrous DMAc (2 mL) were added to the former system at 80 °C for 2 h. After that, NIAM chain extender and anhydrous DMAc (8 mL) were introduced, and the mixture was reacted for another 4 h. Finally, the solution was dried in a vacuum oven at 90 °C for 24 h to obtain PSSNM. The synthetic feed ratios and corresponding properties of PSSNM are summarized in Tables S1–S5, S8 and S12.Synthetic route of PBP
The synthesis route of PBP is shown in Fig. S12. PTMEG (1.50 g, 1.50 mmol) was introduced into a three-necked flask and heated under vacuum at 110 °C for 2 h. Next, 4,4′-dicyclohexylmethane diisocyanate (HMDI), 10 µL of DBTDL, and 3 mL of anhydrous N,N-dimethylformamide (DMF) were added to the flask, and the reaction mixture was stirred at 80 °C for 3 h under Ar atmosphere to form the prepolymer. Subsequently, pre-weighed 4,4′-biphenol (BP) and an additional 3 mL of anhydrous DMF were incorporated into the system and the reaction was carried out at 80 °C for 2 h. Then, 2,6-pyridinedimethanol (PDM) and anhydrous DMF (3 mL) were introduced, and the reaction was continued for another 3 h. Finally, the resulting solution was dried in a vacuum oven at 90 °C for 24 h to yield the desired polymer PBP. The synthetic feed ratios and corresponding properties of PBP are summarized in Table S13.Machine learning section
To predict and optimize the mechanical and self-healing properties of PU systems, we developed a machine learning framework based on GBR, implemented in scikit-learn. GBR is an ensemble learning technique that builds a strong predictive model by sequentially combining multiple weak learners (typically decision trees). Each new tree is trained to correct the errors made by the ensemble of existing trees, focusing on the residual errors from the previous stage. This iterative boosting process makes GBR particularly effective at capturing complex, non-linear relationships even with limited data. Input features were standardized, and mechanical property targets (σ, ε, T) were log-transformed to account for differences in scale. The dataset was divided into training (80%) and testing (20%) subsets. Hyperparameters were tuned via grid search to minimize prediction error. Model performance was assessed using mean absolute error (MAE) and R2. The trained GBR models were integrated with a multi-objective evolutionary algorithm, NSGA-III, to search for optimal formulations across six objectives: σ, ε, T and the corresponding self-healing efficiencies (ησ, ηε, ηT). NSGA-III employs a systematic evolutionary search mechanism that efficiently handles the simultaneous optimization of multiple conflicting performance metrics, particularly in complex scenarios such as six-objective problems. It is capable of stably generating a well-distributed and convergent Pareto optimal solution set. In contrast, other popular multi-objective methods, such as, Thompson sampling efficient multi-objective optimization (TSEMO), particle swarm optimization (PSO), and multi-objective Bayesian optimization (MOBO), are generally more suited for resolving non-contradictory or low-dimensional (2–3 objectives) trade-off optimization problems, which are not utilized in this work.47–49 The optimization was initialized with 500 random compositions and evolved over 500 generations using crossover and mutation operators. All predicted outputs were normalized to [0, 1] and aggregated into two weighted indices representing mechanical (Z1) and self-healing (Z2) performance. This integrated framework enables efficient exploration of the compositional space and identification of candidates with balanced, high-performance properties. Code used in this study is available at the GitHub repository: https://github.com/chemwangl/Active-learning-for-self-healing-polyurethane-materials.Materials, characterization details, mechanical and self-healing testing methods, and other machine learning details are stated in the SI.
Author contributions
Kang Liang: data curation, methodology, conceptualization, formal analysis, investigation, writing – original draft. Xinke Qi: formal analysis, investigation, software, validation. xu xiao: investigation, methodology. Li Wang: resources, supervision, funding acquisition, writing – review & editing. Jinglai Zhang: resources, funding acquisition, project administration.Conflicts of interest
There are no conflicts to declare.Data availability
All data on which this publication is based appear either in the main text or in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sc07752d.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22578099) and Basic Research Program of key scientific research projects in Henan province (23ZX010 (https://www.sciencedirect.com/science/article/pii/S0257897223004498)).Notes and references
- A. Mouren and L. Avérous, Chem. Soc. Rev., 2023, 52, 277–317 RSC.
- H. Wang, T. Li, J. Li, R. Zhao, A. Ding and F.-J. Xu, Prog. Polym. Sci., 2024, 151, 101803 CrossRef CAS.
- A. Delavarde, G. Savin, P. Derkenne, M. Boursier, R. Morales-Cerrada, B. Nottelet, J. Pinaud and S. Caillol, Prog. Polym. Sci., 2024, 151, 101805 CrossRef CAS.
- C. Li, X. Su, C. Cao, X. Li and M. Zou, Chem. Sci., 2025, 16, 2295–2306 RSC.
- R. H. Aguirresarobe, S. Nevejans, B. Reck, L. Irusta, H. Sardon, J. M. Asua and N. Ballard, Prog. Polym. Sci., 2021, 114, 101362 CrossRef.
- T. Liu, X. Wang, F. Sun, L. Wang, C. Hu, B. Yao, J. Xu and J. Fu, Nat. Commun., 2025, 16, 9555 CrossRef CAS PubMed.
- J. Chen, D. Wang and J. Fu, Adv. Mater., 2025, 37, e07548 CrossRef CAS.
- H. Wu, H. Wang, M. Luo, Z. Yuan, Y. Chen, B. Jin, W. Wu, B. Ye, H. Zhang and J. Wu, Mater. Horiz., 2024, 11, 1548–1559 Search PubMed.
- L. Cheng, D. Jiao, L. Cao, P. Hou, K. Deng and C. Liu, Prog. Org. Coat., 2024, 194, 108579 CrossRef CAS.
- Y. Chen, Q. Wang, L. Hou, H. Huang, Z. Gao and Y. Wei, Exploration, 2025, 5, e20240066 CrossRef CAS.
- C. Zhang, Z. Cui, Y. Zhang, Z.-H. Ren and Z.-H. Guan, ACS Appl. Polym. Mater., 2024, 6, 9986–9994 CrossRef CAS.
- J. Huang, W. Yao, X. Cui, L. Si, D. Yang, X. Liu and W. Liu, Chem. Eng. Sci., 2024, 293, 120030 CrossRef CAS.
- Y. Ma, Q.-Y. Tang, J. Zhu, L.-H. Wang and C. Yao, Chin. Chem. Lett., 2014, 25, 680–686 CrossRef CAS.
- W. Yang, Y. Zhu, T. Liu, D. Puglia, J. M. Kenny, P. Xu, R. Zhang and P. Ma, Adv. Funct. Mater., 2023, 33, 2213294 CrossRef CAS.
- D. Zhao, X. Li, Q. Li, C. Yue, Y. Wang and H. Li, Chem. Sci., 2024, 15, 13306–13312 RSC.
- Y. Xu, S. Zhou, Z. Wu, X. Yang, N. Li, Z. Qin and T. Jiao, Chem.–Eng. J., 2023, 466, 143179 CrossRef CAS.
- M. Zhang, Y. Wang, M. Yang, L. Sun, G. Zhao, P. Feng, N. Li, C. Liu, J. Xu, X. Jian and Y. Chen, Macromolecules, 2024, 57, 3047–3057 Search PubMed.
- D. Wang, J. Xu, J. Chen, P. Hu, Y. Wang, W. Jiang and J. Fu, Adv. Funct. Mater., 2020, 30, 1907109 CrossRef CAS.
- C.-H. Li, C. Wang, C. Keplinger, J.-L. Zuo, L. Jin, Y. Sun, P. Zheng, Y. Cao, F. Lissel, C. Linder, X.-Z. You and Z. Bao, Nature Chem., 2016, 8, 618–624 CrossRef CAS PubMed.
- F. Xu, H. Li and Y. Li, Adv. Mater., 2024, 36, 2412317 CrossRef CAS PubMed.
- Y. Su, X. Wang, Y. Ye, Y. Xie, Y. Xu, Y. Jiang and C. Wang, Chem. Sci., 2024, 15, 12200–12233 RSC.
- S. M. McDonald, E. K. Augustine, Q. Lanners, C. Rudin, L. Catherine Brinson and M. L. Becker, Nat. Commun., 2023, 14, 4838 CrossRef CAS PubMed.
- T. Erps, M. Foshey, M. K. Luković, W. Shou, H. H. Goetzke, H. Dietsch, K. Stoll, B. von Vacano and W. Matusik, Sci. Adv., 2021, 7, eabf7435 CrossRef CAS PubMed.
- S.-C. Lai, J. Jin and Z.-H. Luo, React. Chem. Eng., 2025, 10, 942–952 RSC.
- X. Wu, R. C. Turnell-Ritson, P. Han, J.-C. Schmidt, L. Piveteau, N. Yan and P. J. Dyson, Nat. Commun., 2025, 16, 4322 CrossRef CAS PubMed.
- B. Shi, T. Lookman and D. Xue, MGE Advances, 2023, 1, e14 Search PubMed.
- M. Eisenberg and M. Wimmer, Softw. Syst. Model., 2025, 24, 891–921 CrossRef.
- J. Leem, Y. Jiang, A. Robinson, Y. Xia and X. Zheng, Adv. Funct. Mater., 2023, 33, 2304451 Search PubMed.
- L.-Q. Huang, H.-X. Huang, N. Yu, C.-Z. Chen, Y. Liu, G.-H. Hu, J. Du and H. Zhao, Macromolecules, 2025, 58, 1425–1434 CrossRef CAS.
- H. Sun, J. Yao, X. Li, Y. Liu and H. Gu, Sci. Rep., 2025, 15, 17227 CrossRef CAS PubMed.
- T. Miller, I. Durlik, A. Łobodzińska, L. Dorobczyński and R. Jasionowski, Appl. Sci., 2024, 14, 11612 CrossRef CAS.
- G. Chen and D.-M. Tang, Nanomaterials, 2024, 14, 1688 CrossRef CAS PubMed.
- K. Xu, G. Chen, M. Zhao, W. He, Q. Hu and Y. Pu, RSC Adv., 2022, 12, 2712–2720 RSC.
- J. R. Gouveia, R. R. de Sousa Júnior, A. O. Ribeiro, S. A. Saraiva and D. J. dos Santos, Eur. Polym. J., 2020, 131, 109690 CrossRef CAS.
- Q. Qu, J. He, Y. Da, M. Zhu, Y. Liu, X. Li, X. Tian and H. Wang, Macromolecules, 2021, 54, 8243–8254 CrossRef CAS.
- D. Liu, C.-J. Fan, Y. Xiao, K.-K. Yang and Y.-Z. Wang, Polymer, 2022, 263, 125513 CrossRef CAS.
- J. Hu, R. Yang, L. Zhang, Y. Chen, X. Sheng and X. Zhang, Polymer, 2021, 222, 123674 CrossRef CAS.
- X. Liu, X. Liu, W. Li, Y. Ru, Y. Li, A. Sun and L. Wei, Chem.–Eng. J., 2021, 410, 128300 CrossRef CAS.
- P. Müller, A. D. Clayton, J. Manson, S. Riley, O. S. May, N. Govan, S. Notman, S. V. Ley, T. W. Chamberlain and R. A. Bourne, React. Chem. Eng., 2022, 7, 987–993 RSC.
- Q. Gu, Q. Xu and X. Li, Expert Syst. Appl., 2022, 207, 117738 CrossRef.
- X. Wu, M. Li, H. Li, H. Gao, Z. Wang and Z. Wang, Small, 2024, 20, 2311131 CrossRef CAS.
- Y. Yao, Z. Xu, B. Liu, M. Xiao, J. Yang and W. Liu, Adv. Funct. Mater., 2021, 31, 2006944 CrossRef CAS.
- X. Fu, P. Lu, Y. Fan, J. Xu, S. Zhu and J. Zhao, Chem.–Eng. J., 2025, 505, 159568 CrossRef CAS.
- L. Cheng, C. Liu, H. Zhao and L. Wang, Chem.–Eng. J., 2023, 467, 143463 CrossRef CAS.
- C. Liu, L. Cheng, L.-Y. Cui, P. Hou, B. Qian and R.-C. Zeng, J. Mater. Sci. Technol., 2023, 152, 169–180 CrossRef CAS.
- C. Chen, T. Zhang, X. Zhou, H. Lin, J. Cui, X. Liu and H. Li, Prog. Org. Coat., 2022, 167, 106826 CrossRef CAS.
- S. T. Knox, S. J. Parkinson, C. Y. P. Wilding, R. A. Bourne and N. J. Warren, Polym. Chem., 2022, 13, 1576–1585 RSC.
- A. Selvam, S. Mayilswamy, R. Whenish, K. Naresh, V. Shanmugam and O. Das, Sci. Rep., 2022, 12, 16887 CrossRef CAS.
- J. I. Myung, J. R. Deneault, J. Chang, I. Kang, B. Maruyama and M. A. Pitt, Digital Discovery, 2025, 4, 464–476 RSC.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |