Spinel-type Al₄C₃ attainable above 7 GPa and more high-pressure phases of Al₄C₃

Abstract

We predict that Al₄C₃ adopts a cubic, anti-spinel-type structure (Al₄C₃-II) between 7 and 33 GPa, peaking in stability relative to other Al₄C₃ structures at 26 GPa. At ambient pressure, Al₄C₃-II is mechanically robust, with a bulk modulus of 160 GPa and a Vickers hardness of around 30 GPa. Beyond Al₄C₃-II, we identify three additional post-spinel phases appearing in the Al₄C₃ phase diagram, including an anti-Th₃P₄-type at 140 GPa. The clear enthalpy differences under pressure leave little doubt that the known trigonal R3̄m ground state of Al₄C₃ will undergo multiple phase transitions. The accessible pressure window for spinel-type Al₄C₃-II is easily accessible in both laser-heated diamond anvil cell and large-volume multi-anvil cell experiments. We therefore encourage experimental exploration of the Al–C system at high pressure.

---

Introduction

High-pressure chemistry is a rich field in materials research, and advanced synthesis techniques have delivered a variety of new compounds in recent times.^1–4 A notable research method is the laser heating-diamond anvil cell (LH-DAC) used in conjunction with in situ X-ray diffraction (XRD).^5–7 Modern LH-DAC equipment can explore temperatures and pressures above ∼5000 K and 300 GPa,^8–10 and enables dynamic compression rates of several 100 GPa s⁻¹.^11–13 Larger volumes of material can be synthesized using Multi-Anvil-Cells (MAC) at pressures up to 50 GPa.¹⁴

Computational methods are now a standard tool for characterizing synthesized materials and are essential for exploring the phase space and advancing experimental research at high pressure.^15,16 For example, the spinel-type γ-Si₃N₄ was achieved at 15 GPa and 2000 K through a collaborative effort of computation and experiment.¹⁷ Recently, after more than three decades of effort, a crystal phase of C₃N₄ was synthesized at high pressure (>100 GPa).^18–21

Hitherto, the only known polymorph of Al₄C₃ is the trigonal (R3̄m) ground state structure.^22–24 The high-pressure behavior of Al₄C₃ was explored up to 6 GPa at 300 K.²⁵ Exploration at higher temperatures occurred only up to 8 GPa, but resulted in an incongruent thermal decomposition of Al₄C₃.^26,27 Recently, M₄C₃ with anti-Th₃P₄ type structures have been synthesized for Dy₄C₃ at 19 GPa and for Sc₄C₃ at 10 GPa.^28,29 Despite its simplicity, Al₄C₃ appears to have been overlooked,^30,31 and our own efforts had been communicated but not published. However, its composition suggests it may display a similar rich high-pressure chemistry as Si₃N₄.^32–38

Results and discussion

While computing several hundred polymorphs with composition A₄X₃ at different pressures, we ultimately identified four high-pressure modifications of Al₄C₃, indexed with Roman numerals (II, III, IV, and V), that surpass the trigonal ground-state modification Al₄C₃-I. In sequence, these are an anti-spinel type, an anti-CaFe₂O₄-like orthorhombic modification, an anti-CaFe₂O₄-type, and an anti-Th₃P₄ type. Polyhedral structure depictions are shown in Fig. 1.

Fig. 1 The five phases of Al₄C₃ studied. Space groups and (average) coordination numbers (CN) of Al are indicated. Black spheres represent carbon; aluminum is depicted in colored polyhedra.

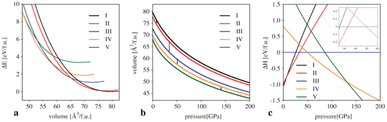
Ground state energies, lattice parameters, volumes, and bulk moduli of the structures are given in Table 1. The energy–volume, ΔE–V, diagram is shown in Fig. 2a, the corresponding pressure–volume diagram in Fig. 2b, and the enthalpy–pressure, ΔH–p, diagram is presented in Fig. 2c. Accordingly, the ground state modification will transform into the denser (anti-) spinel type of Al₄C₃-II at 7 GPa. This is a relatively low-pressure process that can be attained with various experimental equipment, including large-volume presses. The largest enthalpy difference of Al₄C₃-II to another phase, hence the maximum driving force for its formation, about 0.2 eV/Al₄C₃, is attained at 26 GPa. At 33 GPa, cubic Al₄C₃-II will be superseded by an orthorhombic structure that is related to the (anti-) CaFe₂O₄-type. This Al₄C₃-III remains favored up to 50 GPa, at which point it will transform into an (anti-) CaFe₂O₄-type. Finally, at pressures above 140 GPa, an (anti-) Th₃P₄-type of Al₄C₃-V will be the most favorable structure. This final structure resembles the high-pressure phases of Sc₄C₃ and Dy₄C₃, attained at 10 and 19 GPa, respectively.^28,29 Hence, the larger trivalent cations of Sc and Dy attain the (anti-) Th₃P₄-type at much lower pressures than the smaller Al³⁺ – a trend commonly observed in high-pressure chemistry of elements and compounds, including sesquioxides and sesquisulfide.^39–41 As expected, the densities of the Al₄C₃ polymorphs increase from phase I to V. Since the bulk moduli of the polymorphs are comparable, the initial slopes of the pressure–volume graphs (Fig. 2b) are very similar. That they remain so indicates a similar pressure dependence of the compressibility of the polymorphs. The average coordination number of Al₄C₃ polymorphs increases from phase I to V—except for the transition from the ground-state to the spinel-type structure (Fig. 1). This progression of phases thus reflects a systematic densification and coordination enhancement under pressure. The sequence of phase transformations, including transition pressure p_t and volume change at p_t, is summarized by

Table 1 Energy, lattice parameters, and volume of Al₄C₃ structures. The bulk modulus B₀ is computed from E–V data using the Murnaghan equation of state

	Energy (eV/Al4C3)	Lattice parameters (Å)	Volume (Å^3/Al4C3)	Bulk modulus (GPa)
I	−62.89	a = 3.33	79.64	172
		c = 24.88
II	−62.81	a = 8.53	77.65	176
III	−61.83	a = 9.24	72.56	170
		b = 3.12
		c = 10.08
IV	−61.02	a = 8.79	69.61	171
		b = 3.03
		c = 10.45
V	−59.56	a = 6.48	68.00	—

---

Fig. 2 (a) Energy–volume, ΔE–V, diagram of relevant Al₄C₃ polymorphs. The energy is given relative to Al₄C₃-I. (b) Pressure–volume diagram of relevant Al₄C₃ polymorphs. The arrows indicate transition pressures between the phases. Note that Al₄C₃-V is mechanically unstable below 30 GPa. (c) Enthalpy–volume, ΔH–p, diagram of relevant Al₄C₃ polymorphs. The enthalpy is given relative to Al₄C₃-III. The insert in the upper right corner details the transition sequence II–III–IV between 25 and 60 GPa. Black, red, blue, orange, and green lines represent Al₄C₃-I, II, III, IV, and V, respectively.

At ambient pressure, the energy difference between the (anti-) spinel-type of Al₄C₃-II and the ground state modification Al₄C₃-I is only 80 meV/Al₄C₃. LDA calculations even place Al₄C₃-II below Al₄C₃-I by 23 meV/Al₄C₃, although both structures are built up by AlC₄-tetrahedra only, and, thus, the number of nearest atoms (coordination number) of Al is identical.

The elastic constants of Al₄C₃ polymorphs (I–V) computed at zero pressure are shown in Table 2. Based on stability criteria,^42,43 the structures of Al₄C₃-I–IV are mechanically stable at ambient pressure. Thus, the high-pressure phases may be recoverable. While Al₄C₃-V is mechanically stable at 140 GPa, it becomes unstable below ∼30 GPa. A possible distortion along a Bain strain path may transform it into the spinel-type Al₄C₃-II.³³ The elastic constants can be used to compute the aggregate moduli, particularly the elastic shear modulus G. We obtain 123, 148, 70, and 110, for Al₄C₃-I–IV, respectively. Using the formula of Chen,⁴⁴ we estimate the Vickers hardness of Al₄C₃-I to 22 GPa and that of spinel-type Al₄C₃-II to 30 GPa. All polymorphs of Al₄C₃ presented here are semi-conductors, with band gaps of 1.6, 1.4, 1.9, 2.2, and 2.5 eV (GGA values) for Al₄C₃-I–V, respectively.

Table 2 Elastic constants (GPa) of Al₄C₃ polymorphs (I–V) computed at zero pressure (0 GPa)

	I	II	III	IV	V
C11	347	342	306	351	110
C22	347	342	424	510	110
C33	397	342	455	407	110
C44	111	168	17	65	−966
C55	116	168	17	53	−966
C66	116	168	151	141	−966
C12	124	94	65	76	134
C13	55	94	78	44	134
C14	14	0	0	0	0
C23	55	94	47	44	134

---

Computational method

We started our search for potential high-pressure modifications of Al₄C₃ by screening models that we previously considered for Si₃N₄.⁴⁵ The results were confirmed by evolutionary algorithms using the USPEX code,^46–48 with a slight modification to Al₄C₃-III. All structures were computed using density functional theory (DFT), implemented with the Vienna Ab initio Simulations Package (VASP).^49,50 We employed the projector augmented wave (PAW) formalism, along with the strongly constrained and approximately normed (SCAN) functional, for electron correlation and exchange.^51–53 A plane wave energy cutoff of 500 eV was applied, and fine grids sampled the Brillouin zone with spacings of 0.030–0.040 Å⁻¹.⁵⁴ With these parameters, forces, and energies converged to within 5 meV Å⁻¹ and 0.1 meV per atom, respectively. Throughout the work, we approximate Gibbs energy differences by enthalpy differences, hence ΔG ≈ ΔH. Potential contributions from defects, non-stoichiometry, or surface effects during growth may be factors that alter the thermodynamic balance through configurational or vibrational entropy. We assume that if these effects occur, they affect all structures similarly. Remaining entropy differences are, in general, much smaller in comparison to the much larger variation of ΔH within a few GPa of pressure. Justification for this common approach stems from calculations of the phase boundary between the β- and γ-phase of Si₃N₄, with γ-Si₃N₄ adopting the spinel-structure,⁵⁵ and from the prediction of a synthesis of Hf₃N₄ with Th₃P₄-structure from the elements.⁵⁶

Conclusions

We predict a cubic (anti-) spinel-type of Al₄C₃ succeeding the known trigonal ground state modification at higher pressures. While Al₄C₃-II is 0.08 meV/Al₄C₃ above the ground state at ambient pressure, it becomes thermodynamically favored between 7 and 33 GPa with a maximum enthalpy difference (hence, driving force) of 0.2 eV f.u.⁻¹ at 26 GPa. Al₄C₃-II is also stable against decomposition into the elements, by 1.8 and 1.7 eV/Al₄C₃ at ambient pressure and 30 GPa, respectively. The reported energy differences are well above the “uncertainty” of DFT calculations for enthalpies of formation differences, about 10 meV per atom.⁵⁷ The proposed stability range of spinel-type Al₄C₃ is accessible with large-volume presses⁵⁸ or LH-DAC.⁵ However, high temperatures may be required to facilitate the transition. Previous experiments examined pressures up to 8 GPa and maintained temperatures below 2500 K.^26,27 Al₄C₃-II is mechanically stable at ambient pressure, with a bulk modulus of 160 GPa comparable to that of Fe₃C or ThC.^59,60 The hardness of Al₄C₃-II will be substantially higher than that of the known modification, we estimate H_v ≈ 30 GPa for Al₄C₃-II.

Beyond Al₄C₃-II, the phase diagram of Al₄C₃ features three post-spinel modifications. Several other materials also exhibit post-spinel modifications, including CaFe₂O₄, ZnGa₂O₄, and CdCr₂Se₄.^61–66 For Si₃N₄, such phases were also proposed,^45,61 but ultimately a pernitride SiN₂ with N₂⁴⁻-units emerged. Motivated by this analogy, we explored a series of Al–C compounds with C₂-dimers in various oxidation states (C₂²⁻, C₂⁴⁻, and C₂⁶⁻), but none yielded a thermodynamically stable polymorph. In addition to Al₄C₃-I to Al₄C₃-V, we also identified several candidate structures of Al₄C₃ that, at certain pressures, approach the stability of the thermodynamically most favorable structure shown here. These include types related to SrPb₂O₄, P₄S₃, and further variants of the CaFe₂O₄-type. While our calculations neglect possible contributions from defects, non-stoichiometry, or surface effects – factors that could alter the thermodynamic balance through configurational or vibrational entropy – it is evident that Al₄C₃ will undergo pressure-induced phase transitions. We therefore encourage experimental efforts to synthesize the predicted Al₄C₃-II modification and advance the high-pressure chemistry of metal carbides.

Author contributions

Mitchell Falgoust: writing – review & editing, writing – original draft, visualization, methodology, investigation, formal analysis, data curation. Peter Kroll: writing – review & editing, writing – original draft, visualization, supervision, resources, project administration, methodology, investigation, funding acquisition, formal analysis, data curation, conceptualization.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting the article is available from the corresponding author upon reasonable request.

Acknowledgements

This work used Stampede3 at Texas Advanced Computing Center (TACC) through allocation DMR190103 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants #2138259, #2138286, #2138307, #2137603, and #2138296. Additional computational work was made possible by the High-Performance Computing facilities at the University of Texas at Arlington. MF was supported through a Graduate Dean Research Assistance fellowship.

References

1. J. V. Badding, High-Pressure Synthesis, Characterization, and Tuning of Solid State Materials, Annu. Rev. Mater. Res., 1998, 28, 631–658.
2. Y. Fei and M. J. Walter, Static and Dynamic High Pressure Mineral Physics, Cambridge University Press, Cambridge, 2022.
3. W. Zhao, J. Zhang, Z. Sun, G. Xiao, H. Zheng, K. Li, M.-R. Li and B. Zou, Chemical Synthesis Driven by High Pressure, CCS Chem., 2025, 7, 1250–1271.
4. S. Guo, Y. Zhang, K. Bu, Y. Zhan and X. Lü, High-Pressure Chemistry of Functional Materials, Chem. Commun., 2025, 61, 1773–1789.
5. A. Jayaraman, Diamond Anvil Cell and High-Pressure Physical Investigations, Rev. Mod. Phys., 1983, 55, 65.
6. W. A. Bassett, Diamond Anvil Cell, 50th Birthday, High Pressure Res., 2009, 29, Cp5–Cp186.
7. M. E. Alabdulkarim, W. D. Maxwell, V. Thapliyal and J. L. Maxwell, A Comprehensive Review of High-Pressure Laser-Induced Materials Processing, Part I: Laser-Heated Diamond Anvil Cells, J. Manuf. Mater. Process., 2022, 6, 111.
8. L. R. Benedetti and P. Loubeyre, Temperature Gradients, Wavelength-Dependent Emissivity, and Accuracy of High and Very-High Temperatures Measured in the Laser-Heated Diamond Cell, High Pressure Res., 2004, 24, 423–445.
9. S. Tateno, K. Hirose, Y. Ohishi and Y. Tatsumi, The Structure of Iron in Earth's Inner Core, Science, 2010, 330, 359–361.
10. N. Dubrovinskaia, et al., Terapascal Static Pressure Generation with Ultrahigh Yield Strength Nanodiamond, Sci. Adv., 2016, 2, e1600341.
11. M. Ricks, A. E. Gleason, F. Miozzi, H. Yang, S. Chariton, V. B. Prakapenka, S. Sinogeikin, R. L. Sandberg, W. L. Mao and S. Pandolfi, Phase Transition Kinetics Revealed by in Situ X-Ray Diffraction in Laser-Heated Dynamic Diamond Anvil Cells, Phys. Rev. Res., 2024, 6 DOI:10.1103/PhysRevResearch.6.0133316.
12. L. Q. Huston, L. Miyagi, R. J. Husband, K. Glazyrin, C. Kiessner, M. Wendt, H. P. Liermann and B. T. Sturtevant, New Dynamic Diamond Anvil Cell for Time-Resolved Radial X-Ray Diffraction, Rev. Sci. Instrum., 2024, 95, 043904.
13. W. J. Evans, C. S. Yoo, G. W. Lee, H. Cynn, M. J. Lipp and K. Visbeck, Dynamic Diamond Anvil Cell (Ddac): A Novel Device for Studying the Dynamic-Pressure Properties of Materials, Rev. Sci. Instrum., 2007, 78, 073904.
14. J.-a. Xu and H.-k. Mao, Moissanite: A Window for High-Pressure Experiments, Science, 2000, 290, 783–785.
15. N. P. Salke, et al., Prediction and Synthesis of Dysprosium Hydride Phases at High Pressure, Inorg. Chem., 2020, 59, 5303–5312.
16. P. V. Marshall, S. D. Thiel, E. E. Cote, R. Hrubiak, M. L. Whitaker, Y. Meng and J. P. S. Walsh, Combined First-Principles and Experimental Investigation into the Reactivity of Codeposited Chromium-Carbon under Pressure, ACS Mater. Au, 2024, 4, 393–402.
17. A. Zerr, G. Miehe, G. Serghiou, M. Schwarz, E. Kroke, R. Riedel, H. Fuess, P. Kroll and R. Boehler, Synthesis of Cubic Silicon Nitride, Nature, 1999, 400, 340–342.
18. A. Y. Liu and M. L. Cohen, Prediction of New Low Compressibility Solids, Science, 1989, 245, 841–842.
19. P. V. Zinin, L. C. Ming, S. K. Sharma, S. M. Hong, Y. Xie, T. Irifune and T. Shinmei, Synthesis of New Cubic C₃N₄ and Diamond-Like BC₃ Phases under High Pressure and High Temperature, in Joint 21st AIRAPT and 45th EHPRG International Conference on High Pressure Science and Technology, 2008, vol. 121.
20. D. Laniel, et al., Synthesis of Ultra-Incompressible and Recoverable Carbon Nitrides Featuring CN₄ Tetrahedra, Adv. Mater., 2024, 36, 2308030.
21. D. Laniel, et al., High-Pressure Synthesis of Op28-C₃N₄ Recoverable to Ambient Conditions, Adv. Funct. Mater., 2025, 35, 2416892.
22. M. von Stackelberg and E. Schorrenberg, The Structure of Aluminium Carbide Al₄C₃, Z. Phys. Chem. B, 1934, 27, 37.
23. J. H. Cox and L. M. Pidgeon, The X-Ray Diffraction Patterns of Aluminum Carbide Al₄C₃ and Aluminum Oxycarbide Al₄O₄C, Can. J. Chem., 1963, 41, 1414–1416.
24. T. M. Gesing and W. Jeitschko, The Crystal Structure and Chemical Properties of U₂Al₃C₄ and Structure Refinement of Al₄C₃, Z. Naturforsch., B: J. Chem. Sci., 1995, 50, 196–200.
25. V. L. Solozhenko and O. O. Kurakevych, Equation of State of Aluminum Carbide Al₄C₃, Solid State Commun., 2005, 133, 385–388.
26. J. C. Schuster, A Reinvestigation of the Thermal Decomposition of Aluminum Carbide and the Constitution of the Al-C System, J. Phase Equilib., 1991, 12, 546–549.
27. V. Turkevich, A. Garan, O. Kulik and I. Petrusha, Phase Diagram and Diamond Synthesis in the Aluminum–Carbon System at a Pressure of 8 GPa, Innovative Superhard Materials and Sustainable Coatings for Advanced Manufacturing, 2005, pp. 335–343.
28. E. A. Juarez-Arellano, et al., Formation of Scandium Carbides and Scandium Oxycarbide from the Elements at High-(P, T) Conditions, J. Solid State Chem., 2010, 183, 975–983.
29. F. I. Akbar, et al., High-Pressure Synthesis of Dysprosium Carbides, Front. Chem., 2023, 11 DOI:10.3389/fchem.2023.1210081.
30. L. Sun, Y. Gao, K. Yoshida, T. Yano and W. Wang, Prediction on Structural, Mechanical and Thermal Properties of Al₄SiC₄, Al₄C₃ and 4H-SiC under High Pressure by First-Principles Calculation, Mod. Phys. Lett. B, 2017, 31, 1750080.
31. A. Pisch, A. Pasturel, G. Deffrennes, O. Dezellus, P. Benigni and G. Mikaelian, Investigation of the Thermodynamic Properties of Al₄C₃: A Combined DFT and DSC Study, Comput. Mater. Sci., 2020, 171, 109100.
32. E. Kroke, High-Pressure Syntheses of Novel Binary Nitrogen Compounds of Main Group Elements, Angew. Chem., Int. Ed., 2002, 41, 77–82.
33. P. Kroll, Pathways to Metastable Nitride Structures, J. Solid State Chem., 2003, 176, 530–537.
34. P. Kroll and M. Milko, Theoretical Investigation of the Solid State Reaction of Silicon Nitride and Silicon Dioxide Forming Silicon Oxynitride (Si₂N₂O) under Pressure, Z. Anorg. Allg. Chem., 2003, 629, 1737–1750.
35. E. Horvath-Bordon, R. Riedel, A. Zerr, P. F. McMillan, G. Auffermann, Y. Prots, W. Bronger, R. Kniep and P. Kroll, High-Pressure Chemistry of Nitride-Based Materials, Chem. Soc. Rev., 2006, 35, 987–1014.
36. B. H. Yu and D. Chen, Phase Transition Characters and Thermodynamics Modeling of the Newly-Discovered Wii- and Post-Spinel Si₃N₄ Polymorphs: A First-Principles Investigation, Acta Metall. Sin. (Engl. Lett.), 2013, 26, 131–136.
37. L. Cui, M. Hu, Q. Q. Wang, B. Xu, D. L. Yu, Z. Y. Liu and J. L. He, Prediction of Novel Hard Phases of Si₃N₄: First-Principles Calculations, J. Solid State Chem., 2015, 228, 20–26.
38. Q. H. Wu, Z. T. Huo, C. Chen, X. Q. Li, Z. Wang, C. J. Wang, L. J. Zhang, Y. F. Gao, M. Xiong and K. M. Pan, Prediction of Four Si₃N₄ Compounds by First-Principles Calculations, AIP Adv., 2023, 13 DOI:10.1063/5.0130194.
39. A. Mujica, A. Rubio, A. Muñoz and R. J. Needs, High-Pressure Phases of Group-IV, III–V, and II–VI Compounds, Rev. Mod. Phys., 2003, 75, 863–912.
40. L. Liu and W. A. Bassett, Elements, Oxides, Silicates: High Pressure Phases with Implications for the Earth's Interior, Oxford University Press, New York, 1986, p. 250.
41. F. J. Manjón and D. Errandonea, Pressure-Induced Structural Phase Transitions in Materials and Earth Sciences, Phys. Status Solidi B, 2009, 246, 9–31.
42. J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford University Press, 1985.
43. F. Mouhat and F.-X. Coudert, Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
44. X.-Q. Chen, H. Niu, D. Li and Y. Li, Modeling Hardness of Polycrystalline Materials and Bulk Metallic Glasses, Intermetallics, 2011, 19, 1275–1281.
45. P. Kroll and J. von Appen, Post-Spinel Phases of Silicon Nitride, Phys. Status Solidi B, 2001, 226, R6–R7.
46. A. R. Oganov and C. W. Glass, Crystal Structure Prediction Using Ab Initio Evolutionary Techniques: Principles and Applications, J. Chem. Phys., 2006, 124, 244704.
47. A. R. Oganov, A. O. Lyakhov and M. Valle, How Evolutionary Crystal Structure Prediction Works—and Why, Acc. Chem. Res., 2011, 44, 227–237.
48. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, New Developments in Evolutionary Structure Prediction Algorithm USPEX, Comput. Phys. Commun., 2013, 184, 1172–1182.
49. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871.
50. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
51. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
52. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
53. J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402.
54. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 1976, 13, 5188–5192.
55. A. Togo and P. Kroll, First-Principles Lattice Dynamics Calculations of the Phase Boundary between β-Si₃N₄ and γ-Si₃N₄ at Elevated Temperatures and Pressures, J. Comput. Chem., 2008, 29, 2255–2259.
56. P. Kroll, Hafnium Nitride with Thorium Phosphide Structure: Physical Properties and an Assessment of the Hf-N, Zr-N, and Ti-N Phase Diagrams at High Pressures and Temperatures, Phys. Rev. Lett., 2003, 90, 125501.
57. A. Wang, R. Kingsbury, M. McDermott, M. Horton, A. Jain, S. P. Ong, S. Dwaraknath and K. A. Persson, A Framework for Quantifying Uncertainty in DFT Energy Corrections, Sci. Rep., 2021, 11, 15496.
58. L. G. Khvostantsev and V. N. Slesarev, Large-Volume High-Pressure Devices for Physical Investigations, Phys.-Usp., 2008, 51, 1099–1104.
59. M. Umemoto and H. Ohtsuka, Mechanical Properties of Cementite, ISIJ Int., 2022, 62, 1313–1333.
60. C. Yu, et al., Structural Phase Transition of ThC under High Pressure, Sci. Rep., 2017, 7, 96.
61. A. Zerr, A New High-Pressure Delta-Phase of Si₃N₄, Phys. Status Solidi B, 2001, 227, R4–R6.
62. W. Xu, G. Hearne, S. Layek, D. Levy, M. Pasternak, G. K. Rozenberg and E. Greenberg, Interplay between Structural and Magnetic-Electronic Responses of FeAl₂O₄ to a Megabar: Site Inversion and Spin Crossover, Phys. Rev. B, 2018, 97, 085120.
63. M. Sahu, Pressure-induced volume collapse and metallization in inverse spinel Co₂TiO₄, J. Phys.: Condens. Matter., 2025, 37, 345402.
64. I. Efthimiopoulos, Z. T. Y. Liu, M. Kucway, S. V. Khare, P. Sarin, V. Tsurkan, A. Loidl and Y. Wang, Pressure-Induced Phase Transitions in the CdCr₂Se₄ Spinel, Phys. Rev. B, 2016, 94, 174106.
65. D. Errandonea, R. S. Kumar, Y. Ma and C. Y. Tu, High-Pressure Structural Stability of Spinel-Type ZnGa₂O₄: A Synchrotron X-Ray Diffraction Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 024103.
66. T. Yamanaka, A. Uchida and Y. Nakamoto, Structural Transition of Post-Spinel Phases CaMn₂O₄, CaFe₂O₄, and CaTi₂O₄ under High Pressures up to 80 GPa, Am. Mineral., 2008, 93, 1874–1881.

---