Localization of the Au–Au bond strength in the triplet excited state of the [Au(CN)₂⁻] oligomers revealed by ultrafast time-domain Raman spectroscopy

Abstract

Photo-induced Au–Au bond formation and subsequent ultrafast dynamics of the [Au(CN)₂⁻] oligomers have been attracting much interest. To fully understand this unique photochemical process, it is important to elucidate the oligomer size dependence of the structure and dynamics in the excited state. In this study, we use time-resolved impulsive stimulated Raman spectroscopy to obtain Raman spectra of large [Au(CN)₂⁻] oligomers, the tetramer and pentamer, in the lowest excited triplet (T₁) state. We observe a frequency shift of the Au–Au stretch vibration, reflecting an ultrafast bent (zigzag)-to-linear structural change for the T₁ tetramer, as in the case of the T₁ trimer, indicating that this type of structural change commonly occurs with the photo-induced Au–Au bond formation in the [Au(CN)₂⁻] oligomers. With the addition of the Raman spectrum of the T₁ dimer newly measured, we compare the Raman spectra to discuss the structure of T₁ [Au(CN)₂⁻]_n (n = 2–5) with the help of complementary DFT calculations. The results of time-domain Raman spectroscopy and theoretical calculations indicate that the Au–Au bond strength(s) in the T₁ tetramer and T₁ pentamer are significantly stronger in the central dimer-like and trimer-like “core” parts, respectively, compared to the Au–Au bonds connecting two monomer units at both ends. This localization of bond strength highlights the distinct nature of the p_z–p_z σ chemical bond formed in the T₁ [Au(CN)₂⁻]_n oligomers, as a new type of chemical bond. This study expands our understanding of the photo-induced Au–Au bond formation process and the resulting excited-state structure of metal complex assemblies.

---

Introduction

Oligomers, which exist widely in nature, are formed through covalent bonds due to bond rearrangement, or weaker attractive forces such as the hydrogen bond and metallophilic interaction. They play important roles in realizing various functions. For example, in plants, photoactivation and inactivation of some biological functions occur through oligomer formation and dissociation of photoreceptor proteins, such as cryptochrome^1,2 and UVR8.³ In natural and artificial functional systems, oligomers also serve as the working units for light-harvesting and photovoltaic processes in self-assembly dendrimers, ring-shaped porphyrin oligomers,⁴ perylene bisimide dimer/trimer aggregates,⁵ and so on.

Oligomers of complexes containing transition metals like Re(I),⁶ Pt(II),^7,8 and Au(I)^9–11 are used as functional molecular assemblies and light-emissive materials. Among them, the complex of dicyanoaurate(I), [Au(CN)₂⁻], is one of the most prototypical complexes forming oligomers in an aqueous solution. Different sizes of oligomers with loosely bonded structures are formed due to weak aurophilic interaction in the ground state, and covalent bonds are formed among the gold atoms in the monomer unit with photoexcitation that excites an electron from an anti-bonding d_zσ* orbital to a bonding p_zσ orbital.^9,10,12 Therefore, the [Au(CN)₂⁻]_n oligomer has been considered a suitable system for investigating the ultrafast structural dynamics associated with chemical bond formation.

The excited-state dynamics of the [Au(CN)₂⁻] trimer were first studied by femtosecond time-resolved absorption spectroscopy in 2013.¹² This study concluded that the intersystem crossing (ISC) of the excited-state trimer proceeds on a 0.5 ps time scale after photoexcitation and then, a bent-to-linear structural change takes place with a 2.1 ps time constant in the lowest excited triplet (T₁) state. Later, time-resolved X-ray scattering measurements were performed, and it was claimed that the bent-to-linear structural change of the trimer first finishes within 0.5 ps, and then the Au–Au bonds gradually shorten with a 1.6 ps time constant,¹³ which is markedly different from the initial assignment. To solve the controversy, ultrafast time-domain Raman spectroscopy, i.e., time-resolved impulsive stimulated Raman spectroscopy (TR-ISRS), was applied. A characteristic Raman band of the T₁ trimer was observed at 90 cm⁻¹, and the rise and frequency shift of this band revealed that the ISC and the bent-to-linear structural change occur with time constants of 0.4 ps and 3 ps,¹⁴ respectively, which supported the conclusion of the first time-resolved absorption study. This TR-ISRS study also clarified that the controversy arose because oligomers of different sizes coexist in the samples used in the earlier studies. In particular, X-ray scattering measurements cannot clearly distinguish oligomers of different sizes coexisting in solution. Indeed, in 2020, Kim et al. reported wavepacket motions with frequencies at 79 and 125 cm⁻¹ observed in time-resolved X-ray scattering measurements and attributed them to the T₁ trimer.¹⁵ However, the 125 cm⁻¹ vibration is highly likely due to the T₁ dimer (∼130 cm⁻¹), which was observed as an oscillatory component of the femtosecond time-resolved absorption signal reported in an earlier study.¹⁶

Recently, we performed femtosecond time-resolved absorption and emission measurements of K[Au(CN)₂] aqueous solutions while changing the concentration and excitation wavelength systematically, and succeeded in separating the dynamics of the excited-state [Au(CN)₂⁻] oligomers having different sizes. Notably, the time constants of ISC have been determined to be 0.2 ps (dimer), 0.38 ps (trimer), 2.6 ps (tetramer), and 13 ps (pentamer), respectively.¹⁷ Furthermore, coherent wavepacket motions of individual oligomers immediately after photoexcitation were compared, and the center wavelength of the transient absorption band giving rise to each oscillation was determined from the node position of the amplitude of the wavepacket motion detected. Nevertheless, time-resolved absorption and emission spectroscopy can only provide limited information on the excited-state dynamics. For example, it is difficult to obtain unambiguous information about the excited-state structural evolution from featureless electronic spectra. More importantly, direct comparison of the vibrational frequency of the excited-state oligomers having different sizes has not been realized for the excited state having the same spin multiplicity, because the wavepacket motions of the T₁ oligomers were observed for the dimer and trimer, whereas those of the S₁ oligomers were detected for the pentamer and tetramer in time-resolved absorption measurements. Therefore, it is desirable to observe and compare the vibrational spectra of common excited states to obtain a comprehensive understanding of the excited-state properties of the [Au(CN)₂⁻] oligomers with different sizes. In particular, understanding the properties of the T₁ oligomers is important from the viewpoint of application for the emission device because they are directly related to the emission properties of this system.

As already mentioned, ultrafast time-domain Raman spectroscopy has been successfully applied to examine the [Au(CN)₂⁻] trimer¹⁴ and demonstrated that the T₁ oligomer exhibits a distinct Raman spectrum in the low-frequency terahertz region for which time-domain Raman measurements are advantageous. Here, we report a thorough TR-ISRS study of K[Au(CN)₂] aqueous solutions. Through the time-domain Raman data obtained while systematically changing the concentration of the solutions, we succeed in the separation of the Raman spectra of the T₁ [Au(CN)₂⁻] oligomers from the dimer to pentamer, allowing us to clarify the properties and formation process of the T₁ [Au(CN)₂⁻] oligomers from the vibrational viewpoint: the temporal change of the Raman spectra reveals that the structural change of the excited-state tetramer occurs on the T₁ potential energy surface after the formation of covalent Au–Au bonds, as in the case of the trimer. Furthermore, the comparison of the Raman spectra of four T₁ [Au(CN)₂⁻]_n oligomers (n = 2–5) reveals that the spectrum of the T₁ oligomer with even and odd sizes exhibits distinct spectral features from each other, which reflects the difference and localization of the Au–Au bond strengths in large T₁ oligomers.

Methods

Time-resolved impulsive stimulated Raman spectroscopy (TR-ISRS)

Details of the TR-ISRS experimental setup based on a Ti:sapphire amplifier have been described elsewhere.¹⁸ In this study, we used a newly constructed setup based on a Yb:KGW regenerative amplifier (PHAROS-6W, Light Conversion, 1030 nm, 1 kHz). Briefly, the output of the amplifier was split into two parts. One part was used to generate the actinic pump pulse (P₁, 343 nm, 90 nJ) through third-harmonic generation. The pulse duration of the actinic pump pulse was adjusted using a folded 4f grating compressor. To avoid the generation of the coherent nuclear wave packet in the sample, the duration of the actinic pump pulse was set to 450 fs in this study. The second part of the regenerative amplifier output was used for the generation of white light continuum and the third harmonic, which are used as a seed and a pump pulse for a home-built non-collinear optical parametric amplifier (NOPA), respectively, to generate a broadband femtosecond pulse. The output of the NOPA was compressed to 20 fs utilizing a pair of chirp mirrors and glass wedges. The generated ultrashort pulse was split into two, and they served as the Raman pump pulse (P₂, 580–650 nm, 30 nJ) and Raman probe pulse (P₃, 580–650 nm, 2 nJ). The characterization of the Raman pump and Raman probe pulses was carried out by the frequency-resolved optical gating at the sample position. Three pulses (P₁, P₂, and P₃) were focused together onto a flow cell with a 0.5 mm path length, through which the sample solution was flowed during the measurement to avoid photo-degradation. TR-ISRS measurements were conducted at the magic angle polarization condition between the actinic pump (P₁) and Raman pump (P₂) pulses. The polarizations of the Raman pump (P₂) and Raman probe (P₃) pulses were set to be parallel.

Quantum chemical calculations

Quantum chemical calculations of the optimized geometries, vibrational frequencies, and Raman intensities for [Au(CN)₂⁻]_n (n = 2–5) in the T₁ states were carried out with density functional theory (DFT) using GAUSSIAN 16, Rev A03.¹⁹ The density functional employed was a hybrid density functional proposed by Perdew, Burke and Ernzerhof (PBE1PBE).^20,21 The basis functions used were LANL2TZ(f)^22,23 with the Los Alamos relativistic effective core potential for the Au atom, and LANL2DZ extended with polarization functions (d,p) for H, C, and N atoms.²⁴ Although spin–orbit coupling (SOC) can often cause mixing of electronic configurations between T₁ and T_n or S_n, we ignored SOC interaction in the DFT calculations since DFT calculations including SOC for the tetramer revealed that the lowest excited states with three spin states were composed of almost pure T₁ electronic configurations, as shown in Table S1. To mimic the environmental perturbation for the geometry of the excited state and excitation energy, a polarizable continuum model (PCM) was employed using H₂O as solvent.²⁵ The structural dependence of vibrational frequencies and Raman intensities for the tetramer was examined using the T₁ geometries obtained by partial optimization with constraints of the Au–Au–Au angle. The excitation energies calculated with TDDFT at the optimized T₁ geometries were 3.608 eV (344 nm) for the dimer, 3.007 eV (412 nm) for the trimer, 2.707 eV (458 nm) for the tetramer, and 2.542 eV (488 nm) for the pentamer. These values fairly well reproduced the observed peak wavelengths of the phosphorescence spectra: 330 nm (dimer), 390 nm (trimer), 430 nm (tetramer), and 460 nm (pentamer), confirming the reliability of the calculation models used in this study.^16,17

Sample preparation

K[Au(CN)₂] was purchased from TAKANA Precious Metals Co. (99.5% grade) and recrystallized several times from water that was purified by a Milli-Q system (Millipore) before use. The steady-state absorption spectra were measured before and after each TR-ISRS measurement using a commercial UV-visible absorption spectrometer (Hitachi U-3310) to ensure no noticeable photodegradation.

Results & discussion

Steady-state and time-resolved absorption spectra of large oligomers (tetramer and pentamer)

Steady-state UV-visible absorption spectra of K[Au(CN)₂] aqueous solution in the concentration range from 315 mM to 685 mM (C = 315–685 mM) are shown in Fig. 1. The spectrum exhibits significant changes as the concentration increases: although a dilute aqueous solution (C < 0.04 mM) only shows absorption due to the monomer in the wavelength region below 245 nm (data not shown), the red edge of the absorption extends to the longer wavelength side as the concentration increases, reflecting the formation of the oligomer. The analysis of the concentration dependence of the steady-state absorption and emission spectra showed that large oligomers, such as the tetramer and the pentamer, are sequentially formed in the ground state in the high concentration range from 315 mM to 685 mM.^17,26 In our previous study, we measured femtosecond time-resolved absorption spectra of a 0.61 M solution with photoexcitation at 340 nm and found that the excited-state tetramer and pentamer are predominantly generated. The time-resolved absorption spectrum at ΔT = 120 ps after photoexcitation at 340 nm is also shown in Fig. 1. It exhibits a broad absorption band peaked at ∼650 nm, which is attributed to the T_n ← T₁ excited-state absorption (ESA) of the tetramer and the pentamer generated after intersystem crossing.¹⁷ Therefore, in the TR-ISRS measurements to examine the T₁ tetramer and T₁ pentamer, we set the wavelength of the Raman pump/probe (P₂ & P₃) to 580–650 nm, which is in resonance with the T_n ← T₁ ESA band of these large oligomers. The duration of the Raman pump/probe (P₂ & P₃) pulses is 20 fs, whereas the actinic pump (P₁) is stretched to 450 fs, not to induce coherent wavepacket motion with the actinic pump process.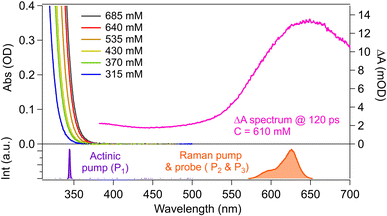

Fig. 1 Steady-state and time-resolved absorption spectra of K[Au(CN)₂] aqueous solution. Steady-state absorption spectra were measured at various concentrations from 315 mM to 685 mM, and the femtosecond time-resolved absorption spectrum was measured at 610 mM at 120 ps after photoexcitation with λ_exc = 340 nm (this time-resolved spectrum is the same as reported in ref. 17). The spectra of the actinic pump (P₁) and the Raman pump/probe (P₂/P₃) pulses are also shown at the bottom.

Femtosecond time-resolved Raman spectra of large oligomers (tetramer and pentamer) obtained by TR-ISRS measurements

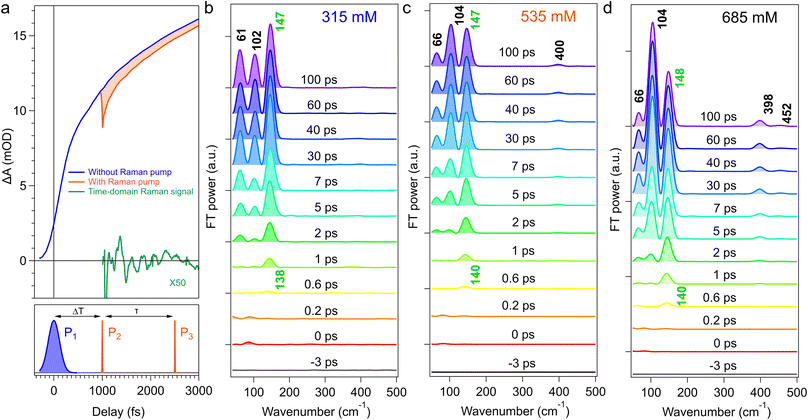
Fig. 2a depicts a typical procedure to obtain raw TR-ISRS data, taking the experiment at 685 mM as an example. In the TR-ISRS measurement, we first introduce the actinic pump pulse P₁ for photoexcitation, and the transient absorption signal appears. Then, at a certain delay time of ΔT, the Raman pump pulse P₂ is irradiated to induce Raman-active coherent nuclear motion of transients, and the P₂-induced difference in the transient absorption signal is measured with the Raman probe pulse P₃ while scanning the time delay (τ) between the P₂ and P₃ pulses. The difference between the transient absorption signals with and without the Raman pump pulse is the raw TR-ISRS data (red shaded). By subtracting population components from the raw TR-ISRS data using multi-exponential curve fitting, the oscillatory component (green curve) is extracted, which provides time-domain Raman data of the transients. Finally, after applying a Hanning window and zero paddings, the Fourier transform (FT) of the oscillatory component provides the femtosecond time-resolved Raman spectrum at the delay time of ΔT (1 ps in this case).

Fig. 2 Femtosecond time-resolved Raman spectra of K[Au(CN)₂] aqueous solution at various concentrations measured with TR-ISRS. (a) Pulse sequence and a typical procedure to obtain raw time-domain Raman signals. The data taken from a K[Au(CN)₂] aqueous solution at 685 mM measured at ΔT = 1 ps are used as an example. Time-resolved FT power spectra at various ΔT delay times at (b) 315 mM, (c) 535 mM, and (d) 685 mM.

We measured femtosecond time-resolved Raman spectra of [Au(CN)₂⁻] oligomers in a wide concentration range from 315 to 685 mM. Fig. 2b–d show time-resolved FT-power Raman spectra in the low-frequency region measured at 315, 535, and 685 mM, obtained with Fourier transformation. The spectra in the high-frequency region are not shown because they only show C≡N stretch vibrations that cannot be measured with the 20 fs pulses used in the present study. The time-resolved Raman spectra at all concentrations are given in Fig. S1 in the SI.

In time-resolved Raman spectra at 315 mM (Fig. 2b), a transient Raman band at ∼140 cm⁻¹ can be noticed at ΔT = 0.6 ps after photoexcitation, and its intensity gradually increases with two other transient Raman bands at ∼60 and ∼100 cm⁻¹ in the first 5 ps. These Raman bands are attributable to the T₁ tetramer.¹⁴ While the intensity of these bands increases in the early picosecond region, the Raman band at ∼140 cm⁻¹ simultaneously exhibits a noticeable upshift from 138 to 147 cm⁻¹, indicating a structural change occurring in the T₁ tetramer. After 10 ps, no further spectral change is observed in the ΔT delay time window of the present measurement (100 ps).

The time-resolved Raman spectra measured at 535 mM and 685 mM are shown in Fig. 2c and d, respectively. As seen in these figures, the relative intensity and temporal evolution of the transient Raman bands change with increasing concentration. For instance, the intensity of the ∼100 cm⁻¹ band relative to the ∼140 cm⁻¹ band at ΔT = 100 ps becomes significantly higher as the concentration increases (the normalized FT power Raman spectra at all concentrations are shown in Section S2 in SI). In fact, the ∼100 cm⁻¹ band keeps growing even after 10 ps at 685 mM, although it remains unchanged after 10 ps at 315 mM. Furthermore, a new ∼400 cm⁻¹ Raman band appears at C > 315 mM. This concentration-dependent change in the time-resolved Raman spectra cannot be rationalized simply by the temporal change of a single excited-state population. It clearly indicates that another oligomer other than the T₁ tetramer, i.e., the T₁ pentamer, contributes to the time-resolved Raman spectra obtained at high concentrations.

To obtain quantitative information from the femtosecond time-resolved Raman spectra, we performed the global fitting analysis. The real-part FT spectrum exhibits the “absorptive” bandshape in the present experiments (Fig. S3 shows the real-part and imaginary-part of the FT spectra). Thus, we analyzed the temporal profiles of the real-part amplitudes at ∼60, ∼100, ∼140, and ∼400 cm⁻¹. The temporal traces observed at all six concentrations from 315 to 685 mM are well fitted with a sum of exponential functions convoluted with the instrumental response function, and the experimental data (open circles) and the best fits (dotted line) are shown in Fig. 3. Note that the sign of the real-part FT amplitude can be negative depending on the resonance condition, but the absolute amplitude represents the population evolution. So, the sign of the real-part FT amplitude at ∼60, ∼100, and ∼400 cm⁻¹ bands is inverted in this figure. The temporal profiles of the FT amplitudes at 60, 100, and 140 cm⁻¹ are well fitted with a single time constant, τ₁ = 2.6 ps, at 315 mM, whereas successful fits for all concentrations at 370–685 mM require two common time constants, τ₁ = 2.6 ps, τ₂ = 13 ps. In contrast, a single time constant τ₁ = 2.6 ps can well reproduce the temporal trace of the ∼140 cm⁻¹ band at all concentrations.

Fig. 3 Temporal profiles of the real-part FT amplitude of the transient Raman bands observed in K[Au(CN)₂] aqueous solution at various concentrations: (a) 60 cm⁻¹, (b) 100 cm⁻¹, (c) 140 cm⁻¹, and (d) 400 cm⁻¹. The best fits are also shown with dotted curves.

Our former studies of time-resolved absorption, time-resolved emission, and TR-ISRS of the [Au(CN)₂⁻] oligomers showed that the ISC times of the tetramer and the pentamer are 2.6 ps¹⁴ and 13 ps,¹⁷ respectively, which agree well with the τ₁ and τ₂ time constants obtained from the temporal traces of transient Raman bands. This confirms that the T₁ tetramer and the T₁ pentamer contribute to the femtosecond time-resolved Raman spectra shown in Fig. 2. Importantly, at 315 mM, lacking the τ₂ component indicates that only the T₁ tetramer is observed at this low concentration with 343 nm photoexcitation, and both the T₁ tetramer and the T₁ pentamer appear in the femtosecond time-resolved Raman spectra at 370–685 mM. Furthermore, the rise of the transient Raman band at ∼140 cm⁻¹ can be fit only with a single time constant (τ₁ = 2.6 ps) at all concentrations (315–685 mM), indicating that the ∼140 cm⁻¹ band is solely attributable to the T₁ tetramer regardless of the concentration because τ₁ is the time constant of the ISC of the tetramer.

Ultrafast structural changes of the tetramer

As described in the previous section, the ∼140 cm⁻¹ Raman amplitude increases single-exponentially under all concentrations, revealing that this Raman band is solely due to the T₁ tetramer. Importantly, this ∼140 cm⁻¹ Raman band exhibits a frequency upshift in the early picosecond time region. Fig. 4 plots the temporal frequency change of this band observed at 685 mM. The peak frequency of this Raman band shifts from 140 to 148 cm⁻¹ with a time constant of ∼4 ps.

Fig. 4 Temporal change of the Au–Au stretch vibration of the T₁ tetramer at ∼140 cm⁻¹. The experimental frequencies are taken from the time-resolved Raman spectra measured at C = 685 mM (black open circles), and the calculated Au–Au stretching frequency at different Au–Au–Au angles is obtained by DFT with geometrical optimization at each Au–Au–Au bent angle (red-filled circles).

It has been reported that the T₁ trimer undergoes a bent-to-linear structural change on a picosecond timescale after the photo-induced Au–Au bond formation.^12,14 Therefore, it is likely that a similar structural change also occurs in the T₁ tetramer. We performed a quantum chemical calculation using DFT to clarify the origin of the frequency shift observed for the ∼140 cm⁻¹ Raman band of the T₁ tetramer. In this calculation, we performed geometrical optimization of the T₁ tetramer at a fixed Au–Au–Au bent angle θ (shown in the inset of Fig. 4) and calculated Raman spectra of the T₁ tetramer (see Section S4 in SI for the details). Fig. 4 shows the Au–Au–Au bent angle dependence of an Au–Au stretching frequency at ∼140 cm⁻¹. As clearly seen, the calculated frequency exhibits an ∼10 cm⁻¹ upshift as the angle changes from 160° to 180°, which well reproduces the frequency upshift of the ∼140 cm⁻¹ band observed in the experiment. The good agreement between the experimental and theoretical results indicates that the frequency upshift of the ∼140 cm⁻¹ band arises from a bent (or a zigzag)-to-linear structural change occurring with an ∼4 ps time constant in the T₁ tetramer.

Analyzing time-resolved Raman spectra, we conclude that the [Au(CN)₂⁻] trimer and tetramer have similar photo-induced scenarios. After the photoexcitation, weak Au–Au bonds in the S₀ oligomers become tightened as covalent bonds are formed between the Au atoms in the S₁ state. Subsequently, the T₁ state is formed with the ISC (trimer 0.38 ps; tetramer 2.6 ps), and the structural change occurs from a bent or zigzag structure to a linear structure (trimer 3 ps;¹⁴ tetramer 4 ps). Considering the time constants for the structural change and ISC, the structural change of the trimer exclusively occurs in the T₁ state, whereas that of the tetramer likely takes place not only in the T₁ state but also in the S₁ state. For both the trimer and the tetramer, the structural changes proceed mainly with the displacement of the two monomer units at the edge, and such geometric constraints may result in similar time constants for the structural change of the T₁ trimer (3 ps) and the T₁ tetramer (4 ps). The larger stabilization energy of the linear structure, which is realized with the greater overlap of the p_z σ orbital, is considered to be the driving force for these photo-induced structural changes.

Comparison of the Raman spectra of the T₁ oligomers (n = 2–5) and the difference in the Au–Au bonds

Now, we are reaching a position to compare the T₁ Raman spectra of the dimer, trimer, tetramer, and pentamer to overview the character of the T₁ [Au(CN)₂⁻] oligomers having different sizes.

To do this, we first separately obtained T₁ Raman spectra of the pentamer and tetramer. In the femtosecond time-resolved Raman spectra at 315 mM, the real-part FT amplitudes of the Raman bands at ∼60, ∼100, and ∼140 cm⁻¹ exhibit a single exponential rise with the ISC time of the tetramer (2.6 ps), implying that they are solely due to the T₁ tetramer. Thus, we adopt the time-resolved Raman spectrum measured at 315 mM and the delay time ΔT = 100 ps (when the frequency upshift of the 140 cm⁻¹ band is finished) as the Raman spectrum of the T₁ tetramer. The Raman spectrum of the T₁ pentamer is obtainable from the data of other concentrations (370–685 mM) by subtracting the contribution of the T₁ tetramer. Because the ∼140 cm⁻¹ band is solely due to the T₁ tetramer, the real-part FT amplitude of the ∼140 cm⁻¹ band is considered a direct measure of the population of the T₁ tetramer. Thus, we subtracted the time-domain Raman data of 315 mM at ΔT = 100 ps, which only contains the T₁ tetramer, from the time-domain Raman data of other concentrations with adequate factors to obtain time-domain Raman signals due to the T₁ pentamer. The FT power Raman spectra of the T₁ pentamer obtained from the time-domain data at different concentrations after the subtraction show bands at ∼110, ∼400, and ∼450 cm⁻¹ with the same relative amplitude ratios, which confirms the adequacy of this analysis. However, another band appearing at <∼50 cm⁻¹ in the spectrum of the T₁ pentamer is considered an artifact arising from imperfect baseline subtraction in the time domain. We note that the Raman band at ∼60 cm⁻¹ of the T₁ tetramer is real, although its intensity is substantially affected by the baseline subtraction for the 315 mM data (the details of the spectral subtraction procedure are given in Section S5 in SI).

The Raman spectrum of the T₁ trimer has been obtained in our previous TR-ISRS experiment carried out for a 100 mM solution, and we adopted the spectrum at ΔT = 0.6 ps.¹⁴ For the T₁ dimer, we newly measured the Raman spectrum of a 10 mM diluted solution with excitation at 260 nm, where the excited-state dimer is predominantly generated¹⁶ (the steady-state absorption spectrum, the spectra of the ultrashort pulses used for TR-ISRS, and the time-resolved Raman spectra obtained are given in Section S6 in the SI). The time-resolved Raman spectra exhibit a strong band at ∼130 cm⁻¹, and the temporal profile of its FT amplitude is well fit with a double exponential function with time constants of 0.8 ps and 20 ps. Although the origin of the 0.8 ps decay is not clear at the moment, the 20 ps decay time constant agrees well with the lifetime of the T₁ dimer (26 ps) measured by time-resolved absorption and emission spectroscopies,^16,17 which confirms that the observed Raman spectra are due to the T₁ dimer. We use the time-resolved Raman spectrum at ΔT = 4 ps as the spectrum of the T₁ dimer.

Fig. 5 compares the T₁ Raman spectra of [Au(CN)₂⁻] oligomers from the dimer to the pentamer, which were obtained as described above (note that a band below ∼50 cm⁻¹ of T₁ pentamer is highly likely an artifact, as already mentioned). This figure clearly shows that the Raman spectral feature changes with the size of the T₁ oligomer. In particular, the strongest band of the T₁ oligomers with even sizes (the dimer and the tetramer) appears in the frequency region of 130–145 cm⁻¹, whereas that of the oligomer with odd sizes (the trimer and the pentamer) appears in a lower frequency range of 90–110 cm⁻¹. To rationalize this frequency difference, we calculated the vibrational frequency of each T₁ oligomer at the optimized linear structure. The computed peak positions and the non-resonant intensities of the Raman bands of each T₁ oligomer are summarized in Fig. 5 and Table 1. The results of the theoretical calculation agree well with the experimental spectra, particularly for the strongest band of each T₁ oligomer. The calculations indicate that the ∼130 cm⁻¹ band of the T₁ dimer is due to the Au–Au stretch, whereas the ∼90 cm⁻¹ band of the T₁ trimer is attributed to the symmetric Au–Au–Au stretch. The corresponding Raman bands of the T₁ tetramer (∼144 cm⁻¹) and T₁ pentamer (∼108 cm⁻¹) are similarly assignable to the Au–Au and Au–Au–Au stretch modes, respectively. Although these modes in the larger T₁ oligomers also include some displacement of the Au atoms at the edge, the displacements of the Au atoms in the central parts are much greater (the displacement magnitudes are shown with the length of the arrows in Fig. 5). Therefore, we can say that the vibrations giving rise to the strongest Raman band of the T₁ oligomers are mainly located in the central parts, i.e., the dimer moiety in the oligomers with even sizes and the trimer moiety in the oligomers with odd sizes.

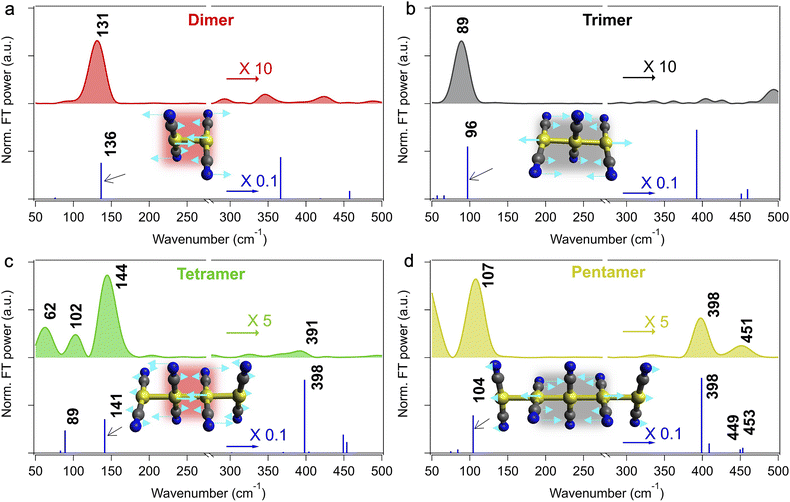Fig. 5 Raman spectra of the T₁ [Au(CN)₂⁻]_n oligomers (n = 2–5). (a) Dimer (C = 10 mM, ΔT = 4 ps), (b) trimer (C = 100 mM, ΔT = 0.6 ps), (c) tetramer (C = 315 mM, ΔT = 100 ps), and (d) pentamer (C = 685 mM and C = 315 mM, ΔT = 100 ps, which were obtained through the data analysis described in the main text). The calculated frequencies and (non-resonant) Raman intensities are shown with sticks at the bottom in each panel. The normal coordinates of the Au–Au and Au–Au–Au stretch vibrations of each T₁ oligomer at 136, 96, 141, and 104 cm⁻¹ are also shown in the inset. Other normal coordinates of the vibrational modes with calculated Raman intensities are greater than 1% of the strongest band are shown in Fig. S7. The original data of the Raman spectrum of the T₁ trimer in (b) have already been reported in ref. 14.

Table 1 Calculated and measured Raman band positions of each oligomer in the T₁ state

	Dimer	Trimer	Tetramer	Pentamer
a Ref. 17 and references therein (fluorescence lifetime).
Measured	131 cm^−1	89 cm^−1	62, 102, 144, 391 cm^−1	107, 398, 451 cm^−1
Calculated	136 cm^−1	96 cm^−1	89, 141, 398 cm^−1	104, 398, 449 cm^−1
ISC time constant^a	<0.2 ps	0.38 ps	2.6 ps	13 ps

---

The similarity between the T₁ oligomers of even and odd sizes is observed not only in the Raman spectra but also in their structures. Table 2 lists the bond lengths of each T₁ oligomer that were obtained with DFT calculations. For the T₁ oligomer with even sizes, the length of the central Au–Au bond (2.74 Å) of the T₁ tetramer is similar to the Au–Au bond length of the T₁ dimer (2.69 Å), and the length of the Au–Au bonds at the edge is substantially longer (2.85 Å). For the T₁ oligomer with odd sizes, on the other hand, the length of the central two Au–Au bonds of the T₁ pentamer (2.77 Å) is almost the same as those of the T₁ trimer (2.76 Å), whereas the length of the edge Au–Au bonds is substantially longer (2.96 Å). In these T₁ oligomers, an electron is excited from an anti-bonding d_zσ* orbital to a bonding p_zσ orbital among the gold atoms, and hence, the Au–Au bonds are tightened compared to the S₀ state. The Au–Au bond tightening occurs in all Au–Au bonds, implying that the bonding p_zσ orbital is delocalized. However, the calculated bond length indicates that the Au–Au bond tightening does not equally occur in all Au–Au bonds in the T₁ oligomers but happens in the central part more greatly: the stronger Au–Au bond of the T₁ oligomer with even size (i.e., tetramer) is seen for the dimer moiety, whereas that of the T₁ oligomer with odd size (i.e., pentamer) is found in the trimer moiety. This makes the Au–Au bonds in the central parts noticeably different from those in the edge parts in the large T₁ oligomers. This inequivalent Au–Au bond strength is considered to be reflected in the similarity and the difference in the normal coordinate and frequency of the Au–Au stretch vibrations that give rise to the strongest transient Raman bands of the T₁ oligomers with even and odd sizes. In fact, these vibrations are well localized in the dimer/trimer central part, rather than equally delocalized over the whole T₁ oligomer (the insets of Fig. 5).

Table 2 Au–Au bond length(s) of each T₁ oligomer at the optimized structure computed by DFT calculation

Oligomers	Bond length(s) Å
Dimer	2.69
Trimer	2.76	2.76
Tetramer	2.85	2.74	2.85
Pentamer	2.96	2.77	2.77	2.96

---

Conclusions

We performed TR-ISRS measurements of aqueous solutions of K[Au(CN)₂] in a wide concentration range, enabling the observation of time-resolved Raman spectra of the tetramer and pentamer in the T₁ state. An ultrafast bent (zigzag)-to-linear structural change was observed for the T₁ tetramer, as in the case of the T₁ trimer, indicating that this type of structural change commonly occurs in the T₁ state after the Au–Au bond formation. A newly performed TR-ISRS measurement of the T₁ dimer enabled comparison of the Raman spectra of T₁ [Au(CN)₂⁻] oligomers from the dimer to pentamer. The strongest Raman bands of the T₁ [Au(CN)₂⁻] oligomers observed in the low frequency region were attributed to the Au–Au stretch or symmetric Au–Au–Au stretch vibrations, and they exhibited an alternative frequency change with changes in the even–odd oligomer size. DFT calculations well reproduced the experimental Raman spectra. They also indicated that the Au–Au bond strength in the large T₁ oligomers (the tetramer and the pentamer) is stronger in the central part, where the observed Au–Au stretch vibrations are mainly located. The structural change in the T₁ oligomers also extends to the two monomer units at both ends, which are dislocated during the ultrafast structural change after photo-induced bond formation. In ordinary cases, σ bonds are localized, and the bond strengths are essentially the same regardless of the difference in their positions in a molecule. In contrast, the p_z–p_z σ bond formed in T₁ [Au(CN)₂⁻] oligomers with photoexcitation has a greater bond strength in the central part and is also delocalized on the Au atoms at both ends. This represents a distinct nature of the p_z–p_z σ chemical bond formed in T₁ [Au(CN)₂⁻] oligomers with photoexcitation. Overall, this study not only provides an overview of the properties and structure of T₁ [Au(CN)₂⁻] oligomers with different sizes but also offers a new type of chemical bond in molecular assemblies.

Author contributions

LL: conceptualization, investigation, writing – original draft, writing – review & editing; HK: conceptualization, investigation, writing – review & editing; MI: conceptualization, writing – review & editing; KN: investigation, computation, writing – review & editing; TT: conceptualization, supervision, writing – original draft, writing – review & editing, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Data availability

The raw experimental data are saved and will be shared upon request.

Supplementary information (SI): substantial details on experimental data and the quantum chemical calculations. See DOI: https://doi.org/10.1039/d5sc05664k.

Acknowledgements

LL acknowledges Dr Tsukasa Takanashi for the useful discussion about recrystallization of the sample and DFT calculations. TT acknowledges JSPS KAKENHI Grant Number JP25K22248.

References

1. Q. Wang, Z. Zuo, X. Wang, L. Gu, T. Yoshizumi, Z. Yang, L. Yang, Q. Liu, W. Liu, Y.-J. Han, J.-I. Kim, B. Liu, J. A. Wohlschlegel, M. Matsui, Y. Oka and C. Lin, Science, 2016, 354, 343–347.
2. L. Ma, X. Wang, Z. Guan, L. Wang, Y. Wang, L. Zheng, Z. Gong, C. Shen, J. Wang, D. Zhang, Z. Liu and P. Yin, Nat. Struct. Mol. Biol., 2020, 27, 472–479.
3. X. Li, Z. Liu, H. Ren, M. Kundu, F. W. Zhong, L. Wang, J. Gao and D. Zhong, Nat. Commun., 2022, 13, 93.
4. Y. Nakamura, I. W. Hwang, N. Aratani, T. K. Ahn, D. M. Ko, A. Takagi, T. Kawai, T. Matsumoto, D. Kim and A. Osuka, J. Am. Chem. Soc., 2005, 127, 236–246.
5. X. Li, L. E. Sinks, B. Rybtchinski and M. R. Wasielewski, J. Am. Chem. Soc., 2004, 126, 10810–10811.
6. Y. Yamamoto, H. Takeda, T. Yui, Y. Ueda, K. Koike, S. Inagaki and O. Ishitani, Chem. Sci., 2014, 5, 639–648.
7. K. M.-C. Wong and V. W.-W. Yam, Acc. Chem. Res., 2011, 44, 424–434.
8. M. Iwamura, A. Fukui, K. Nozaki, H. Kuramochi, S. Takeuchi and T. Tahara, Angew. Chem., Int. Ed., 2020, 59, 23154–23161.
9. M. A. Rawashdeh-Omary, M. A. Omary and H. H. Patterson, J. Am. Chem. Soc., 2000, 122, 10371–10380.
10. M. A. Rawashdeh-Omary, M. A. Omary, H. H. Patterson and J. P. Fackler, J. Am. Chem. Soc., 2001, 123, 11237–11247.
11. N. L. Coker, J. A. Krause Bauer and R. C. Elder, J. Am. Chem. Soc., 2004, 126, 12–13.
12. M. Iwamura, K. Nozaki, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2013, 135, 538–541.
13. K. H. Kim, J. G. Kim, S. Nozawa, T. Sato, K. Y. Oang, T. W. Kim, H. Ki, J. Jo, S. Park, C. Song, T. Sato, K. Ogawa, T. Togashi, K. Tono, M. Yabashi, T. Ishikawa, J. Kim, R. Ryoo, J. Kim, H. Ihee and S.-i. Adachi, Nature, 2015, 518, 385–389.
14. H. Kuramochi, S. Takeuchi, M. Iwamura, K. Nozaki and T. Tahara, J. Am. Chem. Soc., 2019, 141, 19296–19303.
15. J. G. Kim, S. Nozawa, H. Kim, E. H. Choi, T. Sato, T. W. Kim, K. H. Kim, H. Ki, J. Kim, M. Choi, Y. Lee, J. Heo, K. Y. Oang, K. Ichiyanagi, R. Fukaya, J. H. Lee, J. Park, I. Eom, S. H. Chun, S. Kim, M. Kim, T. Katayama, T. Togashi, S. Owada, M. Yabashi, S. J. Lee, S. Lee, C. W. Ahn, D.-S. Ahn, J. Moon, S. Choi, J. Kim, T. Joo, J. Kim, S.-i. Adachi and H. Ihee, Nature, 2020, 582, 520–524.
16. M. Iwamura, R. Wakabayashi, J. Maeba, K. Nozaki, S. Takeuchi and T. Tahara, Phys. Chem. Chem. Phys., 2016, 18, 5103–5107.
17. M. Iwamura, R. Urayama, A. Fukui, K. Nozaki, L. Liu, H. Kuramochi, S. Takeuchi and T. Tahara, Phys. Chem. Chem. Phys., 2023, 25, 966–974.
18. H. Kuramochi, S. Takeuchi and T. Tahara, Rev. Sci. Instrum., 2016, 87, 043107.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, 2016.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. C. Adamo and V. Barone, Chem. Phys. Lett., 1997, 274, 242–250.
22. L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031.
23. A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114.
24. C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert and L. S. Sunderlin, J. Phys. Chem., 2001, 105, 8111–8116.
25. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
26. M. Iwamura, K. Kimoto, K. Nozaki, H. Kuramochi, S. Takeuchi and T. Tahara, J. Phys. Chem. Lett., 2018, 9, 7085–7089.

---

Footnotes

† Current address: Laboratory for Soft Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, 100190, P. R. China.

‡ Current address: Department of Materials Engineering Science, Graduate School of Engineering Science, The University of Osaka, 1-3 Machikaneyama, Toyonaka 560-8531, Japan.

---