Edge magnetism in colloidal MoS₂ triangular nanoflakes

Abstract

The control of localized magnetic domains at the nanoscale holds great promise for next-generation spintronic applications. Colloidal transition metal dichalcogenide nanostructures are experimentally accessible and chemically tunable platforms for spintronics, deserving dedicated research to assess their potential. Here, we investigate from first principles free-standing triangular MoS₂ nanoflakes with sulfur-terminated, hydrogen-passivated edges, to probe intrinsic spin behavior at varying side lengths. We find a critical edge length of approximately 1.5 nm separating nonmagnetic nanoflakes from larger ones with a magnetic ground state emerging from several, energetically competing spin configurations. In these systems, the magnetic activity is not uniformly distributed along the edges but localized on specific “magnetic islands” around molybdenum edge atoms. The localization of magnetic moments is robust even in non-equilateral nanoflake geometries, highlighting their intrinsic stability regardless of the (high) symmetry of the hosting structure. Our findings establish that the S-terminated, H-passivated triangular MoS₂ nanoflakes are an energetically stable and potentially accessible platform via colloidal synthesis for low-dimensional, next-generation spintronic devices.

---

1. Introduction

The rich physics of spin-active materials has opened opportunities for spintronic applications, including high-density memory, logic circuits, and quantum information devices.^1–5 With the emergence of edge-spin quantum magnetism in confined graphene nanostructures,^6–10 an increasing number of two-dimensional (2D) materials are explored for their potential use in spintronics.^11–15 Transition metal dichalcogenides (TMDs) are looked upon as the most promising candidates, thanks to their combined stability and structural flexibility even in confined nanostructured configurations.^11–14

The magnetic behavior typical of materials with reduced dimensionality, has been often observed in TMD nanostructures.^16–25 The local spin domains emerging in these systems is related to the presence of edges, which create a polar discontinuity.^22,26 The resulting electrostatic potential gradient drives the accumulation of charge carriers toward the edge to screen the polarization charges, ultimately leading to an edge-localized magnetization.^22,26,27 As a result, while bulk TMDs are typically non- or very weakly magnetic,²⁸ edge effects and lateral confinement can induce magnetism, with persistent ferromagnetic ordering even at room temperature.^16,17,29,30 For example, TMD nanoribbons with armchair edges are typically nonmagnetic or weakly magnetic,^16,17,30 while those featuring zigzag or sawtooth edges stabilize in a magnetic ground state.^16–25 In these nanostructures with extended zigzag edges, the magnetic moment is generally delocalized along the entire edge, limiting the density of individually addressable magnetic elements.^16–25 The lack of controllable, localized spin centers remains a critical challenge for utilizing TMDs in high-density spintronic devices.^31,32

Magnetism in TMDs can arise either via intentional introduction of defects^33–41 or intrinsically from edge boundaries in confined nanostructures.^16–25 Extrinsic magnetism, introduced by chalcogen vacancies^42,43 or transition-metal dopants,^33,44–46 generates localized spin domains. However, this approach offers limited control of the resulting magnetic properties, which exhibit a sensitive and often unpredictable dependence on the precise concentration, position, and clustering of the dopants. In contrast, intrinsic magnetism is inherently more robust and reliable as it is directly associated with the structural properties of the confined materials, including their edges.^6–10 For magnetic materials, a high density of reactive edges is distinctly advantageous. Edge atoms, due to changes in coordination, often deviate from the bulk-stoichiometric equilibrium, leading to atomic reconfigurations and non-uniform spin distributions.^6–10

Triangular TMD nanoflakes can be highly promising spin hosts, as they exhibit intrinsic magnetism with localized magnetic moments,^{13,14,47–50} similar to their graphene-based analogs.^51–53 Colloidal triangular nanostructures offer the advantage to be synthesized with a uniform elemental termination and a single type of edge (e.g., zigzag) along all sides.^{13,14,47–50} While previous work on TMD nanoribbons focused on delocalized edge spins,^22,26,27 the confined geometry of triangular nanoflakes provides a unique structural platform to stabilize discrete, addressable magnetic units. This feature is crucial, as nanoflakes of other shapes (e.g., rectangular or rhombic) inherently result in a mixture of terminating elements and/or edge types. In TMDs, the structural characteristics of triangular quantum dots prevent the inherent limitations of nanoribbons or nanosheets, where opposite boundaries must contain a mixture of transition-metal (d-orbital magnetism) and chalcogen (p-orbital magnetism) terminations,^16,18,54,55 or where engineering uniform elemental termination forces the adoption of the armchair orientation on one side.^16,24,56 By overcoming these constraints and ensuring uniform magnetic zigzag edges, triangular geometries circumvent constraints imposed by mixed terminations and nonmagnetic regions, making them a viable platform for generating stable, well-defined spin-active islands compared to conventional ribbon-like structures.

In this work, we investigate the magnetic properties of colloidal MoS₂ nanoflakes of triangular shape with hydrogen-passivated sulfur edges. While theoretical studies on similar systems based on first-principles and tight-binding models have been published in the last decade,^{13,14,47–50} we propose a systematic analysis to identify well-defined spin domains intrinsically arising in these systems due to their characteristic topology. By performing density functional theory (DFT) calculations, we show MoS₂ nanoflakes with edge lengths smaller than 1.5 nm are nonmagnetic, whereas larger structures exhibit energetically competing magnetic states separated by less than 50 meV, with varying total magnetic moments due to distinct local spin alignments. Despite S-termination and H-passivation, only specific Mo atoms close to the edges develop local magnetic moments forming symmetric topologies, in pronounced contrast to the delocalized spin density characterizing periodic TMD nanoribbons. Our results highlight triangular MoS₂ nanoflakes with S–H edges as robust, experimentally feasible platforms to create high-density, individually addressable magnetic islands for spin-filtering and next-generation spintronic applications.

2. Computational details

All calculations presented in this work were performed with spin-polarized (SP) DFT⁵⁷ as implemented in the Vienna Ab initio Simulation Package (VASP)⁵⁸ within the projector augmented wave framework.^59,60 We used the generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) implementation,⁶¹ incorporating Grimme's D3 dispersion correction and Becke–Johnson damping.^62,63 Since the considered nanoflakes are non-periodic, we sample the Brillouin zone only at the Γ-point, and add to the simulation box a vacuum layer of 16 Å in all directions, to eliminate spurious interactions between periodic images of the unit cell. We relax the initial structures imposing SP until the Hellmann–Feynman forces acting on each atom were lower than 0.005 eV Å⁻¹. The total energy convergence criterion for the self-consistent runs is set to 10⁻⁸ eV and the plane-wave basis-set cutoff energy to 475 eV.

Due to the possible coexistence of multiple local minima predicted by SP-DFT,⁶⁴ the final magnetic state of a system depends on the starting spin configuration. To account for this uncertainty, we perform our calculations fixing the targeted total magnetic moments while allowing the system to self-consistently rearrange its local spins to satisfy the imposed constraint for the total magnetization µ. This strategy minimizes the dependence on the initial conditions, enabling a systematic energetic comparison among different magnetic states to identify the ground state.

3. Results and discussion

3.1. Structural properties

In this work, we investigate six equilateral triangular MoS₂ nanoflakes with varying edge lengths (L) generated from the 2H monolayer with experimental lattice parameters a = 3.16 Å.^65–67 The nanoflakes are labeled according to the number of MoS₂ rings along their edge (Fig. 1), ranging from the smallest nanoflake with two rings (r₂) to the largest one with seven rings (r₇). Their lateral sizes span approximately 15 Å, ranging from 9.5 Å for r₂ to 25.2 Å for r₇. In each nanoflake, the interior molybdenum (Mo) atoms are sixfold coordinated by sulfur (S), whereas each interior sulfur atom is threefold coordinated by Mo. The edges are terminated by hydrogen-passivated sulfur atoms, which are known to be chemically stable in colloidal MoS₂ nanostructures.^68–72

Fig. 1 Hydrogen-passivated triangular MoS₂ nanoflakes, with an increasing number of rings along the edge length (L) and labeled according to them. The atoms are color-coded according to the magnitude of their displacement from the initial positions after structural optimization.

We first briefly summarize the impact of structural relaxation by analyzing atomic displacements with respect to the initial positions across all nanoflakes (Fig. 1). Note that all atoms were allowed to fully relax, and displacements of the final (f), optimized structures are calculated as the Euclidean distance 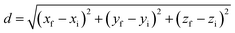relative to the unrelaxed, initial (i) structure. As expected, edge atoms experience the largest shifts, ranging from 0.3–0.8 Å, due to their modified coordination environments. Specifically, H atoms exhibit the most significant displacements (0.5–0.8 Å), owing to their small size and arbitrary initial placement as passivating species. Both Mo and S atoms on the corners show moderate to large positional shifts, on the order of 0.5 Å, whereas atoms in the core are only negligibly affected, with average displacements below 0.2 Å. The atoms undergo highly symmetric displacements, as expected from the equilateral geometry of the structure. As the system size increases, a clear distinction emerges between bulk-like atoms, which exhibit small displacements, and edge-like atoms, which show significantly larger displacements (Fig. 1).

The analysis of the bond distances (Fig. S1) reveals a narrow distribution for the Mo–S and S–H bonds, confirming the structural stability of both the core and the H-passivated edges. In contrast, the Mo–Mo distances vary slightly, within 10% of the experimental value (3.16 Å) of the 2D MoS₂ sheet,^65–67 while S–S distances show the largest deviation, up to approximately 0.6 Å, or around 20% of the lattice parameter of MoS₂ monolayer. This pronounced variation stems from the unique H-passivated environment of the S atoms at the nanoflake corners, which induces enhanced structural relaxation compared to the interior (Fig. 1).

3.2. Magnetic ground-state determination

We next investigate different magnetic configurations of the relaxed structure for each system size to determine their ground state (see Section 2 for details on the procedure). As shown in Fig. 2, where the calculated total energy differences relative to the most stable magnetic state (red squares) are displayed, the smallest nanoflakes (r₂ and r₃) possess a non-magnetic ground state. In these systems, states with higher magnetic moments lead to a sharp increase in total energy, on the order of 800 meV and 1.6 eV for the largest explored magnetization, µ = 4µ_B (Fig. 2, top panels), confirming the superior stability of the non-magnetic phase. In contrast, beginning with r₄ and for all larger nanoflakes, magnetic configurations are energetically favored, suggesting 1.5 nm as a size threshold for the appearance of a magnetic ground state, similar to graphene nanoislands.⁶ In the larger nanoflakes (r₄ to r₇), the total magnetic moment exhibits a non-monotonic size dependence, and the distribution of the local magnetic moments is highly non-uniform. Moreover, whenever a magnetic ground state is present, multiple magnetic orders lead to very similar total energies, within a range of 25.8 meV (Fig. 2, insets), which is comparable to thermal energy at room temperature.

Fig. 2 (a–f) Total energy difference (E_diff) relative to the magnetic ground state (red square) for various fixed total magnetic moments (µ) of the considered r₂–r₇ MoS₂ nanoflake. Less stable configurations discussed in the text are squared in black. Insets: zoom-in to nearly degenerate magnetic orderings.

Among the nanoflakes exhibiting a magnetic ground state, local spins are localized on the unpaired Mo d-electrons. For r₄, the ground state has a total magnetic moment µ = 2µ_B (Fig. 3). This configuration is ferromagnetic, arising from three local moments aligned parallel to each other. A ferrimagnetic spin pattern appears in the energetically competing (ΔE < 10 meV, see Fig. 2) configuration with µ = 1µ_B, while for µ > 1µ_B, only ferromagnetic states appear, where all local magnetic moments are parallel (Fig. 3). The most striking feature is that, in all non-zero magnetic configurations of r₄, the local magnetic domains are localized exclusively on three atoms arranged in a triangular pattern. For the configuration with µ ≥ 2µ_B, these triangularly arranged magnetic domains have nearly the same magnitude. Furthermore, as the magnetization increases, also the remaining Mo atoms in the flake incrementally acquire a non-zero magnetization, as expected.

Fig. 3 Spatial distribution of the local magnetic moments in the r₄ nanoflake at varying total magnetization (in µ_B) indicated in each panel. The color scale for the atoms represents the magnitude and orientation of the local spins.

The r₅ nanoflake shows a ferrimagnetic ground state with a total magnetic moment of µ = 0.5µ_B, where 4 local spins are aligned parallel while 2 are aligned antiparallel (Fig. 4a). This configuration is almost degenerate (ΔE ≈ 12 meV) to two other ferrimagnetic orderings characterized by total magnetization of µ = 1µ_B and µ = 1.5µ_B (Fig. 2). Similar to r₄, the magnetic behavior of the r₅ nanoflake is dominated by six Mo edge atoms (two per edge) forming the same pseudo-triangular spatial pattern regardless of the total magnetic moment, with spins aligning either parallel or antiparallel depending on the value of µ (Fig. 4a and S2 in the SI). Again, for µ > 2µ_B, the non-zero spins align parallel to each other, giving rise to ferromagnetic configurations, with the surrounding Mo atoms acquiring a local magnetization increasing with µ.

Fig. 4 Spatial distribution of the local magnetic moments in selected (a) r₅, (b) r₆, and (c) r₇ magnetic configurations. The color scale for the atoms represents the magnitude and orientation of the local spins.

In the larger nanoflakes, r₆ and r₇ (Fig. 4b, c, S3 and S4 in the SI), a consistent pattern emerges, similar to r₄ and r₅, where only a few Mo edge atoms contribute significantly to the total magnetic moment. The ground state of r₆ has a total magnetic moment of µ = 6µ_B. Like r₄, this state is ferromagnetic, with all spins aligned parallel to each other (Fig. 4b). Other magnetic configurations with µ ≤ 2.5µ_B are ferrimagnetic but energetically much less stable, with shifts from the ground state of the order of 300 meV or more. Ferromagnetic states emerge for µ ≥ 3µ_B. Interestingly, the other ferromagnetic configuration with µ = 5.5µ_B is about 100 meV higher in energy compared to the ground state (see Fig. 2). As shown in Fig. 4b, this state features not only fully parallel spin alignment but also total 9 unpaired spins homogeneously distributed on the nanoflake with similar contribution from each edge.

The ground state of the r₇ nanoflake is ferrimagnetic like r₅, with a total magnetic moment of µ = 2.5µ_B, which is less than the r₆ flake. In this configuration, 9 Mo edge atoms carry the spins, on the order of 0.5µ_B (Fig. 4c), arranged in a pseudo-hexagonal pattern along the edges. Similar to r₅, all spin along one edge are aligned antiparallel to the other two edges. In this largest nanoflake, the competition between ferrimagnetic and ferromagnetic ordering is significantly higher compared to other structures (Fig. 4c and S4 in the SI). This is slightly different behavior compared to r₆ or smaller sizes where a clear boundary between ferrimagnetic and ferromagnetic ordering occurs. Remarkably, many states with in this case are the closest in energy to the ground state, spanning a narrow range of 20 meV, which is comparable with thermal energy at room temperature.

The physical origin of these local magnetic moments is fundamentally linked to the polar discontinuity that emerges at the edge of the nanoflake relative to its bulk-like interior.^22,26,27 When an extended crystal terminates at an edge, the local charge balance is disrupted, creating an electrostatically uncompensated net polarization charge. The resulting electrostatic potential gradient drives the accumulation of charge carriers toward the edge to screen polarization charges, ultimately leading to an edge-localized magnetization. This magnetism is strongly size-dependent and only emerges when the edge length is 1.5 nm (r₄ nanoflakes) or larger. In these larger systems, we can clearly distinguish between a bulk-like core and an edge region, while below this size, the entire nanoflake is dominated by edge effects and the bulk/edge interface is absent.

The non-monotonic dependence of the total magnetic moment of the nanoflake size is attributed to the energetically competing local spin alignments (ferrimagnetic vs. ferromagnetic ordering) that are nearly degenerate (within a 25 meV range) across different nanoflake sizes. As the structure becomes more extended, the larger edge perimeter provides more Mo atoms near the boundary, leading to a complex landscape where the specific total spin alignment that minimizes the energy and defines the ground state depends on the precise arrangement and number of edge atoms. We expect the magnetization to eventually taper down and disappear once the bulk limit is restored. Based on previous estimates for MoS₂ nanoribbons,²² the cutoff length is on the order of 50 Å, almost twice the maximum edge size of the triangular nanoflakes explored in this study.

The (pseudo-)triangular spin arrangement is a topological manifestation of the nanoflake geometry, directly correlated with the number of edges and their type. The emergence of local magnetic moments is a consequence of the polar discontinuities at the edges, generating polarization charges λ = P × n̂, where P is the polarization vector and n̂ is the unit vector orthogonal to the edge. Since each edge is defined by a distinct normal unit vector n̂, it generates a distinct polarization charge density and, consequently, a distinct set of localized, charge-reconstructed edge states on each side. The specific Mo edge atoms hosting the localized magnetic moment are those located at the interface between the inner bulk-like core and the outer edge-like region, where the strong charge reconstruction driven by the H-passivated S-edges is concentrated. Removing a Mo atom from one of these critical corner sites would create S dangling bonds, mirroring the effects seen in non-passivated S-edges, and thus slightly modify the magnetic moments along the affected edge. Likewise, spin localization critically depends on H-passivation, which concentrates the charge reconstruction at these specific Mo atom sites.²⁶

This size-dependent ground-state spin analysis of the MoS₂ nanoflakes reveals a close competition among different magnetic orders. The total magnetic moment of the ground state varies non-monotonically with increasing nanoflake size, and this magnetic behavior is characterized by localized moments confined to specific edge atoms, which form non-trivial spatial arrangements. The presence of nearly degenerate magnetic configurations, with energy differences comparable with thermal energy at room temperature, suggests not only that the ground-state may fluctuate under specific thermodynamic conditions but also indicates a significant potential for tuning the magnetic order using external perturbations. For example, in the most stable ferromagnetic configuration of r₄ flake at T = 0, an external magnetic field could flip the orientation of the spin, enabling a reversible magnetic transition. These possible controllable switching processes highlight the potential of these triangular nanoflakes as active components in spintronic devices, including spin filters and other applications exploiting tunable edge magnetism.

The triangular MoS₂ nanoflakes considered in our analysis are often synthesized as colloidal structures in solution. Although this technique has been refined to allow controlled sample preparation,^73,74 irregularities often emerge especially in the edge region. Likewise, H-passivation may be (locally) absent or replaced by other species. Given this variability, we examined the robustness of the effects discussed above – namely, the presence of magnetic ground states and regular spin patterns formed by specific and spatially ordered edge Mo atoms – against small structural edge distortions and the absence of H-passivation (see Fig. S5 and S6 in the SI for details).

We found a persisting magnetic ordering even in the presence of small deviations from the equilateral nanoflake shape. This is an expected consequence of the polar discontinuity from which this effect originates.^22,26 This mechanism is electronic, not geometric: the magnetic moment is a response to the uncompensated electrostatic potential, which is primarily dictated by the long-range arrangement of the edge termination and the chemical environment (the S–H bond), and is hardly sensitive to small bond length or angle variations within the edge region.

On the other hand, we noticed that H-passivation plays a critical role: it not only saturates the dangling bonds of S atoms but, importantly, introduces a specific charge environment that dictates the polarization direction, leading to spin localization on the Mo atoms near the edges.²⁶ Without H-passivation, the S-edges have a different polarization profile and behave like a closed 1D metallic wire,⁷⁵ suppressing the required charge localization required for the ordered and confined magnetism predicted for their passivated counterparts.

Introducing S vacancies or removing Mo atoms from the non-magnetic core would introduce competing, extrinsic magnetic moments localized at the defect sites. Likewise, substituting Mo with transition metal dopants is expected to introduce strong, localized spins. In all cases, the resulting magnetic ground state would be a complex interplay between the intrinsic edge magnetism (arising from polar discontinuity) and these newly introduced localized moments, likely increasing the total magnetic moment and altering the nearly degenerate spin landscape. Given the complexity and variability of these scenarios, we postpone a dedicated investigation to future work.

3.3. Electronic properties

We conclude our analysis by discussing the electronic structure of the energetically most favorable magnetic configuration of all considered MoS₂ nanoflakes in terms of their spin-polarized atom-projected density of states (PDOS, see Fig. 5). The smallest nanoflakes, r₂ and r₃, which are characterized by a non-magnetic ground state, are semiconducting with non-monotonic band gaps of 0.4 eV and 0.8 eV, respectively, consistent with previous works.^13,76–78 In line with physical intuition, the band edges are dominated by Mo atoms with small contributions from H (especially in the highest occupied state) and S (at the bottom of the conduction band). S states prevail over Mo states deeper in the valence region, starting from approximately −2 eV in both cases. Quantum confinement effects appear in the discrete and energetically separated states characterizing both their occupied and unoccupied regions (Fig. S7).

Fig. 5 (a–f) Spin-polarized atom-projected density of states (PDOS) for the magnetic ground state of r₂–r₇ MoS₂ nanoflake. The Fermi energy (E_F) is set to 0 eV and marked by a vertical dashed bar.

Larger MoS₂ nanoflakes, characterized by a magnetic ground state, display a metallic behavior, with Mo d-states crossing the Fermi energy (Fig. 5). Interestingly, the even-numbered nanoflakes (r₄ and r₆) exhibit a significantly lower density of states at the Fermi level compared to their odd-numbered counterparts. In particular, r₆ exhibits a small gap of a few tens of meV in each spin channel. In r₅ and r₇, where the metallicity is more pronounced, an even larger gap of the order of 100 meV is visible in the spin-down channel, as expected in the presence of a ferromagnetic ground state. The larger number of Mo and S atoms compared to the passivating hydrogens is reflected in the atom-resolved contributions to the PDOS, which are overwhelmingly dominated by the metal and chalcogen species (Fig. 5). Nonetheless, similar to the smaller structures, even in the larger nanoflakes, the gap region hosts predominantly Mo contributions while S states prevail deeper in the valence region, here starting from approximately −1.5 eV, and higher in the conduction band, starting from 1 eV, where they are hybridized with Mo orbitals.

This analysis on the electronic structure of the considered MoS₂ nanoflakes consistently reflects the previous discussion on their magnetic properties. The semiconducting nature of the smallest, non-magnetic nanostructures (r₂ and r₃) is governed by quantum confinement. Conversely, the metallic behavior predicted for the larger magnetic nanoflakes (r₄–r₇) results from the unpaired spins in the Mo d-orbitals crossing the Fermi level. The larger magnetization and the near-degeneracy of magnetic orders of these larger systems are directly manifested in the complex spin-split PDOS near the Fermi level, supporting their potential as platforms for tunable edge magnetism. We note in passing that the results displayed in Fig. 5 are obtained at the PBE + SP + D3 level of theory, which excludes static and dynamic correlations that are crucial for a quantitative description of magnetic nanostructures. As such, our results are intended solely to provide a qualitative picture of the trends arising in the PDOS of the considered nanoflakes, without claiming quantitative predictive accuracy.

4. Summary and conclusions

In summary, we systematically investigated the intrinsic magnetic properties of triangular MoS₂ nanoflakes using spin-polarized DFT. By varying the edge length of S-terminated nanoflakes with hydrogen passivation, we identified a critical size threshold of approximately 1.5 nm, below which the structures remain non-magnetic. Larger nanoflakes exhibit multiple, closely competing magnetic states arising from localized moments on specific Mo edge atoms. All magnetic configurations are metallic, with unpaired Mo d-orbitals crossing the Fermi level. The robustness of this edge-induced magnetism is underscored by finding that edge-localized magnetic moments persist even in structurally modified, non-equilateral geometries. In contrast, removing hydrogen passivation leads to a disordered spin landscape, where magnetic moments become randomly distributed across both Mo and S edge atoms.

In conclusion, our results demonstrate that S-terminated and H-passivated triangular MoS₂ nanoflakes represent a stable, experimentally accessible, and promising platform for nanoscale spin control. The robust and localized magnetic moments in these nanoflakes can be manipulated by external electric or magnetic field to realize advanced spintronic applications, primarily by using electrostatic gating. For instance, if magnetic field with alternating component is applied, it will induce spin rotation and hence results in spin manipulation for the design of low-dimensional spintronic devices such as spin filters and memory elements. Similarly alternating electric field allows manipulation of the spin state at will via electric-dipole-induced spin resonance and therefore can be explored as spin qubit. Given the analogies among TMDs, we anticipate that the physics predicted here also exists in other members of this family, such as W-based nanoflakes. However, a detailed analysis of different metallic and/or chalcogen species, as well as the influence of defects Mo and S vacancy and functionalization, requires dedicated analysis, which will be pursued in future work.

Author contributions

Surender Kumar: conceptualization, methodology, calculations and formal analysis, writing original draft; Stefan Velja: software, review & editing; Muhammad Sufyan Ramzan: review & editing; Caterina Cocchi: conceptualization, resources, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The raw data presented in this study are available free of charge in zenodo DOI: https://doi.org/10.5281/zenodo.17457576 [record: 17457576].

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5ra08271d.

References

1. I. Žutić, J. Fabian and S. Das Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys., 2004, 76, 323.
2. S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami and S. Piramanayagam, Spintronics based random access memory: a review, Mater. Today, 2017, 20, 530.
3. E. C. Ahn, 2D materials for spintronic devices, npj 2D Mater. Appl., 2020, 4, 17.
4. X. Lin, W. Yang, K. L. Wang and W. Zhao, Two-dimensional spintronics for low-power electronics, Nat. Electron., 2019, 2, 274.
5. A. Avsar, H. Ochoa, F. Guinea, B. Özyilmaz, B. J. van Wees and I. J. Vera-Marun, Colloquium: Spintronics in graphene and other two-dimensional materials, Rev. Mod. Phys., 2020, 92, 021003.
6. J. Fernández-Rossier and J. J. Palacios, Magnetism in graphene nanoislands, Phys. Rev. Lett., 2007, 99, 177204.
7. D.-e. Jiang, B. G. Sumpter and S. Dai, First principles study of magnetism in nanographenes, J. Chem. Phys., 2007, 127, 124703.
8. Y. Sun, Y. Zheng, H. Pan, J. Chen, W. Zhang, L. Fu, K. Zhang, N. Tang and Y. Du, Magnetism of graphene quantum dots, npj Quantum Mater., 2017, 2, 5.
9. R. E. Blackwell, F. Zhao, E. Brooks, J. Zhu, I. Piskun, S. Wang, A. Delgado, Y.-L. Lee, S. G. Louie and F. R. Fischer, Spin splitting of dopant edge state in magnetic zigzag graphene nanoribbons, Nature, 2021, 600, 647.
10. O. V. Yazyev, Emergence of magnetism in graphene materials and nanostructures, Rep. Prog. Phys., 2010, 73, 056501.
11. Y. Liu, C. Zeng, J. Zhong, J. Ding, Z. M. Wang and Z. Liu, Spintronics in two-dimensional materials, Nano-Micro Lett., 2020, 12, 93.
12. F. M. O. Brito, L. Li, J. M. V. P. Lopes and E. V. Castro, Edge magnetism in transition metal dichalcogenide nanoribbons: Mean field theory and determinant quantum monte carlo, Phys. Rev. B, 2022, 105, 195130.
13. A. Tiutiunnyk, A. L. Morales, R. Bertel, R. L. Restrepo, F. M. Nava-Maldonado, J. C. Martínez-Orozco, D. Laroze, C. A. Duque, J. D. Correa and M. E. Mora-Ramos, Electronic, optical, and magnetic properties of doped triangular MoS₂ quantum dots: A density functional theory approach, Phys. Status Solidi B, 2022, 259, 2100509.
14. H. Abdelsalam, O. H. Abd-Elkader, N. S. Zaghloul and Q. Zhang, Magnetic and electronic properties of edge-modified triangular WS₂ and MoS₂ quantum dots, Crystals, 2023, 13, 251.
15. N. Sethulakshmi, A. Mishra, P. Ajayan, Y. Kawazoe, A. K. Roy, A. K. Singh and C. S. Tiwary, Magnetism in two-dimensional materials beyond graphene, Mater. Today, 2019, 27, 107.
16. Y. Li, Z. Zhou, S. Zhang and Z. Chen, MoS₂ nanoribbons: High stability and unusual electronic and magnetic properties, J. Am. Chem. Soc., 2008, 130, 16739.
17. A. R. Botello-Méndez, F. López-Urías, M. Terrones and H. Terrones, Metallic and ferromagnetic edges in molybdenum disulfide nanoribbons, Nanotechnology, 2009, 20, 325703.
18. C. Ataca, H. Şahin, E. Aktürk and S. Ciraci, Mechanical and electronic properties of MoS₂ nanoribbons and their defects, J. Phys. Chem. C, 2011, 115, 3934.
19. X. Deng, Z. Li and J. Yang, One-dimensional magnetic order stabilized in edge-reconstructed MoS₂ nanoribbon via bias voltage, J. Phys. Chem. Lett., 2020, 11, 7531.
20. P. P. Shinde, S. P. Adiga, S. Pandian, S. Ramachandran, K. S. Hariharan and S. M. Kolake, MoS₂ quantum dots: Effect of hydrogenation on surface stability and H₂S release, J. Phys. Chem. C, 2019, 123, 28106.
21. P. Cui, J.-H. Choi, W. Chen, J. Zeng, C.-K. Shih, Z. Li and Z. Zhang, Contrasting structural reconstructions, electronic properties, and magnetic orderings along different edges of zigzag transition metal dichalcogenide nanoribbons, Nano Lett., 2017, 17, 1097.
22. M. Gibertini and N. Marzari, Emergence of one-dimensional wires of free carriers in transition-metal-dichalcogenide nanostructures, Nano Lett., 2015, 15, 6229.
23. L. Kou, C. Tang, Y. Zhang, T. Heine, C. Chen and T. Frauenheim, Tuning magnetism and electronic phase transitions by strain and electric field in zigzag MoS₂ nanoribbons, J. Phys. Chem. Lett., 2012, 3, 2934.
24. H. Pan and Y.-W. Zhang, Tuning the electronic and magnetic properties of MoS₂ nanoribbons by strain engineering, J. Phys. Chem. C, 2012, 116, 11752.
25. H. Pan and Y.-W. Zhang, Edge-dependent structural, electronic and magnetic properties of MoS₂ nanoribbons, J. Mater. Chem., 2012, 22, 7280.
26. M. Gibertini, G. Pizzi and N. Marzari, Engineering polar discontinuities in honeycomb lattices, Nat. Commun., 2014, 5, 5157.
27. P. D'Amico, M. Gibertini, D. Prezzi, D. Varsano, A. Ferretti, N. Marzari and E. Molinari, Intrinsic edge excitons in two-dimensional mos₂, Phys. Rev. B, 2020, 101, 161410.
28. F. A. Rasmussen and K. S. Thygesen, Computational 2d materials database: Electronic structure of transition-metal dichalcogenides and oxides, J. Phys. Chem. C, 2015, 119, 13169.
29. S. Dey, A. Phutela, S. Bhattacharya, F. Singh, P. Srivastava and S. Ghosh, Enhanced room-temperature ferromagnetism in nanostructured MoS₂ flakes by hydrogen post-treatment: Combined experimental and first-principles based studies, ACS Appl. Nano Mater., 2024, 7, 25693.
30. F. Ouyang, Z. Yang, X. Ni, N. Wu, Y. Chen and X. Xiong, Hydrogenation-induced edge magnetization in armchair MoS₂ nanoribbon and electric field effects, Appl. Phys. Lett., 2014, 104, 071901.
31. Y. P. Feng, L. Shen, M. Yang, A. Wang, M. Zeng, Q. Wu, S. Chintalapati and C.-R. Chang, Prospects of spintronics based on 2d materials, WIREs Comput. Mol. Sci., 2017, 7, e1313.
32. V. Ortiz Jimenez, Y. T. H. Pham, D. Zhou, M. Liu, F. A. Nugera, V. Kalappattil, T. Eggers, K. Hoang, D. L. Duong, M. Terrones, H. Rodriguez Gutiérrez and M.-H. Phan, Transition metal dichalcogenides: Making atomic-level magnetism tunable with light at room temperature, Advanced Science, 2024, 11, 2304792.
33. S. Fu, K. Kang, K. Shayan, A. Yoshimura, S. Dadras, X. Wang, L. Zhang, S. Chen, N. Liu, A. Jindal, X. Li, A. N. Pasupathy, A. N. Vamivakas, V. Meunier, S. Strauf and E.-H. Yang, Enabling room temperature ferromagnetism in monolayer MoS₂ via in situ iron-doping, Nat. Commun., 2020, 11, 2034.
34. Z. Guguchia, A. Kerelsky, D. Edelberg, S. Banerjee, F. von Rohr, D. Scullion, M. Augustin, M. Scully, D. A. Rhodes, Z. Shermadini, H. Luetkens, A. Shengelaya, C. Baines, E. Morenzoni, A. Amato, J. C. Hone, R. Khasanov, S. J. L. Billinge, E. Santos, A. N. Pasupathy and Y. J. Uemura, Magnetism in semiconducting molybdenum dichalcogenides, Sci. Adv., 2018, 4, eaat3672.
35. Q. Liang, Q. Zhang, X. Zhao, M. Liu and A. T. S. Wee, Defect engineering of two-dimensional transition-metal dichalcogenides: Applications, challenges, and opportunities, ACS Nano, 2021, 15, 2165.
36. T. Zhang, Y. Yang, Y. Guo, Q. Bai, H. Chang, R. Dou and C. Gu, Defect-induced anomalous magnetic response of valley polarization in multilayer-corralled MoS₂ monolayers, Phys. Rev. B, 2024, 110, 104108.
37. M. F. Hossen, S. Shendokar and S. Aravamudhan, Defects and defect engineering of two-dimensional transition metal dichalcogenide (2D TMDC) materials, Nanomaterials, 2024, 14, 410.
38. Z. Jagličić, A. Jeromen, Z. Trontelj, D. Mihailović, D. Arčon, M. Remškar, A. Mrzel, R. Dominko, M. Gaberšček and J. M. Martinez-Agudo, et al., Magnetic properties of MoS₂ nanotubes doped with lithium, Polyhedron, 2003, 22, 2293.
39. D. Mihailovic, Z. Jaglicic, D. Arcon, A. Mrzel, A. Zorko, M. Remskar, V. Kabanov, R. Dominko, M. Gaberscek and C. Gomez-Garcia, et al., Unusual magnetic state in lithium-doped MoS₂ nanotubes, Phys. Rev. Lett., 2003, 90, 146401.
40. D. Gao, S. Shi, K. Tao, B. Xia and D. Xue, Tunable ferromagnetic ordering in MoS₂ nanosheets with fluorine adsorption, Nanoscale, 2015, 7, 4211.
41. R. Sanikop and C. Sudakar, Tailoring magnetically active defect sites in MoS₂ nanosheets for spintronics applications, ACS Appl. Nano Mater., 2019, 3, 576.
42. B. Sun, Q. L. Li and P. Chen, Room-temperature ferromagnetism of single-crystalline MoS₂ nanowires, Micro Nano Lett., 2014, 9, 468.
43. S. Mathew, K. Gopinadhan, T. Chan, X. Yu, D. Zhan, L. Cao, A. Rusydi, M. Breese, S. Dhar and Z. Shen, et al., Magnetism in MoS₂ induced by proton irradiation, Appl. Phys. Lett., 2012, 101, 102103.
44. X. Tian, L. Liu, Y. Du, J. Gu, J.-b. Xu and B. I. Yakobson, Effects of 3d transition-metal doping on electronic and magnetic properties of MoS₂ nanoribbons, Phys. Chem. Chem. Phys., 2015, 17, 1831.
45. L. Martinez, J. Delgado, C. Saiz, A. Cosio, Y. Wu, D. Villagrán, K. Gandha, C. Karthik, I. Nlebedim and S. Singamaneni, Magnetic and electrocatalytic properties of transition metal doped MoS₂ nanocrystals, J. Appl. Phys., 2018, 124, 153903.
46. Y. Wang, L.-T. Tseng, P. P. Murmu, N. Bao, J. Kennedy, M. Ionesc, J. Ding, K. Suzuki, S. Li and J. Yi, Defects engineering induced room temperature ferromagnetism in transition metal doped MoS₂, Mater. Des., 2017, 121, 77.
47. D. Cao, T. Shen, P. Liang, X. Chen and H. Shu, Role of chemical potential in flake shape and edge properties of monolayer MoS₂, J. Phys. Chem. C, 2015, 119, 4294.
48. L. Pei, S. Tao, S. Haibo and X. Song, Structural stability, electronic and magnetic properties of MoS₂ quantum dots based on the first principles, Solid State Commun., 2015, 218, 25.
49. S. Pavlović and F. M. Peeters, Electronic properties of triangular and hexagonal MoS₂ quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155410.
50. Q. Chen, L. L. Li and F. M. Peeters, Magnetic field dependence of electronic properties of MoS₂ quantum dots with different edges, Phys. Rev. B, 2018, 97, 085437.
51. T. Espinosa-Ortega, I. A. Luk'yanchuk and Y. G. Rubo, Magnetic properties of graphene quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205434.
52. M. Maruyama and S. Okada, Magnetic properties of graphene quantum dots embedded in h-BN sheet, J. Phys. Chem. C, 2016, 120, 1293.
53. R. Han, J. Chen, M. Zhang, J. Gao, Y. Xiong, Y. Pan and T. Ma, Zigzag edge ferromagnetism of triangular-graphene-quantum-dot-like system, Phys. Rev. B, 2024, 109, 075117.
54. P. Castenetto, P. Lambin and P. Vancsó, Edge magnetism in mos2 nanoribbons: Insights from a simple one-dimensional model, Nanomaterials, 2023, 13, 3086.
55. P. Vancsó, I. Hagymási, P. Castenetto and P. Lambin, Stability of edge magnetism against disorder in zigzag MoS₂ nanoribbons, Phys. Rev. Mater., 2019, 3, 094003.
56. E. Ridolfi, L. R. F. Lima, E. R. Mucciolo and C. H. Lewenkopf, Electronic transport in disordered MoS₂ nanoribbons, Phys. Rev. B, 2017, 95, 035430.
57. P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864.
58. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
59. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
60. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
62. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (dft-d) for the 94 elements h-pu, J. Chem. Phys., 2010, 132, 154104.
63. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456.
64. M.-T. Huebsch, T. Nomoto, M.-T. Suzuki and R. Arita, Benchmark for ab initio prediction of magnetic structures based on cluster-multipole theory, Phys. Rev. X, 2021, 11, 011031.
65. J. C. Wildervanck and F. Jellinek, Preparation and crystallinity of molybdenum and tungsten sulfides, Z. Anorg. Allg. Chem., 1964, 328, 309.
66. R. Coehoorn, C. Haas, J. Dijkstra, C. J. F. Flipse, R. A. de Groot and A. Wold, Electronic structure of MoSe₂, MoS₂, and WSe₂. I. band-structure calculations and photoelectron spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6195.
67. K. E. Dungey, M. D. Curtis and J. E. Penner-Hahn, Structural characterization and thermal stability of MoS₂ intercalation compounds, Chem. Mater., 1998, 10, 2152.
68. S. Sharifvaghefi, B. Yang and Y. Zheng, New insights on the role of H₂S and sulfur vacancies on dibenzothiophene hydrodesulfurization over MoS₂ edges, Appl. Catal., A, 2018, 566, 164.
69. J. V. Lauritsen, M. Nyberg, R. T. Vang, M. V. Bollinger, B. S. Clausen, H. Topsøe, K. W. Jacobsen, E. Lægsgaard, J. K. Nørskov and F. Besenbacher, Chemistry of one-dimensional metallic edge states in MoS₂ nanoclusters, Nanotechnology, 2003, 14, 385.
70. N. Topsoe and H. Topsoe, Ftir studies of Mo/Al₂O₃-based catalysts: II. evidence for the presence of sh groups and their role in acidity and activity, J. Catal., 1993, 139, 641.
71. K. Y. Ma, S. I. Yoon, A.-R. Jang, H. Y. Jeong, Y.-J. Kim, P. K. Nayak and H. S. Shin, Hydrogenation of monolayer molybdenum diselenide via hydrogen plasma treatment, J. Mater. Chem. C, 2017, 5, 11294.
72. N. U. Din, V. Turkowski and T. S. Rahman, Excited states in hydrogenated single-layer mos₂, J. Phys.: Condens. Matter, 2020, 33, 075201.
73. N. Bertram, J. Cordes, Y. Kim, G. Ganteför, S. Gemming and G. Seifert, Nanoplatelets made from MoS₂ and ws₂, Chem. Phys. Lett., 2006, 418, 36.
74. J. M. Huang, R. A. Laitinen and D. F. Kelley, Spectroscopy and trapping dynamics in ws₂ nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10995.
75. M. V. Bollinger, J. V. Lauritsen, K. W. Jacobsen, J. K. Nørskov, S. Helveg and F. Besenbacher, One-dimensional metallic edge states in mos₂, Phys. Rev. Lett., 2001, 87, 196803.
76. S. Wang, C. Han, L. Ye, G. Zhang, Y. Hu, W. Li and Y. Jiang, Electronic properties of triangle molybdenum disulfide (MoS₂) clusters with different sizes and edges, Molecules, 2021, 26, 1157.
77. R. Bertel, M. Mora-Ramos and J. Correa, Electronic properties and optical response of triangular and hexagonal mos2 quantum dots. a dft approach, Physica E, 2019, 109, 201.
78. T. B. Wendumu, G. Seifert, T. Lorenz, J.-O. Joswig and A. Enyashin, Optical properties of triangular molybdenum disulfide nanoflakes, J. Phys. Chem. Lett., 2014, 5, 3636.

---