 Open Access Article
Open Access ArticleMolecular interactions of cinnamyl and quinoxaline derivatives with Bcl-2 antiapoptotic proteins: a computational study
Imelda L. Lazcano-Carrascoa,
Carlos Z. Gómez-Castrob,
Luis A. Zárate-Hernándeza,
Rosa L. Camacho-Mendozaa,
Simplicio González Montiela,
Marco Franco-Pérez *c and
Julián Cruz-Borbolla*a
*c and
Julián Cruz-Borbolla*a
aÁrea Académica de Química, Centro de Investigaciones Químicas, Universidad Autónoma del Estado de Hidalgo, km. 4.5 Carretera Pachuca-Tulancingo, Ciudad del Conocimiento, C.P. 42184, Mineral de la Reforma, Hidalgo, Mexico. E-mail: jcruz@uaeh.edu.mx; Tel: +52 771 71 72000 x40109
bSECIHTI Research Fellow. Área Académica de Química, Centro de Investigaciones Químicas, Universidad Autónoma del Estado de Hidalgo, km. 14.5 Carretera Pachuca-Tulancingo, Ciudad del Conocimiento, C.P. 42184, Mineral de la Reforma, Hidalgo, Mexico
cDepartamento de Física y Química Teórica, Universidad Nacional Autónoma de México, Av. Universidad No. 3004, Col. Ciudad Universitaria, Alc. Coyoacán, C.P. 04510 CDMX, Mexico. E-mail: qimfranco@quimica.unam.mx
First published on 23rd January 2026
Abstract
Antiapoptotic proteins represent a major obstacle to the success of anticancer therapies, as they promote the survival of malignant cells and contribute to treatment resistance. Among these, Bcl-2 and Bcl-xl are frequently overexpressed in pancreatic cancer, making them important therapeutic targets. In this work, we present a systematic computational study aimed at identifying the molecular features that enable selected cinnamyl and quinoxaline derivatives to inhibit the oligomerization of these proteins. Using a combination of molecular docking and molecular dynamics simulations, we characterized the most plausible binding modes and assessed the stability of the resulting complexes. Key intermolecular interactions responsible for binding were analyzed using the Quantum Theory of Atoms in Molecules (QTAIM), while reactivity descriptors derived from temperature-dependent chemical reactivity theory were employed to rationalize trends in affinity and stability. Our results reveal consistent structural and electronic patterns that govern the effective inhibition of Bcl-2 and Bcl-xl, providing mechanistic insight into their molecular recognition processes. Beyond improving the understanding of antiapoptotic protein inhibition, this study offers practical guidelines for the rational design of new small-molecule inhibitors with potential anticancer activity.
1. Introduction
Cancer is a significant problem for global health due to its high mortality rates. Pancreatic cancer is one of the most unfavorable cancers and is the fourth leading cause of death in the United States, primarily due to its late detection and pronounced resistance to chemotherapy, resulting in a dismal survival rate of less than 5%.1,2 The pancreatic cancer cell line 1 (PANC-1), one of the most significant cancer cell lines, is a keystone target for understanding the mechanisms of uncontrolled pancreatic cell proliferation, potentially resulting in a highly aggressive neoplasia known as adenocarcinoma.3One of the mechanisms of therapeutic resistance in cancer cells is antiapoptotic protection through members of the Bcl-2 family, which are present in PANC-1.4 Proteins from the Bcl-2 family are apoptotic regulators, acting primarily at the mitochondrial membrane, where they modulate its permeability. This modulation facilitates the release of key signaling molecules, such as cytochrome c, which ultimately triggers the cascade of events leading to programmed cell death. By balancing pro-apoptotic and anti-apoptotic signals, Bcl-2 family proteins play a central role in maintaining cellular homeostasis and determining cell fate.5 This family of proteins is primarily constituted by pro-apoptotic members, such as Bcl-2-associated X protein (BAX) and Bcl-2 homologous antagonist/killer (BAK), which serve as the final effectors of apoptosis by forming pores in the external mitochondrial membrane via oligomerization. Conversely, antiapoptotic proteins, such as the antiapoptotic B-cell lymphoma-2 (Bcl-2) and B-cell lymphoma-extra-large (Bcl-xl) proteins, act as cell death inhibitors.5,6 These antagonist proteins can sequester their proapoptotic counterparts, thus preventing cell death.7,8 Immunohistochemical assays have shown that the antiapoptotic members Bcl-2 and Bcl-xl are overexpressed in 50–70% of all pancreatic cancers.9
Another subfamily of Bcl-2 proteins comprises Bcl-2 homology 3 domain (BH3) mimetics, which act as activators of BAX and BAK and inhibitors of Bcl-2 and Bcl-xl. Several studies on different types of cancer have shown uncontrolled overexpression of antiapoptotic members, an alteration that may lead to the development of resistance to oncological treatments.10 Research into the design and development of small molecules that imitate the function of BH3-mimetics has revealed their potential to induce apoptosis in cancer cells. These molecules selectively bind to the active sites of anti-apoptotic proteins such as Bcl-2 and Bcl-xl, disrupting their interaction with pro-apoptotic proteins.9,10 Navitoclax (ABT-263) and venetoclax (ABT-199) are drugs used in the treatment of acute and chronic leukemias acting as BH3-mimetics targeting and inhibiting Bcl-xl.11 Several studies developed to induce cell death in pancreatic cancer have focused on the identification of curcumin derivatives that possess multifunctional pharmacological properties, including anti-oxidant,12 anti-inflammatory13 and anticancer14 activities. However, their clinical utility is limited due to extensive first-pass metabolism, which markedly reduces their oral bioavailability.15 To address this limitation, a key area of active research involves the development of synthetic analogs of curcumin designed to enhance its pharmacological effects. Recent findings suggest that cinnamyl derivatives represent a new class of compounds with significant therapeutic value.16 Cinnamyl-based compounds are commonly synthesized via a standard Claisen–Schmidt reaction, which is conducted via the condensation of diacetyl and benzaldehyde.17,18
Quinoxalines are a second class of highly promising heterocyclic compounds characterized by a benzene ring fused to a pyrazine ring. This unique structure endows them with a broad spectrum of biological activities, including antibacterial, anti-inflammatory, anticancer, and antimalarial effects.19,20 Particularly, polyfunctionalized quinoxaline derivatives have been identified as a new class of chemotherapeutics.21–23
Recent studies have highlighted that cinnamyl (1,6-diarylhexa-1,5-diene-3,4-diones) and quinoxaline (2,3-di((E)-prop-1-en-1-yl)quinoxaline) derivatives (for instance, those shown in Fig. 1) are highly effective apoptosis inducers. It is suggested that these compounds exert their anticancer effects by targeting key signaling pathways associated with Bcl-2 family proteins and caspases. By disrupting the anti-apoptotic functions of Bcl-2 proteins and activating caspase-dependent pathways, they effectively promote programmed cell death in pancreatic cancer cells.24
 | ||
| Fig. 1 Cinnamyl and quinoxaline derivatives considered in this work.24 | ||
This study is focused on elucidating and rationalizing the affinity of some of the members of this new class of anti-pancreatic cancer candidates (Fig. 1) toward their pharmacological targets, the anti-apoptotic proteins Bcl-2 and Bcl-xl. To achieve a comprehensive and reliable understanding, we employed a multi-faceted computational approach. First, molecular docking studies were conducted to rank the candidates based on their binding affinity to these targets. Subsequently, selected protein–inhibitor complexes were then subjected to molecular dynamics simulations to assess their stability and dynamic behavior over time. Weak interactions critical to the stability of these complexes were identified through the analysis of bond critical points (BCPs) using the Quantum Theory of Atoms in Molecules (QTAIM)25 for which we constructed simplified protein–inhibitor models. Furthermore, the inherent molecular affinity of these candidates towards their targets was evaluated using advanced reactivity descriptors, some of which were derived from the temperature-dependent chemical reactivity theory (τ-CRT).26–30 By integrating these methodologies, our work aims to uncover key protein–inhibitor interactions that, in addition to providing a rational explanation for the stability of the studied protein–inhibitor complexes, could guide the design and development of next-generation antineoplastic drugs with enhanced efficacy.
2. Computational strategies
2.1 Geometry optimization of inhibitors
For each inhibitor, an initial exploration of a diverse range of possible rotamers was conducted using Born-Oppenheimer molecular dynamics (BOMD) simulations at the PBE/DZVP31,32 level of theory, under elevated temperature conditions of 600 K to enhance conformational sampling. Each simulation spanned 700 steps for a total simulation time of 2 femtoseconds.The resulting geometries were ranked in terms of their free energies, and the selected structures were then optimized in the gas phase using the ωB97XD33 density functional approximation (DFA), conjointly with the def2-TZVP34 orbital basis set for all atoms. It is well documented that this level of theory is adequate to describe weak chemical interactions, such as those observed in protein-inhibitor complexes.33 The resulting lowest energy conformation was then selected. The effect of the solvent medium on geometries and computed molecular properties was additionally evaluated using a continuum approach, particularly the SMD solvation model35 at the same level of theory as the previous step. We confirm that all the optimized structures (both in the gas and solution phases) corresponded to minima on the potential energy surface (PES) by an analysis of vibrational frequencies. BOMDs were performed with the deMon2k package,36 while geometry optimizations and electronic structure calculations were carried out using Gaussian 16 software.37
2.2 Molecular docking and dynamics
Compounds M1–M7 were selected as ligands for molecular docking and were previously optimized and prepared by adding nonpolar hydrogens and Gasteiger charges using AutoDock Tools 1.5.2 (ADT).38 The crystal structures of proteins from the Bcl-2 family were obtained from the Protein Data Bank (PDB) database (https://www.rcsb.org/) under the PDB IDs 4IEH (Bcl-2) and 3ZK6 (dimeric Bcl-xl). Other studies examined these proteins due to their interaction sites with BH3-activating proteins.39,40 For both proteins, the water molecules and the cocrystallized compounds bound to them were eliminated using visual molecular dynamics (VMD) software.41 Subsequently, hydrogen atoms and Kollman charges were added using ADT 1.5.2. The size of the grid on which the Bcl-2 interaction was established at coordinates x = 10.659, y = 24.4212, and z = 8.479 with 86 points on each dimension, whereas the interaction box for the Bcl-xl protein was established at x = 20.181, y = 52.776, and z = 0.135 with 102 points. The Lamarckian genetic algorithm was realized by employing 100 docking runs, 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generations, and 2.5 × 107 energy evaluations. The minimum energy conformations (EU) and inhibition constants (Ki) were determined using the ADT 1.5.2 interface. For comparison purposes, our docking study was extended to the monomeric Bcl-xl protein, which is suggested as the simplest representative model for this protein.42 The images of the protein–ligand interactions were visualized using the Biovia Discovery Studio43 and Chimera44 software packages.
000 generations, and 2.5 × 107 energy evaluations. The minimum energy conformations (EU) and inhibition constants (Ki) were determined using the ADT 1.5.2 interface. For comparison purposes, our docking study was extended to the monomeric Bcl-xl protein, which is suggested as the simplest representative model for this protein.42 The images of the protein–ligand interactions were visualized using the Biovia Discovery Studio43 and Chimera44 software packages.
The protein–ligand complexes were analyzed via molecular dynamics (MD) to evaluate their stability over time. At this stage, only the monomeric Bcl-xl protein complexes were analyzed. After a short standard thermal and density-fitting equilibration protocol, a 300 ns isothermal–isobaric ensemble at 310 K and 1 atm production simulations were run in duplicate using the open-source software NAMD v. 2.1445 and the CHARMM36 force field.46 The NAMD psfgen program was used to generate the topology file for the protein, while the topologies for the M3 and M5 ligands were recovered with CGenFF (https://cgenff.com/). The final models of the protein–ligand complexes were used to carry out equilibration of the system, density fitting, and production MD simulations. The density equilibrium dynamics was applied to enable the system to achieve a stable thermodynamic state prior to analysis, consisting of five steps to adapt the solvent, perform a heating process, and adjust the volume. Based on the docking results, the complexes exhibiting the lowest (M3-Bcl-xl) and highest (M5-Bcl-xl) binding affinities—consistent, as discussed below, with trends observed in the preliminary 300 ns molecular dynamics simulations—were selected for an additional, third independent simulation replica of 500 ns. The production dynamics were analyzed to assess the stability of these complexes using the root mean square deviation (RMSD), the distance from the center of mass (distCOM), and the root mean square fluctuation (RMSF). Additionally, two replicas were run for 300 ns for the reference Bcl-xl inhibitor Navitoclax (PDB ID: 4LVT), and three replicas were run for the ligand-free Bcl-xl protein. This set of calculations performed here summed up to over 4.3 microseconds of combined MD simulation time.
2.3 Representative models of the Bcl-xl–ligand binding sites
To enable a robust assessment of the energetic stability of the Bcl-xl–ligand complexes under investigation, we performed a systematic relaxation of the binding site for each system using progressively refined levels of approximation. This multistep protocol allowed us to derive reduced, yet chemically representative, binding-site models that are suitable for subsequent first-principles density functional theory (DFT) calculations. First, each ligand–protein complex was subjected to a multistage energy minimization protocol in the presence of the full protein and explicit solvation. This procedure consisted of three consecutive steps. (1) An initial relaxation of 3000 conjugate-gradient minimization steps was performed using the CHARMM36 force field for all atoms. (2) This was followed by 3000 hybrid QM/MM minimization steps. The QM region was defined as the ligand together with all protein residues exhibiting at least one interaction within a distance cutoff of 3.5–3.9 Å from the ligand. This cutoff was systematically adjusted to yield a computationally tractable QM region of approximately 300 atoms. The QM subsystem was treated at the semiempirical PM347 level using ORCA,48 while the MM region was described with the CHARMM36 potential. (3) Using the same QM/MM partitioning, a final set of 200 minimization steps was carried out with the QM region described at the DFT level using the B97-3c/def2-SVPD49 method. No positional restraints were applied during this stage.Following these relaxations, the QM region was extracted by truncating the surrounding MM environment while retaining key backbone atoms. The resulting reduced models were capped and reconnected to preserve the protein backbone continuity, with first-coordination-sphere fragments including up to three residues. To improve model robustness and reduce complexity, non-interacting loop regions were systematically replaced by alanine residues, thereby decreasing the total number of protein fragments while maintaining the structural integrity of the binding site. This reduction strategy follows established protocols previously demonstrated to yield reliable interaction energies in protein–ligand systems.50,51
As a final stage, we computed the interaction energies of the resulting complexes following the supermolecule approximation:
| ΔEint = Ecomplex − (Eprotein + Eligand) | (1) |
2.4 Protein–ligand interactions via QTAIM of generated representative models of the Bcl-xl–ligand binding sites
To elucidate and characterize key inter- and intramolecular interactions between the Bcl-xl protein and the M3 and M5 ligands, we conducted a topological analysis of the electron density, using the theoretical framework of the Quantum Theory of Atoms in Molecules (QTAIM) proposed by Bader.25 For this purpose, we used the simplified representative models optimized in the preceding subsection. Our primary focus was to identify and analyze bond critical points (BCPs) at the interface of the host protein and the inhibitor within the binding pocket, providing insights into the nature and strength of these interactions. QTAIM properties were calculated using MultiWFN 3.8,53 focusing on bond critical points (BCPs) that define interactions between the protein and ligand. Specifically, we extracted key descriptors, including the electron density, Lagrangian kinetic energy, potential energy density, total energy density, the Laplacian of the electron density, and the −G(r)/V(r) ratio.2.5 Chemical reactivity descriptors
We analyzed two sets of chemical reactivity descriptors using the optimized geometries of the isolated inhibitors as the starting point. Standard conceptual reactivity indicators were computed, including the electronic chemical potential (μ), which follows a similar equation to Mulliken electronegativity and serves as a measure of the electronic species’ acidity strength; chemical hardness (η), which reproduces Pearson's empirical hardness scale; and global electrophilicity (ω),54 a descriptor closely related to Pauling electronegativity,55 along with the electroaccepting (ω+) and electrodonating (ω−) powers reported by Gazquez, Cedillo & Vela.56 Their definitions and working equations are provided in the SI (Table S1). The ionization potential (I) and electron affinity (A), required for these calculations, were obtained vertically using an ensemble model comprising three fundamental states: N0 − 1 (cation), N0 (neutral) and N0 + 1 (anion). Additionally, the Fukui function57 was computed in a similar manner conjointly with the Dual Descriptor (DD).58 The corresponding scalar plots were visualized using MultiWFN 3.8, while condensed Fukui values were determined using the response-of-molecular-fragment approach, based on the same three-state ensemble model. Hirshfeld population analysis was employed to calculate the required atomic charges.59,60We also analyzed chemical reactivity descriptors within the finite-temperature regime, focusing on the local counterparts of chemical potential and chemical hardness.61–64 These descriptors illustrate how global properties are distributed across molecular space, helping to identify key reactive sites and providing a chemical interpretation. Specifically, the local chemical potential highlights acidic and basic moieties, while the local hardness pinpoints regions reluctant to charge transfer; this descriptor is also known to be related to the Hard & Soft Acids & Bases (HSAB) principle at the local level.63 In this way, these descriptors offer valuable insights into the contribution of key moieties to the observed binding affinity toward Bcl-2 and Bcl-xl proteins. Conveniently, computing these descriptors requires no additional calculations, as detailed in the SI, where the practical calculation schemes are provided.
2.6 Absorption, distribution, metabolism and excretion profiles
To complete the molecular and pharmacological profiling, we computed absorption, distribution, metabolism, and excretion (ADME) properties using the freely accessible SwissADME web server.65 In total, twelve ADME-related descriptors were evaluated for each compound.3. Results and discussion
3.1 Structural properties
The optimized geometries of the cinnamyl and quinoxaline derivatives under study are shown in Fig. S1 of the SI. For the cinnamyl derivatives M1–M4, the results revealed C–O distances of 1.22 Å and C1–C2 bond lengths ranging from 1.46 to 1.47 Å. These values closely match those typically observed in the cinnamyl group, where C–C distances around 1.39 Å have been reported based on X-ray diffraction data.66 Similarly, in the quinoxaline derivatives (M5–M7), the N–C5 bond distance was found to be 1.32 Å, while the N–C3 bond length ranged from 1.36 to 1.37 Å. These values align well with literature-reported bond lengths for the pyrazine ring in quinoxaline.67 These results suggest that our selected theoretical protocol is adequate for the computation of the geometrical parameters of these two families of compounds.3.2 Molecular docking of M1–M7 ligands with the Bcl-2 protein
We evaluated the protein-inhibitor interactions by analyzing the binding affinity, inhibition constant (Ki), and the most significant noncovalent protein–ligand interactions, as summarized in Table 1. According to these results, the seven ligands under study are able to form stable complexes with the antiapoptotic protein Bcl-2. From the cinnamyl derivatives, the M1 ligand presented the highest affinity for Bcl-2, as indicated by the low values of BE and Ki conjointly with the short distance of its most significant intermolecular interaction. These computed binding energies are close to previous results reported for flavonoids through a similar molecular docking strategy with these proteins.39 Interestingly, the quinoxalines M5–M7 exhibit higher affinity for the Bcl-2 protein than their cinnamyl counterparts, exhibiting lower binding energies and inhibition constants. Overall, the quinoxaline M5 displayed the best affinity parameters for this protein. The computed binding energy values for this ligand (−8.89 and −8.45 kcal mol−1) are close to those reported for a quinoxaline-1,3,4-oxadiazole compound on the Bcl-2 protein in a previous molecular modeling study (−8.3 kcal mol−1).39–68 It is worth noting that the binding distance of the most significant interaction (with Arg105) is the shortest observed, which could be indicative that the interaction with the Arg105 residue is relevant for the inhibition of the Bcl-2 protein.| Protein | Ligand | Binding sites | Binding energy (kcal mol−1) | Inhibition constant (μM) | Binding distance (Å) | Most significant interaction |
|---|---|---|---|---|---|---|
| Bcl-2 | M1 | Arg66 | −6.33 | 22.79 | 1.973 | N–H⋯Olig |
| M2 | Arg105 | −5.53 | 88.50 | 2.201 | N–H⋯Olig | |
| M3 | Arg66 | −5.33 | 124.5 | 2.066 | N–H⋯Olig | |
| M3 | Gly104 | −5.14 | 170.9 | 2.214 | N–H⋯Olig | |
| M4 | Arg66 | −5.87 | 49.83 | 1.970 | N–H⋯Olig | |
| M5 | Arg105 | −8.89 | 0.303 | 1.934 | N–H⋯Olig | |
| M5 | Tyr161 | −8.45 | 0.664 | 2.057 | H–O⋯H-Nlig | |
| M6 | Arg66 | −7.30 | 4.490 | 1.917 | N–H⋯Olig | |
| M7 | Arg105 | −6.75 | 11.30 | 2.127 | N–H⋯N–Clig | |
| Bcl-xl | M1 | Ser106 | −6.78 | 60.80 | 2.984 | N–H⋯Olig |
| M2 | Ser106 | −6.42 | 19.69 | 2.984 | N–H⋯Olig | |
| M3 | Ser106 | −5.29 | 133.5 | 2.989 | N–H⋯Olig | |
| M4 | Ser106 | −5.90 | 47.59 | 2.896 | N–H⋯Olig | |
| M5 | Ser106 | −9.15 | 0.197 | 2.160 | C–O⋯H–Nlig | |
| M5 | Arg139 | −8.35 | 0.762 | 2.951 | N–H⋯Olig | |
| M5 | Gly138 | −9.49 | 0.111 | 2.128 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–Nlig O⋯H–Nlig |
|
| M6 | Ser106 | −7.46 | 3.420 | 2.751 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯N–Clig O⋯N–Clig |
|
| M7 | Ser106 | −8.05 | 1.250 | 2.685 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯N–Clig O⋯N–Clig |
Previous studies of molecular docking39,69,70 have identified Arg66, Arg105, Gly104, Tyr161, and Trp103 as key residues within the Bcl-2 inhibition site, where cinnamyl and quinoxaline derivatives engage in hydrogen bonding, van der Waals, π⋯π, π⋯alkyl, and π⋯σ interactions, among others. Fig. 2a highlights the key interactions observed for the most active derivative, M1 (cinnamyl), demonstrating that these specific interactions dictate the binding pattern of the ligands with Bcl-2 and further validate the findings from our docking analysis. Notably, within the binding pocket, the M1 derivative adopts a folded conformation. However, the intrinsically larger angle between the benzene rings in quinoxaline derivatives—compared to their cinnamyl counterparts—may facilitate interactions with more residues.
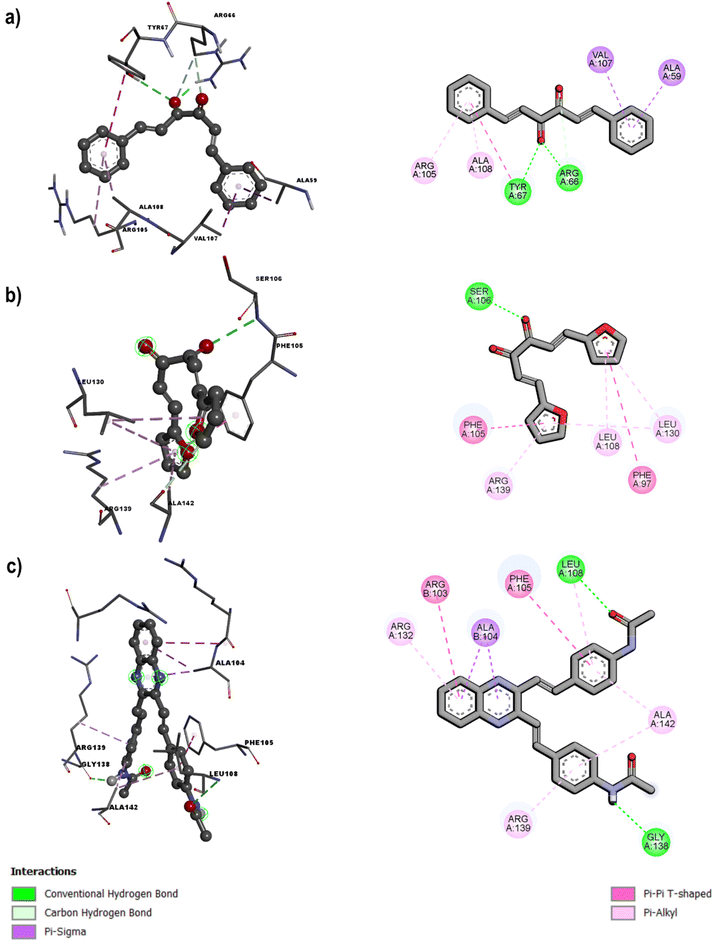 | ||
| Fig. 2 3D and 2D pictures of (a) compound M1 at the active site of Bcl-2 protein, (b) M3 complexed with the active site of Bcl-xl and (c) compound M5 bound to the binding site of Bcl-xl. | ||
3.3 Molecular docking of the ligands M1–M7 with the Bcl-xl protein
As in the case of the Bcl-2 protein, the quinoxaline derivatives exhibited better binding parameters than the cinnamyl-based compounds. M3 and M5 are the lowest and highest binding energy cinnamyl and quinoxaline derivatives for the dimeric protein Bcl-xl, with binding energies of −5.29 kcal mol−1 and −9.49 kcal mol−1, respectively (Fig. 2b). This time M5 exhibited three highly stable coordination patterns (Fig. 2c), with two of them (Ser106 and Gly138) having almost equal probabilities of occurring (Table 1). Note that the oxygen of the α-dicarbonyl and furan moieties of M1 and M5, respectively, are the molecular moieties responsible for their observed high affinities with both proteins. The M6 and M7 compounds bound to Ser106 via the nitrogen in benzopyrazine, whereas the furan and thiophene rings in their structures engaged in π⋯π, π⋯alkyl, and π⋯σ interactions with the Phe105 and Leu108 benzene rings. The different binding patterns observed across the set of ligands here studied can be in part attributed to the flexibility of the protein near the binding pocket; the Phe105, Ser106, and Leu108 residues form part of α-helix 3, which has a high degree of plasticity that enables the structure to be modified via interactions with small molecules, allowing modification of the inhibition site and preventing the protein from oligomerizing with apoptotic proteins and participating in the interruption of apoptosis.71 We extended the docking analysis to the monomeric form of Bcl-xl and observed the same stability trend as that obtained for the dimeric protein, as summarized in Table S2 of the SI. Although the overall trends are consistent, the coordination patterns differ in number, reflecting the reduced availability of coordinating residues in the monomeric protein (see Fig. S2).3.4 Molecular dynamics of the ligands M3 and M5 in complex with the monomeric Bcl-xl protein
As the next step, we conducted molecular dynamics simulations on the ligands with the highest and lowest binding performance toward the Bcl-xl protein, since this protein has been shown to be 10 times more functional than Bcl-2 due to its broader expression in different types of cancer, as well as its role in resistance to chemotherapy and its relevance to solid tumors.72,73 This analysis aimed to uncover potential mechanisms governing binding affinity patterns and to further validate the findings from our molecular docking study. As demonstrated below, the docking protocol employed in this study reproduces stability trends that are consistent with those obtained from ab initio DFT calculations for these systems. These results indicate that the preliminary docking outcomes for Bcl-2 are representative of the underlying interaction energetics and can therefore be reliably used as qualitative guidelines for subsequent, higher-level theoretical analyses. First, we analyzed the protein conformational changes based on the simulation trajectories for each system. Structural modifications at the active inhibition site were examined visually using VMD, comparing the native (ligand-free) protein with the complexes obtained from molecular docking. To quantify these changes, the root mean square deviation (RMSD), the distance between the center of mass (COM) of the ligand and the protein (distCOM), and the residue-based root mean square fluctuation (RMSF) were calculated, with the corresponding graphs presented in Fig. 5. The RMSD graph (Fig. 3a) indicates that the native protein exhibited values less than 2 Å throughout the simulation, a typical value for MD simulations of stable, natively folded proteins. For the Bcl-xl–M3 complex, fluctuations were observed throughout the simulation at 20 ns, 60 ns, and 150 ns; for this reason, the ligand can be considered unstable at the binding site, whereas the Bcl-xl–M5 system exhibited 1.5 Å, remained stabilized during the simulation and was more stable than the Bcl-xl–M3 system.We used the distCOM factor for characterizing the dynamical behavior of the overall molecular system, identifying whether the center of mass of the ligand moves farther away from or closer to the center of mass of the pharmacological target. The orange line in Fig. 3b shows that the M3 ligand remained within the binding site for the initial 40 ns. However, when it reached 45 ns of simulation, the behavior fluctuated, reaching up to 95 Å from the center of mass of the protein, wherein the ligand left the docking groove, meaning that the complex lost its stability. However, at 220 ns, the protein underwent conformational changes within the active site, and the ligand itself docked again within the binding cavity until 500 ns, very close to the original binding mode, showing distances less than 20 Å between the centers of mass, suggesting that the MD calculations could refine the results obtained in the molecular docking. The M5 ligand remained within the active site because the distance to the center of mass was constant for 500 ns. Three replicas of 300 ns were run, and the results were consistent in both cases. The RMSF of the Cα atoms for the residues was calculated for the three systems.
The RMSF set out in Fig. 3c enables the identification of the most flexible regions in the protein system. The orange line corresponds to the complex containing the M3 ligand, where the Cα atoms presented the highest fluctuations, with Bcl-xl as the reference point. The dynamic profile of the Bcl-xl–M5 complex resembled that of the native structure, except for residues 102 and 117, which correspond to Arg and Gly, respectively; those residues were not observed within the active site. Furthermore, amino acids Phe105, Ser106, Leu108, and Arg139 had the lowest fluctuations of 0.4–0.5 Å, suggesting that these residues were involved in stable interactions with the M5 ligand, as previously inferred in our docking study. In contrast, for the M3 ligand, these residues fluctuated above 0.5 Å. These residues are considered conserved in the Bcl-xl protein72 because they play a fundamental role in rational drug design, since they are within the inhibition site.73 Our findings suggest that the M5 ligand stabilizes the Phe105, Ser106, Leu108, and Arg139 residues, minimizing fluctuations due to its hydrogen bond interactions. Together, our docking and molecular dynamics results clearly indicate that the M5 quinoxaline derivative may be considered as an effective inhibitor of Bcl-xl protein and a promising antineoplastic candidate.
3.5 Energetic stability of the representative models of the Bcl-xl–ligand binding sites
Following the optimization and truncation procedures, we observed that the overall binding patterns were largely preserved. The key binding moieties remained essentially unchanged, and the general orientation of the ligands within the binding pocket was maintained. Fig. 4 illustrates the resulting binding-site models for the M3 and M5 ligands bound to Bcl-xl, highlighting the representative configurations from which the most significant interactions are discussed in the following section.The corresponding energetic analysis is summarized in Table 2. For comparative purposes, we included the clinically relevant reference compound Navitoclax (PDB ID: 1XJ), for which a representative binding-site model was generated following the same protocol described in the Computational Details section. As for the derivatives under investigation, the interaction energy for Navitoclax was computed using the supermolecular approach (eqn (1)), ensuring methodological consistency across all systems.
| Ligand | IC50 (μM) | Docking | ωB97XD-3 | B97-3c | PBEh-3c |
|---|---|---|---|---|---|
| def2-SVP | def2-SVP | def2-mTVZP | |||
| M1 | 40.25 | −7.49 | −36.245 | −34.776 | −23.655 |
| M2 | 50.19 | −7.50 | −52.381 | −56.952 | −35.232 |
| M3 | 1.45 | −5.29 | −38.824 | −35.121 | −23.828 |
| M4 | 23.49 | −6.85 | −55.668 | −60.264 | −39.272 |
| M5 | 35.14 | −9.49 | −59.684 | −53.820 | −41.750 |
| M6 | 38.36 | −9.23 | −45.564 | −39.474 | −29.868 |
| M7 | 26.95 | −8.05 | −41.602 | −44.183 | −29.378 |
| Navitoclax | 1.98 | −15.97 | −108.176 | −101.432 | −104.632 |
A first notable observation is that all evaluated compounds exhibit favorable interactions with the Bcl-xl protein. As expected, the reference inhibitor Navitoclax displays the highest binding affinity, with an interaction energy nearly twice as favorable as that of the most stable derivative examined in this study. Among the newly investigated compounds, both the ωB97X-D3 and PBEh-3c density functional approximations consistently identify M5 as the derivative with the strongest affinity toward Bcl-xl, whereas M1 is systematically predicted to be the least affine compound by all three DFAs considered. Importantly, all these energetic trends are fully consistent with the results obtained from the docking analysis.
The close agreement between the ωB97X-D3 and PBEh-3c functionals further supports their suitability for evaluating protein–ligand interaction energetics in this system. Given that both methods reproduce identical stability rankings, ωB97X-D3 emerges as a particularly attractive choice due to its lower computational cost while maintaining reliable energetic discrimination among the ligands.
3.6 Protein–ligand interactions via QTAIM
At this stage, we aimed to characterize protein–ligand interactions at the electronic level using QTAIM-defined bond critical points (BCPs). To achieve this, we used the reduced models of the protein–ligand interaction site previously obtained via equilibrium geometries from MD simulations as starting points. The quantum parameters computed for the most relevant BCPs of the protein–ligand bonds in the reduced Bcl-xl–M3 and Bcl-xl–M5 complexes are presented in Table 3.| ID | Electron density | Ratio | Ligand–residue interaction |
|---|---|---|---|
| BCP | ρ(r) | −G(r)/V(r) | |
| Reduced Bcl-xl–M3 complex | |||
| 1 | 0.016 | 1.025 | Ala95CO⋯HCfuranLig |
| 2 | 0.009 | 1.187 | Val141CH⋯Cfuran |
| 3 | 0.012 | 0.999 | Phe97CH⋯HCLig |
| 4 | 0.005 | 1.334 | Tyr101ringCH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| 5 | 0.008 | 1.177 | Phe97ringCH⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| 6 | 0.008 | 1.064 | Arg103CN⋯HCfuran |
| 7 | 0.015 | 0.984 | Arg139CH⋯HCfuran |
| 8 | 0.010 | 1.011 | Arg139CH⋯Ofuran |
| 9 | 0.005 | 1.213 | Gly138CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| Reduced Bcl-xl–M5 complex | |||
| 1 | 0.004 | 1.226 | Gly138NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| 2 | 0.008 | 1.349 | Gly138CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| 3 | 0.015 | 0.968 | Arg139CH⋯HCLig |
| 4 | 0.013 | 1.105 | Arg139CH⋯HCLig |
| 5 | 0.004 | 1.275 | Leu130CH⋯Npyrazine |
| 6 | 0.015 | 0.928 | Arg139CH⋯HCLig |
| 7 | 0.008 | 1.220 | Ala104CH⋯Cring–Lig |
| 8 | 0.005 | 1.349 | Ala104CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CLig CLig |
| 9 | 0.014 | 1.070 | Phe105ringCH⋯HCLig |
| 10 | 0.008 | 1.169 | Phe97ringCH⋯Cring–Lig |
| 11 | 0.029 | 1.070 | Tyr101CO⋯HNLig |
For the Bcl-xl–M3 complex, the electron density at the BCPs ranged from 0.008 to 0.016 a.u., consistent with hydrogen bonding interactions. This observation is reinforced by the computed −G(r)/V(r) ratios, where positive values indicate that kinetic energy dominates over potential energy, a hallmark of non-covalent interactions typically governed by electrostatics.74–76 A similar behavior was observed for the Bcl-xl–M5 complex; however, the electron density at the BCPs ranged from 0.004 to 0.029 a.u where BCP 11, corresponding to the interaction between the oxygen of the OH group of Tyr101 and the amide N–H proton in quinoxaline, exhibited the highest electron density accumulation among all BCPs. This suggests that this specific interaction plays a crucial role in the higher affinity of M5 toward Bcl-xl. Interestingly, this interaction was not identified in Table 1 as one of the most significant from our docking analysis, underscoring the importance of electronic structure-based approaches for accurately identifying key protein–ligand stabilizing interactions. Note that M3 does not exhibit such relevant interaction, which may have an impact on its affinity for the protein, as our results in Table 1 indicate.
By summing up the electron density at the critical points (BCPs) linking protein residues to ligand moieties, we found that the Bcl-xl–M5 complex accumulated a higher electron density (0.198 a.u. across 32 BCPs) compared to Bcl-xl–M3 (0.142 a.u. across 28 BCPs). This suggests that Bcl-xl–M5 not only engages in more non-covalent interactions than Bcl-xl–M3, but also that its weak intramolecular interactions contribute more significantly to stability, providing a plausible explanation for the observed differences in their binding affinities toward Bcl-xl protein. Fig. 4 depicts the most relevant BCPs for both complexes, revealing that oxygen atoms (α-dicarbonyl and furane in M3 and amide carbonyl in M5) are important electron donors, forming up to three relevant non-covalent interactions for both ligands. This observation complements the results previously inferred from the docking analysis.
3.7 Chemical reactivity analysis
Building on the gathered information, we aim to explore the relationship between ligand affinity for both proteins and their intrinsic reactivity properties. To achieve this, we computed the chemical reactivity descriptors outlined in the computational strategies section and the SI. Our previous findings suggest that electrostatics play a crucial role in the stability of the ligand–protein complex, prompting us to include the dipole moment magnitude of the ligands in our analysis, calculated at the same level of theory as the reactivity descriptors. We examined trends by correlating binding parameters obtained from our docking study and the IC50 values reported for these compounds against the PANC-1 cell line24 with the reactivity descriptors. For consistency and comparative analysis, we adopted the energetic profiles derived from the docking studies, as these data are also available for the corresponding Bcl-2 complexes. Moreover, our theoretical results demonstrate that the docking protocol reproduces the same relative reactivity trends observed with higher-level DFT calculations. This agreement indicates that docking-derived energetics can serve as a reliable and computationally efficient proxy for estimating binding affinities and for prioritizing additional candidate compounds without the need for more demanding ab initio calculations.As a first step, we explored the inherent reactivity trends of our derivatives by analyzing the donor–acceptor map (DAM) diagram (Fig. 5), introduced by Martínez,77 which classifies chemical species based on their electron-donating and electron-accepting capacities. A low ω− value indicates a strong capacity for donating electrons, whereas a high ω+ value suggests an elevated capacity for accepting electrons. Quinoxalines are positioned in the lower left-hand section of the map, indicating their role as electron-donating species, while cinnamyls are in the upper right-hand section, behaving as electron-accepting entities (or weak electron-donors). This trend can be rationalized by direct analysis of their structural features. In cinnamyls, the vinyl group contains a carbon–carbon double bond with significant π-character, enabling electron delocalization. In quinoxalines, however, the π-system extends further, incorporating both the benzene ring and the benzopyrazine moiety, allowing for greater electron delocalization throughout the structure.
Before conducting our analysis using both global and local chemical reactivity indicators to infer the reactivity trends of the studied ligands (Table 4), it is important to highlight that local reactivity indicators were primarily computed for the oxygen atoms in the α-dicarbonyl groups (cinnamyls) and the heteroatoms in benzopyrazine moieties (quinoxalines). This focus is justified for two key reasons: (i) these atoms participate in the most significant interactions, as indicated in Table 1, and (ii) although the electron density at their corresponding critical points was not predominant (see Table 3), our analysis revealed that these atoms exhibit three critical points with notable charge density, suggesting their crucial role in ligand–protein interactions.
| ωB97XD/def2-TZVP | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ligand | IC50 (μM) | I | A | μ | η | ω | ω+ | ω− | Dipole (debye) |
| M1 | 40.25 | 8.42 | 1.29 | −4.86 | 7.13 | 1.65 | 6.18 | 1.32 | 0.001 |
| (6.85) | (3.24) | (−5.05) | (3.6) | (3.53) | (9.81) | (4.77) | (2.48) | ||
| M2 | 50.19 | 8.51 | 1.38 | −4.95 | 7.13 | 1.71 | 6.35 | 1.4 | 0.003 |
| (6.84) | (3.23) | (−5.03) | (3.61) | (3.51) | (9.76) | (4.73) | (1.8) | ||
| M3 | 1.45 | 8.34 | 1.26 | −4.80 | 7.09 | 1.63 | 6.1 | 1.29 | 1.05 |
| (6.06) | (3.26) | (−4.66) | (2.79) | (3.89) | (10.27) | (5.62) | (3.26) | ||
| M4 | 23.49 | 8.36 | 1.32 | −4.84 | 7.04 | 1.67 | 6.19 | 1.35 | 0.97 |
| (6.2) | (3.27) | (−4.73) | (2.94) | (3.82) | (10.19) | (5.45) | (3.04) | ||
| M5 | 35.14 | 7.17 | 0.93 | −4.05 | 6.24 | 1.32 | 5.05 | 0.99 | 6.29 |
| (5.95) | (2.58) | (−4.26) | (3.38) | (2.69) | (7.73) | (3.46) | (10.35) | ||
| M6 | 38.36 | 7.22 | 0.97 | −4.09 | 6.25 | 1.34 | 5.12 | 1.02 | 1.22 |
| (5.86) | (2.64) | (−4.25) | (3.22) | (2.8) | (7.93) | (3.68) | (1.96) | ||
| M7 | 26.95 | 7.29 | 1.06 | −4.18 | 6.23 | 1.4 | 5.27 | 1.1 | 0.75 |
| (5.95) | (2.63) | (−4.29) | (3.32) | (2.78) | (7.91) | (3.61) | (1.43) | ||
For the Bcl-2–ligand complexes, we observed a strong correlation between the ω+/ω− ratio and the binding energies (BEs) calculated in our docking studies, yielding an R2 value of 0.907 (Fig. 6a). To construct this plot, the data for the M3 compound were excluded as it deviated significantly from the correlation trend. However, even when including M3, the computed R2 value of 0.807 remains acceptable. This finding underscores the importance of the inherent balance between electrophilicity and nucleophilicity in the stability of these complexes, suggesting that pronounced back-bonding and/or amphiphilicity effects may be occurring within the binding pocket. This is consistent with the diverse array of weak interactions identified in our docking and molecular dynamics studies and bond critical point (BCP) analyses for these systems. The most active derivative, M5, exhibited the highest ω+/ω− ratio, while the least active compound, M2 (excluding M3), showed the lowest ratio. This indicates that the electron-donating interactions from the protein to the inhibitor likely dominate over electron-accepting interactions. This interpretation is further supported by the higher correlation coefficient observed when using electron affinity (A) as a descriptor (R2 = 0.805) compared to ionization potential (I) (R2 = 0.675), both excluding M3. Consequently, the atypical behavior of M3 may be attributed to mechanisms other than the typical donor–acceptor process that could be hindering its activity against the protein.
Additionally, our analysis using temperature-dependent local descriptors revealed that the activity of these compounds is also influenced by their local hardness properties (Fig. 6b). Notably, the interacting moieties in cinnamyls (e.g., the α-dicarbonyl oxygen atom) are harder than those in quinoxalines, which may partially explain why cinnamyls are generally less reactive than quinoxalines. M5, the most reactive compound, possesses the second least hard atom, surpassed only by M6 by a negligible difference of 0.03 eV. This classifies the amide oxygen in M5 as a strong, soft nucleophile, emphasizing the critical role of the amide moiety in its activity. Interestingly, among the cinnamyls, the least reactive derivative, M3, contains the softest atom, while the oxygen in M1, the most active cinnamyl, is the hardest. This contrasting trend may reflect fundamental differences in the reactivity profiles of cinnamyls and quinoxalines. Specifically, the protein–ligand interactions in cinnamyls may be influenced by the HSAB principle at the local level, where hard ligand fragments preferentially interact with hard enzyme moieties. This statement must be corroborated in further studies by analyzing the influence of hard protein fragments on the formation of protein–ligand complexes.
In contrast to the results observed with the Bcl-2 protein, the ω+/ω− ratio did not exhibit a strong correlation with the affinity data obtained for the Bcl-xl complexes, yielding an R2 value of 0.62. Notably, both M3 and M6 showed the largest deviations from the correlation trend. When these two compounds were excluded, the correlation improved significantly, with an R2 value of 0.94 (Fig. 7a). Interestingly, M6 also deviated from the correlation trend in the Bcl-2 analysis (Fig. 6a), but this deviation was more pronounced for the Bcl-xl complex. Upon closer examination of Fig. 1, it becomes evident that both M3 and M6 contain furan rings, suggesting that this functional group may confer a distinct binding pattern to these proteins compared to other derivatives. Similar to the findings with Bcl-2, good correlations were obtained for Bcl-xl using electron affinity (A) and ionization potential (I) as descriptors, but only when M3 and M6 were excluded. The correlation was stronger for A (R2 = 0.930) than for I (R2 = 0.845), reinforcing the idea that electron donation from the protein to the inhibitor plays a significant role in stabilizing these complexes, as observed with Bcl-2.
The local hardness versus binding energy (BE) profile for Bcl-xl (Fig. S3) closely resembled that of Bcl-2. Specifically, the most active derivative, M5, possessed the second least hard atom, while the most active cinnamyl, M1, displayed the hardest oxygen atom. However, as illustrated in Fig. 5b, the interaction between cinnamyls and Bcl-xl appears to be strongly influenced by the HSAB principle at the local level; when only cinnamyls were considered, the correlation between local hardness and BE was remarkably high, with an R2 value of 0.964. This suggests that the reactivity and binding affinity of cinnamyls to Bcl-xl are governed by local electronic properties, where hard ligand fragments preferentially interact with hard protein moieties.
As a next step, we investigated potential correlations between our reactivity descriptors and the experimentally measured IC50 values reported in a previous study for the PANC-1 cell line.24 It is pertinent to recall that both the Bcl-2 and Bcl-xl proteins are present in this cell line and thus both can interact with inhibitors. Analysis using local descriptors revealed that the local chemical potential is exceptionally linked to the IC50 values when cinnamyls and quinoxalines are analyzed separately. As discussed, their reactive nature is distinct between these families due to several factors. The observed trend provides the following insightful result, the basicity of the α-dicarbonyl oxygen is a key determinant of cinnamyl activity: the more basic the oxygen, the more potent the cinnamyl; the acidity of terminal functional groups in the side chains of quinoxalines determines the activity of this family: the more acidic the substituent, the more potent the quinoxaline. This behavior resembles that observed for local hardness and may reflect the difference and diversity of weak interactions observed in each family of derivatives with the Bcl-2 protein.
It is important to note that IC50 values are not expected to align closely with the BEs calculated in this work, as external factors such as solubility, permeability, and availability—governed partially by electrostatics—can significantly influence a ligand's ability to inhibit its pharmacological target in a biological or in vitro setting. While the IC50 values generally did not correlate with the BEs computed in this study, an intriguing inverse trend was observed among the cinnamyls. Specifically, M3 exhibited the lowest IC50 value, indicating the highest potency, while M1 and M2 showed the highest IC50 values, corresponding to lower activity. This discrepancy with our molecular docking and molecular dynamics results can be partially explained by examining the dipole moments of these compounds. M3 and M4, the most polar cinnamyls, likely benefit from enhanced solubility and relative abundance in aqueous-based environments (including blood), which may contribute to their improved inhibitory performance. In contrast, M1 and M2, with lower dipole moments, are less polar and may suffer from reduced availability, potentially related to their higher IC50 values (Fig. 8a). Interestingly, M5, the most active derivative according to our docking results, displayed a high dipole moment, which can be related to its favorable spatial distribution of its electrophilic/nucleophilic balance (Fig. 8b). However, in terms of IC50 values, it ranked as the third most active compound. This discrepancy indicates that while its pronounced polarity likely enhances its reactivity and binding affinity to the target protein, the substantial dipole moment may hinder its membrane permeability, potentially compromising cellular uptake and overall efficacy. This observation suggests that the binding pockets of these proteins possess a higher polarity profile compared to biological membranes and cell walls. For instance, the Bcl-2 protein binding pocket is considerably composed of hydrophilic residues, including Arg66, Arg105, and Tyr67, which are strategically positioned at the binding interface. As previously reported39,70–72 and confirmed in this study (see Fig. 2), these residues play a crucial role in stabilizing complexes with the Bcl-2 protein. Moreover, our findings suggest that these key residues impose specific polarity requirements on potential inhibitors, highlighting their importance in ligand recognition and binding affinity.
 | ||
| Fig. 8 μ (r) dependence on the experimental IC50 values of Bcl-2 using (a) cinnamyls and (b) quinoxalines as inhibitors. | ||
In a simplified interpretation, ligands bound to these proteins can thus be conceptualized as molecules confined within a medium of relatively high polarity, a scenario that aligns with the foundational principles of continuum solvation models. Consequently, one might hypothesize that molecular descriptors calculated within a polar solvent continuum framework could partially reflect the electrostatic environment experienced by ligands within these protein binding sites. Interestingly, we observed good to notable correlations between several computed descriptors and the binding energies (BEs) in this study, without the need to exclude any derivatives—a limitation encountered with reactivity descriptors calculated in the gas phase. Specifically, the binding energies for Bcl-2 proteins showed significant correlations with the electrophilicity index (Fig. 9a, R2 = 0.716) and electron affinity (R2 = 0.713), while the binding energies for Bcl-xl correlated well with the electrophilicity index (Fig. 9b, R2 = 0.847), electro-donating power (R2 = 0.815), and electron affinity (R2 = 0.768). These findings highlight the critical role of the electron-accepting capacity of ligands in their binding interactions, as well as the importance of electrostatic interactions within the binding pocket, in the inhibition of these proteins.
 | ||
| Fig. 9 ω vs. BE profiles for inhibitors binding to the (a) Bcl-2 and (b) Bcl-xl proteins. Electrophilicities were calculated in the aqueous phase, according to our theoretical protocol. | ||
At the local level, our chemical reactivity analysis, combined with the results from our BCPs study, underscores the critical role of the α-dicarbonyl oxygen in cinnamyls at the quantum mechanical level, indicating that new cinnamyls with enhanced inhibitory properties can be systematically designed following the overall regional properties found for this moiety. While definitive relationships between local descriptors and inhibitory efficacy indices (BEs or IC50) for the quinoxalines cannot be established based on the data gathered in this study, it is evident that the two functional groups (branches) attached to the quinoxaline framework—particularly the electronic properties of their terminal moieties—play a critical role in determining their inhibitory properties. The amide group present in M5 suggests that a strong electron-donating moiety is essential for effective inhibition. However, the small furan-containing chains in M6, along with the unexpected trends observed for this compound, indicate that the length, size, and structural features of these terminal groups also significantly influence their efficacy as inhibitors of the anti-apoptotic proteins under investigation. As previously noted, the binding pockets of these proteins are highly flexible, accommodating ligands of varying sizes. Unlike M5, the M6 and M7 compounds lack a benzene ring in their side chains. This structural difference may contribute to the superior efficacy of M5, as the benzene moiety not only provides an additional site for weak π-bonding interactions but also enhances the electrophilicity of the adjacent terminal functional group.
The key molecular moieties responsible for the inhibitory properties of these candidates—such as the α-dicarbonyl group in cinnamyls and the terminal-branch moieties in quinoxalines—can be effectively identified using the Fukui function, together with the dual descriptor (DD) plots. While the condensed-to-atom representation of neither the Fukui function nor the DD exhibited a direct correlation with the inhibitory efficacy indices of the derivatives studied, their visual representation provides valuable insights into the molecular regions governing inhibitory activity. The donation and acceptance, or back-bonding processes, are critical to the formation of protein–inhibitor complexes, making the left (f−) and right (f+) Fukui functions particularly useful for analysis. In Fig. 10, we present these profiles for the M3 and M5 derivatives. For M3, the f+ function indicates that the α-dicarbonyl C–C bond is the primary site for charge acceptance, followed by the carbon atoms linked to the furan rings. Conversely, the f− function reveals that the main donation sites are located at the oxygen atoms of the α-dicarbonyl group. This suggests that the most reactive site for both acceptance/donation of charge is concentrated in the core chain of M3, which may be hindering the optimal formation of weak interactions with the protein. This information is clearly captured by the DD, which highlights the central chain as the molecular moiety responsible for amphiphilic reactivity. This localization of reactivity may explain the lower inhibitory efficacy of M3, as the central chain's dominance in both donation and acceptance processes could limit its ability to form diverse and stable interactions with the enzyme. In contrast, M5, the most reactive compound, exhibits well-separated and distinct sites for charge acceptance and donation. The quinoxaline moiety, particularly the pyrazine fragment, is identified as the primary site for charge acceptance, while the amide oxygens act as the main sites for charge donation. This spatial separation of reactive sites, captured clearly by the DD, likely contributes to M5's high dipole moment and its superior inhibitory performance. The DD plot of this derivative effectively highlights the molecular regions prone to interact with the proteins, emphasizing the importance of the quinoxaline core for charge acceptance and the amide group for charge donation.
 | ||
| Fig. 10 Electrophilic (left) and nucleophilic (middle) Fukui functions, and the DD (right) for M3 and M5, with an isovalue of 0.05. | ||
3.8 In silico prediction of potential ADME
The computed ADME properties are summarized in Table 5. Overall, all compounds satisfy Lipinski's rule-of-five criteria,65 with the exception of M6, which exhibits a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value slightly above 5, potentially indicating limitations related to aqueous solubility or an increased tendency for accumulation in adipose tissue. Analysis of hydrogen-bond donor and acceptor counts reveals that the compounds possess few proton-donating groups, a feature that is generally favorable for passive membrane permeability. In this context, M1, M3, and M4 exhibit solubility profiles consistent with rapid gastrointestinal absorption.
P value slightly above 5, potentially indicating limitations related to aqueous solubility or an increased tendency for accumulation in adipose tissue. Analysis of hydrogen-bond donor and acceptor counts reveals that the compounds possess few proton-donating groups, a feature that is generally favorable for passive membrane permeability. In this context, M1, M3, and M4 exhibit solubility profiles consistent with rapid gastrointestinal absorption.
| ADME propertiesa | Compounds | ||||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | M7 | |
MW: molecular weight, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P: lipophilicity, log P: lipophilicity, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S: solubility, HD: number of hydrogen donors, HA: number of hydrogen acceptors, TPSA: topological polar surface area, BBB permeant: permeability of the blood–brain barrier.a Parameter calculated using SwissADME65 (https://www.swissadme.ch/). S: solubility, HD: number of hydrogen donors, HA: number of hydrogen acceptors, TPSA: topological polar surface area, BBB permeant: permeability of the blood–brain barrier.a Parameter calculated using SwissADME65 (https://www.swissadme.ch/). |
|||||||
| MW≤500 | 262.3 | 298.28 | 242.23 | 274.36 | 448.52 | 346.47 | 314.34 |
| #HA≤10 | 2 | 4 | 4 | 2 | 4 | 2 | 4 |
| #HD≤5 | 0 | 0 | 0 | 0 | 2 | 0 | 0 |
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
3.5 | 4.13 | 2.04 | 3.36 | 4.18 | 5.12 | 3.8 |
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S S |
−3.95 | −4.26 | −2.66 | −3.63 | −5.2 | −5.65 | −4.67 |
| ESOL Class | Soluble | Moderately soluble | Soluble | Soluble | Moderately soluble | Moderately soluble | Moderately soluble |
| TPSA | 34.14 | 34.14 | 60.42 | 90.62 | 83.98 | 82.26 | 52.06 |
| BBB permeant | Yes | Yes | Yes | No | No | No | Yes |
| CYP1A2 inhibitor | Yes | Yes | Yes | Yes | No | Yes | Yes |
| CYP2C19 inhibitor | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| CYP2C9 inhibitor | No | No | Yes | Yes | Yes | Yes | Yes |
| CYP2D6 inhibitor | No | No | No | No | No | No | No |
| CYP3A4 inhibitor | No | Yes | No | No | Yes | Yes | Yes |
From a safety perspective, central nervous system (CNS) exposure is undesirable in the context of Bcl-xl inhibition, as neuronal apoptosis may lead to neurotoxicity. Notably, M4 and M5 emerge as particularly promising candidates, as their high topological polar surface area (TPSA) values (90.62 and 83.98 Å2, respectively) are associated with negligible blood–brain barrier permeability.
Regarding metabolic liability, most derivatives are predicted to inhibit the CYP2C19 and CYP2C9 isoforms, whereas none show inhibitory activity toward CYP2D6. Importantly, M3 and M4 do not inhibit CYP3A4, the principal cytochrome P450 enzyme involved in the metabolism of many chemotherapeutic agents, suggesting a reduced risk of clinically relevant drug–drug interactions. Although M5 displays a more complex metabolic profile, including predicted CYP3A4 inhibition, its distinctive structural features—particularly the presence of two hydrogen-bond donor sites associated with amide N–H groups—may contribute to its enhanced binding affinity toward the therapeutic target relative to the other derivatives in the series.
4. Conclusions
Our molecular docking and molecular dynamics analyses confirm that both families of compounds can inhibit the anti-apoptotic proteins Bcl-2 and Bcl-xl; however, quinoxaline derivatives exhibit superior activity compared to their cinnamyl counterparts. This difference arises from distinct structural, electronic, and reactivity properties.Structurally, cinnamyls require a folded conformation to maximize intramolecular interactions, whereas quinoxalines are inherently positioned to directly engage key residues, enhancing their binding affinity. Notably, M3 demonstrated poor stability in MD simulations, likely due to insufficient intermolecular interactions with Bcl-xl.
From a reactivity perspective, two primary factors govern complex stability in the binding pocket: electrostatic interactions—given the binding site's polarity—and a donation/acceptance mechanism, where electron-accepting ligands are preferred. It must be highlighted that a solvation continuum model incorporating a polar medium, mimicking the polar environment of the binding pocket, improved the description of these interactions through our reactivity descriptors.
However, IC50 values suggest that excessive polarity may hinder cell membrane permeability, limiting in vitro potency. Strikingly, the local chemical potential at the α-dicarbonyl oxygens of cinnamyls accurately reproduced their in vitro potency trend, highlighting the crucial role of this moiety. This relationship positions local chemical potential as a promising predictive tool for designing more potent cinnamyl derivatives.
Overall, our study offers a comprehensive framework for optimizing protein–ligand stability. While quinoxalines exhibited superior activity in silico, cinnamyls may outperform in vitro if their polarity and electrophilic/nucleophilic balance are fine-tuned. Additionally, designing quinoxaline derivatives with soft electron-rich functional groups on the side-alkyl chains could lead to even more effective inhibitors.
Contributions
Conceptualization, methodology, and formal analysis: I. L. L. C.; investigation: R. L. C. M.; software and figure preparation: L. Z. H.; manuscript revision: S. G. M. and C. Z. G. C.; resources, writing, review, and editing: M. F. P. and J. C. B. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare that they have no competing financial interests.Ethics approval
This study did not involve human or animal subjects; therefore, ethical approval, consent to participate, and consent to publish are not applicable.Data availability
All the data supporting this article are part of the main body of the manuscript (Tables 1–3). This study was carried out using IC50 values from ref. 24 of the manuscript.Supplementary information (SI) is available. Working formulas for the chemical reactivity descriptors used in this work, energetic results from our molecular docking procedures and predicitive performance of the finite temperature chemical reactivity descriptors used in this work, can be found in the Supplementary Information file. See DOI: https://doi.org/10.1039/d5ob02005k.
Acknowledgements
J. C. B. gratefully acknowledges CONAHCYT for grant 1561802.The authors thank the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT or National Humanities, Sciences, and Technologies Council) (SNII distinction as research membership and scholarship) for their financial support.
I. L. L. C. thanks CONAHCYT for the assistant scholarship, whereas J. C. B. acknowledges the support received via the CONAHCYT project 1561802. M. F.-P. thanks CONAHCYT for the support provided through a sabbatical fellowship.
References
- E. Barone, A. Corrado, F. Gemignani and S. Landi, Environmental risk factors for pancreatic cancer: an update, Arch. Toxicol., 2016, 90, 2617–2642 CrossRef CAS.
- A. McGuigan, P. Kelly, R. C. Turkington, C. Jones, H. G. Coleman and R. S. McCain, Pancreatic cancer: A review of clinical diagnosis, epidemiology, treatment and outcomes, World J. Gastroenterol., 2018, 24, 4846–4861 CrossRef PubMed.
- M. Khan, J. I. Qazi, A. Rasul, Y. Zheng and T. Ma, Evodiamine induces apoptosis in pancreatic carcinoma PANC-1 cells via NF κB inhibition, Bangladesh J. Pharmacol., 2013, 8, 8–14 Search PubMed.
- S. Qian, Z. Wei, W. Yang, J. Huang, Y. Yang and J. Wang, The role of BCL-2 family proteins in regulating apoptosis and cancer therapy, Front. Oncol., 2022, 12, 985363 CrossRef CAS PubMed.
- A. N. Hata, J. A. Engelman and A. C. Faber, The BCL2 Family: Key Mediators of the Apoptotic Response to Targeted Anticancer Therapeutics, Cancer Discovery, 2015, 5, 475–487 CrossRef CAS PubMed.
- P. N. Kelly and A. Strasser, The role of Bcl-2 and its pro-survival relatives in tumourigenesis and cancer therapy, Cell Death Differ., 2011, 18, 1414–1424 CrossRef CAS PubMed.
- Z. Zhang, L. Bai, L. Hou, H. Deng, S. Luan and D. Liu, et al., Trends in targeting Bcl-2 anti-apoptotic proteins for cancer treatment, Eur. J. Med. Chem., 2022, 232, 114184 CrossRef CAS PubMed.
- P. E. Czabotar and A. J. Garcia-Saez, Mechanisms of BCL-2 family proteins in mitochondrial apoptosis, Nat. Rev. Mol. Cell Biol., 2023, 24, 732–748 CrossRef CAS PubMed.
- J. M. Galante, M. M. Mortenson, T. L. Bowles, S. Virudachalam and R. J. Bold, ERK/BCL-2 Pathway in the Resistance of Pancreatic Cancer to Anoikis, J. Surg. Res., 2009, 152, 18–25 CrossRef CAS PubMed.
- A. J. García-Sáez, The secrets of the Bcl-2 family, Cell Death Differ., 2012, 19, 1733–1740 CrossRef.
- J. D. Leverson, D. C. Phillips, M. J. Mitten, E. R. Boghaert, D. Diaz and S. K. Tahir, et al., Exploiting selective BCL-2 family inhibitors to dissect cell survival dependencies and define improved strategies for cancer therapy, Sci. Transl. Med., 2015, 7, 279ra40 Search PubMed.
- T. Masuda, T. Maekawa, K. Hidaka, H. Bando, Y. Takeda and H. Yamaguchi, Chemical Studies on Antioxidant Mechanism of Curcumin: Analysis of Oxidative Coupling Products from Curcumin and Linoleate, J. Agric. Food Chem., 2001, 49, 2539–2547 Search PubMed.
- V. P. Menon and A. R. Sudheer, Antioxidant and anti-inflammatory properties of curcumin, in The Molecular Targets and Therapeutic Uses of Curcumin in Health and Disease, Springer US, Boston, MA, 2007, vol. 595, pp. 105–125 Search PubMed.
- P. Anand, C. Sundaram, S. Jhurani, A. B. Kunnumakkara and B. B. Aggarwal, Curcumin and cancer: An “old-age” disease with an “age-old” solution, Cancer Lett., 2008, 267, 133–164 Search PubMed.
- D. Zhou, N. Ding, S. Zhao, D. Li, J. Van Doren and Y. Qian, et al., Synthesis and Evaluation of Curcumin-Related Compounds Containing Inden-2-one for Their Effects on Human Cancer Cells, Biol. Pharm. Bull., 2014, 37, 1977–1981 Search PubMed.
- E. C. Constable, M. J. Hannon and D. R. Smith, Cinnamyl - an oligopyridine precursor, Tetrahedron Lett., 1994, 35, 6657–6660 CrossRef CAS.
- H. A. Ahmad, S. S. Gillani, R. Babar, M. A. Munawar and S. Gulb, A Rapid and Efficient Protocol for the Synthesis of Cinnamyls, INEOS OPEN, 2020, 3, 20–24 CrossRef CAS.
- X. Luo and L. T. Lim, Cinnamyl- and Quinoxaline-Derivative Indicator Dyes for Detecting Volatile Amines in Fish Spoilage, Molecules, 2019, 24, 3673 CrossRef CAS PubMed.
- J. A. Pereira, A. M. Pessoa, M. N. D. S. Cordeiro, R. Fernandes, C. Prudêncio and J. P. Noronha, et al. Quinoxaline, its derivatives and applications: A State of the Art review, Eur. J. Med. Chem., 2015, 97, 664–672 CrossRef CAS PubMed.
- S. Tariq, K. Somakala and A. Mohd, Quinoxaline: An insight into the recent pharmacological advances, Eur. J. Med. Chem., 2018, 143, 542–557 Search PubMed.
- P. Corona, A. Carta, M. Loriga, G. Vitale and G. Paglietti, Synthesis and in vitro antitumor activity of new quinoxaline derivatives, Eur. J. Med. Chem., 2009, 44, 1579–1591 CrossRef CAS PubMed.
- M. Montana, F. Mathias, T. Terme and P. Vanelle, Antitumoral activity of quinoxaline derivatives: A systematic review, Eur. J. Med. Chem., 2019, 163, 136–147 CrossRef CAS.
- H. A. S. Abbas, A. R. M. Al-Marhabi and Y. A. Ammar, Design, synthesis and biological evaluation of 2,3-disubstituted and fused quinoxalines as potential anticancer and antimicrobial agents, Acta Pol. Pharm., 2017, 74, 445–458 CAS.
- R. Wang, C. Li, S. Cho, C. Chang, J. Chen and T. Shih, Synthesis of cinnamyls and quinoxalines and their biological evaluation as anticancer agents, Arch. Pharm., 2022, 355, 2100448 CrossRef CAS PubMed.
- F. Bader Richard, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1990, p. I Search PubMed.
- M. Franco-Pérez, F. Heidar-Zadeh, P. W. Ayers, F. De Proft, A. Vela and J. L. Gázquez, et al., Temperature and external fields in conceptual density functional theory, Chem. Sci., 2024, 15, 20090–20121 Search PubMed.
- J. L. Gázquez and M. Franco-Pérez, Finite Temperature Conceptual Density Functional Theory, in Conceptual Density Functional Theory, Wiley, 2022, pp. 137–160 Search PubMed.
- J. L. Gázquez, M. Franco-Pérez, P. W. Ayers and A. Vela, Conceptual Density Functional Theory in the Grand Canonical Ensemble, in Chemical Reactivity in Confined Systems, Wiley, 2021, pp. 191–211 Search PubMed.
- J. L. Gázquez, M. Franco-Pérez, P. W. Ayers and A. Vela, Temperature–dependent approach to chemical reactivity concepts in density functional theory, Int. J. Quantum Chem., 2019, 119, e25797 CrossRef.
- M. Franco-Pérez and J. L. Gázquez, Charge Transfer Is Promoted by Electronic Heat Exchange in Atoms and Molecules, J. Phys. Chem. Lett., 2025, 2283–2294 CrossRef PubMed.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- S. Chiodo, N. Russo and E. Sicilia, Newly developed basis sets for density functional calculations, J. Comput. Chem., 2005, 26, 175–184 Search PubMed.
- J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valences, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- P. Sarmah and R. C. Deka, Solvent effect on the reactivity of CIS –platinum(II) complexes: A density functional approach, Int. J. Quantum Chem., 2008, 108, 1400–1409 Search PubMed.
- A. Koster, G. Geudtner, A. Álvarez, P. Calaminici, M. E. Casida and J. Carmona-Espindola, et al. deMon2k, The deMon Developers, Cinvestav, Mexico City, 2018 Search PubMed.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb and J. Cheeseman, et al. Gaussian 16, Gaussian, Inc., Wallingford, CT, 2019 Search PubMed.
- S. Forli, R. Huey, M. E. Pique, M. F. Sanner, D. S. Goodsell and A. J. Olson, Computational protein–ligand docking and virtual drug screening with the AutoDock suite, Nat. Protoc., 2016, 11, 905–919 CrossRef CAS PubMed.
- M. Faiz Abd Ghani, R. Othman and N. Nordin, Molecular docking study of naturally derived flavonoids with antiapoptotic BCL-2 and BCL-XL proteins toward ovarian cancer treatment, J. Pharm. Bioallied Sci., 2020, 12, 676–680 CrossRef PubMed.
- G. Lessene, P. E. Czabotar, B. E. Sleebs, K. Zobel, K. N. Lowes and J. M. Adams, et al., Structure-guided design of a selective BCL-XL inhibitor, Nat. Chem. Biol., 2013, 9, 390–397 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graph., 1996, 14, 33–38 Search PubMed.
- S. Muchmore, M. Sattler and H. Liang, et al., X-ray and NMR structure of human Bcl-xl, an inhibitor of programmed cell death, Nat. Lett., 1996, 381, 335–341 Search PubMed.
- B. Ssi, U. Mbiotek, Z. S. Muscifa, W. Destiarani, F. G. Rohmatullah and M. Yusuf, Molecular interaction analysis and visualization of protein-ligand docking using Biovia Discovery Studio Visualizer, IJCB, 2023, 2, 22–30 Search PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt and E. C. Meng, et al., UCSF Chimera—A visualization system for exploratory research and analysis, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid and E. Villa, et al., Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS.
- J. Huang and A. D. MacKerell, CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data, J. Comput. Chem., 2013, 34, 2135–2145 Search PubMed.
- J. J. P. Stewart, Optimization of Parameters for Semiempirical Methods. III Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, T1, Pb, and Bi, J. Comput. Chem., 1991, 12, 320–341 Search PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- J. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, B97–3c: A revised low-cost variant of the B97-D density functional method, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- C. Y. Qiang, S. Y. Jing, M. Y. Qiang and D. H. Ming, Efficient calculation of protein–ligand binding free energy using GFN methods: the power of the cluster model, Phys. Chem. Chem. Phys., 2022, 24, 14339–14347 RSC.
- C. Isert, K. Atz, S. Riniker and G. Schneider, Exploring protein–ligand binding affinity prediction with electron density-based geometric deep learning, RSC Adv., 2024, 14, 4492–4502 RSC.
- J. Gorges, B. Bädorf, A. Hansen and S. Grimme, Efficient Computation of the Interaction Energies of Very Large Non-covalently Bound Complexes, Synlett, 2023, 34, 1135–1146 Search PubMed.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 Search PubMed.
- J. M. López, A. E. Ensuncho and J. R. Robles, Descriptores globales y locales de la reactividad para el diseño de nuevos fármacos anticancerosos basados en cis-platino(II), Quim. Nova, 2013, 36, 1308–1317 Search PubMed.
- M. Franco-Pérez and J. L. Gázquez, Electronegativities of Pauling and Mulliken in Density Functional Theory, J. Phys. Chem. A, 2019, 123, 10065–10071 CrossRef PubMed.
- J. L. Gázquez, A. Cedillo and A. Vela, Electrodonating and Electroaccepting Powers, J. Phys. Chem. A, 2007, 111, 1966–1970 CrossRef.
- J. I. Martínez-Araya, Why is the dual descriptor a more accurate local reactivity descriptor than Fukui functions?, J. Math. Chem., 2015, 53, 451–465 CrossRef.
- C. Morell, A. Grand and A. Toro-Labbé, New Dual Descriptor for Chemical Reactivity, J. Phys. Chem. A, 2005, 109, 205–212 CrossRef CAS PubMed.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- R. F. Nalewajski and R. G. Parr, Information theory, atoms in molecules, and molecular similarity, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8879–8882 Search PubMed.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, Local chemical potential, local hardness, and dual descriptors in temperature dependent chemical reactivity theory, Phys. Chem. Chem. Phys., 2017, 19, 13687–13695 RSC.
- C. A. Polanco-Ramírez, M. Franco-Pérez, J. Carmona-Espíndola, J. L. Gázquez and P. W. Ayers, Revisiting the definition of local hardness and hardness kernel, Phys. Chem. Chem. Phys., 2017, 19, 12355–12364 Search PubMed.
- M. Franco-Pérez, C. A. Polanco-Ramírez, J. L. Gázquez and P. W. Ayers, Local and nonlocal counterparts of global descriptors: the cases of chemical softness and hardness, J. Mol. Model, 2018, 24, 285 Search PubMed.
- M. Franco-Pérez, C. A. Polanco-Ramírez, J. L. Gázquez, P. W. Ayers and A. Vela, Study of organic reactions using chemical reactivity descriptors derived through a temperature-dependent approach, Theor. Chem. Acc., 2020, 139, 44 Search PubMed.
- A. Daina, O. Michielin and V. Zoete, SwissADME: a free web tool to evaluate pharmacokinetics, drug-likeness and medicinal chemistry friendliness of small molecules, Nat. Sci. Rep., 2017, 7, 42717 Search PubMed.
- E. C. Constable, A. H. Redondo, C. E. Housecroft, M. Neuburger and S. Schaffner, Copper(I) complexes of 6,6′-disubstituted 2,2′-bipyridine dicarboxylic acids: new complexes for incorporation into copper-based dye sensitized solar cells (DSCs), Dalton Trans., 2009, 6634–6644 Search PubMed.
- C. Yu, E. Hao, T. Li, J. Wang, W. Sheng and Y. Wei, et al., Dipyrrolylquinoxaline difluoroborates with intense red solid-state fluorescence, Dalton Trans., 2015, 44, 13897–13905 Search PubMed.
- Y. Ono, M. Ninomiya, D. Kaneko, A. D. Sonawane, T. Udagawa and K. Tanaka, et al., Design and synthesis of quinoxaline-1,3,4-oxadiazole hybrid derivatives as potent inhibitors of the anti-apoptotic Bcl-2 protein, Bioorg. Chem., 2020, 104, 104245 CrossRef CAS PubMed.
- A. M. Petros, E. T. Olejniczak and S. W. Fesik, Structural biology of the Bcl-2 family of proteins, Biochim. Biophys. Acta, Mol. Cell Res., 2004, 83–94 CrossRef CAS PubMed.
- N. Saxena, S. P. Katiyar, Y. Liu, A. Grover, R. Gao and D. Sundar, et al., Molecular interactions of Bcl-2 and Bcl-xl with mortalin: identification and functional characterization, Biosci. Rep., 2013, 33, e000073 CrossRef.
- I. Bertini, S. Chevance, R. Del Conte, D. Lalli and P. Turano, The Anti-Apoptotic Bcl-xl Protein, a New Piece in the Puzzle of Cytochrome C Interactome, PLoS One, 2011, 6, e18329 CrossRef CAS PubMed.
- N. Wakui, R. Yoshino, N. Yasuo, M. Ohue and M. Sekijima, Exploring the selectivity of inhibitor complexes with Bcl-2 and Bcl-XL: A molecular dynamics simulation approach, J. Mol. Graph Model., 2018, 79, 166–174 Search PubMed.
- J. Luan, B. Hu, S. Wang, H. Liu, S. Lu and W. Li, et al., Selectivity mechanism of BCL-XL/2 inhibition through in silico investigation, Phys. Chem. Chem. Phys., 2022, 24, 17105–17115 RSC.
- S. J. Grabowski, Ab Initio Calculations on Conventional and Unconventional Hydrogen BondsStudy of the Hydrogen Bond Strength, J. Phys. Chem. A, 2001, 105, 10739–10746 Search PubMed.
- A. Mohajeri, M. Alipour and M. Mousaee, Halogen–Hydride Interaction between Z–X (Z = CN, NC; X = F, Cl, Br) and H–Mg–Y (Y = H, F, Cl, Br, CH3), J. Phys. Chem. A, 2011, 115, 4457–4466 CrossRef CAS PubMed.
- A. Shahi and E. Arunan, Hydrogen bonding, halogen bonding and lithium bonding: an atom in molecules and natural bond orbital perspective towards conservation of total bond order, inter- and intra-molecular bonding, Phys. Chem. Chem. Phys., 2014, 16, 22935–22952 Search PubMed.
- A. Martínez, Toxicity of persistent organic pollutants: a theoretical study, J. Mol. Model, 2024, 30, 97, DOI:10.1007/s00894-024-05890-8.
| This journal is © The Royal Society of Chemistry 2026 |





