Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intrinsic Ohmic contact and electric-field tunable interface in a 2D NbS2/As2C3 metal–semiconductor heterostructure
Nguyen Xuan
Sang
ab,
Nguyen Q.
Cuong†
 *cd and
Le Phuong
Long
*cd and
Le Phuong
Long
 e
e
aAtomic Molecular and Optical Physics Research Group, Institute for Advanced Study in Technology, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: nguyenxuansang@tdtu.edu.vn
bFaculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam. E-mail: nguyenquangcuong3@duytan.edu.vn
dSchool of Engineering & Technology, Duy Tan University, Da Nang 550000, Vietnam
eCenter of Scientific Research and Application, Lac Hong University, No. 10 Huynh Van Nghe Str, Tran Bien Ward, Dong Nai Province, Vietnam. E-mail: phuonglong@lhu.edu.vn
First published on 3rd December 2025
Abstract
Metal–semiconductor heterostructures play a crucial role in determining the performance of nanoelectronic and optoelectronic devices, as they govern charge injection efficiency and contact resistance at the interface. In this work, we design and explore a 2D NbS2/As2C3 metal–semiconductor heterostructure using first-principles calculations. The heterostructure is confirmed to be energetically stable, with weak van der Waals interactions that preserve the intrinsic characteristics of the constituent monolayers. All stacking configurations exhibit metallic behavior and form intrinsic p-type Ohmic contacts, accompanied by the absence of metal-induced gap states and only weak Fermi level pinning at the interface. The tunneling probability and contact resistivity indicate that the heterostructure exhibits low contact resistance. Furthermore, the interfacial contact behavior can be effectively tuned using an external perpendicular electric field. A positive field reduces the hole barrier while maintaining the Ohmic character, whereas a negative field enhances the barrier and induces a transition to a p-type Schottky contact. These results highlight NbS2/As2C3 as a promising 2D heterostructure with efficient charge injection, weak Fermi level pinning, and electric-field–tunable interfacial properties for future nanoelectronic and optoelectronic applications.
1 Introduction
Since the groundbreaking isolation of graphene by Novoselov and Geim in 2004,1 two-dimensional (2D) materials have become a rapidly expanding frontier in condensed matter physics and materials science. Graphene, a monolayer of carbon atoms arranged in a honeycomb lattice, exhibits remarkable properties such as high carrier mobility, mechanical strength, and thermal conductivity.2,3 However, its zero bandgap poses limitations for applications in logic devices and optoelectronics.4 This shortcoming has led to extensive efforts to explore alternative 2D materials with intrinsic semiconducting or magnetic properties. Among them, transition metal dichalcogenides (TMDs),5 hexagonal boron nitride (h-BN),6 black phosphorus (BP),7 and MXenes8 have emerged as promising candidates with a wide range of physical characteristics. These materials often possess tunable bandgaps, high carrier mobility, and layer-dependent phenomena, making them ideal platforms for next-generation nanoelectronics, valleytronics, and energy-related applications.9,10 Despite their promising properties, 2D materials face critical limitations that hinder their practical applications. For instance, although monolayer MoS2 has emerged as a prototypical semiconducting TMD with a direct bandgap and strong spin–orbit coupling, its carrier mobility at room temperature remains relatively low due to strong electron–phonon scattering and defects introduced during synthesis.11,12 In contrast, black phosphorus (BP), also known as phosphorene in its monolayer form, offers high carrier mobility and a tunable direct bandgap, making it attractive for field-effect transistors (FETs). However, BP suffers from severe ambient instability; it readily degrades upon exposure to oxygen and moisture under room temperature conditions.13,14 These intrinsic and extrinsic challenges necessitate strategies to stabilize or enhance the performance of 2D materials in real-world devices.To overcome the intrinsic limitations of individual two-dimensional (2D) materials, constructing van der Waals (vdW) heterostructures has emerged as a powerful and versatile design strategy. By vertically stacking different 2D layers without the constraint of lattice matching, it becomes possible to engineer novel interfacial properties that are absent in the individual 2D materials.15,16 Among various configurations, metal–semiconductor heterostructures are of particular interest due to their critical roles in nanoelectronic and optoelectronic devices, including Schottky diodes, photodetectors, and field-effect transistors.17–19 In these systems, the interfacial band alignment and Schottky barrier height (SBH) are key factors governing charge carrier injection and overall device performance. However, in conventional metal–semiconductor contacts, large SBHs often form, limiting carrier transport. Furthermore, the Fermi level pinning (FLP) effect caused by interfacial states such as defects, metal-induced gap states (MIGSs), or strong chemical bonding can trap charges and effectively fix the Fermi level, rendering the SBH nearly insensitive to the choice of contact metal.17 This fundamentally restricts the tunability of the contact characteristics and often leads to high contact resistance. To address these issues, designing vdW metal–semiconductor heterostructures with weakly bonded interfaces has become an emerging direction.
Recent efforts have focused on designing vdW MSHs with weakly bonded interfaces to mitigate FLP and enhance charge transport. A wide range of such heterostructures have been successfully synthesized20,21 and investigated through first-principles calculations,22–24 encompassing integration of TMDs, graphene, MXenes, and other emerging 2D materials. These studies provide valuable insights into interfacial engineering strategies. Recently, NbS2, a group-V TMD, exhibits metallic conductivity even in its monolayer form, along with excellent chemical stability and strong in-plane bonding. Its high density of states near the Fermi level and good work function alignment make it a promising 2D metallic contact material for forming low-resistance interfaces with semiconducting layers.25–29 Furthermore, a novel 2D material, As2C3, has been computationally predicted to be a semiconductor with excellent mechanical and thermal stability30 that is comparable to or even superior to typical 2D semiconductors like MoS2 (ref. 31) and WS2.32 In its nanosheet form, As2C3 exhibits an ultrahigh carrier mobility of 4.45 × 105 cm2 V−1 s−1, which is comparable to that of graphene33 and even larger than those of other common 2D semiconductors such as MoS2 (ref. 34) and phosphorene.35 In addition, As2C3 has been proposed as a promising candidate for gas sensing applications,36 as well as for integration with a variety of 2D materials, including both metallic and semiconducting systems.37–39 These findings strongly suggest that employing 2D As2C3 as a channel material could open new opportunities for the design of next-generation nanodevices.
In this work, we computationally design and investigate the integration of 2D metallic NbS2 and semiconducting As2C3 to form a novel van der Waals heterostructure. We systematically explore its electronic properties and interfacial contact engineering, with particular emphasis on the effects of external electric fields. Our results reveal the fundamental mechanisms governing charge transfer, band alignment, and contact formation, thereby providing valuable insights into interface engineering strategies for next-generation 2D nanoelectronic devices based on the metal–semiconductor NbS2/As2C3 heterostructure.
2 Computational details
First-principles calculations based on density functional theory (DFT) were carried out using the Vienna Ab initio Simulation Package (VASP).40 The projector augmented wave (PAW) method was employed to describe the interaction between core and valence electrons.41 Electron exchange and correlation were treated using the Perdew–Burke–Ernzerhof (PBE) functional42,43 within the generalized gradient approximation (GGA).44 To account for the weak interlayer van der Waals (vdW) interactions crucial for heterostructure modeling, the DFT-D3 method with Becke–Johnson damping was applied.45 A plane-wave basis set with an energy cutoff of 500 eV was used throughout all simulations. For Brillouin zone sampling, a Monkhorst–Pack k-point grid of 12 × 12 × 1 was employed. These parameters are also consistent with previous DFT studies.46–48 All atomic structures were fully relaxed until the residual forces on each atom were less than 0.01 eV Å−1, and the total energy convergence threshold was set to 10−6 eV. A vacuum region of 20 Å was included along the out-of-plane direction to avoid spurious interactions between periodic images.3 Results and discussion
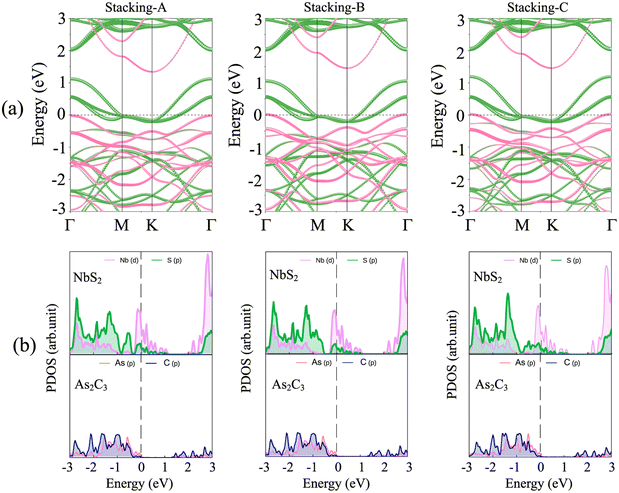
We begin our investigation by examining the atomic and electronic structures of the individual monolayers of NbS2 and As2C3, as shown in Fig. 1. The NbS2 monolayer adopts a layered hexagonal structure belonging to the P63/mmc space group and possesses D 3 h point group symmetry. Its unit cell comprises a single niobium (Nb) atom coordinated by two sulfur (S) atoms, forming a sandwich-like configuration with trigonal prismatic coordination. The optimized lattice constant is found to be 3.41 Å, in good agreement with previous theoretical studies.49 The electronic band structure of NbS2 reveals a metallic character, characterized by a conduction band that intersects the Fermi level. This metallic behavior arises primarily from the strong hybridization between Nb-d orbitals and S-p orbitals, as clearly illustrated in the projected density of states (PDOS) in Fig. 1(a). The presence of a high density of states near the Fermi energy further confirms the suitability of NbS2 as a 2D metallic contact material for heterostructure applications. The atomic structure of the As2C3 monolayer is illustrated in Fig. 1(b). Similar to NbS2, As2C3 adopts a layered hexagonal configuration and crystallizes in the P6/mmm space group. Its unit cell comprises four arsenic (As) atoms and six carbon (C) atoms, forming a stable 2D framework. The optimized lattice constant is calculated to be 5.86 Å, which is consistent with previous theoretical predictions.30,36 At the ground state, monolayer As2C3 exhibits an indirect semiconducting nature with a band gap of 1.43 eV within the PBE functional and 2.31 eV when computed using the HSE06 hybrid functional. The valence band maximum (VBM) is primarily derived from As-p orbitals, while the conduction band minimum (CBM) arises from the hybridization between As-p and C-p states. The sizable band gap indicates that As2C3 is a promising candidate for semiconducting components in 2D heterostructures.To explore the interfacial properties of the 2D NbS2/As2C3 heterostructure, we constructed vertically stacked models by aligning the constituent monolayers along the out-of-plane direction. Owing to the intrinsic symmetry and layered characteristics of both NbS2 and As2C3, three distinct stacking configurations were proposed and systematically investigated, as illustrated in Fig. 2. These configurations are referred to as Stacking-A, Stacking-B, and Stacking-C. Each stacking arrangement was fully relaxed to obtain the energetically favorable atomic structure prior to electronic property analysis. The equilibrium interlayer separations between the NbS2 and As2C3 layers in each heterostructure, denoted as D, are highlighted in Fig. 2. The obtained values of D for Stacking-A, Stacking-B and Stacking-C are 3.50, 3.61 and 3.20 Å, respectively. Among them, Stacking-C exhibits the shortest interlayer distance, suggesting a relatively stronger interlayer interaction. Additionally, as compared with the interlayer separations in other typical vdW heterostructures, such as M, the interlayer separations D obtained for the NbS2/As2C3 heterostructures fall well within the typical vdW interaction range. This observation confirms that the interlayer coupling in the proposed heterostructures is governed by vdW forces. Furthermore, to assess the thermodynamic stability of the proposed NbS2/As2C3 heterostructures, we evaluate the binding energy (Eb) for each stacking configuration. The binding energy is defined as
 | (1) |
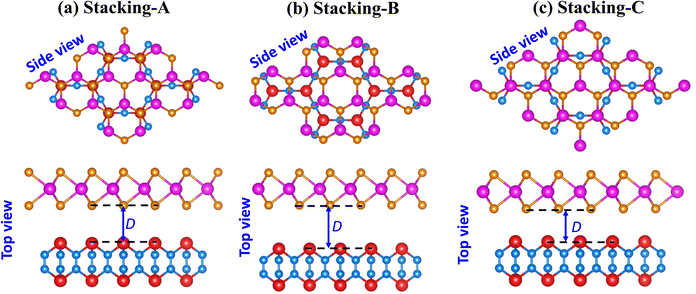 | ||
| Fig. 2 Optimized atomic structures of the NbS2/As2C3 heterostructure for different stacking configurations of (a) Stacking-A, (b) Stacking-B and (c) Stacking-C. | ||
Here, the total energies of the constituent NbS2, As2C3 and their heterostructure are denoted by ENbS2, EAs2C3 and ENbS2/As2C3, respectively. A stands for the area of the considered supercell for the heterostructure. The calculated binding energies per unit area for Stacking-A, Stacking-B, and Stacking-C are −12.73, −11.80 and −20.30 meV Å−2, respectively. All values are negative, indicating that the formation of the NbS2/As2C3 heterostructure is energetically favorable in all three configurations. Among them, Stacking-C exhibits the most negative binding energy, suggesting that it is the most energetically stable configuration. This is consistent with the fact that Stacking-C also possesses the shortest interlayer spacing (3.20 Å), reflecting the weak vdW interaction between the two layers. Importantly, the interaction remains in the vdW regime, which does not alter the intrinsic electronic properties of the constituent monolayers but merely holds them together, similar to the behavior observed in graphite and many other 2D vdW heterostructures. Consequently, in 2D heterostructures, the most stable stacking configurations—those exhibiting the lowest (most negative) binding energies—typically correspond to the smallest interlayer separations. These trends have also been consistently reported in various other 2D systems, further supporting the reliability of our observations.50–52 Additionally, these values of the binding energy are comparable with those obtained in graphite53 and other vdW heterostructures.54,55
We further investigate the electronic characteristics of the NbS2/As2C3 heterostructure by analyzing its electronic band structures and projected density of states (PDOS), as presented in Fig. 3. Remarkably, all three stacking configurations retain a metallic nature, with bands crossing the Fermi level. This observation indicates that the metallic character of the NbS2 layer is preserved upon stacking with the semiconducting As2C3 monolayer, as displayed in Fig. 3(a). The metallicity in the heterostructure is mainly governed by the hybridization between Nb-d and S-p orbitals, as evidenced by the dominant contribution near the Fermi level in the PDOS in Fig. 3(b). The preservation of metallic states is of particular interest for applications in electrical contacts, as it suggests efficient carrier injection. More interestingly, we can observe that in all three stacking configurations, the VBM of the As2C3 layer crosses the Fermi level at the Γ point. This characteristic implies that hole carriers from the semiconducting As2C3 layer can be injected into the metallic NbS2 layer without encountering an energy barrier. Consequently, Ohmic contact is established at the interface for all three configurations. The formation of Ohmic contact is highly desirable for nanoelectronic applications, as it ensures minimal contact resistance and efficient charge transport across the interface. Interestingly, the PDOS analysis reveals that there are no significant electronic states within the band gap region of the As2C3 layer contributed by the metallic NbS2 side. This absence of metal-induced gap states (MIGSs) suggests that the interlayer interaction at the NbS2/As2C3 interface is predominantly governed by vdW forces. Consequently, the Fermi level remains unpinned and aligns closely with the valence band maximum of the semiconductor. This weak FLP behavior enhances the flexibility of designing low-resistance electrical contacts in 2D devices and further underscores the potential of the NbS2/As2C3 heterostructure for application in future nanoelectronic and optoelectronic devices.
To gain deeper insight into the interfacial interactions, we further examine the charge redistribution at the interface of the NbS2/As2C3 heterostructures, as illustrated in Fig. 4(a). The charge density difference is defined as follows:
| Δρ(r) = ρNbS2/As2C3(r) − ρNbS2(r) − ρAs2C3(r) | (2) |
Here, ρNbS2/As2C3(r), ρNbS2(r) and ρAs2C3(r) are the charge densities of the NbS2/As2C3 heterostructure and NbS2 and As2C3 monolayers, respectively. As illustrated in Fig. 4, the yellow regions, indicating charge accumulation, are primarily located on the NbS2 side, whereas the cyan regions, corresponding to charge depletion, are found near the As2C3 layer. This spatial distribution suggests that electrons are transferred from the As2C3 semiconductor to the metallic NbS2 layer upon the formation of the heterostructure. Such a charge transfer results in the formation of an interfacial dipole directed from the semiconductor to the metal, which slightly modifies the local potential at the interface. Furthermore, to obtain the total amount of charge transfer from the As2C3 to the NbS2 layers, we calculate the cumulative charge density along the z direction as follows:
 | (3) |
Furthermore, the electrostatic potential profiles of the NbS2/As2C3 heterostructures are plotted in Fig. 4(b). It is evident that the potential well of the NbS2 layer is deeper than that of the As2C3 layer across all three stacking configurations. This indicates an intrinsic electrostatic field within the NbS2 monolayer. Moreover, the calculated work functions reveal that the As2C3 side possesses a lower work function compared to the NbS2 side. This difference in work function drives a small electron transfer from As2C3 to NbS2, consistent with the observed ΔQ values and the direction of the built-in potential gradient. Additionally, analysis of the electrostatic potential across the NbS2/As2C3 heterostructure enables the extraction of critical interface parameters, such as the contact barrier height (ΦB) and barrier width (WB). These quantities are essential for evaluating charge injection efficiency at the metal–semiconductor junction. Based on the extracted ΦB and WB, we estimate the tunneling probability (TB) using the Wentzel–Kramers–Brillouin (WKB) approximation, which provides insight into the likelihood of carrier transmission across the interface. Furthermore, the contact resistivity (ρt) can be derived from the tunneling probability, offering a quantitative measure of the interfacial transport characteristics. The TB and ρt can be quantitatively estimated using the following expressions:
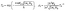 | (4) |
As discussed above, Stacking-C of the NbS2/As2C3 heterostructure is identified as the most energetically favorable configuration. To further assess its suitability for practical applications, we evaluate its mechanical and thermal stability. Mechanical stability is examined through the calculation of elastic constants and Young's modulus. Thermal stability is investigated via ab initio molecular dynamics (AIMD) simulations performed at room temperature T = 300 K over an 8 ps timescale. It is evident that the formation of the NbS2/As2C3 heterostructure induces a notable enhancement in the elastic constants compared to those of the individual monolayers, as illustrated in Fig. 5(a). The calculated in-plane elastic constants for the NbS2/As2C3 heterostructure are C11 = 173.02 N m−1, C12 = 67.77 N m−1 and C44 = 52.62 N m−1. One can find that these values of the elastic constants satisfy the Born-Huang mechanical stability criteria for 2D materials, which require that C11 > 0, C44 > 0 and C11 − C12 > 0.31,57,58 The fulfillment of these conditions confirms that the NbS2/As2C3 heterostructure is mechanically stable under small deformations. Furthermore, we calculated the angular dependence of Young's modulus of the NbS2/As2C3 heterostructure to further assess its mechanical rigidity as follows:59,60
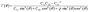 | (5) |
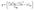 . The polar dependence of the Young's modulus for the NbS2/As2C3 heterostructure is illustrated in Fig. 5(b). The heterostructure exhibits isotropic mechanical behavior in the plane. The Young's modulus reaches a maximum value of 146.47 N m−1, which is higher than that of the constituent monolayers. In addition, this value is comparable with that in other 2D materials, such as MoS2 (130 N m−1)61 and Ti2C MXene (130 N m−1).62 This isotropy suggests that the mechanical response of the heterostructure is uniform regardless of the direction of applied strain, a desirable property for flexible and mechanically stable 2D devices. Furthermore, the ab initio molecular dynamics (AIMD) simulation results for the NbS2/As2C3 heterostructure are presented in Fig. 5(c). Throughout the simulation, no structural distortions, bond breaking, or significant atomic displacements were observed, confirming the thermal robustness of the heterostructure under elevated temperature conditions. All these findings indicate that the NbS2/As2C3 heterostructure demonstrates both mechanical integrity and thermal resilience, reinforcing its promise for reliable integration into next-generation 2D nanoelectronic and optoelectronic devices.
. The polar dependence of the Young's modulus for the NbS2/As2C3 heterostructure is illustrated in Fig. 5(b). The heterostructure exhibits isotropic mechanical behavior in the plane. The Young's modulus reaches a maximum value of 146.47 N m−1, which is higher than that of the constituent monolayers. In addition, this value is comparable with that in other 2D materials, such as MoS2 (130 N m−1)61 and Ti2C MXene (130 N m−1).62 This isotropy suggests that the mechanical response of the heterostructure is uniform regardless of the direction of applied strain, a desirable property for flexible and mechanically stable 2D devices. Furthermore, the ab initio molecular dynamics (AIMD) simulation results for the NbS2/As2C3 heterostructure are presented in Fig. 5(c). Throughout the simulation, no structural distortions, bond breaking, or significant atomic displacements were observed, confirming the thermal robustness of the heterostructure under elevated temperature conditions. All these findings indicate that the NbS2/As2C3 heterostructure demonstrates both mechanical integrity and thermal resilience, reinforcing its promise for reliable integration into next-generation 2D nanoelectronic and optoelectronic devices.
Furthermore, the practical implementation of the metal–semiconductor NbS2/As2C3 heterostructure hinges on its tunability in electronic properties and contact performance, which are critical for optimizing device functionality. To this end, we investigate whether these characteristics can be modulated through external stimuli, such as an applied perpendicular electric field. This approach enables a deeper understanding of the field-induced effects on band alignment and Schottky barriers, thereby assessing the feasibility of tailoring the heterostructure electronic behavior for specific nanoelectronic applications. The direction of the applied external electric field is illustrated in the inset of Fig. 6(a). A positive electric field is defined as pointing from the As2C3 layer toward the NbS2 layer, i.e., perpendicular to the interface and aligned with the out-of-plane axis and its strength varies from −0.5 to +0.5 V Å−1. Such large strengths of applied electric fields can be generated in recent experiments using dual ion-in-liquid gating.63 The application of an external electric field introduces tunability in both the contact barrier heights and the contact types of the NbS2/As2C3 heterostructure. Under a positive electric field, the hole barrier is significantly reduced, while the electron barrier increases correspondingly. This asymmetric modulation preserves the p-type Ohmic contact nature of the heterostructure, facilitating efficient hole injection from NbS2 into As2C3. Conversely, the application of a negative electric field leads to an increase in the hole barrier and a reduction in the electron barrier. Notably, when the field strength exceeds −0.2 V Å−1, the hole barrier becomes significantly enhanced and attains a positive value, indicating the emergence of a p-type Schottky contact at the NbS2/As2C3 interface. The tunability in the contact types and contact barriers of the NbS2/As2C3 heterostructure makes it a promising candidate for next-generation nanoelectronic and optoelectronic devices. The projected band structures of the NbS2/As2C3 heterostructure under external electric fields of +0.5 V Å−1 and −0.5 V Å−1 are shown in Fig. 6(b) and (c), respectively. Under the application of a positive electric field of +0.5 V Å−1, the heterostructure retains its Ohmic contact character, as evidenced by the presence of bands crossing the Fermi level. These crossing bands indicate efficient carrier injection and minimal energy barrier at the interface. The states near the Fermi level arise from the hybridization between the metallic NbS2 layer and the As-p orbitals of the As2C3 layer, as illustrated in the PDOS of the NbS2/As2C3 heterostructure in Fig. 6(d). More interestingly, under the application of a negative electric field of −0.5 V Å−1, as shown in Fig. 6(c), the NbS2/As2C3 heterostructure undergoes a transition from Ohmic to Schottky contact. This shift is characterized by a downshift in the valence band of the As2C3 layer toward lower binding energies, effectively increasing the hole injection barrier and reinforcing the Schottky contact nature. Under the negative electric field, the bands crossing the Fermi level are contributed by the metallic NbS2 layer with no contribution from the As2C3 layer, as confirmed by the projected density of states (PDOS) shown in Fig. 6(e). All these findings suggest that the electric field serves as an effective external stimulus to modulate the electronic properties and contact behavior of the NbS2/As2C3 heterostructure. This tunability highlights the potential of such NbS2/As2C3 heterostructures as promising candidates for next-generation field-effect transistors and nanoelectronic devices.
4 Conclusions
In summary, we have proposed and investigated a novel 2D NbS2/As2C3 metal–semiconductor heterostructure using first-principles calculations. The heterostructure is found to be energetically stable with weak interlayer interactions that preserve the intrinsic properties of the constituent layers. All stacking configurations exhibit metallic features, and importantly, the system forms intrinsic p-type Ohmic contacts owing to the crossing of the As2C3 valence band through the Fermi level. The projected density of states further reveals the absence of metal-induced gap states and only weak Fermi level pinning at the interface. The calculated tunneling probability and contact resistivity indicate that the Stacking-C configuration is the most favorable, offering the lowest resistance due to its narrowest barrier width. Charge transfer analysis also confirms electron transfer from As2C3 to NbS2, consistent with the interfacial band alignment. Furthermore, the application of a perpendicular electric field is shown to effectively tune the interfacial properties. A positive field reduces the hole barrier while preserving the Ohmic character, whereas a negative field enhances the hole barrier and induces a transition to a p-type Schottky contact. These findings demonstrate that NbS2/As2C3 is a promising 2D metal–semiconductor heterostructure with efficient charge injection, weak Fermi level pinning, and tunable contact properties. This work provides valuable insights into interfacial engineering strategies and paves the way for the design of next-generation nanoelectronic and optoelectronic devices based on emerging 2D materials.Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS.
- F. Schwierz, Nat. Nanotechnol., 2010, 5, 487–496 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS.
- C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726 CrossRef CAS PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 Search PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, ACS Nano, 2014, 8, 1102–1120 CrossRef CAS.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- K. Kaasbjerg, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 115317 CrossRef.
- J. O. Island, G. A. Steele, H. S. J. van der Zant and A. Castellanos-Gomez, 2D Materials, 2015, 2, 011002 CrossRef.
- A. Favron, E. Gaufrès, F. Fossard, A.-L. Phaneuf-L’Heureux, N. Y.-W. Tang, P. Lévesque, A. Loiseau, R. Leonelli, S. Francoeur and R. Martel, Nat. Mater., 2015, 14, 826–832 CrossRef CAS.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. Castro Neto, Science, 2016, 353, aac9439 CrossRef CAS.
- S.-J. Liang, B. Cheng, X. Cui and F. Miao, Adv. Mater., 2020, 32, 1903800 CrossRef CAS.
- A. Allain, J. Kang, K. Banerjee and A. Kis, Nat. Mater., 2015, 14, 1195–1205 CrossRef CAS.
- Y. Zhang, L. Yin, J. Chu, T. A. Shifa, J. Xia, F. Wang, Y. Wen, X. Zhan, Z. Wang and J. He, Adv. Mater., 2018, 30, 1803665 CrossRef.
- S. K. Dutta, S. K. Mehetor and N. Pradhan, J. Phys. Chem. Lett., 2015, 6, 936–944 CrossRef CAS.
- Q. Fu, X. Wang, J. Zhou, J. Xia, Q. Zeng, D. Lv, C. Zhu, X. Wang, Y. Shen and X. Li, et al. , Chem. Mater., 2018, 30, 4001–4007 CrossRef CAS.
- X. Wang, Z. Wang, J. Zhang, X. Wang, Z. Zhang, J. Wang, Z. Zhu, Z. Li, Y. Liu and X. Hu, et al. , Nat. Commun., 2018, 9, 3611 CrossRef.
- C. V. Nguyen, P. T. Truong, H. V. Phuc, C. Q. Nguyen, N. T. Hiep and N. N. Hieu, Nano Lett., 2025, 25, 10673 CrossRef CAS.
- C. C. Tho, S.-D. Guo, S.-J. Liang, W. L. Ong, C. S. Lau, L. Cao, G. Wang and Y. S. Ang, Appl. Phys. Rev., 2023, 10, 041307 CAS.
- C. C. Tho, C. Yu, Q. Tang, Q. Wang, T. Su, Z. Feng, Q. Wu, C. Nguyen, W.-L. Ong and S.-J. Liang, et al. , Adv. Mater. Interfaces, 2023, 10, 2201856 CrossRef CAS.
- P. Zhang, C. Bian, J. Ye, N. Cheng, X. Wang, H. Jiang, Y. Wei, Y. Zhang, Y. Du and L. Bao, et al. , Sci. China Mater., 2020, 63, 1548–1559 CrossRef CAS.
- J. Chen, Z. Ma, D. Wang, X. Li, S. Li and B. Bian, Phys. E, 2025, 168, 116179 CrossRef CAS.
- H. G. Shin, H. S. Yoon, J. S. Kim, M. Kim, J. Y. Lim, S. Yu, J. H. Park, Y. Yi, T. Kim and S. C. Jun, et al. , Nano Lett., 2018, 18, 1937–1945 CrossRef CAS.
- X. Ding, S. Zhang, M. Zhao, Y. Xiang, K. H. Zhang, X. Zu, S. Li and L. Qiao, Phys. Rev. Appl., 2019, 12, 064061 CrossRef CAS.
- T. N. Tran, P. T. Truong, H. V. Phuc, N. N. Hieu, V. B. T. Phung and C. V. Nguyen, Dalton Trans., 2025, 54, 7080–7087 RSC.
- P.-F. Liu, T. Bo, Z. Liu, O. Eriksson, F. Wang, J. Zhao and B.-T. Wang, J. Mater. Chem. C, 2018, 6, 12689–12697 RSC.
- S. Singh, L. Lang, V. Dovale-Farelo, U. Herath, P. Tavadze, F.-X. Coudert and A. H. Romero, Comput. Phys. Commun., 2021, 267, 108068 CrossRef CAS.
- X. Liu, P. Zhang, S. Wang, Y. Fang, P. Wu, Y. Xiang, J. Chen, C. Zhao, X. Zhang and W. Zhao, et al. , Nat. Commun., 2024, 15, 1263 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 Search PubMed.
- W. Bao, X. Cai, D. Kim, K. Sridhara and M. S. Fuhrer, Appl. Phys. Lett., 2013, 102, year Search PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed.
- V. Kumar and J. Jung, Appl. Surf. Sci., 2022, 599, 153941 CrossRef CAS.
- C. V. Nguyen, P. T. Truong, L. M. Duc, H. V. Phuc, N. V. Hieu, T. P. Linh, N. T. Hiep, C. Q. Nguyen and N. N. Hieu, Langmuir, 2025, 41, 21768–21779 CrossRef CAS.
- B. Huang, J. Yang, X. Liu, Z.-k. Tang and L. Cao, ACS Appl. Electron. Mater., 2025, 7, 4319–4326 CrossRef CAS.
- J. Mo, L. Li, X. Li, X. Yao, X. Xiang and X. Zu, Int. J. Hydrogen Energy, 2025, 100, 982–993 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- C. Bacaksiz, A. Dominguez, A. Rubio, R. T. Senger and H. Sahin, Phys. Rev. B, 2017, 95, 075423 CrossRef.
- I. Williamson, S. Li, A. C. Hernandez, M. Lawson, Y. Chen and L. Li, Chem. Phys. Lett., 2017, 674, 157–163 CrossRef CAS.
- J. Zhu, H. N. Alshareef and U. Schwingenschlögl, Appl. Phys. Lett., 2017, 111, 043903 CrossRef.
- T. Li, Q. Miao, Y. Wang and H. Yang, Surf. Interfaces, 2023, 42, 103336 CrossRef CAS.
- A. Slassi, RSC Adv., 2022, 12, 12068–12077 RSC.
- N. Ferdous, M. S. Islam, J. Biney, C. Stampfl and J. Park, Sci. Rep., 2022, 12, 20106 CrossRef CAS.
- F. Wang, J. Yuan, Z. Zhang, X. Ding, C. Gu, S. Yan, J. Sun, T. Jiang, Y. Wu and J. Zhou, Phys. Rev. B, 2023, 108, 075416 CrossRef CAS.
- X. Chen, F. Tian, C. Persson, W. Duan and N.-x. Chen, Sci. Rep., 2013, 3, 3046 CrossRef.
- N. Ibrahim, L. Mohammed, S. Umar, D. Ceresoli and Q. Zhang, FlatChem, 2024, 47, 100729 CrossRef CAS.
- Z. Cui, K. Ren, Y. Zhao, X. Wang, H. Shu, J. Yu, W. Tang and M. Sun, Appl. Surf. Sci., 2019, 492, 513–519 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- M. Maździarz, Arch. Mech., 2025, 77, 379–399 Search PubMed.
- M. Maździarz, 2D Materials, 2019, 6, 048001 CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- E. Cadelano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 245434 CrossRef.
- R. C. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 035423 CrossRef.
- S. Wang, J.-X. Li, Y.-L. Du and C. Cui, Comput. Mater. Sci., 2014, 83, 290–293 CrossRef CAS.
- B. I. Weintrub, Y.-L. Hsieh, S. Kovalchuk, J. N. Kirchhof, K. Greben and K. I. Bolotin, Nat. Commun., 2022, 13, 6601 CrossRef CAS PubMed.
Footnote |
| † To whom correspondence should be addressed. |
| This journal is © The Royal Society of Chemistry 2026 |