Open Access Article
Open Access ArticleTheoretical study on the multi-mechanism synergistic bactericidal effect of asymmetric Janus AuNPs–PS microspheres
Lingcong
He
 ,
Hongyang
Xu
,
Hongyang
Xu
 ,
Yonghui
Yang
and
Xue-Bo
Chen
,
Yonghui
Yang
and
Xue-Bo
Chen
 *
*
University of Science and Technology Liaoning, School of Electronic and Information Engineering, Anshan 114051, Liaoning, China. E-mail: xuebochen@126.com
First published on 5th December 2025
Abstract
With the overuse of antibiotics and the emergence of increasingly complex application scenarios, single-strategy bactericidal approaches are proving increasingly inadequate in today's environment. How to simultaneously attack multiple “targets” from multiple dimensions has become one of the hot topics in current research. This study proposes a multi-mechanism synergistic antibacterial platform based on Janus polystyrene–gold nanoparticle (AuNPs–PS) microspheres using COMSOL 6.3. This platform achieves the displacement motion of Janus AuNPs–PS microspheres through the UV-induced photothermal effect (PTT), and combines dielectrophoretic force (DEP) to enable controlled enrichment and directional arrangement of the microspheres. It achieves enhanced sterilization efficiency through the synergistic interaction of the photothermal effect and DEP based on Janus AuNPs. The study first simulated the light absorption–scattering model of AuNPs–PS microspheres under UV irradiation, verifying that the microspheres can generate a temperature field via the photothermal effect. Subsequently, the motion of the microspheres under thermophoresis and their effective separation under DEP were simulated to assess their feasibility in practical applications. Finally, the paper compares the bactericidal rates achieved by the microspheres under UV irradiation alone versus under multi-mechanism synergy. Simulation results indicate that the synergistic effect of multiple mechanisms yields a bactericidal efficacy approximately 30% higher than that of a single strategy. Among these, UV itself has a bactericidal effect. Relevant literature indicates that AuNPs can generate high temperatures under the photothermal effect, thereby disrupting bacterial membrane structures to a certain extent. Furthermore, the photocatalytic effect on the AuNP surface can catalyze the production of large amounts of reactive oxygen species (ROS) under appropriate conditions, facilitating the inactivation of certain bacteria. The PS matrix serves as an ideal carrier for AuNPs, with its excellent functionalization and dielectric properties providing the foundation for DEP manipulation. Furthermore, the spatial targeting and enrichment effect of DEP significantly enhances the local microsphere concentration and contact efficiency with bacteria. This multi-synergistic approach combining “physical enrichment–photothermal–photocatalysis” offers a potential strategy for overcoming bacterial resistance barriers. Under simulated conditions, it demonstrates promising removal potential against persistent biofilms, providing a theoretical mechanism for combating drug-resistant bacterial infections without readily inducing resistance. However, this inference requires validation through biological experiments. The study aims to provide theoretical foundations and simulation guidance for developing highly efficient sterilization technologies.
1. Introduction
The problem of significantly increased bacterial resistance due to antibiotic misuse is becoming increasingly severe. This resistance is primarily induced by continuous drug stimulation, which forces bacterial communities to select for resistant individuals carrying mutations in the relevant genes. These resistant individuals then survive and proliferate extensively, leading to enhanced resistance across the entire bacterial population. To combat resistant bacteria, single-strategy sterilization methods (such as UV sterilization) offer some antibacterial effects but remain significantly limited. This is because a single mechanism typically targets only one or a few bacterial points (e.g., cell wall, single protein, and DNA replication). Bacteria can evade the antimicrobial effects of single-mechanism sterilization methods through various resistance mechanisms. These include altering the structure of the target site for antimicrobial agents, upregulating efflux pump genes to actively expel antimicrobials, producing enzymes that inactivate antimicrobials, or activating metabolic pathways that bypass the target site to form biofilms. Moreover, the use of certain methods (like disinfectants or sterilizing solutions) can easily cause environmental harm.1 Therefore, developing novel, highly effective, and safe antimicrobial strategies has become an urgent task for researchers worldwide. Given the current landscape both domestically and internationally, future antimicrobial research will increasingly focus on multi-mechanism synergistic effects. This shift is not coincidental but rather a strategic response by the scientific community to the survival strategies and evolutionary pressures faced by bacteria, particularly drug-resistant strains. The core concept of multi-mechanism synergistic strategies is to launch simultaneous attacks from multiple dimensions and against multiple targets, leaving bacteria “unable to defend against all threats or adapt to any single one.” Consider the “combination punch effect”—the principle that two fists cannot withstand four hands applies here. Taking ultraviolet (UV) sterilization as an example, UV serves as a traditional physical disinfection method with advantages such as being non-toxic, safe, and environmentally friendly. It has been widely applied in fields including wastewater treatment, food processing, and healthcare.2 However, traditional UV sterilization technology suffers from issues such as significant variations in inactivation efficiency due to water quality and limited effectiveness against certain microorganisms. Single-strategy antimicrobial approaches are increasingly showing limitations. This study introduces DEP into AuNPs–PS microspheres under photothermal effects, developing a more efficient multi-strategy antimicrobial method. Simulations and comparative experiments demonstrate that the combined action of DEP and AuNPs–PS enhances antimicrobial efficacy by nearly 30%. Kesharwani et al.21 noted that the localized surface plasmon resonance (LSPR) of AuNPs can generate significant near-field enhancement and photothermal conversion in the UV-vis spectrum. This process disrupts bacterial biofilm structures and compromises cell membrane integrity, facilitating the entry of reactive oxygen species (ROS) generated by subsequent photocatalysis into the cell interior, thereby achieving bactericidal effects.22,23 Furthermore, dielectrophoretic forces concentrate microspheres in target areas, substantially increasing local concentrations and creating optimal conditions for photothermal and photocatalytic processes, thereby generating a synergistic effect.3,4The photothermal effect refers to the phenomenon where photosensitive materials absorb light energy and efficiently convert it into thermal energy, causing an increase in their own temperature and that of their surroundings. Its core principle lies in the non-radiative relaxation process of light energy.5 When AuNPs are exposed to UV irradiation of specific wavelengths, their internal electrons become excited, transitioning from the ground state to an excited state. Electrons in this unstable excited state release energy through collisions with other electrons or the crystal lattice (atomic nuclei), returning to the ground state. During this process, the kinetic energy of the electrons is converted into thermal vibrations of the crystal lattice. The intensely thermally vibrating lattice transfers thermal energy to its surroundings (such as water molecules) through collisions, manifesting macroscopically as a localized temperature increase.6,7 Due to the Janus-like structure of AuNPs–PS microspheres, the AuNP side efficiently absorbs light energy through the strong LSPR effect and rapidly generates substantial heat, causing a sharp increase in local temperature on this side. In contrast, the PS side being a transparent medium absorbs very little visible/near-infrared light, resulting in negligible heat generation. Consequently, the temperature on this side remains close to that of the surrounding solvent. Consequently, a significant temperature gradient forms across the surface of the nanoscale microsphere, extending from the AuNPs (hot side) to the PS (cold side). Solvent molecules surrounding the hot side exhibit increased kinetic energy due to heating, resulting in more vigorous motion. In contrast, solvent molecules on the cold side possess lower kinetic energy and exhibit relatively calmer motion. This leads to the generation of thermal permeation slip flow, driving the fluid to move along the surface from hot to cold regions. Simultaneously, the presence of slip imposes an equal and opposite reaction force on the microspheres themselves, causing the AuNPs–PS microspheres to roll toward the cold side. This is the principle behind the self-thermophoresis displacement of Janus AuNPs–PS microspheres. The description of thermophoresis can be expressed using the following equation:8
 | (1) |
Dielectrophoresis (DEP) is a force generated by applying a non-uniform electric field to neutral particles, enabling precise manipulation of microparticles and cellular organisms. Consequently, it demonstrates significant potential in the fields of microbial manipulation and separation.9 To date, numerous researchers have undertaken work in this area. For example, Chiou et al. first proposed the optically driven dielectric electrophoresis (ODEP) technique in 2005 for manipulating cells or particles.10 Negr et al. investigated the effects of DEP on nanoparticles in 2017 through the long-term stability of nanofluids in highly divergent fields.11 In 2020, Zhang et al. proposed a dielectrophoresis microfluidic chip for particle separation, which utilizes dielectric properties to achieve size-based separation of blood cells.9 The formation of DEP is often attributed to the polarization of neutral particles in an inhomogeneous electric field, which induces corresponding charges on their surfaces. Simultaneously, the resulting electric dipole moment causes the positive and negative charge ends of the particles to become unevenly distributed under the influence of forces. In a sinusoidally varying electric field, the dielectric electromotive force typically follows the following laws:12
| FDEP = 2πr3ε0εmRe[k(ω)]∇E2 | (2) |
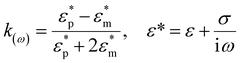 | (3) |
Here, ε0 and εm denote the permittivity of free space and the permittivity of the suspension medium, 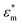 and
and 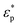 represent the complex permittivities of the suspension medium and particles, E denotes the root-mean-square electric field strength, Re[k(ω)] signifies the real part of the Clausius–Mossotti (CM) factor, and ω is the frequency of the applied electric field. ε and σ denote the dielectric constant and electrical conductivity of the material. Re[k(ω)] typically varies between [−0.5, 1]. When Re[k(ω)] is positive, particles migrate toward regions of higher electric field strength, termed positive dielectrophoresis (pDEP). Conversely, when Re[k(ω)] is negative, particles migrate toward regions of lower electric field strength, termed negative dielectrophoresis (nDEP). Eqn (2) and (3) are both calculated using the static approximation method. Since the actual electrode dimensions are typically much larger than those of the particles, this approximation is generally quite suitable for describing interactions with the applied electric field.
represent the complex permittivities of the suspension medium and particles, E denotes the root-mean-square electric field strength, Re[k(ω)] signifies the real part of the Clausius–Mossotti (CM) factor, and ω is the frequency of the applied electric field. ε and σ denote the dielectric constant and electrical conductivity of the material. Re[k(ω)] typically varies between [−0.5, 1]. When Re[k(ω)] is positive, particles migrate toward regions of higher electric field strength, termed positive dielectrophoresis (pDEP). Conversely, when Re[k(ω)] is negative, particles migrate toward regions of lower electric field strength, termed negative dielectrophoresis (nDEP). Eqn (2) and (3) are both calculated using the static approximation method. Since the actual electrode dimensions are typically much larger than those of the particles, this approximation is generally quite suitable for describing interactions with the applied electric field.
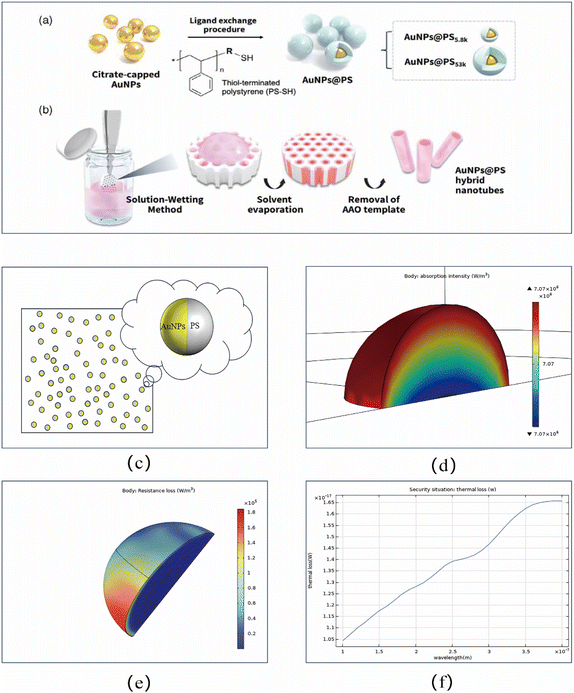
The Janus AuNPs–PS multi-mechanism synergistic bactericidal platform integrates multiple physical fields including light, heat, electricity, and mechanics. The thermophoresis force generated by the photothermal effect provides self-propulsion for Janus spheres, while DEP enables targeted positioning, achieving controlled enrichment and directed arrangement of microspheres in the target area. Fig. 1 illustrates the general workflow of the Janus AuNPs–PS multi-mechanism synergistic bactericidal platform.
To validate the rationality and feasibility of this design, this study employed COMSOL Multiphysics simulation software to establish a multi-mechanism synergistic sterilization model for AuNPs–PS under DEP. This model utilizes multi-physics coupling of light fields, electric fields, fluid flow, and particle tracking. To simulate the self-thermophoresis motion of Janus AuNPs–PS microspheres induced by the photothermal effect, this study first analyzed the thermal dissipation of absorbed and scattered light from AuNPs under UV irradiation. By constructing a thermophoresis model, it successfully demonstrated that the microspheres deflect away from the heat source under an asymmetric temperature field. To highlight the significant efficacy of multi-mechanism synergistic bactericidal action, the paper compares the bactericidal performance of Janus AuNPs–PS microspheres with that achieved solely under UV irradiation. Simulation results indicate that the multi-mechanism synergistic approach enhances bactericidal efficacy by approximately 30%. This precisely validates the rationale for leveraging synergistic effects from UV irradiation, photothermal effects, photocatalysis, and electric fields to achieve bactericidal activity.
2. Model and design
2.1 Photothermal transfer of AuNPs
When a collimated light beam strikes a translucent medium, absorption and scattering occur, and part of the incident light is converted into thermal energy, while another portion undergoes directional alteration. Under specific conditions, both phenomena can be simulated using the diffusion approximation within COMSOL Multiphysics software. Experiment 1 presents the light absorption–scattering model for AuNPs–PS microspheres under UV illumination. The light absorption model employs the irradiation beam in absorbing media interface from the heat transfer module, solving the Beer–Lambert law within the material.12 When using this interface, it is assumed that the intensity of the beam at the illuminated boundary is known. The light absorption can be determined using the following equations: | (4) |
 | (5) |
Although this study is a theoretical investigation based on COMSOL simulations, aiming to explore and demonstrate the potential mechanism and feasibility of the synergistic antibacterial strategy “Janus AuNPs–PS combined with DEP” at the physical level, numerous synthesis methods for AuNPs–PS have been reported with the continuous advancement of nanotechnology. For instance, ref. 27 details two synthesis approaches: the ligand exchange method and the solution wetting method. Fig. 2a and b illustrate the schematic preparation process of gold nanoparticle–polystyrene hybrid nanotubes. Both methods first require the reduction of tetrachloroauric acid aqueous solution using citric acid to prepare gold nanoparticles. Subsequently, either ligand exchange or solution wetting was employed to replace citrate ions which form stronger gold–sulfur bonds with thiol-capped polystyrene (PS-SH). After solvent evaporation, the AuNPs–PS material solidified within the nanopores of the AAO template. Finally, the AAO template is selectively stripped using a 5 wt% NaOH aqueous solution to yield AuNPs–PS hybrid nanotubes. In this experiment, the morphology of AuNPs–PS particles was designed as Janus-like. Due to the high symmetry of the AuNPs–PS microspheres and the extremely weak UV absorption of the transparent PS side medium after adding UV-resistant additives, which generates almost no heat, only 1/4 of the sphere was simulated (Fig. 2c). When UV irradiation strikes the AuNPs, both light absorption and scattering occur. These phenomena are accompanied by simultaneous heat conversion, meaning both light absorption and scattering can be represented through COMSOL simulations of the conversion efficiency between light and heat. Fig. 2d simulates the optical absorption of AuNPs under UV irradiation at a wavelength of 254 nm. The figure clearly shows that the closer to the particle surface, the higher the optical absorption intensity, indicating that the photothermal conversion efficiency of AuNPs is often optimal at the surface. Fig. 2e depicts the resistive losses during light scattering in AuNPs. Compared to the consistent internal losses, significant variations in resistive losses are observed at the particle surface. This indicates that light scattering is strongly correlated with the light-contacting surface, while resistive loss directly manifests as localized heating within the AuNPs. Optimizing the particle size, shape, or material properties can enhance photothermal efficiency. Fig. 2f reflects the overall thermal loss of AuNPs under UV irradiation across the 100–400 nm wavelength range. This figure demonstrates that AuNPs exhibit the most significant absorption efficiency for UV irradiation at longer wavelengths. Of course, the parameters used in this experiment (electromagnetic wave frequency, optical refractive index, and relative permittivity) are all idealized values. Their limitation lies in their extreme susceptibility to interference from external environmental factors. To truly implement this in practical applications, further validation through real-world experiments remains necessary.
3. Results and discussion
3.1 Thermal swimming of Janus microspheres
Self-heating micro/nano motors driven by the photothermal effect remain a prominent focus in current micro/nano actuation research. Particularly in the biomedical field, such motors demonstrate immense potential. For instance, in targeted drug delivery, these motors can be loaded with pharmaceuticals, remotely guided by near-infrared light to navigate to specific pathological sites and release the drugs; in microsurgery and photothermal therapy, they function as “microsurgical scalpels,” utilizing the photothermal effect to generate localized high temperatures that destroy cancer cells; in environmental remediation, they can adsorb and collect pollutants (such as heavy metals and organic toxins) from water, transporting them to designated areas for centralized treatment. In practical applications, such motors are typically composed of advanced photothermal materials that exhibit photothermal effects under illumination at specific wavelengths. The resulting asymmetric temperature field induces self-thermophoresis in the motor. Although this subsection does not involve actual experiments, it employs simulations to verify whether the thermally driven motion of AuNPs–PS microspheres aligns with theoretical predictions. By simulating an asymmetric temperature field around the microspheres, we assess whether they deflect from the hot side toward the cold side as described in the Introduction.According to Newton's second law, the particle position and magnitude of the thermophoretic force can be calculated by solving the second-order equation of motion for the position vector components of the AuNPs–PS particles:
 | (6) |
 | (7) |
The figures below show our results. Among that the AuNPs–PS particles have a particle size of 2–6 µm, a density of 1927 kg m−3, and a thermal conductivity of 160 W m−1 K−1. Fig. 3a depicts a thermophoresis-driven model. Particles will be released at the dashed line position on the left and accumulate along the solid line on the right, driven by a hydrogen flow rate of 2000 sccm. Fig. 3b and c simulate the fluid temperature and velocity, and the motion velocity of AuNPs–PS particles, respectively. According to the principle of molecular thermal motion, particles will undergo vigorous movement at high temperatures, resulting in a significant acceleration of flow velocity in this region. To vividly illustrate the motion state of particles under thermophoresis, Fig. 3d–f capture the particle movement at t = 0 s, t = 1 s, and t = 4 s. Fig. 3d depicts the initial particle release state. Fig. 3e illustrates the process where particles gradually move away from the heat source as they follow the H2 flow. Fig. 3f reflects the continuous accumulation of particles at the baffle. Fig. 3g simulates the overall trajectory of particles sweeping across the heated surface. The white edge at the bottom clearly demonstrates that AuNPs–PS gradually shift toward the cooler side under thermophoresis. Fig. 3h shows a positive correlation between actuator temperature and particle position along the y-axis. Although this experiment successfully simulated the motion of AuNPs–PS under thermophoresis, the H2 fluid environment limits the practical application of AuNPs–PS. We hereby state that the ideal parameters employed in the thermal swimming process (such as particle size, density, thermal conductivity, and so forth) represent a simplification of complex realities and constitute an inherent limitation of this study. To achieve authentic experimental results, subsequent practical verification through specific implementation is required. With the rapid advancement of nanotechnology, literature on the thermophoresis-driven motion of Janus AuNPs microspheres has become increasingly common. Moreover, since AuNPs are photosensitive materials, they can undergo photothermal effects and achieve self-propulsion under irradiation of NIR/UV light at certain intensities. For example, Jiang et al.12 found that for thermophoresis to serve as a mechanism for particle self-propulsion, a local temperature gradient must be generated by the particle itself. They fabricated Janus particles by evaporating gold layers onto hemispheres of silicon or polystyrene spheres. To elucidate the mechanism, they measured for the first time the temperature distribution and thermal slip flow field around microscopic Janus particles. By measuring the temperature drop on the particles, they verified that the autonomous propulsion speed agreed with predictions from measurable parameters. Additionally, they demonstrated the application of this autonomous propulsion to drive micro-rotors in micromachines. Xuan et al.6 developed fuel-free, NIR-driven Janus mesoporous silica nanoparticle motors (JMSNMs) by vacuum sputtering a 10 nm Au layer onto one side of the MSNs. Maric et al.13 developed NIR-driven mesoporous SiO2–Au nanomotors by coating mesoporous silica nanoparticles with a thin gold layer. These motors exhibit highly efficient self-propulsion, enabling them to readily penetrate biofilm matrices and disperse biofilms in situ on the Au portion of the nanomotor due to photothermal effects.
To strike a balance between computational complexity and physical realism, we have introduced necessary simplifications to the thermophoresis model. The primary advantage of this first-order approximation is its ability to clearly reveal and quantify the dominant trends and core physical mechanisms underlying the synergistic interaction between DEP and thermophoresis effects, free from the interference of complex secondary effects. This simplification is crucial for concept-validation studies, providing a clear theoretical framework for understanding the dominant physical forces within the system. However, for nanoparticles, Brownian motion constitutes the primary source of random diffusion. In simulated scenarios, due to the imposition of strong thermophoresis forces, these directed, deterministic forces may significantly dominate particle transport over random Brownian diffusion. Consequently, in regions with weaker force fields or for smaller-sized particles, the influence of Brownian motion becomes more pronounced. Regarding the ideal temperature gradient, this model employs a linear or steady-state temperature field assumption. This differs from the complex, non-uniform temperature field in real microfluidic environments, which arises from the combined effects of localized laser heating, convection, and thermal diffusion. This simplification may overestimate the uniformity and stability of the temperature field, thereby affecting the local accuracy of thermophoresis calculations. Future model improvements are anticipated to include introducing random terms to couple Brownian motion and establishing more complex non-isothermal flow models coupled with fluid dynamics to simulate more realistic temperature distributions, thereby further enhancing prediction accuracy.
3.2 Targeted localization function of dielectrophoretic forces
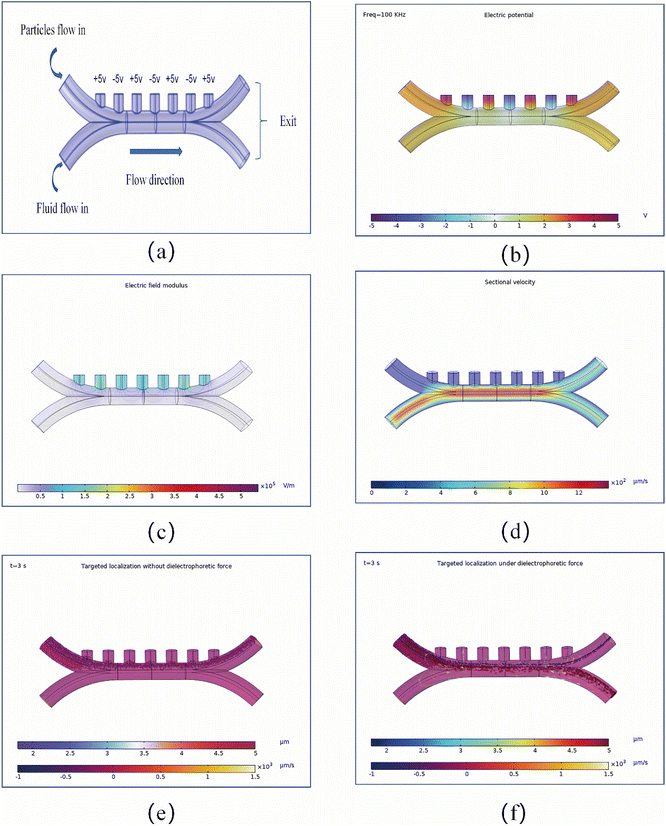
The previous experiment demonstrated that AuNPs–PS microspheres can deflect from the hot side to the cold side under thermophoresis conditions, successfully resolving the power supply issue. However, for AuNPs–PS particles to achieve practical application, the issue of directional control must be resolved. Currently, the practical application of micro- and nano-scale particles remains limited, primarily in the biomedical and environmental remediation fields. Particularly in biomedical applications, targeted drug delivery has already seen numerous clinical trials.14,15 For injuries of varying severity across different pathological sites within a biological organism, the volume of micro- and nanoparticles naturally differs, leading to variations in the amount of drug they carry. Consequently, how to achieve directional control of particles made from identical materials but differing in size has become one of the most pressing challenges to address. However, unlike robots in the macroscopic world equipped with control chips and artificial intelligence algorithms for precise navigation, the movement of micro- and nanoscale particles does not possess such capabilities. Motion in the microscopic realm typically requires external physical fields to assist in control. The currently popular control approaches involve magnetic or electric control. This entails coating the surface of micro- and nano-particles with iron or nickel materials, enabling precise guidance through external magnetic fields or applied electric fields, leveraging electrostatic forces for accurate steering.16 This study employs the second approach—electric field control by applying a 10 V potential difference to generate dielectrophoretic forces, thereby simulating directional control of two distinct sizes of AuNPs–PS particles (6 µm and 12 µm). As a powerful and flexible micro/nano-scale manipulation technique in microfluidics, DEP harnesses forces exerted by non-uniform electric fields on neutral particles. By simply adjusting the electric field frequency and intensity, it enables diverse functions including particle capture, separation, transport, and alignment. This technology holds broad application prospects in biotechnology, medical diagnostics, and nanotechnology.Fig. 4a depicts the dielectrophoretic force model for AuNPs–PS particles. A 10 V potential difference is applied between the positive and negative electrodes. Mixed particles enter through the upper inlet at a flow rate of approximately 100 µm s−1, while the fluid enters through the lower inlet at a flow rate of roughly 600 µm. Fig. 4b–d simulate the potential distribution on the model surface, the electric field distribution across multiple cross-sections, and the fluid velocity distribution in the X–Y plane, respectively. As shown in Fig. 4d, particles closer to the channel central exhibit higher corresponding flow velocities. Fig. 4e and f show the flow patterns of mixed particles with and without dielectrophoretic forces, where purple represents 6 µm particles and red represents 12 µm particles. When no dielectrophoretic force is present (Fig. 4e), mixed particles are released simultaneously from the upper inlet. Since the fluid velocity at the bottom is significantly higher than the particle release velocity at the upper inlet, all particles will concentrate and exit through the upper outlet. When dielectrophoretic forces are present (Fig. 4f), the size difference between particles causes the larger particles to experience significantly stronger dielectrophoretic forces than the smaller particles. Consequently, larger particles exit through the lower outlet while smaller particles exit through the upper outlet. This experiment concludes that DEP can control the outflow direction of particles of varying sizes, enabling precise targeted positioning. However, this study only controlled particle size as a variable and did not validate different particle materials. This is crucial for biomedical applications, as medical practices often fuse different blood cells with micro- and nanoscale particles to achieve targeted drug delivery via blood cells as a medium. Despite the limitations of this experiment, DEP-based targeted positioning of particles differing in size and even material composition is undoubtedly feasible. Ref. 17 demonstrates the precise separation of mixed cells (red blood cells, white blood cells, and platelets), highlighting the broad potential of DEP for particle separation in microfluidic applications. As mentioned several times in the text, the experimental conclusions are limited to the results of this simulation and require verification through real experimental data to confirm their feasibility.
3.3 Sterilization experiment comparison
This experiment investigates the application of multi-mechanism synergistic sterilization, integrating multiple physical fields (light field, electric field, flow field, and particle tracking). The light field was modeled using a 254 nm UV lamp due to UV light's high energy, excellent optical responsiveness, and mature technology. Assuming uniform power distribution across the lamp surface, each light ray's power attenuates as it propagates through water away from the surface, influenced by water's internal transmittance. For distilled water, the internal transmittance of UV irradiation is approximately 98%. This study investigates the impact of photo-induced dielectrophoretic forces on sterilization efficacy. Therefore, the internal transmittance of UV irradiation was set to 70% to represent water of lower purity. When light propagates through water, a dedicated dose rate calculation node combined with the ray tracing module is used to compute the volumetric dose rate. To obtain an accurate distribution of injection rates, it is necessary to emit a sufficient number of rays and employ a sufficiently fine mesh layout within the domain. In this example, we set the number of rays emitted to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to strike a balance between precision, solution time, and file size considerations. The intensity distribution of UV light typically follows a Gaussian function:18
000 to strike a balance between precision, solution time, and file size considerations. The intensity distribution of UV light typically follows a Gaussian function:18 | (8) |
A non-uniform electric field is generated by an alternating electrode arrangement, where the potentials of the positive and negative electrodes remain constant. The anode potential is set to 5 V, and the cathode potential to −5 V. Under steady-state conditions, the electric field distribution within the microchannel is governed by the Laplace equation:9
| ∇ × J = Qi | (9) |
| J = σE + Je | (10) |
| E = −∇V | (11) |
The flow field module simulates the fluid dynamics surrounding the motion of micro- and nanoparticles. This study employs the “turbulence, k–ε” physics interface to solve for fluid velocity and pressure within the reactor, utilizing the built-in fully developed flow option at the inlet boundary to define the inflow velocity distribution. By adjusting the flow velocity magnitude, the movement speed of particles within the aqueous solution can be controlled. The “particle tracking” module is employed to track bacterial particles suspended in aqueous solutions. This module utilizes a simple exponential decay model with a fixed inactivation constant k to predict the proportion of bacteria that are inactivated or killed, as described using the following formulas:19
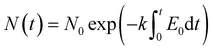 | (12) |
 | (13) |
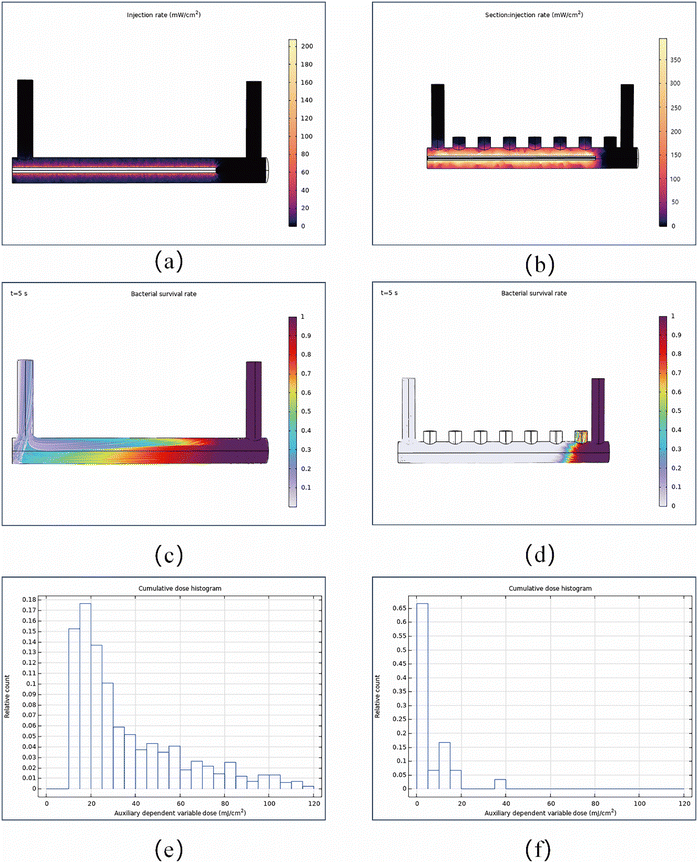
Fig. 5a depicts a ring reactor model primarily composed of three sections: the reaction zone, the ultraviolet lamp zone, and the electrode domain. A non-uniform electric field is generated by an alternating arrangement of seven electrodes. The main body of the reaction zone has a radius of 5 cm and a length of 100 cm. Both the inlet and outlet have a radius of 3 cm and a height of 30 cm. The UV lamp has a radius of 1 cm and a length of 80 cm. Each electrode has a radius of 3 cm and a height of 10 cm, with a spacing of 13 cm between them. Mesh parameters are controlled by the physical field, with elements set to coarse. All regions of the model are in a fluid environment, using the default fluid material from the case library—an aqueous solution at room temperature. During the experiment, the aqueous solution will flow from the inlet to the outlet. Within the electrode region, it will be subjected to the synergistic effects of UV irradiation and DEP. Fig. 5b shows a cross-sectional distribution of the flow velocity field, illustrating the fluid dynamics within the reactor. Compared to the inlet and outlet velocities, the flow velocity in the main reactor is relatively slow, at only 0.2 cm s−1. This low-velocity distribution significantly influences the movement trajectories of bacterial particles, as the low-velocity zones facilitate bacterial retention and aggregation, while high-velocity zones tend to carry some bacteria away from the UV high-intensity region. The dielectrophoretic force provides favourable conditions in the low-velocity zones of the flow field. This spatially heterogeneous distribution is also one of the key factors enabling highly efficient sterilization. Fig. 5c and d show the potential and electric field distributions of the reactor, respectively. Simulation results indicate that under a 5 V AC voltage drive, the average potential difference between electrodes reaches approximately 2 V. The electric field lines reveal that high-field-strength regions are primarily distributed between the electrodes, precisely where the dielectrophoretic forces exert their predominant effects.
To validate the high efficiency of the multi-mechanism synergistic bactericidal effect of AuNPs–PS particles, we compared the bactericidal rates achieved under UV irradiation alone with those achieved through the multi-mechanism synergistic effect. Our findings concluded that the multi-mechanism synergistic effect enhanced the bactericidal rate by approximately 30% compared to the efficacy of a single mechanism. The simulation comparison process is as follows. Fig. 6a shows the irradiance distribution under UV irradiation alone. It is evident that the UV irradiance always reaches its maximum near the light source and decreases outward in a fan-shaped pattern. After introducing AuNPs–PS particles and DEP, Fig. 6b clearly demonstrates that the UV irradiance near the light source has been significantly enhanced. The underlying mechanism lies in the dielectrophoretic force, which enables the controlled enrichment and directed arrangement of microspheres. Simultaneously, it effectively guides bacteria to aggregate toward AuNPs–PS microspheres and migrate toward high-intensity regions on the surface of the UV light source. This significantly increases the probability of particle-UV light contact and exposure duration, thereby substantially enhancing the UV irradiation intensity experienced by particles near the light source. Morphological changes in bacteria and vital staining serve as the “gold standard” experimental evidence for validating the efficacy of any bactericidal strategy. Ref. 21 and 27 employed scanning electron microscopy to observe morphological alterations on particle surfaces and utilized live/dead staining kits to quantitatively assess bacterial survival rates, respectively. However, this paper constitutes preliminary theoretical research and can only analyze particle colour variations simulated through model software. Fig. 6c and d respectively illustrate the particle trajectories of two dynamic sterilization processes. Fig. 6c captures the sterilization effect at t = 5 s under UV irradiation alone. The colour legend indicates that the bacterial survival rate under UV exposure is approximately 30%, demonstrating a sterilization rate of 70%; Fig. 6d captures a schematic at t = 5 s under the synergistic effect of multiple mechanisms. The image clearly shows that bacterial particles within the reactor have been largely eliminated. This demonstrates that, compared to single-mechanism sterilization, the synergistic effect of multiple mechanisms—while leveraging UV's inherent sterilization capability—combines the high-temperature sterilization effect generated by the photothermal effect of AuNPs with the sterilizing power imparted by the reactive oxygen species produced through chemical reactions. This synergistic effect, integrating “physical enrichment–photothermal–photocatalysis,” significantly enhances the sterilization capability. Simulations using idealized parameters (e.g., uniform particle size, consistent drag, and fixed k) cannot reliably simulate complex bacterial behaviour under sterilization. Therefore, the predictions of the current model should be regarded more as theoretical validation of potential efficacy and mechanisms under ideal conditions. Future research will focus on developing more inclusive multiscale models that incorporate parameter distribution functions and dynamic feedback mechanisms to describe population heterogeneity and evolutionary dynamics, thereby enabling more accurate predictions of sterilization efficacy in practical application scenarios. Their potential practical application in real-world scenarios requires subsequent validation through actual experiments.
Finally, to obtain more precise sterilization data, we installed a particle tracking module at the reactor outlet and defined an auxiliary dependent variable. This module employs a simple exponential decay model with a fixed inactivation constant k, enabling tracking of bacterial trajectories within the fluid and displaying the proportion of surviving bacteria via colour expressions. The auxiliary dependent variable can integrate the dosing rate for each particle trajectory. After using a filter to exclude bacterial particles and all AuNPs–PS that ultimately did not reach the outlet in the aqueous solution, the particle counter can perform relative counting of surviving bacteria based on the cumulative UV dose of bacterial particles that finally reached the outlet. Based on studies of UV response performance by Zhang9 and Sozzi20et al., we assumed a bacterial fixed inactivation rate constant k of 0.1 cm2 mJ−1 and predicted the survival rates of bacteria exposed solely to UV irradiation versus those exposed to UV irradiation combined with DEP. Fig. 6e shows the cumulative dose histogram along particle trajectories under UV irradiation alone. This graph indicates that all bacteria received a dose of at least 10 mJ cm−2, but for some particles, the cumulative dose was significantly higher. Fig. 6f presents the cumulative dose histogram under multi-mechanism synergistic effects. This graph shows that counts essentially reach zero after accumulating a dose of 20 mJ cm−2, indicating no surviving bacterial particles were detected. This further validates the potent bactericidal efficacy of multi-mechanism synergistic effects.
This experiment simulates bacterial survival rates in fluids under UV irradiation alone and compares them with survival rates under the combined effect of AuNPs–PS particles and DEP. Simulation results indicate that the enhanced method achieves approximately 30% higher bactericidal efficacy. While antibiotics serve as a traditional sterilization method with some efficacy, they readily disrupt ecosystems and foster drug-resistant strains as the dosage increases. Deepening research reveals microorganisms are unlikely to develop resistance against drug–nanoparticle conjugates. Consequently, therapeutic approaches that load drugs onto nanoparticles via multi-ionic complexation, physical encapsulation, or chemical bonding are being actively explored.24 Gold nanoparticle–antibiotic conjugates are particularly prevalent for selectively photothermally eliminating protozoa and bacteria. For instance, Sreedharan et al.25 coupled ciprofloxacin to Bacillus subtilis RSB64-derived gold nanoflowers (GNFs) via robust adsorption under optimized conditions to evaluate the GNF–ciprofloxacin complex's impact on the antibiotic's cell growth inhibition activity. The results demonstrated that the GNF–ciprofloxacin conjugate exhibited enhanced bactericidal activity against Gram-negative bacteria. Vidya et al. developed an effective drug delivery agent for treating multidrug-resistant (MDR) bacterial infections by using gold nanoparticles (AuNPs) prepared from bacterial extracellular polysaccharides (EPS) both as a reducing agent and stabilizer.26 Numerous real-world cases exist where AuNP particles have been used to selectively eliminate drug-resistant bacteria. Although we have not identified any documented instances of AuNP particles combined with DEP under UV light achieving bactericidal effects, this remains a bold endeavor. Theoretically, this approach is indeed feasible. As analyzed earlier, DEP enables controlled enrichment and directed arrangement of microspheres while effectively adsorbing bacteria. This enhances microbial exposure to UV irradiation and facilitates the localized photothermal killing effect of AuNPs.
4. Conclusion
This study, for the first time, theoretically analysed the limitations of single-mechanism approaches compared to multi-mechanism synergistic effects in bactericidal capabilities, proposing that the synergistic attack of multiple effects, such as “physical enrichment–photothermal–photocatalysis”, delivers potent bactericidal effects. By simulating the light absorption–scattering behaviour of AuNPs–PS microspheres under UV irradiation, their dynamic motion under thermophoresis, and their targeted positioning via DEP, the study substantiates the rationality and feasibility of multi-mechanism synergistic sterilization. This aligns with the practical application of light-driven micro/nanorobots in environmental remediation. With the rapid advancement of micro–nano technology and advanced materials, extensive academic research has demonstrated that micro–nano robots composed of photoactive materials can achieve self-propulsion under external light sources (UV/NIR/VIS) and enable precise positioning through magnetic or electric fields. Finally, to validate that the synergistic effect of multiple mechanisms yields superior sterilization capabilities, the study compared sterilization rates achieved under UV irradiation alone versus under the multi-mechanism synergy. Simulation results indicate that the synergistic approach achieves approximately 30% higher sterilization efficacy than the single-strategy method. Although the latter's sterilization capacity has been enhanced, from an economic perspective, the new system incorporates the precious metal material AuNPs and an external electric field, which moderately increases operational costs. Therefore, more economical and efficient sterilization methods remain worthy of continuous exploration and innovation. Based on the simulation results presented in this paper, we anticipate designing a future microfluidic therapeutic device. When infectious bodily fluids (such as blood or wound exudate) flow through the DEP electrode region, Janus AuNPs–PS will be injected and efficiently capture and kill pathogens under an applied electric field. The treated ‘clean’ fluid will then be reinfused or drained. Of course, for this device to be truly realized, future challenges should focus more on the biocompatibility of the particles and the economic viability of large-scale particle synthesis.Author contributions
Lingcong He: investigation, conceptualization, writing—original manuscript. Hongyang Xu/Yonghui Yang: literature organizing, categorizing, summarizing and framing. Xue-Bo Chen: methodology, conceptualization, guidance, writing—review and editing.Conflicts of interest
We declare that we have no known competing financial interests or personal relationships that have appeared to influence the work reported in this paper.Data availability
This study was completed using COMSOL Multiphysics 6.3. As the software is commercially licensed, we are unable to provide executable programs. Furthermore, this study does not include any software or code, nor does it generate or analyze new data.Acknowledgements
This work was supported by the National Natural Science Foundation of China, under grant number 71571091 and 71771112.References
- G. I. Scott, et al., Antibiotics as CECs: an overview of the hazards posed by antibiotics and antibiotic resistance, Front. Mar. Sci., 2016, 3, 24 CrossRef.
- S. Iwaguch, et al., Sterilization system using microwave and UV light, Colloids Surf., B, 2002, 25(4), 299–304 CrossRef CAS.
- A. Gharatape, et al., A novel strategy for low level laser-induced plasmonic photothermal therapy: the efficient bactericidal effect of biocompatible AuNPs@(PNIPAAM-co-PDMAEMA, PLGA and chitosan), RSC Adv., 2016, 6(112), 110499–110510 RSC.
- E. Park, R. Selvaraj and Y. Kim, High-efficiency photothermal sterilization on PDMS film with Au@CuS yolk-shell nanoparticles, J. Ind. Eng. Chem., 2022, 113, 522–529 CrossRef CAS.
- T. Ding, V. K. Valev and A. R. Salmon, et al., Light-induced actuating nanotransducers, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(20), 5503–5507 CrossRef CAS PubMed.
- M. Xuan, et al., Near Infrared Light-Powered Janus Mesoporous Silica Nanoparticle Motors, J. Am. Chem. Soc., 2016, 138(20), 6492–6497 CrossRef CAS PubMed.
- Z. Wu, et al., Superfast near-infrared light-driven polymer multilayer rockets, Small, 2016, 12(5), 577–582 CrossRef CAS PubMed.
- L. Hernandez-Adame, et al., Biological synthesis of monodisperse AuNPs@Damiana with enhanced antiseptic activity against gram-negative bacteria, J. Inorg. Organomet. Polym. Mater., 2021, 31(10), 4018–4024 CrossRef CAS.
- Y. Zhang and X. Chen, Dielectrophoretic microfluidic device for separation of red blood cells and platelets: a model-based study, J. Braz. Soc. Mech. Sci. Eng., 2020, 42(2), 89 CrossRef CAS.
- P. Yu Chiou, A. T. Ohta and M. C. Wu, Massively parallel manipulation of single cells and microparticles using optical images, Nature, 2005, 436(7049), 370–372 CrossRef CAS.
- F. Negr and A. Cavallini, Effect of dielectrophoretic forces on nanoparticles, IEEE Trans. Dielectr. Electr. Insul., 2017, 24(3), 1708–1717 Search PubMed.
- H. R. Jiang, N. Yoshinaga and M. Sano, Active motion of a Janus particle by self-thermophoresis in a defocused laser beam, Phys. Rev. Lett., 2010, 105(26), 268302 CrossRef PubMed.
- T. Maric, et al., Near‐infrared light‐driven mesoporous SiO2/Au nanomotors for eradication of Pseudomonas aeruginosa biofilm, Adv. Healthcare Mater., 2023, 12(13), 2203018 Search PubMed.
- Z. H. Wang, M. Chu, N. Yin, W. Huang, W. Liu, Z. Zhang, J. Liu and J. Shi, Biological chemotaxis-guided self-thermophoretic nanoplatform augments colorectal cancer therapy through autonomous mucus penetration, Sci. Adv., 2022, 8(26), eabn3917 Search PubMed.
- Z.-H. Wang, et al., Self-thermophoretic nanoparticles enhance intestinal mucus penetration and reduce pathogenic bacteria interception in colorectal cancer, Adv. Funct. Mater., 2023, 33(17), 2212013 Search PubMed.
- W. C. Huang, P. J. Tsai and Y. C. Chen, Multifunctional Fe3O4@Au nano-eggs as photothermal agents for selective killing of nosocomial and antibiotic-resistant bacteria, Small, 2010, 5(1), 51–56 CrossRef.
- H. Xu, et al., A three-dimensional microfluidic model based on dielectrophoresis for the separation of blood cells, Anal. Methods, 2025, 17(23), 4723–4733 RSC.
- Y. M. Ahmed, et al., Ray tracing for fluence rate simulations in ultraviolet photoreactors, Environ. Sci. Technol., 2018, 52(8), 4738–4745 CrossRef CAS PubMed.
- R. Pethig, Review article dielectrophoresis: Status of the theory, Biomicrofluidics, 2010, 4(2), 022811 CrossRef PubMed.
- D. A. Sozzi and F. Taghipour, UV reactor performance modeling by Eulerian and Lagrangian methods, Environ. Sci. Technol., 2006, 40(5), 1609–1615 Search PubMed.
- P. Kesharwani, R. Ma and L. Sang, et al., Gold nanoparticles and gold nanorods in the landscape of cancer therapy, Mol. Cancer, 2023, 22(1), 98 CrossRef CAS.
- A. Gharatape, S. Davaran and R. Salehi, et al., Engineered gold nanoparticles for photothermal cancer therapy and bacteria killing, RSC Adv., 2016, 6(112), 111482–111516 RSC.
- M. A. Dheyab, A. A. Aziz and P. Moradi Khaniabadi, et al., Monodisperse gold nanoparticles: A review on synthesis and their application in modern medicine, Int. J. Mol. Sci., 2022, 23(13), 7400 CrossRef CAS.
- J. K. Patra, G. Das and L. F. Fraceto, et al., Nano based drug delivery systems: recent developments and future prospects, J. Nanobiotechnol., 2018, 16(1), 71 CrossRef PubMed.
- S. M. Sreedharan and R. Singh, Ciprofloxacin functionalized biogenic gold nanoflowers as nanoantibiotics against pathogenic bacterial strains, Int. J. Nanomed., 2019, 9905–9916 CrossRef CAS.
- S. M. Vidya, S. Mutalik and K. U. Bhat, et al., Preparation of gold nanoparticles by novel bacterial exopolysaccharide for antibiotic delivery, Life Sci., 2016, 153, 171–179 CrossRef.
- Y. H. Tseng, C. W. Chu and T. Y. Chiu, et al., Rayleigh-instability-induced transformation for confined polystyrene-grafted gold nanoparticles in anodic aluminum oxide templates, J. Chin. Chem. Soc., 2021, 68(11), 2045–2053 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |