 Open Access Article
Open Access ArticleUnveiling the anodic potential of Janus MNS (M = Sc, Ti; N = Se, Te) monolayers for calcium-ion batteries: insights from DFT and AIMD studies
Sharah Sami
Rifah
,
Bivas Kumar
Dash
,
Afiya Akter
Piya
 and
Siraj Ud
Daula Shamim
and
Siraj Ud
Daula Shamim
 *
*
Department of Physics, Mawlana Bhashani Science and Technology University, Tangail-1902, Bangladesh. E-mail: sdshamim@mbstu.ac.bd
First published on 19th January 2026
Abstract
Rechargeable calcium-ion batteries offer a promising solution for energy storage due to calcium's natural abundance, high deposition potential, and superior energy density compared to magnesium-ion systems. Their divalent nature further enhances their appeal for next-generation battery technologies. In this study, we present a DFT analysis focusing on Janus transition metal dichalcogenides (TMDs) as potential anode materials for Ca ion batteries utilizing the GGA-PBE exchange–correlation functional. The research explores the structural, electronic, and adsorption characteristics of nanosheets such as ScSeS, ScTeS and TiSeS. All investigated TMDs show favorable Ca adsorption with negative adsorption energies that preserve structural integrity without notable distortion, thus confirming structural stability. Band structure analysis further reveals that ScSeS, ScTeS, and TiSeS display metallic behavior, as evidenced by conduction bands that cross the Fermi level. In addition, cohesive energy calculations provide values of −1.28, −2.17, and −2.06 eV per atom for ScSeS, ScTeS, and TiSeS, respectively, underscoring their energetic stability. Low diffusion barriers have been found for the three nanosheets. Furthermore, ScSeS and TiSeS nanosheets demonstrate high theoretical specific capacities of approximately 436.73 mAh g−1 and 428.84 mAh g−1, with low OCVs of 0.64 V and 0.23 V, respectively. These combined properties position ScSeS and TiSeS as promising anode materials for calcium-ion batteries.
1. Introduction
The desire for sustainable energy is on the rise due to the exhaustion of traditional fuel reserves and concerns about their impact on the environment. Rechargeable batteries perform a significant role in the current era, serving as efficient energy storage units that can incorporate renewable sources such as wind and solar power into electrical grids, thereby diminishing reliance on non-renewable energy sources. Lithium-ion batteries (LIBs) are distinguished among rechargeable ion batteries for their impressive performance, significant energy density, and longevity. However, mounting concerns have emerged regarding the safety hazards and limited resources associated with this battery technology. Rechargeable calcium-ion batteries (CIBs) show great potential as substitutes for traditional LIBs because of their desirable features, including a high theoretical capacity and the widespread availability of calcium for use as an anode. Additionally, calcium offers a low redox potential and exhibits divalent electron redox properties, further enhancing the appeal of these batteries as next-generation energy storage solutions.1 Exploring the practicality of CIBs, calcium ranks as the fifth most abundant component of the Earth's crust, surpassing both sodium and magnesium in abundance, and outstripping lithium by 2500 times.2 The ample supply of calcium implies minimal material expenses for battery manufacturing. Furthermore, calcium is non-hazardous, ensuring that its bulk utilization in battery production would not pose environmental risks.In recent days, increasing interest has emerged in utilizing nanostructured materials for electrode applications within energy storage technologies, particularly in next-generation alkali-ion batteries. These substances provide advantages such as fast charging/discharging, excellent longevity, and remarkably high energy storage capacity.3,4 Graphene is widely used as an anode material in rechargeable batteries with a specific capacity of 372 mAh g−1. Current research has highlighted 2D nanomaterials, including modified/defective graphene (762 mAh g−1),5 borophene (1240 mAh g−1),6 phosphorene (865 mAh g−1),7 transition metal carbides (263 mAh g−1),8etc., garnering attention as promising alternatives for anode materials. Transition metal dichalcogenides (TMDs) have attracted considerable attention as promising candidates for diverse energy storage applications.9,10,11,12,13 TMDs, symbolized as MX2 where M denotes a transition metal and X represents a chalcogen, are often compared to inorganic equivalents of graphite. Each TMD layer has a simple three-part structure: one M atom between two X atoms, forming an X–M–X sandwich. The layers are held together by weak van der Waals forces, which facilitate the insertion of ions.14,15,16,17
Many research endeavors have explored the production and analysis of TMDs for their potential as electrode substances in ion storage batteries. E. Yang et al. employed a first-principles approach to investigate the Na ion adsorption and movement characteristics, as well as the potential for phase alteration triggered by Na adsorption, on TiS2, VS2, CrS2, CoTe2, NiTe2, ZrS2, NbS2, and MoS2.18 For sodium-ion batteries (SIBs), Ti, Zr, Nb, and Mo-based materials are identified as suitable anode materials, with theoretical capacities ranging from 260 to 339 mAh g−1 and voltages of 0.49 to 0.95 V. Roman et al. employed first-principles calculations to demonstrate that ScS2 monolayers exhibit exceptional potential as cathodes for Li/Na/Ca-ion batteries, offering high theoretical capacities (982.76 mAh g−1 for Ca), low ion diffusion barriers (<0.3 eV), and metallic conductivity.19 Salavati et al. utilized DFT simulations to evaluate 1T-phase VS2 and VSe2 as anode materials for multivalent ion batteries. Their study revealed high Li, Ca, and Na ion storage capacities (466 and 257 mAh g−1, respectively) but unfavorable adsorption for Al and Mg ions, highlighting their potential for flexible energy storage.20 Zhao et al. used first-principles calculations to study Li+ storage in monolayer and bulk TiSe2.21 Bulk TiSe2, with an intercalation mechanism, has a theoretical capacity of 260 mAh g−1 (1.14–2.09 V). Monolayer TiSe2, using an adsorption mechanism, offers a higher capacity of 780 mAh g−1 (0.18–1.43 V) and low diffusion barriers, 163 m eV at high and 39 m eV at low Li+ concentration, showing great potential as a high-rate anode material for lithium-ion batteries. Previously, our team employed density functional theory (DFT) simulations to examine the structural, electronic, and adsorption properties of ScSeS and TiSeS nanosheets for Mg ion adsorption.22 The study revealed theoretical specific capacities of about 686.18 mAh g−1 for ScSeS and 546.63 mAh g−1 for TiSeS. The calculated average open circuit voltages are 0.43 V for ScSeS and 0.11 V for TiSeS, indicating their potential as promising anode materials.
In this research, we employed DFT calculations to investigate various properties of ScSeS, ScTeS and TiSeS nanosheets. These properties included structural and electronic characteristics, adsorption behavior, diffusion barriers, cycling stability, and electrochemical features such as specific capacity and open circuit voltage. The results demonstrated that the proposed structures maintain excellent structural integrity, contributing to their impressive cycling durability and high specific capacities. Specifically, the specific capacities were approximately 873.46 mAh g−1, 438.07 mAh g−1 and 668.20 mAh g−1, showcasing their strong performance. The average open circuit voltages for ScSeS, ScTeS and TiSeS were 0.33 V, 0.23 V, and 0.10 V, respectively. These findings suggest that the proposed nanosheets are promising candidates for anode materials in future calcium ion battery systems.
2. Computational details
All first-principles calculations were performed using the DMol3 module within the BIOVIA Materials Studio Simulation Package.23 We performed DFT calculations using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional to analyze the electronic structure and energetics.24 The GGA–PBE was chosen over the Local Density Approximation (LDA) for its improved accuracy in predicting lattice parameters and adsorption energies, especially important for layered and open-framework materials like TMD monolayers.25,26 LDA tends to exaggerate bonding strength, resulting in shorter-than-actual interatomic distances.27,28 Considering the significance of long-range van der Waals forces in layered structures and adsorption phenomena, Grimme's DFT-D2 dispersion correction was employed.29 This method was selected over the Tkatchenko–Scheffler (TS) scheme due to its compatibility with DMol3 and proven effectiveness in modeling 2D materials.30 We have employed all-electron double numerical plus polarization (DNP) basis sets for all atoms, which offer accuracy comparable to Gaussian-type basis sets and well-suited to DFT calculations in DMol3.31,32 Simulations used a 3 × 3 supercell of 27 atoms with a 20 Å vacuum space to eliminate interlayer interactions. Electrochemical properties, including open-circuit voltage (OCV) and specific capacity, were evaluated via standard thermodynamic equations. The work function was calculated by determining the energy gap separating the vacuum level from the Fermi level. Periodic boundary conditions and an orbital cutoff of 5.0 Å with a 4 × 4 × 1 k-point mesh were maintained to ensure numerical accuracy and stability.3. Results and discussion
3.1. Structural stability
A 3 × 3 supercell of ScSeS contains 27 atoms which exhibit a sandwich-like structure, consisting of 9 scandium (Sc) atomic layer inserted between one layer of 9 selenium (Se) and one layer of 9 sulfur (S) atoms (Fig. 1). The bond distances are also explicitly marked in Fig. 1. To evaluate the energetic stability of the nanosheets, cohesive energy calculations were performed using the following expression,33 | (1) |
In addition, to evaluate thermodynamic stability of ScSeS, ScTeS and TiSeS, ab initio molecular dynamics (AIMD) simulations were performed using the Nose–Hoover Thermostat (NVT) ensemble with a 1 fs time step at 300 K. Fig. 2 illustrates the fluctuations in potential energy over time at this temperature. The potential energy showed minimal variations, and while slight distortions were observed, no bond breakage occurred. These findings suggest that the structures exhibit strong thermodynamic stability.18,20,21 The band structures were plotted along high-symmetry paths in the Brillouin zone, specifically from Γ (Gamma) to F to M to Γ (Fig. 2). In the band structure, it is seen that the conduction band crosses the Fermi level for ScSeS, ScTeS and TiSeS, indicating that the nanosheets exhibit metallic characteristics. This indicates the absence of a band gap and the presence of free carriers, which is favorable for fast electronic conduction in battery electrodes.
 | ||
| Fig. 2 Variation in the potential energy as a function of time at 300 K and band structures of the (a) ScSeS, (b) ScTeS and (c) TiSeS. | ||
3.2 Single Ca atom adsorption on ScSeS, ScTeS, and TiSeS
Identifying the most stable adsorption site is crucial for examining the adsorption behavior of Ca on ScSeS, ScTeS and TiSeS nanosheets. To determine this, we have evaluated three potential adsorption locations, (a) top of the Sc/Ti denoted by S1, (b) top of the Se/Te denoted by S2 and (c) top of the S denoted by S3. At first, the adsorption energy was determined by positioning a single Ca atom on the nanosheets at three distinct sites to find the most favorable adsorption location. The analysis predicts that all adsorption sites will have negative adsorption energy, meaning an exothermic reaction occurs, leading to a favorable interaction between the Ca atom and the nanosheets. To quantify this, the adsorption energy per atom was calculated using the following equation,34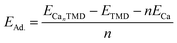 | (2) |
| Nanosheet | Adsorption site | E Ad. | d (Ca−TMD) | Q C a |
|---|---|---|---|---|
| ScSeS | S1 | −4.3 | 3.309 | 1.457 |
| S2 | −4.5 | 4.850 | 1.480 | |
| S3 | −3.5 | 4.608 | 1.431 | |
| ScTeS | S1 | −2.2 | 3.276 | 1.458 |
| S2 | −2.5 | 5.133 | 1.486 | |
| S3 | −0.4 | 5.258 | 1.308 | |
| TiSeS | S1 | −2.0 | 3.252 | 1.437 |
| S2 | −2.2 | 4.453 | 1.463 | |
| S3 | −1.6 | 4.452 | 1.444 |
 | ||
| Fig. 3 Top and side views of Ca adsorbed at the different adsorption sites on the ScSeS, ScTeS, and TiSeS nanosheets. | ||
3.3 Multiple Ca atom adsorption on ScSeS, ScTeS and TiSeS
The strongest interaction between the Ca atom and the nanosheet is indicated by the higher negative adsorption energies. For ScSeS, Ca atoms tend to favor adsorption on the S2 sites which are on the top of Se. After exploring various adsorption sites, different number of Ca atoms, including 2, 3, 4, 6, 10, 14, 18, 22 and 28, were adsorbed onto the ScSeS nanosheet (Fig. 4). The corresponding adsorption energies and the charge transfer from Ca to ScSeS, ScTeS and TiSeS are detailed in Table 2. Since Ca adsorption is closely linked to the efficiency of anode materials, which is crucial for evaluating the performance of Ca-ion battery anodes, multiple atoms were adsorbed for analysis. The ScSeS nanosheet structure remains stable and undistorted with up to 28 Ca atom adsorptions. However, when more than one Ca atom is added, the optimized positions reveal a slight tilt from their original placements. As the quantity of Ca atoms increases, there is a marked decrease in adsorption energy. The calculated adsorption energies are −3.46 eV, −2.51 eV, −2.26 eV, −1.80 eV, −1.36 eV, −1.08 eV, −0.80 eV, −0.49 eV and −0.37 eV for 2, 3, 4, 6, 10, 14, 18, 22 and 28 Ca atoms, respectively. Concurrently, both Hirshfeld and Mulliken charge transfer values decrease as the number of Ca atoms increases. The rising number of positively charged Ca ions leads to greater electrostatic repulsion. Specifically, Hirshfeld charges decrease from 0.550e to 0.053e, while Mulliken charges drop from 1.336e to 0.283e with the increased presence of Ca atoms. Notably, an unusual result was observed for the 14 Ca atom adsorption case. In the case of ScTeS, Ca atoms prefer to adsorb at the S2 site, positioned above Te. After examining multiple adsorption sites, various numbers of Ca atoms, such as 2, 3, 4, 6, 10, 14, and 18, were adsorbed onto the ScTeS nanosheet, as illustrated in Fig. 4. Since Ca adsorption is linked to the efficiency of anode materials, which is important for evaluating the performance of Ca-ion battery anodes, we placed several Ca atoms on the surface. Up to the adsorption of 18 Ca atoms, the structure of the ScTeS nanosheet remained unchanged. However, when more than one Ca atom was placed on the surface, the atoms slightly shifted from their original positions after optimization. As the number of adsorbed Ca atoms increased, the adsorption energy dropped noticeably. The calculated adsorption energies were −1.50 eV, −0.96 eV, −0.91 eV, −0.73 eV, −0.49 eV, −0.22 eV, and −0.15 eV for 2, 3, 4, 6, 10, 14, and 18 atoms, respectively. This downward trend in adsorption energy aligns with previous findings in similar studies. A similar pattern was observed in charge transfer values. According to Hirshfeld analysis, the values gradually decreased from 0.471e to 0.068e, and in Mulliken analysis, from 1.205e to 0.330e as more Ca atoms were added. This reduction is due to the increasing repulsive forces among Ca ions, as they all carry a positive charge. | ||
| Fig. 4 Front and side views of optimized ScSeS, ScTeS and TiSeS structures adsorbed with diverse numbers of Ca atoms: (a) 2 Ca atoms, (b) 6 Ca atoms, (c) 14 Ca atoms, and (d) 18 Ca atoms. | ||
| Nanosheet | Number of atoms (Ca) | E Ad. | Hirshfeld charge | Mulliken charge | Work function (φ) | %Δφ |
|---|---|---|---|---|---|---|
| ScSeS | 2 | −3.46 | 0.550 | 1.336 | 4.87 | −29.73 |
| 3 | −2.51 | 0.386 | 1.100 | 4.68 | −32.47 | |
| 4 | −2.26 | 0.304 | 0.953 | 4.55 | −34.22 | |
| 6 | −1.80 | 0.209 | 0.739 | 4.50 | −34.94 | |
| 10 | −1.36 | 0.157 | 0.533 | 3.95 | −42.89 | |
| 14 | −1.08 | 0.125 | 0.558 | 3.49 | −49.63 | |
| 18 | −0.80 | 0.084 | 0.405 | 3.81 | −45.04 | |
| 22 | −0.49 | 0.063 | 0.340 | 3.49 | −49.63 | |
| 28 | −0.37 | 0.053 | 0.283 | 3.70 | −46.60 | |
| ScTeS | 2 | −1.50 | 0.471 | 1.205 | 4.02 | −31.55 |
| 3 | −0.96 | 0.300 | 0.931 | 4.17 | −28.85 | |
| 4 | −0.91 | 0.252 | 0.841 | 4.01 | −31.62 | |
| 6 | −0.73 | 0.169 | 0.658 | 3.97 | −32.38 | |
| 10 | −0.49 | 0.135 | 0.517 | 3.61 | −38.40 | |
| 14 | −0.22 | 0.105 | 0.468 | 3.55 | −39.50 | |
| 18 | −0.15 | 0.068 | 0.330 | 3.86 | −34.12 | |
| TiSeS | 2 | −1.43 | 0.468 | 1.270 | 4.29 | −27.56 |
| 3 | −0.93 | 0.302 | 1.005 | 4.30 | −27.55 | |
| 4 | −0.84 | 0.249 | 0.912 | 4.16 | −29.77 | |
| 6 | −0.69 | 0.169 | 0.709 | 4.15 | −29.93 | |
| 10 | −0.58 | 0.137 | 0.585 | 3.84 | −35.26 | |
| 14 | −0.41 | 0.121 | 0.582 | 3.44 | −41.97 | |
| 18 | −0.29 | 0.082 | 0.445 | 3.80 | −35.93 | |
| 22 | −0.08 | 0.066 | 0.381 | 3.36 | −43.30 |
For TiSeS, Ca atoms preferentially adsorb at the S2 site (above Se). The nanosheet remains structurally stable with up to 22 Ca atoms, though slight tilting occurs beyond single adsorption. Adsorption energies progressively decrease from −1.43 eV (2 Ca) to −0.08 eV (22 Ca), indicating weaker binding with increasing Ca concentration (Fig. 4). This reduction in adsorption energy aligns with findings from previous research in the same field. Similarly, charge transfer values also decline; for Hirshfeld charges, they decrease steadily from 0.468e to 0.066e, while Mulliken charges decrease from 1.270e to 0.381e with the increasing number of Ca atoms.
The charge density difference (CDD) maps, illustrated in Fig. 5, show how charge redistributes when Ca atoms are adsorbed. In the maps, the red region represents electron depletion around the Ca atoms, while blue regions indicate electron accumulation. This clearly shows that electrons are transferred from Ca to the substrate, creating strong electrostatic attraction and ensuring stable adsorption. The distinct charge separation reflects the ionic nature of the bonding, and the noticeable charge buildup around Ca suggests efficient electron donation, which can promote smoother Ca-ion diffusion and improve the overall electrochemical performance of the materials.
 | ||
| Fig. 5 Charge density difference maps illustrating the charge transfer upon Ca adsorption on the most stable sites of (a) ScSeS, (b) ScTeS, and (c) TiSeS. | ||
Additionally, the increase in positively charged Ca ions leads to greater electrostatic repulsion among them. The DOS and the projected DOS (PDOS) for these configurations were analyzed (Fig. 6). The total DOS profiles for ScSeS, ScTeS, and TiSeS all exhibit non-zero values at the Fermi level, indicating their metallic nature. Such electronic characteristics suggest favorable electrical conductivity. Fig. 6 provides a detailed view of the PDOS profiles for ScSeS, denoted by (a–e) for ScTeS, denoted by (f–j) for TiSeS, and denoted by (k–o) after the adsorption of varying amounts of Ca atoms. The PDOS spectra in the figure clearly show that the addition of Ca atoms onto the nanosheets results in significant peaks appearing near the Fermi energy, indicating an increase in electronic activity at these energy levels. As more Ca atoms are adsorbed, the overall density of states near the Fermi level grows, further emphasizing the enhanced electronic interactions. This behavior suggests that, during the charging process, Ca atoms donate electrons to the nanosheets, becoming Ca cations in the process. This electron transfer from Ca to the nanosheets plays a critical role in the material's capacity for charge storage, further contributing to its potential application in energy storage devices, such as Ca-ion batteries. The increased DOS near the Fermi level also indicates an improved capacity for electron mobility, enhancing the overall conductivity of the material as more Ca atoms are adsorbed.
 | ||
| Fig. 6 PDOS of diverse numbers of Ca atoms adsorbed on ScSeS (a–e), ScTeS (f–j) and TiSeS (k–o); here the dashed line represents the point where the Fermi level is defined as zero. | ||
3.4 Diffusion barrier
To evaluate the effectiveness of the nanosheets as anode materials, it is essential to investigate both the diffusion pathways and energy barriers. For optimal performance, a nanosheet with a low diffusion barrier for Ca ions is required to ensure rapid charging. Since the functionality of a battery is critically dependent on its charging speed, the calculation of diffusion barriers plays a significant role in identifying promising candidates for anode materials. Variations in diffusion barriers can greatly influence the mobility of metals within a material. The diffusion coefficient is known to change exponentially with the diffusion barrier, following an Arrhenius-type equation at a constant temperature,35| D = Doe−Ea/KT | (3) |
 | ||
| Fig. 7 Computed energy barriers for various paths of Ca diffusion on (a–c) ScSeS, (d–f) TiSeS, and (g–i) ScTeS. | ||
For ScSeS, ScTeS, and TiSeS, we conducted calculations to identify multiple possible diffusion pathways by shifting the Ca atom between adjacent adsorption sites. In the case of ScSeS, the lowest energy barriers were estimated to be approximately 0.43 eV, 0.39 eV, 0.54 eV, and 0.35 eV when Ca migrated from Sc to S, S to Sc, Se to Sc, and Sc to Se, respectively, as illustrated in Fig. 7(a and b). Additionally, the Se to Se diffusion pathway exhibited a higher barrier of 1.55 eV, as presented in Fig. 7(c). Similarly, for ScTeS, the energy barriers were calculated to be 0.30 eV, 0.30 eV, 0.33 eV, and 0.56 eV as Ca moved from S to Sc, Sc to S, Sc to Te, and Te to Sc, respectively, while the Te to Te diffusion pathway showed a comparatively higher barrier of 1.45 eV, as shown in Fig. 7(d–f). For TiSeS, the energy barriers were determined to be 0.57 eV, 0.37 eV, 0.43 eV, and 0.48 eV as Ca migrated from Se to Ti, Ti to Se, Ti to S, and S to Ti, respectively, and the Se to Se pathway presented a barrier of 1.46 eV, as depicted in Fig. 7(g–i). These results indicate that all three nanosheets have a lower diffusion energy barrier, suggesting better ion mobility. These results indicate that ScTeS has a lower diffusion energy barrier compared to ScSeS and TiSeS, suggesting better ion mobility in ScTeS. ScSeS exhibits moderate ion mobility due to its relatively low diffusion barrier, ranking second lowest among the studied materials. Additionally, in contrast to previous studies on ScS2, the diffusion barriers for Li, Na, and Ca were found to be 0.67 eV, 0.56 eV, and 1.70 eV in the linear direction, and 0.34 eV, 0.25 eV, and 0.67 eV in the zigzag direction, respectively.19 This comparison highlights the lower diffusion barriers in ScTeS, making it a more efficient material for ion transport. Moreover, the energy barriers we calculated for ScSeS, ScTeS and TiSeS are similar to those of Li ions on pristine graphene, which has an energy barrier of 0.311 eV.36
3.5 Work function
The work function is a critical parameter for understanding the field emission properties of a material. It represents the minimum energy required to extract an electron from the Fermi level and move it into a vacuum. A lower work function generally indicates better electron emission efficiency, making it highly relevant for applications like anode materials in electronic devices. In this study, the work function is calculated as follows,37 | (4) |
The work functions of our bulk ScSeS, ScTeS and TiSeS nanosheets were determined to be 6.92 eV, 5.93 eV and 5.86 eV, respectively. Interestingly, for ScSeS, the work function showed a significant reduction, dropping by 29.73% with the adsorption of 2 Ca atoms and by 46.60% when 28 Ca atoms were adsorbed. A similar trend was observed for ScTeS, where the work function decreased by 31.55% for 2 Ca atoms and by 34.12% for 18 Ca atoms, and also for TiSeS, where the work function decreased by 27.56% for 2 Ca atoms and by 43.30% for 22 Ca atoms. The data presented in Table 2 clearly demonstrate a decline in work function as the concentration of Ca increases on the nanosheet surfaces. This notable reduction strongly indicates enhanced electron transfer during the adsorption of Ca atoms, which could improve the material's electronic properties, making it a promising candidate for energy storage and related applications.
3.6 Electrochemical properties
In the realm of ion storage batteries, understanding the performance of anode materials hinges on two main parameters: specific capacity and open circuit voltage. Specific capacity reflects the quantity of ions that can be accommodated per unit mass of the anode material. It is calculated using the formula,33 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 Coulombs per mole, while z represents the quantity of ions taking part in the electrochemical process. This formula helps quantify the anode's ability to store charge, providing insight into its efficiency and potential energy capacity. High specific capacity indicates greater potential for ion storage, which translates to improved battery performance and energy density.
485 Coulombs per mole, while z represents the quantity of ions taking part in the electrochemical process. This formula helps quantify the anode's ability to store charge, providing insight into its efficiency and potential energy capacity. High specific capacity indicates greater potential for ion storage, which translates to improved battery performance and energy density.
The specific capacity of an ion-based battery increases with the number of Ca ions stored in the anode material during charging, which enhances the amount of electricity the battery can deliver during discharge. To explore this, we systematically increased the Ca atom concentration on the TMD nanosheets, adding varying amounts from 2 to 28 Ca atoms, and monitored the structural integrity of the nanosheets. We discovered that ScSeS can accommodate up to 14 Ca atoms, while ScTeS can incorporate up to 10 Ca atoms and TiSeS can hold up to 14 Ca atoms. The resulting specific capacities are approximately 436.73 mAh g−1 for ScSeS with 14 Ca atoms, 291.54 mAh g−1 for ScTeS with 10 Ca atoms and 428.84 mAh g−1 for TiSeS with 14 Ca atoms. The 2D ScS2 monolayer exhibits a high theoretical specific capacity of 491.36 mAh g−1 for alkali ions (Li, Na, K) and 324.29 mAh g−1 for Mg and Al ions.38 These results indicate that the ScSeS, ScTeS and TiSeS nanosheets investigated in this study offer competitive specific capacities compared to other 2D materials. In case of graphite, the conventional anode for lithium-ion batteries offers a specific capacity of 372 mAh g−1.39 These values reflect the enhanced energy storage capabilities of the studied anode materials, with ScSeS standing out due to its highest specific capacity of 436.73 mAh g−1. This superior capacity indicates greater potential for storing and releasing charge, making ScSeS a particularly promising candidate for high-performance CIBs.
A critical aspect of ion storage battery performance is the average open circuit voltage (OCV), which is derived from the energy changes occurring before and after modifications. In the case of TMD materials used as anodes, this process is represented by:40
| Cax1TMD + (x2 − x1)Ca2+ + (x2 − x1)e− ↔ Cax2TMD |
To calculate the average OCV for CaxTMD within the concentration range x1 < x < x2, the following formula is used:
 | (6) |
 and
and  denote the total energies of the TMD materials containing x1 and x2 Ca atoms, respectively. This approach allows for the estimation of the average OCV based on the changes in energy as Ca ions are added or removed from the anode material.
denote the total energies of the TMD materials containing x1 and x2 Ca atoms, respectively. This approach allows for the estimation of the average OCV based on the changes in energy as Ca ions are added or removed from the anode material.
The calculated OCV is shown in Fig. 8, where it gradually decreases with increasing Ca content. The OCV values for the ScSeS nanosheets are 1.69 V, 0.54 V, 0.44 V, 0.34 V, 0.19 V, −0.08 V, −0.45 V and −0.04 when 2, 4, 6, 10, 14, 18, 22 and 28 Ca atoms are incorporated, respectively. In contrast, for ScTeS nanosheets, the OCV values are 1.28 V, 0.16 V, 0.19 V, 0.06 V, −0.22 V and −0.06 V with 2, 4, 6, 10, 14 and 18 Ca atoms, respectively. Also, for TiSeS nanosheets, the OCV values are 0.66 V, 0.13 V, 0.19 V, 0.001 V, −0.05 V and −0.45 V with 2, 4, 10, 14, 18 and 22 Ca atoms, respectively. The average OCV was calculated up to the positive potential for ScSeS, ScTeS, and TiSeS, yielding values of 0.64 V, 0.42 V, and 0.23 V for 14 Ca, 10 Ca, and 14 Ca atoms, respectively. In contrast, using ScS2 as an intercalation host yields higher average electrode potentials of 3.61 V for Li, 2.68 V for Na, and 1.93 V for Ca.19
 | ||
| Fig. 8 Average OCV of (a) ScSeS, (b) ScTeS and (c) TiSeS nanosheets adsorbed with diverse numbers of Ca atoms. | ||
When we start adsorbing more atoms on both of our nanosheets, the average OCV turns negative. A negative OCV in the context of battery materials generally indicates that the electrochemical reaction is not favorable under the given conditions. It also indicates instability in the battery material and reflects poor performance for energy storage, as the material may not support further ion insertion or might lead to inefficiencies during charging and discharging cycles. Therefore, we conclude the calculation of specific capacity at 14 Ca ions for ScSeS, 10 Ca ions for ScTeS and 14 Ca ions for TiSeS. The analysis indicates a trend where high specific capacities are associated with lower OCV values. This observation aligns with findings from prior research, which suggests that a lower OCV can be beneficial for enhancing battery performance. These results imply that the ScSeS, ScTeS and TiSeS nanosheets, with their high specific capacities and relatively low OCV, could serve as highly effective anode materials in calcium-ion batteries. This conclusion underscores the potential of these nanosheets to improve the efficiency and energy density of such batteries, potentially leading to better performance and longer-lasting energy storage solutions.
4. Conclusions
In this study, we conduct a theoretical investigation of calcium-ion batteries using ScSeS, ScTeS and TiSeS as anode materials, leveraging DFT calculations. Our analysis focuses on evaluating key parameters such as specific capacity, OCV, and the stability of the nanosheets. For both ScSeS and TiSeS, the most favorable adsorption site for Ca ions is identified as the top of the Se atom and for ScTeS, the most favorable adsorption site is the top of the Te atom. After determining this optimal site, we systematically increase the number of adsorbed Ca atoms to 2, 6, 10, 14, 18, 22 and 28. The decrease in both Hirshfeld and Mulliken charge values with the increasing number of Ca atoms indicates the occurrence of charge transfer. In the case of ScSeS, the nanosheet accommodates up to 14 Ca ions. Beyond this point, further adsorption results in a negative OCV, indicating that charge transfer is no longer favorable. A similar observation is made for ScTeS, which can adsorb up to 18 Ca atoms without significant distortion. When more than 18 Ca atoms are adsorbed, the adsorption energy becomes positive, indicating that no additional Ca atoms can be adsorbed. The OCV remains positive up to 10 Ca atoms, after which it turns negative. Furthermore, TiSeS stably adsorbs up to 22 Ca ions without structural deformation. When the OCV becomes negative beyond 14 Ca atoms, further ion insertion is no longer thermodynamically favorable and electrochemical transfer stops, marking the adsorption limit of the material. The band structure and DOS analysis reveal that the nanosheets possess metallic characteristics. When Ca atoms are progressively introduced into the nanosheets, there is a noticeable increase in the density of states, particularly evident at the Fermi level. This rise in the density of states signifies enhanced electron availability, reinforcing the conductive properties of the nanosheets as more Ca is incorporated. We also focus on the work function, which simultaneously decreases with the increase of Ca ions, providing strong evidence of electron transfer. Our calculations reveal theoretical specific capacities of approximately 436.73 mAh g−1 for ScSeS with 14 adsorbed Ca atoms, 291.54 mAh g−1 for ScTeS with 10 Ca atoms and 428.84 mAh g−1 for TiSeS with 14 Ca atoms. Additionally, they exhibit very low OCV, with values of 0.64 V for ScSeS, 0.42 V for ScTeS and 0.23 V for TiSeS. Based on the comprehensive evaluation of the electrical and electrochemical properties, the three examined nanosheets demonstrate potential as promising anode materials. However, when comparing the three, ScSeS emerges as the more favorable option due to its higher specific capacity and lower diffusion barrier, making it a superior candidate for anode applications.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting the findings of this study, including optimized structures, adsorption energy values, charge transfer, work function, etc., are available within the article. All the calculations have been implemented by the DMol3 module. Additional data can be provided by the corresponding author upon reasonable request.Acknowledgements
We gratefully acknowledge the Bangladesh Research and Education Network (BdREN) for providing computational access.References
- L. Yan, W. Yang, H. Yu, L. Zhang and J. Shu, Recent progress in rechargeable calcium-ion batteries for high-efficiency energy storage, Energy Storage Mater., 2023, 60, 102822, DOI:10.1016/J.ENSM.2023.102822
.
- R. J. Gummow, G. Vamvounis, M. B. Kannan and Y. He, Calcium-Ion Batteries: Current State-of-the-Art and Future Perspectives, Adv. Mater., 2018, 30(39), 1–14, DOI:10.1002/adma.201801702
.
- H. Zhou, D. Li, M. Hibino and I. Honma, A Self-Ordered, Crystalline-Glass, Mesoporous Nanocomposite for Use as a Lithium-Based Storage Device with Both High Power and High Energy Densities, Angew. Chem., 2005, 117(5), 807–812, DOI:10.1002/ange.200460937
.
-
A. S. Aricò, P. Bruce, B. Scrosati, J.-M. Tarascon and W. Van Schalkwijk, “WSPC-MATERIALS FOR SUSTAINABLE ENERGY-Reprint Volume Book-Trim Size:-11in x 8.5”, in Nanostructured Materials for Advanced Energy Conversion and Storage Devices, 2010 Search PubMed
.
- C. Ling and F. Mizuno, Boron-doped graphene as a promising anode for Na-ion batteries, Phys. Chem. Chem. Phys., 2014, 16(22), 10419–10424, 10.1039/c4cp01045k
.
- T. Huang, B. Tian, J. Guo, H. Shu, Y. Wang and J. Dai, Semiconducting borophene as a promising anode material for Li-ion and Na-ion batteries, Mater. Sci. Semicond. Process., 2019, 89, 250–255 Search PubMed
.
- V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phosphorene as an anode material for Na-ion batteries: A first-principles study, Phys. Chem. Chem. Phys., 2015, 17(21), 13921–13928, 10.1039/c5cp01502b
.
- J. Rivnay, A. Salleo, N. Stingelin and C. Silva, Multi-phase semicrystalline microstructures drive exciton dissociation in neat plastic semiconductors, J. Mater. Chem. C, 2015, 3, 10715–10722, 10.1039/b000000x
.
- X. Yu, M. S. Prévot, N. Guijarro and K. Sivula, Self-assembled 2D WSe2 thin films for photoelectrochemical hydrogen production, Nat. Commun., 2015, 6(1), 7596 Search PubMed
.
- B. Chen, D. Chao, E. Liu, M. Jaroniec, N. Zhao and S. Z. Qiao, Transition metal dichalcogenides for alkali metal ion batteries: Engineering strategies at the atomic level,
Energy Environ. Sci.
, 2020, 1096–1131 Search PubMed
.
- W. Wu,
et al., Piezoelectricity of single-atomic-layer MoS2 for energy conversion and piezotronics, Nature, 2014, 514(7253), 470–474, DOI:10.1038/nature13792
.
- H. Yuan, L. Kong, T. Li and Q. Zhang, A review of transition metal chalcogenide/graphene nanocomposites for energy storage and conversion, Chin. Chem. Lett., 2017, 28(12), 2180–2194, DOI:10.1016/j.cclet.2017.11.038
.
- D. Voiry, J. Yang and M. Chhowalla, Recent Strategies for Improving the Catalytic Activity of 2D TMD Nanosheets Toward the Hydrogen Evolution Reaction, Adv. Mater., 2016, 28(29), 6197–6206, DOI:10.1002/adma.201505597
.
- M. Chhowalla, H. S. Shin, G. Eda, L. J. Li, K. P. Loh and H. Zhang, The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets, Nat. Chem., 2013, 5(4), 263–275 CrossRef PubMed
.
- W. Choi, N. Choudhary, G. H. Han, J. Park, D. Akinwande and Y. H. Lee, Recent development of two-dimensional transition metal dichalcogenides and their applications, Mater. Today, 2017, 20(3), 116–130 Search PubMed
.
- J. Xu, J. Zhang, W. Zhang and C. S. Lee, Interlayer nanoarchitectonics of two-dimensional transition-metal dichalcogenides nanosheets for energy storage and conversion applications, Adv. Energy Mater., 2017, 7(23), 1700571 Search PubMed
.
- X. Huang, Z. Zeng and H. Zhang, Metal dichalcogenide nanosheets: Preparation, properties and applications, Chem. Soc. Rev., 2013, 42(5), 1934–1946, 10.1039/c2cs35387c
.
- E. Yang, H. Ji and Y. Jung, Two-Dimensional Transition Metal Dichalcogenide Monolayers as Promising Sodium Ion Battery Anodes, J. Phys. Chem. C, 2015, 119(47), 26374–26380, DOI:10.1021/ACS.JPCC.5B09935/SUPPL_FILE/JP5B09935_SI_001
.
- A. Al Roman, M. M. Rahman, K. Hossain, S. Das and F. Ahmed, Development of high-performance ScS2 monolayer as cathode material: A DFT analysis, Solid State Commun., 2022, 352, 114828, DOI:10.1016/j.ssc.2022.114828
.
- M. Salavati and T. Rabczuk, Application of highly stretchable and conductive two-dimensional 1T VS2 and VSe2 as anode materials for Li-, Na- and Ca-ion storage, Comput. Mater. Sci., 2019, 160, 360–367, DOI:10.1016/J.COMMATSCI.2019.01.018
.
- C. Zhao,
et al., Revealing the distinct electrochemical properties of TiSe2 monolayer and bulk counterpart in Li-ion batteries by first-principles calculations, Appl. Surf. Sci., 2021, 540, 148314, DOI:10.1016/J.APSUSC.2020.148314
.
- S. S. Rifah, M. S. Zaman, A. A. Piya and S. U. D. Shamim, Exploring the anodic performance of ScSeS and TiSeS monolayers of modified transition metal dichalcogenides for Mg ion batteries via DFT calculations, Phys. Chem. Chem. Phys., 2024, 26(8), 6667–6677 RSC
.
- O. Obaidullah, U. Habiba, A. A. Piya and S. U. Daula Shamim, Exploring the performance of T-graphene for the anode of Mg-ion and Ca-ion batteries: A first-principles study, AIP Adv., 2023, 13(11), 115031 Search PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865
.
- H. Peng, Z.-H. Yang, J. P. Perdew and J. Sun, Versatile van der Waals Density Functional Based on a Meta-Generalized Gradient Approximation, Phys. Rev. X, 2016, 6(4), 41005, DOI:10.1103/PhysRevX.6.041005
.
- S. Lebègue and O. Eriksson, Electronic structure of two-dimensional crystals from ab initio theory, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 79(11), 115409, DOI:10.1103/PhysRevB.79.115409
.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B, 1981, 23(10), 5048–5079, DOI:10.1103/PhysRevB.23.5048
.
- K. Lejaeghere,
et al., Reproducibility in density functional theory calculations of solids, Science, 2016, 351(6280), aad3000 Search PubMed
.
- V. A. Basiuk and L. V. Henao-Holguín, Dispersion-corrected density functional theory calculations of meso-tetraphenylporphine-C60 complex by using DMol3 module, J. Comput. Theor. Nanosci., 2014, 11(7), 1609–1615 Search PubMed
.
- I. V Lebedeva, A. V Lebedev, A. M. Popov and A. A. Knizhnik, Comparison of performance of van der Waals-corrected exchange-correlation functionals for interlayer interaction in graphene and hexagonal boron nitride, Comput. Mater. Sci., 2017, 128, 45–58, DOI:10.1016/j.commatsci.2016.11.011
.
- B. Delley, Hardness conserving semilocal pseudopotentials, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 66(15), 1–9, DOI:10.1103/PhysRevB.66.155125
.
- Y. Inada and H. Orita, Efficiency of numerical basis sets for predicting the binding energies of hydrogen bonded complexes: Evidence of small basis set superposition error compared to Gaussian basis sets, J. Comput. Chem., 2008, 29(2), 225–232, DOI:10.1002/JCC.20782
.
- T. Ahmed, A. A. Piya and S. U. D. Shamim, Recent advances in Zr and Hf-based MXenes and their hetero-structure as novel anode materials for Ca-ion batteries: theoretical insights from DFT approach, Nanoscale Adv., 2024, 6, 3441–3449 Search PubMed
.
- X. Wang, Z. Zeng, H. Ahn and G. Wang, First-principles study on the enhancement of lithium storage capacity in boron doped graphene, Appl. Phys. Lett., 2009, 95(18), 183103, DOI:10.1063/1.3259650/131974
.
- S. U. D. Shamim, A. A. Piya, M. S. Rahman, S. M. Hasan, M. K. Hossain and F. Ahmed, Tuning the electrochemical behavior of graphene oxide and reduced graphene oxide via doping hexagonal BN for high capacity negative electrodes for Li and Na ion batteries, Phys. Chem. Chem. Phys., 2023, 25(5), 4047–4061 Search PubMed
.
- X. Fan, W. T. Zheng and J. L. Kuo, Adsorption and diffusion of Li on pristine and defective graphene, ACS Appl. Mater. Interfaces, 2012, 4(5), 2432–2438, DOI:10.1021/AM3000962/ASSET/IMAGES/MEDIUM/AM-2012-000962_0009
.
- S. Reza Khoshnobish, T. Ahmed, T. Arefin, A. Akter Piya and S. Ud Daula Shamim, Assessing the sensing performance of Janus transition metal dichalcogenides (ScSSe, TiSSe and ZrSSe) for oxygen-containing toxic gas molecules such as CO, NO, NO2 and SO2, Appl. Surf. Sci., 2025, 679, 161301, DOI:10.1016/j.apsusc.2024.161301
.
- D. Chakraborty, M. Pandey and P. Johari, ScS2 Monolayer as a Potential Cathode Material for Alkali-ion Batteries and Beyond, arXiv, 2022, preprint, arXiv:2201.02268, DOI:10.48550/arXiv.2201.02268..
- J. Xu,
et al., Recent Progress in Graphite Intercalation Compounds for Rechargeable Metal (Li, Na, K, Al)-Ion Batteries, Adv. Sci., 2017, 4(10), 1700146, DOI:10.1002/ADVS.201700146
.
- Y. Zhang, Z. F. Wu, P. F. Gao, S. L. Zhang and Y. H. Wen, Could Borophene Be Used as a Promising Anode Material for High-Performance Lithium Ion Battery?, ACS Appl. Mater. Interfaces, 2016, 8(34), 22175–22181, DOI:10.1021/acsami.6b05747
.
| This journal is © The Royal Society of Chemistry 2026 |

