Open Access Article
Open Access ArticleNanometer-scale confinement of whispering gallery plasmonic modes upon slit excitation
Henrik
Parsamyan
 *,
Roza
Gabrielyan
*,
Roza
Gabrielyan
 ,
Gurgen
Arabajyan
,
Hovhannes
Haroyan
,
Gurgen
Arabajyan
,
Hovhannes
Haroyan
 and
Khachatur
Nerkararyan
and
Khachatur
Nerkararyan

Institute of Physics, Yerevan State University, A. Manoogian 1, Yerevan, 0025, Armenia. E-mail: hparsamyan@ysu.am
First published on 19th January 2026
Abstract
Squeezing optical fields into resonant modes with deep-subwavelength volumes is crucial for advancing quantum optics and nanoscale sensing. A promising approach is to harness surface plasmon modes in resonators composed of stacked metal–insulator–metal cylindrical layers, where optical fields in the visible and infrared ranges are transformed into strongly confined gap modes. In a structure with cylindrical symmetry, whispering gallery modes form a family of eigenmodes with a high azimuthal order, which are typically inaccessible in plasmonic sandwich configurations under plane wave illumination, and their excitation usually requires carefully positioned focused electron probes. Here, we propose an efficient method for exciting whispering gallery modes in gap-surface plasmon resonators using plane wave excitation. The introduction of a nanoscale through-split in the top metal layer enables the formation of a rich set of WGMs in the near-infrared spectrum, resulting in 2–3 orders of magnitude enhancement in total electromagnetic energy accumulated in the spacer. This strategy offers a practical pathway to unveil hidden modal families in plasmonic sandwich resonators to control light–matter interactions at the nanoscale and to drive the further miniaturization of plasmonic devices.
Introduction
Optical nanocavities, devices that are capable of spatially confining and enhancing electromagnetic waves at certain frequencies in small-volume cavity modes, can be perceived as key components in modern photonic systems. The effective concentration and accumulation of electromagnetic energy at optical frequencies in deep-subwavelength volumes play an important role in tailoring the properties of light–matter interactions.1 A widely used optical cavity design incorporates high-index dielectric structures supporting Mie resonances, enabling the efficient confinement of wave fields and minimal losses2 in resonators with sizes comparable to the incident wavelength. An alternative strategy to spatially shrink the optical fields in subwavelength volumes is exploiting hybrid resonators incorporating metal–dielectric layers.3,4 In these systems, electromagnetic fields emerge as surface plasmon waves at metallic interfaces because of the collective oscillations of free electrons in metals,5 providing much smaller confinement volumes of optical fields in contrast to conventional Mie resonators.6,7 Among hybrid plasmonic structures, the so-called gap-surface plasmon (GSP) resonators, comprising a thin dielectric sandwiched by metallic layers, enable extreme light confinement and enhancement within the dielectric spacer.8 This is linked to the presence of hybridized states owing to the coupling of surface plasmons at opposite metal–dielectric interfaces of the spacer, resulting in a series of gap-confined lateral modes.9–11 Due to the rich manifold of possible modes supported by metal–insulator–metal sandwich configurations, GSP resonators have been proposed as efficient platforms for investigations of various phenomena, including the realization of directional scattering,12 optical magnetic modes11,13 and anapole states,9 luminescence enhancement14 and surface-enhanced sensing,15,16 second-harmonic generation,17 nanolasers18 and spontaneous emission control.19,20 Recently, increasing attention has been devoted to GSP resonators with the aim of broadening the range of accessible modes and engineering higher-order resonances, particularly through the excitation of whispering-gallery modes (WGMs) in GSP disk configurations. These resonant modes, concentrated inside the dielectric spacer of MIM structures and having more than two extremums along the perimeter of the disk, are formed by the multiple total internal reflections of the gap plasmons from the curved boundary of the resonator and in-phase interference after each round-trip. Various studies have been devoted to MIM disk-shaped WGM resonators, with different material compositions incorporating silver or gold as the metallic layers and semiconductors and insulators as the spacer.21,22 Compared with their dipolar counterparts (with an azimuthal mode number of 1), higher azimuthal order whispering-gallery modes can provide tighter confinement and stronger electromagnetic energy localization within the spacer.19,21 Specifically, for given resonator dimensions, higher order modes possess a larger effective mode index, which enhances the spatial confinement and reduces the radiation losses owing to the increased contrast between the mode index and the surrounding.23 Conversely, dipolar modes exhibit a strong net electric dipole moment, allowing efficient coupling with the external excitation field.24 However, this results in higher radiation losses, and consequently lower quality factors compared to higher-order modes.Although whispering gallery modes are characteristic eigenmodes in GSP resonators with cylindrical symmetry, similar to disk-shaped resonators, it is challenging to couple the far-field excitation, for instance, normally incident plane or Gaussian waves, with high azimuthal-order modes due to the symmetry mismatch and lack of a wavevector component in the azimuthal direction.25 In theoretical studies based on numerical techniques, this issue is bypassed by using a point dipole with an appropriate dipole moment orientation; placed inside or in the vicinity of the resonator.21,22 This is realized by the Purcell effect, where efficient coupling of an emitter to a specific cavity mode is achieved by spatially overlapping the former with the local intensity maximum and alignment of the emitter dipole moment with the mode electric field direction.26 However, in practice, spectroscopic methods, such as cathodoluminescence and electron energy loss spectroscopy in combination with transmission electron microscopy, with a carefully chosen impinging position of an electron beam can be adopted to excite different high azimuthal- and radial-order WGMs. These methods utilize electrons with kinetic energies of several hundred keV, which can penetrate thin metallic layers and excite plasmons.27 They have been exploited to reveal the so-called “dark” modes in subwavelength metallic disks28 and GSP sandwich resonators.19
In this work, we propose a concept for coupling linearly polarized plane waves to high-azimuthal-order plasmonic modes of a disk-shaped GSP resonator, which otherwise cannot be excited by a normally incident plane wave. This is achieved by introducing a nanoscale through-split in the top metallic disk of the sandwich structure. In this configuration, visible and near-infrared light can efficiently couple to the plasmonic WGMs, leading to a 2–3 orders of magnitude increase in the accumulated total electromagnetic energy within the spacer. Further analysis reveals that each semi-disk, coupled through the split, simultaneously behaves as both a WGM and a Fabry–Pérot resonator. The strong WGM fields confined in deep-subwavelength volumes can enable a Purcell-effect enhancement and high-sensitivity sensing. Additionally, the WGM resonances can be effectively tuned by varying the resonator diameter. Our approach unlocks access to rich sets of modes in hybrid cylindrical resonators, enabling advanced light–matter interaction studies.
Geometry and simulation methods
A schematic illustration of the proposed WGM sandwich resonator is depicted in Fig. 1. The configuration comprises sequential nanodisks of Au–SiO2–Au layers, where td and tm are the thicknesses of the dielectric and metal layers, respectively. The top Au disk layer is split into two equal semi-disks along the diameter, creating a concentric air-filled gap with a length equal to the disk diameter. The resulting split width is g, and the disk diameter is D. The system is illuminated by a plane wave polarized along the x-axis (perpendicular to the gap axis) and propagating along the surface normal of the disks (parallel to the z-axis). To investigate the modes and their characteristics, we performed a full-wave three-dimensional numerical simulation in a finite element method-based COMSOL Multiphysics environment. The simulation model uses the scattered field formulation, enabling proper calculations of the scattered and absorbed fields. The structure is enclosed in a sphere with a radius of 2λmax, where λmax is the maximum wavelength of the spectrum of interest. Finally, the sphere is surrounded by a perfectly matched layer (PML) to eliminate backscattered fields and minimize errors. The discretization of the system employs a tetrahedral scheme with element sizes varying across different material domains. Specifically, the maximum element size is 5 nm in the dielectric spacer and 10 nm in the split and metallic layers. The frequency-dependent complex refractive indices for SiO2 (ref. 29) and Au30 were taken from the experimental data. The primary measures for quantitative analysis are the scattering and absorption cross sections and the energy accumulated in the dielectric region. The total energy accumulated in a material domain is calculated as follows: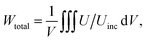 | (1) |
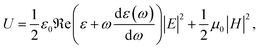 | (2) |
Throughout the simulations, the thicknesses of the Au and SiO2 layers are 40 nm and 10 nm, respectively. The air split width in the top disk is 30 nm, and the diameter of each layer is 450 nm unless otherwise specified.
Results and discussion
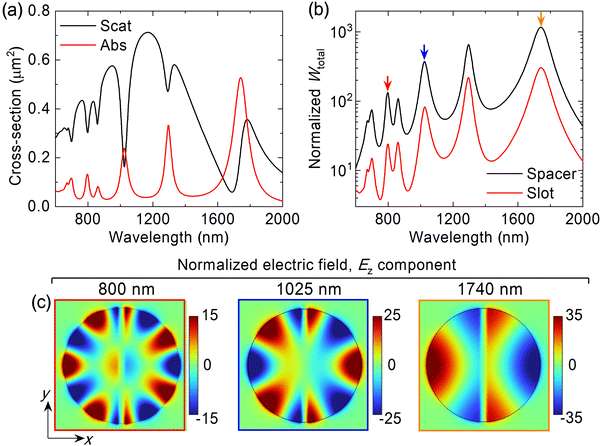
The scattering and absorption cross-sections of the proposed split GSP resonator under an electromagnetic field polarized along the short axis of the split are shown in Fig. 2(a) by black and red lines, respectively. Multiple dips (peaks), corresponding to the GSP modes of the resonator, are observed in the scattering (absorption) spectrum. Sharp resonant drops observed in the scattering spectrum indicate strong confinement of the wavefields in the GSP resonator. Fig. 2(b) shows the normalized total electromagnetic energy accumulated in the spacer and split, calculated according to eqn (1). The appearance of the resonant modes in the structure is accompanied by the strong accumulation of electromagnetic energy in both the spacer and the nanosplit, ranging from 102 to 103 for certain modes.Analysis of the modal family of the split GSP resonator reveals the existence of whispering-gallery-like modes. Fig. 2(c) illustrates the distributions of the out-of-plane electric field Ez components of these modes in the lateral cross-section of the spacer. The modes of a configuration with cylindrical symmetry, such as the one under consideration, are generally characterized by radial 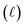 and azimuthal (m) mode numbers. The former is defined by the number of extrema along the radial direction, whereas the latter refers to the number of full oscillations along the circumference (azimuthal direction).31 Hence, the modes, appearing at wavelengths of 800, 1025 and 1740 nm, can be characterized by the radial mode number of
and azimuthal (m) mode numbers. The former is defined by the number of extrema along the radial direction, whereas the latter refers to the number of full oscillations along the circumference (azimuthal direction).31 Hence, the modes, appearing at wavelengths of 800, 1025 and 1740 nm, can be characterized by the radial mode number of 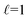 and azimuthal mode numbers of m = 5, 3 and 1, which are also identified by red, blue and orange arrows in Fig. 2(b), respectively. The strong localization of surface plasmons along each half of the perimeter of the MIM disks to the left and right of the nanosized split can be noted. The normalized total electromagnetic energy of the WGM-like modes accumulated in the spacer is approximately 1170, 376, and 134 for the m = 1, 3, and 5 modes, respectively. The Q-factors of these modes are calculated according to the relation Q ≈ λ0/δλ, where λ0 is the resonant wavelength and δλ is the full-width at half maximum of the resonance curve. Accordingly, the Q-factors of the three WGMs are estimated to be 19.3 (m = 1), 24.4 (m = 3) and 35.7 (m = 5), respectively.
and azimuthal mode numbers of m = 5, 3 and 1, which are also identified by red, blue and orange arrows in Fig. 2(b), respectively. The strong localization of surface plasmons along each half of the perimeter of the MIM disks to the left and right of the nanosized split can be noted. The normalized total electromagnetic energy of the WGM-like modes accumulated in the spacer is approximately 1170, 376, and 134 for the m = 1, 3, and 5 modes, respectively. The Q-factors of these modes are calculated according to the relation Q ≈ λ0/δλ, where λ0 is the resonant wavelength and δλ is the full-width at half maximum of the resonance curve. Accordingly, the Q-factors of the three WGMs are estimated to be 19.3 (m = 1), 24.4 (m = 3) and 35.7 (m = 5), respectively.
Decomposition of the scattering spectrum of the split GSP resonator based on spherical harmonics is carried out to further elucidate the contributions of each multipole moment. The results are summarized in SI Fig. S1(a). The enhancement in the electromagnetic field of WGMs in this configuration is contributed by the magnetic dipole moment, co-existing with the electric anapole states.9,32
Additionally, several modes labeled as hybrid modes to distinguish them from WGMs appear in the split GSP resonator, resulting from the strong interplay between the gap-plasmons formed along the half-perimeter of the disk and radial direction perpendicular to the long axis of the nanosplit. The distributions of the Ez components of these modes are shown in SI Fig. S2.
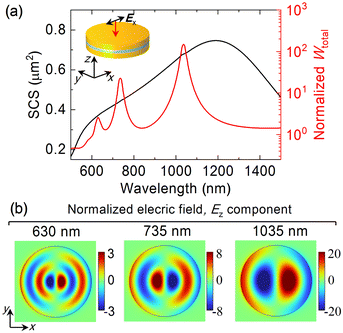
Now, to compare the characteristic modal families of the proposed GSP resonator having a split top disk with that of the solid MIM resonator, we plotted the scattering (left axis) and spacer energy (right axis) spectra of the solid GSP resonator of identical sizes in Fig. 3(a). The inset shows a schematic of the solid MIM resonator. Three characteristic modes emerge in this system upon plane wave excitation at wavelengths of 630 nm, 735 nm, and 1035 nm, corresponding to WGMs with an azimuthal mode number of m = 1 and radial mode numbers of 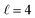 , 3, and 2, respectively.
, 3, and 2, respectively.
The normalized distributions of the electric field Ez components of these modes in the lateral plane of the spacer are shown in Fig. 3(b). It can be seen that the total normalized electromagnetic energy of these modes accumulated in the spacer reaches 2.6, 22 and 150 as the radial mode number decreases from 4 to 2. The overall lower energy of the modes in the solid GSP resonator compared to the high-azimuthal-order WGMs of the split GSP resonator at nearby spectral positions (see Fig. 2) can be attributed to their dominant electric-dipolar character, which, together with Ohmic losses,33 contributes to the total losses in the system. Alternatively, the accumulation of electromagnetic energy is associated with the magnetic dipole and electric quadrupole resonances, as shown in SI Fig. S1(b) in further detail. An important distinction between the characteristic whispering-gallery-like modes of solid and split GSP resonators is that in the latter configuration, the strong electromagnetic field is concentrated around the perimeter of the disk, making it particularly promising for biosensing applications.
Whispering gallery modes in disk-shaped resonators are generally described by solving the Helmholtz equation in cylindrical coordinates.34 In thin disks, where the resonator height is much smaller than the radius, the emerging modes are typically characterized by only azimuthal and radial mode numbers.34,35 In the case of the GSP resonator, its capacitor-like structure leads to dominant vertical field confinement between the metal layers. Consequently, the out-of-plane electric field component Ez can be approximated as follows:35
| Ez(r, φ, t) = E0mJm(kGSPr)sin(mφ)exp(iωt), | (3) |
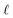 , is implicitly determined by m and the argument of the Bessel function. Outside the resonator, the fields are determined by the Hankel function of the first kind and order m; and exponentially decay away from the resonator surface.
, is implicitly determined by m and the argument of the Bessel function. Outside the resonator, the fields are determined by the Hankel function of the first kind and order m; and exponentially decay away from the resonator surface.
The radial and azimuthal distributions of the normalized electric field Ez component for the 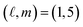 mode at λ = 800 nm are shown in Fig. 4(a). The left panel displays the field profile along the x-axis (perpendicular to the split), corresponding to the radial distribution. The right panel illustrates the azimuthal variation of the mode along the circumference of the disk. Red asterisks in the left plot denote the Bessel function of the fifth order. Green and cyan shaded regions illustrate the separation split and disk diameter, respectively. Perfect agreement can be seen between the Bessel J5 function and the radial distribution of the mode. The field maxima of all these plasmonic WGM-like modes of the split-disk system are located near the resonator edge due to the high-azimuthal orders of these modes, which, along with the stronger field amplitude of WGMs, can enable stronger interaction with the adsorbed molecules at the resonator surface. In contrast, the field maxima of all the modes in the solid MIM resonator are located deeply inside the spacer due to the low azimuthal order of these modes, as seen in Fig. 3(b). Moreover, the azimuthal distribution resembles a sinusoidal function following Relation (3). However, in both plots, discontinuity appears at the separation split edges (green areas). The radial and azimuthal distributions of the (3, 1) mode of the solid GSP resonator are similarly shown in SI Fig. S3. The profile of the normalized electric field Ez component of the (1,5) mode discussed above in the lateral XZ plane is depicted in Fig. 4(b).
mode at λ = 800 nm are shown in Fig. 4(a). The left panel displays the field profile along the x-axis (perpendicular to the split), corresponding to the radial distribution. The right panel illustrates the azimuthal variation of the mode along the circumference of the disk. Red asterisks in the left plot denote the Bessel function of the fifth order. Green and cyan shaded regions illustrate the separation split and disk diameter, respectively. Perfect agreement can be seen between the Bessel J5 function and the radial distribution of the mode. The field maxima of all these plasmonic WGM-like modes of the split-disk system are located near the resonator edge due to the high-azimuthal orders of these modes, which, along with the stronger field amplitude of WGMs, can enable stronger interaction with the adsorbed molecules at the resonator surface. In contrast, the field maxima of all the modes in the solid MIM resonator are located deeply inside the spacer due to the low azimuthal order of these modes, as seen in Fig. 3(b). Moreover, the azimuthal distribution resembles a sinusoidal function following Relation (3). However, in both plots, discontinuity appears at the separation split edges (green areas). The radial and azimuthal distributions of the (3, 1) mode of the solid GSP resonator are similarly shown in SI Fig. S3. The profile of the normalized electric field Ez component of the (1,5) mode discussed above in the lateral XZ plane is depicted in Fig. 4(b).
 | ||
| Fig. 4 (a) Distributions of the normalized Ez field along (left) the x-axis and (right) the circumference of the disk. The red asterisks correspond to the Bessel function of order m = 5. Cyan and green regions in plots show the areas of the disk and split, respectively. (b) Normalized Ez distribution in the XZ plane. (c) Schematic of a Fabry–Perot analogue of the half-disk. (d) Comparison of the scattering cross-section spectra of the GSP resonators with the split widths of 10, 30 and 50 nm. All parameters are same as presented in Fig. 2. (e) Electric charge σ distributions at the upper and lower interfaces of the spacer for the (1,5) mode. | ||
Although the field extrema are located inside the dielectric spacer near the spacer–air interface, a part of the field extended into the surrounding air is relatively strong due to the boundary condition at the spacer–air interface, as also seen in Fig. 4(a), left panel. Specifically, the Ez/Ez,max ratio at the spacer–air interface is nearly 0.89, where Ez,max is the maximum of the mode electric field. The exponential tail of this mode in the surrounding air drops twice at nearly 6 nm away from the resonator surface in the radial direction. This can enable rather strong coupling with a nearby fluorescent molecule.
In solid disk resonators, the localized resonances of WGMs are formed when the round-trip phase shift of the mode is 2π. Consequently, the spectral positions λ0 of the resonance modes with azimuthal mode number m can be approximately determined from the expression πD = mλ0/neff, where D and neff are the disk diameter and effective mode index, respectively.23 However, in the split GSP resonator configuration, the full round-trip propagation of the gap-plasmons along the circumference is interrupted by the air split. As a result, WGMs in this structure are formed by reflections at the edges of the split, with gap-plasmons propagating along the curved perimeter of each semidisk. This geometry closely resembles a Fabry–Pérot resonator, where the separation split functions as two mirrors, and the nearly 180° arc between them forms the propagation path.35 A schematic illustrating this analogy is provided in Fig. 4(c). Continuing this line of reasoning, the resonance condition of the WGMs in the split GSP nanoresonator can be expressed by the Fabry–Perot resonator formula, as follows:36,37
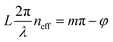 | (4) |
Our numerical simulations further confirm this interpretation. In Fig. 4(d), the dependence of the scattering spectrum on the nanosplit width g is shown for values of 10, 30, and 50 nm. A blueshift in the resonance positions can be seen as the nanosplit width increases from 10 to 50 nm, conditioned by the decrease in the propagation path. Hence, introducing a split in the top disk of the GSP resonator breaks the rotational C4 symmetry of the system, also creating two coupled resonators with a semi-cylindrical base.
Note that the total electromagnetic energy of WGMs accumulated in the spacer remains nearly constant as the split width varies. The influence of the nanosplit asymmetry on the optical response of the proposed GSP resonator is discussed in SI, Section IV. Two types of asymmetries are considered: (i) fixing one side of the nanosplit while increasing its width by 10 nm, and (ii) maintaining the nanosplit width while shifting its center by 20 nm. The resulting optical responses are compared with those of the symmetric configuration in Fig. S4. In the first case, the optical response is identical to that of the symmetric configuration [Fig. S4(a)]. In the second case, splitting of the plasmonic WGM resonances appears [Fig. S4(b)]. This is associated with the formation mechanism of WGMs in the proposed configuration, which originate from reflections at the nanosplit edges and propagate along the curved perimeter of each semidisk. When the nanosplit is displaced from the disk center, the propagation path shortens on one side and equivalently lengthens on the other. Consequently, two semi-cylindrical resonators with different resonant frequencies are formed owing to the contrast between the propagation paths of the gap-plasmons. This results in the splitting of the WGM resonance of the symmetric configuration into two adjacent resonances. One should also note that the presence of nanometer-scale surface roughness on the split interfaces can shift the resonance wavelength by altering the reflection phase, φ, in accordance with eqn (4), as well as can lead to increased radiation losses.36
Finally, it can be observed that all the WGMs formed in the proposed resonator are characterized by odd azimuthal numbers. This is a direct consequence of the excitation symmetry, where a normally incident plane wave induces charges of the same polarity on the edges of each side of the separation split, which in turn forces the fields along the curved (arched) propagation path to form only an odd number of half-oscillations. This is elucidated by inspecting the charge distributions at the upper and lower interfaces of the spacer for the (1,5) mode, as illustrated in Fig. 4(e). Breaking the excitation symmetry, for instance, by considering an oblique incident plane wave with its electric field polarized along the short axis of the split, will introduce a phase difference between the edges of each side of the split. As a result, charges of opposite polarity are induced. In contrast to the symmetric excitation, this condition forces the fields along the semicircular propagation path to form an even number of half-oscillations, thus extending the modal family of the split GSP resonator.
It is also evident that this charge distribution produces a strong Ex component of the electric field within the split, which itself functions as a plasmonic resonator supporting a capacitor-like mode.
The colour maps in Fig. 5 present the scattering cross-section and the total electromagnetic energy stored in the spacer as a function of disk diameter and wavelength. Three characteristic plasmonic WGMs of the system are identified by dashed blue lines. As the disk diameter increases from 350 to 550 nm, the resonance wavelengths of these WGMs exhibit an approximately linear redshift of 230 nm, 360 nm, and 750 nm for the m = 5, 3 and 1 modes, respectively. This trend is consistent with the linear relationship between the resonator diameter and the resonant wavelength of the WGMs.23 This fine control of the dispersion of WGMs of the split GSP disk resonator facilitates an enhancement in nonlinear optical effects. In particular, the resonance wavelengths of WGMs with azimuthal mode numbers (resonance wavelengths 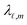 ) m = 1 (λ1,1) and m = 5 (λ1,5) can be matched such that λ1,1 = 2λ1,5 by adjusting the disk diameter. This feature can be exploited for mode-matched second-harmonic generation.38
) m = 1 (λ1,1) and m = 5 (λ1,5) can be matched such that λ1,1 = 2λ1,5 by adjusting the disk diameter. This feature can be exploited for mode-matched second-harmonic generation.38
Another important aspect is the polarization of the incident electromagnetic field, which significantly influences the excitation of plasmonic WGMs. To investigate this, we compared the optical response of the GSP resonator for two polarization states of the incident field, parallel and perpendicular to the split. The results are shown in Fig. 6(a) and (b), which present the scattering cross-section and the normalized total electromagnetic energy stored in the spacer, respectively. When the incident field is polarized along the nanosplit, both the scattering cross-section and spacer energy spectra closely resemble those of the solid MIM sandwich structure (without a nanosplit). Specifically, three distinct resonances appear in the energy spectrum at nearly 630, 730, and 1018 nm, with slightly reduced energy due to leakage through the split. For comparison, the results for the perpendicularly polarized field are reproduced from Fig. 2. The perpendicular polarization of the incident field leads to a strong electric field within the nanosplit, with the dominant field component being Ex, as shown in Fig. 4(e).
The field confinement can be further improved by either reducing the spacer thickness, which will lead to a higher effective mode index,39 or by employing a spacer material with a higher refractive index, such as TiO2.40 SI Section 5 discusses the role of the spacer dielectric in the optical response of the split GSP resonator.
Finally, the presence of multiple high-intensity antinodes enables this configuration of a GSP resonator to be exploited to achieve the Purcell effect.41,42 The associated Purcell factor is a central criterion of the cavity quantum electrodynamics and describes the enhancement of the spontaneous emission rate of a quantum emitter placed inside a cavity compared with that of free space.43 To investigate this, an ideal lossless point dipole is placed at r = 222 nm, approximately corresponding to the antinode positions of the WGMs. The dipole moment is oriented along the z-axis, aligning with the dominant electric field component of the WGMs. This configuration is schematically illustrated in the inset of Fig. 7.
 | ||
| Fig. 7 Radiative (blue), non-radiative (red) and total decay rate enhancement of a point dipole located at r = 222 nm in the spacer corresponding to the maximum intensity point of WGMs with the radial mode number of 1. The inset shows the cross-section of the GSP resonator along xz-plane and the position of the dipole. Red, blue and orange arrows denote the modes with the azimuthal mode numbers of 5, 3 and 1, respectively. All geometrical parameters are same as presented in Fig. 2. | ||
The spectral dependence of the radiative (Γr) and non-radiative (Γnr) decay rate enhancements, along with their sum corresponding to the Purcell factor (Pf), is shown in Fig. 7 by the blue, red, and black lines, respectively. The resonance peaks at wavelengths of approximately 790 nm (red arrow), 1010 nm (blue arrow), and 1742 nm (orange arrow) correspond to the WGMs. These peaks exhibit some of the highest Purcell factor values, reaching approximately 3720, 5850, and 8515 from left to right, respectively. The quantum efficiency44 can be calculated as QE = Γr/Pf, leading to QE values of WGMs of nearly 52%, 54% and 60% for the m = 5, 3 and 1 modes, respectively. Given that the Purcell effect requires spatial overlap between the dipole emitter and the field intensity maximum of the mode, exploiting WGMs with different azimuthal numbers is advantageous, as the intensity maxima of these modes are located close to each another. This, in turn, facilitates the coupling of an emitter to all the WGMs. Note that this is not the case for modes with varying radial order, such as those supported by a solid GSP resonator without a split under linearly polarized plane wave, where the field maximum shifts towards the resonator center as the radial number increases. Another important advantage is that a high Purcell factor in plasmonic systems is achieved due to the ultra-small mode volume of plasmonic modes rather than a high Q-factor.41 Moreover, the inherently low Q-factor of these modes resulting from the metal losses enables a relatively high Purcell factor to be maintained over a broad spectral range. In the estimation of the Purcell factor, the ideal dipole was placed at the center of the separation between the top and bottom disks. However, it should be emphasized that positioning of the dipole emitter close to the metallic disks will result in fluorescence quenching.45
The fabrication of the proposed split MIM resonator can be divided into two main steps. In the first step, cylindrical cavities are defined in a resist layer spin-coated on a low-refractive index substrate (such as SiO2 or MgF2) using conventional electron-beam lithography.46 30-nanometer-thick Au layers can be deposited by the standard thermal evaporation, whereas the 10-nanometer-thin intermediate layer can be introduced via atomic layer deposition. Subsequently, a lift-off process of the resist will reveal the MIM sandwich structure. In the second step, a highly precise 30-nanometer-wide split in the top Au disk can be introduced by using focused gallium or helium ion beam milling.47
Conclusions
In summary, we have demonstrated a practical approach for enabling the coupling of a normally incident plane wave to high-azimuthal-order whispering-gallery-like eigenmodes in a metal–insulator–metal plasmonic disk nanoresonator. This is achieved by introducing a nanoscale through-split in the top metal disk, which functions as a plasmonic nanoantenna and facilitates the conversion of far-field excitation into whispering-gallery modes localized along the perimeter of the disk. This mechanism, combined with an estimated enhancement of up to three orders of magnitude in the total electromagnetic energy accumulated within the spacer, establishes favourable conditions for biosensing applications and Purcell effect enhancement. Furthermore, the presence of two semicircular disks separated by a nanometer-wide air gap can enable dynamic control of the electromagnetic response via electro-optical modulation, particularly through the use of Pockels materials as the spacer.Conflicts of interest
The authors declare no conflict of interest.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: (I) multipolar decomposition: this section includes multipole decomposition of the scattering spectra of split and solid GSP resonators based on spherical harmonics. (II) Hybrid modes of the split GSP resonator: this section shows distributions of the electric field Ez components of hybrid GSP modes of the split nanoresonator. (III) Mode profile in the solid GSP resonator: the section presents distributions of the electric field Ez component of the (3,1) mode of the solid GSP resonator along the circumference and diameter of the disk. (IV) Influence of the nanosplit asymmetry: this section discusses the influence of the nanosplit asymmetry on the spectral and modal characteristics of the split GSP resonator. (V) Role of the spacer dielectric: this section examines the influence of the spacer dielectric material on the spectral characteristics. See DOI: https://doi.org/10.1039/d5na00985e.Acknowledgements
This work was supported by the Scientific Research Grant of the Higher Education and Science Committee of the MESCS of Armenia (23RL-2A034). The authors gratefully thank the three anonymous reviewers for their valuable comments and the Nanoscale Advances editorial office staff for their careful preparation of the manuscript proofs.References
- S. I. Bozhevolnyi and K. V. Nerkararyan, Opt. Express, 2009, 17, 10327 CrossRef CAS PubMed.
- Y. Kivshar, Nano Lett., 2022, 22, 3513–3515 CrossRef CAS PubMed.
- G.-C. Li, Y.-L. Zhang and D. Y. Lei, Nanoscale, 2016, 8, 7119–7126 RSC.
- S. Li, Y. Fang and J. Wang, Opto-Electron. Sci., 2024, 3, 240011 CAS.
- S. Kasani, K. Curtin and N. Wu, Nanophotonics, 2019, 8, 2065–2089 CrossRef CAS.
- L. Huang, L. Xu, D. A. Powell, W. J. Padilla and A. E. Miroshnichenko, Phys. Rep., 2023, 1008, 1–66 CrossRef CAS.
- P. T. Kristensen and S. Hughes, ACS Photonics, 2014, 1, 2–10 CrossRef CAS.
- L. Li, S. Wu, L. Li, Z. Zhou, H. Ding, C. Xiao and X. Li, Nanoscale, 2019, 11, 5467–5473 RSC.
- T. Yezekyan, V. A. Zenin, J. Beermann and S. I. Bozhevolnyi, Nano Lett., 2022, 22, 6098–6104 CrossRef CAS PubMed.
- T. Søndergaard, J. Jung, S. I. Bozhevolnyi and G. Della Valle, New J. Phys., 2008, 10, 105008 CrossRef.
- A. Pors and S. I. Bozhevolnyi, Opt. Express, 2013, 21, 27438 CrossRef PubMed.
- A. Pors, S. K. H. Andersen and S. I. Bozhevolnyi, Opt. Express, 2015, 23, 28808 CrossRef CAS PubMed.
- Y. Zhang, P. Yue, J.-Y. Liu, W. Geng, Y.-T. Bai and S.-D. Liu, Opt. Express, 2019, 27, 16143 CrossRef CAS PubMed.
- A. Das, C. Mao, S. Cho, K. Kim and W. Park, Nat. Commun., 2018, 9, 4828 CrossRef PubMed.
- A. Xomalis, X. Zheng, A. Demetriadou, A. Martínez, R. Chikkaraddy and J. J. Baumberg, Nano Lett., 2021, 21, 2512–2518 CrossRef CAS PubMed.
- K. L. Domina, V. V. Khardikov, V. Goryashko and A. Y. Nikitin, Adv. Opt. Mater., 2020, 8(5), 1900942 Search PubMed.
- B. Krause, D. Mishra, J. Chen, C. Argyropoulos and T. Hoang, Adv. Opt. Mater., 2022, 10(16), 2200510 CrossRef CAS PubMed.
- K. Yu, A. Lakhani and M. C. Wu, Opt. Express, 2010, 18, 8790 CrossRef CAS PubMed.
- M. Kuttge, F. J. García de Abajo and A. Polman, Nano Lett., 2010, 10, 1537–1541 CrossRef CAS PubMed.
- R. Gabrielyan, G. Arabajyan, T. Yezekyan and H. Parsamyan, Opt. Express, 2025, 33, 2593 CrossRef CAS PubMed.
- S.-H. Kwon, Opt. Express, 2012, 20, 24918 CrossRef PubMed.
- F. Lou, M. Yan, L. Thylen, M. Qiu and L. Wosinski, Opt. Express, 2014, 22, 8490 CrossRef CAS PubMed.
- A. Bozzola, S. Perotto and F. De Angelis, Analyst, 2017, 142, 883–898 RSC.
- T. K. Hakala, H. T. Rekola, A. I. Väkeväinen, J.-P. Martikainen, M. Nečada, A. J. Moilanen and P. Törmä, Nat. Commun., 2017, 8, 13687 CrossRef CAS PubMed.
- G. Zhu, L. Qv, Y. Guo and Y. Fang, Plasmonics, 2022, 17, 87–93 CrossRef CAS.
- R. He, M. Meunier, Z. Dong, H. Cai, W. Gao, J. Zuniga-Perez and X. Liu, Nanoscale, 2023, 15, 1652–1660 RSC.
- F. P. Schmidt, H. Ditlbacher, F. Hofer, J. R. Krenn and U. Hohenester, Nano Lett., 2014, 14, 4810–4815 CrossRef CAS PubMed.
- F.-P. Schmidt, H. Ditlbacher, U. Hohenester, A. Hohenau, F. Hofer and J. R. Krenn, Nano Lett., 2012, 12, 5780–5783 CrossRef CAS PubMed.
- L. Gao, F. Lemarchand and M. Lequime, Opt. Express, 2012, 20, 15734 CrossRef PubMed.
- R. L. Olmon, B. Slovick, T. W. Johnson, D. Shelton, S.-H. Oh, G. D. Boreman and M. B. Raschke, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 235147 CrossRef.
- Y. Yang, O. D. Miller, T. Christensen, J. D. Joannopoulos and M. Soljačić, Nano Lett., 2017, 17, 3238–3245 CrossRef CAS PubMed.
- R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton, Opt. Commun., 2018, 407, 17–21 CrossRef CAS.
- E. C. Garnett, W. Cai, J. J. Cha, F. Mahmood, S. T. Connor, M. Greyson Christoforo, Y. Cui, M. D. McGehee and M. L. Brongersma, Nat. Mater., 2012, 11, 241–249 CrossRef CAS PubMed.
- T. Heebner, J. Grover, I. Rohit, Optical Microresonators, Springer New York, New York, NY, 2008, vol. 138 Search PubMed.
- H. Parsamyan, H. Haroyan and K. Nerkararyan, Opt. Commun., 2020, 474, 126122 CrossRef CAS.
- M. G. Nielsen, D. K. Gramotnev, A. Pors, O. Albrektsen and S. I. Bozhevolnyi, Opt. Express, 2011, 19, 19310 CrossRef CAS PubMed.
- T. Abrahamyan, H. Haroyan, D. Hambaryan, H. Parsamyan, A. Babajanyan, K. Lee, B. Friedman and K. Nerkararyan, J. Phys. D Appl. Phys., 2022, 55, 445001 CrossRef CAS.
- A. Noor, A. R. Damodaran, I.-H. Lee, S. A. Maier, S.-H. Oh and C. Ciracì, ACS Photonics, 2020, 7, 3333–3340 CrossRef CAS PubMed.
- H. T. Miyazaki and Y. Kurokawa, Phys. Rev. Lett., 2006, 96, 097401 CrossRef PubMed.
- T. Siefke, S. Kroker, K. Pfeiffer, O. Puffky, K. Dietrich, D. Franta, I. Ohlídal, A. Szeghalmi, E. Kley and A. Tünnermann, Adv. Opt. Mater., 2016, 4, 1780–1786 CrossRef CAS.
- S. Huang, T. Ming, Y. Lin, X. Ling, Q. Ruan, T. Palacios, J. Wang, M. Dresselhaus and J. Kong, Small, 2016, 12, 5190–5199 CrossRef CAS PubMed.
- J. Yuan, J. Hu, Y. Zheng, H. Wei, J. Xiao, Y. Wang, X. Zhao, Y. Xiang, Y. Lei and W. Wang, Opto-Electron. Sci., 2025, 4, 240021 CAS.
- V. Krivenkov, P. Samokhvalov, I. Nabiev and Y. P. Rakovich, J. Phys. Chem. Lett., 2020, 11, 8018–8025 CrossRef CAS PubMed.
- Y. Kan, S. I. Bozhevolnyi and S. Kumar, Adv. Quantum Technol., 2023, 6(12), 2300196 CrossRef CAS.
- G. Sun, J. B. Khurgin and C. C. Yang, Appl. Phys. Lett., 2009, 95(17), 171103 CrossRef.
- F. Dai, A. Horrer, P. Adam and M. Fleischer, Adv. Opt. Mater., 2020, 8(7), 1901734 CrossRef CAS.
- K. Höflich, G. Hobler, F. I. Allen, T. Wirtz, G. Rius, L. McElwee-White, A. V. Krasheninnikov, M. Schmidt, I. Utke, N. Klingner, M. Osenberg, R. Córdoba, F. Djurabekova, I. Manke, P. Moll, M. Manoccio, J. M. De Teresa, L. Bischoff, J. Michler, O. De Castro, A. Delobbe, P. Dunne, O. V. Dobrovolskiy, N. Frese, A. Gölzhäuser, P. Mazarov, D. Koelle, W. Möller, F. Pérez-Murano, P. Philipp, F. Vollnhals and G. Hlawacek, Appl. Phys. Rev., 2023, 10(4), 041311 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |