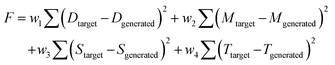Generative inverse design for microstructure control in precursors for Li- and Mn-rich layered-oxide cathodes

Abstract

Microstructures often dictate materials' performance, yet they are rarely treated as an explicit design variable because microstructures are hard to quantify, predict, and optimize. We built an image-centric, closed-loop framework that makes microstructural morphology a controllable objective and demonstrate its use case with precursors for Li- and Mn-rich layered oxide cathodes. This work presents an integrated, AI-driven framework for the predictive design and optimization of lithium-ion battery cathode precursor synthesis. This framework integrates a diffusion-based image generation model, a quantitative image analysis pipeline, and a particle swarm optimization (PSO) algorithm. By extracting key morphological descriptors such as texture, sphericity, and median particle size (D₅₀) from SEM images, the platform accurately predicts SEM-like morphologies resulting from specific co-precipitation conditions, including reaction time-, solution concentration-, and pH-dependent structural changes. We experimentally validated that our optimization pinpoints synthesis parameters yielding user-defined target morphologies of Li- and Mn-rich (LMR) layered oxide materials, with predicted and synthesized structures showing close agreement. This framework offers a practical strategy for data driven materials design, enabling both forward prediction and inverse design of synthesis conditions and paving the way toward autonomous, image-guided microstructure engineering.

---

New concepts

We introduce a generative, image-guided inverse-design framework that elevates microstructures from a passive synthesis outcome to an explicit design variable. Unlike conventional optimization strategies that focus on composition or bulk properties and assess morphology only retrospectively, our approach directly encodes images as quantitative descriptors and embeds them into a closed-loop optimization cycle.

The key breakthrough lies in combining image-based quantification, diffusion-driven forward simulation, and global optimization into an integrated workflow that enables both prediction and inverse design of precursors for Li- and Mn-rich cathodes. This framework achieves experimental realization of user-defined morphologies and links targeted microstructures to improve electrochemical stability.

Beyond batteries, the concept is material-agnostic: by swapping descriptors and training data, the same quantification prediction optimization triad can be extended to catalysts, alloys, and porous membranes where geometry governs function. This work provides the community with a generalizable blueprint for morphology driven discovery, transforming microstructural control from empirical trial and error into a systematic, data driven design paradigm.

1. Introduction

Microstructural morphology plays a pivotal role in materials' performance by orchestrating complex phases and controlling the heterogeneity of microstructural features.¹ Transformation-induced plasticity (TRIP) steels,² for instance, feature a meticulously crafted microstructure that undergoes deformation-driven phase transitions, yielding multiple coexisting phases. The resulting mechanical properties are a product of synergistic interactions, resulting in strengths and ductilities that far surpass the mere sum of each phase's contribution. In the case of cathode active materials for Li-ion batteries, individual particles are never identical; thus, morphological heterogeneity likewise dominates performance. For Li- and Mn-rich (LMR) layered oxide cathodes, tailored composition can provide an initial capacity of over 250 mAh g⁻¹; however, long-term stability and voltage retention are primarily influenced by variations in particle size, morphology, and defect concentration.³ The inherent complexity of LMR microstructures has, in fact, obscured the critical link between morphology, structural defects, and reaction mechanisms, thereby highlighting a persistent challenge in materials design.^4–7 While composition and scalar parameters are routinely optimized, the rich morphology captured in imaging data remains an underexploited design lever.

Conventional material optimization frameworks generally address microstructures in a relatively indirect manner, with a focus on maximizing scalar targets (e.g., capacity and conductivity) or adjusting composition and stoichiometry.⁸ This approach is often predicated on the assumption that microstructural details will emerge because of processing-related decisions. Consequently, electron microscopic image-level features are seldom explicitly delineated as design objectives. In the domain of battery cathode development, for instance, synthesis recipes are optimized to enhance electrochemical properties. The microstructure is evaluated post hoc using bulk average properties such as XRD phase refinement, BET surface area, particle size distribution, and porosity. This approach contrasts with the more conventional practice of designing these proxies upfront. The quantification of an entire SEM or TEM image in a form suitable for optimization remains a non-trivial task. Previous studies have employed a limited set of summary metrics, such as the phase area fraction or characteristic length scales to incorporate morphology into design.^9,10 However, these coarse descriptors may overlook the subtle textural and topological nuances that are crucial for performance. Furthermore, there is a lack of discussion regarding the sufficiency of indirect measures, resulting in a suboptimal representation of rich, image-derived information within the inverse design loop.

In addition to the limitations of coarse descriptors, effective image-based inverse design of microstructures confronts several intertwined challenges. The process of distilling the rich, multi-scale patterns visible in SEM and TEM images into quantitative features is exceptionally difficult. Conventional metrics such as median grain sizes, porosity, or aspect ratios capture only fragmentary aspects of morphology, leaving subtle textural and topological nuances unquantified. The establishment of robust, predictive links between synthesis parameters and the resulting microstructure remains largely empirical. Minor changes in precursor concentration, temperature, or mixing protocol can provoke disproportionate or unpredictable morphological shifts. This forces reliance on laborious trial-and-error tuning. Because of the absence of an integrated closed-loop framework that treats image-derived morphology as an explicit design variable, researchers resort to an inefficient Edisonian cycle (adjust, synthesize, characterize, and repeat), an approach that becomes untenable as materials systems become more complex. In order to surmount the aforementioned impediments, it is imperative to employ methodologies that systematically encode substantial image data, facilitate dependable process-morphology predictions, and underpin autonomous, closed-loop design of targeted microstructures.

To address these gaps, we propose a closed-loop, image-driven inverse design framework that integrates wavelet-based image quantification, diffusion-based generative modelling, and global optimization into a unified methodology. First, microstructure images are transformed into a compact “morphology fingerprint” that captures multi-scale texture, particle sphericity, and size distribution metrics via image-based quantitative morphology analysis.^11,12 Subsequently, a conditional diffusion model functions as a forward simulator, synthesizing realistic SEM images from process parameters or target descriptors with high fidelity.^13,14 Next, a particle swarm optimization (PSO) algorithm is employed to iteratively adjust co-precipitation conditions.¹⁵ This process is intended to direct the generated images toward the desired morphology. The efficacy of each iteration is evaluated using quantitative morphology metrics, which serve to determine the algorithm's “fitness”. By treating the microstructure image itself as the design objective rather than relying on scalar proxies, our approach actively explores the space of possible morphologies in a feedback loop. We validated this framework by synthesizing Li- and Mn-rich layered oxide cathodes under the optimized conditions predicted by our algorithm, and SEM characterization confirmed that the experimentally obtained microstructures closely matched the target morphology fingerprint.

2. Results

2.1. Integrated frameworks for forward prediction and inverse design

The proposed workflow (Fig. 1) reimagines precursor synthesis as a closed-loop, data-driven process, rather than the traditional, time-intensive trial-and-error approach. The system is composed of three synergistic modules that form the backbone of the overall structure. First, a morphology analysis model was developed that extracts three reproducible descriptors directly from SEM micrographs. The developed model supplants qualitative labels such as “needle-like” or “plate-like” with a texture metric,^16–18 and it replaces conventional laser-diffraction PSA measurements with sphericity and particle-size metrics, thereby providing richer, SEM-scale insights. Secondly, a conditional diffusion-based image generator has been developed to learn the mapping between co-precipitation parameters (i.e., pH, concentration of NaOH and NH₄OH, and reaction time)^16,19,20 and realistic SEM-like morphologies. This model enables the reconstruction of multiscale morphological features, thereby facilitating rapid virtual screening of admissible parameter sets.^13,14,21,22 Thirdly, a particle swarm optimization (PSO) routine interrogates the generator iteratively to converge on synthesis conditions that meet user-defined morphological targets.¹⁵ PSO ultimately completes the cycle by sampling the design space, querying the generator for a virtual image, extracting descriptors through the analysis model, and updating its velocity based on the discrepancy between its current state and the target morphology.

Fig. 1 Schematic overview of the integrated AI-based framework for precursor morphology optimization. The framework consists of three key components: (a) a morphology analysis module that quantifies texture, sphericity and D₅₀ from the images, (b) a diffusion-based image generation model that predicts SEM-like precursor morphologies from co-precipitation parameters, and (c) a particle swarm optimization (PSO) algorithm that iteratively refines synthesis conditions to minimize the difference between predicted and target morphologies. Given a user-defined target morphology (right), the framework iteratively generates precursor images under candidate synthesis conditions, quantifies their morphology features, and updates the input parameters until convergence is reached. The bottom table shows an example of the co-precipitation parameters used as model input.

2.2. Image-based quantitative morphology analysis

Domain-knowledge based morphology descriptors are indispensable for correlating precursor microstructures with electrochemical and mechanical behavior. Accordingly, this study employs the two metrics already standard in powder engineering the median equivalent diameter (D₅₀) and the sphericity of secondary particles (agglomerates) reporting both their population means and full distributions.^23–27 To complement these metrics, we introduce a texture descriptor that quantitatively captures the primary-particle shape, which prior qualitative labels could not describe consistently.

Sphericity and D₅₀ of secondary particles are widely used because they predict packing density, stress distribution during electrode calendaring, and fracture resistance under compression.²⁸ AI-assisted segmentation enabled calculation of both D₅₀ and sphericity from the projected area and equivalent radius (Fig. 2b). The resulting D₅₀ values matched laser diffraction data within ±4% (Fig. 2c).

Fig. 2 Quantitative image-based analysis of precursor morphology using texture, sphericity, and D₅₀. Texture and sphericity values are given on a normalized 0–1 scale. (a) Texture quantification based on discrete wavelet transform (DWT), used to distinguish fine primary particle structures reflecting differences in surface microstructural complexity. (b) Sphericity analysis of secondary particles visualized with color-coded segmentation. Average sphericity (Avg) and standard deviation (Std) values are presented for each sample (bottom-left graph). (c) Comparison between D₅₀ values extracted from image analysis and experimental particle-size analyzer measurements across different synthesis times. The close match validates the reliability of the image-based quantification method.

The texture descriptor fills the gap left by subjective terms such as “plate-like”, “rod-like” or “needle-like”.^16–18 Although such qualitative labels may hint at the dominant crystallographic facets, they are inherently unreliable because their meaning is observer-dependent and they reduce complex three-dimensional geometry to a single adjective. Most importantly, they do not provide a continuous metric that can be incorporated into engineering models or statistical analyses.

Because texture is computed directly from voxel-level geometry, it remains reproducible even when phase boundaries are indistinct, enabling robust quantification of the primary particle shape (Fig. 2a). Several groups have attempted to quantify the primary-particle shape by first segmenting the particles and then extracting geometric metrics from the segmented volumes. While conceptually attractive, this “direct segmentation” route becomes highly sensitive to hyper-parameter choices or to the specific distribution of labels in the training set once inter-phase boundaries are diffuse or crystallographic domains intergrow.

To verify that the selected descriptors carry complementary information, we calculated pairwise Pearson correlation coefficients among D₅₀, mean sphericity, and texture (SI Fig. S4). The values were −0.38 (D₅₀ vs. sphericity), −0.17 (D₅₀ vs. texture), and 0.26 (sphericity vs. texture), indicating only weak correlations. This confirms that the domain knowledge-based descriptor set is mutually independent and therefore suitable for quantitative morphology analysis. The correlation with experimental variables further demonstrates how particle shape can be tuned. Texture exhibited a strong dependence on pH, as well as on the concentrations of NaOH and NH₄OH. It reached values ≥0.7 when the concentrations of NaOH and NH₄OH were set to ×0.25 and ×0.09, respectively, under pH 10 conditions that produced high texture value (thin, faceted lamellae). In contrast, texture dropped below 0.3 when the concentrations were changed to ×0.08 and ×0.29 at pH 11, or when O₂ induced Mn²⁺ promoted platelet thickening. Sphericity increased monotonically with reaction time, while its standard deviation decreased, indicating progressive morphological homogenization. Higher concentrations of NaOH enhanced nucleation density and resulted in more spherical particles, whereas lower pH or the presence of oxygen gas reduced sphericity.

2.3. Forward prediction via diffusion-based image generation

The conditional diffusion model translates arbitrary co-precipitation parameters into realistic SEM-like micrographs in <5 s on a consumer GPU. Fig. 3a juxtaposes experimental and generated 15 000× images, highlighting accurate replication of the rapid texture relaxation observed even in the very first nucleation steps (∼ 120 min). In 3000× images (Fig. 3a), secondary particle densification and aggregate coalescence are reproduced with striking visual fidelity.

Fig. 3 Comparison of experimental and model-generated precursor morphologies and their quantitative descriptors across synthesis time. (a) Side-by-side comparison of experimental SEM images (top row) and diffusion model-generated images (bottom row) across different synthesis durations at low magnification (3000×), capturing the development of secondary particle morphology and packing structure. (b) Corresponding comparison at high magnification (15 000×), where the model panel shows one randomly sampled output; texture values are annotated on each panel. (c) Comparison of D₅₀ values (median secondary particle size) estimated from experimental SEM images and model-generated images. Error bars indicate span of particle size distribution (span = (D₉₀–D₁₀)/D₅₀). (d) Model-estimated texture mean and standard deviation obtained from 100 independent samples for each synthesis time. (e) Quantitative comparison of texture values over synthesis time; black points denote experimental data, while blue points represent individual model estimates, demonstrating consistent trends between experimental and model data.

Furthermore, although the model is not constrained by explicit physical equations, it internalizes the mapping between synthesis parameters (pH, NaOH, NH₄OH, time, etc.) and precursor morphology, generating results that mirror the underlying growth dynamics. In practical co-precipitation, nascent nuclei rapidly aggregate, producing abrupt morphological changes; subsequently, crystals embedded within the agglomerates grow more slowly.^29,30 The diffusion model reproduces this sequence: during the first 120 min it tracks the rapid evolution of secondary and primary particles, and at later times it recreates the Ostwald-ripening regime in which convex regions dissolve, concave regions grow, and overall particle sphericity increases.³¹ For each synthesis condition, texture is computed per particle and summarized as the condition-level mean (µ) and standard deviation (SD). To quantify model variability, we draw 100 independent conditional generations per condition and compute the same per-particle texture, reporting the model µ ± SD and overlaying individual sampled estimates. As shown in Fig. 3d, model means track experimental means with R² = 0.98 for texture; D₅₀ trajectories in Fig. 3c align with R² = 0.91. These results indicate that the model preserves underlying structural statistics rather than merely imitating visual style.

Our model demonstrates robust performance within the training manifold, effectively capturing morphology variations across multiple synthesis parameters. Morphology evolution under varying pH conditions is accurately reproduced, and intermediate states are reliably interpolated (Fig. S5). In this univariate pH conditioned case, the model was trained using experimental data at pH 10.0, 10.7, and 11.0; the generated morphologies at these same points closely match the experimental textures, confirming reconstruction fidelity. The interpolated prediction at pH 10.5, which was absent from the training dataset, further highlights the model's capacity to generalize within the same chemical series, consistent with known growth mechanisms such as the directional adsorption of metal–ammonia complexes on the (001) plane.¹⁸

Building on this capability, forward predictions were then performed in a two-dimensional synthesis parameter space in which pH and initial NH₄OH concentration were varied together from pH 10.0/0.29 M NH₄OH to pH 11.0/0.57 M NH₄OH to generate intermediate conditions via linear interpolation of the conditioning inputs (Fig. S6; using the same trained diffusion backbone and protocol as in the pH only case). All other synthesis variables were fixed within that separate experimental series. The predictions reveal a monotonic decrease in D₅₀ with increasing pH and ammonia concentration, while particle sphericity remains essentially constant across the interpolation domain.

2.4. Inverse design validation through PSO optimization

To showcase practical utility, we defined a target morphology characterized by high texture, high sphericity, low σ (sphericity), and elevated D₅₀ traits associated with fast Li⁺ diffusion and high tap density. Motivated by prior studies linking particle geometry to diffusion kinetics, packing behavior, and structural stability, we selected morphological targets comprising high texture, high sphericity, low σ (sphericity), and elevated D₅₀.^32–36 These choices respectively shorten Li⁺ diffusion pathways, promote dense packing and smooth powder flow, enforce uniform particle shape conducive to stable Li⁺ transport, and increase tap density. PSO launched 40 search points across the feasible parameter space, each iteratively querying the generator, quantifying descriptors, and updating its trajectory. Convergence occurred within 50 iterations, yielding the following optimal synthesis conditions. A low-dimensional data projection indicates that the optimized run lies within the empirical manifold derived from experimental data (see Fig. S9).

Experimental validation verified the model's accuracy. SEM images of the synthesized precursor (Fig. 4b, bottom) reveal densely packed secondary particles and finely textured primary networks that mirror virtual predictions (top). Descriptor discrepancies between prediction and experiment remain ≤5% across all metrics. Electrochemical cycling tests show a 3% smaller capacity fade and improved voltage retention (smaller average-voltage decay) relative to baseline LMR cathodes under identical conditions (SI Fig. S7 and S8).

Fig. 4 Optimization of precursor morphology using an integrated image-based inverse design framework. (a) Visualization of the optimization result in a three-dimensional morphological design space defined by sphericity, sphericity standard deviation, and D₅₀ (median secondary particle size). The color scale represents texture, with warmer colors indicating finer primary features. Each point corresponds to an experimentally measured dataset. The green dashed line marks the predefined target morphology, and the green solid line denotes the optimized result. (b) SEM image comparison of the predicted target morphology (top row) and the experimentally synthesized result (bottom row) obtained using the optimized co-precipitation conditions. Low and high magnification images are shown to evaluate both particle shape and primary particle texture.

3. Conclusion

These findings confirm that the proposed inverse-design approach effectively guides experimental synthesis toward target morphological features, underscoring its potential for rational microstructure control in materials design. By replacing vague descriptors with a triad of quantitative metrics (texture, sphericity, and D₅₀), the SEM image itself becomes a first-class design variable. Correlation analysis (the Image based quantitative morphology analysis section) revealed that sphericity, sphericity standard deviation, D₅₀, and texture each exhibit low mutual correlation, indicating that these morphological descriptors independently characterize distinct aspects of secondary-particle structures (SI Fig. S4). This independence delineates a controllable processing window for optimizing tap density, Li-ion diffusivity, and capacity retention.

The high-fidelity synthetic micrographs generated entirely in silico demonstrate the feasibility of rapid morphology scouting across extensive compositional spaces (e.g., the full pH–NH₄OH range) in mere minutes, thereby compressing weeks of wet-lab trial-and-error into GPU time. Every pixel in the conditional diffusion generator is conditioned on the same descriptor set used for experimental quantification, allowing researchers to trace visual motifs back to numerical targets. Tens of thousands of hypothetical conditions can thus be screened per hour on a single consumer GPU (throughput unattainable with conventional CSTR campaigns) and the linear scaling of optimization cost with the descriptor count permits seamless integration of further constraints (impurity limits, BET, and grain-boundary texture) without architectural overhaul.

Some localized deviations from monotonic behavior observed in interpolated morphologies (the Forward prediction via diffusion-based image generation section) can be attributed to nonlinear interactions between chemical equilibria (e.g., complexation efficiency, and supersaturation) and kinetic factors (e.g., nucleation and coarsening). Such discrepancies are common in multivariate synthesis landscapes and highlight opportunities for refinement through expanded data coverage or conditioning guided by physical constraints.

Although demonstrated for Li- and Mn-rich layered-oxide precursors, the framework has the potential to be material agnostic. The framework is morphology first under fixed composition; composition conditioned inputs (e.g., Ni/Mn ratio) can be incorporated in the conditioning vector when harmonized multi-chemistry datasets become available. This potential can be realized by swapping the training image set and descriptor definitions, enabling immediate transfer to catalysts, additively manufactured alloys, or porous membranes where geometry governs function. The key insight is that while each material system requires domain-specific morphological descriptors such as active site exposure area in catalysts or pore connectivity in membranes the core ‘quantification–prediction–optimization’ closed-loop architecture remains universally applicable. This structural invariance suggests that the framework's value lies not in its current implementation but in its systematic approach to bridging the gap between morphological targets and synthesis protocols. By translating explicit morphological targets into experimentally verifiable recipes, the integrated AI system furnishes a blueprint for accelerating morphology-driven discovery not only in battery materials but also in catalytic, pharmaceutical, and structural domains.

Several challenges remain before the full implementation of autonomous morphology design becomes a standard practice. First, applicability is limited to the present training domain and image-based objectives (single reactor and restricted pH-temperature window); extrapolation and strict physical consistency are limited, and federated learning across routes is needed for generality. Second, electrochemical performance is still analyzed offline; incorporating cycling data directly into the loss function would create a fully closed loop that couples structure and property optimization. Third, residual errors associated with complex kinetics–thermodynamics coupling could be reduced by augmenting the training set around these regions or by introducing physics-informed priors.

The ongoing work integrates multi-reactor datasets and streams real-time electrochemical feedback, with all code and pretrained weights to be released under an open-source license. Coupling this image-driven inverse-design paradigm with robotic synthesis and high-throughput imaging holds great promise for achieving truly closed-loop optimization, thereby accelerating the discovery process for lithium-ion batteries and beyond. The framework is modular but transferable only with re-specified inputs/constraints and independent validation for each new system. We anticipate that data-guided morphology engineering will soon advance from proof-of-concept to a standard tool in the materials-by-design platform, ultimately accelerating the decades-long lab-to-fab timeline for morphology-sensitive materials.

4. Experimental section

4.1. Precursor synthesis and data acquisition

A Mn-rich hydroxide precursor, Ni_0.33Mn_0.67(OH)₂, was synthesized via a continuous co-precipitation process in a water-jacketed stirred-tank reactor under a N₂ atmosphere. The concentrations of NaOH and NH₄OH were systematically varied to control pH (9.8–11.0) and ammonia coordination, while maintaining the total metal concentration at 2.0 M (Ni : Mn = 33 : 67). The as-precipitated powders were washed, filtered, and vacuum dried at 100 °C. The detailed reactor setup and synthesis protocol are described in SI (S1.1.1).

The resulting precursors were examined using a SEM (JEOL JCM-6000) at two magnifications (3000 and 15 000) to capture both secondary and primary particle morphologies. A total of 55 distinct synthesis conditions were recorded, each linked with paired SEM images and particle-size data (Microtrac S3500, D₅₀ values). Image acquisition parameters and data-pairing procedures are given in S1.1.2 and S1.1.3.

For lithiation, the hydroxide precursor was mixed with LiOH·H₂O at a Li/(Ni + Mn) molar ratio of 1.38 and calcined at 850 °C for 10 h to obtain Li- and Mn-rich layered oxide (Li_1.16Ni_0.28Mn_0.56O₂). Electrode fabrication and electrochemical assembly details are provided in S1.1.4.

4.2. Morphology quantification and digital image analysis

To transform raw microscopy data into quantitative morphological descriptors, we implemented the digital image analysis framework for characterizing both primary and secondary particle morphologies (details in S1.2).

Primary-particle features were characterized via wavelet-based texture analysis, capturing hierarchical structural roughness and anisotropy directly from 15 000× magnified SEM images without explicit particle segmentation (S1.2.1). The texture energy, computed as the mean-square magnitude of wavelet coefficients, served as a scalar metric, reflecting morphological complexity.

Secondary-particle morphology was quantified through instance segmentation using the Segment Anything Model (SAM) to identify individual particle boundaries from 3000× magnified images. Circularity-based sphericity (Ψ = 4πA P⁻², where Ψ denotes the sphericity, A is the projected area of the particle, and P is its perimeter.) and image-derived D₅₀ values were computed from the segmented masks (S1.2.2). Ensemble-level means (µ) and standard deviations (SD) of these metrics were used as quantitative condition-level descriptors.

4.3. Conditional image generation via diffusion modeling

A diffusion-based generative model (adapted from stable diffusion) was employed to synthesize realistic precursor morphologies under specified synthesis parameters (S1.3). The model operates in the latent space of a variational autoencoder (VAE) and was augmented with a ControlNet module to encode user-defined process conditions (e.g., pH, NH₄OH concentration, and stirring rate).

During training, the base diffusion weights were frozen while ControlNet layers were optimized via denoising score-matching (ε-prediction) using all available labeled images. Model convergence was monitored using the peak signal to noise ratio (PSNR) and structural similarity (SSIM) metrics, applying early stopping when PSNR > 34 dB and SSIM > 0.965 stabilized within 10 epochs. These training details and architectural schematics are fully described in S1.3.

4.4. Inverse design of synthesis conditions

To identify optimal synthesis parameters for desired morphologies, we developed an inverse prediction framework combining the trained ControlNet-guided generator with particle swarm optimization (PSO) (S1.4).

Users may specify target attributes such as D₅₀ (D), sphericity (M), standard deviation of sphericity (S), and texture (T) numerically or through reference images. The algorithm generates candidate parameter sets, produces corresponding synthetic SEM-like images, quantifies their morphology, and iteratively minimizes a weighted objective function:

where w₁, w₂, w₃ and w₄ balance the influence of size, shape, and texture fidelity.

The optimization proceeds until convergence to a minimal F, yielding synthesis conditions that reproduce the target morphological characteristics. Full mathematical formulation and implementation details are provided in S1.4.

This integrated workflow bridges experiment, quantitative image analytics, and generative modeling to establish a closed-loop system for both forward prediction of morphology and inverse design of synthesis conditions. All algorithms, training parameters, and implementation codes are detailed in SI Section S1.

Author contributions

G. C., C. L., K. J., and I. P. conceived the original idea and designed the research project. G. C., J. K., and K. J. carried out precursor co-precipitation and data collection. C. L. and I. Y. performed image analysis, generation, and optimization model development. G. C., J. K., and I. P. conducted electrochemical evaluation. G. C., C. L., K. J., and I. P. wrote the manuscript with input from all authors. K. J. and I. P. supervised all aspects of the research.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data supporting the findings of this study are included in the main article and the supplementary information (SI). The supplementary information contains additional experimental details, model descriptions, and supporting figures and tables related to the main text. See DOI: https://doi.org/10.1039/d5mh01850a.

Due to company data policies, the raw datasets used for model training cannot be made publicly available; however, further details may be provided by the corresponding author upon reasonable request within confidentiality constraints.

The custom code developed for image analysis, diffusion-based image generation, and optimization is provided as a zip file.

Acknowledgements

This work was supported by POSCO Holdings and the National Supercomputing Center with supercomputing resources including technical support (KSC-2022-CRE-0402). This research was also supported by the Regional Innovation System & Education (RISE) program funded by the Ministry of Education (MOE) and the Jeollanamdo, Republic of Korea (2025-RISE-14-003) and the Sunchon National University Glocal University Fund in 2025.

References

1. H. M. Hau, et al., Earth-abundant Li-ion cathode materials with nanoengineered microstructures, Nat. Nanotechnol., 2024, 19, 1831–1839.
2. Y. Li, et al., Ductile 2-GPa steels with hierarchical substructure, Science, 2023, 379, 168–173.
3. W. Zuo, et al., Li-rich cathodes for rechargeable Li-based batteries: reaction mechanisms and advanced characterization techniques, Energy Environ. Sci., 2020, 13, 4450–4497.
4. G. Choi, et al., Unraveling and regulating superstructure domain dispersion in lithium-rich layered oxide cathodes for high stability and reversibility, Energy Environ. Sci., 2024, 17, 4634–4645.
5. Y. Lee, et al., Elucidating and controlling phase integration factors in Co-free Li-rich layered cathodes for lithium-ion batteries, Mater. Horiz., 2025, 12, 3731–3742.
6. L. Chen, et al., Hierarchical Li_1.2Ni_0.2Mn_0.6O₂ Nanoplates with Exposed {010} Planes as High-Performance Cathode Material for Lithium-Ion Batteries, Adv. Mater., 2014, 26, 6756–6760.
7. J. Kim, et al., Data-driven insights into the reaction mechanism of Li-rich cathodes, Energy Environ. Sci., 2025, 18, 4222–4230.
8. Y. Lee, et al., Elucidating and controlling phase integration factor in Co-free Li-rich layered cathode for lithium-ion batteries, Mater. Horiz., 2025, 12(11), 3731–3742.
9. U.-H. Kim, et al., Heuristic solution for achieving long-term cycle stability for Ni-rich layered cathodes at full depth of discharge, Nat. Energy, 2020, 5, 860–869.
10. U.-H. Kim, et al., Microstructure-Controlled Ni-Rich Cathode Material by Microscale Compositional Partition for Next-Generation Electric Vehicles, Adv. Energy Mater., 2019, 9, 1803902.
11. G. Lee, R. Gommers, F. Waselewski, K. Wohlfahrt and A. O’Leary, PyWavelets: A Python package for wavelet analysis, J. Open Source Softw., 2019, 4, 1237.
12. S. Arivazhagan and L. Ganesan, Texture classification using wavelet transform, Pattern Recognit. Lett., 2003, 24, 1513–1521.
13. J. Ho, A. Jain and P. Abbeel, Denoising diffusion probabilistic models, Adv. Neural Inf. Process. Syst., 2020, 33, 6840–6851.
14. L. Zhang, A. Rao and M. Agrawala, Adding conditional control to text-to-image diffusion models, in: Proceedings of the IEEE/CVF international conference on computer vision, (2023).
15. J. Kennedy and R. Eberhart, Particle swarm optimization, in Proceedings of ICNN’95 – International Conference on Neural Networks, 1995.
16. C. Xu, S. Guan, L. Li, C. Sun, B. An and X. Geng, Electrochemical properties of LiNi_0.6Co_0.2Mn_0.2O₂ cathode materials prepared with different ammonia content, Coatings, 2021, 11, 932.
17. Z. Wu, et al., Investigating the effect of pH on the growth of coprecipitated Ni_0.8Co_0.1Mn_0.1(OH)₂ agglomerates as precursors of cathode materials for Li-ion batteries, Ceram. Int., 2023, 49, 15851–15864.
18. W. Hua, et al., Unravelling the growth mechanism of hierarchically structured Ni_1/3Co_1/3Mn_1/3(OH)₂ and their application as precursors for high-power cathode materials, Electrochim. Acta, 2017, 232, 123–131.
19. J. Seo, et al., High quality large-scale nickel-rich layered oxides precursor co-precipitation via domain adaptation-based machine learning, InfoMat, 2025, 7, e70031.
20. S. Yang, X. Wang, X. Yang, Z. Liu, Q. Wei and H. Shu, High Tap Density Spherical Li [Ni_0.5Mn_0.3Co_0.2] O₂ Cathode Material Synthesized via Continuous Hydroxide Coprecipitation Method for Advanced Lithium-Ion Batteries, Int. J. Electrochem., 2012, 2012, 323560.
21. R. Rombach, A. Blattmann, D. Lorenz, P. Esser and B. Ommer, High-resolution image synthesis with latent diffusion models, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2022.
22. D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv, 2013, preprint, arXiv:1312.6114 DOI:10.48550/arXiv.1312.6114.
23. L. Fuchs, et al., Generating multi-scale Li-ion battery cathode particles with radial grain architectures using stereological generative adversarial networks, Commun. Mater., 2025, 6, 4.
24. C. F. Mora and A. K. H. Kwan, Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing, Cem. Concr. Res., 2000, 30, 351–358.
25. H. Wadell, Volume, shape, and roundness of rock particles, J. Geol., 1932, 40, 443–451.
26. K. W. Desmond and E. R. Weeks, Influence of particle size distribution on random close packing of spheres, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022204.
27. H. Y. Sohn and C. Moreland, The effect of particle size distribution on packing density, Can. J. Chem. Eng., 1968, 46, 162–167.
28. S. K. Vanimisetti and N. Ramakrishnan, Effect of the electrode particle shape in Li-ion battery on the mechanical degradation during charge–discharge cycling, Proc. Inst. Mech. Eng., Part C, 2012, 226, 2192–2213.
29. P. Barai, Z. Feng, H. Kondo and V. Srinivasan, Multiscale computational model for particle size evolution during coprecipitation of Li-ion battery cathode precursors, J. Phys. Chem. B, 2019, 123, 3291–3303.
30. Y. Yang, S. Xu, M. Xie, Y. He, G. Huang and Y. Yang, Growth mechanisms for spherical mixed hydroxide agglomerates prepared by wcipitation method: A case of Ni_1/3Co_1/3Mn_1/3(OH)₂, J. Alloys Compd., 2015, 619, 846–853.
31. X. Yang, et al., Growth mechanisms for spherical Ni_0.815Co_0.15Al_0.035 (OH)₂ precursors prepared via the ammonia complexation precipitation method, J. Energy Chem., 2021, 53, 379–386.
32. Y. Su, et al., Improved Stability of Layered and Porous Nickel-Rich Cathode Materials by Relieving the Accumulation of Inner Stress, ChemSusChem, 2020, 13, 426–433.
33. Y. Su, et al., High-rate structure-gradient Ni-rich cathode material for lithium-ion batteries, ACS Appl. Mater. Interfaces, 2019, 11, 36697–36704.
34. Y. Su, et al., Exposing the {010} Planes by Oriented Self-Assembly with Nanosheets To Improve the Electrochemical Performances of Ni-Rich Li[Ni_0.8Co_0.1Mn_0.1]O₂ Microspheres, ACS Appl. Mater. Interfaces, 2018, 10, 6407–6414.
35. N. Anansuksawat, T. Sangsanit, S. Prempluem, K. Homlamai, W. Tejangkura and M. Sawangphruk, How uniform particle size of NMC90 boosts lithium ion mobility for faster charging and discharging in a cylindrical lithium ion battery cell, Chem. Sci., 2024, 15, 2026–2036.
36. A. Hafez, Q. Liu, T. Finkbeiner, R. A. Alouhali, T. E. Moellendick and J. C. Santamarina, The effect of particle shape on discharge and clogging, Sci. Rep., 2021, 11, 3309.

---

Footnote

† These authors contributed equally to this work.

---