Predicting how fast crystals grow at the free surface of molecular glasses
Federico
Caporaletti
 *ab,
Martín Eduardo
Villanueva
*ab,
Martín Eduardo
Villanueva
 b,
Sascha
Molitor
ab,
Biao
Zuo
b,
Sascha
Molitor
ab,
Biao
Zuo
 cd and
Simone
Napolitano
cd and
Simone
Napolitano
 *ab
*ab
aLaboratory of Polymer and Soft Matter Dynamics, Université libre de Bruxelles (ULB), Brussels 1050, Belgium. E-mail: federico.caporaletti@ulb.be; simone.napolitano@ulb.be
bExperimental Soft Matter and Thermal Physics (EST), Université libre de Bruxelles (ULB), Brussels 1050, Belgium
cSchool of Chemistry and Chemical Engineering, Key Laboratory of Surface & Interface Science of Polymer Materials of Zhejiang Province, Zhejiang Sci-Tech University, Hangzhou, 310018, China
dZhejiang Provincial Innovation Center of Advanced Textile Technology, Shaoxing, 312000, China
First published on 6th October 2025
Abstract
Organic glasses can crystallize at their free surfaces far more rapidly than in the bulk, a phenomenon that has challenged our understanding of glass dynamics for more than a decade. This behavior is commonly attributed to the enhanced molecular mobility present at interfaces, yet the microscopic origin of such fluctuations has remained elusive. Here we show that surface crystal growth can be understood in terms of collective small displacements (CSD), local rearrangements that enable reshaping of the amorphous packing leading to equilibration in liquids and glasses. Within this framework, crystal growth is governed by the slow Arrhenius process (SAP), the experimental manifestation of CSD. Building on this concept, we develop a minimal model that quantitatively predicts crystal growth rates at free surfaces from thermodynamic and energetic considerations. The model accurately reproduces both the magnitude and temperature dependence of growth rates for 14 different organic molecules, spanning a large range of glass transition temperatures and intermolecular interactions, with direct implications for pharmaceuticals and organic electronics. More broadly, our results establish CSD as the microscopic mechanism underlying fast surface crystal growth, offering a predictive framework to anticipate and ultimately control the properties of glasses and crystals.
New conceptsThe growth of crystals at the free surface of molecular glasses is known to be anomalously fast, yet the physical origin of this behavior remains elusive. We show that this process can be quantitatively described by collective small displacements (CSD), localized molecular rearrangements that reorganize the amorphous phase and promote equilibration. In this framework, the kinetics of surface crystal growth are governed by the slow Arrhenius process (SAP), which provides the experimental signature of CSD. Linking surface growth rates to the SAP timescale yields a predictive model that accurately captures the temperature dependence of growth across 14 chemically diverse organic molecules. Unlike traditional approaches based on mass transport or structural relaxation, our model reveals a universal scaling law rooted in localized collective displacements at the growth front. Our framework requires only thermodynamic or dielectric relaxation input and can be applied even when growth data are lacking. By connecting ordering kinetics to a well-defined molecular process, this framework enables quantitative and transferable predictions, which may lead to new strategies for controlling order formation in pharmaceuticals, electronics, and hybrid materials through the tuning of intrinsic amorphous dynamics. |
The growth of crystals from glassy materials is of central interest in a wide number of applications that require the formation1 or inhibition of ordered structures.2 In the pharmaceutical industry, for example, optimizing drug crystallization ensures safe and effective control of physical properties that directly impact bioavailability, stability, and toxicity.3 Crystallization is also a critical process in organic electronics: molecular orientation and presence of defects, in fact, significantly influence the optical and electrical properties of the constituent materials;4 in addition to that, precise control of crystal growth can also lead to improved efficiency, stability, and lifespan of electronic devices.5
Predicting how fast crystals form in operational and storage conditions remains, however, a challenging task. The Wilson–Frenkel model6,7 indicates that the growth of crystalline domains is primarily constrained by the mechanisms of mass transport occurring within the liquid phase. This theoretical approach is validated by the empirical relationship found between the growth rate and the self-diffusion coefficient across various classes of substances, particularly when a considerable degree of undercooling is achieved.8
Importantly, this approach cannot predict how fast crystal grow below the glass transition temperature, Tg, the temperature regime where materials are usually stored. Below Tg crystals tend to grow in a molecule-by-molecule fashion9 resulting in growth rates significantly larger—sometimes by several orders of magnitude10—than what is anticipated on the basis of a simple extrapolation from the high-temperature liquid-state behavior. Previous work rationalizes these findings in terms of the glass-to-crystal (GC) mode, a fast growth mechanism typical of glassy materials, whose origin is still debated.9,11–17
Recent evidence suggests the GC growth to be mediated by a nonequilibrium interface between the crystal and liquid phases.15,18 Although this mechanism facilitates the formation of crystalline fibers up to several tens of K above Tg, heating the material to the point where fluidity exceeds a certain threshold results in a decreased efficiency of GC in forming large crystals.17
These abrupt changes in crystal formation18 and enhanced growth rates are also frequently observed on the free surface of glasses.2,19–24 Understanding surface crystal growth has both fundamental and technological importance. Free surfaces of organic glasses exhibit enhanced mobility, offering a unique probe of nonequilibrium crystallization dynamics. In practice, surface growth can limit the stability of amorphous pharmaceuticals by initiating crystallization at exposed interfaces, or degrade organic electronic devices through unwanted ordering at film surfaces. Cracks and defects further accelerate these processes by exposing fresh free surfaces, underscoring the need for a quantitative description of surface crystal growth.
Providing a quantitative description of crystal growth at a free surface is, however, particularly challenging because of the peculiar nature of the process. In bulk crystallization, a growing seed is always surrounded by amorphous molecules, so that virtually any molecule in the vicinity can contribute to growth. In contrast, a surface crystal layer develops at the interface between free space, bulk and an amorphous surface phase, the latter playing the dominant role.20,25 Importantly, these surface crystals may protrude up to a few hundreds of nanometers above the glassy surface,20 such that advancing the crystal front by a single molecular diameter requires the coordinated participation of many surface molecules.25 As an illustration, in the time it takes for a surface indomethacin molecule to diffuse and travel 100 nm, the crystal growth front advances merely 1 nm.25
Over the years, several explanations have been put forward to account for these phenomena, including reductions of crystallization-induced stress26,27 and perturbations in molecular packing.27 The interpretation most widely accepted today is that faster crystal growth reflects enhanced molecular mobility, a feature characteristic of free surfaces in both soft and hard materials.28–32
Interestingly, surface crystal growth and GC mode involve similar thermal barriers,15,22 hinting that these distinct equilibration phenomena are the manifestation of the same underlying microscopic process. This relaxation process, operative not only adjacent to interfacial layers but also within the core of materials, would eventually be more efficient in guiding the conversion of glasses (and liquids) into crystals in the proximity of a free surface.
Previous studies tried to identify such a microscopic process using empirical relationships linking, through comparison of activation energy barriers, molecular-scale fluctuations to macroscopic phenomena.33,34 In practical terms, this approach requires identifying the molecular relaxation process such that the product of its timescale and the growth rate remains constant across different temperatures. The reasoning follows a modified Stokes–Einstein relation, originally expressed as Dη/T ∼ constant. In this formulation, the growth rate u takes the place of the diffusion coefficient D, while the viscosity η is estimated through the molecular time scale tmol. When the relevant thermal activation barriers exceed about 10 kJ mol−1, the explicit temperature dependence becomes negligible, reducing the expression to utmol ∼ constant. The application of this method to commonly studied microscopic processes appears impractical. The α-process, the mechanism responsible for viscous flow, requires creating large gaps and cooperative rearrangements at the intermolecular level to allow substantial movements; below Tg such large displacements are extremely slow, with timescales often exceeding those necessary to crystallize the entire surface. For example, surface crystals of N,N′-bis(3-methylphenyl)-N,N′-diphenylbenzidine (TPD)—a small molecule used as a protipycal hole transport component in organic electronic devices and blue-violet light emitting material35,36—grow up to 1 nm s−1 at room temperature (see Fig. 1), which means more than 30 K below Tg, where the α-relaxation requires geological times. Moreover, the thermal barrier for the surface crystallization of TPD, akin to other small organic molecules,2,15,19,21–23,34,37–43 remains constant across all temperatures, significantly contrasting with the experimental results observed for the α-modes. Instead, temperature-invariant thermal barriers are observed in what are known as secondary (β-, γ-, …) processes,44 but linking these microscopic mechanisms to crystal growth is not possible, because their activation energies do not consistently align with those required for crystal growth.34
 | ||
| Fig. 1 (A) Time evolution of increment in the length, L, of crystals growing at the free surface of TPD above and below the material Tg (= 333 K). Symbols are experimental data, while continuous lines provide the expected time evolution of the crystal length L = L0 + u·t, where the linear growth rate u was predicted by our model using the value of U00, see eqn (3), obtained from measurements conducted on the small molecules listed in Fig. 3 and the thermal barrier provide by CSD model;45 see Fig. S2 for more information on the kinetics. (B) The experimental values of the surface crystallization rates (light blue diamonds) are shown together with the self-diffusion rate31 of TPD estimated from the characteristic timescale of the structural relaxation; the logarithm of these quantities is plotted as a function of the inverse temperature, because in such representation straight lines correspond to constant activation barriers. The continuous light blue line depicts the predictions of eqn (3), with the shaded area indicating one standard deviation. | ||
A possible route to identifying the molecular process that governs crystal growth in the glassy state comes from recent theoretical developments suggesting that materials can also relax through collective small displacements (CSD),45 not requiring the large hops typical of the α-modes. Such molecular rearrangements would be at the origin of the slow Arrhenius process (SAP), a relaxation process observed in the dielectric response of polymers46 and small organic molecules,47 and characterized by a material-dependent, temperature-invariant activation barrier (ESAP on the order of 100 kJ mol−1, ≈40kBT at room temperature), often exceeding those observed for (β-, γ-, …).46
In this Communication, we establish a direct connection between the fast growth of crystals at free surfaces of organic glasses and the collective small displacements that govern local equilibration in amorphous systems. Building on this idea, we develop a minimal model that provides quantitative predictions of surface growth rates from the expected dynamics of amorphous packing consolidation, which can be derived through thermodynamics and simple energetic considerations. Our central assumption is that crystallization proceeds through nonequilibrium kinetics governed by the slow Arrhenius process, the experimental manifestation of CSD. Applied to a broad set of small organic molecules of technological interest, our model successfully captures both the absolute values and the temperature dependence of the observed growth rates. The SAP has a set of interesting properties that strongly distinguish it from other microscopic mechanisms and make it a suitable candidate to achieve a molecular-scale description of crystal growth. The timescale over which this process relaxes, τSAP ∼ exp(ESAP/RT) —where R is the gas constant—is insensitive to changes in mechanical stresses48 and density46,49 equivalent to those experienced by organic materials during temperature jumps as large as 200 K. The SAP is also connected to high-temperature flow,46,50 which shares the same activation barrier. This feature is reminiscent of the behavior observed in densely packed metallic glasses,51,52 where groups of atoms diffuse and flow as if they were in a liquid even at temperatures well below their Tg. This property suggests that molecular rearrangements beneath the SAP occur in a constrained space, significantly smaller than the typical α-relaxation range (1–3 nm at Tg), indicating that SAP-dynamics does not necessitate extensive cooperative movements. These concepts are supported by the detection of the SAP in the glassy state,46,47,49 a regime where large hops and large-scale diffusion do not occur on the laboratory timescale.
Consistently with these ideas, White et al. have recently proposed a mechanistic picture of the SAP in terms of a set of collective displacements,45 whose relaxation involves length scales and timescales smaller than those of the structural process. The energy exchange for each of the single movements that concur to collective small displacements (CSD) is given by RT00 ≈ 3.5 kJ mol−1, with T00 ≈ 435 K, a temperature which—being valid for a broad set of organic molecules—is a signature of the SAP. It is important to note that this energy is indicative of very localized molecular rearrangements; for context, the thermal barriers linked to trans/gauche transitions are five times greater. At the molecular scale, collective motion is limited by the interaction energy between nonbonded species,53 which leads to a description of ESAP in terms of the thermodynamic properties of the system.45 Based on this theoretical framework, the equilibration rate of macroscopic properties facilitated by the SAP is described by:
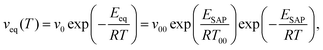 | (1) |
Using eqn (1) to predict the rate at which crystals grow on the surface of glasses requires identifying the molecular rearrangements that contribute to the addition of molecules to a crystalline seed. Unlike for dilute solutions, on a free surface all molecules are already present in proximity of the growth front, meaning that diffusion over distances larger than one molecular diameter should not be considered. Thus, we anticipate that small-scale displacements that result in the SAP45 are sufficient to rearrange the amorphous packing and bring molecules to the correct position and orientation, allowing incorporation in the crystalline phase. Recent work54 supports this hypothesis by demonstrating that the thermal barrier of orientational ordering observed on the free surface of glasses55,56 aligns with that of SAP.
To provide a quantitative picture, and based on the model hypothesis that v00 is a constant, we considered the number of molecules added to the growth front within one SAP relaxation time should not depend on the chemical composition of the glass nor the temperature. Indicating with L the crystal length at a given time t and with a the molecular diameter,57 this rationale implies a scaling law of the type
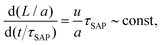 | (2) |
Due to the low nucleation rate in the glassy state, we first annealed the samples at Tg + 5 K for 300 s and then quenched the films at the temperature where crystallization was monitored under isothermal conditions. The surface growth rate was then determined by analyzing images obtained by optical (OM) and atomic force microscopy (AFM); see Fig. S1 and S2 of the SI. The measured values of u (see blue markers in Fig. 1B for the case of TPD) show an Arrhenius temperature dependence, with activation energies of the order of 100 kJ mol−1. Significantly, even when the temperature is over 100 K below Tg (see Fig. 3)—which is many tens of K below the point at which α-relaxation is predicted to involve timescales31 vastly surpassing the universe's age—, crystal growth remains feasible. In contrast, at such temperatures, the SAP relaxes within a few hours. We determined the values of τSAP by analysis of the dielectric spectra of small molecules, using a standard approach;47 see more details in the SI.
We combined the results of these independent sets of experiments in Fig. 2, where we show that the dimensionless ratio 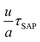 does not change significantly with temperature or material composition, as expected. This condition implies that the thermal barrier for the growth of crystals on a free surface (−R∂
does not change significantly with temperature or material composition, as expected. This condition implies that the thermal barrier for the growth of crystals on a free surface (−R∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u/∂T ≡)Esg ≈ ESAP, which allows us to apply the formalism of eqn (1) to study surface crystallization.
u/∂T ≡)Esg ≈ ESAP, which allows us to apply the formalism of eqn (1) to study surface crystallization.
 | ||
Fig. 2 Experimental validation of eqn (2). For molecules for which we could directly access τSAPvia dielectric measurements we confirm, in panel (A), that the dimensionless quantity  remains unaffected by both temperature and material composition, within experimental uncertainties. In panel (B), we present the temperature-averaged values of remains unaffected by both temperature and material composition, within experimental uncertainties. In panel (B), we present the temperature-averaged values of 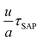 for the materials shown in panel (a) and other compounds where we could prediuct τSAPvia the CSD model45 (crossed-out symbols), which requires PVT data as input; see SI for derivation. The dashed lines in (a) and (b) indicate the expected value of this quantity estimated by multiplying the attempt rate of the SAP relaxation time45 (2.2 ± 0.3) × 10−2 s, for the parameter U00 obtained by fitting the data of Fig. 3 to eqn (3). These results supports the key hypothesis of our model, indicating that crystal growth share the same thermal barrier of the slow Arrhenius process and considering that the number of molecules incorporated at the growth front during one τSAP is constant. Full names of the materials are in Fig. 3 and in the SI. for the materials shown in panel (a) and other compounds where we could prediuct τSAPvia the CSD model45 (crossed-out symbols), which requires PVT data as input; see SI for derivation. The dashed lines in (a) and (b) indicate the expected value of this quantity estimated by multiplying the attempt rate of the SAP relaxation time45 (2.2 ± 0.3) × 10−2 s, for the parameter U00 obtained by fitting the data of Fig. 3 to eqn (3). These results supports the key hypothesis of our model, indicating that crystal growth share the same thermal barrier of the slow Arrhenius process and considering that the number of molecules incorporated at the growth front during one τSAP is constant. Full names of the materials are in Fig. 3 and in the SI. | ||
To this purpose we fitted the growth rate values of the compounds reported in Fig. 2B to the expression
 | (3) |
 | ||
| Fig. 3 For 15 different small organic molecules [tris(4-carbazoyl-9-ylphenyl)amine (TCTA); rubrene (RUB); grisofulvin (GSF); m-mtdata (MMT); trinitrobenzene (TNB); celecoxib (CEL); felodipine (FEL); γ-indomethacin (IMC γ); α-indomethacin (IMC α); nifedepine (NIF); acetaminophen (APAP); clotrimazole (CMZ); nimesulide (NIM) ortho-terphenyl (OTP); clofazimine (CFZ)], we provide the logarithm of the surface growth rate u determined by experiments (symbols) as a function of the inverse temperature. For GSF we also report the crack induced growth rate (white crosses) from Shi et al.41 The continuous lines depict the fits of these data to eqn (3), with the shaded area indicating one standard deviation. We determined log(U00/s−1) = 3.8± 0.2 by fitting data from molecules for which the thermal barrier of the SAP or that of CSD were available (see colored markers). This same attempt rate value was then fixed and considered for all the other molecules (gray markers). R2 is the coefficient of determination quantifying the goodness of the fit to the model for T < Tg: R2 = 1 indicates that the modeled values exactly match the experimentally observed values. In the case of NIF, GSF, FEL and IMG (γ-polymorph) for which data are available also above Tg and the growth is not disrupted by the onset of fluidity, fits of the experimental results over the entire temperature range provide R2 values of 0.96, 0.95, 0.9 and 0.97 respectively. The data for CMZ are available for both polymorphs (form II is reported in the SI, Fig. S11) only above Tg: the corresponding R2 are 0.96 and 0.97, respectively. For TCTA, APAP TNB, CEL, IMC (α and γ polymorphs), for which PVT data were available,59–61 we also provide, with black dashed lines and error bars, the predictions of the temperature dependence of u built up considering the just-mentioned attempt rate and values of the thermal barrier of crystal growth provided by CSD.45 In the case of OTP, we report also u(T) provided by the thermal barrier predicted by the CSD from PVT data62 and an attempt rate 275 times larger than that valid for other molecules (gray dotted-dashed line). See SI for details on this procedure and chemical names of the compounds. | ||
To further test the predictive character of our approach, in Fig. 1 we compare the experimental results of TPD and the predictions of eqn (3), where we used the value of the attempt rate U00—as obtained from the global fitting procedure described above, which did not include TPD data—and the SAP thermal barrier provided by CSD. In Fig. 2(B) we show that eqn (2) also holds for materials where τSAP was estimated from PVT data using the CSD model.45
Fig. 3 also reports the predictions of this approach for all those molecules for which we could determine εLCL based on thermodynamic data from the literature. Importantly, this approach captures the correct thermal barrier of OTP; see dashdotted line in Fig. 3. As shown in Table S2 and Fig. S8, the thermal barrier for surface crystal growth (Esg) quantitatively agrees with the thermal barrier of the SAP and the values predicted by the CSD model for samples where these quantities were available. As already noted, the materials used to determine U00 all exhibit nearly the same activation barrier for the growth rate (≈90 kJ mol−1), despite their very different Tg values, molecular structures, and interaction strengths. In fact, they also share the same thermal expansion coefficient (≈5 × 10−4 K−1), a result that naturally emerges from the implementation of CSD within the LCL model. This finding highlights that commonly used macroscopic or chemical descriptors might not be the key parameters controlling surface crystal growth, which appears instead to governed by more fundamental features of amorphous packing and its collective dynamics.
Although we apply the model only in the glassy state (the R2 values in Fig. 3 refer exclusively to growth rates measured for T < Tg), for some systems the predicted trend extends even above Tg. This observation is consistent with previous findings that needle-like crystals can grow with an activation barrier similar to that of crystal growth at the free surface also in the liquid state. In this context, we stress that our predictions are not limited to thin films but apply as well to crystallization events in bulk samples, such as those driven by crack formation,15,41 thereby reinforcing the generality of the framework; see white crosses in the grisofulvin (GSF) panel. Cracks and bubbles—commonly formed during fast processing, or in the presence of uneven thermal expansion in hybrid materials—introduce free surface-like conditions within the bulk, allowing for a significant acceleration in crystal growth, with respect to unstressed samples.
We anticipate that our method can be also applied to compounds that have not yet been synthesized, for which analytical methods could provide a PVT characterization. With further refinement, the model could also be applied to predict GC growth rates, considering the large affinity between this phenomenon and surface growth. Similarly, we expect that with increasing temperature, the more isotropic-modes will eventually overrule the (surface) ordering driven by the SAP, which leads to changes observed for GC and surface crystallization1 in small organic molecules. We stress that our methodology can be successfully applied to small organic molecules spanning a wide range of glass transition temperatures (301–423 K) and intermolecular interactions—from weak anisotropic van der Waals forces, as in TCTA, to strong directional hydrogen bonding, as in IMC. However, this formalism does not extend to polymers or other large molecules In fact, the enhancement of growth at free surfaces is confined to a very shallow region, decaying within only 2–3 nm of depth. As a result, while smaller molecules are strongly affected—since a significant fraction of their volume lies within the free surface layer30—this effect vanishes for larger molecules, and already for oligomers no appreciable contrast between free-surface growth rates and bulk GC growth is expected.
While our framework reproduces the behavior of many molecular glasses, deviations appear for low-Tg compounds; see the lower part of Fig. 3, where the panels are arranged from high to low Tg, proceeding left to right and then top to bottom and Fig. 4. At comparable reduced temperatures (T/Tg), these systems are at lower absolute T, where the SAP shifts to longer times. This may contribute to an underestimation of the observed growth rates as in this regime other microscopic processes might also become relevant. We further note that the CSD model underpinning our description was developed using approximations valid around T00 (≈435 K),45 which are expected to lose accuracy at sufficiently low or high temperatures. At the lower end of the explored range (T < 300 K), we are likely to approach this limit, suggesting that further refinement of the theoretical framework could extend its predictive power to a broader class of materials.
 | ||
| Fig. 4 Goodness of fit (R2) of eqn (3) as a function of the glass transition temperature for the systems reported in Fig. 3. The gray-dashed line is a guide for the eye. | ||
Finally, we note that earlier work had already hinted, albeit only in an approximate form,25,37 at relations similar to eqn (3). In particular, by analyzing the connection between diffusion coefficients and crystal growth rates, expressions of the type u/D ≈ const were proposed, which closely resemble our assumption u/a·τSAP = const. This correspondence suggests that surface diffusion may represent the manifestation of a molecular mobility akin to that described by collective small displacements. Future studies will be needed to explore this connection in greater depth.
Conflicts of interest
There are no conflicts to declare.Data availability
Data are available upon reasonable request to the corresponding authors.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5mh01335f.
Acknowledgements
We thank Mark Ediger and Lian Yu (University of Wisconsin-Madison, USA) for fruitful discussions on the microscopic origin of surface crystal growth and for valuable comments on our manuscript. F. C. is a Chargé de Recherche of the Fonds de la recherches scientifique-FNRS. We acknowledge financial support from Action de Recherche Concertée ULB under grant ARC “COHESAP”.References
- J. S. Bangsund, T. R. Fielitz, T. J. Steiner, K. Shi, J. R. Van Sambeek and C. P. Clark,
et al., Formation of aligned periodic patterns during the crystallization of organic semiconductor thin films, Nat. Mater., 2019, 18(7), 725–731 CrossRef CAS PubMed
.
- L. Zhu, J. Jona, K. Nagapudi and T. Wu, Fast surface crystallization of amorphous griseofulvin below Tg, Pharm. Res., 2010, 27, 1558–1567 CrossRef CAS
.
- J. Chen, B. Sarma, J. M. Evans and A. S. Myerson, Pharmaceutical crystallization, Cryst. Growth Des., 2011, 11(4), 887–895 CrossRef CAS
.
- J. Xu, S. Wang, G. J. N. Wang, C. Zhu, S. Luo and L. Jin,
et al., Highly stretchable polymer semiconductor films through the nanoconfinement effect, Science, 2017, 355(6320), 59–64 CrossRef CAS PubMed
.
- M. J. Han, D. Wei, Y. H. Kim, H. Ahn, T. J. Shin and N. A. Clark,
et al., Highly oriented liquid crystal semiconductor for organic field-effect transistors, ACS Cent. Sci., 2018, 4(11), 1495–1502 CrossRef CAS
.
- H. W. Wilson, XX. On the velocity of solidification and viscosity of super-cooled liquids, London, Edinburgh Dublin Philos. Mag. J. Sci., 1900, 50(303), 238–250 CrossRef
.
-
I. I. Frenkel, Kinetic theory of liquids, Dover Publications, 1955 Search PubMed
.
- S. F. Swallen and M. Ediger, Self-diffusion of the amorphous pharmaceutical indomethacin near Tg, Soft Matter, 2011, 7(21), 10339–10344 RSC
.
- T. Hikima, Y. Adachi, M. Hanaya and M. Oguni, Determination of potentially homogeneous-nucleation-based crystallization in o-terphenyl and an interpretation of the nucleation-enhancement mechanism, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(6), 3900 CrossRef CAS PubMed
.
- Y. Sun, H. Xi, M. Ediger and L. Yu, Diffusionless crystal growth from glass has precursor in equilibrium liquid, J. Phys. Chem. B, 2008, 112(3), 661–664 CrossRef CAS PubMed
.
- R. Greet and D. Turnbull, Glass transition in o-terphenyl, J. Chem. Phys., 1967, 46(4), 1243–1251 CrossRef CAS
.
- H. Ishida, T. Wu and L. Yu, Sudden rise of crystal growth rate of nifedipine near Tg without and with polyvinylpyrrolidone, J. Pharm. Sci., 2007, 96(5), 1131–1138 CrossRef CAS PubMed
.
- T. Konishi and H. Tanaka, Possible origin of enhanced crystal growth in a glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(22), 220201 CrossRef
.
- J. D. Stevenson and P. G. Wolynes, The ultimate fate of supercooled liquids, J. Phys. Chem. A, 2011, 115(16), 3713–3719 CrossRef CAS PubMed
.
- C. T. Powell, H. Xi, Y. Sun, E. Gunn, Y. Chen and M. Ediger,
et al., Fast crystal growth in o-terphenyl glasses: a possible role for fracture and surface mobility, J. Phys. Chem. B, 2015, 119(31), 10124–10130 CrossRef CAS
.
- M. H. R. Acosta, D. R. Cassar, L. R. Rodrigues, J. M. C. Baldin and E. D. Zanotto, Diffusion proxies reveal the dynamic process in supercooled and glassy lithium diborate, Ceram. Int., 2024, 50(19), 35549–35556 CrossRef
.
- D. Musumeci, C. T. Powell, M. Ediger and L. Yu, Termination of solid-state crystal growth in molecular glasses by fluidity, J. Phys. Chem. Lett., 2014, 5(10), 1705–1710 CrossRef CAS
.
- D. Musumeci, M. Hasebe and L. Yu, Crystallization of organic glasses: How does liquid flow damage surface crystal growth?, Cryst. Growth Des., 2016, 16(5), 2931–2936 CrossRef CAS
.
- T. Wu and L. Yu, Surface crystallization of indomethacin below Tg, Pharm. Res., 2006, 23, 2350–2355 CrossRef CAS PubMed
.
- Y. Sun, L. Zhu, K. L. Kearns, M. D. Ediger and L. Yu, Glasses crystallize rapidly at free surfaces by growing crystals upward, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(15), 5990–5995 CrossRef CAS
.
- M. Hasebe, D. Musumeci, C. T. Powell, T. Cai, E. Gunn and L. Zhu,
et al., Fast surface crystal growth on molecular glasses and its termination by the onset of fluidity, J. Phys. Chem. B, 2014, 118(27), 7638–7646 CrossRef CAS
.
- C. Huang, S. Ruan, T. Cai and L. Yu, Fast surface diffusion and crystallization of amorphous griseofulvin, J. Phys. Chem. B, 2017, 121(40), 9463–9468 CrossRef CAS
.
- K. Wang and C. C. Sun, Crystal growth of celecoxib from amorphous state: polymorphism, growth mechanism, and kinetics, Cryst. Growth Des., 2019, 19(6), 3592–3600 CrossRef CAS
.
- Y. Yang, H. Tian, S. Napolitano and B. Zuo, Crystallization in thin films of polymer glasses: the role of free surfaces, solid interfaces and their competition, Prog. Polym. Sci., 2023, 101725 CrossRef CAS
.
- C. W. Brian and L. Yu, Surface self-diffusion of organic glasses, J. Phys. Chem. A, 2013, 117(50), 13303–13309 CrossRef CAS PubMed
.
- J. Schmelzer, R. Pascova, J. Möller and I. Gutzow, Surface-induced devitrification of glasses: the influence of elastic strains, J. Non-Cryst. Solids, 1993, 162(1–2), 26–39 CrossRef CAS
.
- O. Farrance, R. Jones and J. Hobbs, The observation of rapid surface growth during the crystallization of polyhydroxybutyrate, Polymer, 2009, 50(15), 3730–3738 CrossRef CAS
.
- L. Zhu, C. Brian, S. Swallen, P. Straus, M. Ediger and L. Yu, Surface self-diffusion of an organic glass, Phys. Rev. Lett., 2011, 106(25), 256103 CrossRef CAS
.
- W. Zhang, C. W. Brian and L. Yu, Fast surface diffusion of amorphous o-terphenyl and its competition with viscous flow in surface evolution, J. Phys. Chem. B, 2015, 119(15), 5071–5078 CrossRef CAS
.
- W. Zhang and L. Yu, Surface diffusion of polymer glasses, Macromolecules, 2016, 49(2), 731–735 CrossRef CAS
.
- Y. Zhang and Z. Fakhraai, Decoupling of surface diffusion and relaxation dynamics of molecular glasses, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(19), 4915–4919 CrossRef CAS PubMed
.
- Y. Li, C. Bishop, K. Cui, J. Schmidt, M. Ediger and L. Yu, Surface diffusion of a glassy discotic organic semiconductor and the surface mobility gradient of molecular glasses, J. Chem. Phys., 2022, 156, 094710 CrossRef CAS
.
- Y. Sun, H. Xi, M. Ediger, R. Richert and L. Yu, Diffusion-controlled and “diffusionless” crystal growth near the glass transition temperature: Relation between liquid dynamics and growth kinetics of seven ROY polymorphs, J. Chem. Phys., 2009, 131, 074506 CrossRef
.
- C. T. Powell, K. Paeng, Z. Chen, R. Richert, L. Yu and M. Ediger, Fast crystal growth from organic glasses: comparison of o-terphenyl with its structural analogs, J. Phys. Chem. B, 2014, 118(28), 8203–8209 CrossRef CAS PubMed
.
- S. Tse, S. Tsang and S. So, Polymeric conducting anode for small organic transporting molecules in dark injection experiments, J. Appl. Phys., 2006, 100, 063708 CrossRef
.
- S. S. Swayamprabha, M. R. Nagar, R. A. K. Yadav, S. Gull, D. K. Dubey and J. H. Jou,
et al., Hole-transporting materials for organic light-emitting diodes: an overview, J. Mater. Chem. C, 2019, 7(24), 7144–7158 RSC
.
- S. Ruan, W. Zhang, Y. Sun, M. Ediger and L. Yu, Surface diffusion and surface crystal growth of tris-naphthyl benzene glasses, J. Chem. Phys., 2016, 145, 064503 CrossRef
.
- S. W. Park, J. M. Choi, K. H. Lee, H. W. Yeom, S. Im and Y. K. Lee, Amorphous-to-crystalline phase transformation of thin film rubrene, J. Phys. Chem. B, 2010, 114(17), 5661–5665 CrossRef CAS PubMed
.
- Q. Shi and T. Cai, Fast crystal growth of amorphous griseofulvin: relations between bulk and surface growth modes, Cryst. Growth Des., 2016, 16(6), 3279–3286 CrossRef CAS
.
- Y. Chen, Z. Chen, M. Tylinski, M. Ediger and L. Yu, Effect of molecular size and hydrogen bonding on three surface-facilitated processes in molecular glasses: surface diffusion, surface crystal growth, and formation of stable glasses by vapor deposition, J. Chem. Phys., 2019, 150, 024502 CrossRef
.
- Q. Shi, J. Tao, J. Zhang, Y. Su and T. Cai, Crack-and bubble-induced fast crystal growth of amorphous griseofulvin, Cryst. Growth Des., 2019, 20(1), 24–28 CrossRef
.
- L. Zhu, L. Wong and L. Yu, Surface-enhanced crystallization of amorphous nifedipine, Mol. Pharmaceutics, 2008, 5(6), 921–926 CrossRef CAS
.
- U. S. Kestur and L. S. Taylor, Evaluation of the crystal growth rate of felodipine polymorphs in the presence and absence of additives as a function of temperature, Cryst. Growth Des., 2013, 13(10), 4349–4354 CrossRef CAS
.
- F. Caporaletti, S. Capaccioli, S. Valenti, M. Mikolasek, A. Chumakov and G. Monaco, Experimental evidence of mosaic structure in strongly supercooled molecular liquids, Nat. Commun., 2021, 12(1), 1867 CrossRef CAS PubMed
.
- R. P. White, S. Napolitano and J. E. G. Lipson, Mechanistic picture for the slow Arrhenius process (SAP) in glass forming systems: the collective small displacements model, Phys. Rev. Lett., 2025, 134, 098203 CrossRef CAS PubMed
.
- Z. Song, C. Rodrguez-Tinoco, A. Mathew and S. Napolitano, Fast equilibration mechanisms in disordered materials mediated by slow liquid dynamics, Sci. Adv., 2022, 8(15), eabm7154 CrossRef CAS PubMed
.
- F. Caporaletti and S. Napolitano, The slow Arrhenius process in small organic molecules, Phys. Chem. Chem. Phys., 2024, 26(2), 745–748 RSC
.
- E. Thoms, K. Wang, S. Chandran and S. Napolitano, Fast Processing Affects the Relaxation of Polymers: The Slow Arrhenius Process Can Probe Stress at the Molecular Level, J. Phys. Chem. Lett., 2024, 15, 4838–4843 CrossRef CAS PubMed
.
- E. Thoms, C. Li and S. Napolitano, Tracing the slow Arrhenius process deep in the glassy state-quantitative evaluation of the dielectric relaxation of bulk samples and thin polymer films in the temperature domain, J. Chem. Phys., 2024, 160, 034901 CrossRef CAS
.
- B. Wang, M. Sanviti, A. Alegria and S. Napolitano, Molecular mobility of polymers at the melting transition, ACS Macro Lett., 2023, 12(3), 389–394 CrossRef CAS
.
- C. Chang, H. Zhang, R. Zhao, F. Li, P. Luo and M. Li,
et al., Liquid-like atoms in dense-packed solid glasses, Nat. Mater., 2022, 21(11), 1240–1245 CrossRef CAS PubMed
.
- Y. T. Sun, R. Zhao, D. W. Ding, Y. H. Liu, H. Y. Bai and M. Z. Li,
et al., Distinct relaxation mechanism at room temperature in metallic glass, Nat. Commun., 2023, 14(1), 540 CrossRef CAS PubMed
.
- R. P. White and J. E. Lipson, Chain fluids: Contrasts of theoretical and simulation approaches, and comparison with experimental alkane properties, J. Chem. Phys., 2009, 131, 074109 CrossRef PubMed
.
- F. Caporaletti, H. Boch and S. Napolitano, Slow liquid dynamics promotes orientational ordering in a columnar liquid crystalline glass-former, J. Mol. Liq., 2025, 433, 127902 CrossRef CAS
.
- C. Bishop, Z. Chen, M. F. Toney, H. Bock, L. Yu and M. Ediger, Using deposition rate and substrate temperature to manipulate liquid crystal-like order in a vapor-deposited hexagonal columnar glass, J. Phys. Chem. B, 2021, 125(10), 2761–2770 CrossRef CAS PubMed
.
- D. Chatterjee, S. Huang, K. Gu, J. Ju, J. Yu and H. Bock,
et al., Using 4D STEM to probe mesoscale
order in molecular glass films prepared by physical vapor deposition, Nano Lett., 2023, 23(5), 2009–2015 CrossRef CAS
.
- For each system, the lenght a was determined upon optimization of the molecular geometry, see SI for more details.
-
H. E. Pence and A. Williams, ChemSpider: an online chemical information resource, ACS Publications, 2010 Search PubMed
.
- S. S. Dalal, Z. Fakhraai and M. D. Ediger, High-throughput ellipsometric characterization of vapor-deposited indomethacin glasses, J. Phys. Chem. B, 2013, 117(49), 15415–15425 CrossRef CAS
.
- Y. Jin, A. Zhang, S. E. Wolf, S. Govind, A. R. Moore and M. Zhernenkov,
et al., Glasses denser than the supercooled liquid, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(31), e2100738118 CrossRef CAS
.
- H. N. Yang, S. J. He, T. Zhang, J. X. Man, Y. Zhao and N. Jiang,
et al., Molecular orientation and thermal stability of thin-film organic semiconductors, Org. Electron., 2021, 88, 106014 CrossRef CAS
.
- M. Naoki and S. Koeda, Pressure-volume-temperature relations of liquid, crystal, and glass of o-terphenyl: excess amorphous entropies, and factors determining molecular mobility, J. Phys. Chem., 1989, 93(2), 948–955 CrossRef CAS
.
- Y. Gui, Y. Chen, Z. Chen, K. J. Jones and L. Yu, Improving stability and dissolution of amorphous clofazimine by polymer nano-coating, Pharm. Res., 2019, 36, 1–7 CrossRef CAS
.
- Q. Shi, Y. Wang and J. Kong, Crystallization of amorphous nimesulide: The relationship between crystal growth kinetics and liquid dynamics, Molecules, 2023, 28(7), 2919 CrossRef CAS
.
- Q. Shi, Y. Wang, J. Xu, Z. Liu and C. Y. Chin, Fast crystal growth of amorphous nimesulide: implication of surface effects, Struct. Sci., 2022, 78(1), 33–39 CAS
.
- E. Thoms, Z. Song, K. Wang and S. Napolitano, Simple Model to Predict the Adsorption Rate of Polymer Melts, Phys. Rev. Lett., 2024, 132(24), 248101 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2026 |
