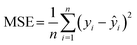Machine learning prediction of acute toxicity with in vivo experiments on tetrazole derivatives

Abstract

This study investigates the application of machine learning techniques to predict the toxicity of tetrazole derivatives, aiding in the identification of environmental risks from chemical exposure. Utilizing LD₅₀ data sourced from the scientific literature and the ChemIDplus database, regression models were developed to forecast acute intraperitoneal toxicity in mice. A machine learning regression model for acute intraperitoneal toxicity in mice was constructed and validated on a test dataset, achieving high accuracy (R² = 0.76 and MSE below 10⁻⁴) and surpassing most of the comparable literature models. Molecular descriptors were computed via Mordred software to explore quantitative structure–activity relationships, and additionally, the model's robustness was demonstrated by measuring the acute toxicity of tetrazole derivatives synthesized through the azido-Ugi reaction.

---

1 Introduction

Organic chemistry plays a crucial role in drug development.^1–5 However, the process of identification and synthesis is complex and time-consuming due to the vast chemical space.^6–8 Researchers often face challenges in identifying effective molecules with low general toxicity.⁹ For example, different acute toxicity in mice is a critical aspect of drug risk management.¹⁰ This toxicity is commonly assessed using 50% lethal dose (LD₅₀), which indicates the quantity of a chemical expected to result in death in 50% of the treated animals within a specified period.^11,12 LD₅₀ studies can be expensive and time-consuming, often requiring large animal cohorts. The chemical space contains an enormous number of different scaffolds. Finding the structures that meet given parameters in such a large array is difficult. Therefore, it is essential to develop alternative methods.^13,14 The use of machine learning algorithms has shown significant promise in the prediction of the general toxicity of compounds.^15,16 The development of predictive models using deep learning and ensemble learning has improved the accuracy and reliability of toxicity predictions. Furthermore, the integration of toxicological data and molecular descriptors enhances the ability of machine learning models to predict toxic outcomes with high accuracy.¹⁷ In particular, such models enable early-stage safety screening in drug discovery by prioritizing low-toxicity candidates from vast libraries, reducing animal testing, and accelerating the transition from synthesis to preclinical evaluation – key steps in identifying safe pharmaceutical leads.

Historically, quantitative structure–activity relationship models have been utilized for the computational prediction of drug promiscuity and toxicity.^18–20 These models establish correlations between biological properties and the specific functional groups present in each compound. While they provide valuable mechanistic insights into predictions, generating these models from random and diverse databases can be challenging. In this context, the growing availability of toxicity databases has facilitated the adoption of machine learning techniques for predicting the toxicity of small molecules, which have gained significant traction in recent years. Currently, numerous quantitative structure–property relationship models have been developed to predict acute toxicity in rodents for organic chemicals. Various mathematical techniques have been employed to create regression models and classification models, including linear regression, random forests, support vector machines, k-nearest neighbors, and neural networks.^21–26 For example, Lei et al. utilized a relevance vector machine in conjunction with other methods (such as k-nearest neighbors, random forest, etc.) to create a regression model for predicting acute oral toxicity in rats, achieving a predictive R² of 0.69 for an external test set comprising 2736 compounds.²⁷ It was highlighted that this method depends on prior knowledge of neighboring experimental data, meaning that the actual predictive capability is influenced by the chemical diversity and structural representation within the training set. Lu et al. constructed prediction models using the local lazy learning method, achieving a maximized coefficient of determination (R²) for large test sets. The regression model based on this technique achieved an R² of 0.608.²⁸ Li et al. proposed that a multi-classification model might be more intuitive for toxicity assessment than a regression model, as classifying toxicity can be easier to interpret.²⁹ The model demonstrated reliable predictive accuracy for each class, achieving overall accuracies of 83.0% and 89.9% on external validation sets I and II, respectively.

It is important to note that classification models are more frequently reported in the literature than regression models. This trend may occur because regression models are often limited by the quantity and quality of available datasets, which are still insufficient when compared to the extensive variety of chemical structures. These limitations can limit the predictive accuracy when utilizing available ML regression models. Consequently, identifying and excluding chemicals that adversely affect the performance of regression models presents a promising approach to address this issue. Moreover, in modern predictive models for vectorizing molecules, fingerprints such as Morgan, the Mol2Vec approach, and Word2Vec are used.³⁰ Despite the satisfactory accuracy of these methods, they have significant limitations, as they do not allow the establishment of direct relationships between the studied properties and the structural parameters of the compounds. This fact can complicate the interpretation of the results and the understanding of the mechanisms of action of drug candidates.

In our study, we utilized molecular descriptors calculated using the Mordred^31,32 software, which provides a detailed analysis of the structural characteristics of the compounds and their influence on the target, which, in turn, contributes to more accurate predictions. Recent advances in deep learning have further revolutionized toxicity prediction, with graph neural networks (GNNs) excelling in capturing structural relationships in molecular graphs, and transformers enabling effective sequence-based modeling for complex chemical representations, providing robust aggregation of multiple models for enhanced generalization.^33–35 However, these state-of-the-art methods, while powerful, often demand significant computational resources and large datasets, posing challenges such as overfitting and scalability issues when applied to moderate-sized toxicity datasets. Herein, we prioritized simpler, interpretable models to ensure accessibility and scalability, and reduce the risk of overfitting, achieving comparable predictive accuracy for early-stage drug safety screening without the complexity of deep learning architectures. To verify the correctness and universality of the model's performance, we synthesized a series of aminotetrazoles whose scaffolds were not present in the original dataset. This decision is driven by the need to assess how the model can predict the properties of new chemical structures that were absent in the training set. Tetrazole rings are known for their promising pharmacological properties and are frequently used in the structure of new pharmaceuticals because all of their parameters matched the Lipinski rule of 5, and they can be easily obtained via azido-Ugi reaction.^36–38 The data obtained by means of the proposed model will help to improve the prediction of the algorithms and reveal new patterns in the relationship between chemical structure and drug activity. Through integration of the toxicological data and molecular descriptors, machine learning models may not only provide valuable insights into the safety and hazards of various chemicals in pharmaceutical and environmental settings, but also spark interest towards potentially promising bioactive molecules, such as aminotetrazoles.

2 Materials and methods

2.1 Dataset and analysis

The compiled dataset contained structures in SMILES format collected from the study by Jain et al., which included data from the ChemIDplus database.^39,40 The original toxicity data consisted of LD50 values measured following intraperitoneal administration in mice.

2.2 Model performance evaluation method

The performance of the machine learning models was evaluated using a holdout dataset: 80% of the data was utilized for training (training set), while 20% remained unused (validation set). The trained machine learning model was then applied to the validation set. To assess the model's efficacy, two key metrics were employed: R² (coefficient of determination) and mean squared error (MSE).

The R² value is calculated using the formula:

where:

• SS_res is the sum of the squares of the residuals (the differences between predicted and actual values);

• SS_tot is the total sum of squares (the variance of the actual values).

A higher R² value suggests a better fit of the model to the data.

The mean squared error (MSE) is calculated using the formula:

where:

• n is the number of observations,

• y_i is the actual value,

• ŷ_i is the predicted value.

Lower MSE values indicate better predictive performance.

2.3 Chemical space analysis

The analysis of the structural diversity was conducted using the open-source software RDKit. For this assessment, the Bemis–Murcko scaffolds were chosen as the evaluation method.⁴¹ This approach allowed the identification and characterization of core structural frameworks within the compounds.

2.4 Descriptors

Molecular descriptors implemented in Mordred were chosen as features reflecting the chemical structure of the compounds. This approach has long proven itself in predicting biological properties based on the structure of compounds. Molecular descriptors are a set of more than a thousand different physicochemical (lipophilicity, molar weight, etc.), quantitative (Lipinski's rule of five, number of aliphatic cycles, etc.) and other descriptors. The use of descriptors from the Mordred library allows for the construction of a more interpretable model, enabling a better understanding of which specific features influence the predicted parameter and how. By leveraging these descriptors, researchers can gain insights into the relationships between molecular characteristics and their effects on the outcomes being studied, facilitating more informed decision-making in the modeling process.

2.5 Approaches to building machine learning models

In this work, we used ordinary linear regression and its variations, such as Lasso and Ridge regression, to combat overfitting. The advantages of linear regression include its simplicity and high interpretability, as the analysis yields a clear formula that describes the dependence of the target variable on various parameters. This approach not only allowed us to establish quantitative relationships between variables but also enabled us to draw conclusions about the influence of individual factors on the resulting outcome. Moreover, many tasks can be reduced to a linear model after appropriate feature processing, making linear regression a universal tool in statistical analysis and machine learning. The use of regularization techniques like Lasso and Ridge regression further helps minimize the risk of overfitting, allowing the model to maintain its generalization capability in the presence of a large number of features or when issues of multicollinearity arise.

2.6 Characterization of the compounds

One-dimensional NMR (¹H, and ¹³C) spectra were obtained using 400 MHz spectrometers. The chemical shifts are expressed in parts per million (ppm) relative to TMS. Deuterated solvent peaks served as internal standards: deuterochloroform at 7.27 ppm for ¹H NMR and 77.00 ppm for ¹³C NMR.

2.7 General procedure for azido-Ugi reaction

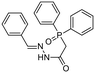
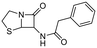
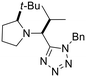
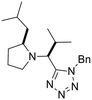
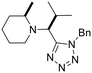
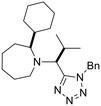
The appropriate cyclic amine (2-tert-butylpyrrolidine, 2-(trifluoromethyl)pyrrolidine, 2-isobutylpyrrolidine, 2-methylpiperidine or 2-cyclohexylazepane, 0.2 mmol) was dissolved in MeOH (5 ml). Subsequently, isobutyraldehyde (0.22 mmol, 0.2 ml), TMSN₃ (0.22 mmol, 0.29 ml), and benzyl isocyanide (0.22 mmol, 0.27 ml) were added to the reaction mixture, which was then maintained at room temperature for 1 day. The reaction progress was monitored by TLC. Once the reaction was finished, the solvent was removed by evaporation, and the resulting product was purified using column chromatography with a solvent mixture of dichloromethane/methanol (30 : 1). ¹H and ¹³C NMR spectra of the products are described in the literature.⁴²

5-{(S)-1-[(S)-2-tert-Butylpyrrolidin-1-yl]-2-methylpropyl}-1-benzyl-1H-tetrazole, 74%. ¹H NMR (400 MHz, CDCl₃): δ 0.19 (d, J = 6.6 Hz, 3H), 0.80 (s, 9H), 1.16 (d, J = 6.6 Hz, 3H), 1.18–1.30 (m, 2H), 1.40–1.54 (m, 2H), 2.06–2.09 (m, 1H), 2.22–2.30 (m, 1H), 2.85–2.87 (m, 1H), 3.57–3.59 (m, 1H), 3.70 (d, J = 10.76 Hz, 1H), 5.51 (d, J_HH = 15.6 Hz, 1H), 5.72 (d, J_HH = 15.6 Hz, 1H), 7.18–7.35 (m, 5H). ¹³C NMR (100 MHz, CDCl₃): δ 19.6, 20.4, 25.2, 26.9, 27.3, 32.9, 36.7, 47.3, 50.8, 63.3, 71.0, 127.3, 128.9, 129.1, 134.0, 153.5.

1-Benzyl-5-{(S)-1-[(S)-2-(trifluoromethyl)pyrrolidin-1-yl]-2-methylpropyl}-1H-tetrazole, 87%. ¹H NMR (400 MHz, CDCl₃): δ 0.23 (d, J_HH = 6.6 Hz, 3H), 1.07 (d, J_HH = 6.6 Hz, 3H), 1.43–1.53 (m, 1H), 1.58–1.64 (m, 1H), 1.66–1.75 (m, 2H), 2.20–2.29 (m, 1H), 2.45–2.53 (m, 1H), 3.03–3.08 (m, 1H), 3.32–3.39 (m, 1H), 3.85 (d, J = 10.9 Hz, 1H), 5.59 (d, J_HH = 15.4 Hz, 1H), 5.61 (d, J_HH = 15.4 Hz, 1H), 7.23–7.36 (m, 5H). ¹³C NMR (100 MHz, CDCl₃): δ 19.3, 19.8, 23.6, 26.3, 31.8, 46.3, 51.0, 60.2, 61.0 (q, CH–CF₃, ²J_CF = 30.0 Hz), 126.8 (q, CF₃, ¹J_CF = 280.8 Hz), 127.7, 129.1, 129.2, 133.5, 154.0. ¹⁹F NMR (376.5 MHz, CDCl₃): δ −75.77 (CF₃).

1-Benzyl-5-{(S)-1-[(S)-2-isobutylpyrrolidin-1-yl]-2-methylpropyl}-1H-tetrazole, 81%. ¹H NMR (400 MHz, CDCl₃): δ 0.14 (d, J_HH = 6.6 Hz, 3H), 0.91 (d, J_HH = 6.6 Hz, 3H), 0.99 (t, J_HH = 7.2 Hz, 6H), 1.19–1.26 (m, 1H), 1.36–1.54 (m, 3H), 1.60–1.69 (m, 3H), 2.23–2.33 (m, 2H), 2.96–3.00 (m, 2H), 3.62 (d, J = 10.6 Hz, 1H), 5.29 (d, J_HH = 15.4 Hz, 1H), 5.81 (d, J_HH = 15.4 Hz, 1H), 7.20–7.22 (m, 2H), 7.33–7.38 (m, 3H). ¹³C NMR (100 MHz, CDCl₃): δ 19.6, 20.3, 22.4, 22.7, 24.5, 25.9, 30.9, 31.0, 44.4, 45.8, 50.9, 58.2, 58.6, 127.6, 128.9, 129.1, 133.8, 154.0.

(R)-1-{(S)-1-[1-Benzyl-1H-tetrazol-5-yl]-2-methylpropyl}-2-methylpiperidine, 88%. ¹H NMR (400 MHz, CDCl₃): δ 0.27 (d, J_HH = 6.5 Hz, 3H), 0.83 (d, J_HH = 5.6 Hz, 3H), 0.98 (d, J_HH = 6.5 Hz, 3H), 1.04–1.20 (m, 3H), 1.43–1.46 (m, 1H) 1.56 (d, J_HH = 12.3 Hz, 1H), 1.82–1.88 (m, 1H), 2.05 (t, J_HH = 10.7 Hz, 1H), 2.41–2.43 (m, 1H), 2.58 (d, J_HH = 9.7 Hz, 1H), 2.88 (d, J_HH = 11.4 Hz, 1H), 3.38 (d, J_HH = 10.4 Hz, 1H), 5.43 (d, J_HH = 15.5 Hz, 1H), 5.71 (d, J_HH = 15.5 Hz, 1H),7.20–7.36 (m, 5H). ¹³C NMR (100 MHz, CDCl₃): δ 19.7, 19.3, 21.8, 29.3, 30.7, 34.3, 34.7, 46.9, 51.0, 52.4, 65.0, 127.8, 128.8, 129.0, 133.8, 153.3.

(S)-1-[(S)-1-(1-Benzyl-1H-tetrazol-5-yl)-2-methylpropyl]-2-cyclohexylazepane, 76%. ¹H NMR (400 MHz, CDCl₃): δ 0.23 (d, J_HH = 6.6 Hz, 3H), 0.66–0.75 (m, 1H), 0.89–0.96 (m, 1H), 0.99 (d, J_HH = 6.6 Hz, 3H), 1.08–1.38 (m, 10H), 1.50–1.57 (m, 2H), 1.62–1.72 (m, 3H), 1.75–1.85 (m, 2H), 2.18–2.22 (m, 1H), 2.42–2.47 (m, 1H), 2.96 (dd, J_HH = 5.1 Hz, J_HH = 9.3 Hz, 1H), 3.15 (q, J_HH = 7.1 Hz, 1H), 3.53 (d, J_HH = 10.5 Hz, 1H), 5.44 (d, J_HH = 15.6 Hz, 1H), 5.70 (d, J_HH = 15.6 Hz, 1H), 7.17–7.21 (m, 2H), 7.32–7.37 (m, 3H). ¹³C NMR (100 MHz, CDCl₃): δ 19.7, 20.1, 26.2, 26.6, 26.8, 26.9, 27.1, 28.3, 28.4, 29.7, 30.5, 31.2, 42.9, 45.7, 51.2, 62.4, 67.8, 127.5, 128.9, 129.1, 133.9, 156.1.

2.8 Assessment of acute toxicity of the compounds

In the experiment to assess the acute toxicity of the compounds, female Balb/c mice (12 weeks, 23–25 g, propagated in the animal facility at Blokhin Cancer Center, Moscow, Russia) were used. The mice received food and water ad libitum. Each compound was reconstituted at 0.5 mM (1.36–1.72 mg kg⁻¹), the maximal concentration that allowed the acquisition of a transparent solution in 0.5% aqueous dimethyl sulfoxide (solvent), and injected i.p. at a volume of 200 μL. Control animals received 200 μL of the solvent (for dosages, see Table S1 in the SI). Each cohort contained 5–10 mice. The animals were monitored for behavior, physical activity, hair cover and nutritional habits for up to 14 d post injection.

3 Results and discussion

3.1 Data analysis

The dataset contained LD₅₀ values for mice of 35 299 small molecular weight compounds and was subject to initial preprocessing to ensure quality and suitability for modeling. Data preprocessing procedures included: removal of compounds lacking LD₅₀ values or structural information in SMILES format, exclusion of duplicates based on identical SMILES representations to prevent bias, and validation of SMILES strings using RDKit to ensure syntactic correctness and convertibility to molecular objects. Following preprocessing, no missing values or duplicates remained. Based on the classification criteria established by the U.S. Environmental Protection Agency (EPA), four groups were presented: category I: (0, 50]; category II: (50, 500]; category III: (500, 5000]; category IV: (5000, +∞); mg kg⁻¹. The toxicity data of the compounds was log-normally distributed, indicating that the values were positively skewed and cannot take negative values (Fig. 1). This type of distribution is particularly suitable for modeling non-negative data that often exhibit exponential growth patterns.

Fig. 1 Distribution of data in datasets by LD₅₀ values: a) histogram of toxicity values by category; b) KDE line of toxicity values.

To analyze this data effectively, we utilized logarithmic transformations, which allowed us to apply regression techniques that assume normally distributed errors. This approach can enhance the interpretability and predictive power of our models when assessing the toxicity levels of compounds. Logarithmic transformation of the KDE line did not give the desired results (Fig. 2a); however, it appears to be significantly closer to a Gaussian normal distribution after dividing the logarithmic toxicity values by molar mass (Fig. 2b).

Fig. 2 KDE line plots after transformation: a) distribution of logarithmic toxicity values; b) distribution of logarithmic toxicity value divided by molar mass.

The effectiveness and predictive power of a machine learning model are strongly linked to the chemical space represented by the training dataset. Generally, as the variety of the data expands, the model's ability to generalize tends to improve. One method for exploring chemical space is through the definition of a scaffold for compounds. The Bemis–Murcko scaffold is obtained from the original chemical compound by isolating cyclic structures and the linkers connecting them, while eliminating the side chains (R-groups). This dataset contains 9776 different scaffolds; however, the majority of them occur only once. The most frequently occurring scaffolds were analyzed within each toxicity group, providing insights into the structural features that may correlate with varying levels of toxicity. This comprehensive analysis aimed to enhance our understanding of the relationship between chemical structure and toxicity. The benzene scaffold is presented in all four toxicity categories; however, categories 1 and 2 and categories 3 and 4 are structurally similar (Table 1).

Table 1 Analysis of the chemical space – most commonly occurring Bemis–Murcko scaffolds in compounds related to different toxicity groups

Category 1
Scaffold structure
Frequency	10.20	1.59	1.08	0.79	0.69
Category 2
Scaffold structure
Frequency	10.74	1.25	1.19	0.78	0.57
Category 3
Scaffold structure
Frequency	9.15	0.75	0.73	0.60	0.57
Category 4
Scaffold structure
Frequency	9.63	1.66	1.33	1.33	1.33

---

3.2 Development of regression models for toxicity prediction

The Mordred descriptors were applied as the input features for the development of various regression models because descriptors have all the molecular information, including structural, topological, electronic, and thermodynamics properties. In total, the descriptors dataset from 35 299 molecules was divided randomly at an 80 : 20 ratio, where the 80% part (28 239 molecules) was used for training and the remaining 20% (7060 molecules) was used for testing. Next, regression models were developed to calculate the toxicity values for the compounds. For this task, we utilized linear regression models, including those with different types of regularization (Lasso and Ridge). Multi-linear regression (MLR) models the relationship between two or more variables based on experimentally obtained data using a linear equation. Typically, the linear equation for MLR with n observations is expressed as y = a¹X₁ + a²X₂ + a³X₃ + … + aⁿX_n + B. In this equation, each independent variable X_i (where i = 1, 2, 3, …, n) is linked to the dependent variable Y according to the specified formula and B is a constant. The coefficient of determination, R², is employed for evaluation when applying the regression algorithm. First, we examined the potential metrics that could be achieved by transforming the target variable. We applied a logarithmic transformation to the toxicity values using base 10, meaning that we predicted not the actual values but their orders of magnitude. Additionally, we normalized the logarithmically transformed values relative to the molecular weight. These transformations significantly improved the model's performance metrics (Table 2).

Table 2 Performance of MLR models using the different transformations of toxicity values

Target transformation	R ^2 for the training part	R ^2 for the testing part
Toxicity values without transformation	0.039	−0.160
Logarithmically transformed values	0.336	0.089
Logarithmically transformed values divided by MW	0.746	0.713

---

To understand the relationship between chemical structure and predicted toxicity, we analyzed the most important features contributing to the model. Among the top features, many belong to the class of autocorrelation descriptors (e.g., AATS2d, GATS1p, GATS1i, AATS0d), which capture how atomic properties correlate across the molecular graph at certain topological distances. These descriptors reflect the distribution of electronic and geometric properties throughout the molecule, indicating that the spatial arrangement and electronic environment of the atoms play a crucial role in toxicity (Fig. 3). Autocorrelation descriptors like these have been previously associated in QSAR studies with toxicological mechanisms involving molecular reactivity and bioavailability; for instance, they often encode information about electron density distribution, which can influence nucleophilic/electrophilic interactions – a common driver of acute toxicity in rodents. While the diverse nature of our dataset precludes direct mechanistic assignment for every compound, these features generally highlight how global electronic properties (e.g., polarizability or ionization potential) modulate LD₅₀ by affecting absorption, distribution, or target interactions, aligning with SAR rules in acute toxicity prediction.⁴³

Fig. 3 Influence of features on a target variable.

For example:

• AATS2d and AATS1d measure the average autocorrelation of atomic properties weighted by distance, suggesting that interactions between atoms separated by specific bond distances influence toxic behavior. This topological weighting may relate to mechanisms like steric accessibility for enzymatic binding or membrane permeation, which are critical in oral LD₅₀ outcomes.⁴⁴

• GATS1p and GATS1i are Geary autocorrelation descriptors weighted by polarizability and ionization potential, respectively, highlighting the importance of electronic properties in the molecule's toxicity profile. Polarizability, in particular, correlates with lipophilicity (log P proxies), a key factor in crossing biological barriers and eliciting systemic toxicity.⁴³

Other significant descriptors include:

• CIC1 and CIC0 (complementary information content indices), which quantify molecular complexity and diversity of atomic environments.

• NdsN (number of donor atoms), indicating the presence of atoms capable of donating electrons, which may affect reactivity and interaction with biological targets.

• ETA_shape_p (a shape index descriptor) reflects the overall molecular shape and size, which can influence membrane permeability and bioavailability.

Overall, the importance of these descriptors suggests that both electronic distribution and molecular topology significantly impact the predicted toxicity. This aligns with chemical intuition that toxicity is often related to how molecules interact at the atomic level with biological systems, governed by structural and electronic factors.

Then, we selected the top 30 features based on their importance and performed polynomial transformations using various degrees. For the polynomial of degree 4, we utilized 15 features due to memory constraints. We employed Lasso and Ridge regression models to combat overfitting. These regularization techniques help to enhance model generalization by penalizing large coefficients, thereby improving the overall performance on unseen data (Table 3). Overfitting in polynomial regression without regularization is pronounced, especially for degrees 3 and 4, leading to extremely poor generalization performance. As the polynomial degree increases, the model's quality on the training set improves significantly: the R² score increases from 0.766 (degree 2) to 0.865 (degree 3), then slightly decreases to 0.845 (degree 4). However, for the test set, the R² score drops sharply and becomes negative, with values becoming catastrophically low as the polynomial degree increases – from −0.029 (degree 2) to −1 283 660.53 (degree 4). This is a clear indication of severe overfitting: the model fits the training data too closely but loses its ability to generalize. Regularization significantly improves model stability by reducing overfitting and maintaining acceptable performance on the test set. The best result was achieved for ridge regression, and the increase in the degree of polynomial transformation does not improve the quality of the model.

Table 3 Performance of regression models using the polynomial features transformation

Model	Polynomial degree	R ^2 for the training part	R ^2 for the testing part
Linear regression	2	0.766	−0.029
	3	0.865	−19.017
	4	0.845	−1 283 660.53
Lasso regression (alpha = 10.0)	2	0.030	0.025
	3	0.16	0.14
	4	0.00	0.00
Ridge regression (alpha = 10.0)	2	0.736	0.730
	3	0.800	0.622
	4	0.783	−1.785

---

Next, we optimized the parameters of the ridge model. The best result, R² = 0.755 and MSE below 10⁻⁴, was achieved for ridge regression with polynomial degree equal to 3 and parameter alpha = 100 (Fig. 4). Further optimization of the chosen model did not result in any visible improvements, which is outstanding in terms of both R² and convenience of the model (see Table S2. Comparison of state-of-the-art machine learning methods for predicting acute toxicity in the SI). Thus, thirty top-ranked features were selected based on the absolute magnitudes of the coefficients from an initial linear regression model and then a third-degree polynomial transformation was applied, generating 5456 transformed features to account for nonlinear relationships (see SI).

Fig. 4 Performance of regression-based models for prediction.

To further validate the robustness of the developed models and ensure that they are not based on chance correlations, a Y-randomization (permutation) test was performed. This involved randomly shuffling the target variable 10 times while keeping the molecular descriptors fixed. For each randomization, the model was retrained using the same hyperparameters and cross-validation procedure as in the original training. Performance metrics (R²) were computed for each permuted model, and the distribution was compared to the original model's performance using a one-sided permutation test (p < 0.05 threshold). This approach confirms that the models capture true structure–activity relationships rather than artifacts from the data (Fig. 5).

Fig. 5 Box-plot for the Y-randomization (permutation) experiment.

Our approach demonstrates competitive performance relative to existing models (Table 4). Notably, some methods, like the quantitative structure–toxicity relationship (QSTR) models and advanced neural networks, show comparable or slightly higher R² values, but often on smaller datasets. Overall, our results indicate that the proposed regression model provides a robust and accurate tool for toxicity prediction, with the advantage of being trained on a large dataset, which enhances its generalizability.

Table 4 Comparison of state-of-the-art machine learning methods for predicting acute toxicity

Dataset size	Method	Root mean square error	R ^2	Ref.
2736	Relevance vector machine and consensus modeling	Up to 0.754	Up to 0.656	27
2896	Local lazy learning	—	0.712	28
6861	Enhanced graph neural network	0.766	0.691	45
554	Multiple linear regression	0.438	0.728	46
Over 80 000	Nonlinear machine learning	0.550	0.700	1
378	Quantitative structure–toxicity relationship	0.396	0.715	47
2633	Evolved transformer model	—	0.781	35
7385	Equivariant graph neural networks	—	0.715	33
131	Quantitative structure–toxicity relationship	0.960	0.748	48
1995	Quantitative structure–toxicity relationship	0.185	0.850	49
35 299	Ridge regression		0.755	This work

---

3.3 Synthesis

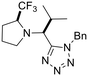
Previously, we have demonstrated that the azido-Ugi reaction with α-substituted cyclic amines allows tetrazole derivatives to be obtained with a high degree of control of diastereoselectivity (up to 100% de).³⁵ We selected several cyclic amines based on availability, diversity, potential bioactivity and diastereomeric purity. For instance, α-trifluoromethylpyrrolidine is interesting due to the biomarker CF₃-group as well as its high diastereoselectivity in the azido-Ugi reaction. Therefore, we have chosen α-trifluoromethyl-, α-cyclohexyl- and α-isobutyl pyrrolidines, α-neopentylpiperidine and α-cyclohexylazepane as starting materials. The reactions of all cyclic amines with TMSN₃, benzylisocyanide, and isobutyral proceeded smoothly at room temperature. The desired tetrazole derivatives were obtained in high yields (74–88%) and individual diastereomers were isolated by means of column chromatography (Scheme 1). In addition, it should be noted that the carbon skeletons of the chosen compounds were absent from both the training and test sets. Thus, the model's predictions for these compounds represent a rigorous test of its ability to generalize to new chemical spaces.

Scheme 1 Azido-Ugi reaction of secondary cyclic amines.

The model predicted low toxicity of all five compounds (LD₅₀ > 270 mg kg⁻¹), with the trifluoromethyl derivative being assessed as the least toxic (563 mg kg⁻¹). To experimentally test these predictions, intraperitoneal injections of these compounds were performed in Balb/c mice. Administration of 0.5 mM solutions in 200 μL did not cause any detectable negative effects during 14 days of observation: the animals maintained normal activity, hair cover and nutritional habits. No toxicity-related death was registered (Table 5).

Table 5 Predicted acute toxicity in mice

No.	Structure	Predicted LD50, mg kg^−1
1		563.0
2		353.1
3		319.1
4		271.4
5		274.7

---

Although we did not measure the LD₅₀ value for the acute intraperitoneal mouse toxicity, the absence of toxic manifestations and lethality confirms the low toxicity of the synthesized compounds and, most importantly, is consistent with the order of toxicity predicted by the model. However, it is important to note that while our ML model provides predictions of endpoints such as LD₅₀, the validation was conducted using single-dose observations rather than graded-dose experiments, which limits the direct assessment of dose–response relationships and precise LD₅₀ estimation. The results nonetheless demonstrate that the developed model has good generalization ability and can be effectively used to predict the toxicity of new compounds not represented in the original data. This is especially important for pharmaceutical research, where the search for new safe candidates requires reliable methods for assessing toxicity at early stages. In addition, the ease of synthesis and favorable toxicological profile of tetrazole derivatives make them attractive for further studies of bioactivity and drug development.

4 Conclusion

In this work, a machine learning regression model for predicting acute intraperitoneal toxicity in mice was successfully built and validated, which showed high accuracy (R² = 0.76) and outperformed similar models from the literature. The universality of the model was confirmed on a series of new tetrazole derivatives synthesized using the azido-Ugi reaction, for which the model adequately predicted low toxicity. Experimental data obtained during intraperitoneal administration of these compounds to mice confirmed the model predictions and the absence of toxic effects. Thus, the presented model is a reliable tool for assessing the toxicity of new chemical compounds and can significantly accelerate the process of finding safe candidates for drug development. The synthesized tetrazole derivatives deserve further in-depth study in order to identify their pharmacological properties and potential use in medicine.

Author contributions

Danil P. Zarezin: synthesis, data treatment, development of ML models, writing – review & editing, visualization; Alexander A. Shtil: assessment of acute toxicity of compounds, writing – review & editing; Valentin G. Nenajdenko: methodology, resources, writing – review & editing; Sophia S. Borisevich: conceptualization, writing – review & editing.

Conflicts of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Data availability

The authors declare that all data regarding the article “Machine Learning-Based Prediction of Acute Toxicity of Chemicals Using Regression Models and Molecular Descriptors” are available at the provided GitHub repository link – https://github.com/Danzar1991/Machine-Learning-Prediction-of-Acute-Toxicity/.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5md00757g.

Acknowledgements

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

References

1. A. Daghighi, G. M. Casanola-Martin, K. Iduoku, H. Kusic, H. González-Díaz and B. Rasulev, Multi-endpoint acute toxicity assessment of organic compounds using large-scale machine learning modeling, Environ. Sci. Technol., 2024, 58(23), 10116–10127,  DOI:10.1021/acs.est.4c01017.
2. Y. C. Xiao and F. E. Chen, The vinyl sulfone motif as a structural unit for novel drug design and discovery, Expert Opin. Drug Discovery, 2024, 19(2), 239–251,  DOI:10.1080/17460441.2023.2284201.
3. D. P. Zarezin, O. I. Shmatova and V. G. Nenajdenko, Chiral β3-isocyanopropionates for multicomponent synthesis of peptides and depsipeptides containing a β-amino acid fragment, Org. Biomol. Chem., 2018, 16, 5987–5998,  10.1039/C8OB01507D.
4. D. P. Zarezin, O. I. Shmatova, A. M. Kabylda and V. G. Nenajdenko, Efficient synthesis of the peptide fragment of the natural depsipeptides jaspamide and chondramide, Eur. J. Org. Chem., 2018, 34, 4716–4722,  DOI:10.1002/ejoc.201800992.
5. D. P. Zarezin and V. G. Nenajdenko, Diazocarbonyl derivatives of amino acids: unique chiral building blocks for the synthesis of biologically active compounds, Russ. Chem. Rev., 2019, 88, 248,  DOI:10.1070/RCR4852.
6. S. Allenspach, J. A. Hiss and G. Schneider, Neural multi-task learning in drug design, Nat. Mach. Intell., 2024, 6, 124–137,  DOI:10.1038/s42256-023-00785-4.
7. Q. Tang and A. Khvorova, RNAi-based drug design: considerations and future directions, Nat. Rev. Drug Discovery, 2024, 23, 341–364,  DOI:10.1038/s41573-024-00912-9.
8. C. S. Carnero, A. R. Pavan, J. L. dos Santos and F. R. Pavan, In silico drug design strategies for discovering novel tuberculosis therapeutics, Expert Opin. Drug Discovery, 2024, 19(4), 471–491,  DOI:10.1080/17460441.2024.2319042.
9. J. Y. Ryu, W. D. Jang, J. Jang and K. S. Oh, PredAOT: a computational framework for prediction of acute oral toxicity based on multiple random forest models, BMC Bioinf., 2023, 24, 66,  DOI:10.1186/s12859-023-05176-5.
10. D. Gadaleta, K. Vukovic, C. Toma, G. J. Lavado, A. L. Karmaus and K. Mansouri, et al. SAR and QSAR modeling of a large collection of LD50 rat acute oral toxicity data, Aust. J. Chem., 2019, 11(1), 58,  DOI:10.1186/s13321-019-0383-2.
11. C. R. Garcia-Jacas, Y. Marrero-Ponce, F. Cortes-Guzman, J. Suarez-Lezcano, F. O. Martinez-Rios and M. Garcia-Gonzalez Pupo-Merino, et al. Enhancing acute oral toxicity predictions by using consensus modeling and algebraic form-based 0D-to-2D molecular encodes, Chem. Res. Toxicol., 2019, 32(6), 1178–1179,  DOI:10.1021/acs.chemrestox.9b00011.
12. J. Chen, H. H. Cheong and S. W. I. Siu, BESTox: a convolutional neural network regression model based on binar encoded SMILES for acute oral toxicity prediction of chemical compounds, Proc. Int. Conf. Algorithms Comput. Biol., 2020, pp. 155–166,  DOI:10.1007/978-3-030-42266-0_12.
13. A. Mayr, G. Klambauer, T. Unterthiner and S. Hochreiter, DeepTox: toxicity prediction using deep learning, Front. Environ. Sci., 2016, 3, 80,  DOI:10.3389/fenvs.2015.00080.
14. G. Klambauer, T. Unterthiner, A. Mayr and S. Hochreiter, DeepTox: toxicity prediction using deep learning, Toxicol. Lett., 2017, 280, 69–75,  DOI:10.1016/j.toxlet.2017.07.175.
15. M. E. Andersen and D. Krewski, Toxicity testing in the 21st century: bringing the vision to life, Toxicol. Sci., 2009, 107, 324–330,  DOI:10.1093/toxsci/kfn255.
16. A. Bender, H. Mussa, R. C. Glen and S. Reiling, Molecular similarity searching using atom environments, information-based feature selection, and a naive Bayesian classifier, J. Chem. Inf. Comput. Sci., 2004, 44, 170–178,  DOI:10.1021/ci034207y.
17. D. Krewski, D. Acosta Jr, M. Andersen, H. Anderson, J. C. Bailar and K. Boekelheide, et al. Toxicity testing in the 21st century: a vision and a strategy, J. Toxicol. Environ. Health, Part B, 2010, 13(2–4), 51–138,  DOI:10.1080/10937404.2010.483176.
18. Y. Xu, J. Pei and L. Lai, Deep learning based regression and multi-class models for acute oral toxicity prediction with automatic chemical feature extraction, J. Chem. Inf. Model., 2017, 57(11), 2672–2685,  DOI:10.1021/acs.jcim.7b00244.
19. C. N. Cavasotto and V. Scardino, Machine learning toxicity prediction: latest advances by toxicity end point, ACS Omega, 2022, 7(42), 47536–47546,  DOI:10.1021/acsomega.2c05693.
20. S. Chen, T. Fan, T. Ren, N. Zhang, L. Zhao and R. Zhong, et al. High-throughput prediction of oral acute toxicity in Rat and Mouse of over 100,000 polychlorinated persistent organic pollutants (PC-POPs) byinterpretable data fusion-driven machine learning global models, J. Hazard. Mater., 2024, 480, 136295,  DOI:10.1016/j.jhazmat.2024.136295.
21. K. Enslein, T. R. Lander, M. E. Tomb and P. N. Craig, A predictive model for estimating rat oral LD50 values, Toxicol. Ind. Health, 1989, 5(2), 127–135,  DOI:10.1177/074823378900500210.
22. A. A. Toropov, B. F. Rasulev and J. Leszczynski, QSAR modeling of acute toxicity for 10 nitrobenzene derivatives towards rats: comparative analysis by MLRA and optimal descriptors, QSAR Comb. Sci., 2007, 26(6), 686–693,  DOI:10.1002/qsar.200610135.
23. J. X. Guo, J. J. Q. Wu, J. B. Wright and G. H. Lushington, Mechanistic insight into acetylcholinesterase inhibition and acute toxicity of organophosphorus compounds: a molecular modeling study, Chem. Res. Toxicol., 2006, 19(2), 209–216,  DOI:10.1021/tx050090r.
24. M. Hamadache, O. Benkortbi, S. Hanini, A. Amrane, L. Khaouane and C. S. Moussa, A quantitative structure activity relationship for acute oral toxicity of pesticides on rats: validation, domain of application and prediction, J. Hazard. Mater., 2016, 303, 28–40,  DOI:10.1016/j.jhazmat.2015.09.021.
25. D. V. Eldred and P. C. Jurs, Prediction of acute mammalian toxicity of organophosphorus pesticide compounds from molecular structure, SAR QSAR Environ. Res., 1999, 10(1), 75–99,  DOI:10.1080/10629369908039170.
26. H. Zhu, T. M. Martin, L. Ye, A. Sedykh, D. M. Young and A. Tropsha, Quantitative structure-activity relationship modeling of rat acute toxicity by oral exposure, Chem. Res. Toxicol., 2009, 22(11), 1913–1921,  DOI:10.1021/tx900189p.
27. T. Lei, Y. Li, Y. Song, D. Li, H. Sun and T. Hou, ADMET evaluation in drug discovery: 15. Accurate prediction of rat oral acute toxicity using relevance vector machine and consensus modeling, J. Cheminf., 2016, 8, 6,  DOI:10.1186/s13321-016-0117-7.
28. J. Lu, J. Peng, J. Wang, Q. Shen, Y. Bi and L. Gong, et al. Estimation of acute oral toxicity in rat using local lazy learning, Aust. J. Chem., 2014, 6, 26,  DOI:10.1186/1758-2946-6-26.
29. X. Li, L. Chen, F. Cheng, Z. Wu, H. Bian and C. Xu, et al. In silico prediction of chemical acute oral toxicity using multi-classification methods, J. Chem. Inf. Model., 2014, 54(4), 1061–1069,  DOI:10.1021/ci5000467.
30. J. Shao, Q. Gong, Z. Yin, W. Pan, S. Pandiyan and L. Wang, S2DV: converting SMILES to a drug vector for predicting the activity of anti-HBV small molecules, Briefings Bioinf., 2022, 23(2), bbab563,  DOI:10.1093/bib/bbab593.
31. H. Moriwaki, Y. S. Tian, N. Kawashita and T. Takagi, Mordred: a molecular descriptor calculator, J. Cheminf., 2018, 10, 4,  DOI:10.1186/s13321-018-0258-y.
32. H. Suhendar, A. Windiyanti and A. Asriani, Prediction of organic molecular optical absorption energy based on deep learning using mordred descriptor features, J. Phys.:Conf. Ser., 2023, 2596, 012020,  DOI:10.1088/1742-6596/2596/1/012020.
33. J. Cremer, L. M. Sandonas, A. Tkatchenko, D.-A. Clevert and G. De Fabritiis, Equivariant Graph Neural Networks for Toxicity Prediction, Chem. Res. Toxicol., 2023, 36, 1561–1573,  DOI:10.1021/acs.chemrestox.3c00032.
34. X. Ma, X. Fu, T. Wang, L. Zhuo and Q. Zou, GraphADT: empowering interpretable predictions of acute dermal toxicity with multi-view graph pooling and structure remapping, Bioinformatics, 2024, 40(7), btae438,  DOI:10.1093/bioinformatics/btae438.
35. C. Shao, F. Shao, S. Huang, R. Sun and T. Zhang, An Evolved Transformer Model for ADME/Tox Prediction, Electronics, 2024, 13, 624,  DOI:10.3390/electronics13030624.
36. D. P. Zarezin, A. M. Kabylda, V. I. Vinogradova, P. V. Dorovatovskii, V. N. Khrustalev and V. G. Nenajdenko, Efficient synthesis of tetrazole derivatives of cytisine using the azido-Ugi reaction, Tetrahedron, 2018, 74, 4315–4322,  DOI:10.1016/j.tet.2018.06.045.
37. I. V. Kutovaya, D. P. Zarezin, O. I. Shmatova and V. G. Nenajdenko, Six-component azido-Ugi reaction: from cyclic ketimines to bis-tetrazole-derived 5–7-membered amines, Eur. J. Org. Chem., 2019, 15, 2675–2681,  DOI:10.1002/ejoc.201900244.
38. I. V. Kutovaya, D. P. Zarezin, O. I. Shmatova and V. G. Nenajdenko, Pseudo-seven-component double azido-Ugi reaction: an efficient synthesis of bistetrazole derivatives, Eur. J. Org. Chem., 2019, 24, 3908–3915,  DOI:10.1002/ejoc.201900662.
39. S. Jain, V. B. Siramshetty, V. M. Alves, E. N. Muratov, N. Kleinstreuer, A. Tropsha, M. C. Nicklaus, A. Simeonov and A. V. Zakharov, Large-scale modeling of multispecies acute toxicity end points using consensus of multitask deep learning methods, J. Chem. Inf. Model., 2021, 61(2), 653–663,  DOI:10.1021/acs.jcim.0c01164.
40. NLM Tech Bull, Mar-Apr;(313), e3.ChemIDplus: a web-based chemical search system, https://www.nlm.nih.gov/pubs/techbull/ma00/ma00_chemid.html/, (accessed 10 August 2025).
41. G. Malakhov and P. Pogodin, Dataset of drugs, their molecular scaffolds and medical indications with interactive visualization, Data Brief, 2024, 54, 110417,  DOI:10.1016/j.dib.2024.110417.
42. D. P. Zarezin, V. N. Khrustalev and V. G. Nenajdenko, Diastereoselectivity of azido-Ugi reaction with secondary amines. Stereoselective synthesis of tetrazole derivatives, J. Org. Chem., 2017, 82(12), 6100–6107,  DOI:10.1021/acs.joc.7b00611.
43. Recent advances in QSAR studies: methods and applications, ed. T. Puzyn, J. Leszczynski and M. T. Cronin, Springer, New York, 2010,  DOI:10.1007/978-1-4020-9783-6.
44. S. B. Olasupo, A. Uzairu and B. Sagagi, Quantitative Structure-Activity relationship (QSAR) models for predicting Toxicity of Dioxin compounds, J. Comput. Methods Mol. Des., 2016, 6(2), 1–12.
45. S. Monem, A. H. Abdel-Hamid and A. E. Hassanien, Drug toxicity prediction model based on enhanced graph neural network, Comput. Biol. Med., 2025, 185, 109614,  DOI:10.1016/j.compbiomed.2024.109614.
46. G. Sun, Y. Zhang, L. Pei, Y. Lou, Y. Mu, J. Yun and F. Li, et al. Chemometric QSAR modeling of acute oral toxicity of Polycyclic Aromatic Hydrocarbons (PAHs) to rat using simple 2D descriptors and interspeciestoxicity modeling with mouse, Ecotoxicol. Environ. Saf., 2021, 222, 112525,  DOI:10.1016/j.ecoenv.2021.112525.
47. Y. Li, T. Fan, T. Ren, N. Zhang, L. Zhao and R. Zhong, et al. Ecotoxicological risk assessment of pesticides against different aquatic and terrestrial species: using mechanistic QSTR and iQSTTR modelling approaches to fill the toxicity data gap, Green Chem., 2024, 26, 839–856,  10.1039/D3GC03109H.
48. X. Lu, X. Wang, S. Chen, T. Fan, L. Zhao and R. Zhong, et al. The rat acute oral toxicity of trifluoromethyl compounds (TFMs):a computational toxicology study combining the 2D-QSTR, read-acrossand consensus modeling methods, Arch. Toxicol., 2024, 98, 2213–2229,  DOI:10.1007/s00204-024-03739-w.
49. J. Xu, T. Ren, F. Li, S. Chen, T. Fan, L. Zhao, R. Zhong, G. Sun and N. Lin, Assessment of the rat acute oral toxicity of quinoline-based pharmaceutical scaffold molecules using QSTR, q-RASTR and machine learning methods, Mol. Diversity, 2025 DOI:10.1007/s11030-025-11265-9.

---