 Open Access Article
Open Access ArticleEnhanced optical, electrical and charge transport properties of NaCaP3O9 ceramics for emerging advanced technologies
Mayssa
Karray
 a,
Iheb
Garoui
a,
Saber
Nasri
a,
Iheb
Garoui
a,
Saber
Nasri
 a,
Nourah A.
Alsobai
b,
Noweir Ahmad
Alghamdi
c and
Abderrazek
Oueslati
a,
Nourah A.
Alsobai
b,
Noweir Ahmad
Alghamdi
c and
Abderrazek
Oueslati
 *a
*a
aLaboratory of Spectroscopic Characterization and Optical Materials, Faculty of Sciences, University of Sfax, B.P. 1171, 3000 Sfax, Tunisia. E-mail: oueslatiabderrazek@yahoo.fr
bDepartment of Physics, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
cDepartement of Physics, Faculty of Science, Al-Baha University, Alaqiq 65779, Saudi Arabia
First published on 13th January 2026
Abstract
Phosphate compounds are promising for next-generation optoelectronic and electronic applications due to their versatile structures and properties. In this work, NaCaP3O9 (NCPO) ceramics were synthesized by a conventional solid-state method and crystallize in a pure triclinic phase (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), as confirmed by XRD and structural refinement. FTIR analysis verified the structural integrity through characteristic vibrational modes. Optical studies revealed a wide direct band gap of about 3.95 eV, highlighting the suitability of NCPO for ultraviolet optoelectronic applications. Dielectric and electrical investigations over wide temperature and frequency ranges demonstrated semiconducting behavior with a negative temperature coefficient of resistance. Impedance and electric modulus analyses indicated grain-dominated conduction and non-Debye relaxation behavior. The frequency-dependent conductivity follows Jonscher's law, and charge transport is governed by a thermally activated correlated barrier hopping mechanism with an activation energy of ∼0.36 eV. The estimated thermal sensitivity constant (β ≈ 3597 K) and low stability factor (SF ≈ 1.5) suggest strong thermistor performance and stable electrical properties. Overall, this study enhances the understanding of the electrical and dielectric behavior of NCPO and underscores its potential for advanced thermistor, sensor, and optoelectronic device technologies.
), as confirmed by XRD and structural refinement. FTIR analysis verified the structural integrity through characteristic vibrational modes. Optical studies revealed a wide direct band gap of about 3.95 eV, highlighting the suitability of NCPO for ultraviolet optoelectronic applications. Dielectric and electrical investigations over wide temperature and frequency ranges demonstrated semiconducting behavior with a negative temperature coefficient of resistance. Impedance and electric modulus analyses indicated grain-dominated conduction and non-Debye relaxation behavior. The frequency-dependent conductivity follows Jonscher's law, and charge transport is governed by a thermally activated correlated barrier hopping mechanism with an activation energy of ∼0.36 eV. The estimated thermal sensitivity constant (β ≈ 3597 K) and low stability factor (SF ≈ 1.5) suggest strong thermistor performance and stable electrical properties. Overall, this study enhances the understanding of the electrical and dielectric behavior of NCPO and underscores its potential for advanced thermistor, sensor, and optoelectronic device technologies.
1. Introduction
Over the past century, the growing demand for advanced technologies with efficient energy usage for modern electronic and industrial applications has become a major focus of scientific research.1–3 Due to their remarkable performance, ceramic materials have emerged as promising alternatives, delivering solutions that lower environmental impact while increasing energy density, often in compact dimensions and at lower cost.4,5 Recently, phosphate-based compounds, known for their structural versatility, have attracted considerable attention due to their exceptional physical properties such as high electrical conductivity, intriguing magnetic behavior, and elevated dielectric constants.6–8 These features make them ideal candidates for various advanced technologies, including ceramic capacitors,9 microwave components,10,11 next-generation 5G/6G communication networks,12 and sensors applications.6,13The search for advanced sodium-based cationic conductors with favorable electrochemical characteristics has intensified in recent years, driven by their potential application in future Na-ion rechargeable battery technologies. Several candidates have been studied, including NaFe(PO3)3,14 Na3V2(PO4)3,15 NaZr2(PO4)3,16 and Na2CoP2O7.17 Structurally, these materials are composed of frameworks that combine PO4 tetrahedra with MOn polyhedra (where M denotes a transition metal and n ranges from 4 to 6). This results in complex connectivity patterns that form tunnels and cavities throughout the structure. The geometry and dimensions of these tunnels directly influence the movement of cations within the material. Therefore, exploring the crystal structures of such materials is essential for gaining insights into their ionic transport mechanisms and optimizing their performance.
In recent years, calcium-based phosphate materials have attracted increasing attention across a wide range of technological fields. Their structural versatility and intrinsic biocompatibility make them particularly suitable for advanced bio-materials and biomedical applications.18–21 Beyond these areas, growing interest has emerged in the use of calcium phosphates for energy-related technologies, where they have shown promising performance in energy storage systems, such as batteries, as well as in energy conversion devices.22 Among the various synthesis approaches for phosphate-based materials, the conventional solid-state reaction technique remains the most prevalent. Its widespread adoption is attributed to its operational simplicity, low production cost, and suitability for large-scale synthesis.6,23,24 Additionally, it supports the formation of phase-pure and highly crystalline compounds, which are key factors in achieving reliable and enhanced material performance. Within this context, considerable attention has been directed toward the NaMP3O9 family, where M denotes divalent or trivalent metal ions such as Fe, Mn, Ca, Sr, Co, Zn, and Mg.11,25–29 Despite progress in their structural characterization, however, the electrical and dielectric behaviors of these materials remain insufficiently explored. This lack of data has spurred efforts to probe their ionic transport mechanisms at the microscopic level. Impedance spectroscopy has emerged as a powerful technique in this regard, offering detailed insights into the distinct roles of grains, grain boundaries, and electrode interfaces in governing charge transport. Moreover, these findings can be effectively linked to morphological and structural attributes, as identified by the impedance spectroscopy technique.3 Beyond this, impedance analysis enables evaluation of the negative temperature coefficient (NTC) of resistance observed in certain pyrophosphate compounds, positioning them as promising candidates for applications such as thermal regulation, temperature sensing, inrush current protection, and accurate thermal monitoring.30,31 Among the NaMP3O9 family, NaCoP3O9 is the only compound synthesized via the solid-state method that has been investigated by impedance spectroscopy. It has demonstrated promising performance, exhibiting an electrical conductivity of 1.01 × 10−5 Ω−1 cm−1 at 753 K and an activation energy of 1.1 eV, as derived from Arrhenius analysis.32 This compound has also gained attention as a potential cathode material for sodium-ion battery applications.25,33
NaCaP3O9, a member of the metaphosphate family, crystallizes in the triclinic system with space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) .29 It is isostructural with NaSrP3O9, and their triclinic forms represent the only polymorphs reported for these compounds, highlighting the unique stability of their linear polyphosphate chains. The relative ionic radii of M+ and M2+ cations strongly influence the degree of polymerization in these metaphosphates. To date, Eu3+-doped NaCaP3O9 exhibits strong photoluminescence with tunable emission, making it promising for high-performance white light-emitting diodes (WLEDs) and other luminescent devices.34,35 However, its electrical and dielectric properties have not yet been explored, underscoring the novelty and significance of the present study.
.29 It is isostructural with NaSrP3O9, and their triclinic forms represent the only polymorphs reported for these compounds, highlighting the unique stability of their linear polyphosphate chains. The relative ionic radii of M+ and M2+ cations strongly influence the degree of polymerization in these metaphosphates. To date, Eu3+-doped NaCaP3O9 exhibits strong photoluminescence with tunable emission, making it promising for high-performance white light-emitting diodes (WLEDs) and other luminescent devices.34,35 However, its electrical and dielectric properties have not yet been explored, underscoring the novelty and significance of the present study.
The objective of this study is to provide the first comprehensive investigation of the structural, optical, and electrical properties of NaCaP3O9 (NCPO) ceramic using the conventional solid-state reaction technique. The relatively low sintering temperature (600 °C) and the affordability of the constituent materials make this ceramic particularly attractive. A multi-technique approach combining X-ray diffraction (XRD), infrared (IR) spectroscopy, UV-visible spectroscopy, and complex impedance spectroscopy is employed to characterize the material. Special emphasis is placed on evaluating the optical parameters relevant for optoelectronic applications. Furthermore, impedance spectroscopy confirms the NTCR behavior and reveals a thermally activated conduction process. To deepen our understanding of charge transport, frequency- and temperature-dependent conductivity data are analyzed. The interplay between conduction and relaxation processes is also explored using the Kohlrausch–Williams–Watts (KWW) model applied to the electric modulus formalism.
2. Experimental work
2.1 Material preparation of NaCaP3O9 (NCPO)
The NaCaP3O9 sample was synthesized using a conventional solid-state reaction method. High-purity precursors NH4H2PO4, CaCO3, and Na2CO3 were accurately weighed according to the required stoichiometric ratios. The methodology of synthesis involved several steps, as depicted in Fig. 1.The powders were thoroughly mixed in an agate mortar at room temperature to ensure uniformity. The resulting mixture underwent dry grinding for one hour, followed by wet grinding for an additional hour. This process yielded a well-homogenized powder. The blended powder was calcined in a programmable furnace, where the temperature was gradually raised to 300 °C and maintained for 6 hours. After cooling, the calcined material was finely reground for 2 hours to obtain a lump-free texture. Cylindrical pellets were then formed using a uniaxial press and subsequently sintered at 600 °C for 3 hours to promote densification and phase formation. The final product consisted of well-sintered pellets, ready for structural and functional characterization.
2.2 Analysis and characterization
The optical properties of the material were studied using a Shimadzu UV-Vis-NIR spectrophotometer (model 3100), operating in the spectral range of 200–800 nm.
Electrical measurements were conducted by coating the opposing faces of the sintered ceramic pellets with silver electrodes through vacuum thermal evaporation, ensuring effective electrical contact. The impedance data were collected using a Solartron 1260 analyzer, covering frequencies from 0.1 Hz to 1 MHz and temperatures ranging from 393 K to 633 K, within this interval, the electrical response exhibits thermally activated behavior with well-defined relaxation and conduction mechanisms. This setup enabled the investigation of electrical transport processes and dielectric relaxation behavior within the material. This allowed for the investigation of electrical transport processes and dielectric relaxation behavior within the material.
3. Results and discussion
3.1 Structural, SEM description, and vibrational characterization
The X-ray diffraction pattern of the synthesized NCPO compound is presented in Fig. 2(a). The presence of sharp, well-defined peaks confirms the material's high crystallinity. By applying Rietveld refinement, the diffraction peaks were successfully indexed to a triclinic crystal system with space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , indicating the successful formation of a single-phase NCPO structure. Table 1 summarizes the crystallographic parameters determined through structural refinement. The obtained goodness-of-fit value (χ2 ≈ 1.01) reflects a strong correlation between the experimental data and the calculated diffraction pattern, confirming the reliability of the refinement process. Moreover, the extracted lattice parameters show excellent consistency with values previously reported in the literature.29
, indicating the successful formation of a single-phase NCPO structure. Table 1 summarizes the crystallographic parameters determined through structural refinement. The obtained goodness-of-fit value (χ2 ≈ 1.01) reflects a strong correlation between the experimental data and the calculated diffraction pattern, confirming the reliability of the refinement process. Moreover, the extracted lattice parameters show excellent consistency with values previously reported in the literature.29
 | ||
| Fig. 2 (a) X-ray diffraction (XRD) pattern of NCPO recorded at room temperature. (b) The unit cell of NCPO. | ||
| Sample | NaCaP3O9 |
|---|---|
| Structure | Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| D SC (nm) | 56.886 |
| Unit cell parameter | |
| a (Å) | 6.735 (6) |
| b (Å) | 6.950 (6) |
| c (Å) | 7.642 (4) |
| V (Å3) | 3160.820 |
| α (°) | 83.502 |
| β (°) | 81.260 |
| γ (°) | 82.804 |
| Agreement factors | |
| R p (%) | 29.40 |
| R exp (%) | 37.77 |
| R wp (%) | 38 |
| R F (%) | 1.665 |
| R Bragg (%) | 2.187 |
| χ 2 | 1.01 |
According to JCPDS file No. 23-0669,39 the unit cell structure of NCPO, shown in Fig. 2(b), features infinite (PO3)n−n chains formed by phosphate tetrahedra with two short and two long P–O bonds and an average P–O–P angle of ∼134.8°. These chains are folded to accommodate Ca2+ ions, which adopt distorted dodecahedral coordination with eight oxygen atoms, forming edge-sharing chains perpendicular to the phosphate backbone. Na+ ions occupy highly distorted octahedral (NaO6) sites, each coordinated to six terminal oxygen atoms from adjacent phosphate chains. NaO6 octahedra link parallel Ca–O chains, reinforcing the rigidity and stability of the triclinic NCPO framework.
The mean crystallite size was estimated using Scherrer's formula,37 based on the full width at half maximum (FWHM) of the (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 01) diffraction peak located at 2θ = 30.97° (refer to Fig. 2(a)):
01) diffraction peak located at 2θ = 30.97° (refer to Fig. 2(a)):
 | (1) |
In this equation, λ denotes the wavelength of the incident X-ray, β corresponds to the full width at half maximum (FWHM) of a prominent diffraction peak (expressed in radians), θ is the associated Bragg angle, and k is the Scherrer constant, generally taken as 0.9.37 Based on this calculation, the crystallite size of NCPO is estimated to be around 56.886 nm, confirming that the synthesized phosphate material exhibits nanoscale dimensions.
The SEM micrographs were employed to analyze the surface morphology of the synthesized phosphors. Fig. 3(a) displays the SEM image of the NCPO sample, revealing agglomerated particles with mixed sizes. The observed grain size lies in the micrometer range rather than the nanometer scale, which can be attributed to the aggregation of smaller particles during the annealing process. This agglomeration occurs because smaller particles, possessing higher surface energy, tend to merge into larger ones to minimize their overall surface free energy. The resulting particle sizes are thus on the order of a few micrometers. The morphology and particle dimensions of the obtained phosphors suggest their potential suitability for white LED (WLED) applications.38Fig. 3(b) presents the Lorentz-fitted grain size distribution histogram. Image analysis indicates an average grain size of approximately 1 µm. The grain size determined from SEM images is larger than that estimated from XRD analysis, a difference that can be explained by the fact that each grain observed in the SEM micrograph is composed of several crystallite domains.39
FTIR spectroscopy plays a crucial role in the structural characterization of the NCPO compound by revealing detailed insights into its vibrational properties. The infrared spectrum of the synthesized sample is shown in Fig. 4, and the corresponding absorption bands, along with their tentative assignments, are summarized in Table 2. These assignments are based on previously reported data29,40,41 and follow a typical order of metaphosphate vibrational modes, arranged by decreasing frequency. The FTIR spectrum exhibits characteristic absorption bands associated with polyphosphate groups, including asymmetric PO2 stretching modes (νas) at 1288, 1262, and 1212 cm−1, and symmetric PO2 stretching modes (νs) at 1150, 1110, and 1085 cm−1. Additionally, the bands observed within the 702–1045 cm−1 range are attributed to symmetric and asymmetric P–O–P stretching vibrations. The lower frequency region, spanning from 446 to 580 cm−1, corresponds to bending modes involving P–O and O–P–O linkages. These regions show medium to strong absorption intensities, confirming the presence of linear (PO3)n−n chains rather than cyclic phosphate units.
| Wave number (cm−1) | Assignments |
|---|---|
| 1288 | υ as (PO2) |
| 1262 | |
| 1212 | |
| 1150 | υ s (PO2) |
| 1110 | |
| 1085 | |
| 1045 | υ as (POP) |
| 897 | |
| 778 | υ s (POP) |
| 745 | |
| 702 | |
| 580 | P–O & O–P–O bend |
| 561 | |
| 531 | |
| 509 | |
| 476 | |
| 454 | |
| 446 |
3.2 Optical characteristics
UV-Visible spectroscopy serves as a fundamental technique for investigating the optoelectronic properties of semiconducting materials, enabling detailed insights into their band structure and electronic transitions. The optical behavior of the synthesized sample was systematically analyzed through its absorbance spectra to elucidate its electronic structure. Prominent absorption features were identified, allowing precise determination of the optical band gap as well as the Urbach energy, which reflects the degree of structural disorder. Additionally, critical optical constants including the extinction coefficient, penetration depth, and refractive index were evaluated as functions of photon energy. This comprehensive analysis provides crucial information for assessing the material's potential suitability and performance in advanced optoelectronic applications.The inset of Fig. 5(a) displays the derivative of the absorbance curve (dA/dλ) plotted against wavelength. The optical bandgap Eg of NCPO was estimated from the curve's minimum using the formula Eg = 1240/λ (with λ in nm). From the main peak at 300 nm, the bandgap is calculated to be about 4.13 eV, placing the material in the wide bandgap semiconductor range, suitable for UV photonics and high-power electronics devices.44,45 However, this method does not allow for distinguishing between direct and indirect bandgaps. To overcome this limitation, Tauc's method, which is well-adapted for powdered materials, was applied using the following relation:
| (αhν)1/n = A(hν − Eg) | (2) |
In this framework, the nature of the bandgap is analyzed by examining the relationship between photon energy (hν) and the absorption coefficient (α) of the material. The exponent n characterizes the type of optical transition, where n = 1/2 corresponds to allowed direct transitions and n = 2 to allowed indirect transitions.46
As illustrated in Fig. 5(b), the plots of (αhν)1/2 and (αhν)2versus photon energy (hν) reveal linear regions. By extrapolating these linear portions to the energy axis, the optical bandgap energies Eg can be determined. The intercepts correspond to the direct and indirect bandgaps, denoted as Egd and Egi, respectively. The estimated values are 3.95 eV and 2.99 eV for the direct transition (n = 1/2) and the indirect transition (n = 2) respectively.
To determine whether the material exhibits a direct or indirect bandgap, a mathematical verification is necessary and should be systematically applied.47
Ln(αhν) = ln(α0) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(hν − Eg) ln(hν − Eg) | (3) |
To confirm the direct nature of the bandgap in our NCPO sample, we utilized the previously determined bandgap energy (Eg = 4.13 eV). We analyzed the relationship between ln(αhν) and ln(hν − Eg), as presented in Fig. 5(c). The resulting linear plot yields a slope of approximately 0.4, consistent with a direct allowed transition. Direct bandgaps are preferred in optoelectronic applications due to their higher luminous efficiency, as they enable radiative recombination without phonon involvement, leading to enhanced light emission.48,49 Consequently, the NCPO sample shows significant potential for light-emitting diode (LED) fabrication. Metaphosphate materials, such as NCPO, typically exhibit wide bandgaps and absorb light in the ultraviolet region, as reported by Abudoureheman et al.,50 making them promising candidates for UV-emitting optoelectronic devices.
Considering that the analyzed NCPO compound exhibits semiconducting behavior with a direct bandgap, we attempted to theoretically estimate the positions of the conduction band minimum (ECB) and valence band maximum (EVB) using the following empirical formula:51
| ECB = χ − Ee − 0.5 × Eg | (4) |
| EVB = ECB + Eg | (5) |
In this equation, χ represents the absolute electronegativity of the compound, while Ee is a fundamental constant corresponding to the free electron energy on the hydrogen scale, typically taken as 4.5 eV. The electronegativity of the sample can be estimated using the following expression:52
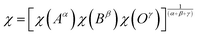 | (6) |
In this context, α, β, and γ denote the multiplicities of atoms Na, Ca, and oxygen positions, respectively. Based on our calculations, the absolute electronegativity of the sample was determined to be 5.7 eV. Using this value along with the calculated EVB, ECB, and Eg, we constructed a schematic representation of the band structure, as illustrated in Fig. 6. These properties further support NCPO's potential for UV-emitting LED applications, as the wide bandgap (Eg = 3.95 eV) enables emission in the ultraviolet region, critical for applications such as sterilization, water purification, and UV sensing. The direct allowed transition enhances radiative recombination efficiency, ensuring high quantum yield, while the calculated ECB and EVB align favorably with common electrode materials, facilitating efficient charge carrier injection in LED device structures.
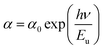 | (7) |
In this equation, α0 is a constant and hν is the photon energy. As shown in Fig. 7(a), the Urbach energy (Eu) for NCPO is estimated to be approximately 0.58 eV, corresponding to 14.68%. This relatively low Eu value suggests high crystallinity and minimal structural disorder, further supporting the material's suitability for efficient UV-emitting LEDs, as low defect densities enhance carrier mobility and radiative recombination efficiency.
 | ||
| Fig. 7 (a) Variation of Ln(α) as a function of incident photon energy. (b) (A/λ)2vs. 1/λ plots for the NaCaP3O9 compound. | ||
Extending Urbach's rule, Skettrup proposed the steepness factor (σ) as an additional optical parameter, which can be used to further evaluate the Urbach energy through the following empirical relation:47
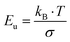 | (8) |
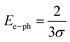 | (9) |
The calculated values for the steepness parameter and the electron–phonon interaction strength are approximately 0.0446 eV−1 and 14.94 eV, respectively. Electron–phonon interaction refers to the coupling between charge carriers and lattice vibrations (phonons) in solids, playing a crucial role in governing fundamental properties such as electrical resistivity, superconductivity, and thermal conductivity.47
In the context of optoelectronic devices, the maximum wavelength of incident radiation denoted as λT or threshold wavelength is a key parameter for assessing a material's suitability for such applications. It represents the shortest wavelength capable of initiating optoelectronic processes, such as absorption or emission, within the material. The λT value in our study was estimated using the following relation:55
 | (10) |
In this equation, α represents the absorption coefficient, λ is the wavelength of the incident radiation, and C is a constant. From the fitted curves, the λT value for our sample was determined to be 325 nm, as shown in Fig. 7(b).
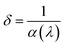 | (11) |
The δ(λ) values for the NCPO sample exhibit distinct regions that correspond to variations in the absorption coefficient, as shown in Fig. 8(a). In the 200–300 nm range, the material effectively blocks UV-vis radiation, indicating its potential as a UV filter.57 As the wavelength shifts toward the visible region, the δ values increase, with a noticeable sharp peak observed at 365 nm. Within the visible spectrum, the δ values then decrease progressively, accompanied by a prominent absorption band.
 | ||
| Fig. 8 (a) Variation of the penetration depth δ against λ for the studied NCPO material. (b) Variation of the extinction coefficient and refractive index as a function of wavelength (λ). | ||
The extinction coefficient (k) can be calculated from the absorption coefficient α(λ) using the relation:57
 | (12) |
which describes the material's ability to absorb and scatter light, indicating its effectiveness in attenuating incident radiation. Similarly, the refractive index (n) is a fundamental optical parameter influenced by electronic polarization and internal fields, and is critical for designing optical devices such as filters, switches, and modulators.58 It can be determined using the following expression:
 | (13) |
Fig. 8(b) shows the variation of the extinction coefficient (k) and refractive index (n) as functions of the incident wavelength. Both n and k decrease with increasing wavelength, exhibiting high values in the UV region and declining to relatively low levels in the visible range. This behavior reflects the excellent optical quality and compactness of the synthesized samples. The gradual decrease in optical opacity from the UV to the visible region confirms strong UV absorption. Based on these observations, the material shows great potential for use in UV sensing applications.59,60 Consequently, it can be considered a promising candidate for integration into optoelectronic devices.
3.3 Frequency-dependent electrical properties assessed by impedance spectroscopy
Impedance spectroscopy is a versatile and powerful technique widely employed to investigate the electrical and electrochemical properties of materials, offering valuable information about charge transport mechanisms and electronic structure in electrochemical and semiconducting systems. By analyzing a material's response to an applied alternating electric field over a broad frequency range, this method allows one to assess the processes governing energy storage and dissipation, which are directly linked to the intrinsic properties of the material.61,62 The electrical response in the high-frequency domain is primarily attributed to the bulk (grain) contribution, where charge carriers move through the crystalline lattice with relatively low resistance. Conversely, the low-frequency region is mainly governed by grain boundary effects, characterized by higher resistive behavior arising from structural disorder, defect accumulation, and the presence of potential barriers at grain interfaces. These grain boundaries function as charge carrier trapping sites, resulting in extended relaxation times compared to those associated with the grain interiors. The observed relaxation phenomena are mainly driven by thermally activated hopping of charge carriers between localized states and across interfacial barriers, and are strongly affected by microstructural heterogeneity. Comparable grain and grain boundary contributions, as well as similar relaxation behavior, have been reported for phosphate- and oxide-based ceramic materials, confirming the effectiveness of impedance spectroscopy in distinguishing bulk and interfacial transport processes.63–66 The complex impedance is expressed as the sum of a real part, representing the resistive component, and an imaginary part, corresponding to the capacitive component, according to the relation Z* = Z′ + jZ″.Fig. 9(a) illustrates how the real part of the complex impedance (Z′) varies with angular frequency across a temperature range of 393 K to 633 K for the studied NCPO system. The curves exhibit two characteristic zones. At low frequencies, Z′ shows a nearly flat response, indicating DC conduction dominated by long-range charge transport, where carriers move between neighboring sites through successful hopping.6,67,68 At higher frequencies, a significant dispersion in Z′ is observed, which is attributed to AC conduction caused by localized motion of carriers, reflecting limited or incomplete hopping processes. This dual behavior highlights two distinct conduction mechanisms: DC conduction is evident at lower frequencies due to extended charge migration, while at higher frequencies, the influence of localized relaxation and short-range motion becomes dominant, contributing to AC conductivity. With rising temperature, the transition point where Z′ begins to depend on frequency shifts to higher frequencies (from 10 rad s−1 at 393 K to 312 rad s−1 at 633 K), suggesting that the system undergoes a thermally driven relaxation process.
At high frequencies, Z′ levels off and reaches a minimum value regardless of temperature, implying that thermal energy helps reduce the number of barriers impeding charge flow. In the low-frequency domain, a clear decrease in Z′ with increasing temperature is noted, which reflects a negative temperature coefficient of resistance (NTCR). This trend is a typical indicator of semiconducting behavior and confirms that the material exhibits NTC thermistor characteristics.69
The imaginary component of the impedance spectrum provides valuable insight into the dielectric relaxation behavior of the NCPO compound, which is influenced by the movement of charge carriers or the reorientation of dipolar entities under an applied electric field. As shown in Fig. 9(b), the −Z″ values are plotted against angular frequency across various temperatures (393–633 K), revealing the evolution of relaxation dynamics with thermal excitation. Each spectrum exhibits a prominent peak, approximately corresponding to the transition region between DC and AC conduction, as previously identified in the real part of the impedance (see Fig. 9(a)). This peak, referred to as the relaxation frequency, signifies the shift from long-range charge transport to localized carrier dynamics. The noticeable broadening of these peaks indicates a departure from the ideal Debye relaxation model,62 reflecting the complex nature of polarization and conduction processes in the material. Below the relaxation peak, charge transport is primarily governed by long-range carrier motion, whereas above this frequency, the conduction behavior is mainly influenced by localized relaxation phenomena.
To get additional information on charge carrier dynamics can be obtained from the analysis of Nyquist plots, which are especially effective in differentiating the electrical responses originating from the bulk (grain) and interfacial (grain boundary) regions of the material. In this work, Fig. 10(a) and (b) displays the Nyquist plots (Z″ vs. Z′) for the NCPO compound. The impedance spectra exhibit clear semi-circular arcs, primarily attributed to the bulk (grain) contribution, with negligible evidence of grain boundary effects.70 These arcs are notably depressed, with centers lying below the real axis (Z′), suggesting a non-ideal relaxation process that deviates from classical Debye behavior and is more accurately described by the Cole–Cole model. As the temperature increases, the diameter of the arcs decreases, reflecting a decline in bulk resistance, which is characteristic of thermally activated conduction.
To model the impedance data accurately, fitting was performed using ZView software,71 which identified the most appropriate equivalent circuit consisting of a parallel combination of a resistor (R), a constant phase element (CPE), and a capacitor (C), as shown in the Fig. 10(c). The corresponding fitting parameters are summarized in Table 3.
| T (K) | R (MΩ) | C (10−11 F) | Q (10−10 F) | α |
|---|---|---|---|---|
| 633 | 42.66 | 3.341 | 1.644 | 0.61925 |
| 613 | 50.379 | 3.342 | 1.593 | 0.61851 |
| 593 | 63.594 | 3.337 | 1.331 | 0.63248 |
| 573 | 80.868 | 3.324 | 0.8607 | 0.67241 |
| 553 | 109.8 | 3.354 | 1.194 | 0.62405 |
| 533 | 145 | 3.287 | 0.6215 | 0.71270 |
| 513 | 204.2 | 3.295 | 0.6148 | 0.70946 |
| 493 | 276.8 | 3.280 | 0.4424 | 0.74262 |
| 473 | 378.8 | 3.304 | 0.3108 | 0.75810 |
| 453 | 535.9 | 3.289 | 0.3576 | 0.75905 |
| 433 | 721.8 | 3.332 | 0.3309 | 0.74483 |
| 413 | 1085 | 3.466 | 0.8024 | 0.50460 |
| 393 | 1364 | 3.356 | 0.1786 | 0.78068 |
The results summarized in Table 3 reveal a noticeable reduction in resistivity as the temperature rises, indicating the sample exhibits semiconducting behavior. To extract key parameters such as activation energy, sensitivity constant, and stability factor, Fig. 10(d) illustrates the variation of ln(R × T) as a function of the reciprocal temperature (1000/T). The resulting plot exhibits a clear linear trend, indicating that resistivity decreases steadily with increasing temperature an expected behavior for materials exhibiting excellent negative temperature coefficient resistance (NTCR) characteristics. Within the investigated temperature range, the data align well with the Arrhenius equation:
 | (14) |
In this expression, “A” denotes the pre-exponential factor, “kB” is Boltzmann's constant, and “Ea” represents the activation energy.
Fig. 10(d) reveals a clear linear trend in the temperature-dependent electrical behavior, supported by a strong correlation coefficient (R2 = 0.99587), which confirms the presence of thermally activated conduction. The slope of the linear fit allowed for the determination of the activation energy, calculated to be 0.31 eV. Using this value, the thermal sensitivity constant β defined by the relation  ,1 was found to be approximately 3597.4 K. This value is notably higher than that reported for similar thermistor materials, such as Cu0.2Ni0.5ZnMn1.3O4 (β ≈ 3356 K),72 indicating the superior thermal response of the NCPO system. In addition, the material's electrical stability over temperature was assessed by calculating the stability factor (SF), which is the logarithmic ratio between the maximum and minimum resistivity recorded within the measured temperature range.73 The resulting SF ≈ 1.5 suggests minimal resistivity fluctuations, which is in the same order of the value reported for ZnO nanoceramics (SF ≈ 1.796),73 indicating stable electrical behavior.
,1 was found to be approximately 3597.4 K. This value is notably higher than that reported for similar thermistor materials, such as Cu0.2Ni0.5ZnMn1.3O4 (β ≈ 3356 K),72 indicating the superior thermal response of the NCPO system. In addition, the material's electrical stability over temperature was assessed by calculating the stability factor (SF), which is the logarithmic ratio between the maximum and minimum resistivity recorded within the measured temperature range.73 The resulting SF ≈ 1.5 suggests minimal resistivity fluctuations, which is in the same order of the value reported for ZnO nanoceramics (SF ≈ 1.796),73 indicating stable electrical behavior.
Together, these results affirm that NCPO exhibits both high thermal sensitivity and electrical stability, making it a strong candidate for use in thermistor and thermal sensing technologies.
3.4 Study of modulus formalism and relaxation behavior
The complex electric modulus formalism is a powerful tool used to examine charge transport mechanisms and relaxation dynamics in ceramic materials, particularly those involving charge carrier accumulation and mobility.74 These phenomena are fundamental contributors to both dielectric polarization and electrical conductivity, which are critical factors in evaluating the dielectric performance and multifunctional behavior of the NCPO ceramic system. The complex electric modulus M*(ω) is mathematically defined in terms of the complex impedance Z*(ω) as follows:75| M*(ω) = jωC0(Z′ + jZ″) = jωC0Z′ − ωC0Z″ | (15) |
Based on this relation, the real and imaginary components of the modulus can be expressed as follows:
| M′(ω) = ωC0Z″ | (16) |
| M″(ω) = ωC0Z′ | (17) |
Fig. 11 displays the M″ versus M′ plots of the complex electric modulus for the studied compound across a range of temperatures. These diagrams consistently exhibit single, well-shaped semicircular arcs, which are indicative of a uniform, single-phase system.74 Utilizing the electric modulus formalism proves advantageous, as it minimizes the effects of electrode polarization and enhances the resolution between bulk (grain) and interfacial (grain boundary) contributions. The consistent presence of one semicircular arc across all measured temperatures suggests that electrical conduction in the material is primarily driven by grain (bulk) processes. In contrast, a multiphase material would typically exhibit multiple arcs or features, each associated with distinct conductive regions. Thus, this analysis not only provides insight into the relaxation dynamics but also reinforces the conclusion that the NCPO sample exhibits single-phase behavior and conduction dominated by the bulk region.
Fig. 12(a) illustrates the evolution of the imaginary part of the complex electric modulus (M″) with angular frequency at various temperatures (393–633 K) for the NCPO compound. At lower frequencies, the M″ values remain nearly negligible, indicating the absence of significant electrode polarization effects in this spectral region.47,76 As the frequency increases, M″ exhibits a notable rise, reaching a distinct peak that signals the onset of a relaxation process. This peak progressively shifts to higher frequencies as the temperature increases, confirming the thermally activated character of the dynamic relaxation behavior. The observed broad and asymmetric nature of the M″ peaks indicate a deviation from ideal Debye relaxation, pointing toward a distribution of relaxation times within the system. Analyzing the curve in two segments, it is evident that frequencies below the characteristic relaxation frequency (ωp) correspond to long-range charge displacement within the bulk, while frequencies above ωp reflect localized carrier dynamics. This crossover underscores the coexistence of extended and confined charge transport processes within the material.
To better capture the asymmetric nature of the modulus spectra, the Bergman model an extension of the modified Kohlrausch–Williams–Watts (KWW) function is commonly used and is expressed as follows:77
 | (18) |
In this formulation,  represents the maximum of the imaginary part of the electric modulus, occurring at the characteristic angular frequency ωp. The parameter β, which lies between 0 and 1, quantifies the extent of relaxation dispersion. A “β” value of 1 signifies ideal Debye-type relaxation, typically associated with uniform dipole–dipole interactions. Conversely, values of β less than 1 reveal deviations from Debye behavior, indicating the involvement of more distributed or complex relaxation mechanisms.74 As illustrated in Fig. 12(b), the β parameter exhibits a temperature-dependent trend. Its values remain consistently below one, indicating a deviation from ideal Debye-type relaxation. This behavior implies a wide distribution of relaxation times, likely arising from irregular dipole–dipole interactions in the NCPO system.
represents the maximum of the imaginary part of the electric modulus, occurring at the characteristic angular frequency ωp. The parameter β, which lies between 0 and 1, quantifies the extent of relaxation dispersion. A “β” value of 1 signifies ideal Debye-type relaxation, typically associated with uniform dipole–dipole interactions. Conversely, values of β less than 1 reveal deviations from Debye behavior, indicating the involvement of more distributed or complex relaxation mechanisms.74 As illustrated in Fig. 12(b), the β parameter exhibits a temperature-dependent trend. Its values remain consistently below one, indicating a deviation from ideal Debye-type relaxation. This behavior implies a wide distribution of relaxation times, likely arising from irregular dipole–dipole interactions in the NCPO system.
Fig. 12(c) illustrates how the relaxation angular frequency (ωp) varies with temperature, showing an upward trend as temperature rises. This increase indicates that the relaxation process shifts to higher frequencies, consistent with thermally activated dynamics. To evaluate the activation energy governing this relaxation, Fig. 12(d) plots ln(ωp × T) against the inverse temperature (1000/T). The linear behavior confirms that the relaxation process follows an Arrhenius-type dependence. From the slope of the fitted curve, the activation energy was calculated to be 0.33 eV. This value closely matches that obtained from electrical resistivity analysis, indicating that both the relaxation dynamics and the charge transport mechanism are governed by similar thermally activated processes.1,52,60
3.5 Modeling the conduction mechanism in NCPO
This section focuses on the detailed investigation of charge transport mechanisms in the NCPO compound by examining the variation of electrical conductivity as a function of both angular frequency and temperature (393–633 K). Fig. 13 illustrates how conductivity evolves with frequency, highlighting complex conduction behavior. In the low-frequency range (region I), particularly below 100 rad s−1, the conductivity spectrum σ(ω) exhibits a plateau corresponding to the DC conductivity (σdc), reflecting frequency-independent behavior. As the frequency increases, the system enters region II, characterized by a dispersive increase in conductivity. The parameter ωh (the hopping frequency) precisely characterizes the onset of the AC conductivity regime (see Table 4). This transition is well-described by Jonscher's empirical universal power law, which characterizes the frequency dependence of AC conductivity as follows:78| σ(ω,T) = σdc(T) + Aωs(T) | (19) |
 | ||
| Fig. 13 Frequency-dependent electrical conductivity spectra of the NCPO compound recorded over the temperature range of 393 K to 633 K. | ||
| T (K) | σ dc × 10−9 | s | A × 10−12 | ω h |
|---|---|---|---|---|
| 393 | 0.123 | 0.83503 | 0.83235 | 396.486 |
| 413 | 0.176 | 0.83377 | 0.86384 | 586.488 |
| 433 | 0.238 | 0.83073 | 0.91021 | 812.860 |
| 453 | 0.331 | 0.82955 | 0.93414 | 1183.724 |
| 473 | 0.473 | 0.82070 | 1.05725 | 1697.398 |
| 493 | 0.610 | 0.80747 | 1.26256 | 2108.914 |
| 513 | 0.827 | 0.80431 | 1.32857 | 2978.074 |
| 533 | 1.18 | 0.78828 | 1.67268 | 4106.998 |
| 553 | 1.52 | 0.77388 | 2.07059 | 5047.692 |
| 573 | 2.06 | 0.76367 | 2.44065 | 6791.591 |
| 593 | 2.66 | 0.74176 | 3.33203 | 8176.163 |
| 613 | 3.35 | 0.73796 | 3.63234 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414.561 414.561 |
| 633 | 4.10 | 0.72678 | 4.33603 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 426.529 426.529 |
In this expression, the parameter A serves as a scaling factor that determines the magnitude of the frequency-dependent component of the conductivity. It reflects the degree of charge carrier polarization in response to an alternating field.79 The exponent s, often referred to as the frequency exponent, characterizes the variation of conductivity with frequency. The first term in the equation corresponds to the DC conductivity, which remains constant regardless of frequency, while the second term accounts for the AC conductivity, which increases with frequency due to dynamic charge transport mechanisms. The “s” parameter is especially informative, as it provides insight into the nature and strength of interactions between mobile charge carriers and the crystal lattice, offering a deeper understanding of the material's conduction behavior.80 The dc conductivity (σdc), pre-exponential factor (A), and frequency exponent (s) were evaluated using eqn (19), and the resulting values are listed in Table 4.
Several models have been proposed to describe the frequency exponent behavior, including the correlated barrier hopping (CBH) model introduced by Elliott.81 In addition, tunneling-based mechanisms such as quantum mechanical tunneling (QMT),82 overlapping large-polaron tunneling (OLPT), and non-overlapping small-polaron tunneling (NSPT) have been considered, all of which involve charge transport between localized states near the Fermi level.83
Fig. 14(a) illustrates the temperature dependence of the frequency exponent s and the parameter ln(A). Both quantities decrease systematically with increasing temperature, while the exponent s remains below unity, indicating non-Debye relaxation behavior.84 This behavior is in good agreement with the correlated barrier hopping (CBH) model,81 which suggests that charge transport in the NCPO system is primarily governed by thermally activated hopping of localized charge carriers. Recent studies on ceramics show that ac conduction is dominated by thermally activated hopping of localized charge carriers, well described by the correlated barrier hopping (CBH) model. This approach accounts for charge transport between defect-related states over potential barriers and explains the temperature-dependent, non-Debye relaxation behavior observed in these materials.84–87
 | ||
| Fig. 14 (a) Temperature dependence of the frequency exponent “s”; (b) variation of DC conductivity (σdc) with temperature. | ||
To further probe the conduction mechanism, we analyzed the variation of DC electrical conductivity (σdc) with temperature across a broad range (393–633 K). This investigation helps elucidate both the nature of electrical conduction and the dominant hopping and scattering processes that influence the transport response of NCPO. Fig. 13(b) presents the evolution of σdc with temperature, revealing an increasing trend indicative of a thermally activated process. This increase is attributed to the activation of a small polaron hopping (SPH) mechanism, as described by Mott and Davis.88 In this framework, the temperature dependence of DC conductivity is expressed by:
 | (20) |
Here, Ea denotes the activation energy required for a charge carrier to hop between localized states, σ0 is the pre-exponential factor, and kB is Boltzmann's constant.
The plot of ln(σdc × T) versus 1/kBT, shown in Fig. 15(a), yields a linear fit with a correlation coefficient R2 = 0.99333. This confirms that the SPH mechanism is the dominant conduction process. From the slope of the Arrhenius plot, the activation energy was calculated to be 0.36 eV. The activation energy corresponds to the minimum energy required for charge carriers to overcome potential barriers or hop between localized states during electrical conduction. It reflects the degree of carrier localization and the ease of charge transport within the material, where a lower activation energy indicates enhanced mobility and more efficient conduction. Consequently, the activation energy provides important insight into the dominant charge transport mechanism governing the electrical behavior of the system.
 | ||
| Fig. 15 (a) Arrhenius plot of ln(σdc × T) versus inverse temperature (1/kBT). (b) Scaled conductivity spectra at various temperatures for the NCPO compound. | ||
In addition, various scaling models have been proposed in the literature to further analyze frequency-dependent conductivity behavior.89–91 Among these, the Ghosh model has gained considerable attention due to its effectiveness in describing hopping conduction mechanisms. It is expressed as:91
 | (21) |
 | (22) |
Fig. 15(b) displays the temperature-dependent evolution of the scaled conductivity, represented as  plotted against the reduced frequency
plotted against the reduced frequency  . The fact that all curves collapse onto a single master curve across the entire temperature range strongly suggests that the underlying charge transport mechanism does not change with temperature.92 This superposition behavior supports the applicability of the time–temperature superposition principle (TTSP) and indicates that the same fundamental conduction dynamics are maintained throughout the measured conditions.93
. The fact that all curves collapse onto a single master curve across the entire temperature range strongly suggests that the underlying charge transport mechanism does not change with temperature.92 This superposition behavior supports the applicability of the time–temperature superposition principle (TTSP) and indicates that the same fundamental conduction dynamics are maintained throughout the measured conditions.93
To establish a correlation between the electrical behavior and structural characteristics and to identify the charge carriers responsible for conduction within the framework of the CBH (correlated barrier hopping) model. According to this model, the frequency-dependent AC conductivity can be expressed using the following equation:94
 | (23) |
In this expression, the polaron number n (typically 1 or 2) reflects the number of polarons participating in the hopping mechanism, while NNp is proportional to the square of the density of available states (NNp = NT2 for the bipolaron case; (NNp = NT2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/2kBT) (for the single polaron case). The term ω represents the angular frequency, and ε′ corresponds to the real part of the dielectric permittivity.
exp(−Ueff/2kBT) (for the single polaron case). The term ω represents the angular frequency, and ε′ corresponds to the real part of the dielectric permittivity.
Additionally, Rω represents the hopping distance. These parameters can be determined using the following expressions:94
 | (24) |
In this relation, e = charge of electron, ε′ = dielectric constant, k = Boltzmann constant, T = temperature, W denotes the binding energy required to move a charge carrier from one site to another and τ0 = characteristic relaxation time.
Fig. 16 presents the variation of ln(σac) as a function of 1000/T. A strong agreement is observed between the experimental data points (represented as scatter) and the theoretical predictions (depicted by the fitted line). The various parameters employed in the fitting procedure are compiled in Table 5. Furthermore, the analysis indicates that the frequency-dependent increase in the density of localized states N in NCPO suggests reduced structural disorder, enabling more efficient ionic hopping. Concurrently, the decline in effective barrier energy Ueff with frequency supports a CBH-type conduction mechanism. These results highlight the key role of localized states in governing AC conductivity, reinforcing the potential of NCPO for solid-state ionic applications.95,96
| Frequency (Hz) | N (1018 eV−1 cm−3) | U eff (eV) |
|---|---|---|
| 100 | 2.538 | 0.1817 |
| 1000 | 2.563 | 0.1425 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
5.456 | 0.1225 |
Fig. 17(a) illustrates the temperature dependence of the hopping distance Rω. According to the correlated barrier hopping (CBH) model, this distance tends to increase with temperature. As thermal energy rises, charge carriers (polarons) gain sufficient energy to hop over longer distances, facilitating improved interchain interactions and enhancing charge transport.95
 | ||
| Fig. 17 (a) The temperature dependence of Rω (Å) at different indicated frequencies. (b) The variation of Rω (Å) with frequency. | ||
On the other hand, Fig. 17(b) presents the evolution of the hopping distance Rω as a function of different frequencies. It is evident that Rω exhibits a stronger temperature dependence in the high-frequency range, whereas this sensitivity progressively diminishes at lower frequencies. This behavior suggests that thermal activation has a more pronounced effect on short-range hopping processes dominating at higher frequencies.
Fig. 18 presents a schematic representation of the CBH conduction model in NCPO. To validate this mechanism, the hopping distance Rω was compared to the Na–Na interatomic spacing. The close agreement between the calculated Rω values (∼4.18 Å) and the average Na–Na distance (∼4.16 Å)29 strongly suggests that charge transport is primarily facilitated by localized Na+ ion migration through a small polaron hopping process, consistent with the CBH model.
4. Conclusion
This comprehensive study presents a detailed investigation of the structural, optoelectronic, and electrical properties of NaCaP3O9 (NCPO) metaphosphate synthesized via a straightforward and scalable solid-state method. The successful structural refinement confirmed the pure triclinic phase crystallizing in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, providing a robust platform for multifunctional properties. The identified wide direct band gap (∼3.95 eV) positions NCPO as a compelling candidate for ultraviolet (UV) optoelectronic devices, including UV photodetectors and transparent electronic components, where strong UV absorption and high optical transparency are essential.
space group, providing a robust platform for multifunctional properties. The identified wide direct band gap (∼3.95 eV) positions NCPO as a compelling candidate for ultraviolet (UV) optoelectronic devices, including UV photodetectors and transparent electronic components, where strong UV absorption and high optical transparency are essential.
Our extensive impedance spectroscopy analysis revealed NCPO's intrinsic semiconducting behavior marked by a negative temperature coefficient of resistance (NTCR), a key attribute for thermistor and sensor applications demanding reliable temperature sensitivity and stability.
The thermally activated conduction with an activation energy ≈0.36 eV and compliance with Jonscher's power law confirm that charge transport is governed by localized Na+ ion hopping within the correlated barrier hopping (CBH) framework, a key factor in tailoring the material's electronic performance.
Based on the activation energy obtained, the thermal sensitivity constant β was estimated to be around 3597.4 K. This relatively high value, compared with those reported for comparable thermistor materials, reflects the enhanced thermal response of the NCPO system. Moreover, the stability factor SF, close to 1.5, indicates low resistivity fluctuations when compared to typical literature values (SF ≈ 1.796), confirming the good electrical stability of the material.
Furthermore, modulus spectroscopy unveiled complex dielectric relaxation behavior with both short- and long-range ionic mobility, captured effectively by the Kohlrausch–Williams–Watts (KWW) function. The close agreement of activation energies obtained from modulus (0.33 eV) and conductivity analyses underscores the interconnected nature of dielectric and electrical processes in NCPO, reflecting a unified thermally activated mechanism.
Collectively, these findings underscore the material's exceptional multifunctionality combining structural stability, favorable optical absorption, and robust electrical conduction making NaCaP3O9 metaphosphate not only a scientifically intriguing system but also a highly promising candidate for next-generation optoelectronic devices, temperature sensors, and energy storage technologies. Our study significantly expands the understanding of phosphate-based metaphosphates and lays a critical foundation for future exploration and optimization of these materials in advanced electronics and photonics.
Author contributions
Mayssa Karray: investigation, data curation, formal analysis, visualization, writing – original draft, writing – review & editing. Iheb Garoui: investigation, data curation, formal analysis, visualization, writing – original draft, writing – review & editing. Saber Nasri: investigation, data curation, formal analysis, visualization, writing – original draft, writing – review & editing. Nourah A. Alsobai: investigation, formal analysis, visualization, writing – original draft, writing. Noweir Ahmad AlGhamdi: investigation, formal analysis, visualization, writing – original draft, writing. Abderrazek Oueslati: conceptualization, methodology, formal analysis, validation, writing review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The authors confirm that the data used to support the findings of this study are included within the article and are available from the corresponding author upon reasonable request.References
- S. B. Yahya, I. Garoui, N. Abid, R. Barillé and B. Louati, K2MgGeO4 orthogermanate: A promising material for optoelectronic applications – Insights from optical absorption, NTCR behavior, and dielectric polarization analysis, Ceram. Int., 2025, 51, 45762, DOI:10.1016/j.ceramint.2025.07.291.
- A. Zaman, et al., Analysis of the effect of nickel substitution on the structural, optical, dielectric, and magnetic properties of SrNb2O6 ceramics synthesized via the solid-state reaction route, J. Mol. Struct., 2025, 1345, 143115, DOI:10.1016/j.molstruc.2025.143115.
- W. H. Shah, et al., Structural, dielectric relaxation, and electrical transport properties of Ca2V2O7 pyrovanadate: Complex impedance spectroscopy and DFT investigations, Ceram. Int., 2025, 51, 46294, DOI:10.1016/j.ceramint.2025.07.337.
- S. Ben Yahya, I. Garoui, M. Zaghrioui, A. Oueslati and B. Louati, Solid-state synthesized Li4GeO4 germanate: an exploration of its structure, vibrational characteristics, electrical conductivity, and dielectric properties, RSC Adv., 2025, 15(12), 9295–9304, 10.1039/d5ra01165e.
- N. Lalotra, V. Kumar and K. Pathania, Structural analysis, charge compensation and down-conversion photoluminescence in LiMgPO4:Sm3+ phosphors for warm light emitting applications, Ceram. Int., 2025, 51, 47295, DOI:10.1016/j.ceramint.2025.07.432.
- I. Garoui, et al., Dielectric relaxation and electrothermal charge carrier transport via correlated barrier hopping in the solid electrolyte TlFeP2O7: Experimental and theoretical modeling, Ceram. Int., 2025, 51, 29510, DOI:10.1016/j.ceramint.2025.04.155.
- S. Aydi, A. Djemli, O. A. Algethami, S. Znaidia, F. Sahnoune and A. Oueslati, Study on morphological, FTIR, optical band-gap and AC conductivity of Li2CoP2O7 for advanced applications, RSC Adv., 2025, 15(33), 27154–27166, 10.1039/d5ra04105h.
- A. Akhrouf, S. Krimi, M. Bouhbou, Y. Laajali and E. K. Hlil, Synthesis, crystal structure, optical, color, thermal, magnetic, and spectroscopic properties of the substituted honeycomb-lattice BaNi2−xCox(PO4)2 (x = 0, 0.5 and 1), Ceram. Int., 2023, 49(3), 5130–5145, DOI:10.1016/j.ceramint.2022.10.030.
- S. K. Choi, et al., Comparative investigation of electrochemical properties of Li1.5Al0.5Ti1.5(PO4)3 ceramic electrolyte synthesized using different chelating agents for all solid-state batteries, Ceram. Int., 2025, 51(8), 10502–10509, DOI:10.1016/j.ceramint.2024.12.482.
- L. Liu, R. Wang, W. Du, X. Zhang, H. Wu and X. Lu, Phase composition, bond characteristics and thermal conductivity of novel Cu4O(PO4)2 microwave dielectric ceramic at low sintering temperature, Ceram. Int., 2025, 51(3), 3926–3933, DOI:10.1016/j.ceramint.2024.11.368.
- Q. Yu, et al., Effect of Mn2+ substitution on the dielectric properties of NaMg(PO3)3 ceramics at microwave and terahertz frequencies, Ceram. Int., 2024, 50(22), 47971–47979, DOI:10.1016/j.ceramint.2024.09.144.
- C. Sun, et al., Low permittivity LiGd(PO3)4 microwave dielectric ceramics and their application in C-band, J. Alloys Compd., 2025, 1033, 181163, DOI:10.1016/j.jallcom.2025.181163.
- I. Mokni, et al., Sr6Y(PO4)5: Nd3+ a novel whitlockite-type phosphor for optical temperature sensing applications: Synthesis and luminescence properties, Ceram. Int., 2024, 50(13), 22936–22946, DOI:10.1016/j.ceramint.2024.04.018.
- R. Gond, et al., Enabling the Electrochemical Activity in Sodium Iron Metaphosphate [NaFe(PO3)3] Sodium Battery Insertion Material: Structural and Electrochemical Insights, Inorg. Chem., 2017, 56(10), 5918–5929, DOI:10.1021/acs.inorgchem.7b00561.
- B. Chen, Z. Peng and Z. Yuan, Constructing sandwich structure of Nb-substituted Na3V2(PO4)3/C nanoparticles enwrapped on three-dimensional graphene with superior sodium storage property, Ceram. Int., 2022, 48(22), 33957–33966, DOI:10.1016/j.ceramint.2022.07.345.
- W. Wang, B. Jiang, L. Hu and S. Jiao, Nasicon material NaZr2(PO4)3: a novel storage material for sodium-ion batteries, J. Mater. Chem. A, 2014, 2(5), 1341–1345, 10.1039/c3ta14310d.
- P. Barpanda, et al., A layer-structured Na2CoP2O7 pyrophosphate cathode for sodium-ion batteries, RSC Adv., 2013, 3(12), 3857, 10.1039/c3ra23026k.
- S. R. Vasant, et al., A Review on calcium pyrophosphate and other related phosphate nano Bio-materials and their applications, Rev. Adv. Mater. Sci., 2017, 48, 44 Search PubMed.
- S. V. Dorozhkin, Calcium orthophosphate-based biocomposites and hybrid biomaterials, J. Mater. Sci., 2009, 44(9), 2343–2387, DOI:10.1007/s10853-008-3124-x.
- T. Safronova, et al., Bioceramics Based on β-Calcium Pyrophosphate, Materials, 2022, 15(9), 3105, DOI:10.3390/ma15093105.
- M. Yang, et al., Humidity-Responsive Amorphous Calcium–Magnesium Pyrophosphate/Cassava Starch Scaffold for Enhanced Neurovascular Bone Regeneration, ACS Appl. Mater. Interfaces, 2024, 16(28), 35964–35984, DOI:10.1021/acsami.4c03204.
- R. M. P. Colodrero, P. Olivera-Pastor, A. Cabeza and M. Bazaga-García, Properties and Applications of Metal Phosphates and Pyrophosphates as Proton Conductors, Materials, 2022, 15(4), 1292, DOI:10.3390/ma15041292.
- M. Karray, I. Garoui, S. Nasri, S. Znaidia, A. Mahmoud and A. Oueslati, Cesium Iron (III) Pyrophosphate Prepared Using a Solid-State Process: Structure, Mössbauer Spectroscopy, and Relaxation Dynamics, ChemistrySelect, 2025, 10(2), 1, DOI:10.1002/slct.202404727.
- P. K. Panda, P.-Y. Sung, P. Dash, C.-T. Hsieh, J.-K. Chang and W.-R. Liu, Exploiting high ionic conductivity of solid-state electrolytes by doping metal ions into NASICON-type ceramics for solid-state lithium batteries, Ceram. Int., 2025, 51, 34203, DOI:10.1016/j.ceramint.2025.05.148.
- X. Lin, et al., Synthesis, structural, and electrochemical properties of NaCo(PO3)3 cathode for sodium-ion batteries, J. Solid State Electrochem., 2016, 20(5), 1241–1250, DOI:10.1007/s10008-015-3114-2.
- X. Lin, Y. Zhao, Y. Dong and Q. Kuang, Synthesis and structural data of a Fe-base sodium metaphosphate compound, NaFe(PO 3) 3, Data Brief, 2015, 4, 217–221, DOI:10.1016/j.dib.2015.05.022.
- R. V. Lavrik, V. V. Trachevsky and V. A. Diamant, Growth of monocrystals of double polyphosphate NaMn (PO3)3 and its structure, Catal. Petrochem., 2019, 28, 61–68, DOI:10.15407/kataliz2019.28.061.
- L. Wu, et al., Defect-Induced Self-Reduction and Anti-Thermal Quenching in NaZn(PO3)3:Mn2+ Red Phosphor, Adv. Opt. Mater., 2021, 9(19), 1, DOI:10.1002/adom.202100870.
- I. Abrahams, G. E. Hawkes, A. Ahmed, T. Di Cristina, D. Z. Demetriou and G. I. Ivanova, Structures of the chain metaphosphates NaM(PO3)3 (M = Ca or Sr), Magn. Reson. Chem., 2008, 46(4), 316–322, DOI:10.1002/mrc.2161.
- M. Amara, A. Jbeli, N. A. Althumairi, J. Dhahri and E. K. Hlil, Investigating the NTC characteristics of (1 − x)BFN − xBCW ceramics via impedance spectroscopy, Ceram. Int., 2025, 51(15), 20371–20380, DOI:10.1016/j.ceramint.2025.02.205.
- R. Meena and R. S. Dhaka, Dielectric properties and impedance spectroscopy of NASICON type Na3Zr2Si2PO12, Ceram. Int., 2022, 48(23), 35150–35159, DOI:10.1016/j.ceramint.2022.08.111.
- Y. Ben Smida, A. Guesmi, S. Georges, M. Avdeev and M. F. Zid, Crystal structure and ionic conductivity of the new cobalt polyphosphate NaCo(PO3)3, J. Solid State Chem., 2016, 234, 15–21, DOI:10.1016/j.jssc.2015.11.029.
- R. Gond, R. P. Rao, V. Pralong, O. I. Lebedev, S. Adams and P. Barpanda, Cubic Sodium Cobalt Metaphosphate [NaCo(PO3)3] as a Cathode Material for Sodium Ion Batteries, Inorg. Chem., 2018, 57(11), 6324–6332, DOI:10.1021/acs.inorgchem.8b00291.
- M. L. Meena, C.-H. Lu, S. Som, R. Chaurasiya and S. D. Lin, Highly efficient and thermally stable Eu3+ activated phosphate based phosphors for wLEDs: An experimental and DFT study, J. Alloys Compd., 2022, 895, 162670, DOI:10.1016/j.jallcom.2021.162670.
- S. Wang, C. Xu and X. Qiao, Synthesis and photoluminescence properties of the novel Eu3 + -activated CaNa(PO3)3 phosphors, J. Mater. Sci.: Mater. Electron., 2020, 31(12), 9605–9613, DOI:10.1007/s10854-020-03503-7.
- J. Faber, EPDIC-8, European Powder Diffraction Conference, Powder Diffr., 2002, 17(4), 337–338, DOI:10.1154/1.1536354.
- O. Amorri, M. Khalfa, R. Jemai, J. Horchani, L. Bessais and K. Khirouni, Structural, optical electrical and magnetic properties of Zn0.5Mg0.5Fe2O4 ferrite, Inorg. Chem. Commun., 2025, 179, 114753, DOI:10.1016/j.inoche.2025.114753.
- P. Khajuria, A. K. Bedyal, M. Manhas, A. Vij, H. C. Swart and V. Kumar, Crystal Structure and Luminescence Dynamics of Highly Pure Lim(Po3)3:Eu3 + [M = Sr, Ca] Red Phosphors for White Light Emitting Diodes, SSRN Electron. J., 2022, 42, 1470, DOI:10.2139/ssrn.4210946.
- H. L. Yakel, On the structures of some compounds of the perovskite type, Acta Crystallogr., 1955, 8(7), 394–398, DOI:10.1107/s0365110x55001291.
- D. Ilieva, D. Kovacheva, C. Petkov and G. Bogachev, Vibrational spectra of R(PO3)3 metaphosphates (R = Ga, In, Y, Sm, Gd, Dy), J. Raman Spectrosc., 2001, 32(11), 893–899, DOI:10.1002/jrs.753.
- M. Ferid, N. K. Ariguib and M. Trabelsi, Etude du système KPO3Sm(PO3)3 et des phases polymorphiques de phosphates condensés KSm(PO3)4, J. Solid State Chem., 1987, 69(1), 1–9, DOI:10.1016/0022-4596(87)90002-8.
- A. Watras, et al., The role of the Ca vacancy in the determination of the europium position in the energy gap, its valence state and spectroscopic properties in KCa(PO3)3, Phys. Chem. Chem. Phys., 2014, 16(12), 5581, 10.1039/c3cp54875a.
- R. Ben Said, N. Moutia, B. Louati, K. Guidara and K. Khirouni, UV–visible characterization of zinc and potassium zinc pyrophosphate, Opt. Quantum Electron., 2021, 54(1), 1, DOI:10.1007/s11082-021-03312-0.
- S. Ben Yahya, H. El Karout, B. Sahraoui, R. Barillé and B. Louati, Innovative synthesis, structural characteristics, linear and nonlinear optical properties, and optoelectric parameters of newly developed A2ZnGeO4 (A = K, Li) thin films, RSC Adv., 2024, 14(33), 23802–23815, 10.1039/d4ra03742a.
- M. Mnakri, H. Souissi, M. Tliha, M. Ben Gzaiel, S. Znaidia and A. Oueslati, Exploring the structural electrical, optical and theoretical study of KCrP2O7: A look through Racah theory, J. Mol. Struct., 2025, 1328, 141359, DOI:10.1016/j.molstruc.2025.141359.
- Amorphous and Liquid Semiconductors, ed. J. Tauc, Springer US, 1974, DOI:10.1007/978-1-4615-8705-7.
- I. Ibrahmi, et al., Synthesis and trigonal structure of a new lead-free zero-dimensional perovskite (CH3NH3)2[SnBr6] with multifunctional optical and electrical properties, J. Phys. Chem. Solids, 2025, 207, 112909, DOI:10.1016/j.jpcs.2025.112909.
- A. B. A. Hajji, et al., MnCr2O4: A suitable material with significant optical response for optoelectronic devices, Opt. Mater., 2025, 162, 116951, DOI:10.1016/j.optmat.2025.116951.
- C. Wang, X. Fan, Y. Tan, W. Wei and Y. Tang, High-Temperature Reversible Phase Transition and Switchable Dielectric and Semiconductor Properties in a 2D Hybrid [(C3H12N2O)CdCl4]n, Eur. J. Inorg. Chem., 2019,(24), 2907–2911, DOI:10.1002/ejic.201900493.
- M. Abudoureheman, et al., MIMIIP3O9 (MI = Rb, MII = Cd, Mg, Ca; MI = Cs, MII = Pb, Sr; MI = K, MII = Mg): Cation Substitution Application in Cyclophosphate Family and Nonlinear Optical Properties, Inorg. Chem., 2018, 57(12), 7372–7379, DOI:10.1021/acs.inorgchem.8b01017.
- A. B. A. Hajji, M. Wali, R. Dhahri, E. Dhahri, J. F. M. L. Mariano and M. Jemmali, A comprehensive study of the structural, magnetic and optoelectronic behavior of Ni0.6Mn0.4Cr2O4 chromite for magneto optical devices, Ceram. Int., 2025, 51(14), 18369–18383, DOI:10.1016/j.ceramint.2025.02.050.
- I. Garoui, S. Ben Yahya, N. A. Alghamdi, I. Chaabane, A. Oueslati and B. Louati, Investigation of electronic parameters, carrier transport mechanisms via the correlated barrier hopping model, electrothermal NTCR effects, and polarization contributions to the dielectric response of Ni3(PO4)2 orthophosphates synthesized by the sintering process, Mater. Adv., 2025, 6(24), 9761–9778, 10.1039/d5ma01096a.
- M. Ben Gzaiel, I. Garoui, F. N. Almutairi, I. Mbarek and A. Oueslati, Lead-Free halide perovskites for optoelectronic application: Investigation of structural, optical, electric and dielectric behaviors, Opt. Mater., 2024, 154, 115664, DOI:10.1016/j.optmat.2024.115664.
- A. S. Hassanien and A. A. Akl, Optical characteristics of iron oxide thin films prepared by spray pyrolysis technique at different substrate temperatures, Appl. Phys. A:Mater. Sci. Process., 2018, 124(11), 1, DOI:10.1007/s00339-018-2180-6.
- A. B. J. Kharrat, K. Kahouli and S. Chaabouni, Detailed investigation of the optical properties of the (C8H11BrN)3BiCl6 compound by UV–visible measurements, Bull. Mater. Sci., 2020, 43(1), 1, DOI:10.1007/s12034-020-02248-7.
- R. Mguedla, et al., Experimental and theoretical investigations on optical properties of multiferroic PrCrO3 ortho-chromite compound, Opt. Mater., 2020, 101, 109742, DOI:10.1016/j.optmat.2020.109742.
- F. Hcini, J. Khelifi and K. Khirouni, Improving of structural, conduction mechanisms, dielectric, optical properties of the sol–gel produced half-doped La0.5Ba0.5CrO3 perovskite for electronics devices, non-linear optical and optoelectronic applications, Appl. Phys. A:Mater. Sci. Process., 2025, 131(6), 1, DOI:10.1007/s00339-025-08612-w.
- S. Heni, S. Hcini, M. L. Bouazizi, L. HajTaieb, A. Dhahri and H. ben Bacha, Improving the optical properties of magnesium spinel chromites through Ni and Cu substitutions for optoelectronic applications, RSC Adv., 2024, 14(36), 26340–26353, 10.1039/d4ra03342f.
- M. Enneffati, M. Rasheed, B. Louati, K. Guidara and R. Barillé, Morphology, UV–visible and ellipsometric studies of sodium lithium orthovanadate, Opt. Quantum Electron., 2019, 51(9), 1, DOI:10.1007/s11082-019-2015-5.
- M. Enneffatia, M. Rasheed, B. Louatia, K. Guidaraa, S. Shihab and R. Barillé, Investigation of structural, morphology, optical properties and electrical transport conduction of Li0.25Na0.75CdVO4 compound, J. Phys.: Conf. Ser., 2021, 1795(1), 012050, DOI:10.1088/1742-6596/1795/1/012050.
- I. Garoui, et al., Synthesis, crystal structure, BFDH morphology, Hirshfeld surface analysis and electrical characterization of the new bi-(2-amino-5-methylpyridinium) hexa-chlorostannate compound, Phys. E, 2024, 158, 115897, DOI:10.1016/j.physe.2024.115897.
- I. Garoui, M. Mallek, F. N. Almutairi, W. Rekik and A. Oueslati, Synthesis, Structural characterization and complex impedance analysis of a novel organic-inorganic hybrid compound based on Mercury (II) chloride, J. Mol. Struct., 2024, 1315, 138881, DOI:10.1016/j.molstruc.2024.138881.
- U. Kumar, H. Cheema, V. Yadav, R. Sundar Maurya, A. Kumar and P. A. Alvi, Influence of La doping on structure, AC conductivity and impedance spectroscopy of Ba2SnO4 Ruddlesden Popper oxide, Mater. Chem. Phys., 2021, 274, 125186, DOI:10.1016/j.matchemphys.2021.125186.
- U. Kumar and M. Jatiya, Structural and Electrical Properties of Perovskite SrSnO 3 and Ruddlesden Popper Oxide Sr 2 SnO 4: A comparative study, 2023 DOI:10.22541/au.168692950.08587515/v1.
- U. Kumar, K. Ankur, D. Yadav and S. Upadhyay, Synthesis and characterization of Ruddlesden-Popper system (Ba1−xSrx)2SnO4, Mater. Charact., 2020, 162, 110198, DOI:10.1016/j.matchar.2020.110198.
- U. Kumar and S. Upadhyay, Structural, Optical and Electrical Properties of Ruddlesden Popper Oxide Ba2SnO4, J. Electron. Mater., 2019, 48(8), 5279–5293, DOI:10.1007/s11664-019-07336-x.
- N. Ortega, et al., Multiferroic properties of Pb(Zr,Ti)O3/CoFe2O4 composite thin films, J. Appl. Phys., 2006, 100(12), 126105, DOI:10.1063/1.2400795.
- S. Karmakar, S. Varma and D. Behera, Investigation of structural and electrical transport properties of nano-flower shaped NiCo2O4 supercapacitor electrode materials, J. Alloys Compd., 2018, 757, 49–59, DOI:10.1016/j.jallcom.2018.05.056.
- P. Satpathy, A. Behera, S. Parhi and S. K. Parida, Electrical characterization of the barium manganite, Mater. Today: Proc., 2022, 67, 1180–1184, DOI:10.1016/j.matpr.2022.07.453.
- S. Nasri, A. Jraba, I. Garoui, A. Oueslati and E. Elaloui, Potassium tin chloride (K2SnCl6) as a lead-free perovskite: anti-solvent synthesis, structural characterization, and charge transport properties, RSC Adv., 2025, 15(7), 5369–5380, 10.1039/d5ra00090d.
- D. Johnson, ZPlot, ZView Electrochemical Impedance Software Version 2.3 b, Scribner Associates Inc., North Carolina, 2000 Search PubMed.
- S. Jagtap, S. Rane, S. Gosavi, U. Mulik and D. Amalnerkar, Infrared properties of ‘lead free’ thick film NTC thermo-resistive sensor based on the mixture of spinel material and RuO2, Sens. Actuators, A, 2013, 197, 166–170, DOI:10.1016/j.sna.2013.03.037.
- B. K. Das, T. Das and D. Das, Structural and electrical properties of mechanically alloyed ZnO nanoceramic for NTC thermistor application, J. Mater. Sci.: Mater. Electron., 2023, 34(3), 230, DOI:10.1007/s10854-022-09670-z.
- S. Chkoundali, I. Garoui, W. Trigui and A. Oueslati, Crystal structure, Hirshfeld surface analysis, conduction mechanism and electrical modulus study of the new organic–inorganic compound [C8H10NO]2HgBr4, RSC Adv., 2024, 14(13), 8971–8980, 10.1039/d4ra00689e.
- N. Chakchouk, B. Louati and K. Guidara, Ionic conductivity and dielectric relaxation studies of a low-temperature form of silver zinc phosphate, J. Alloys Compd., 2018, 747, 543–549, DOI:10.1016/j.jallcom.2018.03.036.
- M. Javed, et al., Investigation on electrical transport and dielectric relaxation mechanism in TbCrO3 perovskite orthochromite, J. Alloys Compd., 2023, 955, 170181, DOI:10.1016/j.jallcom.2023.170181.
- R. Bergman, General susceptibility functions for relaxations in disordered systems, J. Appl. Phys., 2000, 88(3), 1356–1365, DOI:10.1063/1.373824.
- A. K. Jonscher, The ‘universal’ dielectric response, Nature, 1977, 267(5613), 673–679, DOI:10.1038/267673a0.
- B. Louati, F. Hlel and K. Guidara, Ac electrical properties and dielectric relaxation of the new mixed crystal (Na0.8Ag0.2)2PbP2O7, J. Alloys Compd., 2009, 486(1–2), 299–303, DOI:10.1016/j.jallcom.2009.06.148.
- M. Javed, et al., Electro-thermally assisted charge carrier dynamics and dielectric relaxation response of CuAl2O4 spinel aluminate, J. Alloys Compd., 2025, 1012, 178429, DOI:10.1016/j.jallcom.2024.178429.
- S. R. Elliott, A.C. conduction in amorphous chalcogenide and pnictide semiconductors, J. Adv. Phys., 1987, 36(2), 135–217, DOI:10.1080/00018738700101971.
- N. F. Mott, Materials with mixed valency that show a verwey transition, Philos. Mag. B, 1980, 42(3), 327–335, DOI:10.1080/01418638008221874.
- M. Enneffati, B. Louati, K. Guidara, M. Rasheed and R. Barillé, Crystal structure characterization and AC electrical conduction behavior of sodium cadmium orthophosphate, J. Mater. Sci.: Mater. Electron., 2017, 29(1), 171–179, DOI:10.1007/s10854-017-7901-7.
- D. Panda, S. S. Hota and R. N. P. Choudhary, Investigation of structural, microstructural, dielectric, and electrical characteristics of a new lead-free compound: Ca3Bi2MoO9, J. Mater. Sci.: Mater. Electron., 2023, 34(27), 10854, DOI:10.1007/s10854-023-11326-5.
- S. S. Hota, D. Panda and R. N. P. Choudhary, Development of ultra-high energy storage density and ultra-wide operating temperature behavior of a lead-free capacitor sensor; (Bi1/2 K1/2) (Fe1/3Mn1/3W1/3)O3, J. Power Sources, 2024, 599, 234223, DOI:10.1016/j.jpowsour.2024.234223.
- S. Sekhar Hota, D. Panda and R. N. P. Choudhary, Studies of structural, dielectric, and electrical properties of polycrystalline barium bismuth tungstate for thermistor application, Inorg. Chem. Commun., 2023, 153, 110785, DOI:10.1016/j.inoche.2023.110785.
- S. S. Hota, D. Panda and R. N. P. Choudhary, Studies of structural, dielectric, electrical, and optical properties of a multi-doped novel complex perovskite (Bi1/2Na1/2)(Fe1/3Mn1/3W1/3)O3 ceramic for opto-electronic application, Chin. J. Phys., 2024, 87, 430–451, DOI:10.1016/j.cjph.2023.11.021.
- N. F. Mott, Conduction in glasses containing transition metal ions, J. Non-Cryst. Solids, 1968, 1(1), 1–17, DOI:10.1016/0022-3093(68)90002-1.
- S. Summerfield, Universal low-frequency behaviour in the a.c. hopping conductivity of disordered systems, J. Philos. Mag. B, 1985, 52(1), 9–22, DOI:10.1080/13642818508243162.
- B. Roling, C. Martiny and K. Funke, Information on the absolute length scales of ion transport processes in glasses from electrical conductivity and tracer diffusion data, J. Non-Cryst. Solids, 1999, 249(2–3), 201–209, DOI:10.1016/s0022-3093(99)00311-7.
- A. Ghosh and A. Pan, Scaling of the Conductivity Spectra in Ionic Glasses: Dependence on the Structure, J. Phys. Rev. Lett., 2000, 84(10), 2188–2190, DOI:10.1103/physrevlett.84.2188.
- S. O. Mansour, B. Louati and K. Guidara, AC conductivity and dielectric behavior of high-temperature form of copper silver phosphate, Ionics, 2015, 21(7), 1973–1982, DOI:10.1007/s11581-014-1362-2.
- S. Halder, A. Dutta and T. P. Sinha, Time–temperature superposition in the grain and grain boundary response regime of A2HoRuO6(A = Ba, Sr, Ca) double perovskite ceramics: a conductivity spectroscopic analysis, RSC Adv., 2017, 7(69), 43812–43825, 10.1039/c7ra08295a.
- I. Garoui, et al., New organic–inorganic chloride (2-amino-4-methylpyridinium hexachlorostannate): Crystal structure, BFDH morphology, and electrical conduction mechanism, J. Phys. Chem. Solids, 2025, 206, 112840, DOI:10.1016/j.jpcs.2025.112840.
- F. Hamrit, R. Chtourou, D. Taloub, I. Gharbi and A. Oueslati, Synthesis, morphological, electrical, and conduction mechanism studies of a sodium cerium diphosphate compound, RSC Adv., 2023, 13(22), 15356–15365, 10.1039/d3ra02231e.
- S. Nasri, M. Megdiche and M. Gargouri, The investigation of dielectric properties and ac conductivity of new ceramic diphosphate Ag0.6Na0.4FeP2O7 using impedance spectroscopy method, Phys. E, 2016, 84, 182–190, DOI:10.1016/j.physe.2016.06.009.
| This journal is © The Royal Society of Chemistry 2026 |











