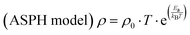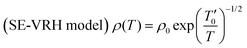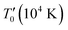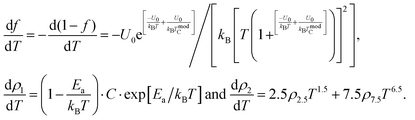DOI:
10.1039/D5MA01272D
(Paper)
Mater. Adv., 2026,
7, 1537-1551
TCR parameter study for examining the possibility of the usefulness of perovskite Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) systems for thermistor and bolometer applications
Received
3rd November 2025
, Accepted 12th December 2025
First published on 5th January 2026
Abstract
We report a comprehensive experimental and theoretical investigation of the electrical transport properties in Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05, and 0.1) compounds synthesized via the sol–gel route. Temperature-dependent resistivity measurements revealed a robust and composition-independent metal–semiconductor transition (TM–SC ≈ 160 K), an uncommon behavior for chemically substituted manganites. The transport characteristics were quantitatively examined using multiple conduction frameworks, including percolation theory, small-polaron hopping (SPH), and Mott variable-range hopping (VRH). These approaches enabled the extraction of activation energies, hopping exponents, charge-carrier localization parameters, and disorder-related scaling factors. Among the tested models, percolation theory yielded the most consistent description of the semiconducting regime across all samples. Temperature coefficient of resistance (TCR) values, calculated within phase-separation and phase-coexistence transport schemes, exhibited pronounced enhancement in the 180–200 K interval. The combined modeling-driven analysis demonstrated that Na substitution substantially modulated the intrinsic electronic transport parameters—even while preserving a fixed transition temperature—establishing these compositions as promising candidates for high-performance uncooled bolometric infrared sensing.
1. Introduction
Perovskite manganites with the universal formula AMnO3 (where A can be a trivalent element like La, Pr, and Sm, bivalent like Sr and Ca or monovalent like Na, K, and Ag) have received extensive attention due to their interesting electrical and magnetic properties, and they have also been extensively studied by researchers both experimentally1,2 and theoretically.3,4 Small changes in dopant concentration,5,6 preparation method or cation deficiency can cause huge changes in structural,7,8 electrical, optical and magnetic characteristics.9 Most of the studies have focused on trivalent rare earth doping in AMnO3 compounds via either partial or complete replacement with a monovalent element such as Ag, Na and K. These doped monovalent cations not only change the structure of the manganites but also affect their magneto-transport properties.10,11 Doped manganite systems exhibit important structural, optical, electrical and magnetic characteristics.3,12,13 Perovskite-like praseodymium manganites display both strong ferromagnetism and metallic conductivity when trivalent Pr3+ ions are partially substituted by monovalent ions like Ag, Na, K, etc.14,15 It has been reported that doped manganite materials exhibit multifunctional properties, including magnetic refrigeration, electrical transport, bolometric applications, and high-density magnetic recording technologies (such as read heads for hard disks and non-volatile magnetic random-access memory, MRAM).16 Significant efforts have been devoted to addressing the challenges associated with uncooled bolometric applications. In this context, and given that doped manganites are composed of phase-separated ferromagnetic metallic and paramagnetic insulating regions. Li et al.17 proposed a simple phenomenological model to describe the temperature dependence of electrical resistivity. Recently, Alexandrov et al.18 described the resistivity of manganites near the ferromagnetic transition using the so-called current carrier density collapse (CCDC). Using this result, Wang et al.19 can explain the behavior of TCR in manganites. In order to study the electrical transport mechanism and correlation between magnetic and electric properties, we prepared Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05 and 0.1) samples. Due to their ability to exhibit a metal–semiconductor transition (TM–SC) near room temperature, Na+- and K+-doped PrMnO3 manganites are considered promising candidates for practical applications.20,21 Specifically, the transport properties above TM–SC are generally interpreted using the small polaron hopping (SPH)22 or variable range hopping (VRH)23 models, while the metallic regime is governed by electron–magnon scattering and polaron formation near the transition. Additionally, Li et al.24 proposed a theoretical percolation model, based on phase separation between metallic and insulating regions, to explain the transport process across the whole temperature range. Typical TCR values are found to be closely related to intrinsic parameters such as activation energy, disorder, and transition temperature.
In this paper, in order to describe the electrical behavior of Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05 and 0.1) synthesized by the sol–gel method, we employed these models to calculate resistivity as a function of temperature and TCRmax, with particular attention paid to the role of adiabatic small polaron hopping conduction in the insulating and ferromagnetic phases. Meanwhile, detailed analysis confirmed that these theoretical approaches are quantitatively consistent with our experimental observations. Interestingly, the Na+ substitution was found to significantly influence the electrical transport mechanism and TCR behavior, opening perspectives for their application in infrared detection devices.
2. Experimental details
In this work, the under-investigated perovskite powders have been formed by using the modified sol–gel method that is known as Pechini. Thus, Pr6O11 (>99.9%), Na2CO3 (>99.9%), K2CO3 (>99.9%), and MnO2 (>99.9%) precursors revealing an elevated purity are mixed according to the following chemical reaction:
| 0.8/6Pr6O11 + (0.2 − x)/2K2CO3 + x/2Na2CO3 + MnO2 → Pr0.8K0.2−xNaxMnO3 + δCO2 + δ′O2 |
After mixing the initial powders, the obtained solution is mixed with citric acid (C6H8O7) and ethylene glycol (C2H6O2). To synthesize the desired manganites, heat treatment was applied in the second step of the preparation. After that, to remove organic matter and obtain a viscous gel, the obtained mixture is evaporated on a thermal plate at 120 °C. To obtain a crude powder, the obtained gel is dried at 300 °C. Two calcination steps at 600 °C for 10 hours and at 800 °C for 14 hours are also effectuated. Such kind of annealing treatment changes the raw powders into materials with a well-established crystalline structure and chemical composition. Using hydraulic press, each package of powder is pressed into pellets to obtain the samples, or they are subjected to different thermal heating (at 900 °C and 1000 °C). After the elaboration of the desired compounds, the obtained materials are electrically characterized using an impedance analyzer (Agilent 4294 A) by taking the materials in the form of electrical dipoles. To conduct the electrical measurements and to obtain a capacitor configuration, thin layers of silver are made on each pellet's two opposite faces to serve as electrodes. The experimental measurements (conductance and capacitance) as a function of frequency are conducted over a wide temperature range from 80 to 500 K to confirm that our compounds facilitate the future applications of manganites.
3. Experimental and theoretical (TCR) parameters for testing the possibility of the usefulness of some manganites for technological applications
3.1. Transport properties
To investigate the electrical properties of Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) samples, the variation of resistivity ρ(T) with temperature was measured in the temperature range [80–500 K]. Using the derivative of resistivity with respect to temperature (dρ/dT) as a criterion for the type of electrical behavior, we observed that the samples (x = 0.0, 0.05 and 0.1) exhibit metallic behavior (dρ/dT > 0) at low temperatures (for T < TM–SC) and adopt semiconductor behavior (dρ/dT < 0) above the TM–SC temperature, where TM–SC represents the temperature associated with the maximum value of resistivity ρmax (Fig. 1). For samples x = 0.0, x = 0.05, and x = 0.1, the transition temperature occurs at TM–SC = 160 K.
 |
| | Fig. 1 Temperature evolution of resistivity ρ and dρ/dT for the Pr0.8Na0.2−xKxMnO3 (x = 0.00 and x = 0.05) compounds. | |
3.1.1 Low-temperature behavior (T < TM–SC).
At low temperatures (T < TM–SC), Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) manganites exhibit metallic behavior. This behavior can be modeled by the charge carrier diffusion model,25 which is often used to fit experimental data for electrical resistivity as a function of temperature. The data are fitted using the following general expression: ρ(T) = ρ0 + ρnTn (n = 1, 2, 2.5, 4.5, 5 and 7.5). To identify the appropriate fit to the resistivity data (ρ(T)) of our manganites, we use the following equations:| | | ρ(T) = ρ0 + ρ2T2 + ρ4.5T4.5 | (4) |
| | | ρ(T) = ρ0 + ρ2T2 + ρ5T5 | (5) |
| | | ρ(T) = ρ0 + ρ2.5T2.5 + ρ7.5T7.5 | (6) |
where the term ρ1T is a thermal diffusive conductive process and ρ2T2 in eqn (2), (4) and (5) represents the electrical resistivity due to the electron–electron process.26,27 The other representation ρ2.5T2.5 is the electrical resistivity caused by the electron-magnon scattering process in the FM phase.28 The term ρ4.5T4.5 is a combination of electron–electron, electron–magnon and electron–phonon scattering processes.29,30 On the other hand, ρ5T5 represents the electron–phonon interaction31 and ρ7.5T7.5 originates partly from the formation of polarons close to metal-semiconductor transition temperature.32
In this case, the experimental data of the Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) sample are fitted to the aforementioned six equations (Fig. 2). The best fit can be derived by comparing the square of the linear correlation coefficient (R2) determined for each equation. The corresponding parameters of the fit are shown in the Table inserted in Fig. 2. It is noteworthy to mention that the obtained values of R2 for all samples were as high as 99.9% for eqn (6), supporting the view that eqn (6) is most suitable to fit the experimental results. This indicates that the electrical characteristics at T < TM–SC are controlled by the effects of the contribution of the electron-magnon scattering processes and the polaron formation. In the metallic regime (T < TM–SC), the reduction of resistivity with increasing Na substitution (x) is primarily attributed to the enhancement of double-exchange (DE) electron hopping between Mn3+ and Mn4+ ions. Introducing Na+ (monovalent) in place of K+ (also monovalent) subtly modifies the local electronic environment around the Mn–O network. Doping K+ with Na+ in manganite oxides primarily affects the structure and electronic bandwidth rather than the Mn mixed valence state, because both K+ and Na+ are monovalent cations. Substituting the larger K+ with the smaller Na+ reduces the A-site ionic radius and lowers the tolerance factor, which increases MnO6 octahedral tilting and decreases the Mn–O–Mn bond angle. These structural distortions weaken the double-exchange interaction, leading to reduced electrical conductivity and lower ferromagnetic transition temperatures. The Mn3+/Mn4+ ratio generally remains unchanged during K+ → Na+ substitution since the charge balance is preserved; however, Mn valence can be indirectly affected if the substitution alters the oxygen stoichiometry of the lattice. Overall, Na doping influences lattice distortion and transport/magnetic properties more significantly than it affects Mn valence. The corresponding parameters of fitting are collected and listed in Table 1.
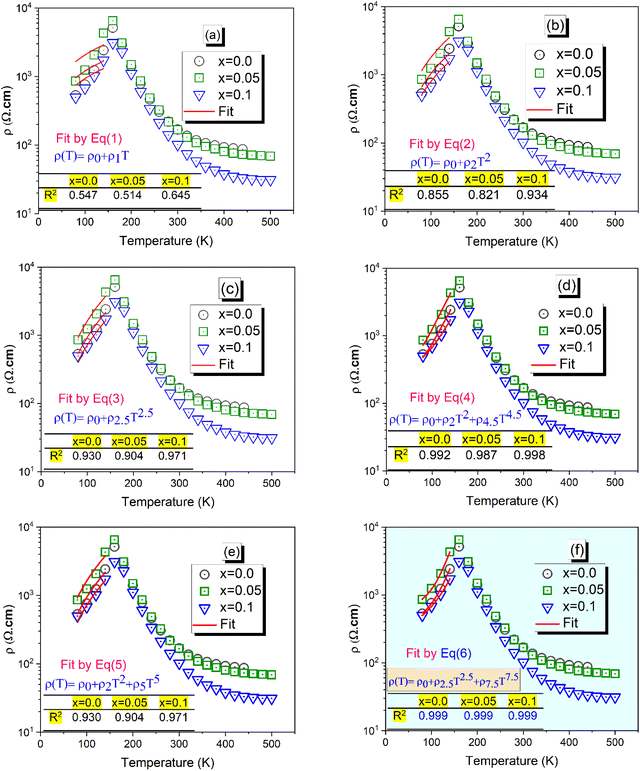 |
| | Fig. 2 The electrical resistivity ρ(T) as a function of temperature for Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05 and 0.1) samples (a–f). The red line is the fit of the experimental data in the metallic region below (TM–SC) using all the six equations. | |
Table 1 The obtained parameters of the experimental data fitted by the appropriate models below and above TM–SC of the Pr0.8K0.2−xNaxMnO3 (0 ≤ x ≤ 0.15) samples
|
|
ρ(T) = ρ0 + ρ2.5T2.5 + ρ7.5T7.5 |
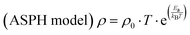
|

|
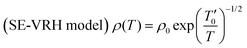
|
|
ρ
0 (Ω cm) |
ρ
2.5 (Ω cm K−2.5) |
ρ
7.5 (Ω cm K−7.5) |
R
2
|
E
a (meV) |
γ
|
R
2
|
E
a (meV) |
R
2
|
|
N′(EF) (1020 e V−1 cm−3) |
R
2
|
|
x = 0.0 |
35.656 |
2.821 × 10−4 |
1.120 × 10−14 |
0.999 |
76 |
2.756 |
0.995 |
92 |
0.997 |
3.3 |
6.156 |
0.996 |
|
x = 0.05 |
62.845 |
3.547 × 10−4 |
2.271 × 10−14 |
0.999 |
81 |
2.937 |
0.990 |
103 |
0.996 |
3.5 |
5.804 |
0.998 |
|
x = 0.1 |
30.983 |
3.105 × 10−4 |
5.527 × 10−15 |
0.999 |
109 |
3.953 |
0.988 |
130 |
0.994 |
3.9 |
5.209 |
0.999 |
3.1.2 High-temperature behavior (T > TM–SC).
In this range of temperature, (T > TM–SC), the variation in the electrical resistivity with temperature can be explained on the basis of two different models:
• Emin–Holstein's theory, called small polaron hopping (SPH), is considered for temperatures above θD/2 (θD is the Debye temperature).33
• The variable range hopping (VRH) model has been suggested to explain the electrical conduction above TM–SC, that is, in the range θD/4 < T < θD/2.34
3.1.2.1 SPH model.
This model is based on the phenomenon of hopping of a self-trapped electron (small polaron) to localized states. The hopping movements, associated with the transport mechanism to the nearest sites, are assisted by phonons.13,25 The conduction mechanism of our manganites at high temperatures (T > θD/2) is governed by the small polaron hopping model according to two possible approximations, one is called adiabatic (ASPH) (eqn (7)) and the other non-adiabatic (NSPH) (eqn (8)). These approximations are given by the following equations:33| | 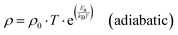 | (7) |
| |  | (8) |
where ρ0 is the residual resistivity and Ea is the energy needed for the activation of a hopping conduction process. For the studied samples, the well-known Debye temperature (θD) values were estimated using the curve of ln(ρ/T) versus 1/T (Fig. 3(a)–(c)). The optical phonon frequency (υph) can be obtained from the relation (h·υph = kB·θD), where h = 4.14375 × 10−15 eV s and kB = 8.61733326 × 10−5 eV K−1 are Planck's and Boltzmann's constants, respectively. For all studied compounds, the deduced υph and θD values are 1.331 × 1013 Hz and 320 K, respectively. These results are in good agreement with the results reported in the literature.35 From eqn (7) and (8), the parameter “Ea” describes the activation energies required for a charge carrier to hopping and participate in electrical conduction in each temperature range. Electrical resistivity is supported by the size imbalance of the cations present in manganite. This imbalance generates cationic disorder energy. The term cation size imbalance refers to the difference in ionic radii between the A-site cations (Pr3+, K+, and Na+) in the perovskite structure. Substituting K+ (ionic radius ≈ 1.64 Å) with the smaller Na+ (≈1.39 Å) increases the A-site size mismatch, which enhances structural disorder and modifies the Mn–O–Mn bond geometry. This disorder contributes to the cationic disorder energy and directly influences the carrier localization and therefore the electrical resistivity. While the electrical changes cannot be attributed to a single numerical value, the degree of A-site mismatch can be estimated through the well-known variance parameter 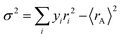 which increases with Na substitution (σ2 = 2.23 Å2 for x = 0.0 and σ2 = 1.72 Å2 for x = 0.05 and σ2 = 1.22 Å2 for x = 0.1).36,37 In regions of high and low temperatures, the activation energy Ea is given by the following equation:38
which increases with Na substitution (σ2 = 2.23 Å2 for x = 0.0 and σ2 = 1.72 Å2 for x = 0.05 and σ2 = 1.22 Å2 for x = 0.1).36,37 In regions of high and low temperatures, the activation energy Ea is given by the following equation:38| | 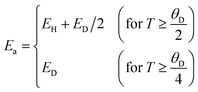 | (9) |
among them, EH is the polaron hopping energy and ED is the disorder energy resulting from the energy difference between neighboring sites. To identify which small-polaron hopping mechanism is dominant in our samples, we compared the experimental resistivity data to both the adiabatic small-polaron hopping (ASPH) and non-adiabatic small-polaron hopping (NSPH) models. As a consequence, the variation in ln(ρ/T) versus (1/kBT) and ln(ρ/T3/2) as a function of (1/kBT) is plotted in Fig. 4(a)–(c) and 5(a)–(c). Then, the aforementioned curves are fitted using the last equations (eqn (7) and (8)), respectively. The obtained parameters are presented in Table 1. It can be clearly seen from this table that the linear correlation coefficients (R2) for the used models are very close. For this reason, it is so difficult to judge the appropriate hopping mechanism SPH model. The orthorhombic perovskite structure and the distortion of the MnO6 octahedra influence the Mn–O–Mn bond angles, lattice strain, and consequently, the electronic bandwidth. These structural factors directly affect the hopping probability between Mn3+/Mn4+ ions and therefore play an essential role in determining the observed electrical transport behavior. To better understand which model is most suitable to describe the electrical transport phenomena at high temperatures, for all compounds, we used Holstein's condition.39 This restriction assumes that the polaron bandwidth represented by “J” should meet the expectations of the following inequality:| |  | (10) |
where J and ϕ are expressed as follows:| | 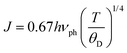 | (11) |
| | 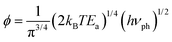 | (12) |
the ratio J/ϕ was expressed as follows:| | 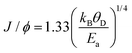 | (13) |
Using the θD and Ea values, computed from the slope of the straight-line curve (above θD/2), the J/ϕ ratios (Table 2) are determined. Although all samples exhibit J/ϕ > 1, which indicates that adiabatic hopping is possible, this criterion alone is not sufficient to identify the correct small-polaron regime. The selection of the adiabatic SPH (ASPH) mechanism is instead based on a combination of quantitative and physical arguments. First, the values predicted by the non-adiabatic model (NSPH) are significantly lower and physically inconsistent. Second, the ASPH model provides superior fitting quality, with higher linear correlation coefficients and smaller residuals compared to NSPH, demonstrating a more accurate description of the temperature dependence of ln(ρ/T) versus 1/(kBT). Finally, the mixed Mn3+/Mn4+ valence and the associated double-exchange pathways lead to a sufficiently large electron-transfer integral and bandwidth to promote adiabatic hopping rather than phonon-assisted non-adiabatic transport. For these combined reasons, ASPH-not NSPH best describes the conduction mechanism in the investigated Pr0.8K0.2−xNaxMnO3 compounds. It is also essential to check if the coupling of small polarons occurs through strong or weak e–ph interactions. According to the theories of Austin and Mott,40 the values of small-polaron coupling constant (γ) can be reckoned from the relation γ = 2Ea/h·υph. According to this standard, the small polaron coupling constant (γ) must satisfy the following conditions:41| | 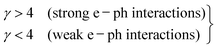 | (14) |
Therefore, the e–ph coupling constant γ is a key parameter to control various characteristics in the sample. Consequently, the value of γ is an important indicator of the type of interactions between electrons and phonons. Table 1 shows that this value ranges from 2.756 to 3.953, suggesting that doping with Na+ cations enlarge the interactions between electrons and phonons. At this point, the rapport between the polaron mass mp and rigid lattice effective mass m* is related to γ using the following equation:42,43| | 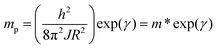 | (15) |
The obtained mp/m* ratio is mp/m* = 15.736, mp/m* = 18.859, and mp/m* = 52.091 for x = 0.0, 0.05 and 0.1, respectively. The ratio mp/m* provides a quantitative indication of the strength of electron–phonon coupling in small-polaron systems. According to the established SPH model in the literature, including the work of Khan et al. on Ca0.85Gd0.15MnO3, the values of mp/m* ≈ 1–5 correspond to weak-to-moderate coupling, whereas the ratios in the range of 10–20 are typically associated with weak adiabatic interaction where charge carriers retain significant mobility.42 In contrast, values exceeding ∼30–40 indicate strong polaron binding and enhanced localization. In our samples, the extracted values mp/m* = 15.736, 18.859, and 52.091 for x = 0.0, 0.05, and 0.1, respectively, fall clearly within these established regimes. The first two compositions lie in the weak-interaction domain, consistent with adiabatic small-polaron hopping, while the composition with x = 0.1 exhibits a significantly larger mass enhancement, indicative of a transition toward strong electron–phonon coupling due to increased structural disorder.42 These results validate the interpretation that the nature of carrier–lattice interaction evolves with Na substitution.
 |
| | Fig. 3 Evolution of Ln (ρ/T) against the inverse of temperature for the Pr0.8Na0.2−xKxMnO3 (x = 0.00 and x = 0.05) compounds (a)–(c). | |
 |
| | Fig. 4 Variation in ln(ρ/T) vs. (1/kBT) for the Pr0.8Na0.2−xKxMnO3 (x = 0.00 and x = 0.05) compounds (a)–(c). | |
 |
| | Fig. 5 Variation in ln(ρ/T3/2) vs. (1/kBT) for the Pr0.8Na0.2−xKxMnO3 (x = 0.00 and x = 0.05) compounds (a)–(c). | |
Table 2 Values of the J/ϕ ratio for the case of adiabatic and non-adiabatic SPH models for the Pr0.8K0.2−xNaxMnO3 (0 ≤ x ≤ 0.15) samples
|
|
x = 0.0 |
x = 0.05 |
x = 0.1 |
|
J/ϕ (adiabatic SPH) |
1.228 |
1.208 |
1.121 |
|
J/ϕ (non adiabatic SPH) |
1.170 |
1.137 |
1.073 |
3.1.2.2 VRH model.
As observed in Fig. 1, we found that all the studied compounds exhibit a metallic behavior below the characteristic Debye temperature θD/4. In this case, we can assume that the Mott-VRH conduction mechanism does not contribute to the transport properties of the materials at low temperatures. Beyond such characteristic temperature θD/4 = 160 K, we found from Fig. 4 and 5 that each curve exhibits two linear slopes, indicating the activation of two mean conduction processes. At high temperatures, the occurrence of semiconductor behavior is attributed to the hopping motion of the small polarons. However, the origin of the observed semiconductor behavior, in the intermediate temperature range, is not yet discussed for the studied compounds. In the literature, the occurrence of a semiconductor behavior, in the intermediate temperature range, is mainly attributed to the contribution of the Shklovskii-Efros-VRH (SE-VRH) conduction mechanism.44 To testify the validity of the SE-VRH on describing the electrical behavior of the materials in the intermediate temperature range, we plotted the evolution of ln(ρ(T)·T−1/2) versus T−1/2 (Fig. 6(a)–(c)) for all the prepared samples. In this temperature range, Shklovskii and Efros suggested that the material has a high density of charge carriers around the Fermi level.44 The SE-VRH model takes into consideration the charge carrier interaction effects on electrical resistivity, as compared to the proposed Mott-VRH model. Based on the SE-VRH model, the variation in DC resistivity as a function of temperature can be examined using the following expression:44| | 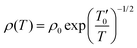 | (16) |
where the characteristic SE-VRH temperature 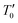 and the pre-exponential factor ρ0 are constants. For the studied compounds, the validity of the SE-VRH model was confirmed via the evolution of ln(ρ(T)·T−1/2) versus T−1/2 (Fig. 6(a)–(c)). In addition, the linear curves are used to calculate the characteristic SE-VRH temperature for each compound. From the relationship between
and the pre-exponential factor ρ0 are constants. For the studied compounds, the validity of the SE-VRH model was confirmed via the evolution of ln(ρ(T)·T−1/2) versus T−1/2 (Fig. 6(a)–(c)). In addition, the linear curves are used to calculate the characteristic SE-VRH temperature for each compound. From the relationship between 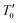 and the density of states at the Fermi level (N′(EF)) given by
and the density of states at the Fermi level (N′(EF)) given by 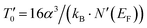 , we can determine N′(EF). The inverse of the localization length of the trapped charge carriers α was found to be 2.22 nm−1.45 The deduced values of
, we can determine N′(EF). The inverse of the localization length of the trapped charge carriers α was found to be 2.22 nm−1.45 The deduced values of 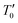 and N′(EF) for all samples are summarized in Table 1. From Table 1, it is obvious that a remarkable decrease in N′(EF) could be observed. In the intermediate temperature interval, more information about the dynamics of the charge carriers can be equally obtained. Using the Shimakawa theory,46 the transfer of localized electrons via tunneling conduction processes also accounts for the origin of the electrical resistivity for θD/4 ≤ T ≤ θD/2. Consequently, the evolution of ρ against temperature, for θD/4 ≤ T ≤ θD/2, can be analyzed using the relation ρ = ρ0·T−n. From Fig. 6(d) and (e), the value of the exponent factor n was deduced. The corresponding parameters of the fit are shown in Table 1 inserted in Fig. 6(d) and (e). The n parameter was employed to examine the electron-lattice interaction force. From Fig. 6(d) and (e), the obtained n value confirmed that the electrical transport is governed by the contribution of the multi-phonon tunnel effect and indicated that Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) system again reveals a weak electron-lattice interaction.46
and N′(EF) for all samples are summarized in Table 1. From Table 1, it is obvious that a remarkable decrease in N′(EF) could be observed. In the intermediate temperature interval, more information about the dynamics of the charge carriers can be equally obtained. Using the Shimakawa theory,46 the transfer of localized electrons via tunneling conduction processes also accounts for the origin of the electrical resistivity for θD/4 ≤ T ≤ θD/2. Consequently, the evolution of ρ against temperature, for θD/4 ≤ T ≤ θD/2, can be analyzed using the relation ρ = ρ0·T−n. From Fig. 6(d) and (e), the value of the exponent factor n was deduced. The corresponding parameters of the fit are shown in Table 1 inserted in Fig. 6(d) and (e). The n parameter was employed to examine the electron-lattice interaction force. From Fig. 6(d) and (e), the obtained n value confirmed that the electrical transport is governed by the contribution of the multi-phonon tunnel effect and indicated that Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) system again reveals a weak electron-lattice interaction.46
 |
| | Fig. 6 Variation in ln(ρT−1/2) vs. T−1/2 (a)–(c). Variation in ln(ρ) vs. ln(T) for the Pr0.8Na0.2−xKxMnO3 (x = 0.00 and x = 0.05) compounds (d and e). | |
3.2. Percolation model
In order to understand the transport properties in the whole temperature range explored, in particular around the transition temperature, a new phenomenological model based on the phase segregation mechanism (percolation approach) was developed.15,17 Following this model and for the determination of the percolation threshold dependence, we carried out a quantitative analysis for the resistivity temperature dependence for the explored samples. According to Li et al.,15,17 due to the competition between FM and PM regions, the total resistivity can be expressed as follows:where ρ1,2 is the resistivity of each phase, f is the volume fraction of the (FM) area, and (1 − f) is the volume fraction of the (PM) area. The volume fractions of FM and PM phases satisfy the Boltzmann distribution expressed as follows:| |  | (18a) |
| | 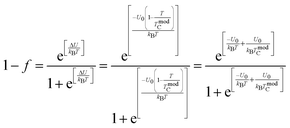 | (18b) |
where 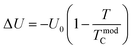 is the energy difference between FM and PM states, TmodC represents the temperature in the vicinity of which the resistivity reaches a maximum value and U0 is the energy difference for temperatures well below TmodC.17 Therefore, the complete expression describing the temperature dependence of resistivity over the entire temperature range can be written in the following form:
is the energy difference between FM and PM states, TmodC represents the temperature in the vicinity of which the resistivity reaches a maximum value and U0 is the energy difference for temperatures well below TmodC.17 Therefore, the complete expression describing the temperature dependence of resistivity over the entire temperature range can be written in the following form:| |  | (19) |
From eqn (18), one can find that,| | 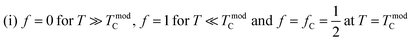 | (20) |
| | 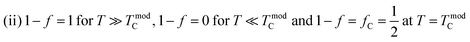 | (21) |
where ƒC is the percolation threshold. It is worth mentioning that when f < ƒC, the sample remains semiconducting, and when f > ƒC, the sample becomes metallic. The simulated curves of the resistivity (red line) of these samples are shown in Fig. 7. Obviously, the calculated results are in good agreement with the experimental data. The best parameters obtained after fitting are summarized in Table 3. In addition, the excellent agreement between the calculated graph and the experimental graph shows that the percolation model is applicable to these samples and confirms the coexistence of the FM domain and the PM area near the TC. In addition, the relationship between the FM phase volume fraction (f) of the sample and the temperature determined by the fitting of the resistivity data is shown in Fig. 8(a). The common behavior between samples was obtained. The function f(T) is equal to 1 under TM–SC, which indicates that the FM score in this part has a strong advantage. Then, above TM–SC, the curve tends to decrease to zero and enter the PM insulator state. The final behavior of f(T) confirms the effectiveness of the percolation method, which assumes that the FM state transitions to the PM state when the temperature rises.
 |
| | Fig. 7 The electrical resistivity ρ(T) as a function of temperature. The red line is the percolation model calculated using eqn (19). | |
Table 3 The obtained parameters of the percolation model using eqn (19) of the Pr0.8K0.2−xNaxMnO3 (0 ≤ x ≤ 0.15) samples
|
|
ρ
0 (Ω cm) |
ρ
2.5 (Ω cm K−2.5) |
ρ
7.5 (Ω cm K−7.5) |
C (Ω cm) |
T
modC (K) |
U
0/kB (K) |
E
a/kB (K) |
R
2
|
|
x = 0.0 |
449.81068 ± 68.32155 |
9.5015 × 10−4 ± 0.0013 |
1.34397 × 10−13 ± 7.28119 × 10−14 |
0.00123 ± 3.16228 × 10−4 |
160 |
2972.92613 ± 136.44094 |
1618.88704 ± 107.13246 |
1 |
|
x = 0.05 |
546.54552 ± 72.11806 |
0.0049 ± 0.0012 |
1.48674 × 10−13 ± 4.00304 × 10−14 |
0.00143 ± 1.78961 × 10−4 |
160 |
3087.13258 ± 65.62395 |
1622.74086 ± 47.21513 |
1 |
|
x = 0.1 |
386.52349 ± 87.54988 |
0.00196 ± 0.00146 |
1.42002 × 10−14 ± 2.15818 × 10−14 |
0.00134 ± 2.62766 × 10−4 |
160 |
2906.38964 ± 349.19834 |
1621.62382 ± 50.2435 |
0.999 |
 |
| | Fig. 8 The temperature dependencies of the volume fractions of the FM (f) for the Pr0.8K0.2−xNaxMnO3 (x = 0, 0.05 and 0.1) compounds (a). The temperature dependencies of the volume fractions of the FM (f), PM (1 − f) phases and df/dT for the Pr0.8K0.2−xNaxMnO3 (x = 0, 0.05 and 0.1) samples using eqn (18a) and (18b) (b)–(d). | |
Fig. 8(b)–(d) shows the temperature dependence of the volume fraction of the FM phase f and the volume fraction of the PM phase 1 − f. In the present approach, as shown in Fig. 8(b)–(d), the transition from the PM state (f = 0) to the FM state (f = 1) occurs over a wide temperature range (∼75 K) near TC. This may be more supported by the values of Curie temperature TC determined by the volume fraction of the FM region df/dT, as shown in Fig. 8(b)–(d). We found that the obtained values of TC for all samples are very close.
3.3. Correlation of the temperature coefficient of resistivity (TCR) for doped manganites to the transition temperature
The temperature coefficient of resistance (TCR), the percentage of which is defined by the following relationship:47,48| | 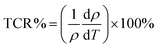 | (22) |
represents the basic parameters of the device application related to the infrared detector (IR) of the night vision technology (bolometer).47,49 TCR% is closely related to the resistivity and the slope of the ρ(T) curve. To understand the sensitivity of the infrared detector to a temperature in manganites, we must have a material with a high TCR value. The curves representing the temperature coefficient of resistance (TCR%) of the samples are shown in Fig. 9(a). In fact, the TCR values of the obtained Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05 and 0.1) samples are comparable to some systems used for infrared sensors such as amorphous silicon (−2.1%) and vanadium oxide (from −2 to −4%).47,50Fig. 9(b) collects the TCR peak and TCR peak temperature changes as a function of Na doping content. With the increase in Na content, the maximum value of TCR first decreases and then increases. Obviously, when x = 0.00, the maximum TCR value reaches −3.748% K−1, and the peak temperature of TCR reaches 200 K. At x = 0.05, the TCR value reaches −4.037% K−1, but the peak temperature of TCR reaches 180 K. At x = 0.1, the TCR value drops to −3.793% K−1, but the peak temperature of TCR reaches 200 K. At this time, the main impact on TCR comes from the slope near the metal semiconductor transition region (160 K), depicting TCR with a downward trend.
 |
| | Fig. 9 The variation in TCR % as a function of temperature for the Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05 and 0.1) samples (a). Peak TCR and Peak TCR temperature curves at different Na doping amounts (b). Temperature evolution of the DC normalization of resistivity and the width of the Gaussian distribution Γ for the Pr0.8K0.2−xNaxMnO3 (x = 0, 0.05 and 0.1) samples (c). The measured TCRmax values and the calculated TCRmax values at different Na doping amounts calculated using eqn (27) and (31) (d). | |
In order to further clarify the suitable measured values of TCR, Alexandrov et al.18 proposed a model called Current Carrier Density Collapse (CCDC), where paramagnetic insulating and ferromagnetic metallic phases exist simultaneously, whose resistivity expression is given by the following formula:
where
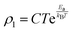
,
ρ2 =
ρ0 +
ρ2.5T2.5 +
ρ7.5T7.5 are the resistivity of each phase, respectively, and
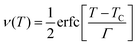
is the volume fraction of the second phase where
Γ is the width of the Gaussian distribution and erfc is the error function given by
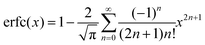
or more precisely
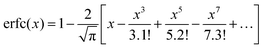
. Using the expression of erfc, we can deduce that
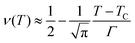
and
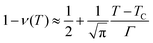
.
Using eqn (23), TCR can be written as follows:
| | 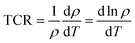 | (24) |
Thus,
| | 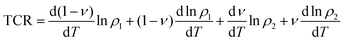 | (25) |
Finally, we can write TCR as follows:
| | 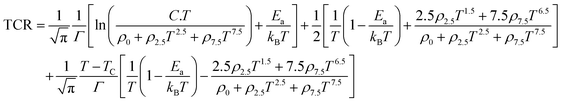 | (26) |
It can be seen from
eqn (26) that the maximum TCR (TCR
max) value occurs at temperature
TC. Therefore, by substituting
T =
TC into
eqn (26) and considering that the residual resistivity is generally much smaller than the resistivity at
TC and
Γ ≪
TC, the TCR
max value is approximately estimated as follows:
| | 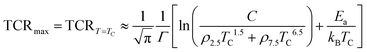 | (27) |
Like the measured TCR
max, we also presented the calculated TCR
max in
Fig. 9(d) using
eqn (27) and the values of the width of the Gaussian distribution
Γ estimated from
Fig. 9(c) for all samples. As shown in
Fig. 9(d), the calculated TCR
max is very close to the measured values of all samples, which shows that
eqn (27) can explain experimental data well for TCR
max for the samples. We also fitted the experimental resistivity data to the phenomenological model based on the percolation mechanism proposed by Li
et al.17 which is studied in the second Section 3.3. Using
eqn (17), TCR can be expressed as follows:
| | 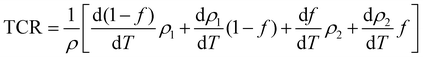 | (28) |
In addition, the following equations are obtained:
By substituting all the above-mentioned results in
eqn (28), TCR is expressed as follows:
| |  | (29) |
It is important to note that
f = 1/2 when
T =
TC, and the residual resistivity
ρ0 is usually much smaller than the resistivity at
TC, TCR
max is expressed as follows:
| | 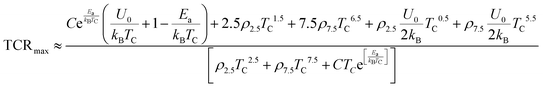 | (30) |
Finally,
| |  | (31) |
As shown in
Fig. 9(d), the calculated TCR
max value is very close to the measured values of all samples, which shows that
eqn (31) can well explain the TCR
max experimental data of the samples. Based on
eqn (27) and (31), TCR
max is governed by several key parameters including the Curie temperature (
TC), the disorder factor (
Γ), the electron–magnon scattering constant (
ρ2.5T2.5), the polaron hopping barrier (
ρ7.5T7.5), and the FM–PM energy separation (
U0). These quantities may originate from intrinsic mechanisms, such as the Mn
3+/Mn
4+ electronic configuration, double-exchange interactions, and intrinsic lattice distortions, or from extrinsic effects arising from A-site substitution (Na/K), oxygen non-stoichiometry, and cationic disorder. Together, these intrinsic and extrinsic contributions modify the charge-carrier hopping landscape, thereby controlling the magnitude and position of TCR
max in the studied manganites.
4. Conclusion
The electrical transport in Pr0.8K0.2−xNaxMnO3 (x = 0.00, 0.05, and 0.1) exhibits two distinct regimes: a low-temperature regime dominated by electron–magnon–phonon scattering and polaron formation near the TM–SC transition (≈160 K) and a high-temperature regime well described by ASPH and VRH models. The percolation model successfully captures resistivity across the full temperature range (80–500 K), highlighting the role of connectivity and phase coexistence. Na substitution for K significantly modifies resistivity and TCR, enabling fine-tuning of the transport mechanism, with ASPH providing the most accurate hopping description. High TCR values and their correlation with intrinsic parameters activation energy, TM–SC, and cationic disorder underscore the sensitivity of these manganites to compositional tuning, establishing them as promising candidates for uncooled bolometric infrared sensors in the 180–200 K range and for advanced thermal sensing applications.
Conflicts of interest
There are no conflicts to declare.
Data availability
All data relevant to this study are available from the corresponding author upon reasonable request.
Acknowledgements
This work was supported by the Laboratory of Advanced Materials and Nanotechnologies (LRMAN), Higher Institute of Applied Sciences and Technology of Kasserine, University of Kairouan, BP 471, 1200 Kasserine, Tunisia.
References
- N. Abdelmoula, E. Dhahri, N. Fourati and L. Reversat, Monovalent effects on structural, magnetic and magnetoresistance properties in doped manganite oxides, J. Alloys Compd., 2004, 365(1–2), 25–30, DOI:10.1016/s0925-8388(03)00639-x
 .
.
- M. Khlifi, M. Bejar, O. E. L. Sadek, E. Dhahri, M. A. Ahmed and E. K. Hlil, Structural, magnetic and magnetocaloric properties of the lanthanum deficient in La0.8Ca0.2−x□xMnO3 (x = 0–0.20) manganites oxides, J. Alloys Compd., 2011, 509(27), 7410–7415, DOI:10.1016/j.jallcom.2011.04.049
 .
.
- C. B. Larsen, S. Samothrakitis, A. D. Fortes, A. O. Ayas, M. Akyol, A. Ekicibil and M. Laver, Basal plane ferromagnetism in the rhombohedral manganite La0.85Ag0.15MnO3+δ, J. Magn. Mater., 2020, 498, 166192, DOI:10.1016/j.jmmm.2019.166192
 .
.
- Y. Bitla, P. D. Babu and S. N. Kaul, Magnetotransport in under and optimally hole-doped bulk nanocrystalline La1−xCaxMnO3 manganites, J. Magn. Magn. Mater., 2020, 501, 166291, DOI:10.1016/j.jmmm.2019.166291
 .
.
- M. Kumar Verma, N. Dutt Sharma, S. Sharma, N. Choudhary and D. Singh, High magnetoresistance in La0.5Nd0.15Ca0.25A0.1MnO3 (A = Ca, Li, Na, K) CMR manganites: correlation between their magnetic and electrical properties, Mater. Res. Bull., 2020, 125, 110813, DOI:10.1016/j.materresbull.2020.110813
 .
.
- B. Panda, K. L. Routray and D. Behera, Studies on conduction mechanism and dielectric properties of the nano-sized La0.7Ca0.3MnO3 (LCMO) grains in the paramagnetic state, Phys. B, 2020, 583, 411967, DOI:10.1016/j.physb.2019.411967
 .
.
- K. Daoudi, S. El-Helali, Z. Othmen, B. M. Suleiman and T. Tsuchiya, Microstructure and electrical transport mechanisms of the Ca-doped LaMnO3 films grown on MgO substrate, J. Materiomics, 2020, 6(1), 17–23, DOI:10.1016/j.jmat.2019.10.002
 .
.
- C. A. Taboada-Moreno, F. Sanchez-De Jesus, F. Pedro-Garcia, C. A. Cortés-Escobedo, J. A. Betancourt-Cantera, M. Ramirez-Cardona and A. M. Bolarín-Miró, Large magnetocaloric effect near to room temperature in Sr doped La0.7Ca0.3MnO3, J. Magn. Magn. Mater., 2020, 496, 165887, DOI:10.1016/j.jmmm.2019.165887
 .
.
- M. V. Subbarao, D. G. Kuberkar, G. J. Baldha and R. G. Kulkarni, Superconductivity of the La3.5−x–yRyCa2xBa3.5−xCu7Oz system (R = Gd, Nd and Dy), Phys. C, 1997, 288(1–2), 57–63, DOI:10.1016/s0921-4534(97)01492-5
 .
.
- M. Battabyal and T. K. Dey, Electrical conductivity in La1−xAgxMnO3 pellets between 10 and 350 K, Phys. B, 2005, 367(1–4), 40–47, DOI:10.1016/j.physb.2005.05.043
 .
.
- S. Bhattacharya, A. Banerjee, S. Pal, P. Chatterjee, R. K. Mukherjee and B. K. Chaudhuri, Transport properties of Na doped La1−xCax−yNayMnO3 measured in a pulsed magnetic field, J. Phys.: Condens. Matter, 2002, 14(43), 10221–10235, DOI:10.1088/0953-8984/14/43/319
 .
.
- P. K. Siwach, U. K. Goutam, P. Srivastava, H. K. Singh, R. S. Tiwari and O. N. Srivastava, Colossal magnetoresistance study in nanophasic La0.7Ca0.3MnO3 manganite, J. Phys. D: Appl. Phys., 2005, 39(1), 14–20, DOI:10.1088/0022-3727/39/1/003
 .
.
- X. Pu, H. Li, K. Chu, Y. Duan, Z. Li and X. Liu, (Pr0.75La0.25)0.7Sr0.3MnO3:Agx (0 ≤ x ≤ 0.25) polycrystalline ceramics with room-temperature TCR improvement for uncooled infrared bolometers, Ceram. Int., 2020, 46(11), 19028–19037, DOI:10.1016/j.ceramint.2020.04.233
 .
.
- A. Jerbi, A. Krichene, R. Thaljaoui and W. Boujelben, Structural, Magnetic, and Electrical Study of Polycrystalline Pr0.55Sr0.45−xNaxMnO3 (x = 0.05 and 0.1), J. Supercond. Novel Magn., 2015, 29(1), 123–132, DOI:10.1007/s10948-015-3217-0
 .
.
- X. Pu, H. Li, G. Dong, K. Chu, S. Zhang, Y. Liu, X. Yu and X. Liu, Electrical transport properties of (Pr1−xLax)0.7Sr0.3MnO3 (0 ≤ x ≤ 0.3) polycrystalline ceramics prepared by sol–gel process for potential room temperature bolometer use, Ceram. Int., 2020, 46(4), 4984–4991, DOI:10.1016/j.ceramint.2019.10.238
 .
.
- J. M. D. Coey, M. Viret and S. Von Molnar, Mixed-Valence Manganites, Adv. Phys., 1999, 48(2), 167–293, DOI:10.1002/chin.199939229
 .
.
- G. Li, H.-D. Zhou, S. J. Feng, X.-J. Fan, X.-G. Li and Z. D. Wang, Competition between ferromagnetic metallic and paramagnetic insulating phases in manganites, J. Appl. Phys., 2002, 92(3), 1406–1410, DOI:10.1063/1.1490153
 .
.
-
A. S. Alexandrov, A. M. Bratkovsky and V. V. Kabanov, Phase Coexistence and Resistivity near the Ferromagnetic Transition of Manganites, arXiv, 2006, preprint, cond-mat/0601712 DOI:10.1103/physrevlett.96.117003.
- L.-M. Wang, Y. Tian, R. Liu and W. Wang, A ‘universal’ criterion for metallic glass formation, Appl. Phys. Lett., 2012, 100(26), 261913, DOI:10.1063/1.4731881
 .
.
- S. L. Ye, W. H. Song, J. M. Dai, K. Y. Wang, S. G. Wang, J. J. Du, Y. P. Sun, J. Fang, J. L. Chen and B. J. Gao, Large room-temperature magnetoresistance and phase separation in La1−xNaxMnO3 with 0.1 ≤ x ≤ 0.3, J. Appl. Phys., 2001, 90(6), 2943–2948, DOI:10.1063/1.1396823
 .
.
- S. Roy, Y. Q. Guo, S. Venkatesh and N. Ali, Interplay of structure and transport properties of sodium-doped lanthanum manganite, J. Phys.: Condens. Matter, 2001, 13(42), 9547–9559, DOI:10.1088/0953-8984/13/42/314
 .
.
- X. J. Chen, C. L. Zhang, C. C. Almasan, J. S. Gardner and J. L. Sarrao, Small-polaron hopping conduction in bilayer manganite, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094426, DOI:10.1103/physrevb.67.094426
 .
.
- R. Banerjee, Banerjee replies, Phys. Rev. Lett., 1993, 70(22), 3519, DOI:10.1103/physrevlett.70.3519
 .
.
- P. T. Phong, N. V. Khiem, N. V. Dai, D. H. Manh, L. V. Hong and N. X. Phuc, Electrical transport of (1 − x)La0.7Ca0.3MnO3+xAl2O3 composites, J. Magn. Magn. Mater., 2009, 321(19), 3330–3334, DOI:10.1016/j.jmmm.2009.06.009
 .
.
- S. Bouzidi, M. A. Gdaiem, A. Dhahri, J. Dhahri and E. K. Hlil, Charge transport mechanism and percolation model in La0.75Ca0.25−xNaxMnO3 (0 ≤ x ≤ 0.10) manganites, J. Mater. Sci.: Mater. Electron., 2020, 31(14), 11548–11559, DOI:10.1007/s10854-020-03703-1
 .
.
- M. Viret, L. Ranno and J. M. D. Coey, Magnetic localization in mixed-valence manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55(13), 8067–8070, DOI:10.1103/physrevb.55.8067
 .
.
- P. Schiffer, A. P. Ramirez, W. Bao and S.-W. Cheong, Low Temperature Magnetoresistance and the Magnetic Phase Diagram of La1−xCaxMnO3, Phys. Rev. Lett., 1995, 75, 3336, DOI:10.1103/physrevlett.75.3336
 .
.
- V. Sen, N. Panwar, G. L. Bhalla and S. K. Agarwal, Structural, magnetotransport and morphological studies of Sb-doped La2/3Ba1/3MnO3 ceramic perovskites, J. Phys. Chem. Solids, 2007, 68(9), 1685–1691, DOI:10.1016/j.jpcs.2007.04.012
 .
.
- G. J. Snyder, R. Hiskes, S. DiCarolis, M. R. Beasley and T. H. Geballe, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(21), 14434–14444, DOI:10.1103/physrevb.53.14434
 .
.
- G. Venkataiah and P. Venugopal Reddy, Structural, magnetic and magnetotransport behavior of some Nd-based perovskite manganites, Solid State Commun., 2005, 136(2), 114–119, DOI:10.1016/j.ssc.2005.04.014
 .
.
- M. Khlifi, M. Bejar, E. Dhahri, P. Lachkar and E. K. Hlil, Influence of Ca-deficiency on the magneto-transport properties in La0.8Ca0.2MnO3 perovskite and estimation of magnetic entropy change, J. Appl. Phys., 2012, 111(10), 103909, DOI:10.1063/1.4718450
 .
.
- C. Xiong, H. Hu, Y. Xiong, Z. Zhang, H. Pi, X. Wu, L. Li, F. Wei and C. Zheng, Electrical properties and enhanced room temperature magnetoresistance in (La0.7Ca0.2Sr0.1MnO3)1−x/Pdx composites, J. Alloys Compd., 2009, 479(1–2), 357–362, DOI:10.1016/j.jallcom.2008.12.087
 .
.
- D. Emin and T. Holstein, Studies of small-polaron motion IV. Adiabatic theory of the Hall effect, Ann. Phys., 1969, 53(3), 439–520, DOI:10.1016/0003-4916(69)90034-7
 .
.
- N. F. Mott, Conduction in glasses containing transition metal ions, J. Non-Cryst. Solids, 1968, 1(1), 1–17, DOI:10.1016/0022-3093(68)90002-1
 .
.
- S. Mnefgui, A. Dhahri, J. Dhahri and E.-K. Hlil, Effects of Transition-Metal V-Doping on the Structural, Magnetic and Transport Properties in La0.67Sr0.33MnO3 Manganite Oxide, J. Supercond. Novel Magn., 2012, 26(2), 251–260, DOI:10.1007/s10948-012-1756-1
 .
.
- H. Ben Khlifa, S. Othmani, I. Chaaba, S. Tarhouni, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Cheikhrouhou and E. K. Hlil, Effect of K-doping on the structural, magnetic and magnetocaloric properties of Pr0.8Na0.2−xKxMnO3 (0 ≤ x ≤ 0.15) manganites, J. Alloys Compd., 2016, 680, 388–396, DOI:10.1016/j.jallcom.2016.04.138
 .
.
- H. Ben Khlifa, R. M’nassri, W. Cheikhrouhou-Koubaa, E. K. Hlil and A. Cheikhrouhou, Effects of synthesis route on the structural, magnetic and magnetocaloric properties of Pr0.8K0.2MnO3, Ceram. Int., 2017, 43(2), 1853–1861, DOI:10.1016/j.ceramint.2016.10.144
 .
.
- E. A. Davis and N. F. Mott, Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors, Philos. Mag., 1970, 22(179), 0903–0922, DOI:10.1080/14786437008221061
 .
.
- T. Holstein, Studies of polaron motion, Ann. Phys., 1959, 8(3), 343–389, DOI:10.1016/0003-4916(59)90003-x
 .
.
- I. G. Austin and N. F. Mott, Polarons in crystalline and non-crystalline materials, Adv. Phys., 1969, 18(71), 41–102, DOI:10.1080/00018736900101267
 .
.
- T. Holstein, Studies of polaron motion, Ann. Phys., 1959, 8(3), 325–342, DOI:10.1016/0003-4916(59)90002-8
 .
.
- M. H. Khan and S. Pal, Nature of electrical hopping conduction and magneto transport studies in the electron doped manganite Ca0.85Gd0.15MnO3, Phys. Lett. A, 2015, 379(5), 401–406, DOI:10.1016/j.physleta.2014.11.017
 .
.
- B. Biswas, R. Nag, S. Mondal, M. H. Khan, M. Debnath and S. Taran, and Sudipta Pal., Magnetic field dependent metal insulator transition by monovalent doping (Na+) in PrMnO3: investigation through structural, magnetic and transport properties, Phys. B, 2023, 652, 414664, DOI:10.1016/j.physb.2023.414664
 .
.
-
A. L. Efros and B. I. Shklovskii, Coulomb Interaction in Disordered Systems with Localized Electronic States, Electron–Electron Interactions in Disordered Systems, 1985, pp. 409–482 DOI:10.1016/b978-0-444-86916-6.50011-9
 .
.
- H. E. Sekrafi, A. Ben Jazia Kharrat, M. A. Wederni, K. Khirouni, N. Chniba-Boudjada and W. Boujelben, Structural, electrical, dielectric properties and conduction mechanism of sol-gel prepared Pr0.75Bi0.05Sr0.1Ba0.1Mn0.98Ti0.02O3 compound, Mater. Res. Bull., 2019, 111, 329–337, DOI:10.1016/j.materresbull.2018.11.041
 .
.
- K. Shimakawa and K. Miyake, Multi phonon Tunneling Conduction of Localized n Electrons in Amorphous Carbon Films, Phys. Rev. Lett., 1988, 61, 994, DOI:10.1103/physrevlett.61.994
 .
.
- S. Vadnala, T. Durga Rao, P. Pal and S. Asthana, Study of structural effect on Eu-substituted LSMO manganite for high temperature coefficient of resistance, Phys. B, 2014, 448, 277–280, DOI:10.1016/j.physb.2014.04.029
 .
.
- I. Ouni, Y. Moualhi and H. Rahmouni, Regarding application in sensor; a comparative study of electrical properties of Pr0.8X0.2MnO3 (X = Na and X = K) ceramics, Inorg. Chem. Commun., 2025, 179, 114756, DOI:10.1016/j.inoche.2025.114756
 .
.
- I. Ouni, Y. Moualhi and H. Rahmouni, Thermistor and capacitor parameter analysis through electrical and dielectric investigations of manganite systems for technological applications, Sens. Actuators, A, 2025, 384, 116300, DOI:10.1016/j.sna.2025.116300
 .
.
- V. Y. Zerov, V. G. Malyarov, I. A. Khrebtov, Y. V. Kulikov, I. I. Shaganov and A. D. Smirnov, Uncooled membrane-type linear microbolometer array based on a VOx film, J. Opt. Technol., 2001, 68(6), 428, DOI:10.1364/jot.68.000428
 .
.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Hedi
Rahmouni
* and
Hedi
Rahmouni


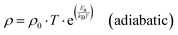

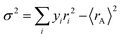 which increases with Na substitution (σ2 = 2.23 Å2 for x = 0.0 and σ2 = 1.72 Å2 for x = 0.05 and σ2 = 1.22 Å2 for x = 0.1).36,37 In regions of high and low temperatures, the activation energy Ea is given by the following equation:38
which increases with Na substitution (σ2 = 2.23 Å2 for x = 0.0 and σ2 = 1.72 Å2 for x = 0.05 and σ2 = 1.22 Å2 for x = 0.1).36,37 In regions of high and low temperatures, the activation energy Ea is given by the following equation:38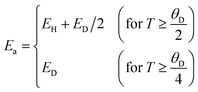

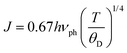
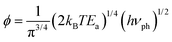
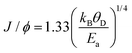
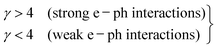
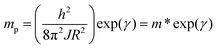



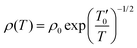
 and the pre-exponential factor ρ0 are constants. For the studied compounds, the validity of the SE-VRH model was confirmed via the evolution of ln(ρ(T)·T−1/2) versus T−1/2 (Fig. 6(a)–(c)). In addition, the linear curves are used to calculate the characteristic SE-VRH temperature for each compound. From the relationship between
and the pre-exponential factor ρ0 are constants. For the studied compounds, the validity of the SE-VRH model was confirmed via the evolution of ln(ρ(T)·T−1/2) versus T−1/2 (Fig. 6(a)–(c)). In addition, the linear curves are used to calculate the characteristic SE-VRH temperature for each compound. From the relationship between 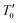 and the density of states at the Fermi level (N′(EF)) given by
and the density of states at the Fermi level (N′(EF)) given by 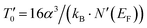 , we can determine N′(EF). The inverse of the localization length of the trapped charge carriers α was found to be 2.22 nm−1.45 The deduced values of
, we can determine N′(EF). The inverse of the localization length of the trapped charge carriers α was found to be 2.22 nm−1.45 The deduced values of 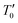 and N′(EF) for all samples are summarized in Table 1. From Table 1, it is obvious that a remarkable decrease in N′(EF) could be observed. In the intermediate temperature interval, more information about the dynamics of the charge carriers can be equally obtained. Using the Shimakawa theory,46 the transfer of localized electrons via tunneling conduction processes also accounts for the origin of the electrical resistivity for θD/4 ≤ T ≤ θD/2. Consequently, the evolution of ρ against temperature, for θD/4 ≤ T ≤ θD/2, can be analyzed using the relation ρ = ρ0·T−n. From Fig. 6(d) and (e), the value of the exponent factor n was deduced. The corresponding parameters of the fit are shown in Table 1 inserted in Fig. 6(d) and (e). The n parameter was employed to examine the electron-lattice interaction force. From Fig. 6(d) and (e), the obtained n value confirmed that the electrical transport is governed by the contribution of the multi-phonon tunnel effect and indicated that Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) system again reveals a weak electron-lattice interaction.46
and N′(EF) for all samples are summarized in Table 1. From Table 1, it is obvious that a remarkable decrease in N′(EF) could be observed. In the intermediate temperature interval, more information about the dynamics of the charge carriers can be equally obtained. Using the Shimakawa theory,46 the transfer of localized electrons via tunneling conduction processes also accounts for the origin of the electrical resistivity for θD/4 ≤ T ≤ θD/2. Consequently, the evolution of ρ against temperature, for θD/4 ≤ T ≤ θD/2, can be analyzed using the relation ρ = ρ0·T−n. From Fig. 6(d) and (e), the value of the exponent factor n was deduced. The corresponding parameters of the fit are shown in Table 1 inserted in Fig. 6(d) and (e). The n parameter was employed to examine the electron-lattice interaction force. From Fig. 6(d) and (e), the obtained n value confirmed that the electrical transport is governed by the contribution of the multi-phonon tunnel effect and indicated that Pr0.8K0.2−xNaxMnO3 (x = 0.0, 0.05 and 0.1) system again reveals a weak electron-lattice interaction.46


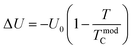 is the energy difference between FM and PM states, TmodC represents the temperature in the vicinity of which the resistivity reaches a maximum value and U0 is the energy difference for temperatures well below TmodC.17 Therefore, the complete expression describing the temperature dependence of resistivity over the entire temperature range can be written in the following form:
is the energy difference between FM and PM states, TmodC represents the temperature in the vicinity of which the resistivity reaches a maximum value and U0 is the energy difference for temperatures well below TmodC.17 Therefore, the complete expression describing the temperature dependence of resistivity over the entire temperature range can be written in the following form:
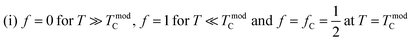
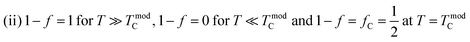


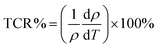

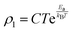 , ρ2 = ρ0 + ρ2.5T2.5 + ρ7.5T7.5 are the resistivity of each phase, respectively, and
, ρ2 = ρ0 + ρ2.5T2.5 + ρ7.5T7.5 are the resistivity of each phase, respectively, and 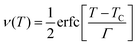 is the volume fraction of the second phase where Γ is the width of the Gaussian distribution and erfc is the error function given by
is the volume fraction of the second phase where Γ is the width of the Gaussian distribution and erfc is the error function given by 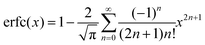 or more precisely
or more precisely 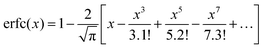 . Using the expression of erfc, we can deduce that
. Using the expression of erfc, we can deduce that 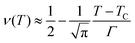 and
and 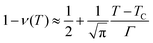 .
.
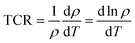
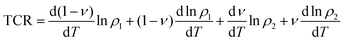
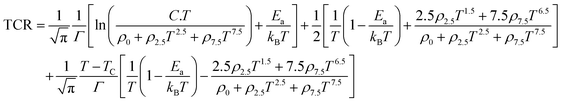
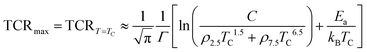
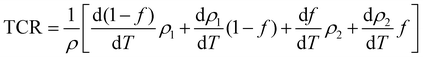

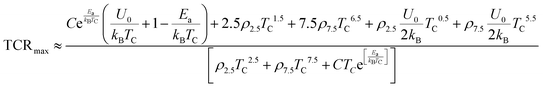

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.