Open Access Article
Open Access ArticleTailoring structural and optical responses in rhombohedral La0.67Sr0.33−xCaxMn1−xNixO3 through dual-site doping
Zouhayra
Aydi
 *a,
Radhia
Dhahri
*a,
Radhia
Dhahri
 a,
Essebti
Dhahri
a,
Essebti
Dhahri
 a,
El-Kébir
Hlil
b and
E.
López-Lago
a,
El-Kébir
Hlil
b and
E.
López-Lago
 c
c
aLaboratoire de Physique et Application, Faculté des Sciences, Université de Sfax, Tunisia. E-mail: aydizouhayra8@gmail.com
bInstitut Néel, CNRS et Université Joseph Fourier, B.P. 166, 38042 Grenoble, France
cDepartamento de Física Aplicada, Facultade de Óptica e Optometríae Instituto de Materiais (iMATUS) Campus Vida, Universidade de Santiago de Compostela (USC), 15782 Galicia, Spain
First published on 12th December 2025
Abstract
Perovskite manganites, due to their strong interplay between crystal structure, electronic states, and magnetic ordering, are highly tunable via chemical substitution. In this study, we investigate the effect of low-level co-doping with Ca2+ at the A-site and Ni2+ at the B-site in rhombohedral La0.67Sr0.33MnO3 (LSMN0), focusing on the composition La0.67Sr0.35Ca0.025Mn0.975Ni0.025O3 (LSMN1). The doping level x = 0.025 was strategically selected to preserve phase stability while inducing measurable modifications in lattice geometry, electronic structure, and optical behavior. Nanocrystalline samples were synthesized via a modified sol–gel route to ensure compositional homogeneity and fine grain sizes. Structural characterization using X-ray diffraction (XRD) and Rietveld refinement confirmed the retention of the rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase, with slight variations in lattice parameters and Mn–O–Mn bond angles upon doping. Fourier-transform infrared (FTIR) and Raman spectroscopy revealed modifications in vibrational modes, indicating reduced Jahn–Teller distortions. Optical absorption measurements in the UV-Vis-NIR range demonstrated a band gap widening, decreased Urbach energy, and notable changes in refractive index dispersion and dielectric functions for the co-doped sample. These findings establish a direct correlation between structural refinement and enhanced optical performance, underscoring the potential of dual-site doping as a powerful tool for tailoring perovskite manganites for applications in optoelectronics, photonic devices, and energy-conversion technologies.
c phase, with slight variations in lattice parameters and Mn–O–Mn bond angles upon doping. Fourier-transform infrared (FTIR) and Raman spectroscopy revealed modifications in vibrational modes, indicating reduced Jahn–Teller distortions. Optical absorption measurements in the UV-Vis-NIR range demonstrated a band gap widening, decreased Urbach energy, and notable changes in refractive index dispersion and dielectric functions for the co-doped sample. These findings establish a direct correlation between structural refinement and enhanced optical performance, underscoring the potential of dual-site doping as a powerful tool for tailoring perovskite manganites for applications in optoelectronics, photonic devices, and energy-conversion technologies.
1. Introduction
In the past few decades, perovskite manganites with the general chemical formula R1−xAxMnO3 (R: trivalent rare-earth ion, A: divalent alkaline-earth ion) have emerged as a class of materials of extraordinary scientific and technological relevance.1–3 Their significance lies in the remarkable diversity of physical phenomena they exhibit colossal magnetoresistance (CMR), charge/orbital ordering, insulator–metal transitions, magnetocaloric effects, and tunable optical responses arising from the intimate coupling between their crystal structure, electronic states, magnetic ordering, and lattice dynamics.4,5 This coupling is exceptionally sensitive to small perturbations in composition, pressure, temperature, and magnetic field, which makes manganites an ideal platform for studying correlated electron systems and for developing functional devices across spintronics, energy conversion, sensing, and photonics.From a structural perspective, these oxides crystallize in the perovskite structure, where Mn occupies the B-site, surrounded by an octahedral cage of oxygen atoms, and R/A cations reside at the A-site in a 12-fold coordination environment. The physical properties are largely determined by the mixed-valence state of Mn ions Mn3+ and Mn4+ and by the associated double-exchange interaction (Mn3+–O–Mn4+) that governs charge transport and magnetic alignment.6–8 Competing with this interaction are Jahn–Teller (JT) distortions of Mn3+O6 octahedra, which localize charge carriers and reduce conductivity. The delicate equilibrium between double exchange and JT distortions is, in turn, strongly dependent on the Mn–O–Mn bond angle, Mn–O bond length, and overall crystal symmetry.
Chemical substitution at the A-site or B-site is an efficient strategy to tune this balance. A-site substitution for example, replacing Sr2+ with the smaller Ca2+ reduces the Goldschmidt tolerance factor, leading to enhanced octahedral tilting and a decrease in the Mn–O–Mn bond angle.9,10 This structural modification narrows the electronic bandwidth and shifts the balance between itinerant and localized electronic states. B-site substitution such as replacing Mn with Ni2+ introduces additional effects: Ni2+ has a larger ionic radius and a 3d8 electronic configuration, which tends to weaken JT distortions, modify the Mn3+/Mn4+ ratio, and alter the hybridization between transition-metal d states and oxygen p states.11,12 These changes affect not only transport and magnetic properties but also optical absorption, dielectric response, and refractive index dispersion.
When both A-site and B-site are substituted simultaneously, the effects can be synergistic rather than simply additive. Such co-doping allows simultaneous control over structural distortions, electronic bandwidth, charge carrier concentration, and defect landscape.13 Low-level co-doping is particularly valuable because it can trigger significant modifications in electronic and optical properties without destabilizing the perovskite framework or introducing parasitic phases. In fact, several previous studies have demonstrated the potential of dual-doped manganite systems such as La1−xSrxMn1−yCoyO3, La1−xCaxMn1−yFeyO3, and La0.67Sr0.33−xCaxMn1−xCoxO3 in enhancing magnetoresistive, dielectric, and optical performances.5,14–16 These works revealed that simultaneous A- and B-site substitutions can tune the Mn–O bond geometry, modify the Mn3+/Mn4+ ratio, and optimize the balance between double-exchange and Jahn–Teller interactions, yet comprehensive optical investigations of such low-level co-doped systems remain scarce.
In the present work, we investigate the La0.67Sr0.33−xCaxMn1−xNixO3 system with a precisely chosen co-doping level of x = 0.025. This specific composition was selected for three main reasons: (i) it is small enough to preserve the rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry, ensuring phase stability; (ii) it is large enough to produce measurable changes in lattice parameters, Mn–O bond geometry, and octahedral tilting.
c symmetry, ensuring phase stability; (ii) it is large enough to produce measurable changes in lattice parameters, Mn–O bond geometry, and octahedral tilting.
(iii) it offers an opportunity to correlate structural refinement (grain growth, reduced micro-strain) with substantial modifications in optical properties such as band gap widening, refractive index behavior, and dielectric performance.17,18
Previous studies have demonstrated that similar co-doping strategies can lead to enhanced crystallinity, reduced lattice disorder, suppression of defect-related localized states, and controlled modulation of the optical band gap.19 These effects are crucial for optoelectronic applications where light-matter interaction must be precisely engineered such as in photodetectors, transparent conducting oxides, optical coatings, and components in the UV-Vis-NIR range.
Here, our objective is to provide a detailed, multi-technique investigation of the influence of Ca2+ (A-site) and Ni2+ (B-site) co-doping on the structure, vibrational dynamics, and optical behavior of nanocrystalline La0.67Sr0.33MnO3. The materials were synthesized using a modified sol–gel method to ensure atomic-level homogeneity, precise stoichiometry, and nanoscale crystallinity. Our research involves the study of optical characteristics, which allow the determination of band gap energies, Urbach energy, refractive index dispersion and dielectric functions. By integrating these experimental results, we aim to establish a clear understanding of the structure–property relationships in low-level co-doped manganites, providing insights for their application in advanced photonic and optoelectronic systems.
2. Experimental study
Nanocrystalline manganites LSMN0 and LSMN1 were synthesized through a modified sol–gel route, a method known for producing highly homogeneous, fine-grained materials with precise stoichiometric control. High-purity precursors were used, including lanthanum nitrate hexahydrate (La(NO3)3·9H2O, 99.9%), strontium nitrate (Sr(NO3)2, 99.9%), calcium nitrate tetrahydrate (Ca(NO3)2·4H2O, 99.9%), manganese nitrate tetrahydrate (Mn(NO3)2·4H2O, 98%), and nickel nitrate hexahydrate Ni(NO3)2·6H2O, all supplied by Sigma-Aldrich. The nitrates were dissolved in deionized water and continuously stirred at 80 °C for 2 h to ensure complete homogenization. Citric acid and ethylene glycol were added as complexing and polymerizing agents, promoting the formation of a stable sol network. The resulting solution was gradually heated to 200 °C to form a viscous gel, which was subsequently dried and calcined in three stages at 300 °C, 400 °C, and 600 °C (12 h each) to remove organic residues and initiate crystallization of the perovskite phase. The obtained powders were finely milled, pressed into pellets, and sintered at 800 °C for 24 h to achieve high crystallinity and phase stability. This synthesis approach enables atomic-scale mixing, uniform cation distribution, and controlled particle growth, key factors in obtaining nanostructured perovskites with enhanced functional performance.The structural, vibrational, and optical properties of LSMN0 and LSMN1 were investigated using complementary techniques. X-Ray diffraction (XRD) patterns were recorded with a Bruker D8 Endeavor diffractometer using Cu Kα1 radiation (λ = 1.5406 Å), operating at 40 kV and 25 mA. Data were collected over the 2θ range of 10°–90° with a step size of 0.01° and a counting time of 1 s per step, ensuring high angular resolution. Phase identification and peak fitting were performed using DIFFRAC.EVA (v2.1, Bruker).
Fourier transform infrared (FTIR) spectra were performed in the 400–4000 cm−1 region using a DTGS detector with a resolution of 4 cm−1 and 32 accumulations, probing the metal–oxygen vibrational modes. Raman spectroscopy at 300 K was performed using a Renishaw Reflex spectrometer coupled with a Leica DM confocal microscope to investigate lattice dynamics and possible Jahn–Teller distortions. The instrument provides automatic alignment and calibration for reproducible signal acquisition. Spectra were recorded with a 514 nm Ar+ laser, a spatial resolution of ≈2 µm, and laser power below 1 mW to avoid local heating. The setup includes a low-noise CCD detector, Rayleigh filters, and a motorized XYZ stage for Raman mapping. Data processing was performed using Wire 3.0 software (Renishaw, UK), with spectra collected in the 100–1000 cm−1 range. Optical absorption spectra were obtained using a UV-3101PC double-beam spectrophotometer operating in the 200–2400 nm range, equipped with a xenon lamp for UV-Vis and a halogen lamp for near-infrared measurements. The experimental results are presented and analyzed in the following section.
3. Results and discussion
3.1. Structural study
The crystal structure of the La0.67Sr0.33−xCaxMn1−xNixO3 nanocrystalline compounds (x = 0.0, LSMN0; x = 0.025, LSMN1) was investigated at room-temperature by X-ray diffraction (XRD) using a Bruker D8 Endeavor diffractometer with Cu–Kα1 radiation (λ = 1.5406 Å). Diffraction patterns were collected over the 10°–90° (2θ) range with high angular resolution, enabling precise evaluation of phase composition and lattice symmetry (Fig. 1(a)).The XRD profiles exhibit sharp and well-defined diffraction peaks, characteristic of highly crystalline single-phase materials, with no detectable secondary phases, confirming the phase purity of both compositions. All main diffraction peaks were indexed and matched with the standard JCPDS card no. 96-152-1757 for rhombohedral La0.7Sr0.3MnO3, confirming that both LSMN0 and LSMN1 crystallize in the same R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase. The most intense reflections correspond to the (012), (104), (110), (113), (202), (024), (122), (214), and (220) planes, which are clearly labeled in Fig. 1(a).20
c phase. The most intense reflections correspond to the (012), (104), (110), (113), (202), (024), (122), (214), and (220) planes, which are clearly labeled in Fig. 1(a).20
When comparing the diffraction profiles of LSMN0 and LSMN1, a slight shift of the major peaks toward lower angles (Fig. 1(a), insect) is evident upon Ni substitution. This shift, interpreted according to Bragg's law, indicates an increase in lattice spacing (d) and therefore a slight expansion of the unit cell in the Ni-doped sample. Such expansion is consistent with the partial replacement of Mn3+/Mn4+ by Ni2+ ions, which possess a slightly larger effective ionic radius and introduce local lattice distortions.21
The rhombohedral symmetry (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) observed in both samples arises from collective rotations of the MnO6 octahedra, a structural response typically associated with the tolerance factor reduction due to Ca2+ substitution at the A-site and Ni2+ substitution at the B-site. These distortions decrease the Mn–O–Mn bond angle, influencing electronic bandwidth and electron–phonon coupling.22 The observed peak broadening also suggests a nanocrystalline nature, which is consistent with the low-temperature sol–gel synthesis route employed.
c) observed in both samples arises from collective rotations of the MnO6 octahedra, a structural response typically associated with the tolerance factor reduction due to Ca2+ substitution at the A-site and Ni2+ substitution at the B-site. These distortions decrease the Mn–O–Mn bond angle, influencing electronic bandwidth and electron–phonon coupling.22 The observed peak broadening also suggests a nanocrystalline nature, which is consistent with the low-temperature sol–gel synthesis route employed.
To quantify these effects, Rietveld refinement was performed using the FullProf suite with the standard R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structural model as an initial input, as shown in Fig. 1(b). The calculated profiles showed excellent agreement with experimental data, confirming the R
c structural model as an initial input, as shown in Fig. 1(b). The calculated profiles showed excellent agreement with experimental data, confirming the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c rhombohedral phase for both LSMN0 and LSMN1. The refined lattice parameters and cell volumes (Table 1) reveal a small increase in unit cell volume for LSMN1, consistent with Ni-induced structural relaxation and modified Mn–O bond lengths.
c rhombohedral phase for both LSMN0 and LSMN1. The refined lattice parameters and cell volumes (Table 1) reveal a small increase in unit cell volume for LSMN1, consistent with Ni-induced structural relaxation and modified Mn–O bond lengths.
| Sample | LSMN0 | LSMN1 | |||
| Structure | Rhombohedral | Rhombohedral | |||
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
|||
| Unit cell parameter | a = b (Å) | 5.495(1) | 5.495(6) | ||
| c (Å) | 13.367(6) | 13.369(3) | |||
| V (Å3) | 349.566(3) | 349.675(8) | |||
| Atoms | Tetrahedral A-site (La/Sr/Ca) | Wyckoff position | (0, 0, 1/4) | 6a | 6a |
| Site summitry | −3 | −3 | |||
| B iso (Å2) | 5.25978 | 1.66489 | |||
| Occupancy: | |||||
| (La) | 0.11650 | 0.11508 | |||
| (Sr) | 0.06017 | 0.05096 | |||
| (Ca) | — | 0.02940 | |||
| Octahedral B-site (Mn/Ni) | Wyckoff position | (0, 0, 0) | 6b | 6b | |
| Site summitry | −3 | −3 | |||
| B iso (Å2) | 5.25019 | 1.32474 | |||
| Occupancy | |||||
| (Mn) | 0.16599 | 0.15608 | |||
| (Ni) | — | 0.01103 | |||
| O | Wyckoff position | (x, 0, 1/4) | 18e | 18e | |
| Site summitry | 1 | 1 | |||
| B iso (Å2) | 6.02641 | 2.88729 | |||
| Occupancy | 0.51585 | 0.56419 | |||
| D SSP (nm) | 40 ± 5 | 75 ± 5 | |||
| 〈O–Mn–O〉 (°) | 90.627(17) | 90.7112(0) | |||
| 〈Mn–O–Mn〉 (°) | 167.0(3) | 165.5401(0) | |||
| 〈La/Sr/Ca–O–La/Sr/Ca〉 (°) | 94.62(11) | 95.1376(0) | |||
| 〈La/Sr–O–Mn〉 (°) | 89.11(3) | 88.9879(0) | |||
| 〈O–La/Sr–O〉 (°) | 114.51(12) | 120.0000(0) | |||
| 〈Mn–O〉 (Å) | 1.9509(6) | 1.95410(0) | |||
| 〈La/Sr–O〉 (Å) | 2.527(5) | 2.50186(0) | |||
| 〈Mn–La/Sr〉 (Å) | 3.34190(11) | 3.34232(0) | |||
| Agreement factors | R p (%) | 9.07 | 12.7 | ||
| R exp (%) | 9.34 | 8.62 | |||
| R wp (%) | 12.3 | 13.8 | |||
| R F (%) | 7.18 | 8.43 | |||
| R B (%) | 1.40 | 1.31 | |||
| χ 2 | 1.23 | 1.46 | |||
These findings demonstrate that low-level Ni substitution (x = 0.025) preserves the global rhombohedral symmetry but subtly modifies the lattice metrics, potentially influencing the electronic bandwidth, Jahn–Teller distortions, and Mn3+/Mn4+ double exchange interactions. Such structural adjustments are known to impact magnetic ordering and transport behavior, as reported for related Ni-doped rhombohedral manganites.17,23
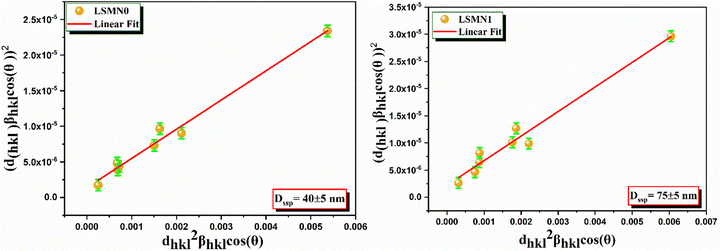
The classical Scherrer equation is commonly employed to estimate the average crystallite size from X-ray diffraction (XRD) line broadening. However, it inherently neglects the contribution of lattice strain, which also affects peak broadening and, in some cases, peak position. In nanocrystalline materials, both particle-size effects and microstructural defects (vacancies, dislocations, and surface stress) contribute significantly to peak broadening, making a more comprehensive approach necessary.
To address this limitation, the size strain plot (SSP) method24 is considered advantageous because it simultaneously accounts for crystallite size and lattice strain. Starting from the Scherrer relation and incorporating strain-induced peak broadening, the SSP equation can be expressed as:
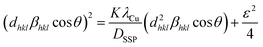 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2versus dhkl2βhklcos
θ)2versus dhkl2βhklcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, yields a slope proportional to (KλCu)/DSSP and an intercept corresponding to ε2/4, from which the strain is derived as
θ, yields a slope proportional to (KλCu)/DSSP and an intercept corresponding to ε2/4, from which the strain is derived as 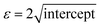 .
.
To ensure data reliability, each diffraction peak was fitted using a pseudo-Voigt profile to minimize instrumental broadening effects, and the full width at half maximum (FWHM) uncertainty (±0.005° in 2θ) was propagated through the SSP calculation. Consequently, the estimated uncertainties in crystallite size and strain are ±5 nm and ±0.02%, respectively. These error bars have been added to Fig. 2 to highlight the reproducibility and statistical confidence of the linear fitting.
Applying this analysis to La0.67Sr0.33−xCaxMn1−xNixO3 (x = 0.0 and 0.025) revealed crystallite sizes of 40 ± 5 nm for LSMN0 and 75 ± 5 nm for LSMN1, indicating that Ni substitution facilitates grain growth and reduces lattice strain. The SSP plot (Fig. 2) clearly reflects these trends, where LSMN0 shows a steeper slope and higher intercept (smaller crystallites and higher micro-strain) compared to LSMN1, which exhibits a gentler slope and reduced intercept (larger crystallites and lower micro-strain). These findings suggest that partial Ni incorporation at the Mn site enhances lattice coherence, reduces defect density, and promotes improved crystal growth kinetics, consistent with similar observations reported in doped perovskite oxides.21
3.2. FT-IR spectroscopy and spectroscopie Raman analysis
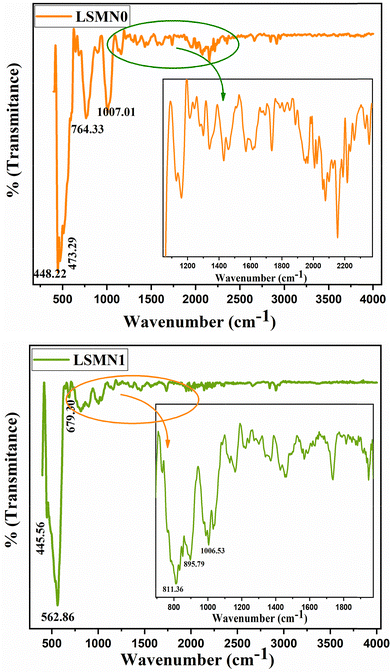
The FT-IR spectra of LSMN0 and LSMN1 were recorded in the range 400–4000 cm−1 (Fig. 3). Both spectra exhibit the typical absorption features of distorted perovskite manganites, with no additional peaks associated with the Ni dopant, indicating that Ni2+ ions are successfully incorporated into the perovskite lattice without forming secondary phases.For LSMN0, strong absorption bands appear at 448, 473, 764, and 1007 cm−1. The bands around 448–473 cm−1 are attributed to Mn–O bending vibrations, while the higher frequency peaks near 764 and 1007 cm−1 correspond to stretching modes of Mn–O bonds within the MnO6 octahedra.25 These features are consistent with the lattice vibrations typically observed in rhombohedral perovskites (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group). Additionally, weaker absorptions observed in the 2000–2500 cm−1 region can be linked to atmospheric CO2 adsorption, which is common for oxide powders.
c space group). Additionally, weaker absorptions observed in the 2000–2500 cm−1 region can be linked to atmospheric CO2 adsorption, which is common for oxide powders.
In comparison, the Ni-doped LSMN1 sample exhibits slight shifts and intensity variations: the main low-frequency band appears at 445 and 562 cm−1, suggesting subtle modifications in Mn–O bond lengths due to Ni2+ substitution at the Mn site. New contributions near 679 and 811 cm−1, as well as a shifted high-frequency component at 1006 cm−1, indicate changes in octahedral distortion and local bonding environments. Similar modifications of FTIR bands upon B-site substitution have been reported for doped manganites, reflecting local structural relaxation and variations in Jahn–Teller distortion intensity.
The presence of broad, low-intensity features in the region around 3400 cm−1 (not highlighted in detail here due to weak signal) is commonly associated with O–H stretching vibrations of surface-adsorbed water and lattice hydroxyl groups. This confirms the hygroscopic nature of perovskite oxide powders.
Overall, both spectra confirm the retention of the perovskite framework after Ni doping, with subtle changes in Mn–O vibrational frequencies suggesting minor lattice distortion and altered bonding strength, in agreement with XRD analysis showing increased crystallite size and reduced micro strain for LSMN1 (Table 2).
| Sample | Band (cm−1) | Vibrational assignment |
|---|---|---|
| LSMN0 | 448–473 | Mn–O bending (MnO6 octahedron) |
| 764 | Mn–O stretching (internal MnO6 mode) | |
| 1007 | Asymmetric Mn–O stretching | |
| 2000–2500 (weak) | Adsorbed CO2 | |
| ∼3400 (weak) | O–H stretching (adsorbed water/lattice OH) | |
| LSMN1 | 445–562 | Mn–O bending modified by Ni2+ substitution |
| 679–811 | Mn–O stretching with local distortion (Ni2+ effect) | |
| 1006 | Asymmetric Mn–O stretching (modified octahedron) | |
| 2000–2500 (weak) | Adsorbed CO2 | |
| ∼3400 (weak) | O–H stretching (adsorbed water/lattice OH) |
The room-temperature Raman spectra of LSMN0 and LSMN1, recorded using a 514 nm excitation laser within the 200–1000 cm−1 range (Fig. 4), exhibit the characteristic vibrational features rhombohedral distorted perovskite manganites (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c).26,27 For the undoped LSMN0 sample, three prominent Raman-active bands can be identified: an A1g mode near 225 cm−1, corresponding to rotational (tilting) motions of the MnO6 octahedra;28 an Eg mode around 410 cm−1, attributed to bending distortions of the Mn–O–Mn bonds; and a broader, more intense Eg band in the 660–670 cm−1 region linked to Mn–O bond stretching and highly sensitive to Jahn–Teller lattice distortions; the broadening reflects local structural disorder.29,30 Additionally, a weak shoulder around 310 cm−1 cans be clearly observed in Fig. 4. This feature is assigned to mixed rotational–bending vibrations of the MnO6 octahedra, in agreement with previous reports on La1−xSrxMnO3-type perovskites.27,31 The significant broadening of this high-frequency band reflects a degree of local structural disorder inherent to the material. Upon partial Ni2+ substitution at the Mn site (LSMN1), distinct spectral changes are observed: all Raman bands exhibit a slight blue shift (toward higher frequencies) for example, from (225 → 230 cm−1, 410 → 420 cm−1, and 670 → 675 cm−1), indicating a local rigidification of the lattice, the high-frequency Eg band becomes sharper with reduced full width at half maximum (FWHM), suggesting reduced Jahn–Teller distortions and enhanced local octahedral symmetry and the overall spectral intensity increases reflecting improved local crystallinity and reduced dynamic disorder. Moreover, the relative enhancement of the 230 and 410 cm−1 modes in LSMN1 evidence stronger Mn/Ni–O–Mn coupling and reduced angular distortion. These modifications indicate a reduction in Jahn–Teller distortions and an enhancement of the local octahedral symmetry, suggesting that Ni doping suppresses dynamic disorder by altering Mn/Ni–O bond lengths and decreasing octahedral tilting. These assignments are consistent with previous Raman studies on La1−xSrxMnO3 (Podobedov et al., 1998;32 Dubroka et al., 200633). This interpretation is consistent with X-ray diffraction (XRD) results, which revealed a significant increase in crystallite size (from ∼40 nm in LSMN0 to ∼75 nm in LSMN1) and a reduction in micro strain. Overall, the Raman analysis confirms that Ni doping preserves the global rhombohedral symmetry while inducing localized structural relaxation and improved crystallinity, in line with the typical effects of B-site substitutions in perovskite manganites.27
c).26,27 For the undoped LSMN0 sample, three prominent Raman-active bands can be identified: an A1g mode near 225 cm−1, corresponding to rotational (tilting) motions of the MnO6 octahedra;28 an Eg mode around 410 cm−1, attributed to bending distortions of the Mn–O–Mn bonds; and a broader, more intense Eg band in the 660–670 cm−1 region linked to Mn–O bond stretching and highly sensitive to Jahn–Teller lattice distortions; the broadening reflects local structural disorder.29,30 Additionally, a weak shoulder around 310 cm−1 cans be clearly observed in Fig. 4. This feature is assigned to mixed rotational–bending vibrations of the MnO6 octahedra, in agreement with previous reports on La1−xSrxMnO3-type perovskites.27,31 The significant broadening of this high-frequency band reflects a degree of local structural disorder inherent to the material. Upon partial Ni2+ substitution at the Mn site (LSMN1), distinct spectral changes are observed: all Raman bands exhibit a slight blue shift (toward higher frequencies) for example, from (225 → 230 cm−1, 410 → 420 cm−1, and 670 → 675 cm−1), indicating a local rigidification of the lattice, the high-frequency Eg band becomes sharper with reduced full width at half maximum (FWHM), suggesting reduced Jahn–Teller distortions and enhanced local octahedral symmetry and the overall spectral intensity increases reflecting improved local crystallinity and reduced dynamic disorder. Moreover, the relative enhancement of the 230 and 410 cm−1 modes in LSMN1 evidence stronger Mn/Ni–O–Mn coupling and reduced angular distortion. These modifications indicate a reduction in Jahn–Teller distortions and an enhancement of the local octahedral symmetry, suggesting that Ni doping suppresses dynamic disorder by altering Mn/Ni–O bond lengths and decreasing octahedral tilting. These assignments are consistent with previous Raman studies on La1−xSrxMnO3 (Podobedov et al., 1998;32 Dubroka et al., 200633). This interpretation is consistent with X-ray diffraction (XRD) results, which revealed a significant increase in crystallite size (from ∼40 nm in LSMN0 to ∼75 nm in LSMN1) and a reduction in micro strain. Overall, the Raman analysis confirms that Ni doping preserves the global rhombohedral symmetry while inducing localized structural relaxation and improved crystallinity, in line with the typical effects of B-site substitutions in perovskite manganites.27
3.3 Optical absorption analysis of La0.67Sr0.33−xCaxMn1−xNixO3 (x = 0.0 and 0.025)
The optical absorption spectra of La0.67Sr0.33−xCaxMn1−xNixO3 were analyzed for x = 0.0 (LSMN0) and x = 0.025 (LSMN1) Fig. 5. Both spectra display features associated with Mn3+/Mn4+ ions in an octahedral crystal field, while the Ni-substituted sample (LSMN1) shows additional signatures due to Ni2+ ions. | ||
| Fig. 5 UV-Vis absorption spectra of La0.67Sr0.33−xCaxMn1−xNixO3 (x = 0.0, LSMN0) and Ni-doped (x = 0.025, LSMN1). | ||
For the parent compound LSMN0, a broad absorption band is observed around 750–800 nm, characteristic of the spin-allowed 5Eg → 5T2g transitions of Mn3+ ions in octahedral coordination. Several additional absorption features are visible in the 300–600 nm region (as revealed by spectral deconvolution):
• 320–350 nm: O2− → Mn3+/Mn4+ charge-transfer transitions, commonly observed in manganite perovskites.34
• 430–450 nm: 4A2g → 4T1g transitions of Mn4+ ions.35
• 520–550 nm: 5Eg → 5T2g transitions of Mn3+.
For the Ni-doped sample LSMN1 (x = 0.025), several changes appear:
• The absorption band in the 700–1100 nm region becomes more pronounced, which can be attributed to Ni2+ electronic transitions, such as 3A2g(F) → 3T2g(F) (∼1100 nm) and 3A2g(F) → 3T1g(F) (∼720 nm).36
• The 500–700 nm range shows slightly increased intensity, indicating overlapping contributions from Mn3+: 5Eg → 5T2g and Ni2+: 3A2g(F) → 3T1g(P) (∼520–590 nm).
• The charge-transfer region (320–350 nm) remains present, but its intensity changes, suggesting local electronic structure modifications due to Ni substitution, which is known to affect the Mn3+/Mn4+ ratio and the electronic bandwidth.
• The broad Mn3+ band near 750–800 nm is reduced in intensity compared to LSMN0, consistent with partial replacement of Mn3+by Ni2+. These absorption bands and their corresponding electronic assignments are summarized in Table 3.
| Composition | λ (nm) | Assigned ion(s) | Transition type |
|---|---|---|---|
| LSMN0 | 320–350 | Mn3+/Mn4+ | O2− → Mn charge transfer |
| 430–450 | Mn4+ | 4A2g → 4T1g | |
| 520–550 | Mn3+ | 5Eg → 5T2g | |
| 750–800 | Mn3+ | Broad 5Eg → 5T2g band | |
| LSMN1 | 320–350 | Mn3+/Mn4+ | O2− → Mn charge transfer |
| 500–700 | Mn3+ + Ni2+ | Mn3+ 5Eg → 5T2g, Ni2+ 3A2g(F) → 3T1g(P) | |
| 720 | Ni2+ | 3A2g(F) → 3T1g(F) | |
| 1100 | Ni2+ | 3A2g(F) → 3T2g(F) | |
| 750–800 | Mn3+ (weakened) | 5Eg → 5T2g |
These changes demonstrate that Ni2+ ions are effectively incorporated into the lattice, introducing additional d–d transitions and altering the crystal field distribution. Similar effects have been reported in other Ni-doped manganites, where Ni2+ doping modifies Jahn–Teller distortions, changes carrier bandwidth, and influences the overall optical response.37,38
3.4 Optical band gap analysis
The optical band gap Eg of LSMN0 and LSMN1 was determined using two complementary spectroscopic approaches: the first derivative of the absorption coefficient (dα/dλ) and the first derivative of the reflectance spectra (dR/dλ), which, although less commonly used than absorption, provides a reliable alternative for polycrystalline powders and thin films where direct absorption measurements can be affected by scattering and sample inhomogeneity.39,40 In both cases, the optical transition edge is defined by the extreme values of the derivative curves, corresponding to the onset of direct electronic transitions between the valence and conduction bands. Both techniques yielded consistent results, confirming the reliability of the optical analysis: Eg = 1.49 eV for the undoped LSMN0 and Eg = 3.46 eV for the Ni- and Ca-codoped LSMN1 (Fig. 6(a) and (b)).This significant increase in Eg is induced by simultaneous A-site (Sr2+ → Ca2+) and B-site (Mn3+/Mn4+ → Ni2+) substitutions originate from combined structural and electronic effects. On one hand, the partial replacement of Sr2+ by the smaller Ca2+ ions decreases the Goldschmidt tolerance factor, thereby increasing the tilt of the (Mn/Ni)O6 octahedra and modifying the orbital overlap between transition-metal d-states and oxygen p-states.41 On the other hand, Ni2+ substitution at the B-site alters the Mn3+/Mn4+ ratio and suppresses Jahn–Teller distortions, which typically generate localized electronic states near the Fermi level. The reduced electronic disorder and improved local symmetry lead to a more delocalized conduction band and a widening of the optical band gap.
In addition, the simultaneous Ca–Ni co-doping introduces a redistribution of charge carriers between Mn3+ and Mn4+ ions, leading to a partial filling of the eg orbitals and a modification of the Mn–O–Mn bond angles. This effect decreases electron–phonon coupling and weakens the polaronic localization typical of undoped manganites. Consequently, optical transitions shift toward higher energies, consistent with the increased band gap observed.
The strong correlation between the optical, structural, and vibrational results further supports this interpretation. XRD and Raman analyses revealed reduced micro-strain, narrower Eg stretching modes (∼670 cm−1), and enhanced crystallinity for LSMN1, all of which contribute to a more ordered lattice and a widening of the electronic gap.
These results demonstrate that dual-site substitution in perovskite manganites can be an effective approach to engineer their electronic structure and tune their optoelectronic properties without disrupting the global rhombohedral framework. The combination of derivative-based optical methods and structural analysis confirms that the observed band gap enhancement is intrinsic, arising from electronic structure modifications rather than secondary phases or measurement artifacts. This synergistic effect of Ca and Ni substitution highlights the interplay between lattice distortions, charge compensation, and orbital hybridization, offering a clear physical basis for the observed trends. Such tunability is promising for designing functional manganite-based materials for ultraviolet-visible optoelectronic devices42,43
The optical properties of LSMN0 and LSMN1 were investigated to evaluate the effect of simultaneous A- and B-site substitutions on the perovskite lattice. The absorption coefficient (α) was derived from the experimental absorbance using Beer–Lambert's law 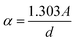 ,44 where A is the absorbance and d is the sample thickness. The optical band gap was then determined using Tauc's formalism:45
,44 where A is the absorbance and d is the sample thickness. The optical band gap was then determined using Tauc's formalism:45
| (αhν)n = β(hν − Eg) | (2) |
Therefore, the observed optical behavior is not a simple measurement artifact but reflects a real modification of the electronic band structure induced by co-doping. These findings bridge the link between lattice distortion, charge redistribution, and optical response, providing a comprehensive physical understanding of the system. These findings highlight that double A/B-site doping preserves the overall rhombohedral symmetry while tuning the local electronic structure, making these materials promising for optoelectronic applications operating in the visible and near-UV regions.46
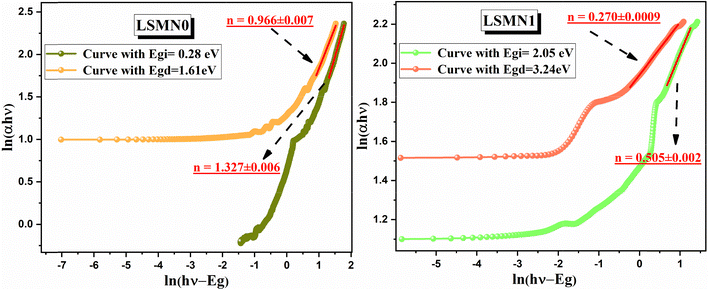
To further elucidate the nature of optical transitions in the x = 0.0, LSMN0 and x = 0.025, LSMN1 compounds, the absorption spectra was analyzed using the logarithmic form of the Tauc relation:
ln(αhν) = ln(β) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(hν − Eg) ln(hν − Eg) | (3) |
For the undoped LSMN0 sample, the fitting procedure yielded n = 0.966 ± 0.007 for the direct gap transition (Egd = 1.61 eV) and n = 1.327 ± 0.006 for the indirect one (Egi = 0.28 eV) (Fig. 7). These values deviate from the ideal parameters of 0.5 and 2, indicating that electronic transitions in LSMN0 are affected by local lattice distortions and defect-related states, which promote phonon-assisted processes and mixed transition behavior. Similar effects have been reported in perovskite manganites where Jahn–Teller distortions and oxygen vacancy states influence optical transitions.49,50 Such deviation also reveals the presence of localized energy levels within the band gap, most likely arising from oxygen vacancies and Mn3+–O–Mn4+ lattice fluctuations. These localized states enhance non-radiative recombination and reduce optical transition probability, leading to the mixed indirect–direct nature observed in LSMN0. The broad absorption tail in this composition supports the presence of such defect-related sub-gap states.
In contrast, the Ni-doped LSMN1 sample exhibited significantly lower indices, with n = 0.270 ± 0.0009 for the direct band gap (Egd = 3.24 eV) and n= 0.505 ± 0.002 for the indirect one (Egi = 2.05 eV) (Fig. 7). These values approach those expected for a direct allowed transition, suggesting that Ni2+ substitution at the Mn site reduces electronic disorder and narrows defect-related tail states, leading to a cleaner and sharper band edge. Such behavior is consistent with the observed increase in crystallite size and reduced micro-strain in LSMN1 (from XRD), as well as the reduced Jahn–Teller distortion evidenced by Raman analysis.51 This finding highlights that Ni2+ incorporation not only widens the band gap but also reorganizes the electronic density of states by strengthening the hybridization between Ni–3d and O–2p orbitals. This enhanced covalency reduces mid-gap states and stabilizes direct electronic transitions, in agreement with the observed structural ordering. Moreover, Ca2+substitution at the A-site complements this effect by tightening the lattice through its smaller ionic radius, thus reducing bond-length fluctuations and phonon scattering. The cooperative action of both dopants contributes to the transition from a disordered to a more coherent electronic structure.
Overall, these results highlight how double substitution on both A-site (Ca2+) and B-site (Ni2+) significantly modifies not only the band gap energy but also the nature of optical transitions, shifting the material response from mixed and defect-affected behavior (LSMN0) toward predominantly direct transitions (LSMN1). This strong correlation between optical transition type, lattice symmetry, and defect suppression demonstrates that co-doping acts as an efficient route to tune carrier localization and electronic transport in perovskite manganites. This electronic structure tuning is particularly relevant for designing manganite-based optoelectronic devices with tailored optical properties.
3.5 Determination of Urbach energy and threshold wavelength
The optical absorption analysis provides further insight into the disorder and localized states present in the studied manganite compounds. In particular, the Urbach energy (Eu) is a key parameter that characterizes the width of the exponential absorption tail in the vicinity of the band edge. This tail originates from localized states in the bandgap, often associated with lattice disorder, structural defects, and phonon interactions.52 While in many cases a high concentration of substitute atoms can increase structural disorder and broaden the absorption tail, carefully selected dopants can reduce local distortions and improve lattice ordering, thereby decreasing Eu and increasing the optical bandgap, as observed in our study.According to the Urbach model, Eu can be extracted from the slope of the linear region in the plot of ln(α) versus photon energy (hν), following the expression:
 | (4) |
Once Eu is known, the steepness parameter S can be calculated using:
 | (5) |
• LSMNO: S ≈ 0.01596
• LSMN1: S ≈ 0.02693
A higher S value corresponds to a sharper absorption edge, typically reflecting a lower degree of structural disorder and a reduced density of localized states. The increase of S from LSMNO to LSMN1 therefore confirms that doping improves lattice ordering, consistent with the observed reduction in Eu.
The S(T) parameter can also be related to the average phonon energy (ħvp) via:54,55
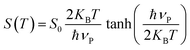 | (6) |
Finally, the threshold wavelength (λi), corresponding to the maximum wavelength of incident radiation capable of initiating electronic transitions, was determined using:56,57
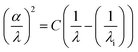 | (7) |
• LSMNO: λi ≈ 314 nm
• LSMN1: λi ≈ 402 nm
The increase in λi after doping suggests that LSMN1 can absorb photons of lower energy (longer wavelength), which is consistent with its reduced optical bandgap and improved structural ordering.
In summary, the combined analysis of Eu, S, and λi demonstrates that doping effectively reduces the Urbach tail, sharpens the absorption edge, and shifts the absorption threshold toward longer wavelengths, confirming a significant improvement in the structural and electronic quality of the material.
The skin depth δ, extinction coefficient k, and refractive index n of LSMN0 and LSMN1 were determined from the optical data. The penetration depth, also referred to as the optical skin depth, represents the distance over which light can propagate into a material before being significantly absorbed or attenuated. It depends on the photon energy and can be obtained from the absorption coefficient (α) according to the relation:58
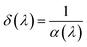 | (8) |
The δ(hν) spectra in Fig. 9(a) show several characteristic minima, each corresponding to strong optical absorption bands associated with interbond or charge-transfer transitions. Low-energy features (<2.3 eV) are generally related to polaronic or d–d excitations, while higher-energy structures (>2.3 eV) correspond to more intense charge-transfer processes involving Mn 3d, Ni 3d, and O 2p states. A direct comparison reveals that the skin depth δ is higher for LSMN1 than for LSMN0 in the 2–4 eV range, indicating that LSMN1 allows deeper light penetration and thus experiences lower absorption. Conversely, the reduced δ values for LSMN0 imply stronger absorption. This behavior can be directly linked to the enhanced structural order and reduced lattice distortions introduced by Ni2+ and Ca2+ co-doping. The improved crystallinity and decreased Jahn–Teller activity in LSMN1 minimize carrier scattering and defect-related absorption, resulting in a longer optical penetration depth. In contrast, the higher disorder and localized states in LSMN0 favor strong photon–phonon interactions, which shorten δ and increase light attenuation.
 | ||
| Fig. 9 (a) Variation of skin depth (δ) as a function of photon energy (hν) for LSMN0 and LSMN1. (b) Extinction coefficient (k) versus photon energy (hν) for LSMN0 and LSMN1. | ||
The extinction coefficient k, which quantifies the absorption and scattering of light by the material, is calculated from α using:59
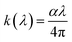 | (9) |
The k(hν) spectra (Fig. 9(b)) display several pronounced peaks in the visible region, consistent with the minima observed in δ(hν). The extinction coefficient k is higher for LSMN0 than for LSMN1, confirming that the Ni substitution reduces absorption in LSMN1.This reduction in k reflects a lower density of defect-induced mid-gap states and a more efficient charge-transfer pathway between Ni/Mn 3d and O 2p orbitals. The smoother electronic landscape in LSMN1 suppresses non-radiative losses, while the smaller ionic radius of Ca2+ enhances lattice compactness, further decreasing optical scattering.
Moreover, the correlated decrease of k and increase of δ indicate a transition toward a more transparent and optically homogeneous lattice in the Ni- and Ca-co-doped compound. This trend is consistent with the observed bandgap widening and Raman/XRD evidence of structural relaxation.
This reduction in k, along with subtle shifts and additional spectral features, indicates modifications in the electronic band structure and Mn–O hybridization induced by Ni doping. Consequently, LSMN1 exhibits weaker visible absorption and a lighter blue color compared to LSMN0, which may be beneficial for optoelectronic or light-harvesting applications requiring tailored absorption properties. Such controlled modulation of δ and k demonstrates the potential of dual-site substitution as a tool to engineer both the optical penetration and the carrier dynamics in perovskite manganites, enabling a rational design of functional transparent or semi-transparent oxide materials.
3.6 Optical dispersion analysis (LSMN0/LSMN1)
The optical response of the synthesized compounds was examined by analyzing the spectral dependence of the refractive index n on the wavelength λ (Fig. 10(a)). This parameter is essential for understanding the interaction of light with the material, as it reflects the reduction of light velocity during propagation through the medium. The refractive index n is related to the reflectance R(λ) and the extinction coefficient k(λ) through the following expression:60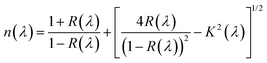 | (10) |
 | ||
| Fig. 10 (a) Refractive index n vs. λ for LSMN0 and LSMN1. (b) Variation of n(λ) curve with Cauchy fit. | ||
The refractive index also depends on the optical band gap Eg, and can be estimated using the empirical relation:61
 | (11) |
From eqn (11), the simplified form becomes:
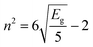 | (12) |
For a more precise description, the experimental refractive index was fitted using the Cauchy dispersion model:62
| n(λ) = n0 + Ax + Bx2 | (13) |
The fitting results reveal notable differences between the two compositions (Fig. 10(b)):
• LSMN0: n0 = 1.92907, A = −0.29326, B = 0.05055, with R2 = 0.99739.
• LSMN1: n0 = 1.35379, A = 0.13405, B = −0.02825, with R2 = 0.99809.
The higher n0 value in LSMN0 indicates a denser electronic polarizability compared to LSMN1, which can be associated with its structural compactness and possibly lower porosity. Conversely, LSMN1 exhibits a lower refractive index baseline, which may enhance light penetration, making it potentially more suitable for optical transmission applications. The decrease of n0 and the change of sign of parameter A upon Ni/Ca co-doping suggest a fundamental alteration of the lattice polarizability and electronic density distribution. The lower n0 in LSMN1 is consistent with its wider optical band gap and reduced defect density, as both factors diminish the contribution of free and localized carriers to the dielectric function. In contrast, the negative A coefficient in LSMN0 indicates stronger wavelength dispersion caused by defect-related electronic transitions and local lattice distortions.
This behavior agrees with Raman and XRD analyses, which showed that Ni incorporation reduces octahedral tilting and Jahn–Teller distortions, thereby suppressing low-energy polarization mechanisms. As a result, LSMN1 exhibits a more stable dielectric response and smoother refractive-index dispersion over the visible range.
The dispersion behavior also differs: LSMN0 shows a stronger wavelength dependence with a negative A parameter, indicating a decrease in n with increasing × (shorter wavelengths), whereas LSMN1 has a positive A, revealing a slight increase in n toward shorter wavelengths This crossover reflects the transition from a disordered to a more ordered electronic structure, where light–matter interactions are governed by well-defined interbond transitions rather than defect-induced scattering. These variations suggest distinct electronic transition characteristics between the two compositions, likely due to differences in local bonding environments and lattice distortions introduced during synthesis.
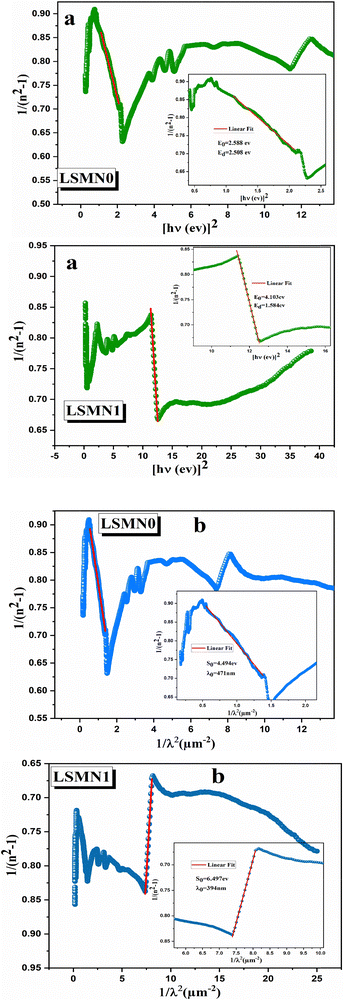
The dispersion behavior of the refractive index n(λ) for LSMN0 and LSMN1 was analyzed using the Wemple–DiDomenico (WDD) single-oscillator model, which relates the optical response to the photon energy Eph through the equation:63
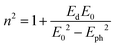 | (14) |
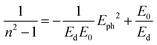 | (15) |
• LSMN0: E0 = 2.588 eV, Ed = 2.508 eV
• LSMN1: E0 = 4.103 eV, Ed = 1.584 eV
The higher E0 value for LSMN1 suggests that its dominant interbond transitions occur at higher energies, consistent with its larger optical band gap. Conversely, the lower Ed for LSMN1 indicates a weaker overall dispersion strength, which can be related to reduced electronic polarizability and lower density of low-energy transition states.
The values of the static oscillator strength (S0) and the oscillator wavelength (λ0) were determined using the alternative WDD relation:64,65
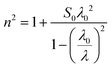 | (16) |
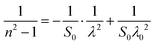 | (17) |
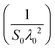 and the slope gives
and the slope gives 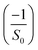 . From the fits of (n2 − 1)−1versus 1/λ2 (Fig. 11(b)), the extracted parameters are:
. From the fits of (n2 − 1)−1versus 1/λ2 (Fig. 11(b)), the extracted parameters are:
• LSMN0: S0 = 4.494, λ0 = 471 nm
• LSMN1: S0 = 6.497, λ0 = 394 nm
The larger S0 value for LSMN1 points to stronger oscillator coupling at its characteristic resonance wavelength λ0, despite its lower dispersion energy Ed. This combination indicates that the Ni-doped compound exhibits sharper and more energetically selective optical transitions, but with a narrower dispersion range compared to the undoped sample. Physically, this reflects a redistribution of oscillator strength toward high-energy transitions, consistent with the Ni-induced shift of the conduction band edge and the suppression of defect-related absorption channels. The shorter λ0 in LSMN1 confirms this upward shift, evidencing a more rigid and electronically ordered lattice.
Overall, the WDD analysis highlights a distinct shift in the optical response upon Ni incorporation: LSMN1 shows a significant increase in E0 and S0 but a decrease in Ed, reflecting an upward shift of interbond transition energies and a modification of the polarizability dynamics within the perovskite lattice. These optical trends are fully consistent with the electronic bandgap widening and reduced structural disorder found in previous sections, providing a coherent picture of how co-doping tunes both dielectric and optical dispersion behaviors.
3.7 Optical and electrical conductivity
The transport behavior of perovskite manganites can be comprehensively understood by examining both their electrical conductivity (σel) and optical conductivity (σop). Electrical conductivity is mainly dictated by the mobility and density of free charge carriers, whereas optical conductivity is associated with photon-induced electronic excitations and the interaction of light with the material's band structure.66In this work, σop(λ) was calculated from the refractive index n(λ) and the absorption coefficient α(λ) using the relation:67
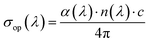 | (18) |
As shown in Fig. 12(a), σop exhibits distinct spectral variations across the measured wavelength range (200–2400 nm). Both LSMN0 and LSMN1 display multiple peaks, reflecting strong interbond transitions and localized state absorptions. LSMN0 shows a more pronounced σop in certain spectral regions (notably around 800–1000 nm), which can be linked to enhanced photon electron interactions due to its specific electronic configuration. In contrast, LSMN1 exhibits smoother variations, possibly indicating reduced scattering centers and altered electronic density of states induced by partial Ca/Ni substitution. The overall magnitude of σop (∼109 S−1) confirms the strong optical response of these materials, which is crucial for optoelectronic applications.
 | ||
| Fig. 12 (a) Spectral variation of optical conductivity σop(λ). (b) Spectral variation of electrical conductivity σel(λ) for LSMN0 and LSMN1. | ||
Electrical conductivity σel(λ) was determined from the refractive index and incident wavelength according to:68
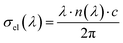 | (19) |
The σel curves (Fig. 12(b)) reveal a monotonic increase with wavelength for both samples, consistent with the wavelength dependence predicted by the above relation. The magnitude of σel is significantly lower than that of σop (σel ≪ σop), emphasizing their different physical origins. While σop is governed by photo-excitation processes, σel primarily reflects charge carrier mobility under an applied electrical field. This behavior indicates that even in regions of strong optical absorption, carriers may remain localized, leading to transport dominated by hopping mechanisms among Mn3+/Mn4+ sites, as previously reported for similar perovskite systems.69
Notably, LSMN1 exhibits slightly higher σel than LSMN0 over much of the investigated range, suggesting that Ca/Ni co-doping may improve charge carrier mobility by tuning lattice distortions and reducing polaron trapping. However, this improvement in σel does not directly correlate with the trends observed in σop, reaffirming that optical and electrical conductivities probe distinct aspects of carrier dynamics.
Similar findings were reported by L. H. Omari et al.70 in Ca3Ti2−xFexO7−δ, where σel was consistently lower than σop, highlighting the independence of optical absorption and direct current transport efficiency.
Overall, the combination of high optical conductivity and moderate electrical conductivity in LSMN compounds underscores their potential for optoelectronic devices, including photodetectors, solar energy converters, and spintronic components. The ability to tailor their transport and optical responses via controlled doping offers a promising route toward application-specific optimization.
3.8 Dielectric constant
The optical dielectric response of LSMN0 and LSMN1 materials was evaluated based on the complex dielectric function defined by eqn (20):71| ε(λ) = ε′(λ) + iε″(λ) | (20) |
| ε′(λ) = n2(λ) − K2(λ); ε″(λ) = 2n(λ)·K(λ) | (21) |
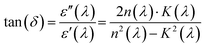 | (22) |
Experimental analysis of the dielectric spectra ε″(hν) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(hν) (within the 0–6 eV energy range) (Fig. 13(a)) reveals a clear distinction between the two samples. LSMN0 exhibits a pronounced ε″ peak in the low-energy range (0.5–1.5 eV), reaching values above 8 × 10−6, suggesting strong optical absorption caused by a high density of localized states or crystal defects near the band edge. In contrast, LSMN1 (co-doped with Ni and Ca) shows significantly reduced ε″ values, reflecting improved crystallinity and lower structural disorder. This reduction in ε″ for LSMN1 directly correlates with the suppression of Jahn–Teller distortions and defect-related states evidenced by Raman spectroscopy and XRD, indicating that the co-doping stabilizes the lattice and minimizes electronic inhomogeneities. Consequently, fewer trap-assisted transitions occur, leading to reduced dielectric losses. This trend is further supported by the behavior of tan
δ(hν) (within the 0–6 eV energy range) (Fig. 13(a)) reveals a clear distinction between the two samples. LSMN0 exhibits a pronounced ε″ peak in the low-energy range (0.5–1.5 eV), reaching values above 8 × 10−6, suggesting strong optical absorption caused by a high density of localized states or crystal defects near the band edge. In contrast, LSMN1 (co-doped with Ni and Ca) shows significantly reduced ε″ values, reflecting improved crystallinity and lower structural disorder. This reduction in ε″ for LSMN1 directly correlates with the suppression of Jahn–Teller distortions and defect-related states evidenced by Raman spectroscopy and XRD, indicating that the co-doping stabilizes the lattice and minimizes electronic inhomogeneities. Consequently, fewer trap-assisted transitions occur, leading to reduced dielectric losses. This trend is further supported by the behavior of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which remains consistently lower for LSMN1, particularly below 2 eV, indicating lower energy dissipation relative to its dielectric polarization a desirable feature for optoelectronic applications. Although the real part ε′ (Fig. 13(b)) ranges between approximately 2.1 and 2.6 for both samples, their spectral behaviors differ: LSMN0 shows a peak near 1.8–2.0 eV, pointing to strong low-energy polarization, while LSMN1 exhibits more prominent ε′ values at higher energies, consistent with its wider optical band gap (estimated at 3.24–3.46 eV for LSMN1 vs. 1.49–1.61 eV for LSMN0), implying a shift of interbond transitions toward the UV region due to the modified electronic structure induced by doping.
δ, which remains consistently lower for LSMN1, particularly below 2 eV, indicating lower energy dissipation relative to its dielectric polarization a desirable feature for optoelectronic applications. Although the real part ε′ (Fig. 13(b)) ranges between approximately 2.1 and 2.6 for both samples, their spectral behaviors differ: LSMN0 shows a peak near 1.8–2.0 eV, pointing to strong low-energy polarization, while LSMN1 exhibits more prominent ε′ values at higher energies, consistent with its wider optical band gap (estimated at 3.24–3.46 eV for LSMN1 vs. 1.49–1.61 eV for LSMN0), implying a shift of interbond transitions toward the UV region due to the modified electronic structure induced by doping.
This upward shift in ε′(hν) for LSMN1 indicates that the main electronic polarization mechanisms are now dominated by higher-energy charge-transfer transitions (Mn/Ni–O hybrid orbitals), confirming that co-doping enhances the covalency and reduces carrier localization. As a result, dielectric polarization becomes more efficient and less lossy, in line with the optical transparency improvement noted previously. Functionally, LSMN0 could be suited for dielectric applications such as IR-range capacitors or components where high low-energy polarizability is needed; however, its higher optical losses (larger ε″ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) limit its performance in transparent devices. On the other hand, LSMN1 achieves an optimized balance between high dielectric response and low absorption losses, with reduced ε″ and minimal tan
δ) limit its performance in transparent devices. On the other hand, LSMN1 achieves an optimized balance between high dielectric response and low absorption losses, with reduced ε″ and minimal tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, making it a strong candidate for photonic and optoelectronic devices operating in the UV-visible range, such as optical windows, filters, or low-loss layers. In summary, chemical control via Ni/Ca co-doping offers an effective approach to tailoring the dielectric and optical behavior by modulating both the polarization capability and loss mechanisms, thereby enhancing the material's performance for targeted functional applications.
δ, making it a strong candidate for photonic and optoelectronic devices operating in the UV-visible range, such as optical windows, filters, or low-loss layers. In summary, chemical control via Ni/Ca co-doping offers an effective approach to tailoring the dielectric and optical behavior by modulating both the polarization capability and loss mechanisms, thereby enhancing the material's performance for targeted functional applications.
In the near-infrared domain, the real (ε′) and imaginary (ε″) parts of the dielectric permittivity can be described by the empirical relations:65,73
| ε′(λ) = M1 − M2λ2; ε″(λ) = M3λ3 | (23) |
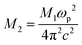 is related to the plasma frequency ωp, and
is related to the plasma frequency ωp, and 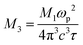 reflects the dielectric loss factor, where τ is the relaxation time. Linear fits of ε′ versus λ2 (Fig. 14(a)) and ε″ versus λ3 (Fig. 14(b)) yield the following parameters.
reflects the dielectric loss factor, where τ is the relaxation time. Linear fits of ε′ versus λ2 (Fig. 14(a)) and ε″ versus λ3 (Fig. 14(b)) yield the following parameters.
 | ||
| Fig. 14 (a) Evolution of ε′ as a function of λ2 and (b) ε″ versus λ3 for the LSMC1 and LSMC2 compounds. | ||
For LSMN0, the fit of ε′(λ) gives M1 = 2.29788 and M2 = (9.51234) × 10−8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm2, with a strong correlation coefficient R2 = 0.96076. For LSMN1, the corresponding values are M1 = 2.24208 and M2 = −(7.31204) × 10−8
nm2, with a strong correlation coefficient R2 = 0.96076. For LSMN1, the corresponding values are M1 = 2.24208 and M2 = −(7.31204) × 10−8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm2 (R2 = 0.96509). The slight sign inversion of M2 for LSMN1 suggests a subtle modification in the dispersion trend, potentially arising from local lattice distortions or changes in carrier screening induced by Ca/Ni co-doping.
nm2 (R2 = 0.96509). The slight sign inversion of M2 for LSMN1 suggests a subtle modification in the dispersion trend, potentially arising from local lattice distortions or changes in carrier screening induced by Ca/Ni co-doping.
For the imaginary part ε″(λ), the fits yield M3 = (4.68064) × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm3 for LSMN0 (R2 = 0.9957) and M3 = (1.27629) × 10−14
nm3 for LSMN0 (R2 = 0.9957) and M3 = (1.27629) × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm3 for LSMN1 (R2 = 0.97447). In both samples, ε″ remains significantly smaller than ε′ across the spectral range investigated, indicating that dielectric losses are minimal and that light propagation through the material occurs with limited energy dissipation. The higher M3 value observed in LSMN1 can be attributed to faster dielectric relaxation and improved carrier mobility within the lattice, reflecting a more coherent polarization response to optical excitation. The inversion of M2 also points to a possible shift in the dominant polarization mechanism, from defect-assisted in LSMN0 to interbond-driven in LSMN1.
nm3 for LSMN1 (R2 = 0.97447). In both samples, ε″ remains significantly smaller than ε′ across the spectral range investigated, indicating that dielectric losses are minimal and that light propagation through the material occurs with limited energy dissipation. The higher M3 value observed in LSMN1 can be attributed to faster dielectric relaxation and improved carrier mobility within the lattice, reflecting a more coherent polarization response to optical excitation. The inversion of M2 also points to a possible shift in the dominant polarization mechanism, from defect-assisted in LSMN0 to interbond-driven in LSMN1.
The high R2 values for all fits confirm the validity of eqn (23) for modeling the dielectric behavior in the near-infrared region. The combination of high ε′ values and low ε″ values highlight the capability of these manganite systems to store electromagnetic energy efficiently while minimizing absorption losses, which is desirable for photonic and optoelectronic applications. Overall, the near-IR dielectric modeling corroborates that Ni/Ca co-doping enhances dielectric stability and optical transparency by modifying the free-carrier screening and reducing defect-mediated polarization. The consistent trends across ε′, ε″, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, and M-parameters demonstrate that structural ordering and bandgap widening jointly govern the improved dielectric performance of LSMN1.
δ, and M-parameters demonstrate that structural ordering and bandgap widening jointly govern the improved dielectric performance of LSMN1.
4. Conclusion
In this study, we carried out an in-depth analysis of the structural, vibrational, optical, electrical, and dielectric properties of nanocrystalline LSMN0 and its Ca/Ni co-doped counterpart LSMN1, synthesized via a modified sol–gel route. Rietveld refinement of the XRD patterns confirmed the retention of the rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c symmetry in both compositions, with slight variations in lattice parameters, Mn–O bond lengths, and Mn–O–Mn bond angles after co-doping. These changes, supported by FTIR and Raman results, indicate a reduction in Jahn–Teller distortions and an enhancement of crystallinity, as reflected by the crystallite size increase from ∼40 nm in LSMN0 to ∼75 nm in LSMN1.
c symmetry in both compositions, with slight variations in lattice parameters, Mn–O bond lengths, and Mn–O–Mn bond angles after co-doping. These changes, supported by FTIR and Raman results, indicate a reduction in Jahn–Teller distortions and an enhancement of crystallinity, as reflected by the crystallite size increase from ∼40 nm in LSMN0 to ∼75 nm in LSMN1.
Optical investigations revealed a pronounced widening of the band gap (from 1.49 eV to 3.46 eV), a substantial decrease in Urbach energy (from 1.62 eV to 0.96 eV), and a refinement of refractive index dispersion, all pointing to reduced electronic disorder and improved optical quality. The analyses based on Wemple DiDomenico and Cauchy models further confirmed a stronger oscillator strength and tunable refractive index in the co-doped sample.
Beyond the optical response, transport and dielectric measurements highlighted additional benefits of Ca/Ni co-substitution. The optical conductivity reached values on the order of 109 S−1, while the electrical conductivity σel was moderately improved in LSMN1, suggesting enhanced carrier mobility through reduced polaron trapping. Dielectric studies showed that LSMN1 exhibits lower dielectric losses (smaller ε″ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) and a more stable real permittivity ε′ across the visible-NIR range, demonstrating improved dielectric efficiency. This balance between strong dielectric response and minimized optical losses makes the material particularly suitable for transparent optoelectronic and photonic applications.
δ) and a more stable real permittivity ε′ across the visible-NIR range, demonstrating improved dielectric efficiency. This balance between strong dielectric response and minimized optical losses makes the material particularly suitable for transparent optoelectronic and photonic applications.
Overall, the dual substitution at the A-site (Ca2+) and B-site (Ni2+) lead to improved crystallinity, wider band gap, enhanced optical transparency, higher optical conductivity, and reduced dielectric losses, while maintaining phase stability. These combined improvements establish low-level Ca/Ni co-doping as a promising strategy for tailoring the multifunctional properties of perovskite manganites, with potential applications in UV-Vis-NIR optoelectronic devices, transparent conducting films, and low-loss dielectric components.
Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting the findings of this study, including X-ray diffraction (XRD), UV-Vis absorption, Fourier-transform infrared (FTIR), Raman spectra, and numerical datasets used for optical and structural analysis, are included within the published article. No additional data, code, or supplementary information (SI) files were generated or are required to access the results.Acknowledgements
ELL thanks Agencia Estatal de Investigación (AEI) for funding through project PID2024-156552OA-I00 and Xunta de Galicia for contract GRC ED431C 2020/10 and GRC ED431C2024/6. Next Generation-EU funds are also greatly acknowledged. Author thanks the support of the Microscopy Unit of the Research and Technological Development Support Infrastructures Network of the University of Santiago de Compostela (RIAIDT-USC).References
- P. R. Nadig, O. Toulemonde, P. Alagarsamy, M. S. Murari and M. D. Daivajna, Multifaceted Roles of Ag+ Ions within and outside La–Ca–MnO3 Perovskite Manganites: Unveiling the Room Temperature Magnetocaloric Effect, J. Phys. Chem. C, 2024, 128, 12686–12703, DOI:10.1021/acs.jpcc.4c03215.
- Z. Aydi, R. Dhahri, S. Kammoun, E. Dhahri, E.-K. Hlil and E. López-Lago, Exploring the environmental potential of LSMO-SG: Critical behavior and magnetocaloric effect for green cooling technologies, J. Alloys Compd., 2025, 1032, 180656, DOI:10.1016/j.jallcom.2025.180656.
- Z. Aydi, A. Dhahri, M. Jeddi, O. R. Alzoubi and E. Dhahri, Magnetocaloric and magneto-transport properties of defective A-site Sr-doped lanthanum manganite, Appl. Phys. A: Mater. Sci. Process., 2025, 131, 772, DOI:10.1007/s00339-025-08877-1.
- M. Dhahri, J. Dhahri and E. K. Hlil, Large magnetic entropy change and prediction of magnetoresistance using a magnetic field in La0.5Sm0.1Sr0.4Mn0.975In0.025O3, RSC Adv., 2018, 8, 5395–5406 RSC.
- Z. Aydi, R. Dhahri, K. Khirouni and E. Dhahri, Dual Ca–Co substitution of La–Sr–Mn–O Perovskite for modulating the multifunctional characteristics to Advanced Optical Functionality, Ceram. Int., 2025, 51(29), 61531–61549, DOI:10.1016/j.ceramint.2025.10.346.
- H. Meskine, H. König and S. Satpathy, Orbital ordering and exchange interaction in the manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 094433, DOI:10.1103/PhysRevB.64.094433.
- A. Wang, T. Liu, Y. Liu and G. Cao, The Jahn–Teller effect of layered perovskite manganites La2−2xSr1+2xMn2O7 studied by Mn K-edge XAFS, Phys. B, 2005, 363, 115–121 CrossRef CAS.
- S. Merten, V. Bruchmann-Bamberg, B. Damaschke, K. Samwer and V. Moshnyaga, Jahn–Teller reconstructed surface of the doped manganites shown by means of surface-enhanced Raman spectroscopy, Phys. Rev. Mater., 2019, 3, 060401(R), DOI:10.1103/physrevmaterials.3.060401.
- S. G. Choi, H.-S. Lee, H. Choi, S.-W. Chung and H.-H. Park, The effect of Ca substitution on the structural and electrical properties of La0.7Sr0.3−xCaxMnO3 perovskite manganite films, J. Phys. D: Appl. Phys., 2013, 46, 425102 CrossRef.
- I. A. Flores Urquizo, Evaluación de las propiedades magnéticas en las perovskitas La0.7Sr0.3−xCaxMnO3 (x = 0.03, 0.05, 0.07 y 0.09) recubiertas con amino silano para su aplicación en hipertermia magnética, PhD Thesis, Universidad Autónoma de Nuevo León, 2018.
- M. Gupta, R. K. Kotnala, W. Khan, A. Azam and A. H. Naqvi, Magnetic, transport and magnetoresistance behavior of Ni doped La0.67Sr0.33Mn1−xNixO3 (0.00 ≤ x ≤ 0.09) system, J. Solid State Chem., 2013, 204, 205–212 CrossRef CAS.
- J. Setiawan, F. B. Susetyo, D. Nanto, S. Simbolon, H. A. Notonegoro, T. Al Farizi and D. Tihera, Preparation, synthesis and characterizations of La0.7Sr0.3Mn(1−y)Ni(y)O3 alloy, Commun. Sci. Technol., 2024, 9(1), 87–93, DOI:10.21924/cst.9.1.2024.1361.
- S. B. Abdelkhalek, N. Kallel, S. Kallel, T. Guizouarn, O. Peña and M. Oumezzine, Transport behavior and mechanism of conduction of simultaneously substituted Y and Fe in La0.7Ba0.3MnO3 perovskite, Phys. B, 2011, 406, 4060–4067 CrossRef.
- S. Daengsakul, C. Thomas, C. Mongkolkachit and S. Maensiri, Thermal Hydro-Decomposition Synthesis, Structural Characterization, and Magnetic Properties of La1−xSrxMn1−yCoyO3, Nanopowders, 2013, 12, 242–253, DOI:10.1166/sam.2013.1451.
- R. Laiho, K. G. Lisunov, E. Lähderanta, P. A. Petrenko, J. Salminen, M. A. Shakhov, M. O. Safontchik, V. S. Stamov, M. V. Shubnikov and V. S. Zakhvalinskii, Variable-range hopping conductivity in La1−xCaxMn1−yFeyO3: evidence of a complex gap in density of states near the Fermi level, J. Phys.: Condens. Matter, 2002, 14, 8043 CrossRef CAS.
- R. Laiho, K. G. Lisunov, E. Lähderanta, J. Salminen and V. S. Zakhvalinskii, Low-field magnetic properties as indication of disorder, frustration and cluster formation effects in La1−xCaxMn1−yFeyO3, J. Magn. Magn. Mater., 2002, 250, 267–274 CrossRef CAS.
- A. M. Ahmed, A. E.-M. A. Mohamed, M. A. Abdellateef and H. A. Abd El-Ghanny, Magnetoresistive properties of Ni-doped La0.7Sr0.3MnO3 manganites, Rare Met., 2016, 35, 551–558, DOI:10.1007/s12598-015-0465-x.
- A. G. Badelin, A. A. Shchepetkin, S. K. Estemirova, V. V. Sorokin and V. K. Karpasyuk, Magnetic and electrical properties of La1−cSrcMn1−xGaxO3 manganites, J. Phys.: Conf. Ser., 2011, 012072 CrossRef.
- K. Dhahri, N. Dhahri, S. Bouzidi, M. Hleili, N. Al-Harbi, N. M. Basfer, N. A. Harqani, J. Dhahri, P. Lachkar and E. K. Hlil, An in-depth insight at the percolation model and charge transport mechanism in La0.7Ca0.1Pb0.2Mn1−2xAlxSnxO3 manganite prepared by sol–gel route, J. Sol-Gel Sci. Technol., 2024, 111, 281–292, DOI:10.1007/s10971-024-06438-1.
- P. G. Radaelli, G. Iannone, M. Marezio, H. Y. Hwang, S.-W. Cheong, J. D. Jorgensen and D. N. Argyriou, Structural effects on the magnetic and transport properties of perovskite A1−xAx′MnO3 (x = 0.25, 0.30), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8265–8276, DOI:10.1103/PhysRevB.56.8265.
- J. Töpfer and J. B. Goodenough, LaMnO3+δ Revisited, J. Solid State Chem., 1997, 130, 117–128, DOI:10.1006/jssc.1997.7287.
- J. B. Goodenough, Electronic and ionic transport properties and other physical aspects of perovskites, Rep. Prog. Phys., 2004, 67, 1915 CrossRef CAS.
- P. Thamilmaran, M. Arunachalam, S. Sankarrajan and K. Sakthipandi, Impact of Ni doping on La0.7Sr0.3Ni Mn1−O3 perovskite manganite materials, J. Magn. Magn. Mater., 2015, 396, 181–189, DOI:10.1016/j.jmmm.2015.08.028.
- Z. Aydi, A. Dhahri, M. Jeddi, K. Khirouni and E. Dhahri, Promising properties and applications in advanced electronic devices of Nd0.6Sr0.3Ba0.1MnO3 Perovskite, J. Inorg. Organomet. Polym. Mater., 2025, 1–24, DOI:10.21203/rs.3.rs-7233919/v1.
- P. Vlazan, C. N. Marin, I. Malaescu, G. Vlase, T. Vlase, M. Poienar and P. Sfirloaga, Revealing the Impact of Ga and Y Doping on Thermal and Electrical Behavior of LaMnO3 Ceramic Materials, Appl. Sci., 2024, 14, 1546 CrossRef CAS.
- C. N. R. Rao and A. K. Raychaudhuri, Colossal Magnetoresistance, Charge Ordering and Other Novel Properties of Manganates And Related Materials, Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides, World Scientific, 1998, pp. 1–42 DOI:10.1142/9789812816795_0001.
- M. V. Abrashev, A. P. Litvinchuk, M. N. Iliev, R. L. Meng, V. N. Popov, V. G. Ivanov, R. A. Chakalov and C. Thomsen, Comparative study of optical phonons in the rhombohedrally distorted perovskites LaAlO3 and LaMnO3, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 4146–4153, DOI:10.1103/PhysRevB.59.4146.
- L. Martín-Carrón, A. De Andrés, M. J. Martínez-Lope, M. T. Casais and J. A. Alonso, Raman phonons as a probe of disorder, fluctuations, and local structure in doped and undoped orthorhombic and rhombohedral manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174303, DOI:10.1103/PhysRevB.66.174303.
- P. T. Phong, S. J. Jang, B. T. Huy, Y.-I. Lee and I.-J. Lee, Structural, magnetic, infrared and Raman studies of La0.8SrxCa0.2−xMnO3 (0 ≤ x ≤ 0.2), J. Mater. Sci.: Mater. Electron., 2013, 24, 2292–2301, DOI:10.1007/s10854-013-1092-7.
- B. C. Behera, A. V. Ravindra, P. Padhan and W. Prellier, Raman spectra and magnetization of all-ferromagnetic superlattices grown on (110) oriented SrTiO3, Appl. Phys. Lett., 2014, 104, 092406, DOI:10.1063/1.4867509.
- X. Liang, Z. Wang, Z. Chen, J. Jiang, J. Han, Y. Wang, H. Wang, Z. Pan, J. Sun, J. Ma, X. Jiang, J. Peng, X. Liu and X. Gu, Refined Sr ion ratio to improve room-temperature TCR of La1−xSrxMnO3 (0.175 ≤ x ≤ 0.235) polycrystalline ceramics, J. Mater. Sci.: Mater. Electron., 2024, 35, 1761, DOI:10.1007/s10854-024-13522-3.
- V. B. Podobedov, A. Weber, D. B. Romero, J. P. Rice and H. D. Drew, Effect of structural and magnetic transitions in La1−xMxMnO3 (M = Sr, Ca) single crystals in Raman scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 43–46, DOI:10.1103/PhysRevB.58.43.
- A. Dubroka, J. Humlíček, M. V. Abrashev, Z. V. Popović, F. Sapiña and A. Cantarero, Raman and infrared studies of La1−ySryMn1−xMxO3 (M = Cr, Co, Cu, Zn, Sc or Ga): Oxygen disorder and local vibrational modes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224401, DOI:10.1103/PhysRevB.73.224401.
- A. B. J. Kharrat, K. Kahouli and S. Chaabouni, Detailed investigation of the optical properties of the (C8H11BrN)3BiCl6 compound by UV-visible measurements, Bull. Mater. Sci., 2020, 43, 275, DOI:10.1007/s12034-020-02248-7.
- E. Jara, R. Valiente, M. Bettinelli and F. Rodríguez, Understanding the Efficiency of Mn4+ Phosphors: Study of the Spinel Mg2Ti1−xMnxO4, J. Phys. Chem. C, 2021, 125, 27118–27129, DOI:10.1021/acs.jpcc.1c08006.
- A. D. Molchanova, Experimental Study and Analysis of Absorption Spectra of Ni2+ Ions in Nickel Orthoborate Ni3(BO3)2, Phys. Solid State, 2018, 60, 1957–1965, DOI:10.1134/S1063783418100219.
- A. Wilk, M. A. Hitchman, W. Massa and D. Reinen, Structure and the electronic properties of a Jahn–Teller distorted tetrahedral nickel(II) complex with sulfur ligands, Inorg. Chem., 1993, 32, 2483–2490, DOI:10.1021/ic00063a047.
- Y. Barak, I. Meir, J. Dehnel, F. Horani, D. R. Gamelin, A. Shapiro and E. Lifshitz, Uncovering the Influence of Ni2+ Doping in Lead–Halide Perovskite Nanocrystals Using Optically Detected Magnetic Resonance Spectroscopy, Chem. Mater., 2022, 34, 1686–1698, DOI:10.1021/acs.chemmater.1c03822.
- O. Taktak, H. Souissi, I. Elhamdi, A. Oueslati, S. Kammoun, M. Gargouri and E. Dhahri, Optical investigations and theoretical simulation of organic-inorganic hybrid: TPA-CoCl4, Opt. Mater., 2024, 150, 115251 CrossRef CAS.
- H. Souissi, S. Kammoun, E. Dhahri, E. López-Lago and B. F. O. Costa, Exploring the structural and optical properties of lithium-chromium phosphate Li3Cr2(PO3)4, Heliyon, 2024, 10(16), e36188 CrossRef CAS PubMed.
- J. B. Goodenough, Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3, Phys. Rev., 1955, 100, 564–573, DOI:10.1103/PhysRev.100.564.
- A. K. Zak, N. Arefipour and A. M. Hashim, Enhancement and refinement of SSP method for XRD analysis and investigation of structural properties of pure and Ca-doped zinc oxide, J. Aust. Ceram. Soc., 2024, 60, 755–762, DOI:10.1007/s41779-024-01032-8.
- R. E. Marotti, D. N. Guerra, C. Bello, G. Machado and E. A. Dalchiele, Bandgap energy tuning of electrochemically grown ZnO thin films by thickness and electrodeposition potential, Sol. Energy Mater. Sol. Cells, 2004, 82, 85–103 CrossRef CAS.
- I. B. Slima, K. Karoui, K. Khirouni, A. Mahmoud, F. Boschini and A. B. Rhaiem, Investigation of the optical and dielectric properties of NaCu0.2Fe0.8−xMnxO2 (x = 0.4; 0.5; 0.6; 0.7) layered oxide materials, Inorg. Chem. Commun., 2023, 157, 111444 CrossRef.
- P. Makuła, M. Pacia and W. Macyk, How To Correctly Determine the Band Gap Energy of Modified Semiconductor Photocatalysts Based on UV-Vis Spectra, J. Phys. Chem. Lett., 2018, 9, 6814–6817, DOI:10.1021/acs.jpclett.8b02892.
- Y. Jiménez-Flores, M. Suárez-Quezada, J. B. Rojas-Trigos, L. Lartundo-Rojas, V. Suárez and A. Mantilla, Characterization of Tb-doped hydroxyapatite for biomedical applications: optical properties and energy band gap determination, J. Mater. Sci., 2017, 52, 9990–10000 CrossRef.
- J. Tauc, R. Grigorovici and A. Vancu, Optical Properties and Electronic Structure of Amorphous Germanium, Phys. Status Solidi B, 1966, 15, 627–637, DOI:10.1002/pssb.19660150224.
- J. I. Pankove, Optical processes in semiconductors, Courier Corporation, 1975 Search PubMed.
- K. Rościszewski and A. M. Oleś, Jahn–Teller distortions and the magnetic order in the perovskite manganites, J. Phys.: Condens. Matter, 2010, 22, 425601 CrossRef PubMed.
- B. Kressdorf, T. Meyer, M. ten Brink, C. Seick, S. Melles, N. Ottinger, T. Titze, H. Meer, A. Weisser, J. Hoffmann, S. Mathias, H. Ulrichs, D. Steil, M. Seibt, P. E. Blöchl and C. Jooss, Orbital-order phase transition in Pr1−xCaxMnO3 probed by photovoltaics, Phys. Rev. B, 2021, 103, 235122, DOI:10.1103/PhysRevB.103.235122.
- E. Hastuti, A. Subhan, P. Amonpattaratkit, M. Zainuri and S. Suasmoro, The effects of Fe-doping on MnO2: phase transitions, defect structures and its influence on electrical properties, RSC Adv., 2021, 11, 7808–7823, 10.1039/D0RA10376D.
- S. Kalyanaraman, P. M. Shajinshinu and S. Vijayalakshmi, Determination of optical constants and polarizability studies on ferroic Tetramethylammonium Tetracholorozincate crystal, Phys. B, 2016, 482, 38–42 CrossRef CAS.
- S. Husain, A. O. Keelani and W. Khan, Influence of Mn substitution on morphological, thermal and optical properties of nanocrystalline GdFeO3 orthoferrite, Nano-Struct. Nano-Objects, 2018, 15, 17–27 CrossRef CAS.
- A. S. Hassanien and A. A. Akl, Influence of composition on optical and dispersion parameters of thermally evaporated non-crystalline Cd50S50−xSex thin films, J. Alloys Compd., 2015, 648, 280–290 CrossRef CAS.
- M. V. Kurik, Urbach rule, Phys. Status Solidi A, 1971, 8, 9 CrossRef CAS.
- H. R. Shakur, A detailed study of physical properties of ZnS quantum dots synthesized by reverse micelle method, Phys. E, 2011, 44, 641–646 CrossRef CAS.
- E. Caponetti, L. Pedone, D. C. Martino, V. Panto and V. T. Liveri, Synthesis, size control, and passivation of CdS nanoparticles in water/AOT/n-heptane microemulsions, Mater. Sci. Eng., C, 2003, 23, 531–539 CrossRef.
- A. Fujishima and K. Honda, Electrochemical photolysis of water at a semiconductor electrode, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- F. Hcini, S. Hcini, M. A. Wederni, B. Alzahrani, H. Al Robei, K. Khirouni, S. Zemni and M. L. Bouazizi, Structural, optical, and dielectric properties for Mg0.6Cu0.2Ni0.2Cr2O4 chromite spinel, Phys. B, 2022, 624, 413439 CrossRef CAS.
- A. M. Mansour, B. A. Hemdan, A. Elzwawy, A. B. Abou Hammad and A. M. El Nahrawy, Ecofriendly synthesis and characterization of Ni2+ codoped silica magnesium zirconium copper nanoceramics for wastewater treatment applications, Sci. Rep., 2022, 12, 9855 CrossRef CAS PubMed.
- M. T. Khan, M. Shkir, A. Almohammedi and S. AlFaify, Fabrication and characterization of La doped PbI2 nanostructured thin films for opto-electronic applications, Solid State Sci., 2019, 90, 95–101 CrossRef CAS.
- D. C. Sati, R. Kumar and R. M. Mehra, Influence of Thickness on Optical Properties of a: As2Se3 Thin Films, Turk. J. Phys., 2006, 30, 519–528 CAS.
- M. DrDomenico Jr and S. H. Wemple, Oxygen-octahedra ferroelectrics. I. Theory of electro-optical and nonlinear optical effects, J. Appl. Phys., 1969, 40, 720–734 CrossRef.
- S. H. Wemple, Refractive-Index Behavior of Amorphous Semiconductors and Glasses, Phys. Rev. B, 1973, 7, 3767–3777, DOI:10.1103/PhysRevB.7.3767.
- N. Tounsi, A. Barhoumi, F. C. Akkari, M. Kanzari, H. Guermazi and S. Guermazi, Structural and optical characterization of copper oxide composite thin films elaborated by GLAD technique, Vacuum, 2015, 121, 9–17 CrossRef CAS.
- A. K. Walton and T. S. Moss, Determination of refractive index and correction to effective electron mass in PbTe and PbSe, Proc. Phys. Soc., London, 1963, 81, 509 CrossRef CAS.
- D. Hcini, S. Hcini, F. Hcini, M. H. Dhaou, A. Mallah, R. Charguia, F. Jabli, A. Dhahri and K. Khirouni, Improving the Properties of Ni0.4Cu0.4Cd0.2Fe2O4 Spinel Ferrites via Heat Treatment for Electrical and Optoelectronic Applications, J. Electron. Mater., 2024, 53, 5706–5727, DOI:10.1007/s11664-024-11239-x (accessed May 8, 2025).
- A. Dhahri, H. Saoudi, S. R. Gavinho, A. Benali, N. Abdelmoula, R. Dhahri, L. Peng, J. Wu, J. Pina and B. F. O. Costa, Particle Size Effect on Optical and Gas-Sensing Properties of La0.67Ca0.2Ba0.13Fe0.97M0.03O3 (M = Ti4+, Mn3+, and Cr3+) Compounds, Crystals, 2024, 14, 173 CrossRef CAS.
- F. Z. Rachid, L. H. Omari, H. Lassri, H. Lemziouka, S. Derkaoui, M. Haddad, T. Lamhasni and M. Sajieddine, Synthesis, structural and optical properties of LaFe1−xCrxO3 nanoparticles, Opt. Mater., 2020, 109, 110332 CrossRef CAS.
- L. H. Omari, H. Lemziouka, R. Moubah, M. Haddad and H. Lassri, Structural and optical properties of Fe-doped Ruddlesden–Popper Ca3Ti2−xFexO7−δ nanoparticles, Mater. Chem. Phys., 2020, 246, 122810 CrossRef CAS.
- R. Mguedla, A. B. J. Kharrat, N. Moutia, K. Khirouni, N. Chniba-Boudjada and W. Boujelben, Gd doping effect on structural, electrical and dielectric properties in HoCrO3 orthochromites for electric applications, J. Alloys Compd., 2020, 836, 155186 CrossRef CAS.
- Z. Raddaoui, B. Smiri, A. Maaoui, J. Dhahri, R. M’ghaieth, N. Abdelmoula and K. Khirouni, Correlation of crystal structure and optical properties of Ba0.97Nd0.0267Ti(1−x)WxO3 perovskite, RSC Adv., 2018, 8, 27870–27880 RSC.
- K. Kahouli, A. B. J. Kharrat and S. Chaabouni, Optical properties analysis of the new (C9H14N)3BiCl6 compound by UV-visible measurements, Indian J. Phys., 2021, 95, 2797–2805, DOI:10.1007/s12648-020-01942-w.
| This journal is © The Royal Society of Chemistry 2026 |