Machine learning screening and high-throughput computation of 3d-transition-metal intercalated Janus PtXY/ζ-phosphorene (X ≠ Y; X, Y = S, Se, Te) heterostructures for photocatalytic water splitting

Abstract

The rising demand for clean and green energy sources has sparked global interest in sustainable hydrogen production technologies. To address this problem, photocatalytic water splitting has emerged as a promising solution for the sustainable production of green hydrogen and oxygen. We investigate the hydrogen adsorption Gibbs free energy for hydrogen evaluation reaction (HER) and rate-limiting Gibbs free energy for oxygen evolution reaction (OER) to analyse the catalytic activity of the transition metal (TM) intercalated PtXY/ζ-phosphorene (X ≠ Y; X, Y = S, Se, Te) van der Waals heterostructures (vdWHs). Our workflow involves generating a large dataset, followed by performing high-throughput first-principles density functional theory (DFT) calculations on a small fraction of the dataset to obtain the training dataset for a machine learning (ML) framework. Incorporating the ML with the DFT workflow, we obtained 13 potential catalysts for HER and 6 potential catalysts for OER. The interlayer distance of the heterostructures and the bond length between the Pt and X atom emerged as the most influential features for HER, whereas the choice of adsorption site is one of the major OER descriptors. Overall, ML approach integrated with high-throughput first principles calculations is promising for the prediction of potential TM-intercalated vdWHs photocatalysts for water splitting.

---

1. Introduction

With the surge in population growth and rising consequences of energy consumption and environmental degradation, the pursuit of green energy sources has emerged as a key priority for research.^1,2 Hydrogen's remarkable properties, such as its high energy density, lack of emissions during combustion, and versatility across diverse applications, make it a highly promising and ideal green fuel. Over the years, green hydrogen has been used in multiple applications such as transportation, power generation and energy storage.^3,4 Despite its promising potential, one of the significant hurdles to utilising hydrogen as a fuel is its high production cost.

Photocatalytic water splitting is a promising and one of the leading methods for hydrogen production, harnessing two of the most abundant and renewable resources, water and sunlight. The low-cost implementation, low energy consumption, and minimal infrastructure requirement for photocatalytic water splitting offer a financially viable and efficient resource.⁵ There are three significant steps in the water splitting photocatalysis process: electron–hole pairs generation by sunlight with photon energy exceeding the semiconductor photocatalyst band gap; photogenerated charge carriers separation and migration to the surface of photocatalyst; the hydrogen evolution reaction (HER) to produce hydrogen and oxygen evolution reaction (OER) to produce oxygen by the photogenerated electrons in conduction band and photogenerated holes in valence band of photocatalyst.^6–8 Unlike conventional hydrogen production methods such as electrolysis, thermal water splitting, and cracking of petroleum, the photocatalytic water splitting is environmentally friendly and less expensive.⁹

Two-dimensional (2D) Janus transition metal dichalcogenides (JTMDCs) exhibit a unique asymmetric structure, where a transition metal layer is sandwiched between two chalcogen layers, thereby breaking the structural symmetry along the z-direction.¹⁰ This asymmetry creates an intrinsic dipole, which can significantly enhance photocatalytic performance compared to conventional symmetric TMDCs.^11,12 Also, JTMDs show high adsorption coefficients and low exciton binding energy, which are beneficial for photocatalysis applications.^13,14 Among the many promising JTMDs, PtSSe is experimentally synthesized and has desirable properties that make it suitable for water splitting photocatalysis.¹⁵ Janus PtSSe demonstrates an impressive solar-to-hydrogen (STH) conversion efficiency (∼18%), considerably higher than other active photocatalytic materials such as Ga₂S₃ (6.4%), Ga₂SSe bilayer (7.42%), pentagonal PdSe₂ (12.59%), and even Janus WSSe (14.46%).¹⁶

In the recent past, phosphorene allotropes have gained the interest of researchers. Heterostructures of blue phosphorene and black phosphorene have shown promising photocatalytic water-splitting activity.^17,18 The PtSSe/ζ-phosphorene heterostructure has been demonstrated to exhibit semiconducting properties with impressively high carrier mobility of ∼10³ cm² V⁻¹ s⁻¹, and a type-II mechanism favourable for water splitting photocatalysis.¹⁹ It has also been shown that the STH conversion efficiency of these heterostructures can exceed 10%, which motivates further investigation into the characteristics of phosphorene.

The unique features, such as effective charge separation due to the interfacial electric field in van der Waals heterostructures (vdWHs), make them suitable candidates for photocatalytic water splitting.²⁰ vdWHs also show excellent solar light absorption ability, e.g., MoSe₂/HfS₂ heterostructures demonstrate a strengthened optical absorption intensity in both the visible and infrared regions compared to the individual HfS₂ and MoSe₂ monolayers;²¹ GeI₂/C₂N vdWHs display a higher redshift around 720 nm than either of its constituent monolayers, enhancing its ability to capture solar energy.²²

Furthermore, Janus heterostructures possess some distinctive characteristics that make them highly desirable for photocatalytic water splitting. The coupling of the intrinsic intralayer polarization in the Janus layer with the interlayer built-in polarisation field provides an additional degree of freedom for tuning the photocatalytic properties. This intrinsic polarization plays a vital role in achieving spatial charge-carrier separation across the interface.²³ Beyond charge separation, the Janus layer polarization also enables modulation of band alignment through variations in stacking order. For instance, in the BlueP/MoSSe heterostructure, altering the stacking sequence transforms the band alignment from type-I to type-II, a configuration particularly favourable for photocatalytic applications.²³ PtSSe-based heterostructures have shown overall excellent results for photocatalytic water splitting.²⁴

Also, the metal atom intercalation can significantly influence the photocatalytic properties of vdWHs, such as improving the charge carrier's transport, alteration in the band gap.²⁵ In addition, metal atoms, when intercalated into layered structures, can create an optimised charge transfer pathway.²⁰ When alkali metals are intercalated into graphitic carbon nitride, it induces the charge redistribution that accelerates the separation efficiency of photogenerated carriers, with intercalated atoms bridging the adjacent layers and enhancing the interlayer charge transportation.²⁶

Although conventional density functional theory (DFT) calculations are computationally intensive for heterostructures, accommodating lattice mismatch often requires a supercell, which can increase the number of atoms and computational costs. Incorporating a machine learning (ML) workflow into the conventional DFT method could significantly reduce the time and resources needed. Furthermore, the size of the dataset for high-throughput computation is often in the order of hundreds or thousands; exploring each of them poses a huge challenge. However, machine learning-assisted screening solves this constraint to a great degree.²⁷ Machine learning is also useful in capturing the complex patterns in the dataset, and analysing these patterns could give us insights into how the results depend upon various material properties.^28–30

Based on the insights gathered from previous research, we have investigated Janus PtSSe/ζ-phosphorene (X ≠ Y, X, Y = S,Se,Te) heterostructures intercalated with 3d-transition-metal elements for photocatalytic water splitting, utilising high-throughput DFT computation and machine learning. Intercalating transition metals into selected sites between the layers of the heterostructures and adsorbing H, O, OH, and OOH on particular adsorption sites, a dataset using high-throughput DFT computation has been generated for machine learning-assisted screening. Machine learning has proven to be a valuable tool, as evident from its performance. The results are further analysed for potential photocatalytic activity descriptors.

2. Methodology

2.1. Computational details

DFT calculations were carried out utilizing the Vienna ab initio simulation package (VASP).³¹ The electron–ion interactions are modelled using the project augmented wave (PAW) method. We used the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional within the generalised gradient approximation (GGA).³² The kinetic energy cut-off for the plane wave expansion is set to 400 eV. The energy convergence criterion for the wave function is set to 10⁻⁵ eV. The Brillouin zone is sampled using a Monkhorst–Pack grid³³ of 12 × 12 × 1 k-point mesh. We utilised the van der Waals DFT-D3 method for long-range vdW interactions.³⁴ To prevent the interaction between neighbouring layers in the perpendicular direction, a vacuum spacing of 25 Å is employed. Gibbs free energy profiling is widely used as a reliable descriptor to examine the HER and OER activity, which are obtained using the method proposed by Nørskov et al.^35,36

2.2. Machine learning

We employed scikit-learn,³⁷ an open-source Python library for ML to train the model, which provides a wide range of methods for feature encoding, cross-validation and feature elimination.³⁸ The library provides a wide variety of ML models for both classification and regression.^39,40 It includes linear models, such as linear regression and Elastic Net, as well as more complex ensemble models, including random forest regressor and AdaBoost regressor. Apart from this, various model selection tools, evaluation metrics and optimisation tools make sci-kit learn a popular tool for machine learning. We utilized “One Hot Encoder” to encode categorical features and the Min-Max Scaler for numerical features.⁴¹ We performed a K-fold cross-validation, with 80% of the dataset used for training and the remaining 20% for validation.

The schematic representation of the methodology is shown in Fig. 1. The features used to train the ML models are presented in Table S2 of the SI. We employed a set of supervised ML regression algorithms, including linear models such as ridge and LASSO, which incorporate regularisation to prevent overfitting, as well as ensemble and tree-based models such as random forest regressor (RFR), gradient boosting regressor (GBR), and ada boost regressor (ABR), which were extensively used previously.⁴² Also, an artificial neural network (ANN), specifically a multi-layer perceptron model (MLP), was considered due to its ability to capture complex non-linear relations.⁴³ Additionally, neighbor-based models such as KNeighbors Regressor (KNR) were also utilized. The various ML models used in the study is given in Table S3, SI.

Fig. 1 The schematic representation of a machine learning workflow integrated with high-throughput DFT computation. The steps include data generation, feature engineering, model optimization, model training and target prediction.

The K-fold cross-validation method is used for model selection with 10-fold splits. The randomized search CV method is used to optimize the hyperparameters. The quantitative evaluation of the optimized model is carried out using standard regression metrics: mean absolute error (MAE) and coefficient of determination (R²). The factors driving the predictions of the ML model are crucial for identifying the key indicators of photocatalytic activity. SHaply Additive explanations (SHAP)⁴⁴ is a robust framework for interpreting ML models. SHAP is based on cooperative game theory, which enables the quantitative assessment of the importance of each input feature and provides insights into the model's final prediction.

3. Results and discussion

2D Janus monolayers (PtSSe, PtSTe, PtSeTe) and ζ-phosphorene monolayer possess a hexagonal and rectangular unit cell, respectively. The calculated lattice constants of PtSSe, PtSTe and PtSeTe are 3.65 Å, 3.80 Å and 3.88 Å, respectively, which are consistent with the previously reported values.^45–47 After obtaining the optimised monolayers, we constructed a 1 × 3 × 1 supercell of PtXY monolayers and a 1x2x1 supercell for ζ-phosphorene to minimise the lattice mismatch. The lattice mismatch of PtSSe/ζ-phosphorene, PtSTe/ζ-phosphorene, PtSeTe/ζ-phosphorene vdWHs along x- and y-directions is 2.01% and 2.46%, 1.07% and 5.47% and 3.14% and 7.35%, respectively.

3.1. High-throughput DFT computation to generate datasets

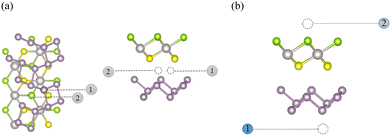
Due to the asymmetrical nature of the Janus PtXY layers, six distinct heterostructures were obtained. Prior to further analysis, we examined various stacking patterns for each of these six heterostructures to determine the minimum energy stacking. The different stacking patterns and their energies are presented in Fig. S1–S6 (SI). In each of the six cases, AF stacking is the most stable stacking method. The six basic heterostructures, arranged in their stable stacking pattern, are shown in Fig. 2. To confirm the stability of these heterostructures, we calculated the binding energy for different AF stacking patterns as:

E_B = E_PtXY/ξ−P − E_PtXY − E_ξ−P (1)

where E_PtXY/ξ−P is the total energy of the heterostructure, E_PtXY and E_ξ−P are the total energies of the individual monolayers.

Fig. 2 The energetically stable heterostructures of (a) PtSSe/ζ-phosphorene (S-side), (b) PtSSe/ζ-phosphorene (Se-side), (c) PtSTe/ζ-phosphorene (S-side), (d) PtSTe/ζ-phosphorene (Te-side), (e), PtSeTe/ζ-phosphorene (Se-side), (f) PtSeTe/ζ-phosphorene (Te-side).

The calculated value of binding energy of PtSSe/ζ-phosphorene (S-side), PtSSe/ζ-phosphorene (Se-side), PtSTe/ζ-phosphorene (S-side), PtSTe/ζ-phosphorene (Te-side), PtSeTe/ζ-phosphorene (Se-side), and PtSeTe/ζ-phosphorene (Te-side), is −37 meV Å⁻², −22 meV Å⁻², −25 meV Å⁻², −21 meV Å⁻², −24 meV Å⁻² and −22 meV Å⁻², respectively. The negative value of the binding energy indicates good energetic stability of these heterostructures. The calculated binding energies are comparable with other layered crystals, such as graphite⁴⁸ and MoS₂.⁴⁹

For the six stable primary heterostructures, we investigated two distinct interlayer sites for the intercalation of ten 3d-transition-metal atoms: Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu and Zn. The relative position of the intercalating sites is illustrated in Fig. 3. In this way, we obtained 120 intercalated configurations from each with two intercalation sites with different metals atoms. After obtaining the optimised 120 structures, we calculated the binding energy of the intercalated transition metal element as:

E_b = E_TM/subtrate − E_TM − E_subtrate (2)

where E_TM/subtrate is the total energy of the TM intercalated heterostructure and E_TM and E_subtrate are the total energies of the transition metal atom and PtXY/ζ-Phosphorene heterostructures, respectively. The intercalated transition metal binding energy is depicted in a heatmap in Fig. 4. The heatmap reveals that the binding energy is highly dependent on the choice of transition metal. Notably, the Zn-intercalated structures exhibit low binding energy, indicating their instability. Even though Cu-intercalated structures show better energetic stability than Zn, they indicate lower stability than the rest of the transition metals.

Fig. 3 (a) Schematic representation of the relative position of intercalation sites for transition metals and (b) adsorption sites in Janus PtXY/ζ-phosphorene (X ≠ Y; X, Y = S, Se, Te) heterostructures.

Fig. 4 Heatmap of the binding energy of transition metals intercalated at site 1 and site 2 of Janus PtXY/ζ-phosphorene (X ≠ Y; X, Y = S, Se, Te) heterostructures.

After obtaining the 120 intercalated vdWHs and evaluating their stability through binding energy, we identified two active sites for hydrogen adsorption, with one on each layer of the heterostructure. The active site ‘one’ is on top of the topmost phosphorus atom of the phosphorene layer, while active site ‘two’ is located above the topmost chalcogen atom of the PtXY layer. The position of the adsorption sites relative to the layers is illustrated in Fig. 3(b). Each of 120 intercalated heterostructures features two distinct adsorption sites, resulting in a total of 240 configurations for hydrogen adsorptions. For hydrogen adsorption, we prepared a set of 240 configurations from which 120 entries (50% of the dataset) were randomly selected for further DFT calculations. We used the Panda's library in Python for the random selection of data entries. Random selection ensures that the training data can represent the entire dataset. For the adsorption calculation, all the atoms of the intercalated vdWHs are kept fixed in their equilibrium positions, and the adsorbed hydrogen atom is allowed to move freely in the z-direction.

Similarly, we have prepared a dataset of 240 entries each for OER calculations involving adsorption of O, OH, and OOH. We separately selected 120 random entries from these datasets for DFT calculation. In the case of OER, rate-limiting Gibbs free energy is the target property, so the rate-limiting step is determined from the Gibbs free energy values. In this way, we obtained the dataset using high-throughput computation for HER and OER, with hydrogen adsorption Gibbs free energy and rate-limiting Gibbs free energy being the target properties for the respective processes. The details of Gibbs free energy calculations are given in SI.

3.2. Machine learning for HER

We evaluated about 18 ML models to identify the best for our problem (Fig. S7–S12, SI). It is observed that linear models exhibited poor performance, as linear models assume a linear relationship between the target and feature values. The poor performance of linear models indicates a highly nonlinear relationship between target and feature values, further supported by the superior performance of ensemble models, which are better at capturing nonlinear patterns. Even though the performance of tree-based models is not acceptable, they show a slightly better performance than linear models. The other models didn’t show satisfactory performance (Table S4, SI). Owing to the superior performance of ensemble models, particularly the RandomForestRegressor, we consider these models for further evaluation.

Next, we addressed the overfitting problem of the ensemble models, when the model is too complicated for the problem at hand, so the model learns from the training dataset, on the underlying noise, so as a result, the model performs exceptionally well for the training dataset but performs worse when presented with an unfamiliar prediction dataset. To check whether the selected model is overfitting, we employed a train-test verification approach. We trained the models with 80% of the available dataset and the remaining 20% test set, which allows us to compare the performance of the seen and unseen datasets. Train-test verification metrics are given in Table S5 (SI). The ExtraTreeRegressor achieved a perfect score for the training dataset, but slightly reduced the lower performance for the testing data, indicating the potential for overfitting. The remaining model exhibits comparable performance on both the training and testing datasets. We used best best-performing model, RandomForestRegressor, for further study.

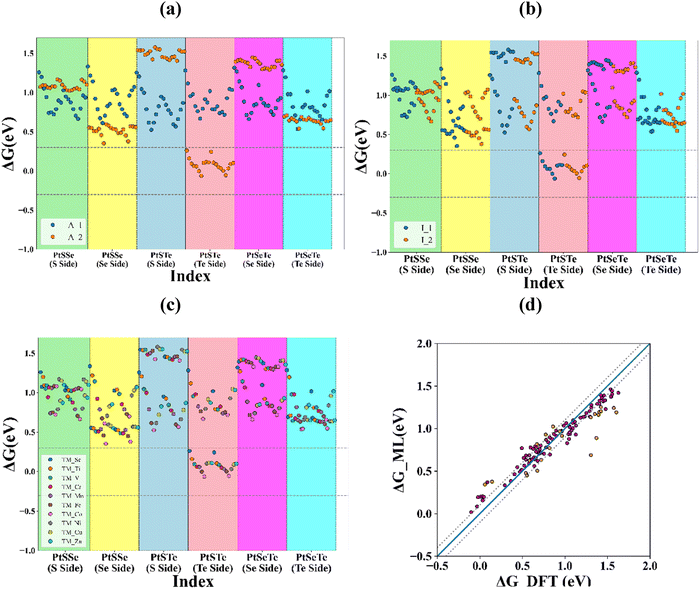
Now we performed the recursive feature elimination process on the random forest regressor (RFR) model with the best combination of hyperparameters (n_estimators = 80, min_samples_split = 2, min_samples_leaf = 1, max_features = 15, max_depth = 30). A learning curve depicting the variation of model accuracy (R²) with the number of samples in the training dataset is plotted (Fig. S13, SI). For a higher number of training samples, the accuracy of both the training dataset and the testing dataset is close to each other. After the feature elimination and hyperparameter optimisation process, the model metrics are obtained as R² = 0.84 and MAE = 0.11 eV. This model, trained on the DFT-generated dataset, is further used to predict the Gibbs free energy of the rest of the dataset. During the filtration of the most promising candidates of the datasets, we only considered those structures with Gibbs free energy lying between −0.3 and 0.3 eV,⁵⁰ and also, while selecting a photocatalyst, we considered the thermodynamic stability of those which having binding energies more than −5 eV.

The plot between Gibbs free energy and dataset index is shown in Fig. 5; the selection criterion for Gibbs free energy is denoted by horizontal dotted lines. We observed that the structures in this region are of PtSTe/ζ-phosphorene (Te side) heterostructures. Also, by flagging the scatter points with the adsorption sites Fig. 5(a), the adsorption site 2 is the most favourable for hydrogen adsorption. Adsorption site 2 is the one on the chalcogen of the Janus layer and is not facing the ζ-phosphorene layer. Fig. 5(d) represents the Gibbs free energy values obtained from DFT calculations and ML predictions, which are plotted for both training and testing data. The blue line shows perfect matching between the two values, indicating that our model closely matches the actual values. The dotted lines show a deviation of ±0.1 eV most of our data points are well within this limit.

Fig. 5 The scatter plot depicting the relationship between Gibbs free energy (ΔG) and index of each adsorbed structure flagged with (a) adsorption site (b) intercalation sites and (c) intercalated transition metal atom. (d) Parity plot of RFR model evaluating the correspondence of predicted values and true values of Gibbs free energy for HER.

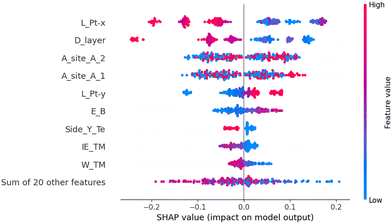
Furthermore, we employed SHAP analysis to examine the influence of each feature on the model's final output, identifying the best descriptors of photocatalytic activity among the selected features. The SHAP analysis results are depicted in Fig. 6. From SHAP analysis, we observed that the Pt–X bond length (L_Pt–X), interlayer thickness (D_layer), choice of intercalation sites (A_site_A_1, A_site_A_2), Pt–Y bond length (L_Pt–Y), and binding energy show the most excellent mean SHAP value. A bar diagram of the average SHAP value for each feature, along with a waterfall plot for a particular prediction, is provided in Fig. S14 and S15 of the SI. The SHAP analysis of two individual predictions (Fig. S15, SI), one corresponding to a promising catalyst i.e. Cr intercalated PtSTe/zeta-P heterostructure (Te side) with ΔG = 0.06 eV and another for a poor catalyst i.e. Zn intercalated PtSSe/zeta-P heterostructure (S side) with (ΔG = 1.11 eV), indicate that the interlayer distance and Pt–X bond length make the most significant contributions to reaching the final prediction. The good catalyst has an interlayer distance of 2.88 Å and whereas poor catalyst has 2.56 Å. It has also been observed in the previous studies that increased interlayer distance leads to the good HER activity by iimproving the Gibbs free energy.^51,52 Based on the benchmark of Gibbs free energy between the limits −0.3 eV to 0.3 eV, the 21 structures are selected (Table S6, SI), out of which 13 structures having binding energy more than −5 eV are given in Table 1.

Fig. 6 SHAP analysis plot depicting the most important descriptors for HER.

Table 1 The predicted adsorbed Janus PtXY/ζ-phosphorene (Z, M, I, A) heterostructures with Gibbs free energy between −0.3 eV to 0.3 eV and intercalates binding energy more than −5 eV for HER. Z, M, I, and A represent the chalcogen side of the heterostructure, the intercalated transition metal atom, the intercalated site, and the adsorption site, respectively

Heterostructures	Gibbs free energy (eV)	Binding energy (eV)
PtSTe/zeta-P(Te,V,I1,A2)	0.09	−5.94
PtSTe/zeta-P(Te,Cr,I1,A2)	0.06	−6.30
PtSTe/zeta-P(Te,Mn,I1,A2)	0.05	−6.23
PtSTe/zeta-P(Te,Fe,I1,A2)	−0.0005	−5.89
PtSTe/zeta-P(Te,Co,I1,A2)	−0.06	−5.42
PtSTe/zeta-P(Te,Ti,I2,A2)	0.10	−5.98
PtSTe/zeta-P(Te,V,I2,A2)	0.08	−6.41
PtSTe/zeta-P(Te,Cr,I2,A2)	0.05	−6.68
PtSTe/zeta-P(Te,Mn,I2,A2)	0.03	−6.79
PtSTe/zeta-P(Te,Fe,I2,A2)	0.003	−6.61
PtSTe/zeta-P(Te,Co,I2,A2)	−0.05	−6.20
PtSTe/zeta-P(Te,Ni,I2,A2)	0.03	−5.58

---

To benchmark the performance of our selected structures, we compared them with the commercially used Pt catalyst, which exhibits a hydrogen evolution Gibbs free energy close to zero. Our calculated Gibb's free energy values span from 0.09 eV to −0.0005 eV, highlighting their excellent catalytic potential relative to the Pt benchmark. Comparable efficiencies have been reported for transition-metal–intercalated Ti-doped WS₂ bilayers, which exhibit Gibbs free energies in the range of 0.003–0.083 eV.⁵³ Similarly, metal-intercalated bilayer borophene demonstrated Gibbs free energy range −0.082 to 0.183 eV.⁵⁴ Furthermore, cation-intercalated 1T-MoS₂ exhibited Gibbs free energies of the same order, further reinforcing the strong catalytic promise of our findings.⁵⁵

3.3. Machine learning for OER

In Gibbs free energy profiling of the OER pathway, the rate-limiting step is the reaction step with the highest energy barrier, and the rate-limiting Gibbs free energy is the corresponding Gibbs free energy value. The overall rate of the whole process is dependent upon this step. In the case of predicting rate-limiting Gibbs free energy for OER using machine learning, the same methodology has been followed as in the case of HER. We have trained 20 different ML models for cross-validation (Fig. S16–S20, SI). The cross-validation results are given in Table S7. From cross-validation, the SVR model with ‘rbf’ kernel is selected as the best-performing model. Also, the train-test verification is performed for SVR models, and the results are given in Table S8. From the results, it is evident that only the SVR model with ‘rbf’ kernel has comparable training and testing metrics scores, hence this model is taken for future predictions.

We now performed recursive feature elimination on the SVR model. After feature elimination, we obtained 30 features for future training. With hyperparameter tuning using Randomised search CV, we were able to find the best set of hyperparameters for the model. The selected final SVR model with the optimised hyperparameters is given as SVR (kernel = ‘rbf’, C = 20, tol = 1 × 10⁻⁵, shrinking = False, gamma = 0.1). The learning curve for the SVR model is depicted in Fig. S13(b), which shows favourable behaviour. The final SVR model exhibits excellent performance with metrics MAE = −0.21 and R² = 0.83.

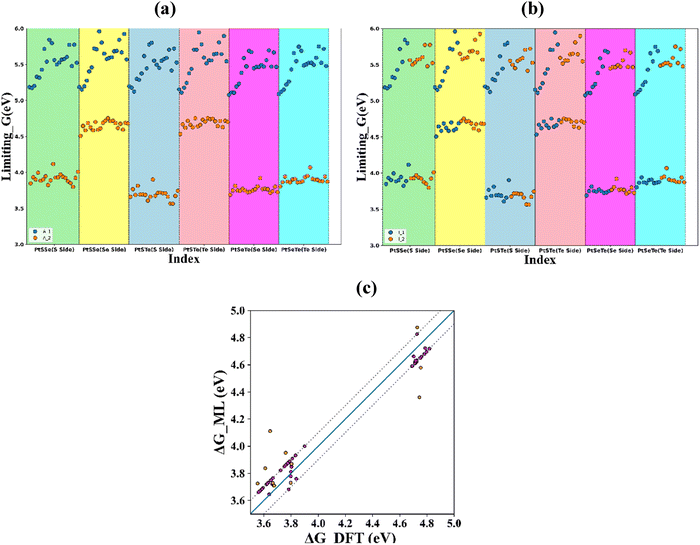
A graph between the rate-limiting value of Gibbs free energy and the dataset index is plotted in Fig. 7. The scatter points are coloured based on the adsorption site in Fig. 7(a). The adsorption site 2 shows the minimum limiting Gibbs free energy value. The intercalation sites do not show any pattern with the rate-limiting Gibbs free energy value (Fig. 7(b)). The graph of rate-limiting Gibbs free energy (true values vs. ML predicted values) is given in Fig. 7(c). The values show a close correspondence with the ideal behaviour and most of the points are within he ±0.1 eV limit as denoted by the dotted lines.

Fig. 7 The scatter plot depicting the relationship between rate-limiting Gibbs free energy and index of each adsorbed structure, flagged with (a) adsorption site (b) intercalation sites and (c) Parity plot of SVR model evaluating the correspondence of predicted values and true values of rate-limited Gibbs free energy for OER.

Next, to identify the most important features among the selected features for OER descriptors, we use a permutation importance technique.⁵⁶ The permutation importance value of each feature is given in Fig. 8. All the selected features have positive permutation importance, which means that shuffling the feature values increases the error of the models or the feature has a positive influence on the model prediction. The choice of the adsorption site is the important feature by far.

Fig. 8 Permutation importance of the features for OER.

From the ML predictions, we have selected 10 structures with the minimum rate-limiting Gibbs free energy values (Table S9, SI), out of which 6 structures exhibit a binding energy greater than −5 eV. The structures, along with their rate-limiting Gibbs free energy value and binding energy, are given in Table 2. The selected structures have rate-limiting Gibbs free energy values more than 3.5 eV. These values are comparable with previous findings or Janus PtSSe-based vdWHs.²⁴ With this, we can narrow down our search to ten promising candidates from a dataset of 240 structures. Feature importance analysis unveils valuable insights into the catalytic activity descriptors. The selected structures also show optimistic binding energy values.

Table 2 The predicted adsorbed Janus PtXY/ζ-phosphorene (Z, M, I, A) heterostructures with rate-limiting Gibbs free energy and intercalated binding for OER. Z, M, I, and A represent the chalcogen side of the heterostructure, the intercalated transition metal atom, the intercalated site, and the adsorption site, respectively

Heterostructure	Rate-limiting Gibbs free energy change (eV)	Binding energy (eV)
PtSTe/zeta-P(S,V,I_1,A_2)	3.68	−6.13
PtSTe/zeta-P(S,Co,I_1,A_2)	3.69	−5.66
PtSTe/zeta-P(S,Sc,I_2,A_2)	3.67	−6.76
PtSTe/zeta-P(S,Fe,I_2,A_2)	3.66	−6.83
PtSTe/zeta-P(S,Co,I_2,A_2)	3.57	−6.33
PtSTe/zeta-P(S,Ni,I_2,A_2)	3.56	−5.62

---

We now calculate the projected electronic bands structure of pristine and intercalated PtSTe/ζ-phosphorene heterostructure as shown in Fig. S21(a) (SI). The corresponding band alignments of pristine heterostructure (Fig. S22, SI) reveals a type-II configuration, favourable to HER and OER activity. In contrast, the Fe- and Mn-intercalated PtSTe/ζ-phosphorene shows a metallic behaviour (Fig. S23, SI), arising from the introduction of states at the Fermi level by the intercalated atoms. Intercalation of a metal atom has been shown to improve photocatalytic activity by acting as a bridge between layers for charge transfer.⁵⁷

4. Conclusions

In this study, we investigated PtXY/ζ-phosphorene heterostructures intercalated with TM atoms, which exhibit promising catalytic activity for HER and OER. TM-intercalated PtSTe/ζ-phosphorene (Te side) exhibits remarkable performance for HER. We have successfully generated a dataset of about 240 adsorbed structures, and 120 have been selected for DFT calculation. After rigorous training of selected machine learning (ML) models on the DFT dataset, we predicted the Gibbs free energy for the entire dataset, yielding 13 candidates for HER and 6 candidates for OER, which satisfied the benchmark. The ML workflow showed exceptional efficiency. The best-performing model for HER is the Random Forest Regressor, which has shown an R² value of 0.83. In contrast, for OER, the SVR model has demonstrated the best performance. Furthermore, we conducted a feature analysis, which provides valuable insight into the catalyst's structural properties that act as descriptors of photocatalytic activity. Among these, the interlayer distance of the heterostructure and the bond length between the Pt and X atom emerged as the most influential factors that affect the Gibbs free energy predictions for HER. In the case of OER, the choice of adsorption site has emerged as a major descriptor of OER. Overall, the ML approach is crucial for identifying different properties that influence the Gibbs free energy for HER and OER processes, and for screening the most promising candidates for photocatalytic water splitting.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included in this article and in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma01011j.

Acknowledgements

This work is supported by the funding from DST-SERB (EEQ/2022/000047), Government of India. RS acknowledges UGC, New Delhi for financial assistance in the form of Senior Research fellowship. The results presented in this work were obtained using the computational resources at the Department of Physics at the Central University of Punjab. Insightful discussions with Nidhi Verma and Sangeeta Meena are highly acknowledged.

References

1. Z. Liu, et al., First-principles high-throughput screening of bulk piezo-photocatalytic materials for sunlight-driven hydrogen production, J. Mater. Chem. A, 2022, 10(35), 18132–18146.
2. D. C. Perera and J. C. Rasaiah, Computational Study of H2O Adsorption, Hydrolysis, and Water Splitting on (ZnO)₃ Nanoclusters Deposited on Graphene and Graphene Oxides, ACS Omega, 2023, 8(35), 32185–32203.
3. M. M. Rampai, et al., Hydrogen production, storage, and transportation: recent advances, RSC Adv., 2024, 14(10), 6699–6718.
4. Ab Jumah, A comprehensive review of production, applications, and the path to a sustainable energy future with hydrogen, RSC Adv., 2024, 14(36), 26400–26423.
5. D. Gunawan, et al., Materials Advances in Photocatalytic Solar Hydrogen Production: Integrating Systems and Economics for a Sustainable Future, Adv. Mater., 2024, 36(42), 2404618.
6. J. L. Fiorio, et al., Nanoengineering of Catalysts for Enhanced Hydrogen Production, Hydrogen, 2022, 3(2), 218–254.
7. S. Kim, N. T. Nguyen and C. W. Bark, Ferroelectric Materials: A Novel Pathway for Efficient Solar Water Splitting, Appl. Sci., 2018, 8(9), 1526.
8. M. A. Ahmed, S. A. Mahmoud and A. A. Mohamed, Interfacially engineered metal oxide nanocomposites for enhanced photocatalytic degradation of pollutants and energy applications, RSC Adv., 2025, 15(20), 15561–15603.
9. T. Ahasan, et al., Advanced TiO₂-Based Photocatalytic Systems for Water Splitting: Comprehensive Review from Fundamentals to Manufacturing, Molecules, 2025, 30(5), 1127.
10. L. Ju, et al., Janus transition metal dichalcogenides: a superior platform for photocatalytic water splitting, J. Phys.: Mater., 2020, 3(2), 022004.
11. L. Ju, et al., Single Selenium Atomic Vacancy Enabled Efficient Visible-Light-Response Photocatalytic NO Reduction to NH₃ on Janus WSSe Monolayer, Molecules, 2023, 28(7), 2959.
12. I. Ahmad, et al., Electronic, mechanical, optical and photocatalytic properties of two-dimensional Janus XGaInY (X, Y;= S, Se and Te) monolayers, RSC Adv., 2021, 11(28), 17230–17239.
13. X. Liu, et al., Polar materials for photocatalytic applications: A critical review, Interdiscip. Mater., 2024, 3(4), 530–564.
14. X. Gao, et al., Boosting the photon absorption, exciton dissociation, and photocatalytic hydrogen-and oxygen-evolution reactions by built-in electric fields in Janus platinum dichalcogenides, J. Mater. Chem. C, 2021, 9(42), 15026–15033.
15. R. Sant, et al., Synthesis of epitaxial monolayer Janus SPtSe, npj 2D Mater. Appl., 2020, 4(1), 41.
16. P. Jamdagni, et al., Photocatalytic properties of anisotropic β-PtX₂ (X = S, Se) and Janus β-PtSSe monolayers, Phys. Chem. Chem. Phys., 2022, 24(36), 22289–22297.
17. X. Wang, et al., Phase Engineering of 2D Violet/Black Phosphorus Heterostructure for Enhanced Photocatalytic Hydrogen Evolution, Small Struct., 2023, 4(10), 2300123.
18. Q. Li, et al., Strain-induced excellent photocatalytic performance in Z-scheme BlueP/γ-SnS heterostructures for water splitting, Phys. Chem. Chem. Phys., 2024, 26(13), 10289–10300.
19. P. Chauhan and A. Kumar, Photocatalytic water splitting and charge carrier dynamics of Janus PtSSe/ζ-phosphorene heterostructure, Sci. Rep., 2024, 14(1), 21618.
20. J. Su, et al., 2D/2D Heterojunctions for Catalysis, Adv. Sci., 2019, 6(7), 1801702.
21. B. Wang, et al., Bilayer MoSe2/HfS2 Nanocomposite as a Potential Visible-Light-Driven Z-Scheme Photocatalyst, Nanomaterials, 2019, 9(12), 1706.
22. F. Opoku, et al., Enhancing the photocatalytic hydrogen generation performance and strain regulation of the vertical GeI₂/C₂ N van der Waals heterostructure: insights from first-principles study, Energy Adv., 2022, 1(3), 146–158.
23. L. Ju, et al., Two-dimensional Janus van der Waals heterojunctions: A review of recent research progresses, Front. Phys., 2020, 16(1), 13201.
24. P. Jamdagni, et al., Janus PtSSe-based van der Waals heterostructures for direct Z-scheme photocatalytic water splitting, Int. J. Hydrogen Energy, 2024, 66, 268–277.
25. Z. Wang, et al., Ultrafast Charge Transfer in Lithium-Ion and Water-Intercalated MoS2/WS2 Heterostructures, Nano Lett., 2024, 24(51), 16383–16390.
26. W. Cui, et al., Alkali/alkaline-earth metal intercalated g-C₃N₄ induced charge redistribution and optimized photocatalysis: status and challenges, J. Phys.: Energy, 2021, 3(3), 032008.
27. C. Duan, et al., Machine Learning Models Predict Calculation Outcomes with the Transferability Necessary for Computational Catalysis, J. Chem. Theory Comput., 2022, 18(7), 4282–4292.
28. R. Singh, et al., Advances in computational design of van der Waals heterostructures for photocatalytic water splitting, J. Mater. Chem. A, 2025, 13(34), 27855–27906.
29. X. Liu, et al., High-throughput computation and machine learning screening of van der Waals heterostructures for Z-scheme photocatalysis, J. Mater. Chem. A, 2025, 13(8), 5649–5660.
30. M. Umer, et al., Machine learning assisted high-throughput screening of transition metal single atom based superb hydrogen evolution electrocatalysts, J. Mater. Chem. A, 2022, 10(12), 6679–6689.
31. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
33. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188–5192.
34. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465.
35. J. K. Nørskov, et al., Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892.
36. J. K. Nørskov, et al., Trends in the Exchange Current for Hydrogen Evolution, J. Electrochem. Soc., 2005, 152(3), J23.
37. F. Pedregosa, et al., Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
38. S. Van Der Walt, S. C. Colbert and G. Varoquaux, The NumPy Array: A Structure for Efficient Numerical Computation, Comput. Sci. Eng., 2011, 13(2), 22–30.
39. Q. Liu, Applications of machine learning in materials science: From a methodological point of view, Appl. Comput. Eng., 2024, 85(1), 262–271.
40. R. Palkovits and S. Palkovits, Using Artificial Intelligence To Forecast Water Oxidation Catalysts, ACS Catal., 2019, 9(9), 8383–8387.
41. K. Koc and A. P. Gurgun, Scenario-based automated data preprocessing to predict severity of construction accidents, Autom. Constr., 2022, 140, 104351.
42. B. M. Abraham, et al., Fusing a machine learning strategy with density functional theory to hasten the discovery of 2D MXene-based catalysts for hydrogen generation, J. Mater. Chem. A, 2023, 11(15), 8091–8100.
43. M. V. Jyothirmai, et al., Machine-Learning-Driven High-Throughput Screening of Transition-Metal Atom Intercalated g-C₃ N₄/MX₂ (M = Mo, W; X = S, Se, Te) Heterostructures for the Hydrogen Evolution Reaction, ACS Appl. Mater. Interfaces, 2024, 16(10), 12437–12445.
44. J. Qi, et al., Study on biomass and polymer catalytic co-pyrolysis product characteristics using machine learning and shapley additive explanations (SHAP), Fuel, 2025, 380, 133165.
45. X. Ge, et al., First-Principles Study of Structural and Electronic Properties of Monolayer PtX2 and Janus PtXY (X, Y = S, Se, and Te) via Strain Engineering, ACS Omega, 2023, 8(6), 5715–5721.
46. D. K. Nguyen, et al., Vacancy-and doping-mediated electronic and magnetic properties of PtSSe monolayer towards optoelectronic and spintronic applications, RSC Adv., 2024, 14(27), 19067–19075.
47. L. Pan, et al., Phonon Transport in Defect-Laden Bilayer Janus PtSTe Studied Using Neural-Network Force Fields, J. Phys. Chem. C, 2024, 128(26), 11024–11032.
48. Z. Liu, et al., Interlayer binding energy of graphite: A mesoscopic determination from deformation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(20), 205418.
49. T. Björkman, et al., van der Waals Bonding in Layered Compounds from Advanced Density-Functional First-Principles Calculations, Phys. Rev. Lett., 2012, 108(23), 235502.
50. M. V. Jyothirmai, et al., Machine-Learning-Driven High-Throughput Screening of Transition-Metal Atom Intercalated g-C₃N₄/MX₂ (M = Mo, W; X = S, Se, Te) Heterostructures for the Hydrogen Evolution Reaction, ACS Appl. Mater. Interfaces, 2024, 16(10), 12437–12445.
51. S. Guo, et al., Tuning interlayer spacing of MoS2 for enhanced hydrogen evolution reaction, J. Alloys Compd., 2021, 864, 158581.
52. J. Yi, et al., Phase and interlayer effect of transition metal dichalcogenide cocatalyst toward photocatalytic hydrogen evolution: The case of MoSe₂, Appl. Catal., B, 2019, 243, 330.
53. Y. Wang, et al., Rational design of transition metal-intercalated Ti-doped WS2 bilayers for enhanced hydrogen evolution catalysis: A synergistic DFT-machine learning approach, Electrochim. Acta, 2025, 538, 147011.
54. Y. Chang, et al., Robust Sandwiched B/TM/B Structures by Metal Intercalating into Bilayer Borophene Leading to Excellent Hydrogen Evolution Reaction, Adv. Energy Mater., 2023, 13(29), 2301331.
55. N. H. Attanayake, et al., Effect of Intercalated Metals on the Electrocatalytic Activity of 1T-MoS₂ for the Hydrogen Evolution Reaction, ACS Energy Lett., 2018, 3(1), 7–13.
56. A. Sabagh Moeini, F. Shariatmadar Tehrani and A. Naeimi-Sadigh, Machine Learning-Driven Band Gap Prediction/Classification and Feature Importance Analysis of Inorganic Perovskites, Int. J. Energy Res., 2025, 2025(1), 9974355.
57. F. Liu, et al., Boosting interlayer charge transfer in polymeric carbon nitride by Mo ions for efficient photocatalytic H₂ evolution, Energy Adv., 2024, 3, 231–240.

---