Deep recurrent neural networks with spectral-statistical fusion for industrial-grade steel alloy classification using femtosecond laser-ablation spark-induced breakdown spectroscopy
Kaiqiang
Que
ab,
Xiaoyong
He†
 *b,
Tingrui
Liang
b,
Zhenman
Gao
b and
Xi
Wu
*a
*b,
Tingrui
Liang
b,
Zhenman
Gao
b and
Xi
Wu
*a
aGuangxi Key Laboratory of Information Functional Materials and Intelligent Information Processing,School of Physics & Electronics, Nanning Normal University, Nanning 530001, China. E-mail: wuxiak@126.com
bSchool of Telecommunications Engineering & Intelligentization, Dongguan University of Technology, Dongguan 523808, China. E-mail: hxy@dgut.edu.cn
First published on 28th October 2025
Abstract
Building on the spectral stability and sensitivity of femtosecond laser-ablation spark induced breakdown spectroscopy (fs-LA-SIBS), and the pattern recognition capacity of deep learning, a DeepRNN spectral-statistical fusion framework is introduced for high-precision classification of industrial-grade steel alloys. The framework fuses two-channel raw spectra with statistical descriptors, and employs configurable bidirectional recurrent encoders (GRU, LSTM, and vanilla RNN) to capture temporal dependencies and shape a robust decision space under end-to-end training. Under a unified evaluation protocol, the DeepRNN framework models are benchmarked against CNN and Transformer, and against traditional machine learning methods including RF, SVM, and PLS-DA; wavelength contribution analysis is performed to identify discriminative regions and interpretable importance profiles. Under the DeepRNN framework, the three encoders consistently outperform CNN, Transformer, and traditional machine learning baselines on core metrics including accuracy, cross-split consistency, and perturbation robustness, with average accuracy improved by approximately 2.35 to 3.50 percentage points compared to CNN and Transformer, and by 6.58 to 15.40 percentage points relative to traditional baselines. They also achieve favorable trade-offs among accuracy, efficiency, and deployability, with wavelength importance aligning with physically meaningful line structures. This sensor-intelligent system enables scenario-oriented deployment: vanilla RNN is chosen when accuracy is paramount; GRU is suitable for low-latency, energy-constrained online monitoring; and LSTM is preferred for the most conservative optimization trajectory and robustness under complex conditions, providing a scalable pathway for real-time industrial alloy identification and quality control.
1. Introduction
The imperative for rapid, high-fidelity classification of industrial steel alloys1 stems from stringent quality demands in aerospace,2 automotive,3 and energy infrastructure,4 where compositional integrity is non-negotiable. While established techniques like X-ray fluorescence (XRF)5 and spark optical emission spectroscopy (OES)6 provide elemental analysis, their constraints in real-time capability, cost, and trace element sensitivity impede deployment for dynamic process control. Laser-induced breakdown spectroscopy (LIBS) has emerged as a transformative solution, enabling rapid, multi-elemental analysis with minimal sample preparation,7–10 driving applications from environmental monitoring11 to industrial quality assurance.12However, unlocking LIBS's full potential for robust, high-precision classification of complex alloys necessitates overcoming challenges in spectral stability and the intricate interpretation of high-dimensional data. Machine learning (ML), particularly deep learning (DL), has become pivotal in addressing these hurdles.13 Moving beyond foundational methods (PLS-DA,14,15 SVM,16,17 RF18,19), sophisticated DL architectures are setting new benchmarks. Optimized artificial neural networks (ANN) have achieved remarkable accuracy (>95%) in ceramic provenance studies,20 while deep belief networks (DBN) significantly outperformed traditional ANN in classifying diverse steel types.21 Convolutional neural networks (CNNs) excel at extracting spatial features from raw spectra, demonstrably reducing prediction errors in soil analysis.22 Recurrent structures and attention mechanisms, exemplified by iTransformer-BiLSTM models, effectively decode complex temporal correlations and non-linearities, achieving exceptional quantification performance (R2 > 0.98, RMSE <0.1 wt%) for rare earth elements.23 Furthermore, innovative multimodal fusion strategies, such as combining LIBS with plasma acoustic signals, have substantially boosted classification accuracy for steels.24 Collectively, these advances underscore the critical role of advanced model architectures and intelligent feature/data utilization in elevating LIBS-based classification.
Femtosecond laser-induced breakdown spectroscopy (fs-LIBS) employs ultrashort pulses to minimize thermal effects and plasma interference, substantially advancing analytical fidelity. The femtosecond laser's extreme peak intensity and narrow pulse width enable rapid energy deposition, promoting immediate ionization and dissociation with negligible plasma shielding. This suppresses blackbody radiation and accelerates plasma cooling, shortening plasma lifetime. Consequently, fs-LIBS offers enhanced spectral line discernibility, richer emission features, and a markedly reduced continuous background compared to ns-LIBS – resulting in significantly improved signal intensity and signal-to-background ratio. The ultrashort interaction also diminishes background noise, allowing near-instantaneous detection. Furthermore, direct vaporization without melting minimizes sample damage and material deposition. These attributes collectively enable superior reproducibility,25 peak power,26 and spatial resolution27 over ns-LIBS. This translates to enhanced resilience against complex matrices, as evidenced by significantly lower prediction errors (<20% vs. 35% for ns-LIBS) in plant analysis.28 Building decisively on this, femtosecond laser ablation spark-induced breakdown spectroscopy (fs-LA-SIBS)29–31 synergizes femtosecond ablation with spark discharge re-excitation, dramatically amplifying emission intensity and analytical sensitivity. Critically, He et al. demonstrated that fs-LA-SIBS achieved 4–12-fold lower detection limits for trace elements in steel alloys compared to fs-LIBS alone, alongside >14-fold increases in calibration slopes, enabling high spatial resolution and simultaneous multi-element analysis at kHz repetition rates32 – positioning it as an exceptionally powerful technique for industrial high-sensitivity detection.
Capitalizing on the spectral stability and sensitivity of fs-LA-SIBS, along with deep learning's strengths in pattern recognition, this study presents a DeepRNN spectral-statistical fusion framework for high-precision identification of industrial-grade steel alloys. The framework integrates two-channel raw spectra with statistical descriptors including peak count, mean peak intensity, global mean, and global standard deviation, and employs configurable bidirectional recurrent encoders (GRU, LSTM, and vanilla RNN) to capture temporal dependencies, shaping a robust decision space under end-to-end training. Under a unified evaluation protocol, the framework is benchmarked against CNN, Transformer, and traditional machine learning methods including RF, SVM, PLS-DA, with wavelength contribution analysis used to identify discriminative regions and interpretable importance profiles. Under the DeepRNN framework, all three encoders consistently outperform CNN, Transformer, and traditional baselines across core metrics like accuracy, cross-split consistency, and perturbation robustness, while balancing accuracy, efficiency, and deployability. Wavelength importance aligns with physically meaningful line structures, supporting scenario-specific deployment: vanilla RNN for accuracy priority, GRU for low-latency, energy-constrained online monitoring, and LSTM for conservative optimization trajectories and robustness under complex conditions, thus providing a scalable technical approach for real-time industrial alloy inspection and quality management.
2. Experimental setup and methodology
2.1 Experimental setup
The fs-LA-SIBS system integrates a femtosecond laser ablation module, spark discharge excitation, and high-resolution spectral detection (Fig. 1). A Ti:sapphire ultrafast laser (central wavelength: 800 nm, pulse width: 35 fs, repetition rate: 1 kHz, maximum single-pulse energy: 7.5 mJ) serves as the ablation source. The collimated laser beam (diameter: 10 mm) is focused onto the surface of steel alloy samples using a plano-convex lens (L1, f = 150 mm) to generate plasma. Samples are mounted on a programmable X–Y translation stage (speed: 3 mm s−1) and electrically isolated via an acrylic plate. | ||
| Fig. 1 Schematic diagram of the femtosecond laser ablation spark-induced breakdown spectroscopy (fs-LA-SIBS) experimental setup. | ||
The synchronized spark discharge unit, triggered by plasma generation, comprises a DC high-voltage source (10 kV, 0.2 A), a current-limiting resistor (R = 100 kΩ), a 10 nF capacitor bank, and a tungsten needle anode tilted at 45° (2 mm from the sample). Plasma emission is collected and collimated by two plano-convex quartz lenses (L2: f = 100 mm; L3: f = 100 mm), then guided through a fiber-optic probe into a triple-channel spectrometer. The spectrometer covers a wavelength range of 200–500 nm, divided into three sub-ranges (200–317 nm, 317–415 nm, and 415–500 nm), each equipped with a 2048-pixel CCD detector (spectral resolution < 0.1 nm) for precise atomic line detection.
2.2 Steel alloy sample and data preprocessing
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 high-resolution continuous spectral samples across the 200–500 nm range. The nine classes demonstrated near-perfect balance (disparity ratio: 0.8%), and post-calibration class proportions were constrained to 10.8–11.6%, eliminating bias and ensuring data representativeness. A stratified 5
804 high-resolution continuous spectral samples across the 200–500 nm range. The nine classes demonstrated near-perfect balance (disparity ratio: 0.8%), and post-calibration class proportions were constrained to 10.8–11.6%, eliminating bias and ensuring data representativeness. A stratified 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 split allocated 50%, 10%, and 40% of the data to training, validation, and test sets, respectively. To rigorously evaluate model robustness, the test set was further partitioned into four 10%-sized subsets. This design enabled multi-scenario validation of model stability and generalization, offering granular insights for performance optimization while maintaining statistical reliability.
4 split allocated 50%, 10%, and 40% of the data to training, validation, and test sets, respectively. To rigorously evaluate model robustness, the test set was further partitioned into four 10%-sized subsets. This design enabled multi-scenario validation of model stability and generalization, offering granular insights for performance optimization while maintaining statistical reliability.
| No. | Sample ID | Al | Cr | Cu | Mn | Mo | Ni | V |
|---|---|---|---|---|---|---|---|---|
| 1 | ZBG021a | 0.872 | 1.510 | 0.029 | 0.443 | 0.175 | 0.025 | — |
| 2 | ZBG214a | 0.017 | 1.040 | 0.029 | 0.387 | 0.016 | 0.025 | — |
| 3 | ZBG216a | — | 0.034 | 0.036 | 0.858 | — | 0.0086 | 0.002 |
| 4 | ZBG217a | — | 4.020 | 0.092 | 0.232 | 0.013 | 0.076 | 1.180 |
| 5 | ZBG235 | — | 4.100 | 0.059 | 0.184 | 1.080 | 0.068 | 4.050 |
| 6 | ZBG247 | 0.032 | 0.126 | 0.056 | 1.160 | 0.006 | 0.017 | 0.096 |
| 7 | ZBG251 | 0.011 | 0.034 | 0.017 | 0.568 | — | 0.012 | 0.003 |
| 8 | ZBG224 | — | 0.151 | 0.018 | 1.210 | — | 0.018 | — |
| 9 | ZBG234a | — | 4.210 | 0.114 | 0.284 | 3.080 | 0.146 | 1.520 |
2.2.2.1 Data loading and normalization. Spectral data comprising wavelength (λ) and intensity (I) values were loaded from CSV files and normalized per channel using min–max scaling to the interval [0, 1] via:
 | (1) |
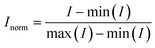 | (2) |
2.2.2.2 Peak feature extraction. A peak detection algorithm identified significant peaks in intensity sequences using a threshold:
| T = 0.8 × max(Inorm) | (3) |
Key metrics of the peak set P were calculated:
| Npeaks = |P| | (4) |
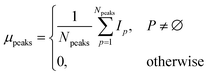 | (5) |
2.2.2.3. Global statistical features. Statistical descriptors of normalized intensity sequences were computed:
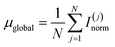 | (6) |
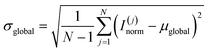 | (7) |
These equations define global statistics where N is the total number of data points in the spectral sequence. I(j)norm represents the normalized intensity value at position j. µglobal calculates the arithmetic mean of all normalized intensity values, while σglobal measures their standard deviation, quantifying the dispersion around the mean.
2.2.2.4. Feature fusion. A bimodal feature matrix was constructed:
| Xspectral = stack([λnorm, Inorm]) ∈ RN×2 | (8) |
| Xstats = [Npeaks, µpeaks, µglobal, σglobal] ∈ R4 | (9) |
The resulting spectral feature matrix Xspectral preserves the sequential information in an N × 2 format, while the statistical feature vector Xstats encapsulates the four extracted characteristics: peak count, average peak intensity, global mean, and global standard deviation.
2.3 Methodology
The DeepRNN framework, illustrated in Fig. 2, comprises five core components for spectral sequence classification:(1) Input layer: the model ingests two complementary inputs: (i) a two-channel spectral sequence [λ, I], where wavelength and intensity are min–max normalized to [0, 1]; and (ii) a four-dimensional statistical descriptor comprising peak count, mean peak intensity, global mean intensity, and global intensity standard deviation. The sequence captures local line shapes and continuum trends, whereas the statistics summarize global distributional properties.
(2) Recurrent layer: to capture sequential dependencies and spectral context, configurable recurrent encoders (GRU, LSTM, and vanilla RNN) are employed with bidirectional processing and stacked depth (default hidden size 256). Inter-layer dropout (rate = 0.2) is used when depth > 1. The final time-step output from both directions is extracted as a global temporal representation that aggregates pre-peak and post-peak contextual information.
(3) Feature fusion layer: the temporal encoding is concatenated with the four-dimensional statistical vector to form a comprehensive representation, enabling the classifier to learn, end-to-end, how to weight dynamic sequence patterns versus global distributional cues.
(4) Fully connected layers: a hierarchical MLP (512 → 256 → 128 → 64) with ReLU and dropout (rate = 0.2) progressively condenses the fused features into a highly discriminative subspace. A final linear layer projects to the number of target classes.
(5) Output layer: the network outputs class logits. During training, a standard multi-class cross-entropy is typically employed (softmax applied implicitly to logits); probabilities at inference can be obtained by explicitly applying softmax. Parameters are optimized end-to-end via backpropagation.
2.4 Computational environment
All computational experiments were conducted on a hardware platform equipped with 64 GB DDR5 RAM, a 12th Gen Intel Core i5-12500T processor, and an NVIDIA RTX A2000 GPU (12 GB VRAM). Model development and training utilized the Windows 11 Pro operating system, Python 3.12.9, and the PyCharm Professional 2023.2.8 integrated development environment. GPU acceleration was enabled via PyTorch 2.6.0 with CUDA 12.4 support, ensuring full utilization of parallel computing capabilities.3. Results and discussion
3.1 Spectral acquisition protocol
Fig. 3 displays the characteristic elemental spectra of steel alloys obtained using fs-LA-SIBS, with Table 2 listing the identified spectral lines based on NIST database and literature ref. 33 and 34. System characterization revealed signal detection limitations in the 200–300 nm range due to reduced transmission efficiency of optical components. Employing a compact triple-channel fiber-optic spectrometer (CCD detector) with 10 ms integration time per channel and 500-pulse accumulation (0.5 mJ per pulse) effectively suppressed noise, while a 2.5 kV/10 nF discharge circuit maintained plasma stability. The non-gated detection mode eliminated temporal synchronization complexities, enabling high-throughput acquisition of up to 30 spectra per second – establishing a robust hardware foundation for rapid multi-element analysis of steel alloys.| Significant element | Main spectral lines (nm) |
|---|---|
| Al | 237.312, 260.089, 308.215, 309.271, 394.401, 396.152 |
| Cr | 357.868, 425.433, 427.480, 428.973 |
| Cu | 324.754, 327.396 |
| Mn | 257.610, 279.482, 403.076, 403.307, 403.449, 404.136 |
| Mo | 202.030, 313.259, 379.825, 386.410 |
| Ni | 341.476, 345.846, 346.165, 346.346, 349.296, 352.454 |
| V | 292.402, 437.923, 438.998, 440.851 |
3.2 Training process of three RNN variants under the DeepRNN framework
Fig. 4a–c depict the training dynamics of GRU, LSTM, and vanilla RNN under the DeepRNN framework. The three models share a common pattern: rapid loss descent followed by smooth refinement and a low plateau. Validation accuracy and Macro-F1 rise concurrently and nearly overlap in the later stage, indicating balanced class improvements and robust generalization. The training loss lying slightly above the validation loss is expected, as dropout is active during training, injecting stochastic noise and increasing the expected training loss, while being disabled during validation, resulting in smoother and lower estimates. In terms of trajectory shapes, vanilla RNN reaches the plateau earlier, with train and validation losses being closer in the later phase, whereas GRU and LSTM exhibit smoother trajectories but settle at a slightly lower plateau. | ||
| Fig. 4 Training dynamics of three RNN architectures under the DeepRNN framework: (a) GRU, (b) LSTM, and (c) vanilla RNN. | ||
In conjunction with Table 3 and architectural factors, the three DeepRNN framework models show a clear profile of performance and efficiency under an identical protocol. Vanilla RNN uses ungated linear recurrence that fits strongly and plateaus early at a moderate computational cost and reaches an accuracy of 99.00% with a training time of 5911.60 s. GRU employs lightweight update and reset gates to balance temporal modeling with reduced parameters and computation and achieves an accuracy of 97.85% with the fastest training time of 1604.83 s, offering the best efficiency. LSTM with input forget output gates and a cell state captures long range dependencies robustly and trains more smoothly and conservatively, reaching an accuracy of 97.99% with a training time of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 529.67 s. Accordingly, choose vanilla RNN when accuracy is paramount, choose GRU when efficiency and real time operation are critical, and choose LSTM when robust long range dependency modeling and smoother optimization are desired.
529.67 s. Accordingly, choose vanilla RNN when accuracy is paramount, choose GRU when efficiency and real time operation are critical, and choose LSTM when robust long range dependency modeling and smoother optimization are desired.
| Model | Average accuracy | Average F1-score | Training time (s) |
|---|---|---|---|
| a GRU, LSTM and vanilla RNN under the DeepRNN framework were evaluated under identical hyperparameters: epochs = 300, dropout = 0.2, learning rate = 5 × 10−4, batch size = 512; these models used the same preprocessing, split, random seed, optimizer, and classification head to guarantee a fair comparison. | |||
| GRU | 97.85% ± 0.34% | 97.86% ± 0.34% | 1604.83 |
| LSTM | 97.99% ± 0.34% | 97.99% ± 0.34% | 10 529.67 |
| RNN | 99.00% ±0.13% | 99.01% ±0.13% | 5911.60 |
3.3 Confusion matrices of three RNN variants under the DeepRNN framework
The confusion matrices for the three RNN variants under the DeepRNN framework are computed as a single global matrix by pooling per-sample predictions across all four test sets under a unified label mapping, which reduces split-specific bias and variance and yields a more reliable view of cross-split error structure and robustness.Under the DeepRNN framework, all three models exhibit strong diagonal dominance, and the micro-averaged and macro-averaged ROC curves are nearly unity. Vanilla RNN shows the sparsest off-diagonal entries; the most salient mistakes are class 0 predicted as class 7 (40 cases) and class 6 predicted as class 5 (34 cases), with most others being single-digit counts. In the low-FPR inset, its class curves cluster closest to the top-left corner with the smallest dispersion; the legend reports Micro-avg AUC = 0.9999 and Macro-avg AUC = 0.9999. GRU presents more visible off-diagonal mass, with representative errors including class 2 predicted as class 7 (41 cases), class 5 as class 6 (37 cases), and class 0 as class 1 (34 cases); its low-FPR curves are more spread out, with Micro-avg AUC = 0.9998 and Macro-avg AUC = 0.9997. LSTM lies between the two: key errors are class 6 predicted as class 5 (38 cases), class 0 as class 7 (27 cases), and class 5 as class 1 (31 cases); its low-FPR stability is better than GRU but slightly below vanilla RNN, with Micro-avg AUC = 0.9997 and Macro-avg AUC = 0.9996 (Fig. 5). Overall, while all three models achieve near-perfect ROC performance, ranking by off-diagonal sparsity and low-FPR stability places the vanilla RNN first, followed by LSTM and then GRU. This difference is primarily attributable to the task's sequence length and quasi-stationary dynamics: the plain recurrent update provides a stronger inductive bias and smoother decision boundaries, yielding more robust low-FPR calibration, whereas LSTM/GRU gating introduces mild over-suppression and variance in this setting, leading to slightly more near-boundary errors.
 | ||
| Fig. 5 Confusion matrices and ROC curves for three RNN variants under the DeepRNN framework: (a) GRU; (b) LSTM; (c) vanilla RNN. | ||
3.4 Significance of statistical features
To clarify the model's decision-making mechanism, a gradient-times-input attribution method is employed to quantify the contribution of each wavelength to the predicted class, with attributions averaged over samples. The L2 norm of RNN hidden states acts as a consistency check. Fig. 6 presents the wavelength contribution curves of GRU, LSTM, and vanilla RNN within the 300–500 nm range: contributions are nearly zero below approximately 360 nm, rise sharply beyond 430 nm, and exhibit several distinct peaks between 450 and 490 nm, indicating key discriminative wavelength bands. Vanilla RNN shows the highest and most fluctuating peaks, suggesting greater sensitivity to fine-scale variations; GRU increases and remains elevated around 470–490 nm, consistent with its gate-controlled mechanism that focuses on salient signals; LSTM curve is smoother with slightly lower peaks, reflecting stronger suppression of noise and artifacts from long-range dependencies. The concurrent increase in contributions beyond 430 nm across all three models indicates robust spectral cues shared by different architectures. From an architectural perspective, the sequence encoder maps wavelength and intensity into hidden representations, and the final classifier is most sensitive near the decision boundary; thus, these peaks correspond to wavelengths that exert the strongest influence on class scores.t-SNE was employed to project the fused penultimate representations from each DeepRNN framework models, with the aim of evaluating class separability, intra-class compactness, and boundary overlap under realistic spectral variability. Fig. 7 demonstrates that all models effectively structure the feature space overall. Vanilla RNN variant forms tighter, more well-separated clusters with clearer boundaries, whereas GRU and LSTM exhibit broader dispersion and greater overlap between adjacent grades – consistent with stronger gating mechanisms that smooth fine spectral contrasts and soften nearby decision boundaries. Local mixing near cluster edges aligns with the chemical similarity of adjacent grades rather than model instability. The dual-branch design, which concatenates the sequence encoder state with explicit statistical descriptors, yields structured manifolds, highlighting the complementary contributions of global temporal context and statistical features.
 | ||
| Fig. 7 Comparative t-SNE analysis under the DeepRNN framework: (a) GRU, (b) LSTM, and (c) vanilla RNN. | ||
As shown in Fig. 8, the ablation study indicates that explicit statistical features are crucial to model discriminative power. When explicit statistics are concatenated with the encoder state, GRU achieves 97.85% accuracy and 97.86% average F1-score, but drops to 11.65% and 2.32% without them. LSTM remains relatively resilient at 88.63% and 88.66% without statistics and rises to 97.99% and 97.99% with them, reflecting stronger modeling of long range dependencies and noise suppression. Vanilla RNN falls from 99.00% and 99.01% to 11.54% and 2.30%, indicating heavier reliance on statistical priors. Architecturally, LSTM's input, forget, and output gates together with its near linear cell state enable additive updates and stable gradient flow, preserving long term context and dampening high frequency perturbations. In industrial spectral applications, these explicit statistics supply stable global profiles and key peak cues that complement temporal representations, markedly improving inter class separability and class balance so that accuracy and average F1-score for all three architectures also increase substantially.
As shown in Fig. 9, we estimate relative contributions using a gradient-based attribution: we measure the output sensitivity to each of the four statistical features, average over the validation set, and normalize to percentages. The descriptors display a consistent hierarchy across models: peak count dominates in GRU, LSTM, and vanilla RNN with 81.98%, 74.15%, and 85.34%, respectively; peak intensity mean contributes 12.88%, 18.77%, and 9.74%; mean intensity and std. intensity are minor at 3.49%, 4.74%, 3.16% and 1.65%, 2.33%, 1.76%. These patterns align with the ablation findings: peak structure and counting provide the primary discriminative prior, while amplitude statistics further tighten decision boundaries; the explicit statistics branch markedly enhances all architectures. Specifically, vanilla RNN shows the strongest dependence and suffers the largest drop when the statistics are removed; LSTM remains comparatively robust without statistics yet gains substantially when peak count and amplitude cues are fused, evidencing complementarity between gated temporal encoding and explicit statistics; additionally, GRU's update and reset gates favor modeling short-to-medium dependencies, placing its no-statistics performance between LSTM and vanilla RNN, while fusing peak count and peak intensity mean noticeably sharpens its decision boundaries, yielding consistent improvements with lower parameter and compute costs.
3.5 Comparison with deep learning models
Under the same dataset and standardized preprocessing pipeline, two representative deep-learning baselines are compared: a 1D CNN and a Transformer. The CNN consists of two 1D convolutional blocks, followed by global average pooling; the pooled feature is concatenated with four statistical descriptors and fed into fully connected layers for classification. The Transformer linearly embeds the two-channel spectra with learnable positional encodings, passes through two Transformer-encoder layers, performs temporal averaging, and concatenates the result with the statistical features before classification. To ensure a fair comparison with DeepRNN, both deep models are trained with the same setup: epochs = 300, dropout = 0.2, learning rate = 5 × 10−4, and batch size = 512. Across four test splits, the Transformer slightly outperforms the CNN: the CNN achieves an average accuracy of 94.91% and an average F1-score of 94.94%, whereas the Transformer reaches 95.50% and 95.48%, with more consistent performance across splits (Table 4).| Model | Average accuracy | Average F1-score |
|---|---|---|
| CNN | 94.91% ± 0.15% | 94.94% ± 0.15% |
| Transformer | 95.50% ± 0.23% | 95.48% ± 0.23% |
Fig. 10a and b show strong diagonal dominance in both confusion matrices, with only a few systematic errors among neighboring classes. For the CNN, the most salient errors are class 5 predicted as class 6 (276 cases) and class 7 predicted as class 0 (153 cases); errors are concentrated on a few class pairs with large counts, forming dominant off-diagonal entries. The transformer reduces these dominant errors without introducing many new ones, yielding overall sparser off-diagonal patterns with only a few scattered low-count entries; its two most frequent errors are class 8 predicted as class 3 (86 cases) and class 6 predicted as class 5 (63 cases). The multi-class ROC results are consistent: the CNN attains a micro-average AUC of 0.9987 and a macro-average AUC of 0.9994, whereas the transformer reaches 0.9979 and 0.9984. Both the main plots and the low-FPR inset indicate high TPR when FPR < 0.05; however, the inset shows the CNN curves lying closer to the top-left corner with smaller class-to-class dispersion, suggesting slightly better stability in the low-FPR regime than the Transformer. Regarding the causes, the concentrated off-diagonal entries indicate class pairs with closely spaced decision boundaries; the CNN's local-convolutional inductive bias is robust when local evidence suffices but is more prone to confusion where stronger global context is required. By contrast, the Transformer's self-attention integrates long-range spectral cues and yields more optimal point decisions around the chosen threshold – thus achieving higher accuracy – whereas AUC evaluates probability ranking and robustness across all thresholds, so it can be slightly lower even when accuracy is higher.
Under the same training protocol, the DeepRNN framework models improves average accuracy and F1 by about 2–4 percentage points over CNN and transformer. Its advantage stems from an inductive bias toward sequential/spectral continuity and gating that preserves long-range dependencies, which stabilizes discrimination near close class boundaries and mitigates overfitting with limited data. Overall, considering the trade-off among performance, efficiency, and stability, the DeepRNN framework is preferred in this study, with CNN/Transformer used as enhancements or ensemble options in specific scenarios.
3.6 Comparison with traditional machine learning methods
A significant performance gap between traditional machine learning methods and the DeepRNN framework models was demonstrated in Table 5 under identical datasets and standardized preprocessing protocols. Following feature engineering optimization and hyperparameter tuning (SVM: RBF kernel with C = 0.3; RF: 100 trees with max_depth = 10; PLS-DA: 30 latent components), traditional models including RF (91.27%), SVM (86.92%), and PLS-DA (84.60%) were observed to exhibit markedly lower classification accuracy compared to the DeepRNN framework models, representing a 6.58–15.40 percentage point improvement over conventional approaches. This performance disparity was attributed to fundamental differences in modeling paradigms, where optimized traditional methods relying on static statistical features and shallow classifiers were found to inadequately capture nonlinear temporal dynamics, while the DeepRNN framework successfully implemented dynamic temporal context updates through statistically initialized hidden states, enabling joint optimization of both the feature space and the temporal domain.| Model | Average accuracy | Average F1-score |
|---|---|---|
| SVM | 86.92% ± 0.49% | 87.21% ± 0.49% |
| PLS-DA | 84.60% ± 0.34% | 84.60% ± 0.35% |
| RF | 91.27% ± 0.40% | 91.27% ± 0.40% |
As shown in Fig. 11, compared with the deep learning models, the traditional methods (SVM, PLS-DA, and RF) display more dispersed off-diagonal entries in their confusion matrices, with more prevalent confusions among neighboring classes. In the low-FPR insets, class curves are less tightly clustered near the top-left corner, indicating weaker stability; this is most pronounced for PLS-DA, while SVM and RF partly mitigate it but still lag behind. Consistently, their macro-average AUCs are lower than those of the deep Learning models, pointing to inferior cross-class consistency and probability-ranking robustness. The gap primarily reflects representational capacity and inductive bias: PLS-DA is constrained by linear projections and struggles with complex or overlapping boundaries; SVM enhances nonlinearity through kernels yet remains limited in modeling long-range dependencies and contextual composition for sequential/spectral data; RF captures nonlinearity via tree ensembles but tends to have weaker probability calibration and limited resolution near fine decision boundaries. In contrast, deep Learning models (CNN/Transformer/DeepRNN) encode multi-scale local-to-global cues and temporal dependencies more effectively, yielding stronger diagonal concentration, better low-FPR stability, and superior macro/micro ROC performance.
 | ||
| Fig. 11 Confusion matrices and ROC curves for Traditional machine learning models (a) SVM; (b) PLS-DA; (c) RF. | ||
4. Conclusion
Leveraging the high stability and sensitivity of fs-LA-SIBS, and combining the deep fusion strategy of spectral temporal and statistical features, the framework presented in this study achieves dual advancements in methodology and engineering for rapid and high-fidelity identification of industrial-grade steel alloys; by tightly coupling bidirectional recurrent units (LSTM, GRU, and vanilla RNN) with four-dimensional statistical descriptors (peak count, mean peak intensity, global mean, and standard deviation), the framework simultaneously models the temporal dependencies of plasma evolution and global spectral distribution; under a unified evaluation protocol, the average accuracy of all three recurrent units exceeds that of CNN and Transformer, and significantly outperforms traditional machine learning baselines (RF, SVM, PLS-DA), with overall accuracy ranging from 97.85% to 99.00% and both macro-average AUC and micro-average AUC exceeding 0.999; compared to CNN and Transformer, the average accuracy is improved by approximately 2.35 to 3.50 percentage points, and relative to traditional baselines, the improvement ranges from 6.58 to 15.40 percentage points; ablation and attribution analyses confirm that explicit statistical features provide key discriminative priors, while wavelength contributions align with physically meaningful line structures, supporting trustworthy interpretability; considering trade-offs among accuracy, latency, and energy consumption, clear deployment guidance is provided: vanilla RNN is recommended when accuracy is paramount, GRU is suitable for low-latency, energy-constrained online monitoring, and LSTM is preferred when robustness under complex conditions is prioritized; this work establishes a scalable sensor-intelligence paradigm for industrial spectral analysis, which can be extended to broader elemental analysis and multimodal spectroscopy, and future research will focus on cross-instrument generalization, weakly supervised and low-data learning, continual and incremental updates, and resource-aware edge deployment to further enhance applicability in real production lines.Author contributions
Kaiqiang Que: methodology, software, formal analysis, investigation, writing-original draft. Xiaoyong He: conceptualization, supervision, writing-review & editing, resources, and funding acquisition. Tingrui Liang: data curation, formal analysis, software, and validation. Zhenman Gao: data curation, software, visualization, and funding acquisition. Xi Wu: supervision, validation, project administration, and funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The data that support the findings of this work are available upon reasonable request from the author.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grants 62204038, 62405052 and 62403132, the Natural Science Foundation of Guangxi Province under Grants 2025GXNSFAA069379.References
- P. Korotaev and A. Yanilkin, Steels classification by machine learning and Calphad methods, Calphad, 2023, 82, 102587 CrossRef CAS.
- M. V. Maisuradze, Y. V. Yudin, A. A. Kuklina and D. I. Lebedev, Formation of Microstructure and Properties During Isothermal Treatment of Aircraft Building Steel, Metallurgist, 2022, 65, 1008–1019 CrossRef CAS.
- R. Rana and S. B. Singh, Automotive Steels: Design, Metallurgy, Processing and Applications, 2016 Search PubMed.
- L. Hughes, N. Bristow, T. Korochkina, P. Sanchez, D. Gomez and J. Kettle, et al., Assessing the potential of steel as a substrate for building integrated photovoltaic applications, Appl. Energy, 2018, 229, 209–223 CrossRef.
- T. D. T. Oyedotun, X-ray fluorescence (XRF) in the investigation of the composition of earth materials: a review and an overview, Geol. Ecol. Landsc., 2018, 2, 148–154 Search PubMed.
- M. A. Khater, Laser-induced breakdown spectroscopy for light elements detection in steel: State of the art, Spectrochim. Acta, Part B, 2013, 81, 1–10 CrossRef CAS.
- R. Noll, C. Fricke-Begemann, S. Connemann, C. Meinhardt and V. Sturm, LIBS analyses for industrial applications – an overview of developments from 2014 to 2018, J. Anal. At. Spectrom., 2018, 33, 945–956 RSC.
- T. Hussain and M. A. Gondal, Laser induced breakdown spectroscopy (LIBS) as a rapid tool for material analysis, J. Phys.: Conf. Ser., 2013, 439, 012050 CrossRef CAS.
- J. M. Tucker, M. D. Dyar, M. W. Schaefer, S. M. Clegg and R. C. Wiens, Optimization of laser-induced breakdown spectroscopy for rapid geochemical analysis, Chem. Geol., 2010, 277, 137–148 CrossRef CAS.
- R. S. Harmon, F. C. DeLucia, C. E. McManus, N. J. McMillan, T. F. Jenkins and M. E. Walsh, et al., Laser-induced breakdown spectroscopy – An emerging chemical sensor technology for real-time field-portable, geochemical, mineralogical, and environmental applications, Appl. Geochem., 2006, 21, 730–747 CrossRef CAS.
- J. B. Sirven, P. Dewalle, C. Quéré, V. Fauvet, M. Tabarant and S. Motellier, et al., Assessment of exposure to airborne carbon nanotubes by laser-induced breakdown spectroscopy analysis of filter samples, J. Anal. At. Spectrom., 2017, 32, 1868–1877 RSC.
- Q. Zeng, G. Chen, X. Chen, B. Wang, B. Wan and M. Yuan, et al., Rapid online analysis of trace elements in steel using a mobile fiber-optic laser-induced breakdown spectroscopy system, Plasma Sci. Technol., 2020, 22, 074013 CrossRef CAS.
- D. Zhang, H. Zhang, Y. Zhao, Y. Chen, C. Ke and T. Xu, et al., A brief review of new data analysis methods of laser-induced breakdown spectroscopy: machine learning, Appl. Spectrosc. Rev., 2022, 57, 89–111 CrossRef CAS.
- J. Lin, X. Lin, L. Guo, Y. Guo, Y. Tang and Y. Chu, et al., Identification accuracy improvement for steel species using a least squares support vector machine and laser-induced breakdown spectroscopy, J. Anal. At. Spectrom., 2018, 33, 1545–1551 RSC.
- W. Zhang, Z. Zhuo, P. Lu, J. Tang, H. Tang and J. Lu, et al., LIBS analysis of the ash content, volatile matter, and calorific value in coal by partial least squares regression based on ash classification, J. Anal. At. Spectrom., 2020, 35, 1621–1631 RSC.
- N. C. Dingari, I. Barman, A. K. Myakalwar, S. P. Tewari and M. Kumar Gundawar, Incorporation of Support Vector Machines in the LIBS Toolbox for Sensitive and Robust Classification Amidst Unexpected Sample and System Variability, Anal. Chem., 2012, 84, 2686–2694 CrossRef CAS PubMed.
- E. Képeš, J. Vrábel, O. Adamovsky, S. Střítežská, P. Modlitbová and P. Pořízka, et al., Interpreting support vector machines applied in laser-induced breakdown spectroscopy, Anal. Chim. Acta, 2022, 1192, 339352 CrossRef.
- T. Zhang, D. Xia, H. Tang, X. Yang and H. Li, Classification of steel samples by laser-induced breakdown spectroscopy and random forest, Chemom. Intell. Lab. Syst., 2016, 157, 196–201 CrossRef CAS.
- L. Zhan, X. Ma, W. Fang, R. Wang, Z. Liu and Y. Song, et al., A rapid classification method of aluminum alloy based on laser-induced breakdown spectroscopy and random forest algorithm, Plasma Sci. Technol., 2019, 21, 034018 CrossRef CAS.
- A. Ramil, A. J. López and A. Yáñez, Application of artificial neural networks for the rapid classification of archaeological ceramics by means of laser induced breakdown spectroscopy (LIBS), Appl. Phys. A:Mater. Sci. Process., 2008, 92, 197–202 CrossRef CAS.
- G. Chen, Q. Zeng, W. Li, X. Chen, M. Yuan and L. Liu, et al., Classification of steel using laser-induced breakdown spectroscopy combined with deep belief network, Opt. Express, 2022, 30, 9428–9440 CrossRef CAS PubMed.
- X. Xu, F. Ma, J. Zhou and C. Du, Applying convolutional neural networks (CNN) for end-to-end soil analysis based on laser-induced breakdown spectroscopy (LIBS) with less spectral preprocessing, Comput. Electron. Agric., 2022, 199, 107171 CrossRef.
- J. Yang, S. Li, Z. Zhang, D. Qian, S. Sun and X. Liu, et al., Transformer-based deep learning models for quantification of La, Ce, and Nd in rare earth ores using laser-induced breakdown spectroscopy, Talanta, 2025, 292, 127937 CrossRef CAS PubMed.
- S. Xiong, N. Yang, H. Guan, G. Shi, M. Luo and Y. Deguchi, et al., Combination of plasma acoustic emission signal and laser-induced breakdown spectroscopy for accurate classification of steel, Anal. Chim. Acta, 2025, 1336, 343496 CrossRef CAS.
- T. A. Labutin, V. N. Lednev, A. A. Ilyin and A. M. Popov, Femtosecond laser-induced breakdown spectroscopy, J. Anal. At. Spectrom., 2016, 31, 90–118 RSC.
- S. P. Banerjee, Z. Chen and R. Fedosejevs, High resolution scanning microanalysis on material surfaces using UV femtosecond laser induced breakdown spectroscopy, Opt. Lasers Eng., 2015, 68, 1–6 CrossRef.
- C. M. Ahamer, K. M. Riepl, N. Huber and J. D. Pedarnig, Femtosecond laser-induced breakdown spectroscopy: Elemental imaging of thin films with high spatial resolution, Spectrochim. Acta, Part B, 2017, 136, 56–65 CrossRef CAS.
- G. G. Arantes de Carvalho, J. Moros, D. Santos, F. J. Krug and J. J. Laserna, Direct determination of the nutrient profile in plant materials by femtosecond laser-induced breakdown spectroscopy, Anal. Chim. Acta, 2015, 876, 26–38 CrossRef CAS.
- O. A. Nassef and H. E. Elsayed-Ali, Spark discharge assisted laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2005, 60, 1564–1572 CrossRef.
- W. Zhou, K. Li, Q. Shen, Q. Chen and J. Long, Optical emission enhancement using laser ablation combined with fast pulse discharge, Opt. Express, 2010, 18, 2573–2578 CrossRef CAS.
- X. He, B. Dong, Y. Chen, R. Li, F. Wang and J. Li, et al., Analysis of magnesium and copper in aluminum alloys with high repetition rate laser-ablation spark-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2018, 141, 34–43 CrossRef CAS.
- X. He, Q. Yang, D. Ling, D. Wei and H. Wang, Elemental Analysis of V, Mo, Cr, Mn, Al, Ni, and Cu in Steel Alloy with Femtosecond Laser Ablation Spark-Induced Breakdown Spectroscopy, Chemosensors, 2022, 10, 370 CrossRef CAS.
- S. M. Azimi, D. Britz, M. Engstler, M. Fritz and F. Mücklich, Advanced Steel Microstructural Classification by Deep Learning Methods, Sci. Rep., 2018, 8, 2128 CrossRef.
- M. Cui, G. Shi, L. Deng, H. Guo, S. Xiong and L. Tan, et al., Microstructure classification of steel samples with different heat-treatment processes based on laser-induced breakdown spectroscopy (LIBS), J. Anal. At. Spectrom., 2024, 39, 1361–1374 RSC.
Footnote |
| † These authors contributed equally and are joint first authors. |
| This journal is © The Royal Society of Chemistry 2026 |






