Time-dependent hydride correction for accurate 240Pu/239Pu isotopic ratio measurements in µm-sized Pu-bearing particles using large geometry-secondary ion mass spectrometry
Received
9th May 2025
, Accepted 28th October 2025
First published on 17th November 2025
Abstract
This paper describes a new methodology based on a time-dependent hydride correction for measuring the isotopic composition of micrometer sized plutonium bearing particles using large geometry secondary ion mass spectrometry. This methodology allows the mitigation of the effect of the hydride interferences on 236U, 239Pu and 240Pu on weapon grade plutonium particles, which contain a low amount of the 240Pu isotope, and on MOX particles, which contain a low amount of plutonium at the weight% level. We successfully applied it on six different samples and demonstrated that the deviations from the reference values of the 240Pu/239Pu isotopic ratios were reduced from +4.6% to +0.24% for the MP2 sample (weapon grade Pu) and from −7% to +0.75% for the UKMOX-100 sample (MOX). We also demonstrated the capabilities for simultaneously measuring the uranium and plutonium isotopic compositions in MOX particles using the dynamic multi-collection mode of LG-SIMS. Moreover, we determined the Pu/U relative sensitivity factor using Pu particles of known ages and applied it to measure the 239Pu/238U atomic ratio in MOX particles. At last, the imaging capabilities of the instrument allowed the detection and discrimination of different types of nuclear particles within the same sample, such as U, Pu or MOX particles. This methodology enhances the range of methods applicable to particle analysis in the field of nuclear safeguards and nuclear forensics.
Introduction
A challenge of international nuclear safeguards is to verify the absence of undeclared nuclear activities. Since 1991, the International Atomic Energy Agency has used environmental sampling to detect the presence of nuclear materials during nuclear facility inspection.1–3 IAEA inspectors routinely collect particulate matter by wiping smooth surfaces at various locations inside the facility using square pieces of cotton cloth, referred to as “swipe samples”. The resulting samples are sent to the IAEA Headquarters for coding and distribution to the IAEA Network of Analytical Laboratories (NWAL), to which the French Commissariat à l’Energie Atomique et aux Energies Alternatives (CEA) has belonged since 2001, for isotopic analysis. The goal of the analyses of such samples is to detect the presence of any particles of nuclear materials, mainly uranium, and to determine their isotopic composition. Because particle isotopic and elementary compositions are representative of the original material, these particles can be considered as fingerprints of specific processes of the nuclear industry.4 Currently, analyses are predominantly performed by fission track combined with thermal ionization mass spectrometry,5,6 FT-TIMS, or by secondary ion mass spectrometry,7–10 SIMS. Whatever the analytical technique, the first step consists in the detection and location of U bearing particles. While the FT-TIMS methodology requires the irradiation of the samples under well-thermalized neutron flux, the SIMS methodology relies on its own imaging capabilities. The detection of U particles has been greatly improved by the development of the Automated Particle Measurement, APM, software.12,13 The APM software is mainly aimed at fast screening measurements by performing a two-dimensional image scan over a large surface using fields of 500 µm by 500 µm at selected masses. The coordinates of the particles and an initial assessment of their isotopic composition are then obtained after data treatment. This pre-analysis being less destructive, a second analysis can be performed on selected particles under microbeam conditions, i.e. without rastering the primary beam, to get an accurate determination of their isotopic composition. Recently, the performance of SIMS measurements has been greatly improved using large geometry-SIMS (LG-SIMS) instruments.9,10 These instruments are equipped with a multi-collection device, which allows the collection of all uranium isotopes simultaneously. Moreover, the mass resolution power at full transmission has increased from about 400 to about 3000, which allows the removal of many of the isobaric interferences that are encountered in U particle analysis.9 Particle analysis by SIMS has also proved its worth in the field of nuclear forensics, as highlighted in the 6th Collaborative Materials Exercise After Action Report.14 Initially focused on U isotopic measurement, the use of this technique has diversified over the last twenty years to provide additional information on the industrial origin of uranium, such as the fluorine content, which is a clue of a conversion process15 and the date of the latest purification, also called uranium age dating.16,17 Beyond U, SIMS has sometimes been applied to plutonium particle characterization for safeguards and nuclear forensics applications.18–22 Isotopes of potential interest are 238Pu, 239Pu, 240Pu, 241Pu and 242Pu. The isotopic compositions depend on the origin of the Pu material, and Pu isotopic measurements are a valuable tool for nuclear forensic, nuclear safeguards and environmental studies.23–25 Unfortunately, Pu isotope analyses suffer from isobaric interferences coming from elemental species, such as 241Am on 241Pu, or hydride ions. Namely, m+1Pu+ is interfered by mPuH+ and 239Pu+ is interfered by 238UH+ in the case of a mixed U–Pu sample. None of these interferences can be resolved even using LG-SIMS because a mass resolution higher than 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is required. Such mass resolution power cannot be used for particle analysis because of the loss in transmission, which avoids the detection of such low signals. These interferences may be all the more problematic (1) when Pu is present as a trace or minor element such as in MOX fuel or irradiated fuel, or (2) in the case of weapon grade Pu where the 240Pu concentration is low, of the order of a few atom percent. To our knowledge, no hydride correction was attempted in any of the cited studies. Contrary to U samples, for which the hydride formation rate can be easily measured using the 238UH/238U ratio, no easy way can be used for the determination of the Pu hydride ratio because mPuH+ ions are interfered by m+1Pu+ ions. Ranebo et al.28 managed to measure the Pu hydride from synthetised mono dispersed Pu particles based on an isotopically pure 242Pu material. They reported a 242PuH/242Pu ratio of around 7 × 10−3, which is in the range of the U hydride ratios they also measured in the U and mixed U–Pu particles they produced. In addition, it should be borne in mind that the hydride formation rate is not a value determined once and for all, but depends largely on the analytical parameters and on the nature of the materials analyzed, and should therefore ideally be determined using standards as similar as possible in nature to the micro-objects of interest, and analyzed, if possible, during the same analytical session as the particles of interest. Nevertheless, such an isotopically pure 242Pu material was not available in the laboratory, and assumptions had to be made to estimate the hydride Pu rate and calculate the 240Pu/239Pu isotopic ratio in Pu bearing particles. These assumptions mainly rely on the similar behaviours of Pu and U hydrides.22,26,27,29 For instance, Ranebo et al. estimated the U hydride rate using the 236/235U ion ratio measured in particles coming from a nuclear weapon material remaining from the Thule accident and used it to give the upper and lower bounds of the real 240Pu/239Pu atom ratio.22 However, as explained by the authors, this H rate is overestimated due to the presence of 236U in the Thule particle. More generally, in the case of a mixed U–Pu material, there are two sources of 236U: the U source material itself and the 236U produced by the decay of 240Pu. Furthermore, in this second case, the amount of 236U that is produced by the 240Pu decay depends on the isotopic composition of Pu, the Pu content and the age of the mixed U–Pu material. This information, along with the isotopic composition of the original uranium, is usually not known at the time of analysis, making it virtually impossible to estimate the amount of 236U. For instance, in the case of the MOX samples that were measured in this study, the 236U content may be calculated using the reference values and resulted in a 236U/235U atomic ratio of about 0.04, which is higher by a factor of 10 to 100 than the 238UH/238U ratio measured on standard U. At least, such hydride rate estimation cannot be applied on a pure Pu material. Consequently, such internal hydride correction was not considered in this paper. In a previous study,29 we demonstrated that an external hydride correction can be applied to Pu in order to improve the accuracy of 240Pu/239Pu isotopic measurements conducted on weapon grade Pu and mixed U–Pu particles. This correction was based on the measurement of the average 238UH/238U ratio on standard U particles. In this paper, we used the same principle, namely measuring an external U hydride ratio to correct the 240Pu/239Pu isotopic ratio, but proposed a novel approach by using a time dependent hydride correction in order to take into account the decrease in the hydride ratio along the analysis. Furthermore, we developed a methodology allowing the simultaneous measurement of the U and Pu isotopic compositions using the multi-collection device of the LG-SIMS. We successfully applied this new methodology to µm-sized particles from three weapon grade Pu samples and three MOX samples with a Pu content ranging from 1 atom % to 10 atom %. In addition, the methodology was also used to measure the U/Pu relative sensitivity factor, RSF, that is required to quantify the Pu content in MOX. The RSF determination is based on the measurement of the 235U/239Pu ratio in well purified Pu particles of known purification date.30 The same approach was applied by Wallenius et al. and the RSF was used to determine the age of Pu particles.19 In summary, in this publication, we (1) show that a time-dependent hydride correction
can be applied to Pu or MOX particles thanks to modeling of the evolution of the 238UH/238U ion ratio over time, (2) demonstrate the capabilities of LG-SIMS to detect and differentiate U, Pu and mixed U–Pu particles using APM analyses, (3) measure the accurate 240Pu/239Pu atom ratio in weapon grade Pu particles and (4) simultaneously measure the 240Pu/239Pu atom ratio, the U isotopic composition and the 239Pu/238U atom ratio in MOX particles.
000 is required. Such mass resolution power cannot be used for particle analysis because of the loss in transmission, which avoids the detection of such low signals. These interferences may be all the more problematic (1) when Pu is present as a trace or minor element such as in MOX fuel or irradiated fuel, or (2) in the case of weapon grade Pu where the 240Pu concentration is low, of the order of a few atom percent. To our knowledge, no hydride correction was attempted in any of the cited studies. Contrary to U samples, for which the hydride formation rate can be easily measured using the 238UH/238U ratio, no easy way can be used for the determination of the Pu hydride ratio because mPuH+ ions are interfered by m+1Pu+ ions. Ranebo et al.28 managed to measure the Pu hydride from synthetised mono dispersed Pu particles based on an isotopically pure 242Pu material. They reported a 242PuH/242Pu ratio of around 7 × 10−3, which is in the range of the U hydride ratios they also measured in the U and mixed U–Pu particles they produced. In addition, it should be borne in mind that the hydride formation rate is not a value determined once and for all, but depends largely on the analytical parameters and on the nature of the materials analyzed, and should therefore ideally be determined using standards as similar as possible in nature to the micro-objects of interest, and analyzed, if possible, during the same analytical session as the particles of interest. Nevertheless, such an isotopically pure 242Pu material was not available in the laboratory, and assumptions had to be made to estimate the hydride Pu rate and calculate the 240Pu/239Pu isotopic ratio in Pu bearing particles. These assumptions mainly rely on the similar behaviours of Pu and U hydrides.22,26,27,29 For instance, Ranebo et al. estimated the U hydride rate using the 236/235U ion ratio measured in particles coming from a nuclear weapon material remaining from the Thule accident and used it to give the upper and lower bounds of the real 240Pu/239Pu atom ratio.22 However, as explained by the authors, this H rate is overestimated due to the presence of 236U in the Thule particle. More generally, in the case of a mixed U–Pu material, there are two sources of 236U: the U source material itself and the 236U produced by the decay of 240Pu. Furthermore, in this second case, the amount of 236U that is produced by the 240Pu decay depends on the isotopic composition of Pu, the Pu content and the age of the mixed U–Pu material. This information, along with the isotopic composition of the original uranium, is usually not known at the time of analysis, making it virtually impossible to estimate the amount of 236U. For instance, in the case of the MOX samples that were measured in this study, the 236U content may be calculated using the reference values and resulted in a 236U/235U atomic ratio of about 0.04, which is higher by a factor of 10 to 100 than the 238UH/238U ratio measured on standard U. At least, such hydride rate estimation cannot be applied on a pure Pu material. Consequently, such internal hydride correction was not considered in this paper. In a previous study,29 we demonstrated that an external hydride correction can be applied to Pu in order to improve the accuracy of 240Pu/239Pu isotopic measurements conducted on weapon grade Pu and mixed U–Pu particles. This correction was based on the measurement of the average 238UH/238U ratio on standard U particles. In this paper, we used the same principle, namely measuring an external U hydride ratio to correct the 240Pu/239Pu isotopic ratio, but proposed a novel approach by using a time dependent hydride correction in order to take into account the decrease in the hydride ratio along the analysis. Furthermore, we developed a methodology allowing the simultaneous measurement of the U and Pu isotopic compositions using the multi-collection device of the LG-SIMS. We successfully applied this new methodology to µm-sized particles from three weapon grade Pu samples and three MOX samples with a Pu content ranging from 1 atom % to 10 atom %. In addition, the methodology was also used to measure the U/Pu relative sensitivity factor, RSF, that is required to quantify the Pu content in MOX. The RSF determination is based on the measurement of the 235U/239Pu ratio in well purified Pu particles of known purification date.30 The same approach was applied by Wallenius et al. and the RSF was used to determine the age of Pu particles.19 In summary, in this publication, we (1) show that a time-dependent hydride correction
can be applied to Pu or MOX particles thanks to modeling of the evolution of the 238UH/238U ion ratio over time, (2) demonstrate the capabilities of LG-SIMS to detect and differentiate U, Pu and mixed U–Pu particles using APM analyses, (3) measure the accurate 240Pu/239Pu atom ratio in weapon grade Pu particles and (4) simultaneously measure the 240Pu/239Pu atom ratio, the U isotopic composition and the 239Pu/238U atom ratio in MOX particles.
Materials and methods
Material and sample preparation
Uranium particles from Certified Reference Materials (CRM) NBS U-100 (New Brunswick Laboratory, Illinois, USA) were used for detector calibration and mass bias determination, as well as for modeling the evolution of the 238UH/238U ion ratio over time. Particles were collected from the powder with a plastic tip and transferred to a cotton cloth (TX 303, Texwipe, NC, USA). They were then transferred from the cotton cloth onto a carbon planchet (grade FP2584 Schunk Electrographite SAS, Germany) under a disposable glove bag filled with nitrogen using the vacuum impactor technique.32 This method consists of sucking off particles with a vacuum impactor head and directly loading them on a carbon planchet beforehand covered with an organic compound, polyisobutylene in nonane, acting as a sticky agent.
The 240Pu/239Pu isotopic ratios were determined in µm-sized Pu particles in three weapon-grade plutonium samples. Particles from MP2 (CETAMA, France) and NBS126 (New Brunswick Laboratory, Illinois, USA) were received as a suspension in ethanol. The particle sizes ranged from 1 to 5 µm. For each sample, a small volume of ethanol was directly loaded onto a carbon planchet using a plastic Pasteur pipette. The third sample, CMX-6, came from the 6th Collaborative Material Exercise, organized by the International Technical Working Group on Nuclear Forensics. This sample consisted of a cerium ingot, whose surface was contaminated with weapon grade Pu particles. These particles were collected by wiping the ingot surface with a cotton cloth. Their sizes ranged from 0.7 to 2 µm. They were transferred onto a carbon planchet using the vacuum impactor technique described above. The simultaneous determination of U and Pu isotopic compositions and of the Pu content was carried out with particles from three MOX samples referred to as UKMOX-010, UKMOX-050 and UKMOX-100 (AEA Technology, United Kingdom). These samples were also received as a suspension in ethanol. For each sample, particles were loaded on a carbon planchet using plastic Pasteur pipettes. UKMOX-010 and UKMOX-050 Pu particle sizes ranged from 0.2 to 5 µm. UKMOX-100 Pu particle sizes ranged from 1 to 5 µm. The isotopic compositions of the three weapon grade Pu samples and the three UKMOX samples are given in Table 1. Only 240Pu/239Pu atom ratios were reported. Beyond the decay correction of the 240Pu/239Pu isotopic ratios, the U isotopic ratios of the UKMOX samples were corrected for the Pu isotope decays, i.e., 240Pu, 239Pu and 238Pu isotopes decay into 236U, 235U and 234U isotopes respectively. The 242Pu isotope decay into the 238U isotope was not taken into account because of the 238U abundance in the UKMOX samples. Likewise, the contribution from 238Pu to 238U was not taken into account.
Table 1 Isotopic composition of the samples. All data are decay corrected. Uncertainties are given with a 95% confidence level. MP2 and NBS126 data come from the certificate value; CMX-6 data come from the exercise action report;14 UKMOX-010 and UKMOX-050 data come from an interlaboratory exercise;30 UKMOX-100 data come from laboratory measurements using ICP-MS
| Sample |
MP2 |
NBS126 |
CMX-6 |
|
240Pu/239Pu (×10−2) |
2.24324 ± 0.00051 |
6.2744 ± 0.0016 |
6.161 ± 0.15 |
| Sample |
UKMOX-010 |
UKMOX-050 |
UKMOX-100 |
|
240Pu/239Pu (×10−2) |
28.6207 ± 0.0046 |
28.6135 ± 0.0038 |
28.6058 ± 0.0054 |
|
239Pu/238U (×10−2) |
8.09 ± 0.81 |
1.51 ± 0.15 |
0.647 ± 0.065 |
|
234U/238U (×10−4) |
2.2352 ± 0.0087 |
1.8414 ± 0.0073 |
1.7739 ± 0.0076 |
|
235U/238U (×10−2) |
1.60024 ± 0.00055 |
1.59075 ± 0.00031 |
1.58914 ± 0.00022 |
|
236U/238U (×10−4) |
6.73 ± 0.18 |
5.78 ± 0.35 |
5.63 ± 0.13 |
Instrumental settings
LG-SIMS measurements were performed with a double focusing IMS 1300HR3 (Cameca Ametek, Gennevillilers, France). This instrument is equipped with an RF plasma oxygen ion source (Oregon physics, Beaverton, OR, USA). A primary ion beam of oxygen ions is typically used to enhance the production of electropositive ions such as U+. All measurements described in this paper were carried out with the O2+ primary beam accelerated to 15 keV. All instrumental settings are given in Table 2. The mass resolving power was set to approximatively 3000 to obtain flat top peaks and a good sensitivity, which improve the accuracy and the reproducibility of the measurements. Ion species were recorded in the multi-collection mode. The multi-collection arrangement allows the simultaneous detection of up to five isotopes using the five electron multipliers. The U useful yield was previously measured with the same instrumental settings on spherical UO2 particles produced at the Institut de Chimie Separative de Marcoule (CEA, France). Its value was 1.37 ± 0.34 (2SD), which is similar to other values obtained using LG-SIMS.9,10 The useful yield refers to the proportion of ions measured in a detector relative to the amount of sputtered or evaporated atoms from the sample material. Following our previous study,29 U and Pu were measured as elemental ions instead of oxide ions in order to reduce the influence of isobaric interferences coming from hydride or carbide ions, such as 238U16O1H on 239Pu16O and 239Pu12C on 235U16O. The multi-collection device configuration allows the simultaneous detection of all U isotopes, 234U+, 235U+, 236U+, 238U+ and the 238UH+ species. For Pu measurements, 239Pu and 240Pu isotopes were acquired simultaneously. Such a configuration would also allow the measurement of the 241Pu isotope but 241Pu is interfered by 241Am. Without any information on the age or the Am content in the sample, no determination of 241Pu is possible. Thus, 241Pu measurement was not discussed in this paper. Dynamic multi-collection analysis was required to measure both Pu and U isotopic compositions. This mode corresponds to the acquisition of two lines with a mass jump between each one. The mass peak switching between the lines was performed by changing the magnetic field. Furthermore, some instrumental parameters, named HC1 stig and DSP2S1, needed to be adjusted between the U and Pu acquisition lines in order (1) to increase the mass dispersion and thus align each U and Pu isotope in the detectors and (2) to improve the peak shapes to obtain flat-top peaks. Actually, the mass differences between U and Pu isotopes differ slightly, which induces a small but significant shift of the peak within the detector. By adjusting these parameters, there is no need to move the detectors. Automated particle measurement analysis was also performed using dynamic multi-collection. However, the software did not allow changes in the HC1stig and DSP2S1 parameters. Thus, as shown in Table 2, only the 240Pu isotope was acquired in the second line of acquisition.
Table 2 IMS 1300HR3 general settings and detailed multi-collection analysis settings. HVI/HVII: primary/secondary voltage; FA/CA: field/contrast apertures; Ip = primary beam intensity; L2/L1/C/H1/H2: names of the different electron multiplier detectors; Ct: counting time; DSP2S1 and HC1stig: names of the parameters that were adjusted between the two lines
| General instrumental settings |
| HVI/HVII/Primary ions |
+ 15 KV/+8 kV/O2+ |
| FA/CA/Field of view |
5000 µm/400 µm/80 µm |
| Exit slit/entrance slit/energy slit |
250 µm/125 µm/50 eV |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
Analytical settings
|
| APM |
Ip = 50 nA/raster size = 500 µm/dynamic multi-collection |
| Line 1: 234U (L2); 235U (L1); 236U + 235UH (C); 238U (H1); 238UH + 239Pu (H2) Ct: 10 s |
| Line 2: 239PuH + 240Pu (L2) Ct: 10 s |
| Hydride rate and IMF factor determinations |
Ip = 70 pA/no raster/static multi-collection/75 cycles |
|
234U (L2); 235U (L1); 236U + 235UH (C); 238U (H1); 238UH (H2) Ct: 8 s |
| U and Pu isotopic measurements |
Ip = 70 pA/no raster/dynamic multi-collection/40 cycles |
| Line 1: 234U (L2); 235U (L1); 236U + 235UH (C); 238U (H1); 238UH + 239Pu (H2) Ct: 6 s |
| Line 2: 238UH + 239Pu (L2); 239PuH + 240Pu (L1) Ct : 6 s |
For the hydride rate and instrumental mass fractionation, IMF, factor determination, static multi-collection measurements were performed in order to simultaneously collect 234U+, 235U+, 236U+, 238U+ and 238UH+. Static multi-collection mode corresponds to a single line of acquisition without any mass shift of the magnet. At last, all recorded intensities are corrected for detector dead-time that was measured independently according to the method described in Hedberg et al.31 Analyses were gathered by one-week analytical sessions. During each analytical session, the detector efficiencies, the IMF factor and the hydride rate were measured on NBS U-100 particles. Then, one to two samples, either weapon grade Pu or MOX samples, were analyzed during the same session. Both U and Pu isotopic ratios were corrected with the previously measured IMF factor. In the literature, a similar approach was used to correct Pu isotopic ratios for the mass fractionation effect.27,28 Prior to individual particle analysis, a particle mapping was carried out using the APM software of the instrument. The imaging of all U isotopes, 239Pu+ and 240Pu+, allowed the detection of U, Pu and MOX particles as will be detailed in the section “Automated particle detection”. Data treatment enabled to get the coordinates of these particles and to give an estimation of the U or Pu, or mixed U and Pu, isotopic composition. Particles were therefore selected according to their isotopic composition and analyzed using the dynamic multi-collection methodology.
Results and discussion
Hydride rate measurement
The 238UH+/238U+ ratio was calculated along with the other U isotopic ratios within individual NBS U-100 particles. The analysis time was set to ten minutes approximately. As can be seen in Fig. 1a, the 238UH/238U ion ratio decreased during the course of the analysis from about 4 × 10−3 to about 5 × 10−4. This trend was similar for all the analyzed particles and has been already observed by other authors.10,11 Based on these experimental data, the 238UH/238U mean ratio was calculated for each time data, allowing an average curve of the 238UH+/238U+ ratio as a function of time to be obtained. This curve can be interpolated as a power law as shown in Fig. 1b with an excellent correlation factor. We can see that hydride levels vary from particle to particle. These rates may depend on the size of the particle. These inter-particle variations lead to relative uncertainties between 16 and 35% for each data point. The uncertainties of a and b coefficients, which were in the order of a few percent, were negligible compared to the variations of the hydride ratio between particles and were therefore not considered.
 |
| | Fig. 1
238UH/238U ion ratio versus analysis time. (a) 238UH/238U ion ratio measured in NBS U-100 particles analyzed during the same analytical session. Each curve corresponds to the analysis of one individual particle. (b) Mean 238UH/238U ion ratio as a function of analysis time in blue and interpolation as a power law in red. Uncertainties correspond to the standard deviation of each 238UH/238U mean value. | |
This time-dependent hydride rate was then used to calculate the abundances of 240Pu eqn (1), of 239Pu eqn (2) and 236U eqn (3) in the case of MOX particle analysis. The calculation of the corresponding 240Pu/239Pu and 236U/238U isotopic ratios and associated uncertainties are given in the SI S1. No correction of abundance sensitivity was applied on 239Pu, 240Pu and 236U. The abundance sensitivity at m + 1 was found to be in the 10−6 range, which can be negligible in comparison with the hydride rate, which is in the 10−4 – 10−3 range.
| | 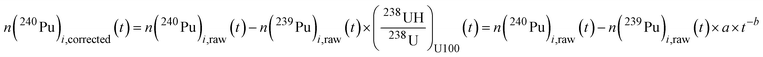 | (1) |
where –
n(
240Pu)
i,raw(
t) and
n(
239Pu)
i,raw(
t) are the measured signals in MOX or Pu particles during cycle i corresponding to the analysis time
t.
n(
240Pu)
i,raw corresponds to the sum of
240Pu and
239PuH signals. In the case of MOX particles,
n(
239Pu)
i,raw(
t) is calculated according to
eqn (2) in order to take into account the
238UH contribution. –
a and
b are the parameters from the
238UH/
238U interpolation curve obtained from the NBS U100 particle analyses during the same analytical session.
| | | n(239Pu)i,corrected(t) = n(239Pu)i,raw(t) − n(238U)i,raw(t) × a × t−b | (2) |
where −
n(
239Pu)
i,raw(
t) and
n(
238U)
i,raw (
t) are the measured signals in MOX particles during cycle
i corresponding to the analysis time
t.
n(
239Pu)
i,raw corresponds to the sum of
239Pu and
238UH signals. –
a and
b are the parameters from the
238UH/
238U interpolation curve obtained from the NBS U-100 particle analyses during the same analytical session.
| | | n(236U)i,corrected(t) = n(236U)i,raw(t) − n(235U)i,raw(t) × a × t−b | (3) |
where –
n(
236U)
i,corrected(
t) and
n(
235U)
i,raw(
t) are the measured signals in MOX particles during cycle i corresponding to the analysis time
t.
n(
236U)
i,corrected corresponds to the sum of
236U and
235UH signals. –
a and
b are the parameters from the
238UH/
238U interpolation curve obtained from the NBS U-100 particle analyses during the same analytical session.
The interpolation curve parameters, a and b, slightly changed between the different analytical sessions, with a ranging from 0.0140 to 0.0197 and b ranging from 0.496 to 0.568. This means that the average hydride ratio slightly changed from one analytical session to another. This could result from different vacuum conditions within the LG-SIMS chamber. Actually, the chamber pressure ranged between 4 × 10−10 and 6 × 10−10 mbar from one analytical session to another. Even if these variations were small, this could have led to the observed changes in the curve parameters. Therefore, it is requested to work under similar vacuum conditions for reference materials, NBS U-100 in our case, and samples to allow accurate hydride correction. The other major sources of hydrogen that can affect the hydride ratio are the substrate on which particles are loaded and the sticky agent. Graphite planchets are commonly used for uranium particle analysis because these materials have high purity and low vapor pressure, and produce no significant high mass polyatomic ions that could create isobaric interferences with uranium ions. However, high purity graphite may contain as much as 1% hydrogen that can be reduced by vacuum annealing, but reabsorption will occur when the graphite is exposed to air. The 238UH may be divided by a factor of ten using a silicon planchet instead of a graphite planchet.10,11 Therefore, the same type of substrate must be used for the reference material and samples. Regarding the sticky agent, a heating treatment at 400 °C could be used to remove the organic compounds responsible for hydride formation. However, it should be noted that this treatment can alter the particles' chemical form if further characterization studies, such as phase determination using micro-Raman spectroscopy, are required. Such heating treatment was not applied in this study and its potential impact on the hydride formation was not investigated.
Static H-correction versus time dependent H-correction
As already mentioned in the Introduction, static H-correction was applied in a previous paper using an IMS 7F instrument.29 This static correction consisted first of calculating the average UH/U ratio, over the entire analysis, for each NBSU-100 particle. The mean UH/U ratio was then used to calculate the net 240Pu+ signal, according to eqn (4). The same calculations were used to determine the net 239Pu+ and 236U+ signals in MOX particles.| |  | (4) |
where – n(240Pu)i,raw and n(239Pu)i,raw are the measured signals in Pu particles during cycle i. n(240Pu)i,raw corresponds to the sum of 240Pu and 239PuH signals. 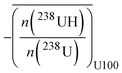 is the mean H ratio obtained from the NBS U-100 particle analyses during the same analytical session.
is the mean H ratio obtained from the NBS U-100 particle analyses during the same analytical session.
Both static and time-dependent hydride corrections were applied to correct the 240Pu/239Pu atomic ratio measured on particles from the three weapon grade Pu samples. Fig. 2 represents the deviation from the reference value, DRV, of the 240Pu/239Pu ratio corrected according to the static hydride correction method versus the 240Pu/239Pu ratio corrected according to the dynamic hydride correction method. Uncertainties were not displayed for a better reading of this figure but they are displayed in Fig. 4. The two correction methods gave roughly equivalent results: most of the data points are fairly well aligned along the straight line with slope 1 (x = y). This was all the more true for particles having been analyzed for the same analysis time as the one used for the NBSU-100 particles, i.e. 578 s. For such particles, the mean static UH/U ratio was representative of the average UH/U ratio prevailing in the Pu particle. Thus, there were no differences between applying this mean UH/U ratio or a point-to-point correction using the time-dependent UH/U ratio. In contrast, the data tended to show that time-dependent corrections gave slightly better results, i.e. a lower DRV, for the shorter analysis times. However, the analysis duration depends on the size of the particles: the larger the particle, the higher and longer the measured signal. In contrast, the signal drops rapidly for the smallest particles, leading to the analysis being stopped before completion. As the range of particle sizes was large, 0.2–5 µm, different analysis durations were encountered during the analysis of particles from the same sample. For these smaller particles, the contribution of 239PuH+ to 240Pu+ was under-estimated when using the mean UH/U ratio calculated during the whole course of the NBS U-100 particle analysis. Actually, the shape of the UH/U ratio evolution, as shown in Fig. 2, clearly indicated that the UH/U ratio was higher at the beginning of the analysis. Thus, the true mean UH/U ratio prevailing in these smaller Pu particles should be higher than the one measured in NBS U-100 particles. In contrast, time-dependent UH/U correction allowed the correction from a more realistic UH/U contribution. Further measurements on monodispersed particles are required to confirm this trend.
 |
| | Fig. 2 Comparison of the DRV of the 240Pu/239Pu atomic ratio measured in single particles from three weapon grade Pu samples using static H-correction eqn (4) and time dependent H-correction eqn (1). Green squares correspond to data obtained from particles analyzed during the full analysis time (578 s). Red triangles correspond to particles analyzed during 60%, or less, of the full analysis time. Blue circles correspond to data obtained from particles analyzed between 60% and full analysis time. The dark line corresponds to the equation x = y. | |
All the following reported data correspond to time-dependent UH/U corrected data.
Automated particle detection
APM threshold parameters were set at 2 counts and 10 pixels for the sum of 238U+ and m/z = 240 ion, using either the Cameca or auto-threshold algorithm, in order to get the particle boundaries. Further details on the threshold parameters and algorithms are given in other papers.12,13 Such settings allowed the detection of micrometer sized particles that contain either U or Pu or mixed U and Pu. However, these settings did not guarantee the detection of high enriched uranium. Thus, a second data treatment is required using the sum of 235U+ and 238U+ instead of the previous one. 235U+, 238U+, m/z = 239 ion (239Pu+ + 238UH+) and m/z = 240 ion (240Pu+ + 238UH+) ion images in one 500 µm × 500 µm field from CMX-6 and UKMOX-100 APM analyses are given respectively in Fig. 3a and b.
 |
| | Fig. 3 Ion images of one APM field from (a) the CMX-6 sample and (b) UKMOX-100. Red circles correspond to ion clusters from a Pu particle (1) and U particles (2-3-4) in (a) and from one MOX particle (1) in (b). | |
The CMX-6 sample contained numerous U particles but only a few Pu particles. The APM data treatment settings allowed the detection of 57 Pu particles and 8315 U particles, meaning that the number of Pu particles was less than 1% of the total number of detected particles. The distinction between Pu and U particles was based on the m/z = 240 signal instead of the m/z = 239 signal. Indeed, the presence of an ion cluster at m/z = 239 may correspond to the 238UH signal from a U particle. Conversely, the detection of a m/z = 240 cluster is necessarily linked to the presence of a Pu particle. The estimated 240Pu/239Pu isotopic ratios of each detected particle were then compiled from APM data and plotted in histogram form. This provided an overview of all the isotopic compositions present in the sample. This isotopic distribution was centered at around 0.08, which was in acceptable agreement with the reference value being 0.06. Data are given in SI S2. The estimated 235U at% of the detected U particles were also plotted in the histogram whose mean value was around 0.2%. This result was in agreement with the reference value. These results confirmed that APM analysis provided relevant and accurate information concerning the isotopic and elemental compositions of the detected particles.
The APM analysis of the UKMOX-100 sample confirmed the detection capabilities of MOX particles containing 1% of Pu. Identification of MOX particles was based on simultaneous and co-located detection of ion clusters at 235U+, 238U+, m/z = 239 and m/z = 240 (Fig. 3b). The estimated 235U at% distribution was centered around 2%, in agreement with the reference value. The estimation of the 240Pu/239Pu isotopic ratios was more scattered and ranged from 0.005 to 0.5, while the reference value was around 0.2. This data scattering may be due to the low Pu content of the particle.
240Pu/239Pu isotopic measurements in weapon grade Pu particles
The 240Pu/239Pu isotopic ratio was measured in 20 particles or more from each MP2, NBL126 and CMX-6 sample (Fig. 4).
 |
| | Fig. 4
240Pu/239Pu isotopic ratio of plutonium particles from MP2 (a); NBS126 (b) and CMX-6 (c) samples. Each point corresponds to the analysis of one particle. Expanded uncertainties are given with a 95% confidence level. The black lines correspond to the reference value and dotted black lines correspond to the expanded uncertainties of the reference value (95% confidence level). | |
Data were corrected from the hydride contribution according to eqn (1). All results were in good agreement with the reference values. Average individual uncertainties ranged from 1% for CMX-6 and NBL126 samples to 2.5% for the MP2 sample (95% confidence level). It is worth noting that the propagation of uncertainties related to the hydride correction increased the final uncertainty by a factor of 2.5 on average. This is due to the scattering of the 238UH/238U ion ratio measured in the different NBS U-100 particles (Fig. 1b). The CMX-6 particle measurements were more scattered than the ones obtained for the other samples. As a reminder, the CMX-6 sample contains many uranium particles. The presence of a U particle in the close vicinity of the Pu particle will result in an increase in the m/z = 239 ion signal due to an additional 238UH+ contribution at the m/z ratio of 239Pu. This will result in a lower 240Pu/239Pu isotopic ratio. Average isotopic ratios are given in Table 3 along with the relative expanded uncertainties, REU, and the deviation from the reference value, DRV, in order to evaluate the efficiency of the hydride correction. MP2 particle measurement was the most challenging because it has the lowest 240Pu abundance. The 239PuH contribution to the total m/z = 240 signal could reach 10% at the beginning of the measurement and stayed above 2% during the course of the analysis. Thus, the uncorrected isotopic ratio differed from the reference value by 4.6%, while the hydride corrected isotopic ratio exhibited no deviation. Hydride correction also greatly improved the result for the NBS126 sample, allowing the reduction of the deviation from the reference value from 2.4% down to 0.31%. The deviation was also reduced for the CMX-6 sample despite the larger relative expanded uncertainties.
Table 3 Comparison of the average 240Pu/239Pu isotopic ratio measured in weapon grade Pu particles from MP2, NBS126 and CMX-6 samples, with and without hydride correction. Expanded uncertainties are given with a 95% confidence level
| Sample |
Hydride-corrected 240Pu/239Pu isotopic ratio |
Uncorrected 240Pu/239Pu isotopic ratio |
| Mean value (×10−2) |
REU (%) |
DRV (%) |
Mean value (×10−2) |
REU (%) |
DRV (%) |
| MP2 |
2.246 ± 0.040 |
1.8 |
0.24 |
2.350 ± 0.040 |
1.7 |
4.6 |
| NBS126 |
6.284 ± 0.054 |
0.86 |
0.31 |
6.415 ± 0.076 |
1.5 |
2.4 |
| CMX-6 |
6.14 ± 0.12 |
1.9 |
−0.37 |
6.25 ± 0.13 |
2.1 |
1.3 |
U and Pu isotopic measurements in MOX particles
The 240Pu/239Pu isotopic ratio was measured in 15 particles from each UKMOX-100, UKMOX-050 and UKMOX-010 sample (Fig. 5). All data were corrected from the hydride contribution according to eqn (1) and (2). The U isotopic ratios were also measured simultaneously and results are given in SI data (S3). All results were in good agreement with reference values, except for some particles from UKMOX-050 (analysis number # 17 and 26) and UKMOX-10 (# 33, 36 and 45). The differences from the reference values may be attributed to an inaccurate hydride correction or an inhomogeneous isotopic composition of the samples at the particle scale. A careful study of the results of analysis # 17, 26 and 45 suggested that the bias was due to an underestimation of the local hydride rate. Actually, the 236U/238U isotopic ratio measured in the same particle was above the reference value, meaning the 235UH correction was undervalued (see Fig. S3). Accurate results could have been obtained by increasing the local hydride ratio by a factor of 5 to 10. We do not have any explanation of this potential local increase in the hydride rate. The lower values of the 240Pu/239Pu isotopic ratios of UKMOX-010 #33 and #36 were associated with the 235U/238U isotopic ratio above the reference value (Fig. S3). This supported the hypothesis of an inhomogeneity of the material at the particle scale. However, these few deviations from the reference values did not affect the overall results. The 240Pu/239Pu average individual uncertainties were 1.3%, 1.7% and 2.2% for UKMOX-010, UKMOX-050 and UKMOX-100 respectively (95% confidence level). The differences in the average individual uncertainties were first attributed to the relatively low Pu content of the particles. The one of UKMOX-100 was the lowest with about 1%. Thus, lower 239Pu+ and 240Pu+ count rates were acquired, which resulted in lower counting statistics. In addition, the increase in the 238UH contribution to 239Pu also led to the enlargement of the uncertainties. Actually, this contribution increased from less than 1% in UKMOX-010 particles to more than 10% in UKMOX-100 particles. As a result, the H-corrections increased the individual uncertainties by a factor of 2 for the UKMOX-100 sample and by a factor of 1.3 for the UKMOX-050 sample. These corrections had practically no effect on the uncertainties for the UKMOX-010 sample. The contribution of 239PuH to 240Pu is negligible, less than 1%, due to the 240Pu abundance, which is close to 28%. Average isotopic ratios are given in Table 4 along with the REU and DRV in order to evaluate the effectiveness of the hydride correction. The DRV has been significantly reduced for UKMOX-100, from −7.0% down to 0.75%. The impact of the hydride correction was less significant for the other samples, due to more scattered results and higher Pu content. Following the removal of the anomalous analyses from these samples (#17 and 26 for UKMOX-050 and #33, 36 and 45 for UKMOX-010), the DRV was greatly reduced thanks to the hydride correction.
 |
| | Fig. 5
240Pu/239Pu atom ratio of MOX particles from UKMOX-100 (orange circles), UKMOX-050 (blue triangles) and UKMOX-010 (green squares). Each point corresponds to the analysis of one particle. Expanded uncertainties are given with a 95% confidence level. The black line corresponds to the reference value. Expanded uncertainties of the reference value are too small to be seen in this figure. | |
Table 4 Comparison of the average 240Pu/239Pu isotopic ratios measured in MOX particles from UKMOX-100, UKMOX-050 and UKMOX-100 samples with and without hydride correction. Expanded uncertainties are given with a 95% confidence level
| Sample |
Hydride-corrected 240Pu/239Pu isotopic ratio |
Uncorrected 240Pu/239Pu isotopic ratio |
| Mean value (×10−1) |
REU (%) |
DRV (%) |
Mean value (×10−1) |
REU (%) |
DRV (%) |
| UKMOX-100 |
2.89 ± 0.18 |
4.1 |
0.75 |
2.66 ± 0.16 |
6.2 |
−7.0 |
| UKMOX-050 |
2.77 ± 0.28 |
10 |
−3.1 |
2.71 ± 0.28 |
10 |
−5.1 |
| UKMOX-050 without #17 and 26 |
2.816 ± 0.064 |
2.3 |
−1.6 |
2.755 ± 0.097 |
3.5 |
−3.7 |
| UKMOX-010 |
2.82 ± 0.13 |
4.7 |
−1.3 |
2.82 ± 0.13 |
4.6 |
−1.6 |
| UKMOX-010 without #33, 36 and 45 |
2.851 ± 0.043 |
1.5 |
−0.37 |
2.843 ± 0.045 |
1.6 |
−0.65 |
Quantification of the Pu content in MOX particles
The determination of the Pu content in MOX particles required the determination of the RSF U:Pu. This factor allows the difference of the U and Pu ionization yields to be taken into account and the conversion of the ion ratio into the elemental ratio using eqn (5).| |  | (5) |
RSF should usually be measured using a reference material with known U and Pu concentrations and whose matrix is similar to the sample's one. To our knowledge at the time of this study, there was no commercially-available U–Pu oxide reference material certified at the particle scale. Hence, this factor was calculated from well purified Pu particles of known ages, whose 235U/239Pu ratio, governed by their decay periods, can be calculated using Bateman's equation. This methodology was previously described19,29 and similar approaches were used to determine the RSF of U and Th for U age dating studies.16,17 In our case, we calculated the RSF(235U/239Pu) of CMX-6 and NBS126 samples. Actually, previous determination of the model ages of these samples based on the radiochronometer 235U/239Pu, using ICP-MS or TIMS methodologies, was in agreement with the real purification dates.14,33 The RSF(239Pu/238U) can be then calculated according to equ (6).
| |  | (6) |
where IMFamu is the instrumental fractionation factor per mass unit previously measured on NBS U-100 particles. M
238U and M
235U are the molar masses of
238U and
235U.
The RSF(239Pu/238U) obtained from CMX-6 and NBS126 samples were similar with a value of 0.450 ± 0.030 and 0.410 ± 0.098 respectively (expanded uncertainties at the 95% confidence level). The slight difference may be due to the matrix effect, although the measurement uncertainties for the NBS126 sample do not allow this to be confirmed. Moreover, the RSF may be dependent on the sample matrix and on the chemical form of the particles. CMX-6 particles came from an old PuF4 neutron source material whereas NBL126 particles consisted of oxidized Pu metal. Small differences were already observed between the RSF measured in Pu oxidized metal and Pu sulfate.19 RSF U:Pu data are few in the literature and the RSF obtained in this work for oxidized metal is in agreement with other data.19,26 In any case, this RSF value means that the measured isotopic ratio is higher by a factor of approximately two than the real ratio. In other words, the Pu content is overestimated by a factor of two if no RSF correction is performed. The Pu content, expressed as the 239Pu/238U isotopic ratio, was measured in 15 particles from UKMOX-100, UKMOX-050 and UKMOX-010 samples (Fig. 6). The average 239Pu/238U ratios were in agreement with the reference values whatever the UKMOX sample. However, the results were highly scattered in comparison with individual uncertainties. This dispersion was also observed within individual particles, with a 239Pu/238U ratio variation up to a factor of three during an analysis. Such identical results were also obtained in other studies.20,29 This can be explained by the fact that uranium and plutonium did not form a homogeneous solid phase when mixed. The UKMOX samples were prepared by blending solutions of uranium and plutonium in dilute nitric acid to obtain the desired bulk U/Pu ratio. Then, after co-precipitation using ammonia, the mixture was calcined in 4% hydrogen in argon at 850 °C. Such process may not allow homogeneity of the Pu distribution at the micrometric scale. However, the results demonstrated that the determination of the RSF allowed the accurate determination of the Pu content of MOX particles, whose 239Pu/238U ratio ranged from 0.007 to 0.08.
 |
| | Fig. 6
239Pu/238U isotopic ratio of MOX particles from UKMOX-100 (orange circles), UKMOX-050 (blue triangles) and UKMOX-010 (green squares). Each point corresponds to the analysis of one particle. Expanded uncertainties are given with a 95% confidence level. Black lines correspond to the reference values and dotted black lines correspond to the expanded uncertainties of the reference values. | |
Analytical calculations of the 240Pu detection limit in WG Pu particles and of the 236U and 239Pu/238U ratio in MOX particles
The 240Pu/239Pu detection limit in WG Pu particles can be calculated from eqn (7) and (8). We assumed that the detector noise, measured at approximately 0.03 cps, can be neglected. The uncertainty of the background can be derived from eqn (7) using a propagation of error approach, where the terms are assumed to be statistically independent. The uncertainties in the measured signals were determined by Poisson counting statistics, except for the hydride ratio. We considered an average hydride ratio of 10−3, corresponding to the average ratio measured in NBSU-100 particles over all analytical sessions. The associated relative standard deviation was set at 24.8%. We also considered the consumption of approximately 10 pg of Pu, equivalent to 3.26 × 1010 atoms, which corresponds to the amount contained in a pure spherical Pu metal particle with a diameter of 0.5 µm. As can be observed, the detection limit was driven by the standard deviation of the hydride ratio measurement. Therefore, the 240Pu/239Pu detection limit in WG Pu particles was 7.25 × 10−4 for typical values of the hydride ratios measured on NBSU-100 particles over the analytical sessions.| |  | (7) |
with the average hydride  ratio measured over all analytical sessions
ratio measured over all analytical sessions| |  | (8) |
with  : standard deviation of the hydride ratios measured over all analytical sessions.
: standard deviation of the hydride ratios measured over all analytical sessions.
The calculation of the 236U detection limit in MOX particles was based on the same principle. The 236U/238U detection limit can be calculated from eqn (9) and (10). The 236U detection limit in at% can be calculated from eqn (11), assuming that (1) the sum of the abundances of 234U, 235U, 236U and 238U corresponds to 100% and (2) 234U/235U = 0.01. A similar approach was used by Ranebo et al.9 and Simon et al.11 to calculate the 236U detection limit in U particles. However, the hydride correction in MOX particles required the use of the hydride ratio measured in NBSU-100 particles, because of the presence of 239Pu that prevented the in situ hydride ratio measurement, as in U particles. In comparison with the data for U particles and for the equivalent hydride ratio, the 236U detection limits in MOX particles were significantly degraded due to the larger standard deviation in the hydride ratio measurement. They were even more degraded when the abundance of 235U was high. For instance, considering the consumption of 1 pg of U, or 2.5 × 109 atoms, the 236U detection limit in MOX particles, in at%, increased from 0.0005 at%, for a 235U abundance of 0.7%, to 0.062 at%, for high-enriched uranium with 235U = 90 at%. The corresponding 236U detection limit calculated by Ranebo et al.9 was 0.0001 at% and 0.009 at% for pure UO2 particles.
| |  | (9) |
| |  | (10) |
| |  | (11) |
At last, we calculated the lowest 239Pu/238U ratio that can be detected in MOX particles, from eqn (12) and (13). As previously considered, the detector noise, measured at approximately 0.03 cps, can be neglected. Once again, the hydride ratio standard deviation was the main source of uncertainty, compared to counting statistics.
| |  | (12) |
| |  | (13) |
Therefore, the lowest 239Pu/238U ratio was 1.7 × 10−3 for typical values of the hydride ratios measured on NBSU-100 particles over the analytical sessions.
These detection limits can be further improved by reducing the hydride ratio and its standard deviation. For instance, the vacuum pressure can be lowered inside the chamber using a nitrogen trap. As previously written, other types of substrate, such as silicon planchets, could be used to reduce the U hydride formation. At least, particles can be calcined to remove organic compounds that are H-rich.
Conclusion
Particle analysis is the most powerful technique to detect clandestine nuclear activities. Due to hydride interferences, the use of (LG-) SIMS has been limited for the characterization of Pu bearing particles. This paper focuses on the development of a new methodology for correcting theses hydride interferences based on a time-dependent correction, which took into account the decrease in the hydride rate over the course of an analysis. This has enabled the calculation of a more realistic hydride ratio at each analysis time. Thus, for hydride levels of around 0.08%, corresponding to those measured during this study, we have demonstrated that hydride related interference can contribute up to 10% or more of the total signal measured for the Pu isotopes of interest under the most unfavourable conditions, specifically for WG Pu, with low 240Pu abundance and mixed U–Pu samples, with low Pu content. Consequently, the discrepancies between the raw and hydride-corrected 240Pu/239Pu ratios are around 5% for particles from the MP2 sample, the most challenging WG Pu sample due to its lowest 240Pu abundance of around 2%. They can reach 8% for particles from the MOXUK-100 sample, which has the lowest Pu content of 1%. As a result, the deviations from the reference values (DRV) of the 240Pu/239Pu isotopic ratio were greatly improved both for WG Pu and MOX particles. The accuracy was greatly improved by a factor of 20 for MP2 particles and by a factor of 9 for UKMOX-100 particles. Moreover, results on weapon grade Pu particles indicated that this method was particularly relevant for small particles, which typically had shorter analysis times than the reference particles used to calculate the hydride rate. This trend could be confirmed by analyzing monodispersed particles that were not commercially available at the time of this study. This paper also describes the newly developed dynamic multi-collection methodology to simultaneously measure the Pu and U isotopic composition at the particle scale. This requires the adjustment of some specific parameters, namely DSP2S1 and HC1stig, to keep the beam centered in each detector. Although the results on UKMOX samples were in good agreement with the reference values, the determination of the U isotopic composition of MOX samples should be treated with caution because of the decay of Pu to the U isotope. Deviations from the initial composition can reach 10% or more depending on the Pu content, the Pu isotopic composition and the age of the material. We also calculated the RSF U:Pu using WG Pu particles of known ages. It was successfully applied to MOX particles to calculate the 239Pu/238U atomic ratio. Despite large inter- and intra-particle variations, the mean ratios were in agreement with the reference values. Finally, we have shown that the automated particle measurement software, called APM, is suitable for the precise detection and discrimination of various types of particles, such as U, Pu or mixed U–Pu particles, within the same sample and for reliable estimation of their isotopic composition.
Author contributions
Anne-Laure Fauré: wrote the paper, developed the methodology, performed analysis, and developed data treatment. Manon Cornaton: performed analysis.
Conflicts of interest
There are no conflicts to declare.
Data availability
Data supporting this article and supplementary data have been included as part of the supplementary information (SI). Supplementary Information is available. See DOI: https://doi.org/10.1039/d5ja00190k.
Acknowledgements
The authors are grateful to Guillaume Stadelmann, Urska Repinc, Andrey Bosko, Mathieu Rosenzweig, and Michael Minixhofer (IAEA, Office of Safeguards Analytical Services) for providing the UKMOX, MP2 and NBL126 samples. The authors are also grateful to Jean Aupiais and Fabien Pointurier (CEA, DAM, DIF) for their help with the mathematical processing of the data and detection limit calculations.
References
- D. L. Donohue and R. Zeisler, Anal. Chem., 1993, 65, 359A CrossRef CAS.
- D. L. Donohue, IAEA Bull., 2002, 44(2), 17 Search PubMed.
- D. L. Donohue, J. Alloys Compd., 1998, 271–273, 11 CrossRef CAS.
-
A. J. Pidduck, M. R. Houlton, G. M. Williams and D. L. Donohue, Institute of Nuclear Materials Management Annual Meeting, Nashville, TN, 2006 Search PubMed.
- Y. Chen, Y. Shen, Z. Y. Chang, Y. G. Zhao, S. L. Guo, J. Y. Cui and Y. Liu, Radiat. Meas., 2013, 50, 43–45, DOI:10.1016/j.radmeas.2012.10.015.
- F. Esaka, C. G. Lee, M. Magara and T. Kimura, Anal. Chim. Acta, 2012, 721, 122–128, DOI:10.1016/j.aca.2012.01.045.
- F. Esaka and M. Magara, Talanta, 2014, 54(120), 349–354, DOI:10.1016/j.talanta.2013.12.029.
- G. Tamborini, M. Betti, V. Forcina, T. Hiernaut, B. Giovannone and L. Koch, Spectrochim. Acta, Part B, 1998, 53(9), 1289–1302, DOI:10.1016/S0584-8547(98)00121-9.
- Y. Ranebo, M. Hedberg, M. Whitehouse, K. Ingeneri and S. Littmann, J. Anal. At. Spectrom., 2009, 24, 277–287, 10.1039/B810474C.
- P. M. L. Hedberg, P. Peres, F. Fernandes, N. Albert and C. Vincent, J. Vac. Sci. Technol., B, 2018, 36(3), 03F108, DOI:10.1116/1.5016943.
- D. S. Simons and J. D. Fassett, J. Anal. At. Spectrom., 2017, 32, 393–401, 10.1039/C6JA00402D.
- P. M. L. Hedberg, P. Peres, J. B. Cliff, F. Rabemananjara, S. Littmann, H. Thiele, C. Vincent and N. Albert, J. Anal. At. Spectrom., 2011, 26, 406, 10.1039/C0JA00181C.
- P. Peres, M. Hedberg, S. Walton, N. Montgomery, J. Cliff, F. Rabemananjara and M. Schuhmacher, Surf. Interface Anal., 2013, 45, 561–565, DOI:10.1002/sia.5015.
-
C. Skónis, 6th Collaborative Materials Exercise After Action Report Release Rev. 2.2, 2021 Search PubMed.
- A.-L. Fauré, C. Rodriguez, O. Marie, J. Aupiais and F. Pointurier, J. Anal. At. Spectrom., 2013, 29, 145–151, 10.1039/C3JA50245G.
- A.-L. Fauré and T. Dalger, Anal. Chem., 2017, 89, 6663–6669, DOI:10.1021/acs.analchem.7b00887.
- C. Skazal, D. S. Simons, J. D. Fasset and A. J. Fahey, Analyst, 2019, 144, 4219–4232, 10.1039/C9AN00774A.
- M. Betti, G. Tamborini and L. Koch, Anal. Chem., 1999, 71, 2616–2622, DOI:10.1021/ac981184r.
- M. Wallenius, G. Tamborini and L. Koch, Radiochim. Acta, 2001, 89, 55–58 CrossRef CAS.
-
M. Aleshin, T. Tanpraphan, O. Bildstein, L. Sangely, U. Repinc, A. Bosko, J. Poths, S. Vogt, Y. Kuno, IAEA-CN-357 Search PubMed.
- J. J. Bellucci, M. J. Whitehouse, M. Aleshin and M. Eriksson, Anal. Chem., 2019, 91, 5599–5604, DOI:10.1021/acs.analchem.8b04809.
- Y. Ranebo, M. Eriksson, G. Tamborini, N. Niagolova, O. Bildstein and M. Betti, Microsc. Microanal., 2007, 13, 179–190, DOI:10.1017/S1431927607070353.
- M. Wallenius, P. Peerani and L. Koch, J. Radioanal. Nucl. Chem., 2000, 246, 317–321, DOI:10.1023/A:1006774524272.
- Z. Varga, Anal. Bioanal. Chem., 2007, 389(3), 725–732, DOI:10.1007/s00216-007-1371-3.
- T. Bisinger, S. Hippler, R. Michel, L. Wacker and H.-A. Synal, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2010, 268, 1269–1272, DOI:10.1016/j.nimb.2009.10.150.
- J. J. Stoffel(s), J. K. Briant and D. S. Simons, J. Am. Soc. Mass Spectrom., 1994, 5, 852–663, DOI:10.1016/1044-0305(94)87008-X.
-
SIMS VIII: Proceedings of the Eighth International Conference on Secondary Ion Mass Spectrometry, ed. D. S. Simons, A. Benninghoven, K. T. F. Janssen, J. Tümpner and H. W. Werner, John Wiley & Sons, 1992, Chichester, England, pp. 715–718 Search PubMed.
- Y. Ranebo, N. Niagolova, N. Erdmann, M. Eriksson, G. Tamborini and M. Betti, Anal. Chem., 2010, 82(10), 4055–4062, DOI:10.1021/ac9029295.
- A. Diacre, A. L. Fauré, M. Cornaton, F. Pointurier and O. Evrard, Talanta, 2023, 252, 123848, DOI:10.1016/j.talanta.2022.123848.
-
IAEA nuclear material round robin 2015 report, SG-RP-13613, 2015/11/23 Search PubMed.
- M. Hedberg, P. Peres, F. Fernandes and L. Renaud, J. Anal. At. Spectrom., 2015, 30, 2516–2524, 10.1039/C5JA00382B.
- F. Esaka, K. Watanabe, H. Fukuyama, T. Onodera, K. T. Esaka, M. Magara, S. Sakurai and S. Usuda, J. Nucl. Sci. Technol., 2004, 41(11), 1027–1032, DOI:10.1080/18811248.2004.9726327.
- B. L. Byerly, F. Stanley and K. Spencer,
et al.
, J. Radioanal. Nucl. Chem., 2016, 310, 623–632, DOI:10.1007/s10967-016-4919-x.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Manon
Cornaton
* and
Manon
Cornaton
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is required. Such mass resolution power cannot be used for particle analysis because of the loss in transmission, which avoids the detection of such low signals. These interferences may be all the more problematic (1) when Pu is present as a trace or minor element such as in MOX fuel or irradiated fuel, or (2) in the case of weapon grade Pu where the 240Pu concentration is low, of the order of a few atom percent. To our knowledge, no hydride correction was attempted in any of the cited studies. Contrary to U samples, for which the hydride formation rate can be easily measured using the 238UH/238U ratio, no easy way can be used for the determination of the Pu hydride ratio because mPuH+ ions are interfered by m+1Pu+ ions. Ranebo et al.28 managed to measure the Pu hydride from synthetised mono dispersed Pu particles based on an isotopically pure 242Pu material. They reported a 242PuH/242Pu ratio of around 7 × 10−3, which is in the range of the U hydride ratios they also measured in the U and mixed U–Pu particles they produced. In addition, it should be borne in mind that the hydride formation rate is not a value determined once and for all, but depends largely on the analytical parameters and on the nature of the materials analyzed, and should therefore ideally be determined using standards as similar as possible in nature to the micro-objects of interest, and analyzed, if possible, during the same analytical session as the particles of interest. Nevertheless, such an isotopically pure 242Pu material was not available in the laboratory, and assumptions had to be made to estimate the hydride Pu rate and calculate the 240Pu/239Pu isotopic ratio in Pu bearing particles. These assumptions mainly rely on the similar behaviours of Pu and U hydrides.22,26,27,29 For instance, Ranebo et al. estimated the U hydride rate using the 236/235U ion ratio measured in particles coming from a nuclear weapon material remaining from the Thule accident and used it to give the upper and lower bounds of the real 240Pu/239Pu atom ratio.22 However, as explained by the authors, this H rate is overestimated due to the presence of 236U in the Thule particle. More generally, in the case of a mixed U–Pu material, there are two sources of 236U: the U source material itself and the 236U produced by the decay of 240Pu. Furthermore, in this second case, the amount of 236U that is produced by the 240Pu decay depends on the isotopic composition of Pu, the Pu content and the age of the mixed U–Pu material. This information, along with the isotopic composition of the original uranium, is usually not known at the time of analysis, making it virtually impossible to estimate the amount of 236U. For instance, in the case of the MOX samples that were measured in this study, the 236U content may be calculated using the reference values and resulted in a 236U/235U atomic ratio of about 0.04, which is higher by a factor of 10 to 100 than the 238UH/238U ratio measured on standard U. At least, such hydride rate estimation cannot be applied on a pure Pu material. Consequently, such internal hydride correction was not considered in this paper. In a previous study,29 we demonstrated that an external hydride correction can be applied to Pu in order to improve the accuracy of 240Pu/239Pu isotopic measurements conducted on weapon grade Pu and mixed U–Pu particles. This correction was based on the measurement of the average 238UH/238U ratio on standard U particles. In this paper, we used the same principle, namely measuring an external U hydride ratio to correct the 240Pu/239Pu isotopic ratio, but proposed a novel approach by using a time dependent hydride correction in order to take into account the decrease in the hydride ratio along the analysis. Furthermore, we developed a methodology allowing the simultaneous measurement of the U and Pu isotopic compositions using the multi-collection device of the LG-SIMS. We successfully applied this new methodology to µm-sized particles from three weapon grade Pu samples and three MOX samples with a Pu content ranging from 1 atom % to 10 atom %. In addition, the methodology was also used to measure the U/Pu relative sensitivity factor, RSF, that is required to quantify the Pu content in MOX. The RSF determination is based on the measurement of the 235U/239Pu ratio in well purified Pu particles of known purification date.30 The same approach was applied by Wallenius et al. and the RSF was used to determine the age of Pu particles.19 In summary, in this publication, we (1) show that a time-dependent hydride correction
can be applied to Pu or MOX particles thanks to modeling of the evolution of the 238UH/238U ion ratio over time, (2) demonstrate the capabilities of LG-SIMS to detect and differentiate U, Pu and mixed U–Pu particles using APM analyses, (3) measure the accurate 240Pu/239Pu atom ratio in weapon grade Pu particles and (4) simultaneously measure the 240Pu/239Pu atom ratio, the U isotopic composition and the 239Pu/238U atom ratio in MOX particles.
000 is required. Such mass resolution power cannot be used for particle analysis because of the loss in transmission, which avoids the detection of such low signals. These interferences may be all the more problematic (1) when Pu is present as a trace or minor element such as in MOX fuel or irradiated fuel, or (2) in the case of weapon grade Pu where the 240Pu concentration is low, of the order of a few atom percent. To our knowledge, no hydride correction was attempted in any of the cited studies. Contrary to U samples, for which the hydride formation rate can be easily measured using the 238UH/238U ratio, no easy way can be used for the determination of the Pu hydride ratio because mPuH+ ions are interfered by m+1Pu+ ions. Ranebo et al.28 managed to measure the Pu hydride from synthetised mono dispersed Pu particles based on an isotopically pure 242Pu material. They reported a 242PuH/242Pu ratio of around 7 × 10−3, which is in the range of the U hydride ratios they also measured in the U and mixed U–Pu particles they produced. In addition, it should be borne in mind that the hydride formation rate is not a value determined once and for all, but depends largely on the analytical parameters and on the nature of the materials analyzed, and should therefore ideally be determined using standards as similar as possible in nature to the micro-objects of interest, and analyzed, if possible, during the same analytical session as the particles of interest. Nevertheless, such an isotopically pure 242Pu material was not available in the laboratory, and assumptions had to be made to estimate the hydride Pu rate and calculate the 240Pu/239Pu isotopic ratio in Pu bearing particles. These assumptions mainly rely on the similar behaviours of Pu and U hydrides.22,26,27,29 For instance, Ranebo et al. estimated the U hydride rate using the 236/235U ion ratio measured in particles coming from a nuclear weapon material remaining from the Thule accident and used it to give the upper and lower bounds of the real 240Pu/239Pu atom ratio.22 However, as explained by the authors, this H rate is overestimated due to the presence of 236U in the Thule particle. More generally, in the case of a mixed U–Pu material, there are two sources of 236U: the U source material itself and the 236U produced by the decay of 240Pu. Furthermore, in this second case, the amount of 236U that is produced by the 240Pu decay depends on the isotopic composition of Pu, the Pu content and the age of the mixed U–Pu material. This information, along with the isotopic composition of the original uranium, is usually not known at the time of analysis, making it virtually impossible to estimate the amount of 236U. For instance, in the case of the MOX samples that were measured in this study, the 236U content may be calculated using the reference values and resulted in a 236U/235U atomic ratio of about 0.04, which is higher by a factor of 10 to 100 than the 238UH/238U ratio measured on standard U. At least, such hydride rate estimation cannot be applied on a pure Pu material. Consequently, such internal hydride correction was not considered in this paper. In a previous study,29 we demonstrated that an external hydride correction can be applied to Pu in order to improve the accuracy of 240Pu/239Pu isotopic measurements conducted on weapon grade Pu and mixed U–Pu particles. This correction was based on the measurement of the average 238UH/238U ratio on standard U particles. In this paper, we used the same principle, namely measuring an external U hydride ratio to correct the 240Pu/239Pu isotopic ratio, but proposed a novel approach by using a time dependent hydride correction in order to take into account the decrease in the hydride ratio along the analysis. Furthermore, we developed a methodology allowing the simultaneous measurement of the U and Pu isotopic compositions using the multi-collection device of the LG-SIMS. We successfully applied this new methodology to µm-sized particles from three weapon grade Pu samples and three MOX samples with a Pu content ranging from 1 atom % to 10 atom %. In addition, the methodology was also used to measure the U/Pu relative sensitivity factor, RSF, that is required to quantify the Pu content in MOX. The RSF determination is based on the measurement of the 235U/239Pu ratio in well purified Pu particles of known purification date.30 The same approach was applied by Wallenius et al. and the RSF was used to determine the age of Pu particles.19 In summary, in this publication, we (1) show that a time-dependent hydride correction
can be applied to Pu or MOX particles thanks to modeling of the evolution of the 238UH/238U ion ratio over time, (2) demonstrate the capabilities of LG-SIMS to detect and differentiate U, Pu and mixed U–Pu particles using APM analyses, (3) measure the accurate 240Pu/239Pu atom ratio in weapon grade Pu particles and (4) simultaneously measure the 240Pu/239Pu atom ratio, the U isotopic composition and the 239Pu/238U atom ratio in MOX particles.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
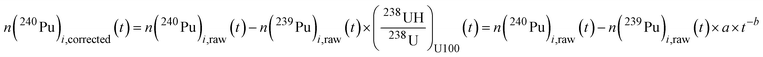

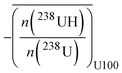 is the mean H ratio obtained from the NBS U-100 particle analyses during the same analytical session.
is the mean H ratio obtained from the NBS U-100 particle analyses during the same analytical session.




 ratio measured over all analytical sessions
ratio measured over all analytical sessions
 : standard deviation of the hydride ratios measured over all analytical sessions.
: standard deviation of the hydride ratios measured over all analytical sessions.










