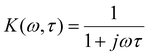Open Access Article
Open Access ArticleMeasurement, interpretation, and application of electrochemical impedance spectroscopy to lithium-ion batteries
Yuhao
Zhang
a,
Jiayuan
Xu
a,
Xinyi
Xie
a,
Qiu-An
Huang
*b,
Shijie
Cheng
a and
Jia
Xie
 *a
*a
aState Key Laboratory of Advanced Electromagnetic Engineering and Technology, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, P. R. China. E-mail: ziqizeng@hust.edu.cn; xiejia@hust.edu.cn
bFaculty of Physics/College of Sciences, Shanghai University, Shanghai 200444, P. R. China. E-mail: hqahqahqa@163.com
First published on 9th December 2025
Abstract
With the widespread application of lithium-ion batteries, thermal safety and state monitoring have emerged as critical issues that hinder the advancement of high-energy-density battery systems. Faced with the above challenges, multidimensional sensing technologies such as gas, pressure, temperature, imaging, and sound have been explored for critical alerts. But the effect is not satisfactory. For instance, traditional temperature sensing technologies, constrained by localized measurement hysteresis and insufficient spatial resolution, struggle to rapidly and in real-time capture the dynamic evolution of internal thermal anomalies in batteries. In contrast, electrochemical impedance spectroscopy (EIS) serves as a non-invasive diagnostic technique that elucidates internal electrochemical–thermal coupling mechanisms through frequency response analysis. This approach paves the way for innovative paradigms in thermal state monitoring and health management of lithium battery systems. The present paper systematically reviews the latest advancements in EIS technologies pertaining to battery safety, focused on analyzing innovations in impedance measurement chips and devices, impedance data processing algorithms, and impedance-based intelligent applications. Our primary objective is to promote the implementation and widespread adoption of high-reliability, low-cost battery management systems utilizing alternating current (AC) impedance.
Broader contextAs the global energy system undergoes an unprecedented transition toward electrification, lithium-ion batteries have emerged as a critical technology for integrating renewable energy and enabling electric mobility. This energy transition has exposed key flaws in existing battery safety frameworks, as traditional monitoring methods are unable to effectively address the complex interplay between electrochemical kinetics and thermodynamics under large-scale conditions. Different from traditional single-temperature sensing, Electrochemical Impedance Spectroscopy (EIS) enables timely warnings of safety issues because it provides wide-band and high-precision kinetic information from bulk to interfaces. The emergence of chip-level EIS measurement solutions and impedance deconvolution technologies based on DRT is driving a shift in safety measures from reactive responses to a predictive battery health ecosystem. These advancements have profound implications for expanding secondary battery applications, optimising fast-charging protocols, and achieving safe battery architectures. |
1. Introduction
The global energy infrastructure is at a critical juncture, facing the challenges of surging electricity demand and increasingly severe environmental pollution issues. Although fossil fuels still dominate the current primary energy supply, related carbon neutrality regulations and policies have significantly spurred an unprecedented expansion of renewable energy.1,2 Meanwhile, the levelized cost of electricity (LCOE) for solar and wind power is gradually decreasing, coupled with rapid breakthroughs in energy storage technology, enabling renewable energy projects to achieve scalable profitability for the first time. As a result, global green capital is rapidly converging towards the renewable energy sector.3With the rapid development of new energy technologies, lithium-ion batteries, as the current representative energy storage medium, have seen substantial expansion in both demand scale and application scenarios.4–6 Although the battery systems demonstrate excellent performance metrics in terms of energy/power density,7 cycle life,8 and capacity retention,9 the thermal safety issues under different operating conditions,10 particularly the severe consequences induced by thermal runaway,11 impose more stringent technical requirements on the accompanying safety management systems. For practical applications, current energy storage systems have established a multimodal collaborative safety monitoring framework, utilizing information such as temperature, pressure, gas, SOC, and crack formation as early warning indicators, supplemented by multidimensional sensing technologies.12–14 Usually, Battery Management Systems (BMSs) can effectively prevent and provide early warnings for safety risks due to mechanical and electrical abuse by means of electrical signal-based voltage monitoring, over-voltage protection, current limiting, balancing, and disconnection.15–18 However, there is currently no highly reliable method to provide safety warnings for thermal abuse.11,19 The problem of thermal abuse has become increasingly severe due to significant temperature differences between the inside and outside of the battery, which are not only difficult to monitor but also have hysteresis effects. Moreover, common temperature monitoring methods struggle to balance cost and efficiency. Thermistors are low-cost but have a slow thermal response and limited accuracy; thermocouples provide high-precision measurements and have a rapid thermal response, but they are expensive and susceptible to noise interference;20 resistance temperature detectors (RTDs) face challenges such as large size and manufacturing difficulties. New temperature sensing techniques, such as Fiber Bragg Grating (FBG) sensors,21–23 in spite of being compact and potentially integrable within the battery, still face considerable challenges regarding feature analysis and the onboard application of optical signals. Furthermore, conventional monitoring of voltage, current, and even pressure and gas offers limited assistance for real-time temperature monitoring.
In contrast, the impedance characteristics of batteries exhibit a strong correlation with temperature over a wide temperature range. In most thermal abuse scenarios, the changes in relevant impedance characteristics are notably pronounced and generally occur earlier than the onset of thermal runaway. In addition, within the battery module, issues such as connector aging,24 contamination,25 and looseness can be monitored through DC resistance measurements, while problems like battery aging, localized lithium plating, and electrolyte corrosion can be evaluated through AC impedance measurements. Due to the need for a certain amplitude of current in DC resistance measurement, it can also be equivalently represented by AC impedance around 1 kHz, thus standardizing DC resistance acquisition into AC impedance measurement. It is essential to emphasize that, given the current trend of increasing capacity in individual battery cells, the welding impedance between the cell and the tab has become comparable to the internal resistance of the battery unit itself, and the safety risks from the connection should not be ignored.
In summary, the current temperature sensors and the associated integration challenges pose an urgent need for non-invasive thermal safety monitoring methods.26 Faced with the above demands, Electrochemical Impedance Spectroscopy (EIS) might provide a new approach, not only for temperature detection inside batteries but also for other safety monitoring of batteries.27 EIS has attracted increasing attention in evaluating electrode performance, diagnosing kinetic mechanisms, and monitoring the operating state of LIBs. Therefore, review articles on battery impedance continue to emerge. These reviews are mainly concentrated on the following aspects.
(1) Fundamental concepts. Orazem et al. presented EIS as a transfer function technique applied to electrochemical systems.28 Lazanas et al. gave a tutorial for EIS from the theoretical background, the principles, and applications in detail.29
(2) Theoretical models. Single et al. took planar electrodes as an example to derive a physics-based impedance model in which a SEI is considered.30 Chen et al. also reviewed how to model porous electrodes and how to apply the developed models to LIBs.31
(3) Fast measurement. Wang et al. reviewed the impedance measurement for onboard battery management.32
(4) Typical applications. Mc Carthy et al. reviewed how to use EIS to estimate SOC, SOH, and temperature for LIBs.33 Qu et al. briefly reviewed how to probe process kinetics using EIS of batteries.34 Iurilli et al. reviewed how to characterize and model the aging phenomena using EIS of LIBs.35 Hu et al. gave a critical review on rapidly developing impedance techniques for degradation and aging investigation of LIBs.36
(5) Broad range introductions. Concentrated on EIS, Vivier et al. systematically reviewed model development, measurement model analysis, and model interpretation in terms of the proposed reaction mechanism.37 Du et al. reviewed impedance definition, impedance acquisition, impedance analysis, and impedance application for LIBs.38 Meddings et al. critically assessed impedance measurement, calibration, interpretation, validation, and equivalent circuit models, all of which are applied to commercial LIBs.39
Although there are abundant literature reviews on impedance spectroscopy, most of them were focused on basic concepts, theoretical models, rapid testing, typical applications, and broad range introductions. Up to now, there is a lack of a systematic review on testing methods, testing safety, testing nonlinearity, data validation, and data interpretation. The above contents are the premise and foundation in impedance data-driven battery safety monitoring and intelligent diagnosis. In view of this, this work reviews the technological closed-loop of innovative impedance applications from measurement to processing to implementation. In detail, this work reviews these technological frontiers as follows:
(1) Classify various impedance measurement methods and devices, focusing on two mass-produced impedance measurement chips, and analyze their application prospects.
(2) Review recent advancements in impedance data acquisition, validation and interpretation, and evaluate the applicability and inherent technical limitations of various methodologies.
(3) Discuss impedance-based safety management such as SOC/SOH monitoring and temperature estimation, and investigate physics-informed thermal models and data-driven neural networks.
2 Measurement of impedance spectra
2.1 Basic knowledge of impedance measurement
Due to the strongly nonlinear and time-varying characteristics of lithium-ion batteries (LIBs), small-signal perturbation is commonly employed for AC impedance measurement. By applying small-amplitude multi-frequency AC excitation signals40 near the operating point, the system response satisfies the fundamental assumptions of causality (response solely caused by excitation), linearity (response approximately proportional to excitation), stability and boundedness (finite excitation energy and bounded response frequency range). Under these conditions, the battery's voltage or current response is measured synchronously. To express the impedance concept with the imposed time-domain excitation and response signals, the complex phasor method is typically employed. Via Fourier transform analysis at the specific frequency ω, the AC current excitation and voltage response signals are converted into their complex phasor representations: Δİ(jω) = Iejϕi and Δ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) (jω) = Uejϕu where I and U represent the magnitudes, and ϕi and ϕu denote their respective phase angles. The complex impedance at frequency ω is then calculated from the ratio of these phasors:
(jω) = Uejϕu where I and U represent the magnitudes, and ϕi and ϕu denote their respective phase angles. The complex impedance at frequency ω is then calculated from the ratio of these phasors: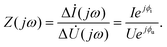 | (1) |
This formula directly provides both the magnitude and phase information of the complex impedance Z(jω), enabling the construction of detailed Nyquist plots for battery characterization. These plots effectively capture the kinetics of charge transfer reactions and conform to the causal constraints required by the Kramers–Kronig relations, thereby providing a reliable basis for the non-destructive evaluation and diagnosis of LIBs.
The typical impedance measurement is primarily sorted into two modes based on excitation signals: galvanostatic (constant current) and potentiostatic (constant potential). In large-scale battery modules, the galvanostatic mode is predominantly adopted due to advantages in current control stability and ease of realization.41 The predominant perturbation signal in EIS measurement is single-frequency sinusoidal excitation, whose key advantage lies in its highly concentrated power spectral density enabling a superior signal-to-noise ratio (SNR) and inherent noise rejection. However, it suffers from prolonged measurement durations and strong dependency on DAC module precision during waveform generation. To reduce the EIS measurement period and simplify excitation signal generation, the research focus has shifted from frequency sweep to novel strategies including multi-sine, multi-pulse, step signals, PRBSs42 and so on. These approaches leverage time-frequency domain transformations to achieve parallel multi-frequency high-gain measurements with optimized noise suppression. The characteristics and implementation of these innovative methods will be discussed in detail in the subsequent sections.
Besides, the typical Nyquist plot of LIBs usually exhibits four characteristic regions from high to low frequencies, i.e. parasitic inductance, SEI medium, charge transfer and solid–liquid diffusion, respectively. In the high-frequency region, the intersection with the real axis can be quantified as ohmic resistance, which includes contributions from electrolyte ionic conductivity, current collector contact, and separator resistance. The mid-to-high frequency semicircle represents the impedance of the solid-electrolyte interphase (SEI). A stable SEI layer manifests as a small, consistent semicircle, while repeated cycling often enlarges this feature due to SEI thickening or crack formation. In the mid-to-low frequency range, the semicircle corresponds to charge transfer resistance at the electrode surface. A larger semicircle diameter suggests sluggish reaction kinetics, which may stem from degraded active materials, insufficient electrolyte wetting, or reduced catalytic activity.43 At the lowest frequencies, the inclined line reflects lithium-ion diffusion dynamics. This region is sensitive to the particle size, porosity, solid/electrolyte diffusion coefficient, and ion transfer number, with deviations in slope often indicating inhomogeneous diffusion or phase separation.44,45
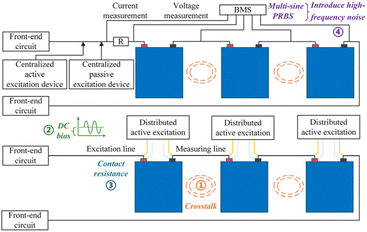
2.2 Challenges of impedance measurement
The effectiveness of EIS modules in analyzing LIBs relies on their ability to perform long-term measurements accurately. However, module-level implementation faces four major challenges: inter-cell crosstalk causing signal contamination, DC bias-induced nonlinear distortion in measurements, contact resistance compromising impedance data reliability, and high-frequency noise from advanced excitation signals degrading measurement accuracy.46 Whether adopting a centralized or distributed architecture, inherent trade-offs involving cost, complexity, robustness, and measurement bandwidth must be considered when addressing these issues. Each system configuration presents specific limitations: centralized systems are prone to DC bias and contact resistance effects, whereas distributed systems47 may encounter constraints in excitation signal amplitude, crosstalk interference, and increased costs.48 Furthermore, under dynamic operating conditions, additional polarization interference can arise, necessitating high-precision synchronous acquisition techniques to isolate artifacts and ensure measurement accuracy.49L. H. J. Raijmakers et al. and NXP Semiconductors50 noted this issue over time, revealing the crosstalk interference mechanism in multi-cell synchronous impedance measurements of battery packs (i.e. higher crosstalk at higher frequencies) through experimental and modeling approaches. This crosstalk originates from electromagnetic coupling between cells and can be expressed using the transfer function 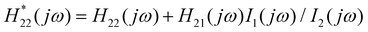 , which is very similar to the mutual inductance between coils. Importantly, their research also showed that crosstalk impedance is independent of battery temperature and SOC, simplifying both modelling and compensation. To address crosstalk, the perturbation frequencies of adjacent cells can be set to slightly different values. However, this prolongs the overall measurement period and is typically only applicable to distributed EIS systems.48 Although most EIS systems could eliminate crosstalk components by embedding transfer function matrices in impedance algorithms, it remains challenging to obtain such matrices in multi-cell coupling scenarios.50,51
, which is very similar to the mutual inductance between coils. Importantly, their research also showed that crosstalk impedance is independent of battery temperature and SOC, simplifying both modelling and compensation. To address crosstalk, the perturbation frequencies of adjacent cells can be set to slightly different values. However, this prolongs the overall measurement period and is typically only applicable to distributed EIS systems.48 Although most EIS systems could eliminate crosstalk components by embedding transfer function matrices in impedance algorithms, it remains challenging to obtain such matrices in multi-cell coupling scenarios.50,51
The DC bias in impedance measurements fundamentally manifests as an external representation of system nonlinearity, arising from dynamic coupling between operating current and perturbation signals.46,52,53 Experimental results suggest that when the DC component exceeds fivefold the AC perturbation amplitude (Idc/Iac > 5), it induces significant Warburg impedance distortion (low-frequency phase angle deviation up to ±7°).54 This effect is particularly pronounced during the discharge, exhibiting impedance variation rates 2–3 times higher than charging states.54 To better compensate/reject the DC bias effect, the nonlinear decay characteristics of the Li-ion diffusion coefficient DLi+ need to be considered, along with a compensation formula that takes into account the enhancement of concentration polarisation coupled with harmonic mixing.
Whether using laser welding or ultrasonic welding, it relies on the contact resistance between busbars and battery terminals/tabs. In EIS measurement systems, only the approach to solder the FPC flexible circuit boards close to the battery tabs (clamped between collector bars and battery lugs) can be considered virtually free from contact resistance effects. These contact resistances from common welding methods have been extensively reported and are summarized in Table 1, where they are compared in magnitude to the ohmic resistance of high-capacity batteries. The contact resistance of connectors may vary with pressure during soldering, contact area, and surface roughness. It can also increase as a result of fatigue caused by continuous vibration. Usually, it is difficult to predict these variations. Currently, they are roughly classified as components of ohmic resistance or as components of resistive/inductive coupled interference. A uniform mean compensation is usually applied during impedance measurements according to the following formula:
| Re(Z)comp = Re(Z)meas + Mre·f + Rpar | (2) |
| Im(Z)comp = Im(Z)meas + Mim·f + Ipar. | (3) |
In the above contact resistance correction for EIS measurement, Re(Z)comp and Im(Z)comp denote the corrected real and imaginary parts, respectively; Re(Z)meas and Im(Z)meas represent the measured real and imaginary parts, respectively; Mre and Mim are the inductive compensation coefficients for the real and imaginary parts, respectively; f is the frequency; and Rpar and Ipar are the resistive compensation terms for the real and imaginary parts,47 respectively.
Finally, multi-sine perturbation and PRBS methods have become integral components of contemporary battery AC impedance measurement techniques, offering significant improvements in both speed and accuracy for impedance spectra. These approaches are particularly valuable for on-board and real-time applications where conventional frequency-sweep methods are impractical due to time constraints. A multi-sine signal can typically be expressed as:
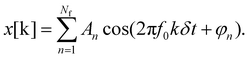 | (4) |
The superimposed multi-sine configuration maintains a relatively uniform power distribution across the frequency points of interest, resulting in lower noise amplification. Although multi-sine perturbation signals are gaining increasing recognition, the superposition of multiple signals may induce nonlinear distortion, which results in technical challenges in signal generation. To achieve better results, Kallel and Kanoun's multi-sine method enhances measurement performance by 78% time reduction (from 1440 s to 315 s) and 84% stability improvement (from 201.21 ppm to 31.70 ppm) through frequency/crest factor optimization.58 This method holds significant practical implications because it improves the stability of multi-sinusoidal impedance measurement by introducing a virtual excitation time interval that merely disturbs with no measurement under dynamic conditions, replacing the original static relaxation time. In addition, optimization methods for multi-sine perturbation signals also include the evolutionary role-playing game theory (ERPGT) based phase optimization,58 the crest factor optimization using the bee swarm algorithm,59 and the genetic algorithm-based phase optimization.60 These advanced computational methods have substantially improved the performance of multi-sine measurements, making them particularly suitable for centralized EIS applications (Fig. 1).61
 | ||
| Fig. 1 Schematic of the impedance spectra of LIBs based on small-signal perturbation measurement.36 | ||
Compared to multi-sine signals, PRBSs exhibit an approximately uniform power spectral density over the measured frequency range and have some high-frequency harmonic gain beyond the measurement band, thereby resulting in increased intrinsic noise and complexity in design/decoding signals. In spite of the above challenges, advantages such as hardware compatibility and multi-frequency acquisition make them one of the most important research directions for fast impedance measurement. Related technological innovations include third-order ternary sequences,62 which improve low-frequency performance while reducing injection amplitudes; discrete interval binary sequences (DIBSs)42 that eliminate spectral leakage and amplify target frequency energy by 4–8 times; and post-processing algorithms incorporating filtering techniques such as Gaussian filters,63 moving average filters63 and so on. In order to speed up the practical implementation of PRBSs, a unified evaluation framework is urgently required for these technological innovations.
Fig. 2 gives a brief summary of section 2.2.
2.3 Impedance measurement methods
This section summarizes various AC impedance measurement methods and the corresponding devices for lithium-ion batteries. Compared with specialized laboratory electrochemical workstations, these devices exhibit lower cost, faster measurement, higher portability, and better compatibility with BMS architectures, though with generally slightly inferior accuracy. These methods are divided into two categories: centralized EIS and distributed EIS.| Front-end circuit | Control algorithm | Range/amplitude | Time | Error | Battery |
|---|---|---|---|---|---|
| TAB DC–DC | Phase shift control64 | 0.1–200 Hz/20 A | — | — | 350 V pack 2p |
| DAB | PI/closed-loop65 | 0.1–500 Hz/2 A | — | RMSE 4% | 8 A h 6s1p |
| Boost | ACMC/DIBS66 | 0.1 Hz–1 kHz/100 mA | — | ±1.7% | 1.2 A h/2 A h |
| DC–DC | Step/DFT67 | 10 Hz–9 kHz/0.2 C | — | <3% | 2.6 A h 3s1p |
| DC–DC | Multi-sine/FIBC61 | 0.1 Hz–1 kHz/0.75 A | 150 s | <3.2% | 150 W Fuel cell |
| DC–DC | FFT68 | 0.1 Hz–5 kHz/5 A | 81 s | 5.6 mΩ | 40 A h 3s1p |
| PCC DC–DC | PI + PR/closed-loop69 | 1 Hz–2 kHz/2 A | — | — | Fuel cell stack |
| DC—DC | Three-level/PI70 | 0.1 Hz–2 kHz/0.4 A | — | — | 20 A h 6s1p |
| DC–DC | Interleaved converter71 | 0.1–100 Hz/0.1 A | — | 3.85% | 9 A h 12 V |
| DC–DC | DP control72 | 0.1 Hz–25 kHz/50 mA | 59.2 s | 1.61% | 3.35 A h |
| Full-bridge | DRBS/FFT73 | 0.1–800 Hz/0.1 C | 10.13 s | ≈3.5% | 3.5/10/50 A h |
| Full-bridge | Phase shift/dual-loop74 | 0.1 Hz–1 kHz/— | — | — | 48 V 365 A h |
| DC–AC | Dual d/q decouple75 | 0.1 Hz–10 kHz/0.5 A | 300 s | <5 mΩ | 3 A h 8s1p |
| NFC DC–AC | Multi-sine/PI76 | 0.01 Hz–4 kHz/— | — | — | 800 V 2.6 A h |
| DC–AC | PI/LCL53 | 0.1–500 Hz/400 mA | — | <4.5% | 8 A h 12s1p |
| DC–AC | PI + PR77 | 1–50 Hz/— | — | — | 2.9 A h 8s1p |
| Active | S-Transform78 | 0.1 Hz–1 kHz/0.2–1.4 A cm−2 | — | <6% | 90 kW fuel cell |
The current research mainly focuses on electric vehicle charger OBCs, electric vehicle front-end DC–DC converters, and DC–AC inverters under three-phase motor backgrounds, with the corresponding passive excitation AC impedance measurement introduction schemes designed, which matches well the actual battery peripheral circuit situation. The related scheme incurs almost no additional cost, as it can be implemented using an existing DSP controller and BMS. However, switching tube-based PWM control strategies for generating the perturbation signal also produce triangular wave noise approximating half of the switching frequency, which is inherently present in the circuit while simultaneously imposing restrictions on the highest-frequency disturbances. For application scenarios, switching frequencies of 10 kHz, 20 kHz, and 40 kHz correspond to the possible limiting disturbance frequencies of 2 kHz, 4 kHz, and 8 kHz, or even lower.69
Next, the three scenarios of electric vehicle charger OBCs, electric vehicle front-end DC–DC converters, and DC–AC inverters are discussed separately. (i) For the on-board charger, the introduction of excitation signals can help monitor the overcharging of batteries. However, a large charging current bias requires compensation of the measured low-frequency impedance in order to achieve a high-precision impedance measurement. (ii) For the front-end converter, the introduction of excitation signals can help to enhance dynamic thermal management for batteries. But due to power fluctuations, excitation signals need to be accelerated and a certain rest time should be reserved in order to achieve a high-precision impedance measurement for batteries. (iii) For the three-phase motor, the introduction of impedance measurement needs to ensure no impact on motor torque and electromagnetic power. Due to the nonlinearity caused by motor magnetic saturation, low-frequency excitation disturbances require larger currents, which bring larger AC ohmic losses while also requiring reasonable disturbance current amplitudes to be designed for the corresponding equipment.75,77 In short, these three scenarios have their own advantages and problems to be solved.
Additionally, attention should also be paid to selecting suitable control algorithms for specific control implementation. Although open-loop configurations combined with filtering elements (LC hardware filtering or DFT software filtering) can achieve sinusoidal perturbations for impedance measurements across battery terminals in certain scenarios, it is difficult for practical applications to maintain stable perturbation amplitudes and to avoid nonlinear distortion. The above difficulty significantly impedes the algorithm implementation in practical applications. Currently, perturbation schemes in various DC–DC circuits include half-bridge, full-bridge, DAB, TAB, and n-stage hybrid configurations, which predominantly employ conventional PI control strategies. Despite these strategies being effective in stabilizing routine DC, they might amplify noise for higher-frequency measurement due to the PI controller resonance under larger perturbation amplitude conditions. In order to address the above challenge, it is necessary to implement advanced control strategies such as PR controllers (enhancing specific frequency band tracking accuracy through resonant peaks) or d/q-axis transformation (converting AC quantities to DC quantities for decoupled control),69,75 aiming at expanding the frequency response bandwidth and improving the measurement precision in the high-frequency range.
Besides, multi-sine perturbation and PRBS-like algorithms can significantly improve impedance measurement speed,61,73 which are of great significance in monitoring the battery state.
A better understanding of section 2.3.1 can be realized by viewing the diagram in Fig. 3.
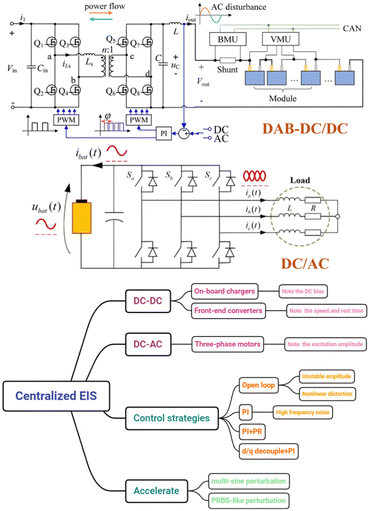 | ||
| Fig. 3 A summary of centralized EIS scenarios and control strategies.65,75 | ||
The history of the distributed EIS system is not short in academic and industrial practice. The disturbance design of this system ranges from small DC–DC circuits79 to equalization circuits,80–82 and subsequently from an on-board BMS83 to the chip-level.84 Although there are differences in development methods and technical routes, the above efforts have collectively promoted the technological maturity and commercial application of the distributed EIS system.
It should be noted that the on-board acquisition of AC impedance is straightforward. A high-precision DAC functionality or switching control algorithm is required for integrated circuits or modules to generate and amplify various current perturbation waveforms through basic external components. A high-precision analog front-end (AFE) or equivalently expressed as an ADC can synchronously acquire voltage signals. The basic computational unit is capable of analyzing AC perturbation signals and calculating the single-frequency impedance. While these functional modules have been embedded into most microcontroller units (MCUs), practically, it is still a notable challenge to achieve fast impedance acquisition for lithium batteries with a low cost. The challenge is rooted in error analysis and compensation under multi-frequency perturbations, the synchronous control of voltage and current sampling, fast impedance calculation with noise reduction, and noise suppression and filtering control in measurement circuits. Usually, it is challenging to ensure the measurement accuracy of milliohm-level impedance that truly reflects the internal characteristics of the battery without prior design, specifically for AC impedance measurement. Currently, there are two commercially available distributed EIS chips for lithium batteries: the AD5941 chip from Analog Devices Inc.85 and the DNB1168 chip from Datang NXP Co., Ltd.86 Unlike the bulky and expensive potentiostats and electrochemical workstations, these chip-level solutions have fewer peripheral components, a smaller on-board size, and a lower cost.
The AD5941 high-precision low-power analog front-end measurement chip integrates a 16-bit successive approximation ADC (with dual sampling rates of 800 kSPS and 1.6 MSPS), a 12-bit high-speed DAC, a potentiostatic biasing module, a DFT-based AC impedance data processing engine and so on.85 The company's related products include AD5933 (an earlier-generation product featuring a 12-bit ADC AFE), AD5940 (with different packaging), CN0510 (a single-cell EIS measurement system based on the AD5941 chip), and ADuCM35587 (a system-in-package chip incorporating a Cortex-M3 core processor and the same AFE as AD5941). Besides, the newly launched battery pack management chip ADBMS2970 also supports EIS and boasts up to 20 voltage measurement channels.88 If these specifications are validated, the first pack-level management chip with AC impedance modules will become true for lithium batteries. The application case of the AD5941 chip in related battery research is shown in Fig. 4.
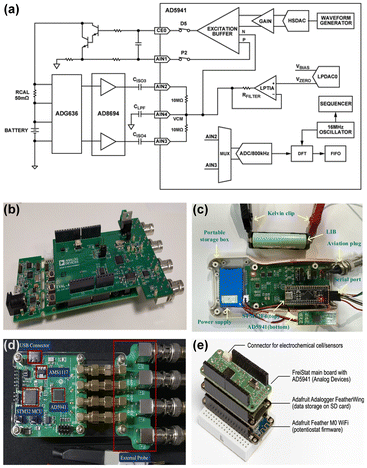 | ||
| Fig. 4 The application cases of the AD5941 chip. (a and b) Official case CN0510;85 (c) portable EIS device;89 (d) cost-effective EIS device;90 and (e) IoT-enabled device.91 | ||
In the official reference design for CN0510, the sinusoidal excitation signal is first generated using an on-chip waveform generator and 12-bit high-speed DAC, then amplified through an external Darlington transistor configuration, and finally applied to the battery. Before being routed to the ADC input pin for voltage measurement, the perturbation voltage is amplified using the gain amplifier AD8694, and parasitic capacitance is eliminated through the ADG636 multiplexer. After the amplitude and phase are extracted with the DFT module, battery impedance is calculated according to the calibration resistor Rcal:85
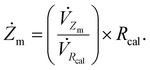 | (5) |
In other designs, in addition to modifying the original mechanical and circuit structure, Wu et al.89 incorporated a differential amplifier, AD830, to construct a broadband constant current source with DC servo loop, generating a perturbation current signal with enhanced precision. Based on the above architecture, Tran et al.90 developed a Qt-based interface. David Bill et al.91 further integrated the system into the Arduino framework for developing AD5941 across various MCU platforms. All the above innovations have greatly promoted the progress of AC impedance measurement technology.
DNB1168 represents a cell-level battery management system based on the EIS monitoring functionality embedded in the integrated circuit. This chip integrates an on-chip temperature sensor for thermal monitoring except for voltage monitoring, SPI daisy-chain communication, cell balancing operations, and so on.86 Featuring a 14-bit ADC architecture, it implements current perturbation signals through external battery balancing circuits from 7.5 mHz to 7.8 kHz. The dedicated low-frequency noise suppression circuitry further enhances impedance measurement accuracy. For practical applications, flexible printed circuit (FPC) interconnects are adopted to enable direct contact with the cell negative terminal and busbar. This configuration not only improves the measurement precision of both temperature and impedance but also eliminates conventional sampling wires and connectors. Within the Datang NXP product family, EIS solutions include DNB1101 – optimized for energy storage systems – whereas DNB1168 targets vehicular environments with AEC-Q100 automotive-grade certification.86 The relevant specific details are shown in Fig. 5.
 | ||
| Fig. 5 Relevant details of DNB1101/DNB1168.47,86 (a) Chip connection schematic diagram; (b and c) official demo. | ||
The DNB1168 series supports SPI daisy-chaining with differential I/O interfaces, enabling single-chain expansion up to 250 chips while maintaining stable communication with minimal electromagnetic interference. Current academic reports primarily focus on the official evaluation boards of the DNB1168 series, with limited documentation on optimized improvements.47,92–94 Nevertheless, partial production deployment has been achieved in industrial applications.
Definitely, distributed EIS solutions extend beyond the two aforementioned chips. For example, Young-Nam Lee et al.95 developed EIS measurement systems using custom AFEs, FPGAs, and STM32 microcontrollers; Luigi Mattia et al.83 implemented EIS battery pack measurements through FPGA and a battery management chip, L9963E; Bliss G. Carkhuff et al.96 designed a Battery Internal Temperature Sensor-based BMS (BITS-BMS). Currently, the distributed EIS system mostly combines an on-chip internal signal generator and DAC to generate sinusoidal excitation signals. In the future, it is possible to generate multi-sine signals and PRBS-like signals with the corresponding processing algorithms for faster impedance measurement in practical applications.
3 Interpretation of impedance spectra
3.1 Acquisition of impedance spectra
For on-board battery impedance measurement based on single-frequency or multi-frequency perturbations, a low-pass or band-pass filter is used to smoothen the waveforms due to the limited resolution and conversion rate of the waveform generator. However, there is no ideal filter in reality; residual high-frequency noise, phase noise, and spectral leakage, all of them together will complicate the acquisition of AC impedance from voltage/current signals in the time domain. Accurate and efficient impedance extraction algorithms can significantly reduce measurement time and computational cost, thereby facilitating the development of its applications.Currently, the two widely used impedance extraction algorithms are the multiplier scheme and the Fourier transform scheme. The multiplier scheme serves single-frequency sinusoidal perturbation and has quite a lot of advantages such as low computational cost, fast processing speed, and easy programming implementation. In addition, it can effectively suppress random white noise. However, when confronted with significant harmonic noise, its processing capability is insufficient, and if the temporal processing is not synchronized, it can introduce additional noise. The voltage response Vac to an injection current iac = a0sin(ωt) is expressed using the following equation:97,98
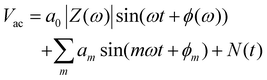 | (6) |
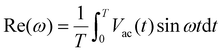 | (7) |
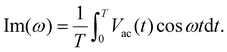 | (8) |
Usually, the integral of random noise is assumed to be zero. If the harmonic interference can be neglected, substituting eqn (5) in eqn (6) and (7) yields:97
Re(ω) ≈ a0|Z(ω)|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(ω) ϕ(ω) | (9) |
Im(ω) ≈ a0|Z(ω)|sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(ω). ϕ(ω). | (10) |
Eqn (8) and (9) indicate that under low harmonic interference conditions the real and imaginary parts of the impedance can be accurately obtained through the multiplier scheme based on the voltage signal in the time domain.
In contrast, the Fourier transform approach has undergone numerous methodological improvements during its development, such as Fast Fourier Transform (FFT), Short-Time Fourier Transform (STFT),99 and Variable Window Fourier Transform. With these technical improvements, the Fourier transform approach not only can handle single-frequency disturbance but also acts as the basis for analyzing multi-frequency disturbance. The most significant feature of this approach is to effectively suppress high-frequency noise and accurately extract single-frequency impedance. Furthermore, high-efficiency Fourier transform embedded in various kernel modules has improved processing speed in practical applications. In FFT-based EIS measurement,100 the aliased battery current yI(t) combines DC offset, multi-frequency sinusoidal disturbances, and random noise. The resulting voltage response yV(t) shares this structure. Both signals undergo Hanning windowing and optimization-based preprocessing before Fourier transform to derive YI(ω) and YV(ω). Impedance is then calculated as Z(ω) = YV(ω)/YI(ω), where the Hanning window mitigates spectral leakage in embedded systems.
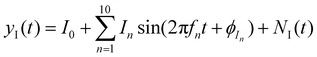 | (11) |
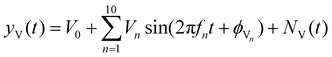 | (12) |
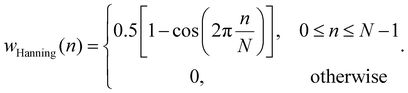 | (13) |
The Fourier transform has inherent limitations, as it extracts the frequency components from the given signal but discards the specific time location. In addition to various windowing techniques, wavelet transform and S-transform have been developed to address the above limitations. These approaches introduce innovative basis functions, leading to the discrimination of frequency characteristics in impedance extraction. Li et al.101 utilized the Complex Morlet Wavelet Transform (CMWT) to acquire and reconstruct impedance spectra in the frequency range of 0.1 Hz to 1 kHz. This method takes ∼28 seconds and achieves average phase and amplitude errors of 2.6% and 0.7%, respectively. Geng et al.102 employed Airy wavelet transform and Short Inverse Repeated Binary Sequence (SIRBS) injection to acquire impedance spectra in 10 seconds and achieved an average error of less than 1%. Besides, Yuan et al.78 used the S-transform to achieve fast calculation of impedance spectra. Under square wave excitation, the average relative error is less than 3%. Compared with the Morlet wavelet transform, S-transform saves 95% of computed time. In spite of excellent performance, these algorithms are still far away from practical application due to their complex implementations and computational requirements.
Other innovations in impedance acquisition include the filter design based on second-order generalized integrators (SOGIs)103 and digital lock-in amplifiers (DLIAs) that incorporate second-order Hilbert transforms,104 among others. These specialized designs can enhance the accuracy of impedance acquisition and reduce overall measurement time, and at the same time, they demonstrate strong feasibility in hardware implementation.
3.2 Validation of impedance spectra
Usually, the Kramers–Kronig transformation is used to assess the quality of the measured impedance data. The specific formulas are defined as follows:105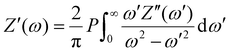 | (14) |
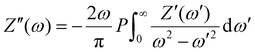 | (15) |
However, in practical impedance measurements, the limited frequency range will introduce inaccurate boundary initial values for the Kramers–Kronig transformation and will directly affect the validation accuracy. Additionally, to ensure the validation of the Kramers–Kronig transformation, the measurement density of the impedance spectra over the given frequency range must be high enough. To simplify the calculation, the linear Kramers–Kronig transformation (LKK) takes the place of the aforementioned validation. LKK is achieved by generalized linear equivalent circuit models, such as R//C parallel configurations, to approximately assess the measurement error through fitting errors. The relevant formulas are expressed as follows:106
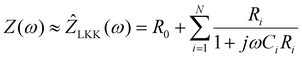 | (16) |
The Kramers–Kronig transformation is very sensitive to violations of causality and stability, but it may have poor feedback regarding violations of linear conditions.110–114 Using numerical simulations, Hirschorn et al.115 revealed that the nonlinear response in electrochemical systems originates from the potential dependence of faradaic processes. Their findings highlight that the Kramers–Kronig relation can only be used to evaluate nonlinear behavior in systems with relatively high ohmic resistance. In other cases, the relation is not very sensitive. They define the ratio Rt,obs/Re and the characteristic frequency ft. When the ratio Rt,obs/Re is small and the characteristic frequency ft is below or close to the lower limit of the measurement range, nonlinear errors exceeding 4% violate the K–K relation. When these conditions are not met, the K–K relation is less sensitive to nonlinear errors.116
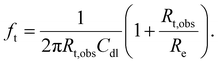 | (17) |
Some other studies117,118 have also demonstrated the aforementioned findings and have assessed the linearity of real impedance spectra experimentally. The nonlinear responses were quantitatively evaluated with respect to sensitivity for three methods: Lissajous figures, total harmonic distortion (THD), and the Kramers–Kronig relationship. It was found experimentally that nonlinear distortion mainly occurs at mid to low frequencies, specifically below the frequency ft. Lissajous figures show that nonlinear distortion is primarily manifested as changes in the shape and symmetry of the figures; however, it is a challenge for this method to determine the boundary points of nonlinearity. Regarding THD, random noise can be quantified through small perturbation harmonic analysis, but due to the heavy computation burden, it is difficult to establish accurate and universal numerical standards. In the experimental evaluation of the latter paper118 for a nonlinear response of 20 mVrms, the low-frequency Lissajous figure exhibited a distorted elliptical shape, and the low-frequency THD showed a significant increase exceeding 4%. In contrast, the Kramers–Kronig relationship was satisfied. It is only when the perturbation amplitude exceeds 60 mVrms do those violations of the Kramers–Kronig relationship occur due to its low sensitivity to nonlinearity.
Certainly, for single-frequency perturbation, the nonlinear effect can be mitigated by reducing the perturbation amplitude and applying data analysis techniques.40 However, for multi-frequency perturbation, the measurement sensitivity to nonlinear effects is markedly reduced, while the influence of amplitude limitation is concurrently weakened. The lack of visualization of Lissajous figures, the decrease in Kramers–Kronig validation sensitivity, and the increase in total harmonic distortion with ambiguous nonlinear characteristics collectively make the nonlinear assessment complex for multi-frequency perturbation. Furthermore, for the onboard impedance applications, verification after electrochemical measurement often fails to ensure that the battery state operating point is not affected by external interference. The study112 revealed the potential invalidity of the Kramers–Kronig relationship for multi-sinusoidal perturbation, while THD analysis might amplify the parasitic nonlinearity from the external measurement artifact. The optimized Kramers–Kronig transformations or THD analysis combined with the device properties may be a feasible method for assessing the nonlinearity for multi-frequency perturbation in the future.
3.3 Analysis of impedance spectra
Regarding the development of electrochemical models, the research focus has gradually evolved from the early Single Particle Model (SPM)120 to a multi-scale coupling framework. For instance, the Pseudo-Two-Dimensional Model (P2D)121 enables dynamic simulation of solid–liquid phase reactions by integrating porous electrode theory, while the Transmission Line Model (TLM)122 proposes an equivalent circuit description property for porous electrodes. Additionally, the classical Doyle–Fuller–Newman (DFN)123 model establishes a unified analysis framework from particles to electrodes to cells. Moreover, Huang et al.124 summarized the theoretical framework for the impedance response of porous electrodes. Similarly, Bai et al.119 unified the DFN-like model under various physical scenarios using the complex phasor method in order to analyze the competitive mechanisms of charge transfer reactions. These developments and progress greatly improve the understanding of charge transfer reactions in batteries.
Regarding the computational efficiency of electrochemical models, model reduction techniques have been introduced, such as the extended single particle model, polynomial approximations, and Padé approximations.125 These techniques allow for the typical impedance characteristics under specific conditions without sacrificing key dynamic characteristics. With the rapid development of computing power, electrochemical models have been increasingly applied in various application scenarios. For example, the PyBaMM (Python Battery Mathematical Modeling) tool126 employs a modular architecture design and matrix optimization techniques, reducing the basic computation time of traditional SPM, DFN models, and other physical–chemical coupling models to the millisecond level. It can be foreseen that electrochemical models will become increasingly accessible and comprehensively applied, extending from academic research to industrial applications.
Regarding the ECM method, the current focus is on how to optimize model structures and improve the reliability of parameter identification. In order to optimize the ECM structure, Warburg circuit elements are introduced to facilitate the transition from integer-order to fractional-order models. AI-based algorithms can be used to improve reliability and to accelerate the speed of parameter identification for ECMs. Table 3 summarizes the latest research development of ECMS. Some typical ECM structures expressed in circuit description codes (CDCs) are shown in Fig. 6.
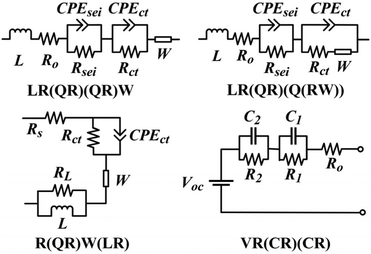 | ||
| Fig. 6 Some typical equivalent circuit models for EIS data analysis.127 | ||
| Ref. | Model structure (CDC) | Fitting error | Identification method | Application scenario |
|---|---|---|---|---|
| 128 | Various circuits | — | CNLS | EQIVCT/manually |
| 129 | Various circuits | Chi-squares 10–3 < χ2 < 10–2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
CNLS | ZsimpWin/manually |
| 131 | 26 equivalent circuits | — | CNLS | Python environment |
| 132 | R(QR)W(LR) | F min < 10–3 | PRO | Optimization |
| 130 | Selected by machine learning | Chi-squares 10–2 < χ2 < 10–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
GOA | Automated processing |
| 133 | LR(QR)(QR)W | RMSE < 0.05 | GSK | Dynamic conditions |
| 134 | LR(QR)(QR)W | RMSE 2.30% | Neural network | Automatic identification |
| 135 | CR(QR) | Success rate 0.875 | Neural network | Automatic identification |
| 127 | LR(QR)(Q(RW)) | MAPE 2.87% | Machine learning | AR-ECM/dynamic |
| 136 | VR(CR)(CR) | Min RMSE 4.893 × 10–3 | INFO | OCV estimation |
Fitting impedance data to ECMs usually adopts the complex nonlinear least-squares algorithm and mainly relies on manually-operated platforms such as EQIVCT, ZView, ZSimpWin,129 and PyEIS. The fitting accuracy generally depends on manually defined initial values and parameter locking procedures. With the rapid development of intelligent technologies, programming methods such as Python and MATLAB have accelerated automatic parameter identification, but their accuracy is still inferior to manual recognition in complex scenarios.
It must be emphasized that ECMs fail to characterize the intricate physicochemical processes in lithium-ion batteries, thereby limiting their practical applications. Luckily, the parameterization methodology marks a solid step forward in deeply understanding battery impedance characteristics.119
In essence, DRT analysis is to deconvolve frequency-domain data into time-domain relaxation time distribution functions g(τ). The logarithmic form of this function can be expressed as γ(τ) = τg(τ). This expression enhances spectral resolution and electrochemical process separability. Its most prevalent mathematical expression is given as follows:138
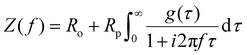 | (18) |
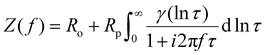 | (19) |
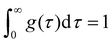 .
.
For non-ideal or fractional-order model elements such as Warburg elements and constant phase elements (CPEs), they can only be approximated by connecting in series a number of aggregate RC elements with different time constants and polarization strengths. For the inductance L parameter, with the time constant defined as t, it can be studied in generalized DRT (gDRT).139,140
From the mathematical perspective, DRT has similar properties to radial basis function expansion, and therefore can be compared and analyzed with common Fourier and Laplace transforms. The comparison results of the three transforms are shown in Table 4.
For DRT techniques, the exponential decay function e−t/τ as the central mathematical model is used to describe the relaxation dynamics. However, the non-orthogonal basis function in DRT leads to the limitation in signal decomposition. Different from the orthogonal bases in Fourier transform, the inversion transform process is essentially a pathological inverse problem because there is a certain linear correlation between the basis groups of the exponential function in DRT. Therefore, it is difficult to fully deconvolute the exponential decay components corresponding to different time constants τ with the finite frequency-domain data, and the multiple inversions in the solution space might lead to a non-unique reconstruction for the relaxation time distribution function g(τ).
To address the aforementioned challenges, regularization methods (e.g., Tikhonov regularization,141 ridge regression,142 neural networks, etc.) are introduced to constrain the solution space and incorporate additional conditions through physical prior knowledge. The regularization method could stabilize inversion results and enhance resistance to noise interference. However, this method potentially suppresses the contribution of signals with negative features. As a result, rigorous validation is necessary to prevent erroneous data interpretation due to regularization parameters. Most recently, the Bayesian probabilistic method was combined with the regularization method in order to improve back-convolution and confirm the optimal number of decoded peaks through prior knowledge and weighting matrices.142 Nevertheless, these attempts require a trade-off between computational complexity and physical interpretation, and cannot overcome the theoretical bottleneck due to the lack of orthogonality. Nowadays, the traditional inversion transforms for DRT are shifting toward machine learning-assisted inversion algorithms. In the above intelligent inversion, deep neural networks are used to learn the implicit features of relaxation processes, which are just the limitations of traditional basis functions.
Table 5 summarizes various DRT decoding technologies with respect to the optimization method, fitting error, and application scenario.
| Ref. | DRT basic method | Optimization method | Fitting error | Application scenario |
|---|---|---|---|---|
| 142 | Ridge regression | Frequency analysis | — | Optimize regularization parameter |
| 143 | Tikhonov regularization | Shape factor co-analysis | MAE < 0.425 | Optimize regularization parameter |
| 144 | Tikhonov regularization | Total outlier assessment | — | Quality-indicator-based preprocess |
| 145 | — | DRT/DDC symmetry analysis | — | Analyse the causes of pseudo-peaks |
| 146 | Hyper-λ algorithm/hierarchical Bayesian | Dual inversion framework/PFRT | — | Dual regression-classification framework/DRT valuation |
| 147 | Hierarchical Bayesian | Hyperparameter optimization | — | Bayesian estimation |
| 148 | Gaussian process | Hyperparameter optimization | Probabilistic method | |
| 149 | Loewner framework | Linear systems theory | — | Without the regularization procedure |
| 150 | FFT-based DRT | — | ε γ = 2.04 × 10–4 | Time-domain DRT extraction |
| 151 | DNN/deep-DRT | Neural network deconvolution | — | Break the limits of regularisation |
| 152 | DNN-DRT | Neural network deconvolution |
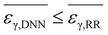
|
For negative peak deconvolution |
| 153 | ANN-DRT | ANN-assisted prediction | R 2 0.9667 | Only predict different DRT data |
Other deconvolution methods such as the Distribution of Capacitive Time (DCT)154 and the Distribution of Differential Capacity (DDC)145,155 have also regained attention. DCT first converts impedance data into admittance data, while DDC transforms complex impedance data into complex capacitance data. Subsequently, the same deconvolution operations as DRT are conducted to obtain the corresponding distribution functions. The formula expressions of related technologies are as follows:
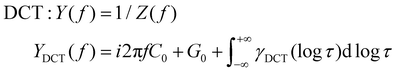 | (20) |
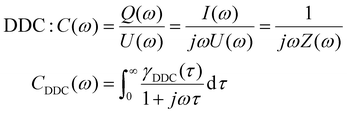 | (21) |
To complement the shortcoming of DRT technology, DCT and DDC are proposed, as defined above. Impedance spectra do not always converge at low frequencies, for example, solid–liquid diffusion impedance spectra for batteries. In this situation, DRT fails; however both DCT and DDC can directly deconvolute successfully. In addition, there is inherent symmetry between DRT and DDC methods, which includes the symmetry of the circuit structure, spectrum, deconvolution algorithm, and deconvolution results.145 Our understanding of the relaxation time characteristics for batteries is still limited. Both DCT and DDC technologies can help us obtain more accurate relaxation time distribution functions and deepen our understanding of impedance reconstruction operations.
In summary, the distribution of relaxation time is very valuable, but it is still a challenge how to precisely deconvolute impedance spectra and how to exactly understand the deconvoluted results. Artificial intelligence assisted deconvolution techniques may provide better solutions to deconvolute impedance spectra and better understand the deconvoluted results.
4 Applications of impedance spectra
4.1 Battery state estimation
In order to fully utilize energy storage systems while ensuring their safety, their state estimation becomes crucial. Among the various states of batteries, the State of Charge (SOC) and the State of Health (SOH) might be the most important. The SOC can indicate the remaining capacity of the battery and prevent overcharging or over-discharging, and the SOH can indicate capacity degradation and identify deterioration patterns.For the current battery management systems, the estimation of the SOC mainly relies on the compensated Coulomb counting method, and the estimation of the SOH mainly depends on the capacity degradation model. The compensation methods for SOC estimation typically include OCV model approaches or terminal voltage calibration at the end of discharge, rooted in the SOC–OCV mapping relationship. The degradation model methods for SOH estimation are based on the impedance characteristics. Therefore, incorporating impedance spectra into state estimation is beneficial for the compensation of the Coulomb counting method and the construction of health indicators by improving the data-driven algorithm.
Table 6 gives a brief summary of SOC estimation and SOH prediction based on impedance spectra. It should be noted that most of the state estimation algorithms reported in the literature have not been validated in practical battery management systems. In detail, both accuracy and universality of the reported state estimation algorithms also need to be strictly verified in embedded environments.
| Ref. | Type | Estimation method | Estimation error | Scenario |
|---|---|---|---|---|
| 156 | SOC | Impedance Track algorithm compensated Coulomb counting | — | Embedded application |
| 157 | SOC | Pearson's r correlation matrix analysis | GOF 0.917 | Theoretical analysis |
| 158 | SOC | Linear regression model and Gaussian process regression | <3.8% | Initial projections |
| 159 | SOC | Low-complexity machine learning based on the ECM | Accuracy 93.9% | Online application |
| 160 | SOC | Random forest combined with convolutional neural networks | R 2 0.9926 | Small sample prediction |
| 161 | SOC | Fractional-order hysteresis thermoelectric coupling model | <2.5% | Wide temperature scene |
| 162 | SOC | Fractional-order adaptive square-root cubature Kalman filter | MAE < 0.5% | BMS application |
| 163 | SOC | Fractional-order multi-innovation unscented Kalman filter | RMSE 0.28% | BMS application |
| 164 | SOH | Fractional order modelling and analysis of relaxation effects | RMSE < 1% | Empirical method |
| 165 | SOH | Deep neural network transfer learning (DNN-TL) | R 2 0.9683 | Data-driven scenario |
| 166 | SOH | 1 kHz data interpolation and correlation analysis | PE 0.241% | Quick application |
| 167 | SOH | The ratio between the real part of 0.99 Hz and 1.976 Hz | MAPE 4.46% | Quick application |
| 168 | SOH | Automatic relevance determination and Gaussian process | — | Data-driven scenario |
| 169 | SOH | Convolutional autoencoder and deep neural network | RMSE 1.29% | Unsupervised application |
| 170 | SOH | Deep neural network transfer learning (DNN-TL) | MSE 0.1117 | Prospective assessment |
| 171 | SOH | ECM with an added capacitor/Gaussian process regression | RMSE 1.77% | BMS application |
| 172 | SOH | DRT-CNN and gradient-weighted class activation mapping | R 2 0.9883 | Embedded application |
| 173 | SOH | Simplified timescale information method and DRT | RMSE 1.36% | Real-time application |
There are still some differences in the estimation framework between the SOC and SOH. SOC estimation mainly aims at improving the accuracy of Coulomb counting by the real-time compensation based on circuit models. In contrast, SOH estimation aims at extracting health features from historical operational data based on the data-driven method. This difference is rooted in the fact that the SOC can rely on Coulomb counting results as a real-time baseline with inherent confidence, while SOH estimation lacks a similar real-time data anchor. In terms of methodology, SOC solutions emphasize lightweight algorithms for data processing and compensation, while SOH implementation requires extra computational resources for pattern recognition across battery datasets. In addition, SOC estimation requires a more stringent temporal resolution and is more sensitive to deviations of the identified parameters than SOH estimation.
In order to establish a stable mapping relationship between impedance features and the SOC for batteries, it is necessary to identify or extract impedance characteristics that are strongly correlated with the SOC but independent of the SOH, temperature, and other factors. However, AC impedance not only is a comprehensive reflection of the complex and coupled physicochemical processes inside batteries, but also extremely sensitive to the SOC. Therefore, it is difficult to standardize and generalize impedance characteristics to estimate the SOC and SOH of batteries. The open-circuit voltage (OCV) compensation method for SOC estimation affects the SOH, temperature, and relaxation processes. In contrast, impedance-based SOC estimation still has significant potential for application and accuracy advantages. With Pearson's r correlation matrix analysis on the LCO battery, Mc Carthy et al.157 demonstrated that the impedance imaginary part at 10 Hz and the impedance real part at 2 Hz are very sensitive to the SOC. Furthermore, Buchicchio et al.159 demonstrated that it is possible to estimate the SOC with a very sparse impedance spectra, and also demonstrated the potential application of lightweight machine learning algorithms. To some extent, impedance features can replace the OCV-based compensation methods for SOC estimation. Moreover, incorporating impedance characteristics into the OCV method can improve the accuracy of SOC estimation. If the impedance characteristics of fractional-order impedance models are incorporated, better SOC estimation results can be obtained because fractional-order models are closer to the physical reality of batteries. For example, Chen et al.162 and Zeng et al.163 used fractional-order and Kalman filtering methods to significantly reduce the root mean square error of the SOC estimation results.
In early stages of impedance-based SOH estimation for batteries, researchers extracted initial features from raw impedance spectra based on the integer-order circuit model. Later, in order to derive more universal and widely applicable features, which can resist interference from other variables to a certain extent, complex fractional-order impedance models combined with DRT techniques are applied in machine learning algorithms and neural network models to extract impedance features. For example, Li et al.171 constructed an equivalent circuit model with additional capacitance to improve the accuracy of impedance fitting and SOH estimation with Gaussian Process Regression (GPR). Kim et al.172 used DRT to extract effective features, and train a compact Convolutional Neural Network (CNN) in embedded micro neural processing units. In spite of fewer parameters, their model demonstrated performance comparable to more complex models. Qian et al.173 used a Gradient Boosting Decision Tree algorithm combined with Simplified Time Scale Information (STI) for data-driven SOH estimation, obtained strongly correlated STI features from raw data, multiple ECM structures, and DRT data, and finally achieved an average error of 1.36%. Obregon et al.169 employed convolutional autoencoders (CAEs) to automatically extract features from impedance data, and subsequently, they used Deep Neural Networks (DNNs) to estimate the SOH, and finally, they achieved a maximum RMSE of 1.29% for test batteries. Fig. 7 summarizes four kinds of model frameworks for SOH estimation. The results suggest that most data-driven methods achieve excellent performance. These above frameworks improve the accuracy and applicability of SOH estimation, but a series of practical issues need further consideration, such as scale, computing power, and real-time. Currently, most data-driven state estimation models use uncorrelated features, whereas impedance spectra can reflect some intrinsic connections of physics. It is believed that the Physical Information Neural Network (PINN) established based on relevant features might promote better development of data-driven SOH estimation.174
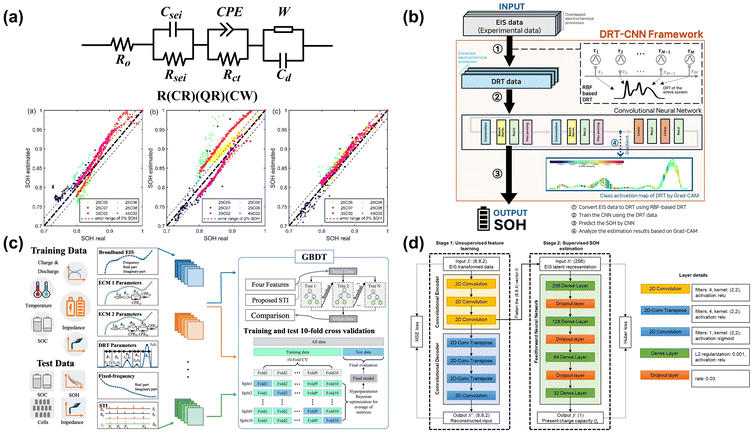 | ||
| Fig. 7 Summary of four kinds of model frameworks for SOH estimation. (a) ECMC;171 (b) DRT-CNN;172 (c) STI-GBDT;173 and (d) CAE-DNN.169 | ||
Despite promising accuracy, data-driven SOC/SOH estimation faces four implementation barriers. First, complex models exceed the computational limits of affordable hardware, preventing real-time use. Second, models trained on limited datasets fail to generalize across battery types and aging conditions. Third, scarce full-lifecycle data hinder robust validation. Finally, slow multi-frequency EIS measurements conflict with real-time operational needs. Overcoming these requires lightweight algorithms, standardized datasets, and faster impedance techniques to bridge lab and practical applications.
4.2 Battery temperature estimation
It is insufficient to monitor the surface temperature of batteries for their diverse application scenarios. Therefore, it is crucial to detect the temperature inside batteries for ensuring their safe operation and long-term cycle life. In order to obtain reliable temperature inside the battery, researchers often use temperature estimation based on electrical signals or thermal models, where AC impedance and DC resistance play an important role. Temperature has a substantial impact on charge transfer reactions in the battery and, in turn, the evolution trend of charge transfer reactions with respect to temperature can be reflected by impedance spectra. Regarding impedance-based temperature estimation, early research is mainly focused on single frequency characteristics or ECM characteristics, while current research emphasizes the integration of impedance data with machine learning models and thermal models. Relevant studies for impedance-based temperature estimation are summarized in Table 7.| Ref. | Type | Estimation method | Estimation error | Temperature range |
|---|---|---|---|---|
| 175 | Feature | The real part at 10.3 kHz/Arrhenius equation fitting | MAPE < 2.5 K | 0–30 °C/transient |
| 176 | Feature | 10\50\100 Hz phase shift/impedance matrix analysis | — | −10/20/50 °C |
| 177 | Feature | 200 Hz impedance data/parametric fitting | RMSE 1.41 °C | 10–55 °C |
| 48 | Feature | 133 and 630 Hz impedance data/Monte Carlo simulations | MAPE ± 1 °C | −20–50 °C |
| 178 | Feature | Zero-crossing frequency fzero/Newton–Raphson method | MAE 1.2 °C | −20–50 °C |
| 179 | Feature | 10 Hz impedance data/Pearson correlation coefficient | RMSE 0.79 °C | 0–60 °C |
| 180 | Feature | SEI layer impedance phase/DRT-based frequency selection | RMSE < 1% | −10–50 °C |
| 181 | Feature | The imaginary part at 600\800\1000 Hz/Arrhenius-like function | RMSE < 2.19 °C | −10–60 °C |
| 182 | Feature | 850 mHz–3.15 kHz EIS data/least squares estimator | RMSE < 0.6 °C | −20–20 °C |
| 183 | Feature | The imaginary part at 26.83\273.27\377.45 Hz/GPR | RMSE < 1.12 °C | 10–50 °C |
| 184 | Model | Voltage, current, and EIS data/multi-layer perceptron model | MAPE 1.086 °C | 0–30 °C |
| 185 | Model | EIS data/DRT and six machine learning methods | MAE < 0.319 °C | 0–30 °C |
| 186 | Model | EIS data/artificial neural networks (ANNs) | ΔT = 1 K | 10–60 °C |
| 187 | Model | Voltage, current, and EIS data/LSTM-RNNs | RMSE < 0.46 °C | −20–50 °C |
| 188 | Model | Voltage, current, and the 215 Hz data/coupled electrothermal model | RMSE 0.23% | 8–30 °C |
| 189 | Model | Voltage, current, and the pulse test/second-order RC ETCM | MAE 3.09% | 15–45 °C |
| 190 | Model | R ohm\Rct\τd\Rth\τth parameters/electrothermal model | MAPE ≤ 0.68 °C | 0–50 °C |
| 191 | Model | Internal resistance/two-step resistance transfer algorithm (RTA) | MAPE < 1.515 °C | 10–50 °C |
| 192 | Model | EIS data/fractional-order ECM and Kalman filter | MAPE < 1.5 °C | −30–80 °C |
| 193 | Model | Resistance entropy thermal model/digital twin framework | MAE < 0.73 °C | 25–45 °C |
The single frequency impedance method aims to identify the feature which is not sensitive to parameters such as the SOC and SOH but sensitive to temperature. Due to the lack of the ability to fully decouple impedance spectra, extensive thermal tests are conducted to identify the relevant features. Furthermore, we cannot exclude all other environmental interferences in a compensatory manner.119 Correlation analysis is usually used to select parameters for temperature estimations. For example, Pearson correlation coefficients or Spearman rank correlation indices can be used to assess the linear or monotonic relationships between impedance characteristics and temperature. The selected parameters require a sensitivity analysis to quantify the temperature impact on them. For the identified feature parameters, application evaluation must be conducted under normal operating conditions to avoid potential influences from the testing environment. Because different batteries may have different formulations and materials, temperature estimation based on a single feature often lacks universality. The successful temperature estimation method for a certain type of battery may result in significant estimation errors when applied to other types of batteries. Ezahedi et al.179 conducted a correlation analysis on a 70 A h large-capacity battery and found a high sensitivity to temperature at 5–25 Hz and 250–1000 Hz and a low sensitivity to SOC/SOH at 10/20/25 Hz. The Gaussian regression model based on AC impedance at 10 Hz achieved an outstanding RMSE of 0.79 °C.
The core purpose of integrating impedance data into machine learning and thermal models is to construct a nonlinear and multi-physics field framework for predicting temperature. Combining the impedance sensitivity with the nonlinear modelling capability of machine learning algorithms, and at the same time, fusing the knowledge constraints from thermodynamic models, they can to some extent address the limitations of the dimensional perception of a single impedance feature. Regarding technical implementation, machine learning can be used to establish the nonlinear mapping relationship between impedance and temperature through supervised learning, and partial decoupling of interference factors can also be achieved through unsupervised learning. Regarding the electro-thermal coupled model, it mainly involves the ECM, full-order thermal model,194 reduced-order lumped model, and thermal ECM. Among the above models, the single-cell thermal sub-model based on the lumped parameter model might be the most extensively used.188
Regarding machine learning, Liu et al.184 extracted features of ECMs with Pearson analysis and principal component analysis. Based on inductance L, charge-transfer resistance Rct, and double layer CPE parameters Y0, n0, they established multiple linear regression, Gaussian process regression, and multilayer perceptron models. Chen et al.185 used DRT to extract impedance features and found that the deconvoluted results have fewer outliers and are more stable models than the original impedance. Both Ströbel et al.186 and Zheng et al.187 validated the feasibility in using neural network models to estimate temperature. The ANN model constructed by the former186 was concise, fast, and effective, while the latter187 utilized operando impedance characteristics for real-time temperature estimation based on a long short-term memory recurrent neural network. Different from the classical static EIS, operando dynamic EIS was performed under the relaxed conditions and may violate the linearity and the smooth range.187Fig. 8 shows that both the real and imaginary parts of the operando dynamic EIS spectra are smaller than those of the classical static EIS spectra, but both exhibit the same trend of contracting towards the origin as the SOC increases. Regarding the above impedance spectra from these two measurement methods, the trend of the imaginary part and the phase angle are very similar with respect to the SOC; however, the real parts have a big difference. These results support the rationality of applying operando EIS for temperature detection.
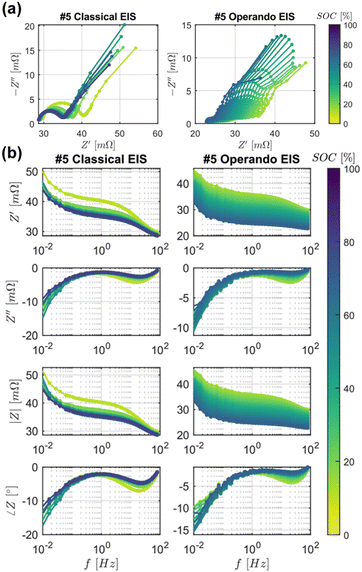 | ||
| Fig. 8 Comparison between the classical static EIS and the operando dynamic EIS. (a) Nyquist diagram; (b) Bode diagram.187 | ||
Regarding electro-thermal coupling models, both Bai et al.188 and Ma et al.189 used a second-order RC thermal circuit model to simulate the cylindrical battery, while a three-dimensional multi-grid geometric thermal model was used to simulate the blade battery. Building on this foundation, Rodríguez-Iturriaga et al.190 considered the heat generated by solid diffusion via ohmic resistance Rohm, charge transfer resistance Rct and solid state diffusion characteristic time τd. The reduced-order thermal model provides some explanatory power for battery behaviors under conditions of different ambient temperatures and charge/discharge rates.
With a two-step resistance transfer algorithm, Xie et al.191 established a thermal resistance network by replacing the lumped parameter model with a three-dimensional heat conduction equation. The presented method demonstrates superior computational speed compared to the finite element method and achieved an online value of 0.496 seconds for model computation. Based on fractional-order equivalent circuit models, Sun et al.192 developed a frequency-domain distributed multi-point thermal model, in which the circuit model is in good agreement with the offline EIS analysis. This approach used a joint Kalman filter to achieve a joint estimation of tab temperature and time-varying thermal conductivity, with a maximum error of less than 1.5 °C. Currently, Shen et al.193 integrated electro-thermal coupling models with deep learning technology. Based on experimental data, a finite element physical model was constructed to quantify the relationship between battery internal resistance and entropy production coefficient. After a convolutional neural network was integrated into the above model, the temperature field distribution could be predicted with a mean absolute error of less than 0.73 °C within 2.92 seconds. The framework constructed for temperature distribution prediction is shown in Fig. 9.
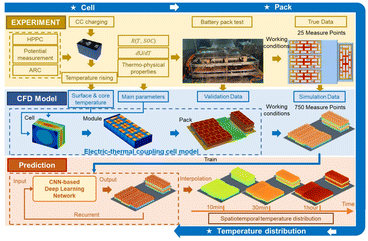 | ||
| Fig. 9 Overview of a CNN-based framework for temperature distribution prediction from cell to pack.193 | ||
While these advanced methods show promise, EIS-based temperature estimation faces unique challenges distinct from those in state estimation. A fundamental obstacle lies in decoupling the impedance response's inherent sensitivity to both temperature and state-of-health, as aging-induced degradation can mimic or mask thermal effects. Furthermore, the technique struggles with spatial resolution, providing a bulk internal value that may obscure critical localized hot spots. Translating lab-based models to real-world applications is also hindered by the complex heat transfer dynamics in battery packs, where cell-to-cell thermal interactions and cooling conditions significantly alter the core temperature–impedance relationship. Finally, achieving the required accuracy for safety-critical management under dynamic loads remains difficult, as transient conditions affect both the battery's thermal time constant and the impedance measurement itself.
4.3 Battery early safety warning
Early safety warning for batteries are extremely important, as there is often not enough time to issue warnings when thermal runaway occurs due to different reasons.195 Current methods such as gas detection, surface temperature monitoring, internal short-circuit monitoring, and pressure detection generally fail to achieve perfect integration and information fusion. If overly reliant on a single data source, it may lead to false alarms or omissions in security alerts. Under normal operating conditions, frequent false alarms from the early warning system may actually lower the vigilance of management personnel, leading to more serious consequences. As a result, early warning systems not only require enough measured data related to thermal runaway caused by various misuse and abuse but also can integrate multidimensional data to reduce false alarm rates and issue warning signals earlier. On the one hand, EIS can reflect charge transfer reactions in batteries and can issue the early warning of thermal runaway; on the other hand, the advancement for impedance-based state estimation algorithms has significantly lowered the difficulty in integrating and processing impedance data. Safety warnings solely based on impedance features might cause false alarms, which could be addressed by multidimensional data fusion with impedance features. Impedance characteristics used to issue early warning for thermal runaway have been discussed above and a summary of it is listed in Table 8.| Ref. | Type | Impedance characteristics | Alarm temperature | Scenario |
|---|---|---|---|---|
| 196 | Single frequency | Impedance phase at 40 Hz | 120 °C | TR test |
| 197 | Multi-frequency | The real part of EIS/ohmic resistance/ISC | — | Mechanical abuse |
| 198 | Single frequency | Dynamic impedance slope at 70 Hz | — | Overcharge |
| 199 | Multi-frequency | Full EIS data and DRT/DNN methods | — | ISC prediction |
| 200 | Multi-frequency | 31.62 Hz phase/circular arc/linear slope | 80 °C/120 °C/120 °C | ARC constant |
| 201 | Multi-frequency | EIS arc contraction or disappearance | 55 °C | Pulse heating |
| 202 | Single frequency | Impedance amplitude at 0.1 Hz | 82 °C/100 °C | Battery module |
| 47 | Single frequency | Impedance amplitude and phase at 1 kHz | 45 °C/90 °C/fail T | ARC constant |
| 203 | Multi-frequency | Impedance phase at 200–600 Hz | 45 °C | Charger |
| 204 | Single frequency | 400.15 Hz phase < −0.5°/stabilized-phase |Z| increase | 55 °C/100 °C | ARC constant |
In the early warning for thermal runaway based on impedance characteristics, the single-frequency feature is primarily focused on phase declination196 at specific frequencies or amplitude attenuation197 under high-temperature conditions, while multi-frequency analyses are focused on the shrinkage or variation of impedance arcs in the low-frequency regime under high-temperature conditions. Regarding warning temperatures, the arc curve change or magnitude attenuation of impedance spectra is suitable to the thermal runaway warning at relatively low temperatures, typically between 60 and 80 °C,201 while the phase and magnitude of impedance spectra transited from decreasing to increasing are suitable to the thermal runaway warning at middle temperatures, around 100 to 120 °C, which are regarded as the onset temperatures of thermal runaway in some situations. Furthermore, due to the minimal change in amplitude or phase of impedance spectra under thermal runaway conditions, single battery impedance monitoring is preferred for practical applications because the module-level impedance spectra often fail to monitor the thermal runaway. Impedance spectra are sampled at multiple dispersed mid-to-high frequency points for the purpose of capturing the dynamics of charge transfer reactions as fast as possible, and at the same time avoiding or mitigating false alarms inherent in single-frequency phase/amplitude methods. Nevertheless, these approaches may fail completely when addressing specific circuit failures such as conductor burnout or collector fracture induced by thermal runaway.201 Current research mainly aims at utilizing the impedance technique to identify the cause or root of the thermal runaway, detect overcharging and lithium plating phenomena, and actively prevent and diagnose the risk of thermal runaway from the source.198
Conclusions
In spite of many challenges and uncertainties, the engineering and practical application of EIS-based state estimation and intelligent diagnosis of batteries are becoming increasingly clear. EIS-based battery management systems facilitate a deeper monitoring and understanding of the internal states of batteries under various operating conditions. Regarding practical applications, the technical roadmap for AC impedance includes at least three key nodes: miniaturization of measurement equipment, real-time data analysis, and accuracy of electrochemical models. These three key nodes play a critical role in achieving truly intelligent state monitoring and battery management systems. Currently, the progress of various impedance measurement schemes has nearly reached the first node of the technical roadmap for EIS-based intelligent diagnosis. Driven by artificial intelligence, continuous breakthroughs have been made in both real-time data analysis and the accuracy of electrochemical models. However, transforming EIS from a research tool into industrialized, large-scale applications still faces multiple challenges, including measurement robustness, model universality, and system integration. This requires multidisciplinary collaboration and standardization efforts to drive industrial implementation.This paper comprehensively discusses EIS technology for batteries from three core aspects: AC impedance measurement, AC impedance data interpretation, and AC impedance applications.
(i) AC impedance measurement is focused on four potential sources of noise interference and centralized/distributed impedance measurement devices. Interferences such as crosstalk, DC bias, connection resistance, and ripple noise require certain considerations for impedance compensation. The design of impedance measurement equipment needs the consideration of different application scenarios in order to achieve higher speed and stability without sacrificing much accuracy.
(ii) The impedance data interpretation is focused on three key points: data acquisition, data validation, and data analysis, with emphasis on investigating data validation under various rapid measurement conditions and automatic processing of impedance data based on ECM models or DRT techniques.
(iii) How to understand impedance data for intelligent applications? Although uniquely designed impedance features perform well in some cases, further exploration in interpreting impedance data, innovative research on artificial intelligence algorithms, and theoretical development of thermoelectric coupling models, are still urgently needed in order to achieve better universality and interpretability.
In order to achieve breakthroughs in accuracy, efficiency, and intelligence for EIS-based battery management and thermal management strategies, multidimensional and systematic research and practice are required. Promising future development directions include establishing standardized EIS testing protocols and open impedance databases to facilitate comparative studies and accelerate model generalization. Integrating AI-driven interpretability frameworks with physical models will enhance the credibility and actionability of EIS-based diagnostics.205,206 Ultimately, transitioning EIS from laboratory validation to field deployment requires industry endorsement and the development of new hardware platforms.
Author contributions
Y. Zhang developed the initial concept for this review. J. Xu and X. Xie contributed to conceptual discussion and refinement. Y. Zhang conducted extensive literature search and drafted the initial manuscript. Y. Zhang and J. Xu developed the methodology for analyzing the literature, created the figures and tables, and ensured the clarity and accuracy of the visual representation. Q. Huang modified the language and conducted thorough proofreading to ensure the manuscript's clarity and readability. Y. Zhang, Q. Huang, and J. Xie reviewed and revised the paper. J. Xie guided the research direction and critically reviewed and edited the manuscript. J. Xie proposed the systematic framework and provided overall supervision of this review.Conflicts of interest
The authors declare no competing interests.Abbreviations
| ACMC | Average current-mode control |
| ADC | Analog to digital converter |
| AFE | Analog front end |
| ARC | Accelerating rate calorimetry |
| BMS | Battery management system |
| BTMS | Battery thermal management system |
| CMWT | Complex Morlet wavelet transform |
| CNLS | Complex nonlinear least squares |
| CPE | Constant phase element |
| DAB | Dual active bridge |
| DAC | Digital to analog converter |
| DCT | The distribution of capacitive time |
| DDC | The distribution of differential capacity |
| DFN | Doyle–Fuller–Newman |
| DFT | Discrete Fourier transform |
| DIBS | Discrete interval binary sequence |
| DLIA | Digital lock-in amplifier |
| DP | Discrete pulse |
| DRBS | Discrete random binary sequence |
| DRT | Distribution of relaxation time |
| ECM | Equivalent circuit model |
| EIS | Electrochemical impedance spectroscopy |
| EMF | Electromotive force |
| ERPGT | Evolutionary role-playing game theory |
| ESC | External short-circuit |
| ETCM | Electro-thermal coupling model |
| FBG | Fiber Bragg grating |
| FFT | Fast Fourier transform |
| FIBC | Floating-interleaving boost converter |
| GOA | Global optimization algorithm |
| GPR | Gaussian process regression |
| GSK | Gaining-sharing knowledge metaheuristic algorithm |
| INFO | Innovative weighted mean of vectors |
| IOT | Internet of things |
| ISC | Internal short-circuit |
| LCOE | Levelized cost of electricity |
| LKK | Linear Kramers–Kronig |
| LSTM | Long short-term memory |
| MAPE | Mean absolute percentage error |
| MCU | Microcontroller unit |
| MSE | Mean square error |
| NTC | Negative temperature coefficient |
| OBC | On-board charger |
| P2D | Pseudo-two-dimensional model |
| PDE | Partial differential equation |
| PE | Percentage error |
| PFRT | Probability function of relaxation time |
| PHM | Prognostics and health management |
| PI | Proportional integral |
| PR | Proportional resonant |
| PRBS | Pseudo-random binary sequence |
| PRO | Partial reinforcement optimizer |
| PSC | Phase shift control |
| PWM | Pulse width modulation |
| RMSE | Root mean square error |
| RTA | Resistance transfer algorithm |
| RTD | Resistance temperature detector |
| SEI | Solid-electrolyte interphase |
| SIRBS | Short inverse repeated binary sequence |
| SNR | Signal-to-noise ratio |
| SOC | State of charge |
| SOGI | Second-order generalized integrator |
| SOH | State of health |
| SPM | Single particle model |
| SPS | Samples per second |
| STFT | Short-time Fourier transform |
| TAB | Triple-active-bridge |
| THD | Total harmonic distortion |
| TLM | Transmission line model |
| TR | Thermal runaway |
Data availability
No primary research results, software or codes have been included and no new data have been generated or analysed as part of this review.Acknowledgements
This work was supported by the National Science Fund for Distinguished Young Scholars (No. 52425706) and the National Natural Science Foundation of China (No. 22479092).References
- M. Deehan, I. Renta, S. Yaary, J. Fillingham, S. Sarkar, G. Matlock, L. Newcomb, E. Bayler, J. Ghirardelli and M. Grasso, 2023 NOAA Science Report, 2024, DOI:10.25923/x0x7-f622.
- D. Raimi and R. G. Newell, Resources for the Future, Washington, DC, USA, 2024, https://www.rff.org/publications/reports/global-energy-outlook-2023 Search PubMed.
- D. Raimi, Y. Zhu, R. G. Newell and B. C. Prest, Resources for the Future, Washington, DC, USA, 2024, https://www.rff.org/publications/reports/global-energy-outlook-2024 Search PubMed.
- D. Yang, Y. Lv, M. Ji and F. Zhao, Int. J. Low-Carbon Technol., 2024, 19, 18–23 CrossRef CAS.
- A. Hamdan, C. D. Daudu, A. Fabuyide, E. A. Etukudoh, S. Sonko and J. World, Adv. Res. Rev., 2024, 21, 1984–1998 CAS.
- H. Song, C. Liu, A. M. Amani, M. Gu, M. Jalili, L. Meegahapola, X. Yu and G. Dickeson, Energy and AI, 2024, 17, 100378 Search PubMed.
- H. Niu, N. Zhang, Y. Lu, Z. Zhang, M. Li, J. Liu, W. Song, Y. Zhao and Z. Miao, J. Energy Storage, 2024, 88, 111666 CrossRef.
- M. Lecompte, J. Bernard, E. Calas, L. Richardet, A. Guignard, F. Duclaud, D. Voyer, M. Montaru, B. Crouzevialle and L. Lonardoni, J. Energy Storage, 2024, 94, 112443 CrossRef.
- Y. Li, J. Li, Y. Ding, X. Feng, X. Liu, P. Yan, M. Sui and M. Ouyang, Energy Storage Mater., 2024, 65, 103167 CrossRef.
- D. Ouyang, J. Weng, J. Hu, J. Liu, M. Chen, Q. Huang and J. Wang, J. Electrochem. Soc., 2019, 166, A559 CrossRef CAS.
- X. Feng, M. Ouyang, X. Liu, L. Lu, Y. Xia and X. He, Energy Storage Mater., 2018, 10, 246–267 CrossRef.
- J. Fan, C. Liu, N. Li, L. Yang, X.-G. Yang, B. Dou, S. Hou, X. Feng, H. Jiang and H. Li, Nature, 2025, 641, 639–645 CrossRef CAS.
- J. B. Robinson, M. Maier, G. Alster, T. Compton, D. J. Brett and P. R. Shearing, Phys. Chem. Chem. Phys., 2019, 21, 6354–6361 RSC.
- B. Gulsoy, T. Vincent, J. Sansom and J. Marco, J. Energy Storage, 2022, 54, 105260 CrossRef.
- F. Ren, T. Cox and H. Wang, J. Power Sources, 2014, 249, 156–162 CrossRef CAS.
- X. Feng, X. He, M. Ouyang, L. Wang, L. Lu, D. Ren and S. Santhanagopalan, J. Electrochem. Soc., 2018, 165, A3748–A3765 CrossRef CAS.
- H. Wang, E. Lara-Curzio, E. T. Rule and C. S. Winchester, J. Power Sources, 2017, 342, 913–920 CrossRef CAS.
- Y. Xiao, F. Yang, Z. Gao, M. Liu, J. Wang, Z. Kou, Y. Lin, Y. Li, L. Gao and Y. Chen, J. Energy Storage, 2023, 64, 107145 CrossRef.
- X. Feng, S. Zheng, D. Ren, X. He, L. Wang, H. Cui, X. Liu, C. Jin, F. Zhang and C. Xu, Appl. Energy, 2019, 246, 53–64 Search PubMed.
- Y. Y. Kee, Y. Asako, T. L. Ken and N. A. C. Sidik, J. Adv. Res. Fluid Mech. Therm. Sci., 2020, 68, 54–62 CrossRef.
- D. Chen, Q. Zhao, Y. Zheng, Y. Xu, Y. Chen, J. Ni and Y. Zhao, Sensors, 2023, 23, 5609 CrossRef CAS.
- A. Raghavan, P. Kiesel, L. W. Sommer, J. Schwartz, A. Lochbaum, A. Hegyi, A. Schuh, K. Arakaki, B. Saha and A. Ganguli, J. Power Sources, 2017, 341, 466–473 CrossRef CAS.
- A. Ganguli, B. Saha, A. Raghavan, P. Kiesel, K. Arakaki, A. Schuh, J. Schwartz, A. Hegyi, L. W. Sommer and A. Lochbaum, J. Power Sources, 2017, 341, 474–482 CrossRef CAS.
- M. Zwicker, M. Moghadam, W. Zhang and C. Nielsen, J. Adv. Join. Process, 2020, 1, 100017 CrossRef.
- P. Lyu, X. Liu, C. Liu and Z. Rao, Int. J. Heat Mass Transfer, 2023, 211, 124279 CrossRef CAS.
- R. R. Richardson, P. T. Ireland and D. A. Howey, J. Power Sources, 2014, 265, 254–261 CrossRef CAS.
- W. Ma, Y. Xie, S. Guo, W. Li, R. Yang, S. Panchal and Y. Zhang, J. Energy Storage, 2024, 102, 114066 CrossRef.
- M. E. Orazem and B. Tribollet, ChemTexts, 2020, 6, 12 CrossRef CAS.
- A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3, 162–193 CrossRef CAS.
- F. Single, B. Horstmann and A. Latz, J. Phys. Chem. C, 2019, 123, 27327–27343 CrossRef CAS.
- Z. Chen, D. L. Danilov, R. A. Eichel and P. H. Notten, Adv. Energy Mater., 2022, 12, 2201506 CrossRef CAS.
- X. Wang, X. Wei, J. Zhu, H. Dai, Y. Zheng, X. Xu and Q. Chen, eTransportation, 2021, 7, 100093 CrossRef.
- K. Mc Carthy, H. Gullapalli, K. M. Ryan and T. Kennedy, J. Electrochem. Soc., 2021, 168, 080517 CrossRef.
- D. Qu, W. Ji and H. Qu, Commun. Mater., 2022, 3, 61 CrossRef.
- P. Iurilli, C. Brivio and V. Wood, J. Power Sources, 2021, 505, 229860 CrossRef.
- W. Hu, Y. Peng, Y. Wei and Y. Yang, J. Phys. Chem. C, 2023, 127, 4465–4495 CrossRef.
- V. Vivier and M. E. Orazem, Chem. Rev., 2022, 122, 11131–11168 Search PubMed.
- X. Du, J. Meng, Y. Amirat, F. Gao and M. Benbouzid, J. Energy Chem., 2024, 95, 464–483 Search PubMed.
- N. Meddings, M. Heinrich, F. Overney, J.-S. Lee, V. Ruiz, E. Napolitano, S. Seitz, G. Hinds, R. Raccichini and M. Gaberšček, J. Power Sources, 2020, 480, 228742 CrossRef.
- J. R. Macdonald, W. B. Johnson, I. Raistrick, D. Franceschetti, N. Wagner, M. McKubre, D. Macdonald, B. Sayers, N. Bonanos and B. Steele, Impedance spectroscopy: theory, experiment, and applications, John Wiley & Sons, 2018 Search PubMed.
- J. R. Macdonald, Ann. Biomed. Eng., 1992, 20, 289–305 CrossRef PubMed.
- W.-h. Li, Q.-a. Huang, W.-m. Yang, C.-p. Yang and J.-j. Zhang, J. Electrochem., 2020, 26, 10 Search PubMed.
- W. Choi, H.-C. Shin, J. M. Kim, J.-Y. Choi and W.-S. Yoon, J. Electrochem. Sci. Technol., 2020, 11, 1–13 CrossRef.
- S. S. Zhang, K. Xu and T. Jow, Electrochim. Acta, 2006, 51, 1636–1640 CrossRef.
- I. Santos-Mendoza, J. Vázquez-Arenas, I. González, G. Ramos-Sánchez and C. Castillo-Araiza, Int. J. Chem. React. Eng., 2019, 17, 20180095 Search PubMed.
- X. Wang, X. Wei, J. Zhu, H. Dai, Y. Zheng, X. Xu and Q. Chen, eTransportation, 2021, 7, 100093 CrossRef.
- Y. Li, L. Jiang, N. Zhang, Z. Wei, W. Mei, Q. Duan, J. Sun and Q. Wang, J. Energy Chem., 2024, 92, 74–86 CrossRef.
- H. Beelen, K. Mundaragi Shivakumar, L. Raijmakers, M. Donkers and H. J. Bergveld, Int. J. Energy Res., 2020, 44, 2889–2908 CrossRef.
- J. P. Christophersen, W. H. Morrison, J. L. Morrison, C. G. Motloch and D. M. Rose, IEEE Aerospace Conference, 2012, pp. 1–16.
- L. Raijmakers, K. M. Shivakumar, M. Donkers, M. Lammers and H. Bergveld, IFAC-PapersOnLine, 2016, 49, 42–47 CrossRef.
- L. Raijmakers and Delft University of Technology, 2018, ISBN 978-94-6228-861-4.
- M. Oldenburger, B. Beduerftig, A. Gruhle, F. Grimsmann, E. Richter, R. Findeisen and A. Hintennach, J. Energy Storage, 2019, 21, 272–280 CrossRef.
- X. Wei, X. Wang and H. Dai, Energies, 2018, 11, 64 CrossRef.
- E. Karden, S. Buller and R. W. De Doncker, J. Power Sources, 2000, 85, 72–78 CrossRef CAS.
- M. J. Brand, E. I. Kolp, P. Berg, T. Bach, P. Schmidt and A. Jossen, J. Energy Storage, 2017, 12, 45–54 CrossRef.
- M. J. Brand, P. A. Schmidt, M. F. Zaeh and A. Jossen, J. Energy Storage, 2015, 1, 7–14 CrossRef.
- C. Bolsinger, M. Zorn and K. P. Birke, J. Energy Storage, 2017, 12, 29–36 CrossRef.
- A. Y. Kallel and O. Kanoun, J. Energy Storage, 2023, 58, 106267 CrossRef.
- F. M. Janeiro, Y. Hu and P. M. Ramos, Measurement, 2020, 150, 107040 CrossRef.
- Z. Guo, Q. Wang, W. Yang, M. Hu, G. Wang, D. Lu, M. Bai and C. Lyu, 2022 17th ICIEA, 2022, 1252–1256 Search PubMed.
- Z. Liu, X. Wang, G. Chang, H. Yuan, W. Tang, X. Wei and H. Dai, IEEE Trans. Power Electron., 2024, 39, 16826–16838 Search PubMed.
- J. Sihvo, D.-I. Stroe, T. Messo and T. Roinila, IEEE Trans. Power Electron., 2019, 35, 2548–2557 Search PubMed.
- J. Sihvo, T. Roinila and D.-I. Stroe, IEEE Trans. Ind. Electron., 2020, 68, 4916–4926 Search PubMed.
- S. A. Assadi, Z. Gong, C. F. Wang, J. Piruzza, J. Xu, D. Jokic, S. Sarofim and O. Trescases, 2022 IEEE APEC, 2022, 1056–1063 Search PubMed.
- X. Wang, X. Wei, Q. Chen and H. Dai, IEEE Trans. Ind. Electron., 2020, 68, 7380–7390 Search PubMed.
- H. H. Abbasali and S. J. Ashtiani, IEEE Trans. Instrum. Meas., 2022, 71, 1–8 Search PubMed.
- J. A. A. Qahouq and Z. Xia, IEEE Trans. Ind. Electron., 2017, 64, 7019–7029 Search PubMed.
- S. R. Islam and S.-Y. Park, IEEE Trans. Ind. Appl., 2019, 56, 1661–1669 Search PubMed.
- J. Shen, H. Homayouni and J. Wang, IEEE Trans. Ind. Electron., 2020, 68, 8819–8828 Search PubMed.
- O. M. Faloye and P. Barendse, 2019 IEEE ECCE, 2019, 2682–2689 Search PubMed.
- S. K. Dam and V. John, IEEE Trans. Ind. Appl., 2017, 54, 1502–1512 Search PubMed.
- J. Sha, X. Li and G. Qiu, IEEE Trans. Power Electron., 2024, 39, 14167–14171 Search PubMed.
- K. Zhang, R. Xiong, S. Qu, B. Zhang and W. Shen, IEEE Trans. Transp. Electrif., 2024, 1–1, DOI:10.1109/tte.2024.3362992.
- V.-T. Doan, V.-B. Vu, H.-N. Vu, D.-H. Tran and W. Choi, 2015 9th ICPE-ECCE Asia, 2015, 1644–1649 Search PubMed.
- H. Qu, D. Luo, D. Jiang, M. Zhou, X. Zhao and W. Sun, IEEE Trans. Power Electron., 2025, 40, 3490–3504 Search PubMed.
- K.-P. Liu, G. Orfanoudakis, S. M. Sharkh and A. Cruden, 2023 IEEE 14th SDEMPED, 2023, 606–612 Search PubMed.
- H. Qu, B. Li, M. Zhou, D. Jiang and W. Sun, ICPE 2023-ECCE Asia, 2023, 3138–3143 Search PubMed.
- H. Yuan, R. Du, X. Wang, X. Wei and H. Dai, IEEE Trans. Ind. Electron., 2022, 70, 3740–3750 Search PubMed.
- L. Wang, X. Zeng, L. Chen, L. Lv, L. Liao and J. Jiang, J. Electrochem. Energy Convers. Storage, 2025, 22, 011008 CrossRef CAS.
- E. Din, C. Schaef, K. Moffat and J. T. Stauth, IEEE Trans. Power Electron., 2016, 32, 5688–5698 Search PubMed.
- P.-H. La and S.-J. Choi, 2021 IEEE APEC, 2021, 975–980 Search PubMed.
- G. Chen, W. Liu, S. Wang, K. Yang, Z. Song and J. Meng, 2024 21st ICHQP, 2024, 236–241 CAS.
- L. Mattia, G. Petrone, F. Pirozzi and W. Zamboni, J. Energy Storage, 2024, 81, 110330 CrossRef.
- N. Datang, Battery Management IC (DNB1168), 2014 Search PubMed.
- AD5941 product description, https://www.analog.com/en/products/ad5941.html.
- DNB1168 product description, https://www.datangnxp.com/details/products/43.
- ADuCM355 product description, https://www.analog.com/en/products/aducm355.html.
- ADBMS2970 product description, https://www.analog.com/en/products/adbms2970.html.
- J. Wu, W. Bai, L. Zhang, X. Zhang, H. Lin, H. Dai, J. Liu, F. Zhang and Y. Yang, J. Energy Storage, 2024, 84, 110856 CrossRef.
- N. L. Tran, N. Q. Ha-Phan, T. L. Phan, C. T. S. Ching and M. K. Ha, IEEJ Trans. Electr. Electron. Eng., 2024, 19, 1730–1736 CrossRef.
- D. Bill, M. Jasper, A. Weltin, G. A. Urban, S. J. Rupitsch and J. Kieninger, Anal. Chem., 2023, 95, 13003–13009 CrossRef CAS.
- L. Wang, X. Zhao, Z. Deng and L. Yang, J. Energy Storage, 2023, 57, 106275 CrossRef.
- Q. Li, D. Yi, G. Dang, H. Zhao, T. Lu, Q. Wang, C. Lai and J. Xie, World Electr. Veh. J., 2023, 14, 321 CrossRef.
- G. Huang and X. Zhu, 2024 9th ICETIS, 2024, 144–147 Search PubMed.
- Y.-N. Lee, S.-W. Jo, G. Rahim, S.-G. Lee and K. Kwon, IEEE Trans. Ind. Electron., 2025, 72, 3202–3212 Search PubMed.
- B. G. Carkhuff, P. A. Demirev and R. Srinivasan, IEEE Trans. Ind. Electron., 2018, 65, 6497–6504 Search PubMed.
- H. Homayouni, J. DeVaal, F. Golnaraghi and J. Wang, IEEE Trans. Transp. Electrif., 2018, 4, 418–431 Search PubMed.
- Impedance Spectroscopy: Theory, Experiment, and Applications, ed. E. Barsoukov and J. R. Macdonald, John Wiley & Sons Inc.: Hoboken, NJ, 2005 Search PubMed.
- D. Klotz, M. Schönleber, J. P. Schmidt and E. Ivers-Tiffée, Electrochim. Acta, 2011, 56, 8763–8769 CrossRef CAS.
- P. Lu, M. Li, L. Zhang and L. Zhou, 2019 PHM-Qingdao, 2019, 1–6 CrossRef.
- W. Li, Q.-A. Huang, C. Yang, J. Chen, Z. Tang, F. Zhang, A. Li, L. Zhang and J. Zhang, Electrochim. Acta, 2019, 322, 134760 CrossRef CAS.
- A. Geng, H. Hu, Z. Zhao, J. Chen, Y. Ge, K. Wang and Z. He, IEEE Trans. Transp. Electrif., 2024, 11, 2444–2455 Search PubMed.
- S. Fan, Z. Li, C. Yu, D. Li, Y. Zhang, D. Wen and Z. Shao, IEEE Trans. Power Electron., 2024, 39, 10675–10681 Search PubMed.
- Y.-N. Lee, K.-S. Choi, S.-W. Jo, G. Rahim, K. Kwon and S.-G. Lee, 2023 I2MTC, 2023, 1–6 Search PubMed.
- M. Schönleber, D. Klotz and E. Ivers-Tiffée, Electrochim. Acta, 2014, 131, 20–27 CrossRef.
- J. Luo, X. Liang, Y. Zhang, C. Liang, H. Yassine, G. Leroy, J.-C. Carru and M. Mascot, J. Solid State Electrochem., 2021, 25, 2225–2233 CrossRef CAS.
- V. Yrjänä and J. Bobacka, Electrochim. Acta, 2024, 504, 144951 CrossRef.
- A. Y. Kallel and O. Kanoun, 2021 IWIS, 2021, 7–10 Search PubMed.
- F. Fasmin and R. Srinivasan, J. Solid State Electrochem., 2015, 19, 1833–1847 CrossRef CAS.
- M. A. Zabara, C. B. Uzundal and B. Ulgut, J. Electrochem. Soc., 2019, 166, A811 CrossRef CAS.
- R. Reséndiz, A. Rodríguez, E. Larios, J. Torres, F. Castañeda and R. Antaño-López, J. Electroanal. Chem., 2022, 904, 115879 CrossRef.
- C. You, M. A. Zabara, M. E. Orazem and B. Ulgut, J. Electrochem. Soc., 2020, 167, 020515 CrossRef CAS.
- K. J. Szekeres, S. Vesztergom, M. Ujvári and G. G. Láng, ChemElectroChem, 2021, 8, 1233–1250 CrossRef CAS.
- G. Katırcı, F. E. Civan, S. Jung, C. B. Lee and B. Ülgüt, Electrochim. Acta, 2024, 481, 143984 CrossRef.
- B. Hirschorn and M. E. Orazem, J. Electrochem. Soc., 2009, 156, C345 CrossRef CAS.
- B. Hirschorn, B. Tribollet and M. E. Orazem, Isr. J. Chem., 2008, 48, 133–142 CrossRef CAS.
- J. J. Giner-Sanz, E. Ortega and V. Pérez-Herranz, Electrochim. Acta, 2015, 186, 598–612 Search PubMed.
- J. M. Goh, C. Eluagu, J. Babauta and M. E. Orazem, J. Electrochem. Soc., 2024, 171, 036508 CrossRef.
- Y. Bai, Q.-A. Huang, K. Wu and J. Zhang, J. Energy Chem., 2024, 92, 759–798 CrossRef CAS.
- N. Hallemans, N. E. Courtier, C. P. Please, B. Planden, R. Dhoot, R. Timms, D. Howey and S. R. Duncan, J. Electrochem. Soc., 2025, 172, 060507 CrossRef CAS.
- M. Pathak, M. D. Murbach, C. Pathak, T.-J. Jang, Y. Qi, D. T. Schwartz and V. R. Subramanian, J. Electrochem. Soc., 2018, 165, A1324 CrossRef.
- X. Kong, G. L. Plett, M. S. Trimboli, Z. Zhang and Y. Zheng, J. Electrochem. Soc., 2020, 167, 013539 CrossRef.
- J. Zhao and J. A. A. Qahouq, Next Energy, 2024, 5, 100153 CrossRef.
- J. Huang, Y. Gao, J. Luo, S. Wang, C. Li, S. Chen and J. Zhang, J. Electrochem. Soc., 2020, 167, 166503 CrossRef.
- H. A. A. Ali, L. H. Raijmakers, K. Chayambuka, D. L. Danilov, P. H. Notten and R.-A. Eichel, Electrochim. Acta, 2024, 493, 144360 CrossRef.
- V. Sulzer, S. G. Marquis, R. Timms, M. Robinson and S. J. Chapman, J. Open Res. Softw., 2021, 9, 1 CrossRef.
- Q. You, Y. Zhang, R. Xiong and H. Ruan, J. Electrochem. Soc., 2025, 172, 020518 CrossRef.
- B. A. Boukamp, Solid State Ionics, 1986, 20, 31–44 CrossRef.
- B. Yeum, Ann Arbor, Michigan, USA (1999–2005), 1999 Search PubMed.
- Z. Zhao, Y. Zou, P. Liu, Z. Lai, L. Wen and Y. Jin, Electrochim. Acta, 2022, 418, 140350 CrossRef.
- K. B. Knudsen, ECS Meeting Abstracts, 2019, 235, 1937–1937 CrossRef.
- A. AbdelAty, M. E. Fouda, A. Elwakil and A. Radwan, J. Electrochem. Soc., 2024, 171, 050553 Search PubMed.
- H. Nunes, J. Martinho, J. Fermeiro, J. Pombo, S. Mariano and M. do Rosário Calado, IEEE Trans. Ind. Appl., 2024, 60, 5048–5060 Search PubMed.
- J. Wang, B. Jiang, Y. Ou, X. Wang, X. Wei and H. Dai, 2024 ITEC Asia-Pacific, 2024, 978–983 Search PubMed.
- Q. Hua and M. Shen, 2023 IEEE NorCAS, 2023, 1–6 Search PubMed.
- W. Merrouche, B. Lekouaghet, E. Bouguenna and Y. Himeur, J. Energy Storage, 2024, 76, 109891 CrossRef.
- A. Maradesa, B. Py, J. Huang, Y. Lu, P. Iurilli, A. Mrozinski, H. M. Law, Y. Wang, Z. Wang and J. Li, Joule, 2024, 8, 1958–1981 CrossRef.
- Y. Lu, C.-Z. Zhao, J.-Q. Huang and Q. Zhang, Joule, 2022, 6, 1172–1198 CrossRef.
- C. Plank, T. Rüther, L. Jahn, M. Schamel, J. P. Schmidt, F. Ciucci and M. A. Danzer, J. Power Sources, 2024, 594, 233845 CrossRef.
- M. A. Danzer, Batteries, 2019, 5, 53 Search PubMed.
- T. H. Wan, M. Saccoccio, C. Chen and F. Ciucci, Electrochim. Acta, 2015, 184, 483–499 CrossRef CAS.
- P. Carbone, A. De Angelis, A. Bertei, A. Maradesa and F. Ciucci, J. Electrochem. Soc., 2025, 172, 020533 CrossRef CAS.
- J. Wang, Q.-A. Huang, J. Wang and J. Zhang, J. Electroanal. Chem., 2024, 962, 118272 CrossRef CAS.
- N. Schlüter, T. Bergmann, S. Ernst and U. Schröder, ChemElectroChem, 2021, 8, 1167–1182 CrossRef.
- J. Wang, Q.-A. Huang, W. Li, J. Wang, Y. Bai, Y. Zhao, X. Li and J. Zhang, J. Electroanal. Chem., 2022, 910, 116176 CrossRef CAS.
- J. Huang, N. P. Sullivan, A. Zakutayev and R. O'Hayre, Electrochim. Acta, 2023, 443, 141879 CrossRef CAS.
- F. Ciucci and C. Chen, Electrochim. Acta, 2015, 167, 439–454 CrossRef CAS.
- J. Liu and F. Ciucci, Electrochim. Acta, 2020, 331, 135316 CrossRef CAS.
- A. Sorrentino, B. Patel, I. V. Gosea, A. C. Antoulas and T. Vidaković-Koch, J. Power Sources, 2023, 585, 233575 CrossRef CAS.
- B. Py and F. Ciucci, J. Electrochem. Soc., 2025, 172, 026504 CrossRef CAS.
- E. Quattrocchi, T. H. Wan, A. Belotti, D. Kim, S. Pepe, S. V. Kalinin, M. Ahmadi and F. Ciucci, Electrochim. Acta, 2021, 392, 139010 CrossRef CAS.
- E. Quattrocchi, B. Py, A. Maradesa, Q. Meyer, C. Zhao and F. Ciucci, Electrochim. Acta, 2023, 439, 141499 CrossRef CAS.
- X. Liu, Z. Yan, J. Wu, J. Huang, Y. Zheng, N. P. Sullivan, R. O'Hayre, Z. Zhong and Z. Pan, J. Energy Chem., 2023, 78, 582–588 CrossRef CAS.
- B. Py, A. Maradesa and F. Ciucci, Electrochim. Acta, 2024, 479, 143741 CrossRef CAS.
- M. Schönleber and E. Ivers-Tiffée, Electrochem. Commun., 2015, 61, 45–48 CrossRef.
- Texas Instruments BQ40Z50, https://www.ti.com/product/BQ40Z50.
- K. Mc Carthy, H. Gullapalli, K. M. Ryan and T. Kennedy, J. Energy Storage, 2022, 50, 104608 CrossRef.
- I. Babaeiyazdi, A. Rezaei-Zare and S. Shokrzadeh, Energy, 2021, 223, 120116 CrossRef CAS.
- E. Buchicchio, A. De Angelis, F. Santoni, P. Carbone, F. Bianconi and F. Smeraldi, Energy, 2023, 283, 128461 CrossRef.
- X. Zhang, L. Zhang, J. Wu, W. Bai, H. Dai, H. Lin, F. Zhang and Y. Yang, J. Electroanal. Chem., 2025, 119093 CrossRef CAS.
- J. Zeng, S. Wang, P. Takyi-Aninakwa, M. Zhang, W. Cao, C. Fernandez and J. M. Guerrero, Int. J. Circuit Theory Appl., 2025, 53, 655–680 CrossRef.
- L. Chen, W. Yu, G. Cheng and J. Wang, Energy, 2023, 271, 127007 CrossRef.
- J. Zeng, S. Wang, M. Zhang, W. Cao, C. Fernandez and J. M. Guerrero, J. Energy Storage, 2024, 86, 111283 CrossRef.
- M. Messing, T. Shoa and S. Habibi, J. Energy Storage, 2021, 43, 103210 CrossRef.
- I. Babaeiyazdi, A. Rezaei-Zare and S. Shokrzadeh, IEEE Trans. Transp. Electrif., 2022, 9, 886–895 Search PubMed.
- K. Mc Carthy, H. Gullapalli and T. Kennedy, Appl. Energy, 2022, 307, 118210 CrossRef CAS.
- Z. Pang, K. Yang, Z. Song, P. Niu, G. Chen and J. Meng, J. Energy Storage, 2023, 72, 108693 CrossRef.
- J. Wang, R. Zhao, Q.-A. Huang, J. Wang, Y. Fu, W. Li, Y. Bai, Y. Zhao, X. Li and J. Zhang, J. Power Sources, 2023, 561, 232737 CrossRef CAS.
- J. Obregon, Y.-R. Han, C. W. Ho, D. Mouraliraman, C. W. Lee and J.-Y. Jung, J. Energy Storage, 2023, 60, 106680 CrossRef.
- Y. Li, M. Maleki and S. Banitaan, J. Energy Storage, 2023, 73, 109185 CrossRef.
- C. Li, L. Yang, Q. Li, Q. Zhang, Z. Zhou, Y. Meng, X. Zhao, L. Wang, S. Zhang and Y. Li, J. Energy Storage, 2024, 86, 111167 CrossRef.
- K. Kim, K. Park, K. Yoon, H. Moon, H. Pyeon, J. Kim and S. Han, J. Power Sources, 2025, 631, 236169 CrossRef CAS.
- G. Qian, Y. Zheng, X. Li, Y. Sun, X. Han and M. Ouyang, Appl. Energy, 2025, 382, 125272 CrossRef CAS.
- Y. Luo, S. Ju, P. Li and H. Zhang, Electrochim. Acta, 2025, 525, 146110 CrossRef CAS.
- J. P. Schmidt, S. Arnold, A. Loges, D. Werner, T. Wetzel and E. Ivers-Tiffée, J. Power Sources, 2013, 243, 110–117 CrossRef CAS.
- J. Zhu, Z. Sun, X. Wei and H. Dai, J. Power Sources, 2015, 274, 990–1004 CrossRef CAS.
- K. Mc Carthy, H. Gullapalli and T. Kennedy, J. Power Sources, 2022, 519, 230786 CrossRef CAS.
- A. A. Hussein and A. A. Fardoun, IEEE Trans. Ind. Appl., 2020, 56, 3043–3051 CAS.
- S. E. Ezahedi, M. Kharrich and J. Kim, J. Energy Storage, 2024, 94, 112467 CrossRef.
- S. S. Bhoir, G. Thenaisie, C. Brivio and M. Paolone, J. Energy Storage, 2024, 97, 112754 CrossRef.
- A. Geng, H. Hu, J. Chen, Y. Ge and Z. He, IEEE Trans. Power Electron., 2025, 40, 6454–6458 Search PubMed.
- X. Du, J. Meng, J. Peng, Y. Zhang, T. Liu and R. Teodorescu, IEEE Trans. Power Electron., 2022, 37, 10101–10105 Search PubMed.
- J. Li, T. Li, Y. Qiao, Z. Tan, X. Qiu, H. Deng, W. Li, X. Qi and W. Wu, J. Energy Storage, 2025, 118, 116287 CrossRef.
- Y. Liu, L. Yang, R. Liao, C. Hu, Y. Xiao, J. Wu, C. He, Y. Zhang and S. Li, J. Energy Storage, 2024, 87, 111426 CrossRef.
- X. Chen, Q. Li, B. Shao, W. Dou, C. Lai, T. Lu and J. Xie, Energy, 2025, 320, 135493 CrossRef CAS.
- M. Ströbel, J. Pross-Brakhage, M. Kopp and K. P. Birke, Batteries, 2021, 7, 85 CrossRef.
- Y. Zheng, Y. Che, J. Guo, N. A. Weinreich, A. Kulkarni, A. Nadeem, X. Sui and R. Teodorescu, IEEE Trans. Power Electron., 2024, 39, 13853–13868 Search PubMed.
- W. Bai, X. Zhang, Z. Gao, S. Xie, K. Peng and Y. Chen, Int. J. Energy Res., 2023, 2023, 4021256 CrossRef.
- X. Ma, Y. Zhang, R. Liu, P. Chang, D. Li, G. Bai and S. Liu, Appl. Therm. Eng., 2025, 269, 126063 CrossRef.
- P. Rodríguez-Iturriaga, V. M. García, S. Rodríguez-Bolívar, E. E. Valdés, D. Anseán and J. A. López-Villanueva, Appl. Energy, 2024, 367, 123327 CrossRef.
- Y. Xie, W. Ma, W. Li, R. Yang, X. Hu, Y. Luo and Y. Zhang, IEEE Trans. Power Electron., 2025, 40, 7453–7465 Search PubMed.
- Y. Sun, Z. Zhang, Y. Jin, R. Cao, B. Xu, X. Liu and S. Yang, Int. J. Heat Mass Transfer, 2024, 235, 126157 CrossRef CAS.
- K. Shen, Y. Ling, X. Meng, X. Lai, Z. Zhu, T. Sun, D. Li, Y. Zheng, H. Wang and C. Xu, J. Energy Storage, 2025, 113, 115676 CrossRef.
- S. Ludwig, M. Steinhardt and A. Jossen, Batteries, 2022, 8, 60 Search PubMed.
- Y. Dai and A. Panahi, Next Energy, 2025, 6, 100186 CrossRef.
- R. Srinivasan, P. A. Demirev and B. G. Carkhuff, J. Power Sources, 2018, 405, 30–36 CrossRef CAS.
- M. Spielbauer, P. Berg, M. Ringat, O. Bohlen and A. Jossen, J. Energy Storage, 2019, 26, 101039 CrossRef.
- N. Lyu, Y. Jin, R. Xiong, S. Miao and J. Gao, IEEE Trans. Ind. Electron., 2021, 69, 1929–1936 Search PubMed.
- B. Cui, H. Wang, R. Li, L. Xiang, J. Du, H. Zhao, S. Li, X. Zhao, G. Yin and X. Cheng, J. Power Sources, 2023, 563, 232824 Search PubMed.
- P. Dong, Z. Liu, P. Wu, Z. Li, Z. Wang and J. Zhang, J. Electrochem. Soc., 2021, 168, 090529 CrossRef CAS.
- S. Yang, X. Wang, S. Zhou, Y. Zhuang, H. Jin, J. Chen, J. Liu, Z. Gao, X. Zhou and Q. Wang, J. Energy Storage, 2024, 99, 113393 CrossRef.
- L. Torres-Castro, A. M. Bates, N. B. Johnson, G. Quintana and L. Gray, J. Electrochem. Soc., 2024, 171, 020520 Search PubMed.
- J. Ning, B. Xiao and W. Zhao, Eng. Rep., 2025, 7, e13082 CrossRef.
- J. Perez, E. Garayalde, J. Lorente, M. Arrinda, M. Oyarbide, H. Macicior, U. Iraola and H. J. Grande, Int. J. Electr. Power Energy Syst. 2025171111053 Search PubMed.
- Y. Bai, Q.-A. Huang, Z. Wu, J. Wang, J. Chen, K. Wu and J. Zhang, J. Energy Chem., 2025, 107, 939–979 CrossRef CAS.
- Z. Wu, Q.-A. Huang, Y. Bai, J. Zhang and K. Wu, J. Energy Chem., 2025, 112, 1026–1045 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |