Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluating large language models for inverse semiconductor design
Muhammed Nur Talha
Kilic
 a,
Daniel
Wines
a,
Daniel
Wines
 *b,
Kamal
Choudhary
*b,
Kamal
Choudhary
 *bcd,
Vishu
Gupta
*bcd,
Vishu
Gupta
 efg,
Youjia
Li
efg,
Youjia
Li
 e,
Sayak
Chakrabarty
e,
Sayak
Chakrabarty
 a,
Wei-Keng
Liao
e,
Alok
Choudhary
e and
Ankit
Agrawal
a,
Wei-Keng
Liao
e,
Alok
Choudhary
e and
Ankit
Agrawal
 *e
*e
aDepartment of Computer Science, Northwestern University, Evanston, IL 60201, USA. E-mail: talha.kilic@u.northwestern.edu
bMaterial Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, MD, USA. E-mail: daniel.wines@nist.gov
cDepartment of Materials Science and Engineering, Whiting School of Engineering, The Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: kchoudh2@jh.edu
dDepartment of Electrical and Computer Engineering, Whiting School of Engineering, The Johns Hopkins University, Baltimore, MD 21218, USA
eDepartment of Electrical and Computer Engineering, Northwestern University, Evanston, IL 60201, USA. E-mail: ankit-agrawal@northwestern.edu
fLewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ, USA
gLudwig Institute for Cancer Research, Princeton University, Princeton, NJ, USA
First published on 16th January 2026
Abstract
Large Language Models (LLMs) with generative capabilities have garnered significant attention in various domains, including materials science. However, systematically evaluating their performance for structure generation tasks remains a major challenge. In this study, we fine-tune multiple LLMs on various density functional theory (DFT) datasets (including superconducting and semiconducting materials at different levels of DFT theory) and apply quantitative metrics to benchmark their effectiveness. Among the models evaluated, the Mistral 7 billion parameter model demonstrated excellent performance across several metrics. Leveraging this model, we generated candidate semiconductors and further screened them using a graph neural network property prediction model and validated them with DFT. Starting from nearly 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated candidates, we identified six semiconductor materials near the convex hull with DFT that were not present in any known datasets, one of which was found to be dynamically stable (Na3S2). This study demonstrates the effectiveness of a pipeline spanning fine-tuning, evaluation, generation, and validation for accelerating inverse design and discovery in computational materials science.
000 generated candidates, we identified six semiconductor materials near the convex hull with DFT that were not present in any known datasets, one of which was found to be dynamically stable (Na3S2). This study demonstrates the effectiveness of a pipeline spanning fine-tuning, evaluation, generation, and validation for accelerating inverse design and discovery in computational materials science.
1 Introduction
Semiconductors are foundational to the digital age, powering technologies from smartphones and laptops to advanced sensors and quantum processors. Unlike metals, which are relatively abundant and functional in their natural state, semiconductors are rare in nature due to the precise electronic band alignments required for their performance. Designing new semiconducting materials with tailored bandgap properties remains one of the most challenging problems in materials science.1–3In recent years, the surge in data availability, fueled by initiatives such as the Materials Genome Initiative4 and advances in computational tools,5,6 has created fertile ground for accelerating materials discovery. AI-driven generative models such as generative adversarial networks (GANs), variational autoencoders (VAEs), and diffusion models have shown strong potential in proposing chemically valid material candidates far more efficiently than traditional random sampling methods.7,8 Specifically, GANs generate samples by mapping noise from a prior distribution, while VAEs encode high-dimensional inputs into a lower-dimensional latent space, which is then used to reconstruct or generate new samples. Diffusion models,9 on the other hand, progressively denoise samples from a noise distribution to generate new structures. While these approaches have demonstrated success in materials generation, they require specific input–output formats and often struggle with variable-length or highly diverse representations.10 In contrast, LLMs can naturally handle textualized representations of chemical formulas and crystal structures, allowing flexible encoding of composition, structural, and property information in a single sequence. This makes them particularly suitable for generative tasks in materials discovery where data may vary significantly in complexity and format. However, LLM-based approaches also have limitations, including reliance on accurate tokenization and the need for sufficiently large datasets to capture complex structural patterns effectively.11,12 Nevertheless, representing complex material systems for modeling remains difficult. This has led to the exploration of advanced data representations,13 including graph neural networks and atomistic image-based approaches, to better capture structure-property relationships.14–16 Traditional methods such as Density Functional Theory (DFT),17,18 though reasonably accurate, are computationally intensive. To overcome this bottleneck, various diffusion, transformer-based, and large language models (LLMs) have been employed to accelerate inverse design workflows.9,19–21 Enhancing the efficiency of inverse design-particularly for material generation, not only expedites scientific discovery22 but also shortens innovation cycles23,24 and significantly reduces the costs associated with traditional trial-and-error experimentation and material synthesis.24
Among these, Large Language Models (LLMs) have shown particular promise. Originally developed for natural language tasks, LLMs are now being repurposed for scientific domains, including materials science.25–28 They excel at integrating heterogeneous data, ranging from text to tabular values and time series, and have improved tasks such as data extraction, annotation, and materials validity assessments.29–33
Beyond text mining, LLMs are revolutionizing property prediction and inverse design applications. Recent research shows that fine-tuned LLMs can not only match but often exceed traditional machine learning models in predicting material properties, such as formation energy and bandgap.34,35 Additionally, hybrid models that integrate LLMs with graph neural networks significantly enhance performance in materials property prediction.36 Notable foundation models tailored for chemistry include Simplified Molecular Input Line Entry System BERT (SMILES-BERT),37 a BERT-style encoder pretrained on large collections of SMILES38 strings to predict masked tokens and learn chemical context, and Molecular Language Transformer (MoLFormer),39 a Transformer-based chemical language model that captures molecular structure–property relationships directly from SMILES sequences. Both models have demonstrated strong performance in encoding molecular representations for downstream regression tasks, such as property prediction. In parallel, LLMs are making substantial contributions to inverse design applications, aiming to create innovative materials with targeted properties. For instance, Atomistic Generative Pre-trained Transformer (AtomGPT)40 is a Large Language Model built on GPT-241![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and Mistral42 architectures, designed to perform both forward modeling, predicting material properties from atomic structures, and inverse design, where target properties are used to generate plausible atomic structures. By leveraging the generative and contextual capabilities of LLMs, AtomGPT bridges property prediction and structure generation within a unified framework for materials discovery. Remarkably, the model of Wei, Lai, et al.8 that uses LLM-based discovery pipelines shows that the proposed structures can achieve up to 90% chemical neutrality, compared to only 20–25% for pseudo-random generation,8 highlighting their potential to generate high-quality, plausible candidates. Moreover, Metal–Organic Framework Generative Pre-trained Transformer (MOFGPT)43 utilizes a Transformer architecture adapted from GPT-2 to generate metal–organic frameworks (MOFs) based on specific property constraints while integrating reinforcement learning for property optimization. It comprises of 12 Transformer decoder layers, each with an embedding dimension of 768, 12 attention heads, and a feed-forward network with a dimensionality of 3072. Together, these advancements highlight the growing power of LLMs not only to interpret and extract scientific knowledge, but also to actively generate novel functional materials, fundamentally transforming the traditional design-make-test cycle in materials science.
and Mistral42 architectures, designed to perform both forward modeling, predicting material properties from atomic structures, and inverse design, where target properties are used to generate plausible atomic structures. By leveraging the generative and contextual capabilities of LLMs, AtomGPT bridges property prediction and structure generation within a unified framework for materials discovery. Remarkably, the model of Wei, Lai, et al.8 that uses LLM-based discovery pipelines shows that the proposed structures can achieve up to 90% chemical neutrality, compared to only 20–25% for pseudo-random generation,8 highlighting their potential to generate high-quality, plausible candidates. Moreover, Metal–Organic Framework Generative Pre-trained Transformer (MOFGPT)43 utilizes a Transformer architecture adapted from GPT-2 to generate metal–organic frameworks (MOFs) based on specific property constraints while integrating reinforcement learning for property optimization. It comprises of 12 Transformer decoder layers, each with an embedding dimension of 768, 12 attention heads, and a feed-forward network with a dimensionality of 3072. Together, these advancements highlight the growing power of LLMs not only to interpret and extract scientific knowledge, but also to actively generate novel functional materials, fundamentally transforming the traditional design-make-test cycle in materials science.
Despite these gains, challenges remain. Materials datasets are often sparse, inconsistent, and diverse in format, limiting the performance of traditional machine learning (ML) approaches.20,44 This is primarily because traditional ML models typically assume that input data is well-structured, uniform, and of fixed length, which limits their ability to handle the diverse and irregular formats often found in materials science datasets.45 In contrast, LLMs can learn from contextually encoded representations, making them more adaptable to such variability with minimal domain specific feature engineering. They have demonstrated a remarkable capacity to generalize across domains capable of generating executable code,46 integrating multimodal data such as text and images for grounded reasoning tasks,47 and solving complex mathematical problems through multi-step reasoning.48 This adaptability across varied data modalities and problem types makes LLMs particularly promising for addressing inverse design challenges in materials science.
In this study, we investigate the potential of fine-tuned LLMs for inverse materials design. The overall workflow is depicted in Fig. 1. Using Alpaca-style prompts, composed of instructions, inputs, and responses, we train several LLMs on three distinct datasets to generate crystal structures, including lattice constants, angles, and atomic coordinates. Through a rigorous benchmarking process on test datasets, comprising 12 models evaluated across three datasets with four LLM variants each, we identify the highest-performing model and use it to generate new candidate materials by giving randomly generated prompts. These candidates are further screened using the Atomistic Line Graph Neural Network (ALIGNN) model49 to predict material properties and stability. Final validation is performed via density functional theory (DFT) calculations. This end-to-end workflow, spanning fine-tuning, generation, prediction, and validation, offers a robust framework for accelerating data-driven discovery of functional materials.
2 Methods
2.1 String formatting
Crystals obtained from the JARVIS-DFT database50–52 are represented as periodically repeating unit cells, defined by lattice constants (l1, l2, l3) and angles (θ1, θ2, θ3). The number of atoms in each cell depends on the chemical formula.Assuming there are n atoms (ei), each with fractional coordinates (xi, yi, zi), the structure can be represented as:
| C = (l1, l2, l3, θ1, θ2, θ3, e1, x1, y1, z1,…,en, xn, yn, zn). | (1) |
This numerical representation is converted into a text format suitable for LLMs, as illustrated in Fig. 1d. Coordinates are space-separated, while different atoms are listed on new lines. There is no restriction on the number of atomic entries, allowing for flexible structural complexity.
2.2 Prompt design
During fine-tuning, we employ the Alpaca prompt format, which consists of three sections: instruction, input, and response. The response is structured as a bulk crystal format string, containing all relevant lattice and atomic details, as shown in Fig. 1c.2.3 LLM models
We used four LLMs from the Unsloth project on Hugging Face:53 unsloth/tinyllama-chat, unsloth/mistral-7b-bnb-4bit, unsloth/gemma-7b-bnb-4bit, and unsloth/llama-3-8b-bnb-4bit. Parameter-Efficient Fine-Tuning (PEFT)54 was applied to reduce the number of trainable parameters, thereby accelerating training while preserving model generalizability. The learning rate, 2 × 10−4, and number of epochs, 8, were determined empirically based on extensive experimentation with the Unsloth models, providing the best balance between training efficiency and the ability of the models to generate correctly formatted structures.2.4 Screening and validation
To assess material properties, we used the ALIGNN model,49 which is a graph neural network-based model trained on DFT calculations that predicts material properties directly from crystal structures. In our benchmarking calculations, we tested the impact of relaxing the LLM generated structures with the ALIGNN-FF universal machine learning force field.55 This force field was used as a calculator along with the atomic simulation environment (ASE),56 where the Fast Inertial Relaxation Engine (FIRE) algorithm,57 with a maximum of 250 optimization steps and a force convergence threshold of 0.1 eV Å−1, was applied to perform full geometry optimization of the structures (lattice parameters and atomic positions). If a structure did not reach convergence after 250 steps, the final structure was used for evaluation. In our inverse design (discovery) workflow (Fig. 1b), we performed DFT calculations with the Vienna Ab initio Simulation Package (VASP) using the projector augmented wave (PAW) method.58,59 We used JARVIS-Tools to facilitate these VASP calculations with automated k-point and kinetic energy cutoff convergence.60 We primarily used the OptB88vdW61 functional for all DFT calculations, which is a Generalized Gradient Approximation (GGA) functional that includes van der Waals (vdW) effects. We also used the Tran-Blaha Modified Becke–Johnson (TB-MBJ)62–65meta-GGA functional to compute the bandgap at a degree of higher accuracy (to correct for bandgap underestimation). Phonon calculations were carried out using the finite displacement method66 along with the phonopy67,68 package. Prior to the DFT calculations, we pre-relaxed the LLM generated structures with the Mattersim69 universal machine learning force field (in order to accelerate convergence at the DFT level). We used the Open Databases Integration for Materials Design (OPTIMADE)70–72 infrastructure to compare our LLM generated structures to materials in several other databases. The DFT data (including input and output files) is included with this manuscript for full reproducibility.3 Results and discussion
The performance of each model is assessed through various metrics within an inverse design framework. The top-performing LLM is used to generate candidate structures, which are further refined using ALIGNN predictions to reduce the search space. Finally, top candidates are validated with DFT after searching if they exist in other materials databases.The data used in this study was obtained from the JARVIS-DFT database,50,51 uploaded in 2022-12-12, which includes a total of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993 materials. We focused on three specific subsets: the Tc Superconductor dataset, which includes materials labeled with their critical temperatures (1058 entries), and two bandgap datasets. One bandgap dataset at the OptB88vdW level of theory (23
993 materials. We focused on three specific subsets: the Tc Superconductor dataset, which includes materials labeled with their critical temperatures (1058 entries), and two bandgap datasets. One bandgap dataset at the OptB88vdW level of theory (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 entries) and the other at the TB-MBJ (meta-GGA) level of theory (19
061 entries) and the other at the TB-MBJ (meta-GGA) level of theory (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 805 entries). For the OptB88vdW dataset, entries with bandgap values greater than 0 eV were selected. Specifically, 52
805 entries). For the OptB88vdW dataset, entries with bandgap values greater than 0 eV were selected. Specifically, 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932 entries with a bandgap of 0 eV were removed from the OptB88vdW subset, resulting in the final dataset of 23
932 entries with a bandgap of 0 eV were removed from the OptB88vdW subset, resulting in the final dataset of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 061 entries. The dataset was split into a training set (90%) and a test set (10%), with no separate validation set. Although the target property distributions are not uniform, all available data, except for the test set, is intentionally included in the training process to maximize diversity which is highly important given the limited dataset size. Excessive data removal would limit the LLM's ability to learn robust structure-property relationships, particularly for the smallest dataset (Tc Superconductor). Additionally, in generative AI settings, lower training loss does not necessarily correlate with better generation quality.73 As a result, model comparison is based on multiple performance metrics, including inference time, MAE, RMSE, the ratio of valid structures, rather than training loss alone, ensuring a comprehensive assessment of generative model performance.
061 entries. The dataset was split into a training set (90%) and a test set (10%), with no separate validation set. Although the target property distributions are not uniform, all available data, except for the test set, is intentionally included in the training process to maximize diversity which is highly important given the limited dataset size. Excessive data removal would limit the LLM's ability to learn robust structure-property relationships, particularly for the smallest dataset (Tc Superconductor). Additionally, in generative AI settings, lower training loss does not necessarily correlate with better generation quality.73 As a result, model comparison is based on multiple performance metrics, including inference time, MAE, RMSE, the ratio of valid structures, rather than training loss alone, ensuring a comprehensive assessment of generative model performance.
Fig. 2 presents the distribution of properties across the three datasets. Although the dataset is not uniformly distributed, the primary aim of this study is to develop a pipeline capable of generating valid chemical structures from given formulas and target properties, rather than solely optimizing property prediction accuracy. Fig. S1 in the SI illustrates the impact of applying different property-value splitting thresholds on dataset sizes. We evaluate the performance of the models using a range of metrics. The test datasets, distinct from those used during fine-tuning, consist of 106 samples for Tc Supercon, 2307 for OptB88vdW bandgap, and 1981 for MBJ bandgap, representing approximately 10% of the total data available for each case. A composition-based overlap analysis was also conducted across the training and test sets for all three datasets. The results indicate that only the Tc Superconductor dataset contains any overlap, with 5 polymorph pairs out of 1058 entries (approximately 0.5%; see Table S2 in the SI for details). For the OptB88vdW and TB-MBJ datasets, no composition overlaps were observed between the training and test splits. Given this extremely small degree of overlap (limited to 0.5% in a single dataset) and the fact that all model comparisons are performed within each dataset, data leakage does not meaningfully influence the evaluation. Following the training phase, the models enter the inference stage, where the response sections of the prompts are initially left blank, as illustrated in Fig. 1d.
Our initial experiment focused on comparing the predicted structures with the ground truth from the test set across different models. The four selected models, TinyLlama-Chat,74 Mistral-7B-bnb-4bit,75 Gemma-7B-bnb-4bit,76 and LLaMA 3-8B-bnb-4bit,77 were chosen based on their public availability and suitability for fine-tuning on standard research hardware, ensuring reproducibility. All selected models have approximately 7–8 billion parameters (except TinyLlama with 1.1 billion), which allows efficient fine-tuning while retaining strong generative capabilities. TinyLlama-Chat is a lightweight model featuring approximately 1.1 billion parameters, designed specifically for fast, low-resource chat applications. Both Mistral-7B and Gemma-7B are robust models with 7 billion parameters, quantized to 4-bit precision through the BitsAndBytes (bnb) framework.78 This quantization significantly reduces memory usage while preserving strong performance. Mistral stands out with its innovative sliding window attention mechanism and demonstrates solid capabilities across a range of natural language processing benchmarks. Conversely, Gemma, developed by Google, is focused on multilingual support and safety alignment, positioning it as a strong candidate for responsible AI applications. Finally, LLaMA 3-8B-bnb-4bit, the new addition to Meta's LLaMA series, delivers state-of-the-art performance with its 8-billion-parameter architecture, also quantized to 4-bit for improved efficiency. It excels in complex reasoning, natural language generation, and general understanding. Fig. 3 shows the distribution of lattice constants for both the target structures and the predictions generated by these four models on the Tc Supercon dataset. Each subfigure represents the distribution along one of the three lattice parameters: a, b, and c. The lattice constant a distribution substantially overlaps with that of b, making a difficult to visually distinguish in the figure; however, in most models, the a distribution remains visible as a blue overlay on top of b. Visually, the Llama3 model appears to align closest to the target distribution. However, quantitative results from the lattice constant error analysis in Table 1 indicate that the Gemma model achieves the lowest lattice constant loss value. Additional lattice constant distribution figures for the OptB88vdW and MBJ bandgap datasets are included in the SI.
| Model | Test set size | Valid structures | 3D coord. MAE | Lat. Const. MAE (Å) | Lat. Angle MAE (°) |
|---|---|---|---|---|---|
| a Bold values indicate the highest performance for each metric within each dataset (Tc Supercon, OptB88vdW bandgap, and MBJ bandgap). | |||||
| T c supercon | |||||
| tinyllama-chat | 106 | 74 | 0.226 | 0.486 | 8.72 |
| mistral-7b-bnb-4bit | 106 | 92 | 0.183 | 0.486 | 8.72 |
| gemma-7b-bnb-4bit | 106 | 87 | 0.154 | 0.375 | 5.042 |
| llama-3-8b-bnb-4bit | 106 | 85 | 0.203 | 0.422 | 7.447 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| OptB88vdW bandgap | |||||
| tinyllama-chat | 2307 | 1314 | 0.272 | 0.861 | 12.144 |
| mistral-7b-bnb-4bit | 2307 | 1529 | 0.243 | 0.741 | 9.427 |
| gemma-7b-bnb-4bit | 2307 | 1490 | 0.247 | 0.765 | 10.366 |
| llama-3-8b-bnb-4bit | 2307 | 1458 | 0.247 | 0.734 | 9.804 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| MBJ bandgap | |||||
| tinyllama-chat | 1981 | 1369 | 0.222 | 0.594 | 11.249 |
| mistral-7b-bnb-4bit | 1981 | 1495 | 0.210 | 0.591 | 10.522 |
| gemma-7b-bnb-4bit | 1981 | 1479 | 0.211 | 0.593 | 10.626 |
| llama-3-8b-bnb-4bit | 1981 | 1474 | 0.215 | 0.597 | 10.738 |
We extend the comparison by computing the Mean Absolute Error (MAE) for structural attributes, including lattice constants, atomic coordinates, and angles within each unit cell. The equations below defines the loss calculations, where N denotes the number of valid structures available for each dataset and model. Lattice constants and lattice angles are represented by three values each for every data in the dataset, while the number of atomic coordinates varies depending on the number of atoms in the structure.
 | (2) |
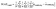 | (3) |
 | (4) |
• alattice/coord/angle,i: Target value of lattice/coordinates/angle for the i-th data.
• âlattice/coord/angle,i: Predicted value of lattice/coordinates/angle for the i-th data.
A comprehensive summary is provided in Table 1, which lists the total number of test samples and the corresponding number of valid structures produced by each model. Here, valid structures are defined as those preserving the same number of atoms as the target, thereby allowing a direct one-to-one comparison of structural components.
While the quantitative evaluation of valid structures in Table 1 is informative, analyzing invalid structures offers additional insight into model failure modes. A qualitative examination of these cases revealed three primary sources of invalidity in our calculations.
(1) Composition mismatches: The generated structure contains an incorrect number of atoms for one or more elements relative to the target formula (e.g., producing ZrB8 instead of ZrB6, or MnBe2P instead of MnBe2P2).
(2) Lattice-parameter inconsistencies: The generated lattice constants or angles deviate substantially from physically plausible values.
(3) Parsing and formatting errors: The output sequence is truncated or corrupted, leading to syntactically invalid structural descriptions.
The distribution of these error types varies across datasets. The Tc Superconductor dataset exhibits a higher proportion of invalid outputs, largely due to its small size and a higher frequency of parsing-related failures. In contrast, the OptB88vdW and TB-MBJ datasets show fewer invalid structures overall, with most errors arising from composition mismatches rather than formatting issues. Among the four LLMs, TinyLlama-Chat exhibits the highest rate of invalid generations across all datasets, likely due to its smaller parameter count. Conversely, the Mistral model achieves the strongest overall performance (Table 1), although differences in MAE values remain relatively modest among the larger models. Representative failure cases corresponding to each error category are summarized in Table S1 of the SI.
Our second evaluation metric focuses on comparing the inference times of the fine-tuned LLMs. This analysis provides a comprehensive evaluation of the models from multiple perspectives, specifically assessing how the number of model parameters and prompt structures influence computational performance. Table 2 reports the results in seconds for each model based on 20 generated samples. In the random comparison, 20 sample prompts are randomly selected from the test set and passed to the models, with the time required for output generation recorded. In the consistent comparison, a single fixed prompt is used across all datasets and models, allowing for a controlled comparison of inference speed. In the empty prompt scenario, the prompt contains no input, and the models generate outputs based solely on this blank input. Inference with empty prompts tends to be slower than in the random and consistent cases, likely due to the lack of input constraints. In both the consistent and empty cases, because the input remains unchanged, the models generate identical outputs. This deterministic behavior is ensured by disabling random sampling in the model's output generation (do_sample = False), which guarantees reproducibility. As shown in Table 2, inference time varies substantially depending on the prompt type, and inference-time variability is driven primarily by sample complexity (e.g., formulas containing many elements leading to longer output sequences) rather than intrinsic model efficiency alone. Despite being a larger model, Mistral exhibits slower inference while achieving the best performance across metrics, highlighting the relationship between model complexity and generative success.
| Model | Statistic | T c Supercon | OptB88vdW bandgap | MBJ bandgap | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Random | Consistent | Empty | Random | Consistent | Empty | Random | Consistent | Empty | ||
| mistral-7b-bnb-4bit | Min (seconds) | 2.54 | 4.15 | 6.66 | 4.31 | 4.18 | 20.59 | 2.68 | 5.44 | 10.11 |
| Max (seconds) | 5.59 | 4.32 | 6.80 | 195.18 | 4.24 | 20.85 | 17.54 | 5.49 | 11.37 | |
| Mean (seconds) | 4.31 | 4.20 | 6.71 | 22.31 | 4.21 | 20.67 | 6.26 | 5.46 | 10.28 | |
| Std (seconds) | 1.01 | 0.05 | 0.03 | 40.54 | 0.01 | 0.05 | 4.16 | 0.01 | 0.26 | |
| gemma-7b-bnb-4bit | Min (seconds) | 2.51 | 3.81 | 7.01 | 3.31 | 3.81 | 18.45 | 1.80 | 4.12 | 7.68 |
| Max (seconds) | 7.88 | 3.91 | 7.67 | 25.43 | 4.89 | 18.61 | 15.62 | 4.34 | 7.74 | |
| Mean (seconds) | 4.20 | 3.83 | 7.49 | 10.08 | 4.22 | 18.53 | 6.35 | 4.16 | 7.71 | |
| Std (seconds) | 1.38 | 0.02 | 0.13 | 6.37 | 0.44 | 0.04 | 3.72 | 0.04 | 0.01 | |
| llama-3-8b-bnb-4bit | Min (seconds) | 2.30 | 3.56 | 6.59 | 2.82 | 4.60 | 14.45 | 2.28 | 3.82 | 8.10 |
| Max (seconds) | 16.77 | 3.67 | 6.66 | 39.81 | 4.63 | 14.99 | 14.58 | 3.88 | 8.16 | |
| Mean (seconds) | 4.47 | 3.58 | 6.61 | 12.80 | 4.61 | 14.61 | 5.00 | 3.88 | 8.13 | |
| Std (seconds) | 3.10 | 0.02 | 0.01 | 9.33 | 0.00 | 0.15 | 3.53 | 0.01 | 0.01 | |
Our final metric for selecting the highest-performing model is based on the structural similarity (evaluated via the RMS distance), and its corresponding material property values, both of which are critical inputs for the model (target value, formula, and structural information) comparison. This analysis is part of the evaluation phase in the workflow, prior to the discovery phase, as shown in Fig. 1a. The target value refers to the superconductivity value for the Tc Supercon dataset, the OptB88vdW bandgap value for the OptB88vdW dataset, and the MBJ bandgap value for the MBJ bandgap dataset. To compare the material property values, we use the Mean Error Value as shown in Table 3. This analysis evaluates the original structure values in the test set against those predicted by the ALIGNN model, which takes atomic structural information and predicts the corresponding material property value. Additionally, we place particular emphasis on the structural similarity between the generated and reference structures. To quantify this, we compute the root mean square (RMS) distance for each predicted-reference structure pair, as implemented in the pymatgen library,79 and evaluate the mean of the RMS distance values across all data points. All model comparisons were conducted within each dataset to ensure a fair evaluation, given the substantial differences in dataset sizes. The Tc Superconductor dataset, due to its small size and limited data, was not treated as a primary target but rather serves as a benchmark to assess model performance in low-data cases.
| Model | Before relaxation | After relaxation | ||||||
|---|---|---|---|---|---|---|---|---|
| NaN ratio (RMS) | Mean (RMS) | NaN ratio (MPV) | MAE (MPV) | NaN ratio (RMS) | Mean (RMS) | NaN ratio (MPV) | MAE (MPV) | |
| T c Supercon | ||||||||
| tinyllama-chat | 0.62 | 0.046 | 0.06 | 2.634 | 0.62 | 0.041 | 0.06 | 2.678 |
| mistral-7b-bnb-4bit | 0.36 | 0.035 | 0.009 | 2.062 | 0.377 | 0.020 | 0.009 | 2.259 |
| gemma-7b-bnb-4bit | 0.38 | 0.025 | 0.00 | 2.092 | 0.37 | 0.028 | 0.00 | 2.29 |
| llama-3-8b-bnb-4bit | 0.43 | 0.037 | 0.037 | 2.500 | 0.43 | 0.024 | 0.037 | 2.142 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| OptB88vdW bandgap | ||||||||
| tinyllama-chat | 0.79 | 0.016 | 0.107 | 1.302 | 0.78 | 0.133 | 0.109 | 1.192 |
| mistral-7b-bnb-4bit | 0.62 | 0.011 | 0.022 | 0.848 | 0.62 | 0.099 | 0.023 | 0.832 |
| gemma-7b-bnb-4bit | 0.65 | 0.010 | 0.022 | 0.941 | 0.66 | 0.109 | 0.022 | 0.928 |
| llama-3-8b-bnb-4bit | 0.67 | 0.012 | 0.034 | 0.885 | 0.66 | 0.090 | 0.034 | 0.887 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| MBJ bandgap | ||||||||
| tinyllama-chat | 0.59 | 0.058 | 0.048 | 0.706 | 0.59 | 0.057 | 0.049 | 0.697 |
| mistral-7b-bnb-4bit | 0.53 | 0.045 | 0.012 | 0.532 | 0.53 | 0.051 | 0.013 | 0.595 |
| gemma-7b-bnb-4bit | 0.54 | 0.043 | 0.008 | 0.547 | 0.54 | 0.048 | 0.008 | 0.580 |
| llama-3-8b-bnb-4bit | 0.54 | 0.049 | 0.017 | 0.566 | 0.54 | 0.056 | 0.017 | 0.597 |
We also evaluated the impact of relaxing the structures generated by LLMs using the universal machine learning force field ALIGNN-FF. Our findings, summarized in Table 3, indicate that structural relaxation affected the mean absolute error (MAE) in different ways across the various models, depending on the dataset. In the case of the Tc Supercon dataset, three out of the four models, excluding LLaMA-3, experienced an increase in MAE following the relaxation process. Conversely, for the OptB88vdW bandgap dataset, all models except LLaMA-3 demonstrated a decrease in MAE, suggesting that relaxation generally enhanced their performance. For instance, the Mistral model had the lowest overall MAE within OptB88vdW bandgap dataset before relaxation (0.848), and after ALIGNN-FF relaxation, its MAE improved further to 0.832. Although the Mistral model outperformed the other models prior to relaxation, the relaxation process did not improve performance for the Tc Supercon and MBJ bandgap datasets, and instead increased the mean error. Without relaxation, it achieved an MAE of 0.53 on the MBJ bandgap dataset which is the lowest among all models and datasets. Additionally, for cases where the RMS distance could not be measured (RMS Not a Number (NaN) ratio), the Mistral model exhibited the lowest NaN ratio in OptB88vdW and MbJ bandgap datasets. Overall, relaxing with ALIGNN-FF does not result in a significant gain or loss of accuracy. Lower accuracy can be due to: (a) ALIGNN-FF relaxation resulting in a local minimum structure instead of the global minimum, (b) the relaxed structure from ALIGNN-FF being too far from the training distribution of the ALIGNN property prediction models, resulting in higher errors.
Fig. 1b illustrates the inverse design workflow for material discovery (after training and evaluating the performance of each LLM model). In our case, we were interested in leveraging our trained LLM model to generate new semiconductor candidates as a proof-of-concept application. For this reason, we focused on the models trained on the MBJ bandgap dataset and found that among the four models we considered, the Mistral 7B model demonstrated the highest performance. After selecting the Mistral 7B model trained on the MBJ dataset, we generated a set of binary and ternary wide bandgap semiconductor candidates for further exploration. For binary and ternary structures, we assigned a random bandgap value, ranging from 2.5 eV to 5 eV in the prompt. We generated binary candidates by swapping the positions of elements in formulas, such as converting OH2 to H2O, recognizing that the correct representation of a chemical formula in databases may not always be the first-listed combination for a given set of elements. Subsequently, a chosen set of elements, particularly those often found in semiconductor devices, was combined with random elements from the periodic table. This set of elements included Si, O, C, N, Al, Ga, Cd, Te, Ge, Se, S, As, B, Zn, Cu, P, Pb, Sn, Mo, In, and Ag. To reduce the sampling space for ternary compounds, we swapped the same set of elements with combinations of themselves. This resulted in 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 binary candidates and 74
000 binary candidates and 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ternary candidates.
000 ternary candidates.
In order to down-select from the structures generated by Mistral 7B, we used various pretrained ALIGNN models to predict the formation energy, energy above the convex hull and bandgap. After predicting these properties with ALIGNN, we filtered candidates based on whether they had negative formation energy, energy above the convex hull below 0.3 eV per atom, and a bandgap (at the MBJ level of theory) above 2 eV. The distributions of the ALIGNN predictions that satisfy this criterion are given in Fig. S12. Although a promising number of candidate structures satisfy this ALIGNN-based screening criteria, we are only concerned with candidates that are previously undiscovered (theoretically and experimentally). To further screen candidates that satisfy our ALIGNN-based screening criteria (in Fig. S12), we utilized the Open Databases Integration for Materials Design (OPTIMADE) infrastructure to search various databases (Materials Project,80 JARVIS-DFT, Alexandria,81–83 Open Quantum Materials Database,84,85 and Materials Cloud Three-Dimensional Structure Database86) for matching chemical compositions and crystal structures. After this additional filtering step, we performed DFT calculations to verify that these candidates were in fact semiconductors and thermodynamically and dynamically stable. Thermodynamic stability, which uses the energy above the convex hull as a metric, and dynamical stability, which uses the phonon spectra (absence of imaginary frequencies) as a metric, can both be quantified with the final DFT step in the screening workflow. Prior to the DFT relaxation, we relaxed the structures with the Mattersim universal machine learning force field to accelerate convergence.
Table 4 depicts a summary of our results for the top candidate structures (after being filtered by ALIGNN and OPTIMADE and verified with DFT). In addition to relaxing the structures with the OptB88vdW functional to obtain Eform, Ehull and Egap, we computed Egap at the MBJ level of theory (to partially correct for underestimation of the bandgap). For these top 6 candidates, we went on to perform phonon calculations to confirm dynamical stability (no imaginary phonon frequencies). Out of these 6 structures, we find that Na3S2 contains all positive phonon frequencies (see Fig. S13), while the remaining 5 structures contain some negative phonon frequencies (which can be due in part to instability, meta-stability or artifacts of the DFT calculations/simulation settings). Fig. 4a depicts the electronic band structure of the top candidate Na3S2 (OptB88vdW), which has a bandgap of 2.13 eV (OptB88vdW) and 2.45 (MBJ), making it a good candidate for wide bandgap applications. Specifically, we find that the mixed valence nature of Na3S2 results in a lowering of the valence band maxima (VBM), resulting in an increase of the bandgap. Fig. 4b depicts the remaining candidate structures that are reported in Table 4. We find that most of these candidate structures have low symmetry, which is common in other generative approaches.87–91 These DFT results highlight the difficulty in finding previously undiscovered semiconductors that are thermodynamically and dynamically stable. Our results also highlight how using LLMs for this difficult inverse design task (in conjunction with graph neural networks and DFT) can accelerate the process of finding new materials with targeted properties.
 | ||
| Fig. 4 (a) The electronic band structure of top candidate Na3S2, which is thermodynamically and dynamically stable. (b) The remaining candidate structures that are presented in Table 4. | ||
| Chemical formula | E form (OptB88vdW) eV per atom | E hull (OptB88vdW) eV per atom | E gap (OptB88vdW) eV | E gap (MBJ) eV |
|---|---|---|---|---|
| Zn2F3 | −2.09 | 0.10 | 0.75 | 2.20 |
| Mg3Te2 | −0.63 | 0.13 | 0.43 | 0.75 |
| Na3S2 | −1.06 | 0.06 | 2.13 | 2.45 |
| Rb3S2 | −1.10 | 0.04 | 2.11 | 3.15 |
| Zn2GaS2 (I) | −0.45 | 0.26 | 0.73 | 1.25 |
| Zn2GaS2 (II) | −0.48 | 0.23 | 0.66 | 1.31 |
4 Conclusion
In this work, we evaluated four Large Language Models (LLMs): TinyLlama-Chat, Mistral-7B, Gemma-7B, and LLaMA 3-8B, utilizing them on three materials datasets: Tc Supercon, OptB88vdW Bandgap, and MBJ Bandgap. Our evaluation of model performance encompassed both structural comparisons, such as atomic coordinates, lattice constants, and lattice angles, and an analysis of material property values of the predicted outcomes. Through our comparative analysis, we identified the Mistral-7B evaluated on the MBJ Bandgap as the top-performing model–dataset pair. Using this model, we developed an inverse design pipeline that generates candidate crystal structures based on specified chemical formulas and randomly sampled target property values. The resulting structures were subjected to validation and screening processes. From the initial pool of approximately 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidate structures, this rigorous process ultimately led to the identification of six semiconducting materials validated through density functional theory (DFT) calculations. Our findings underscore both the inherent challenges of materials discovery and the significant potential of LLMs to expedite materials discovery by enabling a data-driven exploration approach. In the future, we aim to extend this work by developing a domain-specific structured LLM optimized for materials science, with the objective of further accelerating the discovery process and improving the performance through the integration of larger datasets and more advanced model architectures.
000 candidate structures, this rigorous process ultimately led to the identification of six semiconducting materials validated through density functional theory (DFT) calculations. Our findings underscore both the inherent challenges of materials discovery and the significant potential of LLMs to expedite materials discovery by enabling a data-driven exploration approach. In the future, we aim to extend this work by developing a domain-specific structured LLM optimized for materials science, with the objective of further accelerating the discovery process and improving the performance through the integration of larger datasets and more advanced model architectures.
Conflicts of interest
The authors declare no competing interests.Data availability
Code availablity: source codes used in this study are currently available at https://github.com/mntalha/LLM_Atom_Gen.Training data for the LLMs used in this study is available at https://jarvis.nist.gov. DFT data generated from this work is available via Figshare: https://doi.org/10.6084/m9.figshare.30740288
Supplementary information (SI): detailed statistical analyses of the datasets used in this study, including distributions of lattice constants, lattice angles, elemental compositions, and target property values; training performance metrics of the fine-tuned large language models (training time, loss evolution, and throughput), comparisons between predicted and target properties, and structural relaxation analyses across all three datasets; additional validation results include lattice distribution comparisons, stability and electronic property screening of generated structures, density functional theory-computed phonon density of states for selected candidates, dataset splitting analyses, and examples of invalid structure generation with error categorization, as well as a composition-based overlap analysis for the Tc Superconductor dataset. See DOI: https://doi.org/10.1039/d5dd00544b.
Acknowledgements
This work was performed under the following financial assistance award 70NANB24H136 from U.S. Department of Commerce, National Institute of Standards and Technology as part of the Center for Hierarchical Materials Design (CHiMaD). Partial support is also acknowledged from NSF awards CMMI-2053929, OAC-2331329, DOE award DE-SC0021399, and Northwestern Center for Nanocombinatorics. All authors thank the National Institute of Standards and Technology for funding, computational, and data-management resources. This work was performed with funding from the CHIPS Metrology Program, part of CHIPS for America, National Institute of Standards and Technology, U.S. Department of Commerce. Certain commercial equipment, instruments, software, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identifications are not intended to imply recommendation or endorsement by NIST, nor it is intended to imply that the materials or equipment identified are necessarily the best available for the purpose.References
- D. D. Awschalom and M. E. Flatté, Challenges for semiconductor spintronics, Nat. Phys., 2007, 3(3), 153–159 Search PubMed.
- S. Coffa, F. Priolo, E. Rimini and J. M. Poate, Crucial Issues in Semiconductor Materials and Processing Technologies vol. 222. Springer, Dordrecht, Netherlands, 2012 Search PubMed.
- J. Xie, Y. Zhou, M. Faizan, Z. Li, T. Li, Y. Fu, X. Wang and L. Zhang, Designing semiconductor materials and devices in the post-moore era by tackling computational challenges with data-driven strategies, Nat. Comput. Sci., 2024, 4(5), 322–333 Search PubMed.
- Science, N., (US), T.C.: Materials Genome Initiative for Global Competitiveness. Executive Office of the President, National Science and Technology Council, Washington, DC, 2011 Search PubMed.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From dft to machine learning: recent approaches to materials science–a review, JPhys Mater., 2019, 2(3), 032001 Search PubMed.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design, npj Comput. Mater., 2019, 5(1), 21 Search PubMed.
- R. Dong, N. Fu, E. M. Siriwardane and J. Hu, Generative design of inorganic compounds using deep diffusion language models, J. Phys. Chem. A, 2024, 128(29), 5980–5989 CrossRef CAS PubMed.
- L. Wei, Q. Li, Y. Song, S. Stefanov, R. Dong, N. Fu, E. M. Siriwardane, F. Chen and J. Hu, Crystal composition transformer: Self-learning neural language model for generative and tinkering design of materials, Advanced Science, 2024, 11(36), 2304305 CrossRef PubMed.
- J. Ho, A. Jain and P. Abbeel, Denoising diffusion probabilistic models, NeurIPS, 2020, 33, 6840–6851 Search PubMed.
- A. Bandi, P. V. S. R. Adapa and Y. E. Kuchi, The power of generative ai: A review of requirements, models, input–output formats, evaluation metrics, and challenges, Future Internet, 2023, 15(8), 260 CrossRef.
- M. Ali, M. Fromm, K. Thellmann, R. Rutmann, M. Lübbering, J. Leveling, K. Klug, J. Ebert and N. Doll, J. Buschhoff, et al., Tokenizer choice for llm training: Negligible or crucial? in Findings of the Association for Computational Linguistics: NAACL 2024, pp. 3907–3924, 2024 Search PubMed.
- X. Zhu, C. Vondrick, C. C. Fowlkes and D. Ramanan, Do we need more training data?, Int. J. Comput. Vis., 2016, 119(1), 76–92 CrossRef.
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data, Nat. Commun., 2021, 12(1), 6595 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed.
- G. Schwartz and K. Nishino, Recognizing material properties from images, IEEE Trans Pattern Anal Mach Intell, 2019, 42(8), 1981–1995 Search PubMed.
- K. M. Jablonka, Q. Ai, A. Al-Feghali, S. Badhwar, J. D. Bocarsly, A. M. Bran, S. Bringuier, L. C. Brinson, K. Choudhary and D. Circi, et al. , 14 examples of how llms can transform materials science and chemistry: a reflection on a large language model hackathon, Digital Discovery, 2023, 2(5), 1233–1250 RSC.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, 864–871, DOI:10.1103/PhysRev.136.B864.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, 1133–1138, DOI:10.1103/PhysRev.140.A1133.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola: Crystal diffusion variational autoencoder for periodic material generation. arXiv:2110.06197, 2021 Search PubMed.
- N. Gruver, A. Sriram, A. Madotto, A. G. Wilson, C. L. Zitnick and Z. Ulissi, Fine-tuned language models generate stable inorganic materials as text. arXiv:2402.04379, 2024 Search PubMed.
- D. Flam-Shepherd and A. Aspuru-Guzik, Language models can generate molecules, materials, and protein binding sites directly in three dimensions as xyz, cif, and pdb files. arXiv:2305.05708, 2023 Search PubMed.
- E. O. Pyzer-Knapp, J. W. Pitera, P. W. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, Accelerating materials discovery using artificial intelligence, high performance computing and robotics, npj Comput. Mater., 2022, 8(1), 84 CrossRef.
- L. J. Falling, A vision for the future of materials innovation and how to fast-track it with services, ACS Phys. Chem. Au, 2024, 4(5), 420–429 CrossRef CAS PubMed.
- L. Scotti, H. Basoalto, J. Moffat and D. Cogswell, Review of material modeling and digitalization in industry: Barriers and perspectives, Integr. Mater. Manuf. Innov, 2023, 12(4), 397–420 CrossRef.
- J. Choi and B. Lee, Accelerating materials language processing with large language models, Commun. Mater., 2024, 5(1), 13 CrossRef.
- N. Walker, S. Lee, J. Dagdelen, K. Cruse, S. Gleason, A. Dunn, G. Ceder, A. P. Alivisatos, K. A. Persson and A. Jain, Extracting structured seed-mediated gold nanorod growth procedures from scientific text with llms, Digital Discovery, 2023, 2(6), 1768–1782 RSC.
- Z. Zheng, O. Zhang, C. Borgs, J. T. Chayes and O. M. Yaghi, Chatgpt chemistry assistant for text mining and the prediction of mof synthesis, J. Am. Chem. Soc., 2023, 145(32), 18048–18062 CrossRef CAS PubMed.
- Z. Zheng, Z. Rong, N. Rampal, C. Borgs, J. T. Chayes and O. M. Yaghi, A gpt-4 reticular chemist for guiding mof discovery, Angew. Chem., Int. Ed., 2023, 62(46), 202311983 Search PubMed.
- J. E. Saal, A. O. Oliynyk and B. Meredig, Machine learning in materials discovery: confirmed predictions and their underlying approaches, Annu. Rev. Mater. Res., 2020, 50, 49–69 Search PubMed.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, et al. , Recent advances and applications of deep learning methods in materials science, npj Comput. Mater., 2022, 8(1), 59 CrossRef.
- O. N. Oliveira Jr and M. C. F. Oliveira, Materials discovery with machine learning and knowledge discovery, Front. Chem., 2022, 10, 930369 Search PubMed.
- J. Dagdelen, A. Dunn, S. Lee, N. Walker, A. S. Rosen, G. Ceder, K. A. Persson and A. Jain, Structured information extraction from scientific text with large language models, Nat. Commun., 2024, 15(1), 1418 Search PubMed.
- X. Zhao, J. Greenberg, Y. An and X. T. Hu, Fine-tuning bert model for materials named entity recognition, in 2021 IEEE International Conference on Big Data (Big Data), IEEE, 2021, pp. 3717–3720 Search PubMed.
- R. Jacobs, M. P. Polak, L. E. Schultz, H. Mahdavi, V. Honavar and D. Morgan, Regression with large language models for materials and molecular property prediction. arXiv:2409.06080, 2024 Search PubMed.
- S. S. Srinivas and V. Runkana: Cross-modal learning for chemistry property prediction: Large language models meet graph machine learning. arXiv:2408.14964, 2024 Search PubMed.
- Y. Li, V. Gupta, M. N. T. Kilic, K. Choudhary, D. Wines, W.-k. Liao, A. Choudhary and A. Agrawal, Hybrid-llm-gnn: integrating large language models and graph neural networks for enhanced materials property prediction, Digital Discovery, 2025, 4, 376–383, 10.1039/D4DD00199K.
- S. Wang, Y. Guo, Y. Wang, H. Sun and J. Huang, Smiles-bert: large scale unsupervised pre-training for molecular property prediction. in Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, 2019, pp. 429–436 Search PubMed.
- D. Weininger, Smiles, a chemical language and information system. 1. introduction to methodology and encoding rules, J. Chem. Doc., 1988, 28(1), 31–36 CAS.
- F. Wu, D. Radev and S. Z. Li, Molformer: Motif-based transformer on 3d heterogeneous molecular graphs, in Proceedings of the AAAI Conference on Artificial Intelligence, 2023, vol. 37, pp. 5312–5320 Search PubMed.
- K. Choudhary, Atomgpt: Atomistic generative pretrained transformer for forward and inverse materials design, J. Phys. Chem. Lett., 2024, 15(27), 6909–6917 CrossRef CAS PubMed.
- A. Radford, J. Wu, R. Child, D. Luan, D. Amodei and I. Sutskever, et al. , Language models are unsupervised multitask learners, OpenAI blog, 2019, 1(8), 9 Search PubMed.
- D. Jiang, Y. Liu, S. Liu, J. Zhao, H. Zhang, Z. Gao, X. Zhang, J. Li and H. Xiong, From clip to dino: Visual encoders shout in multi-modal large language models. arXiv:2310.08825, 2023 Search PubMed.
- S. Badrinarayanan, R. Magar, A. Antony, R. S. Meda and A. B. Farimani: Mofgpt: Generative design of metal-organic frameworks using language models. arXiv:2506.00198, 2025 Search PubMed.
- Z. Zhu, Y. Xue, X. Chen, D. Zhou, J. Tang, D. Schuurmans and H. Dai, Large language models can learn rules, arXiv:2310.07064, 2023 Search PubMed.
- L. M. Ghiringhelli, C. Carbogno, S. Levchenko, F. Mohamed, G. Huhs, M. Lüders, M. Oliveira and M. Scheffler, Towards efficient data exchange and sharing for big-data driven materials science: metadata and data formats, npj Comput. Mater., 2017, 3(1), 46 CrossRef.
- T. Ahmed, C. Bird, P. Devanbu and S. Chakraborty, Studying llm performance on closed-and open-source data. arXiv:2402.15100, 2024 Search PubMed.
- J. Y. Koh, R. Salakhutdinov and D. Fried, Grounding language models to images for multimodal inputs and outputs. in International Conference on Machine Learning, PMLR, 2023, pp. 17283–17300 Search PubMed.
- A. Didolkar, A. Goyal, N. R. Ke, S. Guo, M. Valko, T. Lillicrap, D. Jimenez Rezende, Y. Bengio, M. C. Mozer and S. Arora, Metacognitive capabilities of llms: An exploration in mathematical problem solving, NeurIPS, 2024, 37, 19783–19812 Search PubMed.
- K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 185 CrossRef.
- K. Choudhary, K. F. Garrity, A. C. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne and A. Centrone, et al. , The joint automated repository for various integrated simulations (jarvis) for data-driven materials design, npj Comput. Mater., 2020, 6(1), 1–13 CrossRef.
- D. Wines, R. Gurunathan, K. F. Garrity, B. DeCost, A. J. Biacchi, F. Tavazza and K. Choudhary, Recent progress in the jarvis infrastructure for next-generation data-driven materials design, Appl. Phys. Rev., 2023, 10(4), 041302 CAS.
- K. Choudhary, The jarvis infrastructure is all you need for materials design, Comput. Mater. Sci., 2025, 259, 114063 CrossRef CAS.
- M. H. Daniel Han, team, U.: Unsloth. http://github.com/unslothai/unsloth.
- L. Xu, H. Xie, S.-Z. J. Qin, X. Tao and F. L. Wang, Parameter-efficient fine-tuning methods for pretrained language models: A critical review and assessment. arXiv:2312.12148, 2023 Search PubMed.
- K. Choudhary, B. DeCost, L. Major, K. Butler, J. Thiyagalingam and F. Tavazza, Unified graph neural network force-field for the periodic table: solid state applications, Digital Discovery, 2023, 2(2), 346–355 RSC.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , The atomic simulation environment—a python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002 CrossRef PubMed.
- A. V. Smirnov, Algorithm fire—feynman integral reduction, J. High Energy Phys., 2008, 2008(10), 107 CrossRef.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for ab initio Total-energy Calculations Using a Plane-wave Basis Set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- K. Choudhary and F. Tavazza, Convergence and machine learning predictions of monkhorst-pack k-points and plane-wave cut-off in high-throughput dft calculations, Comput. Mater. Sci., 2019, 161, 300–308, DOI:10.1016/j.commatsci.2019.02.006.
- J. Klimeš, D. R. Bowler and A. Michaelides, Van der waals density functionals applied to solids, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83(19), 195131 CrossRef.
- A. D. Becke and E. R. Johnson, A simple effective potential for exchange, J. Chem. Phys., 2006, 124(22), 221101, DOI:10.1063/1.2204597.
- B. Traoré, G. Bouder, W. Lafargue-Dit-Hauret, X. Rocquefelte, C. Katan, F. Tran and M. Kepenekian, Efficient and accurate calculation of band gaps of halide perovskites with the tran-blaha modified becke-johnson potential, Phys. Rev. B:Condens. Matter Mater. Phys., 2019, 99, 035139, DOI:10.1103/PhysRevB.99.035139.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401, DOI:10.1103/PhysRevLett.102.226401.
- F. Tran and P. Blaha, Importance of the kinetic energy density for band gap calculations in solids with density functional theory, J. Phys. Chem. A, 2017, 121(17), 3318–3325, DOI:10.1021/acs.jpca.7b02882.
- D. Alfè, Phon: A program to calculate phonons using the small displacement method, Comput. Phys. Commun., 2009, 180(12), 2622–2633 CrossRef.
- A. Togo, First-principles phonon calculations with phonopy and phono3py, J. Phys. Soc. Jpn., 2023, 92(1), 012001 CrossRef.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35(35), 353001 CrossRef CAS PubMed.
- H. Yang, C. Hu, Y. Zhou, X. Liu, Y. Shi, J. Li, G. Li, Z. Chen, S. Chen and C. Zeni, et al., Mattersim: A deep learning atomistic model across elements, temperatures and pressures. arXiv:2405.04967, 2024 Search PubMed.
- C. W. Andersen, R. Armiento, E. Blokhin, G. J. Conduit, S. Dwaraknath, M. L. Evans, Á. Fekete, A. Gopakumar, S. Gražulis and A. Merkys, et al. , Optimade, an api for exchanging materials data, Scientific data, 2021, 8(1), 217 CrossRef PubMed.
- M. L. Evans, J. Bergsma, A. Merkys, C. W. Andersen, O. B. Andersson, D. Beltrán, E. Blokhin, T. M. Boland, R. Castañeda Balderas, K. Choudhary, A. Díaz Díaz, R. Domínguez García, H. Eckert, K. Eimre, M. E. Fuentes Montero, A. M. Krajewski, J. J. Mortensen, J. M. Nápoles Duarte, J. Pietryga, J. Qi, F. Trejo Carrillo, A. Vaitkus, J. Yu, A. Zettel, P. B. Castro, J. Carlsson, T. F. T. Cerqueira, S. Divilov, H. Hajiyani, F. Hanke, K. Jose, C. Oses, J. Riebesell, J. Schmidt, D. Winston, C. Xie, X. Yang, S. Bonella, S. Botti, S. Curtarolo, C. Draxl, L. E. Fuentes Cobas, A. Hospital, Z.-K. Liu, M. A. L. Marques, N. Marzari, A. J. Morris, S. P. Ong, M. Orozco, K. A. Persson, K. S. Thygesen, C. Wolverton, M. Scheidgen, C. Toher, G. J. Conduit, G. Pizzi, S. Gražulis, G.-M. Rignanese and R. Armiento, Developments and applications of the optimade api for materials discovery, design, and data exchange, Digital Discovery, 2024, 3, 1509–1533, 10.1039/D4DD00039K.
- M. L. Evans, C. W. Andersen, S. Dwaraknath, M. Scheidgen, A. Fekete and D. Winston, ‘optimade-python-tools‘: a python library for serving and consuming materials data via optimade apis, J. Open Source Softw., 2021, 6(65), 3458, DOI:10.21105/joss.03458.
- B. W. Carvalho, A. S. Garcez, L. C. Lamb and E. V. Brazil, Grokking explained: A statistical phenomenon. arXiv:2502.01774, 2025 Search PubMed.
- P. Zhang, G. Zeng, T. Wang and W. Lu, Tinyllama: An open-source small language model, arXiv:2401.02385, 2024 Search PubMed.
- F. Jiang, Identifying and mitigating vulnerabilities in llm-integrated applications. Master's thesis, University of Washington, 2024 Search PubMed.
- G. Team, T. Mesnard, C. Hardin, R. Dadashi, S. Bhupatiraju, S. Pathak, L. Sifre, M. Rivière, M. S. Kale and J. Love, et al., Gemma: Open models based on gemini research and technology, arXiv:2403.08295, 2024 Search PubMed.
- A. Grattafiori, A. Dubey, A. Jauhri, A. Pandey, A. Kadian, A. Al-Dahle, A. Letman, A. Mathur, A. Schelten and A. Vaughan, et al., The llama 3 herd of models, arXiv:2407.21783, 2024 Search PubMed.
- T. Dettmers, A. Pagnoni, A. Holtzman and L. Zettlemoyer, Qlora: Efficient finetuning of quantized llms. arXiv:2305.14314, 2023 Search PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python materials genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002, DOI:10.1063/1.4812323 https://www.pubs.aip.org/aip/apm/article-pdf/doi/10.1063/1.4812323/13163869/011002_1_online.pdf .
- J. Schmidt, N. Hoffmann, H.-C. Wang, P. Borlido, P. J. M. A. Carriço, T. F. T. Cerqueira, S. Botti and M. A. L. Marques, Machine-learning-assisted determination of the global zero-temperature phase diagram of materials, Adv. Mater., 2023, 35(22), 2210788, DOI:10.1002/adma.202210788 https://www.advanced.onlinelibrary.wiley.com/doi/pdf/10.1002/adma.202210788 .
- J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. L. Marques, Crystal graph attention networks for the prediction of stable materials, Sci. Adv., 2021, 7(49), 7948, DOI:10.1126/sciadv.abi7948 https://www.science.org/doi/pdf/10.1126/sciadv.abi7948 .
- H.-C. Wang, J. Schmidt, M. A. L. Marques, L. Wirtz and A. H. Romero, Symmetry-based computational search for novel binary and ternary 2d materials, 2D Materials, 2023, 10(3), 035007, DOI:10.1088/2053-1583/accc43.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials design and discovery with high-throughput density functional theory: The open quantum materials database (oqmd), JOM, 2013, 65(11), 1501–1509, DOI:10.1007/s11837-013-0755-4.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The open quantum materials database (oqmd): assessing the accuracy of dft formation energies, npj Comput. Mater., 2015, 1(1), 15010, DOI:10.1038/npjcompumats.2015.10.
- S. Huber, M. Bercx, N. Hörmann, M. Uhrin, G. Pizzi and N. Marzari, Materials Cloud three-dimensional crystals database (MC3D), Materials Cloud Archive., 2022, 38 DOI:10.24435/materialscloud:rw-t0.
- D. Wines, T. Xie and K. Choudhary, Inverse design of next-generation superconductors using data-driven deep generative models, J. Phys. Chem. Lett., 2023, 14(29), 6630–6638, DOI:10.1021/acs.jpclett.3c01260.
- P. Lyngby and K. S. Thygesen, Data-driven discovery of 2d materials by deep generative models, npj Comput. Mater., 2022, 8(1), 232, DOI:10.1038/s41524-022-00923-3.
- R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu and Y. Liu, Crystal Structure Prediction by Joint Equivariant Diffusion, 2024, https://arxiv.org/abs/2309.04475.
- B. K. Miller, R. T. Q. Chen, A. Sriram and B. M. Wood, FlowMM: Generating Materials with Riemannian Flow Matching, 2024, https://arxiv.org/abs/2406.04713.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal Diffusion Variational Autoencoder for Periodic Material Generation, 2022. https://www.arxiv.org/abs/2110.06197.
| This journal is © The Royal Society of Chemistry 2026 |