Open Access Article
Open Access ArticlePEMD: a high-throughput simulation and analysis framework for solid polymer electrolytes
Shendong
Tan
 ab,
Bochun
Liang
ac,
Dexin
Lu
ab,
Chaoyuan
Ji
ab,
Bochun
Liang
ac,
Dexin
Lu
ab,
Chaoyuan
Ji
 a,
Wenke
Ji
a,
Zihui
Li
a and
Tingzheng
Hou
a,
Wenke
Ji
a,
Zihui
Li
a and
Tingzheng
Hou
 *a
*a
aShenzhen All-Solid-State Lithium Battery Electrolyte Engineering Research Center, Institute of Materials Research (IMR), Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China. E-mail: tingzhenghou@sz.tsinghua.edu.cn
bSchool of Materials Science and Engineering, Tsinghua University, Beijing, 100084, China
cDepartment of Materials Science and Engineering, City University of Hong Kong, Hong Kong, 999077, China
First published on 12th December 2025
Abstract
Solid polymer electrolytes exhibit limitations in room-temperature ionic conductivity and electrochemical stability. While molecular simulations and electronic-structure theory are able to sample these key properties at the molecular scale, the field currently lacks integrated, automated tools for end-to-end assessment. We introduce polymer electrolyte modeling and discovery (PEMD), an open-source Python framework that unifies polymer construction, force field parameterization, multiscale simulation, and property analysis for polymer electrolytes. The comprehensive analysis suite spans transport properties, transport mechanisms, and electrochemical stability. PEMD achieves a 100% success rate in constructing a collection of 656 homopolymers. The automated molecular dynamics workflow reproduces experimental ionic conductivities for 18 reported systems (Spearman ρ = 0.819; MAE = 0.684 in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (S cm−1)). Specifically, for poly(ethylene oxide)/LiTFSI electrolytes, PEMD captures the canonical non-monotonic dependence of ionic conductivity on salt concentration with built-in default settings. The workflow is further applied at scale to compute ionic conductivities for 200 polymer electrolytes. Moreover, automated oxidation window screening on 15 representative polymer electrolytes recovers experimental rankings for the oxidation potential (Spearman ρ = 0.754; MAE = 0.473 V). With standardized protocols and traceable workflows, PEMD provides a reliable platform for high-throughput screening and data-driven design of solid polymer electrolytes.
10 (S cm−1)). Specifically, for poly(ethylene oxide)/LiTFSI electrolytes, PEMD captures the canonical non-monotonic dependence of ionic conductivity on salt concentration with built-in default settings. The workflow is further applied at scale to compute ionic conductivities for 200 polymer electrolytes. Moreover, automated oxidation window screening on 15 representative polymer electrolytes recovers experimental rankings for the oxidation potential (Spearman ρ = 0.754; MAE = 0.473 V). With standardized protocols and traceable workflows, PEMD provides a reliable platform for high-throughput screening and data-driven design of solid polymer electrolytes.
1 Introduction
Solid polymer electrolytes are promising candidates for next-generation solid-state lithium battery technology owing to their inherent advantages, including low cost, enhanced safety, and manufacturing compatibility.1–5 Despite the benefits, their limited room-temperature ionic conductivity and electrochemical stability represent the primary impediments to practical applications.6–8 The transport mechanism in polymer electrolytes is intrinsically coupled across scales: local Li+ solvation, coordination, and ion pairing phenomena dictate the mesoscale structure and constrain polymer segmental motion. This coupling ultimately results in poor ion transport and the formation of concentration gradients that induce electrode polarization.9–12 Given that experimental characterization is frequently limited by resolution, timescale, and compositional complexity, theoretical and computational methodologies offer a complementary and powerful route that affords atomistic insight under controlled conditions to systematically uncover fundamental structure–property relationships.13–17Over the past decades, established simulation engines such as GROMACS,18 LAMMPS,19 and Gaussian20 have served as theoretical platforms for performing molecular dynamics (MD) simulations and quantum mechanics (QM) calculations, enabling a wide range of studies on polymer systems.21–23 Moreover, the polymer modeling community has developed diverse specialized tools, including PSP,24 mBuild,25 PySoftK,26 and the high-throughput workflow package RadonPy.27 Despite the extensive toolkit (Table S1), the utility of most existing computational resources is limited to either structural model generation or data-driven polymer informatics. Most recent developments have begun to couple modeling with electrolyte-specific analyses.9,28–30 Nevertheless, end-to-end, domain-tailored platforms for data-driven screening and design of polymer electrolytes remain inadequate. The absence of such a unified toolchain currently forces researchers to assemble fragmented toolchains via manual scripting, a process which fundamentally compromises reproducibility, scalability, and computational efficiency. Therefore, to address the current data scarcity for electrolyte-specific polymer properties, including transport properties,31–33 transport mechanisms,34–36 and electrochemical stability,37,38 an integrated computational workflow is fundamentally necessiary.
In this work, we present PEMD (polymer electrolyte modeling and discovery), an open-source Python package for high-throughput simulation and analysis of polymer electrolytes. PEMD establishes an integrated and modular platform that seamlessly automates the entire computational workflow, from polymer construction and force field generation to multiscale simulation and property analysis. Compared with existing tool, PEMD achieves substantial efficiency gains in polymer structure modeling, capable of OPLS-AA force field generation and conformer search for polymer chains of effectively unlimited length. Utilizing this foundation, the embedded analysis module is designed to evaluate key electrolyte properties, including ionic conductivity, transference numbers, solvation structure distributions, and electrochemical stability windows (ESW), while supporting scalable, high-throughput calculations. By enabling standardized, reproducible, and scalable computational protocols, PEMD bridges atomistic modeling with data-driven materials discovery, offering a versatile and essential tool for the design and optimization of next-generation polymer electrolytes.
2 Architecture and methods
As schematically outlined in Fig. 1, the PEMD framework provides an integrated, high-throughput pipeline designed for the comprehensive assessment of polymer electrolyte behavior. The workflow comprises four key stages: polymer construction, OPLS-AA force field parameterization, multiscale simulation, and physicochemical property analysis.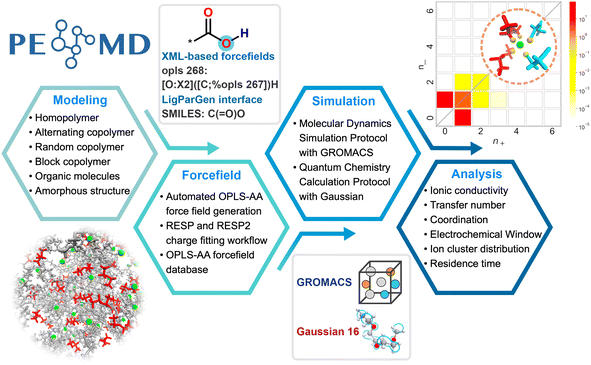 | ||
| Fig. 1 Overview of the PEMD workflow: modeling, force field parameterization, simulation, and analysis. | ||
2.1 Polymer model construction
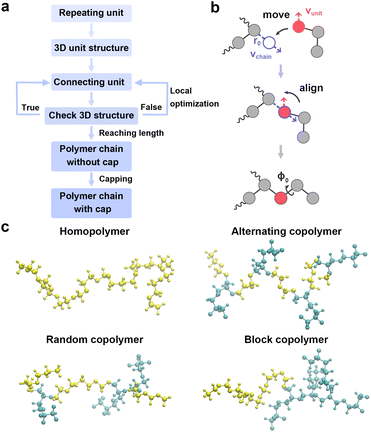
Reliable, automated construction of representative polymer conformers is fundamental for enabling credible simulations and subsequent analyses of polymer electrolytes. Fig. 2a shows the automated polymer structures generation algorithm. The workflow initiates by generating the 3D structure of the constituent monomer. Monomer units are then repeatedly attached to the growing polymer chain at predefined connection sites. Fig. 2b details the geometric operations of a move-align connection operator. First, the local neighborhood of the chain's tail atom is analyzed to compute the outward extension vector vchain, pointing in the direction of minimal steric hindrance. A virtual joining site is subsequently placed along vchain at the prescribed bond length, r0 = 1.5 Å. The incoming monomer unit is then translated such that its head atom coincides with this designated site. Based on the local environment around the head atom, its own extension vector vunit is determined, and the unit is rigidly rotated to achieve the antiparallel alignment of vunit with vchain. To mitigate close atomic contacts, an additional dihedral rotation (φ0) is applied around vunit. Following each connection step, the resulting geometry is rigorously evaluated for steric conflicts or unrealistic conformations (Fig. 2a). If such structural defects are detected, a local geometric optimization is performed to relieve strain and preserve structural integrity. Otherwise, the chain construction proceeds directly to the next connection step. Upon completion of the polymer backbone, users can specify capping groups for the head and tail termini (e.g., –H, –CH3, –OH). By default, saturated sp3-carbon termini are hydrogen-capped, while all other termini are methyl-capped.Based on this workflow, PEMD facilitates the construction of diverse polymer architectures, including homopolymers, alternating copolymers, random copolymers, and block copolymers (Fig. 2c). Given that previous reports has highlighted the profound influence of amorphous morphology on ion transport and segmental dynamics in polymer electrolytes,5,39 the constructed polymer chains are subsequently used to automatically generate amorphous simulation cells through the integrated PACKMOL interface.40 Example code snippets illustrating the polymer construction and amorphous cell generation processes are provided in Fig. S1 and S2.
2.2 OPLS-AA force field parameterization
OPLS-AA force field has been widely implemented and benchmarked for polymer electrolyte simulations due to its established robustness and universality.30,36,41,42 However, the utility of existing parameterization tools, such as LigParGen,43 is restricted by a maximum molecule size, typically fewer than 200 atoms. The inherent limitations render direct parameter generation unsuitable for the long polymer chains that are typically required for accurate representation of polymer electrolyte systems.To effectively address this size limitation, we employ a two-stage parameterization strategy (Fig. 3a). The first stage involves generating initial OPLS-AA parameters for a short-chain polymer segment. The resultant parameters are then converted into an XML-based force field file via the XMLGenerator class in PEMD. This step establishes an explicit and verifiable mapping between atom types and their corresponding bonded and non-bonded parameters. In the second stage, these XML definitions are systematically extended to arbitrarily larger polymer chains without atom-count restrictions. Atom typing is performed using Foyer44 through a hierarchical SMARTS-based pattern matching algorithm. As illustrated in Fig. 3b with a polyethylene oxide (PEO) oligomer (degree of polymerization = 3), each atom is uniquely identified by a SMARTS string that encodes both its elemental identity and its local chemical environment. Based on this precise atom-type matching, GROMACS-compatible OPLS-AA force field files are generated automatically, ensuring high fidelity and scalability.
 | ||
| Fig. 3 (a) Flowchart of the OPLS-AA force field parameterization in PEMD. (b) Atom-typing logic implemented via SMARTS pattern matching, illustrated on a PEO oligomer (degree of polymerization = 3). | ||
Furthermore, PEMD integrates automated support for RESP and RESP2 charge fitting (detailed subsequently), enabling the direct incorporation of optimized partial charges into the generated OPLS-AA force field file. For enhanced convenience and standardization, PEMD maintains an internal OPLS-AA force field database, which houses curated entries for a wide selection of representative polymers and electrolyte components. This provides users with flexible access to OPLS-AA parameters, allowing them to be either dynamically generated by calling oplsaa() via LigParGen or readily loaded from the internal database (Fig. S3).
2.3 Automated simulations framework
We employ a funnel-type conformer search strategy (Fig. 4a) that is applicable to both oligomers and small molecules, with a PEO oligomer presented as a representative example. The procedure begins by using the monomer's SMILES notation and the specified degree of polymerization to generate 1000 initial 3D conformers using RDKit.45 A subsequent rapid MMFF46 prescreening step retains the 100 lowest-energy, diversity-aware candidates. These candidates are then refined through a semi-empirical GFN1-xTB47 method, which reduces the set to the 10 most promising structures. Finally, these structures undergo density functional theory (DFT) geometry optimizations, utilizing a user-specified functional and basis set, to ultimately converge on 5 local energy minima. | ||
| Fig. 4 (a) Multi-level conformer search workflow in PEMD. (b) RESP/RESP2 charge fitting with multi-conformer averaging and end-preserving charge reassignment. | ||
Once the lowest-energy geometries are identified following the protocol, they serve as the input structures for subsequent QM calculations. Fig. 4b summarizes an automated RESP/RESP2 charge-fitting workflow. A procedure includes calculating the electrostatic potential (ESP) of representative oligomers at the DFT level, followed by fitting atom-centered charges using Multiwfn48 with either the RESP or RESP2 formalism. To mitigate the geometry dependence of the fitted charges, we implement a multi-conformer averaging scheme. Specifically, charges for each member of the low-energy conformer ensemble are fitted separately, and the final per-atom charges are determined by averaging these values across all conformers. To extend these derived charges to arbitrary polymer chain lengths, the oligomer is structurally decomposed into terminal caps and a repeat unit. A user-selected parameter, nend, specifies the number of terminal repeat units that will retain their explicit fitted charges, while the interior are assigned translationally invariant charges obtained by averaging the charges over the core repeat unit and subsequently tiling this averaged set across the remaining interior segments. The final set of charges is then renormalized to match the required net charge of the system. This end-preserving, interior-periodic mapping strictly follows established best practices for polymer parameterization based on oligomer ESP fitting.41 Fig. S4 provides the PEMD code snippets implementing the conformer search and automated RESP/RESP2 charge fitting.
To accurately sample the transport properties of polymer electrolytes, we adopt a standardized classical MD protocol implemented within GROMACS (Fig. 5a). Initial amorphous cell at the target density is prepared in the modeling module (Fig. S2). Following a steepest-descent energy minimization to eliminate unphysical close contacts, the systems undergo NVT equilibration at the target temperature. This is immediately succeeded by a linear up-down temperature ramp implemented via the simulated-annealing control points in GROMACS, which accelerates the relaxation of local entanglements characteristic of amorphous polymer systems. The annealing stage, which is automated in PEMD, exposes user-tunable parameters (temperature window, ramp rate, number of control points) to ensure efficient and reproducible equilibration. Subsequently, a 5 ns NPT equilibration is performed to further relax the systems. The time evolution of the potential energy, temperature, volume, mean-squared end-to-end distance <R2>, and radius of gyration Rg for representative systems is shown in Fig. S5. All of these quantities fluctuate around stable mean values without systematic drift, indicating that both the thermodynamic state and the polymer chain conformations are well equilibrated before the production runs. A representative snapshot at the mean plateau volume was extracted as the starting configuration for production MD run. Given that amorphous polymer electrolytes typically require tens to hundreds of nanoseconds for obtaining converged transport statistics, the production simulations are conducted at the target temperature with a default simulation time of 200 ns. To quantify the computational cost of the MD workflow, Table S2 summarizes the wall-clock runtime of each MD stage for PEO/LiTFSI electrolytes at various Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO ratios. For example, for a system with Li
EO ratios. For example, for a system with Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO = 0.05 (7900 atoms), the total wall-clock time required for the full MD workflow is 53.83 h. Fig. 5b visually compares the initial PACKMOL packing with the equilibrated amorphous polymer electrolyte structures obtained following this complete workflow. The PEMD code snippets automateing this MD protocol are provided in Fig. S6. In fact, similar MD workflows have been implemented in the GroPoB framework developed by Gudla and Zhang,49 which focuses on determining the glass transition temperature of PEO/LiTFSI polymer electrolytes. By contrast, PEMD is integrated with a general polymer builder and supports high-throughput analysis of both transport properties and redox stability across diverse polymer electrolytes.
EO = 0.05 (7900 atoms), the total wall-clock time required for the full MD workflow is 53.83 h. Fig. 5b visually compares the initial PACKMOL packing with the equilibrated amorphous polymer electrolyte structures obtained following this complete workflow. The PEMD code snippets automateing this MD protocol are provided in Fig. S6. In fact, similar MD workflows have been implemented in the GroPoB framework developed by Gudla and Zhang,49 which focuses on determining the glass transition temperature of PEO/LiTFSI polymer electrolytes. By contrast, PEMD is integrated with a general polymer builder and supports high-throughput analysis of both transport properties and redox stability across diverse polymer electrolytes.
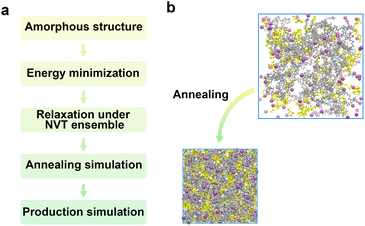 | ||
| Fig. 5 (a) General MD simulation protocol in PEMD. (b) Visualization of the annealing process, showing the initial and post-annealed amorphous polymer electrolyte configurations. | ||
Electrochemical stability is defined as the voltage window bounded by the reduction and oxidation limits over which a polymer electrolyte can operate without undergoing irreversible redox decomposition.8 The oxidative limit is particularly critical as it dictates compatibility with high-voltage cathodes,50 and thus imposes constraints on the energy density, cycle lifetime, and safety of solid-state batteries. Prior work has found that reliable and converged estimates of the oxidative window are achieved using a polymer-anion complex with three repeat units38,51–53 (Fig. S7). Herein, we automated the oxidation potentials (Eox) calculation of polymer electrolytes based on the polymer-anion cluster model (Fig. 6a). First, ion-polymer complexes are extracted from MD trajectories by specifying the repeat unit, chain length, and capping group. Illustrated using the PEO/LiTFSI (Fig. 6b), the construction of these ion-polymer clusters begins by identifying the anion's first coordination shell with respect to the H atoms of the PEO chain. The covalently bound heavy atom (X in X–H) nearest to the coordinating H is designated as the chain anchor. Starting from this anchor, a contiguous polymer segment is grown in both symmetrically along the backbone until the prescribed chain length is reached. This segment, alongside the coordinating anion, is then excised from the trajectory structure. Finally, the extracted clusters are capped using the identical algorithm empolyed in the initial polymer model construction.
 | (1) |
 | ||
| Fig. 6 (a) Automated computational framework for oxidative window. (b) Extraction of ion-polymer complexes from MD trajectories. | ||
2.4 Post-processing and analysis
PEMD is designed to provide comprehensive property analyses of polymer electrolytes. As summarized in Fig. 7, the schematic presents three core modules: transport properties, transport mechanisms, and electrochemical stability. Within the transport properties module, current functionalities include evaluating self-diffusion coefficients, ionic conductivity, and the cation transference number. Specifically, the self-diffusion coefficients are evaluated from the Einstein relation (eqn (2) in Table 1). Ionic conductivity is computed from the fluctuation-dissipation theorem via the Green–Kubo relation (eqn (3) in Table 1). Additionally, the cation transference number is precisely determined from the Onsager transport matrix Lij (eqn (4) in Table 1). To obtain physically meaningful transport properties from MD simulations, PEMD employs automated analysis procedures to ensure that the system has reached the diffusive regime (Fig. S9).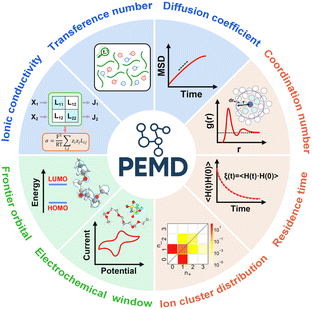 | ||
| Fig. 7 (a) Schematic of the PEMD post-analysis, including transport properties (blue panels), transport mechanisms (orange panels), and electrochemical stability (green panels). Next, we specify the bulk dielectric constant and perform DFT single-point energy calculations to identify plausible starting geometries. The oxidative limit Eox is then computed by evaluating the adiabatic ionization free energy and converting it to a voltage viaeqn (1). | ||
| Transport property | Formulaa |
|---|---|
| a List of symbols: α denotes an index over particles (ions, polymer and solvent); i and j denote indices of ionic species; kB is the Boltzmann constant; T is the temperature; V is the cell volume; qi and qj are the charge of species i and j; z+ and z− are the charge numbers of the cation. and anion, respectively. | |
| Self-diffusion coefficient (Dα) |
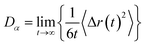 (2) (2) |
| Ionic conductivity (σ) |
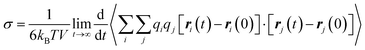 (3) (3) |
| Cation transference number (t+) |
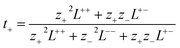 (4) (4) |
The design of higher-performance polymer electrolytes fundamentally necessitates a mechanistic understanding of ion transport at the atomistic level. Accordingly, PEMD provides a comprehensive suite of mechanistic analyses, including solvation structure distributions, cation transport mechanisms, ion clustering statistics, and residence times. We quantified the solvation structure distributions directly from MD trajectories, leveraging the capabilities of MDAnalysis.55 The requisite distance cutoffs for defining Li+-donor contacts were rigorously determined from the first minima of the radial distribution functions (RDF). For every simulation frame and each individual Li+, PEMD records the composition of specific coordination motifs, m = (npolymer, nanion, nsolvent). These motifs were then histogrammed to yield the statistical distribution of distinct solvation structures within the electrolyte. Additional analysis methods, including the detailed characterization of cation transport mechanisms, ion clustering statistics, and residence times, are thoroughly discussed in Fig. S10–S13.
Electrochemical stability is assessed using two complementary approaches. Firstly, the frontier orbital energies (HOMO and LUMO) of polymer electrolytes can provide a rapid, qualitative estimate of the stability window (Fig. S14). A lower HOMO energy typically correlates with higher oxidative stability, while a higher LUMO energy suggests greater resistance to reduction. Although this approach is low-cost and highly suitable for large-scale pre-screening and ranking, it inherently neglects geometry relaxation, local coordination, and environmental polarization. Consequently, the absolute values derived from frontier orbitals should be treated as qualitative or at most semi-quantitative. For the definitive electrochemical stability window (ESW) determination, PEMD incorporates the calculation of Eox and Ered values obtained by a more rigorous approach: sampling chemically representative MD snapshots, prescreening candidate geometries at the low-level DFT, and then computing adiabatic ionization/electron-attachment free energies that are mapped to voltages versus Li/Li+ (Fig. 6).
3 Results and discussion
3.1 Modeling performance
To quantify the efficiency and robustness for polymer structure generation and simulation initialization, we benchmarked PEMD against existing platforms, specifically mBuild, PSP, PySoftK, and RadonPy on 656 homopolymers spanning a broad range of molecular weights (Mw) (Fig. 8). PEMD successfully generated terminally capped chains for every target system, exhibiting no discernible dependence on Mw. By contrast, both PSP and PySoftK demonstrated a steep decline in their success rate as Mw increased, with PSP showing the most significant decrease. While mBuild exhibited no clear Mw dependence, its overall success rate was consistently below 60%. RadonPy maintained a high success rate across the molecular weight spectrum but did not achieve 100% completion. Collectively, these comparative results establish PEMD as a highly robust and scalable front-end for the large-scale computational modeling of polymer structures, particularly in the domain of experimentally relevant polymer electrolyte systems with high Mw.3.2 Transport properties
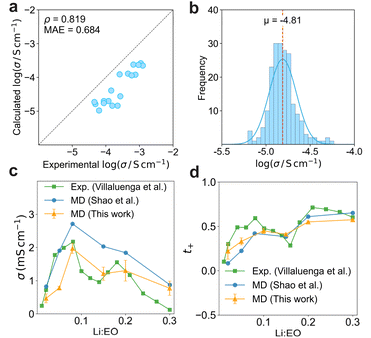
To assess the fidelity of the MD workflow, we performed fully automated MD simulations on 18 literature-reported polymer electrolytes and systematically compared the resultant ionic conductivities (σ) against experimental data (Fig. 9a and Table S3; see computational details in Part S1). The calculated and experimental σ show a strong monotonic relationship, quantified by a Spearman correlation coefficient (ρ) of 0.819 and a mean absolute error (MAE) of 0.684 in log10 (S cm−1). This strong correlation directly supports the quantitative reliability of the automated computational workflow. Glass transition temperature (Tg) plays an important role in governing polymer chain mobility and thus influences the dynamics of polymer electrolytes.5,6 In PEMD, Tg can also be computed automatically using a protocol adapted from the GroPoB workflow.49 Fig. S16 depicts the calculated Tg values plotted against experimental ionic conductivity. A strong negative correlation is observed, with a Spearman rank coefficient ρ of −0.962 and a coefficient of determination R2 of 0.949. We further applied this validated workflow to automatically compute σ for 200 polymer electrolytes (Fig. 9b). Across this expanded chemical space, the distribution of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ is unimodal with a mean centered at −4.81 (approximately 1.5 × 10−5 S cm−1 in linear units). Within this benchmarked set, PEO/LiTFSI remains the top-performing electrolyte. A small distribution on the high-conductivity side suggests that only a limited subset of candidates is likely to be promising. This finding underscores the necessity of expanding the accessible chemical space, for instance by utilizing generative models to propose novel polymer chemistries, in order to accelerate the identification of superior polymer electrolytes.56–59
σ is unimodal with a mean centered at −4.81 (approximately 1.5 × 10−5 S cm−1 in linear units). Within this benchmarked set, PEO/LiTFSI remains the top-performing electrolyte. A small distribution on the high-conductivity side suggests that only a limited subset of candidates is likely to be promising. This finding underscores the necessity of expanding the accessible chemical space, for instance by utilizing generative models to propose novel polymer chemistries, in order to accelerate the identification of superior polymer electrolytes.56–59
We further benchmarked the dependence of ionic conductivity on salt concentration within PEO/LiTFSI electrolytes (Fig. 9c and Table S4). The MD workflow accurately reproduces the canonical non-monotonic dependence of σ on salt concentration, characterized by an initial rise at low salt, a maximum concentration near Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO ratios of 0.10 to 0.12, and a subsequent decline at higher salt loadings. The predicted ionic conductivity trend shows close quantitative agreement with prior experimental observation by Villaluenga et al.60 and computation studies by Shao et al.61 This result underscores the robustness and fidelity of the default MD protocol across a broad range of electrolyte formulations.
EO ratios of 0.10 to 0.12, and a subsequent decline at higher salt loadings. The predicted ionic conductivity trend shows close quantitative agreement with prior experimental observation by Villaluenga et al.60 and computation studies by Shao et al.61 This result underscores the robustness and fidelity of the default MD protocol across a broad range of electrolyte formulations.
The cation transference number was subsequently determined directly from the MD trajectories. Fig. 9d illustrates the dependence of t+ on salt concentration for PEO/LiTFSI (Table S4). t+ exhibits an increasing trend with salt loading, consistent with both experimental reports and prior MD investigations.61 Therefore, the built-in MD workflow provides a robust, automated framework for the comprehensive evaluation of key transport properties in polymer electrolytes.
3.3 Transport mechanisms
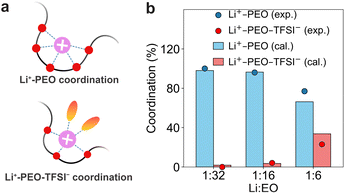
Designing high-performance polymer electrolytes requires a fundamental mechanistic understanding of Li+ transport. In PEO/LiTFSI electrolytes, the tight coordination of Li+ by ether oxygens suppresses ion mobility. Recent studies show that fine-tuning the salt content can partially release Li+ from the PEO cage, enhancing both ionic conductivity and the cation transference number.62 The solvation structure distributions, specifically Li+-PEO and Li+-PEO-TFSI− species, are quantified using PEMD and compared with the experiments. The experimental data was derived from Raman spectral fits of the TFSI− bands, characterizing the dissociated and associated ion fractions (Fig. 10). As the salt concentration increases from Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EO = 1
EO = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 to 1
32 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6, the computed results show a monotonic increase in the Li+-PEO fraction and a concurrent suppression of the Li+-PEO-TFSI− aggregates. The measured values based on the Raman spectral analysis agrees well with the computed distributions across the range of concentrations.63 This agreement indicates that PEMD faithfully recovers the Li+ solvation-structure distribution, providing support for the reliability of the mechanistic analysis module.
6, the computed results show a monotonic increase in the Li+-PEO fraction and a concurrent suppression of the Li+-PEO-TFSI− aggregates. The measured values based on the Raman spectral analysis agrees well with the computed distributions across the range of concentrations.63 This agreement indicates that PEMD faithfully recovers the Li+ solvation-structure distribution, providing support for the reliability of the mechanistic analysis module.
To further demonstrate that the current analysis workflow is not limited to ether-based polymer electrolytes, we additionally applied the same protocol to a representative polycarbonate system, poly(ethylene carbonate) (PEC)/LiTFSI. Fig. S17 depicts the coordination fractions of Li+-PEC and Li+-PEC-TFSI− species at Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) carbonyl oxygen (CO) ratios of 1
carbonyl oxygen (CO) ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32, 1
32, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16, and 1
16, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. We observed that, at low salt concentration, the fraction of Li+-PEC-TFSI− species in PEC/LiTFSI is clearly higher than the Li+-PEO-TFSI− fraction in the corresponding PEO/LiTFSI system. This suggests that the polycarbonate host provides a weaker coordination environment for Li+ than PEO, allowing TFSI− anions to enter the first solvation shell more readily.
6. We observed that, at low salt concentration, the fraction of Li+-PEC-TFSI− species in PEC/LiTFSI is clearly higher than the Li+-PEO-TFSI− fraction in the corresponding PEO/LiTFSI system. This suggests that the polycarbonate host provides a weaker coordination environment for Li+ than PEO, allowing TFSI− anions to enter the first solvation shell more readily.
3.4 Electrochemical stability
To evaluate the external validity of the electrochemical stability calculation protocol, we applied the framework to 15 representative polymer electrolytes and benchmarked the predicted Eox against reported oxidation onsets (Fig. 11 and Table S5). Eox values were computed at the B3LYP-D3(BJ)/def2-TZVP64–68 level of theory. The functional sensitivity relative to M06-2X69 and ωB97X-D70 is shown in Fig. S18. B3LYP yielded the highest Spearman ρ (0.754) and the lowest MAE (0.473 V). Specifically, PPO, PEO, PDOL, and PTHF exhibit lower oxidative window. Spin density maps of the cationic states reveal hole localization along the backbone C–C bonds in PPO, consistent with the C–C bond weakening and subsequent elongation. By contrast, the preferred oxidation pathway in PEO, PDOL, and PTHF is anion-mediated hydrogen abstraction (deprotonation), where the anion extracts a proton from the polymer. Using the automated computational workflow for Eox, our predictions show strong agreement with experiment, validating the methodology for electrochemical stability calculations.4 Conclusion
We developed PEMD, an open-source Python framework that unifies polymer construction, OPLS-AA force field parameterization, multiscale simulation, and property analysis into a single, automated workflow specifically tailored to polymer electrolytes. Rigorous benchmarking demonstrates that PEMD achieves a 100% build success rate across 656 homopolymers. Furthermore, the automated MD workflow accurately reproduces experimental ionic conductivity trends with high statistical fidelity (Spearman ρ = 0.819; MAE = 0.684 in log10 (S cm−1)), and captures the canonical dependence of transference numbers on salt concentration. The automated oxidation window screening protocol further recovers the experimental ranking of 15 representative polymer electrolytes (Spearman ρ = 0.754; MAE = 0.473 V). Collectively, these results establish PEMD as a reproducible and scalable platform that advances the capability of electrolyte-specific computational modeling for polymer materials design.By formulating standardized protocols and high-throughput calculation framework, PEMD enables the systematic exploration of diverse polymer chemistries, generating robust data sets suitable for mechanistic analysis and data-driven materials discovery. We note that the current tool has several inherent limitations. First, due to practical limits on the number of atoms, the polymer chain lengths accessible to atomistic MD are considerably shorter than those in experimental samples.30 While convergence tests in concerning chain length have been performed to verify certain transport properties, a limited chain length has been reported to cause deviations in other properties, such as rheological properties.71–73 Second, polymer electrolytes often exhibit significant crystallinity,39 whereas PEMD currently focuses exclusively on amorphous phases, which are widely reported to be more relevant to ion transport.39,74,75 Finally, at high salt concentrations, strong ion–ion correlations make it computationally challenging for the system to reach a diffusive regime within an accessible simulation timeframe,36 thereby demanding significantly larger consumption of computing power.
Future extensions of this work will focus on three key aspects: (i) enriching the underlying physical models, including the incorporation of polarizable and reactive force fields; (ii) coupling the workflow with active learning and generative design strategies to enable accelerated closed-loop discovery; and (iii) extending applicability to more complex systems, including graft polymers, multicomponent composite electrolytes, and interfacial systems. These potential improvements will offer a versatile foundation for the predictive design and rapid screening of next-generation polymer electrolytes essential for solid-state battery technologies.
Author contributions
S. T. and T. H. conceived the idea. T. H. supervised the project. S. T., B. L. and C. J. developed the algorithms, implemented the code, and performed validation. S. T., B. L., C. J, D. L., W. J., Z. L. discussed the results. S. T. and T. H. wrote the initial manuscript, which was approved by all authors.Conflicts of interest
The authors have no conficts of interest to declare.Data availability
The PEMD source code used to generate the results is openly available on GitHub repository (https://github.com/HouGroup/PEMD) and has been archived on Zenodo as an immutable snapshot: PEMD v1.1.0, DOI https://doi.org/10.5281/zenodo.17695865 (accessed 24 November 2025). The dataset corresponding to the enhanced Table S3, in CSV format, together with example input and output files for representative ionic-conductivity and oxidation window calculations (topologies, coordinates, GROMACS mdp files, and analysis scripts), is provided in the same Zenodo record. Example notebooks and workflow scripts are also included in the GitHub and Zenodo releases.All data supporting the findings of this study are available within the article and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00454c.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (22409121), the Natural Science Foundation of Guangdong Province (2025A1515012161), Shenzhen All-Solid-State Lithium Battery Electrolyte Engineering Research Centre Upgrade Project (XMHT20240108008), the Shenzhen Technical Plan Project (JCYJ20240813112111015), the Shenzhen Stable Support Program for Higher Education Institutions (WDZC20231126215806001).Notes and references
- X.-Y. Huang, C.-Z. Zhao, W.-J. Kong, N. Yao, Z.-Y. Shuang, P. Xu, S. Sun, Y. Lu, W.-Z. Huang, J.-L. Li, L. Shen, X. Chen, J.-Q. Huang, L. A. Archer and Q. Zhang, Nature, 2025, 646, 343–350 CrossRef CAS PubMed.
- J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Nat. Rev. Mater., 2019, 4, 312–330 CrossRef CAS.
- D. Zhou, D. Shanmukaraj, A. Tkacheva, M. Armand and G. Wang, Chem, 2019, 5, 2326–2352 CAS.
- Z. Xue, D. He and X. Xie, J. Mater. Chem. A, 2015, 3, 19218–19253 RSC.
- Z. Song, F. Chen, M. Martinez-Ibañez, W. Feng, M. Forsyth, Z. Zhou, M. Armand and H. Zhang, Nat. Commun., 2023, 14, 4884 CrossRef CAS PubMed.
- K. G. Stakem, F. J. Leslie and G. L. Gregory, Chem. Sci., 2024, 15, 10281–10307 RSC.
- Z.-Y. Wang, C.-Z. Zhao, S. Sun, Y.-K. Liu, Z.-X. Wang, S. Li, R. Zhang, H. Yuan and J.-Q. Huang, Matter, 2023, 6, 1096–1124 CrossRef CAS.
- C. Bai, Y. Li, G. Xiao, J. Chen, S. Tan, P. Shi, T. Hou, M. Liu, Y.-B. He and F. Kang, Chem. Rev., 2025, 125, 6541–6608 CrossRef CAS PubMed.
- Y. Shao, H. Gudla, J. Mindemark, D. Brandell and C. Zhang, Acc. Chem. Res., 2024, 57, 1123–1134 CrossRef CAS PubMed.
- A. A. Franco, A. Rucci, D. Brandell, C. Frayret, M. Gaberscek, P. Jankowski and P. Johansson, Chem. Rev., 2019, 119, 4569–4627 CrossRef CAS PubMed.
- C. Y. Son and Z.-G. Wang, J. Chem. Phys., 2020, 153, 100903 CrossRef CAS PubMed.
- T. Hou, K. D. Fong, J. Wang and K. A. Persson, Chem. Sci., 2021, 12, 14740–14751 RSC.
- A. Alvarez-Fernandez, G. Hernández and J. Maiz, JACS Au, 2025, 5, 3701–3715 CrossRef CAS PubMed.
- K. Wang, H. Shi, T. Li, L. Zhao, H. Zhai, D. Korani and J. Yeo, Digital Discovery, 2023, 2, 1660–1682 RSC.
- D. O. Möhrle, M. Schammer, K. Becker-Steinberger, B. Horstmann and A. Latz, J. Electrochem. Soc., 2024, 171, 020549 CrossRef.
- T. Hou, X. Chen, L. Jiang and C. Tang, J. Electrochem., 2022, 28, 2219007 Search PubMed.
- C. Ji, S. Tan, B. Liang, K. Yang, Z. Li, Y. Zhu, Y. Xie, Y.-B. He, J. Li and T. Hou, Chem. Commun., 2025, 61, 10989–10992 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- W. Zhang, V. Koverga, S. Liu, J. Zhou, J. Wang, P. Bai, S. Tan, N. K. Dandu, Z. Wang, F. Chen, J. Xia, H. Wan, X. Zhang, H. Yang, B. L. Lucht, A.-M. Li, X.-Q. Yang, E. Hu, S. R. Raghavan, A. T. Ngo and C. Wang, Nat. Energy, 2024, 9, 386–400 CrossRef CAS.
- N. J. Shah, C. Fang, N. C. Osti, E. Mamontov, X. Yu, J. Lee, H. Watanabe, R. Wang and N. P. Balsara, Nat. Mater., 2024, 23, 664–669 CrossRef CAS PubMed.
- D. Lu, R. Li, M. M. Rahman, P. Yu, L. Lv, S. Yang, Y. Huang, C. Sun, S. Zhang, H. Zhang, J. Zhang, X. Xiao, T. Deng, L. Fan, L. Chen, J. Wang, E. Hu, C. Wang and X. Fan, Nature, 2024, 627, 101–107 CrossRef CAS PubMed.
- H. Sahu, K.-H. Shen, J. H. Montoya, H. Tran and R. Ramprasad, J. Chem. Theory Comput., 2022, 18, 2737–2748 CrossRef CAS PubMed.
- C. Klein, J. Sallai, T. J. Jones, C. R. Iacovella, C. McCabe and P. T. Cummings, in Foundations of Molecular Modeling and Simulation: Select Papers from FOMMS 2015, ed. R. Q. Snurr, C. S. Adjiman and D. A. Kofke, Springer Singapore, Singapore, 2016, pp. 79–92 Search PubMed.
- A. Santana-Bonilla, R. López-Ríos de Castro, P. Sun, R. M. Ziolek and C. D. Lorenz, J. Chem. Inf. Model., 2023, 63, 3761–3771 CrossRef CAS PubMed.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- T. Xie, A. France-Lanord, Y. Wang, J. Lopez, M. A. Stolberg, M. Hill, G. M. Leverick, R. Gomez-Bombarelli, J. A. Johnson, Y. Shao-Horn and J. C. Grossman, Nat. Commun., 2022, 13, 3415 CrossRef CAS PubMed.
- L.-T. Wu, J. Mindemark, D. Brandell and J.-C. Jiang, ACS Appl. Polym. Mater., 2025, 7, 3636–3646 CrossRef CAS.
- J. Ruža, P. Leon, K. Jun, J. Johnson, Y. Shao-Horn and R. Gómez-Bombarelli, Macromolecules, 2025, 58, 6732–6742 CrossRef.
- K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2021, 54, 2575–2591 CrossRef CAS.
- K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2020, 53, 9503–9512 CrossRef CAS.
- K. D. Fong, J. Self, K. M. Diederichsen, B. M. Wood, B. D. McCloskey and K. A. Persson, ACS Cent. Sci., 2019, 5, 1250–1260 CrossRef CAS PubMed.
- J. Self, K. D. Fong and K. A. Persson, ACS Energy Lett., 2019, 4, 2843–2849 CrossRef CAS.
- A. Maitra and A. Heuer, Phys. Rev. Lett., 2007, 98, 227802 CrossRef CAS PubMed.
- H. Gudla, Y. Shao, S. Phunnarungsi, D. Brandell and C. Zhang, J. Phys. Chem. Lett., 2021, 12, 8460–8464 CrossRef CAS PubMed.
- M. A. Cabañero Martínez, N. Boaretto, A. J. Naylor, F. Alcaide, G. D. Salian, F. Palombarini, E. Ayerbe, M. Borras and M. Casas-Cabanas, Adv. Energy Mater., 2022, 12, 2201264 CrossRef.
- C. F. N. Marchiori, R. P. Carvalho, M. Ebadi, D. Brandell and C. M. Araujo, Chem. Mater., 2020, 32, 7237–7246 CrossRef CAS.
- C.-D. Fang, Y. Huang, Y.-F. Sun, P.-F. Sun, K. Li, S.-Y. Yao, M.-Y. Zhang, W.-H. Fang and J.-J. Chen, Nat. Commun., 2024, 15, 6781 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- C.-E. Fang, Y.-C. Tsai, C. Scheurer and C.-C. Chiu, Polymers, 2021, 13, 1131 CrossRef CAS PubMed.
- N. S. V. Barbosa, Y. Zhang, E. R. A. Lima, F. W. Tavares and E. J. Maginn, .J. Mol. Model., 2017, 23, 194 CrossRef PubMed.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, 331–336 CrossRef PubMed.
- C. Klein, A. Z. Summers, M. W. Thompson, J. B. Gilmer, C. McCabe, P. T. Cummings, J. Sallai and C. R. Iacovella, Comput. Mater. Sci., 2019, 167, 215–227 CrossRef CAS.
- G. Landrum, RDKit: Open-Source Cheminformatics Software, http://www.rdkit.org Search PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theor. Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- H. Gudla and C. Zhang, J. Phys. Chem. B, 2024, 128, 10537–10540 CrossRef CAS PubMed.
- J. Wang, S. L. Guillot, M. L. Usrey, T. Hou and K. A. Persson, J. Am. Chem. Soc., 2025, 147, 8841–8851 CrossRef CAS PubMed.
- K. Zhour, A. Heuer and D. Diddens, J. Chem. Phys., 2024, 161, 214302 CrossRef CAS PubMed.
- E. R. Fadel, F. Faglioni, G. Samsonidze, N. Molinari, B. V. Merinov, W. A. Goddard Iii, J. C. Grossman, J. P. Mailoa and B. Kozinsky, Nat. Commun., 2019, 10, 3360 CrossRef PubMed.
- X. Jiao and X. Pan, J. Electroanal. Chem., 2021, 882, 114995 CrossRef CAS.
- O. Borodin, X. Ren, J. Vatamanu, A. von Wald Cresce, J. Knap and K. Xu, Acc. Chem. Res., 2017, 50, 2886–2894 CrossRef CAS PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- Z. Yang, W. Ye, X. Lei, D. Schweigert, H.-K. Kwon and A. Khajeh, npj Comput. Mater., 2024, 10, 296 CrossRef CAS.
- A. Khajeh, X. Lei, W. Ye, Z. Yang, L. Hung, D. Schweigert and H.-K. Kwon, Digital Discovery, 2025, 4, 11–20 RSC.
- H. Qiu and Z.-Y. Sun, npj Comput. Mater., 2024, 10, 273 CrossRef CAS.
- H. Tran, R. Gurnani, C. Kim, G. Pilania, H.-K. Kwon, R. P. Lively and R. Ramprasad, Nat. Rev. Mater., 2024, 9, 866–886 CrossRef CAS.
- I. Villaluenga, D. M. Pesko, K. Timachova, Z. Feng, J. Newman, V. Srinivasan and N. P. Balsara, J. Electrochem. Soc., 2018, 165, A2766 CrossRef CAS.
- Y. Shao, H. Gudla, D. Brandell and C. Zhang, J. Am. Chem. Soc., 2022, 144, 7583–7587 CrossRef CAS PubMed.
- R. Chang, Y. Liu, Y. Zhang, Y. Shi, J. Tang, Z.-L. Xu, X. Zhou and J. Yang, Adv. Energy Mater., 2025, 15, 2405906 CrossRef CAS.
- B. A. Fortuin, J. Otegi, J. M. López del Amo, S. R. Peña, L. Meabe, H. Manzano, M. Martínez-Ibañez and J. Carrasco, Phys. Chem. Chem. Phys., 2023, 25, 25038–25054 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- H. Watanabe, Prog. Polym. Sci., 1999, 24, 1253–1403 CrossRef CAS.
- A. J. Tsamopoulos, A. F. Katsarou, D. G. Tsalikis and V. G. Mavrantzas, Polymers, 2019, 11, 1194 CrossRef PubMed.
- D. Choe, S. H. Jeong and C. Baig, J. Theol., 2024, 68, 591–601 CAS.
- J. Fu, Z. Li, X. Zhou and X. Guo, Mater. Adv., 2022, 3, 3809–3819 RSC.
- J. Chattopadhyay, T. S. Pathak and D. M. F. Santos, Polymers, 2023, 15, 3907 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |