Workflows and principles for collaboration and communication in battery research

Abstract

Interdisciplinary collaboration in battery science is required for rapid evaluation of better compositions and materials. However, diverging domain vocabulary and non-compatible experimental results slow down cooperation. We critically assess the current state-of-the-art and develop a structured data management and interpretation system to make data curation sustainable. The techniques we utilize comprise ontologies to give a structure to knowledge, database systems tenable to the FAIR principles, and software engineering to break down data processing into verifiable steps. To demonstrate our approach, we study the applicability of the Galvanostatic Intermittent Titration Technique on various electrodes. Our work is a building block in making automated material science scale beyond individual laboratories to a worldwide connected search for better battery materials.

---

1 Introduction

Li-ion batteries are widely deployed for transportation, grid stabilization, and power tools. These applications require specialized batteries, e.g., with long service life, or performance under extreme conditions. Enhancing the usable lifespan and power density of future batteries will greatly aid in their successful deployment. The following work focuses on current challenges in the exchange of domain-specific knowledge, and proposes a workflow that both aids the researchers directly, and is machine-readable for the automatic collation of results from multiple laboratories.

Discovering new battery compositions requires a comprehensive understanding of the physicochemical processes taking place within them. Building this understanding starting from a candidate battery material requires thorough collaboration across a wide variety of disciplines: chemists to formulate the material, physicists to develop the experimental machinery, experimental electrochemists to perform and interpret the experiments, and theoretical electrochemists to find patterns in the data. Due to the many mechanisms that happen in a battery during this chain of events,¹ interdisciplinary communication between all scientists involved in battery characterization is needed.

However, the exchange between theoretical and experimental electrochemistry has always been challenging due to a divergence in discipline-specific language and domain knowledge. This is a direct consequence of the necessarily different challenges in battery characterization and the diverse backgrounds. On the one hand, model-based interpretation of experiments introduces bias by assigning processes to measurement features. However, the underlying assumptions may not be transparent. On the other hand, most experimental procedures have to be repeated multiple times to overcome challenges around accuracy and reproducibility. Yet, the concise publication of a representative single dataset may not make that transparent.

To bring the community forward and better align theoretical and experimental efforts, workflows and methods need to be established, with which we can produce high-quality data in an up-scalable manner while increasing its compliance with the FAIR principles:² Findable, Accessible, Interoperable, and Reusable.

Current efforts to achieve this task span many disciplines and problems. Describing the data such that it can be collected and analyzed across institutions requires common requirements and a formalized language, e.g., ontologies.^3–5 Maximizing the throughput of any one institution is aided by automation and digitalization of the experiments.^6–9 Interpreting the rich amount of data requires a close integration with advanced machine learning techniques.^10,11

This paper demonstrates a semi-autonomous, FAIR-compliant workflow to create reusable measurement data and use it to parameterize electrochemical battery models. We show how it allows us to identify and resolve mismatching biases in data interpretation. First, we detail the theory behind the battery models we use, the measurement techniques we employ, the FAIR principles, and the algorithms we use for parameterization. Second, we present a case study of how we elucidated a commonly occurring mismatch between active material diffusivities, depending on the measurement technique or theoretical model treatment. Third, we report on our findings on enhancing the collaboration between experimentalists and theoreticians. Finally, we conclude with a summary of our findings.

2 Methods

2.1 Ensuring FAIR workflows

We present the methods we investigated to apply the FAIR principles in practice for battery measurements. We implement the four methods to improve compliance with the FAIR principles: data annotation with ontologies, data publication in open repositories, automated data processing workflows, and data review.

Findability requires structured metadata that make datasets searchable and discoverable. We achieve this by creating metadata based on key-value pairs. The structure and terms used in the metadata are taken from the Battery Interface Ontology (BattINFO).¹² BattINFO is a domain ontology that expresses knowledge about batteries using a formal and machine-readable vocabulary. To give context, ontologies relate to the philosophical study of the nature and structure of knowledge. Metadata that is structured according to an ontology hence can be algorithmically translated for other domains, and is especially suitable as a basis for research data search machines. Our goal here is to provide the proof-of-concept for producing datasets that can be searched and collated across multiple laboratories from all over the world. Hence, we only read out the structure and terms around the concept of a lithium-ion battery within BattINFO, and fill them in with the specific properties of our battery. To open and browse BattINFO, we use the software Protégé,¹³ from which we show example screenshots in the SI Fig. 4 and 5. BattINFO is an extension of the Elementary Multiperspective Materials Ontology (EMMO¹⁴). Within the ecosystem of ontologies based on EMMO, like for example the Crystallography Domain Ontology, the Battery Value Chain Ontology, or BattINFO, we may combine multiple ontologies if needed. For our purposes, BattINFO provides all relevant concepts. Still, our dataset is thus compatible with datasets annotated according to those other ontologies. Find our metadata example in the appended dataset within the record “INR18650-LG-3500-MJ1 Lithium-Ion Battery Cell Direct Characterization Data”. This allows metadata annotated with BattINFO terms to be understood within the broader scope of physics and materials science and enables interoperability with other datasets annotated with EMMO. Furthermore, annotating datasets with semantic vocabularies and linking to other datasets adheres to World Wide Web Consortium (W3C) recommendations for publishing linked data on the Web, which extends the findability for web-based queries. The structured and semantically annotated metadata is serialized as JSON-LD files and stored alongside the data using the database software Kadi4Mat.¹⁵ As Kadi4Mat is only one possible database solution in our modular workflow, we will not discuss its specifics. For an exemplary FAIR-compliant use case with Kadi4Mat, please refer to Brandt et al.¹⁶

Accessibility ensures that datasets, once discovered, can be retrieved. Open data repositories act as publishers of datasets, providing long-term storage, persistent identifiers, and version control. Using third-party repositories such as Zenodo, operated by CERN, suitable datasets can be made available with central access venues. Kadi4Mat simplifies this process with a three-click integration, preserving metadata and data files for immediate access and citation. See the Zenodo dataset appended to this paper as our gold standard proof-of-concept, especially the way it conserves the contextual information about knowledge flows and applications.

Interoperability allows datasets and workflows to be reused in new contexts. We achieve this by adhering to standardized formats with ontology-annotated data models and breaking the data processing pipeline into modular workflows. These workflows define clear inputs, processes, and outputs, enabling automation and machine-readability. Structuring data to support automation incidentally makes the process much more transparent and requires machine-readable (intermediate) results. Kadi4Mat provides an infrastructure to keep the data and the workflows acting on it in one. You'll find the workflows and their data linked in the appended Zenodo dataset, and we print one example of how the workflows appear on Kadi4Mat in the SI Fig. 6.

Reproducibility ensures that others can understand, verify, and adapt the developed workflows. External reviews help validate data pipelines and uncover any missing documentation. For reusability, we incorporate a checklist-based review to confirm that datasets meet legal and practical requirements, such as licensing and accessibility.

2.2 Electrochemical battery parameterization

Our goal is to obtain material parameters that, when plugged into predictive models of the cell state, will give the results that we would observe in validation measurements. On the cell level without access to microstructure imaging data, our most accurate dynamic model is the Doyle–Fuller–Newman (DFN¹⁷) model. For a thermodynamically consistent derivation and treatment of the general class of models that the DFN belongs to, we refer to Latz et al.¹⁸ Limitations of the DFN appear when considering the complex microstructures that arise in thick electrodes or novel materials,¹⁹ as well as previously negligible effects in novel electrolytes.²⁰ To account for microstructure effects in the context of the DFN, please refer to Traskunov et al.²¹ Recent research showed that 3D microstructure models do not offer higher short-term voltage prediction accuracy than the DFN for commercial-like batteries.²² 3D microstructure models do, however, offer higher predictive capability for cell degradation.²³ Hence, we do not consider microstructure effects here.

We demonstrate the challenges in systematically treating complex and diverse characterization data, starting with inverse modelling of the DFN as “most accurate method” and work our way down via simplifications of the DFN to direct parameter extraction from graphs. The single particle model with electrolyte (SPMe²⁴) is the linearized version of the DFN concerning electrolyte dynamics. Effectively, it approximates the DFN with only one representative particle per electrode, while resolving the electrolyte dynamics spatially.

The single particle model (SPM²⁵) is the constant term of the DFN concerning electrolyte dynamics. It may be considered a DFN that neglects the electrolyte dynamics and treats the electrodes as one representative particle each. We use PyBaMM²⁶ to simulate these models. Marquis et al.²⁴ documented their equations and distinguishable parameter groupings.

2.3 Measuring and interpreting GITT battery response

We now introduce the experimental methods and their interpretations we will consider. The Galvanostatic Intermittent Titration Technique (GITT) was introduced in 1977 to study molecule transport phenomena in electrochemistry.²⁷ With GITT, the battery experiences a short constant-current pulse, followed by a sufficiently long rest period. GITT is used most commonly for the determination of diffusion coefficients. Please refer to the SI Subsection 2.4 for the formula and its modernization.^28,29 Later in the paper, we will only use the square-root slope of the voltage signal shortly after current changes, abbreviated as

Applying inverse modelling to GITT can utilize the measurement more comprehensively.³⁰ Escalante et al.³¹ have already discussed the differences that can arise due to the model choice, in the case of the SPM vs. the SPMe. We will elaborate on that by additionally including the DFN.

GITT also yields the most accurate measurement of the Open-Circuit Potential (OCP) at any one State-of-Charge (SOC), i.e., the degree of lithiation between the maximally delithiated and maximally lithiated states. Measurement of voltage at a low current, typically cycling the battery in 50 h or more (quasi-OCP), gives many SOC points but mixes static and dynamic parts and flattens features in the OCP curve. With GITT, the cell gets cycled with short constant-current pulses only changing the SOC by a small percentage value. Longer rest phases in-between let the voltage signal exponentially decay close to the OCP, and we take the exponential asymptote as the OCP. Hence, compared to quasi-OCP, the SOC resolution has to be lower, but each measurement is more accurate. One can alleviate this a bit by shortening the rest phases between GITT pulses and recovering their terminal voltage from exponential extrapolation.³⁰ In any case, a reliable rest phase must have the material exhibit only one mode of exponential relaxation at its end. A plot of voltage over logarithmic time easily verifies this for graphite and NMC for rest phases as short as 15 min; long-term hysteresis can require rest phases as long as weeks for other materials like silicon.^32,33

The algorithm we use to fit simulation models to data is called Expectation Propagation with Bayesian Optimization for Likelihood-Free Inference (EP-BOLFI³⁰). It can tackle the high nonlinearity, i.e., the complexity of our models, while not only managing but also incorporating uncertainties in data, model, and model parameters into the fits. As the original case study for EP-BOLFI also studied GITT, there for a battery without an extra reference electrode, we refer to its paper for a more thorough introduction.

3 Experimental

3.1 Cell composition

We conduct our experiments on the INR18650-MJ1, a cylindrical 3500 mAh Li-ion battery cell in the 18 650 format manufactured by LG Chem. With its high cycle life, an energy density of 710 Wh  L⁻¹, and a specific energy of 260 Wh kg⁻¹, measured at reference current 0.2 C, it is often employed for high energy applications. For an overview of the experimental techniques we employ and which aspect of the battery each covers, please refer to Table 1.

Table 1 Overview of the measurement techniques we employ to completely characterize a battery. PE refers to the positive electrode and NE to the negative electrode. References are recommended literature for the measurement techniques

Property	Technique	Technique type
Chemical properties
PE max. lithiation	ICP-OES	Spectroscopy
PE active material	ICP-OES^34	Spectroscopy
Electrolyte composition	GC-MS^35	Spectroscopy
NE max. lithiation	OCP extrapol.^36	Electrochemical
NE active material	µCT^37	Microscopy
Geometric or microstructural properties
Electrode coating thickness	SEM	Microscopy
Particle size distributions	µCT^37	Microscopy
Porosity	Hg porosimetry^38	Physical
Tortuosity	EIS^39,40	Electrochemical
Kinetic, transport, or thermodynamic properties
Electrolyte ionic transport	Literature^41	Physical
Electrode electronic transport	4-Point-probe	Physical
Exchange-current densities	EIS^42	Electrochemical
Electrode lithium transport	GITT^29	Electrochemical
Open-circuit potentials	GITT^36	Electrochemical

---

The positive electrode active material is a high-nickel NMC-840511 (LiNi_0.84Mn_0.05Co_0.11O₂) positive electrode, based on our measurements using inductively coupled plasma atomic emission spectroscopy (ICP-OES) performed on a Varian Vista-MPX. The element ratios are consistent with scanning electron microscopy (SEM) from a Zeiss Gemini Ultra plus and energy-dispersive X-ray spectroscopy (EDX) from a Bruker XFlash detector 5010, which report the average ratios Ni : Mn : Co 83 : 5 : 12. Both ratio results are consistent with a report by Li et al.,³⁴ stating Ni : Mn : Co 82 : 6 : 11 from ICP and EDX. From ICP-OES also the lithium concentration is obtained which can be converted to a maximum lithium concentration of 19 812 mol m⁻³via the active material loading and Faraday's Law. The negative electrode active material is a graphite/silicon oxide composite, as confirmed via SEM-EDX. The ratio of graphite to silicon oxide is determined from Micro Computer Tomography (µCT),³⁷ as 96.5 volume-% graphite and 3.5 volume-% silicon oxide. The maximum lithium concentration is calculated to be 29 254 mol m⁻³ at full lithiation from the extrapolation of the OCP model fit.³⁶ Electrolyte harvested from the cell was measured via gas chromatography-mass spectrometry (GC-MS) by Sturm et al.,³⁵ revealing it to be 1 mol L⁻¹ LiPF₆ in a solvent based on EC : EMC : DMC (ethlyene carbonate : ethyl methyl carbonate : dimethyl carbonate) with 1 : 1 : 1 volume ratios. The transport parameters for this electrolyte are well-documented and, therefore, taken from the literature.⁴³ For an exemplary electrolyte measurement workflow, we refer to Landesfeind et al.⁴¹

3.2 Cell disassembly

To study materials and perform experiments on the electrode level, the cell is disassembled and the electrodes extracted. To this end, the cell is discharged to the discharge cut-off voltage of 2.5 V at 0.1 A (C/50), transferred to an argon-filled glove box, and opened with a pipe cutter. After the cell is dismantled, positive and negative electrodes are extracted and carefully separated from the separator to avoid cross-contamination. For all measurements, the electrode and separator samples were washed twice for one minute with DMC and dried in the glove box. For Electrochemical Impedance Spectroscopy (EIS) to measure tortuosities, to remove any residual salts, the electrodes were immersed in DMC overnight and left to dry for 30 minutes before re-assembly. For electrochemical experiments, the coating on one side of the double-sided electrodes must be removed from the current collector foil. The positive electrode coating is removed with N-Methyl-2-Pyrrolidone (NMP). In contrast, the coating of the negative electrode is removed outside of the glove box with deionized water, as a water-soluble binder is commonly used there. Images of the jelly roll removed from the cell can and the subsequent removal of the coatings are depicted in the SI Fig. 1. The process of dismantling the commercial cell and preparing the components for different types of measurements is described in more detail by Schmitt et al.,⁴² together with a comprehensive description and assessment of various techniques for parameter identification.

3.3 Cell geometry and microstructure

Electrode coating thicknesses are determined with the same SEM setup as above (Zeiss Gemini Ultra plus) to be 73 µm for the positive and 87 µm for the negative electrode. The thicknesses are averaged over several SEM images to accommodate for local variations. Exemplary SEM images are shown in the SI Fig. 3 to get an impression of particle morphology. The separator is a ceramic-coated polymer with a thickness of approximately 12 µm. The images of the electrode surface reveal that the active materials on the negative and positive electrodes are in flake and spherical shape, respectively. Parameters describing the microstructure of the electrode are quantitatively assessed by analyzing the 3D reconstruction of the porous structure obtained by µCT.³⁷ For that purpose, the microstructural data of the MJ1 cell provided in Heenan et al.⁴⁴ is analyzed. For the reconstruction of the raw data, the 3D stack of images is segmented with the program ImageJ⁴⁵ (from NIH). Due to non-uniform illumination, setting a single threshold for all micrographs is not feasible. Therefore, a Sauvola algorithm⁴⁶ is used to perform local thresholding of the data. The Sauvola algorithm works by dividing the input image into square windows and setting thresholds for each based on the mean and standard deviation of the pixel intensities.

Fig. 1 shows the visualizations of the 3D reconstructions of the analyzed data. The data visualization uses Mayavi,⁴⁷ a Python-based data visualization library. The Particle Size Distributions (PSD) of the various phases are calculated with MATLAB and TauFactor,⁴⁸ using a method introduced by Münch et al.⁴⁹ For a comprehensive microstructural analysis, we refer to Heenan et al.⁴⁴ The porosities of the electrode and separators are measured by mercury porosimetry,³⁸ using the Pascal 140 + 240 system by Thermo Scientific, resulting in 0.26, 0.38, and 0.23, for the negative electrode, separator, and positive electrode, respectively. A maximum pressure of 200 MPa is applied to the evacuated samples.

Fig. 1 Visualization of the 3D reconstructions of the (a) NMC active phase in the positive electrode and of the (b) graphite and (c) silicon-oxide phases in the negative electrode. Below those are the calculated particle size distributions for the (d) NMC, (e) graphite, and (f) silicon phases. Image data taken from Heenan et al.⁴⁴

3.4 Cell assembly and electrochemical measurements

For all electrochemical measurements (GITT, EIS, tortuosity evaluation), electrodes with 18 mm diameter are punched out from the harvested electrodes with a die cut (EL-Cut from EL-CELL) and assembled in ECC-PAT-Core-Cells (EL-CELL) in three-electrode configuration, if not otherwise mentioned. For the GITT measurements (also the ones with intermittent EIS), the counter electrodes are the ones from the original cell to adjust for the respective full cell SOC in the measurements. To measure tortuosities, EIS is performed in symmetrical cells of the negative and of the positive electrodes, respectively. In all cases, a 260 µm thick Whatman GF/A separator with porosity 0.93 and Bruggeman coefficient 1.0 replaces the original one, with an integrated lithium reference ring from EL-CELL for measuring the working electrode versus the reference electrode potential at 0 V versus Li/Li⁺. Following the EL-CELL protocol, the cell plungers are chosen such that the reference ring is located approximately in the middle of the separator to prevent measurement artefacts. The plungers for the EIS tortuosity measurement are copper-coated to minimize additional ohmic resistance. For GITT, LiPF₆ in EC : EMC : DMC 1 : 1 : 1 volume ratios (ethylene carbonate, ethyl methyl carbonate, dimethyl carbonate) with 2 weight-% VC (vinylene carbonate) from Solvionic is used to represent the original electrolyte whereas a non-intercalating electrolyte consisting of 10 mmol Tetrabutylammonium Perchlorate (TBAClO₄, Merck) in EC (Alfa Aesar) : EMC (Solvionic) 3 : 7 weight ratio is used to perform EIS under blocking conditions to measure tortuosity of the electrodes. In both cases 120 µl is used. For EIS of the separator, 50 µl EC : EMC : DMC 1 : 1 : 1 volume ratios are used again instead. To ensure proper wetting, the cells were allowed to rest for 12 hours before measurements.

Cycling is conducted with a BaSyTec Cell Test System (CTS) inside an IPP750 climate chamber by Memmert operating at 25 °C. For the GITT measurements, three full charge–discharge cycles at C/5 current between 2.5 V and 4.2 V of the full cell voltage were performed before each measurement to equilibrate the cell and reform potentially damaged SEI. The pulse charges corresponding to the SOC steps in the subsequent GITT sequence are given relative to a scale between 0% and 100% corresponding to the capacity between 2.5 V and 4.2 V at C/50 obtained directly after the equilibration step. For determination of the capacity, voltage was measured between working and counter electrode whereas during the GITT sequence, it is measured between working and reference electrode. Between 10% and 90% SOC, the GITT pulses were carried out with C/10 current in 5% steps, and beyond that with C/20 current in 1% steps to avoid reaching cut-off voltages early and get a higher resolution at the edges. The relaxation criterion signalling the end of the rest phases is a voltage change smaller than 0.0005 V within the last 30 minute segment – an expedient, programmable termination criterion in the BaSyTec software to account for different relaxation time at different SOC. The resulting capacity obtained from these measurements is 12 mA h, as estimated from an OCP model fit.³⁶

The tortuosity of both electrodes and the separator is determined with EIS according to the procedure thoroughly described by Landesfeind et al.,^39,40 giving the values in Table 2. EIS measurements are conducted under blocking conditions in potentiostatic mode, employing a Gamry 1010E instrument with a 5 mV amplitude over a frequency range of 1–1000 kHz. To ensure measurement reproducibility, this is repeated for three cells for each component. For the impedance spectra, Equivalent Circuit Models (ECM) are used to obtain the ionic resistance R_ion from which the tortuosity is then calculated. With A denoting cross-section area and L_k denoting coating thicknesses, R_ion can be obtained according to

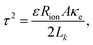with the conductivity of the electrolyte at κ_e = 0.32 mS cm⁻¹ 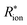and the 2 referring to the fact that we have two identical coatings in the symmetrical cell. The ECM for the separator consists of a resistor in series with a constant-phase element. The ECM for the electrodes consists of a resistor R_ion in series with a simplified Transmission Line Model (TLM). For the latter, blocking conditions, reflective boundary conditions, and R_ion ≫ R_electrolyte are assumed. See Schmitt et al.⁴² for further elaborations. An ECM consisting of a resistor and capacitor in parallel fits the impedance semicircle at 4–100 Hz and yields the exchange-current densities.

Table 2 Path-length tortuosity τ², MacMullin number N_M, and Bruggeman exponent β of different components of the MJ1 cell determined by EIS

Component	τ ^2	N M	β
Negative el.	4.6 ± 0.9	17.5 ± 3.5	1.1 ± 0.2
Separator	4.64 ± 0.05	12.2 ± 0.1	1.59 ± 0.01
Positive el.	2.5 ± 0.1	11.0 ± 0.6	0.6 ± 0.0

---

The electronic conductivities of the electrodes are determined from a four-point-probe measurement (Ossila) to be and 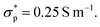An adhesive tape is used to delaminate the coating from the current collector to ensure that only the conductivity of the porous electrode is measured.

3.5 Data for results and discussions

We emulate the state-of-the-art of the research field by considering data from one of our previously finished experiments, which had little interaction between experimentalists and theoreticians. We use this as a basis for discussion between the two disciplines and to motivate how a more FAIR-compliant version of the experiment and its interpretation improve results. This dataset comprises GITT and EIS measurements from a BaSyTec device setup on the EL-CELL setup. The GITT measurements and EIS measurements were performed interspersed with each other. The precise timings and order of operations are collected in the SI Table 1 and the SI Table 2 for the lithiation and delithiation direction, respectively.

Our discussions revealed the necessity of a GITT measurement without performing EIS intermittently for parameterization. The exact measurement protocol is listed in the SI Table 3 and the SI Table 4 in lithiation and delithiation direction, respectively.

To handle the measurement data, we first need to convert it into a consistent format suited to our analysis. The battery measurement devices (“cyclers”) commonly output data in a proprietary format. The most raw export from the cyclers is a CSV file. We stripped redundant measurement columns, like various representations of time or empty columns, reducing file size by 77%. We packaged the remaining table in a Parquet file, reducing file size by another 87%. Parquet is a minimal file size container, exploiting common redundancies in time-series data. Parquet also provides fast access with its column-oriented data structure.

4 Results

Our developed workflow is summarized in Fig. 2. We group its components into four categories: converting raw measurement data into interoperable data (highlighted in blue), collating laboratory reports into interoperable characterization results (highlighted in green), distinguishing static from dynamic measurement features (highlighted in orange), and parameterizing an electrochemical model (highlighted in red). We now discuss these in order.

Fig. 2 Finalized workflow for handling GITT and/or EIS data. Solid lines indicate a record/dataset, while dashed lines indicate a workflow/sub-task. The four bigger coloured sections represent the raw-to-interoperable data conversion (top left, blue), laboratory-to-interoperable report conversion (bottom left, green), discerning static and dynamic measurement features (top right, orange), and model parameterization (bottom right, red).

4.1 Creating interoperable data

We aim to standardize data processing by establishing one consistent data format internally. With this approach, reusing our existing data processing scripts for future datasets becomes seamless – requiring only a single script each time to convert new datasets into the standardized format, or maybe even just different settings in the same script. We showcase our data conversion on the CSV conversion of our proprietary cycler output file, as CSV is the most generally accessible non-proprietary format. The first standardization here deals with general tabular data interpretation regardless of format, e.g., conversion to SI units or structuring according to measurement protocol.

The development of such an interpretation script against multiple datasets revealed the following adjustments it needs to be able to perform.

• Normalizing column descriptors, e.g., from “Applied current/A m⁻²” to “I [A]”; the re-formatted unit denotion is intentional, and ambiguous extra scalings like the m² obfuscate magnitudes.

• Stripping redundant or empty data columns, as these would slow down network-intensive data processing and obscure the information content.

• Stripping superfluous data rows, e.g., measurement channels that were logged even though no experiment was connected to them.

• Storing non-data comments in a separate file.

• Converting the file encoding into a global format.

• Converting localized column delimiters and decimal symbols into a global format.

• Interpreting the contents of a “cycler state” column of the user's choice, based on state changes of which the measurement will be segmented.

• Collating multiple measurement files into one while preserving the numbering of the original files for consistency.

• Normalizing current sign conventions based on cycler state, as some cyclers might imply current sign change by stating “Charge” and “Discharge”, while others will additionally explicitly denote it.

• Normalizing voltage sign conventions globally, as the direction of the battery in the cycler should not affect further data processing.

• Normalizing the sign convention for the imaginary part of an impedance measurement, as only some cyclers will report the true impedance. In contrast, others already negated the imaginary part for Nyquist plots.

• Lastly, normalizing current and voltage signs to align with the convention of the battery model and extract the working conditions to input into the battery simulator.

Identifying the correct adjustments and even the data structure itself in unfamiliar data may take several trial-and-error runs. In the specific case of time series measurements such as battery cycling and GITT, we at least know that the data has to be tabular in some way. If the table is laid out in plain text, such as CSV, issues about formatting, encoding, and segmentation may waste extensive amounts of time, if errors are caught late. The pipeline may still run through, but the results necessitate an investigation back through the various steps, which takes a lot of time on top of having to re-run the whole pipeline again. To accelerate the trial-and-error process, we instead recommend a visual validation of this preprocessing step, as shown for example in Fig. 3. Parsing more involved data formats like HDF5 introduces an entirely new problem, as such files may have only ever been intended to be used with one specific program, so the investigation into the data structure may take several days. We provide our parsers for CSV and HDF5 data as examples, including the tools to perform the aforementioned adjustments. If one wants to use those tools, one may parse the data into CSV table format and then use the presented utilities to perform the adjustments from there.

Fig. 3 Visualization of the preprocessed data of the GITT measurement on the graphite electrode in lithiation direction. Each “cycle” is one GITT pulse with its following rest phase.

To store the standardized measurement, we use the file format Apache Parquet, as it features an optimally small file size, fast reads, and broad software support. The conversion to a Parquet file happens with one central script to ensure that the structure of the files is consistent. We showcase the general tool usage on this interpretation step in the SI Section 4. We document unstructured metadata, like the operating states of each segment, via a separate JSON file. Still, the reusability of our data processing scripts requires us to keep them file-agnostic, as they should work with minimal adjustments for data stored as CSV or HDF5. Therefore, we handle in-memory sharing between data processing scripts with a Python object structure. Reusing our data processing scripts with different file formats involves writing one script that parses them into that Python object structure.

4.2 Challenges in creating interoperable laboratory reports

We want to be able to handle any information on material and cell properties programmatically. Then, all further data processing steps document exactly how we used that information, and future reuse can build on that. We showcase our laboratory report standardization on the documents as they come, as this elucidates some of the common challenges in the communication and data exchange between experimentalists and theoreticians. A more ideal setup than what we show here would be to introduce ontology-based checklists and data sheets to the laboratory. You may find both the original documents as well as our BattINFO-compliant data-metadata representation of them within the dataset we published on Zenodo, in the record “INR18650-LG-3500-MJ1 Lithium-Ion Battery Cell Direct Characterization Data”.

The laboratory report was summarized into two files that act as interfaces to users. The experimentalist side intended to curate the data in a self-explanatory way and devised the following attempt to structure and describe the information and results from the parameterization works. The first file, an Excel file, contained all geometry and material parameters in a minimal format. The second file, a PowerPoint file, repeated some of the parameters while also giving error bars, additional context on the methods used, and diagrams for the non-scalar information and images from the microscopy measurements. The PowerPoint file acts as metadata for the data in the Excel file. Nevertheless, the Excel file is not interoperable, as there is no machine-readable information about its data structure. Manual extraction is the only avenue here; ideally, the experimentalists would have been provided with an interoperable structure to input. Such a structure would also have given the theoreticians a central document to align their requirements to ensure that the experiments cover all required material properties. As an example, the thermodynamic factor of the electrolyte was initially missed on both sides. We filled such gaps with literature data gleaned from LiionDB.⁵⁰

As standardization efforts are still rapidly developing (such as the BPX physics-based battery modelling standard), we opted not to adopt them during our methodology's long development period. However, once all the required features are present, BPX will be the most interoperable way to present our parameter file. Alternatively, our parameter file is a Python script that stores the parameters in a key-value structure. The keys correspond to the simulation software PyBaMM.²⁶

4.3 Data preprocessing to enhance signal interpretability

We want to dissect our data into signal and background. More accurately, we only want to use the part of the data containing a signal for a specific parameter of interest. Then, the sensitivity and precision of the following parameterization step are much more easily assessed. The time-series voltage response of a battery can be split into a static part (OCP), and a dynamic part, termed “overpotential”. Since we want to study transport properties, which only appear in the dynamic part here, we must first consider the static part.

We extract OCP data of both electrodes from GITT measurements as described in Section 2.2. We store the extracted OCV data in a JSON file; as this dataset is rather small, JSON is more appropriate here than Parquet, for human-readability. To increase the SOC resolution and filter noise, we interpolate the OCP data with the OCP model of Birkl et al.³⁶ These steps entail many small adjustments and a carefully crafted optimization algorithm, which are documented by our code and the workflow files describing its invocation. See Yao et al.⁵¹ for another example. Finally, we store the OCV model and the metadata of its optimization in a JSON file. The data, the fit parameters, a directly usable representation of the fit function, and the optimization metadata are stored with respective keys.

We want to parameterize our data in a way that considers as many uncertainties as possible, as battery measurements, in particular, entail a lot of them.³⁰ Then, our results will transparently encode how accurately the battery response reflects its material properties and allow us to update the range of possible parameters with future measurements. First, we subtract the optimized OCP model from the GITT data. To verify the accuracy and alignment of the OCP model, we plot the resulting overpotential measurement and check that the voltage asymptotes of the rest phases are close to zero. The overpotential is stored as a Parquet file with an identical internal structure to the original data, including timestamps, current, and voltage.

4.4 Probabilistic parameterization

We now prepare and perform the parameterization according to the algorithm EP-BOLFI.³⁰ EP-BOLFI splits into a preprocessing step for Expectation Propagation for Likelihood-Free Inference (EP-LFI⁵²) and a parameterization step for Bayesian Optimization for Likelihood-Free Inference (BOLFI⁵³). The application to GITT is part of the EP-BOLFI publication. Preprocessing for EP allows you to apply domain knowledge by transforming the data into characteristic features. A typical GITT pulse or rest phase for materials like graphite and NMC can be entirely described by only two features, if no phase changes are occurring during the measurement, comprising of a total of five scalar values: the square-root behaviour for short times consisting of offset and square-root slope, and the exponential behaviour for long times consisting of offset, magnitude, and decay rate.³⁰ We choose a suitable subset of features that relate to the quantity we wish to measure; here, it is the short-time square-root slopes for diffusivities. The remaining central input EP-BOLFI requires are our prior assumptions about the parameters of interest. The spread of sensible parameters that is known a priori is encoded as a probability distribution, denoted as the Prior.

All inputs for the parameterization get encapsulated as a JSON file containing model information, model discretization, experimental conditions, experimental data, experimental features, and EP-BOLFI settings. We now visualize that our parameterization is set up correctly. We do so by collecting the spread of simulation results over the parameter sets that are at the 95% probability bounds of the Prior. After visually confirming that the Prior we set contains the true parameters in its 95% probability bounds, we run the parameterization. See the GITT analysis in the EP-BOLFI paper³⁰ for a detailed explanation of this process.

The parameterization result is also a probability distribution over the parameter sets. Compared to the Prior, it only contains the subset of the Prior that also agrees with the data. As the result is a posteriori knowledge about the true parameters, it is aptly denoted the Posterior. We can visualize the Posterior similarly to the Prior, as it is structurally identical. Hence, the plots are consistent and can emphasize that the Posterior is a knowledge update of the Prior. Once the parameterization is done for each GITT pulse, we collect the individual SOC point parameters into a function of SOC. The SOC-dependent functions are stored as JSON files alongside a B-spline interpolation in Python format and their plot.

4.5 GITT characterization results

Fig. 4a shows the results of state-of-the-art direct diffusivity extraction from the GITT data in delithiation direction. The limited error propagation we can consider here only displays the effect of voltage measurement resolution. It naturally becomes an issue in the SOC range 0.6–1.0, where graphite has a voltage plateau that is shallower than the measurement can resolve. Hence, we observe large error bars in that range.

Fig. 4 Results for the diffusivity of the active material from one set of GITT data in delithiation direction, via direct calculations (a) and from fitting electrochemical models (b). The labels read as follows: ΔU_s/ΔU_t refers to the original GITT method,²⁷ ΔU_s/ΔU_t(Δt ↓) refers to the same method applied to only a suitably small time segment (90 s), refers to the differential formulation of the original GITT method, refers to a correction for overlapping relaxation phenomena,²⁹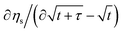 additionally removes the OCP prior to diffusivity calculation, and SPM, SPMe, and DFN refer to the fitted electrochemical models. The best direct approach is plotted in black in (b) as well for comparison.

Fig. 4b shows the results of our model-based diffusivity extration from the same GITT data in delithiation direction. Our approach includes more sources of uncertainty in its error propagation, especially parameter uncertainties and their correlations. We observe a significant decrease in diffusivity accuracy at a much wider SOC range 0.3–1.0.

The DFN simulations for the individual GITT pulses, where one exemplary one is shown in Fig. 5, hint at the reason. Traditional GITT relies on the assumption that the overpotential response grows monotonously, which we do not observe there. We investigate the unexpected shape of the overpotential further in an analysis of the overpotential components in Fig. 6a.

Fig. 5 The predictive parameterization posterior of a GITT measurement in delithiation direction. The highlighted square-root slopes γ are used for fitting. The constant-current pulse lasts 0.6 h, and we show only the relevant part of the following rest. The square-root features used for parameterization are noted down for experiment (orange) and optimal simulation (green) in . The large posterior 95% confidence interval is a consequence of the non-matchable pulse square-root feature.

Fig. 6 A plot detailing the overpotential components in a GITT measurement in delithiation (a) and lithiation (b) direction. Only the two largest contributions are relevant in the delithiation direction, which are the OCP and particle concentration overpotential. The oscillation between the two is a result of a rapid change in OCP slope. All contributions are equally important in the lithiation direction. In particular, we see that the particle concentration overpotential shows a minor contribution overall, which makes this a measurement of the electrolyte rather than of the electrode.

Oscillations between SOC and overpotential occur, showing unexpected retrograde SOC change. The SOC at which this happens is near a bend in the OCP, originating from crystal structure rearrangements in the active material. While the voltage response grows monotonously, the overpotential response does not, which would be missed in traditional GITT. With our approach, though, the similarity of the shape and the relaxation square-root accuracy tell us that the OCV and model accuracy are sufficiently high for parameterization.

Furthermore, we observe a fundamental phenomenon in statistical estimation in the model-based diffusivities Fig. 4b: the bias-variance tradeoff. Since the SPM neglects electrolyte effects, it is the wrong model and can not fit the data, which we call a high bias. Consequently, as seen from the error bars, the variance is suspiciously low, which we colloquially call “confidently incorrect”. As we approach a more correct model with the SPMe, the variance grows, which we now know is expected but may be counterintuitive.³¹ Only the DFN, as a sufficient model, can exhibit low bias and variance simultaneously. This example cautions us to trust a parameterization with a single model without considering the context from adjacent models.

Fig. 7a shows the results of state-of-the-art direct diffusivity extraction from the GITT data, this time in the lithiation direction. The limited error propagation we can consider here again only displays the effect of voltage measurement resolution. This time, it is much less of an issue due to the measurement happening in the direction of increasing OCP slope, which results in voltage responses comfortably beyond measurement accuracy. The exception is at the very beginning of the GITT lithiation measurement at high negative electrode SOC, as the surface concentrations do not reach the non-plateau region of the OCP yet.

Fig. 7 Results for the diffusivity of the active material from one set of GITT data in lithiation direction, via direct calculations (a) and from fitting electrochemical models (b). The labels read as follows: ΔU_s/ΔU_t refers to the original GITT method,²⁷ ΔU_s/ΔU_t(Δt↓) refers to the same method applied to only a suitably small time segment (90 s), refers to the differential formulation of the original GITT method, refers to a correction for overlapping relaxation phenomena,²⁹ and additionally removes the OCP prior to diffusivity calculation, and SPM, SPMe, and DFN refer to the fitted electrochemical models. The best direct approach is plotted in black in (b) as well for comparison.

Fig. 7b shows the results of our model-based diffusivity extraction on the same GITT data in lithiation direction. We observe almost no improvement over the prior parameter assumptions for the SOC range 0.3–1.0. The SPM fit shows suspiciously low variance, which can be attributed to an insufficient model introducing significant bias.³¹ We see a marked decrease in diffusivity accuracy in the SOC range 0.0–0.1 across all models this time. Similar to the delithiation direction, we observe that GITT measurements towards the edge of the SOC range can not uniquely parameterize the active material diffusivity. When the local electrode concentration hits an SOC limit, a “depletion shockwave” runs from the current collector to the separator, which has a different dynamic than a diffusivity response.

The DFN simulations can't capture the magnitude of the overpotential this time, as we see in one of the parameterized pulses in Fig. 8.

Fig. 8 The predictive parameterization posterior of a GITT measurement in lithiation direction. The highlighted square-root slopes γ are used for fitting. The constant-current pulse lasts 0.6 h, and we show only the relevant part of the following rest. The square-root features used for parameterization are noted down for experiment (orange) and optimal simulation (green) in . The overfitted posterior 95% confidence interval is a consequence of the prior 95% confidence interval not enveloping the data either.

The shallow OCP curve is one reason, as the negative electrode concentration overpotential scales with it. Consequently, it is small with regards to the electrolyte overpotential, as shown in the overpotential analysis in Fig. 6b.

We repeat the identical procedure for the positive NMC electrode in the SI Section 5. As NMC has a benign OCP with no bends and small slope changes, traditional GITT works well and our approach is not needed.

We can ensure the compatibility of other measurements to our GITT parameterization by utilizing the fact that we treated it according to Bayesian principles. In Bayesian statistics, results from insufficient data are described as probability distributions reflecting the uncertainty that the data and model contain. To give context: the posterior (the “result”) in Bayesian statistics is obtained as the product of the prior (the “informed researcher's intuition”) and the likelihood (the “model”). We generalize this multiplication update by multiplying the likelihoods of multiple measurements or multiple parts of a measurement by the prior, which is the EP-LFI⁵² approach. This allows us to cast a much wider net with the prior than before, moving from a rather narrow subjectively influenced prior to one that collects all physically feasible parameter values. As batteries are highly variable even within one production batch,⁴ we prefer this approach over averaged calibration. The mathematical justification for this “trick” stems from summary statistics.⁵⁴ More straightforwardly, this is equivalent to a semi-parallelized EP-LFI, which is stated by Barthelmé et al.⁵⁵ to be valid. This “simple” step is only possible when the models used for the parameterization in both cases are compatible. See Zhu et al.⁵⁶ and Deng et al.⁵⁷ for the challenges that combining GITT and, e.g., Electrochemical Impedance Spectroscopy otherwise entail.

5 Discussions

Here we describe the generally applicable issues and improvements we found in our collaboration. We will discuss these in order: measurement protocol communication, measurement objective communication, measurement accuracy assessment, uncertainty treatment, documentation via metadata, elucidating domain knowledge, checking model compatibility, interoperable laboratory reports, and software dependency review.

Communication of measurement protocol is the first step that may induce issues. We found different understandings of a measurement technique (GITT) amongst the parties involved. With different requirements and limitations, one may select a different interpretation. For example, a theoretician might prefer a rigid GITT set for consistency or an arbitrary, but uninterrupted one for error mitigation. At the same time, an experimentalist is concerned about maximizing expensive equipment time and might interweave other measurements in the rest phase “downtime”. By joining all parties on what may be considered the domain of only one party, we could find an optimal solution for all: shortening the rest phases. While shorter rest phases down to 15 min may suffice,³⁰ this only applies after one verification GITT pulse on the material at hand with the usual hours-long relaxation. Additionally, GITT as a measurement protocol can be adapted to provide diagnostic fingerprints during charging of a battery,²⁸ and inversely, our approach can also utilize similar patterns in actual battery usage data. As modern (battery) materials science relies on an interdisciplinary approach to progress further, it becomes all the more important to discuss the intricacies of any given measurement technique with all involved parties.

Measurement objective communication is a separate step that needs to be considered. The issue we found was different quantities of interest. This may sound trivial without knowledge of experimental setups, but to use resources optimally, they can be much more complex than what their output files suggest. For example, a multiplexer setup can seamlessly switch between the time-domain measurements for GITT and the frequency-domain measurements for EIS. However, specific quantities can only be logged by one device at once, leading to gaps in the record for the other device. For example, an EIS measurement device may not be set up to track the total charge transferred, which is necessary for the GITT measurement device to assign SOCs to data points. A solution to avoid this is to agree on a verbose spreadsheet with exact cycler instructions beforehand. Some issues only appear in such simplified discussions, as they eliminate the application of advanced knowledge. For example, a theoretician might not know the time, current, or voltage resolution limits. So after a discussion on the measurement technique in general, we recommend to separately discuss requirements for recorded data.

Measurement accuracy assessment refers to a human-interpretable representation of the intermediate steps in the data pipeline. On the one hand, it allows for the re-calibration and fine-tuning of the intermediate steps. On the other hand, it reduces the individual errors that accumulate in the final error propagation calculation. The issue we found was a lack of checks of assumptions. For example, a GITT measurement may be idealized as per theory. Each segment starts with a short-term square-root behaviour and smoothly merges into an exponential decay towards a (quasi-)equilibrium. To verify this, we subtracted the electrode OCP from the data. But we found oscillations of the overpotential around bends in the electrode OCP, e.g., in Fig. 5. While it is well understood that the original GITT formula from 1977 (ref. 27) does not apply in such situations, we show that GITT with a model-based analysis can still yield a suitable parameterization. This point generalizes to the mutual progress between measurements and manufacturing in materials science, as new issues may arise in workflow steps that were straightforward for established materials.

Uncertainty treatment is a step that can not be overstated in its importance in battery research. We found that the magnitude of uncertainty sources is easily underestimated when only considering one at a time. With EP-BOLFI,³⁰ we turn to a black-box optimizer with a stochastical framework that allows us to evaluate any uncertainties simultaneously that we can incorporate into a simulation model. Voltage measurement precision and material/geometrical property uncertainty can be tacked onto any simulation model. Meanwhile, material/geometrical property correlation is an intrinsic property of the model equations that EP-BOLFI uncovers. For example, the influence of electrolyte properties and their geometry on the complete parameterization is often underestimated. To verify the extent of this influence, we perform the overpotential analyses in Fig. 6 for selected SOC points in both the delithiation and lithiation directions. We see that in delithiation direction, most of the signal stems from the electrode concentration gradients, which is desired. But in lithiation direction, only about 10–20% of the signal stems from the phenomenon of interest, while the electrolyte concentration gradient effects dominate the signal. Any uncertainty in the electrolyte properties has a proportionally increased influence on the parameterization of the active material diffusivity. Checking the influence of the electrolyte this way tells us how much we need to optimize the experimental setup for a sufficient signal from the electrodes. The same principle applies when measuring the intact battery, where we have overlapping signals from both electrodes and the electrolyte. As we have shown in the GITT case study of the original EP-BOLFI publication,³⁰ our approach is still suitable in this case, with comparably large error bars. The workflow machinery stays the same, as a two-electrode setup is its default mode. Commercial batteries give us a unique test case for advanced uncertainty treatment, as they are mass-manufactured with strict regulatory requirements, yet still remain elusive for diagnostics. Having verified that the stochastic optimization approach is suitable for the present case, we believe it to be a promising venue in other challenging diagnostics issues in and beyond materials science, e.g., astronomy⁵⁸ or the medical sciences.⁵⁹ These disciplines have their own sophisticated workflow engines to process data per given requirements, and develop them to decrease the amount of manual supervision and improve quality control.

Documentation via metadata is often considered an ungrateful task, as it is thought not to have an immediate benefit. The issue we found is that domain-specific language between experimentalists and theoreticians did not diverge in the words used but in the meaning of those words. For example, the term “tortuosity τ” has different defaults depending on one's own research field. More accurately, one may refer to “path-length tortuosity τ” if the ratio between material and effective transport properties is ε/τ², or “effective tortuosity τ” if it is ε/τ. With ontology-backed descriptions of each use of the term “tortuosity”, one could directly translate sources from other disciplines into one's own requirements. So we make the case that an ontology-structured documentation workflow can have immediate benefits, while also allowing cross-disciplinary exchange of material knowledge. For example, graphite is a ubiquitous material, so information from or findings communicated to other fields in material science may accelerate further research.

Elucidating domain knowledge is critical for successful communication across disciplines. The issue we found is the unconscious application of domain knowledge. For example, initial communication about the difference between a commercial cell and its modified experimental sample was kept “simple” in the interest of each party's time: the theoreticians got the description that the experimental setup minimizes “the effect” of the separator. But this “simple” statement encodes a large volume of expectations of the measurement, an assumption on the quantities that will be extracted from it, and the method by which the separator was made “negligible”. Theoreticians would assume that the new separator would be a marginally thick glass fibre with unity tortuosity. We show the actual picture in the SI Fig. 2. The separator is “removed” from the measurement by it having unity tortuosity and high porosity. But, as the commercial electrolyte influences the signal greatly³⁰ compared to a purely academic cell, combined with the considerable thickness of the separator, the removal is imperfect, which must be communicated back and forth. Hence, we recommend graphical communication as a way to transfer domain knowledge. While it may feel like a non-worthwhile time investment, we found that communicating verbosely rather than abstractly consistently saves time, as early misunderstandings can be caught before they infiltrate a whole workflow. This naturally grows more important the more different specialties need to be brought together to elucidate a given question in material science.

Checking model compatibility thoroughly by checking assumptions between models can be arbitrarily difficult. The issue we found was the pragmatic reliance on the fact that different models of one phenomenon are supposed to approximate the same physical reality. For example, while Transmission Line Models claim that they reproduce a Finite Volume discretization of porous microstructures, from the differences found in 1D + 1D impedance simulations,⁶⁰ we can infer that TLM parameters do not map onto those of 1D + 1D models. The motivation behind our modular workflow approach is to make it even feasible to retry a parameterization with various models, possibly with multiple calibrations. This opens up the field of data-driven model comparison and model building in multiphysics simulations.

Interoperable laboratory reports may seem like an extra step on top of the measurement documentation. The issue we found is the loss of auxiliary information, e.g., meanings of data column descriptors, differences between a battery cell and its sample for measurement, known noise sources, or even specifics of the preceding equipment use. With ontologies, we have a tool to make checklists and input masks for metadata, automatically converting laboratory notes into a complete picture. For example, we encountered data segments from a multiplexer setup that were not interpretable independently. One device seemed to have arbitrary gaps in voltage data. But both devices were active simultaneously, passing their electrical connection to the battery cell back and forth. Another example is the common description of current via A m⁻², which, out of context, lacks the information if the area it refers to is the total surface area of one of the electrodes or the cross-section of one of the electrodes, and which electrode it refers to. A very natural issue we want to emphasize here is human error when transcribing non-machine-readable laboratory reports. Apart from the translation of domain-specific knowledge, there can also be very practical issues, like missing tabs in an Excel sheet or forgetting to check for data outside of the initial viewport.

Software dependency review entails not only the log of software versions used but, more importantly, the effects each piece of software has on the workflow. The issue we found is the sometimes non-interoperable implementation of file formats. For example, Pandas is a popular Python library for handling tabular data, offering data export into the HDF5 file format. While it is possible to store interoperable data this way,⁶¹ the default behaviour is a file that can only be reasonably read by Pandas. This raises an unnecessary barrier to future reuse. In the worst case, one must find the same Pandas version and make it run on their system. Therefore, we recommend verifying the standard adherence of your data by opening it in a “third” software, as in, one neither party initially used. Additionally, the choice of file format depends on the size of one's organization. To show that HDF5 is appropriate for organizations with dedicated resources for data curation, we refer you to Moradpour et al.⁶² With no dedicated resources, a file format is preferable that can not be misconstrued as the highly flexible HDF5 can. For example, we choose Apache Parquet because it forces us to organize our data in a single table each time. For unstructured data, we choose JSON, since it sacrifices file compactness for structural simplicity and universal readability. You may find examples for each file type in the appended Zenodo record, specifically for Pandas-only HDF5 within “INR18650-LG-3500-MJ1 Anode Raw Data Collection” in “INR18650-LG-3500-MJ1 Anode”, for its compact and normalized Parquet version in “INR18650-LG-3500-MJ1 Anode Structured Data Collection” there, and for JSON as used for logging within “INR18650-LG-3500-MJ1 Anode GITT OCV Model Fit” there as well.

6 Conclusions

We conclude that improving adherence to the FAIR principles and refactoring data treatment to be automatable improve transparency and reusability of the data and the software that interprets it while simultaneously allowing us to bridge disciplines. We summarize our findings by FAIR principle.

Findable is the principle with which we identify our first issue, the low availability of appropriate data. The emphasis lies on “appropriate”, as in, the data you find has to match the material you are studying. For example, there are numerous incongruent material characterizations for “graphite”;^43,63–84 this exhaustive list was generated with LiionDB.⁵⁰ Here, the main cause is that several different configurations of graphite are commonly referred to as just “graphite”, independent of structure, morphology, or crystallinity. The other cause is the wide range of values one gets from different parameterization approaches, not all of which may take into account the effects from voltage plateaus and their transitions.

Accessible is the principle with which we identify our second issue, the low accessibility of raw data. The usual way to “use” data is to extract it from a plot of the data manually. This greatly obscures phenomena on vastly differing timescales, as in virtually all battery phenomena. Storing the measurement files instead of just their plots on a data publisher like Zenodo provides raw data.

Interoperable is the principle with which we identify our third issue, proprietary data formats. Each manufacturer of battery cyclers has their own format. With incomplete documentation of the settings used in a particular measurement, retrieving the data completely can become challenging. Providing a data format and the code that can handle it allows retrieval of the original measurement data.

Reproducible is the principle with which we identify our fourth issue, the failure to apply novel methods. Without a completely documented example it can be impossible to identify whether the method does not apply or if one implemented it wrong. Ultimately, the novel method may get dropped in favour of an obsolete but established one. We observe this in the still widespread use of the ΔU_s/ΔU_t GITT variant over the 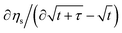one or our inverse modelling approach. We document our analysis by providing the raw data and the code analyzing it Open Source.

Reusable is the principle with which we identify our last issue, one of a purely legal nature. It is common to forget that measurement data is, by default, protected by copyright, depending on your jurisdiction. So, if no contract clauses or other legal documents like licenses have been prepared, when the researcher who curated the data has left the field, that data is now unusable. To protect themselves against legal proceedings, institutes and industry will not use that data, even if that is not what the researcher intended. A consistent workflow protects against such bureaucratic issues.

Automation has benefits separate from the FAIR principles. Segmentation into sub-tasks allows for flexible tool adaptation and reuse for new tools. Automation is thus accessible to an ontology treatment, enabling translations between disciplines. The automation forces any manual adjustments to be documented, leading to a machine-readable version of any intermediate step for future use. Undocumented adjustments vanish when one commits to generally usable sub-tasks. The workflows are also more human-readable. Every intermediate step is inspectable for error correction. The whole data pipeline or parts of it can be quickly re-run with different settings. Incidentally, the data pipeline's clear structure makes it much more user-friendly. This clarity may also bear benefits for individual datasets. We regard our work as an important step forward in incorporating automation and digitalization techniques into the battery characterization workflow. This both accelerates the progress of individual research initiatives and fosters collaboration between the various disciplines involved in next-generation batteries.

Author contributions

Yannick Kuhn: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, validation, visualization, writing – original draft, writing – review & editing. Bhawna Rana: data curation, formal analysis, investigation, validation. Micha Philipp: writing – review & editing. Christina Schmitt: data curation, formal analysis, investigation, validation. Roberto Scipioni: formal analysis, investigation, visualization. Eibar Flores: conceptualization, methodology, writing – review & editing. Dennis Kopljar: conceptualization, data curation, funding acquisition, investigation, methodology, project administration, validation, writing – original draft, writing – review & editing. Simon Clark: conceptualization, data curation, funding acquisition, methodology, project administration, resources, software, visualization, writing – original draft, writing – review & editing. Arnulf Latz: supervision, writing – review & editing. Birger Horstmann: conceptualization, funding acquisition, project administration, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The dataset comprising of the raw experimental data, its preprocessed derivatives, and the whole parameterization workflow and results is publicly available on Zenodo: https://doi.org/10.5281/zenodo.15407849. The program needed to translate the parameterization workflow files into series of command line statements is part of the Open Source Kadi4Mat software https://doi.org/10.5281/zenodo.4088269, specifically the subpackages to manage https://doi.org/10.5281/zenodo.4442552 and execute https://doi.org/10.5281/zenodo.4442562 the workflow files. The code these command line statements call which is performing the preprocessing and analysis, as well as the code neede to reproduce the figures, is collected within the Open Source Python library EP-BOLFI: https://doi.org/10.5281/zenodo.6967238 or “pip install ep-bolfi”. To enable reusability, we provide datasets under a permissive Creative Commons license, which allows others to access, share, and adapt the data as long as proper credit is given. This licensing approach maximizes the potential for collaboration, innovation, and integration of our work into broader research efforts.

Supplementary information: precise experimental protocols, illustrations of the battery disassembly, background information on Protegé and GITT, and the diffusivity analysis on the NMC electrode. See DOI: https://doi.org/10.1039/d5dd00247h.

Acknowledgements

This work was supported by the German Aerospace Center (DLR). The authors acknowledge support by the Helmholtz Association through grant no. KW-BASF-6 (Initiative and Networking Fund as part of the funding measure “ZeDaBase-Batteriezelldatenbank”) and by the European Union's Horizon 2020 innovation program under grant agreement numbers 875527 (HYDRA) and 101103997 (DigiBatt). This work was conducted using Protégé. This work contributes to the research performed at CELEST (Center for Electrochemical Energy Storage Ulm-Karlsruhe).

References

1. R. Xu, X. Li, S. Tang, Z. Wang, H. Guo, W. Peng, D. Wang, J. Duan, J. Wang and G. Yan, Appl. Energy, 2024, 371, 123630.
2. M. D. Wilkinson, M. Dumontier, I. J. Aalbersberg, G. Appleton, M. Axton, A. Baak, N. Blomberg, J. W. Boiten, L. B. da Silva Santos, P. E. Bourne, J. Bouwman, A. J. Brookes, T. Clark, M. Crosas, I. Dillo, O. Dumon, S. Edmunds, C. T. Evelo, R. Finkers, A. Gonzalez-Beltran, A. J. Gray, P. Groth, C. Goble, J. S. Grethe, J. Heringa, P. A. t Hoen, R. Hooft, T. Kuhn, R. Kok, J. Kok, S. J. Lusher, M. E. Martone, A. Mons, A. L. Packer, B. Persson, P. Rocca-Serra, M. Roos, R. van Schaik, S. A. Sansone, E. Schultes, T. Sengstag, T. Slater, G. Strawn, M. A. Swertz, M. Thompson, J. V. D. Lei, E. V. Mulligen, J. Velterop, A. Waagmeester, P. Wittenburg, K. Wolstencroft, J. Zhao and B. Mons, Sci. Data, 2016, 3, 160018.
3. A. Mistry, A. Verma, S. Sripad, R. Ciez, V. Sulzer, F. B. Planella, R. Timms, Y. Zhang, R. Kurchin, P. Dechent, W. Li, S. Greenbank, Z. Ahmad, D. Krishnamurthy, A. M. Fenton Jr, K. Tenny, P. Patel, D. J. Robles, P. Gasper, A. Colclasure, A. Baskin, C. D. Scown, V. R. Subramanian, E. Khoo, S. Allu, D. Howey, S. DeCaluwe, S. A. Roberts and V. Viswanathan, ACS Energy Lett., 2021, 6, 3831–3835.
4. P. Dechent, S. Greenbank, F. Hildenbrand, S. Jbabdi, D. U. Sauer and D. A. Howey, Batteries Supercaps, 2021, 4, 1821–1829.
5. S. Clark, F. L. Bleken, S. Stier, E. Flores, C. W. Andersen, M. Marcinek, A. Szczesna-Chrzan, M. Gaberscek, M. R. Palacin, M. Uhrin and J. Friis, Adv. Energy Mater., 2022, 12, 2102702.
6. A. Dave, J. Mitchell, K. Kandasamy, S. Burke, B. Paria, B. Poczos, J. F. Whitacre and V. Viswanathan, ECS Meeting Abstracts, 2020, MA2020-01, p. 527.
7. A. Lewis-Douglas, L. Pitt and D. A. Howey, arXiv, 2020, preprint, arXiv:2010.14959,  DOI:10.48550/arXiv.2010.14959.
8. M. Vogler, S. K. Steensen, F. F. Ramírez, L. Merker, J. Busk, J. M. Carlsson, L. H. Rieger, B. Zhang, F. Liot, G. Pizzi, F. Hanke, E. Flores, H. Hajiyani, S. Fuchs, A. Sanin, M. Gaberšček, I. E. Castelli, S. Clark, T. Vegge, A. Bhowmik and H. S. Stein, Adv. Energy Mater., 2024, 14, 2403263.
9. S. P. Stier, C. Kreisbeck, H. Ihssen, M. A. Popp, J. Hauch, K. Malek, M. Reynaud, T. P. Goumans, J. Carlsson, I. Todorov, L. Gold, A. Räder, W. Wenzel, S. T. Bandesha, P. Jacques, F. Garcia-Moreno, O. Arcelus, P. Friederich, S. Clark, M. Maglione, A. Laukkanen, I. E. Castelli, J. Carrasco, M. C. Cabanas, H. S. Stein, O. Ozcan, D. Elbert, K. Reuter, C. Scheurer, M. Demura, S. S. Han, T. Vegge, S. Nakamae, M. Fabrizio and M. Kozdras, Adv. Mater., 2024, 36, 2407791.
10. G. Houchins and V. Viswanathan, J. Chem. Phys., 2020, 153, 054124.
11. A. Sanin, J. K. Flowers, T. H. Piotrowiak, F. Felsen, L. Merker, A. Ludwig, D. Bresser and H. S. Stein, Adv. Energy Mater., 2025, 2404961.
12. P. Dechent, E. Barbers, S. Clark, S. Lehner, B. Planden, M. Adachi, D. A. Howey and S. Paarmann, arXiv, 2024, preprint, arXiv:2410.23303,  DOI:10.48550/arXiv.2410.23303.
13. M. A. Musen, AI Matters, 2015, 1, 4–12.
14. G. Goldbeck, E. Ghedini, A. Hashibon, G. J. Schmitz and J. Friis, A world of engineering simulation. NWC 2019, NAFEMS World Congress, 2019, pp. 19–86.
15. N. Brandt, L. Griem, C. Herrmann, E. Schoof, G. Tosato, Y. Zhao, P. Zschumme and M. Selzer, Data Sci. J., 2021, 20, 1–14.
16. N. Brandt, N. T. Garabedian, E. Schoof, P. J. Schreiber, P. Zschumme, C. Greiner and M. Selzer, Data, 2022, 7, 1–15.
17. M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533.
18. A. Latz and J. Zausch, J. Power Sources, 2011, 196, 3296–3302.
19. I. Traskunov and A. Latz, Electrochim. Acta, 2021, 379, 138144.
20. M. Schammer, B. Horstmann and A. Latz, J. Electrochem. Soc., 2021, 168, 026511.
21. I. Traskunov and A. Latz, Energy Technol., 2021, 9, 2000861.
22. E. C. Tredenick, A. M. Boyce, S. Wheeler, J. Li, Y. Sun, R. Drummond, S. R. Duncan, P. S. Grant and P. R. Shearing, J. Electrochem. Soc., 2025, 172, 030503.
23. I. Squires, A. Galvis, J. M. Foster and S. J. Cooper, J. Electrochem. Soc., 2024, 171, 050536.
24. S. G. Marquis, V. Sulzer, R. Timms, C. P. Please and S. J. Chapman, J. Electrochem. Soc., 2019, 166, A3693–A3706.
25. S. Santhanagopalan, Q. Guo, P. Ramadass and R. E. White, J. Power Sources, 2006, 156, 620–628.
26. V. Sulzer, S. G. Marquis, R. Timms, M. Robinson and S. J. Chapman, J. Open Res. Software, 2021, 9, 1–8.
27. W. Weppner and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1569–1578.
28. Y.-C. Chien, H. Liu, A. S. Menon, W. R. Brant, D. Brandell and M. J. Lacey, Nat. Commun., 2023, 14, 2289.
29. S. D. Kang and W. C. Chueh, J. Electrochem. Soc., 2021, 168, 120504.
30. Y. Kuhn, H. Wolf, A. Latz and B. Horstmann, Batteries Supercaps, 2023, 6, e202200374.
31. J. M. Escalante, S. Sahu, J. M. Foster and B. Protas, Electrochem. Soc., 2021, 168, 110519.
32. L. Köbbing, Y. Kuhn and B. Horstmann, ACS Appl. Mater. Interfaces, 2024, 16, 67609–67619.
33. D. Wycisk, G. K. Mertin, M. Oldenburger, O. von Kessel and A. Latz, J. Energy Storage, 2024, 89, 111617.
34. X. Li, A. M. Colclasure, D. P. Finegan, D. Ren, Y. Shi, X. Feng, L. Cao, Y. Yang and K. Smith, Electrochim. Acta, 2019, 297, 1109–1120.
35. J. Sturm, A. Rheinfeld, I. Zilberman, F. B. Spingler, S. Kosch, F. Frie and A. Jossen, J. Power Sources, 2019, 412, 204–223.
36. C. R. Birkl, E. McTurk, M. R. Roberts, P. G. Bruce and D. A. Howey, J. Electrochem. Soc., 2015, 162, A2271–A2280.
37. J. Scharf, M. Chouchane, D. P. Finegan, B. Lu, C. Redquest, M. cheol Kim, W. Yao, A. A. Franco, D. Gostovic, Z. Liu, M. Riccio, F. Zelenka, J.-M. Doux and Y. S. Meng, Nat. Nanotechnol., 2022, 17, 446–459.
38. S. C. Carniglia, J. Catal., 1986, 102, 401–418.
39. J. Landesfeind, J. Hattendorff, A. Ehrl, W. A. Wall and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, A1373–A1387.
40. J. Landesfeind, M. Ebner, A. Eldiven, V. Wood and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, A469–A476.
41. J. Landesfeind and H. A. Gasteiger, J. Electrochem. Soc., 2019, 166, A3079–A3097.
42. C. Schmitt, M. Gerle, D. Kopljar and K. A. Friedrich, J. Electrochem. Soc., 2023, 170, 070509.
43. J. Schmalstieg, C. Rahe, M. Ecker and D. U. Sauer, J. Electrochem. Soc., 2018, 165, A3799–A3810.
44. T. M. M. Heenan, A. Jnawali, M. D. R. Kok, T. G. Tranter, C. Tan, A. Dimitrijevic, R. Jervis, D. J. L. Brett and P. R. Shearing, J. Electrochem. Soc., 2020, 167, 140530.
45. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, 2012.
46. J. Sauvola and M. Pietikäinen, Pattern Recogn., 2000, 33, 225–236.
47. P. Ramachandran and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 40–51.
48. S. J. Cooper, A. Bertei, P. R. Shearing, J. A. Kilner and N. P. Brandon, SoftwareX, 2016, 5, 203–210.
49. B. Münch and L. Holzer, J. Am. Ceram. Soc., 2008, 91, 4059–4067.
50. A. A. Wang, S. E. O'Kane, F. B. Planella, J. L. Houx, K. O'Regan, M. Zyskin, J. Edge, C. W. Monroe, S. J. Cooper, D. A. Howey, E. Kendrick and J. M. Foster, Prog. Energy, 2022, 4, 032004.
51. A. M. Yao and V. Viswanathan, Open-Circuit Voltage Models Should Be Thermodynamically Consistent, 2024.
52. S. Barthelmé and N. Chopin, J. Am. Stat. Assoc., 2014, 109, 315–333.
53. M. U. Gutmann and J. Corander, J. Mach. Learn. Res., 2016, 17, 1–47.
54. T. P. Minka, A family of algorithms for approximate Bayesian inference, 2001, https://tminka.github.io/papers/ep/minka-thesis.pdf.
55. S. Barthelmé, N. Chopin and V. Cottet, Handbook of Approximate Bayesian Computation, Chapman and Hall/CRC, 1st edn, 2018, ch. 13.
56. Y. Zhu, T. Gao, X. Fan, F. Han and C. Wang, Acc. Chem. Res., 2017, 50, 1022–1031.
57. C. Deng and W. Lu, J. Power Sources, 2020, 473, 228613.
58. W. Freudling, S. Zampieri, L. Coccato, S. Podgorski, M. Romaniello, A. Modigliani and J. Pritchard, Astron. Astrophys., 2024, 681, A93.
59. E. Williams, S. Niehaus, J. Reinelt, A. Merola, P. G. Mihai, K. Villringer, K. Thierbach, E. Medawar, D. Lichterfeld, I. Roeder, N. Scherf and M. d. C. Valdés Hernández, arXiv, 2021, preprint, arXiv:2112.03277,  DOI:10.48550/arXiv.2112.03277.
60. N. Hallemans, N. E. Courtier, C. P. Please, B. Planden, R. Dhoot, R. Timms, S. J. Chapman, D. Howey and S. R. Duncan, J. Electrochem. Soc., 2025, 1–20.
61. N. H. Paulson, L. T. Ward, J. J. Kubal and B. J. Blaiszik, Battery-data-toolkit, 2021, https://github.com/ROVI-org/battery-data-toolkit.
62. A. Moradpour, M. Kasper, M. Moertelmaier, N. A. Z. R-Smith and F. Kienberger, Batteries Supercaps, 2024, 7, e202300514.
63. M. Ecker, T. K. D. Tran, P. Dechent, S. Käbitz, A. Warnecke and D. U. Sauer, J. Electrochem. Soc., 2015, 162, A1836–A1848.
64. S. Tang, Z. Wang, H. Guo, J. Wang, X. Li and G. Yan, Solid State Ionics, 2019, 343, 115083.
65. M. Doyle, J. Newman, A. S. Gozdz, C. N. Schmutz and J.-M. Tarascon, J. Electrochem. Soc., 1996, 143, 1890–1903.
66. M. D. Levi and D. Aurbach, J. Phys. Chem. B, 1997, 101, 4641–4647.
67. M. D. Levi, C. Wang, E. Markevich, D. Aurbach and Z. Chvoj, J. Solid State Electrochem., 2003, 8, 40–43.
68. E. Prada, D. D. Domenico, Y. Creff, J. Bernard, V. Sauvant-Moynot and F. Huet, J. Electrochem. Soc., 2012, 159, A1508–A1519.
69. K. Smith and C. Y. Wang, J. Power Sources, 2006, 161, 628–639.
70. G.-H. Kim, K. Smith, K.-J. Lee, S. Santhanagopalan and A. Pesaran, J. Electrochem. Soc., 2011, 158, A955.
71. M. Doyle and Y. Fuentes, J. Electrochem. Soc., 2003, 150, A706.
72. V. Srinivasan and J. Newman, J. Electrochem. Soc., 2004, 151, A1530.
73. G. Liebig, G. Gupta, U. Kirstein, F. Schuldt and C. Agert, Batteries, 2019, 5, 62.
74. M. A. Cabañero, N. Boaretto, M. Röder, J. Müller, J. Kallo and A. Latz, J. Electrochem. Soc., 2018, 165, A847–A855.
75. K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. V. D. Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180.
76. M. W. Verbrugge and B. J. Koch, J. Electrochem. Soc., 1999, 146, 833–839.
77. G. Hua-Jun, X.-H. Li, X.-M. Zhang, H.-Q. Wang, Z.-X. Wang and W.-J. Peng, New Carbon Mater., 2007, 22, 7–11.
78. J. Li, F. Yang, X. Xiao, M. W. Verbrugge and Y. T. Cheng, Electrochim. Acta, 2012, 75, 56–61.
79. P. Arora, M. Doyle and R. E. White, J. Electrochem. Soc., 1999, 146, 3543–3553.
80. R. D. Perkins, A. V. Randall, X. Zhang and G. L. Plett, J. Power Sources, 2012, 209, 318–325.
81. F. Jiang and P. Peng, Sci. Rep., 2016, 6, 32639.
82. M. Mastali, M. Farkhondeh, S. Farhad, R. A. Fraser and M. Fowler, J. Electrochem. Soc., 2016, 163, A2803–A2816.
83. K. Kumaresan, G. Sikha and R. E. White, J. Electrochem. Soc., 2008, 155, A164.
84. O. Chaouachi, J. M. Réty, S. Génies, M. Chandesris and Y. Bultel, Electrochim. Acta, 2021, 366, 137428.

---