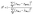Automated synthesis and fragment descriptor-based machine learning for retention time prediction in supercritical fluid chromatography

Abstract

The integration of automated synthesis and machine learning (ML) is transforming analytical chemistry by enabling data-driven approaches to method development. Chromatographic column selection, a critical yet time-consuming step in separation science, stands to benefit substantially from such advances. Here, we report a workflow that combines automated synthesis of a structurally diverse amide library with fragment descriptor-based ML for retention time prediction in supercritical fluid chromatography (SFC). Retention data were systematically acquired on the recently developed DCpak® PBT column, providing one of the first structured datasets for this stationary phase. Benchmarking revealed that fragment-count descriptors (ChyLine and CircuS) substantially outperformed conventional molecular fingerprints, delivering higher predictive accuracy and more interpretable relationships between substructures and retention behavior. External validation underscored the role of chemical space coverage, while visualization techniques such as ColorAtom analysis offered mechanistic insight into model decisions. By uniting automated synthesis with chemoinformatics-driven ML, this study demonstrates a scalable approach to generating high-quality training data and predictive models for chromatography. Beyond retention prediction, the framework exemplifies how data-centric strategies can accelerate column characterization, reduce reliance on trial-and-error experimentation, and advance the development of autonomous, high-throughput analytical workflows.

---

Introduction

Chromatography is an indispensable analytical technique for the separation and analysis of components within complex mixtures, with widespread applications in pharmaceuticals,¹ food science,² and environmental monitoring.³ Among the various factors influencing the efficiency and success of chromatographic separations, column selection is paramount. Consequently, the characterization of both new and existing columns is a crucial step in optimizing separation conditions. High-throughput evaluation methods facilitate the rapid and efficient screening of numerous columns, significantly accelerating analytical workflows.

In recent years, artificial intelligence (AI) and machine learning (ML) have attracted considerable attention for their predictive capabilities across various scientific disciplines, including analytical chemistry.^4–6 In liquid chromatography (LC), AI and ML have emerged as powerful tools for retention time prediction, enabling faster, more accurate, and more efficient chromatographic method development. Furthermore, supercritical fluid chromatography (SFC) has gained increasing attention due to its ability to provide even faster analyses, and its adoption has been expanding rapidly.^7,8

Despite these advancements, the adoption of newly developed chromatography columns remains challenging for analytical chemists, as their separation characteristics are often unknown. Consequently, trial-and-error experimentation with unfamiliar columns can be impractical and time-consuming. To address this issue, we propose a machine learning model capable of predicting retention times based on molecular structures, thereby providing analytical chemists with valuable insights into the separation characteristics of new columns and facilitating their selection and use.

In this study, we employed an automated synthesis robot to rapidly generate a diverse set of amide compounds with varying molecular structures. Retention times were measured using an SFC system, and a machine learning model was developed to predict retention times based on molecular structures. Furthermore, we explored the relationship between molecular substructures and retention times through visualization, which is also discussed in this study.

Materials and methods

Experimental setup

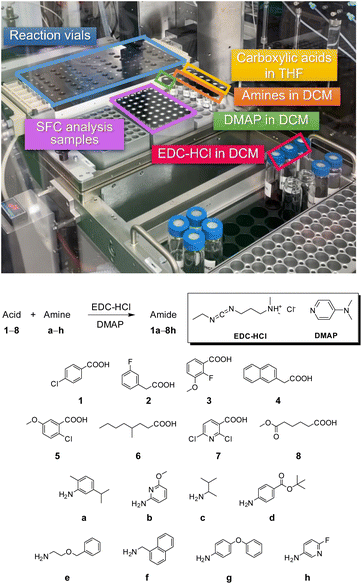
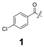
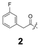
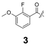
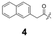
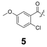
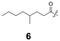
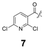
To construct a library of amide compounds with diverse molecular structures, we obtained a comprehensive list of commercially available reagents from Tokyo Chemical Industry Co., Ltd (TCIDATA, no. 43, 202007). For both carboxylic acid derivatives and amine derivatives, we calculated their Morgan fingerprints and selected eight structurally diverse compounds from each category based on Tanimoto similarity coefficients, ensuring minimal structural redundancy. The library of amide compounds consisted mainly of aromatic amide compounds. This composition reflects the structural bias present in commercially available amines and carboxylic acids, which tend to include a large proportion of aromatic derivatives. Such a bias likely originates from the pharmaceutical importance of aromatic amides, as compounds such as aniracetam, agomelatine, and benorilate are well known marketed drugs. Therefore, aromatic amides play a significant role in screening libraries used in drug discovery. Nevertheless, the dataset also contains aliphatic amides such as 6c and amides with ester functionalities such as 8c, ensuring structural diversity for reliable model development.

Subsequently, the automated synthesis of various amide compounds was carried out through condensation reactions between the selected amines and carboxylic acids (Fig. 1 and Table 1). Tetrahydrofuran (THF) solutions of the selected eight carboxylic acid derivatives and dichloromethane (DCM) solutions of the eight selected amines were prepared. A dichloromethane solution of 4-dimethylaminopyridine (DMAP) and 3-ethylcarbodiimide hydrochloride (EDC-HCl) was then added, and the mixtures were stirred at 40 °C for 8 hours to synthesize various amide compounds. After the reaction was complete, 0.1 mol L⁻¹ HCl aqueous solution was added, and the mixture was shaken. The organic layer was separated using a phase separation filter, collected, and diluted with a heptane/2-propanol (50/50) mixture to prepare the chromatography sample solutions. For the synthesis of compound 7b, a catalytic amount of hydroxybenzotriazole (HOBt) was additionally employed under otherwise identical conditions. Chromatographic analysis was carried out on a Daicel DCpak® PBT column⁹ (3 µm, 4.6 mm i.d. × 100 mm, fully porous particles) with supercritical CO₂ and 2-propanol (90 : 10, v/v) as the mobile phase at a flow rate of 2.0 mL min⁻¹. The column temperature was maintained at 40 °C. Samples (1 mg mL⁻¹ in n-hexane/2-propanol) were injected at a volume of 5 µL. Detection was performed using a two-dimensional photo diode array detector, and one-dimensional chromatograms were obtained at 220.0 nm. For samples that eluted at retention times close to that of the sample solvent, chromatograms were compared with those of previously measured other samples to identify solvent-derived peaks, and the analyte retention times were determined accordingly. When the reaction did not proceed completely, chromatograms of the starting materials were measured, and the newly appeared peak that was not derived from the starting materials was identified as the amide product.

Fig. 1 Automated synthesis of amides 1a–8h. Carboxylic acids were dissolved in THF. Amines, DMAP, and EDC-HCl were dissolved in DCM. For SFC measurements, sample solutions were diluted with a heptane/2-propanol (50/50) mixture in 2 mL vials.

Table 1 Retention time t_R (s) of the 64 amides (1a–8h). Column; DCpak® PBT, eluent; sCO₂/2-PrOH = 90/10, flow rate; 2.0 mL min⁻¹, column temperature; 40 °C, concentration of the sample; 1 mg mL⁻¹ in heptane/2-PrOH (50/50) mixture, injection volume; 5 µL, detection; absorption at 220 nm^a

a Retention time tR (s), 220 nm, t0 ∼ 39.8 s.
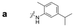
	148.0	97.8	130.4	201.6	149.2	81.6	174.8	88.0
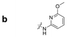
	132.6	105.6	131.8	240.6	150.6	77.0	180.8	86.6
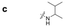
	76.0	61.8	66.2	103.0	78.8	56.4	88.0	59.6
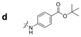
	220.2	133.4	179.4	315.6	221.1	102.8	224.4	107.8
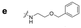
	132.2	104.8	130.4	228.2	149.4	98.0	168.6	110.2
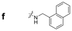
	381.0	238.2	300.0	654.4	408.8	158.6	488.6	183.8
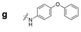
	504.4	262.0	371.8	719.8	503.2	179.2	534.0	193.2
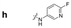
	161.0	107.6	168.8	260.4	185.6	80.6	182.4	87.6

---

Here, we employed the DCpak® PBT column, which is a silica gel-modified column with polybutylene terephthalate (PBT). This column was developed relatively recently, and its use remains limited. The retention times of the 64 synthesized amide compounds are summarized in Table 1.

In general, compounds containing aromatic rings tended to exhibit strong retention, whereas those with alkyl chains showed shorter retention times. However, interpreting the column characteristics intuitively based solely on this retention time table is challenging. Therefore, based on these results, we attempted to develop a machine learning model to predict retention times from molecular structures.

Computational details

Experimental data (chromatograms) was processed using in-house scripts to extract the retention time in an automatic manner with the peak detection and integration by Python. The code and intermediate results are available as SI.

The ML model for prediction of retention time was built following the best practices in QSPR modelling.¹⁰ In this work, we chose structural descriptors to represent the molecules, as it is the most relevant part in our dataset. Widely used molecular fingerprints (FP) – binary vectors indicating the absence or the presence of certain structural features – were selected for their simplicity.¹¹ We have used Morgan FP¹² (capturing the circular substructures), RDkit FP¹³ (circular, linear, and branched substructures), AtomPairs¹⁴ (pairs of atoms with the topological distance between them), Torsion¹⁵ (substructures consisting of 4 connected atoms with torsion angles) and Avalon¹⁶ (various drug-likeness features). The binary nature of the FP, however, limits their expressiveness and may lead to lower performance of a model. To circumvent that, we also use fragment features that account not only for the presence of certain substructure, but count their occurrences in each molecule, enriching the information content in the descriptor vector. Two types of fragment descriptors were used – CircuS (Circular Substructures) to account for circular fragments, and ChyLine (Chython Linear) for linear substructures. Both fragment descriptors were calculated using DOPtools library (ver.1.2),¹⁷ all fingerprints – using RDkit (ver.2024.9.6). Each descriptor type generates a number of features for the dataset: for fingerprints, the length of the feature vector was set to 1024; for fragment counts, the number varies depending on the fragment topology and size. The calculated matrices of descriptors for each setting are available in SI.

The best descriptor type was selected in a benchmarking study. It was performed using DOPtools library and the following parameters were optimized: (1) descriptor space – only one type of descriptors were used at a time by each model; (2) ML algorithm – Support Vector Machines (SVM),¹⁸ Random Forest (RF)¹⁹ and XGBoost (XGB)²⁰ were tested in a regression model; (3) ML hyperparameters, depending on the algorithm. The models were scored by the prediction results of a repeated 5-fold cross-validation (CV_k=5). Determination coefficient (R²) and root mean squared error (RMSE) are used to quantify the model's quality:

where N is the number of points in the set, y_obs,i is the experimentally observed value of the ith data point, y_pred,i is the predicted value of the ith data point, and ŷ_obs,i is the average observed value across the set.

The following Python libraries were used for data processing and calculations: Chython (ver.1.78),²¹ RDkit (ver.2024.9.6), DOPtools (ver.1.2), Scikit-learn (ver.1.5),²² Optuna (ver.3.6).²³ Other libraries were installed as dependencies to the latest available versions.

Results and discussion

Model benchmark

The model for the prediction of retention time was based on the ensemble of data presented in the Table 1. In the initial stages, we have modelled the retention time directly, and a benchmark study on molecular descriptors was performed along with the hyperparameter optimization, so that every type of descriptors achieves the best possible predictivity in CV_k=5. Additionally, performing the benchmark on different ML methods, we have observed better predictive power of the SVM, so the results henceforth are only shown for this method (all benchmark results are available in SI). Its results show the clear advantage of fragment descriptors over fingerprints: all fingerprints have shown much higher error of prediction and have especially struggled with the compounds in the higher ranges (see Fig. S141). Indeed, as fragment counts contain more information, it is expected that they would retain more knowledge on the relationship between the structure and the modelled property. Moreover, as the higher retention times are often associated with the repeating substructures (e.g., in this case, more aromatic rings in a structure lead to higher RT), which the fingerprints fail to effectively retain as they only encode the presence and absence of substructures.

Yet, the retention time by itself depends not only on the chemical structure, but also on the experimental setup and conditions. To eliminate the effect of changes in the chromatography column size and eluent speed, we have then selected the retention factor as the modelled property. The retention factor (k) is given by (t_R − t₀)/t₀, where t_R is the analyte retention time and t₀ is the column dead time. Considering the range of the values, we also transform the retention factor value to a logarithmic scale to reduce the effect of the range on the error of prediction (ln k). As the Fig. 2 shows, the fragment descriptors have again shown the best performance in cross-validation, although the performance was excellent across the board. For this property, the fingerprints still have difficulties with predicting values in lower and higher ranges. Since the models for ln k with fragments have shown the best performance, further we only discuss these.

Fig. 2 (Top) benchmark results (RMSE in repeated CV_k=5 for the logarithmic retention factor model) for each descriptor type in SVM. Each boxplot represents the distribution of scores (RMSE, in log units) for 5 repeats of CV_k=5 on the training set with random shuffling (white square for the mean score, the box for the interquartile range IQR, whiskers for 1.5 IQR, other points are outliers). (Bottom) observed vs. predicted RT in CV_k=5 for the three best models: ChyLine fragments (left), CircuS fragments (middle), Morgan features FP (right).

External predictions and interpretation

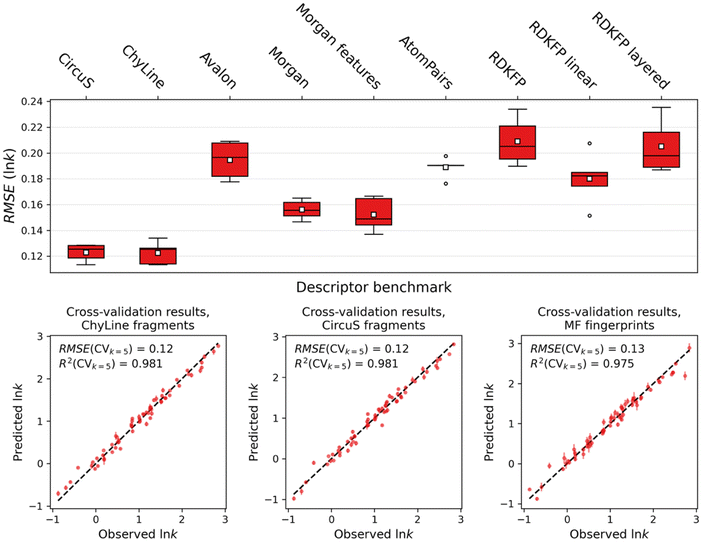
Fragment-based models for ln k were applied to a series of molecules from external sources to verify the chemical space coverage by the models. The compounds used here (1x–12x) included various amide compounds with structures relatively similar to those used in model training, as well as arbitrarily selected compounds with completely dissimilar structures. The results of predictions are shown in Fig. 3. As the figure shows, both models struggle with this test set, with the RMSE being over 1 compared to 0.12 for cross-validation. However, such high prediction error is due to two main factors.

Fig. 3 The external predictions for the test set (1x–12x, right) made by the model built on ChyLine fragments (left plot) and CircuS fragments (right plot). The outliers (data points for which the prediction error is greater than 1 logarithmic unit) are indicated in red and annotated by text. Statistical scores in blue are for the subset excluding the outliers.

First, there are several notable outliers for both models, especially compounds 10x and 12x. If the outliers are removed, the statistical scores for the models improve significantly. Moreover, outside of these outliers, model built on ChyLine performs quite well across most of the range of ln k values. The CircuS model, on the other hand, shows a more restrictive coverage.

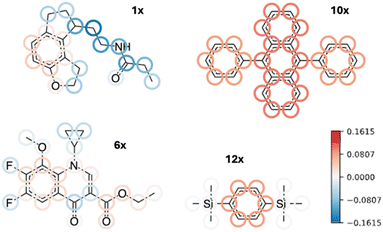
Second, the chemical space of the test set is quite different from that of the training set. First of all, not all molecules are amides, although they are the main target of the model. The special cases are the aforementioned compounds 10x and 12x, the former of which (9,10-diphenylanthracene) is a polycyclic aromatic compound, and the latter (1,4-bis(trimethylsilyl)benzene) contains trimethylsilyl groups which are completely outside of the initial chemical space. One can also interpret these errors using the ColorAtom methodology,²⁴ which allows to assign atomic contributions to predictions by coloring them according to their importance. Fig. 4 shows ColorAtom interpretations for the predictions on outliers by the ChyLine model. Indeed, for the compound 10x, the aromatic groups show positive contribution, i.e., increasing the retention time as it would be expected. However, due to the high number of these groups compared to the training set, the model overestimates the ln k which leads to a high prediction error. On the other hand, the silyl groups in the compound 12x are completely ignored by the model and their contribution cannot be correctly estimated. Similar observations can be made about other outliers, as well, where some groups' contributions are over- or underestimated.

Fig. 4 Interpretation of ChyLine-based model for prediction of ln k by ColorAtom. The contributions of atoms are coded blue for negative contributions and red for positive, with the intensity of color indicating the scale of the effect. White-coded atoms have virtually no contribution to the prediction. The contributions are scaled to the maximum in the test set (colorbar on the right), to allow the comparison of the effect.

It could also be assumed that the compounds of the test set are outside of the applicability domain (AD)²⁵ of the training set. Indeed, when estimating Fragment Control (FC)²⁶ AD, which excludes the compounds possessing new fragments, and Bounding Box (BB)²⁷ AD, which excludes compounds which have descriptors values outside of the training set, all compounds of the test set would be considered outside of AD, although these are very strict definitions (see details in SI). To demonstrate that the AD of the model is not extremely restrictive, we performed validation by excluding a random portion of the training set to an external test set and repeated the optimization and validation process on these new sets. The predictions for these sets are excellent, which shows that the model works well on external data of amides, as expected (all details are presented in SI).

Conclusions

In this study, we demonstrated a machine learning-based approach for predicting the retention times of amide compounds in supercritical fluid chromatography (SFC), aimed at facilitating high-throughput evaluation of recently developed chromatography columns. By combining automated synthesis of a structurally diverse amide library with rigorous chemoinformatics modelling, we generated a dataset of retention times measured on the DCpak® PBT column, which is a relatively new stationary phase with limited prior characterization.

We benchmarked a range of molecular descriptors and machine learning algorithms, showing that fragment-count-based descriptors (ChyLine and CircuS) substantially outperformed traditional molecular fingerprints in cross-validated prediction of both raw retention times and logarithmic retention factors (ln k). These fragment descriptors provided richer, more quantitative representations of structural features that correlate with chromatographic behavior, especially for compounds with repeating or aromatic substructures that drive retention on the PBT column.

External validation using structurally diverse test compounds highlighted important limitations of model extrapolation, with notable prediction errors for molecules well outside the training set's chemical space. Nonetheless, interpretation methods such as ColorAtom analysis clarified the origins of prediction errors, confirming that the model's learned relationships remain chemically meaningful within its applicability domain. Moreover, controlled experiments excluding subsets of the training data demonstrated robust predictive performance for amide structures within the expected chemical space.

Overall, our approach shows that machine learning models trained on systematically designed reaction libraries can provide accurate, interpretable predictions of SFC retention times for new columns. This can reduce the need for trial-and-error experimentation, accelerate method development, and improve column selection workflows. Future work will expand the training data to broader chemical classes and columns, refine applicability domain estimation, and integrate these predictive tools into automated analytical workflows for high-throughput chromatography.

Author contributions

S. S. was responsible for the synthesis and measurements. Y. N. contributed to the automated synthesis and measurements. S. B. and P. S. conducted the informatics analyses. P. S. and Y. N. contributed to the writing of the manuscript. Y. N. supervised and coordinated the overall project.

Conflicts of interest

The authors declare no competing financial interest. (PBT columns were provided by Daicel Corporation, and a compound data list was provided by Tokyo Chemical Industry Co., Ltd; neither had any influence on the impartiality of this study).

Data availability

All experimental data and code for reproducing the modelling results are freely available in the GitHub repository: https://github.com/icredd-cheminfo/chromatography-modeling, as well as in the Zenodo repository at DOI: https://doi.org/10.5281/zenodo.17655751.

Supplementary information (SI): experimental data and code for reproducing the modelling results. See DOI: https://doi.org/10.1039/d5dd00437c.

Acknowledgements

This work was supported by JSPS KAKENHI grant numbers JP23H03810, JP23H03807 and JP JP23H03806. Support was also provided by JST-ERATO (JPMJER1903) and the Institute for Chemical Reaction Design and Discovery (ICReDD), which was established by the World Premier International Research Initiative (WPI), MEXT, Japan.

Notes and references

1. H. H. Maurer, J. Chromatogr. A, 2013, 1292, 19–24.
2. H. M. Merken and G. R. Beecher, J. Agric. Food Chem., 2000, 48, 577–599.
3. S. Montesdeoca-Esponda, A. del Toro-Moreno, Z. Sosa-Ferrera and J. J. Santana-Rodríguez, J. Sep. Sci., 2013, 36, 2168–2175.
4. A. G. Usman, S. Işik, S. I. Abba and F. Meriçli, J. Sep. Sci., 2021, 44, 843–849.
5. Y. Fan, Y. Deng, Y. Yang, X. Deng, Q. Li, B. Xu, J. Pan, S. Liu, Y. Kong and C.-E. Chen, Environ. Sci.:Adv., 2024, 3, 198–207.
6. Z.-M. Win, A. M. Y. Cheong and W. S. Hopkins, J. Chem. Inf. Model., 2023, 63, 1906–1913.
7. L. T. Taylor, J. Supercrit. Fluids, 2009, 47, 566–573.
8. V. Desfontaine, D. Guillarme, E. Francotte and L. Nováková, J. Pharm. Biomed. Anal., 2015, 113, 56–71.
9. K. Nagai, T. Shibata, S. Shinkura and A. Ohnishi, J. Chromatogr. A, 2018, 1549, 85–92.
10. A. Tropsha, Mol. Inf., 2010, 29, 476–488.
11. Danishuddin and A. U. Khan, Drug Discovery Today, 2016, 21, 1291–1302.
12. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
13. G. Landrum, RDKit: Open-source cheminformatics, https://www.rdkit.org.
14. R. E. Carhart, D. H. Smith and R. Venkataraghavan, J. Chem. Inf. Comput. Sci., 1985, 25, 64–73.
15. R. Nilakantan, N. Bauman, J. S. Dixon and R. Venkataraghavan, J. Chem. Inf. Comput. Sci., 1987, 27, 82–85.
16. P. Gedeck, B. Rohde and C. Bartels, J. Chem. Inf. Model., 2006, 46, 1924–1936.
17. S. Byadi, P. Gantzer, T. Gimadiev and P. Sidorov, Digital Discovery, 2025, 4, 1188–1198.
18. H. Drucker, C. J. C. Burges, L. Kaufman, A. J. Smola and V. Vapnik, in Advances in neural information processing systems, 1996, pp. 155–161.
19. L. Breiman, Mach. Learn., 2001, 45, 5–32.
20. T. Chen and C. Guestrin, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, New York, NY, USA, 2016, pp. 785–794.
21. R. Nugmanov, N. Dyubankova, A. Gedich and J. K. Wegner, J. Chem. Inf. Model., 2022, 62, 3307–3315.
22. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
23. T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, ACM, New York, NY, USA, 2019, pp. 2623–2631.
24. G. Marcou, D. Horvath, V. Solov’Ev, A. Arrault, P. Vayer and A. Varnek, Mol. Inf., 2012, 31, 639–642.
25. T. I. Netzeva, A. P. Worth, T. Aldenberg, R. Benigni, T. D. Mark, P. Gramatica, J. S. Jaworska, S. Kahn, G. Klopman, A. Carol, G. Myatt, N. Nikolova-jeliazkova, G. Y. Patlewicz and R. Perkins, Altern. Lab. Anim., 2005, 2, 155–173.
26. P. Polishchuk, T. Madzhidov, T. Gimadiev, A. Bodrov, R. Nugmanov and A. Varnek, J. Comput.-Aided Mol. Des., 2017, 31, 829–839.
27. V. P. Solov’ev, I. Oprisiu, G. Marcou and A. Varnek, Ind. Eng. Chem. Res., 2011, 50, 14162–14167.

---