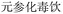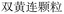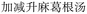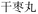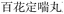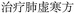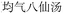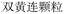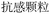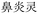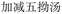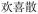Open Access Article
Open Access ArticleSemantic repurposing model for traditional Chinese ancient formulas based on a knowledge graph
Xu
Dong
a,
Wenyan
Zhao
a,
Feifei
Li
a,
LiHong
Hu
 *a,
Hongzhi
Li
a and
Guangzhe
Li
*bc
*a,
Hongzhi
Li
a and
Guangzhe
Li
*bc
aSchool of Information Science and Technology, Northeast Normal University, Changchun, 130117, P. R. China. E-mail: lhhu@nenu.edu.cn
bChangchun University of Chinese Medicine, Changchun, Jilin 130117, P. R. China. E-mail: ligz@nenu.edu.cn
cJilin Province Technology Innovation Center of Traditional Chinese Medicine Health Food, Changchun University of Chinese Medicine, Changchun, Jilin 130117, P. R. China
First published on 29th October 2025
Abstract
Drug repurposing can dramatically decrease cost and risk in drug discovery and it can be very helpful for recommending candidate drugs. However, as traditional Chinese medicine (TCM) formulas are multi-component, the repurposing methods for western medicine are usually not applicable for TCM formulas. In this study, we proposed a concept/strategy for multi-component formula/recipe discovery with network and semantics. With this concept, we establish a semantic formula-repurposing model for TCM based on a link-prediction algorithm and knowledge graph (KG). The proposed model integrating semantic embedding with KG networks facilitates the effective repurposing of traditional Chinese medicine formulas. First, we construct a KG that consists of more than 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ancient formulas, including over 120
600 ancient formulas, including over 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 entities, 415
000 entities, 415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 triples and 12 relations that are extracted from non-structural textual data by deep-learning techniques. Then, a link-prediction model is built on KG triplets for entity and edge semantic vectors. The formula-repurposing task is considered as computing the similarity of semantic vectors in KG between entities and query formulas. In the current version of the proposed model, two ways of repurposing are tested: one is searching for a similar formula to the query one, and the other is seeking a possible formula for rare, emerging diseases or epidemics. The former is based on the name of a formula; the latter is carried out through symptom entities. The experiments are exemplified with existing formulas, Fufang Danshen Tablets (
900 triples and 12 relations that are extracted from non-structural textual data by deep-learning techniques. Then, a link-prediction model is built on KG triplets for entity and edge semantic vectors. The formula-repurposing task is considered as computing the similarity of semantic vectors in KG between entities and query formulas. In the current version of the proposed model, two ways of repurposing are tested: one is searching for a similar formula to the query one, and the other is seeking a possible formula for rare, emerging diseases or epidemics. The former is based on the name of a formula; the latter is carried out through symptom entities. The experiments are exemplified with existing formulas, Fufang Danshen Tablets (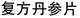 ) and the symptoms of COVID-19. The results agree well with existing clinical practices. This suggests our model can be a comprehensive approach to constructing a knowledge graph of TCM formulas and a TCM formula-repurposing strategy, which is able to assist compound formula development and facilitate further research in multi-compound drug/prescription discovery.
) and the symptoms of COVID-19. The results agree well with existing clinical practices. This suggests our model can be a comprehensive approach to constructing a knowledge graph of TCM formulas and a TCM formula-repurposing strategy, which is able to assist compound formula development and facilitate further research in multi-compound drug/prescription discovery.
1 Introduction
It is well-known that the development of new drugs requires substantial financial and time resources.1 Drug repurposing has been considered an efficacious approach to enhancing the efficiency and lowering the costs of drug development. Drug repurposing is a concept of reevaluating and using existing drugs for the treatment of different diseases. It involves using known drugs or compounds to treat diseases or conditions beyond their original intended scopes, i.e., drug repurposing employs drugs that are already on the market for treating other diseases. Therefore, drug repurposing not only helps scientists discover new therapeutic strategies, but also leverages existing drugs, reducing the risks and costs associated with developing new drugs. There are many successful examples of drug repurposing. Sildenafil, originally developed as an antihypertensive drug, was later repurposed by Pfizer for the treatment of erectile dysfunction, capturing 47% of the market share.2 Quinacrine, an antimalarial drug, has been recently reevaluated for its potential in treating rheumatoid arthritis and other autoimmune diseases.3 Baricitinib, initially developed as a treatment for rheumatoid arthritis, was found during the COVID-19 pandemic to have anti-inflammatory properties, making it a candidate drug for treating COVID-19.4 In recent years, drug repurposing has been gradually gaining traction and increasingly recognized by scientists.Traditional Chinese medicine (TCM) is a distinct and intricate medical system that has evolved over thousands of years. Some external treatments in TCM, such as acupuncture, moxibustion and manipulation (Tuina), have earned recognition in many countries as a complementary and alternative approach to healthcare. During the COVID-19 pandemic, TCM played a significant role through collaboration with western medicine to effectively support epidemic treatment and prevention in China.5 Nowadays, Chinese herbs have been an important repository of druggable compounds from natural sources, which are harnessed for the discovery and development of novel natural compounds, active ingredients, individual herbs, and compound formulations or prescriptions with therapeutic selectivity. In addition, Chinese herbs are also increasingly emerging as a source of novel anticancer agents6 and they have become valuable natural resources in the development of anticancer drugs. These advancements enable the precise targeting and eradication of cancer cells, effectively curbing their proliferation while minimizing significant toxicity.7,8 In various other disease treatments, TCM is also gradually playing a significant role. It has been revealed that the Chinese herb Salvia miltiorrhiza possesses protective effects on the cardiovascular system. Asian countries have extensively applied Salvia miltiorrhiza in the treatment of cardiovascular diseases, particularly those affecting the heart and brain.9 The development of pharmaceuticals based on TCM has attracted growing attention.
TCM is founded on a holistic theoretical framework, and its treatment is fundamentally different from Western medicine. Unlike Western medicine, which typically consists of single, pure compounds targeting specific biological pathways,10,11 TCM prescriptions are composed of multiple compounds that act on multiple targets and exhibit various therapeutic functions. Regarding TCM complexity, apparently TCM formula/prescription repurposing cannot directly adopt Western drug repurposing approaches, as they primarily focus on known drugs with explicit drug structures and components. In recent years, multi-target or multi-compound drugs that are principally similar to the TCM prescription concept have started to become prevalent in drug development.12 Therefore, our model for TCM formula repurposing may enlighten multi-compound drug discovery.
The existing methods of the main components of TCM repurposing can be categorized as follows: molecule-based (or ligand-based) methods, target-based methods, network-theory-based strategies, and knowledge-graph-based methods. Knowledge-graph-based methods have shown great potential in the field of TCM repurposing in recent years. A knowledge graph (KG) can store, manage and utilize knowledge efficiently, and it is able to reason based on existing knowledge to uncover potential drug–target–disease relationships. Moreover, KGs possess excellent scalability, allowing them to continuously update and expand with the addition of new data; thereby the models combining KG and deep learning show superior performance when dealing with complex problems.13 In recent years, significant progress has been made in constructing knowledge graphs in the field of TCM, such as the establishment of multiple databases containing traditional Chinese medical literature.14 Jia et al. introduced the foundation of knowledge graphs and subsequently delved into the construction of a knowledge graph specific to TCM.15 Some researchers have also focused on constructing KGs for specific domains within TCM. For instance, the construction of a KG for TCM-related gastrointestinal disorders, such as spleen and stomach diseases, has been undertaken.16 Furthermore, a variety of applications based on TCM KGs have emerged, including a prescription recommendation system for Chinese herbal medicine,17 intelligent question-answering systems,18 and pattern-based diagnostic decision-making systems.19
However, for the development of new formulas and medications, a KG with component herb nodes, the relations of diseases and various prescriptions are prerequisite. To deeply excavate and exploit ancient formulas, we constructed a TCM KG and proposed a formula-repurposing model for TCM formulas based on link-prediction algorithms and the built TCM KG. First, we constructed named-entity recognition and relation-extraction models to automatically extract over 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 entities and 410
600 entities and 410![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 relations from unstructured text data for building a KG with more than 50
000 relations from unstructured text data for building a KG with more than 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 formulas. Then, we obtained KG embedding via the semantic hierarchic link-prediction model Hierarchy-Aware Knowledge Graph Embedding (HAKE).20 Finally, with KG embedding, we sought out similar formulas for a target TCM formula or discovery of new possible formula candidates for diseases.
000 formulas. Then, we obtained KG embedding via the semantic hierarchic link-prediction model Hierarchy-Aware Knowledge Graph Embedding (HAKE).20 Finally, with KG embedding, we sought out similar formulas for a target TCM formula or discovery of new possible formula candidates for diseases.
Our main contributions include three aspects:
• A Chinese medicine entity terminology lexicon has been constructed containing a total of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 terms. These terms are categorized into eight entity types: TCM diseases, Western medicine diseases, efficacy, syndromes, therapeutic methods, symptoms, formula, and Chinese herbs. Based on this lexicon, a dataset for Chinese herbal medicine named-entity recognition was created, comprising over 50
000 terms. These terms are categorized into eight entity types: TCM diseases, Western medicine diseases, efficacy, syndromes, therapeutic methods, symptoms, formula, and Chinese herbs. Based on this lexicon, a dataset for Chinese herbal medicine named-entity recognition was created, comprising over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Chinese herbal formulas.
000 Chinese herbal formulas.
• A TCM formula KG was constructed using triples obtained through entity and relation-extraction models. We defined 12 types of relationships among the eight categories of entities and performed TCM formula relationship extraction, consisting of 415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 relationship data records.
900 relationship data records.
• A semantic formula-repurposing model based on self-developed TCM KG and a link-prediction model is proposed for TCM formulas. The experimental results agree well with clinical practice, which further validate the usability of the TCM formula KG we built.
2 Related work
2.1 Traditional Chinese medicine knowledge graph
A knowledge graph can be defined by G = (V, E), where V is the set of nodes and E is the set of edges. TCM knowledge graphs are increasingly being used in various applications to enhance understanding and treatment related to TCM. These KGs help primary care physicians improve their diagnostic and treatment skills by providing a structured representation of TCM concepts and relations. Zheng et al. developed a deep-learning-based platform, TCMKG, to effectively manage TCM knowledge and provide a comprehensive understanding of TCM concepts.21 Furthermore, KGs play a crucial role in systematically organizing and analyzing health knowledge related to TCM, contributing to the preservation and development of TCM as a cultural heritage.22 Furthermore, TCM knowledge graphs have been utilized in information exchange frameworks to support clinical applications and enhance diagnostic pattern discovery in precision medicine.23 Guo et al. explored knowledge reasoning based on traditional rules and features within TCM knowledge graphs to infer new facts and improve the TCM decision-making process.24 Xie et al. constructed a KG using ancient TCM texts and proposed a syndrome reasoning method based on the TCM knowledge graph, combining reinforcement learning algorithms with Term Frequency-Inverse Document Frequency (TF-IDF) concepts to infer the relationships between symptoms and syndromes, thereby improving the accuracy of computer-aided diagnosis.252.2 Named-entity recognition for TCM formulas
Named-entity recognition (NER) for TCM literature records is a challenging task, as they span a long history, and are thus dispersed, with inconsistent recording methods and chaotic formats. Additionally, TCM formulas often contain entities nested within one another, forming a hierarchical structure known as nested entities. The representation of nested entities in text frequently exhibits this hierarchy, which poses challenges for natural language processing tasks such as information extraction, entity or relation extraction, and semantic understanding. Therefore, when dealing with nested entities in TCM data, it is essential to correctly identify the hierarchical relations between entities to achieve accurate text comprehension and analysis. In 2023, Su et al. proposed a model called GlobalPointer (GP), which utilizes a globally normalized approach for named-entity recognition, allowing for the indistinguishable recognition of both nested and non-nested entities.26 To tackle the nested-entity recognition, we use GP as one of modules in our NER model.The structure of GP consists of two layers: token representation and span prediction. In the token representation layer, assuming the input sequence is represented as X = [x1, x2, xn], an output matrix H is obtained based on Bidirectional Encoder Representations from Transformers (BERT) (eqn (1)). H = [h1, h2, hn] represents the input sequence embedding.
| h1,h2,hn = BERT(x1,x2,…xn) | (1) |
In the span-prediction layer, two feedforward layers are employed, which rely on the beginning word embedding and the end word embedding of the span. The sentence representation H is then used to compute the span representation based on these word embeddings.
| qi,α = Wq,αhi + bq,α | (2) |
| ki,α = Wk,αhi + bk,α | (3) |
In eqn (2) and (3), the vectors 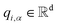 and
and 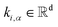 are representations of the entity type α, and they represent the start and end positions of the span score[i
are representations of the entity type α, and they represent the start and end positions of the span score[i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j] for the entity type α, respectively. The score of the span score[i
j] for the entity type α, respectively. The score of the span score[i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j] as an entity of type α is calculated in eqn (4).
j] as an entity of type α is calculated in eqn (4).
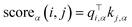 | (4) |
To leverage boundary information, positional encoding is introduced by incorporating relative position information into the model. Rotary Position Embedding (ROPE) coding27 is added to the entity word vectors, where the helical positional encoding is a transformation matrix Ri, and it satisfies RTiRj = Rj−i. The score function is calculated in eqn (5).
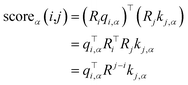 | (5) |
In addition, to further enhance the model's ability for NER, we employ a Gated Attention Unit (GAU) to enhance the model's contextual awareness.28 Since BERT uses absolute position encoding, it cannot capture relative positional information. Therefore, we incorporate relative position encoding into BERT. The employed GAU model is used to capture long-distance dependencies of the word vectors with relative position encoding, which are then input into GP. These aforementioned components (BERT, GP and GAU) are combined to form the NER model, BGGNER, which can achieve excellent results in the NER task on TCM formulas.
2.3 Relation-extraction in TCM
TCM formula texts are from important literature sources of TCM, recording numerous combinations of medicinal materials and treatment methods, which hold significant value for research and applications in drug development. However, the recording and descriptive methods of TCM formulas vary owing to the time of their emergence, making it impossible to use rules for relation extraction. Therefore, relation extraction in TCM formula literature is also tough work. With the rapid development of deep-learning techniques, employing deep-learning methods is currently one of the most popular means. However, there are few publicly available datasets for relation extraction in TCM, which presents a major difficulty for deep-learning modeling.To address data deficiency issues, we used a manual plus regular matching approach to tag the formula text, which resulted in a relational extraction dataset. Additionally, due to the complexity of one-to-many, many-to-many, and many-to-one relations in TCM formula texts, a relation-extraction model, CASREL, is adopted for relation extraction.29 CASREL is a novel cascading binary tagging framework that introduces a new perspective to reevaluate the task of extracting relation triples, aiming to address the issues of overlapping triples and multi-entity relationships. In our study, we improved the CASREL model to enhance its performance with relation extraction in TCM. Building upon the previous NER work, we annotated the TCM formula relation-extraction dataset and trained the dataset using the improved CASREL model, achieving promising results.
2.4 Semantic embedding based on a link-prediction model
Link prediction in KGs is a vital task in the fields of knowledge representation and reasoning. Given a head entity and a relation in a KG, it is possible to predict the tail entity; alternatively, given a head entity and a tail entity, one can predict the relationship between them. Various link-prediction models have been proposed to fulfill this task, aiming to improve the accuracy and scalability. Existing knowledge graph embedding models primarily focus on capturing relational patterns such as symmetry, asymmetry, inversion, and composition, but tend to overlook semantic information, which is the most important feature for TCM formula repurposing. The HAKE model addresses this limitation by proposing a method for modeling semantic hierarchies, mapping entities into a polar coordinate system where entities with different semantics are distributed across distinct hierarchical levels. Its goal is to automatically learn and represent the semantic hierarchies within knowledge graphs. By distinguishing entities at different levels and leveraging modulus information to reflect the hierarchical depth of entities, HAKE enhances link-prediction performance. Moreover, HAKE effectively captures hierarchical relations without requiring additional hierarchical information or clustering algorithms.20 Therefore, we chose HAKE as the KG embedding model.3 Materials and methods
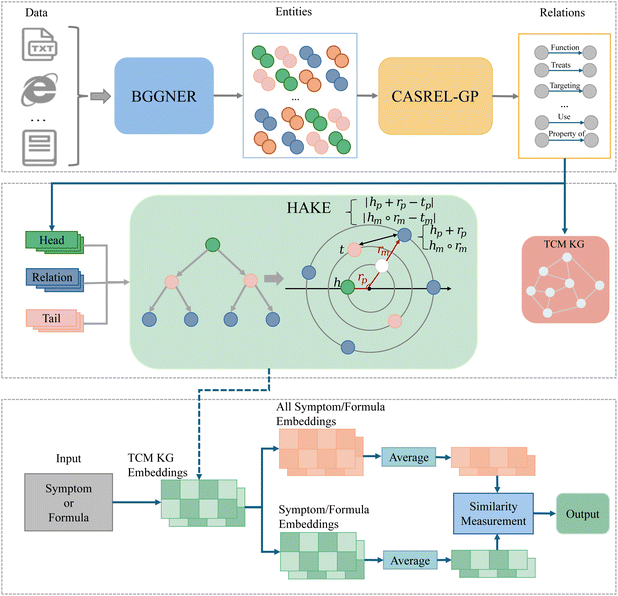
We first used the NER model and relation-extraction model to extract entities and relations, which formed a TCM formula knowledge graph; then, the built KG served as the foundation for building a formula-repurposing model for TCM formulas. The following includes data preparation, entity recognition, relation extraction, and the construction of the formula-repurposing model.3.1 Data preprocessing
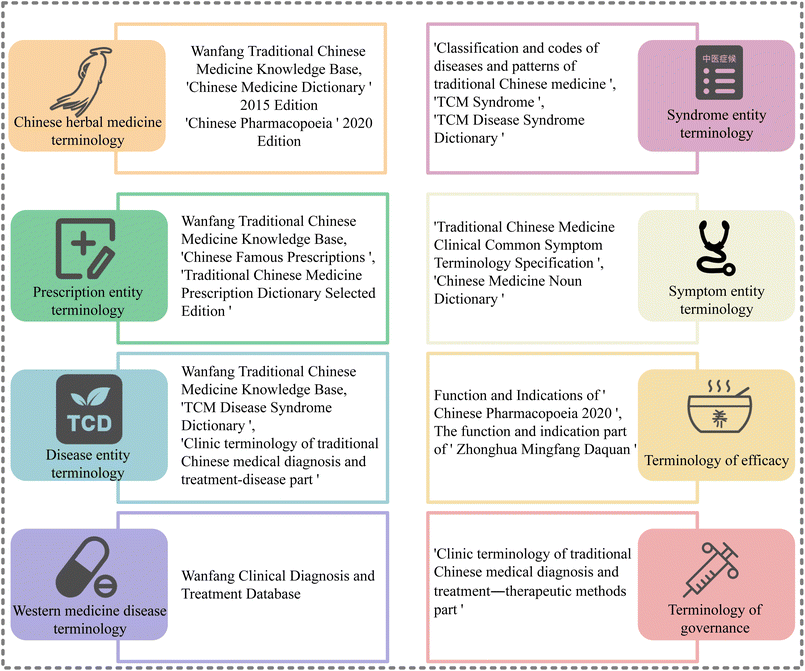
Regarding NER tasks, it is essential to construct a comprehensive terminology lexicon, which is significant for improving the performance of NER models. Our TCM terminology is derived from the following sources:(1) The Wanfang traditional Chinese medicine knowledge base already contains well-organized categories of terms such as “diseases”, “formulas”, “Chinese herbs”, and “patent Chinese medicines”, where these terms can be directly collected.30
(2) The internet hosts a plethora of relevant data, albeit often in a disorganized structure. We utilize web crawlers for data collection and then cleaning data from the internet.
(3) Textbooks and various published books also contain numerous terms within TCM. The terms in textbooks have been screened and organized by experts in the relative fields, making them more accurate than other data sources.31
(4) “Clinic terminology of traditional Chinese medical diagnosis and treatment diseases”, released by the National Health Commission and the State Administration of traditional Chinese medicine, consists of three sections. The first section covers disease terminology, the second section encompasses syndrome terminology, and the third section pertains to therapeutic method terminology. These highly reliable terms, collected and published by relevant national authorities, are readily available to use and possess.32
Finally, the collected terminologies have been categorized into eight classes: “formula”, “herbs”, “traditional Chinese medicine diseases”, “Western medicine diseases”, “syndromes”, “symptoms”, “treatment methods”, and “efficacy”. The entity terminology is illustrated in Fig. 1.
The sources of the Chinese herbal formula data in this study include two main parts:
(1) Chinese medicine formula books: Chinese medicine formula books are treasures that have been passed down through generations, representing the accumulated wisdom of traditional Chinese medicine. They contain verified and effective classical formulas. In this study, books such as “Compendium of Chinese Classic Formulas”33 and “Dictionary of Traditional Chinese Medical Formulae”31 were used. In “Compendium of Chinese Classic Formulas”, each formula consists of sections such as “Composition”, “Usage”, “Effects”, “Indications”, “Explanation of the Formula”, “Annotations”, and “Additional Formulas”. In “Dictionary of Traditional Chinese Medical Formulae”, each formula is composed of sections including “Origin”, “Alternative Names”, “Composition”, “Usage”, “Functions”, “Indications”, and “Selected Excerpts from Discussions on the Formula”.
(2) Internet: with the continuous advancement of internet technology, a vast amount of textual data is available on various websites. Unlike books, these data do not require extensive processing and often come in relatively standardized formats. After being collected and cleaned through web scraping, these data can be directly utilized on computers for further analyses.
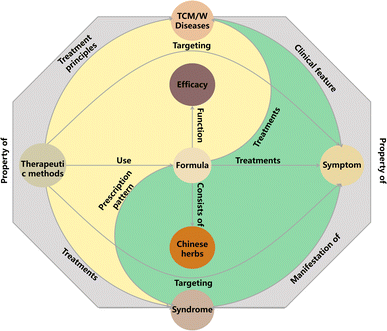
The summary of term entities in the obtained terminology entity lexicon for each category is presented in Fig. 2. Then, our formed entity-relation schema of the KG is shown in Fig. 3.
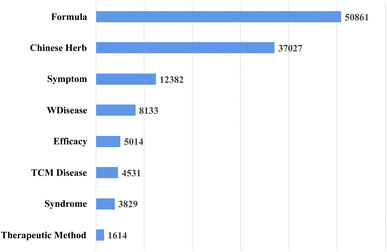 | ||
| Fig. 2 The quantities of various types of term entities in our Chinese medicine entity terminology lexicon. | ||
3.2 Named-entity recognition model
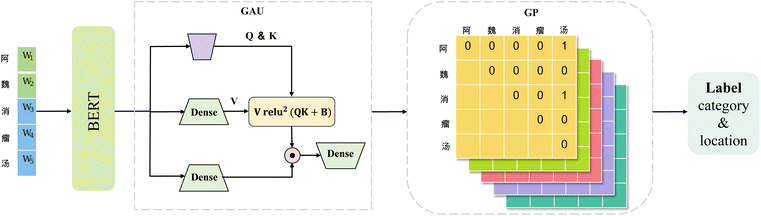
Our NER model (shown in Fig. 4), referred to as BGGNER, is composed of three modules: BERT, GAU and GP, which are utilized for information modeling of word vectors, long-range dependency capture and entity recognition, respectively, to achieve effective nested-entity recognition. At first, the non-structural texts are input into BERT to obtain word embedding. GAU is subsequently employed to more effectively capture the dependencies among different segments of the input word embedding. Finally, GP is employed to identify nested entities.During data preprocessing, the formula texts are first segmented based on a predefined maximum text length. The segmented texts are then tokenized using the BERT tokenizer to generate corresponding character token lists. A mapping process is performed to align the original character positions with the tokenized outputs, which are then fed into the BERT model to obtain contextualized embeddings. These embeddings are further processed by the GAU module to enhance contextual information.
Positional information plays a crucial role in entity recognition, as it enables the determination of entity start and end positions. The word embeddings produced by BERT, augmented with positional encodings, are input into the GAU module to capture long-range dependencies. The output of the GAU module is passed to the GP decoder, which produces eight entity recognition matrices, with their dimensions determined by the maximum text length. In these matrices, a value of 1 at position (i, j) indicates that an entity of the corresponding type begins at position i and ends at position j. By traversing the matrix and selecting elements with scores above a predefined threshold, the start and end positions of entities, as well as their types, can be accurately determined. Owing to its ability to mark multiple entities within the same matrix, GP effectively handles nested-entity recognition, demonstrating strong capability in capturing both entity boundaries and entity types.
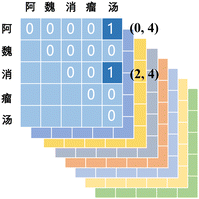
Nested entities are commonly found in TCM documents. For instance, as shown in Fig. 5, prescriptions such as “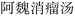 ” (Awei Xiaoliu Decoction – a formula for hemangioma) and “
” (Awei Xiaoliu Decoction – a formula for hemangioma) and “ ” (Xiaoliu Decoction – a formula for carcinoma) constitute two distinct entities, despite the fact that “
” (Xiaoliu Decoction – a formula for carcinoma) constitute two distinct entities, despite the fact that “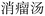 ” is nested within “
” is nested within “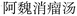 ”. In early deep-learning-based approaches, NER was framed as a sequence labeling task, where each character was individually tagged with its entity type and position. However, such methods are inherently limited in handling nested entities.
”. In early deep-learning-based approaches, NER was framed as a sequence labeling task, where each character was individually tagged with its entity type and position. However, such methods are inherently limited in handling nested entities.
To address the challenge of nested-entity recognition and enhance model efficiency, we propose a hybrid named-entity recognition framework, as depicted in Fig. 4. The core idea of the GP module is to reformulate the task as a multi-label classification problem. The label generation process is illustrated in Fig. 5. The size of the label matrix is determined by the predefined maximum text length. For example, if the maximum text length is set to 5, the corresponding label matrix is of size 5 × 5. Each row in the matrix denotes a potential start position of an entity, while each column denotes a potential end position. For example, the entity “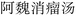 ” corresponds to coordinates (0, 4), and “
” corresponds to coordinates (0, 4), and “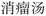 ” to (2, 4).
” to (2, 4).
GP's ability to recognize nested entities lies in its departure from traditional sequence labeling methods (e.g., BIO tagging). Instead, it adopts a span-based multi-label classification strategy. By constructing independent score matrices for each entity type, it allows the same span to be simultaneously assigned multiple entity types. This design decouples boundary detection from type classification, allowing the recognition processes for different entity types to operate independently, and thereby naturally supports nested structures. In contrast to conventional sequence labeling, this approach directly models inclusion and overlap relationships among entities, enabling nested-entity recognition without the need for complex post-processing. It effectively distinguishes both nested and non-nested entities. Given the eight entity types, the model generates eight corresponding label matrices, each dedicated to recognizing one specific entity type.
3.3 Relation-extraction model
We categorized the relations between entities into 12 classes based on expert opinions, as shown in Table 1. After defining the relation types, we manually labeled the herbal formula texts using a combination of human annotation and regular expression matching. By this means, we process 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 herbal formula texts and obtain a total of 413
000 herbal formula texts and obtain a total of 413![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 relation instances. When modeling, the dataset is divided into training, validation, and testing sets with an 8
733 relation instances. When modeling, the dataset is divided into training, validation, and testing sets with an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The division was carried out by randomly shuffling to ensure fair data distribution.
1 ratio. The division was carried out by randomly shuffling to ensure fair data distribution.
| Entities | Relations | Entities |
|---|---|---|
| Formula | Function | Efficacy |
| Formula | Treatments | Disease |
| Formula | Prescription pattern | Syndrome |
| Formula | Treatments | Symptom |
| Formula | Consists of | Chinese herbs |
| Disease | Clinical feature | Symptom |
| Disease | Property of | Syndrome |
| Syndrome | Manifestation of | Symptom |
| Therapeutic methods | Use | Formula |
| Therapeutic methods | Targeting | Symptom |
| Therapeutic methods | Treatment principles | Disease |
| Therapeutic methods | Treatments | Syndrome |
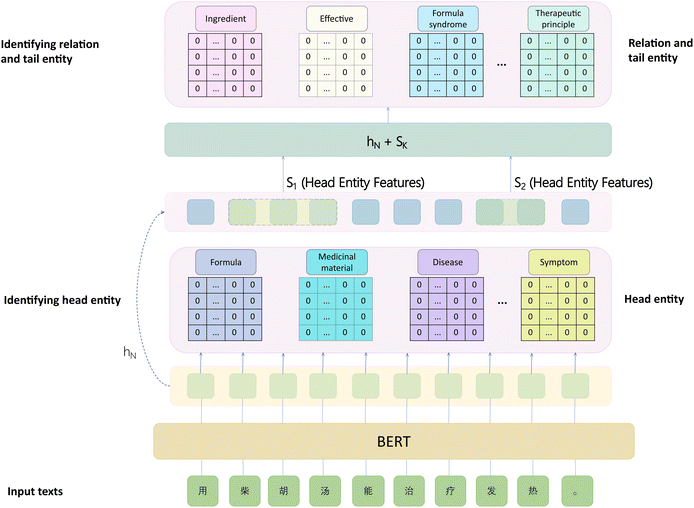
Due to the multiple types of relations presenting in the constructed TCM formula dataset, we employ the relation-extraction model, CASREL,29 which excels in both speed and accuracy, and use BERT as the word embedding model. In CASREL, the extraction of entity triplets involves two main steps: first, identifying all potential head entities within the text; then, for each relation category, extracting all potential tail entities that exhibit a relation with the identified head entities.
Though the CASREL relation-extraction model offers good speed, it suffers from a drawback in terms of the separate recognition of the start and end entities. This arises from the two-linear-layer architecture, where each layer is dedicated to recognizing the start and end positions of entities, respectively. The procedure introduces inconsistency between training and prediction phases. In detail, during training, the model identifies the start and end positions of entities separately, but during final prediction, it recognizes the entire entity directly. This training-prediction discrepancy may degrade performance. Additionally, the original CASREL model cannot handle nested entities.
To address the aforementioned issues, we replaced the stacked pointer tagging model with the GP module. Furthermore, the CASREL model, after identifying the head entity, incorporates the head entity's embeddings into the BERT word embeddings for recognizing tail entities and relations. However, only incorporating the start and end positions of the head entity is insufficient, so we integrated all word embeddings of the head entity into the recognition of relations and tail entities.
Moreover, we replaced the original model's loss function with a multi-label cross-entropy loss function. This change can not only enhance the convergence speed of the model but also improve the final performance. The resulting improved relation-extraction model, CASREL-GP, is illustrated in Fig. 6.
The multi-label cross-entropy loss function is represented in eqn (6).
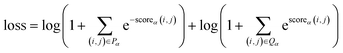 | (6) |
Where Pα is the set of all head-tail pairs for entities with a type α in the given sample, Qα is the set of all non-entities or entities with types other than α in the sample, and scoreα(i, j) represents the score of the fragment t[i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j] being an entity of type α.
j] being an entity of type α.
3.4 Traditional Chinese medicine formula-repurposing model
After constructing the TCM prescription knowledge graph, we proposed a formula-repurposing model based on the KG and a link-prediction model HAKE,20 as shown in Fig. 7. First, the HAKE model was trained by the constructed TCM formula KG, and obtained the embedding representations of entities and relations in KG. Then, the embedding representation of the query formula was generated through the obtained entity embedding representations. Finally, by calculating the similarity between the query and all the same category of entities in library, we may find similar therapeutic formulas or possible formulas for some target diseases.HAKE is a link-prediction model that focuses on modeling the semantic hierarchy by computing the phase and modulus of entities, like concentric circles in a polar coordinate system. The modulus part is the radius of an entity embedding, and the phase part is the rotational angle of the angular coordinates in a polar coordinate system. This semantic hierarchy enhances the information of the entity embeddings.
To differentiate the modulus and phase components of the embeddings, we denote the modulus embeddings for entities and relations as hm, rm, and tm and the phase embeddings as hp, rp, and tp. The modulus separates entities of different hierarchical structures, which corresponds to entities with varying radii in the polar coordinate system. Given that the hierarchical structure can be viewed as a tree, the entities at different hierarchical levels can be interpreted as various depths within that tree. The representation of the modulus part is expressed as follows in eqn (7), where  and
and 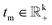 , and the corresponding distance function is expressed as shown in eqn (8).
, and the corresponding distance function is expressed as shown in eqn (8).
| hm·rm = tm | (7) |
| dr,m(hm,tm) = ‖hm·rm − tm‖2 | (8) |
The phase part models entities on the same hierarchical structure, which corresponds to entities on the same concentric circle. Since entities on the same concentric circle have different phases, this allows for the differentiation of entities within the same hierarchical structure. The modeling of the phase part is expressed as shown in eqn (9).
| (hp + rp)mod 2π = tp | (9) |
| dr,p(hp,tp) = ‖sin((hp + rp − tp)/2)‖1 | (10) |
The sin function is used because the phase exhibits periodicity on the circle.
Finally, the modulus and phase are combined and the distance function is shown in eqn (11).
| dr(h,t) = dr,m(hm,tm) + λdp(hp,tp) | (11) |
When dr(h,t) gets closer to 0, it indicates that the triplet, composed of the head entity, tail entity, and relation, is valid.
In our modeling, after obtaining the embedding representations of entities and relations, let S be the set of all symptoms in the graph. For each symptom s ∈ S, its corresponding embedding vector is denoted as es. Let F be the set of all formulas, and for each formula f ∈ F, and its corresponding set of treated symptoms is denoted as Cs ∈ S. For a given formula f, the average embedding vector of its treated symptoms can be represented in eqn (12).
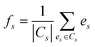 | (12) |
Then, applying the above operation to all formulas in the knowledge graph F, we obtain the embedding vector set εF, for all formulas, represented in eqn (13).
| εF = {fs∣f∈F} | (13) |
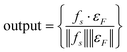 | (14) |
4 Results and discussion
The proposed NER and relation-extraction models are firstly constructed using public databases and evaluated using parameters, precision, recall and F1. To build our TCM KG, the established models are used to obtain entities and relations from TCM databases. The TCM formula-repurposing model is built upon TCM KG to conduct specific formula prediction. This can not only help find new indications for a formula but also verify the usability of the TCM KG.4.1 Experimental analysis
4.1.1.1 NER model. To ensure the performance of the proposed entity extraction model, we use two publicly available named-entity recognition databases to construct our NER model, including a general-domain dataset from the People's Daily, and the latest clinical medical entity dataset CMeEE (Chinese Medical Entity Extraction dataset) in the medical field. Subsequently, the well-trained NER model is adopted for our collected Chinese medicine formula dataset for TCM entity extraction. The detailed information of the datasets is shown in Table 2. People's Daily consists solely of non-nested entities. The CMeEE dataset contains both nested and non-nested entities. Our collected TCM dataset consists of much higher nested entities than CMeEE in terms of the number of final data points.34 Additionally, the number of entities in our own dataset is also much higher than that of CMeEE.
| Dataset | Training set | Test set | Average sentence length | Average number of entities per sentence |
|---|---|---|---|---|
| TCM | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 225 |
4653 | 227.81 | 25.12 |
| People's Daily | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 271 |
7585 | — | — |
| CMeEE | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
5000 | 54.15 | 9 |
We employed the classical combination NER models, BERT + BiLSTM + CRF and BERT + GP, as baseline models for comparison with our proposed model BERT + GAU + GP (BGGNER). The experimental results are presented in Table 3.
| Dataset | Model | Precision | Recall | F1 |
|---|---|---|---|---|
| CMeEE | BERT + GP | 0.7936 | 0.6922 | 0.7375 |
| BERT + BiLSTM + CRF | 0.696 | 0.725 | 0.710 | |
| BGGNER (our model) | 0.7650 | 0.7430 | 0.7458 | |
| People's Daily | BERT + GP | — | — | 0.9551 |
| BERT + BiLSTM + CRF | — | — | 0.9546 | |
| BGGNER (our model) | 0.9560 | 0.9604 | 0.9580 | |
| TCM (our dataset) | BERT + GP | 0.9531 | 0.9506 | 0.9518 |
| BERT + BiLSTM + CRF | 0.9422 | 0.9368 | 0.9337 | |
| BGGNER (our model) | 0.9558 | 0.9615 | 0.9586 |
For the CMeEE dataset, Table 3 shows that the models with the GP decoder are the best, while the addition of the GAU model, which effectively captures feature information, leads to varying degrees of improvement in the final results. However, for CMeEE, we can see that the difference between the precision and recall values is relatively large, which implies that BERT-GP tends to overpredict positive samples. For the People's Daily dataset, which consists solely of non-nested entities, the results show that our proposed NER model with the GP decoder and GAU enhanced position information is better than the one with CRF. This indicates that the GP labeling scheme performs well in recognizing nested entities and non-nested entities. For the TCM dataset, our model outperforms baseline models according to all evaluation metrics.
It is noticeable that the proposed BGGNER model demonstrates improved performance compared with the baseline models, particularly in handling nested entities. This can be attributed to GP’s ability of recognizing nested entities in the dataset; moreover, the added GAU module captures long-distance dependency information between words in sentences. The incorporation of the GAU module and the GP decoder contributes to the model's ability to capture complex entity relations and dependencies, making it an effective alternative for nested-entity recognition tasks.
In terms of overall performance, it is evident that the proposed NER model, BGGNER, outperforms both the BERT + GP and BERT + BiLSTM + CRF models. Therefore, we use BGGNER to extract entities from our collected TCM texts. It can be seen that the GP decoder exhibits a clear advantage over the CRF decoder, showing an improvement of nearly 2% in F1 performance.
4.1.1.2 Relation extraction. To ensure the performance of the relation-extraction model, we also conduct experiments on the public relation-extraction dataset DuIE2.0, which was released as part of the Baidu Information Extraction Competition.35 DuIE2.0 stands as the largest schema-based Chinese relation-extraction dataset, boasting a wide-ranging source collection that includes Baidu Baike, Baidu Tieba, and Baidu Information Flow. Comprising over 430
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 triple data points and 210
000 triple data points and 210![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sentences, and encompassing 48 distinct relation types, this dataset enjoys a broad and extensive data source. The utilization of the DuIE2.0 dataset in our evaluation strategy serves to verify the model performance and mitigate the possibility of the enhancements being specific to a single dataset.
000 sentences, and encompassing 48 distinct relation types, this dataset enjoys a broad and extensive data source. The utilization of the DuIE2.0 dataset in our evaluation strategy serves to verify the model performance and mitigate the possibility of the enhancements being specific to a single dataset.
In the relation-extraction model, we compared our improved model CASREL-GP with the original CASREL model, and the results are shown in Table 4.
| Dataset | Model | Precision | Recall | F1 |
|---|---|---|---|---|
| DuIE2.0 | CASREL | 0.7253 | 0.7221 | 0.7176 |
| CASREL-GP (our model) | 0.7434 | 0.7313 | 0.7318 | |
| TCM | CASREL | 0.9299 | 0.9099 | 0.9156 |
| CASREL-GP (our model) | 0.9419 | 0.9160 | 0.9280 |
In Table 4, training and evaluating the improved relation-extraction model on the DuIE2.0 dataset yielded a comprehensive superiority over the original relation-extraction model. This outcome serves as substantial evidence that our proposed enhancements are leading to a notable improvement in the performance of the model. It is also shown for our constructed TCM dataset that the modifications of the model have led to a notable improvement in performance. This suggests that the enhanced relation-extraction model CASREL-GP outperformed CASREL in relation extraction.
Therefore, we further compared the improved model with two state-of-the-art models in the current field of relation extraction. This comparison was conducted on our self-constructed TCM dataset for extracting relationships from Chinese herbal formula texts. The experimental results are presented in Table 5, where it can be seen that the improved relation-extraction model outperforms SOTA baseline models.
| Models | Precision | Recall | F1 |
|---|---|---|---|
| TPLinker | 0.9242 | 0.9220 | 0.9224 |
| SpERT | 0.9355 | 0.9016 | 0.9174 |
| CASREL-GP (our model) | 0.9419 | 0.9160 | 0.9280 |
4.2 HAKE embedding
We leverage a link-prediction model, HAKE, to generate KG embedding for our TCM KG. Fig. 8 shows the visualized entity embeddings from the trained HAKE model. Fig. 8(a) displays all the entity embeddings included in the TCM formula knowledge graph. Since HAKE employs a hierarchical modeling approach, treating entities as part of a concentric circle structure, the resulting overall entity distribution exhibits a circular outline (shown in Fig. 8(a)). For different types of entities, they distribute across various radial levels due to the hierarchical modeling. This can be clearly seen in Fig. 8(b), where different types of entities are located on their respective concentric circles with each entity forming a circle with the same color embedding points. This embedding distribution also indirectly validates the clarity and rationality of the hierarchical structure within the trained TCM formula knowledge graph. | ||
| Fig. 8 Semantic hierarchy visualization of embeddings: (a) visualization of all entities; (b) visualization of the hierarchical structure of four entities. | ||
4.3 Formula-repurposing applications
The study for formula repurposing can be approached from two perspectives: first, identifying formulas with similar therapeutic effects based on a given formula's name (“formula-to-formula”), and second, finding corresponding formulas based on known symptoms (“symptom-to-formula”).In the “formula-to-formula” experiment, using the names of existing formulas as input, the repurposing model predicts formulas with similar therapeutic effects. We present the top 5 similar results from the experiment in Table 6.
In the case of Fufang Danshen Tablets, they are known for regulating Qi, relieving pain, and promoting blood circulation, primarily used to treat coronary heart disease and angina. The predicted top 5 results include Fufang Danshen Drops Pills, Kuangxiong Pills, Jingzhi Guanxin Tablets, Guanxin Danshen Tablets, and Taoren Porridge, all of which share therapeutic effects for coronary heart disease and angina. More experimental cases are provided in Table S1 of the SI.
To visually present the relationship between the input formula and the predicted results, we applied multidimensional scaling (MDS) to reduce the dimensions of the embeddings of the input formula and its predicted top 5 counterparts. In Fig. 9, the similarities on a 2D plane between formulas are shown, where the shorter the distance, the higher the similarity to the input formula. As shown in Fig. 9, we visualized several cases: the red dot at the center represents the input formula, while the other colored dots represent the predicted formulas. It is evident that the closer the dots are to the central red dot, the higher the similarity. More visualization results are shown in Fig. S1 of the SI. It demonstrates that these results are consistent with practical clinical scenarios.
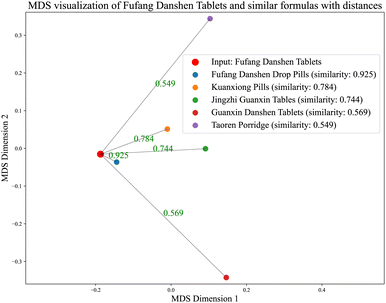 | ||
| Fig. 9 MDS dimensionality reduction representation and distance to the 5 closest formulas from the input formula. | ||
Symptom-to-formula prediction involves predicting TCM formulas that can possibly treat specific diseases, such as epidemic outbreaks or rare diseases, based on their manifest symptoms. By computing the embedding of the symptoms associated with a disease, we can identify formulas that address those particular symptoms. The detailed experimental results are displayed in Table 7.
It can be seen that ID 1 represents a symptom set typical of the common cold, such as headaches and fever. The model's predicted formulas are closely aligned with treatments for these symptoms, showcasing its ability to identify and recommend formulas for common cold.
When additional symptoms related to pulmonary conditions, such as fatigue, shortness of breath, and dry cough, are incorporated into the symptom set to form ID 2 in Table 7, the model adaptively predicts formulas more appropriate to these new symptoms. Examples include Baihua Dingchuan Pills, Zhiliao Feixuhan Fang, and Junqi Baxian Decoction, all of which primarily target cough and dyspnea. By examining the predicted outcomes for various symptom combinations, the model demonstrates flexibility and adaptability. It adjusts its predictions when specific symptoms are added or removed from the set, reflecting its ability to comprehend and process complex medical data. Particularly for the symptom sets associated with COVID-19 patients (ID 3 and ID 4), the model accurately predicts Kanggan Granules as the top 1 choice, which have been effective in treating COVID-19 and are included in the treatment guidelines for COVID-19 patients in China.36 From experiments, it is evident that by inputting different combinations of symptoms, the model demonstrates the ability to predict TCM formulas related to specific symptoms. This suggests that the symptom-to-formula approach may provide insights and assistance in quickly discovering treatments for outbreaks or rare diseases.
4.4 Embedding analyses
To demonstrate the superiority of HAKE-based embeddings in the proposed drug repurposing model, we compared them with embeddings generated by the classical link-prediction model, TransE.37 As illustrated in Fig. 10, we visualized the embeddings of the formula Yuanshen Huadu Yin and its principal ingredient, Yuanshen, obtained using the two models, respectively. Notably, in the semantic hierarchy, the formula Yuanshen Huadu Yin contains the principal herb Yuanshen, connected via the relation “consists of”, indicating that they occupy different semantic levels. As shown in Fig. 10(a), the embeddings produced by TransE are intermingled and fail to reflect this hierarchical relationship. In contrast, Fig. 10(b) shows that the embeddings generated by HAKE exhibit a hierarchical structure, capturing the inclusion relationship between Yuanshen Huadu Yin and Yuanshen. These results indicate that HAKE provides more informative embeddings that encode semantic hierarchies compared to TransE. Consequently, when HAKE embeddings are used for drug repurposing, the hierarchical semantics can be incorporated into similarity measurements, leading to more accurate predictions than those based on TransE embeddings. In addition, this result underscores the importance of the embedding algorithm choice, prompting us to further refine this component in our repurposing model. | ||
| Fig. 10 The visualizations of (a) TransE and (b) HAKE embeddings generated for entities, a formula-Yuanshen Huadu Yin (blue dots), and its principal herbal ingredient-Yuanshen (yellow dots). | ||
To further elucidate the key entities and relations influencing drug repurposing predictions, we visualized similarities between the input symptoms and the treatment symptoms predicted by the model (Fig. 11). Taking the common cold symptoms (ID 1, Yuanshen Huadu Yin in Table 7) as an example, a heatmap was generated comparing the input symptoms with those corresponding to the predicted formula. The results indicate that the predicted formula effectively addresses symptoms such as fever, headache, and sore throat, while certain symptoms, including fever–thirst, fever–sore throat, headache–aversion to cold, and sore throat–thirst, exhibit relatively high correlations. These patterns reflect the latent relationships among symptoms, where fever may induce headache, sore throat, and thirst. Intuitively, the symptom aversion to cold may be closely correlated to fever, but in fact it is often accompanied by headache with intolerance to cold, so it is not necessarily linked to fever; thus, it shows a stronger correlation with headache and a comparatively weaker association with fever. Overall, this analysis for symptom and formula associations demonstrates that the model effectively captures both direct and approximately synonymous entity correspondences, highlighting its ability to uncover latent entity associations. These findings may shed light on underlying treatment principles and provide a promising tool for practitioners to understand TCM systematically and comprehensively.
 | ||
| Fig. 11 Heatmap of the similarity between input symptoms and the symptoms of the formula predicted by the model. | ||
For broader applications, our repurposing model can predict new indications for existing formulas and recommend suitable formulas for specific diseases, among other applications. It should be noted, however, that the model's performance is highly dependent on the quality of the underlying KG, and predictions may change as the KG grows in scale and complexity. To improve both the accuracy and robustness of the model, we are actively working to enrich and refine our TCM KG and enhance its embedding algorithm.
5 Conclusions
We proposed a full-chain strategy for TCM formula repurposing, starting from KG construction to semantic repurposing. Firstly, we build a TCM formula knowledge graph from scratch. We constructed an entity terminology lexicon for TCM formulas. To address the issue of entity nesting in TCM terminology, we constructed the BGGNER model, which effectively resolves the nesting problem and outperforms other baseline models, achieving fine results in experiments. Given the presence of one-to-many, many-to-many, and many-to-one relations in TCM formula texts, we adopted the improved CASREL relation-extraction model, CASREL-GP, for TCM relation extraction. This led to the successful construction of the TCM formula knowledge graph, which was further used in formula-repurposing experiments. The semantic repurposing experimental results closely aligned with clinical practices, validating the usability of the TCM formula knowledge graph and our repurposing strategy. This indicates the proposed formula-repurposing strategy can be utilized for deeply understanding ancient prescriptions and assisting in efficient new indications and prescription development, especially in the situation of an epidemic outbreak. Additionally, the proposed strategy can also be easily extended to various recipe discoveries, such as health care products, health foods and cuisine.Author contributions
XD: writing – original draft, validation, software, methodology. WZ: validation, investigation, modeling. FL: validation, software, methodology. LHH: writing – review & editing, supervision, investigation, conceptualization. HL: software, investigation. GL: validation, methodology, supervision, investigation, conceptualization.Conflicts of interest
There are no conflicts to declare.Data availability
The code and data for TCM repurposing can be found at either https://github.com/Djiutian/TCMRepurposing, or https://doi.org/10.5281/zenodo.17427048. The CMEE dataset is available at DOI: https://doi.org/10.1007/978-3-030-81197-6_55. The People's Daily dataset is available at the following link: https://github.com/InsaneLife/ChineseNLPCorpus/tree/master/NER/renMinRiBao. The DuIE2.0 dataset is available at URL: https://aistudio.baidu.com/datasetdetail/180082.Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00344j.
Acknowledgements
This work was supported by National Natural Science Foundation of China (22273010) and Jilin Province Science and Technology Development Plan Item (20250301008YY).References
- N. Nosengo, Nature, 2016, 534, 314–316 CrossRef PubMed.
- D. J. Phillips, Pfizer's expiring Viagra patent adversely affects other drugmakers too, Forbes, 2013, https://www.forbes.com/sites/investor/2013/12/20/pfizers-expiring-viagra-patent-adversely-affects-other-drugmakers-too Search PubMed.
- D. J. Wallace, Semin. Arthritis Rheum., 1989, 282–296 CrossRef CAS PubMed.
- E. G. Favalli, M. Biggioggero, G. Maioli and R. Caporali, Lancet Infect. Dis., 2020, 20, 1012–1013 CrossRef CAS PubMed.
- E. L. H. Leung, H. D. Pan, Y. F. Huang, X. X. Fan, W. Y. Wang, F. He, J. Cai, H. Zhou and L. Liu, Engineering, 2020, 6, 1099–1107 CrossRef CAS PubMed.
- C. L. Yao, J. Q. Zhang, J. Y. Li, W. L. Wei, S. Wu and D. A. Guo, Nat. Prod. Rep., 2021, 38, 1618–1633 RSC.
- C. Y. Wang, X. Y. Bai and C. H. Wang, Am. J. Chin. Med., 2014, 42, 543–559 CrossRef CAS PubMed.
- Q. Sun, M. He, M. Zhang, S. Zeng, L. Chen, H. Zhao, H. Yang, M. Liu, S. Ren and H. Xu, Front. Pharmacol, 2021, 12, 685002 CrossRef CAS PubMed.
- Z. M. Li, S. W. Xu and P. Q. Liu, Acta Pharmacol. Sin., 2018, 39, 802–824 CrossRef CAS PubMed.
- D. Wang, W. Li, X. Dong, H. Li and L. Hu, J. Chem. Inf. Model., 2023, 63, 782–793 CrossRef CAS PubMed.
- D. Wang, X. Dong, X. Zhang and L. Hu, Briefings Bioinf., 2025, 26, bbae676 CrossRef CAS PubMed.
- C. Li, W.-w. Jia, J.-l. Yang, C. Cheng and O. E. Olaleye, Acta Pharmacol. Sin., 2022, 43, 3080–3095 CrossRef CAS PubMed.
- L. Zhong, J. Wu, Q. Li, H. Peng and X. Wu, ACM Comput. Surv., 2023, 56, 1–62 CrossRef.
- Z. Liu, E. Peng, S. Yan, G. Li and T. Hao, Proceedings of the 27th international conference on computational linguistics: system demonstrations, 2018, pp. 15–19 Search PubMed.
- L. Jia, J. Liu, T. Yu, Y. Dong, L. Zhu, B. Gao and L. Liu, J. Med. Inf., 2015, 51–53 CAS.
- C. Li, F. Lin and D. Xie, Proceedings of the 3rd International Symposium on Artificial Intelligence for Medicine Sciences, 2022, pp. 294–301 Search PubMed.
- Y. Wang, J. Phys.: Conf. Ser., 2020, 012019 Search PubMed.
- Y. Zou, Y. He and Y. Liu, 2020 39th Chinese Control Conference (CCC), 2020, pp. 4266–4272 Search PubMed.
- R. Yang, Q. Ye, C. Cheng, S. Zhang, Y. Lan and J. Zou, Evid. base Compl. Alternative Med., 2022, 2022, 8693937 Search PubMed.
- Z. Zhang, J. Cai, Y. Zhang and J. Wang, Proceedings of the AAAI conference on artificial intelligence, 2020, pp. 3065–3072 Search PubMed.
- Z. Zheng, Y. Liu, Y. Zhang and C. Wen, 2020 IEEE international conference on knowledge graph (ICKG), 2020, pp. 560–564 Search PubMed.
- T. Yu, J. Li, Q. Yu, Y. Tian, X. Shun, L. Xu, L. Zhu and H. Gao, Artif. Intell. Med., 2017, 77, 48–52 CrossRef PubMed.
- Z. Liu, J. Yang, K. Chen, T. Yang, X. Li, B. Lu, D. Fu, Z. Zheng and C. Luo, IEEE Internet Things J., 2024, 11, 20002–20014 Search PubMed.
- Z. Guo, Q. Liu and B. Zou, Digital Chin. Med., 2022, 5, 386–393 CrossRef.
- Y. Xie, L. Hu, X. Chen, J. Feng and D. Zhang, Comput. Mater. Continua, 2020, 65, 481–494 Search PubMed.
- J. Su, A. Murtadha, S. Pan, J. Hou, J. Sun, W. Huang, B. Wen and Y. Liu, arXiv, 2022, preprint, arXiv:2208.03054, DOI:10.48550/arXiv.2208.03054.
- J. Su, M. Ahmed, Y. Lu, S. Pan, W. Bo and Y. Liu, Neurocomputing, 2024, 568, 127063 CrossRef.
- W. Hua, Z. Dai, H. Liu and Q. Le, International conference on machine learning, 2022, pp. 9099–9117 Search PubMed.
- Z. Wei, J. Su, Y. Wang, Y. Tian and Y. Chang, Proceedings of the 58th annual meeting of the association for computational linguistics, 2019, pp. 1476–1488 Search PubMed.
- Wanfang Data, Traditional Chinese Medicine Medical Resource Platform, 2025, https://tcm.med.wanfangdata.com.cn/, accessed: 15 September 2025 Search PubMed.
- H. Peng, Dictionary of Traditional Chinese Medical Formulae (Zhongyi Fangji Dacidian, in Chinese), The People’s Health Press Co., Ltd, Beijing, 2nd edn, 2016 Search PubMed.
- National Administration of Traditional Chinese Medicine and National Health Commission of the People's Republic of China, Notice on Issuing the “Classification and Codes of Diseases and Syndromes in Traditional Chinese Medicine” and the “Clinical Terminology of Traditional Chinese Medical Diagnosis and Treatment”, 2020, https://www.gov.cn/zhengce/zhengceku/2020-11/24/content_5563703.htm, accessed: 15 September 2025 Search PubMed.
- Y. Li, Compendium of Chinese Classic Formulas (Zhonghua Mingfang Daquan, in Chinese), Heilongjiang Science &Technology Press, 2011 Search PubMed.
- H. Zan, W. Li, K. Zhang, Y. Ye, B. Chang and Z. Sui, Workshop on Chinese Lexical Semantics, 2020, pp. 652–664 Search PubMed.
- S. Li, W. He, Y. Shi, W. Jiang, H. Liang, Y. Jiang, Y. Zhang, Y. Lyu and Y. Zhu, CCF International Conference on Natural Language Processing and Chinese Computing, 2019, pp. 791–800 Search PubMed.
- Beijing Municipal Health Commission, Medication Guide for COVID-19 Patients (First Edition), Official Press Release, 2022, https://wjw.beijing.gov.cn/xwzx_20031/wnxw/202212/t20221212_2877983.html Search PubMed.
- A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston and O. Yakhnenko, Translating Embeddings for Modeling Multi-relational Data, in Advances in Neural Information Processing Systems, 2013, 26 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |