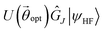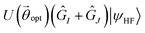Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum state preparation of multiconfigurational states for quantum chemistry
Gabriel
Greene-Diniz
 *,
Georgia
Prokopiou
*,
Georgia
Prokopiou
 ,
David Zsolt
Manrique
,
David Zsolt
Manrique
 and
David
Muñoz Ramo
and
David
Muñoz Ramo

Quantinuum Ltd, 13-15 Hills Road, CB2 1NL Cambridge, UK. E-mail: gabriel.greene-diniz@quantinuum.com
First published on 12th December 2025
Abstract
The ability to prepare states for quantum chemistry is a promising feature of quantum computers, and efficient techniques for chemical state preparation is an active area of research. In this paper, we implement and investigate two methods of quantum circuit preparation for multiconfigurational states for quantum chemical applications. It has previously been shown that controlled Givens rotations are universal for quantum chemistry. To prepare a selected linear combination of Slater determinants (represented as occupation number configurations) using Givens rotations, the gates that rotate between the reference and excited determinants need to be controlled on qubits outside the excitation (external controls), in general. We implement a method to automatically find the external controls required for utilizing Givens rotations to prepare multiconfigurational states on a quantum circuit. We compare this approach to an alternative technique that exploits the sparsity of the chemical state vector and find that the latter can outperform the method of externally controlled Givens rotations; highly reduced circuits can be obtained by taking advantage of the sparse nature (where the number of basis states is significantly less than 2nq for nq qubits) of chemical wavefunctions. We demonstrate the benefits of these techniques in a range of applications, including the ground states of a strongly correlated molecule, matrix elements of the Q-SCEOM algorithm for excited states, as well as correlated initial states for a quantum subspace method based on quantum computed moments and quantum phase estimation.
1 Introduction
Quantum computation has the potential to make a large impact on quantum chemistry and condensed matter physics. This has motivated a recent rapid development of techniques for representing quantum chemical states on gate-based quantum computers.1–12 From the point of view of general quantum state preparation, many research works have focused on maximizing the efficiency of loading classical data into a quantum processor and preparing a quantum state to represent those data.13–18 It is interesting to consider applications of the latter approach to quantum chemistry, where the classical data represent previously obtained chemical information, and the quantum computer can be used to further evolve the quantum chemical state (for example, to increase the accuracy of the representation of the ground or excited states of a molecule).The existence of gate sets that are universal for quantum chemistry (in the sense of spanning the space of all states that preserve fermionic symmetries) has recently been proved.3 These gates take the form of Givens rotations (GRs) to represent particle-number-conserving excitations that correlate the occupations of different fermionic modes. GRs have also been used to construct gate fabrics that can navigate fermionic Fock spaces.1 Regarding the preparation of multiconfigurational states (where each configuration represents electrons distributed throughout a molecular orbital basis, in a second quantized framework), if the configurations are specified a priori then a sequence of GRs can be applied to the circuit to prepare the desired state vector.3 However, GRs will mix any basis states with qubit subspaces that match those involved in the rotation. To ensure that only the desired basis states are included in the state vector, GRs can be controlled by qubits outside the rotation space3 (which we refer to as “external” controls to distinguish these from internal CNOTs within the GR gate decomposition). However, externally controlling each GR on all qubits not directly involved in the rotation leads to very large circuits when decomposed into typical hardware gate sets. The question then remains as to how to apply external controls to guarantee the desired state vector is produced, while avoiding, when possible, externally controlling all GRs on all qubits outside the excitation. A specific example of this was presented in3 for a 6-qubit state consisting of 4 occupation number (ON) configurations. In this paper, we provide a general algorithm for finding external GR controls automatically for any particle-number-preserving fermionic state.
We also consider the previously proposed method of Gleinig and Hoefler to prepare sparse quantum states.19 Initially designed to overcome the problem of exponentially scaling resources for arbitrary quantum state preparation,14,20,21 the sparse state preparation (SSP) method takes advantage of the fact that many interesting quantum states span a relatively small section of the full Hilbert space, where the number of non-zero basis coefficients is far less than O(2n). This is the case for typical states of interest in quantum chemistry; the full configuration interaction (FCI)22 wavefunction obeys fundamental fermionic symmetries (e.g. spin and particle number conservation) which rule out many basis states of the entire Hilbert space. Additionally, the success of methods such as semistochastic heat-bath configuration interaction (SHCI)23 and perturbatively selected configuration interaction (CIPSI)24 exemplify the fact that a relatively small number of configurations can often provide a good approximation to the full wavefunction.
The importance of the sparsity of chemical wavefunctions is emphasized when considering approximations to the ground state, particularly in situations requiring “warm start” states, i.e. those states with large overlap with the true ground state (relative to single configuration Hartree–Fock (HF) states) yet remain sparse enough to be efficiently prepared. Considering the example of quantum phase estimation (QPE) in which the success probability is proportional to the overlap between the initial state and the true ground state, and the fact that in many interesting cases (e.g. strongly correlated systems) the HF state has significantly low overlap, the ability to efficiently and conveniently prepare multiconfigurational states can be highly beneficial. A recently published work25 noted the method of Gleinig and Hoefler as a non-variational approach to quantum chemical state preparation, and provided a comparison to other sparse state preparation approaches in terms of asymptotic scaling. Here, an implementation of Gleinig and Hoefler's approach suitable for quantum chemistry, along with its integration with various ground and excited state methods, is reported and applied to a strongly correlated chemical system.
In this paper we compare the techniques of externally controlled GRs3 and Gleinig and Hoefler's scheme19 for preparing quantum circuits corresponding to selected linear combinations of computational basis states, where the latter represent occupation number configurations (Slater determinants). These techniques are implemented in the InQuanto26–28 software package, and we demonstrate their utility for a wide range of quantum algorithms useful for quantum chemistry.
2 Preparation of multiconfigurational states in quantum circuits
2.1 Givens rotations with external controls
Consider an arbitrary single electronic configuration specified by an ON configuration22 in a finite basis of spin orbitals |…, fi, …, fj, …〉 with fermionic occupation numbers fi, fj ∈ {0, 1}, where fi ≠ fj, and i, j label orbitals involved in the excitation. An excitation can be viewed as a mixing between ON configurations with different occupations. Adopting the Jordan–Wigner (JW) transformation between fermionic and qubit algebras29,30 |…, fi, …, fj, …〉↦|…, qi, …, qj, …〉 where qi, qj ∈ {0, 1} are individual qubit states, a fermionic excitation can be encoded as a unitary operation applied to a register of qubits representing the ON configuration, rotating it to a convex combination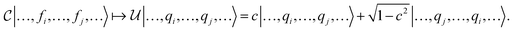 | (1) |
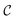 is a fermionic excitation operator, and
is a fermionic excitation operator, and  is a unitary operator (encoded as quantum gates) applied to the qubit register. Note that
is a unitary operator (encoded as quantum gates) applied to the qubit register. Note that 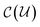 should preserve the total number of electrons (the qubit register Hamming weight).
should preserve the total number of electrons (the qubit register Hamming weight).
Eqn (1) corresponds to a 1-body excitation. Using a 2-qubit state as a minimal example, the excitation can be expressed in the computational basis as a GR,1–3 whose action on the 2nq=2 dimensional Hilbert space is to rotate in a 2 dimensional subspace of the state vector
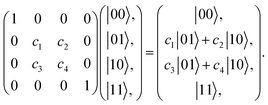 | (2) |
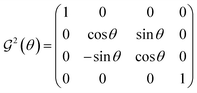 | (3) |
The Hamming distance between two binary strings x and y, defined as
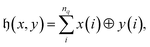 | (4) |
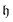 is related to the excitation order
is related to the excitation order 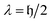 for λ-body excitations between two ON configurations. The qubits on which the excitation unitary acts can be specified using
for λ-body excitations between two ON configurations. The qubits on which the excitation unitary acts can be specified using 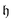 and its decomposition into an array of qubit-wise XOR values (x(0) ⊕ y(0), x(1) ⊕ y(1), …, x(nq) ⊕ y(nq)). The indexes of non-zero elements of this array correspond to the GR qubit indexes, while the value of
and its decomposition into an array of qubit-wise XOR values (x(0) ⊕ y(0), x(1) ⊕ y(1), …, x(nq) ⊕ y(nq)). The indexes of non-zero elements of this array correspond to the GR qubit indexes, while the value of 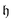 specifies the excitation order.
specifies the excitation order.
Selected linear combinations of ON configurations with fixed coefficients can be prepared using sequences of GRs applied to the circuit. Each GR mixes a pair of basis states (i.e. excitation) and its rotation angle θ can be obtained from state vector coefficients via recursive normalization (see Arrazola et al.3). Alternatively, optimized coefficients can be found by varying the gate angles within each rotation in a variational algorithm. As mentioned in the introduction (and elaborated in previous work3), the gates that encode each GR may need to be externally controlled to ensure that the sequence of GRs does not yield unwanted basis states. Thus, all the steps necessary to prepare a linear combination of ON configurations on a quantum circuit are at hand, apart from a general method to specify the external controls.
In the following subsection, we outline a procedure to automatically accomplish this task given a selected set of ON configurations, which specifies the excitation unitaries and the external controls needed to accomplish each GR. This can be used to build the circuit representing the multiconfigurational state.
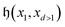 and their qubit components are then stored. Gate angles of each GR, dependent on the ON coefficients, can be found by using recursive normalization of ON coefficients (a specific example is also discussed in Section 3.1.1).
and their qubit components are then stored. Gate angles of each GR, dependent on the ON coefficients, can be found by using recursive normalization of ON coefficients (a specific example is also discussed in Section 3.1.1).
Let  represent a rotation that linearly mixes the reference with a basis state indexed by e = 2, …, D. The excitation indexes are obtained from a decomposition of the Hamming distance (non-zero contributions to the sum in eqn (4)), which specifies each GR unitary in the (D – 1)-length sequence, i.e.
represent a rotation that linearly mixes the reference with a basis state indexed by e = 2, …, D. The excitation indexes are obtained from a decomposition of the Hamming distance (non-zero contributions to the sum in eqn (4)), which specifies each GR unitary in the (D – 1)-length sequence, i.e.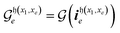 , where
, where 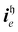 is a tuple of indexes of length 2λ corresponding to nonzero contributions to
is a tuple of indexes of length 2λ corresponding to nonzero contributions to 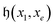 . Note that for the basis state index e = 2, external controls are not needed by definition.
. Note that for the basis state index e = 2, external controls are not needed by definition.
For a given ordered set of input configurations, the search for external controls required for 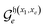 depends on whether a “previous” (p < e) basis state is “rotatable” by
depends on whether a “previous” (p < e) basis state is “rotatable” by 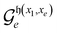 , and if so controls are applied to ensure that
, and if so controls are applied to ensure that 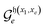 will not act on any basis state with index p = 2, …, e – 1.
will not act on any basis state with index p = 2, …, e – 1.
For basis states xe separated from the reference x1 by 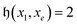 or
or 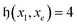 , Givens rotations
, Givens rotations 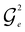 or
or 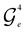 , respectively, can be used to mix xe with x1, and the external controls found by Algorithm 1 ensure that the circuit maintains the desired state vector. For
, respectively, can be used to mix xe with x1, and the external controls found by Algorithm 1 ensure that the circuit maintains the desired state vector. For 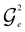 and
and 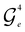 , we use the gate decompositions presented in previous works for 1-body and 2-body GRs1,3 (compilations of these circuits in the H-series gate set31 are given in the Appendix Fig. 10). However, when
, we use the gate decompositions presented in previous works for 1-body and 2-body GRs1,3 (compilations of these circuits in the H-series gate set31 are given in the Appendix Fig. 10). However, when 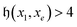 , a unitary is required that encodes the (λ > 2)-body excitation. To this end, we adapt a gadget described by Arrazola et al.3 consisting of (a) a sequence of multi-controlled SWAPs, (b) a central
, a unitary is required that encodes the (λ > 2)-body excitation. To this end, we adapt a gadget described by Arrazola et al.3 consisting of (a) a sequence of multi-controlled SWAPs, (b) a central 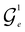 , and (c) the reverse of (a). In the Appendix section A.1, Algorithm 2 describes how the indexes of these unitaries and their external controls are found. Compared to Arrazola et al.,3 our scheme achieves a lower overhead of external controls for SWAPs and the central
, and (c) the reverse of (a). In the Appendix section A.1, Algorithm 2 describes how the indexes of these unitaries and their external controls are found. Compared to Arrazola et al.,3 our scheme achieves a lower overhead of external controls for SWAPs and the central 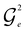 to combine ON configurations separated by λ > 2. An example of this for a 3-body excitation of the |111000〉 configuration is shown in Fig. 12.
to combine ON configurations separated by λ > 2. An example of this for a 3-body excitation of the |111000〉 configuration is shown in Fig. 12.
Once the 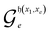 for all xe are found, along with their external controls (if required), the desired state |ψ〉 can be prepared as
for all xe are found, along with their external controls (if required), the desired state |ψ〉 can be prepared as
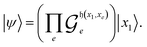 | (5) |
2.2 Sparse state preparation for quantum chemistry
In this section, we briefly describe Gleinig and Hoefler's sparse state preparation (SSP) method. For more details, we refer the reader to the original article.19 Here, we provide a brief description for completeness and highlight those aspects most relevant to multiconfigurational state preparation for quantum chemistry. This method essentially solves the problem of finding some n-qubit circuit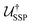 such that
such that 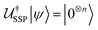 , where |ψ〉 is the desired n-qubit state to be prepared. Knowing
, where |ψ〉 is the desired n-qubit state to be prepared. Knowing 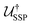 , one can reverse this to obtain the state preparation unitary
, one can reverse this to obtain the state preparation unitary 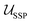 such that the desired state is
such that the desired state is 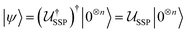 . The input to the SSP method is an unordered set
. The input to the SSP method is an unordered set  of bit strings representing ON configurations, with normalized coefficients cd such that the state to be prepared is
of bit strings representing ON configurations, with normalized coefficients cd such that the state to be prepared is 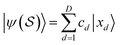 and
and 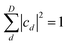 .
.
In the ith iteration of the algorithm,19 an arbitrary angle (possibly controlled) 1-qubit rotation gate along with an arrangement of NOT and CNOT gates (collectively labeled here as 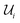 ) are found, which if applied to the state at the ith iteration results in a new state hosting
) are found, which if applied to the state at the ith iteration results in a new state hosting 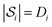 < Di−1 non-zero basis coefficients (where
< Di−1 non-zero basis coefficients (where 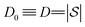 ). This is accomplished by “merging” two bit strings x1,i, x2,i contained in
). This is accomplished by “merging” two bit strings x1,i, x2,i contained in 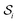 , where merging amounts to applying
, where merging amounts to applying 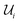 such that
such that 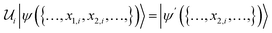 (up to global phase). The arrangement of gates in each
(up to global phase). The arrangement of gates in each 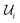 are determined by the distribution of binary values throughout the D bit strings.19 We note that for real-valued cd the Ry(θ) gate parameterized by angle θ is sufficient to represent the 1-qubit rotation in each
are determined by the distribution of binary values throughout the D bit strings.19 We note that for real-valued cd the Ry(θ) gate parameterized by angle θ is sufficient to represent the 1-qubit rotation in each 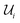 .
.
The gate angles of the SSP method, which determine the values of cd, are obtained on-the-fly and enter in the 1-qubit rotations, each of which mixes 2 basis states x1,i, x2,i at a given iteration i of the SSP algorithm; the ith rotation angle is obtained by normalizing the x2,i coefficient c2,i to 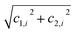 and taking the arcsin. For the next i + 1 iteration, the coefficient c2,i is replaced by the previous normalizer
and taking the arcsin. For the next i + 1 iteration, the coefficient c2,i is replaced by the previous normalizer 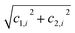 , and the angle of the (i + 1)th single qubit rotation is obtained for x1,i+1, x2,i+1 as in the previous iteration. For an example of this, see Gleinig and Hoefler's paper.19
, and the angle of the (i + 1)th single qubit rotation is obtained for x1,i+1, x2,i+1 as in the previous iteration. For an example of this, see Gleinig and Hoefler's paper.19
An important consequence of this algorithm is that the sequence of 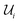 applied to the initial circuit |0⊗n〉 is independent of the order of bit strings provided by the user at input. This is a major difference with the GR method described in Section 2.1, and highlights the lack of a “reference” ON configuration for excitations in the SSP method (whereas in the GR method the excitation reference is fixed as the first member of the ordered set of input bit strings, and all GRs subsequently applied can be considered as rotations relative to the reference). While this does not affect the behavior of SSP-prepared circuits for fixed (non-variational) cd, variational applications of this method (in which gate angles are variationally optimized, hence leading to variationally optimized cd) can be affected, as discussed in Section 3.1.1.
applied to the initial circuit |0⊗n〉 is independent of the order of bit strings provided by the user at input. This is a major difference with the GR method described in Section 2.1, and highlights the lack of a “reference” ON configuration for excitations in the SSP method (whereas in the GR method the excitation reference is fixed as the first member of the ordered set of input bit strings, and all GRs subsequently applied can be considered as rotations relative to the reference). While this does not affect the behavior of SSP-prepared circuits for fixed (non-variational) cd, variational applications of this method (in which gate angles are variationally optimized, hence leading to variationally optimized cd) can be affected, as discussed in Section 3.1.1.
2.3 Methods which benefit from multiconfigurational state preparation
In the following subsections we mention a non-exhaustive list of methods which we use to demonstrate the utility of circuit preparation to represent selected linear combinations of ON configurations. We also mention previous applications, namely the preparation of N ± 1-particle states for Green's functions,32 and quantum circuit representations of CASSCF (complete active space self-consistent field) wavefunctions to study orbital entanglement.33On present-day noisy intermediate scale quantum (NISQ) hardware, the originally proposed form of VQE is significantly limited by various sources of noise (e.g. qubit decoherence, gate error rates, state preparation and measurement errors). Hence, in this work, VQE is utilized as a classical optimizer of gate angles 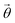 in multiconfigurational state circuits, which directly translates into optimization of basis state (ON configuration) coefficients of the circuit state vector. This demonstrates how the methods for preparing multiconfigurational state circuits (Section 2.1 and Section 2.2) can be used to prepare variational ansatzes for VQE applied to quantum chemistry. In this context, VQE is run in an ideal setting in which quantum measurements are classically simulated so that
in multiconfigurational state circuits, which directly translates into optimization of basis state (ON configuration) coefficients of the circuit state vector. This demonstrates how the methods for preparing multiconfigurational state circuits (Section 2.1 and Section 2.2) can be used to prepare variational ansatzes for VQE applied to quantum chemistry. In this context, VQE is run in an ideal setting in which quantum measurements are classically simulated so that 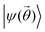 consists of ideally optimized basis coefficients.
consists of ideally optimized basis coefficients. 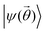 can then be used as the initial (warm start) state in subsequent methods (such as quantum subspace methods, or quantum phase estimation). One can also measure expectation values of the Hamiltonian in a noisy setting using offline optimized
can then be used as the initial (warm start) state in subsequent methods (such as quantum subspace methods, or quantum phase estimation). One can also measure expectation values of the Hamiltonian in a noisy setting using offline optimized 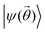 to quantum compute estimates of the ground state energy corresponding to ideal VQE parameters (see Section 3.1.1).
to quantum compute estimates of the ground state energy corresponding to ideal VQE parameters (see Section 3.1.1).
By deriving a truncation of the Lanczos expansion at m = 4,37 a non-perturbative approximation to the ground state energy referred to as QCM4 can be expressed using cumulants 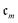 (also referred to as connected moments)
(also referred to as connected moments)
 | (6) |
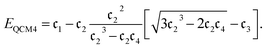 | (7) |
In this work, we also utilize the connected moments expansion38–41 in which the “t-expansion” of Horn and Weinstein42 can be expressed in terms of 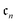 . This leads to alternative expressions of the energy to various orders of moments. Here we consider the CMX2 formula, in which “2” refers to the dimension of the associated subspace l
. This leads to alternative expressions of the energy to various orders of moments. Here we consider the CMX2 formula, in which “2” refers to the dimension of the associated subspace l
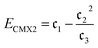 | (8) |
To obtain expectation values 〈Ĥm〉, the fermionic Hamiltonian is JW encoded as 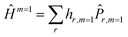 (where Pauli strings
(where Pauli strings ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) r,m are tensor products of Pauli gates spanning the qubit register and hr,m are real coefficients), then Ĥm > 1 are obtained by recursive multiplication of Ĥ. 〈Ĥm〉 can then be computed from quantum hardware measurements in the computational basis via Pauli string averaging. For ideal simulations, expectation values are computed classically (considered as the limit of infinite sampling in the absence of device noise).
r,m are tensor products of Pauli gates spanning the qubit register and hr,m are real coefficients), then Ĥm > 1 are obtained by recursive multiplication of Ĥ. 〈Ĥm〉 can then be computed from quantum hardware measurements in the computational basis via Pauli string averaging. For ideal simulations, expectation values are computed classically (considered as the limit of infinite sampling in the absence of device noise).
We note that the use of multiconfigurational (or multireference) initial states for connected moment expansions of the energy has a long history in classical computational chemistry.38 In Section 3.1.2 we show a quantum computational version of this approach, where the circuit corresponding to the initial state is tailored to linear combinations of specific ON configurations (Slater determinants).
| Z(t) = 〈ψ|e−itĤ|ψ〉, | (9) |
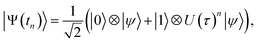 | (10) |
| Re Zn = 〈Ψ(tn)|X⊗I|Ψ(tn)〉, | (11) |
| Im Zn = 〈Ψ(tn)|Y⊗I|Ψ(tn)〉. | (12) |
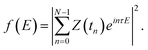 | (13) |
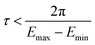 , where Emax and Emin are the largest and smallest eigenvalues of the simulated Hamiltonian. This choice ensures τE ∈ (–π, π) for every eigenvalue E, therefore avoiding phase aliasing and enabling unambiguous extraction viaeqn (13). In practice, the spectrum can be centered by using
, where Emax and Emin are the largest and smallest eigenvalues of the simulated Hamiltonian. This choice ensures τE ∈ (–π, π) for every eigenvalue E, therefore avoiding phase aliasing and enabling unambiguous extraction viaeqn (13). In practice, the spectrum can be centered by using 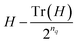 , so that the ground state energy corresponds to the smallest eigenphase.
, so that the ground state energy corresponds to the smallest eigenphase.
In Section 3 we demonstrate how multiconfigurational state preparation can increase the overlap with the ground state and therefore impacts the performance of the QCELS method.
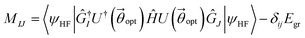 | (14) |
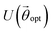 is a unitary ansatz with angles
is a unitary ansatz with angles 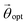 optimized for the ground state. A simplified form of the off-diagonal elements can be obtained44
optimized for the ground state. A simplified form of the off-diagonal elements can be obtained44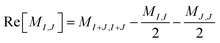 | (15) |
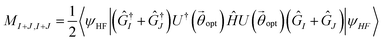 | (16) |
Here we discuss the application of the multiconfigurational state preparation methods presented in Section 2, comparing both approaches, each being a building block of the Q-SCEOM implementation in InQuanto.26,28
2.4 Computational details
To demonstrate the use of multiconfigurational state preparation as a useful approach to prepare initial states for strongly correlated systems, we study the ground and excited states of twisted C2H4 in the minimal basis set STO-3G. The ground state corresponds to a singlet at torsion angles close to 0° or 180°, while at 90° the ground state is quasi-degenerate with the triplet having a slightly lower energy. In terms of classical preprocessing, the PySCF code53 is used to build the fermionic (second quantized) Hamiltonian and to run complete active space configuration interaction (CASCI) and unrestricted HF calculations. Active spaces are selected based on the ordering of mutual information54 between orbital pairs (see Fig. 15 in the Appendix for the plots of the molecular orbitals (MOs) that were used in the active spaces). For all active spaces and all torsion angles, the natural orbitals are dominated by the carbon 2p shell, with small admixtures of H 1s that grow (but remain minority) as the torsion angle tends to 90°. For larger (8-qubit and 12-qubit) active spaces, higher orbitals that contribute to correlation in the ground state also contain mixtures of 2s and 2p. Fermionic Hamiltonians are JW transformed to obtain Ĥ as a sum of Pauli strings, for each active space. For VQE optimizations, the L-BFGS-B method as implemented in the SciPy package55 was used. The multiconfigurational state preparation methods are implemented in the InQuanto software package,26–28 and all quantum calculations are carried out using InQuanto. Quantum circuits are compiled using the architecture agnostic software compiler TKET.563 Results
3.1 Ground state of C2H4
Here we demonstrate the use of multiconfigurational state circuits to calculate the ground state energy of twisted C2H4, using variational and non-variational techniques. A common bottleneck in these eigensolvers is the large overhead in measurements needed to accurately represent the required expectation values (typically by averaging over Pauli string measurements). This issue is exacerbated in strongly correlated systems in which a single reference (single ON configuration) state does not have a large overlap with the true ground state. A warm start initial state can be highly beneficial in this regard, particularly for quantum subspace methods, as the measurement overhead can be reduced, for example by requiring a smaller number of Hamiltonian moments or a smaller dimensionality of the subspace.Before discussing results for the ground state energies of specific active spaces, we mention a popular quantum computational method to approximate the ground state which is Unitary Coupled Cluster Singles and Doubles (UCCSD),12 with excitation parameters θk optimized by VQE. This ansatz can be expressed as a series of unitary operators applied to a reference state (e.g. to the Hartree–Fock state |ψHF〉)
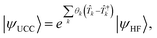 | (17) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) k consist of single, double, triple, …, excitations, which excite 1, 2, 3, …, fermions between occupied and virtual orbitals. In UCCSD, the excitations are truncated to singles and doubles, corresponding to each
k consist of single, double, triple, …, excitations, which excite 1, 2, 3, …, fermions between occupied and virtual orbitals. In UCCSD, the excitations are truncated to singles and doubles, corresponding to each ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) k operating over a maximum four spin oribtal indexes. (In practise, a Trotterized form of UCCSD is used as the variational ansatz, since individual excitations may not commute. Here we omit the Trotterization from eqn (17) for brevity).
k operating over a maximum four spin oribtal indexes. (In practise, a Trotterized form of UCCSD is used as the variational ansatz, since individual excitations may not commute. Here we omit the Trotterization from eqn (17) for brevity).
If one applies the second quantized fermionic operators Tk directly to |ψHF〉, a series of ON configurations can be generated which correspond to all possible single and double excitations relative to the HF state. The latter in fact correspond to the basis states of Configuration Interaction Singles and Doubles (CISD),22 and the CISD wavefunction is obtained once the coefficients of those basis states are found (typically by diagonalization of the Hamiltonian in the CISD basis). While UCCSD can be more accurate than CISD (due to size extensivity, for example), CISD contains a significant portion of electronic correlation and often yields reasonable approximations to the ground state. Due to the framework we developed for preparing multiconfigurational states, a variational circuit corresponding to the CI expansion can easily be generated once the ON configurations of the expansion are given. In Fig. 1, we compare CISD circuit sizes prepared using the SSP and GR methods to UCCSD circuits (with all gate angles represented symbolically) for a range of active spaces. For each active space, the ON configurations are obtained by applying ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) k to the closed shell singlet HF state. Therefore, the states prepared using these ON configurations retain the same spin symmetry as the ground states of C2H4 for torsion angles close to 0° or 180°.
k to the closed shell singlet HF state. Therefore, the states prepared using these ON configurations retain the same spin symmetry as the ground states of C2H4 for torsion angles close to 0° or 180°.
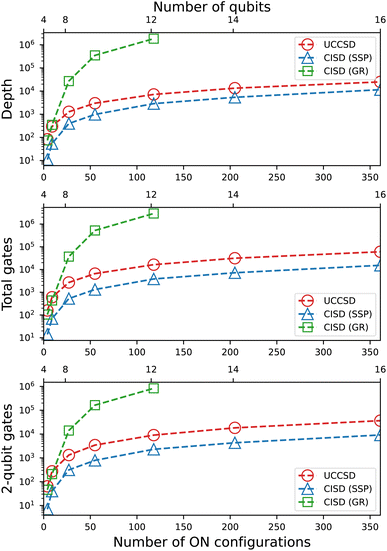 | ||
Fig. 1 Circuit resources obtained for UCCSD and CISD, where the latter are prepared using the GR (Section 2.1) or the SSP19 (Section 2.2) methods. Number of qubits nq ∈ {4, 6, 8, 10, 12, 14, 16}. For a given nq (equal to number of spin orbitals), the number of electrons is 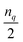 if if 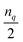 is even or is even or 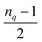 if if 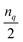 is odd, for which the HF reference is a closed shell singlet configuration. For a given nq and number of electrons, the number of configurations corresponds to the number of single and double excitations plus the HF reference. Circuits are compiled to the standard gate set using the Qiskit57 extension of TKET.56 is odd, for which the HF reference is a closed shell singlet configuration. For a given nq and number of electrons, the number of configurations corresponds to the number of single and double excitations plus the HF reference. Circuits are compiled to the standard gate set using the Qiskit57 extension of TKET.56 | ||
We observe that the SSP method produces circuits significantly smaller than the GR method over the range of active spaces chosen (4–16 qubits correspond to 2–8 active molecular orbitals). This is primarily due to the scaling in the number of external controls required for the GR method as the state becomes more complex with size, in addition to the decomposition of GR 1-body and 2-body rotations. The circuits produced by SSP are also consistently smaller than those produced by UCCSD for the same active space, implying the lower susceptibility to gate fidelity errors and qubit decoherence of the SSP CISD circuits, despite the generally lower accuracy of CISD compared to that of UCCSD.
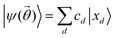 for VQE optimization
for VQE optimization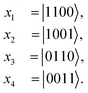 | (18) |
 and coefficients cd are described as follows.
and coefficients cd are described as follows.
For the GR method, as described in Section 2.1 each GR linearly combines the reference (x1) with another ON configuration in the input set. 3 GRs are required to linearly combine the configuration pairs 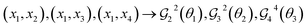 . In this case, externally controlling
. In this case, externally controlling 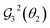 on the second qubit (q2) is required to maintain the desired state vector (see Fig. 2): since x2 = |1001〉 is “rotatable” by
on the second qubit (q2) is required to maintain the desired state vector (see Fig. 2): since x2 = |1001〉 is “rotatable” by 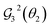 , then the external control is placed so that
, then the external control is placed so that 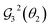 only operates on basis states in which q2 = 1 (and hence has no effect on |1001〉). The corresponding pairs of coefficients (elements of the
only operates on basis states in which q2 = 1 (and hence has no effect on |1001〉). The corresponding pairs of coefficients (elements of the  matrices related to rotation angle, see Eq. (3)) are obtained through recursive normalization of the cd state vector coefficients,3 which here become
matrices related to rotation angle, see Eq. (3)) are obtained through recursive normalization of the cd state vector coefficients,3 which here become 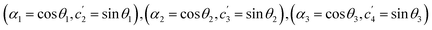 where
where 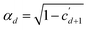 and
and 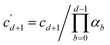 with α0 = 1†. For the SSP method, coefficients are related to gate angles as described in sec. 2.2 and exemplified in Gleinig and Hoefler's paper.19
with α0 = 1†. For the SSP method, coefficients are related to gate angles as described in sec. 2.2 and exemplified in Gleinig and Hoefler's paper.19
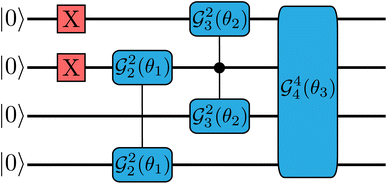 | ||
Fig. 2 Circuit corresponding to state c1|1100〉 + c2|1001〉 + c3|0110〉 + c4|0011〉 prepared using the GR method (see Section 2.1). Algorithm 1 found that externally controlling 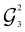 on the second qubit is required. Substituting the gate parameters for 90° torsion as an example and compiling to the H-series gate set,31 this circuit can be represented using 61 PhasedX gates, 4 Rz gates, and 44 2-qubit ZZMax gates. on the second qubit is required. Substituting the gate parameters for 90° torsion as an example and compiling to the H-series gate set,31 this circuit can be represented using 61 PhasedX gates, 4 Rz gates, and 44 2-qubit ZZMax gates. | ||
Fig. 2 and 3 show the VQE ansatz circuits of 4 ON configurations (Eq. (18)), built using the SSP and GR methods. Depending on the optimized VQE parameters 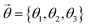 , this ansatz spans both singlet and triplet eigenstates (with spin number restricted to sz = 0). For example, at torsion angle = 0°, optimization of
, this ansatz spans both singlet and triplet eigenstates (with spin number restricted to sz = 0). For example, at torsion angle = 0°, optimization of 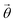 results in (up to global phase) a doubly excited closed shell singlet with negligible contributions from singly excited configurations
results in (up to global phase) a doubly excited closed shell singlet with negligible contributions from singly excited configurations 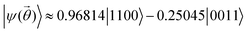 (with |c2|, |c3| < 2 × 10−6). Whereas for torsion angle = 90°, with sz = 0 the ground state is dominated by a superposition of open shell configurations, with small but non-negligible contributions from the closed shell configurations.
(with |c2|, |c3| < 2 × 10−6). Whereas for torsion angle = 90°, with sz = 0 the ground state is dominated by a superposition of open shell configurations, with small but non-negligible contributions from the closed shell configurations. 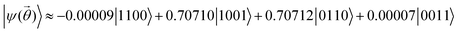 (as all 4 ON configurations have non-negligible weight, this state vector is used as the example for circuit resources reported in the captions of Fig. 2 and 3). We note that following the optimization of all VQE parameters for torsion angles between 0° and 180°, ideal energies
(as all 4 ON configurations have non-negligible weight, this state vector is used as the example for circuit resources reported in the captions of Fig. 2 and 3). We note that following the optimization of all VQE parameters for torsion angles between 0° and 180°, ideal energies 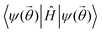 match the lowest eigenvalues obtained from exact diagonalization of Ĥ in the 2-particle sector (see Fig. 4) (and in the absence of device or measurement noise, ideal energies obtained from the GR and SSP methods are identical). Hence, the multiconfigurational state ansatz reproduces the ground state manifold for all torsion angles after VQE optimization.
match the lowest eigenvalues obtained from exact diagonalization of Ĥ in the 2-particle sector (see Fig. 4) (and in the absence of device or measurement noise, ideal energies obtained from the GR and SSP methods are identical). Hence, the multiconfigurational state ansatz reproduces the ground state manifold for all torsion angles after VQE optimization.
 | ||
| Fig. 3 Circuit corresponding to state c1|1100〉 + c2|1001〉 + c3|0110〉 + c4|0011〉 prepared using the SSP method19 (see Section 2.2). Substituting the gate parameters for 90° torsion as an example and compiling to the H-series gate set,31 this circuit can be represented using 10 PhasedX gates, 4 Rz gates, and 5 2-qubit ZZMax gates. | ||
 | ||
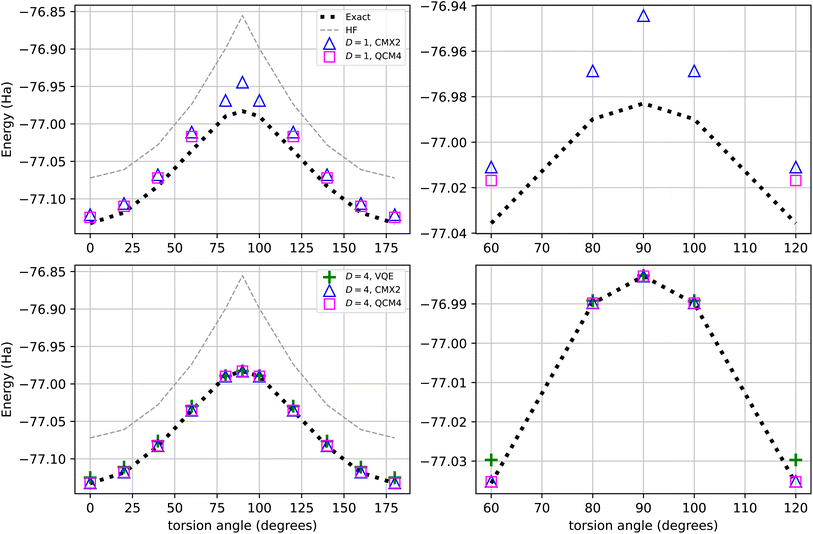
| Fig. 4 Energies obtained from VQE-optimized multiconfigurational states for the 4-qubit (2 electrons in 4 spin orbitals) active space of C2H4. Simulated measurements correspond to 104 shots per circuit, and the Hamiltonian consists of 14 Pauli operators. Top graph: GR method (see Section 2.1). Bottom graph: SSP method (see Section 2.2). C2H4 structure at torsion angles 0°, 90°, and 180° shown above graphs. H11E corresponds to emulations of hardware experiments with a noise model calibrated to the H1 trapped ion device.31 | ||
Emulations of quantum hardware experiments use a noise model calibrated to the H1 trapped ion quantum computer,31 labeled as “H11E”. As shown in Fig. 4, quantum computations of the expectation value are subject to greater amounts of noise for the GR method due to the larger circuits (compare circuit resources reported in Fig. 2 and 3), related to the decompositions of particle-conserving GRs1,3 in addition to the external control (for 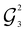 ) required for this case. Despite the negligible coefficients of singly excited configurations for some torsion angles ≠90°, we retain all 4 ON configurations in the circuit state vector for all torsion angles for ease of comparison. However, we note that shorter circuits (which represent only 2 ON configurations) for some torsion angles (at this active space) will likely lead to similar ideal energies.
) required for this case. Despite the negligible coefficients of singly excited configurations for some torsion angles ≠90°, we retain all 4 ON configurations in the circuit state vector for all torsion angles for ease of comparison. However, we note that shorter circuits (which represent only 2 ON configurations) for some torsion angles (at this active space) will likely lead to similar ideal energies.
Despite the smaller circuits produced by SSP for the same state, and hence its lower susceptibility to device errors, the GR method does exhibit a conceptual advantage over SSP, which can be particularly useful when interpreting a variational state in a chemical context: when all gate angles of a circuit produced by the GR method are 0, the state vector falls back to the first ON configuration of the input set (x1 in (x1, …, xD)). If x1 is chosen to be the HF state, then the GR unitaries added to this circuit can be readily interpreted as excitations on top of the HF reference. This is not necessarily the case for the SSP method, whose  state is non-trivial to predict as it depends on the distribution of binary values throughout the set of input ON configuration bit strings.19 Hence, the reference state for chemical excitations is not necessarily accessible as the
state is non-trivial to predict as it depends on the distribution of binary values throughout the set of input ON configuration bit strings.19 Hence, the reference state for chemical excitations is not necessarily accessible as the  state of SSP method. This issue can be exacerbated in variational optimizations of the gate angles, which can terminate in local minima at small gate angles: for the SSP method this local minimum state can be unpredictable, whereas for the GR method it is likely close or equal to the HF state. For the small VQE applications presented here, this issue can be bypassed by random initialization of SSP parameters (avoiding
state of SSP method. This issue can be exacerbated in variational optimizations of the gate angles, which can terminate in local minima at small gate angles: for the SSP method this local minimum state can be unpredictable, whereas for the GR method it is likely close or equal to the HF state. For the small VQE applications presented here, this issue can be bypassed by random initialization of SSP parameters (avoiding  initialization). However, difficulties may arise in larger systems with more complicated parameter landscapes.
initialization). However, difficulties may arise in larger systems with more complicated parameter landscapes.
| Torsion angle (°) | c 1|x1〉 | c 2|x2〉 | c 3|x3〉 | c 4|x4〉 | PhasedX | R z | ZZMax |
|---|---|---|---|---|---|---|---|
| 0/180 | 0.9690|11110000〉 | −0.2345|11001100〉 | 0.0546|10011001〉 | 0.0547|01100110〉 | 174 (22) | 7 (6) | 128 (17) |
| 20/160 | 0.9683|11110000〉 | −0.2380|11001100〉 | 0.0533|10011001〉 | 0.0534|01100110〉 | 174 (22) | 7 (6) | 128 (17) |
| 40/140 | 0.9617|11110000〉 | −0.2648|11001100〉 | 0.0503|10011001〉 | 0.0503|01100110〉 | 174 (22) | 7 (6) | 128 (17) |
| 60/120 | 0.9354|11110000〉 | −0.3481|11001100〉 | 0.0441|10011001〉 | 0.0441|01100110〉 | 174 (22) | 7 (6) | 128 (17) |
| 80/100 | 0.8281|11110000〉 | −0.5522|11001100〉 | −0.0681|10011100〉 | 0.0681|01101100〉 | 66 (18) | 4 (3) | 40 (13) |
| 90 | 0.7044|11100100〉 | 0.7044|11011000〉 | 0.0615|10110100〉 | 0.0615|01111000〉 | 52 (16) | 4 (3) | 32 (11) |
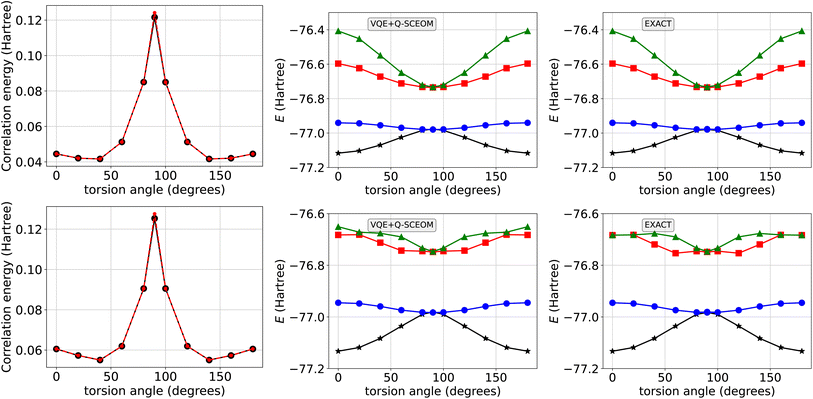
The multiconfigurational states from Table 1 are then used as initial states for the QCM4 and CMX2 methods, with energies obtained from expectation values of Hamiltonian moments. Ideal results (noiseless and infinite shot limit) are shown in Fig. 5. We first note that for torsion angles of 0° to 60° and 120°–180° (representing relatively weak electronic correlation), the ideal energy values are reasonably accurate for the D = 1 HF input state, and highly accurate for the D = 4 multiconfigurational states.
At torsion angles near the transition point (80°, 90°, 100°, strongly correlated as the singlet and triplet eigenstates become quasi-degenerate) we find that the D = 1 closed shell HF input state results in numerically very small cumulants 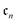 , leading to the term
, leading to the term 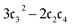 approaching 0 or negative and an ill-defined QCM4 formula when taking the square root (see eqn (7)). Noting that the original derivation assumed the condition,
approaching 0 or negative and an ill-defined QCM4 formula when taking the square root (see eqn (7)). Noting that the original derivation assumed the condition,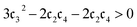 ,37 we omit the QCM4 energies from these angles for D = 1 (also considering that the closed shell HF state insufficiently represents the strongly correlated ground state, leading to a poor description of the correlation represented by the moment expectation values). However, for the D = 4 multiconfigurational states, both the QCM4 and CMX2 calculations recover the exact lowest energies for all torsion angles. This shows the benefit of multiconfigurational input states for methods involving connected moments, as not only does the QCM4 formula avoid the issue of negative
,37 we omit the QCM4 energies from these angles for D = 1 (also considering that the closed shell HF state insufficiently represents the strongly correlated ground state, leading to a poor description of the correlation represented by the moment expectation values). However, for the D = 4 multiconfigurational states, both the QCM4 and CMX2 calculations recover the exact lowest energies for all torsion angles. This shows the benefit of multiconfigurational input states for methods involving connected moments, as not only does the QCM4 formula avoid the issue of negative 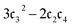 (we assume due to a higher quality input state), but the lower order theory (CMX2) can obtain a similar accuracy, hence necessitating a lower order of moments and ultimately less Pauli strings to measure. The latter point is further emphasized by considering that the VQE energies at torsion angle near 90° are < 1mHa above the exact values; at these geometries the expectation of Ĥ with respect to the multiconfigurational state already captures most of the electronic correlation, obviating the need for higher order moments with a small overhead in circuit depth (see circuit resources reported in Table 1).
(we assume due to a higher quality input state), but the lower order theory (CMX2) can obtain a similar accuracy, hence necessitating a lower order of moments and ultimately less Pauli strings to measure. The latter point is further emphasized by considering that the VQE energies at torsion angle near 90° are < 1mHa above the exact values; at these geometries the expectation of Ĥ with respect to the multiconfigurational state already captures most of the electronic correlation, obviating the need for higher order moments with a small overhead in circuit depth (see circuit resources reported in Table 1).
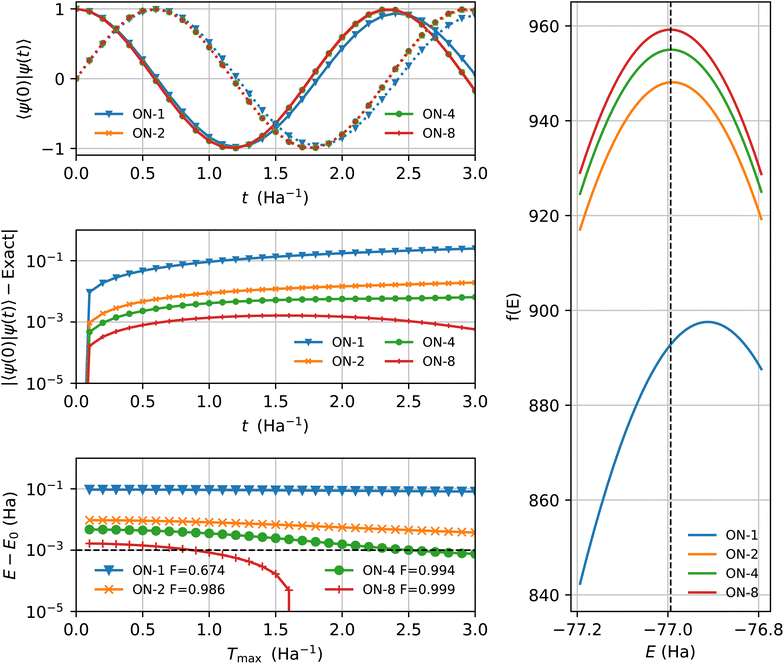
Fig. 6 summarizes the simulations. The top panel shows the complex time series Z(tn) (real and imaginary parts) for each initial state. All curves except the HF case lie almost on top of each other. The middle panel plots the relative error with respect to the exact value, e−itn〈ψ0|H|ψ0〉. We chose τ = 0.1 Ha−1 and N = 31, giving a total evolution time Tmax = (N – 1)τ, long enough to capture at least one full period of the exact Z(t). The right panel displays the QCELS objective, whose maximum was located with the BFGS method. Finally, the bottom-left panel shows the energy errors obtained by repeating the simulations with smaller Tmax while keeping N = 31, effectively choosing a smaller time step. The energies derived from the initial states |ϕON-1〉 and |ϕON-2〉 do not reach the typical target precision ε = 1mHa within the time window, even at the largest Tmax, whereas those from |ϕON-4〉 and especially |ϕON-8〉 do, and importantly, the latter hits the target precision at approximately half the evolution time.
Because the depth of the circuit representation of e−itH scales linearly with t, compact, high fidelity state representation can save significant amount of gate operations by reducing the evolution time. Preparing |ϕON-4〉 via the SSP requires 13 two-qubit gates, while |ϕON-8〉 needs 40. Although the state preparation thus costs 27 additional 2-qubit gates, the shorter evolution time is expected to result a net saving well beyond the 27 gates.
3.2 Excited states of C2H4
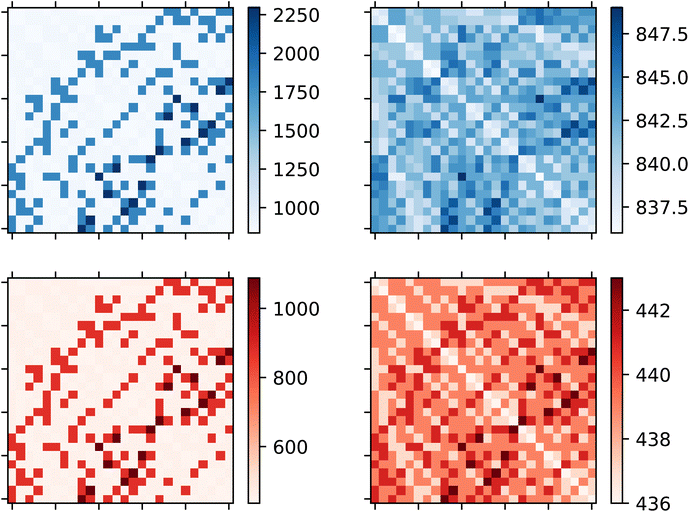
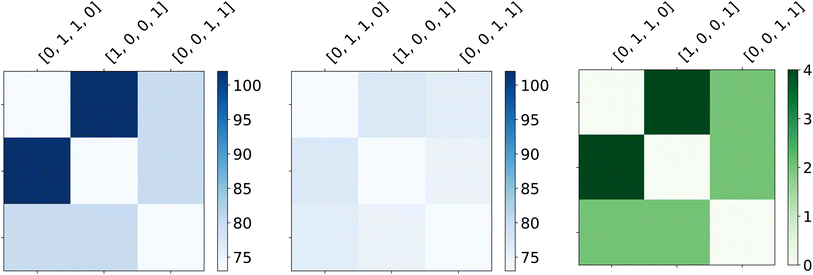
Consequently, we look at the excited states of C2H4 using the Q-SCEOM method. The UCCSD ansatz, optimized by VQE for the ground state, was used for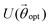 in eqn (14). We also used particle and spin conserving singles and doubles excitation operators. We compare the efficiency of the GR and SSP methods for the construction of the off-diagonal elements of the M matrix (see Sec. 2.3.4 for details). In Fig. 7 we present the total number of gates (upper panel) and the total number of 2-qubit gates (lower panel) (the circuits were compiled with the H-series emulator) for each element of the M matrix for the C2H4 molecule using the 8-qubit active space with torsion angle of 90°. More specifically, the circuits correspond to
in eqn (14). We also used particle and spin conserving singles and doubles excitation operators. We compare the efficiency of the GR and SSP methods for the construction of the off-diagonal elements of the M matrix (see Sec. 2.3.4 for details). In Fig. 7 we present the total number of gates (upper panel) and the total number of 2-qubit gates (lower panel) (the circuits were compiled with the H-series emulator) for each element of the M matrix for the C2H4 molecule using the 8-qubit active space with torsion angle of 90°. More specifically, the circuits correspond to 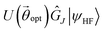 for the diagonal elements and
for the diagonal elements and 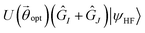 for the off-diagonal elements. There are 26 excitation particle and spin conserving operators. Therefore the M matrix consists of 676 elements. Only the diagonal and the upper-half part of the matrix were calculated since M is a symmetric matrix. The GR method was used for the plots in the left side while the SSP method was used for plots in the right side. It is evident that the SSP method reduces significantly the number of gates. This is in accordance to results presented in Section 3.1 for the calculation of ground state energies. We note here that in the case of the GR method, the structure of the matrices shown in Fig. 7 is directly analogous to the Hamming distance of the associated states to be combined. In particular, the improvement of the SSP method over the GR method becomes greater for values of the Hamming distance larger than 4, for which the GR method requires the construction exemplified in Fig. 12. (see Section A.2 in the Appendix for more details).
for the off-diagonal elements. There are 26 excitation particle and spin conserving operators. Therefore the M matrix consists of 676 elements. Only the diagonal and the upper-half part of the matrix were calculated since M is a symmetric matrix. The GR method was used for the plots in the left side while the SSP method was used for plots in the right side. It is evident that the SSP method reduces significantly the number of gates. This is in accordance to results presented in Section 3.1 for the calculation of ground state energies. We note here that in the case of the GR method, the structure of the matrices shown in Fig. 7 is directly analogous to the Hamming distance of the associated states to be combined. In particular, the improvement of the SSP method over the GR method becomes greater for values of the Hamming distance larger than 4, for which the GR method requires the construction exemplified in Fig. 12. (see Section A.2 in the Appendix for more details).
Additionally, the gate decompositions of the multiconfiguration states for Hamming distances ≤4 also contribute to the reduced circuit sizes obtained from the SSP for the M matrix elements. This is exemplified in Fig. 8, where the GR and SSP circuits are shown for the construction of the |ψI+J〉 state for the M20 element for the Q-SCEOM calculation of the 8-qubit C2H4 at 90° torsion. We observe that 3 2-qubit entangling gates are needed for the SSP method, whereas the GR method requires 14 (see also Fig. 10).
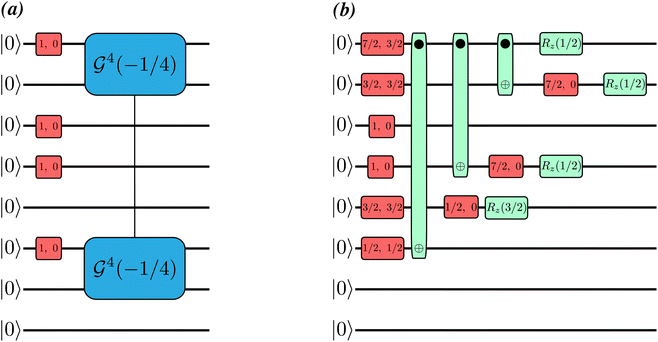 | ||
Fig. 8 Circuits to construct the multiconfigurational state |(Ĝ2 + Ĝ0)|ψHF〉 for the M20 element. Green vertical bars represent the ZZMax 2-qubit entangling gate, while red horizontal bars represent PhasedX(α, β) = Rz(β)Rx(α)Rz(−β) 1-qubit rotations.31 The circuits represent (up to global phase) the state 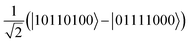 . All gate angles are in units of π. (a) GR method, for which the . All gate angles are in units of π. (a) GR method, for which the 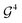 rotation decomposes into 14 ZZMax gates (see bottom panel of Fig. 10 for the representation of rotation decomposes into 14 ZZMax gates (see bottom panel of Fig. 10 for the representation of 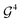 in the H-series gate set). (b) SSP method, containing only 3 ZZMax gates. in the H-series gate set). (b) SSP method, containing only 3 ZZMax gates. | ||
Next, we look at the ground state and excited energies of C2H4 at various torsion angles. We present in Fig. 9 the results for the 4-qubit and 8-qubit case in the upper and lower parts, respectively. In the left panel we plot in red the correlation energy of the ground state energy as the absolute difference of the HF energy with respect to the exact result (first eigenvalue obtained with diagonalization of the Hamiltonian). As expected, the degree of correlation increases as we approach the 90° torsion. We also plot in black the absolute difference of the HF energy with respect to the VQE result obtained through optimization of the UCCSD ansatz. It is evident that at 90° torsion angle, VQE yields a higher energy compared to the exact result. We attribute this to the fact that the VQE optimization results in an unstable singlet state whereas the stable solution is a triplet, as discussed in Section 3.1. Note here, that for all the VQE calculations reported in this section, prior to the calculation of the M matrix, we limited our search to open-shell singlet states. Consequently, we plot in the middle panel the VQE result for the ground state energy and the energy of the first three excited states obtained with Q-SCEOM. We employed the SSP method for the construction of the off-diagonal elements of the M matrix for C2H4 at various torsion angles. We compare the Q-SCEOM results to the eigenvalues obtained through diagonalization of the Hamiltonian. For both active spaces, Q-SCEOM reproduces qualitatively the exact result. Interestingly, at the 90° angle, Q-SCEOM recovers the correct total energy (which matches the exact result) even though VQE (which affects the Q-SCEOM result through the optimized ansatz that is used for the calculation of the M matrix) yields a higher energy.
4 Discussion
In this work, quantum circuit preparation of multiconfigurational states for quantum chemistry has been demonstrated and compared as the state preparation step for a range of applications, including ground state energy calculations using VQE, QCM, and QPE, as well as excited state energies calculated using Q-SCEOM. The use-case to demonstrate these techniques is twisted C2H4, whose energy surface passes through a strongly correlated point as a function of torsion angle.Multiconfigurational state preparation allows initial states that are more accurate than the single configuration HF state, which for QCM can facilitate a reduction in measurement overhead at a relatively small cost of extra circuit depth for the initial state, whereas for QPE the probability of accurately measuring the phase can be increased by a multiconfigurational initial state (relative to HF) since this probability is proportional to the overlap between the initial state and true ground state.58 For Q-SCEOM, the off-diagonal elements of the M matrix can be generated using multiconfigurational state preparation, hence the latter facilitates a framework for automatically building and running the Q-SCEOM algorithm for a given molecule.
Overall, we observe significantly more efficient circuits using the SSP method compared to the GR method. This is largely due to the utilization of the sparsity of chemical states that can be exploited by the SSP, in addition to the gate decomposition of particle-conserving GRs and their required external controls leading to larger gate and depth overheads for the GR method. A conceptual advantage of the GR method can be seen when considering the state preparation as transformations of a reference state; setting the rotation angle of all GRs to 0 is guaranteed to result in the state |x1〉 where x1 is the first ON configuration in the ordered input set. Since x1 can be chosen from HF, each GR can be considered as an excitation of the HF reference, preserving familiar notions from classical computational chemistry. In the context of variational searches of the ground state energy, this property of the GR method prevents unpredictable local minima at small values of variational parameters (which the SSP method can be susceptible to), and may be beneficial for analyzing contributions of specific basis states to the total electronic correlation.
In terms of future applications, our implementation easily allows for the composition of different ansatz circuit structures. For example, appending generalized59 UCC unitaries to a multiconfigurational state circuit prepared using the GR or SSP methods provides a framework for multireference methods60 at the quantum circuit level, such as multireference UCC. We also note a recent work that extended the reference state error mitigation scheme61 to multireference states62 using GRs. An interesting future direction would be to apply the SSP method to prepare the multireference states used for error mitigation, with the potential of significant reduction in circuit resources.
In addition, since multiconfigurational state preparation as presented here can be seen as an approach of loading classical (chemical) data to a quantum processor and preparing a quantum state to represent this data, this could be compared to preparation of multi-determinant states using quantum read-only memory (QROM),63 or to sparse state preparation using quantum random access memory.18 We note that while these techniques achieve a similar asymptotic scaling to the SSP method in the number of 2-qubit gates (O(Dnq), our implementation of multiconfigurational state preparation does not require controlled operations between auxiliary qubits and state qubits. We also note a recent work64 that utilizes QROM to reduce the Toffoli count for matrix product state preparation.
In conclusion, this work provides a framework for preparing quantum circuit representations of multiconfigurational states, as implemented in InQuanto.26–28 Overall, the impact of this work can be summarized by the following points.
(i) We provide a novel implementation for the use of externally controlled GRs for multiconfigurational state preparation, which automatically finds the required external controls of GRs for a given ordered set of ON configurations.
(ii) While the SSP algorithm was published in a previous article,19 this work demonstrates novel applications of the SSP method for a range of algorithms currently proposed for studying the ground and excited states of molecules quantum computationally, i.e. VQE, QCM4, QPE, and Q-SCEOM.
(iii) Specific to the application of the SSP method to VQE, our implementation allows for the use of SSP to generate a variational ansatz, in which the lowest energy state vector can be obtained by optimizing the angles of the 1-qubit unitaries within the SSP circuit.
The utility of multiconfigurational initial states is shown for various quantum computational approaches to quantum chemistry. In particular, when the state to be prepared exhibits sparsity in the sense of D ≪ 2nq, very efficient circuit representations can be achieved, therefore boosting the accuracy of QPE, for example, or reducing the measurement overhead of quantum subspace methods, without a large overhead in circuit depth. In addition, multiconfigurational state preparation is useful for enabling certain methods (such as Q-SCEOM) which require circuit constructions of selected excitations of a reference state, thus enhancing the tool set for quantum approaches to ground and excited states of molecules.
Author contributions
All authors contributed to the conceptualization of the work. G. G. D, G. P., and D. Z. M. contributed to the implementation of methods and analysis of results. All authors contributed to the manuscript.Conflicts of interest
The authors declare no conflict of interest.Note added after first publication
This article replaces the version published on 12th December 2025, which contained a typographical error in the set of basis states where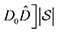 should have been
should have been  as well as inconsistent italicisation of eqn (10)–(12).
as well as inconsistent italicisation of eqn (10)–(12).
Data availability
The data and binary version of the software supporting the conclusions of this paper are available from the corresponding author upon request. Any provision of the software or data is at the discretion of the providing company. A trial version of InQuanto is available at https://www.quantinuum.com/products-solutions/inquanto-trial. InQuanto version 5.0 (https://inquanto.quantinuum.com/index.html) is used in this work. Pseudocode for the GR method is presented in this article (see Algorithms 1 and 2). See also pseudocode for the SSP method reported in the original paper by Gleinig and Hoefler (https://doi.org/10.1109/DAC18074.2021.9586240). A repository is available that contains representative starting datasets and notebooks to allow similar conclusions to be drawn to those of the manuscript based on the workflow in the notebooks and self-written replacements for calls to proprietary code (https://doi.org/10.5281/zenodo.17466867).A Appendices
A.1 Circuit decompositions for GR method
In Fig. 10 we show the gate decompositions of the 1-body and 2-body
and 2-body 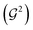 rotations. Compared to the corresponding circuits shown in previous work,3 we observe a similar number of 2-qubit entangling gates (ZZMax31 here and CNOTs in Arrazola et al.3). The Hadamard gates of the decompositions shown in3 are absorbed into the PhasedX(α, β) = Rz(β)Rx(α)Rz(−β)31 1-qubit rotations, and additional Rz and PhasedX rotations are required to achieve a 2-qubit operation equivalent to a CNOT, resulting in differences in the total number of 1-qubit gates. For completeness, the action of the 2-qubit ZZMax is depicted in Fig. 11 in terms of CNOTs and Rz.
rotations. Compared to the corresponding circuits shown in previous work,3 we observe a similar number of 2-qubit entangling gates (ZZMax31 here and CNOTs in Arrazola et al.3). The Hadamard gates of the decompositions shown in3 are absorbed into the PhasedX(α, β) = Rz(β)Rx(α)Rz(−β)31 1-qubit rotations, and additional Rz and PhasedX rotations are required to achieve a 2-qubit operation equivalent to a CNOT, resulting in differences in the total number of 1-qubit gates. For completeness, the action of the 2-qubit ZZMax is depicted in Fig. 11 in terms of CNOTs and Rz.
 | ||
Fig. 10 Circuits for 1-body (2-qubit) 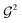 and 2-body (4-qubit) and 2-body (4-qubit) 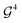 rotations, where state vectors are obtained up to global phase. Green vertical bars represent the ZZMax 2-qubit entangling gate, while red horizontal bars represent PhasedX(α, β) = Rz(β)Rx(α)Rz(−β) 1-qubit rotations.31 All gate angles are in units of π. Subscripts on rotations, where state vectors are obtained up to global phase. Green vertical bars represent the ZZMax 2-qubit entangling gate, while red horizontal bars represent PhasedX(α, β) = Rz(β)Rx(α)Rz(−β) 1-qubit rotations.31 All gate angles are in units of π. Subscripts on  and and  are omitted. are omitted. | ||
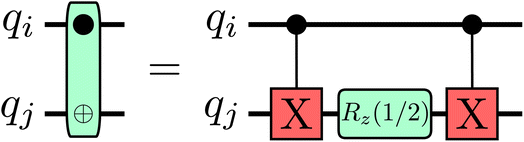 | ||
| Fig. 11 The 2-qubit entangling gate ZZMax31 in terms of CNOT and Rz gates. The equality is up to global phase. Gate angles are in units of π. | ||
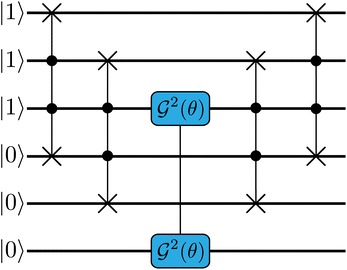 | ||
Fig. 12 Circuit to perform a (λ = 3)-body excitation of the ON configuration |111000〉, yielding cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|111000〉 + sin θ|111000〉 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|000111〉, where θ is in units of π. The subscript e in θ|000111〉, where θ is in units of π. The subscript e in 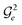 is omitted in the figure. See top panel of Fig. 10 for the decomposition of the central is omitted in the figure. See top panel of Fig. 10 for the decomposition of the central 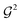 in the H-series gate set.31 in the H-series gate set.31 | ||
This section also describes our scheme to build the excitation gadget that connects basis states separated by 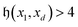 Hamming distance (λ > 2 – body excitation), when preparing the multiconfigurational state using the GR method. Unlike Fig. 5 of in Arrazola et al.,3 here each SWAP is not controlled on all other qubits in the circuit, but only on “minority” qubits, i.e. those qubits with minority binary values (see qminor in Algorithm 2). This results in lower overhead of external controls that scale with the number of minority qubits nminor rather than nq as in Arrazola et al.3 However, this leads to the possibility that (i) the control states (conditions of the external control) of a SWAP are matched by the qubits of one of the previous basis states, or (ii) a swapped version of the first basis state
Hamming distance (λ > 2 – body excitation), when preparing the multiconfigurational state using the GR method. Unlike Fig. 5 of in Arrazola et al.,3 here each SWAP is not controlled on all other qubits in the circuit, but only on “minority” qubits, i.e. those qubits with minority binary values (see qminor in Algorithm 2). This results in lower overhead of external controls that scale with the number of minority qubits nminor rather than nq as in Arrazola et al.3 However, this leads to the possibility that (i) the control states (conditions of the external control) of a SWAP are matched by the qubits of one of the previous basis states, or (ii) a swapped version of the first basis state 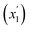 becomes equal to one of the previous basis states (note that qubits of
becomes equal to one of the previous basis states (note that qubits of  at a given iteration of the WHILE loop lines 5–13 of Algorithm 2 form the control states for the next iteration). If (i) or (ii) occurs, it is not necessarily a problem once the central
at a given iteration of the WHILE loop lines 5–13 of Algorithm 2 form the control states for the next iteration). If (i) or (ii) occurs, it is not necessarily a problem once the central  is also controlled on the minority qubits of (“fully swapped”)
is also controlled on the minority qubits of (“fully swapped”)  . The latter implies that the external controls of the central
. The latter implies that the external controls of the central  also scale with nminor, while a cheaper alternative would be to use the usual
also scale with nminor, while a cheaper alternative would be to use the usual 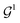 controls from Algorithm 1. However, in order for the external controls found by Algorithm 1 to be usable for the central
controls from Algorithm 1. However, in order for the external controls found by Algorithm 1 to be usable for the central  of the λ > 2 excitation gadget, we find that both (i) and (ii) must not occur.
of the λ > 2 excitation gadget, we find that both (i) and (ii) must not occur.
A.2 Circuit resources and hamming distances for the M matrix in Q-SCEOM
In this section, we plot the Hamming distances between the |ψI+J〉 and |ψHF〉 states, used to build the M matrix for Q-SCEOM. The Hamming distances have a significant impact on the circuit resources used for each element of the M matrix, particularly for the GR method. Fig. 13 corresponds to the 4-qubit active space, where the left and middle panels show the total number of gates for the GR and SSP methods, respectively, while the right panel shows the Hamming distances. Fig. 14 shows the Hamming distances for the 8-qubit active space. | ||
| Fig. 14 Hamming distance between the I, J states that are combined to construct the |ψI + ψJ〉 states for C2H4 using the 8-qubit active space. | ||
A.3 Plots of orbitals
In this section we plot the spatial orbitals used in the active spaces of C2H4, shown in Fig. 15. | ||
| Fig. 15 UHF spatial orbitals of C2H4 at 0° torsion angle that were used for the construction of the active spaces. The HOMO and LUMO shown in (a) were used for the 4-qubit case. The 8-qubit case was augmented with the orbitals shown in (b) and the 12-qubit case used all six orbitals shown in the figure. Occupied and virtual orbitals are shown in the upper and lower part respectively. The isosurface level was set to 0.02. PySCF53 was used for the HF calculation. | ||
Acknowledgements
We thank Alec Owens and Carlo Gaggioli for helpful feedback and comments. We also acknowledge Josh J. M. Kirsopp and Iakov Polyak for useful discussions.References
- G.-L. R. Anselmetti, D. Wierichs, C. Gogolin and R. M. Parrish, New J. Phys., 2021, 23, 113010 CrossRef.
- C. H. Chee, D. Leykam, A. M. Mak and D. G. Angelakis, Shallow quantum circuits for efficient preparation of Slater determinants and correlated states on a quantum computer, 2023, arXiv:2301.07477, DOI:10.48550/arXiv.2301.07477.
- J. M. Arrazola, O. D. Matteo, N. Quesada, S. Jahangiri, A. Delgado and N. Killoran, Quantum, 2022, 6, 742 CrossRef.
- S. Fomichev, K. Hejazi, M. S. Zini, M. Kiser, J. F. Morales, P. A. M. Casares, A. Delgado, J. Huh, A.-C. Voigt, J. E. Mueller and J. M. Arrazola, Initial state preparation for quantum chemistry on quantum computers, 2024, arXiv:2310.18410, DOI:10.48550/arXiv.2310.18410.
- Y. S. Yordanov, D. R. M. Arvidsson-Shukur and C. H. W. Barnes, Phys. Rev. A, 2020, 102, 062612 CrossRef.
- Y. S. Yordanov, V. Armaos, C. H. W. Barnes and D. R. M. Arvidsson-Shukur, Commun. Phys., 2021, 4, 228 CrossRef.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth and J. Tennyson, Phys. Rep., 2022, 986, 1–128 CrossRef.
- I. G. Ryabinkin, T.-C. Yen, S. N. Genin and A. F. Izmaylov, J. Chem. Theory Comput., 2018, 14, 6317 CrossRef PubMed.
- F. A. Evangelista, G. K.-L. Chan and G. E. Scuseria, J. Chem. Phys., 2019, 151, 244112 CrossRef PubMed.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, ACS Cent. Sci., 2019, 5, 167 CrossRef PubMed.
- H. R. Grimsley, D. Claudino, S. E. Economou, E. Barnes and N. J. Mayhall, J. Chem. Theory Comput., 2020, 16, 1–6 CrossRef PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- L. Grover and T. Rudolph, Creating superpositions that correspond to efficiently integrable probability distributions, 2002, arXiv:0208112, DOI:10.48550/arXiv.0208112.
- M. Möttönen, J. J. Vartiainen, V. Begholm and M. M. Salomaa, Quantum Inf. Comput., 2005, 5, 467–473 Search PubMed.
- V. Shende, S. Bullock and I. Markov, IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, vol. 25, pp. 1000–1010 Search PubMed.
- I. F. Araujo, D. K. Park, F. Petruccione and A. J. da Silva, Sci. Rep., 2021, 11, 6329 CrossRef PubMed.
- X.-M. Zhang, T. Li and X. Yuan, Phys. Rev. Lett., 2022, 129, 230504 Search PubMed.
- T. M. L. de Veras, L. D. da Silva and A. J. da Silva, Quantum Inf. Process., 2022, 21, 204 CrossRef.
- N. Gleinig and T. Hoefler, 58th ACM/IEEE Design Automation Conference (DAC), 2021, pp. 433–438 Search PubMed.
- M. Plesch and i. c. v. Brukner, Phys. Rev. A, 2011, 83, 032302 CrossRef.
- P. Niemann, R. Datta and R. Wille, IEEE 46th International Symposium on Multiple-Valued Logic (ISMVL), 2016, pp. 247–252 Search PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, in Second Quantization, John Wiley & Sons, Ltd, 2000, pp. 1–33 Search PubMed.
- J. Li, M. Otten, A. A. Holmes, S. Sharma and C. J. Umrigar, J. Chem. Phys., 2018, 149, 214110 CrossRef PubMed.
- M. Dash, S. Moroni, A. Scemama and C. Filippi, J. Chem. Theory Comput., 2018, 14, 4176–4182 CrossRef CAS PubMed.
- C. Feniou, O. Adjoua, B. Claudon, J. Zylberman, E. Giner and J.-P. Piquemal, J. Phys. Chem. Lett., 2024, 15, 3197–3205 Search PubMed.
- A. Tranter, C. Di Paola, D. Muñoz Ramo, D. Z. Manrique, D. Gowland, E. Plekhanov, G. Greene-Diniz, G. Christopoulou, G. Prokopiou, H. D. J. Keen, I. Polyak, I. T. Khan, J. Pilipczuk, J. J. M. Kirsopp, K. Yamamoto, M. Tudorovskaya, M. Krompiec, M. Sze, N. Fitzpatrick, R. J. Anderson and V. Bhasker, InQuanto: Quantum Computational Chemistry, 2022, https://www.quantinuum.com/products-solutions/inquanto Search PubMed.
- A. Tranter, C. Di Paola, D. Muñoz Ramo, D. Z. Manrique, D. Gowland, E. Plekhanov, G. Greene-Diniz, G. Christopoulou, G. Prokopiou, H. D. J. Keen, I. Polyak, I. T. Khan, J. Pilipczuk, J. J. M. Kirsopp, K. Yamamoto, K. Sorathia, M. Tudorovskaya, M. Krompiec, M. Sze, N. Fitzpatrick, O. Backhouse, R. J. Anderson and V. Bhasker, Introduction to the InQuanto Computational Chemistry Platform For Quantum Computers, 2022 Search PubMed.
- A. Tranter, C. Di Paola, D. Muñoz Ramo, D. Z. Manrique, D. Gowland, E. Plekhanov, G. Greene-Diniz, G. Christopoulou, G. Prokopiou, H. D. J. Keen, I. Polyak, I. T. Khan, J. Pilipczuk, J. J. M. Kirsopp, K. Yamamoto, K. Sorathia, M. Tudorovskaya, M. Krompiec, M. Sze, N. Fitzpatrick, O. Backhouse, R. J. Anderson and V. Bhasker, InQuanto User Guide, 2024, https://inquanto.quantinuum.com/index.html Search PubMed.
- P. Jordan and E. Wigner, Z. Phys., 1928, 47, 631–651 Search PubMed.
- S. Szalay, Z. Zimborás, M. Máté, G. Barcza, C. Schilling and Ö. Legeza, J. Phys. A: Math. Theor., 2021, 54, 393001 CrossRef CAS.
- Quantinuum H1-1, 2025, https://docs.quantinuum.com/h-series/ Search PubMed.
- G. Greene-Diniz, D. Z. Manrique, K. Yamamoto, E. Plekhanov, N. Fitzpatrick, M. Krompiec, R. Sakuma and D. M. Ramo, Quantum, 2024, 8, 1383 CrossRef.
- G. Greene-Diniz, C. N. Self, M. Krompiec, L. Coopmans, M. Benedetti, D. Muñoz Ramo and M. Rosenkranz, Sci. Rep., 2025, 15, 28409 CrossRef CAS PubMed.
- M. Motta, W. Kirby, I. Liepuoniute, K. J. Sung, J. Cohn, A. Mezzacapo, K. Klymko, N. Nguyen, N. Yoshioka and J. E. Rice, Electron. Struct., 2024, 6, 013001 CrossRef.
- H. J. Vallury, M. A. Jones, C. D. Hill and L. C. L. Hollenberg, Quantum, 2020, 4, 373 CrossRef.
- M. A. Jones, H. J. Vallury, C. D. Hill and L. C. L. Hollenberg, Sci. Rep., 2022, 12, 8985 CrossRef PubMed.
- L. C. L. Hollenberg and N. S. Witte, Phys. Rev. D, 1994, 50, 3382–3386 CrossRef PubMed.
- J. Cioslowski, Phys. Rev. Lett., 1987, 58, 83–85 CrossRef PubMed.
- P. J. Knowles, Chem. Phys. Lett., 1987, 134, 512–518 CrossRef.
- K. Kowalski and B. Peng, J. Chem. Phys., 2020, 153, 201102 CrossRef PubMed.
- D. Claudino, B. Peng, N. P. Bauman, K. Kowalski and T. S. Humble, Quantum Sci. Technol., 2021, 6, 034012 CrossRef.
- D. Horn and M. Weinstein, Phys. Rev. D, 1984, 30, 1256–1270 CrossRef.
- Z. Ding and L. Lin, PRX Quantum, 2023, 4, 020331 CrossRef.
- A. Asthana, A. Kumar, V. Abraham, H. Grimsley, Y. Zhang, L. Cincio, S. Tretiak, P. A. Dub, S. E. Economou, E. Barnes and N. J. Mayhall, Chem. Sci., 2023, 14, 2405–2418 RSC.
- A. Kumar, A. Asthana, V. Abraham, T. D. Crawford, N. J. Mayhall, Y. Zhang, L. Cincio, S. Tretiak and P. A. Dub, J. Chem. Theory Comput., 2023, 19, 9136–9150 CrossRef PubMed.
- M. D. Prasad, S. Pal and D. Mukherjee, Phys. Rev. A, 1985, 31, 1287–1298 CrossRef PubMed.
- B. Datta, D. Mukhopadhyay and D. Mukherjee, Phys. Rev. A, 1993, 47, 3632–3648 CrossRef PubMed.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, P. K. Barkoutsos, A. Mezzacapo, M. Pistoia, S. Sheldon, S. Woerner, J. M. Gambetta and I. Tavernelli, Phys. Rev. Res., 2020, 2, 043140 CrossRef.
- M. Motta, W. Kirby, I. Liepuoniute, K. J. Sung, J. Cohn, A. Mezzacapo, K. Klymko, N. Nguyen, N. Yoshioka and J. E. Rice, Electron. Struct., 2024, 6, 013001 CrossRef.
- P. F. Kwao, S. P. Sundar, B. Gupt and A. Asthana, On the generalized eigenvalue problem in subspace-based excited state methods for quantum computers, 2025, arXiv:2503.09670, DOI:10.48550/arXiv.2503.09670.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- J. R. McClean, Z. Jiang, N. C. Rubin, R. Babbush and H. Neven, Nat. Commun., 2020, 11, 636 CrossRef PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, WIREs Comput. Mol. Sci., 2018, 8, e1340 CrossRef.
- K. Boguslawski and P. Tecmer, Int. J. Quantum Chem., 2015, 115, 1289–1295 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef PubMed.
- S. Sivarajah, S. Dilkes, A. Cowtan, W. Simmons, A. Edgington and R. Duncan, Quantum Sci. Technol., 2020, 6, 014003 CrossRef.
- A. Javadi-Abhari, M. Treinish, K. Krsulich, C. J. Wood, J. Lishman, J. Gacon, S. Martiel, P. D. Nation, L. S. Bishop, A. W. Cross, B. R. Johnson and J. M. Gambetta, Quantum Computing with Qiskit, 2024, arXiv:2405.08810, DOI:10.48550/arXiv.2405.08810.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, 2010 Search PubMed.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2019, 15, 311–324 CrossRef PubMed.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef PubMed.
- P. Lolur, M. Skogh, W. Dobrautz, C. Warren, J. Biznárová, A. Osman, G. Tancredi, G. Wendin, J. Bylander and M. Rahm, J. Chem. Theory Comput., 2023, 19, 783–789 CrossRef PubMed.
- H. Zou, E. Magnusson, H. Brunander, W. Dobrautz and M. Rahm, Multireference error mitigation for quantum computation of chemistry, 2025, arXiv:2505.08291, DOI:10.48550/arXiv.2505.08291.
- N. M. Tubman, C. Mejuto-Zaera, J. M. Epstein, D. Hait, D. S. Levine, W. Huggins, Z. Jiang, J. R. McClean, R. Babbush, M. Head-Gordon and K. B. Whaley, Postponing the orthogonality catastrophe: efficient state preparation for electronic structure simulations on quantum devices, 2018, arXiv:1809.05523, DOI:10.48550/arXiv.1809.05523.
- D. W. Berry, Y. Tong, T. Khattar, A. White, T. I. Kim, G. H. Low, S. Boixo, Z. Ding, L. Lin, S. Lee, G. K.-L. Chan, R. Babbush and N. C. Rubin, PRX Quantum, 2025, 6, 020327 CrossRef.
Footnote |
† This is consistent with 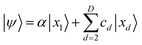 where where 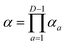 . The sequence of GRs applied to the circuit returns the desired state vector through this recursive mapping of the normalized coefficients, as discussed in Arrazola et al.3 . The sequence of GRs applied to the circuit returns the desired state vector through this recursive mapping of the normalized coefficients, as discussed in Arrazola et al.3 |
| This journal is © The Royal Society of Chemistry 2026 |