Open Access Article
Open Access ArticleExtrapolating beyond C60: advancing prediction of fullerene isomers with FullereneNet
Bin
Liu†
ab,
Jirui
Jin†
ab and
Mingjie
Liu
 *ab
*ab
aDepartment of Chemistry, University of Florida, Gainesville, FL 32611, USA. E-mail: mingjieliu@ufl.edu
bQuantum Theory Project, University of Florida, Gainesville, FL 32611, USA
First published on 11th November 2025
Abstract
Fullerenes, carbon-based nanomaterials with sp2-hybridized carbon atoms arranged in polyhedral cages, exhibit diverse isomeric structures with promising applications in optoelectronics, solar cells, and medicine. However, the vast number of possible fullerene isomers complicates efficient property prediction. In this study, we introduce FullereneNet, a graph neural network-based model that predicts fundamental properties of fullerenes using topological features derived solely from unoptimized structures, eliminating the need for computationally expensive quantum chemistry optimizations. The model leverages topological representations based on the chemical environments of pentagonal and hexagonal rings, enabling efficient capture of local structural details. We show that this approach yields superior performance in predicting the C–C binding energy for a wide range of fullerene sizes, achieving mean absolute errors of 3 meV per atom for C60, 4 meV per atom for C70, and 6 meV per atom for C72–C100, surpassing the values of the state-of-the-art machine learning interatomic potential GAP-20. Additionally, the FullereneNet model accurately predicts 11 other properties, including the HOMO–LUMO gap and solvation free energy, demonstrating robustness and transferability across fullerene types. This work provides a computationally efficient framework for high-throughput screening of fullerene candidates and establishes a foundation for future data-driven studies in fullerene chemistry.
1 Introduction
Fullerenes are carbon-based nanomaterials composed of sp2 hybridized carbons with the general formula C20+2n (n ≥ 0, n ≠ 1).1,2 These carbon atoms form pentagonal and hexagonal rings on the spherical polyhedral cages. The different arrangements of these rings lead to numerous isomeric structures for each fullerene size, with the number of possible isomers increasing at a rate of O(N9) for N = 20 + 2n carbon atoms, resulting in a diverse family of fullerenes.3 Thanks to their unique spherical cage structure and remarkable physicochemical properties, various fullerenes have been synthesized and applied in optoelectronics, solar cells, gas storage and separation, biology, and medicine.4–11 For example, fullerenes—C60, C70, and C84—and their derivatives, which conform to the isolated pentagon rule (IPR) with 12 pentagons separated by hexagons to minimize steric strain and ensure high stability, are used as electron acceptors in organic solar cells.12,13 Pristine non-IPR fullerenes, such as C20 and C36, which are unstable and highly reactive due to their condensed pentagons and increased strain, have been successfully synthesized and isolated.14,15 Additionally, non-IPR fullerenes with endohedral functionalization (encapsulation of metal and/or nonmetal atoms, e.g., Sc2@C66 and Sc3N@C68) or exohedral functionalization (anchoring functional groups on the cage surface, e.g., chlorinated C50Cl10, C60Cl12, and C60Cl8) exhibit unusual electronic, magnetic, and mechanical properties.16–19 So far, only a small portion of fullerenes has been investigated for real-world applications through a laborious trial-and-error approach. To fully harness their capabilities in customizing electronic properties and functionalization for practical uses, it is crucial to accurately and efficiently predict the fundamental properties, including stability, electronic properties, and solubility, for high-throughput screening of potential fullerene candidates. However, the expansive fullerene family—with its range of sizes and numerous isomers for each size (e.g., C84 has 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 isomers)—not only poses significant challenges to mathematical enumeration and topological analysis20 but also surpasses the computational capacity of current high-performance resources for quantum chemistry calculations.
592 isomers)—not only poses significant challenges to mathematical enumeration and topological analysis20 but also surpasses the computational capacity of current high-performance resources for quantum chemistry calculations.
To circumvent this computational bottleneck, early studies explored connections between the graph-theoretical properties of fullerenes and their physical characteristics. Schwerdtfeger et al.’s review21 provides an extensive account of such topological indicators, demonstrating how graph-based indices derived from adjacency matrices can qualitatively predict properties, such as the HOMO–LUMO gap through approaches like Hückel theory, and even anticipate phenomena such as Jahn–Teller distortions. However, these traditional approaches rely heavily on human-derived heuristics and predefined physical approximations, which constrain their predictive power to the limits of established chemical intuition.
Data-driven machine learning (ML) techniques have become powerful tools for predicting properties of fullerenes and their functionalized derivatives. For example, García-Risueño et al.22 trained various conventional ML models to predict the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO), and gap renormalization energies using a dataset of 163 fullerenes and their derivatives, ranging from C28 to C180. They tested numerous variables as input representations, including density functional theory (DFT)-calculated electronic properties, geometric features, phonon features, bond length features, and bond order features. Liu et al.23 trained a SchNet model-based neutral network potential (NNP), which uses molecular coordinates as input representations and a dataset of 120 k non-isomorphic C2nClm chlorofullerene isomers generated from 500 pristine cages of C40, C50, C60, and C70. The NNP achieved a mean absolute error (MAE) of 0.37 eV for relative energy prediction with respect to DFT benchmarks and demonstrated excellent transferability to other exohedral functionalized fullerenes C2nXm (X = H, F, I, Cl, Br, OH, CF3, CH3) across different functional groups, number of addends, and cage sizes. However, previous studies have relied on DFT-calculated features or those derived from DFT-optimized geometry for ML training, which requires significant computational cost, making it unsuitable for high-throughput screening of fullerene candidates. Machine Learning Interatomic Potentials (MLIPs) have also been employed for fullerene systems. Aghajamali and Karton24 applied the Gaussian Approximation Potential (GAP-20)25 force field to investigate the isomerization energies and thermal stabilities of C40 fullerenes, while Karasulu et al.26 used GAP-20 to predict large carbon clusters and search for novel isomers, overcoming the computational limits of first-principles approaches. However, GAP-20 is limited to energy-potential surface prediction and cannot predict other fundamental properties which are crucial for real-world applications, such as molecular orbital levels, HOMO–LUMO gaps, and solubilities. More importantly, employing MLIPs requires geometry optimization to determine ground-state energies, resulting in additional computational costs.
Graph neural networks (GNNs) have gained considerable attention in chemistry due to their exceptional performance in molecular and materials science.27–30 Their effectiveness stems from the ability to represent molecules and materials as graphs, where nodes correspond to atoms and edges to bonds. For example, TensorNet,31 which utilizes Cartesian tensor representations, demonstrates state-of-the-art (SOTA) performance on the small organic molecule dataset QM9.32 MatFormer,33 incorporating a transformer architecture for learning periodic graph representations, is considered a leading GNN model for predicting crystal properties such as formation energy and band gap. However, these models require optimized structures as inputs, since precise structural information is essential for training, significantly increasing computational costs. Moreover, fullerenes, consisting solely of carbon, present unique challenges due to identical node features, complicating the design of effective GNN models for this system. To the best of our knowledge, no existing GNN model can accurately and efficiently predict a wide range of fundamental properties for fullerenes of any size without relying on quantum chemistry-optimized structures as inputs.
In this work, we developed a GNN-based model to predict the fundamental properties of fullerenes using two sets of topological features based on the arrangement of pentagons and hexagons over the cage surface, as proposed in our previous study.34 These topological features rely solely on carbon atom connectivity and can be efficiently extracted from unoptimized geometries, eliminating the need for quantum chemistry-based geometry optimization. Our results show that these features can effectively capture the intricate local structural environments of carbon atoms in fullerene, enabling excellent accuracy and extrapolation capability for predicting the C–C binding energy beyond C60. Notably, our GNN model trained with a C20–C58 dataset achieved MAEs of 3, 4, and 6 meV/atom for test sets C60, C70, and C72–C100, respectively, surpassing the accuracy of the SOTA MLIP GAP-20. More profoundly, with the same topological features as structural representations, our retrained GNN models demonstrated high prediction accuracy for 11 other properties, including the HOMO, LUMO, gap, solvation free energies, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. Our study highlights the superior capability of topological features for predicting various fundamental properties of fullerenes with excellent accuracy and transferability. Our study lays a fundamental basis for future data-driven research in fullerene chemistry.
P. Our study highlights the superior capability of topological features for predicting various fundamental properties of fullerenes with excellent accuracy and transferability. Our study lays a fundamental basis for future data-driven research in fullerene chemistry.
2 Methodology
2.1 Dataset construction
In this study, we constructed three datasets for model training and testing. The C20–C60 dataset, consisting of 5770 structures, was adopted from our previous work.34 This dataset provides a complete set of C20–C60 structures, with properties such as the HOMO–LUMO gap, formation energy, and IP-EA computed using DFT (with the same methods applied in this work). The C70 dataset, comprising 8149 isomers, was generated using the FULLERENE program (version 4.5) and subsequently optimized with a harmonic oscillator approximation-based force field,35 which provides a good compromise between computational efficiency and accuracy in reproducing fullerene geometries. The C72–C100 dataset (except C88) with 1171 IPR-conforming isomers was obtained from the Fullerene Library created by M. Yoshida.36 Tables S1 and S2 list the number of possible isomers, C–C bonds, and hexagonal rings for each fullerene size in each set.2.2 Computational details
We applied the Gaussian 16 package37 for all the DFT calculations. We used the B3LYP hybrid functional38–40 with D3 dispersion correction41 and the 6-31G* basis set for geometry optimization. The maximum force threshold was 0.02 eV Å−1. Then, we conducted a single-point calculation in the singlet state with the B3LYP functional and 6-311G* basis set to compute energies and electronic properties of the isomers. The solvation energies were calculated using the Solvation Model based on Density (SMD).42 The dielectric constants for water and ODCB solvents were set at 78 and 10, respectively.Geometry optimization with the GAP-20 potential was performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package,43 compiled with the Quantum mechanics and Interatomic Potentials (QUIP) library44,45 including GAP routines. Geometry relaxation and energy minimization were conducted with the conjugate gradient method. The convergence criteria were set to 10−4 eV for the total energy and 10−6 eV Å−1 for the atomic forces.
2.3 Feature space construction
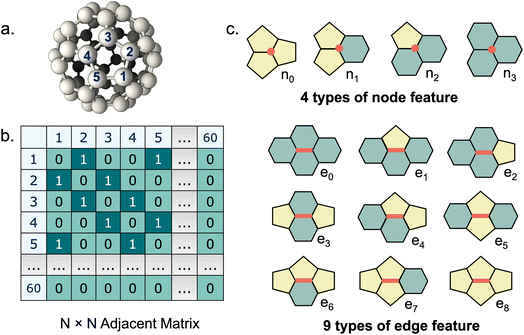
We used atom and bond representations from our previous work34 as node and edge features for GNN model training. In fullerene molecules, each carbon atom is fused to three adjacent polygonal rings, and each C–C bond is surrounded by four polygonal rings, either pentagons or hexagons. Atom features categorize carbon atoms into four types {vi|i = 0, 1, 2, 3}, based on the number of adjacent pentagons (ranging from 0 to 3). The node feature is one-hot encoded with four digits to represent the local geometry of each carbon atom. Similarly, bond features categorize C–C bonds into nine types {ei|i = 0, …, 8}, based on the number and arrangement of the surrounding polygonal rings. The edge feature is one-hot encoded with nine digits to indicate the local geometry of each C–C bond. The detailed atom and bond features are shown in Fig. 1.Beyond the canonical fullerenes studied in this work, our methodology may also be applied to non-canonical fullerenes that include other polygons such as heptagons and octagons. While the present study focused exclusively on canonical fullerenes, we propose an extension of the current methodology to address non-canonical cases (see Section S1), which will be carefully investigated in future work.
2.4 GNN model architecture
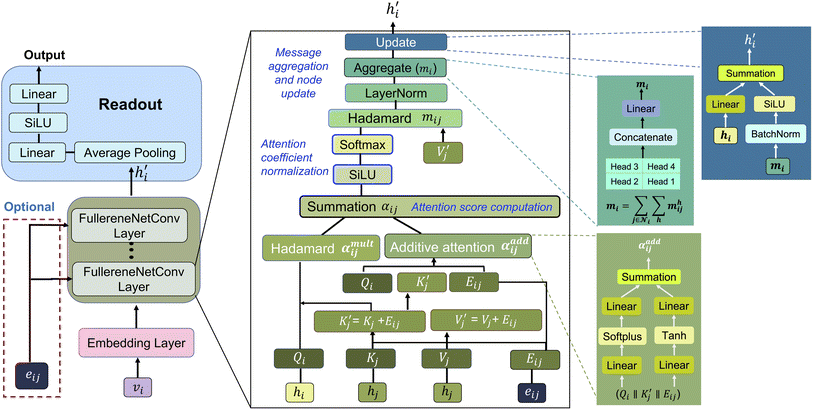
Here, we present our model named FullereneNet, inspired by the transformer-based architecture utilized in MatFormer33 (model details are in Section S2). This model is designed to eliminate the need for quantum mechanical optimization of fullerene structures, as illustrated in Fig. 2. We define the molecular graph as G = (V, E), where V and E represent the set of atoms and bonds in a molecule, respectively. Let vi ∈ V denote the node feature of atom i, and eij ∈ E represent the edge feature between atoms i and its neighbor atom j. The overall model architecture consists of an embedding layer, multiple convolutional layers, and a readout function. The embedding layer projects the atomic feature vi to a higher-dimensional vector, denoted as hi. The convolutional layers are the core of the GNN model, where message passing occurs.46,47 This process is essential for capturing interactions between atoms. The readout function aggregates the updated atomic representations into a molecular-level feature, which is then used for property prediction via a pooling function.Our proposed message passing scheme is composed of three steps: attention score computation, attention coefficient normalization, and message computation with node information updating. In the first step, query Qi, key Kj, and value Vj are calculated following the regular attention mechanism.48 These vectors serve to evaluate how relevant each neighboring node is to the node being updated. By comparing the query of a node with the keys of its neighbors, the model calculates attention scores that determine the influence each neighbor should have. Specifically,
| Qi = LNQ(hi), Kj = LNK(hj), Vj = LNV(hj), and Eij = LNE(eij) | (1) |
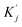 and
and 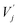 are obtained by summing Kj or Vj with Eij, respectively. Next, we compute the attention score using both additive and multiplicative components. The additive attention computes attention scores by processing the concatenation of Qi,
are obtained by summing Kj or Vj with Eij, respectively. Next, we compute the attention score using both additive and multiplicative components. The additive attention computes attention scores by processing the concatenation of Qi, 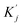 , and Eij through two separate multi-layer perceptrons (MLPs) with different activation functions:
, and Eij through two separate multi-layer perceptrons (MLPs) with different activation functions: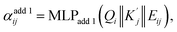 | (2) |
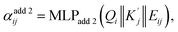 | (3) |
| αaddij = αadd 1ij + αadd 2ij, | (4) |
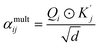 | (5) |
After obtaining the attention score αij, we then move to the second part. A non-linear activation function, such as SiLU, is first applied to the combined attention scores αij. To ensure that the attention coefficients are properly normalized, a softmax function is applied over the neighbors of atom i:
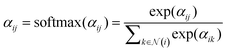 | (6) |
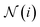 denotes the set of neighbor nodes of atom i.
denotes the set of neighbor nodes of atom i.
Finally, in the third part, messages from neighbors are aggregated and updated to the original atom representations. The messages from neighbors are first computed by weighting the value vectors 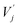 with the attention coefficients αij using the Hadamard product:
with the attention coefficients αij using the Hadamard product:
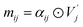 | (7) |
The processed messages are then passed through a layer normalization function. Subsequently, the messages from each node and attention head are aggregated using a summation method:
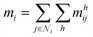 | (8) |
The last step is the node update with a residual connection:
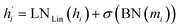 | (9) |
MatFormer introduces an effective transformer variant tailored for crystal graph learning. However, our proposed model, FullereneNet, diverges from MatFormer in terms of feature construction and message passing schemes. While MatFormer leverages elemental diversity to extract a broad range of atomic features, it struggles with fullerenes, which consist solely of carbon and exhibit uniform atomic properties. To overcome this limitation, we design topological atomic features that distinguish pentagon and hexagon arrangements around carbon atoms, effectively capturing structural variations and enhancing representation. Additionally, MatFormer takes a DFT-optimized structure to derive bond distances and angles, whereas FullereneNet, with its bespoke feature design, bypasses the need for geometry optimization via ab initio methods as input, significantly reducing computational costs. Regarding message passing, MatFormer combines multiple information streams through a complex triple concatenation process. In comparison, FullereneNet employs a streamlined method that separately processes atomic interactions through two complementary pathways—one capturing linear relationships and another capturing non-linear relationships between connected atoms. This dual-pathway design eliminates redundant computational steps while better preserving the essential topological information that determines fullerene stability. Given the uniform node degree (i.e., three) in fullerenes, FullereneNet does not encounter the challenge to distinguish nodes with different degrees as MatFormer.33 Instead, it benefits from applying softmax normalization, which enhances training stability and model focus. The hyperparameter search range for FullereneNet is summarized in Table S3.
2.5 Model training strategy for extrapolation
In this study, we aim to develop a GNN model with strong extrapolation capabilities for predicting the stability of larger fullerenes. To achieve this, we trained and validated our model on a dataset of small fullerenes ranging from C20 to C58, including 3958 distinct isomers. Three larger fullerene groups were utilized as test sets: the complete C60 dataset containing 1812 isomers, a C70 dataset consisting of 100 randomly selected non-IPR isomers from a total of 8149 entries, and a C72–C100 dataset comprising 1171 IPR-conforming isomers. The random selection of C70 isomers ensures unbiased sampling across the energy landscape while avoiding the prohibitive computational cost of evaluating all 8149 isomers, while the curated C72–C100 dataset provides validation against established structural benchmarks. Moreover, the inclusion of both IPR and non-IPR fullerenes in the test sets allows us to demonstrate the model's reliable extrapolation capability.Previous studies49,50 have shown that different data-splitting strategies can enhance a model's extrapolation ability. To explore their impact on improving the robustness and effectiveness of extrapolation, we applied four distinct strategies to partition the training and validation sets (Fig. 3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Five GNN models were trained, each using a different random seed.
1 ratio. Five GNN models were trained, each using a different random seed.
The extrapolation performance of each strategy was evaluated by averaging the prediction outcomes of the corresponding five GNN models across the three test sets: the C60, C70, and C72–C100 datasets.
3 Results and discussion
3.1 Stability prediction
We evaluated the extrapolation performance of FullereneNet trained using the four strategies discussed in Section 2.5. The performance metrics for predicting the binding energies of fullerene in three test sets—C60, C70, and C72–C100—are summarized in Table 1. For each strategy, the final prediction value was obtained by averaging the prediction values of the five corresponding GNN models on the test set. As shown in Table 1, all FullereneNet models trained on the C20–C58 dataset, irrespective of the training strategies employed, consistently demonstrate high accuracy in predicting binding energies of the C60, C70, and C72–C100 datasets, as indicated by MAE and root mean squared error (RMSE) values. Notably, these models achieve small MAE values ranging from 3 meV per atom to 7 meV per atom.| Dataset | Method | R 2 | MAE | RMSE |
|---|---|---|---|---|
| C60 | LOGO | 0.988 | 0.003 | 0.004 |
| LOCO | 0.988 | 0.003 | 0.004 | |
| 5-Fold CV | 0.989 | 0.003 | 0.004 | |
| Random split | 0.989 | 0.003 | 0.003 | |
| C70 (non-IPR) | LOGO | 0.969 | 0.004 | 0.005 |
| LOCO | 0.972 | 0.004 | 0.005 | |
| 5-Fold CV | 0.973 | 0.004 | 0.005 | |
| Random split | 0.974 | 0.004 | 0.005 | |
| C72–C100 (IPR) | LOGO | 0.304 | 0.007 | 0.009 |
| LOCO | 0.431 | 0.006 | 0.008 | |
| 5-Fold CV | 0.391 | 0.006 | 0.008 | |
| Random split | 0.563 | 0.005 | 0.007 |
The strong extrapolation capabilities of FullereneNet highlight the effectiveness of atom and bond features as input representations for predicting fullerene's stability. Based on our results, the four different data split strategies did not exhibit a statistically significant difference in their predictive performance for large-sized fullerenes. Furthermore, the prediction error for the C72–C100 test set was consistently larger than that for the other two test sets, regardless of the training strategy employed. For instance, using the random split method, the FullereneNet model achieved a coefficient of determination (R2) of 0.563 and an MAE of 5 meV per atom for C72–C100, compared to 0.989 and 3 meV per atom for C60 and 0.974 and 4 meV per atom for C70. This slightly lower accuracy for the C72–C100 test set can be attributed to the fact that the binding energy distribution of the C72–C100 set is markedly different from that of the training set (C20–C58), as illustrated in Fig. S1.
As detailed in Section 2, FullereneNet incorporates node and edge features extracted from unoptimized fullerene structures as input. In contrast, MatFormer, the predecessor of FullereneNet, relies on atomic attributes such as atomic volume, valence electron count, and bond distances calculated from optimized Cartesian coordinates. However, since fullerene consists exclusively of carbon atoms, these conventional atomic descriptors become uniform across the structure, limiting their discriminative power for property prediction. Herein, we evaluated the performance of MatFormer, trained on the bond distance obtained from atomic coordinates of unoptimized fullerene structures, against FullereneNet in predicting the binding energies of fullerenes ranging from C60 to C100. As shown in Fig. S2, MatFormer performs poorly with unoptimized structures, whereas optimizing fullerene structures significantly improves the prediction accuracy. For example, in the C70 dataset, utilizing optimized structures to train MatFormer increases the R2 value from 0.542 to 0.977 and reduces the MAE from 19 meV per atom to 4 meV per atom, as illustrated in Fig. S3.
The state-of-the-art MLIP, GAP-20, has been developed to accurately and efficiently predict isomerization energies, assess thermal stability, and identify new carbon clusters and fullerene isomers.26 We evaluated the performance of GAP-20 on DTF optimized structures by predicting the relative binding energies for the C60, C70, and C72–C100 datasets, using the binding energy of C60-isomer-1 as the reference (Fig. S4). We emphasize that GAP-20 exhibits excellent accuracy in geometry optimization when benchmarked against the DFT method. For the C60 dataset, we confirmed strong correlations between relative binding energies calculated using GAP-20 with both DFT-optimized and GAP-20-optimized structures, achieving an impressive R2 value of 0.97 and a low MAE of 5 meV per atom (Fig. S5), consistent with previous studies.52
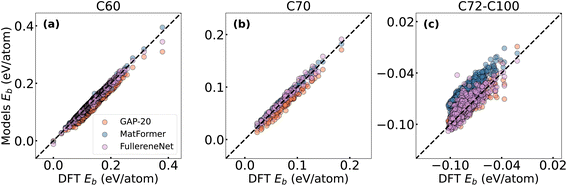
Fig. 4 presents a comprehensive comparison of binding energy prediction performance among FullereneNet (using unoptimized structures), MatFormer, and GAP-20 (both using optimized structures). Our results demonstrate that FullereneNet consistently outperforms the other two models across all three datasets. MatFormer exhibits poor performance on the C72–C100 test sets, achieving an MAE of 0.020 eV per atom. Similarly, GAP-20 shows suboptimal performance on the C60 test set, with an MAE of 0.016 eV per atom. Detailed MAE and R2 values for all methods are summarized in Table S4.
Besides the accuracy, one significant benefit of our model is that it can avoid the huge computational cost associated with computing large-size fullerenes. Take one C720 isomer36 as an example, which represents a computationally challenging system due to its substantial size. To quantify the computational advantages, we performed a detailed cost analysis comparing FullereneNet with DFT and MLIP approaches. The DFT calculations (using Gaussian 1637 on 48 CPU cores), geometry optimization with B3LYP/6-31G* required 33 hours 56 minutes of wall time, followed by an additional 6 hours 4 minutes for single-point energy calculations with B3LYP/6-311G*, totaling approximately 40 hours of computation time. In contrast, GAP-20 calculation (using LAMMPS with convergence criteria of 10−4 eV for total energy and 10−6 eV Å−1 for atomic forces) completed geometry optimization in approximately 1 minute on a single CPU core. Remarkably, FullereneNet prediction required less than 5 seconds with one NVIDIA L4 GPU, representing a tremendous speedup compared to DFT calculations. This dramatic computational acceleration arises from FullereneNet's ability to directly predict binding energies based on the arrangement of polygonal rings, eliminating the need to compute energies from optimized geometry using DFT or MLIP.
In summary, our results demonstrate that FullereneNet effectively leverages topological features from unoptimized structures to accurately predict binding energies, showcasing strong extrapolation capabilities for larger fullerenes. In contrast, MatFormer and GAP-20 rely heavily on optimized structures for accurate prediction. Given GAP-20's exceptional ability to generate optimized geometries closely matching DFT results, integrating it with FullereneNet could enhance predictions of additional properties, such as ionization potential and electron affinity. This combined approach will be explored further in Section 3.3.
3.2 Feature analysis
Feature engineering remains a fundamental challenge in materials and molecules discovery, where the choice of structural representations significantly impacts model performance. For conventional GNN models designed for molecules, researchers typically utilize atom features such as element type and hybridization, along with bond features including bond types and distances.53 However, these conventional features become inadequate for fullerene modeling, as they consist exclusively of sp2-hybridized carbon atoms, resulting in uniform node features across the structure. In this study, we developed topologically informed node and edge features based on pentagon and hexagon arrangements and investigated whether these features can capture the structural nuances of fullerene systems composed of chemically identical atoms.As detailed in Section 2.3, all node and edge features were derived from the adjacency matrix, whose elements reflect the connectivity between pairs of carbon atoms within a fullerene molecule (see Fig. 1). Given that the connectivity among carbon atoms varies across different fullerene structures, each yields a distinctive adjacency matrix, thereby enabling a unique representation of each structure. However, when using only the adjacency matrix, along with Gaussian-random-sampled node and edge features as inputs, the GNN model demonstrates extremely low predictive capability (see Fig. S6). These findings indicate that, while the node and edge features are derived from the adjacency matrix, they offer distinct structural dimensions crucial for interpreting structure–property relationships. Specifically, the adjacency matrix records atom-pair connectivity, capturing local connectivity within a fullerene molecule. In contrast, node features specify the types of three rings each atom shares, and edge features detail the types of four rings shared by each bond, providing semi-local structural information that cannot be effectively inferred by the GNN model but must be incorporated through human domain expertise. This strategic integration of chemical knowledge about ring types and arrangements enables our model to differentiate between carbon atoms that would otherwise appear indistinguishable, establishing a hierarchical representation that captures both local connectivity and higher-order topological patterns essential for stability prediction. Our findings highlight the crucial role of human domain knowledge in feature extraction and representation design, contributing to the development of more robust, reliable, and accurate ML models.
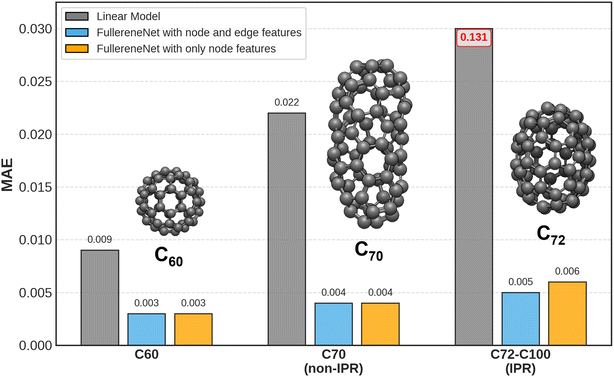
The manually derived node and edge features enable the GNN-based model, FullereneNet, to achieve superior performance in binding energy predictions, as demonstrated above. Since both node and edge features are derived from a single adjacency matrix to capture the semi-local chemical environment of pentagons and hexagons, we further evaluated the necessity of incorporating both feature types. To this end, we retrained the FullereneNet model using only node features to predict C–C binding energies across three test sets. The corresponding performance metrics are presented in Fig. 5 and Table S5. Similar to the model trained with both node and edge features, the model utilizing only node features demonstrates excellent extrapolation performance across four training strategies, yielding an average R2 of 0.989 and an MAE of 3 meV per atom for C60, 0.974 and 4 meV per atom for C70, and 0.364 and 6 meV per atom for C72–C100. The slightly reduced accuracy for the C72–C100 test set can be attributed to its binding energy distribution, which falls outside the range of the training set (see Fig. S1). These results suggest that since both node and edge features originate from the adjacency matrix, the inclusion of edge features offers minimal additional advantage in enhancing the extrapolation performance of GNN models when node features are already incorporated.
3.3 Further discussion
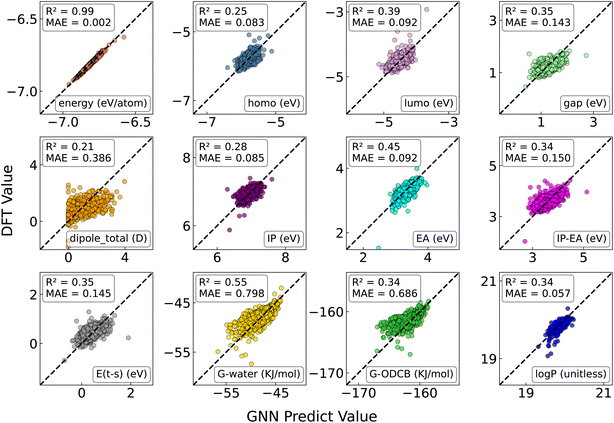
One of the key challenges in the computational design of molecules and materials is the high computational cost associated with structural optimization.54,55 In previous sections, we demonstrated that the FullereneNet achieves superior performance in predicting fullerene stability through carefully designed topological features rather than relying on optimized 3D Cartesian coordinates. This approach offers a substantial advantage by eliminating the computational cost associated with geometry optimization, which can be prohibitively expensive for high-throughput screening. To reinforce this advantage, we evaluated FullereneNet's predictive capability across a broader range of properties beyond stability. We tested FullereneNet on 11 other essential properties relevant for practical applications,56 including various electronic characteristics and solubility metrics, as summarized in Table S6.First, we benchmarked the MatFormer model using both unoptimized and optimized structural data as input. It is important to note that GAP-20 is limited to predicting the stability of fullerenes and cannot forecast other fundamental properties. As shown in Fig. S7, the MatFormer model struggles to accurately capture the structure–property relationships when using unoptimized structures on 11 properties. In contrast, structure optimization leads to significant improvements in both R2 and MAE values. For example, in predicting the HOMO–LUMO gap, the R2 value increased from −0.64 to 0.51, while the MAE decreased from 0.23 eV to 0.12 eV (Fig. S7 and S8).
Subsequently, we retrained the FullereneNet model using both node and edge features derived from unoptimized structures and applied the model to extrapolate predictions for the C60 dataset. As illustrated in Fig. 6 and S8, FullereneNet achieves comparable predictions to MatFormer with optimized structures for electronic properties while outperforming MatFormer in solubility-related property predictions with higher average R2 and lower MAE values. Specifically, when predicting free solvation energies in water (ΔGsol(water)) and 1,2-dichlorobenzene (ΔGsol(ODCB)), and the 1,2-dichlorobenzene–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), FullereneNet achieves MAE values of 0.80 kJ mol−1, 0.69 kJ mol−1, and 0.06, respectively. In contrast, the MatFormer model trained on optimized structures yielded MAE values of 0.85 kJ mol−1, 1.74 kJ mol−1, and 0.26 (Fig. S8). These results highlight the effectiveness of our feature design in capturing the chemical characteristics of fullerene systems, thereby enhancing the transferability of the FullereneNet model in predicting a diverse range of fundamental properties of fullerenes.
P), FullereneNet achieves MAE values of 0.80 kJ mol−1, 0.69 kJ mol−1, and 0.06, respectively. In contrast, the MatFormer model trained on optimized structures yielded MAE values of 0.85 kJ mol−1, 1.74 kJ mol−1, and 0.26 (Fig. S8). These results highlight the effectiveness of our feature design in capturing the chemical characteristics of fullerene systems, thereby enhancing the transferability of the FullereneNet model in predicting a diverse range of fundamental properties of fullerenes.
It is important to note that while FullereneNet achieves exceptional accuracy in predicting binding energies (R2 = 0.99), its performance varies across other properties. For instance, electronic properties such as the HOMO–LUMO gap and electron affinity exhibit moderate predictive accuracy (R2 = 0.35 and 0.45, respectively), indicating that these quantum mechanical properties are influenced by factors beyond the current topological descriptors. This observation is consistent with established chemical principles, as electronic properties often require more sophisticated quantum mechanical descriptors to accurately capture electron density distributions and orbital interactions.57 Nonetheless, FullereneNet provides reliable predictions across multiple properties without costly geometric optimization, marking a significant advancement in high-throughput fullerene screening. By effectively balancing computational efficiency and predictive accuracy, our model enables the rapid identification of promising candidates for further computational or experimental validation. These findings also highlight the limitations of topological descriptors in capturing complex electronic properties while underscore the broader applicability of FullereneNet in efficient property prediction.
4 Conclusion
In this work, we developed a graph neural network (GNN)-based model, FullereneNet, to predict a wide range of fundamental properties of fullerenes using topological features derived from unoptimized structures. By leveraging the chemical environments of pentagons and hexagons within the fullerene cage, we demonstrated that these topological features efficiently capture the local structural details of fullerenes, enabling accurate property predictions without the need for computationally expensive quantum chemistry optimizations. Our model significantly outperforms existing machine learning interatomic potentials GAP-20 and MatFormer, achieving superior accuracy in predicting C–C binding energies across various fullerene sizes. Additionally, FullereneNet exhibits robust performance in predicting 11 other properties, including HOMO–LUMO gaps, solvation free energies, and partition coefficients, demonstrating its versatility and transferability. This study provides a computationally efficient framework for high-throughput screening of fullerene candidates, offering a valuable tool for advancing the exploration and application of fullerenes in various fields, from optoelectronics to materials science.Author contributions
B. L. and M. L. initiated this study. B. L. conducted the theoretical calculations, while J. J. trained the machine learning models. All authors contributed to data analysis and manuscript writing.Conflicts of interest
There are no conflicts to declare.Data availability
The fullerene structures, including both unoptimized and optimized geometries, are available in the Zenodo repository.58Code availability: the Python implementation of FullereneNet is openly accessible on GitHub and Zenodo for long-term availability and reproducibility.59
Supplementary information: including details on extension of feature construction method, MatFormer model's details; figures on dataset distribution, model performance on different test sets; tables of fulluerene isomer numbers, model parameters, and property units is available. See DOI: https://doi.org/10.1039/d5dd00241a.
Acknowledgements
This work was financially supported by the University of Florida's new faculty start-up funding. The authors acknowledge the University of Florida Research Computing for providing computational resources and support that have contributed to the research results reported in this publication.References
- M. Chen, R. Guan and S. Yang, Hybrids of fullerenes and 2D nanomaterials, Adv. Sci., 2019, 6, 1800941 CrossRef PubMed.
- M. Gaur, C. Misra, A. B. Yadav, S. Swaroop, M. FÓ and M. Bechelany, et al., Biomedical applications of carbon nanomaterials: fullerenes, quantum dots, nanotubes, nanofibers, and graphene, Materials, 2021, 14, 5978 CrossRef CAS PubMed.
- W. P. Thurston, Shapes of polyhedra and triangulations of the sphere, arXiv, 1998, preprint, arXiv: arXiv.math/9801088, DOI:10.48550/arXiv.math/9801088.
- J. Weaver and D. Poirier, Solid state properties of fullerenes and fullerene-based materials, in Solid State Physics. Elsevier, 1994, Vol. 48, pp. 1–108 Search PubMed.
- D. M. Guldi, and N. Martin, Fullerenes: from synthesis to optoelectronic properties, Springer Science & Business Media, 2002, Vol. 4 Search PubMed.
- A. Kausar, Breakthroughs of fullerene in optoelectronic devices—an overview, Hybrid Adv., 2024, 100233 CrossRef.
- B. C. Thompson and J. M. Fréchet, Polymer–fullerene composite solar cells, Angew. Chem., Int. Ed., 2008, 47, 58–77 CrossRef CAS.
- O. O. Adisa, B. J. Cox and J. M. Hill, Methane storage in spherical fullerenes, J. Nanotechnol. Eng. Med., 2012, 3, 041002 CrossRef.
- D. Mao, X. Wang, G. Zhou, L. Chen, J. Chen and S. Zeng, Fullerene-intercalated graphene nanocontainers for gas storage and sustained release, J. Mol. Model., 2020, 26, 1–6 CrossRef PubMed.
- S. Goodarzi, T. Da Ros, J. Conde, F. Sefat and M. Mozafari, Fullerene: Biomedical engineers get to revisit an old friend, Mater. Today, 2017, 20, 460–480 CrossRef CAS.
- E. Castro, A. H. Garcia, G. Zavala and L. Echegoyen, Fullerenes in biology and medicine, J. Mater. Chem. B, 2017, 5, 6523–6535 RSC.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganäs and J. V. Manca, On the origin of the open-circuit voltage of polymer–fullerene solar cells, Nat. Mater., 2009, 8, 904–909 CrossRef CAS PubMed.
- H. K. H. Lee, A. M. Telford, J. A. Röhr, M. F. Wyatt, B. Rice and J. Wu, et al., The role of fullerenes in the environmental stability of polymer: fullerene solar cells, Energy Environ. Sci., 2018, 11, 417–428 RSC.
- H. Prinzbach, A. Weiler, P. Landenberger, F. Wahl, J. Wörth and L. T. Scott, et al., Gas-phase production and photoelectron spectroscopy of the smallest fullerene, C20, Nature, 2000, 407, 60–63 CrossRef CAS PubMed.
- C. Piskoti, J. Yarger and A. Zettl, C36, a new carbon solid, Nature, 1998, 393, 771–774 CrossRef CAS.
- M. Yamada, H. Kurihara, M. Suzuki, J. D. Guo, M. Waelchli, M. M. Olmstead, A. L. Balch, S. Nagase, Y. Maeda, T. Hasegawa and X. Lu, J. Am. Chem. Soc., 2014, 136(21), 7611–7614 CrossRef CAS PubMed.
- A. R. Puente Santiago, M. F. Sanad, A. Moreno-Vicente, M. A. Ahsan, M. R. Cerón and Y. R. Yao, et al., A new class of molecular electrocatalysts for hydrogen evolution: Catalytic activity of M3N@ C2 n (2 n= 68, 78, and 80) fullerenes, J. Am. Chem. Soc., 2021, 143, 6037–6042 CrossRef CAS.
- S. Y. Xie, F. Gao, X. Lu, R. B. Huang, C. R. Wang and X. Zhang, et al., Capturing the labile fullerene [50] as C50Cl10, Science, 2004, 304, 699 CrossRef CAS.
- Y. Z. Tan, Z. J. Liao, Z. Z. Qian, R. T. Chen, X. Wu and H. Liang, et al., Two I h-symmetry-breaking C60 isomers stabilized by chlorination, Nat. Mater., 2008, 7, 790–794 CrossRef CAS PubMed.
- A. Bille, V. Buchstaber and E. Spodarev, Some open mathematical problems on fullerenes, J. Chem. Inf. Model., 2025, 65, 2911–2923 CrossRef CAS PubMed.
- P. Schwerdtfeger, L. N. Wirz and J. Avery, The topology of fullerenes, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 96–145 CAS.
- P. García-Risueño, E. Armengol, À. García-Cerdaña, J. M. Garcia-Lastra and D. Carrasco-Busturia, Phys. Chem. Chem. Phys., 2024, 26(30), 20310–20324 RSC.
- M. Liu, Y. Han, Y. Cheng, X. Zhao and H. Zheng, Exploring exohedral functionalization of fullerene with automation and Neural Network Potential, Carbon, 2023, 213, 118180 CrossRef CAS.
- A. Aghajamali and A. Karton, Correlation between the energetic and thermal properties of C40 fullerene isomers: an accurate machine-learning force field study, Micro Nano Eng., 2022, 14, 100105 CrossRef CAS.
- P. Rowe, V. L. Deringer, P. Gasparotto, G. Csányi and A. Michaelides, J. Chem. Phys., 2020, 153, 034702 CrossRef CAS.
- B. Karasulu, J. M. Leyssale, P. Rowe, C. Weber and C. de Tomas, Accelerating the prediction of large carbon clusters via structure search: Evaluation of machine-learning and classical potentials, Carbon, 2022, 191, 255–266 CrossRef CAS.
- X. Fang, L. Liu, J. Lei, D. He, S. Zhang and J. Zhou, et al., Geometry-enhanced molecular representation learning for property prediction, Nat. Mach. Intell., 2022, 4, 127–134 CrossRef.
- S. S. Ziaee, H. Rahmani, M. Tabatabaei, A. H. Vlot and A. Bender, DCGG: drug combination prediction using GNN and GAE, Prog. Artif. Intell., 2024, 13, 17–30 CrossRef.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou and C. Shao, et al., Graph neural networks for materials science and chemistry, Commun. Mater., 2022, 3, 93 CrossRef CAS PubMed.
- K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7, 185 CrossRef.
- G. Simeon and G. De Fabritiis, Tensornet: Cartesian tensor representations for efficient learning of molecular potentials, Adv. Neural Inf. Process. Syst., 2024, 36, 37334–37353 Search PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and L. O. A. von, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1, 1–7 Search PubMed.
- K. Yan, Y. Liu, Y. Lin and S. Ji, Periodic graph transformers for crystal material property prediction, Adv. Neural Inf. Process. Syst., 2022, 35, 15066–15080 Search PubMed.
- B. Liu, J. Jin and M. Liu, Mapping structure-property relationships in fullerene systems: a computational study from C20 to C60, npj Comput. Mater., 2024, 10, 227 CrossRef CAS.
- P. Schwerdtfeger, L. Wirz and J. Avery, Program fullerene: a software package for constructing and analyzing structures of regular fullerenes, J. Comput. Chem., 2013, 34, 1508–1526 CrossRef CAS PubMed.
- M. Yoshida. C72 Fullerenes. Accessed: 2025-02-24. 2025. url: https://nanotube.msu.edu/fullerene/fullerene-isomers.html.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, and J. R. Cheeseman, et al., Gaussiañ16 Revision C.01, Gaussian Inc. Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 15 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown and P. S. Crozier, et al., LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- G. Csányi, S. Winfield, J. R. Kermode, A. De Vita, A. Comisso and N. Bernstein, et al., Expressive Programming for Computational Physics in Fortran 95+, IoP Comput. Phys. News., 2007, 1–24 Search PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. Daigavane, B. Ravindran and G. Aggarwal, Understanding convolutions on graphs, Distill, 2021, 6, e32 Search PubMed.
- B. Sanchez-Lengeling, E. Reif, A. Pearce and A. B. Wiltschko, A gentle introduction to graph neural networks, Distill, 2021, 6, e33 Search PubMed.
- Y. Liu, H. Yuan, Z. Wang and S. Ji, Global pixel transformers for virtual staining of microscopy images, IEEE Trans. Med. Imag., 2020, 39, 2256–2266 Search PubMed.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling and S. Paradiso, et al., Can machine learning identify the next high-temperature superconductor? Examining extrapolation performance for materials discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- Z. W. Zhao, C. M. Del and A. Troisi, Limitations of machine learning models when predicting compounds with completely new chemistries: possible improvements applied to the discovery of new non-fullerene acceptors, Digital Discovery, 2022, 1, 266–276 RSC.
- J. Wu, Advances in K-means clustering: a data mining thinking, Springer Science & Business Media, 2012 Search PubMed.
- A. Aghajamali and A. Karton, Can force fields developed for carbon nanomaterials describe the isomerization energies of fullerenes?, Chem. Phys. Lett., 2021, 779, 138853 CrossRef CAS.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- D. Packwood, J. Kermode, L. Mones, N. Bernstein, J. Woolley and N. Gould, et al., A universal preconditioner for simulating condensed phase materials, J. Chem. Phys., 2016, 144, 164109 CrossRef PubMed.
- M. Chen, R. Baer and E. Rabani, Structure optimization with stochastic density functional theory, J. Chem. Phys., 2023, 158, 2 Search PubMed.
- J. Nelson, Polymer: fullerene bulk heterojunction solar cells, Mater. Today, 2011, 14, 462–470 CrossRef CAS.
- S. C. Li, H. Wu, A. Menon, K. A. Spiekermann, Y. P. Li and W. H. Green, When do quantum mechanical descriptors help graph neural networks to predict chemical properties?, J. Am. Chem. Soc., 2024, 146, 23103–23120 CrossRef CAS PubMed.
- B. Liu, J. Jin and M. Liu, Extrapolating Beyond C60: Advancing Prediction of Fullerene Isomers with FullereneNet, Zenodo, 2025, DOI:10.5281/zenodo.17400608.
- B. Liu, J. Jin and M. Liu, Extrapolating Beyond C60: Advancing Prediction of Fullerene Isomers with FullereneNet, Version v1.0.0. 2025, DOI:10.5281/zenodo.17426461.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |