Evaluating the transfer learning from metals to oxides with GAME-Net-Ox

Abstract

The estimation of the strength of the bond of adsorbates on the surface is key to the design of novel materials for heterogeneous catalysis. Machine learning (ML) methodologies have proven effective in rapidly and accurately evaluating adsorption energies on transition metal surfaces. However, the complexity of metal oxides and their diverse adsorbate–catalyst interactions hinder the sound transfer of ML approaches to these catalytically relevant materials. To address this challenge, we have evaluated the transferability of GAME-Net, a graph neural network developed for transition metals, by following an approach of increasing complexity, leading to GAME-Net-Ox. A density functional theory dataset was built with organic molecules on conductive (IrO₂ and RuO₂) and semiconductive (TiO₂) rutile oxides to evaluate GAME-Net's transferability. While the original GAME-Net failed to directly generalize between metals and metal oxides, GAME-Net-Ox trained exclusively on oxides achieved high accuracy (MAE = 0.16 eV) and both families of materials can be treated in GAME-Net-Ox with the same accuracy (MAE = 0.16 eV). This work demonstrates the adaptability of the GAME-Net architecture, enabling the screening of adsorbates on metal oxides, materials with complex electronic properties.

---

1 Introduction

Understanding the adsorption of molecules on surfaces is key to evaluate the catalytic properties of heterogeneous catalysts,^1,2 which is paramount to advance the development of green processes aimed at tackling climate change.^3,4 The integration of machine learning (ML) predictive models into materials science holds promise to accelerate the discovery, design, and optimization of materials across a wide range of chemical systems.^5–8 Existing models consistently demonstrate high accuracy and reliability when predicting physicochemical properties of bulk materials. This success is largely attributed to the well-defined, periodic crystal structures of bulk materials, including features such as elemental composition, lattice parameters, and electronic structure, and the availability of large, consistent and open-access density functional theory (DFT) datasets^9–13 adhering to the FAIR principles.¹⁴ As a result, ML models can effectively utilize simple yet robust descriptors to achieve strong predictive performance.^15–17

In contrast, the transferability to surface properties seems more complex. For example, computational databases for the adsorption energies of molecules on metal and alloy surfaces have only been available recently.^18–22 Our understanding of the interaction of adsorbates with metals is associated with a covalent contribution described by the d-band model and a smaller redox contribution.^21,23–26 Thus, by leveraging physically meaningful descriptors and large high-quality available databases, several ML models can now rapidly and accurately predict adsorption energies.^22,27 Moreover, these models can also be used as pre-optimizers²⁸ and the obtained structures can be later refined with DFT methods. Such approaches greatly reduce both computational time and cost associated with quantum mechanical calculations. The success of these approaches is underpinned by the relative simplicity of the metal electronic structure, where catalytic activity trends follow the smooth variation in electronic properties.²⁵

However, extending ML-based methodologies to metal oxides, active industrial catalytic materials in oxidation, hydrotreating, and acid–base processes,²⁹ present substantial challenges. Unlike metals, metal oxides display a much broader spectrum of complexity.^30–36 Metal oxides (i) adopt different crystal structures; (ii) exhibit a broad range of electronic properties (insulators, semiconductors, or conductors); (iii) contain acid–base and redox sites; and (iv) exhibit metal–oxygen bonds ranging from highly covalent to predominantly ionic. Therefore, the adsorption of molecules on metal oxides spans a wide range of interaction types and strengths, including electrostatics, acid–base and redox chemistry, and both homolytic and heterolytic dissociation pathways. Furthermore, the synthesis of metal oxides results in defective (oxygen depleted) and/or hydroxylated surfaces in an uncontrolled manner that significantly influences their properties.^30,37,38 Moreover, the study of their catalytic properties by means of atomistic simulations is highly sensitive to the level of theory employed, further hampering a rational and systematic understanding.^39–42

The largest open-access DFT database targeting adsorption on metal oxide surfaces is the OC22 dataset.⁴³ OC22 includes 4728 unary (A_xO_y) and binary (A_xB_yO_z) oxides with and without the most typical defects, oxygen vacancies, and 9 small adsorbates (C*, H*, O*, N*, CO*, OH*, 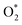, H₂O*, and OOH*). This database has been employed to develop ML potentials reaching a mean absolute error (MAE) of the total energy of 1.10 eV.²⁷ However, there is a lack of comprehensive databases and systematic studies on the adsorption of closed-shell small organic molecules on metal oxides, which makes the use of reliable ML models for adsorption on these materials challenging.

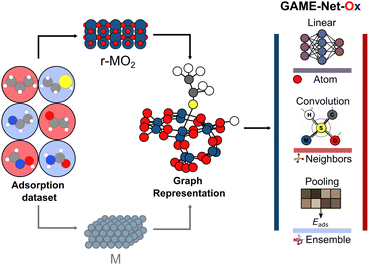
In this paper, we aim at investigating the transferability of the GAME-Net²² architecture from metals to oxides. GAME-Net is a very light (285 761 parameters) graph neural network (GNN) targeted to directly predict the adsorption energy of molecules on transition metal surfaces of close-shell molecules. GAME-Net is an initial structure to relaxed energy model (IS2RE), that when provided a guess adsorption configuration directly predicts its energy based on the graph representation. We present GAME-Net-Ox as the corresponding model designed to target the adsorption energy on both metals and metal oxide surfaces (Fig. 1).

Fig. 1 Conceptual schematics of this work. Starting from a dataset of DFT adsorption relaxations on transition metal catalysts, this work presents GAME-Net-Ox, an extension of the GAME-Net graph neural network that enables the prediction of the adsorption energy on conductive and semiconductive rutile metal oxides.

Because of the wide range of electronic and geometric properties of metal oxides, the selection of the materials and adsorbed molecules to explore is non-trivial. We selected three isostructural rutile-type (r) metal oxides, two conductors (RuO₂ and IrO₂) and one semiconductor (TiO₂). We initially select RuO₂ and IrO₂ for their conductive nature similar to that of pure metals. With this strategy we isolate the structural complexity and acid–base properties of the metal oxides while keeping the electronic properties relatively constant. Subsequently, we incorporate r-TiO₂, to address the role of a much richer electronic structure with a semiconductor nature. Regarding the selection of adsorbed molecules, we exploited the chemistry of our problem. Accordingly, we chose molecules that capture the diversity of the most relevant functional groups in organic chemistry. This approach differs from common models, which are typically based solely on small molecules and fragments (typically containing C, H, and O). We found that the new model, GAME-Net-Ox, was able to predict the adsorption energy of closed shell molecules (including some dissociative adsorptions) with comparable accuracy to GAME-Net for transition metal surfaces (MAE_GAME-Net-Ox = 0.16 eV and MAE_GAME-Net = 0.18 eV). This paves the way to explore the robustness of GAME-Net architecture to build very light alternative models to predict adsorption energies of a wide set of molecules and materials.

2 Methods

2.1 Density functional theory settings

Density functional theory (DFT) simulations for developing GAME-Net-Ox were carried out with the Vienna Ab initio Simulation Package (VASP) 5.4.4.^44,45 We used the Perdew–Burke–Ernzerhof (PBE)⁴⁶ density functional complemented by Grimmes's D3 approach⁴⁷ to account for van der Waals interactions. Core electrons were represented by projector-augmented wave pseudopotentials^48,49 and valence electrons were described with plane waves with a kinetic energy cutoff of 450 eV. Electronic convergence was set to 10⁻⁶ eV and atomic positions were converged until residual forces fell below 0.025 eV Å⁻¹. Bulk lattice parameters of rutile (P4₂/_mnm space group) RuO₂, IrO₂, and TiO₂ were optimized with a kinetic energy cut-off of 700 eV. Then, the MO₂(110) termination, which is the corresponding lowest surface energy orientation for rutiles,^50,51 was used to build the slab model of the three metal oxides with periodic boundary conditions. The surfaces were represented with p(2 × 2) slabs with five tri-layers (O–M–O), where the upper 2 tri-layers were fully relaxed and the bottom ones were fixed to the bulk distances. The vacuum between the slabs was set to 15 Å and a dipole correction was applied in the z direction.⁵² The Brillouin zone was sampled by a Γ-centered 5 × 3 × 1 k-point mesh generated through the Monkhorst–Pack method.⁵³

The close-shell molecules selected follow our Functional Groups (FG) dataset strategy, which is based on the principles of organic chemistry.⁵⁴ 38 gas-phase molecules comprising alkanes, alkenes, alkynes, alcohols, aldehydes, ketones, ethers, thiols, thials, thioketones, thioethers, amines, imines, carbonates, carboxylic acids, esters, carbamate esters, amides, oximes, and amidines up to C₃ (Table S1) were relaxed in a 20 Å cubic box. The molecules were then placed on the surfaces with DockOnsurf⁵⁵ on five sites (Fig. S1) with up to three different conformations. The adsorption center was placed between 1.5 and 3 Å above the surface, depending on the adsorption site and molecular size. To prevent unphysical configurations, atomic clashes are detected using the collision of spheres method. In this approach, the sphere radius is calculated by multiplying the covalent radius of each atom by a collision threshold factor, set to 1.3. A surface coverage of 0.01 molecules per Å⁻² was defined for all adsorption structures to neglect lateral interactions. The number of sampling points per angle is set to three, except for molecules with threefold rotational symmetry, where it is reduced to two to prevent the generation of symmetry-equivalent configurations degenerated in energy. To further minimize the initial generation of equivalent adsorbed configurations, the root mean square deviation (RMSD) of atomic positions was used as a similarity metric. Structures with an RMSD below 0.15 Å were considered duplicates and removed from the dataset. This strategy reduced the pool of 10 initial adsorption configurations generated with DockOnSurf for each adsorbate-surface pair to 1–3 unique structures depending on the molecule size. RMSD values were computed using the StructureMatcher class from the pymatgen (2024.11.13) library.⁵⁶

As for the adsorption on metal database, we retrieved from the FG-dataset⁵⁴ for Ag, Au, Cd, Co, Cu, Fe, Ir, Ni, Os, Pd, Pt, Rh, Ru, and Zn. Moreover, adsorptions on the (0001) termination of hexagonal close-packed Ti were generated retaining equivalent DFT details. We used a 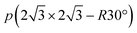supercell modeled by a four-layer slab, where the two bottom layers were fixed to the bulk positions while the two uppermost ones were allowed to relax. The vacuum between the slabs was set to more than 13 Å and a dipole correction was applied in the z direction.⁵² The Brillouin zone was sampled by a Γ-centered 3 × 3 × 1 k-point mesh generated through the Monkhorst–Pack method.⁵³

Overall, in this work we have generated a new dataset of the adsorption of different molecules on RuO₂, IrO₂, TiO₂, and metallic Ti, and we have merged it with an already existing dataset of the adsorption of the same molecules on different metal surfaces. Thus, we have employed analogs DFT setting, such as the VASP version, the density functional of choice, the van der Waals contributions, the pseudopotentials and the energy cut-off of the plane waves used to represent the electrons, and the k-point meshes (among other settings), to ensure that the merging of the two data sets was completely accurate and transparent.

2.2 Machine learning settings

GAME-Net-Ox has been developed with Pytorch Geometric 2.6.1 (ref. 57) and Pytorch 2.6.0,⁵⁸ and its training has been performed on a NVIDIA RTX A2000 12GB GPU with CUDA 12.4. The adsorption graphs used as input to train the graph neural network (GNN) are constructed starting from the relaxed three-dimensional (3D) atomic coordinates obtained from DFT relaxations. The graphs encode atoms as nodes represented by its chemical identity (element) via one-hot encoding, while chemical bonds between atoms are modeled as edges. Within the graphs, there is no distinction between adsorbate–adsorbate (A–A), surface–surface (S–S), and adsorbate–surface (A–S) bonds. Graph edges do not include any chemical feature, providing information only on the atom connectivity. The xyz → graph conversion algorithm is that of the original GAME-Net model,²² which employs a distance-based criterion to define the bonds between atoms. Two atoms are considered connected if (i) their distance in the DFT-relaxed structure is smaller than the sum of their covalent radii from Cordero et al.⁵⁹ plus a tolerance of 0.3 Å, and (ii) they are adjacent after applying the Voronoi tessellation. In GAME-Net, the graph representing the metal was limited only to the surface atoms directly interacting with the adsorbate (1^st-order neighbors). Here, the bi-elemental nature of metal oxides requires extending the surface representation to the 3^rd-order neighbors to always capture the full composition of the catalyst within the graph (Fig. S2). Each adsorption graph is labeled with its DFT adsorption energy, defined as:

E_ads = E_tot − E_slab − E_mol (1)

where E_tot is the energy of the relaxed adsorption structure, E_slab is the energy of the clean metal oxide slab and E_mol is the energy of the gas-phase molecule. In GAME-Net-UQ,⁶⁰ an improved version of the original GNN, the generalized coordination number (gCN),⁶¹ a descriptor for the local coordination including the second nearest neighbors, was encoded in the surface atom nodes. As this descriptor is suited for pure metal surfaces, GAME-Net-Ox encodes the coordination number (CN), which enables the effective capture of the local environment (first nearest neighbors) of the surface atoms in a simpler yet effective manner. The CN for a specific surface atom is obtained by counting the number of edges connecting it to other atoms belonging to the oxide surface, while for adsorbate atoms this feature is set to zero.

After converting the DFT adsorption structures to the corresponding graph representations, the same systematic filtering procedure employed for the FG-dataset used to train GAME-Net has been applied. This involves discarding duplicate isomorphic graphs representing the same adsorbate/surface pair.²² Two graphs representing the same adsorbate/surface pair are considered as different adsorption configurations if their DFT adsorption energy differs by at least 0.01 eV. For instance, for the adsorbate/surface pairs of the metal oxides, we retain approximately 86% of the original DFT dataset (Table S2).

Once constructed, the graph representation of the adsorbed molecule serves as input to the neural network. The input graphs are represented by a set of node feature vectors, each of them being a 21-dimensional array (15 metals + C, H, O, N, and S + coordination number), and by the graph connectivity in coordinate format (COO). GAME-Net-Ox architecture consists of three main building blocks: fully connected layers, convolutional layers, and a pooling layer.²² First, each node feature vector is transformed by a dense layer that increases its size from 21 to 160 dimensions without a bias term. Next, three GraphSAGE⁶² and one TAG⁶³ convolutional layers process these node embeddings, using the graph's connections to gather information from neighboring nodes while retaining the same size of 160. Finally, the Graph Multiset Transformer (GMT)⁶⁴ pooling layer compresses the information embedded in the nodes into a graph representation, which predicts the target energy of the whole adsorption structure.²² The ReLU⁶⁵ activation function is used throughout all the node-level layers. GAME-Net-Ox uses the same convolutional and pooling methods as GAME-Net-UQ, but as the node feature vectors include Ti as an additional one-hot encoded element and the reduced layer width (from 192 to 160), the final model contains 387 840 trainable parameters. While the number of parameters of GAME-Net-Ox is similar to that of GAME-Net (0.3 M) and GAME-Net-UQ (0.5 M), it is 2–3 orders of magnitude more lightweight than state-of-the-art ML interatomic potentials like EquiformerV2 trained on OC22 (31 M–153 M) or MACE-MP-0 (15 M).⁵ Details on the internal architecture of the model layers can be found in Tables S3–S5.

In the GNN learning processes, the graph dataset was randomly split into 60% training, 20% validation, and 20% testing sets. Since the dataset is balanced in terms of the catalyst surface and adsorbate, random splitting was suitable. The filtering strategies used to avoid equivalent adsorption structures in the dataset ensure the absence of data leakage. We employed a five-fold nested cross-validation to get a robust assessment of GAME-Net-Ox in-distribution performance, following the same procedure employed for GAME-Net. Each of the five splits is employed once as a test set, while the remaining four are iteratively rotated between training and validation roles. This results in 20 independent training runs, each using a distinct combination of splits for the training, validation, and test sets. The generalization performance of the model is finally assessed by concatenating the test sets from the independent trainings.

The ML trainings have been performed by minimizing the mean absolute error (MAE) loss function with the AMSGrad optimizer⁶⁶. A target scaling (standardization) based on the energy values in the training and validation sets has been performed to improve numerical stability during trainings. Training-related hyperparameters were selected in accordance with the original GAME-Net's hyperparameter optimization.²² The initial learning rate was set to 10⁻⁴ and is adjusted using a ReduceLROnPlateau PyTorch scheduler,⁶⁷ which lowers the learning rate by a factor of 0.7 if there is no improvement after 5 epochs (patience) in the MAE of the validation set. The learning rate was allowed to decrease down to a minimum of 10⁻⁸. In each training, 250 epochs were performed. During each epoch, the training data are fed to the GNN in batches of 16 samples, performing a backward propagation and updating the model parameters after each batch.

3 Results

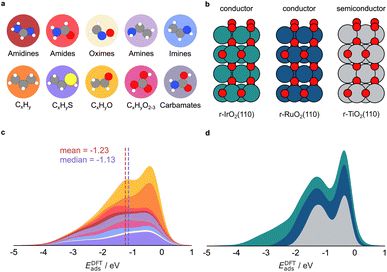
We aim to transfer the architecture of GAME-Net²² to predict the adsorption energy (E_ads) on RuO₂, IrO₂, and TiO₂ oxides (Fig. 1) rendering GAME-Net-Ox. First, we built an analogue FG-dataset to the one used in GAME-Net.²² We included 38 closed-shell organic molecules up to C₃ with the most common functional groups in organic chemistry adsorbed on the (110) surface of three rutile metal oxides (Fig. 2a and b). Particularly, we used DFT (PBE + D3) to relax the structure of the following molecules on the metal oxide surfaces: (i) non-cyclic hydrocarbons; (ii) O-functionalized (alcohols, ketones, aldehydes, ethers, carboxylic acids, and carbonates); (iii) N-functionalized (amines, imines, and amidines); (iv) S-functionalized (thiols, thioaldehydes, and thioketones); and (v) N- and O-functionalized combinations (amides, oximes, and carbamate esters) (Table S1). For each molecule, we assessed its adsorption on different sites of the three metal oxide surfaces, following the procedure described in detail in the Methods section. The distribution of adsorption energies depicts two distinct peaks, corresponding to chemisorption (strong adsorption, E_ads < −1.0 eV) and physisorption (weak adsorption, E_ads between −0.1 and −1.0 eV) events on the three metal oxides (Fig. 2c).⁶⁸ Moreover, adsorption energy span is broader for IrO₂ compared to RuO₂ and TiO₂. In some cases, due to the acid–base properties of the metal oxides, the molecules are dissociatively adsorbed (i.e., the adsorbates are dissociated into two or more fragments, both or all of which are bound to the surface of the adsorbent).⁶⁹ The molecules adsorbed on 14 transition metal surfaces were retrieved from our previous work,²² and we have now included the Ti(0001) surface. All the structures, inputs, and outputs of the DFT simulations can be found in the ioChem-BD repository.^70,71

Fig. 2 DFT adsorption dataset. (a) Closed-shell molecules included as adsorbates, and (b) metal oxide surfaces included in this study. The adsorption energy (E^DFT_ads) distribution grouped by (c) chemical family and (d) metal oxide follows the same color code of the molecules/materials depicted in the top part.

With the FG-dataset at hand and its graph-based representation, we performed different data splits to identify the data required to build an accurate model for predicting adsorption energies on metal oxides. First, we evaluated the predictive performance of GAME-Net, trained on transition metals, on the adsorption energy on the conductive metal oxides IrO₂ and RuO₂ (Fig. S3). GAME-Net achieves on these materials an MAE of 2.00 eV (n = 536), an expected result due to the fundamentally different nature of adsorbate interactions on the two types of surfaces. An additional aspect to consider is the minimal graph representation employed by GAME-Net, which includes as surface nodes only the atoms directly in contact with the adsorbate, thus implying a loss of information about the metal oxide composition (Fig. S2). This observation shows the need of expanding the surface representation within the input graphs. Then, we evaluated GAME-Net-UQ architecture to capture the higher structural complexity of metal oxides compared to transition metals. We trained a model exclusively on the conductive metal oxides IrO₂ and RuO₂. The resulting model achieved an MAE of 0.34 eV (Fig. S4), which is higher than the one obtained by GAME-Net for transition metal surfaces. Thus, we modified the original graph representation of the metal oxides (1^st-order neighbors) leading to GAME-Net-Ox including further neighbors. Particularly, we extended the surface representation to the 3^rd-order neighbors and incorporated the coordination number (CN) when generating the graph representation of the adsorbate–surface interaction (Fig. S2 and S4).

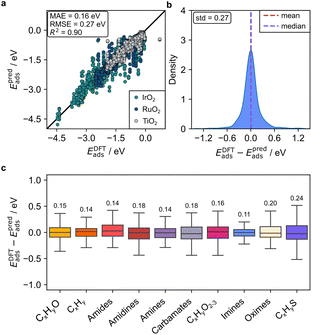
Upon this improvement, GAME-Net-Ox on the two conductive metal oxides achieves a global MAE of 0.22 eV, comparable to the MAE obtained by GAME-Net (0.18 eV) for transition metal surfaces (Fig. 3). Thus, the extended surface representation captured by the graphs of GAME-Net-Ox enhances the material representation and provides better insights into the structure sensitivity of the surface. The in-distribution error is balanced across the different chemical families represented by the adsorbate, with S-containing molecules showing the highest error since S is the least represented atom in the FG-dataset and it is the only heteroatom included that contains d orbitals. The results indicate that, despite the differences in structure, adsorption sites, adsorbate nature, and interaction phenomena between metal oxides and transition metal surfaces, GAME-Net-Ox is sufficiently robust to accurately model the adsorption of closed-shell molecules on the conductive metal oxides. Indeed, it must be highlighted that because of the presence of acid–base pairs in the metal oxides, some molecules with acid protons (i.e., carboxylic and carbonic acids and thiols) evolved to dissociated configurations during DFT structural relaxations (Table S6). Particularly, 64 out of 524 adsorptions on the conductive metal oxides exhibit a dissociated proton. This subset presents an MAE of 0.23 eV (Fig. S5), showing that the predictive accuracy of the model is robust with respect to this feature (MAE of 0.22 eV). As dissociative adsorptions are key for metal oxide catalytic properties, the predictive accuracy of GAME-Net-Ox towards this type of adsorptions is crucial.

Fig. 3 GAME-Net-Ox performance on conductive oxides (IrO₂, RuO₂). Plotted data come from the test sets of the trainings performed for the 5-fold nested cross validation. (a) Parity plot of predicted vs. DFT adsorption energies, and (b) corresponding error distribution. (c) Boxplot of the GAME-Net-Ox error grouped by chemical family. The number of top of each box represents the MAE of the specific family (n = 2096).

Then, we introduced an additional layer of complexity by incorporating TiO₂ (Fig. 4), which despite being isostructural with IrO₂ and RuO₂, is a semiconductor. Training GAME-Net-Ox on the three oxides leads to an MAE of 0.16 eV. Interestingly, the different conductive properties of the metal oxides do not affect the final predictive accuracy. These results demonstrate that the GAME-Net architecture is robust enough to accurately model the adsorption of closed-shell molecules on metal oxides, when their electronic properties differ and dissociative adsorptions are included.

Fig. 4 GAME-Net-Ox performance on conductive (IrO₂ and RuO₂) and semiconductive (TiO₂) oxides. Plotted data come from the test sets of the trainings performed for the 5-fold nested cross validation. (a) Parity plot of predicted vs. DFT adsorption energies, and (b) corresponding error distribution. (c) Boxplot of the GAME-Net-Ox error grouped by chemical family. Number of top of each box represents the MAE of the specific family (n = 3440).

Since the span of adsorption energies differs among the three metal oxides (Fig. 2), we implemented a leave-one-out strategy, using the data from two metal oxides as the training set and the data from the third as the test set (Fig. S6). A higher MAE was observed when adsorptions on IrO₂ were used as the test set (MAE = 0.75 eV), consistent with the widest span of adsorption energies for this material.

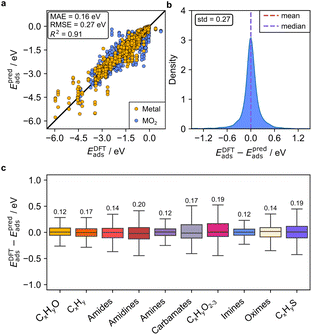
We then merged the data for the adsorption of the 38 closed-shell organic molecules on the three metal oxides and 14 transition metal surfaces to evaluate the predictive ability of GAME-Net-Ox when mixing the two types of surfaces. We performed again fivefold nested cross-validations with data splits 60 : 20 : 20 and the results show that GAME-Net-Ox robustly maintains the same predictive accuracy (MAE = 0.16 eV, Fig. 5). Thus, GAME-Net-Ox is able to predict the adsorption of closed-shell molecules with the same accuracy as GAME-Net, despite the added complexity of metal oxides. However, to achieve these excellent values both types of materials must be included in the training set since the model trained solely on adsorption data for transition metals cannot accurately predict adsorption on metal oxides, and vice versa (Fig. S7).

Fig. 5 GAME-Net-Ox performance on conductive (IrO₂ and RuO₂) and semiconductive (TiO₂) oxides, including the adsorption on the 14 transition metal surfaces from the FG-dataset. Plotted data come from the test sets of the trainings performed for the 5-fold nested cross validation. (a) Parity plot of predicted vs. DFT adsorption energies, and (b) corresponding error distribution. (c) Boxplot of the GAME-Net-Ox error grouped by chemical family. Number of top of each box represents the MAE of the specific family (n = 2384).

Finally, we have performed a benchmark of GAME-Net-Ox against two state-of-the-art ML interatomic potentials (MACE-MP-0 large and EquiformerV2-122M-OC22). The results in Fig. S8 and Table S7 show similar accuracy between GAME-Net-Ox and MACE-MP-0 (MAE = 0.25 eV), while EquiformerV2-122M leads to a one order of magnitude higher MAE (MAE = 2.80 eV). Initially, we attributed this difference in performance to the lack of S-containing adsorbates in the OC22 training dataset. Filtering out these adsorbates, the MAE improved by 50% (MAE = 1.39 eV). Regardless, the MAE is still 10× higher than that of GAME-Net-Ox and MACE-MP-0. We point that the constrained diversity of adsorbates in the training set (9 small molecules and fragments: O, H, N, C, OH, OOH, H₂O, CO, and O₂) has a significant impact on the performance of the model when evaluating adsorbates with a high variability of functional groups.

4 Conclusions

The present work demonstrates the transferability of GAME-Net-like architectures to predict the adsorption energy of closed-shell organic molecules on metal oxides with rutile structures and diverse electronic properties. As expected, models trained on transition metal surfaces only fail to generalize to metal oxides due to differences in their inherent properties as well as different adsorbate–surface interactions. In contrast, GAME-Net-Ox (i.e., GAME-Net-UQ with an oxide-specific graph representation) trained on conductive (IrO₂ and RuO₂) and semiconductive (TiO₂) rutile-type metal oxides, achieves an accuracy comparable to its original performance on metals, even for dissociative acid–base adsorptions and semiconductors such as TiO₂. Therefore, it is possible to build light models directly targeting adsorption energies like GAME-Net-Ox with a reasonable balance of accuracy across materials. Such methodologies pave the way to a more efficient prediction of the adsorption energy on metal oxides with different geometric motifs and electronic structures, as well as on a broader range of adsorbates relevant for catalysis.

Author contributions

T. V. H.: data generation and curation, formal analysis, investigation, methodology, software, visualization. O. L.: conceptualization, data generation, formal analysis, investigation, methodology, visualization, writing – original draft preparation. J. M.-V.: conceptualization, data generation, formal analysis, investigation, methodology, writing – original draft preparation. S. M.: conceptualization, data curation, formal analysis, methodology, software, visualization, writing – original draft preparation. N. L.: conceptualization, funding acquisition, project administration, writing – original draft preparation, editing, and supervision.

Conflicts of interest

There are no conflicts to declare.

Data availability

Code availability: the code for training and evaluation GAME-Net-Ox has been publicly released under the MIT license and is available on https://github.com/LopezGroup-ICIQ/oxides_ML. To improve the reproducibility of this work, a snapshot of the code, graph datasets, and trained models is available in Zenodo at https://doi.org/10.5281/zenodo.17900954.

The DFT data used to develop GAME-Net-Ox are available in ioChem-BD at https://doi.org/10.19061/iochem-bd-1-396 (metal oxides and metallic Ti FG-dataset) and https://doi.org/10.19061/iochem-bd-1-257 (transition metals FG-dataset).

Supplementary information (SI): the results of the considered metal oxide adsorption sites, the expansion on the graph-representation, and the detailed performance results of the different test models. See DOI: https://doi.org/10.1039/d5dd00331h.

Acknowledgements

We thank the Spanish Ministry of Science and Innovation (PID2024-157556OB-I00 and Severo Ochoa Excellence Accreditation CEX2024-001469-S funded by MCIU/AEI/10.13039/501100011033) for the financial support. O. L. acknowledges the Joan Oró Predoctoral Programme of the Generalitat de Catalunya, and the European Social Fund Plus (2023 FI-1 00769). J. M.-V. and N. L. thank Generalitat de Catalunya and AGAUR (2023 CLIMA 00105) for financial support. We thank Barcelona Supercomputing Center-MareNostrum (BSC-RES) for providing generous computational resources.

Notes and references

1. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
2. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
3. J. B. Zimmerman, P. T. Anastas, H. C. Erythropel and W. Leitner, Science, 2020, 367, 397–400.
4. T. P. Araújo, S. Mitchell and J. Pérez-Ramírez, Adv. Mater., 2024, 36, 2409322.
5. I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, arXiv, 2023, preprint, arXiv:2206.07697,  DOI:10.48550/arXiv.2206.07697.
6. K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185.
7. K. Choudhary, B. DeCost, L. Major, K. Butler, J. Thiyagalingam and F. Tavazza, Digital Discovery, 2023, 2, 346–355.
8. M. Neumann, J. Gin, B. Rhodes, S. Bennett, Z. Li, H. Choubisa, A. Hussey and J. Godwin, arXiv, 2024, preprint, arXiv:2410.22570,  DOI:10.48550/arXiv.2410.22570.
9. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
10. K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. H. Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173.
11. B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041.
12. L. Barroso-Luque, M. Shuaibi, X. Fu, B. M. Wood, M. Dzamba, M. Gao, A. Rizvi, C. L. Zitnick and Z. W. Ulissi, arXiv, 2024, preprint, arXiv:2410.12771,  DOI:10.48550/arXiv.2410.12771.
13. J. Schmidt, T. F. Cerqueira, A. H. Romero, A. Loew, F. Jäger, H.-C. Wang, S. Botti and M. A. Marques, Mater. Today Phys., 2024, 48, 101560.
14. M. D. Wilkinson, M. Dumontier, I. J. Aalbersberg, G. Appleton, M. Axton, A. Baak, N. Blomberg, J.-W. Boiten, L. B. da Silva Santos, P. E. Bourne, J. Bouwman, A. J. Brookes, T. Clark, M. Crosas, I. Dillo, O. Dumon, S. Edmunds, C. T. Evelo, R. Finkers, A. Gonzalez-Beltran, A. J. Gray, P. Groth, C. Goble, J. S. Grethe, J. Heringa, P. A. 't Hoen, R. Hooft, T. Kuhn, R. Kok, J. Kok, S. J. Lusher, M. E. Martone, A. Mons, A. L. Packer, B. Persson, P. Rocca-Serra, M. Roos, R. van Schaik, S.-A. Sansone, E. Schultes, T. Sengstag, T. Slater, G. Strawn, M. A. Swertz, M. Thompson, J. van der Lei, E. van Mulligen, J. Velterop, A. Waagmeester, P. Wittenburg, K. Wolstencroft, J. Zhao and B. Mons, Sci. Data, 2016, 3, 160018.
15. W. Yong, H. Zhang, H. Fu, Y. Zhu, J. He and J. Xie, Comput. Mater. Sci., 2022, 204, 111181.
16. A. E. A. Allen and A. Tkatchenko, Sci. Adv., 2022, 8, eabm7185.
17. S.-D. Xue and Q.-J. Hong, arXiv, 2023, preprint, arXiv:2311.05133,  DOI:10.48550/arXiv.2311.05133.
18. J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44.
19. L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072.
20. C. T. Campbell, J. Fingerhut and A. M. Wodtke, Surf. Sci., 2025, 756, 122714.
21. R. García-Muelas and N. López, Nat. Commun., 2019, 10, 4687.
22. S. Pablo-García, S. Morandi, R. A. Vargas-Hernández, K. Jorner, Ž. Ivković, N. López and A. Aspuru-Guzik, Nat. Comput. Sci., 2023, 3, 433–442.
23. B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240.
24. B. Hammer, Y. Morikawa and J. K. Nørskov, Phys. Rev. Lett., 1996, 76, 2141.
25. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105.
26. F. Calle-Vallejo, J. Martínez, J. M. García-Lastra, J. Rossmeisl and M. Koper, Phys. Rev. Lett., 2012, 108, 116103.
27. Y.-L. Liao, B. Wood, A. Das and T. Smidt, arXiv, 2024, preprint, arXiv:2306.12059,  DOI:10.48550/arXiv.2306.12059.
28. B. Wander, M. Shuaibi, J. R. Kitchin, Z. W. Ulissi and C. L. Zitnick, ACS Catal., 2025, 15, 5283–5294.
29. J. C. Védrine, ChemSusChem, 2019, 12, 577–588.
30. V. E. Henrich and P. A. Cox, The Surface Science of Metal Oxides, Cambridge university press, Cambridge, 1994.
31. R. K. Grasselli, Top. Catal., 2002, 21, 79–88.
32. E. M. Fernández, P. G. Moses, A. Toftelund, H. A. Hansen, J. I. Martínez, F. Abild-Pedersen, J. Kleis, B. Hinnemann, J. Rossmeisl, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2008, 47, 4683–4686.
33. A. Seitsonen and G. Ertl, Science, 2000, 287, 1474–1476.
34. H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Pérez-Ramírez, B. R. Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Nature, 2020, 587, 408–413.
35. V. Korpelin, M. M. Melander and K. Honkala, J. Phys. Chem. C, 2022, 126, 933–945.
36. M. Capdevila-Cortada, G. Vilé, D. Teschner, J. Pérez-Ramírez and N. López, Appl. Catal., B, 2016, 197, 299–312.
37. J. Jia, C. Qian, Y. Dong, Y. F. Li, H. Wang, M. Ghoussoub, K. T. Butler, A. Walsh and G. A. Ozin, Chem. Soc. Rev., 2017, 46, 4631–4644.
38. M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219–270.
39. N. Daelman, F. S. Hegner, M. Rellán-Piñeiro, M. Capdevila-Cortada, R. García-Muelas and N. López, J. Chem. Phys., 2020, 152, 050901.
40. B. W. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2020, 121, 1007–1048.
41. S. Divanis, T. Kutlusoy, I. M. I. Boye, I. C. Man and J. Rossmeisl, Chem. Sci., 2020, 11, 2943–2950.
42. M. Capdevila-Cortada, Z. Łodziana and N. López, ACS Catal., 2016, 6, 8370–8379.
43. R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, F. Therrien, J. Abed, O. Voznyy, E. H. Sargent, Z. Ulissi and C. L. Zitnick, ACS Catal., 2023, 13, 3066–3084.
44. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
45. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
48. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
49. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
50. M. J. S. Abb, T. Weber, D. Langsdorf, V. Koller, S. M. Gericke, S. Pfaff, M. Busch, J. Zetterberg, A. Preobrajenski, H. Grönbeck, E. Lundgren and H. Over, J. Phys. Chem. C, 2020, 124, 15324–15336.
51. P. M. Kowalski, B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115410.
52. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
53. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
54. S. Morandi, S. Pablo-García and Ž. Ivković, ioChem-BD Data Repository.
55. C. Martí, S. Blanck, R. Staub, S. Loehlé, C. Michel and S. N. Steinmann, J. Chem. Inf. Model., 2021, 61, 3386–3396.
56. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
57. M. Fey and J. E. Lenssen, arXiv, 2019, preprint, arXiv:1903.02428,  DOI:10.48550/arXiv.1903.02428.
58. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Advances in Neural Information Processing Systems 32, Curran Associates, Inc., 2019, pp. 8024–8035.
59. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832.
60. S. Morandi, O. Loveday, T. Renningholtz, S. Pablo-García, R. A. Vargas-Hernández, R. R. Seemakurthi, P. Sanz-Berman, R. García-Muelas, A. Aspuru-Guzik and N. López, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-bfv3d.
61. F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410.
62. W. Hamilton, Z. Ying and J. Leskovec, Advances in Neural Information Processing Systems, 2017.
63. J. Du, S. Zhang, G. Wu, J. M. F. Moura and S. Kar, arXiv, 2018, preprint, arXiv:1710.10370,  DOI:10.48550/arXiv.1710.10370.
64. J. Baek, M. Kang and S. J. Hwang, arXiv, 2021, preprint, arXiv:2102.11533,  DOI:10.48550/arXiv.2102.11533.
65. A. F. Agarap, arXiv, 2019, preprint, arXiv:1803.08375,  DOI:10.48550/arXiv.1803.08375.
66. S. J. Reddi, S. Kale and S. Kumar, arXiv, 2019, preprint, arXiv:1904.09237,  DOI:10.48550/arXiv.1904.09237.
67. A. Paszke, S. Gross, S. Chintala and G. Chanan, ReduceLROnPlateau—PyTorch 2.7 documentation, 2024, https://pytorch.org/docs/stable/generated/torch.optim.lr_scheduler.ReduceLROnPlateau.html#torch.optim.lr_scheduler.ReduceLROnPlateau, accessed: 2024-07-15.
68. J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, Hoboken, 2014.
69. R. L. Burwell, Pure Appl. Chem., 1976, 46, 71–90.
70. M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2014, 55, 95–103.
71. C. Bo, F. Maseras and N. López, Nat. Catal., 2018, 1, 809–810.

---