Open Access Article
Open Access ArticleElectric fields at hydrophobic water interfaces: spectroscopic evidence, physical origin, and implications on reactivity
Kwing Yeung
Chan
,
Chenjie
Zhuang
,
Vinh Gia
Vuong
,
Naixin
Qian
,
Xin
Gao
 and
Wei
Min
and
Wei
Min
 *
*
Department of Chemistry, Columbia University, New York, NY 10027, USA. E-mail: wm2256@columbia.edu
First published on 24th November 2025
Abstract
Water at interfaces exhibits unique properties that differ markedly from those of bulk water. In particular, a myriad of water-interface-related enhanced reactivities including on-water catalysis and microdroplet chemistry have been documented since the 1980s but remain mechanistically unclear. This review focuses on recent advances in optical spectroscopy and imaging techniques—including fluorescence imaging, vibrational Stark spectroscopy, electrochromism, sum-frequency generation, and high-resolution Raman micro-spectroscopy—that have successfully enabled the detection of interfacial electric fields at different hydrophobic water interfaces (air, liquid and solid). We summarize how both probe-based and label-free optical spectroscopic techniques can consistently quantify the on-water electric field strengths to be on the order of tens of MV cm−1, corroborated by independent non-spectroscopic techniques, such as electrokinetic and surface charge measurements. The surprisingly close agreement among these different measurements and across broad experimental systems strongly hints at the existence of strong electric fields being a general feature of water–hydrophobe interfaces. We further discuss the physical origins of the interfacial electric field with a particular emphasis on the mechanism of preferential hydroxide accumulation at hydrophobic interfaces. Finally, we examine the implications of strong interfacial electric fields for chemical kinetics, radical generation and thermodynamics, thereby making important connections to interfacial water reactivity. These insights not only contribute to our fundamental understanding of water at interfaces but also point toward new strategies for harnessing interfacial water electrostatics in biomedicine, catalysis, green chemistry, and environmental science.
Interfacial water reactivity: from on-water catalysis to microdroplet chemistry and beyond
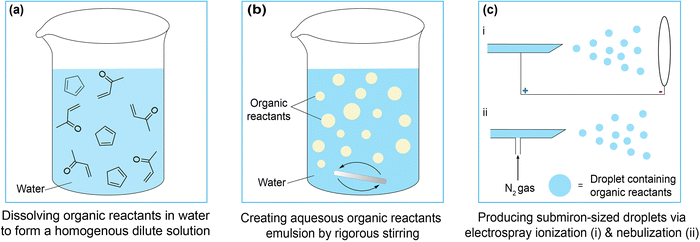
Water is likely the most mysterious, yet universal, substance on Earth. Although its physical and chemical properties have been well studied as a bulk solvent, much evidence suggests that water at interfaces (interfacial water) has intriguing behaviors and properties that are vastly distinct from those of bulk water. In the realm of chemistry, water playing a role in organic reactions was perhaps first recognized by Breslow more than 40 years ago.1,2 It was shown in this pioneering study that Diels–Alder reactions could proceed at a much higher rate in water than in common organic solvents. Breslow intuitively attributed this observation to “hydrophobic effects” with the remarkable conclusion that the reaction acceleration occurs because of, rather than in spite of, the poor solubility of the organic substances in water (Fig. 1a).3In the 2000s, Sharpless and co-workers revisited this phenomenon and systematically studied the unique reactivity of organic compounds in aqueous suspension, coining the term “on-water” catalysis.4 Their approach involved vigorous stirring of organic reactants in water to create suspensions with extensive interfaces between water and organic molecules (Fig. 1b). Importantly, this “on-water” catalysis was demonstrated to be a general mechanism beyond Diels–Alder reactions. They suggested that the phase heterogeneity—the coexistence of organic (oil) and aqueous (water) phases—has a crucial role in the drastic acceleration of reaction kinetics. Though without direct evidence at the time, they hypothesized that the mesoscopic phase boundary itself might be responsible for the observed effect. Jung and Marcus later proposed a molecular theory for this, in which “dangling” OH groups arising from the water's broken hydrogen bonding network at the interface could stabilize the transition state of nearby organic reactions.5 Since then, on-water catalysis has continued to attract attention in the field of organic chemistry.6,7
While on-water catalysis highlights the role of water–oil interfaces in accelerating reactions, the emergence of microdroplet chemistry is a parallel and perhaps more remarkable development.8,9 In microdroplet chemistry, these micron-sized droplets containing reactants are generated through methods such as electrospray ionization and inert gas nebulization, to name but a few (Fig. 1c). These droplets form extensive interfaces with air, and the reaction outcome is analyzed with a mass spectrometer. In the 2010s, several groups, particularly Cooks and Zare, reported substantial (up to a million folds) rate acceleration of reactions in microdroplets compared to their counterparts in bulk water.10–20 These reactions occur entirely in the aqueous phase, hence complementing “on-water” catalysis in the water–oil systems. One striking demonstration is that the on-water chemistry reaction ([2σ + 2σ + 2π] cycloaddition studied earlier by Sharpless and co-workers4) was reproduced in microdroplets with another 100-fold higher rate.21 Thus, these examples underscore a broader principle: the acceleration of chemical reactions is not exclusive to water–oil mixtures but also applicable to water–air interfaces.
Among a plethora of microdroplet reactions, the spontaneous generation of H2O2 from sprayed water microdroplets, initially reported by Zare and co-workers, took the field by surprise, although this discovery is surrounded by ongoing debates.22–33 Its production did not require any obvious oxidants/reductants or an applied potential. It seemingly contradicts one's intuition: the standard potential for oxidizing water to hydroxyl radicals is −2.8 V (against the standard hydrogen electrode),34 which is thermodynamically highly unfavorable. This suggests that water interfaces not only accelerate the reaction kinetics but also reshape thermodynamic landscapes of reactions. Since then, an expanding list of reactions (mostly redox by nature) has been explored and realized in microdroplets, for instance, C(sp3)–N bond formation, Menshutkin reactions, C–H/N–H cross-coupling, reduction of transition metal ions, even simultaneous oxidation and reduction of phosphonates, etc.35–54 These unique chemical reactivities have implications across broad fields including chemical synthesis, green chemistry, atmospheric chemistry and environmental science. For example, nitrogen fixation,55 CO2 capture,56–59 greenhouse gas formation,60 sulfate formation in aerosol,61 degradation of PFAS,62 high-throughput synthesis,63 photochemical synthesis,64,65 and prebiotic chemistry66–71 have all recently been demonstrated in microdroplets.
In addition to water–oil interfaces as in “on-water” catalysis and water–air interfaces as in microdroplet chemistry, similar reactivity has also been found at water–solid interfaces. For example, water droplets have been demonstrated to spontaneously degrade organic dye molecules when sliding over a hydrophobic polymer surface.72 Redox reactivity like that of microdroplets has also been discovered at glass–water interfaces.73 Even biological systems have been reported to exhibit similar behaviors.74,75 Together, decades of experimental evidence accumulated from a wide range of different water interfaces (oil, air and solid) seem to all suggest that interfacial water on hydrophobic surfaces has a chemical reactivity distinct from that of bulk water.
Electrostatic properties of interfacial water
Mechanistic studies over the years have attributed the unique chemistry in microdroplets to several intrinsic properties of water interfaces, such as partial solvation of reactants,76 kinetic confinement,17 stabilization of transition states,5 entropic factor,8,67 extreme pH values (super-acid or super-base),77–79etc. These effects can be amplified in micron-sized droplets due to their high surface-to-volume ratios. Among various explanations, one particularly intriguing hypothesis is the existence of a strong electric field across the aqueous interface.9,80–85While the underlying mechanism may not appear obvious (which will be discussed later), several pieces of evidence and considerations imply the unique interfacial electrostatics and the potential existence of a localized electric field.
(1) Firstly, unlike in a bulk solution, the symmetry is broken at the interface at the molecular level. The ordered orientation of water molecules, which have a large dipole moment at the interface, can generate a local electric field. This picture is adopted in some theoretical calculations of the surface potential.86–89
(2) Secondly, although there are debates on the direction of pH deviation, nearly all studies agree that the pH of the water interface is not neutral, with more evidence supporting that it is basic in nature.90–95 Since only pure water is present in the system, a non-neutral interface means either anions or cations, presumably hydroxide (OH−) or hydronium (H3O+), are preferentially enriched at water interfaces. This ionic imbalance can also generate an interfacial electric field.
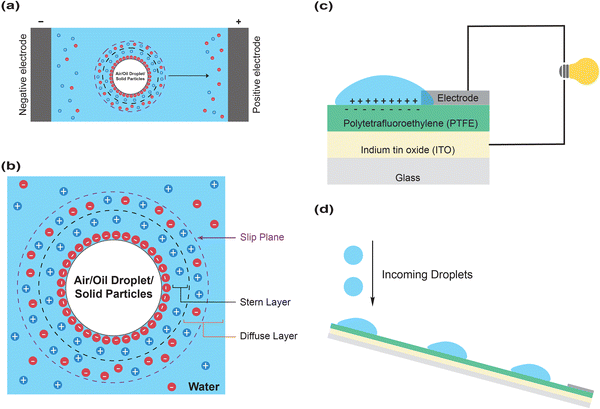
(3) Thirdly, micron-sized objects such as oil droplets, air bubbles and solid particles have been repeatedly and robustly shown to be electrokinetically active in electrophoresis experiments (Fig. 2a).91,96–98 Zeta (ζ) potential is typically around −60 to −90 mV at pH 7, supporting excellent long-term colloidal stability. The electrokinetic response of micron-sized objects to an external electric field unescapably implies that they carry net charges, likely due to the structured distribution of cations and anions, which gives rise to an interfacial electrical double layer (Fig. 2b).
(4) Fourthly, there is an accumulation of negative charges on the hydrophobic polymer surface when in contact with water.93 When water droplets move across a hydrophobic surface, such as polytetrafluoroethylene (PTFE), two phases (water and polymer, respectively) become oppositely charged—a phenomenon called slide electrification. While this had been observed nearly a century ago in a largely curious manner, it has been recently harnessed to generate electrical energy to power light-emitting diodes (LEDs) (Fig. 2c and d).99 Further experiments suggested that slide electrification could yield an electric potential exceeding 1 kilovolt.100 In addition, electrostatic breakdown has also been observed at liquid–solid–gas triple-phase interfaces most recently,101 further suggesting the involvement of strong electric fields.
These pieces of evidence, albeit from different communities, are not isolated. For example, the surface pH measurement can be viewed as the static (only contact) version of slide electrification between water and air; electrokinetic measurement of micron-size objects can be viewed as the miniaturized version of slide electrification. Taken together, non-neutral surface pH, negative ζ potential and water electrification all point to the electrically active nature of aqueous interfaces and may be indicative of a local electric field. Such a convergence of findings raises two fundamental questions for physical chemistry: is there direct experimental evidence for the existence of such an electric field? And if so, how can their strength be quantitatively determined?
Evidence of on-water electric fields by optical imaging
Investigating the interfacial electric field poses both a valuable opportunity and a formidable challenge for experimentalists. Due to water's high dielectric constant and the associated strong screening effect, this interfacial electric field is expected to decay very quickly into the bulk phase, making its detection inherently difficult. Moreover, one cannot prepare only interfacial water without its bulk counterpart in an experiment. Therefore, either strict interfacial selectivity or rigorous separation is required to isolate the interfacial component from the bulk counterpart, which creates another hurdle.However, if an interfacial electric field does exist, it will exert a directional force on polar probe molecules, attracting them to the interface and aligning their dipoles (Fig. 3a). This physical consequence provides an indirect route to test the presence of the interfacial electric field. Optical imaging offers a powerful means to examine this hypothesis by directly visualizing the spatial and orientational distribution of fluorescent probes in microdroplets. Studies aiming to examine the electrostatics of the interface were performed on water–oil emulsions using either single-photon confocal fluorescence or two-photon excited fluorescence microscopy.80–82,102 They investigated the spatial (translational degree of freedom) and orientational (rotational degree of freedom) distributions of the probe at interfaces to evaluate whether such interfacial electric fields exist. These studies showed two consistent observations:
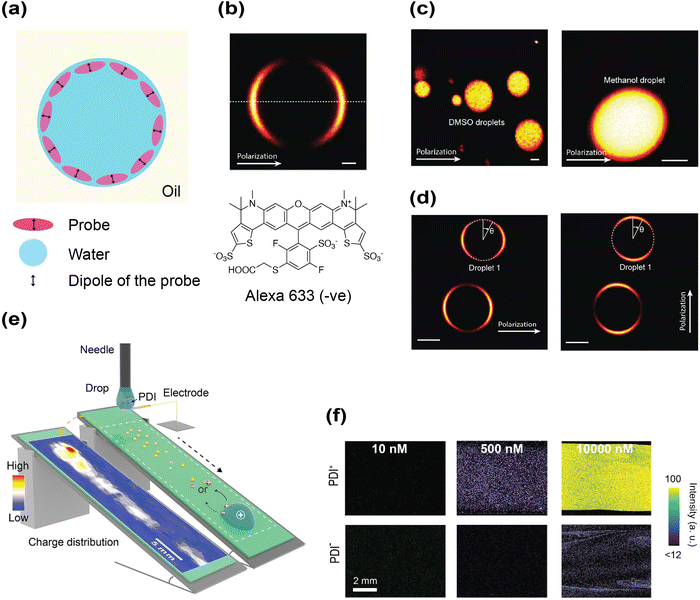 | ||
| Fig. 3 Probing the interfacial electric field using optical imaging of fluorophores. (a) A Schematic diagram showing how a probe can enrich and orient at the water–oil interface (b) Two-photon fluorescence imaging showing the spatial distribution of Alexa 633 (negatively charged) for aqueous droplets emulsified in hexadecane. A similar ring pattern was observed for rhodamine 101 (zwitterionic) and rhodamine 6G (positively charged). Scale bar: 1 µm. Reproduced with permission from ref. 81. Copyright 2020, the American Chemical Society. (c) The probe showed no interfacial enrichment or oriental preference in microdroplets prepared from DMSO/MeOH in hexadecane. Scale bar: 2 µm. Reproduced with permission from ref. 81. Copyright 2020, the American Chemical Society. (d) Strong anisotropy of rhodamine 800 can be observed by rotating the polarization direction of the excitation laser. The fluorescence signal is most intense along the excitation polarization vector where the coupling between the transition dipole and the incident laser's electric field is the strongest. Scale bar: 5 µm. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (e) An experimental setup for demonstrating slide electrification between water and a hydrophobic material, PFOTS. Water droplets containing either a positively charged fluorophore (PDI+) or a negatively charged fluorophore (PDI−) slide down PFOTS and their fluorescence distribution pattern is recorded using a confocal microscope. Reproduced with permission from ref. 104. Copyright 2025, Wiley-VCH. (f) PDI+ is deposited on the surface when its concentration reaches 0.5 µM, but PDI− only begins to deposit on the surface when its concentration reaches 10 µM. Reproduced with permission from ref. 104. Copyright 2025, Wiley-VCH. | ||
Firstly, probe localization at the interface with a clear ring pattern was observed in water microdroplets suspended in hexadecane oil (Fig. 3b).80–82,102 Although Fig. 3b only shows the localization image of a negatively charged dye (Alexa 633), the zwitterionic and positively charged probe exhibited the same ring pattern. As mentioned before, preferential adsorption of certain ions to interfaces leads to an ionic imbalance, which can produce an electrical double layer and attract probes to the interface. Interestingly, when water was replaced by other organic solvents immiscible with the oil such as methanol (MeOH) and dimethyl sulfoxide (DMSO), this characteristic ring pattern disappeared, and the probes distributed uniformly (Fig. 3c). Remarkably, the hexadecane oil does not form stable emulsions in MeOH, DMSO or acetonitrile (MeCN) environments, which implies that their resulting ζ potentials were negligible (i.e., high tendency towards aggregation). This would be accompanied by a much weaker interfacial electric field, which agrees with the disappearance of the ring pattern (Fig. 3c). Therefore, these two observations convey a consistent conclusion—water–oil interfaces possess uniquely strong electric fields.
Secondly, the detected fluorescence signal was not evenly distributed around the ring (Fig. 3d).80–82,102 The angular dependence of fluorescence intensity is known as excitation anisotropy. Fluorescence intensity is the highest when the transition dipole of the probe aligns with the polarization vector of the excitation beam and it is the weakest when perpendicular to it.103 In their studies, by rotating the laser polarization direction, the fluorescence signal distribution rotated accordingly, but the distribution pattern remained nearly the same. This phenomenon can be readily rationalized by the presence of an interfacial electric field, which is shown to be perpendicular to the water–oil interface in simulations,84 recruiting and strictly aligning the dipole of fluorescent probes on the interface through electrostatic interactions. Therefore, this intensity modulation is a strong manifestation for the rigid alignment of the probe's dipoles perpendicular to the water–oil interface. Again, this anisotropic effect was absent in droplets formed between oil and MeOH, MeCN or DMSO.
Similar surface enrichment of fluorescent probes has also been imaged on the water–solid planar interface.104 In this study, water droplets containing either positively or negatively charged fluorescent dyes were allowed to slide down an inclined hydrophobic surface coated with perfluorodecyltrichlorosilane (PFOTS). Fluorophore deposition on the surface was monitored using a confocal fluorescence microscope (Fig. 3e). Both dyes, PDI+ and PDI−, are perylene derivatives and share very similar chemical structures. At a concentration of 0.5 µM, PDI+ could readily deposit on the surface, whereas the deposition of PDI− required at least a 20-fold higher concentration (10 µM) (Fig. 3f). Such a disparity between two dyes with nearly identical molecular structures would hardly be explained by common hydrophobic interactions towards the interface. The positively charged dye having more pronounced surface partition than its negative counterpart is consistent with previous literature that hydrophobic water–solid interfaces are negatively charged,93 thereby recruiting the dye of opposite charge through the electric field.
Quantifying on-water electric fields with probe-based optical spectroscopy
Optical imaging experiments on water–oil/solid interfaces provide strong evidence to support the presence of the on-water electric field. However, quantitative measurement of the field strength is more challenging, as the exact relation between the electric field and the probe distribution (either translational or orientational) at interfaces could be non-trivial and depend on multiple parameters. One approach that has proven fruitful is to examine the spectroscopic shift of vibrational or fluorescence emission frequency of molecules on the interface. It is well established in physical chemistry that the energy eigenvalues are sensitive to the local electrostatic environment, and the amount of energy shift can be used to calculate the strength of the local electric field after proper calibration. Both probe-based and label-free spectroscopic experiments have been implemented to this end, and we will first introduce the former.The first reported field strength was measured by Xiong et al. when studying the vibrational frequency shift of a nitrile (CN) group in a probe molecule on the water–oil interface.82 The influence of an external electric field on a bond's vibrational frequency is known as the vibrational Stark effect (VSE) (Fig. 4a). VSE typically occurs in chemical bonds with anharmonic molecular potential. The first vibrational excited state usually has a larger dipole moment than the ground state. Hence, when the dipole aligns with the external electric field, the first excited state will be energetically more stabilized than the ground state does, leading to a slightly lower energy (redshift) of the vibrational transition between the ground state to the excited state. Mathematically, linear VSE is described by the following equation:
Δ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = −Δ = −Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) · ·![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) | (1) |
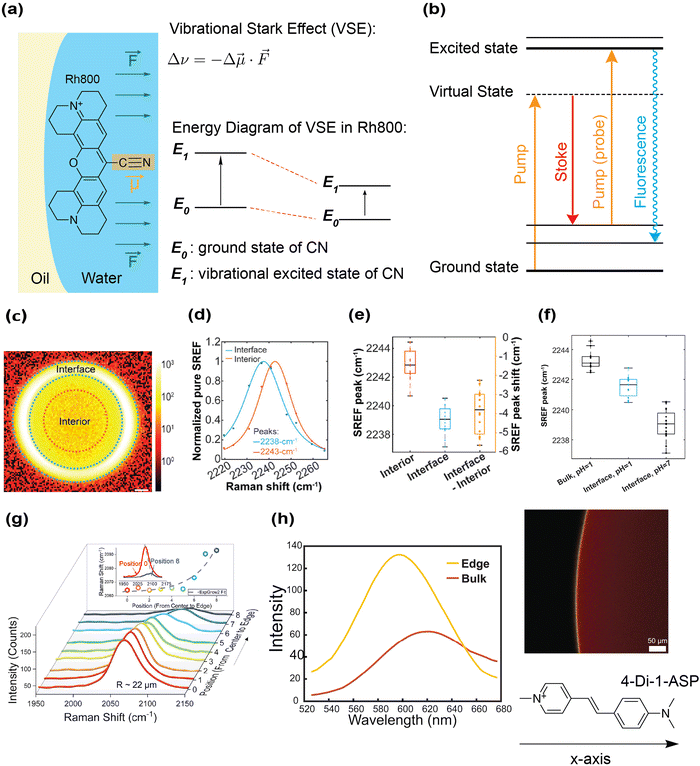 | ||
Fig. 4 Quantifying the interfacial electric field's strength by probe-based spectroscopy. (a) A schematic diagram showing how VSE decreases the vibrational frequency of the CN bond of rhodamine 800 at the water–oil interface. The dipole moment vector on rhodamine 800 aligns almost parallel to the CN bond axis, allowing good projection of the electric field onto the vibrational bond axis. Δv: shift in vibrational frequency, Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) : Stark tuning rate, and : Stark tuning rate, and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) : the external electric field that exerts on the CN bond. The vibrational excited state of the CN bond is more stabilized than its ground state, thus causing a redshift of the CN vibrational frequency. (b) Energy diagram of stimulated Raman excited fluorescence (SREF) spectroscopy. (c) First frame of SREF of the Rh 800 CN mode. The signal from a droplet is divided into three regions: interface, interface-interior and interior. Scale bar: 2 µm. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (d) Background-subtracted SREF spectrum. A redshift of 4 ± 1 cm−1 is recorded for the CN vibrational frequency on the interface. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (e) 16 independent measurements of the CN vibrational frequency on different droplets. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (f) SREF measurement of the CN group on Rh800 under different pH. At pH = 1, the Stark effect on the interface is less prominent. The CN vibrational frequency for Rh800 in the droplet interior remains unaffected at pH = 1. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (g) Probing the electric field at water–air interfaces using SERS spectroscopy. The VSE is studied by comparing the vibrational frequency of CN on gold nanoparticles (dissolved in the droplet) functionalized with SCN between the droplet interface and center. A shift in the CN vibrational frequency is observed on the interface compared with the center. Reproduced with permission from ref. 108. Copyright 2024, the Cell Press. (h) Probing the electric field at the water–air interface using a voltage-sensitive fluorophore (4-Di-1-ASP). The interfacial electric field can affect its fluorescence emission maximum (electrochromism). The emission maximum on the interface is shifted by 18 nm, suggesting that the electrostatic property on the interface and the bulk phase differs. Reproduced with permission from ref. 109. Copyright 2025, ChemRxiv. : the external electric field that exerts on the CN bond. The vibrational excited state of the CN bond is more stabilized than its ground state, thus causing a redshift of the CN vibrational frequency. (b) Energy diagram of stimulated Raman excited fluorescence (SREF) spectroscopy. (c) First frame of SREF of the Rh 800 CN mode. The signal from a droplet is divided into three regions: interface, interface-interior and interior. Scale bar: 2 µm. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (d) Background-subtracted SREF spectrum. A redshift of 4 ± 1 cm−1 is recorded for the CN vibrational frequency on the interface. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (e) 16 independent measurements of the CN vibrational frequency on different droplets. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (f) SREF measurement of the CN group on Rh800 under different pH. At pH = 1, the Stark effect on the interface is less prominent. The CN vibrational frequency for Rh800 in the droplet interior remains unaffected at pH = 1. Reproduced with permission from ref. 82. Copyright 2020, the American Chemical Society. (g) Probing the electric field at water–air interfaces using SERS spectroscopy. The VSE is studied by comparing the vibrational frequency of CN on gold nanoparticles (dissolved in the droplet) functionalized with SCN between the droplet interface and center. A shift in the CN vibrational frequency is observed on the interface compared with the center. Reproduced with permission from ref. 108. Copyright 2024, the Cell Press. (h) Probing the electric field at the water–air interface using a voltage-sensitive fluorophore (4-Di-1-ASP). The interfacial electric field can affect its fluorescence emission maximum (electrochromism). The emission maximum on the interface is shifted by 18 nm, suggesting that the electrostatic property on the interface and the bulk phase differs. Reproduced with permission from ref. 109. Copyright 2025, ChemRxiv. | ||
Δ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , Δ
, Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , and
, and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) are the shift in vibrational frequency, the Stark tuning rate of the vibrational mode, and the strength of the external electric field, respectively.105 To probe the electric field strength at the water–oil interface, a fluorescent probe, rhodamine 800 (Rh800), was employed. The bond axis of its CN group is almost parallel to the dipole moment of the molecule, allowing a good projection of the local electric field onto the vibrational CN bond axis.82
are the shift in vibrational frequency, the Stark tuning rate of the vibrational mode, and the strength of the external electric field, respectively.105 To probe the electric field strength at the water–oil interface, a fluorescent probe, rhodamine 800 (Rh800), was employed. The bond axis of its CN group is almost parallel to the dipole moment of the molecule, allowing a good projection of the local electric field onto the vibrational CN bond axis.82
To study the shift in the vibrational frequency of the CN bond, the vibrational Stark measurement was implemented through stimulated Raman excited fluorescence (SREF) microscopy (Fig. 4b). In SREF, the vibrational spectrum of a chemical bond is mapped into the fluorescence excitation spectrum, allowing superb detection sensitivity down to single molecule level.106 Thus, the SREF signal can serve as a basis for direct comparison of the CN group's vibrational frequency in different environments (i.e., interface vs. bulk) (Fig. 4c). By scanning the SREF images across the line shape of the CN vibrational mode, SREF spectra at different regions (interface and interior) were obtained. Direct comparisons of the SREF spectra from 16 independent measurements between the interface and the interior on different water droplets showed a clear redshift of the CN vibrational frequency (∼4 ± 1 cm−1) at the interface (Fig. 4d and e). The same SREF experiment was repeated with a lower Rh800 concentration to circumvent the possible interference from high probe concentration. Although the SREF signal was no longer detectable in the droplet interior with a low probe concentration, a similar redshift of CN vibrational frequency (∼3 ± 1 cm−1) was observed on the interface. Applying the eqn (1) with Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) of ∼0.53 ± 0.09 cm−1 MV−1 cm−1) for the CN group (estimated based on vibrational solvatochromic measurements and Onsager reaction field theory),107 this redshift corresponds to a local interfacial electric field of approximately 8 MV cm−1. The redshift's magnitude is also found to be pH dependent (Fig. 4f) but is much less sensitive to the concentation of salt ions such as Cl−, suggesting there is a chemical selectivity of the water-hydrophobe interface in attracting anionic species. The observed pH dependent redshift is also consistent with the pH-dependent ζ-potential of oil droplets.91,94
of ∼0.53 ± 0.09 cm−1 MV−1 cm−1) for the CN group (estimated based on vibrational solvatochromic measurements and Onsager reaction field theory),107 this redshift corresponds to a local interfacial electric field of approximately 8 MV cm−1. The redshift's magnitude is also found to be pH dependent (Fig. 4f) but is much less sensitive to the concentation of salt ions such as Cl−, suggesting there is a chemical selectivity of the water-hydrophobe interface in attracting anionic species. The observed pH dependent redshift is also consistent with the pH-dependent ζ-potential of oil droplets.91,94
Another VSE-based measurement was later performed at the water–air interface of aerosol particles.108 In this study, gold nanoparticles self-assembled with the vibrational thiocyanate (SCN) probes were utilized. The vibrational frequency of the CN mode inside aerosol particles was measured using surface-enhanced Raman scattering (SERS) spectroscopy. By spatially resolving the Raman signal from the droplet center to the surface, a Stark shift of 28.89 cm−1 of the CN mode was detected (droplet radius ∼22 µm) (Fig. 4g). A negative correlation between the Stark shift and droplet size was also found: Stark shift in droplets with a radius of 39 µm was 3.31 cm−1. Based on their calculation, the electric field on the surface of droplets was around 10 to 100 MV cm−1, which appears to be in line with the 8 MV cm−1 field strength obtained above by SREF microscopy on the water–oil interface, although the use of SERS nanoparticles, which are much larger than fluorophores, might suffer from a higher chance of perturbing the local air–water interface.
In addition to VSE, the shift in the fluorescence emission frequency, a phenomenon known as electrochromism, is another method to probe the strength of the on-water electric field. In their experiment studying the water–air interface in a water droplet (diameter ∼4 mm), a voltage-sensitive dye, 4-Di-1-ASP, was applied and imaged using spectral confocal fluorescence microscopy.109 On the water–air interface, the emission maximum of the dye was shifted by 18 nm (Fig. 4h). Their computational results further showed that only an electric field applied along the x-axis (from pyridinium to the amine group) of the molecule could lead to such a shift. Therefore, this shift suggested that the dye is oriented perpendicularly to the water–air interface. Moreover, since the transition dipole of 4-Di-1-ASP is also parallel to the x-axis of the molecule,110 its perpendicular alignment at the interface allows efficient perturbation of its transition dipole.111 Hence, the Stark effect experienced by the dye can probe the strength of the local electric field at the interface. By comparing the emission maximum on the interface and that in the bulk phase, the strength of the interfacial electric field can be estimated. Depending on the exact solvent polarity model employed, this shift corresponds to an electric field of 7.2 to 13 MV cm−1, which again is comparable to the 8 MV cm−1 field strength obtained above by SREF microscopy.82 When water was replaced by either anhydrous DMSO or dimethylformamide (DMF) under a nitrogen atmosphere, no shift in the emission maximum was observed, indicating vanishing electrostatics. This is consistent with solvent-dependent probe localization discussed above.80–82 This result confirmed that water is essential for generating the electrochromic shift of dye on the water–air interface.
Probing on-water electric fields with label-free optical spectroscopy
While the probe-based spectroscopic techniques, including SREF, SERS and electrochromism, successfully measured the interfacial electric field strength with largely comparable magnitudes of about 10 MV cm−1, interference or perturbation from the probe (either organic dyes or SERS nanoparticles) to the interfacial water layer is inevitable. Moreover, the size of the probe could be comparable or even larger than the length (presumably on the order of nanometers) of the interfacial water layer, which may lead to systematic deviation. Therefore, a label-free technique that can directly detect the interfacial electric field would be an important complement to existing probe-based techniques. To this end, the intrinsic water OH stretching mode offers a valuable opportunity to investigate the on-water electrostatics in a label-free manner.Due to the sensitivity of the OH stretching frequency to the local electrostatic environment, vibrational spectroscopy has long been a desirable tool to investigate the electrostatics of interfacial water.112–114 One approach to achieve the required surface selectivity is to decompose the Raman/IR spectrum of a mixture containing water and a hydrophobe using the multivariate curve resolution (MCR) algorithm. While this approach was initially developed to study the hydration shell of small solutes for homogenous solutions such as water–methane and water–alcohol mixtures,115–118 Shi et al. reported the first Raman-MCR spectroscopic study of mesoscale water–oil emulsions in 2025.80 Although Raman spectroscopy is inherently not a surface selective technique, the measured Raman spectrum of emulsions can be modeled and decomposed into a pure water spectrum and a solute-correlated (SC) spectrum with high interface selectivity for an in-solution sample (Fig. 5a).117 The decomposition algorithm is described by the following equation:
| D = CBSB + CSCSSC + E | (2) |
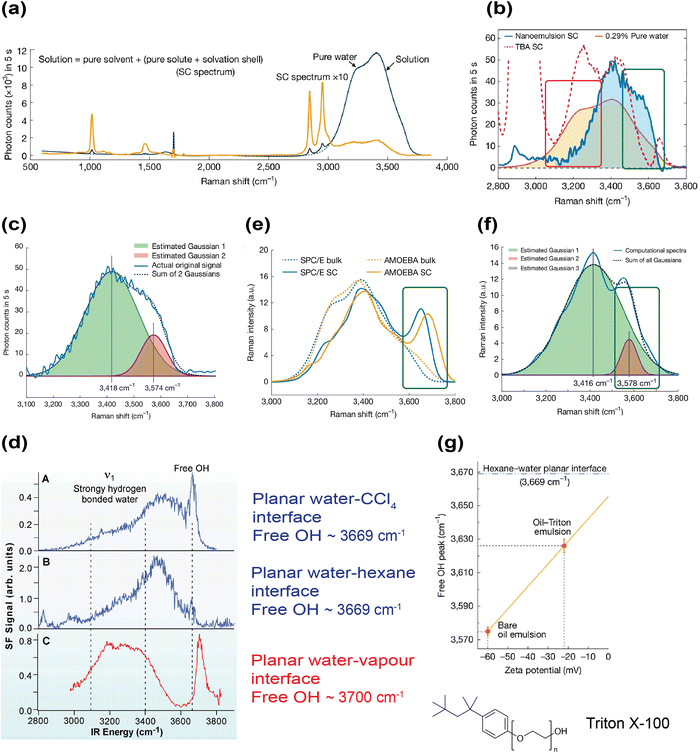 | ||
| Fig. 5 Quantifying the interfacial electric field's strength using Raman-MCR spectroscopy. (a) A proof-of-concept experiment (0.5 M MeOH in water) showing that the high-resolution Raman spectrum of the solution can be decomposed into the solvent (water) and the SC spectrum (contribution from the solute and the solvation shell) using the MCR algorithm. Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. (b) Area-scaled Raman spectrum of pure water (orange line), SC spectrum of water-hexadecane (deuterated) emulsion (blue line) and SC spectrum of 0.5 M TBA solution (red dotted line), respectively. Two characteristic features are highlighted in the SC spectrum of water-hexadecane emulsions, namely reduction of the 3250 cm−1 peak intensity (comparing with the pure water spectrum; highlighted in the red box) and redshift of the free OH stretching frequency to 3575 cm−1 (comparing with the SC spectrum of TBA; highlighted in the green box). Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. (c) Dual Gaussian fit of the water-hexadecane SC spectrum. Note the subpeak at 3574 cm−1. Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. (d) The vibrational sum frequency spectrum of the planar water–oil (tetrachloromethane and hexane) and water-vapor interface. Note the free OH stretching frequency, which is ∼110 cm−1 higher than that in water-hexadecane emulsions. Reproduced with permission from ref. 123. Copyright 2001, the American Association for the Advancement of Science. (e) Computational Raman spectrum using the monomer-field model, which is parametrized by either the SPC/E or AMOEBA model. Before applying the interfacial electric field, the free OH group stretching frequency (ranging from 3650 to 3700 cm−1) on the simulated SC spectra resembles the case in small solute/planar water–oil/air interface. Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. (f) By applying an external electric field (92.5 MV cm−1) on free OH group for the AMOEBA model, the free OH stretching frequency on the simulated SC spectrum is redshifted to 3578 cm−1, similar to the experimental observation. Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. (g) Correlation between free OH stretching frequency and the ζ potential. Addition of Triton X-100 reduces the ζ potential of hexadecane droplets in water and the magnitude of the free OH stretching frequency's redshift. Reproduced with permission from ref. 80. Copyright 2025, Nature Portfolio. | ||
D is the measured Raman spectrum of the emulsion, CB and CSC are the fractions of the solvent (water) and the oil, respectively, SB and SSC are the solvent and solute-corrected (contributed from both the oil and the OH stretching mode perturbed by the oil) spectrum, respectively, and E is the residual error matrix.80 Its application to water–oil emulsions successfully achieved a mesoscale-resolution measurement of the interfacial water. Furthermore, unlike sum frequency generation spectroscopy (which does not produce a signal on bulk materials), the interfacial water spectrum obtained from Raman-MCR can be readily compared to the bulk water Raman spectrum, as well as hydration shells of other small hydrophobic solutes such as alcohols.115,116,118
Raman-MCR spectroscopy revealed several noteworthy features. Firstly, the characteristic shoulder peak of OH stretching at 3250 cm−1 that typically appears in the bulk water's spectrum almost disappeared (Fig. 5b; see the red box).80 In bulk water, this shoulder peak is associated with strong hydrogen bonding and structural order.119,120 Hence, the vanishing of this spectral feature at 3250 cm−1 suggests that the hydrogen bonding network is weakened and more disordered on the mesoscopic water–oil interface. This observation was absent in previously reported SC spectra of small solutes such as tert-butyl alcohol.80,115 This insight was further supported by molecular-dynamics (MD) simulations. Near the water–oil interface, the Errington–Debenedetti order parameter was substantially reduced, indicating a significantly more disordered and weakened (nearly truncated) hydrogen bonding network at the interface. Secondly, there was a substantial water population with free OH groups on the mesoscopic water–oil interface.80 Both the experimental and simulated SC spectrum revealed that the amount of free OH groups made up about 13% of all OH groups within 2 Å of the Willard–Chandler Interface (WCI).121 The emergence of these free OH groups is also in line with the weakened hydrogen bonding network at the interface. Thirdly, the stretching frequency of free OH groups in the experimental SC spectrum of water–oil emulsions appeared at ∼3575 cm−1 (Fig. 5b and c; see the green box), which is redshifted by ∼95 cm−1 compared to the free OH peak of the planar water–oil (hexane and tetrachloromethane) interface (∼3670 cm−1) and water–vapor interface (∼3700 cm−1) (Fig. 5d).122,123 One likely explanation for this redshift is the VSE, in which a strong electric field at the water–oil interface modifies the free OH vibrational frequency. Using the previously reported Stark tuning rate Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) of 1.6 cm−1 MV−1 cm−1,124 the observed 95 cm−1 redshift corresponds to an electric field of ∼60 MV cm−1. Note that the previously reported interfacial electric field was ∼8.5 MV cm−1 in the probe-based method (CN group in Rh800),82 which is likely to be an underestimation since the probe's size is comparable to or even larger than the length of the interfacial water layer.
of 1.6 cm−1 MV−1 cm−1,124 the observed 95 cm−1 redshift corresponds to an electric field of ∼60 MV cm−1. Note that the previously reported interfacial electric field was ∼8.5 MV cm−1 in the probe-based method (CN group in Rh800),82 which is likely to be an underestimation since the probe's size is comparable to or even larger than the length of the interfacial water layer.
Computational Raman spectrum (both interface and bulk) using a monomer-field Raman model of water reproduced similar spectral features (Fig. 5e).80 The shoulder peak at 3250 cm−1 was greatly reduced, which is consistent with the more disordered and weakened hydrogen bonds at the interface. However, this model did not consider the presence of interfacial charges, thereby showing a free OH peak between 3650![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 3700
and 3700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−1. This resembles the reported value in the planar water–oil/air interface. By applying an extra interfacial electric field of 67.5 (SPC/E model) or 92.5 MV cm−1 (AMOEBA model) to free OH groups at the interface, the stretching frequency of free OH in the simulated SC spectrum would be redshifted to ∼3575 cm−1 and become nearly identical to the experimental free OH stretching frequency (Fig. 5f). This computational resemblance supports the experimental spectral redshift being a result of the influence of interfacial electric field on free OH groups.
cm−1. This resembles the reported value in the planar water–oil/air interface. By applying an extra interfacial electric field of 67.5 (SPC/E model) or 92.5 MV cm−1 (AMOEBA model) to free OH groups at the interface, the stretching frequency of free OH in the simulated SC spectrum would be redshifted to ∼3575 cm−1 and become nearly identical to the experimental free OH stretching frequency (Fig. 5f). This computational resemblance supports the experimental spectral redshift being a result of the influence of interfacial electric field on free OH groups.
Another important evidence to support the electrostatic origin of the redshift came from surfactant modulation of the interface.80 The ζ potential of pristine oil droplets in water was −60 mV. Addition of 0.01% Triton X-100, an amphiphilic, non-ionic surfactant that inserts into the water–oil interface, reduced the oil droplets’ ζ potential to −22 mV (Fig. 5g). Correspondingly, the free OH peak then appeared at ∼3626 cm−1, and the extent of redshift was much lower compared to the surfactant-free emulsion. A smaller ζ potential reflects a weaker interfacial electric field, hence a correspondingly smaller redshift of the free OH group.
Besides spectral decomposition in Raman-MCR, vibrational sum frequency generation (VSFG) spectroscopy, thanks to the inherent surface selectivity of the second-order nonlinear susceptibility χ(2), has been a widely adopted technique to study interfaces.125 In VSFG experiments, an IR and visible beam are spatially and temporally focused on the interface-of-interest. The sum frequency signal is resonantly enhanced when the frequency of the IR beam matches the water vibrational mode on the interface.126 VSFG implemented with heterodyne detection also reveals the orientations of interfacial water molecules.127,128 Strazdaite et al. used heterodyne-detected VSFG to study a wide range of D2O-hydrophobe interfaces, including air and various oils.129 Interestingly, the structure of interfacial water differs markedly between D2O–air and D2O–oil interfaces. Compared to D2O–air interfaces, D2O–oil interfaces exhibited enhanced hydrogen-bond ordering, as evidenced by their much stronger OD stretch signals in the lower frequency region (2390 to 2500 cm−1) (Fig. 6a). Moreover, Im(χ(2)) of this OD stretch band in the D2O–air interface was negative, while that in the D2O–oil interface was positive. This indicated that hydrogen-bonded OD groups point toward bulk water at the air interface but toward the hydrophobic phase at the oil interface (Fig. 6b). The only similarity was that, in both D2O–air/oil interfaces, their free OD groups at higher stretching frequency (∼2750 cm−1) oriented toward the hydrophobic phase (Fig. 6b). Their observed spectra were consistent with what Tian et al. measured for the water-silane/hexane interface, where Im(χ(2)) likewise exhibited an enhanced positive band for the OH stretch band (∼3200 cm−1) relative to water–air interface, suggesting that the OH groups point towards the hydrophobic phase.130 They reasoned that such OH orientation was likely due to the negative surface field arising from OH− adsorption on the interface.
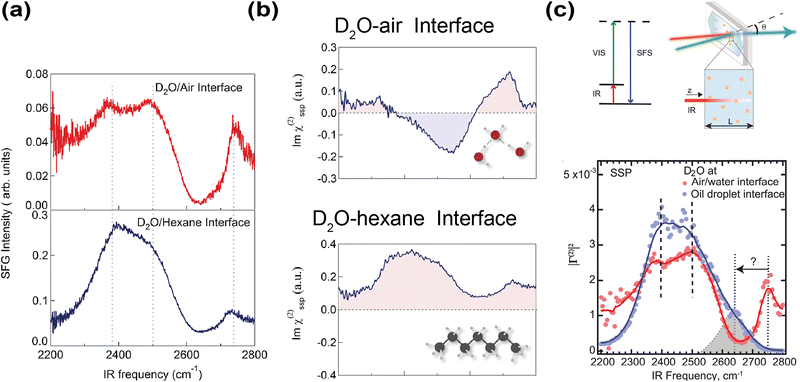 | ||
| Fig. 6 Probing hydrophobic water interface using sum frequency-based spectroscopy. (a) VSFG spectrum of D2O–hexane and D2O–air interface, respectively. Reproduced with permission from ref. 129. Copyright 2015, the American Institute of Physics. (b) VSFG spectrum showing Im(χ(2)) of D2O–hexane and D2O–air interfaces, respectively. Reproduced with permission from ref. 129. Copyright 2015, the American Institute of Physics. (c) Energy level diagram of VSFS and a schematic diagram of the experimental setup. Sum frequency scattering spectrum of D2O-hexadecane (blue) and water–air interface (red), respectively. Similar to the Raman-MCR spectrum, the stretching frequency of the free OD on the D2O–hexadecane interface is redshifted compared to the D2O–air interface. Reproduced with permission from ref. 132. Copyright 2021, the American Association for the Advancement of Science. | ||
While these VSFG studies on planar interfaces yielded valuable information about the interfacial water structure, planar interfaces may not accurately capture chemistry in microdroplets. Moreover, planar interfaces are also more prone to surface contaminations because of a much smaller surface-to-volume ratio. Despite these shortcomings, most VSFG studies have focused on planar interfaces, as probing water–oil emulsions was long considered impossible due to strong IR attenuation and spectral distortion in water.131 Nevertheless, in 2020, Pullanchery et al. demonstrated that vibrational sum frequency scattering (VSFS) could overcome this challenge by correcting the signal with a frequency-dependent normalization factor accounting for IR absorption and efficiency of optical collection, thereby enabling reliable measurements from water–oil emulsions (Fig. 6c).132 Compared to planar D2O–oil/air interfaces, the VSFS spectrum of D2O–oil emulsions did not show the high-frequency free OD stretching peak (∼2750 cm−1) (Fig. 6c). Instead, a new shoulder peak at around 2640 cm−1 was observed, so there was a redshift of around 110 cm−1 compared to the planar D2O–air interface (Fig. 6c). Note the magnitude of this redshift is comparable to that of the free OH peak in Raman-MCR.80 Thus, Raman-MCR and VSFS are largely consistent regarding the appearance and stretching frequency of the free OH(D) groups. The VSFS study attributed this redshift to a charge-transfer mechanism, in which electron density was transferred from water to oil molecules, as an explanation for the redshift of the free OD in their VSFS experiments and for the negative ζ potential of oil droplets dispersed in water.132,133 However, a recent energy decomposition analysis argued that the forward and backward charge transfer between water and oil nearly cancel so that the net flow charge is negligible.134 On the other hand, if one were to interpret the redshift of free OH in VSFS using VSE, nearly identical conclusions about the electric field strength would have been reached.
Apart from the interfacial water structure, VSFG can also provide insight about the adsorption of ions on the hydrophobic water interface, which has been a highly debated topic. For instance, by monitoring the change in Im(χ(2)) at 3200 cm−1 upon ion titration, Tian et al. showed that OH− had the highest adsorption energy (ΔG = −45 kJ mol−1) compared to H3O+ (ΔG = −39.5 kJ mol−1) and Cl− (ΔG = −28 kJ mol−1) on a water–silane interface.130 Their findings were later substantiated by Gan et al. in the water–hexadecane interface.135 Using second harmonic generation spectroscopy and a Langmuir adsorption model, they concluded that OH− has an adsorption free energy of −8.3 kcal mol−1, while H3O+ subsequently localizes to the interface due to electrostatic attraction with OH−. On the other hand, claims about preferential adsorption of H3O+ on the water surface do exist from VSFG experiments. For instance, the sum frequency response of the water–air interface collected by Tarbuck et al. at different pH levels revealed that the addition of H3O+ caused profound perturbation to the interfacial water structure, including orientation, coordination and strength of hydrogen bond, whereas the perturbation is much less significant when OH− was added.136 Therefore, they concluded that H3O+ is enriched on the interface. Their finding is also supported by some subsequent studies.137–139 Again, it is worth emphasizing that VSFG experiments employed a planar water interface, not a curved interface where ζ potential is present or where microdroplet chemistry happens. The planar model can potentially neglect the effect of local curvature on interfacial water structure and charge distribution. Although the precise origin and nature of interfacial ions remain debated, extensive evidence supports the presence of excess charges at water interfaces (Table 1), leaving the detailed physical picture an open question.
| Methods | Interfaces | Measured field strengths |
|---|---|---|
| SREF-VSE | Water-hexadecane interface (emulsion) | ∼4 MV cm−1 |
| SERS | water–air interface (aerosol) | ∼10–100 MV cm−1 (size dependent) |
| Spectral confocal fluorescence microscopy | water–air interface | ∼10 MV cm−1 |
| Raman-MCR | Water–hexadecane interface (emulsion) | ∼60 MV cm−1 |
| Electroacoustic Measurement | Water–hexadecane interface (emulsion) | ∼55 MV cm−1; deduced from a charge density (−4.9 µC cm−2 at pH = 9) |
| Potentiometric mass titration | Water–Teflon interface (nanoparticles in water) | ∼50 MV cm−1; deduced from a charge density (−4.5 µC cm−2 at pH = 5) |
| pH Measurement | water–air interface (microbubbles in water) | ∼45 MV cm−1; deduced from surface OH− excess (4.2 × 10−11 mol cm−2 at pH = 7) |
Connection and consistency with other experimental studies
Is the interfacial electric field of ∼60 MV cm−1, as concluded by Raman-MCR and VSE, consistent with other studies performed on similar samples? We would like to point out that there exists a striking consistency between this value and those deduced from non-spectroscopic approaches. In 2004, Beattie and Djerdjev designed an ingenious experiment to estimate the surface charge density of pristine oil-in-water emulsions.94 They conducted pH-stat experiments combined with an electroacoustic technique to measure the size and surface charge of oil droplets as new water–oil interfaces were being formed. In their method, an emulsion of hexadecane in water was homogenized in a nitrogen atmosphere. The pH was kept constant by titrating with a proper amount of NaOH. As homogenization proceeded, new water–oil interfaces were generated and the amount of OH− added to maintain a constant pH was recorded. Meanwhile, electroacoustic measurements allowed real-time monitoring of droplet size and ζ potential during the entire homogenization process. It was revealed that there was a linear relationship between the amount of added OH− and the increase in surface area (Fig. 7a). Thus, this suggested an intrinsic and constant surface charge density on the oil–water interface, for which hexadecane oil droplets in water were fitted to be −4.9 µC cm−2. Using a similar pH-stat approach, Gan et al. estimated a charge density of −0.14 e nm−2 for hexadecane oil droplets in water, corresponding to −2.3 µC cm−2,135 comparable to the value obtained by Beattie and Djerdjev. The difference might be from the higher pH (∼13) used in Gan et al. and/or the error associated with the estimation of the surface area. They also emphasized that if the observed ζ potential arose from carboxylic acid contaminants in hexadecane, such species would have been spectroscopically detectable, as a charge density of −0.14 e nm−2 corresponds to a concentration of mM, far above the detection limit of second harmonic generation spectroscopy.135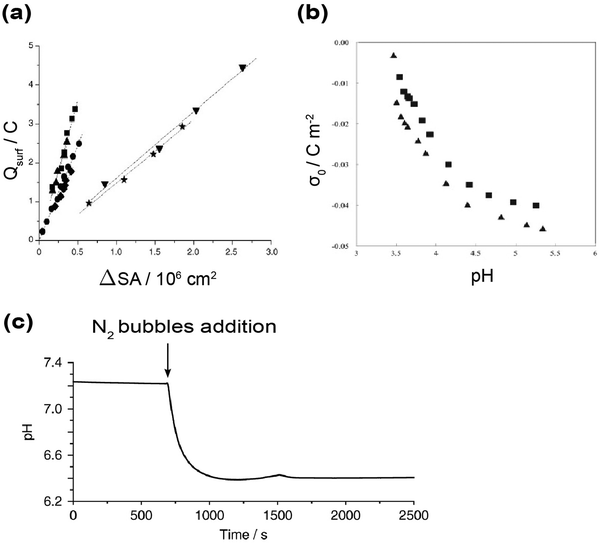 | ||
| Fig. 7 Non-spectroscopic studies on the electrostatics of hydrophobic water interfaces. (a) Correlation between the change in surface area (ΔSA) and surface charge (Qsurf) in different water–oil emulsions: perfluoromethyldecalin (■) at pH = 9: −7.3 µC cm−2, squalene (▲) at pH = 9: −6.7 µC cm−2, hexadecane (●) at pH = 9: −4.9 µC cm−2, hexadecane (✦) at pH = 7: −4.6 µC cm−2, hexadecane with 2 mM SDS (▼) at pH = 9: −1.7 µC cm−2, and squalene with 2 mM SDS (★) at pH = 9: −1.6 µC cm−2 respectively. Reproduced with permission from ref. 94. Copyright 2004, Wiley-VCH. (b) Teflon surface charge density as a function of pH. At pH = 5, the surface charge density on Teflon is around −4.5 µC cm−2. Reproduced with permission from ref. 142. Copyright 2012, Elsevier. (c) Reported pH drop when nitrogen bubbles are added to ultrapure water. Based on the pH drop, the calculated surface OH− excess is calculated to be 4.2 × 10−11 mol cm−2 in nearly neutral pH. This corresponds to a surface charge density of around −4 µC cm−2. Reproduced with permission from ref. 143. Copyright 2020, Nature Portfolio. | ||
The mathematical relationship between the surface charge density and the electric field strength is described by the Gauss's law (in a vacuum):
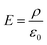 | (3) |
E is the electric field, ρ is the surface charge density, and ε0 is the vacuum permittivity (absolute dielectric constant in vacuum). When using eqn (3) to water interfaces, it should be recognized that the dielectric response of interfacial water differs significantly from the bulk water (whose dielectric constant is ∼78). The effective permittivity of interfacial water, however, has been shown to rapidly approach the vacuum value.140,141 Thus, applying eqn (3) and ε0, the surface charge density (−4.9 µC cm−2) estimated by Beattie and Djerdjev can generate an interfacial electric field of ∼55 MV cm−1, remarkably consistent with the Raman-MCR inferred value of ∼60 MV cm−1.80
In addition to the water–oil emulsions above, similar densities (∼4 to 5 µC cm−2) of negative surface charge have been observed in solid Teflon nanoparticles (Fig. 7b) and nitrogen gas microbubbles dispersed in water (Fig. 7c).142,143 It would be hardly coincidental that all three mesoscopic (i.e., nanodroplets, microbubbles and nanoparticles) hydrophobic phases (lipid, air and solid) of aqueous interfaces exhibit a fairly similar level of surface charge density. Even two-dimensional materials such as hexagonal boron nitride, when in contact with water, were found to acquire a surface charge density of approximately −2.3 µC cm−2 at pH = 7, which was assigned to OH− chemisorption and physisorption.144 Applying the Gauss's law again to these systems would result in an interfacial electric field with comparable strength to the one determined for the water–oil interface. Considering the wide range of experimental techniques employed and interfacial water samples examined, the close agreement among these electric field strengths is notable and strongly suggests a common underlying principle for all water-hydrophobe interfaces.
Possible mechanism of hydroxide accumulation on hydrophobic interfaces
Despite still being a controversial topic with ongoing debates, mounting experimental evidence has indicated the preferential accumulation of OH− ions on water–hydrophobe interfaces,91,94,96 regardless of the specific hydrophobic material involved (e.g., air and oil). Unfortunately, the underlying driving force of this phenomenon remains sparsely discussed in the literature. Here, we highlight an insightful work of Gray-Weale and Beattie, who proposed a thermodynamically grounded framework that coherently accounts for the available experimental observations.78 They attribute the interfacial adsorption of OH− to a suppression in the collective dipole-moment fluctuations of nearby water, which leads to a free energy reduction near interfaces. The depth of the potential well (∼20 kBT) quantitatively underscores the energetic favorability and strength of this adsorption preference. More broadly, this mechanism unifies seemingly disparate systems, including water–oil, water–air, and water–solid interfaces.Central to this so-called fluctuation-suppression model is the ion's ability to lower the relative permittivity of an aqueous solution, and this can be quantitatively described by the following equation:
| ε(c) = εw − δ·c | (4) |
c is the molar concentration of the electrolyte, εw is the relative permittivity of pure water (∼78), and δ is the dielectric decrement. Experimental studies have shown that OH− exhibits almost the largest dielectric decrement among all monovalent anions, such as Cl−.145,146 This is plausibly related to the unique solvation structure proposed in other studies, where water molecules are tightly coordinated to the oxygen atom of OH−.147–150 This property uniquely positions OH− to accumulate at the interface, a behavior made even more remarkable by the fact that OH− is a natural product of water's autoionization and is inherently present in all aqueous systems.
As illustrated in Fig. 8a, an anion in a homogeneous polar solvent imposes constraints on its solvation shell, suppressing local collective dipole-moment fluctuations. The surrounding region, which would normally exhibit correlated fluctuations with the constrained shell, is disrupted—resulting in a free energy penalty. Although the correlation strength decays smoothly with distance, the two-region model (inner constrained zone and outer correlation zone) serves as a useful conceptual simplification. However, when the ion approaches a hydrophobic interface, as shown in Fig. 8b, this energetic penalty is reduced. This is because part of the fluctuation-affected region overlaps with the low-permittivity phase (air, oil or solid, compared to that of water), where water molecules are absent. As a result, fewer “broken” correlations occur within range, and the corresponding free energy cost is diminished. This translates into a net force that attracts ions towards the interface with a vacuum or another medium of low permittivity, which is analogous in form to Hamaker-type dispersion interactions.151
 | ||
| Fig. 8 The fluctuation–suppression model and the potential profiles for OH− and Cl−. (a) An ion in a polar solvent: molecules in the constrained solvation shell (yellow) are not as free as the others to fluctuate, breaking correlations in the surrounding region (larger blue circle). (b) When the same ion is near a hydrophobic interface (gray), part of the correlation zone overlaps with the low-permittivity phase, reducing the number of broken correlations and thus the free energy cost. (c) Calculated potentials of mean force for hydroxide and chloride ions. OH− (red) exhibits a deep potential well (∼20 kBT) at ∼6.7 Å, consistent with strong interfacial adsorption; Cl− (blue) shows a much shallower well. Reproduced with permission from ref. 78. Copyright 2009, the Royal Society of Chemistry. | ||
The full derivation of the fluctuation–suppression force can be found in the original work. Here we briefly summarize the key result. Total free energy is modeled as the sum of two components: a fluctuation-suppression term v(z) and a self-image repulsion term u(z), where z is the distance from the ion. The former arises from the loss of solvent dipole correlations as discussed above. The latter accounts for electrostatic image forces that act to repel the ion from the low-permittivity phase, which dominates at very short distances.151 The total potential of mean force, v(z) + u(z), is calculated and plotted as shown in Fig. 8c. In the case of OH−, a conservatively estimated dielectric decrement (δ− = 10.7 ± 3.1 M−1) is employed. The model predicts a deep potential well with a minimum around 6.7 Å and a depth of approximately 20 kBT.
This magnitude has been validated by a very recent experimental study, which reported an even higher adsorption free energy of 28.4 kBT per OH− at the water–oil interface.152 This value was determined by analyzing the heat released during acid-induced breaking of pristine oil-in-water emulsions, after subtracting the estimated contributions from neutralization and interfacial tension. Consistent results for the desorption enthalpy were observed across three systems: two emulsions with isopropyl myristate and one with hexadecane.
According to Boltzmann statistics, surface ion concentration is expected to scale exponentially with the depth of this potential well. Thus, the ∼20 kBT well for OH− leads to a significant interfacial enrichment, while other anions such as Cl−, with much shallower wells, show lower surface affinity. The study calculated that each OH− within the shear plane occupies an area of approximately 4.5 nm2. This theoretical estimate closely matches the experimental value of ∼3.2 nm2 reported earlier by Beattie and Djerdjev.94 Such close agreement between theory and experiment reinforces the credibility of the model and confirms the high interfacial density of OH−.
Notably, this model successfully reproduces a wide range of experimental observations, including low isoelectric points of hexadecane emulsions,153 the pH dependence of ζ potentials of hexadecane droplets,94 and the Jones-Ray effect as reflected in surface tension measurements.154–156 To predict ζ potential, by numerically solving a modified Poisson–Boltzmann equation that incorporates the fluctuation–suppression potential, the electrostatic potential profile near the interface can be obtained. The slip plane was assumed to lie 2.5 nm away from the interface, and the potential at that position was taken as the ζ potential. By varying the fluctuation-suppression radius a, the simulated ζ potential curves show excellent agreement with experimental data across a wide pH range, with the best fit achieved at a = 6.7 Å. This value corresponds to a potential well depth of 20 kBT, as discussed above. In addition, the predicted isoelectric point was shown to be highly sensitive to both the dielectric decrement δ and the value of a. A decrement as small as that of chloride (5 M−1), or a slightly larger a, would shift the isoelectric point upward toward neutral pH, in conflict with experimental results. The model thus naturally explains the low isoelectric point near pH 3 to 4. Importantly, these predictions arise directly from the computed potential well, without reliance on empirical fitting parameters. Moreover, it accounts for previous contradictions in surface-sensitive spectroscopic data, such as VSFG,137,139 by suggesting that OH− mostly resides below the outermost molecular layers, beyond the typical probing depth of those interface selective techniques.
Implications of on-water electric fields on chemical reactivity
What are the consequences of a strong electric field on chemistry? One elegant and well-established example to demonstrate the effect of electric field on chemistry is enzyme catalysis. As demonstrated by Boxer and co-workers, the active site of an enzyme can exert a large and homogenous electric field on the substrate through pre-organizing its residues to stabilize the transition state, thereby reducing the activation barrier.157 Different from reactions in bulk solution, where solvent molecules mostly interact and stabilize the ground state of the reactant molecule, the active site of an enzyme has evolved to orient the dipoles and charges of amino acid residues so that the resulting electric field is strong and precisely focused on specific bonds of the substrate, especially those undergoing charge rearrangement in the transition state. An enzyme to showcase this principle is ketosteroid isomerase (KSI).158 KSI catalyzes the isomerization of 3-oxo-Δ5-steroid to 3-oxo-Δ4-steroid, which involves the conversion of a ketone (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) to a charged enolate (C–O−). Using the vibrational frequency of the ketone group as the Stark probe, KSI was shown to exert a strong electric field (∼150 MV cm−1) via the OH and COOH groups in Tyr16 and Asp103, respectively. Moreover, by mutating the wild-type residues, the kinetic barrier for forming the enolate intermediate was found to increase from ∼11 to 16 kcal mol−1 while the electric field was reduced from ∼150 to 60 MV cm−1. Taken together, enzyme catalysis highlights how an electric field can be a robust regulator of reactivity.
O) to a charged enolate (C–O−). Using the vibrational frequency of the ketone group as the Stark probe, KSI was shown to exert a strong electric field (∼150 MV cm−1) via the OH and COOH groups in Tyr16 and Asp103, respectively. Moreover, by mutating the wild-type residues, the kinetic barrier for forming the enolate intermediate was found to increase from ∼11 to 16 kcal mol−1 while the electric field was reduced from ∼150 to 60 MV cm−1. Taken together, enzyme catalysis highlights how an electric field can be a robust regulator of reactivity.
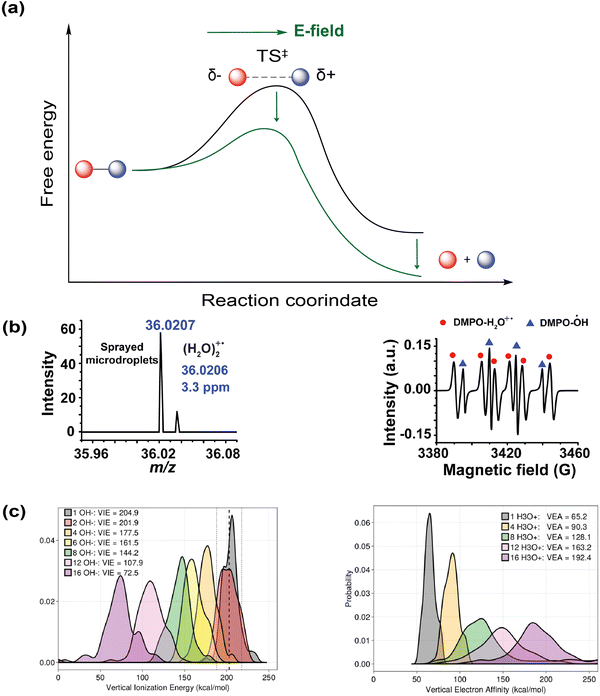
Just as enzymes exploit localized electric fields in their active sites to stabilize transition states, aqueous microdroplets have also been experimentally shown to possess a strong electric field at their interfaces, to which their unusual reactivity is often attributed. Herein, we would like to focus on the chemical reactivity of microdroplets. If such an electric field truly exists on microdroplet interfaces, it can potentially account for the accelerated kinetics and altered thermodynamics in microdroplet chemistry (Fig. 9a). We will illustrate by using simple chemical principles.
 | ||
| Fig. 9 Implications of the interfacial electric field on chemical kinetics and thermodynamics. (a) A schematic diagram showing the altered reaction kinetics and thermodynamics under the influence of an external electric field. (b) Generation of water dimer radical cation is detected using high-resolution mass spectrometry (note the peak with m/z = 36.0207) and electron paramagnetic resonance spectroscopy. Reproduced with permission from ref. 33. Copyright 2025, the American Chemical Society. (c) MD simulations showing that in the presence of excess charges in a microdroplet, the vertical ionization energy of OH− is greatly reduced, whereas the vertical electron affinity of H+ is significantly increased. Reproduced with permission from ref. 169. Copyright 2024, Nature Portfolio. | ||
A strong interfacial electric field will greatly impact the chemical kinetics observed in microdroplets. The effect of electric field on the activation energy can be captured by the following equation:
ΔΔG† = −Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) rxn· rxn·![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) | (5) |
ΔΔG†, Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) rxn and
rxn and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) are the change in activation free energy, the change in dipole moment between ground state and transition state, and the external electric field, respectively.157,159 Assuming a dipole moment difference of 2 Debye between the transition state and the reactant ground state, which is a reasonable magnitude for many reactions (for instance the dipole moment difference for tert-butylchoride in a SN1 reaction is ∼5.5 Debye),157 a lower bound of the interfacial electric field (∼50 MV cm−1) can lower the free energy barrier by 4.8 kcal mol−1. According to simple transition state theory, this will accelerate the rate constant by 3 to 4 orders of magnitude and thus it is a key factor for explaining the rate acceleration of many reactions in aqueous microdroplets relative to the bulk solvent.
are the change in activation free energy, the change in dipole moment between ground state and transition state, and the external electric field, respectively.157,159 Assuming a dipole moment difference of 2 Debye between the transition state and the reactant ground state, which is a reasonable magnitude for many reactions (for instance the dipole moment difference for tert-butylchoride in a SN1 reaction is ∼5.5 Debye),157 a lower bound of the interfacial electric field (∼50 MV cm−1) can lower the free energy barrier by 4.8 kcal mol−1. According to simple transition state theory, this will accelerate the rate constant by 3 to 4 orders of magnitude and thus it is a key factor for explaining the rate acceleration of many reactions in aqueous microdroplets relative to the bulk solvent.
Take the conversion of OH− to hydroxyl radicals as a concrete example with an immediate implication to redox chemistry. While examining the energetics of water back in 1988, Kloss suggested that a minor fraction of OH− exists as a radical-electron pair (OH˙–e−), which may reversibly dissociate into a hydroxyl radical and an electron when it is subject to an external perturbation such as an electric field in pure water.160
 | (6) |
Along this line, a sophisticated calculation using MD simulations from Head-Gordon and co-workers suggested that OH− are under-coordinated on the droplet surface relative to the bulk, exhibiting much lower vertical ionization energy.161 Such partial solvation is likely related to the significantly weakened (nearly-truncated) hydrogen bonding network of the interfacial water itself, as unveiled by the recent Raman-MCR spectroscopic study.80 Consistent with Kloss's vision, this simulation further revealed that a field strength of 80 MV cm−1 exerting ∼5 Å is sufficient to convert the interfacial OH− to a hydroxyl radical.161 Note that the Raman-MCR inferred value of ∼60 MV cm−1 is an average over space and time. Thus, its fluctuations around the average are inevitable, resulting in a rather large probability of reaching the required 80 MV cm−1,84,162 thereby catalyzing the radical generation. The interfacial electric field is also believed to be connected to the curvature of microdroplets.163 Different from the above mechanism of hydroxyl radical oxidizing from OH−, it has been recently hypothesized that the strong electric field can also promote the natural dissociation of water into radical cation/anion pairs (H2O+˙/H2O−˙) and separate the free radical ions into different layers.164,165 While water is more abundant than OH− at the interface, the loss of an electron from OH− is expected to be much lower in energy. Experimentally, Zare, Zhang and co-workers reported the capture of hydroxyl radicals in the form of OH˙–H3O+ (hydrogen bonding with a hydronium cation) using a mass spectrometer.29 Moreover, its isomeric configuration, water dimer radical cation (H2O)2+˙, has been recently detected using both high-resolution mass spectrometry (observed peak at m/z 36.0207 vs. the calculated exact mass of 36.0206 with a mass accuracy error of 3.3 ppm) and electron paramagnetic resonance spectroscopy (Fig. 9b).33 The hydroxyl radicals and hydrated free electrons from interfacial OH− can trigger a plethora of downstream redox reactions.
Besides, the electric field and the associated electrostatic charge can also alter the thermodynamics of reactions profoundly. Intuitively, an electric field can align and enrich charged or polar molecules near the interface and consequently minimize the entropic barrier of chemical reactions. However, chemical thermodynamics textbooks virtually neglect the effect of matter's electrification. This had promoted McCarthy and Whitesides to ask “One of the basic assumptions of chemical thermodynamics is that bulk matter is electrically neutral…. What is the chemistry of materials that bear a net electrostatic charge?”166 Quantitatively, the electrochemical potential µi of an ionic species i in an aqueous solution is governed by the following equation:
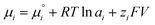 | (7) |
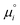 is the standard chemical potential of species i, ai is the thermodynamic activity of species i, R is the ideal gas constant, T is the temperature, zi is the charge of species i, F is the Faraday constant, and V is the local potential.167,168 The first part of the equation
is the standard chemical potential of species i, ai is the thermodynamic activity of species i, R is the ideal gas constant, T is the temperature, zi is the charge of species i, F is the Faraday constant, and V is the local potential.167,168 The first part of the equation 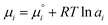 is the textbook knowledge when describing chemical thermodynamics. However, the ziFV term is often neglected (V = 0) unless the reaction involves a charged interface (i.e., an electrode), an external potential, or the material's electrification.
is the textbook knowledge when describing chemical thermodynamics. However, the ziFV term is often neglected (V = 0) unless the reaction involves a charged interface (i.e., an electrode), an external potential, or the material's electrification.
If one puts the above equation in the context of redox microdroplet chemistry, it can provide an explanation of why some thermodynamically unfavorable reactions (i.e., H2O2 generation) can occur spontaneously in a microdroplet environment. Head-Gordon and co-workers elucidated the role of charge in microdroplet chemistry and explicitly emphasized that the reaction thermodynamics in charged microdroplets, especially for redox reactions, are not the same as those occurring in bulk solution.169 In their simulations, they examined the following reaction:
| OH− + H+ → OH˙ + H˙ | (8) |
This reaction is normally highly endothermic (+107 kcal mol−1), yet in a water microdroplet with excess charge (∼20 to 50% of the Rayleigh limit), it is shown that the reaction thermodynamics can be altered dramatically. The strong Coulombic repulsion within the droplet destabilizes solvated ions. Increasing the net charge of a 4-nm water microdroplet (from ±1 to ±16) substantially reduces the hydration enthalpy, shifting from −126 to +10 kcal mol−1 for OH− and from −263 to −146 kcal mol−1 for H+. Thus, the thermodynamic penalty in bulk solution for removing charged species is relieved due to the presence of excess charges in microdroplets, i.e., eqn (8) becomes favorable. At the same time, the vertical ionization energy of OH− decreases whereas the vertical electron affinity of the H+ increases in the presence of charges, indicating that electron transfer between these species becomes more electronically favored (Fig. 9c). Moreover, these results are not confined to nanoscale droplets but can be directly extended to the micro-sized ones, which are more relevant to real experimental conditions. Altogether, in charged microdroplets, the combined shifts in hydration and ionization energy levels act together to make radical formation thermodynamically spontaneous. This provides a molecular-level explanation to rationalize why simultaneous reduction and oxidation become possible in a microdroplet environment,36 despite the thermodynamic barrier.
Conclusions and outlook
Building upon and inspired by pioneering work in “on-water” catalysis and the emerging microdroplet chemistry, this review systematically summarizes the presence, characteristics, and implications of strong electric fields on different water–hydrophobe interfaces. A wide variety of experimental methods, including fluorescence imaging, SREF-vibrational Stark spectroscopy, electrochromism, Raman-MCR, and VSFG spectroscopy, among others, have collectively provided extensive evidence substantiating the existence of an electric field at water interfaces. Remarkably, the inferred strengths of these fields all fall within the range of tens of MV cm−1, in close agreement with values independently estimated from electrokinetic and surface charge measurements. This strongly hints at the existence of strong electric fields being a general feature of water–hydrophobe interfaces. Moreover, this review highlights an intriguing thermodynamic mechanism proposed by Gray-Weale and Beattie that is able to explain the accumulation of OH− at interfaces and reproduce a wide range of experimental observations such as high interfacial density of OH−, isoelectric points of hexadecane emulsions, and the pH dependence of ζ potentials of hexadecane droplets. Central to this mechanism is the suppression of dielectric fluctuations and the associated reduction in free energy near the interface.Our current understanding of hydrophobic water interfaces is still not complete.170–173 Firstly, all aforementioned spectroscopic/microscopic studies of water interfaces capture steady-state response. Important dynamic features, including hydrogen bond rearrangements, vibrational relaxation timescales, transient fluctuations of ions on interfaces, etc. are still unclear. To this end, time-resolved spectroscopy, such as time-resolved VSFG, can offer a powerful method moving forward. It can directly probe how the vibrational frequency of water fluctuates in time (spectral diffusion) and water reorientation kinetics.174–176 Beyond the temporal aspect, another incomplete puzzle lies in the spatial resolution, as the reported electric field strength was derived from ensemble-averaged measurements. Future progress will benefit from methods that can directly probe the spatially resolved water structure and electric fields. Moreover, it should also be recognized that the role of the interfacial electric field may be coupled to, or confounded with, other effects like solvation. For instance, a recent simulation has indicated that the solvation structure of a molecule on the interface can largely determine the electric field it experiences.177 Further studies on disentangling the relative contributions to the observed reactivity are highly desirable. Finally, current studies have not conclusively determined the identity of the charged species on the interface. While ζ potential measurements for solids, gas bubbles and oil droplets dispersed in water almost unequivocally suggest that hydrophobic water interfaces are negatively charged,93,96,98 spectroscopic evidence remains less conclusive. On the theoretical side, some earlier simulations predicted preferential accumulation of H3O+ on the interface,90,178,179 and recent ones suggest the presence of both H3O+ and OH−.180,181 Thus, experiments that can reconcile the measured ζ potential with the identity of the charged species will be incredibly constructive.
The presence of these intrinsic electric fields would reshape our understanding of how interfacial environments influence chemical reaction kinetics and thermodynamics. As shown by simple chemical principles, strong electric fields can potentially account for the accelerated kinetics, altered thermodynamics and radical-based redox reactions. Harnessing interfacial electrostatics thus offers a promising engineering strategy for modulating chemical reactivity and aqueous-phase synthesis, as being implemented most recently.182 Continued advances in spectroscopy and imaging are anticipated to illuminate the intricate relationships between interfacial water structure, electrostatic environment, and chemical reactivity. Such advances will be critical to developing predictive models of interfacial chemistry. This will also pave the way for future innovations across different areas, ranging from catalysis and materials synthesis to atmospheric chemistry and environmental remediation, where interfacial processes play a central role.
Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.Acknowledgements
W. M. acknowledges support from the Multi-University Research Initiative (MURI) of the Air Force Office of Scientific Research (FA9550-21-1-0170), the National Institute of Health (R35 GM149256), and Chan Zuckerberg Initiative (Dynamic Imaging 2023-321166). K. Y. C. acknowledges Croucher Scholarships for Doctoral Study (Croucher Foundation, Hong Kong).References
- D. C. Rideout and R. Breslow, J. Am. Chem. Soc., 1980, 102, 7816–7817 CrossRef CAS.
- R. Breslow, U. Maitra and D. Rideout, Tetrahedron Lett., 1983, 24, 1901–1904 CrossRef CAS.
- R. Breslow, Acc. Chem. Res., 1991, 24, 159–164 CrossRef CAS.
- S. Narayan, J. Muldoon, M. G. Finn, V. V. Fokin, H. C. Kolb and K. B. Sharpless, Angew. Chem., Int. Ed., 2005, 117, 3339–3343 CrossRef.
- Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502 CrossRef CAS.
- A. Chanda and V. V. Fokin, Chem. Rev., 2009, 109, 725–748 CrossRef CAS PubMed.
- M. F. Ruiz-Lopez, J. S. Francisco, M. T. Martins-Costa and J. M. Anglada, Nat. Rev. Chem., 2020, 4, 459–475 CrossRef CAS PubMed.
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Annu. Rev. Phys. Chem., 2020, 71, 31–51 CrossRef CAS PubMed.
- R. A. LaCour, J. P. Heindel, R. Zhao and T. Head-Gordon, J. Am. Chem. Soc., 2025, 147, 6299–6317 CrossRef CAS.
- X. Jia, J. Wu and F. Wang, JACS Au, 2024, 4, 4141–4147 CrossRef CAS PubMed.
- H. Chen, X. Li, B. Li, Y. Chen, H. Ouyang, Y. Li and X. Zhang, J. Am. Chem. Soc., 2025, 147, 11399–11406 CrossRef CAS PubMed.
- M. F. Ruiz-López and M. T. Martins-Costa, Phys. Chem. Chem. Phys., 2022, 24, 29700–29704 RSC.
- Y. Wang, Y. Ju, J. He, J. Zhao, Z. Zhou, J. Jiang and H. Zhang, J. Phys. Chem. Lett., 2025, 16, 2621–2626 CrossRef CAS.
- Y.-W. Zhou, M.-Y. Jia, J.-L. Yang, Q. Liu and Z.-F. Cai, Chem. Sci., 2025, 16, 8470–8477 RSC.
- X. Yan, R. M. Bain and R. G. Cooks, Angew. Chem., Int. Ed., 2016, 55, 12960–12972 CrossRef CAS PubMed.
- G. Rovelli, M. I. Jacobs, M. D. Willis, R. J. Rapf, A. M. Prophet and K. R. Wilson, Chem. Sci., 2020, 11, 13026–13043 RSC.
- K. R. Wilson and A. M. Prophet, Annu. Rev. Phys. Chem., 2024, 75, 185–208 CrossRef CAS PubMed.
- S. Banerjee, E. Gnanamani, X. Yan and R. N. Zare, Analyst, 2017, 142, 1399–1402 RSC.
- M. Girod, E. Moyano, D. I. Campbell and R. G. Cooks, Chem. Sci., 2011, 2, 501–510 RSC.
- J. K. Lee, S. Banerjee, H. G. Nam and R. N. Zare, Q. Rev. Biophys., 2015, 48, 437–444 CrossRef CAS.
- R. M. Bain, S. Sathyamoorthi and R. N. Zare, Angew. Chem., Int. Ed., 2017, 56, 15083–15087 CrossRef CAS PubMed.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19294–19298 CrossRef CAS.
- M. A. Mehrgardi, M. Mofidfar and R. N. Zare, J. Am. Chem. Soc., 2022, 144, 7606–7609 CrossRef CAS.
- D. Nguyen and S. C. Nguyen, J. Phys. Chem. B, 2022, 126, 3180–3185 CrossRef CAS PubMed.
- A. Gallo Jr, N. H. Musskopf, X. Liu, Z. Yang, J. Petry, P. Zhang, S. Thoroddsen, H. Im and H. Mishra, Chem. Sci., 2022, 13, 2574–2583 RSC.
- M. Angelaki, Y. Carreira Mendes Da Silva, S. Perrier and C. George, J. Am. Chem. Soc., 2024, 146, 8327–8334 CrossRef CAS PubMed.
- K. Li, Y. Guo, S. A. Nizkorodov, Y. Rudich, M. Angelaki, X. Wang, T. An, S. Perrier and C. George, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2220228120 CrossRef CAS.
- M. A. Eatoo and H. Mishra, Chem. Sci., 2024, 15, 3093–3103 RSC.
- D. Xing, Y. Meng, X. Yuan, S. Jin, X. Song, R. N. Zare and X. Zhang, Angew. Chem., Int. Ed., 2022, 134, e202207587 CrossRef.
- A. J. Colussi, J. Am. Chem. Soc., 2023, 145, 16315–16317 CrossRef CAS PubMed.
- C. J. Chen and E. R. Williams, Angew. Chem., Int. Ed., 2024, 136, e202407433 CrossRef.
- D. Xing, X. Gao, H. Chen, J. Zhang, M. E. Edwards, C. Liang, C. Zhu, Y. Meng, R. N. Zare, Y. Xia and X. Zhang, Anal. Chem., 2025, 97, 7995–8000 CrossRef CAS.
- X. Zhang, M. Duan, K. Chingin, R. Balabin, L. Liu, X. Zhang and H. Chen, Anal. Chem., 2025, 97, 16004–16010 CrossRef CAS PubMed.
- Y. Tian, L. Kong, H. Zou, M. Liu and G. Liu, Sustain. Horiz., 2024, 11, 100103 CrossRef.
- S. Jin, H. Chen, X. Yuan, D. Xing, R. Wang, L. Zhao, D. Zhang, C. Gong, C. Zhu, X. Gao, Y. Chen and X. Zhang, JACS Au, 2023, 3, 1563–1571 CrossRef CAS PubMed.
- L. Qiu and R. G. Cooks, Angew. Chem., Int. Ed., 2022, 134, e202210765 CrossRef.
- C. Zhu, L. N. Pham, X. Yuan, H. Ouyang, M. L. Coote and X. Zhang, J. Am. Chem. Soc., 2023, 145, 21207–21212 CrossRef CAS PubMed.
- Y. Meng, E. Gnanamani and R. N. Zare, J. Am. Chem. Soc., 2022, 144, 19709–19713 CrossRef.
- Z. Song, C. Liang, K. Gong, S. Zhao, X. Yuan, X. Zhang and J. Xie, J. Am. Chem. Soc., 2023, 145, 26003–26008 CrossRef CAS.
- D. Zhang, X. Yuan, C. Gong and X. Zhang, J. Am. Chem. Soc., 2022, 144, 16184–16190 CrossRef CAS.
- X. Yuan, D. Zhang, C. Liang and X. Zhang, J. Am. Chem. Soc., 2023, 145, 2800–2805 CrossRef CAS.
- A. Nandy, A. Kumar, S. Mondal, D. Koner and S. Banerjee, J. Am. Chem. Soc., 2023, 145, 15674–15679 CrossRef CAS PubMed.
- H. Chen, R. Wang, J. Xu, X. Yuan, D. Zhang, Z. Zhu, M. Marshall, K. Bowen and X. Zhang, J. Am. Chem. Soc., 2023, 145, 2647–2652 CrossRef CAS PubMed.
- L. Zhao, X. Song, C. Gong, D. Zhang, R. Wang, R. N. Zare and X. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200991119 CrossRef CAS.
- K. Gong, Y. Meng, R. N. Zare and J. Xie, J. Am. Chem. Soc., 2024, 146, 8576–8584 CrossRef CAS PubMed.
- X. Chen, Y. Xia, Y. Wu, Y. Xu, X. Jia, R. N. Zare and F. Wang, J. Am. Chem. Soc., 2024, 146, 10868–10874 CrossRef CAS.
- A. Kumar, V. S. Avadhani, A. Nandy, S. Mondal, B. Pathak, V. K. N. Pavuluri, M. M. Avulapati and S. Banerjee, Anal. Chem., 2024, 96, 10515–10523 CrossRef CAS.
- C. J. Chen, V. S. Avadhani and E. R. Williams, Angew. Chem., Int. Ed., 2025, 64, e202424662 CrossRef CAS.
- Y.-G. Fang, X. Li, C. Yuan, X. Li, X. Yuan, D. Zhang, X. Zhang, C. Zhu and W.-H. Fang, Angew. Chem., Int. Ed., 2025, 137, e202417920 CrossRef.
- J. Dong, J. Xu, Z.-D. Meng, Z.-A. Nan, W. Li, R. N. Zare, Z.-Q. Tian and F. R. Fan, J. Am. Chem. Soc., 2025, 147, 16060–16069 CrossRef CAS PubMed.
- J. Zhou, Q. Wang, G. Cheng, W. Shen, R. N. Zare and X. Sun, J. Am. Chem. Soc., 2025, 147, 10916–10924 CrossRef CAS.
- S. Wei, Q. Wan, S. Zhou, W. Nie and S. Chen, J. Am. Chem. Soc., 2024, 146, 32777–32784 CrossRef CAS.
- K. Li, W. You, Y. Zhu, W. Wang, L. Wang, Q. Ge, Y. Liu, X. Ruan, H. Cheng, M. A. Tahir and L. Zhang, J. Hazard. Mater., 2025, 493, 138311 CrossRef CAS PubMed.
- R. Zhang, Z. Zhang, X. Chen, J. Jiang, L. Hua, X. Jia, R. Bao and F. Wang, J. Am. Chem. Soc., 2024, 146, 8528–8535 CrossRef CAS.
- Y. Wang, J. Luo, Y.-G. Fang, Z.-A. Nan, X. Cui, T. Chen, X. Zeng, X. Wang, X. Song, J. Zhao, W. Li, C. Zeng, D. Chen, C. Zhu, Z. Wei, Z.-Q. Tian and F. R. Fan, J. Am. Chem. Soc., 2025, 147, 2756–2765 CrossRef CAS.
- M. A. Mehrgardi, M. Mofidfar, J. Li, C. F. Chamberlayne, S. R. Lynch and R. N. Zare, Adv. Sci., 2024, 11, 2406785 CrossRef CAS.
- J. Dong, J. Chen, W. Wang, Z. Wei, Z.-Q. Tian and F. R. Fan, J. Am. Chem. Soc., 2024, 146, 2227–2236 CrossRef CAS.
- X. Liu, X. Li, X. Wang, Y. Li, X. Hu, Z. Zhou, F. Zhang, Z. Zhang and Y. Chen, J. Am. Chem. Soc., 2025, 147, 3529–3538 CrossRef CAS.
- Q. Ge, Y. Liu, K. Li, L. Xie, X. Ruan, W. Wang, L. Wang, T. Wang, W. You and L. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202304189 CrossRef CAS.
- Q. Jiang, D. Xia, X. Li, H. Zhang, R. Yin, H. Xie, H. Xie, J. Jiang, J. Chen and J. S. Francisco, Angew. Chem., Int. Ed., 2025, 64, e202421002 CrossRef CAS.
- W. Wang, Y. Liu, T. Wang, Q. Ge, K. Li, J. Liu, W. You, L. Wang, L. Xie, H. Fu, J. Chen and L. Zhang, J. Am. Chem. Soc., 2024, 146, 6580–6590 CrossRef CAS PubMed.
- D. Xia, H. Zhang, Y. Ju, H. Xie, L. Su, F. Ma, J. Jiang, J. Chen and J. S. Francisco, J. Am. Chem. Soc., 2024, 146, 11266–11271 CAS.
- K.-H. Huang, K. Chen, N. M. Morato, T. C. Sams, E. T. Dziekonski and R. G. Cooks, Chem. Sci., 2025, 16, 7544–7550 RSC.
- K. Li, K. Gong, J. Liu, L. Ohnoutek, J. Ao, Y. Liu, X. Chen, G. Xu, X. Ruan, H. Cheng, J. Han, G. Sui, M. Ji, V. K. Valev and L. Zhang, Cell Rep. Phys. Sci., 2022, 3, 100917 CrossRef CAS.
- K. Li, Q. Ge, Y. Liu, L. Wang, K. Gong, J. Liu, L. Xie, W. Wang, X. Ruan and L. Zhang, Energy Environ. Sci., 2023, 16, 1135–1145 RSC.
- I. Nam, J. K. Lee, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12396–12400 CrossRef CAS.
- I. Nam, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2017, 115, 36–40 CrossRef.
- D. Xia, F. Zeng, W. Chen, H. Zhao, H. Xie, J. Chen and J. S. Francisco, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2501323122 CrossRef CAS.
- D. T. Holden, N. M. Morato and R. G. Cooks, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2212642119 CrossRef CAS.
- Y. Meng, Y. Xia, J. Xu and R. N. Zare, Sci. Adv., 2025, 11, eadt8979 CrossRef CAS PubMed.
- M. Piejko, J. E. Alfonso-Ramos, J. Moran and T. Stuyver, ChemistryEurope, 2025, 3, e202400093 CrossRef CAS.
- W.-Z. Song, M. Zhang, H.-J. Qiu, C.-L. Li, T. Chen, L.-L. Jiang, M. Yu, S. Ramakrishna, Z.-L. Wang and Y.-Z. Long, Water Res., 2022, 226, 119242 CrossRef CAS PubMed.
- B. Chen, Y. Xia, R. He, H. Sang, W. Zhang, J. Li, L. Chen, P. Wang, S. Guo, Y. Yin, L. Hu, M. Song, Y. Liang, Y. Wang, G. Jiang and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2209056119 CrossRef CAS PubMed.
- H. Gu, C. Gu, A. Du Toit, W. Yu, M. W. Chen, H. L. Struckman, J. R. Silva, Y. Dai and A. G. Ewing, J. Am. Chem. Soc., 2025, 147, 27020–27029 Search PubMed.
- M. W. Chen, X. Ren, X. Song, N. Qian, Y. Ma, W. Yu, L. Yang, W. Min, R. N. Zare and Y. Dai, J. Am. Chem. Soc., 2025, 147, 8267–8279 Search PubMed.
- L. Qiu, Z. Wei, H. Nie and R. G. Cooks, ChemPlusChem, 2021, 86, 1362–1365 Search PubMed.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7272–7277 Search PubMed.
- A. Gray-Weale and J. K. Beattie, Phys. Chem. Chem. Phys., 2009, 11, 10994–11005 Search PubMed.
- K. Gong, J. Ao, K. Li, L. Liu, Y. Liu, G. Xu, T. Wang, H. Cheng, Z. Wang, X. Zhang, H. Wei, C. George, A. Mellouki, H. Herrmann, L. Wang, J. Chen, M. Ji, L. Zhang and J. S. Francisco, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219588120 CrossRef CAS.
- L. Shi, R. A. LaCour, N. Qian, J. P. Heindel, X. Lang, R. Zhao, T. Head-Gordon and W. Min, Nature, 2025, 640, 87–93 CrossRef CAS PubMed.
- H. Xiong, J. K. Lee, R. N. Zare and W. Min, J. Phys. Chem. B, 2020, 124, 9938–9944 CrossRef CAS PubMed.
- H. Xiong, J. K. Lee, R. N. Zare and W. Min, J. Phys. Chem. Lett., 2020, 11, 7423–7428 CrossRef CAS.
- C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2020, 152, 184702 CrossRef CAS.
- H. Hao, I. Leven and T. Head-Gordon, Nat. Commun., 2022, 13, 280 CrossRef CAS.
- C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2022, 156, 054705 CrossRef CAS PubMed.
- J. R. Cendagorta and T. Ichiye, J. Phys. Chem. B, 2015, 119, 9114–9122 CrossRef CAS PubMed.
- M. Matsumoto and Y. Kataoka, J. Chem. Phys., 1988, 88, 3233–3245 CrossRef CAS.
- M. A. Wilson, A. Pohorille and L. R. Pratt, J. Chem. Phys., 1988, 88, 3281–3285 CrossRef CAS.
- S. M. Kathmann, I.-F. W. Kuo and C. J. Mundy, J. Am. Chem. Soc., 2008, 130, 16556–16561 CrossRef CAS.
- V. Buch, A. Milet, R. Vácha, P. Jungwirth and J. P. Devlin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7342–7347 CrossRef CAS.
- J. K. Beattie, A. M. Djerdjev and G. G. Warr, Faraday Discuss., 2009, 141, 31–39 RSC.
- M. Takahashi, J. Phys. Chem. B, 2005, 109, 21858–21864 CrossRef CAS.
- R. Zimmermann, S. Dukhin and C. Werner, J. Phys. Chem. B, 2001, 105, 8544–8549 CrossRef CAS.
- J. K. Beattie and A. M. Djerdjev, Angew. Chem., Int. Ed., 2004, 43, 3568–3571 CrossRef CAS.
- H. Mishra, S. Enami, R. J. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard III and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18679–18683 CrossRef CAS.
- K. G. Marinova, R. G. Alargova, N. D. Denkov, O. D. Velev, D. N. Petsev, I. B. Ivanov and R. P. Borwankar, Langmuir, 1996, 12, 2045–2051 CrossRef CAS.
- R. Vácha, S. W. Rick, P. Jungwirth, A. G. de Beer, H. B. de Aguiar, J.-S. Samson and S. Roke, J. Am. Chem. Soc., 2011, 133, 10204–10210 CrossRef.
- N. Agmon, H. J. Bakker, R. K. Campen, R. H. Henchman, P. Pohl, S. Roke, M. Thämer and A. Hassanali, Chem. Rev., 2016, 116, 7642–7672 CrossRef CAS.
- W. Xu, H. Zheng, Y. Liu, X. Zhou, C. Zhang, Y. Song, X. Deng, M. Leung, Z. Yang, R. X. Xu, Z. L. Wang, X. C. Zeng and Z. Wang, Nature, 2020, 578, 392–396 CrossRef CAS.
- P. Bista, A. D. Ratschow, H.-J. Butt and S. A. Weber, J. Phys. Chem. Lett., 2023, 14, 11110–11116 CrossRef CAS PubMed.
- C. Ye, D. Liu, Y. Gao, F. Liu, H. Xu, T. Jiang and Z. L. Wang, Matter, 2025, 8, 102007 CrossRef CAS.
- Z. Zhou, X. Yan, Y.-H. Lai and R. N. Zare, J. Phys. Chem. Lett., 2018, 9, 2928–2932 CrossRef CAS PubMed.
- R. F. Steiner, Topics in fluorescence spectroscopy: Principles, Springer, 1991, pp. 1–52 Search PubMed.
- X. Zhou, Y. Ji, Z. Ni, J. G. Lopez, K. Peneva, S. Jiang, N. Knorr, R. Berger, K. Koynov and H.-J. Butt, Adv. Mater., 2025, 37, 2420263 CrossRef CAS.
- S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998–1006 CrossRef CAS.
- N. Qian, H. Xiong, L. Wei, L. Shi and W. Min, Annu. Rev. Phys. Chem., 2025, 76, 279–301 CrossRef CAS PubMed.
- L. Shi, F. Hu and W. Min, Nat. Commun., 2019, 10, 4764 CrossRef.
- Y. Liu, Q. Ge, T. Wang, R. Zhang, K. Li, K. Gong, L. Xie, W. Wang, L. Wang, W. You, X. Ruan, Z. Shi, J. Han, R. Wang, J. Chen, C. K. Chan and L. Zhang, Chem, 2024, 10, 330–351 CAS.
- A. M. Kol, T. Herriman, W. Salmon, G. DiLabio and M. Jackson, ChemRxiv, 2025, preprint DOI:10.26434/chemrxiv-2025-dh30c-v2.
- L. M. Loew and L. L. Simpson, Biophys. J., 1981, 34, 353–365 CrossRef CAS.
- S. G. Boxer, J. Phys. Chem. B, 2009, 113, 2972–2983 CrossRef CAS.
- A. Montenegro, C. Dutta, M. Mammetkuliev, H. Shi, B. Hou, D. Bhattacharyya, B. Zhao, S. B. Cronin and A. V. Benderskii, Nature, 2021, 594, 62–65 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Phys. Rev. Lett., 1994, 72, 238–241 CrossRef CAS PubMed.
- Y. Zhang, H. B. de Aguiar, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2020, 11, 624–631 CrossRef CAS PubMed.
- J. G. Davis, K. P. Gierszal, P. Wang and D. Ben-Amotz, Nature, 2012, 491, 582–585 CrossRef CAS PubMed.
- X. Wu, W. Lu, L. M. Streacker, H. S. Ashbaugh and D. Ben-Amotz, Angew. Chem., Int. Ed., 2018, 57, 15133–15137 CrossRef CAS.
- D. Ben-Amotz, J. Am. Chem. Soc., 2019, 141, 10569–10580 CrossRef CAS PubMed.
- P. N. Perera, K. R. Fega, C. Lawrence, E. J. Sundstrom, J. Tomlinson-Phillips and D. Ben-Amotz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 12230–12234 CrossRef CAS.
- K. M. Hunter, F. A. Shakib and F. Paesani, J. Phys. Chem. B, 2018, 122, 10754–10761 CrossRef CAS PubMed.
- R. A. LaCour, J. P. Heindel and T. Head-Gordon, J. Phys. Chem. Lett., 2023, 14, 11742–11749 CrossRef CAS PubMed.
- A. P. Willard and D. Chandler, J. Phys. Chem. B, 2010, 114, 1954–1958 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Science, 1994, 264, 826–828 CrossRef CAS.
- L. F. Scatena, M. G. Brown and G. L. Richmond, Science, 2001, 292, 908–912 CrossRef CAS PubMed.
- J. D. Smith, R. J. Saykally and P. L. Geissler, J. Am. Chem. Soc., 2007, 129, 13847–13856 CrossRef CAS.
- Y. R. Shen, Nature, 1989, 337, 519–525 CrossRef CAS.
- A. G. Lambert, P. B. Davies and D. J. Neivandt, Appl. Spectrosc. Rev., 2005, 40, 103–145 CrossRef CAS.
- S. Nihonyanagi, J. A. Mondal, S. Yamaguchi and T. Tahara, Annu. Rev. Phys. Chem., 2013, 64, 579–603 CrossRef CAS PubMed.
- Y. R. Shen, Annu. Rev. Phys. Chem., 2013, 64, 129–150 CrossRef CAS PubMed.
- S. Strazdaite, J. Versluis and H. J. Bakker, J. Chem. Phys., 2015, 143, 084708 CrossRef PubMed.
- C. S. Tian and Y. R. Shen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15148–15153 CrossRef CAS.
- S. Kulik, S. Pullanchery and S. Roke, J. Phys. Chem. C, 2020, 124, 23078–23085 CrossRef CAS.
- S. Pullanchery, S. Kulik, B. Rehl, A. Hassanali and S. Roke, Science, 2021, 374, 1366–1370 CrossRef CAS.
- E. Poli, K. H. Jong and A. Hassanali, Nat. Commun., 2020, 11, 901 CrossRef CAS.
- R. Zhao, H. Shen, R. A. LaCour, J. P. Heindel, M. Head-Gordon and T. Head-Gordon, Angew. Chem., Int. Ed., 2025, 64, e202508145 CrossRef CAS PubMed.
- W. Gan, W. Wu, F. Yang, D. Hu, H. Fang, Z. Lan and Q. Yuan, Soft Matter, 2017, 13, 7962–7968 RSC.
- T. L. Tarbuck, S. T. Ota and G. L. Richmond, J. Am. Chem. Soc., 2006, 128, 14519–14527 CrossRef CAS.
- C. Tian, N. Ji, G. A. Waychunas and Y. R. Shen, J. Am. Chem. Soc., 2008, 130, 13033–13039 CrossRef CAS PubMed.
- L. M. Levering, M. R. Sierra-Hernández and H. C. Allen, J. Phys. Chem. C, 2007, 111, 8814–8826 CrossRef CAS.
- P. B. Petersen and R. J. Saykally, Chem. Phys. Lett., 2008, 458, 255–261 CrossRef CAS.
- K.-Y. Chiang, T. Seki, C.-C. Yu, T. Ohto, J. Hunger, M. Bonn and Y. Nagata, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2204156119 CrossRef CAS.
- M. Dinpajooh and D. V. Matyushov, J. Chem. Phys., 2016, 145, 014504 CrossRef PubMed.
- T. Preočanin, A. Selmani, P. Lindqvist-Reis, F. Heberling, N. Kallay and J. Lützenkirchen, Colloids Surf., A, 2012, 412, 120–128 CrossRef.
- Y. B. Vogel, C. W. Evans, M. Belotti, L. Xu, I. C. Russell, L.-J. Yu, A. K. Fung, N. S. Hill, N. Darwish, V. R. Gonçales, M. L. Coote, K. S. Iyer and S. Ciampi, Nat. Commun., 2020, 11, 6323 CrossRef CAS.
- Y. Wang, H. Luo, X. R. Advincula, Z. Zhao, A. Esfandiar, D. Wu, K. D. Fong, L. Gao, A. S. Hazrah, T. Taniguchi, C. Schran, Y. Nagata, L. Bocquet, M.-L. Bocquet, Y. Jiang, A. Michaelides and M. Bonn, J. Am. Chem. Soc., 2025, 147, 30107–30116 CrossRef CAS PubMed.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS.
- R. Buchner, G. Hefter, P. M. May and P. Sipos, J. Phys. Chem. B, 1999, 103, 11186–11190 CrossRef CAS.
- T. Megyes, S. Bálint, T. Grósz, T. Radnai, I. Bakó and P. Sipos, J. Chem. Phys., 2008, 128, 044501 CrossRef.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- B. Chen, J. M. Park, I. Ivanov, G. Tabacchi, M. L. Klein and M. Parrinello, J. Am. Chem. Soc., 2002, 124, 8534–8535 CrossRef CAS PubMed.
- C. D. Cappa, J. D. Smith, B. M. Messer, R. C. Cohen and R. J. Saykally, J. Phys. Chem. A, 2007, 111, 4776–4785 CrossRef CAS PubMed.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- A. M. Djerdjev and J. K. Beattie, Molecules, 2025, 30, 785 CrossRef CAS.
- P. Creux, J. Lachaise, A. Graciaa, J. K. Beattie and A. M. Djerdjev, J. Phys. Chem. B, 2009, 113, 14146–14150 CrossRef CAS PubMed.
- P. B. Petersen, J. C. Johnson, K. P. Knutsen and R. J. Saykally, Chem. Phys. Lett., 2004, 397, 46–50 CrossRef CAS.
- G. Jones and W. A. Ray, J. Am. Chem. Soc., 1935, 57, 957–958 CrossRef CAS.
- P. B. Petersen and R. J. Saykally, J. Am. Chem. Soc., 2005, 127, 15446–15452 CrossRef CAS.
- S. D. Fried and S. G. Boxer, Annu. Rev. Biochem., 2017, 86, 387–415 CrossRef CAS PubMed.
- S. D. Fried, S. Bagchi and S. G. Boxer, Science, 2014, 346, 1510–1514 CrossRef CAS.
- S. H. Schneider and S. G. Boxer, J. Phys. Chem. B, 2016, 120, 9672–9684 CrossRef CAS PubMed.
- A. I. Kloss, Dokl. Akad. Nauk SSSR, 1988, 303, 1403–1407 CAS.
- J. P. Heindel, H. Hao, R. A. LaCour and T. Head-Gordon, J. Phys. Chem. Lett., 2022, 13, 10035–10041 CrossRef CAS.
- M. T. Martins-Costa and M. F. Ruiz-López, J. Am. Chem. Soc., 2023, 145, 1400–1406 CrossRef CAS.
- K. Lee, M. A. Mehrgardi and R. N. Zare, J. Am. Chem. Soc., 2025, 147, 33240–33247 CrossRef CAS PubMed.
- D. Ben-Amotz, Science, 2022, 376, 800–801 CrossRef CAS.
- L. Qiu and R. G. Cooks, Angew. Chem., Int. Ed., 2024, 136, e202400118 CrossRef.
- L. S. McCarty and G. M. Whitesides, Angew. Chem., Int. Ed., 2008, 47, 2188–2207 CrossRef CAS PubMed.
- F. Galembeck, L. P. Santos, T. A. Burgo and A. Galembeck, Chem. Soc. Rev., 2024, 53, 2578–2602 RSC.
- Y. Dai, Z.-G. Wang and R. N. Zare, Nat. Chem. Biol., 2024, 20, 1420–1433 CrossRef CAS PubMed.
- J. P. Heindel, R. A. LaCour and T. Head-Gordon, Nat. Commun., 2024, 15, 3670 CrossRef CAS.
- K. D. Judd, S. W. Parsons, T. Majumder and J. M. Dawlaty, Chem. Rev., 2025, 125, 2440–2473 CrossRef CAS.
- S. W. Devlin, F. Bernal, E. J. Riffe, K. R. Wilson and R. J. Saykally, Faraday Discuss., 2024, 249, 9–37 RSC.
- G. Gonella, E. H. G. Backus, Y. Nagata, D. J. Bonthuis, P. Loche, A. Schlaich, R. R. Netz, A. Kühnle, I. T. McCrum, M. T. M. Koper, M. Wolf, B. Winter, G. Meijer, R. K. Campen and M. Bonn, Nat. Rev. Chem., 2021, 5, 466–485 CrossRef CAS.
- Z. L. Wang and A. C. Wang, Mater. Today, 2019, 30, 34–51 CrossRef CAS.
- W. Sung, K. Inoue, S. Nihonyanagi and T. Tahara, Nat. Commun., 2024, 15, 1258 CrossRef CAS PubMed.
- D. Ojha, N. K. Kaliannan and T. D. Kühne, Commun. Chem., 2019, 2, 116 CrossRef.
- D. Ojha and T. D. Kühne, Sci. Rep., 2021, 11, 2456 CrossRef CAS PubMed.
- S. D. Pino, D. Banerjee, M. Monti, G. D. Miron, G. Cassone and A. Hassanali, arXiv, 2025, preprint DOI:10.48550/arXiv.2506.23988.
- R. Vácha, D. Horinek, M. L. Berkowitz and P. Jungwirth, Phys. Chem. Chem. Phys., 2008, 10, 4975–4980 RSC.
- Y.-L. S. Tse, C. Chen, G. E. Lindberg, R. Kumar and G. A. Voth, J. Am. Chem. Soc., 2015, 137, 12610–12616 CrossRef CAS.
- P. Zhang and X. Xu, Langmuir, 2025, 41, 3675–3683 CrossRef CAS PubMed.
- P. Zhang, M. Feng and X. Xu, ACS Phys. Chem. Au, 2024, 4, 336–346 CrossRef CAS PubMed.
- Z. Chen, Y. Zhang, P. Lv, T. Wu, J. He, J. Du, Q. Sun, Q. Wu, J. Yang, Y. Zhang, Y. Zhang, F. He, C. Cui, G. Hong, H. Zhu, Y. Li, J. Guo and X. Deng, Nat. Nanotechnol., 2025, 1–9 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |