Dissecting the single-electron C–C bond: NBO and AIM perspectives

Abstract

In this work, we present a comprehensive electronic structure analysis of the highly praised oxidation product of tricyclic compound spiro-dibenzocycloheptatriene (1p), with emphasis on characterizing the nature of the non-covalent interaction between ipso carbon atoms (C1 and C2), which has been characterized as an allegedly single electron sigma C–C bond. Our NCI analysis reveals that the interaction between the tricyclic moieties is weak and predominantly van der Waals in character (regardless of the counterion). AIM theory identifies a persistent bond critical point between C1 and C2 across all structures, albeit with low electron density indicative of a weak interaction. A comparison of the Laplacian density contour between C1–C2 and a previously reported B–B single-electron σ-bond (herein labeled as 1p-B), shows charge depletion between C1–C2 whereas in B1–B2 there is charge accumulation, characteristic of a σ-bond. The spin density population shows that half the radical is distributed among the two tricyclic structures. Our NBO and NRT analyses indicate that a single-electron σ-bond is present in some resonance structures, although its overall contribution is minimal. The calculated natural bond order for C1–C2 in the cationic form is only 0.066, suggesting limited bond character. Finally, NBO deletion analysis quantifies the interaction energy between the rings, showing that the C1–C2 interaction contributes only ∼9.5% to the total π–π interaction energy, primarily through donor–acceptor interactions between bonding orbitals and Rydberg orbitals. These results converge to show that the C1–C2 interaction is a weak, highly delocalized interaction governed by subtle electronic effects rather than a single electron σ-bond.

---

Introduction

The traditional concept of a σ-bond was long considered to involve the sharing of two electrons. However, in 1931, Linus Pauling expanded this concept to include σ-bonds in which only one electron is shared.¹ Since then, several experimental examples of single-electron σ-bonds have been reported, among them P·P,² B·B,^3,4 Cu·B,⁵ and Sn·Sn.⁶

Recently, the first example of a C·C single-electron σ-bond (1p-I₃, Fig. 1) was reported.⁷ This was achieved through the one-electron oxidation of spiro-dibenzocycloheptatriene (1), producing the cationic radical 1p-I₃. Experimental findings confirmed the presence of a C·C single-electron σ-bond in this species. Furthermore, the two-electron oxidation of compound 1 yielded the dicationic compound 1pp-I₃.

Fig. 1 One and two-electron oxidation of 1.

Despite the few examples of single-electron σ-bonds mentioned above, there are numerous studies on the so-called single-electron σ-hole bonds, in which no true σ-bonding is present. In most of these studies, the radical (typically a methyl radical) interacts with either the σ-hole or π-hole of a neutral molecule. Examples include interactions of H₃C· with H₃CF,⁸ NCX,⁹ S(Cl)(H),¹⁰ BrH,^11,12 NaF,¹³ XeO₃,¹⁴ XF (where X is a halogen).¹⁵ Most of these studies agree that the key characteristic of these single-electron interactions is their weak nature and their electron density features, which resemble those of hydrogen bonds. Due to these similarities, the authors referred to these weak interactions as single-electron tetrel, chalcogen, halogen, or aerogen bonds,^8,10–14 however, they do not display a formal σ-bond. In orbital terms, the interaction occurs between the singly occupied p-orbital of the methyl radical and the σ* (antibonding) orbital of the neutral molecule. Furthermore, these σ-hole interactions are also known to promote unconventional reactivity in functional groups such as –CCl₃.¹⁶

While investigating the experimentally reported C·C single-electron bond using the most recent version of natural bonding orbital (NBO) software (version 7.0),¹⁷ we found discrepancies with the previously reported analysis of 1p-I₃, which was based on NBO version 3.1 included in the Gaussian software package. In the calculated natural Lewis structure (NLS) obtained with NBO 7.0, no single-electron σ-bond is identified. Instead, several orbital interactions are observed between these atoms, specifically between an occupied orbital and an antibonding or Rydberg orbital, resembling those seen in single-electron σ-hole bonds.

Upon further literature review, we found that NBO version 3.1 employs the expanded valency algorithm in its calculations, which may lead to inaccuracies in computed natural charges and the default natural Lewis structure (NLS).^18,19 Therefore, in this study, we explore the electronic structure of the experimentally reported 1p-I₃, using the advanced tools provided in NBO 7.0: natural resonance theory (NRT),²⁰ natural bond critical point (NBCP)²¹ and natural orbital deletion (NBOdel) analysis.²²

Computational methodology

We retrieved the reported crystal structure of the neutral species 1²³ from the Cambridge structural database²⁴ (CCDC number 1567402), the cationic species 1p-I₃ (CCDC number 2301032), the dicationic species 1pp-I₃ (CCDC number 2301040)⁷ and the diboron structure 1p-B (CCDC number 984404).⁴ These structures were then optimized in gas-phase using Gaussian 16 (version C.01) both with and without the corresponding counter anion. We employed the long-range corrected functional ωB97X-D²⁵ along with Dunning's cc-pVTZ basis set²⁶ for carbon and hydrogen atoms, and the quasirelativistic LANL2TZ(f) pseudopotential²⁷ for iodine. The optimized geometries were confirmed to be minima on the potential energy surface through frequency calculations, which showed no imaginary frequencies. The stability of the wavefunction of both the optimized and X-ray structure of 1p-I₃ was tested via the keyword “stable” and the results proved the stability of the wavefunction as a doublet; unrestricted calculations were employed for the cationic species and restricted for the dicationic and neutral ones.

The atoms in molecule (AIM),²⁸ non-covalent interactions (NCI) index,²⁹ and spin population, in the AIM partition, analysis were performed using Multiwfn (version 3.8).³⁰ Further comparison of the AIM results obtained with Multiwfn was made with DensToolKit2 (DTK2)³¹ (see Table S1). The analyzed wavefunctions were obtained from single-point calculations on both the optimized and X-ray structures. Visualization of the results was carried out using the VMD software.³² Further, the calculated root mean square deviation (RMSD) was calculated using ChemCraft³³ excluding the [I₃]⁻ from each geometry.

Natural bond orbital (NBO) analyses^22,34 were conducted using two versions of the software; NBO 7.0¹⁷ and NBO 3.1 over the optimized structures 1, 1p-I₃ and 1pp-I₃. The latter version is implemented within Gaussian 09 and 16, and it was used solely for the calculation of the natural Lewis structure (NLS). NBO 7.0 was used for more advanced analysis, including natural resonance theory (NRT),²⁰ natural bond critical point (NBCP),²¹ and natural bond orbital deletion (NBOdel) calculations. Furthermore, the NBOdel and NRT analysis were performed at the HF/cc-pVTZ//ωB97X-D/cc-pVTZ level as NBOdel energies are known to be more reliable when calculated using Hartree–Fock (HF) since functionals are sometimes poorly parameterized to evaluate the energetic deletion densities.³⁵

Results

Geometry optimization

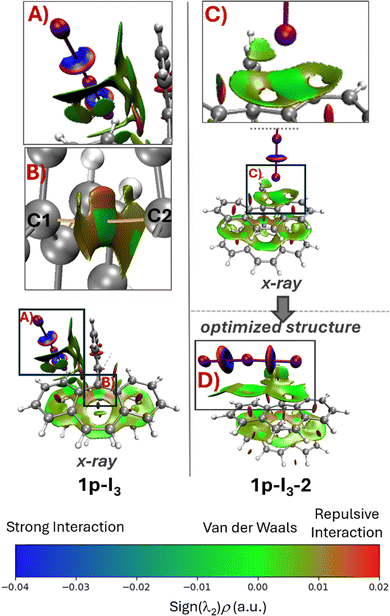
The optimization procedure was performed by using the reported crystal structure of 1p-I₃. We considered three possible configurations for geometry optimization (Fig. 2). In the first configuration, the cation 1p is optimized without its counterion [I₃]⁻ (Ax). In the second, the counterion is positioned side-on relative to the cyclic structure of (1p-I₃) (Bx). In the third, the anion is placed above the plane of the rings, 1p-I₃-2 (Cx). The results show that the optimization of the cation 1p without the anion [I₃]⁻ (Ax) leads to a symmetry-breaking transformation, where the tricyclic structures losses its parallel alignment (Ao), yielding a root mean square deviation (RMSD) of 0.519, which is calculated excluding the anion [I₃]⁻. In contrast, optimization of 1p with the [I₃]⁻ anion positioned side-on (Bo) results in the lowest geometric deviation, with an RMSD of 0.256. However, when the anion is placed perpendicular to the tricyclic structure, above the plane Cx, [I₃]⁻ shift into a nearly parallel orientation, interacting with the rings (Co). This interaction breaks the symmetry of 1p, increasing the RMSD to 0.579.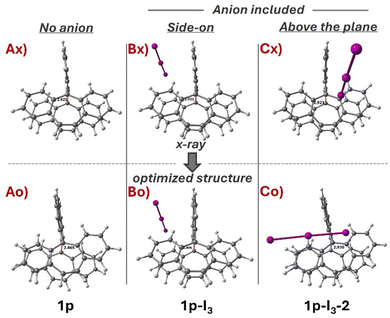

Fig. 2 Comparison between the X-ray structure and optimized structure of 1p with and without the counterion [I₃]⁻.

Analysis of the geometrical parameters (Table 1) shows that the optimized structure with the closest C1–C2 distance to the X-ray structure (2.9207 Å) is 1p-I₃-2 where the anion lies above the plane. However, this structure also exhibits the highest RMSD (0.579), indicating a significant symmetry loss in the tricyclic framework. In contrast, the structure with the lowest RMSD (0.252) and a closely matching C1–C2 distance (2.896 Å) to the X-ray structure is 1p-I₃, where the anion is positioned side-on.

Table 1 Distance (Å) between the ipso carbons, C1–C2, and the calculated RMSD between the cationic structure of the X-ray structure and the cationic structure of the given optimized structures

Structure	X-ray/opt	d(C1–C2)	RMSD^a
a RMSD calculated without the anion [I3]^−.
1p	X-ray	2.9207	0.000
1p	Optimized	2.8649	0.519
1p-I3		2.8958	0.256
1p-I3-2		2.9302	0.579

---

These results clearly demonstrate that the counterion plays a key role in preserving the correct symmetry and alignment of the tricyclic structures, as observed in 1p-I₃. In the previous study, the electronic structure was analyzed without including the counterion.

Furthermore, the experimental and theoretical distance of C1–C2 in 1p-I₃ (2.921 and 2.896 Å, respectively) are quite large compared to the C–C σ-bond of ethane, which is about 1.54 Å. Rzepa investigated, in the Crystal Structure Database (CSD), the X-ray structures that contained a central C–C distance ranging from 2.8 to 3.0 Å.³⁶ He found that only dication structures have these distances. Therefore, the interaction C1–C2 in 1p-I₃ should resemble that of the weak interaction in the dication molecule.

NCI analysis

Further analysis of the electron density was performed for all X-ray and optimized structures. Using non-covalent interaction (NCI) analysis, we obtained an intuitive, qualitative visualization of the interactions between the carbon atoms of the tricyclic structures (Fig. S1). Across all NCI calculations, the results indicate that the interaction between the tricyclic structures corresponds to a van der Waals interaction or other weak interaction. Furthermore, when the counterion is positioned either side-on or above the plane of the rings, the interaction between the anion and cation is also classified as weak. Despite its weak nature, this interaction has two critical consequences (Fig. 3): (1) it preserves the symmetry of the tricyclic during the optimization of Ip-I₃ (A); (2) when the anion [I₃]⁻ is initially positioned perpendicular to the tricyclic structure (C), the optimization leads to a structure in which [I₃]⁻ reorients to a parallel position (D), likely due to stronger non-covalent interactions with the tricyclic framework.

Fig. 3 Non-covalent interaction (NCI) iso-surfaces of the X-ray structures of 1p-I₃ and Ip-I₃-2, as well as for the optimized structure of 1p-I₃-2. For clarity, in 1p-I₃, panels (A) and (B) show close-up views of the NCI iso-surface between the anion [I₃]⁻ and cation (A), and between the centers C1 and C2 (B) in the X-ray structure. In 1p-I₃-2, panels (C) and (D) display the NCI iso-surface between the anion [I₃]⁻ and cation in the X-ray (C) and in the optimized (D) structures, respectively.

Of particular interest is the interaction between atoms C1 and C2, where a single-electron σ-bond has been proposed (B). NCI analysis reveals a weak interaction (indicated by a green isosurface) between these carbon atoms for all the calculated X-ray and optimized structures (see Fig. S1). This suggests that the weak ipso C–C interaction is invariant with respect to the symmetry of the tricyclic structures and the presence or orientation of the anion.

AIM analysis

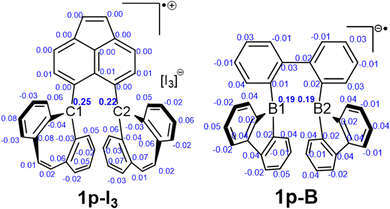
Recently, it was reported a single electron σ-bond between two borane moieties (Fig. 4, 1p-B). This structure is analogous to that of 1p-I₃. In 1p-B, the centrals atoms are the borons (B1 and B2) located within a five-membered ring framework, while the bridging unit differs. Other theoretical studies have been performed over this structure and have concluded that there is, indeed, a B–B single electron σ-bond.³⁷ Therefore, we have performed an atoms in molecules (AIM) analysis over the structure 1p-B in order to compare the results with those of 1p-I₃.

Fig. 4 Contour line map of Laplacian of electron density of the 1p-B (I) and 1p-I₃ (II) X-ray structures in the C1–C2 and B1–B2 region showing their corresponding BCP (A and A′) and bond path. The X and Y units are given in angstroms (Å).

Consistent with the results of Hübner and coworkers (Table 2),⁴ we found a bond critical point (BCP) between the B1 and B2 atoms in 1p-B. At the BCP A′, the density, ρ(r), has a value of 0.040, a negative Laplacian, ∇²ρ(r), and total energy density, H(r), with values of −0.001 and −0.010 atomic units, respectively (entry 4). These negative values are characteristic of a covalent bond interaction.³⁸ Further, the contour line map of Laplacian of the electron density between B1 and B2 atoms, reveals a charge accumulation between these atoms (Fig. 4, I). In contrast, in 1p-I₃ the BCP between C1 and C2 has a low-density value and a positive Laplacian value (entry 2), which is comparable to the BCP C1–C2 found in the dication 1pp-I₃ (entry 3). The contour line map of the Laplacian of electron density between these atoms in 1p-I₃ shows that there is charge depletion as there are only positive Laplacian values (Fig. 4, II). This is a characteristic of a weak interaction. Therefore, this comparison shows that instead of chemical bonding between C1–C2 in 1p-I₃, there is, rather, a weak interaction.

Table 2 Bond critical points (BCP) for the following X-ray structures showing the electron density, ρ(r), Laplacian density, ∇²ρ(r), energy density, H(r), spin density, s(r), shown in atomic units

Entry	Structure	BCP	ρ(r)	∇^2ρ(r)	H(r)	s(r)
1	1	A	0.147	−0.141	−0.0661
2	1p-I3		0.013	0.029	0.0004	0.005
3	1pp-I3		0.009	0.029	0.0013
4	1p-B	A′	0.040	−0.001	−0.0102	0.023

---

The topological features of this interaction can be further studied with the natural bond critical point (NBCP) analysis, in which the density at BCP A is described in terms of natural bond orbitals (see Table S2). The results show that there are many NBOs that contribute to the critical point, but none correspond to the NBO σ-bond C1–C2, in fact, in NBO version 7.0 the natural Lewis structure (NLS) does not contain this bond.

Spin density population

A comparison of the spin density population of 1p-I₃ and 1p-B demonstrates how the radical is delocalized in the tricyclic structures (Fig. 5). In 1p-I₃, the results indicate that C1 and C2 atoms contribute with 0.25 and 0.22 electrons, which accounts to 47% of the total contribution to the spin density population. The rest of the radical is distributed in the tricyclic structure. In 1p-B, the spin density at B1 and B2 atoms contribute both with 0.19, therefore, the total contribution of the borons to the spin density population is 38% and the rest of the radical is delocalized in the molecule framework. This shows that in both systems the radical is highly delocalized in the adjacent rings and that the radical is partially localized in the central atoms C1/C2 and B1/B2. Nonetheless, inspection of the spin density at BCP A and A′ (0.005 and 0.023 electrons, respectively) indicates that the radical is weakly delocalized between C1 and C2 atoms, whereas in 1p-B the partly radical is more delocalized across B1 and B2 atoms.

Fig. 5 Computed spin density population of the X-ray 1p-I₃ and 1p-B structures.

Natural bond orbitals

An important insight to be gained from the optimized 1p-I₃ molecule is how the π-orbitals are localized within the tricyclic framework. Natural bond orbital (NBO) theory provides a Lewis-like representation that includes 2c/2e and 3c/2e bonds and hyperbonding interactions. This representation, known as the natural Lewis structure (NLS), offers a chemically intuitive interpretation of the bonding pattern. Upon examining the NLS calculated using the latest version of the NBO software (NBO 7.0), we observed a significant difference compared to the NLS generated by NBO 3.1, which is implemented in the Gaussian-09 and Gaussian-16 packages (Fig. 6). In NBO 3.1, the NLS includes an alpha NBO corresponding to the single-electron bond (SEB) (a3-SEB). However, in NBO 7.0, the NLS does not include any alpha NBO indicating a SEB. Instead, the alpha electron appears localized on either side of the tricyclic structure. Due to the high delocalization of the bonding pattern, NBO 7.0 allows for further analysis through natural resonance theory (NRT), which quantifies the contributions of various resonance structures and identifies how many of them involve a single-electron σ-bond.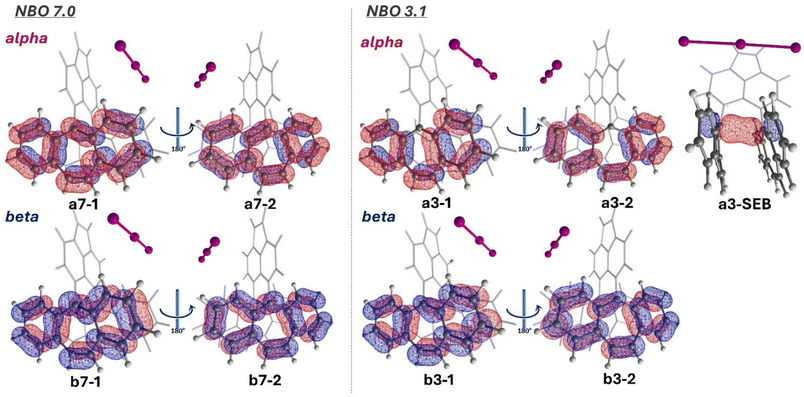

Fig. 6 Calculated natural Lewis structure (NLS) for 1p-I₃ (optimized) using NBO 7.0 and 3.1 program versions. Only relevant NBOs are shown on each side of the tricyclic structure.

Natural resonance theory

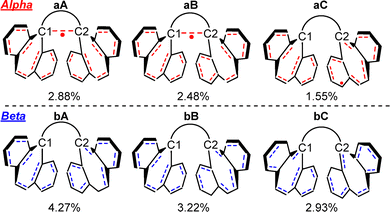
We applied the NRT method to 1p-I₃, and it calculated a total of 256 alpha and 142 beta NRT resonance structures. The highly delocalized character of the system results in low individual structure weights, all below 5.0% (Fig. 7), indicating that no single resonance structure dominates the bonding picture.

Fig. 7 Calculated NRT resonance structures of optimized 1p-I₃ (optimized) along with the resonance weight. Each dashed bond represents a single electron. Only the three most contributing NRT resonance structures are shown.

Closer inspection of the NRT results reveals that the two most significant alpha resonance structures include a single-electron σ-bond between C1 and C2. As shown in Fig. 7, alpha structures aA and aB display this SEB, with respective weights of 2.88% and 2.48%, while structure aC does not. For the beta electrons, as expected, none of the leading resonance structures (bA-bC) show a C1–C2 bond.

Although the two most contributing alpha NRT structures have a C1–C2 bond, their low individual weights do not provide strong evidence of a bond on their own. To evaluate the presence of a bond more comprehensively, one must consider the entire set of alpha resonance structures. By summing the contributions of all structures that include a C1–C2 bond (multiplying each by its corresponding weight) we obtain the natural bond order. If the bond is present in a substantial number of these structures, the resulting C1–C2 bond order should approach 0.500.

The NRT results indicate that the calculated natural bond order between C1 and C2 in 1p-I₃ is 0.066 (Fig. 8). Since this is an open-shell system, the bond order is divided into its alpha and beta contributions. In this case, only the alpha component contributes to the bond order, with a value of 0.066. This is significantly lower than the expected value of 0.500 for a single-electron σ-bond, indicating that the C1–C2 interaction has only 13.2% alpha σ-bond character. These results suggest that, although the two most contributing alpha NRT resonance structures feature a C1–C2 bond, this interaction is not present in most of the full set of resonance structures.

Fig. 8 Calculated natural bond orders from NRT analysis for 1p-I₃ (optimized) between the C1 and C2.

Natural bond orbitals deletion

One method to quantitatively characterize non-covalent interactions is the natural bond orbital deletion (NBOdel) approach. This analysis allows to estimate the intramolecular interaction energy between the tricyclic rings (Table 3, blue rings) by deleting the specific elements of the Fock matrix associated with selected NBOs.²²

Table 3 Natural bond orbital deletion analysis applied for the rings marked in blue of the following optimized structures. Energies are shown in kcal mol⁻¹

Structure	Formula	Fragments	ΔE	ΔE(α)	ΔE(β)
a The interaction between C1–C2 is not considered.
1	[1]	Rings^a ↔ rings^a	40.9
		C1 ↔ C2	40.0
1p-I3	[1]^+	Rings ↔ rings	55.4	39.8	15.6
		C1 ↔ C2	5.2	2.8	2.4
1pp-I3	[1]^2+	Rings ↔ rings	29.9
		C1 ↔ C2	5.0

---

We first applied this method to neutral compound 1, focusing on the interaction between the π-orbitals of the relevant rings, without deleting the σ(C1–C2) bond (Table 3). The results indicate an interaction energy of ΔE = 40.9 kcal mol⁻¹ and deleting only the NBO σ(C1–C2) result of 40.0 kcal mol⁻¹, together account for a total interaction energy of 80.9 kcal mol⁻¹. The same analysis was then applied to the cationic form, 1p-I₃, now including the carbons C1 and C2. The calculated interaction energy is ΔE = 55.4 kcal mol⁻¹. The energy increase of 14.5 kcal mol⁻¹ relative to the neutral species 1 can be explained in terms of the geometry difference; in 1, one of the tricyclic structures is bent away from the other tricyclic moiety, whereas in 1p-I₃, the rings are parallel (Fig. 9). This parallel feature allows for better orbital alignment and, thus, there are stronger interactions between occupied and empty orbitals that increase the interaction energy of 1p-I₃. Since 1p-I₃ is an open shell system, the total interaction energy can be further decomposed into α and β contributions. The α electrons contribute ΔE(α) = 39.8 kcal mol⁻¹, while the β electrons contribute only ΔE(β) = 15.6 kcal mol⁻¹. This demonstrates that the α-electron interaction is more than twice as strong as that of the β electrons. However, it remains to be determined whether this increased interaction energy upon oxidization is primarily due to the C1–C2 interaction. To evaluate this, we selectively deleted only the NBO interactions between C1 and C2. The resulting interaction energy is ΔE = 5.2 kcal mol⁻¹, accounting for just 9.5% of the total interaction. Further decomposition shows nearly equal contributions from the α and β electrons (2.8 and 2.4 kcal mol⁻¹, respectively) indicating a slightly greater contribution from the α electrons.

Fig. 9 Upper view of the neutral 1, cationic 1p-I₃, and dicationic 1pp-I₃ optimized structures showing the structural arrangement of the tricyclic moieties.

Although the C1–C2 interaction is weak, NBO analysis allows us to identify the specific donor–acceptor orbital interactions responsible for this energy. This is done by deleting specific sets of donor and acceptor NBOs interactions associated with C1 and C2 (Fig. 10). The donor orbitals include σ(C–C) and π(C–C) bonds; however, only the α NBOs contain the π-bonding character. The acceptor orbitals can be categorized into three types: (1) antibonding orbitals σ*(C–C) and π*(C–C) (σ*/π*); (2) Rydberg p-orbitals of C1 and C2 (Ry [p(C)]); and (3) other Rydberg orbitals of these atoms. Our results show that no single donor–acceptor NBO interaction dominates the overall interaction energies for either spin component (ΔE(α) = 2.8 kcal mol⁻¹, ΔE(β) = 2.4 kcal mol⁻¹). Instead, several weak interactions contribute (Table 4). Among these, deletion of the donor-Rydberg p-orbital interactions yields the large contributions: 1.687 kcal mol⁻¹ (60.3%) for α electrons and 1.506 kcal mol⁻¹ (62.6%) for β electrons. In contrast, deletion of interactions with antibonding orbitals contributes 0.552 kcal mol⁻¹ (19.7%) and 0.516 kcal mol⁻¹ (21.5%), for α and β electrons, respectively. The remaining interaction energy comes from other Rydberg orbitals of C1 and C2.

Fig. 10 NBO donor (red and blue contour) and acceptor (green and yellow contour) orbitals considered for the NBO deletion analysis of 1p-I₃ (optimized). The donor orbitals are those that involve the C1 and C2 atoms: σ(C–C) and π(C–C). The acceptor orbitals correspond to the antibonding (σ*(C–C) and π*(C–C) (σ*/π*)), low valence (p(C)) and Rydberg orbitals p-orbitals of C1 and C2 (Ry [p(C)]). For clarity, only relevant carbon atoms are shown.

Table 4 Natural bond orbital deletion energies (kcal mol⁻¹) of the interacting donor–acceptor orbitals of C1 and C2. The acceptor orbitals considered are the σ* and π* antibonding (σ*/π*) and the Rydberg p-orbitals of C1 and C2 (Ry [p(c)]) (see Fig. 10). Occupancies (Occ) are given in electrons

Entry	Spin	Donor	Occ	Acceptor	σ*/π*	Ry [p(C)]	Total
a Percentages are obtained dividing by ΔE(α) = 2.8 or ΔE(β) = 2.4 kcal mol^−1.
1A	Alpha	σ(C2–C6)	0.984	[C1]	0.036	0.181	0.217
2A		σ(C2–C8)	0.987		0.008	0.229	0.237
3A		σ(C2–C7)	0.987		0.032	0.248	0.280
4A		π(C2–C7)	0.825		0.179	0.127	0.306
5A	Alpha	σ(C1–C3)	0.984	[C2]	0.053	0.235	0.288
6A		σ(C1–C4)	0.987		0.007	0.246	0.253
7A		σ(C1–C5)	0.987		0.019	0.233	0.252
8A		π(C1–C5)	0.831		0.218	0.188	0.406
	Total				0.552	1.687	2.239
					(19.7%)	(60.3%)	(80.0%)^a
1B	Beta	σ(C2–C6)	0.984		0.074	0.238	0.312
2B		σ(C2–C8)	0.987	[C1]	0.082	0.228	0.310
3B		σ(C2–C7)	0.987		0.087	0.240	0.327
4B	Beta	σ(C1–C3)	0.983		0.134	0.280	0.414
5B		σ(C1–C4)	0.987	[C2]	0.072	0.265	0.337
6B		σ(C1–C5)	0.987		0.067	0.255	0.322
	Total				0.516	1.506	2.022
					(21.5%)	(62.6%)	(84.1%)^a

---

In summary, the dominant interactions between the C1 and C2 are between the donor orbitals, specifically σ-bonds and π-bonds, and the Rydberg orbitals of these atoms, supporting a multi-orbital, non-covalent interaction framework.

Conclusions

We performed a detailed quantum chemical investigation of the weak interaction between ipso carbon atoms (C1 and C2) in tricyclic structures of a neutral compound and its oxidized forms. Our results show that the interaction between the tricyclic moieties is weak, with NCI revealing only van der Waals or non-covalent contact and no evidence of strong through-space bonding. Moreover, a persistent bond critical point (BCP) is observed between C1 and C2 in both X-ray and optimized structures, but the low electron density values suggest a non-covalent nature. Comparing the contour line map of the Laplacian of electron density of 1p-I₃ and 1p-B, shows that 1p-I₃ has depletion charge at the BCP between C1–C2, characteristic of a weak interaction, whereas 1p-B has charge accumulation and a negative energy density value at the BCP between B1–B2, which is representative of a covalent bond. The calculated spin density distribution in 1p-I₃ indicates that C1 and C2 contribute with 0.25 and 0.22 electrons, which accounts to the 47% of the total distribution. The rest is distributed in the two tricyclic structures.

Our NBO and NRT analyses indicate the presence of resonance structures containing a single-electron σ-bond (SEB) between C1 and C2, though their contribution is minor (<3%) and insufficient to define a dominant bonding interaction. The calculated natural bond order (0.066) between C1 and C2 in the monocation shows only a 13.2% character of a typical SEB, confirming the weak and partial nature of this interaction.

Furthermore, NBCP theory reveals no single NBO dominating the electron density at BCP A, indicating that the interaction arises from a broad, delocalized contribution of multiple NBOs, including both Lewis and non-Lewis types. Using the NBOdel analysis, which quantifies the intramolecular interaction, showed that the C1–C2 contribution accounts for only ∼9.5% of the total interaction energy between the rings. This interaction is mainly mediated by donor–acceptor interactions involving bonding orbitals and the Rydberg orbitals of the carbon atoms.

Thus, our theoretical results converge to show that the C1–C2 interaction is not a conventional covalent bond but rather a subtle, delocalized electronic effect with minor bonding character. This weak interaction helps to preserve the geometry and symmetry of the tricyclic systems upon oxidation and provides new insight into the bonding in open-shell π-delocalized systems.

Conflicts of interest

There are no conflicts to declare.

Data availability

Aside from the cartesian coordinates found in the supplementary information (SI) output files for the natural population analysis and other electronic structure computations are available from the authors upon request.

Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04041h.

Acknowledgements

We thank DGTIC – UNAM for granting access to their supercomputer ‘Miztli’ under a LANCAD grant, and Mrs Citlalit Martínez-Soto for keeping our local computers running. L. I. L. F. (1080463) and D. I. M. V. (1080287) acknowledges SECIHTI for financial support.

References

1. L. Pauling, J. Am. Chem. Soc., 1931, 53, 3225–3237.
2. L. Cataldo, S. Choua, T. Berclaz, M. Geoffroy, N. Mézailles, L. Ricard, F. Mathey and P. L. Floch, J. Am. Chem. Soc., 2001, 123, 6654–6661.
3. J. D. Hoefelmeyer and F. P. Gabbaï, J. Am. Chem. Soc., 2000, 122, 9054–9055.
4. A. Hübner, A. M. Diehl, M. Diefenbach, B. Endeward, M. Bolte, H. Lerner, M. C. Holthausen and M. Wagner, Angew. Chem., 2014, 126, 4932–4935.
5. M.-E. Moret, L. Zhang and J. C. Peters, J. Am. Chem. Soc., 2013, 135, 3792–3795.
6. K. Chan, F. Ying, D. He, L. Yang, Y. Zhao, J. Xie, J.-H. Su, B. Wu and X.-J. Yang, J. Am. Chem. Soc., 2024, 146, 2333–2338.
7. T. Shimajiri, S. Kawaguchi, T. Suzuki and Y. Ishigaki, Nature, 2024, 634, 347–351.
8. Q. Li, X. Guo, X. Yang, W. Li, J. Cheng and H.-B. Li, Phys. Chem. Chem. Phys., 2014, 16, 11617–11625.
9. M. D. Esrafili, M. Vakili and M. Solimannejad, Mol. Phys., 2014, 112, 2078–2084.
10. M. D. Esrafili and F. Mohammadian-Sabet, J. Mol. Model., 2015, 21, 65.
11. Q. Li, X. An, B. Gong and J. Cheng, J. Mol. Struct. THEOCHEM, 2008, 866, 11–14.
12. Y. Wang, J. Zou, Y. Lu, Q. Yu and H. Xu, Int. J. Quantum Chem., 2007, 107, 501–506.
13. Z. Li, Y. Zhu, G. Zuo, H. Tang and H. Li, Int. J. Quantum Chem., 2011, 111, 570–577.
14. M. D. Esrafili, F. Mohammadian-Sabet and M. Solimannejad, Chem. Phys. Lett., 2016, 659, 196–202.
15. Q. Li, R. Li, S. Yi, W. Li and J. Cheng, Struct. Chem., 2012, 23, 411–416.
16. G. Caballero-García, M. Romero-Ortega and J. Barroso-Flores, Phys. Chem. Chem. Phys., 2016, 18, 27300–27307.
17. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, jcc.25873.
18. C. R. Landis and F. Weinhold, J. Comput. Chem., 2007, 28, 198–203.
19. C. R. Landis, R. P. Hughes and F. Weinhold, Organometallics, 2015, 34, 3442–3449.
20. E. D. Glendening, C. R. Landis and F. Weinhold, J. Am. Chem. Soc., 2019, 141, 4156–4166.
21. F. Weinhold, J. Comput. Chem., 2012, 33, 2440–2449.
22. E. D. Glendening, C. R. Landis and F. Weinhold, WIREs Comput. Mol. Sci., 2012, 2, 1–42.
23. Y. Ishigaki, T. Shimajiri, T. Takeda, R. Katoono and T. Suzuki, Chem, 2018, 4, 795–806.
24. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
25. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
26. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
27. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
28. R. F. W. Bader and T. T. Nguyen-Dang, Advances in Quantum Chemistry, Elsevier, 1981, pp. 63–124.
29. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
30. T. Lu, J. Chem. Phys., 2024, 161, 082503.
31. J. M. Solano-Altamirano, J. M. Hernández-Pérez, J. Sandoval-Lira and J. Barroso-Flores, J. Chem. Phys., 2024, 161 DOI:10.1063/5.0239835.
32. J. Hsin, A. Arkhipov, Y. Yin, J. E. Stone and K. Schulten, Curr. Protoc. Bioinf., 2008, 24 DOI:10.1002/0471250953.bi0507s24.
33. J. Han, Extended Abstracts of the 2021 CHI Conference on Human Factors in Computing Systems, ACM, Yokohama Japan, 2021, pp. 1–5.
34. F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440.
35. F. Weinhold and E. D. Glendening, NBO 7.0 Program Manual Natural Bond Orbital Analysis Programs, 2018, p. B-30.
36. H. Rzepa, Henry Rzepa's Blog, 2024 DOI:10.59350/xp5a3-zsa24.
37. G. Mierzwa, A. J. Gordon and S. Berski, J. Mol. Struct., 2020, 1221, 128530.
38. ed. C. F. Matta, R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley, 2007.

---