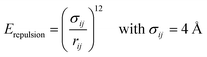Differential sequence charge clustering and mixing ratio affect stability and dynamics of heterotypic peptide condensates
Milan Kumar
Hazra

Department of Chemistry, Indian Institute of Technology, Jodhpur NH 62, Surpura Bypass Rd, Karwar, Jheepasani, Rajasthan 342030, India. E-mail: milanhazra@iitj.ac.in
First published on 25th November 2025
Abstract
Phase separation has emerged as a central mechanism through which cells organize their material components, and it is extremely important in tuning various biological regulations. However, such condensates in cellular media are often heterogeneous in nature in terms of proteins and the presence of polynucleotides in different concentrations. This study explored the stability and dynamics of heterotypic coacervates formed by polyampholyte binary peptides having differential charge-clustering limits. A systematic increase in the differential charge-clustering in the peptide pairs tuned the origin of the heterogeneity and resulted in an enhanced stability of the droplet compared to the homogeneous ones with the same average charge clustering of the two peptide pairs. In addition, the stability of the condensate phase was linearly enhanced with an increase in the high charge-clustering polymers in the system. The peptides with higher charge-clustering diffused 3–4 times slower within the condensate phase than the lower charge-clustering ones due to heterogeneity in the structural morphology of the droplets, which diminished when the difference of charge clustering among the sequence pairs forming the condensate was lowered. Coupled with the differential diffusivity of the polymers in the condensates, droplet diffusion was nearly 7–35 times lower than that of the bulk phase, depending upon the mixing fractions of the polymers and variable sequence charge clustering. The condensates with moderate heterogeneity showed an enhanced arrestation than the most heterogeneous condensates, likely due to their complementarity and better packing, as indicated by the energetics of the condensate. This study quantifies the fundamental microscopic properties of heterotypic condensates formed through long-range electrostatic forces, particularly how they can be modulated by the differential charge patterns in sequences and the systematic mixing of fractions.
Introduction
Phase separation has emerged as a central mechanism through which cells accomplish spatiotemporal compositional control1 and modulate various biological rhythms, namely, RNA metabolism2 and regulation, stress regulation,3 mechano-transduction,4 mitochondrial signaling,5 intracellular storage6 and an enhanced concentration of substrates that facilitate specific biochemical reactions.7,8 Even aberrant condensations lead to disease-like states, e.g., ALS, FTD, Alzheimer's8,9 and cancer.10 It has been extensively shown that protein disorder plays a crucial role in the recognition11 and multi-body association of an assembly.12–15 Given their multicomponent nature and complex functionalities, these condensates are very much context-dependent16,17 and display distinct internal architecture.18,19 Multivalent interactions20–26 stemming from the organizational pattern of a sequence27,28 dictate a condensate's stability and dynamics.28 A stickers-and-spacers model successfully depicts the organizational framework and sequence-specific driving forces of phase separation.21,29–31 The cross-linking of the sticker motifs induces a network mesh, and the binding energy of the peptides dictates the material properties and shape of a condensate.32,33 Biomolecular condensates are complex fluids with extensive liquid-like nature, spanning a broad range of viscoelasticities, and are programmable as sequence features of the proteins involved; altering the degree and the strength of cross-linking can lead to variations in the viscoelastic nature of the network.34 From an engineering viewpoint, condensates can be thought of as tunable, membrane-less organelles having a significant soft colloid-like character35,36 and can be very useful as artificial carriers for intracellular cargo delivery, the time-dependent control and efficient release of cargo, and designing stimuli-responsive artificial materials.36 Therefore, it is of utmost importance to decode the material properties, as well as the underlying physics of homotypic and heterotypic condensate formation involving multiple biologically relevant components, namely, proteins and polynucleotides, which are derived as a function of the sequence characteristics.37,38The phase separation of various single-component proteins with disordered domains has been studied in detail, revealing the important role of various sequence features, namely, charge clustering, sequence hydrophobicity, polar residues, and cation–pi interactions, in underlying the formation kinetics, stability and dynamics of coacervates.26,27,29,31,39–41 Several order parameters have been introduced in this regard, namely, sequence-charge decoration,42 charge-pattern parameter27,29 and fraction hydrophobicity,28 for delineating the features of condensates in a systematic way and for analyzing the conformational ensembles of intrinsically disordered proteins and their corresponding efficiency toward homotypic phase separation. The composition as well as the organization of amino acids in sequences affect their stability and dynamics through a balance between enthalpy and entropic components.43,44 For example, elastin-like hydrophobic protein domains induce entropy-mediated phase separations, which have been determined by direct NMR relaxation measurements and diffusion data.45 Disorder plays an important role in the formation of condensates, as efficient and finite lifetime multivalent interactions are required for dynamic multi-body assembly.20 This aspect is even connected to diffusivity inside the condensates and Tau protein's torsional fluctuation, which were determined through picosecond time-resolved fluorescent depolarization measurements and have been shown to be inherently connected to the liquid-like nature of an assembly.46
From a cellular context, condensates are often heterogeneous and not a single-component phase, and hence they involve many components with diverse binding affinities to each other. Experimental studies with microrheology techniques have shown the significant sticker-strength dependence of network reconfiguration timescales in ARG-GLY-rich, intrinsically disordered regions (IDRs) and single-stranded DNA in heterogeneous condensates. The chain length of SS-DNA influences its phase stability and internal viscosity, but the diffusivity of the peptides remains unaltered due to variations in the chain length.36 Arrhenius’ law of activation energy has been observed to hold true in predicting the viscous nature of such a heterotypic mesh.36 Organizational heterogeneity has also been observed in the heterotypic protein condensates of prion-like domains in stress granule proteins, namely, FUS and hnRNPA. In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary peptide systems, heterotypic interactions have been reported to enhance the stability of the condensate phase. This enhancement has been reported to have originated from complementary electrostatic interactions, even in a system where only 10% of the residues are charged. α-Synuclein and Prp form a dynamic condensate with the nanoscale electrostatic clusters within its microscopic assembly. The breaking and making of non-covalent interactions have been reported to influence the hierarchical structures in the formation of such condensates with a diffusive nature.47 The cellular condensates of basic FGF (BFGF) with a highly charged protein and negatively charged heparin show an enhanced stability of the binary condensates compared to the homotypic condensates in the presence of crowders. As observed in confocal microscopy, BFGF mixed with heparan sulphate proteoglycans at a 1
1 binary peptide systems, heterotypic interactions have been reported to enhance the stability of the condensate phase. This enhancement has been reported to have originated from complementary electrostatic interactions, even in a system where only 10% of the residues are charged. α-Synuclein and Prp form a dynamic condensate with the nanoscale electrostatic clusters within its microscopic assembly. The breaking and making of non-covalent interactions have been reported to influence the hierarchical structures in the formation of such condensates with a diffusive nature.47 The cellular condensates of basic FGF (BFGF) with a highly charged protein and negatively charged heparin show an enhanced stability of the binary condensates compared to the homotypic condensates in the presence of crowders. As observed in confocal microscopy, BFGF mixed with heparan sulphate proteoglycans at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio exhibited larger droplets, which indicates a stronger phase separation.48 The possible reason for this observation has been hypothesized as an enhancement of the multivalent interactions in binary condensates.
10 ratio exhibited larger droplets, which indicates a stronger phase separation.48 The possible reason for this observation has been hypothesized as an enhancement of the multivalent interactions in binary condensates.
Theoretical formulations and molecular simulations have extensively complemented the experimental understanding with an all-atom or a reduced resolution of proteins and polynucleotides due to the long timescale required for such an assembly's equilibration.28–31,41,49–55 These studies however lack an explicit effect of counter-ions or solvent, and water's role; they have captured basic structural aspects as well as the phase behaviours of the relatively reduced miniature models of proteins and peptides. The sequence-dependent, re-entrant phase behaviour observed in patchy particles56–58 and network-forming systems has been reported in heterotypic protein–polynucleotide condensates and could play an important role in the tuning dynamics and solubilization of droplets.59–61
This present study provides a first step towards systematically uncovering the sequence-feature dependence of a heterotypic phase separation. To that end, we first planned to understand the effect of charge-clustering variability of the sequences on the stability and dynamics of the phases formed by the polyampholyte binary pair peptides. The various degrees of charge clustering of like charges along a peptide chain can be quantified by a charge-pattern order parameter, κ.27 The variability of charge clustering among the sequence pairs was quantified as the difference of the charge pattern parameters of the sequence pairs (Δκ). In addition, we systematically mixed the two peptides, where xlow-κ denoted the fraction of the low-κ polymers in the system. We quantitatively compared the stability, internal dynamics, and the chain-reconfiguration timescales of the homotypic vs. heterotypic condensates composed of designed polyampholyte sequence pairs, examining how the peptide mixing fractions and charge-clustering variations impacted the sequence heterogeneity of the condensate phase.
Models and simulations
Designed systems
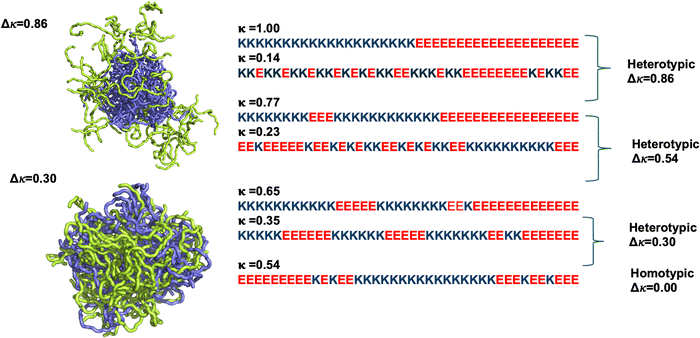
To investigate how differential charge clustering of the sequence pairs and their mixing fractions altered the stability and dynamics of the binary protein coacervates, we designed three 40-residue sequence pairs that were used for condensate formation with a gradual enhancement in the difference of the charge-pattern parameter (Δκ) between the two sequences (Fig. 1). The representative condensates and the structural morphologies of these condensates at Δκ = 0.86 and 0.30 are shown in Fig. 1. While the slate color denotes the polymers with high-κ values, the lemon-green color denotes the polymers with low-κ values. We ensured that the average κ of the two sequences was close to 0.5 and compared our data with the condensates formed by the homotypic phase separation of a sequence (κ = 0.54). Several mixing fractions of the two polymers were simulated namely, at xlow-κ = 0.10, 0.25, 0.40, 0.50, 0.60, 0.75 and 0.90. For clarity, we have reported only five of the simulated mixing fractions. We ensured the neutrality of the sequences and the only order parameters that varied systemwide were the sequence-specific charge clustering and mixing fractions (xlow-κ) of the polymers.Simulation details
Because all-atom, explicit solvent simulations are expensive to achieve, and considering the timescales required to form mesoscopic condensates at equilibrium, a structure-based coarse-grained model62–64 was implemented to investigate the equilibrated heterotypic condensates, which allowed for a comprehensive dissection of the effect of heterogeneity on the condensates’ stability and dynamics. Each residue in the designed polyampholytes was represented by a single bead and was assigned as either a positively or negatively charged residue. The potential energy functional consists of the following terms: the harmonic bonded and angular interactions for designing the polymers, the electrostatic interactions among all the charged beads, both intra- and inter-molecular, and short-range dispersion interactions. We did not implement any dihedral interactions as the designed peptides behave as IDRs.An embedded implicit solvent model and the salt effect were used for screening the electrostatic interactions between the charged beads using the Debye–Hückel potential,63 which is expressed as:
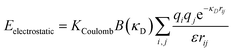 | (1) |
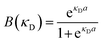 | (2) |
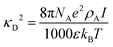 | (3) |
A Langevin dynamics simulation was performed with 100 copies of the binary polymer pairs at different mixing fractions (xlow-κ), as detailed above in a box of dimension 300 × 300 × 300 angstroms.3 To quantify single molecular properties in the bulk (dilute) phase, single polymers were simulated in the same box length at various temperatures below the critical point of the corresponding droplets. From an analysis, the stability of the condensates and the dynamics of the polymers within the same system were quantified at an ionic concentration of 0.04 M, using an implicit solvent medium with a dielectric constant of 80 and multiple temperatures below the critical point of the system. At each temperature, we simulated two independent trajectories with 107 steps by solving the Langevin equation, which confirmed the convergence and averaging of the analysis shown herein. The trajectories were saved at every 500th step. Each trajectory consisted of 20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames. The initial 5000 frames (2500
000 frames. The initial 5000 frames (2500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps) were discarded for equilibration. The final 15
000 steps) were discarded for equilibration. The final 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames were analysed. A clustering algorithm was used to identify the condensates and the largest clusters from the trajectories. We used two different colour schemes: (i) blue-green shades showcase all the mixing fractions, and (ii) the dark red-yellowish red shades showcase the trends for the three different Δκ systems studied at a particular mixing fraction. While the charge-clustering variation in the designed peptide pairs showcase inherent peptide differentiability, the systematic variation of mixing among the peptides allowed us to elucidate the temporal cellular environment alteration, which is immensely important in decoding the functionality of the condensates and their enrichment.
000 frames were analysed. A clustering algorithm was used to identify the condensates and the largest clusters from the trajectories. We used two different colour schemes: (i) blue-green shades showcase all the mixing fractions, and (ii) the dark red-yellowish red shades showcase the trends for the three different Δκ systems studied at a particular mixing fraction. While the charge-clustering variation in the designed peptide pairs showcase inherent peptide differentiability, the systematic variation of mixing among the peptides allowed us to elucidate the temporal cellular environment alteration, which is immensely important in decoding the functionality of the condensates and their enrichment.
Results
Sequence-dependent phase stability in the heterotypic condensates
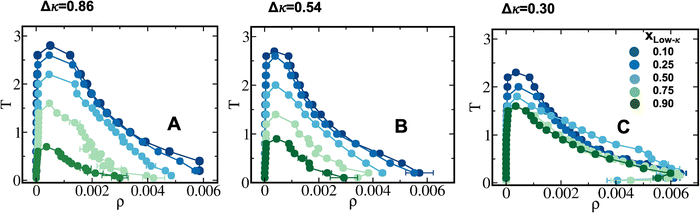
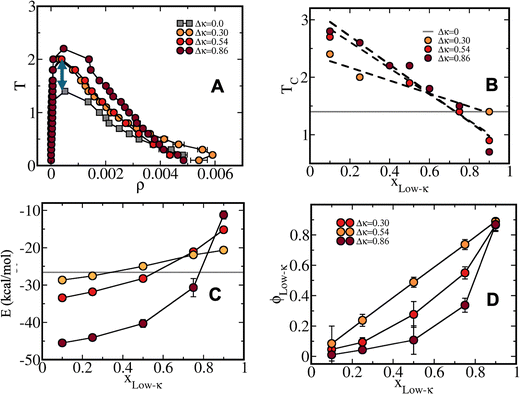
To elucidate the effect of differential charge clustering (as a measure of sequence heterogeneity) on droplet stability, temperature-density phase diagrams were plotted for the three different sequence-pairs along with a gradual decrease in Δκ between the two sequences, as shown in Fig. 2(A)–(C). Each panel shows five different mixing fractions of the low and high-κ polymers and was denoted with the mixing fraction of the low-κ polymer, xlow-κ. At each timestep, we computed the density of the polymers in the condensate phase by counting the number of polymer beads in the largest cluster within a 5-nm distance from the center of mass of the cluster. We employed a Cayley Tree-like clustering algorithm that can capture the information of a network mesh and can help in identifying the largest cluster. The critical point was determined by fitting the density–temperature data to an Ising model with the following expression: | (4) |
Underlying energetics of phase separation and connection to the origin of criticality
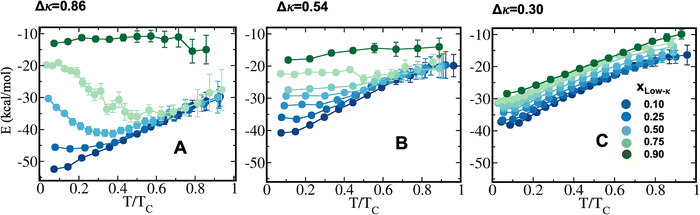
To decode the origin of such heterogeneity in the induced stability pattern of the designed binary peptide condensates, the total energy experienced by each polymer in the condensate phase was computed as a function of the temperature scaled with respect to criticality for all the mixing fractions (Fig. 3). In addition, we dissected the total energy into components, namely, the self-interactions within the high-κ polymers, the low-κ polymer and the cross interactions among these two polymers (Fig. S1–S3). For the highly heterogeneous condensates with sequence pairs at κ = 1.00 and κ = 0.14, the peptide–peptide interaction energy stabilized the condensate phase up to 55 kcal mol−1 at a very low temperature, which ensured that it was far away from criticality (T/Tc = 0.1), and it decreased with the mixing of the low-κ polymers to 18 kcal mol−1, exactly three times that observed for the phase diagram's stability (Fig. 2A). Similarly, along with temperature, the depletion of the attractive energy was linear at the extreme xlow-κ values of 0.1 and 0.9 due to the presence of one kind of polymer at its maximum, but an enhanced stabilization was observed in the condensates formed by the sequence pairs (κ = 1.00 and κ = 0.14) at the mixing fractions, xlow-κ = 0.25–0.75 (where heterogeneity peaked in the condensate phase) in the range of T/Tc = 0.2–0.6 due to the temperature-induced entropy in the system and better mixing at the relatively higher temperatures under significant sequence heterogeneity. The stabilization loss along with temperature also decreased along a gradient where the mixing fraction ranged up to three times that of the electrostatic energy loss at xlow-κ = 0.1, after it reached a critical point of 1.2-fold at an extremely low-κpolymer concentration in the droplet (xlow-κ = 0.9). When there was a slight reduction in the heterogeneity of the charge clustering of the sequence pairs (Δκ = 0.54), stabilization increased up to 40 kcal mol−1 for the mixing fraction, xlow-κ = 0.1, which is a value far away from the criticality of the system (T/Tc = 0.1), and a stabilization energy of nearly 18 kcal mol−1 was observed for the mixing fraction, xlow-κ = 0.9.At a moderate heterogeneity of the sequence pairs (Δκ = 0.30), an enhanced stabilization was observed for the condensate systems with higher xlow-κ values relative to the other sequence pairs with greater heterogeneity (Δκ = 0.86 and 0.54), and the effect of the mixing fraction (xlow-κ) was low. The drop in energetic stabilization was nearly 1.3 times that at T/Tc = 0.1 compared to 3 times that observed in Fig. 3A and B for the condensates of the sequence pairs with Δκ = 0.86 and 0.54 along the mixing fraction (xlow-κ), signifying a better complementarity among the sequence pairs and effective packing, which was unable to be altered by the mixing fractions. This observation was in complete agreement with the phase diagrams shown in Fig. 2. Along with temperature, there was 2–3-fold loss of energy in the droplet phase as it approached criticality (Fig. 3).
A dissection of the pairwise energies among the different kinds of polymers is shown in Fig. S1–S3 for Δκ = 0.86, 0.54 and 0.30, respectively, demonstrating the self-interactions among high-κ polymers, low-κ polymers and the cross interactions between these two polymers (Panels A, B and C, respectively in each figure). The major gain in energy was mostly dominated by the interactions among the high-κ polymers at a lower mixing fraction (xlow-κ) in all three Δκ systems (nearly 40 kcal mol−1 at T/Tc = 0.1), pointing to an enhanced stability at xlow-κ values, as shown in Fig. 2. The low-κ polymers contributed to nearly 9–12 kcal mol−1, with their highest enrichment at xlow-κ = 0.9 in the system (Fig. S1B–S3B). To some extent, the energetic stabilization of the condensates stems from values of 10–18 kcal mol−1 when the droplet was enriched with low-κ polymers, and values of 40–50 kcal mol−1 when it was enriched with high-κ polymers. Similar contributions have been observed from the cross κ interaction energy at Δκ = 0.86 and 0.54 and at mixing fractions, xlow-κ = 0.25–0.75, where mixing plays an important role. At Δκ = 0.54 (Fig. S3B), we quantified a significant increase in the interactions up to 25 kcal mol−1 among the polymers (κ = 0.35) at their maximum enrichment (xlow-κ = 0.9). In addition, the interaction energy among the polymers (κ = 0.35 and κ = 0.65) also increased up to 15 kcal mol−1 at the mixing fractions, xlow-κ = 0.25–0.75, signifying a better complementarity between the two sequences, as pointed out earlier (Fig. S3C).
The possible origin of the enhanced stability of the heterotypic condensates compared to the homotypic ones could pertain to an entropic advantage related to the availability of significantly different charged patches with differential sequences and enthalpic favourability. The additional availability of variably charged patches in the two different sequences enhanced the additional possibility of several complementary multivalent interactions and may have contributed to an enhanced stability of the heterotypic condensates with respect to the homotypic ones. At extreme mixing fractions, the self-interactions within each kind of polymer were the main contributors to an enhanced stability of the heterotypic condensates compared to the homotypic condensates, while there were smaller relative contributions from the cross interactions; overall, these contributions resulted in relatively high Δκ variant pairs primarily due to an enthalpic gain (Fig. S1). Hence, the high-κ polymers formed the droplet's core, and the low-κ polymers remained on the droplet's surface. The cross interactions between the two sequences at the low limit of Δκ (moderately heterotypic) and near xlow-κ = 0.5 dominated the enhanced stability of the condensates compared to the homotypic condensates, and primarily originated from an availability of multiple complementary multivalent patches of interactions among the different sequences (Fig. S3). As the low-κ polymers started entering the core of the droplets, there was a decrease in the Δκ values of the sequence pairs.
A comparative stability analysis of homotypic vs. heterotypic phase separation
To understand the effect of the heterotypic sequence pairs on the phase stability, the phase diagrams for all three Δκ sequence pairs are shown along with the homogeneous condensate of a sequence at κ = 0.54 (the sequence is shown in Fig. 1) and at a mixing fraction, xlow-κ = 0.5. One must note that a significant enhancement of stability was observed for the heterotypic sequence pairs compared to the homotypic sequence pairs, while the homotypic condensates reached a critical point around a reduced temperature of 1.4, and the heterotypic condensates reached critical points at 2–2.2, depending upon the variation in Δκ (Fig. 4A). We tried to map the correlation between the occurrence of the critical points and the energy experienced by each polymer in the homotypic and heterotypic condensate phases along the mixing fractions (Fig. 4B and C) at a fixed distance from criticality. The slope along xlow-κ gradually diminished as the Δκ of the sequence pairs decreased. One should also note the crossover of the critical point of the homotypic and heterotypic condensates at a xlow-κ regime (0.80–0.90) when the stability of the dense phase was lesser than that of the homotypic condensates. This same crossover was observed in the energy each polymer experienced in the droplet phase with respect to the mixing fraction (xlow-κ). In correlation with energy, we also showed the that there was enrichment of the low-κ polymers in the dense phase, determined from the fraction of the low-κ polymers present in the droplet phase relative to the total polymers in the droplet (ϕlow-κ) along the mixing fractions (xlow-κ) at a particular distance from the critical point (Fig. 4D). As Δκ decreased, the relationship between xlow-κ and ϕlow-κ shifted towards a linear correlation. However, at a significantly high heterogeneity, the enrichment was non-linear and showcased an underpopulation of the low-κ polymers in the droplet phase.Liquid-like nature and translational diffusivity in the condensate phase
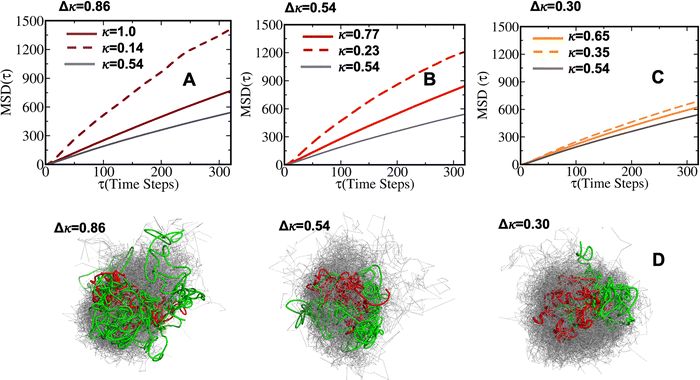
To quantify the internal dynamics within the heterotypic condensates, we measured the diffusion coefficients of the high and low-κ polymers within the droplets at different temperatures as they approached criticality. The diffusion coefficients were evaluated as the slope of the mean squared displacement (Fig. S4 for the MSD of the polymers in the droplet phase), and were computed using the equation: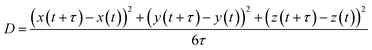 | (5) |
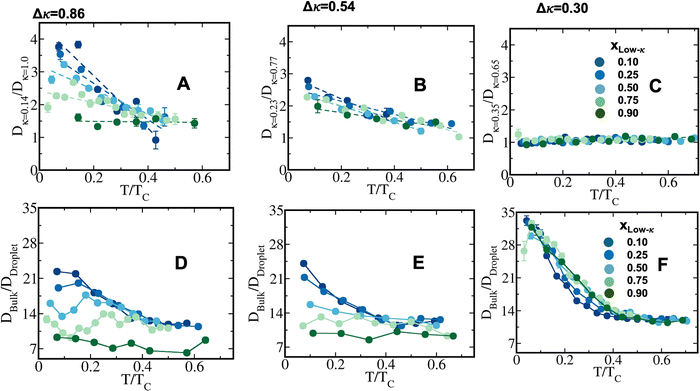
 , along the temperature scaled to the critical point for all the mixing fractions. For Δκ = 0.86, the low-κ polymers diffused into the condensates almost four times higher that of the high-κ polymers that were far away from reaching criticality (T/Tc = 0.1) due to an enhanced interaction of high-κ polymers at a lower mixing fraction (xlow-κ). This ratio gradually diminished to 1 as the temperature approached a critical point. For Δκ = 0.54, the sequence pairs in the condensate phase with the same ratio tended to be at a maximum at T/Tc = 0.1 and were 2–3 times that of the high-κ polymers that were subjected to a mixing fraction. As the mixing fraction xlow-κ increased, the slope of the ratio with respect to T/Tc gradually decreased. At a given temperature scaled by Tc,
, along the temperature scaled to the critical point for all the mixing fractions. For Δκ = 0.86, the low-κ polymers diffused into the condensates almost four times higher that of the high-κ polymers that were far away from reaching criticality (T/Tc = 0.1) due to an enhanced interaction of high-κ polymers at a lower mixing fraction (xlow-κ). This ratio gradually diminished to 1 as the temperature approached a critical point. For Δκ = 0.54, the sequence pairs in the condensate phase with the same ratio tended to be at a maximum at T/Tc = 0.1 and were 2–3 times that of the high-κ polymers that were subjected to a mixing fraction. As the mixing fraction xlow-κ increased, the slope of the ratio with respect to T/Tc gradually decreased. At a given temperature scaled by Tc, 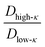 for Δκ = 0.86 and 0.54 had higher values, as xlow-κ tended to 0, the droplet was enriched with high-κ polymers. Surprisingly, at a moderate heterogeneity of the sequence pairs (Δκ = 0.30), we observed that both the low-κ and high-κ polymers had a nearly similar translational diffusivity irrespective of the mixing fraction and temperature. Better packing and enhanced cross-κ polymer interactions drove such a scenario.
for Δκ = 0.86 and 0.54 had higher values, as xlow-κ tended to 0, the droplet was enriched with high-κ polymers. Surprisingly, at a moderate heterogeneity of the sequence pairs (Δκ = 0.30), we observed that both the low-κ and high-κ polymers had a nearly similar translational diffusivity irrespective of the mixing fraction and temperature. Better packing and enhanced cross-κ polymer interactions drove such a scenario.
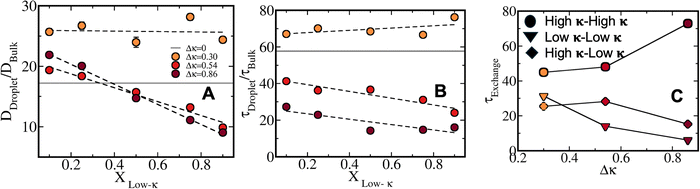
The average diffusivity in the bulk phase was nearly 7–20 times higher than that of the condensate phase, which was subjected to different mixing fractions and temperatures for Δκ = 0.86 and 0.54 (Panels D and E in Fig. 6). The diffusivity in the dilute (bulk) phase was calculated by simulating a single polymer in the same box length given by eqn (5).
However, diffusion was liquid-like for the condensates formed by all three Δκ pairs. For the condensates formed by the sequence pairs with Δκ = 0.86 and 0.54, 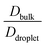 gradually decreased along xlow-κ, indicating an enhanced mobility in the dense phase, correlated to a lower stability (Fig. 2A and B). However, for the condensates formed by the sequence pairs with Δκ = 0.30, we observed an extensive decrease of diffusivity in the condensate phase, resulting in a bulk diffusivity that was 14–35 times higher than that of the droplet phase that was subjected to temperature variations (Fig. 6 panel F). Similar to a previous analysis, we observed no evidence of the effect of mixing on
gradually decreased along xlow-κ, indicating an enhanced mobility in the dense phase, correlated to a lower stability (Fig. 2A and B). However, for the condensates formed by the sequence pairs with Δκ = 0.30, we observed an extensive decrease of diffusivity in the condensate phase, resulting in a bulk diffusivity that was 14–35 times higher than that of the droplet phase that was subjected to temperature variations (Fig. 6 panel F). Similar to a previous analysis, we observed no evidence of the effect of mixing on 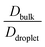 .
.
Reconfiguration lifetime in the dense phase
To understand the relationship between the average translational diffusivity and the conformational kinetics of the polymers in a condensate, we computed a polymer end-to-end distance vector's time correlation function as follows: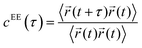 | (6) |
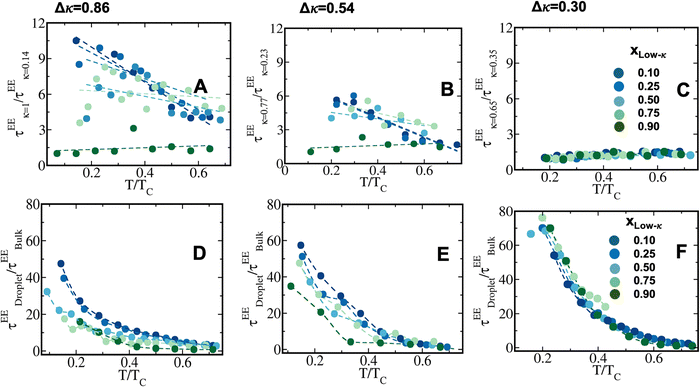
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) represents the end-to-end distance vector of the peptides (Fig. S5A–C). A bi-exponential function was fitted to derive the average time-constants for the end-to-end distance dynamics of the polymers. The average timescale of the correlated end-to-end distance fluctuation in the condensate phase for the high-κ and low-κ polymers is shown in Fig. 7 (panels A–C) as
(t) represents the end-to-end distance vector of the peptides (Fig. S5A–C). A bi-exponential function was fitted to derive the average time-constants for the end-to-end distance dynamics of the polymers. The average timescale of the correlated end-to-end distance fluctuation in the condensate phase for the high-κ and low-κ polymers is shown in Fig. 7 (panels A–C) as  . We observed a 1.5–12-fold enhancement in the slowdown of the conformational dynamics for the high-κ polymers relative to the low-κ polymers that were subjected to increased heterogeneity (Δκ), temperatures and mixing fractions. For the condensate formed by the sequence pairs at Δκ = 0.86, we found a 10-times slowdown for the high-κ polymers relative to the low-κ polymer, with a pronounced population of high-κ polymers at T/Tc = 0.1 (Fig. 7A). A slowdown of nearly 6-fold was observed at similar conditions for Δκ = 0.54 (Fig. 7B). As the temperature approached criticality, the ratio tended to decrease and at around T/Tc = 0.6 we observed that the slowdown for the high-κ polymer was nearly 1.5–3-times that of the low-κ polymers for both the Δκ = 0.86 and Δκ = 0.54 pairs. As the low-κ polymer enriched the droplet, we observed a gradual decrease in the ratio at the same distance from the critical point. For the mixing fraction, xlow-κ = 0.5,
. We observed a 1.5–12-fold enhancement in the slowdown of the conformational dynamics for the high-κ polymers relative to the low-κ polymers that were subjected to increased heterogeneity (Δκ), temperatures and mixing fractions. For the condensate formed by the sequence pairs at Δκ = 0.86, we found a 10-times slowdown for the high-κ polymers relative to the low-κ polymer, with a pronounced population of high-κ polymers at T/Tc = 0.1 (Fig. 7A). A slowdown of nearly 6-fold was observed at similar conditions for Δκ = 0.54 (Fig. 7B). As the temperature approached criticality, the ratio tended to decrease and at around T/Tc = 0.6 we observed that the slowdown for the high-κ polymer was nearly 1.5–3-times that of the low-κ polymers for both the Δκ = 0.86 and Δκ = 0.54 pairs. As the low-κ polymer enriched the droplet, we observed a gradual decrease in the ratio at the same distance from the critical point. For the mixing fraction, xlow-κ = 0.5,  was nearly at a value of 6 at T/Tc = 0.1 and decreased to a value of 3 at T/Tc = 0.6, indicating enhanced dynamics for the high-κ polymers.
was nearly at a value of 6 at T/Tc = 0.1 and decreased to a value of 3 at T/Tc = 0.6, indicating enhanced dynamics for the high-κ polymers.  behaved similarly to
behaved similarly to 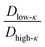 along temperatures scaled to Tc. The translational diffusivity was obtained at a maximum value, 4 times that of the slowdown for the high-κ polymer with respect to the low-κ polymers, while the single-molecule conformational dynamics experienced a 9–10 times slowdown at a value far away from the critical point. As observed earlier at Δκ = 0.30, in terms of translational diffusion, we observed a similar chain reconfiguration timescale for both the low-κ and high-κ polymers irrespective of the temperature and mixing, which was consistent with the translational diffusivity, as shown in Fig. 6C.
along temperatures scaled to Tc. The translational diffusivity was obtained at a maximum value, 4 times that of the slowdown for the high-κ polymer with respect to the low-κ polymers, while the single-molecule conformational dynamics experienced a 9–10 times slowdown at a value far away from the critical point. As observed earlier at Δκ = 0.30, in terms of translational diffusion, we observed a similar chain reconfiguration timescale for both the low-κ and high-κ polymers irrespective of the temperature and mixing, which was consistent with the translational diffusivity, as shown in Fig. 6C.
The end-to-end distance vector dynamics in the droplet phase was 20–60-fold slower than that of the bulk phase at Δκ = 0.86, and the slowdown was nearly 40–60 times at a value of Δκ = 0.54, which was associated with the various mixing fractions, and was the farthest away from criticality (Panels D and E in Fig. 7 and Fig. S5D–E). As the temperatures tended to toward criticality,  decreased to 1. Similar to a previous analysis of the translational diffusivity in the condensate phase of the sequence pairs with a moderate heterogeneity (Δκ = 0.30), we observed an enhanced slowdown up to 70–80 times that of the bulk phase for the end-to-end distance vector reconfiguration, which was far away from criticality at T/Tc = 0.1. Additionally, no effect of the mixing fraction was observed (Panel F in Fig. 7 and Fig. S5F).
decreased to 1. Similar to a previous analysis of the translational diffusivity in the condensate phase of the sequence pairs with a moderate heterogeneity (Δκ = 0.30), we observed an enhanced slowdown up to 70–80 times that of the bulk phase for the end-to-end distance vector reconfiguration, which was far away from criticality at T/Tc = 0.1. Additionally, no effect of the mixing fraction was observed (Panel F in Fig. 7 and Fig. S5F).
To elucidate the effect of heterogeneity in the sequence pairs and mixing fraction on the conformational dynamics and translational diffusivity, and to compare these parameters with the dynamics of the homogeneous condensates, we used 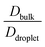 , which is a function of the mixing fraction, xlow-κ, as shown in Fig. 8A, and
, which is a function of the mixing fraction, xlow-κ, as shown in Fig. 8A, and  in Fig. 8B at a constant T/Tc = 0.2. The grey line depicts the same conditions for the homogeneous condensates of the sequence (κ = 0.54) with Δκ = 0.00.
in Fig. 8B at a constant T/Tc = 0.2. The grey line depicts the same conditions for the homogeneous condensates of the sequence (κ = 0.54) with Δκ = 0.00. 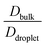 and
and  showed a steady decrease as xlow-κ increased at Δκ = 0.86 and 0.54, while at Δκ = 0.30 there was no dependence on the mixing fractions. The ratio of the bulk phase to droplet diffusivity decreased from 20-fold to 10-fold within xlow-κ = 0.1 to 0.9 at a constant T/Tc = 0.2, showing that there was an enhanced mobility alongside an enrichment of the low-κ polymers, and this ratio was correlated to the variation in the critical point, as shown in Fig. 2B, which exhibits a linear relationship with the stability of the dense phase. Comparatively,
showed a steady decrease as xlow-κ increased at Δκ = 0.86 and 0.54, while at Δκ = 0.30 there was no dependence on the mixing fractions. The ratio of the bulk phase to droplet diffusivity decreased from 20-fold to 10-fold within xlow-κ = 0.1 to 0.9 at a constant T/Tc = 0.2, showing that there was an enhanced mobility alongside an enrichment of the low-κ polymers, and this ratio was correlated to the variation in the critical point, as shown in Fig. 2B, which exhibits a linear relationship with the stability of the dense phase. Comparatively,  decreased from 40-fold to 15-fold as the droplet became enriched with low-κ polymers at a significantly high heterogeneity in the sequence charge clustering of the pairs.
decreased from 40-fold to 15-fold as the droplet became enriched with low-κ polymers at a significantly high heterogeneity in the sequence charge clustering of the pairs.
For the polymers, the conformational kinetics in the droplet phase as well as its translational diffusion are inherently connected to the average lifetime of its interchain contacts (Fig. S6). To elucidate the timescale at which a polymer stays in contact with another polymer in its droplet phase, we used a time correlation function:
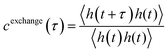 | (7) |
Droplet shape anisotropy
To correlate the stability pattern of the condensate phase to its geometry, we estimated the deviation of the shape of the condensates from that of a sphere under the same conditions. Droplet shape anisotropy (p) has been defined as: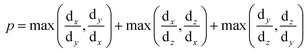 | (8) |
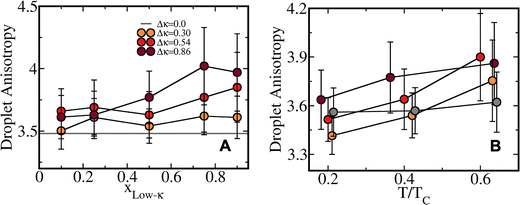
Fig. 9A plots the relative anisotropy from a spherical condensate along with the mixing fractions at T/Tc = 0.4 for Δκ = 0.86, 0.54 and 0.30, respectively. At lower mixing fractions, all the variations in Δκ had relatively similar anisotropy values, which were enhanced as xlow-κ increased for Δκ = 0.86 and 0.54, and remained nearly similar for Δκ = 0.30, indicating the complementarity of the sequence pairs, and this result is similar to the energy analysis in Fig. 3 and Fig. S3. One must note that the complementarity was at a maximum for the homogeneous condensates and they have minimum anisotropy values in the studied systems (shown in grey). Along with temperature, there was an increase in the anisotropy values as the stability of the dense phase diminished for the heterotypic condensates at a mixing fraction, xlow-κ = 0.5, while the homotypic condensates remained fairly stable within the time window of T/Tc = 0.2 to 0.7 (Fig. 9B and Fig. S7).
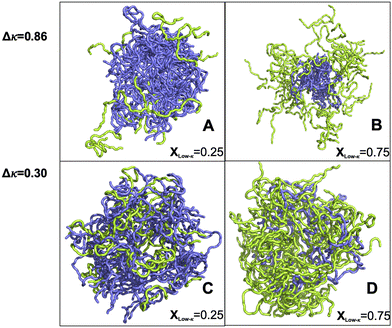
A visual representation of the structural morphology, heterogeneity, and the droplet shape is shown in Fig. 10 for the two extreme mixing fractions, xlow-κ = 0.25 and 0.75, and for the extremely heterotypic (Δκ = 0.86) (Fig. 10A and B) and moderately heterotypic (Δκ = 0.30) sequence pairs (Fig. 10C and D). It is very interesting to note that at a higher heterogeneity of the sequence pairs (Δκ = 0.86), the low-κ polymer formed the surface of the dense phase, while the high-κ polymer formed the core. The differential diffusivity obtained in Fig. 6(A)–(C) and the end-to-end distance vector dynamics in Fig. 7(A)–(C) are essentially related to the structural morphology and surface diffusivity. As the heterogeneity in the pairs of sequence was lowered, the low-κ polymer penetrated the droplet and lowered the dynamic heterogeneity, as shown in Fig. 10(C) and (D).
Convergence of the reported data
The convergence of the density profiles (Fig. S8), energetics (Fig. S9), mean square displacements (Fig. S10–S12), chain reconfiguration time correlation functions (Fig. S13) and exchange correlation functions (Fig. S14 and S15) were studied for all the Δκ systems at T/Tc = 0.4 and xLow-κ = 0.5 from two independent simulation runs, showing that equilibrium was achieved.The finite-size effect on the reported results was also verified. The reproducibility of the trends was shown in the phase diagram, energetics and dynamics by varying the chain length for Δκ = 0.86 for all the mixing fractions (Fig. S16 and S17). A convergence of the phase diagram after varying the number of chains in the simulation box was performed, ensuring that the influence of the finite-size effect of the systems was checked (Fig. S18).
Conclusions
In conclusion, this study lays the foundation for a systematic investigation into how sequence features influence the phase separation of heterotypic proteins. Biological heterotypic condensates are linked to physiological and disease-like behaviours. Condensates formed by different peptides along with nucleic acids offer spatiotemporal control and efficient cellular function. Various components can be part of more than one condensate at different stoichiometries, leading to a difficulty in identifying condensates with a specific component's enrichment. On the other hand, a typical condensate can have multiple different compositions and can act differently in a functional context each time. It is important to note that the composition of a condensate defined at a particular instance might not necessarily indicate its biologically relevant state and can likely be insufficient to describe the array of functions it possesses. Often such condensates are liquid-like, enriched in specific components and are formed through electrostatic cross-linking. Examples often showcase, prion and Tau proteins, two neuronal proteins that often comingle and can even form solid-like aggregates; this occurrence is also observed between prions and alpha-synuclein.47,66 The acidic N-terminal domain of Tau proteins interacts with the basic N-terminal of prion proteins, mediating domain-specific, short-range nanoclusters. Time-resolved experiments have showcased a symphony of molecular events that range on the timescale of nanoseconds to even seconds inside condensates. Emerging evidence suggests that the compositions of heterotypic condensates (namely, nuclear and transcriptional condensates, PML bodies, and m-RNA transport granules) alter with time and in response to stimuli. The composition of stress granules changes with the different types of stresses applied.67 In this context, this study and its findings unravel unique molecular-level stability and dynamic insights into the phase separation of multi-component heterotypic proteins formed through networks mediated by long-range electrostatics. Moreover, our study captures the temporal dynamics of the cellular environment by designing a systematic mixing of peptides and the effect on droplets, which are relevant in a functional context.To achieve our initial goal of unravelling how variations in charge clustering within binary sequences affect the stability and dynamics of phases, we showcased a temperature-density phase diagram, translational dynamics in the condensates, and chain reconfiguration timescales of homotypic versus heterotypic phase separations in designed polyampholyte sequence pairs, and we examined how these properties varied with the mixing fractions of the peptides and with charge-clustering differences. A detailed microscopic view of the relative composition and sequence heterogeneity driven by the alteration in the structural morphology of the condensate phase revealed a fascinating connection between the stability and dynamics profiles and the altered condensate morphology. Among the many valuable outcomes of this study, we observed that there was an enhanced stability of the condensates of binary peptides possessing significantly different charge clustering compared to their homotypic counterparts possessing only one kind of sequence, which had a charge-pattern parameter similar to the binary peptides formed from heterotypic condensates. However, better packing and interaction energy in the moderate heterotypic condensates favored an enhanced droplet stability when the population of low-κ polymers was enriched, which was not the case for the binary peptides with a higher charge-clustering heterogeneity. Differential charge clustering influenced the structural morphology of the formed condensates and enhanced their shape anisotropy rapidly with temperature. At a relatively higher difference in the charge clustering of the two sequences forming condensates, the high-κ peptides formed the core of the droplet, while the low-κ peptides formed the surface of the droplet, which led to the low-κ peptides possessing a 3–4 times higher diffusivity than the high-κ peptides due to surface rolling. As the charge-clustering heterogeneity diminished, the low-κ polymers penetrated more into the droplet phase and possessed a diffusivity nearly similar to that of the high-κ polymers. The average timescale of the chain reconfiguration of the low-κ polymers on the surface was nearly 3–12 times faster than that of the high-κ polymers forming the core, and this difference depended on the extent of composition and sequence charge-clustering heterogeneity. Overall diffusivity in the condensate phase was 7–35 times slower than that in the bulk phase, consistent with a slowdown of 5–70 times in the chain reconfiguration timescale at a value far away from criticality, and this difference depended on the differential variation of charge clustering and the mixing fractions. The conclusions are highly relevant in explaining various experimental observations in FUS, hnRNPA1, or Tau condensates.66 While FUS undergoes condensation with a balance of electrostatic and cation–π interactions involving RGG domains and low complexity domains (LCDs), Tau condensation is highly dominated by heterotypic electrostatic interactions. FUS often undergoes co-condensation in the presence of hnRNPA1, indicating that it is a binary condensate. Organizational heterogeneity has been observed in heterotypic protein condensates of the prion-like domains in FUS and hnRNPA. In 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary peptide systems (same as xlow-κ = 0.5), heterotypic interactions have been reported to enhance the stability of the condensate phase. As observed in confocal microscopy, BFGF mixed with heparan sulphate proteoglycans at a 1
1 binary peptide systems (same as xlow-κ = 0.5), heterotypic interactions have been reported to enhance the stability of the condensate phase. As observed in confocal microscopy, BFGF mixed with heparan sulphate proteoglycans at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratio, showcased larger condensates that indicated a stronger phase separation.48
10 ratio, showcased larger condensates that indicated a stronger phase separation.48
All these experimental results are consistent with our findings.66 The possible origin of the enhanced stability of heterotypic condensates compared to homotypic condensates could pertain to an entropy–enthalpy synergy, which is further related to the availability of significantly different charged patches with different sequences. The additional availability of variable charged patches in two different sequences enhances the possibility of several possible complementary multivalent interactions, enhances at moderately heterotypic condensates and can contribute to an enhanced stability of heterotypic condensates compared to homotypic condensates, which have limited options of charged patches. One must note that self-interactions within each kind of polymer dominate the stability of the condensates with relatively small contributions from cross polymers at relatively higher Δκ values and extreme mixing fractions. Hence, high-κ polymers will form the droplet core, and low-κ polymers will remain on the droplet's surface, possessing high mobility and exchangeability with the bulk phase. In this study, cross interactions among the two sequences dominated the stability of the sequence variants possessing lower Δκ values at an equalized mixing fraction. The low-κ polymers started entering the core of droplet when the Δκ of the sequence pairs decreased.
In short, our study delineates the effect of charge-clustering heterogeneity on the condensates of binary peptides, in terms of their formation and inherent dynamics, providing a first step to systematically understand heterotypic condensation. In this same line of thoughts, our upcoming studies will dissect how the balance between long-range electrostatic interactions and short-range hydrophobic, and cation–π interactions influences the stability and dynamics of heterotypic condensates.
Author contributions
Milan Kumar Hazra: conceptualization, methodology, investigation, formal analysis, writing – original draft, review, editing, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
Due to the large amount of data generated in this study and the data-sharing restrictions of our institution, it is not possible to upload all the data to a public network. Therefore, we disclose the relevant script files used for the simulation and analysis protocol in GitHub. https://github.com/milanxy/CG.MD, https://github.com/milanxy/HETEROTYPIC.CONDENSATE.ANALYSIS, https://github.com/milanxy/LLPS_ANALYSIS.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03436a.
Acknowledgements
This work was funded by the Prime Minister Early Career Research Grant (ANRF/ECRG/2024/000734/LS) from the Anusandhan National Research Foundation (ANRF), India and seed grant from IIT Jodhpur (I/SEED/MKZ/20230169). MKH also thanks the High Performance Computing facility at IIT Jodhpur for computational support.References
- L. B. Case, X. Zhang, J. A. Ditlev and M. K. Rosen, Stoichiometry controls activity of phase-separated clusters of actin signaling proteins, Science, 2019, 363, 1093–1097 CrossRef CAS PubMed.
- R. J. Ries, S. Zaccara, P. Klein, A. Olarerin-George, S. Namkoong, B. F. Pickering, D. P. Patil, H. Kwak, J. H. Lee and S. R. Jaffrey, m6A enhances the phase separation potential of mRNA, Nature, 2019, 571, 424–428 CrossRef CAS.
- T. M. Franzmann, M. Jahnel, A. Pozniakovsky, J. Mahamid, A. S. Holehouse, E. Nüske, D. Richter, W. Baumeister, S. W. Grill, R. V. Pappu, A. A. Hyman and S. Alberti, Phase separation of a yeast prion protein promotes cellular fitness, Science, 2018, 359, eaao5654 CrossRef PubMed.
- Y. Wang, C. Zhang, W. Yang, S. P. Shao, X. Xu, Y. Sun, P. Li, L. Liang and C. Wu, LIMD1 phase separation contributes to cellular mechanics and durotaxis by regulating focal adhesion dynamics in response to force, Dev. Cell, 2021, 56, 1313–1325.e7 CrossRef CAS PubMed.
- Q. Chen, S. An, C. Wang, Y. Zhou, X. Liu and W. Ren, Phase separation in mitochondrial fate and mitochondrial diseases, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2422255122 CrossRef CAS PubMed.
- M. V. Garabedian, W. Wang, J. B. Dabdoub, M. Tong, R. M. Caldwell, W. Benman, B. S. Schuster, A. Deiters and M. C. Good, Designer membraneless organelles sequester native factors for control of cell behavior, Nat. Chem. Biol., 2021, 17, 998–1007 CrossRef CAS PubMed.
- A. M. Küffner, M. Prodan, R. Zuccarini, U. Capasso Palmiero, L. Faltova and P. Arosio, Acceleration of an Enzymatic Reaction in Liquid Phase Separated Compartments Based on Intrinsically Disordered Protein Domains, ChemSystemsChem, 2020, 2, 1–7 CrossRef.
- D. Ramírez de Mingo, P. López-García, M. E. Vaquero, R. Hervás, D. V. Laurents and M. Carrión-Vázquez, Phase separation modulates the functional amyloid assembly of human CPEB3, Prog. Neurobiol., 2023, 231, 102540 CrossRef PubMed.
- C. Alquezar, S. Arya and A. W. Kao, Tau Post-translational Modifications: Dynamic Transformers of Tau Function, Degradation, and Aggregation, Front. Neurol., 2021, 11, 555932 Search PubMed.
- J. Lu, J. Qian, Z. Xu, S. Yin, L. Zhou, S. Zheng and W. Zhang, Emerging Roles of Liquid–Liquid Phase Separation in Cancer: From Protein Aggregation to Immune-Associated Signaling, Front. Cell Dev. Biol., 2021, 9, 1–15 Search PubMed.
- K. Teilum, J. G. Olsen and B. B. Kragelund, Globular and disordered-the non-identical twins in protein–protein interactions, Front. Mol. Biosci., 2015, 2, 40 Search PubMed.
- S. Elbaum-Garfinkle, Y. Kim, K. Szczepaniak, C. C. H. Chen, C. R. Eckmann, S. Myong and C. P. Brangwynne, The disordered P granule protein LAF-1 drives phase separation into droplets with tunable viscosity and dynamics, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7189–7194 CrossRef CAS PubMed.
- H. X. Zhou, V. Nguemaha, K. Mazarakos and S. Qin, Why Do Disordered and Structured Proteins Behave Differently in Phase Separation, Trends Biochem. Sci., 2018, 43, 499–516 CrossRef CAS.
- T. J. Nott, E. Petsalaki, P. Farber, D. Jervis, E. Fussner, A. Plochowietz, T. D. Craggs, D. P. Bazett-Jones, T. Pawson, J. D. Forman-Kay and A. J. Baldwin, Phase Transition of a Disordered Nuage Protein Generates Environmentally Responsive Membraneless Organelles, Mol. Cell, 2015, 57, 936–947 CrossRef CAS PubMed.
- A. Statt, H. Casademunt, C. P. Brangwynne and A. Z. Panagiotopoulos, Model for disordered proteins with strongly sequence-dependent liquid phase behavior, J. Chem. Phys., 2020, 152, 075101 CrossRef CAS PubMed.
- M. Fuxreiter, Context-dependent, fuzzy protein interactions: Towards sequence-based insights, Curr. Opin. Struct. Biol., 2024, 87, 102834 CrossRef CAS PubMed.
- A. S. Holehouse and R. V. Pappu, Functional Implications of Intracellular Phase Transitions, Biochemistry, 2018, 2415–2423, DOI:10.1021/acs.biochem.7b01136.
- T. Kaur, M. Raju, I. Alshareedah, R. B. Davis, D. A. Potoyan and P. R. Banerjee, Sequence-encoded and composition-dependent protein-RNA interactions control multiphasic condensate morphologies, Nat. Commun., 2021, 12, 872 CrossRef CAS PubMed.
- M. Farag, S. R. Cohen, W. M. Borcherds, A. Bremer, T. Mittag and R. V. Pappu, Condensates formed by prion-like low-complexity domains have small-world network structures and interfaces defined by expanded conformations, Nat. Commun., 2022, 13, 7722 CrossRef CAS PubMed.
- P. Li, S. Banjade, H. C. Cheng, S. Kim, B. Chen, L. Guo, M. Llaguno, J. V. Hollingsworth, D. S. King, S. F. Banani, P. S. Russo, Q. X. Jiang, B. T. Nixon and M. K. Rosen, Phase transitions in the assembly of multivalent signalling proteins, Nature, 2012, 483, 336–340 CrossRef CAS PubMed.
- J. M. Choi, F. Dar and R. V. Pappu, LASSI: A lattice model for simulating phase transitions of multivalent proteins, PLoS Comput. Biol., 2019, 15, e1007028 CrossRef CAS PubMed.
- F. Zhang, M. W. A. Skoda, R. M. J. Jacobs, S. Zorn, R. A. Martin, C. M. Martin, G. F. Clark, S. Weggler, A. Hildebrandt, O. Kohlbacher and F. Schreiber, Reentrant condensation of proteins in solution induced by multivalent counterions, Phys. Rev. Lett., 2008, 101, 3–6 Search PubMed.
- G. Kim, S. E. Lee, S. Jeong, J. Lee, D. Park and S. Chang, Multivalent electrostatic pi–cation interaction between synaptophysin and synapsin is responsible for the coacervation, Mol. Brain, 2021, 14, 137 CrossRef CAS PubMed.
- S. E. Farr, E. J. Woods, J. A. Joseph, A. Garaizar and R. Collepardo-Guevara, Nucleosome plasticity is a critical element of chromatin liquid–liquid phase separation and multivalent nucleosome interactions, Nat. Commun., 2021, 12, 1–17 CrossRef PubMed.
- K. Kamagata, S. Kanbayashi, M. Honda, Y. Itoh, H. Takahashi, T. Kameda, F. Nagatsugi and S. Takahashi, Liquid-like droplet formation by tumor suppressor p53 induced by multivalent electrostatic interactions between two disordered domains, Sci. Rep., 2020, 10, 1–12 CrossRef PubMed.
- E. Jordan, F. Roosen-Runge, S. Leibfarth, F. Zhang, M. Sztucki, A. Hildebrandt, O. Kohlbacher and F. Schreiber, Competing salt effects on phase behavior of protein solutions: Tailoring of protein interaction by the binding of multivalent ions and charge screening, J. Phys. Chem. B, 2014, 118, 11365–11374 CrossRef CAS.
- R. K. Das and R. V. Pappu, Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13392–13397 CrossRef CAS PubMed.
- Y. Levy and M. K. Hazra, Biophysics of phase separation of disordered proteins is governed by balance between short- And long-range interactions, J. Phys. Chem. B, 2021, 125, 2202–2211 CrossRef.
- M. K. Hazra and Y. Levy, Charge pattern affects the structure and dynamics of polyampholyte condensates, Phys. Chem. Chem. Phys., 2020, 22, 19368–19375 RSC.
- S. Das, A. N. Amin, Y. H. Lin and H. S. Chan, Coarse-grained residue-based models of disordered protein condensates: Utility and limitations of simple charge pattern parameters, Phys. Chem. Chem. Phys., 2018, 20, 28558–28574 RSC.
- S. Das, A. Eisen, Y. H. Lin and H. S. Chan, A Lattice Model of Charge-Pattern-Dependent Polyampholyte Phase Separation, J. Phys. Chem. B, 2018, 122, 5418–5431 CrossRef CAS PubMed.
- M. Tempel, G. Isenberg and E. Sackmann, Temperature-induced sol-gel transition and microgel formation in α-actinin cross-linked actin networks: a rheological study, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 1802–1810 CrossRef CAS.
- T. Mittag and R. V. Pappu, A conceptual framework for understanding phase separation and addressing open questions and challenges, Mol. Cell, 2022, 2201–2214, DOI:10.1016/j.molcel.2022.05.018.
- I. Alshareedah, M. M. Moosa, M. Pham, D. A. Potoyan and P. R. Banerjee, Programmable viscoelasticity in protein–RNA condensates with disordered sticker-spacer polypeptides, Nat. Commun., 2021, 12, 6620, DOI:10.1038/s41467-021-26733-7.
- P. R. Banerjee, A. N. Milin, M. M. Moosa, P. L. Onuchic and A. A. Deniz, Reentrant Phase Transition Drives Dynamic Substructure Formation in Ribonucleoprotein Droplets, Angew. Chem., Int. Ed., 2017, 56, 11354–11359 CrossRef CAS PubMed.
- I. Alshareedah, A. Singh, S. Yang, V. Ramachandran, A. Quinn, D. A. Potoyan and P. R. Banerjee, Determinants of viscoelasticity and flow activation energy in biomolecular condensates, Sci. Adv., 2024, 10, eadi6539 CrossRef CAS PubMed.
- M. Ramaswami, J. P. Taylor and R. Parker, Altered ribostasis: RNA-protein granules in degenerative disorders, Cell, 2013, 154, P727–P736 CrossRef PubMed.
- I. Alshareedah, M. M. Moosa, M. Raju, D. A. Potoyan and P. R. Banerjee, Phase transition of RNA–protein complexes into ordered hollow condensates, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 15650–15658 CrossRef CAS PubMed.
- A. Chowdhury, A. Borgia, S. Ghosh, A. Sottini, S. Mitra, R. S. Eapen, M. B. Borgia, T. Yang, N. Galvanetto, M. T. Ivanović, P. Łukijańczuk, R. Zhu, D. Nettels, A. Kundagrami and B. Schuler, Driving forces of the complex formation between highly charged disordered proteins, Proc. Natl. Acad. Sci. U. S. A., 2023, 41, e2304036120 CrossRef PubMed.
- D. Sundaravadivelu Devarajan, S. Rekhi, A. Nikoubashman, Y. C. Kim, M. P. Howard, J. Mittal and A. McFerrin, Effect of Charge Distribution on the Dynamics of Polyampholytic Disordered Proteins, Macromolecules, 2022, 55, 8987–8997 CrossRef PubMed.
- S. Das, Y.-H. Lin, R. M. Vernon, J. D. Forman-Kay and H. Sun Chan, Comparative roles of charge, π, and hydrophobic interactions in sequence-dependent phase separation of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 28795–28805 CrossRef CAS.
- L. Sawle and K. Ghosh, A theoretical method to compute sequence dependent configurational properties in charged polymers and proteins, J. Chem. Phys., 2015, 143, 085101 CrossRef PubMed.
- N. Galvanetto, M. T. Ivanović, A. Chowdhury, A. Sottini, M. F. Nüesch, D. Nettels, R. B. Best and B. Schuler, Extreme dynamics in a biomolecular condensate, Nature, 2023, 619, 876–883 CrossRef CAS PubMed.
- M. K. Hazra and Y. Levy, Affinity of disordered protein complexes is modulated by entropy-energy reinforcement, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2120456119 CrossRef CAS PubMed.
- K. K. Kumashiro, K. Ohgo, D. W. Elliott, T. F. Kagawa and W. P. Niemczura, Backbone motion in elastin's hydrophobic domains as detected by 2H NMR spectroscopy, Biopolymers, 2012, 97, 882–888 CrossRef CAS.
- A. Majumdar, P. Dogra, S. Maity and S. Mukhopadhyay, Liquid–Liquid Phase Separation Is Driven by Large-Scale Conformational Unwinding and Fluctuations of Intrinsically Disordered Protein Molecules, J. Phys. Chem. Lett., 2019, 10, 3929–3936 CrossRef CAS PubMed.
- A. Agarwal, L. Arora, S. K. Rai, A. Avni and S. Mukhopadhyay, Spatiotemporal modulations in heterotypic condensates of prion and α-synuclein control phase transitions and amyloid conversion, Nat. Commun., 2022, 13, 1154 CrossRef CAS PubMed.
- S. Xue, F. Zhou, T. Zhao, H. Zhao, X. Wang, L. Chen, J. Ping Li and S. Z. Luo, Phase separation on cell surface facilitates bFGF signal transduction with heparan sulphate, Nat. Commun., 2022, 13, 1112 CrossRef CAS PubMed.
- A. N. Amin, Y. H. Lin, S. Das and H. S. Chan, Analytical Theory for Sequence-Specific Binary Fuzzy Complexes of Charged Intrinsically Disordered Proteins, J. Phys. Chem. B, 2020, 124, 6709–6720 CrossRef CAS PubMed.
- Y. H. Lin, J. D. Forman-Kay and H. S. Chan, Theories for Sequence-Dependent Phase Behaviors of Biomolecular Condensates, Biochemistry, 2018, 2499–2508, DOI:10.1021/acs.biochem.8b00058.
- U. Kapoor, Y. C. Kim and J. Mittal, Coarse-Grained Models to Study Protein–DNA Interactions and Liquid–Liquid Phase Separation, J. Chem. Theory Comput., 2024, 20, 1717–1731 CrossRef CAS PubMed.
- R. M. Regy, G. L. Dignon, W. Zheng, Y. C. Kim and J. Mittal, Sequence dependent phase separation of protein–polynucleotide mixtures elucidated using molecular simulations, Nucleic Acids Res., 2020, 48, 12593–12603 CrossRef CAS PubMed.
- G. L. Dignon, W. Zheng, R. B. Best, Y. C. Kim and J. Mittal, Relation between single-molecule properties and phase behavior of intrinsically disordered proteins, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9929–9934 CrossRef CAS PubMed.
- P. Mohanty, U. Kapoor, D. Sundaravadivelu Devarajan, T. M. Phan, A. Rizuan and J. Mittal, Principles Governing the Phase Separation of Multidomain Proteins, Biochemistry, 2022, 2443–2455, DOI:10.1021/acs.biochem.2c00210.
- G. L. Dignon, W. Zheng, Y. C. Kim, R. B. Best and J. Mittal, Sequence determinants of protein phase behavior from a coarse-grained model, PLoS Comput. Biol., 2018, 14, e1005941 CrossRef PubMed.
- W. M. Jacobs and D. Frenkel, Phase Transitions in Biological Systems with Many Components, Biophys. J., 2017, 112, 683–691 CrossRef CAS PubMed.
- J. R. Espinosa, A. Garaizar, C. Vega, D. Frenkel and R. Collepardo-Guevara, Breakdown of the law of rectilinear diameter and related surprises in the liquid–vapor coexistence in systems of patchy particles, J. Chem. Phys., 2019, 150, 224510 CrossRef PubMed.
- V. Nguemaha and H. X. Zhou, Liquid-Liquid Phase Separation of Patchy Particles Illuminates Diverse Effects of Regulatory Components on Protein Droplet Formation, Sci. Rep., 2018, 8, 6728 CrossRef PubMed.
- R. M. Regy, G. L. Dignon, W. Zheng, Y. C. Kim and J. Mittal, Sequence dependent phase separation of protein–polynucleotide mixtures elucidated using molecular simulations, Nucleic Acids Res., 2020, 48, 12593–12603 CrossRef CAS.
- P. Y. Chew, J. A. Joseph, R. Collepardo-Guevara and A. Reinhardt, Aromatic and arginine content drives multiphasic condensation of protein–RNA mixtures, Biophys. J., 2024, 123, 1342–1355 CrossRef CAS PubMed.
- I. Sanchez-Burgos, L. Herriott, R. Collepardo-Guevara and J. R. Espinosa, Surfactants or scaffolds? RNAs of varying lengths control the thermodynamic stability of condensates differently, Biophys. J., 2023, 122, 2973–2987 CrossRef CAS.
- A. Azia and Y. Levy, Nonnative Electrostatic Interactions Can Modulate Protein Folding: Molecular Dynamics with a Grain of Salt, J. Mol. Biol., 2009, 393, 527–542 CrossRef CAS PubMed.
- O. Givaty and Y. Levy, Protein Sliding along DNA: Dynamics and Structural Characterization, J. Mol. Biol., 2009, 385, 1087–1097 CrossRef CAS PubMed.
- P. C. Whitford and J. N. Onuchic, Simulating biomolecules for physiological timescales, Curr. Opin. Struct. Biol., 2025, 92, 103039 CrossRef CAS PubMed.
- N. A. Erkamp, M. Farag, Y. Qiu, D. Qian, T. Sneideris, T. Wu, T. J. Welsh, H. Ausserwöger, T. J. Krug, G. Chauhan, D. A. Weitz, M. D. Lew, T. P. J. Knowles and R. V. Pappu, Differential interactions determine anisotropies at interfaces of RNA-based biomolecular condensates, Nat. Commun., 2025, 16, 3463 CrossRef CAS.
- S. K. Rai, R. Khanna, A. Avni and S. Mukhopadhyay, Heterotypic electrostatic interactions control complex phase separation of tau and prion into multiphasic condensates and co-aggregates, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2216338120 CrossRef CAS PubMed.
- C. Chin Sang, S. Upadhyay, M. L. Nosella, J. D. Forman-Kay and H. O. Lee, The dynamic and heterogeneous composition of biomolecular condensates and its functional relevance, Nat. Rev. Mol. Cell Biol., 2025 DOI:10.1038/s41580-025-00897-2.
| This journal is © the Owner Societies 2026 |