Active learning-enhanced neuroevolution potential for predictive modeling of UO2 thermophysical properties
Junying
Zhong
 abc,
Lei
Zhang
abc,
Lei
Zhang
 bc and
Tao
Bo
bc and
Tao
Bo
 *bc
*bc
aSchool of Materials Science and Chemical Engineering, Ningbo University, Ningbo, 315211, China
bZhejiang Key Laboratory of Data-Driven High-Safety Energy Materials and Applications, Ningbo Key Laboratory of Special Energy Materials and Chemistry, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo, 315201, China. E-mail: botao@nimte.ac.cn
cQianwan Institute of CNITECH, Ningbo, 315336, China
First published on 20th November 2025
Abstract
Accurately characterizing the temperature dependence of UO2 thermal conductivity is crucial for evaluating its performance under nuclear reactor operating conditions. However, experimental measurements are costly, density functional theory (DFT) calculations are constrained by small spatiotemporal scales, and traditional empirical potentials struggle to capture strong anharmonic effects. To this end, we developed a machine-learned neuroevolution potential (NEP) with near-DFT accuracy using an active learning strategy, and we systematically evaluated and cross-validated the thermal conductivity of UO2 using equilibrium molecular dynamics (EMD), homogeneous nonequilibrium molecular dynamics (HNEMD), and nonequilibrium molecular dynamics (NEMD). The results demonstrate that HNEMD delivers a high signal-to-noise ratio, low uncertainty, and rapid convergence, exhibiting superior computational efficiency and robustness. At 500 K, the spectral phonon mean free path spans approximately one order of magnitude, and heat-transport channel lengths exceeding about 5 µm approach the bulk thermal conductivity limit. In the 800–1500 K range, the NEP reproduces the experimental temperature dependence of UO2 thermal conductivity, while at lower temperatures (300–800 K), it achieves predictive accuracy comparable to that of DFT+U. Systematic validation of UO2 fundamental properties including the equation of state, phonon dispersion relations, elastic constants, heat capacity, and linear thermal expansion coefficient demonstrates that the constructed NEP is reliable and broadly applicable. This work provides methodological support for multiscale thermal transport modeling of nuclear fuels and reactor safety assessment.
Introduction
Uranium dioxide (UO2) is widely used as a nuclear fuel in commercial reactors due to its excellent thermal stability and high melting point. As a ceramic fuel, UO2 exhibits heat transfer that is predominantly governed by quantized lattice vibrations (phonons).1 The propagation of phonons within the material determines its thermal conductivity, which significantly influences the temperature distribution and thermal stresses within UO2 fuel pellets.2 These factors are critical to the safe and efficient operation of nuclear reactors. Therefore, accurate prediction of the thermophysical properties of UO2, especially its thermal conductivity, is of paramount importance.Traditionally, the thermophysical properties of UO2 have been investigated using a combination of experimental and theoretical approaches. Numerous experimental correlations for predicting thermal conductivity have been proposed.3–5 Fink et al.6,7 systematically compiled experimental data on enthalpy, heat capacity, thermal expansion coefficients, and other properties. Their compilations remain highly valuable references to this day. However, experiments under harsh conditions such as high temperatures and intense radiation are technically demanding and costly. In addition, although theoretical approaches such as density functional theory (DFT) have been extensively applied to UO2,8–14 their computational expense limits simulations of large systems and long timescales. To address these limitations, empirical interatomic potentials (EIPs) have been developed.15 These potentials are typically built from physically analytical functions with parameters fitted to experimental data. Widely recognized EIPs for UO2 include the Basak,16 Morelon,17 Yakub,18 and CRG19 potentials, among others. Using these potentials, one can study the properties of UO2 over a wide temperature range such as lattice constants, bulk moduli, defect formation energies, and defect migration barriers. Nevertheless, due to their limited number of parameters and reliance on simplified analytical forms, EIPs often struggle to accurately capture complex interatomic interactions.
In recent years, machine learning interatomic potential (MLIP) has emerged as a promising computational tool. Trained on high-precision datasets, MLIPs can achieve near first-principles accuracy while significantly reducing computational costs. For instance, Dubois et al.20 developed two types of MLIPs, namely the spectral neighbor analysis potential (SNAP) and a high-dimensional neural network potential (HDNNP), for simulating elastic properties, phonon dispersion relations, and defect formation energies in UO2. Stippell et al.21 combined active learning with transfer learning to construct an MLIP for UO2 that achieves DFT+U accuracy, enabling efficient prediction of properties such as lattice constants, bulk modulus, and radial distribution functions. Konashi et al.22 developed a neural network potential (NNP) for UO2 and computed various thermophysical properties from room temperature to the melting point, including the molten state.
However, studies on MLIPs for UO2 remain relatively limited, particularly in terms of systematic evaluations and public comparisons of thermal conductivity predictions. Moreover, most empirical potentials for UO2 (e.g., Buckingham/Coulomb-types, CRG, etc.) were constructed without explicit constraints on phonon dispersion, Grüneisen parameters, or higher-order anharmonic interactions (such as three-phonon and four-phonon scattering). This often results in the predicted temperature dependence of thermal conductivity deviating from experiments and carrying substantial uncertainty.23–25 Furthermore, the implementation of microscopic heat flux in molecular dynamics packages is method-dependent and may introduce biases unrelated to the potentials. For example, in the widely used large-scale atomic/molecular massively parallel simulator (LAMMPS),26 the heat flux for many-body potentials typically relies on specific decompositions of atomic energy and stress, whose non-uniqueness generally precludes equivalence with the rigorous Hardy heat flux.27–29 Within the Green–Kubo framework, using inconsistent heat-flux expressions can induce significant shifts in the computed thermal conductivity. By contrast, the graphics processing units molecular dynamics (GPUMD) package30 developed by Fan et al. implements a Hardy-type heat flux that is consistent with energy conservation for many-body potentials.31–33 It provides modules for thermal conductivity calculations via equilibrium molecular dynamics (EMD), homogeneous nonequilibrium molecular dynamics (HNEMD), and nonequilibrium molecular dynamics (NEMD). In addition, the neuroevolution potential (NEP) proposed by Fan et al.34–36 has attracted widespread attention due to its exceptional computational efficiency. Nowadays, NEP has been successfully applied to a variety of material systems, including bulk crystals, two-dimensional materials, and amorphous phases, and has shown outstanding performance in thermal transport studies by combining GPUMD.
Therefore, we first generate an initial seed dataset of representative configurations and enrich it through active learning iterations to achieve sufficient sampling of the structural phase space across a wide temperature range, yielding a high-fidelity training dataset. On this basis, we train a NEP machine-learning potential. The reliability of the NEP is systematically assessed by comparisons with DFT for the equations of state, elastic constants, and phonon dispersion relations. Using the GPUMD package, we investigate the temperature dependence of the thermophysical properties of UO2, including heat capacity and the linear thermal expansion coefficient. We provide accurate predictions of the thermal conductivity of UO2 by cross-validating results from EMD, NEMD, and HNEMD, and we quantify the consistency among these methods.
Computational details
Construction of the initial dataset
To construct an initial training dataset for active learning, we adopted a stratified sampling strategy. First, using the NepTrainKit37 software, we imposed lattice deformations ranging from −6% to 6% (including uniaxial, biaxial, and triaxial strains) on the UO2 unit cell and a 2 × 2 × 2 supercell, together with a random atomic displacement of 0.1 Å. In total, 400 initial configurations were generated (313 UO2 unit cells and 87 supercells). Subsequently, we augmented the dataset by applying uniform lattice expansions with scaling factors of 1.07–1.12 to the 2 × 2 × 2 supercell, with atomic displacement perturbations of 0.05 Å. Finally, using the NEP8938 universal machine learning potential (covering 89 elements), we performed temperature-ramp molecular dynamics (MD) simulations on 3 × 2 × 2 and 3 × 3 × 2 supercells, heating from 1100 to 2500 K with a time step of 0.5 fs and a total duration of 7.5 ns. Representative configurations were then selected using the farthest point sampling (FPS) method integrated into NepTrainKit.37 This approach systematically captures structural features from static deformations to dynamical evolution, ensuring dataset diversity while reducing redundancy.Active learning
The configuration-space diversity of the training dataset and the accuracy of first-principles calculations are key determinants of the predictive accuracy of machine learning models. To enhance generalization capability and learning efficiency, we adopted an active learning (AL) strategy that iteratively selected and labeled high-value configurations to progressively improve model performance.In this work, the active learning strategy consists of three steps: training, sampling, and labeling. (I) Training: four NEP models were trained with different random seeds on the initial dataset to enable subsequent configuration sampling and uncertainty estimation. (II) Sampling: one of these NEP models was randomly selected to perform MD simulations over a wide temperature range, generating diverse configuration samples. These configurations were then evaluated by all four models and those with high uncertainty indicated by disagreement among the model predictions were selected as candidates for labeling. (III) Labeling: the labeling criterion for candidate configurations is based on the maximum standard deviation of atomic forces,30 denoted by σf:
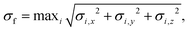 | (1) |
Across 13 rounds of active learning, we progressively optimized the quality and size of the training dataset by increasing MD simulation durations to more thoroughly explore the diversity and dynamical evolution of the configuration space. Ultimately, we constructed a high-quality dataset comprising 1918 independent configurations and 148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 632 atoms, including 506 UO2 unit cells, 1129 2 × 2 × 2, 162 3 × 2 × 2, 30 3 × 3 × 2, and 91 4 × 1 × 1 supercells. The settings for individual active learning iterations are summarized in SI, Table S1.
632 atoms, including 506 UO2 unit cells, 1129 2 × 2 × 2, 162 3 × 2 × 2, 30 3 × 3 × 2, and 91 4 × 1 × 1 supercells. The settings for individual active learning iterations are summarized in SI, Table S1.
DFT calculation settings
All first-principles calculations were performed using the Vienna ab initio simulation Package (VASP).39 In line with our focus on lattice thermophysical properties, which are dominated by lattice dynamics with negligible electronic contributions, and to ensure structural diversity and stable labels in active-learning, we used non-spin-polarized DFT without Hubbard corrections. Electron–ion interactions were described by the projector augmented-wave (PAW)40 method, and exchange–correlation effects were treated within the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)41,42 functional. The 6s27s26p66d25f2 and 2s22p4 orbitals were treated as valence electrons for U and O, respectively. A plane-wave cutoff of 600 eV was employed, with Gaussian smearing (σ = 0.02 eV). The Brillouin zone was sampled on Γ-centered Monkhorst–Pack (MP)43 grids. To balance sampling with the size of cells, we used 5 × 5 × 5 for the UO2 unit cell; 2 × 5 × 5 for the 48-atom supercells (fewer divisions along the elongated direction and more along the shorter ones); and 2 × 2 × 2 for the 96-, 144-, and 216-atom supercells. A K-point convergence test on the 2 × 2 × 2 supercell (SI Fig. S1) shows that a 2 × 2 × 2 mesh meets our accuracy targets. With the increase of the supercell size, the Brillouin zone shrinks, so this mesh provides an equal or higher k-point sampling density for the larger cells. For all self-consistent field (SCF) calculations, the energy convergence threshold was set to 2 × 10−6 eV.NEP configuration
NEP encodes the relative positions and interactions of each atom with its neighbors into compact descriptors and maps these local environments to per-atom energies via a single-hidden-layer feed-forward neural network.35 This compact architecture enables efficient regression while retaining sufficient flexibility. The total potential energy is obtained by summing the energy Ui of each particle i, which is given by: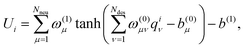 | (2) |
A clear definition of the loss function is critical during the optimization of model parameters. In NEP training, the loss is primarily based on the root mean square error (RMSE) between model predictions and reference values from first-principles calculations. To enhance interpolation and extrapolation capabilities, appropriate regularization is included. The loss function is defined as:
 | (3) |
Based on the preliminary tests of key hyperparameters (see SI Table S2), we finalized the NEP training configuration. The cutoff radii for the radial and angular descriptors were set to 6 Å and 5 Å, respectively. The neural network hidden layer contained 50 neurons. During training, the loss weights on energy, atomic forces, and virial tensor terms were set to 1, 1, and 0.1, respectively. Both L1 and L2 regularization were applied to enhance generalization. Other training hyperparameters are listed in SI Table S3. The overall NEP training workflow is shown in Fig. 1.
 | ||
| Fig. 1 Construction of the initial UO2 dataset, the active learning workflow of NEP model training, and the structural types along with their counts in the final dataset. | ||
To assess dataset representativeness, we analyzed the final dataset using scikit-learn.44 As shown in Fig. 2a, the density distribution is approximately the Gaussian profile, indicating good coverage of the structural space. Fig. 2b shows a principal component analysis (PCA) projection of the UO2 structural descriptors. This analysis demonstrates that active learning effectively broadened structural sampling, enabling exploration of a wider space phase. Finally, after 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of full-batch training, we obtained the NEP model applicable to bulk UO2 across a temperature range of approximately 0–2500 K.
000 steps of full-batch training, we obtained the NEP model applicable to bulk UO2 across a temperature range of approximately 0–2500 K.
Molecular dynamics simulations
All molecular dynamics simulations were performed with the GPUMD package using a 0.5 fs time step at a target pressure of 0 GPa. Unless otherwise specified, we used an 8 × 8 × 8 supercell (6144 atoms; a = b = c = 42.98 Å) of the conventional fluorite UO2 unit cell. NPT (isothermal–isobaric) simulations employed the stochastic cell rescaling (SCR)45 barostat, and NVT (canonical) simulations employed the Bussi–Donadio–Parrinello (BDP)46 thermostat.For structural properties, radial distribution functions (RDFs) were obtained after equilibrating the system for 100 ps in NPT–SCR and sampling for an additional 100 ps in NVT–BDP; RDFs were computed over 0–7 Å. Thermomechanical behavior was characterized by elastic constants, evaluated by applying a small strain of 0.01 to configurations that had first relaxed for 200 ps in NPT–SCR and then equilibrated for 400 ps in the NVE (microcanonical) ensemble. Thermal responses were quantified from NPT–SCR thermal-expansion simulations carried out from 200 to 2100 K in 100 K increments. At each temperature, we ran 400 ps of MD (200 ps equilibration and 200 ps production) and recorded thermodynamic quantities every 1 ps to extract the heat capacity and the linear thermal expansion coefficient.
For thermal transport, the thermal conductivity was cross validated by EMD, HNEMD, and NEMD. We assessed finite-size effects and the dependence on the magnitude and direction of the driving force (SI Fig. S2–S4). In EMD, a 200 ps NPT–SCR equilibration preceded a 1 ns NVT–BDP production run; the heat flux was sampled every 20 fs with a 100 ps correlation time. In HNEMD, we performed a 2 ns NVT–BDP production run after 200 ps of NPT–SCR equilibration, applying a uniform per-atom driving force of 2 × 10−4 Å−1 along the y-direction and recording running averages of the thermal conductivity every 2 ps. In NEMD, heat transport along y was modeled using 8 × 26 × 8 (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 atoms; a = c = 42.98 Å, b = 139.68 Å) and 8 × 30 × 8 (23
968 atoms; a = c = 42.98 Å, b = 139.68 Å) and 8 × 30 × 8 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 atoms; a = c = 42.98 Å, b = 161.17 Å) supercells; the system was partitioned into eight groups along y (SI Fig. S5). After 1 ns of NVT–BDP equilibration, Langevin heat baths47 were applied to the first and last groups as a heat source and cold sink, and the system was propagated for 2 ns. For both HNEMD and NEMD, spectral decomposition along y was performed with a correlation-time window of ±2 ps.
040 atoms; a = c = 42.98 Å, b = 161.17 Å) supercells; the system was partitioned into eight groups along y (SI Fig. S5). After 1 ns of NVT–BDP equilibration, Langevin heat baths47 were applied to the first and last groups as a heat source and cold sink, and the system was propagated for 2 ns. For both HNEMD and NEMD, spectral decomposition along y was performed with a correlation-time window of ±2 ps.
Results and discussion
Model training
Using the fourth-generation NEP framework as implemented in GPUMD, we performed full-batch training for 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps on the training dataset comprising 1918 structures. As shown in Fig. 3a, the loss functions for energies, atomic forces, and virial tensors converged during training, while the L1 and L2 regularization terms stabilized, indicating robust convergence of the NEP model. As presented in Fig. 3b–d, NEP predictions are in close agreement with DFT reference values, with RMSEs of 3.16 meV per atom for energies, 115.02 meV Å−1 for forces, and 22.16 meV per atom for virial tensors. Across these metrics, NEP outperforms previously reported HDNNP,20 SNAP20 and NNP22 potentials. In addition, we assembled an independent test dataset of 200 structures for comparative evaluation (see SI Fig. S6). The RMSEs on this test dataset are likewise low, with no signs of overfitting, preliminarily indicating that the model generalizes well to new samples drawn from the same distribution as the training dataset. Overall, the NEP model trained in this study exhibits high predictive accuracy and robustness.
000 steps on the training dataset comprising 1918 structures. As shown in Fig. 3a, the loss functions for energies, atomic forces, and virial tensors converged during training, while the L1 and L2 regularization terms stabilized, indicating robust convergence of the NEP model. As presented in Fig. 3b–d, NEP predictions are in close agreement with DFT reference values, with RMSEs of 3.16 meV per atom for energies, 115.02 meV Å−1 for forces, and 22.16 meV per atom for virial tensors. Across these metrics, NEP outperforms previously reported HDNNP,20 SNAP20 and NNP22 potentials. In addition, we assembled an independent test dataset of 200 structures for comparative evaluation (see SI Fig. S6). The RMSEs on this test dataset are likewise low, with no signs of overfitting, preliminarily indicating that the model generalizes well to new samples drawn from the same distribution as the training dataset. Overall, the NEP model trained in this study exhibits high predictive accuracy and robustness.
Model validation
To systematically evaluate the reliability of the developed UO2–NEP model, we selected three metrics that are highly sensitive to the accuracy of potential and have clear physical significance, and used them to benchmark the NEP model against DFT. These metrics include the zero-temperature equation of state (EOS), single-crystal elastic constants, and phonon dispersion relations across the full Brillouin zone. The EOS describes the response of materials under variations in pressure, volume, and temperature, provides a fundamental basis for determining the equilibrium lattice constant, quantifying compressibility, analyzing phase transition behavior, and assessing other thermodynamic properties. We sampled 12 volume points within the lattice scaling factor range of 0.94 to 1.05 and performed static total energy calculations on the corresponding structures to obtain EOS. Fig. 4 shows that the energy–volume (E–V) and pressure–volume (P–V) curves from NEP and DFT exhibit excellent agreement near the equilibrium volume. This indicates that the NEP model accurately captures the E–V relationship and pressure response of UO2, providing a reliable foundation for subsequent simulations of thermodynamic properties. | ||
| Fig. 4 Energy–volume and pressure–volume curves for UO2 at 0 K computed with NEP (blue) and DFT (yellow). | ||
Elastic constants are critical indicators for evaluating the mechanical fidelity of an interatomic potential, as they are directly related to the mechanical performance and structural stability of materials. In this study, the elastic constants were calculated from the linear stress–strain constitutive relation. Within the small stress–strain regime, stress and strain obey Hooke's law:
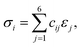 | (4) |
| NEP | DFT | MLIP-DFT | CRG | Exp. | |
|---|---|---|---|---|---|
| C11 (GPa) | 400.5 | 405.2 | 389.5 | 406.3 | 395.0 |
| C12 (GPa) | 118.6 | 110.4 | 121.2 | 124.7 | 121.0 |
| C44 (GPa) | 81.1 | 77.0 | 78.0 | 63.9 | 64.1 |
| B (GPa) | 212.5 | 208.6 | 207.8 | 218.6 | 212.3 |
| G (GPa) | 101.4 | 100.1 | 97.1 | 88.1 | 87.4 |
| E (GPa) | 262.4 | 259.0 | 252.0 | 233.0 | 230.6 |
| ν | 0.294 | 0.293 | 0.298 | 0.322 | 0.319 |
Phonon dispersion relations are a key tool for investigating lattice dynamical behavior and are crucial for understanding thermal transport. To evaluate the predictive performance of the NEP model, we computed the phonon dispersion relations of UO2 using both the NEP model and DFT. After high-precision optimization of the UO2 unit cell, the optimized structure was expanded to a 2 × 2 × 2 supercell for both calculations. NEP-based phonon dispersions were obtained in GPUMD with the finite-displacement method using a displacement of 0.01 Å. For the DFT reference, it was processed with PHONOPY50 using the same displacement to construct the force-constant matrix. As shown in Fig. 5, neither approach yields imaginary frequencies throughout the Brillouin zone, indicating that the UO2 structure is dynamically stable. In the low-frequency region, the acoustic branches show excellent agreement with the DFT results, demonstrating that the NEP model accurately captures the behavior of acoustic phonons, which dominate lattice thermal transport.2
 | ||
| Fig. 5 Phonon dispersion relations for UO2 at 0 K obtained from the NEP model (solid blue lines) and DFT (yellow circles). | ||
Radial distribution function
The radial distribution function (RDF) describes the probability density of the relative distances between any two particles in a many-particle system, thereby providing a direct measure of local structural order and the coordination environment. For a system of volume V containing Na atoms of type a and Nb atoms of type b, the RDF gab(r) for the a–b pair is defined as: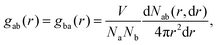 | (5) |
 | ||
| Fig. 6 Partial (U–U, O–O, and U–O) and total radial distribution functions (RDFs) over the temperature range of 300–2500 K. | ||
Elastic constants
We systematically calculated the three independent isothermal elastic constants, C11, C12, and C44, over the range of 300–2000 K (see Fig. 7). Overall, the elastic constants predicted by different force-field models show deviations of varying magnitude from experimental values. These discrepancies primarily arise from: (I) inherent limitations of the interatomic potentials, including approximations to the potential energy surface and limited coverage of the training datasets; (II) intrinsic constraints of MD simulations, such as finite-size effects, implementation differences between the stress–strain and fluctuation approaches, and comparability between the computed isothermal elastic constants and the adiabatic elastic constants commonly measured experimentally; (III) technical challenges in experimental measurements, including uncertainty at high temperature, non-stoichiometry in UO2±x, defects, and effects of polycrystalline; and (IV) the intrinsic complexity of the mechanical behavior with temperature and microstructural evolution. | ||
| Fig. 7 Comparison of the elastic constants C11, C12, and C44 as a function of temperature (300–2000 K). NEP (blue circles), NNP22 (yellow squares), SNAP20 (green upward triangles), and HDNNP20 (red downward triangles) are machine learning potentials; CRG19 (purple diamonds) is an empirical potential; experimental values from Hutchings51et al. are shown as brown crosses. | ||
Specifically, for C11, the HDNNP20 and SNAP20 models systematically underestimate the experimental values over most of the temperature range, whereas NNP,22 CRG,19 and the NEP models developed in this study tend to overestimate slightly. Notably, the experimentally reported scatter in C11 at 300 K is about 60 GPa, indicating substantial uncertainty in the experimental reference data, thereby complicating model assessment. For C12, except for a slight overestimation by the NNP22 model at 300 K, the other models generally lie below the experimental values. All models predict a monotonic decrease in C12 with increasing temperature, in marked contrast to the nearly constant experimental trend of around 120 GPa. For C44, the CRG,19 HDNNP,20 and SNAP20 models yield values lower than experimental values, whereas the NNP22 and NEP models show closer agreement with the experimental data. Overall, the NEP model exhibits smaller deviations from experimental data for both C11 and C44, showing a potential advantage in characterizing the elastic properties of UO2.
Heat capacity and the linear thermal expansion coefficient
For three-dimensional isotropic systems, the linear thermal expansion coefficient αL at constant pressure is approximated here by a central finite difference: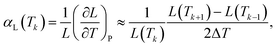 | (6) |
Similarly, the isobaric molar heat capacity Cp is given by:
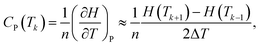 | (7) |
 | ||
| Fig. 8 Temperature dependence of (a) the isobaric molar heat capacity and (b) the linear thermal expansion coefficient. The black circles with error bars represent the NEP results from this work. Crosses denote experimental reference values, taken from Ronchi5 and Martin et al.52 Data for other potentials are taken from ref. 16,19–22. | ||
Thermal conductivity
Thermal conductivity is a critical parameter that characterizes the heat transfer capability and is essential for the design and optimization of nuclear fuels. In this work, we employed EMD, HNEMD, and NEMD to compute the thermal conductivity of UO2 over a range of temperatures.In the EMD approach, the thermal conductivity is obtained from the Green–Kubo relation via the heat current autocorrelation function (HCACF) of an equilibrium system. The Green–Kubo expression reads:
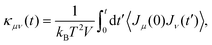 | (8) |
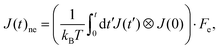 | (9) |
The thermal conductivity is then given by:
 | (10) |
 | (11) |
To efficiently obtain the apparent thermal conductivity κ(L) at arbitrary lengths, we take the Fourier transforms of the virial-velocity cross-correlation function K(t) in both HNEMD and NEMD, thereby establishing a unified spectral decomposition framework. Within this framework, the spectral thermal conductivity κ(ω) in HNEMD is defined as:
 | (12) |
Correspondingly, the spectral thermal conductance G(ω) along the same transport direction in NEMD is given by:
 | (13) |
The spectral mean free path λ(ω) is then defined as:
 | (14) |
The length-dependent thermal conductivity κ(L) is then obtained from the above spectral quantities:
 | (15) |
In this study, we computed the thermal conductivity at 500 K using EMD, HNEMD, and NEMD. The results are shown in Fig. 9. For the EMD results shown in Fig. 9a, because the method relies on integrating the HCACF, the long tail exhibits a low signal-to-noise ratio and is prone to drift, necessitating multiple independent simulations to reduce uncertainty. We conducted 30 independent runs reducing the uncertainty to about 7%. In contrast, the HNEMD in Fig. 9b directly drives a steady-state heat flux via a perturbative field, yielding stronger signals and faster convergence. Only three independent simulations were required to obtain stable estimates, with markedly lower statistical uncertainty than in EMD. NEMD requires large supercells to establish a stable temperature gradient, leading to the highest computational cost per simulation. SI Fig. S7 verifies satisfactory group thermostatting; the spectral thermal conductivity from HNEMD and the spectral thermal conductance from NEMD are shown in SI Fig. S8 and S9, respectively. Fig. 9c shows that the spectral phonon mean free path in UO2 at 500 K spans roughly one order of magnitude, from approximately 50 nm at high frequencies to approximately 500 nm in the low-frequency limit. Correspondingly, in Fig. 9d, κ(L) increases with L and approaches a constant for L exceeding about 5 µm. This asymptotic value can be regarded as bulk (macroscopic) thermal conductivity. Consistent with this, Watanabe et al. reported a pronounced finite-size dependence of thermal conductivity on characteristic length.53 This behavior originates from the temperature-dependent distribution of the phonon mean free path: at high temperatures, enhanced Umklapp scattering shortens the mean free path, making κ less sensitive to the geometric size, whereas at low temperatures the fraction of long-mean-free-path phonons increases, allowing them to propagate over longer distances with fewer scattering events.
Given the comparative efficiency of the three methods assessed above, we adopted the HNEMD approach, which possesses faster convergence and lower uncertainty, to simulate the thermal conductivity of UO2 over 300–1500 K. Ronchi et al.5 noted that the dominant thermal transport mechanisms vary with temperature: lattice contributions prevail at low temperatures, whereas non-lattice channels such as electronic contributions become markedly enhanced above 1300 K. Since classical MD explicitly describes phonons and diffusive carriers (e.g., ions, defects) but excludes electronic contributions, we restricted our simulations to temperatures below 1500 K. As shown in Fig. 10, the NEP model is in overall agreement with the experimental results of Ronchi et al.5 and with the EIP predictions of Zhou et al.54 above 800 K. Below 800 K, the NEP slightly overestimates the experimental values yet remains lower than the results obtained from the CRG19 empirical potential and the modified Busker potential of Liu et al.55 (fitted via the Callaway model with spin phonon relaxation corrections), and it aligns closely with the PBE+U calculations reported by Zhou et al.54 These discrepancies mainly stem from the use of an ideal, defect-free model, which omits impurities, defects, and electronic contributions present in experimental specimens. We note that electronic thermal conduction is non-negligible in experiments within the 1300–1500 K range, which partly explains why our predictions are slightly lower than the measurements in this range. Overall, the NEP model combined with the HNEMD reproduces experimental trends at intermediate temperatures and yields predictions consistent with first-principles calculations at lower temperatures, demonstrating its utility for characterizing the thermal transport properties of nuclear fuels.
 | ||
| Fig. 10 Thermal conductivity of UO2 over 300–1500 K. The solid lines represent the results obtained from the CRG19 empirical potential (blue), PBE+U54 calculations reported by Zhou et al. (yellow), the EIP54 of Zhou et al. (green), and the modified Busker55 potential of Liu et al. (red). Experimental data points are from Fink et al.6 (blue crosses), Ronchi et al.5 (yellow squares), and Lucuta et al.4 (green plus signs). NEP predictions are shown as purple circles, with error bars denoting uncertainties. | ||
Conclusions
The actinide oxide UO2 is the primary fuel in commercial nuclear reactors, and its thermal transport properties are pivotal to reactor-core thermal management and safety margins. In this work, we developed an NEP machine learning potential approaching DFT-level accuracy and combined with the energy-conserving Hardy-type heat flux framework in GPUMD, and we systematically evaluated and cross-validated the thermal conductivity of UO2.Initially, by manually generating an initial dataset and adopting an active learning strategy of “training–sampling–labeling”, we constructed a training dataset that covers both static and dynamic configurations with a balanced density distribution. After iterative refinements, we obtained an NEP applicable for UO2 over 0–2500 K, which agrees closely with DFT for predicted energies, forces, and virials. Further validation confirmed that the equation of state derived from NEP closely matches that of DFT near the equilibrium volume. The predicted elastic constants C11, C12, and C44 deviate from DFT reference values by −1.16%, 7.43%, and 5.32%, respectively. Phonon dispersion relations show no imaginary modes across the Brillouin zone, and the acoustic branches align well with DFT. Overall, the NEP exhibits high accuracy, strong robustness, and reliable capability for characterizing the fundamental physical properties of UO2.
Subsequently, we further examined the temperature dependence of various thermophysical properties. The radial distribution functions indicate that the first-neighbor distances for U–U and O–O pairs increase with increasing temperature, while the average U–O bond length decreases slightly. For elastic constants, the NEP predictions for C11 and C44 are closer to experimental data than those from other MLIPs, and C12 decreases monotonically with temperature. The heat capacity shows good agreement with experimental data in the range of 300–2000 K. The linear thermal expansion coefficient agrees with the Basak potential at T ≤ 1000 K and increases rapidly at higher temperatures. These results underscore the strong applicability and promising potential of the NEP for characterizing the thermophysical properties of UO2.
Finally, we systematically evaluated the EMD, NEMD, and HNEMD methods for thermal conductivity calculations and cross-validated the consistency of the NEP predictions across methods. Among them, the HNEMD delivers the highest computational efficiency, characterized by a high signal-to-noise ratio, low uncertainty, and rapid convergence, outperforming EMD (which requires multiple independent repetitions) and NEMD (with substantial length-scale requirements). At 500 K, the spectral phonon mean free path distribution spans roughly one order of magnitude, and the thermal conductivity reaches the bulk limit once the transport channel length exceeds about 5 µm. Based on HNEMD, the NEP-predicted thermal conductivity from 300 to 1500 K shows good agreement with experimental data above 800 K and aligns closely with the PBE+U results from Zhou et al. below 800 K. Thus, the NEP combined with HNEMD reliably captures the intermediate-temperature thermal transport behavior of UO2 while balancing efficiency and accuracy and yields predictions near first-principles precision in the low-temperature regime.
This work demonstrates the applicability and utility of the NEP for modeling thermal transport in nuclear fuels and provides methodological support for multiscale integration. Beyond UO2, the same framework is applicable to other actinide oxide fuels, as well as to non-stoichiometric compositions, interfaces and grain boundaries, and irradiation-damaged microstructures that govern heat conduction. Such applications can help assess transferability across chemistries and operating conditions and broaden the use of NEP-based simulations in fuel-performance modeling.
Author contributions
Junying Zhong: writing – original draft, writing – review and editing, investigation, methodology, software, visualization, data curation, formal analysis, and validation. Lei Zhang: investigation, conceptualization, resources, and supervision. Tao Bo: writing – review and editing, data curation, methodology, investigation, conceptualization, software, resources, formal analysis, validation, supervision, project administration, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this study are included as part of the Supplementary information (SI). The SI also provides the GPUMD input files for all MD simulations (RAR archive with nep.txt, model.xyz, a README, and per-property folders each containing run.in). See DOI: https://doi.org/10.1039/d5cp03760c.Acknowledgements
We acknowledge financial support from the National Natural Science Foundation of China (No. 12575387, U2167218 and U2267222) and the Yongjiang Talent Introduction Programme (2021A-161-G).Notes and references
- X. Yang, J. Tiwari and T. Feng, Mater. Today Phys., 2022, 24, 100689 CrossRef.
- D. H. Hurley, A. El-Azab, M. S. Bryan, M. W. D. Cooper, C. A. Dennett, K. Gofryk, L. He, M. Khafizov, G. H. Lander and M. E. Manley, et al. , Chem. Rev., 2022, 122, 3711–3762 CrossRef CAS PubMed.
- J. H. Harding and D. G. Martin, J. Nucl. Mater., 1989, 166, 223–226 CrossRef CAS.
- P. G. Lucuta, H. Matzke and I. J. Hastings, J. Nucl. Mater., 1996, 232, 166–180 CrossRef CAS.
- C. Ronchi, M. Sheindlin, M. Musella and G. J. Hyland, J. Appl. Phys., 1999, 85, 776–789 CrossRef CAS.
- J. K. Fink, J. Nucl. Mater., 2000, 279, 1–18 CrossRef CAS.
- J. J. Carbajo, G. L. Yoder, S. G. Popov and V. K. Ivanov, J. Nucl. Mater., 2001, 299, 181–198 CrossRef CAS.
- M. Sanati, R. C. Albers, T. Lookman and A. Saxena, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014116 CrossRef.
- Y. Yun, D. Legut and P. M. Oppeneer, J. Nucl. Mater., 2012, 426, 109–114 CrossRef CAS.
- B.-T. Wang, P. Zhang, R. Lizárraga, I. Di Marco and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 104107 CrossRef.
- B.-T. Wang, J.-J. Zheng, X. Qu, W.-D. Li and P. Zhang, J. Alloys Compd., 2015, 628, 267–271 CrossRef CAS.
- T. P. Kaloni, N. Onder, J. Pencer and E. Torres, Ann. Nucl. Energy, 2020, 144, 107511 CrossRef CAS.
- S. Sheykhi and M. Payami, Iran. J. Sci. Technol., Trans. A: Sci., 2020, 44, 1585–1593 CrossRef.
- E. Torres, I. Cheik Njifon, T. P. Kaloni and J. Pencer, Comput. Mater. Sci., 2020, 177, 109594 CrossRef CAS.
- S. T. Murphy, M. J. D. Rushton and R. W. Grimes, Prog. Nucl. Energy, 2014, 72, 27–32 CrossRef CAS.
- C. B. Basak, A. K. Sengupta and H. S. Kamath, J. Alloys Compd., 2003, 360, 210–216 CrossRef CAS.
- N.-D. Morelon, D. Ghaleb, J.-M. Delaye and L. Van Brutzel, Philos. Mag., 2003, 83, 1533–1555 CrossRef CAS.
- E. Yakub, C. Ronchi and D. Staicu, J. Chem. Phys., 2007, 127, 094508 CrossRef PubMed.
- M. W. D. Cooper, M. J. D. Rushton and R. W. Grimes, J. Phys.: Condens. Matter, 2014, 26, 105401 CrossRef CAS.
- E. T. Dubois, J. Tranchida, J. Bouchet and J.-B. Maillet, Phys. Rev. Mater., 2024, 8, 025402 CrossRef CAS.
- E. Stippell, L. Alzate-Vargas, K. N. Subedi, R. M. Tutchton, M. W. D. Cooper, S. Tretiak, T. Gibson and R. A. Messerly, Artif. Intell. Chem., 2024, 2, 100042 CrossRef.
- K. Konashi, N. Kato, K. Mori and K. Kurosaki, J. Nucl. Mater., 2025, 607, 155660 CrossRef CAS.
- K. Govers, S. Lemehov, M. Hou and M. Verwerft, J. Nucl. Mater., 2008, 376, 66–77 CrossRef CAS.
- S. Nichenko and D. Staicu, J. Nucl. Mater., 2014, 454, 315–322 CrossRef CAS.
- C. I. Maxwell and J. Pencer, Ann. Nucl. Energy, 2019, 131, 317–324 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al. , Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. P. Thompson, S. J. Plimpton and W. Mattson, J. Chem. Phys., 2009, 131, 154107 CrossRef PubMed.
- P. Boone, H. Babaei and C. E. Wilmer, J. Chem. Theory Comput., 2019, 15, 5579–5587 CrossRef CAS PubMed.
- S. T. Tai, C. Wang, R. Cheng and Y. Chen, J. Chem. Theory Comput., 2025, 21, 3649–3657 CrossRef CAS.
- Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren and J. M. Rahm, et al. , J. Chem. Phys., 2022, 157, 114801 CrossRef CAS PubMed.
- Z. Fan, L. F. C. Pereira, H.-Q. Wang, J.-C. Zheng, D. Donadio and A. Harju, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094301 CrossRef.
- Z. Fan, H. Dong, A. Harju and T. Ala-Nissila, Phys. Rev. B, 2019, 99, 064308 CrossRef CAS.
- Z. Li, S. Xiong, C. Sievers, Y. Hu, Z. Fan, N. Wei, H. Bao, S. Chen, D. Donadio and T. Ala-Nissila, J. Chem. Phys., 2019, 151, 234105 CrossRef PubMed.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Phys. Rev. B, 2021, 104, 104309 CrossRef CAS.
- Z. Fan, J. Phys.: Condens. Matter, 2022, 34, 125902 CrossRef CAS PubMed.
- K. Song, R. Zhao, J. Liu, Y. Wang, E. Lindgren, Y. Wang, S. Chen, K. Xu, T. Liang and P. Ying, et al. , Nat. Commun., 2024, 15, 10208 CrossRef CAS PubMed.
- C. Chen, Y. Li, R. Zhao, Z. Liu, Z. Fan, G. Tang and Z. Wang, Comput. Phys. Commun., 2025, 317, 109859 CrossRef CAS.
- T. Liang, K. Xu, E. Lindgren, Z. Chen, R. Zhao, J. Liu, E. Berger, B. Tang, B. Zhang, Y. Wang and et al., arXiv, 2025, preprint, arxiv:2504.21286 DOI:10.48550/arXiv.2504.21286.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- A. Dal Corso, A. Pasquarello, A. Baldereschi and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1180–1185 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- G. Bussi and M. Parrinello, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 056707 CrossRef PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- J. B. Wachtman Jr., M. L. Wheat, H. J. Anderson and J. L. Bates, J. Nucl. Mater., 1965, 16, 39–41 CrossRef.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- M. T. Hutchings, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 1083–1103 RSC.
- D. G. Martin, J. Nucl. Mater., 1988, 152, 94–101 CrossRef.
- T. Watanabe, S. B. Sinnott, J. S. Tulenko, R. W. Grimes, P. K. Schelling and S. R. Phillpot, J. Nucl. Mater., 2008, 375, 388–396 CrossRef CAS.
- S. Zhou, C. Jiang, E. Xiao, S. Bandi, M. W. D. Cooper, M. Jin, D. H. Hurley, M. Khafizov and C. A. Marianetti, J. Phys.: Condens. Matter, 2025, 37, 255901 CrossRef CAS PubMed.
- X.-Y. Liu, M. W. D. Cooper, K. J. McClellan, J. C. Lashley, D. D. Byler, B. D. C. Bell, R. W. Grimes, C. R. Stanek and D. A. Andersson, Phys. Rev. Appl., 2016, 6, 044015 CrossRef.
| This journal is © the Owner Societies 2026 |



