A TMA and DSC study of the kinetics of the solid-state reaction in an Al2O3–Y2O3 system
Nathan
Kerkad
a,
Loïck
Bonnet
b,
Loic
Favergeon
 c,
Alexandre
Maître
a and
Rémy
Boulesteix
c,
Alexandre
Maître
a and
Rémy
Boulesteix
 *a
*a
aUniv. Limoges, IRCER, UMR CNRS 7315, F-87068 Limoges, France. E-mail: remy.boulesteix@unilim.fr
bMarion Technologies, F-09340 Verniolle, France
cMines Saint-Etienne, Univ. Lyon, CNRS, UMR 5307 LGF, Centre SPIN, F-42023 Saint-Etienne, France
First published on 28th November 2025
Abstract
This study focuses on the kinetic analysis of the solid-phase reactivity of mixtures of Al2O3 and Y2O3 powders, introduced in stoichiometric proportions for the formation of the YAG phase (Y3Al5O12). Structural and microstructural analyses using XRD, TEM, STEM, and SEM provided a better understanding of the reaction mechanism of the formation of the YAG phase, which appears to be of a heterogeneous nucleation-growth type. The second part of this study focused on a kinetic analysis of these reactions, using the Kissinger model applied to data obtained by differential scanning calorimetry (DSC) and thermomechanical analysis (TMA). Activation energies equal to 560 kJ mol−1 for the formation of YAP and 660 kJ mol−1 for the formation of the YAG phase were obtained by both methods, meaning that the reaction should be limited by the diffusion of Y3+ ions.
1. Introduction
Polycrystalline ceramics of the rare-earth oxide garnet family, like yttrium aluminum garnet (Y3Al5O12–YAG), are attractive materials to use for various applications like the medium in solid-state laser amplifiers,1 high-temperature windows, LED phosphors2–5 and jewelry.6 For these applications, powders are generally made by chemical synthesis,7–9 but solid-state reactions are also used.10–12 The latter appears better adapted for the mass production of YAG powder today, as it only requires low-cost, high-purity primary oxide nanopowder.The Y3Al5O12 garnet (YAG) phase is a defined compound with no deviation from the exact stoichiometry as reported in its binary phase diagram.13,14 The optical properties of YAG ceramics are controlled by the microstructure and especially by the content of residual defects like secondary phases (Y2O3, Al2O3, Y4Al2O9, YAlO3, etc.), whose refractive indices differ from that of YAG. These defects can occur during different steps of the synthesis process, e.g., due to the poor control of the Y/Al stoichiometric ratio or the reaction-sintering process. In this context, a good understanding of solid-state reaction mechanisms leading to the YAG phase is necessary.15–19 Kong et al.20 suggested a hypothetical mechanism that could occur in a Y2O3–Al2O3 binary powder mixture. This mechanism was schematized based on a core–shell model, represented by Al2O3 submicrometric grains covered by nanometric Y2O3 grains. According to this model, Al2O3 grains were progressively enriched with Y from the surface with increasing temperature, leading to the successive formation of concentric shells of Y4Al2O9 (YAM), then YAlO3 (YAP), and finally Y3Al5O12 (YAG). At around 1873 K, the reaction was almost completed. Nevertheless, this model was based neither on an analytical study of reaction kinetics nor on microstructural observations. Moreover, from our previous works,21–23 we observed a similar reaction sequence with increasing temperature, but none of our microstructural observations are in accordance with this model.
Several recent studies have shed significant light on this subject. Korte and Franz24,25 studied the kinetics of YAG formation from thin layers of Y2O3 and Al2O3. They demonstrated coexistence and competition between the YAG, YAP, and YAM phases by quantifying growth rates at high temperatures (1473–1673 K). Kupp et al.26 showed that the size of the reactive particles strongly influenced the kinetics of YAG formation. They demonstrated that reducing the size of the Y2O3 grains accelerates the reaction and alters the limiting mechanism, which depends on the size ratio of the starting oxides. In addition, Dabulytė-Bagdonavičienė et al.27 developed a mathematical model of YAG synthesis, integrating diffusion and reaction kinetics in a non-stationary system. This model makes it possible to simulate the temporal evolution of YAG formation and to evaluate the influence of various diffusive parameters on the overall kinetics. Finally, Tinkova et al.28 explored a multi-step approach combining mechanical grinding and successive thermal stages, demonstrating that careful control of intermediate treatments can significantly increase the purity of the obtained YAG phase, while identifying a critical YAG concentration beyond which the kinetics become unfavorable.
Consequently, the purpose of this work is to bring a better understanding of the reaction mechanism during YAG phase formation, macroscopically on the scale of particles. With this aim, the reaction sequence was studied by various complementary techniques (thermal, microstructural and structural). The as-obtained results were analyzed by using classical and modified Kissinger's kinetic models.
2. Experimental
Al2O3 powder (pure alpha hexagonal variety, mean particle size: 400 nm, specific surface area: 6 m2 g−1, Baïkowski, France) and Y2O3 powder (pure cubic bixbyite structure, mean particle size: 40 nm, specific surface area: 25 m2 g−1, Solvay, Belgium) with high chemical purity (>99.99%) were weighed and mixed at the stoichiometric ratio to obtain Y3Al5O12 after the final reaction. Thermal treatments were performed in air for different durations (0 to 16 hours) at temperatures ranging from 973 K to 1673 K. The thermal behavior of the Al2O3–Y2O3 mixture was studied by means of differential scanning calorimetry (DSC) measurements carried out using a thermal analyzer (TG-ATD-DSC STA 449 F3 Jupiter™, Netzsch, Germany). The powder mixture was placed in an alumina pan (4 mm in diameter and 6 mm in height), with a total sample mass of about 50 mg. The weighed samples were heated in a flow of air (200 cm3 min−1) from room temperature up to 1773 K at different heating rates (10 ≤ β ≤ 50 K min−1). Thermomechanical analyses were performed under vacuum in a Setaram dilatometer (TMA Setsys evo). The sample was heated from ambient temperature to 1723 K at three different heating rates (1 ≤ β ≤ 10 K min−1). Morphological (FEG-ESEM, TEM-STEM coupled with EDXS chemical analysis, 2100F, Jeol, Japan; BET, 3 Flex, Micrometrics, Canada) and structural (XRD, D8 advanced Da Vinci Cu Kα, Brüker, USA; He pycnometry, Accupyc 1340, Micrometrics, Canada) characterization was performed to study sample changes during heat treatment and to understand local mechanisms. The fractional reaction α of powder mixing was calculated from the sample's apparent density measured by pycnometry and by calculating the mass percentage of each phase (YAP, Al2O3 and YAG) from the mixing density formulae (see the SI for details).3. Results and discussion
3.1. Study of reaction kinetics by structural analyses
First, the reaction sequence between Al2O3 and Y2O3 powders was studied using XRD. Fig. 1 presents the evolution of the XRD patterns as a function of the thermal treatment temperature in air. In agreement with previously published works,3,13,14,20–22 the macroscopic reaction sequence can be described in three successive stages. First, the primary oxides react together to form the YAM phase at a temperature of around 1473 K (eqn (1)):| Al2O3 + 2Y2O3 → Y4Al2O9 | (1) |
 | ||
| Fig. 1 The evolution of XRD patterns as a function of the thermal treatment temperature in air for Y2O3–Al2O3 mixing. | ||
Second, YAM reacts with remaining alumina to form the YAP phase at around 1573 K (eqn (2)):
| Y4Al2O9 + Al2O3 → 4YAlO3 | (2) |
Finally, YAP reacts with alumina to form the YAG phase according to eqn (3):
| 3YAlO3 + Al2O3 → Y3Al5O12 | (3) |
The reaction was also studied by helium pycnometry. Fig. 2 presents the evolution of powder density as a function of the calcination temperature under air with a dwell time of 1 h for two powder-mixing processes: Al2O3–Y2O3 (Y/Al = 1) for YAP phase formation and 5Al2O3–3Y2O3 (Y/Al = 0.6) for YAG phase formation. One has to recall here the theoretical densities of the studied phases: dYAP is the density of the pure YAP phase, equal to 5.35 g cm−3; dAl2O3 is the density of the pure α-Al2O3 phase, equal to 3.98 g cm−3; and dYAG is the density of the pure YAG phase, equal to 4.55 g cm−3. From these results, one can see that the density of mixing is well correlated with the expected behavior and with the reaction sequence observed by XRD. The density during the two powder-mixing processes starts to increase at temperatures higher than 1373 K, due to the formation of the denser YAP phase (1st and 2nd mixing processes), then the density of the 2nd mixing process decreases at temperatures higher than 1500 K due to the replacement of the YAP phase by the YAG one of lower density. At 1773 K, the densities measured for both mixing processes are very close (difference less than 1% due to experimental uncertainty) to the expected ones (marked as dth in Fig. 2).
 | ||
| Fig. 2 The evolution of powder bed density versus temperature for Y2O3–Al2O3 mixtures with Y/Al = 0.6 (YAG) and Y/Al = 1 (YAP). | ||
From complementary density measurements by pycnometry, the fractional reaction α of powder mixing was calculated by considering the unique reaction between YAP and Al2O3 described by eqn (3). According to this hypothesis, the fractional reaction α was determined from the mass percentage and density of each phase (YAP, Al2O3 and YAG). Fig. 3 presents the evolution of the fractional reaction α during the formation of the YAG phase from YAP and Al2O3 powders as a function of the thermal treatment time at 1473 K in air. One can notice the very strong evolution of the fractional reaction during the first hours of thermal treatment at 1473 K. In addition, these results show that the complete reaction (α = 1) is reached at thermal processing times longer than 60 h. From these measurements, one can see that the kinetics of the reaction under isothermal conditions decrease over time. This will help to determine the kinetic model as discussed below.
 | ||
| Fig. 3 Evolution of the reaction advancement rate for Al2O3–YAP mixing as a function of treatment time at 1473 K. | ||
3.2. Study of reaction kinetics by DSC
Then, the reaction sequence and kinetics were studied analytically by DSC. The classically determined general expression to describe the reaction rate of a single-step reaction is given by eqn (4):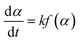 | (4) |
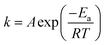 | (5) |
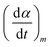 at the peak temperature Tp during transformation. The expression of the derived function eqn (6) takes the following form:
at the peak temperature Tp during transformation. The expression of the derived function eqn (6) takes the following form: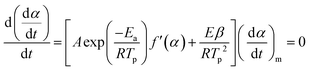 | (6) |
By admitting that the value of the fractional reaction αm related to the maximal rate does not change with heating rate, eqn (6) becomes:
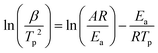 | (7) |
Thus, plotting the evolution of 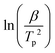 as a function of
as a function of 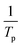 should result in a straight line, and the apparent activation energy Ea can be calculated from the slope of the line. While aware of the limitations of Kissinger's method, which were discussed elsewhere,31 this analysis enables the determination of apparent activation energy values for single-step reactions.
should result in a straight line, and the apparent activation energy Ea can be calculated from the slope of the line. While aware of the limitations of Kissinger's method, which were discussed elsewhere,31 this analysis enables the determination of apparent activation energy values for single-step reactions.
By considering this kinetic analysis, measurements by differential scanning calorimetry (DSC) were carried out at different constant heating rates (β). Fig. 4 shows curves of heat flow obtained by DSC between 1173 K and 1773 K for various heating rates β between 10 K min−1 and 50 K min−1.
 | ||
| Fig. 4 Evolution of DSC heat flow versus temperature at different heating rates for the Y2O3–Al2O3 mixture with Y/Al = 0.6. | ||
One can note that two different exothermic phenomena are observed, at around 1523 K–1573 K and at around 1623 K–1673 K. These two peaks can be attributed to the formation of YAP and YAG phases, respectively. The formation of YAM that occurs at lower temperatures between 1373 K and 1473 K, according to XRD results (Fig. 1), seems to be linked to the endothermic peaks detected at temperatures around 1400 K in Fig. 4. One can also see in Fig. 4 that all of these peaks are shifted to higher temperatures with increasing heating rate, as expected.
From Fig. 4, the temperature for the maximum rate of reaction (Tp) was determined for each reaction step and heating rate. The as-obtained Arrhenius diagrams are presented in Fig. 5a for the second step (YAP formation) and Fig. 5b for the final step (formation of YAG). Fig. 5 shows that straight lines with very good agreement with the model are obtained in both cases. This indicates that only one mechanism should be predominant for each reaction step. The apparent activation energy values were determined to be around 560 ± 3 kJ mol−1 and 660 ± 24 kJ mol−1 for YAP and YAG phase formation, respectively. Interestingly, these two values are close to the values reported for the synthesis of YAG fibers.32 Similar values were also reported for rare-earth solid-state diffusion in the bulk or at grain boundaries (i.e. the faster diffusion path) in YAG polycrystalline and dense ceramics.24,25 That means the formation of YAG grains could be controlled by Y3+ solid-state diffusion. Diffusion coefficients for ionic species in ceramics generally follow this trend at a given temperature: Ds > Dgb > Dv, where Ds, Dgb and Dv are the surface, grain boundary and volume diffusion coefficients, respectively.33,34 For Al2O3, it is well known that surface diffusion starts to be activated at relatively low temperatures (i.e. T < 1200 K).35 From this knowledge, it can be supposed that Al3+ species can diffuse rapidly at grain surfaces to form YAP and YAG particles.
3.3. Study of reaction kinetics by TMA
The activation energy associated with YAP formation was also measured by TMA using the Kissinger approach, modified by Oliver.36 The approach is based on the densification equation adapted to dilatometry, which leads to the expression of the densification rate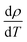 at a constant heating rate
at a constant heating rate 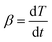 given by eqn (8). The term f(ρ) is associated with sintering, and A combines several terms such as surface energy, grain size, and molar volume, which are dependent on neither temperature nor density. Q, T and R are the activation energy, the temperature and the ideal gas constant, respectively:
given by eqn (8). The term f(ρ) is associated with sintering, and A combines several terms such as surface energy, grain size, and molar volume, which are dependent on neither temperature nor density. Q, T and R are the activation energy, the temperature and the ideal gas constant, respectively: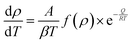 | (8) |
The method assumes that the peak temperature Tp during thermal transformation corresponds to the maximum speed of the reaction, so the second derivative cancels out at this point, enabling eqn (9) and (10) to be written as follows:
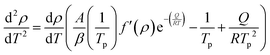 | (9) |
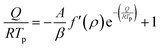 | (10) |
By re-arranging the terms, we can also generate eqn (11), which seems to be the one stated by Kissinger:
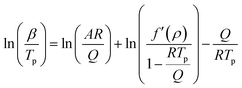 | (11) |
Several assumptions are made to simplify the equation: the grain size is assumed to be constant or of negligible variation, the heating rate is a constant β, and the activation energy Q and the parameter A are assumed to be constant during the reaction. As in Kissinger's work, density variations are neglected. This approach enabled Oliver to establish the following equation (eqn (12)), slightly different from the original Kissinger analysis:
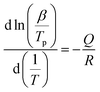 | (12) |
Based on this model, we carried out TMA at different heating rates ranging from 1 to 10 K min−1. The results are shown in Fig. 6. Two different phenomena are observed: first, shrinkage at around 1451 K–1528 K and second, expansion at around 1591 K–1700 K. These two peaks can be attributed to the formation of YAP and YAG phases, respectively. As in DSC, YAM formation is not clearly observed by TMA.
 | ||
| Fig. 6 Evolution of the shrinkage rate versus temperature at different heating rates for the Y2O3–Al2O3 mixture with Y/Al = 0.6. | ||
Using these data, the temperature corresponding to the maximum reaction rate (Tp) for the formation of YAP and YAG was determined for each heating rate. The Arrhenius diagrams obtained are shown in Fig. 7, corresponding to the formation of YAP and YAG. Fig. 7 shows that straight lines are obtained in both cases, in accordance with eqn (12). This indicates that a single mechanism should be predominant for each reaction step. The apparent activation energies were determined to be around 543 ± 30 kJ mol−1 for the formation of the YAP phase and 461 ± 200 kJ mol−1 for the formation of the YAG phase. The error in the activation energy determined by TMA in the case of YAG (Fig. 7b) can be explained either by the low resolution of the formation peak or by the limited number of experiments (only three heating rates were tested). The value obtained for the YAP phase by TMA is very close to that obtained by DSC analysis. Oliver has suggested that the relative error in apparent activation energies was a function of Q/RT. Taking this point into account, the error in calculating the apparent activation energy by TMA should be less than 5%. As a result of this kinetic study, the various apparent activation energy values are reported in Table 1.
Fig. 8 presents TEM and HR-TEM micrographs of YAP–Al2O3 powder mixtures at various fractional reaction values from α = 0 to α = 0.39 during thermal treatment in air at 1473 K. All phases were indexed by elementary chemical analyses, carried out by EDXS. The findings are as follows:
α = 0 (Fig. 8a): YAP (YAlO3) particles appear slightly bigger than Al2O3 particles. Both powders are well crystallized with an isotropic and round shape. This observation also reveals that the mixture is homogeneous at the level of the aggregates of elementary particles, with a diameter of approximately 1 µm. Also, the primary oxide particles show a limited amount of contact between them.
α = 0.23 (Fig. 8b): at this fractional reaction value, the YAG phase is expected to be observed in the primary mixture, as revealed by XRD analyses shown in Fig. 1. Surprisingly, the YAG phase was not observed at the interface between Al2O3 and YAP but instead at the free surface of YAP grains in the form of nanosized grains of about 10 nm in diameter (white arrows in Fig. 8b). These grains are crystallized, as evidenced by the HR-TEM micrograph in Fig. 8d, and correspond to the cubic Ia3d space group of Y3Al5O12. At the same time, one can notice the evolution of the alumina grain surface. The observed example appears to be faceted and accompanied by the creation of crystallographic “steps” (black arrows in Fig. 8e). The amount of observed YAG on the surface of YAP grains is significantly lower than expected based on XRD, suggesting YAG nucleation also occurs within YAP grains.
α = 0.39 (Fig. 8c): the presence of the YAG phase is confirmed and YAG grains of about 150–200 nm in diameter are observed. These grains are in contact with either Al2O3 or YAP primary particles (Fig. 8c). They are still well crystallized, as evidenced by Fig. 8f. Also, the Al2O3 particle surface appears more and more disturbed but still well crystallized (see the Al2O3 grain on the right in Fig. 8f). Such observations are in accordance with a nucleation and growth mechanism for the formation of the YAG phase.
Therefore, the various observations obtained from SEM and TEM allow us to propose original interpretations for the initiation of YAG phase formation from YAP and Al2O3 phases. First, YAG grains appear to be quite far from one reactant source (i.e. Al2O3 grains), which contradicts a simple solid-state reaction mechanism at grain interfaces. Moreover, YAG clearly nucleates in contact with YAP in the form of nanosized nuclei homogeneously distributed on the surface of YAP grains; these nuclei then grow via coalescence to form bigger and bigger grains. Based on these observations, several models can be proposed, which have been developed to simulate the evolution of the advancement rate as a function of time. These include the KJMA (for Kolmogorov, Johnson, Mehl, and Avrami) nucleation-growth model, often referred to as the Avrami model. Such a nucleation-growth model was initially developed for solid-phase transformations37–41 and is based on the random appearance of nuclei in the reactant bulk followed by their recovery during isotropic growth. One assumption of this model is that the reactant volume is considered to be infinite, i.e. nucleation is not influenced by the border of this volume. In the present case, we have demonstrated that YAG nuclei appear at the surface of YAP grains but not at the interface between both reactants. This means that nucleation is not affected by this interface. Once these nuclei have appeared, they grow due to their overlap. Avrami's model incorporates the effects of site saturation and the overlap of expanding nuclei through the use of “ghost nuclei”. These ghost nuclei are germs that would have appeared at certain points if the growth of other nuclei had not covered the volume where they should be born. Markov et al.42 have shown that in the case of crystallization, such an approach can be applied to both the 2D and 3D growth of crystals by considering overlapping areas or volumes, respectively, to calculate the rate of crystallization. Berthier et al. have also demonstrated that Avrami's approach allows the expression of the time evolution of coverage during Ag atom electrodeposition on a copper surface,43 for example. Thus, the assumptions of the Avrami model appear to be applicable. The Avrami model is based on the following eqn (13):44
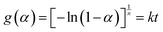 | (13) |
According to this study, an apparent activation energy of 660 kJ mol−1 was determined for the formation of YAG by using the Kissinger approach applied to DSC measurements. This apparent activation energy is of the same order of magnitude as the energies involved in rare-earth diffusion in YAG.48,49 The apparent activation energies for aluminum and oxygen diffusion are too low compared with those measured.50 These results seem to indicate that the YAG formation reaction is controlled by a growth nucleation mechanism in which yttrium is the limiting diffusing species.
Conclusions
In this study, the reaction kinetics and mechanisms of Al2O3–Y2O3 powder mixing were investigated by structural, thermal and microscopic characterization. The Kissinger method was applied successfully to the DSC results and adapted for TMA. It enables the determination of the apparent activation energies of YAP and YAG phase formation, which are approximately 560 kJ mol−1 and 660 kJ mol−1, respectively. The reaction kinetics under isothermal conditions agree very well with a KJMA nucleation-growth model with an exponent n = 0.79. This reaction mechanism can be explained based on the rapid surface diffusion of aluminum species, leading to the formation of crystallized YAG nuclei close to the Y source (i.e. YAP grains), and the formation of YAG grains should be controlled by Y3+ solid-state diffusion.Author contributions
Conceptualization: R. B. and A. M.; methodology: F. D., R. B. and A. M.; validation: L. F., R. B. and A. M.; formal analysis: F. D., N. K. and L. F.; investigation: F. D., N. K. and L. B.; data curation: F. D., N. K. and L. B.; writing – original draft preparation: F. D., N. K.: writing – review and editing, N. K., F. D., L. B., R. B., L. F. and A. M.: supervision, R. B. and A. M.; project administration: R. B.; funding acquisition: R. B. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03930d.Acknowledgements
This study was carried out with financial support from the Region Nouvelle-Aquitaine (HICEMIR program no 2020-RNA20435) and was also supported by an institutional grant from the National Research Agency under the Investments for the Future program with the reference ANR-10-LABX-0074-01 Sigma-LIM.Notes and references
- A. Ikesue and Y. L. Aung, Ceramic laser materials, Nat. Photonics, 2008, 2, 721–727, DOI:10.1038/nphoton.2008.243.
- I. Matsubara, M. Paranthaman, S. W. Allison, M. R. Cates, D. L. Beshears and D. E. Holcomb, Preparation of Cr-doped Y3Al5O12 phosphors by heterogeneous precipitation methods and their luminescent properties, Mater. Res. Bull., 2000, 35, 217–224 CrossRef CAS.
- K. M. Kinsman, J. McKittrick, E. Sluzky and K. Hesse, Phase Development and Luminescence in Chromium-Doped Yttrium Aluminum Garnet (YAG:Cr) Phosphors, J. Am. Ceram. Soc., 1994, 77, 2866–2872, DOI:10.1111/j.1151-2916.1994.tb04516.x.
- J. S. Cho, K. Y. Jung and Y. C. Kang, Two-step spray-drying synthesis of dense and highly luminescent YAG:Ce3+ phosphor powders with spherical shape, RSC Adv., 2015, 5, 8345–8350, 10.1039/C4RA14302G.
- N. Wei, T. Lu, F. Li, W. Zhang, B. Ma, Z. Lu and J. Qi, Transparent Ce:Y3Al5O12 ceramic phosphors for white light-emitting diodes, Appl. Phys. Lett., 2012, 101, 061902, DOI:10.1063/1.4742896.
- A. Krell, T. Hutzler and J. Klimke, Transmission physics and consequences for materials selection, manufacturing, and applications, J. Eur. Ceram. Soc., 2009, 29, 207–221, DOI:10.1016/j.jeurceramsoc.2008.03.025.
- S. A. Kumar and J. Senthilselvan, Co-precipitation Synthesis and Spectroscopic Studies of YAG and Yb:YAG Nanopowder for Opto-Electronic Applications, Trans. Indian Inst. Met., 2015, 68, 153–159, DOI:10.1007/s12666-015-0539-3.
- X. Y. Zou, H. B. Zhang and C. H. Su, Synthesis of Nd:YAG Powders by the Co-Precipitation Method, Adv. Mater. Res., 2011, 239–242, 3306–3309, DOI:10.4028/www.scientific.net/AMR.239-242.3306.
- J.-G. Li, T. Ikegami, J.-H. Lee, T. Mori and Y. Yajima, Co-precipitation synthesis and sintering of yttrium aluminum garnet (YAG) powders: the effect of precipitant, J. Eur. Ceram. Soc., 2000, 20, 2395–2405, DOI:10.1016/S0955-2219(00)00116-3.
- A. Ikesue, I. Furusato and K. Kamata, Fabrication of polycrystalline, transparent YAG ceramics by a solid-state reaction method, J. Am. Ceram. Soc., 1995, 78, 225–228 CrossRef CAS.
- J. Carreaud, R. Boulesteix, A. Maître, Y. Rabinovitch, A. Brenier, A. Labruyère and V. Couderc, From elaboration to laser properties of transparent polycrystalline Nd-doped Y3Al5O12 and Y3ScAl4O12 ceramics: A comparative study, Opt. Mater., 2013, 35, 704–711, DOI:10.1016/j.optmat.2012.07.021.
- S.-H. Lee, S. Kochawattana, G. L. Messing, J. Q. Dumm, G. Quarles and V. Castillo, Solid-State Reactive Sintering of Transparent Polycrystalline Nd:YAG Ceramics, J. Am. Ceram. Soc., 2006, 89, 1945–1950, DOI:10.1111/j.1551-2916.2006.01051.x.
- O. Fabrichnaya, H.-J. Seifert, T. Ludwig, F. Aldinger and A. Navrotsky, The assessment of thermodynamic parameters in the Al2O3–Y2O3 system and phase relations in the Y-Al-O system, Scand. J. Metall., 2001, 30, 175–183, DOI:10.1034/j.1600-0692.2001.300308.x.
- H. Mao, M. Selleby and O. Fabrichnaya, Thermodynamic reassessment of the Y2O3–Al2O3–SiO2 system and its subsystems, Calphad, 2008, 32, 399–412, DOI:10.1016/j.calphad.2008.03.003.
- S.-H. Lee, S. Kochawattana, G. L. Messing, J. Q. Dumm, G. Quarles and V. Castillo, Solid-State Reactive Sintering of Transparent Polycrystalline Nd:YAG Ceramics, J. Am. Ceram. Soc., 2006, 89, 1945–1950, DOI:10.1111/j.1551-2916.2006.01051.x.
- C. Sallé, A. Maître, J.-F. Baumard and Y. Rabinovitch, A First Approach of Silica Effect on the Sintering of Nd:YAG, Opt. Rev., 2007, 14, 169–172, DOI:10.1007/s10043-007-0169-z.
- A. Ikesue, K. Yoshida, T. Yamamoto and I. Yamaga, Optical Scattering Centers in Polycrystalline Nd:YAG Laser, J. Am. Ceram. Soc., 1997, 80, 1517–1522, DOI:10.1111/j.1151-2916.1997.tb03011.x.
- X. Y. Chen, L. Yang, R. E. Cook, S. Skanthakumar, D. Shi and G. K. Liu, Crystallization, phase transition and optical properties of the rare-earth-doped nanophosphors synthesized by chemical deposition, Nanotechnology, 2003, 14, 670, DOI:10.1088/0957-4484/14/6/320.
- J. Carreaud, R. Boulesteix, A. Maître, Y. Rabinovitch, A. Brenier, A. Labruyère and V. Couderc, From elaboration to laser properties of transparent polycrystalline Nd-doped Y3Al5O12 and Y3ScAl4O12 ceramics: a comparative study, Opt. Mater., 2013, 35, 704–711, DOI:10.1016/j.optmat.2012.07.021.
- L. B. Kong, Y. Z. Huang, W. X. Que, T. S. Zhang, S. Li, J. Zhang, Z. L. Dong and D. Y. Tang, Transparent Ceramics, Springer, 2015 Search PubMed.
- A. Maître, C. Sallé, R. Boulesteix, J.-F. Baumard and Y. Rabinovitch, Effect of silica on the reactive sintering of polycrystalline Nd:YAG ceramics, J. Am. Ceram. Soc., 2008, 91, 406–413 CrossRef.
- R. Boulesteix, A. Maître, J.-F. Baumard, C. Sallé and Y. Rabinovitch, Mechanism of the liquid-phase sintering for Nd:YAG ceramics, Opt. Mater., 2009, 31, 711–715 CrossRef CAS.
- L. Bonnet, R. Boulesteix, A. Maître, R. Belon, L. Chrétien and C. Sallé, Influence of (Nd + Y)/Al ratio on sintering behavior and optical features of Y3-xNdxAl5O12 ceramics for laser applications, Opt. Mater., 2018, 77, 264–272, DOI:10.1016/j.optmat.2018.01.028.
- C. Korte and B. Franz, Reaction kinetics in the system Y2O3/Al2O3 – A solid state reaction forming multiple product phases investigated by using thin film techniques, Solid State Ionics, 2021, 368, 115699, DOI:10.1016/j.ssi.2021.115699.
- C. Korte and B. Franz, Reaction kinetics in the system Y2O3/Al2O3 – Use of an external electric field to control the product phase formation in a system forming multiple product phases, Solid State Ionics, 2022, 383, 115978, DOI:10.1016/j.ssi.2022.115978.
- E. R. Kupp, S. Kochawattana, S.-H. Lee, S. Misture and G. L. Messing, Particle size effects on yttrium aluminum garnet (YAG) phase formation by solid-state reaction, J. Mater. Res., 2014, 29, 2303–2311, DOI:10.1557/jmr.2014.224.
- J. Dabulytė-Bagdonavičienė, A. Nečiporenko, F. Ivanauskas and A. Kareiva, Influence of different diffusion rates of reaction reagents on the synthesis of yttrium aluminium garnet (YAG), J. Math. Chem., 2022, 60, 172–183, DOI:10.1007/s10910-021-01303-w.
- V. Tinkova, J. Kajan, G. Damazyan, A. Prnová, M. Michálková, P. Švančárek, T. Gregor, B. Hruška and D. Galusek, Preparation of monophasic YAG raw material by multi-stage process, Discover Appl. Sci., 2024, 6, 73, DOI:10.1007/s42452-024-05718-3.
- H. E. Kissinger, Reaction Kinetics in Differential Thermal Analysis, Anal. Chem., 1957, 29, 1702–1706, DOI:10.1021/ac60131a045.
- H. E. Kissinger, Variation of peak temperature with heating rate in differential thermal analysis, J. Res. Natl. Bur. Stand., 1956, 57, 217, DOI:10.6028/jres.057.026.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- H. Tan, X. Ma, C. Wang and K. Li, Kinetics of grain-growth of yttrium aluminum garnet fibers prepared by sol-gel method, Ceram.-Silik., 2013, 57, 285–289 CAS.
- M. N. Rahaman, Sintering of Ceramics, CRC Press Inc, 2007 Search PubMed.
- K. Hirota and W. Komatsu, Concurrent Measurement of Volume, Grain-Boundary, and Surface Diffusion Coefficients in the System NiO-Al2O3, J. Am. Ceram. Soc., 1977, 60, 105–107, DOI:10.1111/j.1151-2916.1977.tb15481.x.
- Y. Moriyoshi and W. Komatsu, Surface diffusion in the initial sintering of alumina, J. Ceram. Assoc. Jpn., 1976, 84, 348–349, DOI:10.2109/jcersj1950.84.971_348.
- C. Oliver and C. A. Schuh, Kissinger-Style Kinetic Analysis for Sintering Dilatometry Data, Metall. Mater. Trans. A, 2021, 52, 4479–4487, DOI:10.1007/s11661-021-06399-y.
- M. Avrami, Kinetics of Phase Change. I General Theory, J. Chem. Phys., 1939, 7, 1103–1112, DOI:10.1063/1.1750380.
- M. Avrami, Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei, J. Chem. Phys., 1940, 8, 212–224, DOI:10.1063/1.1750631.
- W. A. Johnson and R. F. Mehl, Reaction Kinetics in Processes of Nucleation and Growth, Transactions of the American Institute of Mining and Metallurgical Engineers, 1939, vol. 135, pp. 416–442. – References – Scientific Research Publishing, (n.d.). https://www.scirp.org/reference/referencespapers?referenceid=598556 (accessed September 22, 2025) Search PubMed.
- A. N. Kolmogorov, On the Statistical Theory of the Crystallization of Metals, Bulletin of the Academy of Sciences of the USSR, Mathematics Series, 1937, vol. 1, pp. 355–359. – References – Scientific Research Publishing, (n.d.). https://www.scirp.org/reference/referencespapers?referenceid=880675 (accessed September 22, 2025) Search PubMed.
- M. Avrami, Granulation, Phase Change, and Microstructure Kinetics of Phase Change. III, J. Chem. Phys., 1941, 9, 177–184, DOI:10.1063/1.1750872.
- I. V. Markov, Crystal Growth for Beginners, Fundamentals of Nucleation, Crystal Growth and Epitaxy, 2nd edn, 2003 DOI:10.1142/5172.
- F. Berthier, B. Legrand, J. Creuze and R. Tétot, Atomistic investigation of the Kolmogorov–Johnson–Mehl–Avrami law in electrodeposition process, J. Electroanal. Chem., 2004, 561, 37–52, DOI:10.1016/j.jelechem.2003.07.018.
- T. J. W. De Bruijn, W. A. De Jong and P. J. Van Den Berg, Kinetic parameters in Avrami—Erofeev type reactions from isothermal and non-isothermal experiments, Thermochim. Acta, 1981, 45, 315–325, DOI:10.1016/0040-6031(81)85091-5.
- G. R. Williams, A. I. Khan and D. O’Hare, Mechanistic and Kinetic Studies of Guest Ion Intercalation into LayeredDouble Hydroxides Using Time-resolved, In-situ X-ray Powder Diffraction, in Layer. Double Hydroxides, ed. X. Duan and D. G. Evans, Springer, Berlin, Heidelberg, 2006, pp. 161–192 DOI:10.1007/430_002.
- M. Shamim, S. Sinhamahapatra, J. Hossain, S. Lahiri and K. Dana, Kinetic analysis of magnesium aluminate spinel formation: Effect of MgO:Al2O3 ratio and titania dopant, Ceram. Int., 2018, 44, 1868–1874, DOI:10.1016/j.ceramint.2017.10.124.
- S. Sinhamahapatra, M. Shamim, H. S. Tripathi, A. Ghosh and K. Dana, Kinetic modelling of solid-state magnesium aluminate spinel formation and its validation, Ceram. Int., 2016, 42, 9204–9213, DOI:10.1016/j.ceramint.2016.03.017.
- D. J. Cherniak, Rare earth element and gallium diffusion in yttrium aluminum garnet, Phys. Chem. Miner., 1998, 26, 156–163, DOI:10.1007/s002690050172.
- J. P. Hollingsworth, J. D. Kuntz and T. F. Soules, Nd3+ ion diffusion during sintering of Nd:YAG transparent ceramics, J. Phys. Appl. Phys., 2009, 42, 052001 CrossRef.
- C. Jun, C. Dong-Quan and Z. Jing-Lin, Molecular dynamics simulation of thermodynamic properties of YAG, Chin. Phys., 2007, 16, 2779–2785, DOI:10.1088/1009-1963/16/9/047.
| This journal is © the Owner Societies 2026 |




