Strain-selected magnetic ordering in 1T′α-CrXY (X, Y = S, Se, Te) monolayers
Deju
Zhang
 ab and
Yanning
Zhang
ab and
Yanning
Zhang
 *ab
*ab
aInstitute of Fundamental and Frontier Sciences, University of Electronic Science and Technology of China, Chengdu 611731, People's Republic of China. E-mail: yanningz@uestc.edu.cn
bKey Laboratory of Quantum Physics and Photonic Quantum Information (University of Electronic Science and Technology of China), Ministry of Education, Chengdu 611731, People's Republic of China
First published on 11th December 2025
Abstract
Two-dimensional magnetic materials have garnered considerable attention in recent years owing to their interesting phenomena and potential applications in spintronic devices. In this work, we report that the 1T′α-CrTeSe monolayer, where tellurium atoms are intermittently arranged line by line within the layer, exhibits strain-tuned magnetic properties. We find that the anisotropic nearest-neighbor exchange interactions in this monolayer result in a chiral helimagnetic state. The in-plane biaxial tensile strain suppresses the antiferromagnetic direct exchange interaction and leads to a transition from helimagnetism to ferromagnetism. Its transition temperature is estimated to be about 66 K and can also be tuned to near room temperature by applying strain. Furthermore, we also demonstrate the structural stabilities and strain-tuned magnetic ordering in the CrSeS monolayer. Our study provides not only an ideal platform to explore exotic compounds but also an important opportunity to design controllable magnetic materials in low-dimensional systems.
I. Introduction
The discoveries of ferromagnetism in the CrI3 monolayer1 and the Cr2Ge2Te6 bilayer2 have spurred a surge of interest in the theoretical design and experimental preparation of two-dimensional (2D) intrinsic magnetic materials. These materials provide an ideal platform to reveal long-range magnetic ordering in 2D materials and to develop the corresponding applications in next-generation spintronic devices. From the perspective of theoretical design, a large number of 2D magnetic materials have been predicted to be stable and potentially achievable, such as transition-metal dihalides,3–6 trihalides,7,8 and dichalcogenides.9–13 Transition-metal dihalide monolayers have garnered considerable attention in terms of their excellent stabilities and exfoliation,3 such as chromium dichalcogenides.9,10 Based on these materials, more and more novel structural and physical properties have been revealed by elemental substitution,14–19 strain engineering20,21 and so forth.Element-substituted 2D materials provide an important opportunity to explore interesting polarization22,23 and intrinsic ferromagnetism with high transition temperature.19,24 However, there are still some issues that require further investigation. For example, many element-substituted 2D materials with a Janus pattern were studied, while the corresponding experimental characterization efforts are lacking.25 This indicates that some patterns with lower or degenerate energies have not been revealed yet. Furthermore, the phenomenon of non-collinear magnetic ordering arising from geometric frustration is a topic of significant interest.26–28 Therefore, it is essential to investigate more element-substituted patterns with positive stabilities that may guide experimental synthesis. Moreover, it is necessary and interesting to establish the correlation between their structural and magnetic coupling so as to enhance their performance for promising device applications.
In this paper, based on first-principles calculations and Monte Carlo (MC) simulations, we confirm the structural stabilities and reveal the switchable magnetic coupling of the 1T′α-CrTeSe monolayer. Due to the competition between different intrinsic exchange interactions, the nearest-neighbor ferromagnetic (FM) coupling can be enhanced by applying in-plane biaxial tensile strain, resulting in a chiral helimagnetic (CHM)-to-FM transition. Its transition temperature can also be modified to approach room temperature under biaxial strain. Also, these significant modifications can also be achieved in the CrSeS monolayer. These results offer a promising platform for understanding the tunable magnetic coupling and present an opportunity for manipulating their magnetic ordering in low-dimensional materials.
II. Methods
All first-principles calculations are carried out within the framework of density functional theory as implemented in the Vienna ab initio simulation package.29,30 The exchange–correlation potential is described by using the Perdew–Burke–Ernzerhof functional within the generalized gradient approximation,31 in which the projector-augmented-wave method is adopted, with an energy cutoff of 600 eV.32,33 The effective U values are tested and the value of U = 3.0 eV is adopted to consider the strong correlation effect among Cr-3d electrons, which is reasonable to describe the critical magnetic properties,14,34 as shown in Fig. S1 of the SI. The c-axis-fixed structural optimization is performed until the energy convergence criterion of 1 × 10−6 eV is met and the force on each atom is less than 1 × 10−3 eV Å−1. The electronic configurations 3d54s1, 2s22p4, 3s23p4, 4s24p4, and 5s25p4 are considered as the valence states of chromium, oxygen, sulfur, selenium, and tellurium atoms, respectively. A vacuum region larger than 15 Å is added so that the interactions between the monolayer and its periodic image can be neglected. A k-point mesh of 5 × 9 × 1 is used for structural relaxation, and a 7 × 11 × 1 mesh is used for the calculation of magnetocrystalline anisotropy energy (MAE) and electronic structure. A 2 × 2 × 1 supercell with a 3 × 5 × 1 k-point mesh is used to calculate the exchange coupling parameters. The phonon spectra are calculated by using the finite displacement method as implemented in the PHONOPY code.35,36 A 3 × 3 × 1 supercell and Γ-point are considered in the ab initio molecular dynamics (AIMD) simulations at 300 K up to 8 ps, in which the NVT ensemble with a Nosé–Hoover thermostat37 is used. A 40 × 50 × 1 supercell including 4000 magnetic atoms is used in MC simulations.III. Results and discussion
III.A. Structural stabilities
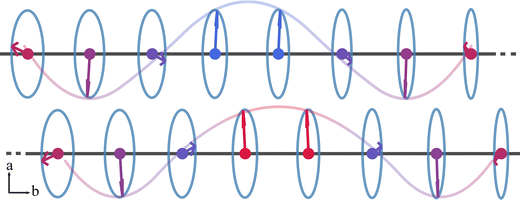
Half-element-substituted trigonal transition metal dihalide monolayers have three common crystal structures, namely the 1T′α, 1T′β,25,38 and Janus patterns.15,18 We have recently reported that the 1T′α pattern is the most energetically favored state of the half-halogen-substituted trigonal CrS2 monolayer, in which both additional electrons and external strains are induced.39 Here, we consider the effects of chalcogen substitution on the structural and magnetic properties in this pattern. Structurally, the selenium and tellurium atoms are alternately arranged in the plane line by line and form the 1T′α-CrTeSe monolayer with the P21/m space group, as shown in Fig. 1(a). The calculated lattice parameters, nearest Cr–Cr distances, and Wyckoff sites of the CrTeSe monolayer are listed in Table S1 of the SI. The optimized lattice parameters are a = 6.642 and b = 3.352 Å, and the nearest Cr–Cr distances are d1 = 3.979, d2 = 3.352, and d3 = 3.470 Å, respectively. The Cr–Se–Cr path is 14.7% shorter than the Cr–Te–Cr path as a result of the smaller ionic radius of selenium, indicating a non-negligible local deformation induced by elemental substitution.To confirm the dynamical and thermal stabilities, we calculate the phonon spectrum and carry out the AIMD simulations of the 1T′α-CrTeSe monolayer at 300 K up to 8 ps. The lattice dynamics calculations have demonstrated its dynamical stability, as evidenced by the absence of imaginary frequencies throughout the Brillouin zone (see Fig. S2 in the SI). Moreover, the CrTeSe monolayer maintains its structure up to 8 ps during the AIMD simulation, which confirms its thermal stability (see Fig. S3 in the SI). In order to examine its potential for experimental synthesis, we also calculate the formation energy of the monolayer by using the following formula:
| Ef = (ECrTeSe − ECr − ETe − ESe)/3 | (1) |
III.B. Magnetic ground state
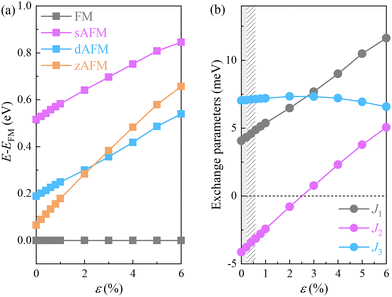
To calculate the magnetic exchange parameters and reveal the magnetic ground states of the 1T′α-CrTeSe monolayer, we consider a 2 × 2 × 1 supercell with four magnetic configurations, namely, FM, striped antiferromagnetic (sAFM), doubly striped antiferromagnetic (dAFM), and zigzag antiferromagnetic (zAFM), as shown in Fig. 1(b), in which the blue and yellow arrows represent the directions of magnetic moments on chromium atoms. We determine the exchange parameters based on the Heisenberg model as follows: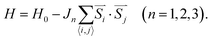 | (2) |
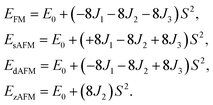 | (3) |
The energies of these four magnetic configurations are listed in Table S2 of the SI, and we derive the parameters as J1 = 4.065, J2 = −8.95, and J3 = 7.035 meV. Direct exchange interactions between cations are highly distance-dependent, as reflected in the Bethe–Slater interaction curve.40–42 In this monolayer, atomic distances of 3.35–3.98 Å indicate AFM direct exchange interactions along these paths, consistent with previous reports.13 They act in competition with the ferromagnetic interactions such as superexchange and Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions. For the Cr–Se/Te–Cr path, the AFM direct exchange interactions are the dominant interactions and cause a negative J2 value.
We consider the spin–orbit coupling and calculate the MAEs of the 1T′α-CrTeSe monolayer with the spin moments parallelly oriented along different directions. The magnetic-easy axis of the CrTeSe monolayer lies in the xz plane with a rotational angle of 60° with respect to the z axis, as shown in Fig. S5 of the SI. This can be attributed to the competition between the in-plane contribution from selenium and the out-of-plane contribution from tellurium (see Fig. S6 in the SI), which is in line with the previous studies.43,44 The MAEs along the x′, y′, and z′ directions are listed in Table S3 of the SI, in which x′ is the magnetic-easy axis, y′ and z′ are rotated y and z axes with the same rotation as the x to x′ axis, respectively. Based on the calculated magnetic exchange parameters and MAEs, we then solve the following Heisenberg model by means of MC simulations to reveal the magnetic ground state of the 1T′α-CrTeSe monolayer:
 | (4) |
Fig. 2(a) depicts the magnetic ground state of the 1T′α-CrTeSe monolayer. When both J1 and J3 are positive, the negative J2 gives rise to a non-collinear magnetic ground state. For each chromium line along the y direction, magnetic moments rotate in the xz-plane with a step size of π/2. Due to the strong AFM coupling of Cr–Se/Te–Cr paths, magnetic moments invert their rotation direction and continue rotating with a step size of −π/2, leading to a CHM state. In the x direction, two chromium lines with a phase difference of about π/6 form a translation period.
The spin-resolved band structure of the 1T′α-CrTeSe monolayer reveals its metallicity, as evidenced by several bands crossing the Fermi level around the Γ and Y points (see Fig. S7 in the SI). Given its metallic properties, we evaluate the potential impact of long-range exchange interactions on the magnetic ground state, where these interactions are primarily mediated by the RKKY mechanism. We incorporate an additional parameter, Jlr_eff, into our spin Hamiltonian to describe the net effect of long-range exchange interactions, as illustrated in Fig. S8 of the SI. Here we scan Jlr_eff across a wide range from −1.0 to 1.0 meV. Our analysis demonstrates that the stability of the ground state is maintained for effective long-range coupling strengths up to |Jlr_eff| ≤ 0.4 meV.
III.C. Biaxial strain
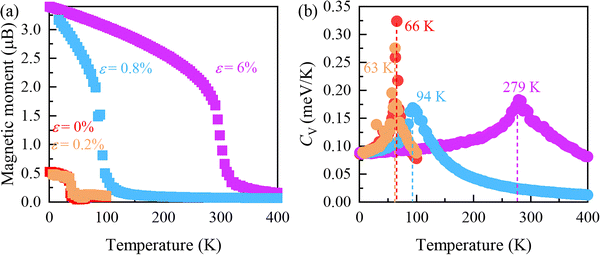
The nearest exchange interactions in the 1T′α-CrTeSe monolayer depend mainly on the atomic distances, which is sensitive to biaxial strain. Thus, it is interesting to explore the effects of in-plane biaxial tensile strain on the modification of the magnetic coupling in the CrTeSe monolayer. Biaxial strain is defined as ε = (l − l0)/l0 × 100%, in which l (l0) is the lattice parameters under an applied (free from) strain. As shown in Fig. 3, within the considered tensile strain range, the energies of the FM and sAFM states are always lowest and highest, respectively. The energy of the dAFM state is sandwiched between those of the zAFM and sAFM states at strains smaller than 3% and becomes lower than that of the zAFM state at strains larger than 3%. Meanwhile, J3 slightly increases up to a strain of 2% and then decreases slightly, while J1 and J2 monotonically increase over the entire strain range considered, in which J2 undergoes a transition from negative to positive at a strain of 3%. The strain induced increase of atomic distance suppresses the AFM direct exchange interaction more than the FM interaction and triggers a monotonical increase of J2. To confirm the magnetic ground state of the CrTeSe monolayer under strain, we calculate its MAEs and the values are shown in Table S4 of the SI. Further MC simulations demonstrate that, at strains below 0.8%, the system resides in a transitional magnetic state characterized by a non-collinear configuration, where all the moments are not fully parallel but maintain a net magnetization along the z-direction. At strains exceeding 0.8%, the moments become fully parallel, indicating the FM state. In particular, although J2 remains negative when the strain is larger than 0.8% and smaller than 3%, its absolute values are clearly decreased and thus lead to FM states.Based on the calculated magnetic phase transition and magnetic exchange parameters and MAEs, we carry out MC simulations to estimate the magnetic transition temperature of the 1T′α-CrTeSe monolayer under strain. Here, we consider the strain-free case and typical strains of 0.2%, 0.8% and 6% as examples. As shown in Fig. 4, owing to the tensile strain enhanced magnetic coupling strength, the magnetic transition temperatures for the strain-free case and strains of 0.2%, 0.8%, and 6% are estimated to be about 66, 63, 94, and 279 K, respectively. To demonstrate that the supercells in MC simulations are enough for correct calculations of the transition temperatures, we test several supercells as shown in Fig. S9 of the SI. It is clear that the 40 × 50 supercell is enough for these simulations. We also use the MAEs along the x, y, and z directions that maintain the transition temperature, as shown in Fig. S9 of the SI. The TC of the CrTeSe monolayer is higher than that of the CrI3 monolayer (45 K)1 and the Cr2Ge2Te6 bilayer (28 K),2 which indicates its possibilities for further applications.
The small strains in the 1T′α-CrTeSe monolayer notably reduce the energy consumption and mechanical complexity required for potential strain-controlled devices. In experiments, strain can be applied to monolayers using various methods, such as lattice mismatch between substrates and epitaxial thin films.45 Based on this method, flexible graphene-based transistors with a large range of strains have been successfully achieved,46–49 indicating the potential spintronic applications of the CrTeSe monolayer.
III.D. CrSO and CrSeS monolayers
To systematically explore the structural and magnetic properties of chalcogen-substitution 1T′α patterns, we further consider the structural stabilities of CrSO and CrSeS monolayers. We calculate the phonon spectra and find that the CrSO monolayer exhibits obvious imaginary frequency, while the CrSeS monolayer is dynamically stable (see Fig. S10 in the SI). We also carry out the AIMD simulation and confirm the thermal stability of the CrSeS monolayer (see Fig. S11 in the SI). The formation energy of −0.496 eV per atom indicates its possibilities of experimental synthesis. By comparing the energies of the four magnetic configurations of the CrSeS monolayer, we derive its exchange parameters as J1 = 5.94, J2 = −4.14, and J3 = 4.00 meV. Meanwhile, we calculate the MAEs and the obtained values of Ey and Ez are 1348 and 161 µeV, respectively. MC simulations suggest that these comparable exchange parameters lead to a 120°-AFM ground state in the CrSeS monolayer.In order to understand the effect of biaxial strain on the magnetic properties of the 1T′α-CrSeS monolayer, we calculate its exchange parameters and MAEs under a biaxial strain (ε) of 6%. Under biaxial strain, its exchange parameters are increased to J1 = 10.23, J2 = 6.28, and J3 = 10.30 meV, and the values of Ey and Ez are changed to 2026 and 588 µeV, respectively. All positive exchange parameters indicate the FM ground state of the tensile CrSeS monolayer. By solving the Heisenberg model, we calculate the transition temperatures of strain-free and tensile CrSeS monolayers and the values are shown in Fig. S12 of the SI. The transition temperature of the strain-free monolayer is estimated to be about 45 K, while that of the tensile monolayer increases above room temperature and reached 315 K. The tensile strain induced change in the magnetic properties of this monolayer confirms the Cr–Cr distance-dominated modification of magnetic coupling in the CrTeSe monolayer and provides another switchable 2D magnetic material.
IV. Conclusions
In conclusion, we performed systematic first-principles investigations on the half-element-substituted CrTeSe monolayer with a line-by-line 1T′α pattern. In this case, the 1T′α and Janus structures have almost degenerate energies and both their formation energies are negative, in which the 1T′α structure is also dynamically and thermally stable. Under in-plane tensile biaxial strain, the antiferromagnetic nearest-neighbor coupling can be tuned to ferromagnetic coupling, resulting in a transition from chiral helimagnetism to ferromagnetism. The strain-tuned magnetic properties of the CrTeSe monolayer are attributed to the competition between different intrinsic exchange interactions, in which the competition depends mainly on the nearest Cr–Cr distances. By applying strain, the transition temperature of this monolayer can be tuned to approach room temperature. Furthermore, based on the same mechanism, the transition from the AFM to the FM coupling can be achieved in the CrSeS monolayer. Our calculations unveiled that the intermittently element-substituted 1T′α monolayers have interesting nearest-neighbor exchange interactions with remarkable controllability, making them promising candidates for use in next-generation low-dimensional spintronic applications.Conflicts of interest
There are no conflicts to declare.Data availability
All data generated or analyzed during this study are included in this article and its supplementary information (SI). See supplementary information for the tests of computational parameters, analyses of MAEs and structural stabilities and long-range exchange interactions, calculated energies of different configurations and band structure for the 1T′α-CrTeSe monolayer, and the discussions of structural stabilities and transition temperatures for the CrSO and CrSeS monolayers. See DOI: https://doi.org/10.1039/d5cp03532e.References
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270, DOI:10.1038/nature22391.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Intrinsic long-range ferromagnetic order is observed in few-layer Cr2Ge2Te6 crystals, with a transition temperature that can be controlled using small magnetic fields, Nature, 2017, 546, 265, DOI:10.1038/nature22060.
- V. V. Kulish and W. Huang, Single-layer metal halides MX2 (X = Cl, Br, I): stability and tunable magnetism from first principles and Monte Carlo simulations, J. Mater. Chem. C, 2017, 5, 8734, 10.1039/C7TC02664A.
- A. S. Botana and M. R. Norman, Electronic structure and magnetism of transition metal dihalides: Bulk to monolayer, Phys. Rev. Mater., 2019, 3, 044001, DOI:10.1103/PhysRevMaterials.3.044001.
- X. Bo, L. Fu, X. Wan, S. Li and Y. Pu, Magnetic structure and exchange interactions of transition metal dihalide monolayers: First-principles studies, Phys. Rev. B, 2024, 109, 014405, DOI:10.1103/PhysRevB.109.014405.
- Y. Zhao, H. Liu, J. Gao and J. Zhao, Transition of CrI2 from a two-dimensional network to one-dimensional chain at the monolayer limit, Phys. Chem. Chem. Phys., 2021, 23, 25291, 10.1039/D1CP03789G.
- S. Tomar, B. Ghosh, S. Mardanya, P. Rastogi, B. S. Bhadoria, Y. S. Chauhan, A. Agarwal and S. Bhowmick, Intrinsic magnetism in monolayer transition metal trihalides: A comparative study, J. Magn. Magn. Mater., 2019, 489, 165384, DOI:10.1016/j.jmmm.2019.165384.
- L. Webster and J.-A. Yan, Strain-tunable magnetic anisotropy in monolayer CrCl3, CrBr3, and CrI3, Phys. Rev. B, 2018, 98, 144411, DOI:10.1103/PhysRevB.98.144411.
- C. Wang, X. Zhou, Y. Pan, J. Qiao, X. Kong, C.-C. Kaun and W. Ji, Layer and doping tunable ferromagnetic order in two-dimensional CrS2 layers, Phys. Rev. B, 2018, 97, 245409, DOI:10.1103/PhysRevB.97.245409.
- L. Wu, L. Zhou, X. Zhou, C. Wang and W. Ji, In-plane epitaxy-strain-tuning intralayer and interlayer magnetic coupling in CrSe2 and CrTe2 monolayers and bilayers, Phys. Rev. B, 2022, 106, L081401, DOI:10.1103/PhysRevB.106.L081401.
- Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X = S, Se) and Their Strain-Induced Tunable Magnetic Properties, ACS Nano, 2012, 6, 1695, DOI:10.1021/nn204667z.
- M. Kan, S. Adhikarib and Q. Sun, Ferromagnetism in MnX2 (X = S, Se) monolayers, Phys. Chem. Chem. Phys., 2014, 16, 4990, 10.1039/C3CP55146F.
- H. Y. Lv, W. J. Lu, D. F. Shao, Y. Liu and Y. P. Sun, Strain-controlled switch between ferromagnetism and antiferromagnetism in 1T-CrX2(X = Se, Te) monolayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214419, DOI:10.1103/PhysRevB.92.214419.
- Y. Wu, Q. Liu, P. Shi, J. Su, Y. Zhang and B. Wang, High temperature ferromagnetic metal: a Janus CrSSe monolayer, Phys. Chem. Chem. Phys., 2023, 25, 9958, 10.1039/D3CP00537B.
- R. Jiao, Q. Wei, L. Zhang, Y. Xie, J. He, Y. Zhou, L. Shen and J. Yuan, Enhancement and modulation of valley polarization in Janus CrSSe with internal and external electric fields, Phys. Chem. Chem. Phys., 2024, 26, 13087, 10.1039/D3CP05298B.
- S. Chen, Z. Zeng, B. Lv, S. Guo, X. Chen and H. Geng, Large tunable Rashba spin splitting and piezoelectric response in Janus chromium dichalcogenide monolayers, Phys. Rev. B, 2022, 106, 115307, DOI:10.1103/PhysRevB.106.115307.
- Q. Alam, S. Sardar, H. U. Din, S. A. Khan, M. Idrees, B. Amin, F. Rehman, S. Muhammad and A. Laref, A first principles study of a van der Waals heterostructure based on MS2 (M = Mo, W) and Janus CrSSe monolayers, Nanoscale Adv., 2024, 4, 3557, 10.1039/D2NA00298A.
- Y. Hou, F. Xue, L. Qiu, Z. Wang and R. Wu, Multifunctional two-dimensional van der Waals Janus magnet Cr-based dichalcogenide halides, npj Comput. Mater., 2022, 8, 120, DOI:10.1038/s41524-022-00802-x.
- S.-D. Guo, X.-S. Guo, Y.-T. Zhu and Y.-S. Ang, Predicted ferromagnetic monolayer CrSCl with large vertical piezoelectric response: A first-principles study, Appl. Phys. Lett., 2022, 121, 062403, DOI:10.1063/5.0109033.
- B. Li, Z. Wan, C. Wang, P. Chen, B. Huang, X. Cheng, Q. Qian, J. Li, Z. Zhang, G. Sun, B. Zhao, H. Ma, R. Wu, Z. Wei, Y. Liu, L. Liao, Y. Ye, Y. Huang, X. Xu, X. Duan, W. Ji and X. Duan, van der Waals epitaxial growth of air-stable CrSe2 nanosheets with thickness-tunable magnetic order, Nat. Mater., 2021, 20, 818, DOI:10.1038/s41563-021-00927-2.
- J.-J. Xian, C. Wang, J.-H. Nie, R. Li, M. Han, J. Lin, W.-H. Zhang, Z.-Y. Liu, Z.-M. Zhang, M.-P. Miao, Y. Yi, S. Wu, X. Chen, J. Han, Z. Xia, W. Ji and Y.-S. Fu, Spin mapping of intralayer antiferromagnetism and field-induced spin reorientation in monolayer CrTe2, Nat. Commun., 2022, 13, 257, DOI:10.1038/s41467-021-27834-z.
- P. Jiang, X. Zheng, L. Kang, X. Tao, H.-M. Huang, X. Dong and Y.-L. Li, Mn2P2S3Se3: a two-dimensional Janus room-temperature antiferromagnetic semiconductor with a large out-of-plane piezoelectricity, J. Mater. Chem. C, 2023, 11, 2703, 10.1039/D2TC04799C.
- J. Luo, H. Meng, X.-X. Xue, K.-Q. Chen and L.-M. Tang, Intrinsic ferrovalley non-Janus FeXI (X = Cl,Br) with large valley polarization and nonvolatile reversible control of the anomalous valley Hall effect in multiferroic heterojunctions, Phys. Rev. B, 2024, 110, 085401, DOI:10.1103/PhysRevB.110.085401.
- J. Tian, J. Li, H. Liu, Y. Li and J. Shi, Two-dimensional Janus 1T-CrXY (X = S, Se, Te, Y = F, Cl, Br, I): Multifunctional ferromagnetic semiconductor with large valley and piezoelectric polarizations, Phys. Rev. B, 2024, 109, 125413, DOI:10.1103/PhysRevB.109.125413.
- P. Han, Z. Jingtong, S. Shi, Y. Zhao, Y. Zhang and J. Wang, Machine learning assisted screening of two dimensional chalcogenide ferromagnetic materials with Dzyaloshinskii Moriya interaction, npj Comput. Mater., 2024, 10, 232, DOI:10.1038/s41524-024-01419-y.
- D.-L. Bao, A. O’Hara, S. Du and S. T. Pantelides, Tunable, Ferroelectricity-Inducing, Spin-Spiral Magnetic Ordering in Monolayer FeOCl, Nano Lett., 2022, 22, 3598, DOI:10.1021/acs.nanolett.1c05043.
- Y. Kousaka, T. Ogura, J. Jiang, K. Mizutani, S. Iwasaki, J. Akimitsu and Y. Togawa, An emergence of chiral helimagnetism or ferromagnetism governed by Cr intercalation in a dichalcogenide CrNb3S6, APL Mater., 2022, 10, 090704, DOI:10.1063/5.0101351.
- C. Zhang, J. Zhang, C. Liu, S. Zhang, Y. Yuan, P. Li, Y. Wen, Z. Jiang, B. Zhou, Y. Lei, D. Zheng, C. Song, Z. Hou, W. Mi, U. Schwingenschlögl, A. Manchon, Z. Q. Qiu, H. N. Alshareef, Y. Peng and X.-X. Zhang, Chiral Helimagnetism and One-Dimensional Magnetic Solitons in a Cr-Intercalated Transition Metal Dichalcogenide, Adv. Mater., 2021, 33, 2101131, DOI:10.1002/adma.202101131.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169, DOI:10.1103/PhysRevB.54.11169.
- J. U. Hafner, Materials simulations using VASP—a quantum perspective to materials science, Comput. Phys. Commun., 2007, 177, 6, DOI:10.1016/j.cpc.2007.02.045.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865, DOI:10.1103/PhysRevLett.77.3865.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, First-Principles Determination of the Soft Mode in Cubic ZrO2, Phys. Rev. Lett., 1997, 78, 4063, DOI:10.1103/PhysRevLett.78.4063.
- N. Holzwarth, A. Tackett and G. Matthews, A Projector Augmented Wave (PAW) code for electronic structure calculations, Part I: atompaw for generating atom-centered functions, Comput. Phys. Commun., 2001, 135, 329, DOI:10.1016/S0010-4655(00)00244-7.
- F. Han, X. Yan, A. Bergara, W. Li, H. Yu and G. Yang, A Janus CrSSe monolayer with interesting ferromagnetism, Phys. Chem. Chem. Phys., 2023, 25, 29672, 10.1039/D3CP04584F.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515, DOI:10.1103/RevModPhys.73.515.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106, DOI:10.1103/PhysRevB.78.134106.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695, DOI:10.1103/PhysRevA.31.1695.
- J. Luo, H. Meng, R. Xu, X.-X. Xue and Y. S. Ang, Two-dimensional 1T′α-VXY (X = S, Se, Te; Y = Cl, Br, I): A multifunctional vanadium chalcohalide family with room temperature ferromagnetism and sliding ferroelectricity, Appl. Phys. Lett., 2024, 124, 113101, DOI:10.1063/5.0190261.
- D. Zhang, Z. Yang, T. Wu, W. Ji and Y. Zhang, Switchable magnetic and electronic properties in CrSX (X = Cl, Br, I) monolayers, Phys. Rev, Materials, 2025, 9, 054004, DOI:10.1103/PhysRevMaterials.9.054004.
- K. Azumi and J. E. Goldman, Volume Magnetostriction in Nickel and the Bethe-Slater Interaction Curve, Phys. Rev., 1954, 93, 630, DOI:10.1103/PhysRev.93.630.
- R. Cardias, A. Szilva, A. Bergman, I. D. Marco, M. I. Katsnelson, A. I. Lichtenstein and Y. O. Kvashnin, The Bethe-Slater curve revisited; new insights from electronic structure theory, Sci. Rep., 2017, 7, 4058, DOI:10.1038/s41598-017-04427-9.
- X. Qing, H. Li, C. Zhong, P. Zhou, Z. Dong and J. Liu, Magnetism and spin exchange coupling in strained monolayer CrOCl, Phys. Chem. Chem. Phys., 2020, 22, 17255, 10.1039/D0CP01160F.
- J. Phillips, A. O. Fumega, S. Blanco-Canosa and V. Pardo, An ab initio description of the family of Cr selenides: structure, magnetism and electronic structure from bulk to the single-layer limit, arXiv, preprint, arXiv:2412.14763, 2024 DOI:10.48550/arXiv.2412.14763.
- L. Meng, Z. Zhou, M. Xu, S. Yang, K. Si, L. Liu, X. Wang, H. Jiang, B. Li, P. Qin, P. Zhang, J. Wang, Z. Liu, P. Tang and Y. Gong, Anomalous thickness dependence of Curie temperature in air-stable two-dimensional ferromagnetic 1T-CrTe2 grown by chemical vapor deposition, Nat. Commun., 2021, 12, 809, DOI:10.1038/s41467-021-21072-z.
- G. Gao, S. Jin and W. Wu, Lattice-mismatch-strain induced inhomogeneities in epitaxial films, Appl. Phys. Lett., 2007, 90, 012509, DOI:10.1063/1.2429903.
- B. J. Kim, H. Jang, S.-K. Lee, B. H. Hong, J.-H. Ahn and J. H. Cho, High-Performance Flexible Graphene Field Effect Transistors with Ion Gel Gate Dielectrics, Nano Lett., 2010, 10, 3464, DOI:10.1021/nl101559n.
- S.-K. Lee, B. J. Kim, H. Jang, S. C. Yoon, C. Lee, B. H. Hong, J. A. Rogers, H. Cho and J.-H. Ahn, Stretchable Graphene Transistors with Printed Dielectrics and Gate Electrodes, Nano Lett., 2011, 11, 4642, DOI:10.1021/nl202134z.
- C.-C. Lu, Y.-C. Lin, C.-H. Yeh, J.-C. Huang and P.-W. Chiu, High Mobility Flexible Graphene Field-Effect Transistors with Self-Healing Gate Dielectrics, ACS Nano, 2012, 6, 4469, DOI:10.1021/nn301199j.
- M. Sun, S. Wang, Y. Liang, C. Wang, Y. Zhang, H. Liu, Y. Zhang and L. H. Han, Flexible Graphene Field-Effect Transistors and Their Application in Flexible Biomedical Sensing, Nano-Micro Lett., 2025, 17, 34, DOI:10.1007/s40820-024-01534-x.
| This journal is © the Owner Societies 2026 |