The catalytic role of triphenyl bismuth in curing reactions: a theoretical study

Abstract

Triphenyl bismuth (TPB), a bismuth-based organometallic compound, has been extensively utilized as a curing catalyst. However, the relevant catalytic mechanism is unclear. In this work, we employ density functional theory to elucidate the reaction mechanism of TPB-catalyzed curing reactions with methyl isocyanate and methanol as representative reactants. In contrast to simplified conceptual models in the literature, which suggested a catalytic mechanism (4C mechanism) involving a high-energy four-membered cyclic transition state, our calculations demonstrate that TPB only exhibits a catalytic ability when following a reaction mechanism (6C mechanism) with a six-membered cyclic transition state structure, in which an additional methanol molecule assists in the breaking of the OH bond and the subsequent proton transfer. In the optimal reaction pathway, which follows the 6C mechanism, a reduction in the energy barrier of 3.5 kcal mol⁻¹ in a vacuum is expected to be achieved by including the TPB catalyst, which significantly accelerates the curing process.

---

1. Introduction

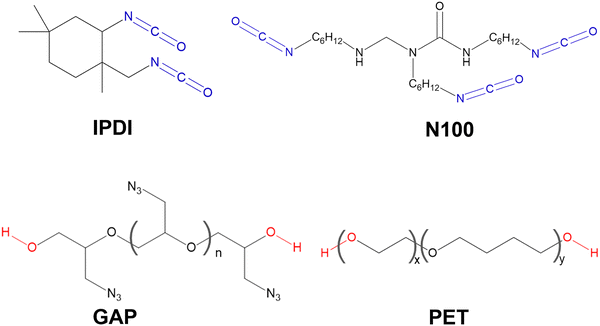
The curing reaction plays a vital role in preparing solid composite propellants,^1,2 which converts a liquid polymer material to a solid state by the cross-linking of polymer chains.^3–6 For example, polyurethanes (PUs) formed by the curing reaction of diol-like (e.g., poly(ethylene oxide-co-tetrahydrofuran) (PET)⁷ and glycidyl azide polymer (GAP)^8,9) and diisocyanate-like ((e.g., poly-isocyanate (N100))⁷ and isophorone diisocyanate (IPDI)¹⁰) polymer molecules are widely used as prepolymer binders in solid propellants and polymer-bonded explosives. The chemical structures of PET, GAP, N100, and IPDI are illustrated in Fig. 1, where their main functional groups, the hydroxyl and isocyanate groups, are highlighted in red and blue, respectively. The urethane group, the main repeating unit in PUs, is produced just through the interaction between these hydroxyl and isocyanate groups.^11–13 The intrinsic slowness of the curing reaction requires the use of suitable catalysts to accelerate the curing process and reduce the curing temperature, thereby ensuring complete and safe curing.

Fig. 1 Structural formulas of IPDI, N100, GAP, and PET.

Organotin compounds, for example, dibutyltin dilaurate, have historically been dominant catalysts for the curing reactions, however, their significant biotoxicity and environmental concerns have driven the industry to seek safer, high-performance alternatives.^14–17 In this context, bismuth (Bi)-based organometallic compounds, such as triphenyl bismuth (TPB),¹⁸ have been widely used to catalyze polyurethane formation and have demonstrated their superior catalytic performance due to their advantages of low toxicity, high stability, and excellent catalytic activity.^12,19,20 Correspondingly, the catalytic activity and mechanism of TPB attract great attention, and various, often conflicting, catalytic mechanisms have been proposed.^{14,17,21–24}

These mechanisms can be broadly classified on the basis of the key intermediate complex generated by binding TPB to isocyanates or hydroxyl groups. In 1998, Luo et al. observed a change in the chemical shift of the hydroxyl proton and attributed this phenomenon to the formation of hydrogen bonds between the Bi atom in TPB and the hydroxyl group of the alcohol, which disrupts the existing alcohol–alcohol hydrogen-bond network. Hence, it was concluded that TPB preferentially binds to alcohol, thus activating the hydroxyl group through Bi–H interactions to facilitate the reaction.¹⁴ Although this mechanism has been widely cited, direct evidence remains limited.^17,22,24 More recently, some studies proposed the isocyanate activation mechanism based on the indirect observation of the TPB–isocyanate complex during the curing reaction. For example, Park et al. observed a color change in the curing system, which indirectly suggested that the Bi atom in TPB is oxidized by isocyanate, leading to the formation of a TPB–isocyanate complex.²³ These conflicting findings highlight the complexity of TPB–reactant interactions and their role in catalytic curing reaction systems.

In addition, experimental studies usually focused on analyzing heat release during the catalytic process and reaction rate. It has been concluded that the curing reaction is a complex process that involves more than one heat-release stage, and the catalytic effects of TPB are manifested as a reduction in the activation energy of approximately 10–20 kJ mol⁻¹.^{7,21,22,25,26} However, there is still a lack of direct experimental evidence to elucidate the precise structures of the intermediates. Moreover, detailed reaction pathways are usually difficult to be determined experimentally. Consequently, theoretical investigations are urgently required to offer microscopic perspectives on the reaction mechanisms.

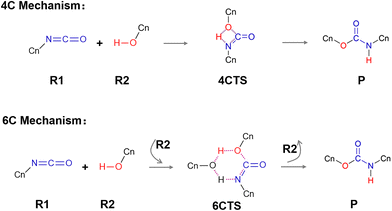
In addition, the mechanism of the isocyanate–alcohol reaction itself is complex. Previous literature on TPB catalysis conceptualized the reaction pathway using a four-membered cyclic transition state,^14,21,23 which is shown in Fig. 2 and called the 4C mechanism here. A recent work reported by Li et al.²⁴ has presented a density functional theory study based on this 4C mechanism. However, we noticed that for reactions of isocyanates with alcohols and water molecules, some studies have also suggested an alternative mechanism involving a six-membered ring transition state with a lower energy barrier, in which the reaction is accelerated by proton transfer mediated by an additional alcohol molecule^27–29 or a water molecule.^6,30,31 This mechanism, the 6C mechanism in Fig. 2, inspired us to speculate that a similar mechanism might be applicable to the TPB catalyzed curing reaction. Thus, in this work, we also investigated this possible mechanism for the curing reaction with or without the catalysis of TPB.

Fig. 2 Possible mechanisms of the curing reaction.

2. Computational details

2.1. Electronic structure calculations

We performed density functional theory (DFT) calculations to deeply investigate the curing reaction mechanism catalyzed by TPB, in which the ωB97X-D functional³² combined with the def2-TZVP or ma-TZVP basis set^33–35 was used. All DFT calculations were carried out with Gaussian 16³⁶ software. Molecular structures were visualized using the GaussView 6 software.³⁶ The ωB97X-D functional was selected because it explicitly includes empirical dispersion correction and has been shown to be effective in dealing with intermolecular interactions and energy barrier calculations for organic systems and systems containing Bi atoms in previous studies,^37,38 thus benefiting the investigation of the current system in which the weak interaction plays an important role.^39,40 Structural optimizations, vibrational frequency analysis, and CM5 charge⁴¹ calculations were performed with the def2-TZVP basis set, and then the single-point energies of these optimized structures were further corrected by using the ma-TZVP basis set. Basis set superposition error (BSSE) in the interaction energy calculation was corrected by the Boys and Bernardi Counter Poise (CP) method.⁴² All energies reported in the main text incorporate zero-point energy (ZPE) corrections, which were calculated with the frequencies obtained by the ωB97X-D/def2-TZVP model chemistry and a frequency scaling factor of 0.975.⁴³ Due to the pronounced weak interactions present in the complexes, there exist many low-frequency vibrational modes, and to accurately account for the contributions of these low-frequency vibrations in computing thermodynamic properties,⁴⁴ the quasi-rigid rotor-harmonic oscillator (quasi-RRHO) approach proposed by Grimme was employed.⁴⁵

To elucidate the nature of intermolecular interactions within the complex formed by TPB and reactants, an energy decomposition analysis based on the generalized Kohn–Sham (GKS-EDA)⁴⁶ was performed at the ωB97X-D/def2-TZVP level with the Xiamen energy decomposition analysis (XEDA) program interfaced with the XACS Cloud,^47,48 and a principal interacting orbital (PIO) analysis was carried out using PIO software.^49,50 The total energy E^tot in GKS-EDA analysis was decomposed into the following components:

E^tot = E^ele + E^ex−rep + E^pol + E^corr/disp

where E^ele, E^ex−rep, E^pol, and E^corr/disp represent electrostatic, exchange/repulsion, polarization, and correlation/dispersion energies contributing to the interaction between TPB and reactant fragments in the complex, respectively.

2.2. Solvation energy calculations

It has been demonstrated that the curing reaction exhibits considerable tolerance toward a wide range of solvent conditions.^29,51–53 Informed by this finding, in this work, we considered toluene, which has been applied in the experimental study of curing reactions,⁵¹ as a representative of solvents to take into account the solvent effect on the curing reaction. Gibbs free energies in toluene were calculated using the SMD implicit solvent model⁵⁴ based on the gas-phase optimized structures and frequencies, and are labeled G_s, where the subscript “s” represents the solvent, distinguished from the subscript “v”, which denotes the results in a vacuum.

Accurate determination of the Gibbs free energy change for bimolecular reactions in solution is a challenging task. Previous analyses have shown that the solvent imposes restrictions on the translational and rotational degrees of freedom of the solute species, leading to a significant overestimation of these entropic contributions when the ideal gas approximation is applied.^55–61 Here, we adopted a rather conservative method, that is, we take translational and rotational entropies at 50% of their calculated values.^56,58 A potentially more reasonable, albeit more radical, alternative would entail completely neglecting all translational and rotational entropies,⁵⁷ which might result in more negative formation Gibbs free energies. However, we stress that, in the calculation of Gibbs free energy barriers for the reaction steps starting from the intermediate, because the number of molecules remains unchanged, the results are less sensitive to the treatment of entropic contributions.

3. Results and discussion

In this work, we focus on the role of TPB in catalyzing the formation of a urethane group by the interaction of the hydroxyl group and the isocyanate group, a key reaction step in the curing reactions.^11,12 Considering that commonly used curing reactants, such as GAP, IPDI, PET, and N100 shown in Fig. 1, usually do not include functional groups and conjugated structures that can significantly affect the reaction mechanism,^4,5,62 to reduce computational cost, in the calculations, we used a simplified reaction model, namely the curing reaction of methyl isocyanate (designated as R1) and methanol (designated as R2) catalyzed by TPB.

3.1. TPB–reactant complex

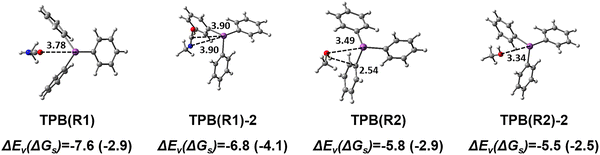
As we mentioned earlier, it was believed that the association of TPB with reactant molecules might activate the characteristic functional groups of the reactants to catalyze the reaction by lowering the barrier. Thus, forming a complex of TPB and reactants may be a key step in the catalysis reaction. Therefore, we first investigated possible association products. Hereafter, the complex of the TPB molecule and reactant molecule will be called the TPB–reactant complex.

TPB spontaneously associates with one R1 or R2 molecule to form a complex in a vacuum, with formation energies (labeled ΔE_v, in which the subscript “v” denotes the vacuum) of −7.6 kcal mol⁻¹ and −5.8 kcal mol⁻¹, respectively. For each of TPB(R1) and TPB(R2), we located two conformers, the high-energy one of which is labeled with the suffix “−2” as shown in Fig. 3. TPB(R1) is 0.8 kcal mol⁻¹ more stable in energy in a vacuum than TPB(R1)-2. Compared to TPB(R1)-2, where the isocyanate group of R1 is nearly parallel to one of the phenyl rings of TPB, the phenyl rings in TPB(R1) show a significant torsional distortion to effectively sandwich the R1 molecule between two phenyl rings, leading to a stronger interaction between TPB and R1. CM5 charge analysis indicates a slight increase in positive charge on the bismuth atom of TPB upon the formation of the TPB(R1) complex (from +0.39 e to +0.41 e), which is consistent with the literature.²³

Fig. 3 Structures and Gibbs free energies of formation of the TPB–reactant complexes. Two relatively stable structures were found for each of the TPB + R1 and TPB + R2 systems. The structure with a higher energy in each case is labeled with the suffix “−2”. Unit of energy: kcal mol⁻¹; unit of bond distance: Å. Color code for atoms: H, white; C, gray; N, blue; O, red; and Bi, purple.

For the complex of TPB with R2, the energy difference between TPB(R2) and TPB(R2)-2 is small, only 0.2 kcal mol⁻¹ in a vacuum. As shown in Fig. 3, the primary distinction in the two structures lies in the orientations of R2. Notably, in contrast to the experimental speculation of Luo et al.,¹⁴ we did not observe the formation of an O–H⋯Bi hydrogen bond between the hydroxyl group and the Bi atom of TPB in both of the complex structures located. This observation is corroborated by the CM5 charge analysis. CM5 charge of the bismuth atom in TPB is positive (+0.39 e) due to the bonding to phenyl rings, making it unsuitable to function as a hydrogen bond acceptor. Nevertheless, we calculated a slight shortening of the R2 hydroxyl bond from 0.966 Å in the hydrogen bond of the R2⋯R2 dimer to 0.961 Å in the TPB(R2) complex. This computed bond shortening (i.e., reduction in H-bond character) makes the hydroxyl proton less deshielding, which aligns with the experimentally observed upfield shift of the hydroxyl proton signal. This finding theoretically confirms the experimental conclusion that the addition of TPB effectively disrupts the existing strong alcohol–alcohol H-bond network.¹⁴

Fig. 4 GKS-EDA results of TPB(R1) and TPB(R2). E^ele, E^ex−rep, E^pol, and E^corr/disp represent electrostatic, exchange/repulsion, polarization, and correlation/dispersion energies contributing to the interaction between TPB and reactant fragments in the complex, respectively.

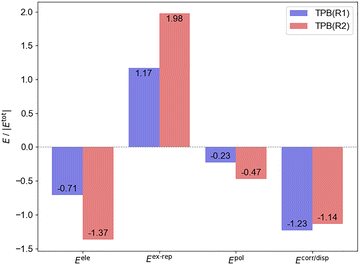
We further performed GKS-EDA and PIO analyses to understand the formation of TPB(R1) and TPB(R2). We analyzed the percentage contribution of each attractive term of the GKS-EDA results (electrostatics E^ele, polarization E^pol, and correlation/dispersion E^corr/disp) to the total attractive interaction (E^ele + E^pol + E^corr/disp). For TPB(R1), the correlation/dispersion constitutes the dominant stabilizing component (57%), followed by electrostatics (33%). In contrast, for TPB(R2), the electrostatics provides the largest contribution (46%), and the correlation/dispersion also plays a substantial role (38%). This energy decomposition indicates that both the complexes adopt a “hybrid correlation/dispersion–electrostatics binding mode”.⁶³ However, their binding characteristics differ: TPB(R1) exhibits a dispersion-dominated hybrid interaction, which indicates the possible role of the π–π interaction between the isocyanate group of R1 and the phenyl rings of TPB. While for the TPB(R2) complex, electrostatic interactions are more pronounced in magnitude than dispersion, implying a partial covalent character in the association of TPB and R2 (Fig. 4).

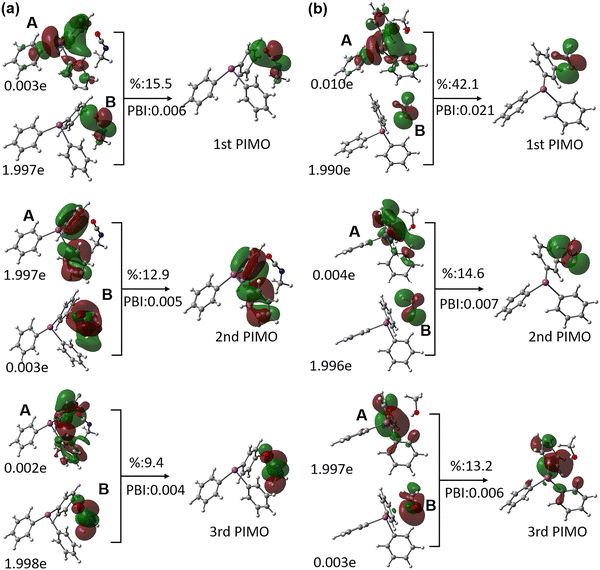
PIO analysis corroborates these conclusions. For TPB(R1), all principal interacting molecular orbitals (PIMOs) exhibit low PIO-based bond indices (PBIs) (smaller than 0.01) and small contribution (smaller than 20%) to the intermolecular interaction, confirming the dominance of dispersion interactions. Further analysis, shown in Fig. 5a, reveals that the first dominant PIMO (1st PIMO) of TPB(R1) can be attributed to the long-pair p electron donation from the O atom of isocyanate to the Bi atom of TPB; the second and third dominant PIMOs (2nd and 3rd PIMO) demonstrate the interaction between the π orbitals of the phenyl rings in TPB and the π* orbitals of isocyanate.

Fig. 5 PIO analysis of (a) TPB(R1) and (b) TPB(R2). Two fragments (TPB and reactant) are labeled as A and B, respectively. The PIMOs with three largest contributions (%) were displayed. The orbital populations (occupation numbers) and the PIO-based bond indices (PBI) are also given in the figure. The red and green colors of orbitals represent two different phases of isosurfaces. Color code for atoms: H, white; C, gray; N, blue; O, red; and Bi, purple.

For TPB(R2), as shown in Fig. 5b, the primary PIMO (1st PIMO) with the largest contribution (42%) to the intermolecular interaction arises from a PIO pair showing the electron donation from the oxygen lone pair orbital of methanol to the p orbital of Bi. Furthermore, the 2nd PIMO and the 3rd PIMO show the electronic donation from the C–H and O–H σ-bonding orbitals of methanol to the π*-antibonding orbital of phenyl rings in TPB and the electronic back-donation from the phenyl π orbital to the O–H σ*-antibonding orbitals of methanol, respectively, indicating a weak σ(C–H/O–H)⋯π interaction between TPB and R2.

We also considered possible combinations of TPB with the hydrogen-bonding stabilized reactant cluster, for example, the formation of TPB(R1⋯R2), TPB(R2⋯R2) (with R1/R2⋯R2 denoting the hydrogen-bonded cluster of R1/R2 and R2), or TPB(R1⋯R2⋯R2) (with R1⋯R2⋯R2 denoting a hydrogen-bonded trimolecular cluster). The optimized TPB–(reactant cluster) complexes are shown in Fig. 6, in which the corresponding formation energies in a vacuum and the Gibbs free energies of formation in toluene are given. Note, hereafter, for the same species with more than one structure, we will always use the suffixes, such as “−1” and “−2”, to distinguish the structures, and the number in the suffix indicates the energy order of the structure in a vacuum, for example, the lower-energy one is always with the suffix “−1”. We found that these TPB–(reactant cluster) complexes can also be formed spontaneously due to the negative formation energy.

Fig. 6 Structures and Gibbs free energies of formation of the TPB-(reactants cluster) complexes. Unit of energy: kcal mol⁻¹; unit of bond distance: Å. Color code for atoms: H, white; C, gray; N, blue; O, red; and Bi, purple.

3.2. Reaction mechanism

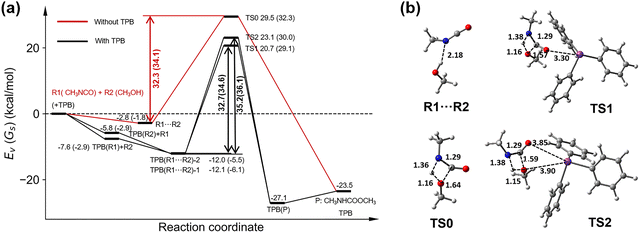
We first investigated the curing reaction mechanism of R1 and R2 via a transition state with a four-membered cyclic structure, namely, the 4C mechanism shown in Fig. 2.^14,21,23 The located four-membered cyclic transition state is given in Fig. 7b, and marked with TS0. The reaction path traced from the TS0 structure by the intrinsic reaction coordinate (IRC) calculations revealed that the TS0 connects to a hydrogen-bond stabilized R1⋯R2 complex, that is, the R1⋯R2 complex can be spontaneously formed once the reactants R1 and R2 approach each other and then pass through TS0 to produce the product P. The energetic diagram along the reaction path is plotted in Fig. 7a. Thus, when TPB is added as a catalyst, we can assume that if a TPB–reactant complex (TPB(R1) or TPB(R2)) is formed, another reactant molecule (R2 or R1) can be spontaneously combined with it to form a TPB(R1⋯R2) complex and then produce the curing product also via a four-membered cyclic transition-state. We have located the corresponding TS structures and shown them in Fig. 7b, which are TS1 and TS2, respectively, directly connecting to TPB(R1⋯R2)-2 and TPB(R1⋯R2)-1 intermediates. The energetics for the TPB-involved pathways are compared to those of the curing reaction pathways without the TPB in Fig. 7a.

Fig. 7 (a) Energy step diagram of the curing reaction in the 4C mechanism. The values within and outside the parentheses, respectively, refer to the Gibbs free energy in toluene at 298.15 K and the energy calculated in a vacuum with ZPE. (b) Structures of some key stationary points along the reaction pathways. Unit: Å. Color code for atoms: H, white; C, gray; N, blue; O, red; and Bi, purple.

We can see that following the 4C mechanism, the curing reaction has to conquer a high energy barrier because of the inherent ring-strain instability of the four-membered cyclic transition state, which is 32.3 kcal mol⁻¹ in a vacuum for the TPB-free reaction, 32.7 or 35.2 kcal mol⁻¹ for the TPB-involved reactions with TPB-R1 or TPB-R2 as the precursor, respectively. In nonpolar toluene, the corresponding Gibbs free energy barriers of these reaction pathways are 34.1 kcal mol⁻¹ (for TPB-free reaction) and 34.6 and 36.1 kcal mol⁻¹ (for TPB-involved reactions), respectively. These results indicate that TPB cannot catalyze the curing reaction in the 4C mechanism, which implies that the reaction may follow a more complex mechanism.

TPB-induced aggregation of reactants motivated us to explore an alternative mechanistic pathway: proton transfer facilitated by an additional alcohol molecule, namely the 6C mechanism with a significantly more stable six-membered cyclic transition state, as depicted in Fig. 2.^6,27–31

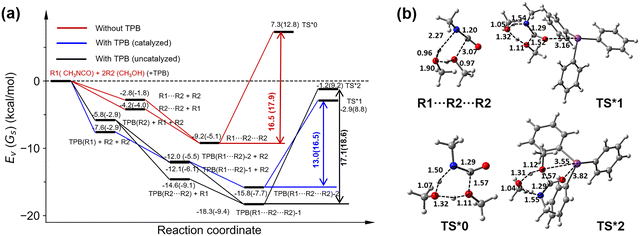
In the 6C mechanism, the formation of a six-membered cyclic transition state for the current isocyanate–methanol reaction means the simultaneous participation of two methanol (R2) molecules and one isocyanate (R1) molecule, however, the collision probability of multiple molecules is relatively low,⁶⁴ and thus, a stepwise reaction mechanism is proposed: a hydrogen-bonded reactant complex (R1⋯R2 or R2⋯R2) is pre-formed and then associated with an additional reactant molecule R2 or R1 to form the key intermediate R1⋯R2⋯R2, which will react via the six-membered cyclic transition state to complete the curing reaction. The energy diagram and optimized structures of some key stationary points along this 6C reaction pathway are plotted in Fig. 8. Note, hereafter, we use the asterisk to distinguish the six-membered cyclic transition state from the four-membered cyclic transition state. As shown in Fig. 8, in the 6C mechanism, the curing reaction barrier in a vacuum is significantly reduced to 16.5 kcal mol⁻¹, and the corresponding Gibbs free energy barrier in toluene at 300 K is estimated to be 17.9 kcal mol⁻¹.

Fig. 8 (a) Energy step diagram of the curing reaction in the 6C mechanism. The values within and outside the parentheses, respectively, refer to the Gibbs free energy in toluene at 298.15 K and the energy calculated in a vacuum with ZPE. (b) Structures of some key stationary points along the reaction pathways. Unit: Å. Color code for atoms: H, white; C, gray; N, blue; O, red; and Bi, purple.

Extending to TPB catalysis, key precursor complexes, TPB(R1)(or TPB(R2)), TPB(R1⋯R2) (or TPB(R2⋯R2)), and TPB(R1⋯R2⋯R2), may be generated sequentially, and then passed through a six-membered cyclic transition state to produce the curing product. Fig. 8 shows two six-membered cyclic transition states that we located, TS*1 and TS*2, and we can see that the pathway through the relatively higher-energy complex TPB(R1⋯R2⋯R2)-2 and the lower-energy transition state TS*1 is optimal and the corresponding rate-determining barrier is only 13.0 kcal mol⁻¹ in a vacuum, achieving a barrier reduction of 3.5 kcal mol⁻¹ compared to the TPB-free reaction. In toluene, the calculated Gibbs free energy barrier of this reaction pathway is 16.5 kcal mol⁻¹, 1.4 kcal mol⁻¹ lower than that of the TPB-free reaction. The other pathway via TPB(R1⋯R2⋯R2)-1 and TS*2 exhibits a higher (Gibbs free) energy barrier, (18.6) 17.1 kcal mol⁻¹, which is less competitive in dynamics.

It is interesting to understand why TPB exhibits catalytic activity for the curing reaction in the 6C mechanism rather than in the 4C mechanism. The activity of the catalyst is reflected mainly by the reduction of the reaction barrier. Numerically, the reduction of barrier height originates from two distinct contributions of the catalyst upon association with reactants: (1) its ability to activate (i.e., destabilize) the reactants, and (2) its ability to stabilize the transition state.

The formation energies of R1⋯R2 and TPB(R1⋯R2)-2 in the 4C pathway are −2.8 and −12.0 kcal mol⁻¹, and their difference is −9.2 kcal mol⁻¹; the formation energies of R1⋯R2⋯R2 and TPB(R1⋯R2⋯R2)-2 in the 6C pathway are −9.2 and −15.8 kcal mol⁻¹, and their difference is −6.6 kcal mol⁻¹. It indicates a significant difference of 2.6 kcal mol⁻¹ in the relative stabilization of reactant complexes in the two mechanisms. That is, relative to the 4C pathway, the 6C pathway destabilizes the reactant complex by 2.6 kcal mol⁻¹. In the same way, we can compare the relative energy differences between the transition states without and with a TPB catalyst in the two mechanisms. The energies of TS0 and TS1 relative to their own reactants in the 4C pathway are 29.5 and 20.7 kcal mol⁻¹, respectively, and thus their relative energy difference is −8.8 kcal mol⁻¹, while that between TS*0 and TS*1 in the 6C pathway is −10.2 kcal mol⁻¹ (which is calculated to be −2.9–7.3 kcal mol⁻¹). Thus, the lowering of the transition state in energy due to the introduction of TPB in the two mechanisms differs by −1.4 kcal mol⁻¹. That is, in the 6C pathway, the TPB catalyst can stabilize the transition state more significantly by 1.4 kcal mol⁻¹ compared to that in the 4C pathway.

These results clearly indicate that while the stabilization of the transition state in the key reaction step by using the TPB catalyst is substantial, the destabilization of the reactant complex by TPB in the 6C mechanism is indeed a major contributing factor to the decreased reaction barrier. This behavior largely stems from the steric hindrance imposed by the unique structure of TPB. As illustrated in Fig. 6 and 8, in the 6C mechanism, upon association with reactants, TPB imposes a significant structural strain on the reactant complex, which is mainly driven by steric clashes from the bulky phenyl moieties and the Bi–O interaction. Conversely, for the less crowded 4C reactant complex, this steric hindrance is less pronounced, allowing TPB to stabilize the reactant complex more effectively and thereby influencing the catalytic outcome.

4. Summary

We thoroughly investigated the microscopic mechanism of the TPB-catalyzed curing reactions using density functional theory, with the reaction of methyl isocyanate and methanol as a model reaction. We first studied the interaction between TPB and the curing reactants and found that TPB can spontaneously combine with both reactants, mainly through the dispersion force and the electronic donation from the O atom of isocyanate or hydroxyl groups to the Bi atom of TPB. In addition, the π orbital of the isocyanate group and the σ (OH or CH) orbital of methanol also interact with the π orbitals of the phenyl ring of TPB, contributing to the stabilization of the TPB–reactant complexes. Thus, various TPB–reactant complexes may be formed during the TPB-catalyzed curing reactions, which explains why different TPB–reactant complexes were identified in different experimental studies.

Further mechanistic analysis reveals that the curing reaction free of TPB and the curing reaction included with TPB both can occur via two mechanisms, which, respectively, involve a four-membered cyclic transition state or a six-membered cyclic transition state with the aid of an additional methanol molecule and are called 4C and 6C mechanisms. The 6C mechanism with a significantly lower reaction barrier is more efficient in dynamics due to the less rigid transition state ring structure than the 4C mechanism. More interestingly, TPB can only exhibit catalytic activity in the 6C mechanism rather than in the 4C mechanism. Based on the current calculations, the energy barrier for the curing reaction in a vacuum is reduced by 3.5 kcal mol⁻¹ when using TPB as a catalyst, in good agreement with the experimental data of 10–20 kJ mol⁻¹ (2.4–4.8 kcal mol⁻¹).^7,21,22 The present study sheds new light on the catalytic mechanism of TPB in the curing reaction system and helps to reconcile the complex and occasionally seemingly contradictory interpretations reported in previous experimental studies.

Conflicts of interest

The authors declare no competing financial interest.

Data availability

The data supporting this article have been included in the supplementary information (SI). Supplementary information: the Cartesian coordinates of all optimized structures and the imaginary frequencies of the transition states. See DOI: https://doi.org/10.1039/d5cp03608a.

References

1. A. Das and P. Mahanwar, Adv. Ind. Eng. Polym. Res., 2020, 3, 93–101.
2. J. C. Quagliano Amado, P. G. Ross, L. Mattos Silva Murakami and J. C. Narciso Dutra, Propellants, Explos., Pyrotech., 2022, 47, e202100283.
3. D. K. Chattopadhyay and K. Raju, Prog. Polym. Sci., 2007, 32, 352–418.
4. J. O. Akindoyo, M. Beg, S. Ghazali, M. Islam, N. Jeyaratnam and A. Yuvaraj, RSC Adv., 2016, 6, 114453.
5. M. Ates, S. Karadag, A. A. Eker and B. Eker, Polym. Int., 2022, 71, 1157–1163.
6. J. Zhou, Z. Liu, Z. Zhu, Z. Zeng and L. Sun, React. Chem. Eng., 2025, 10, 38–47.
7. Y. Li, J. Li, S. Ma and Y. Luo, Int. J. Polym. Anal. Charact., 2016, 21, 495–503.
8. N. Kubota and T. Kuwahara, Propellants, Explos., Pyrotech., 1991, 16, 51–54.
9. N. Kubota, Y. Yano, K. Miyata, T. Kuwahara, M. Mitsuno and I. Nakagawa, Propellants, Explos., Pyrotech., 1991, 16, 287–292.
10. A. Prabhakar, D. Chattopadhyay, B. Jagadeesh and K. Raju, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 1196–1209.
11. X. Zhao and W. Zhu, J. Chin. Chem. Soc., 2022, 69, 419–439.
12. S. Ma, Y. Li, Y. Li, G. Li and Y. Luo, Cent. Eur. J. Energ. Mater., 2017, 14, 708–725.
13. H. He, Z. Shao, S. Hu, Y. Lu and F. Li, Polymer, 2024, 290, 126541.
14. S.-G. Luo, H.-M. Tan, J.-G. Zhang, Y.-J. Wu, F.-K. Pei and X.-H. Meng, J. Appl. Polym. Sci., 1997, 65, 1217–1225.
15. W. J. Blank, Z. He and E. T. Hessell, Prog. Org. Coat., 1999, 35, 19–29.
16. V. De Lima, N. da Silva Pelissoli, J. Dullius, R. Ligabue and S. Einloft, J. Appl. Polym. Sci., 2010, 115, 1797–1802.
17. Y. Ou, S. Chang and B. Zhang, Chin. J. Energ. Mater., 2015, 23, 568–572.
18. P. Jones, A. Blaschette, D. Henschel and A. Weitze, Z. Kristallogr. - Cryst. Mater., 1995, 210, 377–378.
19. E. Landsem, T. L. Jensen, F. K. Hansen, E. Unneberg and T. E. Kristensen, Propellants, Explos., Pyrotech., 2012, 37, 581–591.
20. D. Gui, Y. Zong, S. Ding, C. Li, Q. Zhang, M. Wang, J. Liu, X. Chi, X. Ma and A. Pang, Propellants, Explos., Pyrotech., 2017, 42, 410–416.
21. S. Chang, J. Tang, X. Liu and W. Yan, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 012057.
22. Y. Ou, Q. Jiao, S. Yan and Y. Zhu, Cent. Eur. J. Energ. Mater., 2018, 15, 131–149.
23. S. Park and J. Park, Propellants, Explos., Pyrotech., 2022, 47, e202100135.
24. H. Li, G. Luo, L. Sang and W. Zhu, J. Solid Rocket Technol., 2023, 46, 96–101.
25. S. Lee, C. H. Choi, I.-K. Hong and J. W. Lee, Korean J. Chem. Eng., 2015, 32, 1701–1706.
26. S. Lee, J. H. Choi, I.-K. Hong and J. W. Lee, J. Ind. Eng. Chem., 2015, 21, 980–985.
27. G. Raspoet, M. T. Nguyen, M. McGarraghy and A. F. Hegarty, J. Org. Chem., 1998, 63, 6878–6885.
28. W. Cheikh, Z. B. Rózsa, C. O. Camacho Lopez, P. Mizsey, B. Viskolcz, M. Szöri and Z. Fejes, Polymers, 2019, 11, 1543.
29. C. Gertig, E. Erdkamp, A. Ernst, C. Hemprich, L. C. Kröger, J. Langanke, A. Bardow and K. Leonhard, ChemistryOpen, 2021, 10, 534–544.
30. G. Raspoet, M. T. Nguyen, M. McGarraghy and A. F. Hegarty, J. Org. Chem., 1998, 63, 6867–6877.
31. M. E. Wolf, J. E. Vandezande and H. F. Schaefer, Phys. Chem. Chem. Phys., 2021, 23, 18535–18546.
32. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
35. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmin-ylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT.
37. E. Semidalas and A. Chrissanthopoulos, Comput. Theor. Chem., 2019, 1149, 41–48.
38. K. Ruffell, L. C. Gallegos, K. B. Ling, R. S. Paton and L. T. Ball, Angew. Chem., Int. Ed., 2022, 61, e202212873.
39. A. A. Auer, D. Mansfeld, C. Nolde, W. Schneider, M. Schürmann and M. Mehring, Organometallics, 2009, 28, 5405–5411.
40. A. M. Toma, A. Pop, A. Silvestru, T. Rüffer, H. Lang and M. Mehring, Dalton Trans., 2017, 46, 3953–3962.
41. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541.
42. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
43. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
44. Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2008, 10, 2813–2818.
45. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
46. P. Su, Z. Jiang, Z. Chen and W. Wu, J. Phys. Chem. A, 2014, 118, 2531–2542.
47. P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460.
48. Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu, W. Wu and P. Su, J. Comput. Chem., 2021, 42, 2341–2351.
49. J.-X. Zhang, F. K. Sheong and Z. Lin, Chem. – Eur. J., 2018, 24, 9639–9650.
50. J.-X. Zhang, F. K. Sheong and Z. Lin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1469.
51. S. Monaghan and R. A. Pethrick, Macromolecules, 2012, 45, 3928–3938.
52. S. Monaghan and R. A. Pethrick, Ind. Eng. Chem. Res., 2012, 51, 11038–11044.
53. C. O. C. López, Z. Fejes and B. Viskolcz, J. Flow Chem., 2019, 9, 199–204.
54. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
55. R. Tanaka, M. Yamashita, L. W. Chung, K. Morokuma and K. Nozaki, Organometallics, 2011, 30, 6742–6750.
56. T. Wang, Y. Liang and Z.-X. Yu, J. Am. Chem. Soc., 2011, 133, 9343–9353.
57. B. Mondal, F. Neese and S. Ye, Inorg. Chem., 2015, 54, 7192–7198.
58. M. Besora, P. Vidossich, A. Lledos, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392–1399.
59. A. J. Garza, J. Chem. Theory Comput., 2019, 15, 3204–3214.
60. S.-C. Liu, X.-R. Zhu, D.-Y. Liu and D.-C. Fang, Phys. Chem. Chem. Phys., 2023, 25, 913–931.
61. J. Ariai and U. Gellrich, Phys. Chem. Chem. Phys., 2023, 25, 14005–14015.
62. F. V. Rossi, Additives in Composite Materials: Synthesis and Characterization of Innovative Promoters in Polyurethane Blends, Master's thesis, Instituto Superior Técnico, Universidade de Lisboa, 2016.
63. Z.-Y. Zhao, T. Chen, K. Zhou, P. Su, Z. Xie, Y.-G. Huang, L. Meng, Z.-A. Nan and C.-Z. Lu, J. Phys. Chem. Lett., 2025, 16, 11064–11073.
64. J. Wu, L. G. Gao, Z. Varga, X. Xu, W. Ren and D. G. Truhlar, Angew. Chem., 2020, 132, 10918–10922.

---