Quantum chemical rovibrational spectroscopic data for possible observation of thiocarbonic acid (H2CS3) in interstellar environments
Received
7th October 2025
, Accepted 4th December 2025
First published on 4th December 2025
Abstract
The second-lowest conformer of thiocarbonic acid (cis–trans-H2CS3) lies 0.64 kcal mol−1 above the global minimum and possesses a 2.17 D dipole moment compared to the 0.75 D dipole moment of the cis–cis global minimum. While these properties are qualitatively similar to those of standard carbonic acid (H2CO3), the relative energy is lower, and the dipole moment of cis–cis-H2CS3 is higher than in cis–cis-H2CO3. As such, the quantum chemically computed spectroscopic constants and fundamental vibrational frequencies of these two conformers of thiocarbonic acid are provided in this work as well as those for the trans–trans conformer. Previous quantum chemical work has highlighted that the provided rotational constants should be within 3.5 MHz, if not 1.5 MHz, of experiment, and prior experimental work implies that this molecule can form on interstellar ices and be easily desorbed into the gas phase thereafter. Hence, these data will be able to assist in laboratory characterization or even potential interstellar searches for thiocarbonic acid.
1. Introduction
Sulfur has long been thought to be missing in the universe due to the discrepancy between its astronomically-observed atomic abundance versus its observed molecular abundance when compared to such ratios from other volatile elements.1,2 However, recent work has shown that molecular sulfur is most likely just hidden in plain sight abiding in previously unknown molecules, notably including sulfur allotropes and high-sulfur content hydrides (SnH(1,2) where n > 2) that exhibit numerous conformers and, subsequently, relatively weak individual molecular signals.3 The high number of conformers dilutes the rotational signal of any one molecule such that unique molecular detection through the most common means of astronomical molecular observation is difficult. Even so, several sulfur-containing molecules are known in the astrochemical census4,5 including carbon monosulfide first detected as far back as 19716,7 and trans-propenethiol as recently as 2025.8 Various other sulfur-containing molecules have been observed including four others besides trans-propenethiol in the past 18 months.9–12 Hence, sulfur appears not necessarily to be hiding as much as we have not been looking for it in the proper places.
One of these very recent observations of a sulfurous molecule is trans-dithioformic acid (HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SSH) in 2024.9 Formic acid has been known in astronomical environments since the same time as CS,13 but the fully sulfurous form only emerged recently, more than 50 years later. Formic acid is found throughout biochemistry, and its significance is well-known. For instance this molecule is produced by ants here on Earth which gives them their distinctive odor when crushed. Regardless, this pairing of astronomically-observed formic acid and its sulfur analogue is not unique. More than 30 pairs of oxygen–sulfur analogue molecules where the oxygen form has an exact match to the sulfurous form have been observed towards astronomical sources.14 These include alcohols/thiols, aldehydes/thioaldehydes, eithers/thioethers, and various other chalcogen analogues. These pairs alone constitute roughly a quarter of the known, unique interstellar molecules,4,5 implying a growing role that sulfur is playing in our understanding of interstellar chemistry.
SSH) in 2024.9 Formic acid has been known in astronomical environments since the same time as CS,13 but the fully sulfurous form only emerged recently, more than 50 years later. Formic acid is found throughout biochemistry, and its significance is well-known. For instance this molecule is produced by ants here on Earth which gives them their distinctive odor when crushed. Regardless, this pairing of astronomically-observed formic acid and its sulfur analogue is not unique. More than 30 pairs of oxygen–sulfur analogue molecules where the oxygen form has an exact match to the sulfurous form have been observed towards astronomical sources.14 These include alcohols/thiols, aldehydes/thioaldehydes, eithers/thioethers, and various other chalcogen analogues. These pairs alone constitute roughly a quarter of the known, unique interstellar molecules,4,5 implying a growing role that sulfur is playing in our understanding of interstellar chemistry.
A similar organic, oxygen-rich molecule akin to formic acid is carbonic acid (HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OOH or H2CO3). This molecule is an isomer of water complexed with carbon dioxide and is related to formic acid where the lone C–H group in formic acid is replaced with a hydroxyl group in H2CO3. Carbonic acid is both a diol and a ketone giving it several hallmarks of organic functionalization and, recently, has been shown to form unique helical microscopic complexes for increasingly larger monomolecular clusters.15 It also likely plays a role in ocean acidification but is notoriously unstable due to its preference to form H2O + CO2.16–18 Despite this instability and its chronic elusiveness in the laboratory except at cold temperatures, carbonic acid is now known to exist in astronomical environments.19 The radioastronomical detection of this molecule toward a molecular cloud in the vicinity of the central region of our galaxy was actually for the second-lowest energy conformer (cis–trans). The dipole moment of the cis–cis global minimum is close enough to 0.0 D (specifically 0.2 D) for its signal to be insufficient for observation. That of the higher cis–trans conformer is over 3.0 D, high enough for this version to be observed over its more stable corresponding conformer. Even so, carbonic acid does not appear to be as elusive in space as it can be in the atmosphere or the laboratory. This opens the door for the examination of related molecules observed in astronomical environments. As such, the astronomical presence of the formic acid/dithioformic acid chalcogen analogue pair along with the known interstellar detection of carbonic acid implies that similar chemistry could be at play in the interstellar medium for the sulfurous analogues of H2CO3, as well.
OOH or H2CO3). This molecule is an isomer of water complexed with carbon dioxide and is related to formic acid where the lone C–H group in formic acid is replaced with a hydroxyl group in H2CO3. Carbonic acid is both a diol and a ketone giving it several hallmarks of organic functionalization and, recently, has been shown to form unique helical microscopic complexes for increasingly larger monomolecular clusters.15 It also likely plays a role in ocean acidification but is notoriously unstable due to its preference to form H2O + CO2.16–18 Despite this instability and its chronic elusiveness in the laboratory except at cold temperatures, carbonic acid is now known to exist in astronomical environments.19 The radioastronomical detection of this molecule toward a molecular cloud in the vicinity of the central region of our galaxy was actually for the second-lowest energy conformer (cis–trans). The dipole moment of the cis–cis global minimum is close enough to 0.0 D (specifically 0.2 D) for its signal to be insufficient for observation. That of the higher cis–trans conformer is over 3.0 D, high enough for this version to be observed over its more stable corresponding conformer. Even so, carbonic acid does not appear to be as elusive in space as it can be in the atmosphere or the laboratory. This opens the door for the examination of related molecules observed in astronomical environments. As such, the astronomical presence of the formic acid/dithioformic acid chalcogen analogue pair along with the known interstellar detection of carbonic acid implies that similar chemistry could be at play in the interstellar medium for the sulfurous analogues of H2CO3, as well.
A concrete clue that other sulfur-containing molecules of this ketone-alcohol/thioketone-thiol family may be present in space has emerged from recent ice experiments under simulated interstellar conditions. In one of these, fully sulfurous thiocarbonic acid (HSC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SSH or H2CS3) has been synthesized and desorbed into the gas phase from irradiation of mixed H2S and CS2 ices with simulated cosmic rays.14 These experiments highlight that ice present in protostellar environments could be ionized as star formation begins and create thiocarbonic acid. This molecule could then be desorbed into the gas phase making it possible for radioastronomical observation. Additionally, once thiocarbonic acid is present in such regions, its density of sulfur could allow it to form other sulfurous molecules leading to molecules yet to be observed, increasing the sulfur population in space.14 Of course, such is speculation until observation of the parent molecules like H2CS3 can be achieved.
SSH or H2CS3) has been synthesized and desorbed into the gas phase from irradiation of mixed H2S and CS2 ices with simulated cosmic rays.14 These experiments highlight that ice present in protostellar environments could be ionized as star formation begins and create thiocarbonic acid. This molecule could then be desorbed into the gas phase making it possible for radioastronomical observation. Additionally, once thiocarbonic acid is present in such regions, its density of sulfur could allow it to form other sulfurous molecules leading to molecules yet to be observed, increasing the sulfur population in space.14 Of course, such is speculation until observation of the parent molecules like H2CS3 can be achieved.
As such, this present study will supply the full set of quantum chemically-computed anharmonic, fundamental vibrational frequencies and spectroscopic constants to aid in the laboratory characterization and potential interstellar observation of thiocarbonic acid. The theoretical methods employed have recently predicted the principle A0, B0, and C0 constants of carbonic acid to within 3.3 MHz (average of less than 1.5 MHz) of experiment.20 The higher masses of sulfur will reduce the rotational constants and, thus, reduce the absolute error for the rotational constants. Hence, the predicted values should be accurate enough for clear identification of thiocarbonic acid. As such, the role that this sulfur-dense molecule in its three conformers plays can possibly be characterized with such data. Even if direct astronomical observation is not yet possible, these data will help to inform laboratory spectroscopic characterization of these molecules for both rotational spectroscopy as well as IR, fundamental vibrational frequency comparison especially with the current influx of data from the James Webb Space Telescope (JWST).
2. Computational details
This quantum chemical study relies upon the trusted quartic force field (QFF) approach,21 a fourth-order Taylor series approximation to the potential portion of the internuclear Watson Hamiltonian. The most accurate forms of this approach require the most accurate underlying electronic structure methods for defining the QFF potential,22–24 and coupled cluster singles, doubles, and perturbative triples within the explicitly correlated formalism [CCSD(T)-F12b]25–29 is chosen for this work due to its known accuracy and its performance for carbonic acid.20 The tightly converged geometry is optimized with the cc-pCVTZ-F12 basis set30–34 in conjunction with its complementary auxiliary basis set, and displacements of 0.005 Å and radians are made for the following coordinate systems with “Rn” coordinates of the same type used previously for carbonic acid.20 For C2vcis–cis – and trans–trans thiocarbonic acid, the below symmetry-internal coordinate system is employed:| | 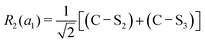 | (2) |
| | 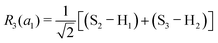 | (3) |
| | 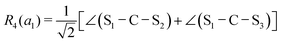 | (4) |
| | 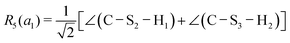 | (5) |
| | 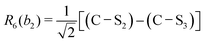 | (6) |
| | 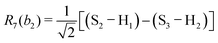 | (7) |
| | 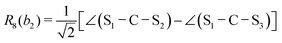 | (8) |
| | 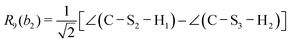 | (9) |
| | | R10(b1) = OPB(S1–C–S2–S2) | (10) |
| |  | (11) |
| | 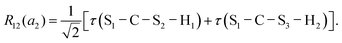 | (12) |
The S2 and S3 atoms are the thiol atoms, and S1 is the thioketone. H1 and H2 are also equivalent by symmetry as they are bonded to S2 and S3, respectively. Additionally, the “out-of-plane-bend” is abbreviated as “OPB” here. This QFF, as a result, requires 4493 total points. For Cscis–trans-H2CS3, the reduction in symmetry for the simple-internal coordinate system employs just shy of double the number of points (8965) for the below coordinates, again with the same atomic number as the C2v conformers:
| | | R10(a″) = OPB(S1–C–S2–S2) | (22) |
| | | R11(a″) = τ(S1–C–S2–H1) | (23) |
| | | R12(a″) = τ(S1–C–S3–H2) | (24) |
At each point, regardless of the symmetry and resulting coordinate system, CCSD(T)-F12/cc-pCVTZ single point energies are computed. To these, the differences in CCSD(T)/cc-pVTZ-DK energies for inclusion and exclusion of scalar relativity35 are added. This so-called “F12-TcCR” (for triple-zeta “T”, core correlation “cC”, and relativity “R”) QFF is known to provide accuracies for rotational constants to within 5.0 MHz and vibrational frequencies within 6.0 cm−1 or better compared to experimental benchmarks.36 Again, this approach produces rotational constants for carbonic acid to as close as 1.1 MHz and as “far” as 3.3 MHz compared to experiment.20 This F12-TcCR QFF methodology builds upon earlier, composite canonical CCSD(T) QFFs37–39 shown to be just as accurate,23,40–45 but the faster basis set convergence in F1246 allows this method to utilize only triple-zeta besis sets instead of quintuple-zeta basis sets. Hence, this F12-TcCR QFF is much faster than the previous generation and, consequently, is capable of computing accurate anharmonic vibrational and spectroscopic data for molecules of the size of thiocarbonic acid and its six atoms.47–49
Once the F12-TcCR QFF is computed, the resulting energies are fit via a least squares procedure and refit to zero the gradients. The force constants derived from this algorithm are fed into rotational and vibrational perturbation theory at second-order (VPT2) procedures50–53 based on the SPECTRO program.54 Both the QFF process and the VPT2 computations are fully and automatically treated within the PBQFF program, a Rust-written code that can compute anharmonic frequencies and spectroscopic data starting from the initial guess to the geometry all the way through computation of the QFF and into generating the final VPT2 analysis.55 PBQFF calls other quantum chemistry programs to compute the required energies allowing for QFFs to be created for any electronic structure method desired. For this work, the geometry optimizations, dipole moments, and single-point energies that define the QFF are computed with the molpro quantum chemistry program.56,57 Finally, anharmonic, infrared intensities are computed with B3LYP/aug-cc-pV(T+d)Z within the Gaussian16 program.30,58–63
3. Results & discussion
3.1. Relative energies & rotational spectra considerations
The two higher-energy conformers of thiocarbonic acid both are relatively close in energy to the cis–cis minimum as shown in Fig. 1. The thiocarbonic acid Cscis–trans conformer resides 0.64 kcal mol−1 above the minimum as corrected with the zero-point (ZPT) vibrational energy (with a 7.23 kcal mol−1 barrier in between), and the trans–trans conformer lies 2.53 kcal mol−1 higher than the cis–cis with an 8.18 kcal mol−1 barrier between the trans–trans and the cis–trans minima. However, cis–trans-H2CO3 is roughly 2 kcal mol−1 higher than the cis–cis,15 showing that the sulfur analogues are closer in energy and should be more thermally accessible. While the cis–trans-thiocarbonic acid dipole moment (2.17 D; Table 1) is much higher than the cis–cis (0.75 D), somewhat similar to the relative energy and dipole moment distribution of H2CO3, the dipole moment for cis–cis-H2CS3 is larger than its pure oxygen analogue by nearly a factor of four. Hence, both cis–cis and cis–trans-thiocarbonic acid may both be observable via radioastronomical searches.
 |
| | Fig. 1 Visual depictions for the three conformers of thiocarbonic acid and their relative energies (in kcal mol−1). S (yellow), C (gray), and H (white). | |
Table 1 Spectroscopic constants (in MHz) for the three conformers of thiocarbonic acid
|
|
Units |
cis–cis |
trans–trans |
cis–trans |
|
A
e
|
MHz |
3572.6 |
3608.5 |
3551.1 |
|
B
e
|
MHz |
3409.1 |
3368.6 |
3439.2 |
|
C
e
|
MHz |
1744.5 |
1742.2 |
1747.1 |
|
A
0
|
MHz |
3566.7 |
3586.1 |
3534.3 |
|
B
0
|
MHz |
3383.4 |
3354.0 |
3421.0 |
|
C
0
|
MHz |
1735.0 |
1732.3 |
1737.0 |
|
κ
|
|
0.80 |
0.75 |
0.87 |
|
Δ
J
|
Hz |
689.866 |
687.426 |
676.610 |
|
Δ
K
|
Hz |
1788.542 |
600.765 |
851.531 |
|
Δ
JK
|
Hz |
−571.801 |
163.918 |
94.943 |
|
δ
J
|
Hz |
299.140 |
296.983 |
292.028 |
|
δ
K
|
Hz |
478.332 |
860.290 |
771.077 |
|
Φ
J
|
µHz |
727.031 |
223.870 |
325.306 |
|
Φ
K
|
µHz |
−940.246 |
10977 |
11765 |
|
Φ
JK
|
mHz |
−3.524 |
4.904 |
4.436 |
|
Φ
KJ
|
mHz |
5.762 |
−13.965 |
−14.378 |
|
ϕ
j
|
µHz |
364.429 |
113.052 |
163.647 |
|
ϕ
jk
|
µHz |
−935.806 |
2470 |
2428 |
|
ϕ
k
|
µHz |
4963 |
878.207 |
423.262 |
|
µ
|
D |
0.75 |
3.26 |
2.17 |
|
µ
x
|
D |
0.00 |
0.00 |
0.00 |
|
µ
y
|
D |
0.00 |
0.00 |
0.27 |
|
µ
z
|
D |
0.75 |
3.26 |
2.15 |
For the spectroscopic data, the A0 and B0 rotational constants of these near-oblate molecules, with κ approaching 1.0, are more than three times smaller than in standard carbonic acid as would be expected for inclusion of the heavier sulfur atoms. The rotational constants for standard carbonic acid are within 3.0 MHz of experiment,20 implying that these three times smaller values for the thiocarbonic acid should be equally, if not more, accurate here. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond length of 1.625 Å and C–S bond length of 1.751 Å in the cis–cis conformer are within 0.02 Å of the single crystal X-ray diffraction experimental data,64 implying that these isolated molecule computations are performing as expected. The two C2v conformers have the strongest similarity between rotational constants of the three forms of H2CS3. The dipole moment of the highest-energy trans–trans conformer is the greatest of the set at 3.26 D, implying that the close spectroscopic constants and the larger dipole moment compared to the cis–cis could have the trans–trans conformer cloud the observation of the global minimum. However, temperatures of greater than the freezing point of water would be required for the population of thiocarbonic acid to populate the trans–trans conformer beyond 1%. Temperatures would have to surpass 800 K and populations of trans–trans above 15% before the rotational signals of the cis–cis and trans–trans conformers would approach parity in a Boltzmann averaging of the dipole moment contributions. However, the fairly low-lying and strongly polar cis–trans-thiocarbonic acid form would likely dominate the rotational spectrum for a thermal distribution of thiocarbonic acid beyond 200 K, but most astronomical regions are colder and non-thermal in nature. While cis–cis-H2CS3 will likely have some contribution to the rotational spectrum of thiocarbonic acid, the cis–trans form may yet be the most observable anyway, as with standard carbonic acid, due to its stronger dipole moment and comparatively low relative energy.
S bond length of 1.625 Å and C–S bond length of 1.751 Å in the cis–cis conformer are within 0.02 Å of the single crystal X-ray diffraction experimental data,64 implying that these isolated molecule computations are performing as expected. The two C2v conformers have the strongest similarity between rotational constants of the three forms of H2CS3. The dipole moment of the highest-energy trans–trans conformer is the greatest of the set at 3.26 D, implying that the close spectroscopic constants and the larger dipole moment compared to the cis–cis could have the trans–trans conformer cloud the observation of the global minimum. However, temperatures of greater than the freezing point of water would be required for the population of thiocarbonic acid to populate the trans–trans conformer beyond 1%. Temperatures would have to surpass 800 K and populations of trans–trans above 15% before the rotational signals of the cis–cis and trans–trans conformers would approach parity in a Boltzmann averaging of the dipole moment contributions. However, the fairly low-lying and strongly polar cis–trans-thiocarbonic acid form would likely dominate the rotational spectrum for a thermal distribution of thiocarbonic acid beyond 200 K, but most astronomical regions are colder and non-thermal in nature. While cis–cis-H2CS3 will likely have some contribution to the rotational spectrum of thiocarbonic acid, the cis–trans form may yet be the most observable anyway, as with standard carbonic acid, due to its stronger dipole moment and comparatively low relative energy.
Additionally, the positions of the hydrogen atoms do not significantly shift the mass of the C axis which lies along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 bond for any of the conformers. The Watson A-reduced spectroscopic constants are close in magnitude for the ΔJ values, but they shift for the other Δ and Φ constants given in Table 1. These given values should assist with high resolution classification of the rotational spectra for the conformers of H2CS3. The Cartesian coordinates for the optimized conformers of thiocarbonic acid are given in the SI, which can be utilized to interpret the cis–trans dipole moment vectors.
S1 bond for any of the conformers. The Watson A-reduced spectroscopic constants are close in magnitude for the ΔJ values, but they shift for the other Δ and Φ constants given in Table 1. These given values should assist with high resolution classification of the rotational spectra for the conformers of H2CS3. The Cartesian coordinates for the optimized conformers of thiocarbonic acid are given in the SI, which can be utilized to interpret the cis–trans dipole moment vectors.
3.2. Fundamental vibrational frequencies
As with most ketone- and thioketone-containing molecules, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch provides the most intense fundamental vibrational frequency for all of the conformers, including the lowest energy cis–cis-thiocarbonic acid conformer. As shown in Table 2, the ν3 C
S stretch provides the most intense fundamental vibrational frequency for all of the conformers, including the lowest energy cis–cis-thiocarbonic acid conformer. As shown in Table 2, the ν3 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch of cis–cis-thiocarbonic acid at 1143.8 cm−1 exhibits an intensity of 163 kcal mol−1 which is more than double the antisymmetric stretch in water. Somewhat surprisingly, the hydride stretches possess small intensities, but their bends exhibit more intensity. The b2 ν6 antisymmetric C–S stretch at 726.3 cm−1 has a notable intensity of more than 100 km mol−1, and most of the low frequency fundamentals do not exhibit large intensities save for the symmetric hydrogen atom OPB at 283.3 cm−1 with its 26 km mol−1 intensity. However, in the age of JWST, only those frequencies above 333 cm−1 would be observable, but the resolution of the MIRI instrument onboard is actually somewhat unreliable below 500 cm−1. As such ν3 and ν5 would be the most observable features with JWST, but all of the mid-IR features should be observable in laboratory experiments. Additionally, the harmonic intensities (given in Table S8) are notably different from these anharmonic values with the C
S1 stretch of cis–cis-thiocarbonic acid at 1143.8 cm−1 exhibits an intensity of 163 kcal mol−1 which is more than double the antisymmetric stretch in water. Somewhat surprisingly, the hydride stretches possess small intensities, but their bends exhibit more intensity. The b2 ν6 antisymmetric C–S stretch at 726.3 cm−1 has a notable intensity of more than 100 km mol−1, and most of the low frequency fundamentals do not exhibit large intensities save for the symmetric hydrogen atom OPB at 283.3 cm−1 with its 26 km mol−1 intensity. However, in the age of JWST, only those frequencies above 333 cm−1 would be observable, but the resolution of the MIRI instrument onboard is actually somewhat unreliable below 500 cm−1. As such ν3 and ν5 would be the most observable features with JWST, but all of the mid-IR features should be observable in laboratory experiments. Additionally, the harmonic intensities (given in Table S8) are notably different from these anharmonic values with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch shifting by more than 30 cm−1 and the S–H stretches by more than 120 cm−1. Hence, anharmonicity is essential for accurate depictions of the vibrational frequencies.
S stretch shifting by more than 30 cm−1 and the S–H stretches by more than 120 cm−1. Hence, anharmonicity is essential for accurate depictions of the vibrational frequencies.
Table 2 The fundamental vibrational frequencies (in cm−1 of cis–cis-H2CS3)
| Mode |
Sym. |
Description |
F12-TcCR |
f
|
|
“In-plane bend”.
|
| ν1 |
a
1
|
S–H sym. stretch |
2587.2 |
1 |
| ν2 |
b
2
|
S–H antisym. stretch |
2582.2 |
4 |
| ν3 |
a
1
|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch S1 stretch |
1143.8 |
163 |
| ν4 |
b
2
|
HSC antisym. IPBa |
949.2 |
23 |
| ν5 |
a
1
|
HSC sym. IPB |
891.8 |
58 |
| ν6 |
b
2
|
Antisym. C–S stretch |
726.3 |
105 |
| ν7 |
a
1
|
Sym. C–S stretch |
497.4 |
4 |
| ν8 |
b
1
|
C OPB |
366.2 |
5 |
| ν9 |
b
2
|
S1 IPB |
285.3 |
2 |
| ν10 |
b
1
|
H sym. OPB |
283.3 |
26 |
| ν11 |
a
1
|
S2–C–S3 IPB |
248.7 |
1 |
| ν12 |
a
2
|
H antisym. OPB |
68.0 |
0 |
| ZPT |
|
5536.2 |
|
Similar to the lowest energy conformer, the highest intensity trans–trans-H2CS3 fundamental vibrational frequency is the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 (ν3) vibration at 1137.7 cm−1 with an intensity of 152 km mol−1 as given in Table 3. Hence, this fundamental is 6.1 cm−1 less than its counterpart in the cis–cis form. Beyond this most intense fundamental frequency, a majority of the trans–trans fundamentals below 1000 cm−1 are higher than the corresponding cis–cis frequencies save for ν6 and ν7. Even so, both conformers showcase similar intensities between the two for their corresponding atomic motions.
S1 (ν3) vibration at 1137.7 cm−1 with an intensity of 152 km mol−1 as given in Table 3. Hence, this fundamental is 6.1 cm−1 less than its counterpart in the cis–cis form. Beyond this most intense fundamental frequency, a majority of the trans–trans fundamentals below 1000 cm−1 are higher than the corresponding cis–cis frequencies save for ν6 and ν7. Even so, both conformers showcase similar intensities between the two for their corresponding atomic motions.
Table 3 The fundamental vibrational frequencies (in cm−1 of trans–trans-H2CS3)
| Mode |
Sym. |
Description |
F12-TcCR |
f
|
| ν1 |
a
1
|
S–H sym. stretch |
2581.0 |
8 |
| ν2 |
b
2
|
S–H antisym. stretch |
2587.5 |
1 |
| ν3 |
a
1
|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 S1 |
1137.7 |
152 |
| ν4 |
b
2
|
HSC antisym. IPB |
997.5 |
31 |
| ν5 |
a
1
|
HSC sym. IPB |
921.5 |
75 |
| ν6 |
b
2
|
Antisym. C–S stretch |
836.7 |
69 |
| ν7 |
a
1
|
Sym. C–S stretch |
483.9 |
10 |
| ν8 |
b
1
|
C OPB |
416.4 |
6 |
| ν10 |
b
1
|
H sym. OPB |
333.5 |
1 |
| ν12 |
a
2
|
H antisym. OPB |
297.5 |
0 |
| ν9 |
a
1
|
S2–C–S3 IPB |
275.4 |
22 |
| ν11 |
b
2
|
S1 IPB |
261.3 |
1 |
| ZPT |
|
|
5632.1 |
|
The S–H stretches (ν1 & ν2) of the cis–trans conformer localize notably into their respective portions and do not couple as they do in either of the Cs conformations. These frequencies are in line with the 2550 cm−1 and 2525 cm−1 S–H stretches recorded in dilute solution 60 years ago.65 The localization breaks down for the C–S/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches (ν3, ν5, & ν7) as these have contributions from either their C–S counterparts and/or from the HSC bends. The lower-frequency IPBs are also comprised of several simple-internal coordinates combined together, making delineation of these modes difficult to classify. Hence, they are left generically labeled in Table 4.
S stretches (ν3, ν5, & ν7) as these have contributions from either their C–S counterparts and/or from the HSC bends. The lower-frequency IPBs are also comprised of several simple-internal coordinates combined together, making delineation of these modes difficult to classify. Hence, they are left generically labeled in Table 4.
Table 4 The fundamental vibrational frequencies (in cm−1 of cis–trans-H2CS3)
| Mode |
Sym. |
Description |
F12-TcCR |
f
|
| ν1 |
a′ |
cis-S–H stretch |
2598.7 |
1 |
| ν2 |
a′ |
trans-S–H stretch |
2570.8 |
2 |
| ν3 |
a′ |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch S1 stretch |
1149.4 |
162 |
| ν4 |
a′ |
IPB |
1017.7 |
24 |
| ν5 |
a′ |
cis-C–S stretch |
896.2 |
61 |
| ν6 |
a′ |
IPB |
806.7 |
56 |
| ν7 |
a′ |
trans-C–S stretch |
495.2 |
6 |
| ν8 |
a″ |
C OPB |
508.2 |
7 |
| ν9 |
a″ |
OPB |
348.8 |
4 |
| ν10 |
a′ |
IPB |
284.8 |
2 |
| ν11 |
a″ |
OPB |
304.6 |
23 |
| ν12 |
a′ |
IPB |
257.6 |
1 |
| ZPT |
|
|
5691.4 |
|
The ν3 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch in the cis–trans conformer (Table 4) is, once more, the most intense fundamental frequency. Its intensity of 162 km mol−1 is nearly the same as the lowest energy cis–cis conformer. The frequency is higher here for the cis–trans at 1149.4 cm−1, giving the C
S1 stretch in the cis–trans conformer (Table 4) is, once more, the most intense fundamental frequency. Its intensity of 162 km mol−1 is nearly the same as the lowest energy cis–cis conformer. The frequency is higher here for the cis–trans at 1149.4 cm−1, giving the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches a span from 1150 cm−1 to 1135 cm−1; the near-coincident family of C
S stretches a span from 1150 cm−1 to 1135 cm−1; the near-coincident family of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch features across the three isomers is shown in Fig. 2 with the inlay giving finer detail. These C
S stretch features across the three isomers is shown in Fig. 2 with the inlay giving finer detail. These C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches are notably higher in frequency than that of thioformaldehyde (H2CS) which lies at 1059 cm−1.66 Hence, the C
S stretches are notably higher in frequency than that of thioformaldehyde (H2CS) which lies at 1059 cm−1.66 Hence, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch in thiocarbonic acid should be a distinguishing feature between H2CS3 and H2 CS if they are synthesized in the gas phase simultaneously. Furthermore, the thiocarbonic acid C
S stretch in thiocarbonic acid should be a distinguishing feature between H2CS3 and H2 CS if they are synthesized in the gas phase simultaneously. Furthermore, the thiocarbonic acid C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches correspond to 8.73 µm which is on the edge of known spectral features commonly attributed to polycyclic aromatic hydrocarbon (PAH) cations.67 The thiocarbonic acid C
S stretches correspond to 8.73 µm which is on the edge of known spectral features commonly attributed to polycyclic aromatic hydrocarbon (PAH) cations.67 The thiocarbonic acid C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching frequencies should be distinctive enough, though, for the H2CS3 features not to be swallowed up by the PAH cations if the thiocarbonic acid conformers are in high enough abundance and/or observed in carbon-poor regions.
S stretching frequencies should be distinctive enough, though, for the H2CS3 features not to be swallowed up by the PAH cations if the thiocarbonic acid conformers are in high enough abundance and/or observed in carbon-poor regions.
 |
| | Fig. 2 A visual depiction of the IR spectrum for the three conformers of thiocarbonic acid artificially broadened with a FWHM of 3.0 cm−1. | |
None of the other cis–trans conformer fundamental frequency intensities are greater than 61 km mol−1 (ν5, C–S stretch) akin to the same behavior in trans–trans. Again, such behavior becomes evident in analyzing the IR spectra of the three conformers (with equal concentrations) modeled in Fig. 2. Clearly, the range from 750 cm−1 to 1050 cm−1 share similar intensities for similar transitions across these two conformers and even the lowest-energy cis–cis. However, again, the ν6 antisymmetric C–S stretch in cis–cis showcases the uniquely intensive behavior of this conformer in the range below 750 cm−1. Fig. 2 further highlights that S–H stretches in the region around 2600 cm−1 are not going to be major contributors to thiocarbonic acid IR spectra and subsequent observations in any environment including the laboratory.
Of course, the spectrum in Fig. 2 assumes the same population for all three conformers. Boltzmann probabilities of the relative energies produce a more physically-meaningful representation of the vibrational spectrum for H2CS3. At 300 K, the cis–cis conformer dominates the spectrum (Fig. S1), but the cis–trans contributes somewhat with the trans–trans conformer only giving any intensity to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch. At 10K, however, (Fig. S2) only the cis–cis conformer has any population and will be the sole carrier of any vibrational spectrum of thiocarbonic acid.
S stretch. At 10K, however, (Fig. S2) only the cis–cis conformer has any population and will be the sole carrier of any vibrational spectrum of thiocarbonic acid.
Finally, the treated Fermi and Coriolis resonances are listed in the SI along with the vibrationally excited rotational constants. The latter provide for any future constructions of a full rovibronic model for each thiocarbonic acid conformer's rotational ladder and spectrum.
4. Conclusions
While the dipole moment of the lowest energy cis–cis conformer of thiocarbonic acid (0.75 D) is notably greater than that of the analogous carbonic acid, the factor of three increase in the dipole moment (2.17 D) for the 0.64 kcal mol−1 higher cis–trans-H2CS3 conformer implies that the cis–trans could still be more observable than the cis–cis. While this behavior would follow the pattern for standard carbonic acid,19 either or potentially both of these low energy conformers could be observable in regions where thiocarbonic acid may be present. Since recent laboratory experiments imply that the warming of ices in the regions surrounding protostars during their formation could form and desorb H2CS3 into the gas phase, star-forming regions would be a natural place to look for thiocarbonic acid in any of its conformational forms. Additionally, the principle rotational and spectroscopic constants in this work should be accurate to within 3 MHz, or potentially even 1 MHz, of experiment, implying that the data produced here could be utilized for direct observation of these molecules. Even if not, these data will certainly assist in laboratory characterization of the rotational lines for thiocarbonic acid for comparison to observed spectra.
Beyond the rotational and radioastronomical implications, the fundamental vibrational frequencies and IR spectra are showcasing the unique nature of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch in thiocarbonic acid. These fundamental stretches for each of the three conformers are all within 15 cm−1 of each other in the range of 1135 cm−1 to 1150 cm−1. The group of C
S stretch in thiocarbonic acid. These fundamental stretches for each of the three conformers are all within 15 cm−1 of each other in the range of 1135 cm−1 to 1150 cm−1. The group of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching frequencies are also 75 cm−1 to 90 cm−1 greater than the same motion in H2CS. Hence, the additional sulfur atoms in the larger molecule shift the behavior of the C
S stretching frequencies are also 75 cm−1 to 90 cm−1 greater than the same motion in H2CS. Hence, the additional sulfur atoms in the larger molecule shift the behavior of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch. Beyond this most intense frequency in each conformer, the low frequency fundamentals have little intensity as do the hydride stretches, leaving the mid-IR as the best place to find potential tell-tale IR signatures of thiocarbonic acid.
S stretch. Beyond this most intense frequency in each conformer, the low frequency fundamentals have little intensity as do the hydride stretches, leaving the mid-IR as the best place to find potential tell-tale IR signatures of thiocarbonic acid.
Conflicts of interest
There are no conflicts to declare.
Data availability
The datasets supporting this article have been uploaded as part of the article or the supplementary information (SI). The SI contains the harmonic frequencies, Cartesian molecular coordinates, resonance treatments, and temperature-based simulated infrared spectra for the three conformers of thiocarbonic acid. See DOI: https://doi.org/10.1039/d5cp03877d.
Acknowledgements
This work is supported by NASA Grants 22-A22ISFM-0009 and 80NSSC24M0132 as well as NSF Grant CHE-2150352. Computational support from the Mississippi Center for Supercomputing Research funded in part by NSF Grant OIA-1757220 is also acknowledged.
References
- S. S. Prasad and W. T. Huntress, Astrophys. J., 1982, 260, 590–598 CrossRef CAS.
- E. B. Jenkins, Astrophys. J., 2009, 700, 1299–1348 CrossRef CAS.
- A. Herath, M. McAnally, A. M. Turner, J. Wang, J. H. Marks, R. C. Fortenberry, J. C. Garcia-Alvarez, S. Gozem and R. I. Kaiser, Nat. Commun., 2025, 16, 5571 CrossRef PubMed.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17 CrossRef CAS.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2021, 259, 30 CrossRef.
- A. A. Penzias, P. M. Solomon, R. W. Wilson, A. A. Penzias and K. B. Jefferts, Astrophys. J., 1971, 168, L53–L58 CrossRef CAS.
- B. Zuckerman, M. Morris, P. Palmer and B. E. Turner, Astrophys. J., 1972, 173, L125–L129 CrossRef.
- C. Cabezas, K. Vávra, G. Molpeceres, L. Kolesniková, M. Agúndez, G. Vylitová, N. Marcelino, L. Hrubčik, R. Fuentetaja, T. Uhliková, B. Tercero, J. Koucky, G. Esplugues, P. Kania, P. de Vicente, S. Urban and J. Cernicharo, Astron. Astrophys., 2025, 698, L24 CrossRef CAS.
- A. Manna and S. Pal, ACS Earth Space Chem., 2024, 8, 2401–2410 CrossRef CAS.
- M. Agúndez, G. Molpeceres, C. Cabezas, N. Marcelino, B. Tercero, R. Fuentetaja, P. de Vicente and J. Cernicharo, Astron. Astrophys., 2025, 693, L20 CrossRef.
- M. Sanz-Novo, V. M. Rivilla, C. P. Endres, V. Lattanzi, I. Jiménez-Serra, L. Colzi, S. Zeng, A. Megias, A. López-Gallifa, A. Martinez-Henares, D. S. Andrés, B. Tercero, P. de Vicente, S. Martin, M. A. Requena-Torres, P. Caselli and J. Martin-Pintad, Astrophys. J., Lett., 2025, 980, L37 CrossRef CAS.
- A. J. Remijan, P. B. Changala, C. Xue, E. Q. H. Yuan, M. Duffy, H. N. Scolati, C. N. Shingledecker, T. H. Speak, I. R. Cooke, R. Loomis, A. M. Burkhardt, Z. T. P. Fried, G. Wenzel, A. Lipnicky, M. C. McCarthy and B. A. McGuire, Astrophys. J., 2025, 982, 191 CrossRef.
- B. Zuckerman, J. A. Ball and C. A. Gottlieb, Astrophys. J., 1971, 163, L41–45 CrossRef CAS.
- L. Coulaud, J. Wang, A. Herath, A. M. Turner, R. C. Fortenberry and R. I. Kaiser, Phys. Chem. Chem. Phys., 2025, 27, 19324–19337 RSC.
- A. M. Wallace and R. C. Fortenberry, J. Phys. Chem. A, 2021, 125, 4589–4597 CrossRef CAS.
- P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Chem. Phys., 2007, 126, 204315 CrossRef PubMed.
- X. Wang and T. Bürgi, Angew. Chem., Int. Ed., 2021, 60, 7860–7865 CrossRef CAS PubMed.
- S. Ioppolo, Z. Kanuchová, R. L. James, A. Dawes, A. Ryabov, J. Dezalay, N. C. Jones, S. V. Hoffmann, N. J. Mason and G. Strazzulla, Astron. Astrophys., 2021, 646, A172 CrossRef CAS.
- M. Sanz-Novo, V. M. Rivilla, I. Jiménez-Serra, J. Martín-Pintado, L. Colzi, S. Zeng, A. Megías, Á. López-Gallifa, A. Martínez-Henares, S. Massalkhi, B. Tercero, P. de Vicente, S. Martín, D. San Andrés and M. A. Requena-Torres, Astrophys. J., 2023, 954, 3 CrossRef CAS PubMed.
- R. C. Fortenberry and V. J. Esposito, Astrophys. J., 2024, 961, 164 CrossRef.
- R. Thackston and R. C. Fortenberry, J. Math. Chem., 2018, 56, 103–119 CrossRef CAS.
- R. C. Fortenberry and T. J. Lee, Annu. Rep. Comput. Chem., 2019, 15, 173–202 Search PubMed.
- M. B. Gardner, B. R. Westbrook and R. C. Fortenberry, Planet. Space Sci., 2020, 193, 105176 CrossRef.
-
R. C. Fortenberry and T. J. Lee, Vibrational Dynamics of Molecules, World Scientific, Singapore, 2022, pp. 235–295 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
-
I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, Cambridge, 2009 Search PubMed.
-
T. D. Crawford and H. F. Schaefer III, Reviews in Computational Chemistry, Wiley, New York, 2000, vol. 14, pp. 33–136 Search PubMed.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- J. G. Hill and K. A. Peterson, Phys. Chem. Chem. Phys., 2010, 12, 10460–10468 RSC.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- A. G. Watrous, B. R. Westbrook and R. C. Fortenberry, J. Phys. Chem. A, 2021, 125, 10532–10540 CrossRef CAS.
- X. Huang and T. J. Lee, J. Chem. Phys., 2008, 129, 044312 CrossRef PubMed.
- X. Huang and T. J. Lee, J. Chem. Phys., 2009, 131, 104301 CrossRef.
- X. Huang, P. R. Taylor and T. J. Lee, J. Phys. Chem. A, 2011, 115, 5005–5016 CrossRef CAS PubMed.
- R. C. Fortenberry, X. Huang, J. S. Francisco, T. D. Crawford and T. J. Lee, J. Chem. Phys., 2011, 135, 134301 CrossRef PubMed.
- R. C. Fortenberry, X. Huang, J. S. Francisco, T. D. Crawford and T. J. Lee, J. Chem. Phys., 2011, 135, 214303 CrossRef PubMed.
- R. C. Fortenberry, X. Huang, J. S. Francisco, T. D. Crawford and T. J. Lee, J. Chem. Phys., 2012, 136, 234309 CrossRef PubMed.
- K. D. Doney, A. Candian, T. Mori, T. Onaka and A. G. G. M. Tielens, Astron. Astrophys., 2016, 586, A65 CrossRef.
- M. J. R. Kitchens and R. C. Fortenberry, Chem. Phys., 2016, 472, 119–127 CrossRef CAS.
- L. Bizzocchi, V. Lattanzi, J. Laas, S. Spezzano, B. M. Giuliano, D. Prudenzano, C. Endres, O. Sipilä and P. Caselli, Astron. Astrophys., 2017, 602, A34 CrossRef.
- W. Györffy and H.-J. Werner, J. Chem. Phys., 2018, 148, 114104 CrossRef PubMed.
- M. C. Davis, N. R. Garrett and R. C. Fortenberry, Phys. Chem. Chem. Phys., 2022, 24, 18552–18558 RSC.
- A. G. Watrous, B. R. Westbrook and R. C. Fortenberry, Mon. Not. R. Astron. Soc., 2024, 527, 11090–11094 CrossRef CAS.
- B. R. Westbrook and R. C. Fortenberry, Vib. Spectrosc., 2024, 132, 103690 CrossRef CAS.
-
J. K. G. Watson, Vibrational Spectra and Structure, Elsevier, Amsterdam, 1977, pp. 1–89 Search PubMed.
-
I. M. Mills, Molecular Spectroscopy - Modern Research, Academic Press, New York, 1972, pp. 115–140 Search PubMed.
-
D. Papousek and M. R. Aliev, Molecular Vibration-Rotation Spectra, Elsevier, Amsterdam, 1982 Search PubMed.
- P. R. Franke, J. F. Stanton and G. E. Douberly, J. Phys. Chem. A, 2021, 125, 1301–1324 CrossRef CAS PubMed.
-
J. F. Gaw, A. Willets, W. H. Green and N. C. Handy, Advances in Molecular Vibrations and Collision Dynamics, JAI Press, Inc., Greenwich, Connecticut, 1991, pp. 170–185 Search PubMed.
- B. R. Westbrook and R. C. Fortenberry, J. Chem. Theory Comput., 2023, 19, 2606–2615 CrossRef CAS PubMed.
-
H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version, a package of ab initio programs, see https://www.molpro.net.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- W. T. Yang, R. G. Parr and C. T. Lee, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 4586–4590 CrossRef CAS PubMed.
- C. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT Search PubMed.
- B. Krebs and G. Henkel, Z. Kristallogr. – Cryst. Mater., 1987, 179, 373–382 CrossRef CAS.
- P. Tice and D. Powell, Spectrochim. Acta, 1965, 21, 835–839 CrossRef CAS.
- J.-M. Flaud, W. Lafferty, A. Perrin, Y. Kim, H. Beckers and H. Willner, J. Quant. Spectrosc. Radiat. Transfer, 2008, 109, 995–1003 CrossRef CAS.
- A. Li and B. T. Draine, Astrophys. J., 2001, 554, 778 CrossRef CAS.
|
| This journal is © the Owner Societies 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  *
*
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SSH) in 2024.9 Formic acid has been known in astronomical environments since the same time as CS,13 but the fully sulfurous form only emerged recently, more than 50 years later. Formic acid is found throughout biochemistry, and its significance is well-known. For instance this molecule is produced by ants here on Earth which gives them their distinctive odor when crushed. Regardless, this pairing of astronomically-observed formic acid and its sulfur analogue is not unique. More than 30 pairs of oxygen–sulfur analogue molecules where the oxygen form has an exact match to the sulfurous form have been observed towards astronomical sources.14 These include alcohols/thiols, aldehydes/thioaldehydes, eithers/thioethers, and various other chalcogen analogues. These pairs alone constitute roughly a quarter of the known, unique interstellar molecules,4,5 implying a growing role that sulfur is playing in our understanding of interstellar chemistry.
SSH) in 2024.9 Formic acid has been known in astronomical environments since the same time as CS,13 but the fully sulfurous form only emerged recently, more than 50 years later. Formic acid is found throughout biochemistry, and its significance is well-known. For instance this molecule is produced by ants here on Earth which gives them their distinctive odor when crushed. Regardless, this pairing of astronomically-observed formic acid and its sulfur analogue is not unique. More than 30 pairs of oxygen–sulfur analogue molecules where the oxygen form has an exact match to the sulfurous form have been observed towards astronomical sources.14 These include alcohols/thiols, aldehydes/thioaldehydes, eithers/thioethers, and various other chalcogen analogues. These pairs alone constitute roughly a quarter of the known, unique interstellar molecules,4,5 implying a growing role that sulfur is playing in our understanding of interstellar chemistry.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OOH or H2CO3). This molecule is an isomer of water complexed with carbon dioxide and is related to formic acid where the lone C–H group in formic acid is replaced with a hydroxyl group in H2CO3. Carbonic acid is both a diol and a ketone giving it several hallmarks of organic functionalization and, recently, has been shown to form unique helical microscopic complexes for increasingly larger monomolecular clusters.15 It also likely plays a role in ocean acidification but is notoriously unstable due to its preference to form H2O + CO2.16–18 Despite this instability and its chronic elusiveness in the laboratory except at cold temperatures, carbonic acid is now known to exist in astronomical environments.19 The radioastronomical detection of this molecule toward a molecular cloud in the vicinity of the central region of our galaxy was actually for the second-lowest energy conformer (cis–trans). The dipole moment of the cis–cis global minimum is close enough to 0.0 D (specifically 0.2 D) for its signal to be insufficient for observation. That of the higher cis–trans conformer is over 3.0 D, high enough for this version to be observed over its more stable corresponding conformer. Even so, carbonic acid does not appear to be as elusive in space as it can be in the atmosphere or the laboratory. This opens the door for the examination of related molecules observed in astronomical environments. As such, the astronomical presence of the formic acid/dithioformic acid chalcogen analogue pair along with the known interstellar detection of carbonic acid implies that similar chemistry could be at play in the interstellar medium for the sulfurous analogues of H2CO3, as well.
OOH or H2CO3). This molecule is an isomer of water complexed with carbon dioxide and is related to formic acid where the lone C–H group in formic acid is replaced with a hydroxyl group in H2CO3. Carbonic acid is both a diol and a ketone giving it several hallmarks of organic functionalization and, recently, has been shown to form unique helical microscopic complexes for increasingly larger monomolecular clusters.15 It also likely plays a role in ocean acidification but is notoriously unstable due to its preference to form H2O + CO2.16–18 Despite this instability and its chronic elusiveness in the laboratory except at cold temperatures, carbonic acid is now known to exist in astronomical environments.19 The radioastronomical detection of this molecule toward a molecular cloud in the vicinity of the central region of our galaxy was actually for the second-lowest energy conformer (cis–trans). The dipole moment of the cis–cis global minimum is close enough to 0.0 D (specifically 0.2 D) for its signal to be insufficient for observation. That of the higher cis–trans conformer is over 3.0 D, high enough for this version to be observed over its more stable corresponding conformer. Even so, carbonic acid does not appear to be as elusive in space as it can be in the atmosphere or the laboratory. This opens the door for the examination of related molecules observed in astronomical environments. As such, the astronomical presence of the formic acid/dithioformic acid chalcogen analogue pair along with the known interstellar detection of carbonic acid implies that similar chemistry could be at play in the interstellar medium for the sulfurous analogues of H2CO3, as well.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) SSH or H2CS3) has been synthesized and desorbed into the gas phase from irradiation of mixed H2S and CS2 ices with simulated cosmic rays.14 These experiments highlight that ice present in protostellar environments could be ionized as star formation begins and create thiocarbonic acid. This molecule could then be desorbed into the gas phase making it possible for radioastronomical observation. Additionally, once thiocarbonic acid is present in such regions, its density of sulfur could allow it to form other sulfurous molecules leading to molecules yet to be observed, increasing the sulfur population in space.14 Of course, such is speculation until observation of the parent molecules like H2CS3 can be achieved.
SSH or H2CS3) has been synthesized and desorbed into the gas phase from irradiation of mixed H2S and CS2 ices with simulated cosmic rays.14 These experiments highlight that ice present in protostellar environments could be ionized as star formation begins and create thiocarbonic acid. This molecule could then be desorbed into the gas phase making it possible for radioastronomical observation. Additionally, once thiocarbonic acid is present in such regions, its density of sulfur could allow it to form other sulfurous molecules leading to molecules yet to be observed, increasing the sulfur population in space.14 Of course, such is speculation until observation of the parent molecules like H2CS3 can be achieved.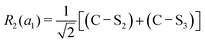
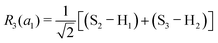
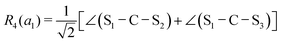
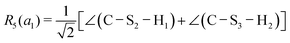
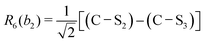
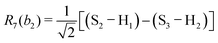
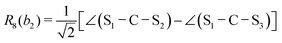
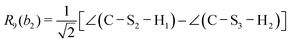

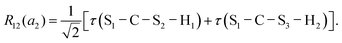

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond length of 1.625 Å and C–S bond length of 1.751 Å in the cis–cis conformer are within 0.02 Å of the single crystal X-ray diffraction experimental data,64 implying that these isolated molecule computations are performing as expected. The two C2v conformers have the strongest similarity between rotational constants of the three forms of H2CS3. The dipole moment of the highest-energy trans–trans conformer is the greatest of the set at 3.26 D, implying that the close spectroscopic constants and the larger dipole moment compared to the cis–cis could have the trans–trans conformer cloud the observation of the global minimum. However, temperatures of greater than the freezing point of water would be required for the population of thiocarbonic acid to populate the trans–trans conformer beyond 1%. Temperatures would have to surpass 800 K and populations of trans–trans above 15% before the rotational signals of the cis–cis and trans–trans conformers would approach parity in a Boltzmann averaging of the dipole moment contributions. However, the fairly low-lying and strongly polar cis–trans-thiocarbonic acid form would likely dominate the rotational spectrum for a thermal distribution of thiocarbonic acid beyond 200 K, but most astronomical regions are colder and non-thermal in nature. While cis–cis-H2CS3 will likely have some contribution to the rotational spectrum of thiocarbonic acid, the cis–trans form may yet be the most observable anyway, as with standard carbonic acid, due to its stronger dipole moment and comparatively low relative energy.
S bond length of 1.625 Å and C–S bond length of 1.751 Å in the cis–cis conformer are within 0.02 Å of the single crystal X-ray diffraction experimental data,64 implying that these isolated molecule computations are performing as expected. The two C2v conformers have the strongest similarity between rotational constants of the three forms of H2CS3. The dipole moment of the highest-energy trans–trans conformer is the greatest of the set at 3.26 D, implying that the close spectroscopic constants and the larger dipole moment compared to the cis–cis could have the trans–trans conformer cloud the observation of the global minimum. However, temperatures of greater than the freezing point of water would be required for the population of thiocarbonic acid to populate the trans–trans conformer beyond 1%. Temperatures would have to surpass 800 K and populations of trans–trans above 15% before the rotational signals of the cis–cis and trans–trans conformers would approach parity in a Boltzmann averaging of the dipole moment contributions. However, the fairly low-lying and strongly polar cis–trans-thiocarbonic acid form would likely dominate the rotational spectrum for a thermal distribution of thiocarbonic acid beyond 200 K, but most astronomical regions are colder and non-thermal in nature. While cis–cis-H2CS3 will likely have some contribution to the rotational spectrum of thiocarbonic acid, the cis–trans form may yet be the most observable anyway, as with standard carbonic acid, due to its stronger dipole moment and comparatively low relative energy.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 bond for any of the conformers. The Watson A-reduced spectroscopic constants are close in magnitude for the ΔJ values, but they shift for the other Δ and Φ constants given in Table 1. These given values should assist with high resolution classification of the rotational spectra for the conformers of H2CS3. The Cartesian coordinates for the optimized conformers of thiocarbonic acid are given in the SI, which can be utilized to interpret the cis–trans dipole moment vectors.
S1 bond for any of the conformers. The Watson A-reduced spectroscopic constants are close in magnitude for the ΔJ values, but they shift for the other Δ and Φ constants given in Table 1. These given values should assist with high resolution classification of the rotational spectra for the conformers of H2CS3. The Cartesian coordinates for the optimized conformers of thiocarbonic acid are given in the SI, which can be utilized to interpret the cis–trans dipole moment vectors.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch provides the most intense fundamental vibrational frequency for all of the conformers, including the lowest energy cis–cis-thiocarbonic acid conformer. As shown in Table 2, the ν3 C
S stretch provides the most intense fundamental vibrational frequency for all of the conformers, including the lowest energy cis–cis-thiocarbonic acid conformer. As shown in Table 2, the ν3 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch of cis–cis-thiocarbonic acid at 1143.8 cm−1 exhibits an intensity of 163 kcal mol−1 which is more than double the antisymmetric stretch in water. Somewhat surprisingly, the hydride stretches possess small intensities, but their bends exhibit more intensity. The b2 ν6 antisymmetric C–S stretch at 726.3 cm−1 has a notable intensity of more than 100 km mol−1, and most of the low frequency fundamentals do not exhibit large intensities save for the symmetric hydrogen atom OPB at 283.3 cm−1 with its 26 km mol−1 intensity. However, in the age of JWST, only those frequencies above 333 cm−1 would be observable, but the resolution of the MIRI instrument onboard is actually somewhat unreliable below 500 cm−1. As such ν3 and ν5 would be the most observable features with JWST, but all of the mid-IR features should be observable in laboratory experiments. Additionally, the harmonic intensities (given in Table S8) are notably different from these anharmonic values with the C
S1 stretch of cis–cis-thiocarbonic acid at 1143.8 cm−1 exhibits an intensity of 163 kcal mol−1 which is more than double the antisymmetric stretch in water. Somewhat surprisingly, the hydride stretches possess small intensities, but their bends exhibit more intensity. The b2 ν6 antisymmetric C–S stretch at 726.3 cm−1 has a notable intensity of more than 100 km mol−1, and most of the low frequency fundamentals do not exhibit large intensities save for the symmetric hydrogen atom OPB at 283.3 cm−1 with its 26 km mol−1 intensity. However, in the age of JWST, only those frequencies above 333 cm−1 would be observable, but the resolution of the MIRI instrument onboard is actually somewhat unreliable below 500 cm−1. As such ν3 and ν5 would be the most observable features with JWST, but all of the mid-IR features should be observable in laboratory experiments. Additionally, the harmonic intensities (given in Table S8) are notably different from these anharmonic values with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch shifting by more than 30 cm−1 and the S–H stretches by more than 120 cm−1. Hence, anharmonicity is essential for accurate depictions of the vibrational frequencies.
S stretch shifting by more than 30 cm−1 and the S–H stretches by more than 120 cm−1. Hence, anharmonicity is essential for accurate depictions of the vibrational frequencies.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch
S1 stretch![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 (ν3) vibration at 1137.7 cm−1 with an intensity of 152 km mol−1 as given in Table 3. Hence, this fundamental is 6.1 cm−1 less than its counterpart in the cis–cis form. Beyond this most intense fundamental frequency, a majority of the trans–trans fundamentals below 1000 cm−1 are higher than the corresponding cis–cis frequencies save for ν6 and ν7. Even so, both conformers showcase similar intensities between the two for their corresponding atomic motions.
S1 (ν3) vibration at 1137.7 cm−1 with an intensity of 152 km mol−1 as given in Table 3. Hence, this fundamental is 6.1 cm−1 less than its counterpart in the cis–cis form. Beyond this most intense fundamental frequency, a majority of the trans–trans fundamentals below 1000 cm−1 are higher than the corresponding cis–cis frequencies save for ν6 and ν7. Even so, both conformers showcase similar intensities between the two for their corresponding atomic motions.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1
S1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches (ν3, ν5, & ν7) as these have contributions from either their C–S counterparts and/or from the HSC bends. The lower-frequency IPBs are also comprised of several simple-internal coordinates combined together, making delineation of these modes difficult to classify. Hence, they are left generically labeled in Table 4.
S stretches (ν3, ν5, & ν7) as these have contributions from either their C–S counterparts and/or from the HSC bends. The lower-frequency IPBs are also comprised of several simple-internal coordinates combined together, making delineation of these modes difficult to classify. Hence, they are left generically labeled in Table 4.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch
S1 stretch![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1 stretch in the cis–trans conformer (Table 4) is, once more, the most intense fundamental frequency. Its intensity of 162 km mol−1 is nearly the same as the lowest energy cis–cis conformer. The frequency is higher here for the cis–trans at 1149.4 cm−1, giving the C
S1 stretch in the cis–trans conformer (Table 4) is, once more, the most intense fundamental frequency. Its intensity of 162 km mol−1 is nearly the same as the lowest energy cis–cis conformer. The frequency is higher here for the cis–trans at 1149.4 cm−1, giving the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches a span from 1150 cm−1 to 1135 cm−1; the near-coincident family of C
S stretches a span from 1150 cm−1 to 1135 cm−1; the near-coincident family of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch features across the three isomers is shown in Fig. 2 with the inlay giving finer detail. These C
S stretch features across the three isomers is shown in Fig. 2 with the inlay giving finer detail. These C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches are notably higher in frequency than that of thioformaldehyde (H2CS) which lies at 1059 cm−1.66 Hence, the C
S stretches are notably higher in frequency than that of thioformaldehyde (H2CS) which lies at 1059 cm−1.66 Hence, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch in thiocarbonic acid should be a distinguishing feature between H2CS3 and H2 CS if they are synthesized in the gas phase simultaneously. Furthermore, the thiocarbonic acid C
S stretch in thiocarbonic acid should be a distinguishing feature between H2CS3 and H2 CS if they are synthesized in the gas phase simultaneously. Furthermore, the thiocarbonic acid C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretches correspond to 8.73 µm which is on the edge of known spectral features commonly attributed to polycyclic aromatic hydrocarbon (PAH) cations.67 The thiocarbonic acid C
S stretches correspond to 8.73 µm which is on the edge of known spectral features commonly attributed to polycyclic aromatic hydrocarbon (PAH) cations.67 The thiocarbonic acid C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching frequencies should be distinctive enough, though, for the H2CS3 features not to be swallowed up by the PAH cations if the thiocarbonic acid conformers are in high enough abundance and/or observed in carbon-poor regions.
S stretching frequencies should be distinctive enough, though, for the H2CS3 features not to be swallowed up by the PAH cations if the thiocarbonic acid conformers are in high enough abundance and/or observed in carbon-poor regions.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch. At 10K, however, (Fig. S2) only the cis–cis conformer has any population and will be the sole carrier of any vibrational spectrum of thiocarbonic acid.
S stretch. At 10K, however, (Fig. S2) only the cis–cis conformer has any population and will be the sole carrier of any vibrational spectrum of thiocarbonic acid.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch in thiocarbonic acid. These fundamental stretches for each of the three conformers are all within 15 cm−1 of each other in the range of 1135 cm−1 to 1150 cm−1. The group of C
S stretch in thiocarbonic acid. These fundamental stretches for each of the three conformers are all within 15 cm−1 of each other in the range of 1135 cm−1 to 1150 cm−1. The group of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretching frequencies are also 75 cm−1 to 90 cm−1 greater than the same motion in H2CS. Hence, the additional sulfur atoms in the larger molecule shift the behavior of the C
S stretching frequencies are also 75 cm−1 to 90 cm−1 greater than the same motion in H2CS. Hence, the additional sulfur atoms in the larger molecule shift the behavior of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S stretch. Beyond this most intense frequency in each conformer, the low frequency fundamentals have little intensity as do the hydride stretches, leaving the mid-IR as the best place to find potential tell-tale IR signatures of thiocarbonic acid.
S stretch. Beyond this most intense frequency in each conformer, the low frequency fundamentals have little intensity as do the hydride stretches, leaving the mid-IR as the best place to find potential tell-tale IR signatures of thiocarbonic acid.