Fe–N–C electrocatalysts derived from a 1,10-phenanthroline–iron complex: kinetic insights into the acidic oxygen reduction reaction
Matheus
Martins
a,
Bianca Tainá
Ferreira
b,
Carlos
Sant’ana Vasconcellos
b,
Nelson A.
Galiote
 b,
Fabio Henrique Barros
Lima
b,
Fabio Henrique Barros
Lima
 b and
Fritz
Huguenin
b and
Fritz
Huguenin
 *a
*a
aDepartamento de Química, Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto – Universidade de São Paulo, 14040-901 Ribeirão Preto (SP), Brazil. E-mail: fritz@ffclrp.usp.br; Tel: +55 16 3315 4862
bInstituto de Química de São Carlos – Universidade de São Paulo, 13560-970 São Carlos (SP), Brazil
First published on 21st November 2025
Abstract
Iron–nitrogen–carbon (Fe–N–C) electrocatalysts have emerged as promising alternatives to platinum for the oxygen reduction reaction (ORR) in acidic media. Herein, we report the synthesis of an Fe–N–C catalyst via impregnation and complexation of iron(III) nitrate and 1,10-phenanthroline onto carbon black, followed by pyrolysis at high temperature. Transmission electron microscopy and X-ray energy-dispersive spectroscopy revealed a uniform distribution of Fe within the porous carbon matrix. The ORR performance was investigated using rotating ring-disk electrode experiments in oxygen-saturated 0.5 mol L−1 H2SO4. The material exhibited an onset potential of approximately 0.83 V vs. RHE, with a maximum turnover frequency of 5.4 O2 s−1 per active site at 10 mA cm−2. A Tafel slope of approximately 118 mV dec−1 identified the first electron transfer as the rate-determining step. A comprehensive kinetic model was developed in the frequency domain, accounting for both interfacial electron transfer and mass transport in the porous electrode, enabling the extraction of intrinsic rate constants and surface coverage parameters. The findings demonstrate the mechanistic and kinetic advantages of Fe–N–C catalysts synthesized using 1,10-phenanthroline, offering valuable insights for the design of advanced ORR electrocatalysts for fuel cells and metal–air batteries.
Introduction
Energy storage and conversion devices, such as metal–air batteries and fuel cells, have been extensively investigated due to growing concerns regarding environmental impacts and sustainability. Among the electrochemical reactions occurring within these systems, the oxygen reduction reaction (ORR) at the cathodic side during discharge is of particular importance. However, the inherently slow kinetics of this multi-electron reaction significantly limits current density, thereby restricting power output and overall energy efficiency. Consequently, extensive research efforts have been directed toward the development of highly active electrocatalysts to enhance ORR performance.1–4Among the various electrocatalysts proposed and investigated, single-atom catalysts synthesized via the pyrolysis of carbonaceous materials doped with transition metals and nitrogen have emerged as promising candidates for ORR applications. Transition metals such as iron and cobalt have garnered particular attention due to their high abundance in the Earth's crust and relatively low cost.5,6 Fe–N–C catalysts, in particular, have demonstrated notable stability and resistance to methanol/CO poisoning, making them among the most promising alternatives to platinum-based catalysts in fuel cells. The high catalytic activity of Fe–N–C is attributed to several key factors, including variations in electron density at the metal center due to the π-electron deficiency in the carbon matrix support, the anodic shift in the redox potential of the metal ion, and the reduction in the energy of the eg (dz2) orbital. These effects promote enhanced adsorption of O2 and key intermediates by facilitating stronger interactions between the oxygen σ orbital and the eg (dz2) orbital of the metal center.7
Spectroscopic studies have confirmed that Fe–Nx moieties serve as the primary active sites in Fe–N–C catalysts, where Fe cations coordinate with pyridinic nitrogen atoms at the edges of graphitic carbon surfaces.8 The high-temperature pyrolysis typically employed for the synthesis of these catalysts often leads to the sintering of Fe atoms, thereby hindering the formation of well-defined Fe–Nx moieties. Thus, controlling the chemical environment during synthesis is essential, as precursor selection strongly influences the catalytic activity of the final material.9 The heteroaromatic chelating agent 1,10-phenanthroline (Phen), which contains two nitrogen atoms and forms stable coordination complexes with Fe2+, has been explored as a nitrogen precursor to enhance the number of host sites for anchoring isolated Fe atoms.10 This approach increases the density of electroactive sites with high catalytic activity. Kim et al. investigated the use of three different Phen isomers and observed that the strong stability of the Fe–1,10-phenanthroline complex suppressed iron migration at high temperatures.11 This resulted in a more uniform distribution of iron within the carbonaceous matrix while preserving a significant proportion of nitrogen dopants at pyridinic sites. Such findings underscore the importance of precursor selection in optimizing Fe–N–C catalysts for ORR applications.
Although Fe–N–C materials containing FeNx moieties are considered among the most promising platinum-free ORR catalysts, their performance remains inferior to that of platinum-based catalysts in proton exchange membrane fuel cells (PEMFCs).12 As a result, further advancements are necessary to bridge this performance gap. A comprehensive kinetic study of the ORR on Fe–N–C catalysts is crucial for understanding the mechanistic effects introduced by specific modifications to the catalyst structure.13
Vasconcellos and co-workers carried out a systematic investigation aimed at enhancing both the oxygen reduction reaction (ORR) activity and durability of Fe–N–C electrocatalysts through the rational optimization of a straightforward 1,10-phenanthroline–iron complexation synthesis route.14 Critical synthesis parameters—including the Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) phenanthroline molar ratio, the textural properties of the carbon support, and the pyrolysis temperature—were deliberately tuned to assess their effect on the structural and catalytic properties of the resulting materials. A notable finding of this study was the pronounced improvement in catalyst stability during accelerated durability testing (104 potential steps) as the pyrolysis temperature increased from 700 to 1300 °C, albeit accompanied by a progressive decrease in ORR activity. Among the catalysts prepared at different temperatures, the sample pyrolyzed at 1050 °C exhibited the most favorable trade-off between kinetic activity and long-term stability. Consequently, this material was selected for detailed kinetic analysis under hydrodynamic (convective) control in the acidic electrolyte.
phenanthroline molar ratio, the textural properties of the carbon support, and the pyrolysis temperature—were deliberately tuned to assess their effect on the structural and catalytic properties of the resulting materials. A notable finding of this study was the pronounced improvement in catalyst stability during accelerated durability testing (104 potential steps) as the pyrolysis temperature increased from 700 to 1300 °C, albeit accompanied by a progressive decrease in ORR activity. Among the catalysts prepared at different temperatures, the sample pyrolyzed at 1050 °C exhibited the most favorable trade-off between kinetic activity and long-term stability. Consequently, this material was selected for detailed kinetic analysis under hydrodynamic (convective) control in the acidic electrolyte.
To further clarify the underlying mechanisms, we developed a frequency-domain model for process identification, incorporating a transmission line transfer function to account for the porous nature of the carbon-based material.
Theoretical section
Electrochemical impedance spectroscopy, combined with time-domain electrochemical data under diffusional-convective control, is a powerful technique for investigating interfacial electrochemical reactions and contributes significantly to the evaluation of catalyst performance.15,16In acidic media, the mechanism of the oxygen reduction reaction (ORR) can be described using the following steps:
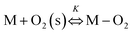 | (I) |
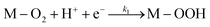 | (II) |
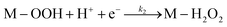 | (III) |
 | (IV) |
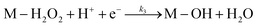 | (V) |
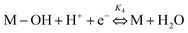 | (VI) |
In step I, a chemical equilibrium is established at the interface between dissolved molecular oxygen and oxygen adsorbed at an active site (M) of the catalyst. Steps II, III, V, and VI each involve the transfer of one electron and one proton, leading to the formation of adsorbed intermediates, and ultimately yielding water and hydrogen peroxide as the final products. Assuming step VI is at equilibrium, the rate-determining step is identified as step II, while the desorption of hydrogen peroxide occurs at step IV, as will be corroborated in the Results and discussion section.
Although adsorbed hydroperoxo (M–OOH) and hydroxyl (M–OH) intermediates were not experimentally detected in this study, their transient formation is consistent with an oxygen reduction pathway in acid media involving H2O2 generation—confirmed by rotating ring-disk electrode (RRDE) measurements—and a sequential 2e− + 2e− mechanism. Other adsorbed intermediates, such as M–O, may also participate in the overall reaction sequence.17–20 Nevertheless, the proposed mechanistic framework adequately captures the key intermediates that govern the observed reaction kinetics. Considering the intrinsic instability of these transient species and the identification of step II as the rate-determining stage (as discussed below), both the transfer function and the theoretical Butler–Volmer behavior remain unaffected within the adopted kinetic model, even in the presence of additional intermediates. Therefore, the individual surface coverages of each intermediate were not explicitly computed; instead, only the total adsorbate coverage and that of molecular oxygen were considered.
The steady-state faradaic current, based on the Butler–Volmer equation, the Langmuir isotherm, and assuming a geometric electrode area of 1 cm2, is given by the following equation:
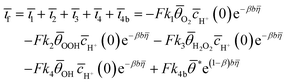 | (1) |
Here, F is the Faraday constant, β is the transfer coefficient, b = RT/nF, where R is the ideal gas constant, T the absolute temperature, if the faradaic current, η the overpotential, and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+(0) the surface proton concentration. The terms θOOH, θH2O2, θOH and θ* represent surface coverages of the adsorbed OOH, H2O2, and OH species and the fraction of free active sites on the catalyst surface, respectively. Each ki represents the rate constant corresponding to a specific elementary step. The currents ī1, ī2, ī3, and ī4 correspond to the faradaic contributions from the elementary steps II, III, V, and VI. The symbol ‘–’ denotes steady-state values.
H+(0) the surface proton concentration. The terms θOOH, θH2O2, θOH and θ* represent surface coverages of the adsorbed OOH, H2O2, and OH species and the fraction of free active sites on the catalyst surface, respectively. Each ki represents the rate constant corresponding to a specific elementary step. The currents ī1, ī2, ī3, and ī4 correspond to the faradaic contributions from the elementary steps II, III, V, and VI. The symbol ‘–’ denotes steady-state values.
The time-dependent variation of the fraction of free active sites was used to establish its relationship with the resulting faradaic current:
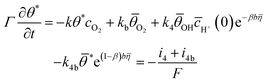 | (2) |
Under steady-state conditions, 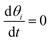 , and considering the pre-equilibrium of step I, the following relationships are obtained:
, and considering the pre-equilibrium of step I, the following relationships are obtained:
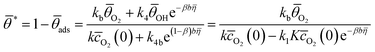 | (3) |
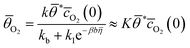 | (4) |
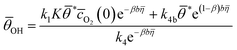 | (5) |
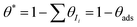 ,
, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) O2(0) is the surface concentration of molecular oxygen, and
O2(0) is the surface concentration of molecular oxygen, and  . When the first electron transfer step is rate-determining, eqn (1) simplifies to the following:
. When the first electron transfer step is rate-determining, eqn (1) simplifies to the following: | (6) |
For the oscillatory regime
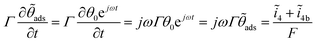 | (7) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ads and ω is the angular frequency of the perturbation. The symbol “∼” denotes quantities under oscillatory conditions. Expanding eqn (7) in terms of
ads and ω is the angular frequency of the perturbation. The symbol “∼” denotes quantities under oscillatory conditions. Expanding eqn (7) in terms of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ,
, ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ads, and
ads, and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O2(0),
O2(0), | (8) |
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ads:
ads: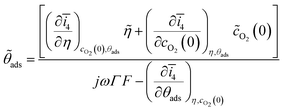 | (9) |
Fick's first law was employed to relate the surface concentration of molecular oxygen to the faradaic current 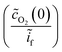 :
:
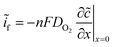 | (10) |
 | (11) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O2/
O2/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O2(0) and
O2(0) and  , the dimensionless differential equation becomes,
, the dimensionless differential equation becomes,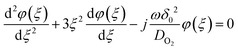 | (12) |
The hydrodynamic diffusion layer thickness (δ0) is given by21
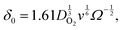 | (13) |
Applying the boundary conditions (φ(1) = 0 and φ(0) = 1), in conjunction with the Nernst hypothesis,
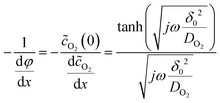 | (14) |
Expanding ĩf in terms of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ,
, ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ads, and
ads, and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) O2(0),
O2(0),
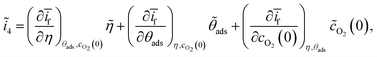 | (15) |
 | (16) |
We add the capacitive reactance associated with the electrical double layer capacitance (Cdl) to the faradaic impedance Zf, generating the transfer function Z1:
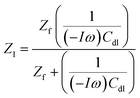 | (17) |
The porosity of the electrode creates two phases within the material: the ionic conductive phase (electrolyte inside the pores) and the electronic conductive phase (solid material). Additionally, there is charge transfer between these phases and a potential gradient within the pores. Due to these effects, we incorporate a transmission line model.16 Starting from differential equations and boundary conditions, we integrate the transfer function Z1 into a transmission line model and obtain the transfer function Z2:
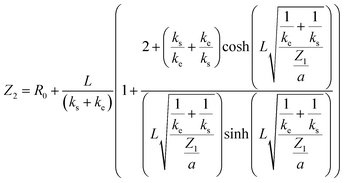 | (18) |
Experimental
Initially, 26 mg of iron(III) nitrate and 160 mg of 1,10-phenanthroline (Phen) were dissolved in 50 mL of absolute ethanol under magnetic stirring. The solution was refluxed at 80 °C for 1 h before adding 200 mg of Black Pearls carbon (Cabot Co.). The suspension was stirred at the same temperature for an additional 4 h. Ethanol was then gradually evaporated at 80 °C under stirring to promote iron nitrate impregnation, and the resulting material was dried overnight. Finally, the obtained powder was subjected to pyrolysis at 1050 °C (heating rate: 5 °C min−1) under an argon atmosphere for 1 h, yielding nitrogen-coordinated iron atoms within the carbon matrix, with an Fe content of 1 wt%.14,22 For catalyst ink preparation, 1 mg of Fe–N–C was dispersed in 200 µL of anhydrous isopropanol (Sigma-Aldrich) and 10 µL of Nafion (Sigma-Aldrich). The mixture was sonicated for 40 min, and 10 µL was drop-cast onto a glassy carbon electrode, resulting in a catalyst loading of 238 µg cm−2. Scanning transmission electron microscopy measurements (STEM), with elemental mapping measurements, were performed using a JEOL JEM-F200 microscopy, operated at 200 kV, equipped with a cold field emission gun (FEG), and a 100 mm2 silicon detector with drift correction and an EDS detector. The iron content relative to the total mass of the electrocatalysts was quantified using inductively coupled plasma mass spectrometry (ICP-MS) on a PerkinElmer NexION 2000c MS instrument. Further details regarding material characterization can be found in ref. 14. Raman spectroscopy of the Fe–N–C Phen BP samples revealed a progressive enhancement in the graphitic character of the carbon framework with increasing temperature from 700 to 1300 °C.14 X-ray photoelectron spectroscopy (XPS) of the same material confirmed the presence of characteristic Fe and N signals, evidencing pyridinic and graphitic nitrogen species as well as Fe(II) and Fe(III) components.14 Based on N2 adsorption measurements analyzed using the BET isotherm method, the specific surface area of the Fe–N–C material corresponds to 840 m2 g−1,14 which falls within the range commonly observed for porous solids.23Electrochemical experiments were conducted using an Autolab PGSTAT30 potentiostat/galvanostat. The Fe–N–C activity for the oxygen reduction reaction (ORR) was evaluated in a three-electrode electrochemical cell, with a saturated calomel electrode (SCE) as the reference electrode, a graphite rod as the counter electrode, and a rotating ring-disk electrode (RRDE). The RRDE consisted of a glassy carbon disk (area was 0.2 cm2) and a platinum ring. The electrolyte was 0.5 mol L−1 H2SO4 (Sigma-Aldrich, pH = 0.30). After bubbling molecular oxygen through the electrolyte solution, the measurements were performed under a continuous oxygen flow directed above the electrolyte in the electrochemical cell. All potentials were corrected against the reversible hydrogen electrode (RHE).
Chronoamperometric measurements were performed to assess the steady-state behavior of the electrode. Additionally, electrochemical impedance spectroscopy (EIS) was conducted over a frequency range of 10 MHz to 10 mHz with an ac perturbation amplitude of 5 mV at different rotation speeds. Experimental data were fitted using the kinetic model described in the Theoretical section.
The surface density of iron ions was determined via the nitrite stripping technique.24 Linear potential sweeps were performed to quantify the electrochemically accessible active-site density at 1600 rpm and a scan rate of 5 mV s−1 (Fig. S1). The reference charge (9.0 mC cm−2), recorded for the electrode in deoxygenated acetate buffer (pH 5.2), represented the non-poisoned surface. Nitrosyl adsorption onto Fe(III) sites was subsequently induced by the addition of NaNO2 (125 mmol L−1) to the electrolyte. Following the procedure described in ref. 24, an analogous potential sweep was then carried out, yielding a stripping charge of 11.2 mC cm−2. Considering the difference between pre- and post-adsorption charges and assuming a five-electron reduction per stripped nitrosyl species, the surface density of Fe ions was calculated as Γ = 4.5 × 10−9 mol cm−2.”
Results and discussion
Fig. 1 displays high-resolution STEM images alongside the corresponding elemental mapping of the Fe–N–C material, providing direct insight into the spatial distribution of iron, nitrogen, and carbon within the carbonaceous framework. The elemental maps clearly reveal that iron is homogeneously dispersed throughout the matrix, with no detectable presence of iron-rich agglomerates or discrete particles. These micrographs are consistent with the X-ray diffraction data, which showed no evidence of particulate structures—only two broad diffraction peaks characteristic of amorphous carbon.14 This uniform distribution strongly suggests the successful formation of isolated iron single-atom sites, in accordance with the design strategy based on high-temperature pyrolysis of the Fe–1,10-phenanthroline complex under optimized synthetic conditions.11 The absence of clustered or metallic iron phases, often associated with catalytic inactivity or side reactions, highlights the efficiency of the synthesis protocol in stabilizing iron atoms at the atomic scale. Furthermore, the iron content determined by inductively coupled plasma mass spectrometry (ICP-MS) was 1.1 wt%,14 which is in close agreement with the theoretical value, confirming the reproducibility and compositional precision of the material preparation. | ||
| Fig. 1 STEM images and the corresponding elemental mapping: iron (red), nitrogen (green), and carbon (blue), for the synthesized Fe–N–C electrocatalyst. | ||
To evaluate the catalytic effect of Fe–N–C in the ORR, linear sweep voltammetry is performed in a 0.5 mol L−1 H2SO4 solution saturated with molecular oxygen. The sweep is conducted over a potential window from 0.95 to 0.25 V vs. RHE, at a scan rate of 5 mV s−1. To investigate the mass transport effect, measurements are carried out at different electrode rotation speeds, as shown in Fig. 2a. We observe an onset potential of approximately 0.83 V vs. RHE. This value is consistent with ref. 24, which reports a similar catalyst loading (270 µg cm−2). Despite these favorable properties, the ORR activity of the Fe–N–C material remained below that of a commercial 20 wt% Pt/Vulcan XC-72 catalyst (E-TEK) under equivalent experimental conditions. The Pt-based catalyst displayed substantially higher current densities at more positive potentials (≈0.3 mA cm−2 at 0.9 V).14
Increasing the electrode rotation speed promotes a rise in current density (jD), indicating its dependence on the gradient of dissolved molecular oxygen concentration in the solution. This is due to the reduction in the Nernst diffusion layer (eqn (18)). At higher overpotentials, the faradaic current density progressively approaches its limiting value. This incomplete approach can be ascribed to the relatively low density of catalytically active sites, which results from the use of high-surface-area Black Pearls carbon to promote atomic dispersion of iron species and to suppress metal aggregation.14
Fig. 2b presents the ring currents (iR) recorded at various rotation rates during linear potential sweeps. The observed current corresponds to the reduction of hydrogen peroxide molecules that have partially desorbed from active sites into the bulk solution, as illustrated in step IV of the proposed reaction mechanism. Determining the number of electrons transferred per oxygen molecule is critical for optimizing energy efficiency. For this purpose, eqn (19) was employed, accounting for the electrode collection efficiency (N = 0.25), as well as the disk (iD, obtained from jD in Fig. 2a) and ring currents obtained during potential sweeps (Fig. 2a). The calculated number of electrons transferred per oxygen molecule decreased from 3.9 at higher potentials to 3.2 at lower potentials (Fig. S2). Unlike in alkaline media, where the intermediate species is negatively charged (HO2−), in acidic media the electroneutral character of hydrogen peroxide facilitates its desorption from active sites when the reaction proceeds through the pathway involving its formation, as described in the proposed mechanism.25
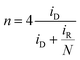 | (19) |
The Koutecký–Levich equation was used to determine the kinetic current density (jk). Fig. 3a shows the inverse of the current density as a function of the inverse square root of the rotation speed for various potentials between 0.7 and 0.6 V. From the linear fittings and extrapolating to infinite rotation speeds, the Butler–Volmer curve (Fig. 3b) and the Tafel plot (Fig. 3c) were obtained. Based on the Tafel slope of approximately 118 mV dec−1, it suggests that the rate-determining step of the reaction is the first electron transfer.26 By extrapolating the Tafel curve to a zero overpotential, the exchange current density was determined to be 2.5 × 10−7 A cm−2, which is about three orders of magnitude higher than that of other Fe–N–C electrocatalysts used for the ORR.25
Using the kinetic current density values and the number of active sites (4.56 nmol cm−2), we calculated the TOF values for potentials ranging from 0.7 V to 0.6 V (Fig. 3d). These values ranged from 1.5 to 13 oxygen molecules consumed per second per active site, which are in the same order of magnitude as those reported for Fe–N–C catalysts synthesized via other routes.24 At a kinetic current density of 10 mA cm−2, the TOF value was approximately 5.4 O2 per second per active surface site.
Fig. 4 illustrates the Nyquist plot for the ORR electrocatalyzed by Fe–N–C at 500, 1000, and 1600 rpm. The low-frequency semicircle corresponds to charge transfer at the interface and to the mass transport of molecular oxygen from solution to the interface during the ORR. Increasing the electrode rotation speed enhances the convective diffusion of molecular oxygen from the bulk solution to the electrode surface, thereby decreasing the faradaic impedance. This phenomenon is integrated into the proposed kinetic model through equations that account for diffusion–convection in solution within a system involving electron transfer, and its influence is reflected in the transfer function (eqn (16)). Meanwhile, the high-frequency semicircle is attributed to mass transport within the electrode pores.16 Since this process is not associated with the potential barrier at the electrode/solution interface for the ORR, increasing the rotation speed does not affect the impedance response. The experimental data, without any fitting, are shown in Fig. S3. Fig. 5 presents Bode diagrams, highlighting the improved fitting of the experimental data using the proposed transfer function.
 | ||
| Fig. 5 Bode plot at rotation speeds of 500 rpm, 1000 rpm, and 1500 rpm. Open circles (○) represent experimental data, while closed circles (●) represent theoretical data. Edc = 0.6 V. | ||
Based on Fick's first law and the current density values obtained under hydrodynamic layer control (Fig. 1a), the surface concentration of molecular oxygen was determined as a function of the applied potential (Fig. 6a). This enabled the use of ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) O2(0) in the analysis of impedance data, reducing the number of fitting parameters. Notably, the oxygen concentration approaches zero at the lower limit of the potential window, defining the limiting current density. Fick's first law was also applied to estimate the surface proton concentration, which is assumed to be approximately equal to the bulk value due to the high proton concentration in the solution.
O2(0) in the analysis of impedance data, reducing the number of fitting parameters. Notably, the oxygen concentration approaches zero at the lower limit of the potential window, defining the limiting current density. Fick's first law was also applied to estimate the surface proton concentration, which is assumed to be approximately equal to the bulk value due to the high proton concentration in the solution.
Fig. 4 and 5 also present the theoretical impedance data derived from fitting the experimental data using eqn (18). The parameters used to fit the impedance diagrams—whether obtained experimentally, extracted from the literature, or determined using alternative models—were as follows: ν = 0.01 cm2 s−1,21DO2 = 2 × 10−5 cm2 s−1,27E = −0.6 V, T = 298 K, Γ = 4.5 × 10−9 mol cm−2, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) O2(0) = 1.5 × 10−7 mol cm−3,
O2(0) = 1.5 × 10−7 mol cm−3, 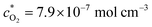 ,28
,28![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+(0) = 0.51 × 10−3 mol cm−3, and Ω = 52.3, 102.7, and 167.5 rad s−1. Due to the lack of information on the location of the transition state within the electrical double layer and to avoid introducing unnecessary degrees of freedom, the symmetry factor was fixed at β = 0.5.21 The values of δ0 for each rotation speed were calculated using eqn (13). Together with the fitting shown in Fig. 3b, where the kinetic current corresponds to
H+(0) = 0.51 × 10−3 mol cm−3, and Ω = 52.3, 102.7, and 167.5 rad s−1. Due to the lack of information on the location of the transition state within the electrical double layer and to avoid introducing unnecessary degrees of freedom, the symmetry factor was fixed at β = 0.5.21 The values of δ0 for each rotation speed were calculated using eqn (13). Together with the fitting shown in Fig. 3b, where the kinetic current corresponds to
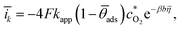 | (20) |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) O2 = 0.480 ± 0.005,
O2 = 0.480 ± 0.005, ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) * = 0.042 ± 0.0004 (
* = 0.042 ± 0.0004 (![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) ads = 0.958 ± 0.01), Cdl = 61.0 ± 0.1 mF cm−2, ks = 1.85 ± 0.01 mS cm−1, ke = 0.25 ± 0.01 mS cm−1, L = 410 ± 1 µm, a = 2500 ± 13 cm−1, and R0 = 0.65 Ω. The corresponding uncertainty analysis and error propagation are presented in the SI (Fig. S4). The values of
ads = 0.958 ± 0.01), Cdl = 61.0 ± 0.1 mF cm−2, ks = 1.85 ± 0.01 mS cm−1, ke = 0.25 ± 0.01 mS cm−1, L = 410 ± 1 µm, a = 2500 ± 13 cm−1, and R0 = 0.65 Ω. The corresponding uncertainty analysis and error propagation are presented in the SI (Fig. S4). The values of 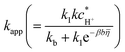 were also used to simulate the Tafel plot, which is shown in Fig. 3c.
were also used to simulate the Tafel plot, which is shown in Fig. 3c.
The data indicate that the observed behavior follows Langmuir adsorption characteristics, which is consistent with the expected response for single-atom catalysts. In such systems, the absence of lateral interactions between adsorbed species—owing to the isolated nature of the active sites—favors ideal Langmuir-type adsorption. When the Frumkin adsorption isotherm was incorporated into the impedance model and fitted simultaneously in both the time and frequency domains (Fig. S5–S7), the term (g) associated with lateral interactions among adsorbed species converged to zero.29 Consequently, the transfer function simplified to that given in eqn (16), supporting the assumption that the catalytic surface is composed of well-dispersed, non-interacting adsorption sites, as typically observed in single-atom catalyst architectures.
The high equilibrium constant (K ≈ 107) reflects a strong binding affinity between isolated iron sites and molecular oxygen, playing a pivotal role in enhancing the electrocatalytic activity toward the oxygen reduction reaction. This strong adsorption capability, combined with the high turnover frequency, ensures that even a limited number of active sites in single-atom catalysts can sustain efficient catalytic performance—an essential requirement for technologies demanding high current densities, such as metal–air batteries and fuel cells.
The rate constant of the rate-determining step was successfully calculated, providing a key kinetic parameter for characterizing the ORR mechanism. Determining this intrinsic constant is crucial, as it enables the quantitative prediction of electrocatalytic behavior under varying operating conditions. With this information, it becomes possible to simulate and anticipate the system's response under current- or potential-controlled regimes, as well as to evaluate the effect of changes in molecular oxygen pressure or concentration. Moreover, the rate constant offers insights into the intrinsic activity of the catalytic sites, independent of mass transport limitations, and serves as a benchmark for comparing different electrocatalysts or reaction environments. This level of mechanistic understanding is essential for process optimization in practical energy conversion systems.
Because of the experimental challenges associated with probing intermediate adsorption on a limited number of electroactive sites (≈4.5 × 10−9 mol cm−2) dispersed within the carbon matrix, the transfer function was formulated exclusively from kinetic data concerning (i) the rate constant of the rate-determining step, (ii) the pre-equilibrium related to molecular oxygen adsorption on the electroactive sites, and (iii) the cumulative surface coverage of the reaction intermediates. The proposed mechanistic model thus relies on RRDE data, Tafel slope analysis, and literature-reported insights.17,21 Nevertheless, the future detection of additional surface intermediates—beyond H2O2—through in situ spectroscopic methods would enable further refinement of this kinetic framework, including the determination of rate constants for additional elementary steps and the evaluation of individual coverage degrees. Complementary characterization and kinetic measurements after extensive potential cycling would likewise contribute to a more comprehensive mechanistic understanding and guide the design of improved catalyst formulations.
Conclusions
This work presents a detailed kinetic and mechanistic study of an Fe–N–C electrocatalyst synthesized by pyrolysis of iron(III) nitrate and 1,10-phenanthroline supported on carbon black. The choice of 1,10-phenanthroline as a nitrogen precursor promoted a uniform dispersion of Fe active sites, which contributed to the catalyst's high ORR performance. The observed onset potential (≈0.83 V vs. RHE), high exchange current density (0.25 µA cm−2), and turnover frequency (5.4 O2 s−1 per site at 10 mA cm−2) indicate a high intrinsic activity for the ORR in acidic media. The kinetic model developed here, which incorporates mass transport and porous electrode effects via a frequency-domain transfer function, enabled the extraction of fundamental parameters such as the apparent rate constant, active site density, and surface oxygen concentration. The Langmuir-type adsorption behavior is consistent with expectations for single-atom catalysts, where the isolated nature of the active sites leads to ideal adsorption characteristics. Despite the limited number of accessible atoms, the high O2 binding constant (≈107) indicates a strong affinity for molecular oxygen at the active centers. Combined with the high turnover frequency values, this suggests a high catalytic efficiency, positioning the material as a promising candidate for use as a positive electrode in metal–air batteries and fuel cells. The kinetic modeling approach employed here can also be extended to other media, such as neutral or alkaline environments, allowing the extraction of analogous kinetic parameters. These parameters not only enable the simulation of electrochemical behavior under various experimental conditions but also provide a predictive basis for the optimization of Fe–N–C-based electrocatalysts for the oxygen reduction reaction. However, further experimental studies remain necessary to resolve additional intermediates and to quantify their respective surface coverages and rate constants, thereby providing deeper mechanistic insight into the ORR process.Conflicts of interest
There are no conflicts of interest to declare.Data availability
Data supporting this article are available at: https://sites.google.com/ffclrp.usp.br/fencelectrocatalysts?usp=sharing.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the linear potential sweep for determining the active site density of the Fe–N–C electrode (Fig. S1), the number of electrons transferred per oxygen molecule as a function of potential (Fig. S2), the experimental Nyquist plots without any fitting (Fig. S3), the determination of kinetic parameter errors (Fig. S4), the Nyquist diagrams for different values of k1 and g at 1500 rpm (Fig. S5) and 500 rpm (Fig. S6), and the kinetic current profile as a function of potential using the Frumkin isotherm (Fig. S7). See DOI: https://doi.org/10.1039/d5cp03000e.
Acknowledgements
F. H. acknowledges financial support from FAPESP (grants 2017/11986-5 and 2021/12735-1) and CAPES (grant 88887.706230/2022-00). F. H. B. L. acknowledges funding from FAPESP (Thematic Project, grant 2019/22183-6). F. H. B. L. and C. S. A. V. also acknowledge support from CNPq under grants 308948/2022-0, 406933/2021-9, 134577/2018-3, and 140893/2021-0. The authors thank Dr Richard F. Webster and Prof. Dr Richard Tilley for their valuable contributions, and gratefully acknowledge the facilities and the scientific and technical support provided by Microscopy Australia at the Electron Microscope Unit (EMU), part of the Mark Wainwright Analytical Centre (MWAC), UNSW Sydney. B. T. F. acknowledges financial support from FAPESP (grant 2024/19994-0).References
- S. M. Alfaifi, R. Balu, K. Chiang, N. R. Choudhury and N. K. Dutta, ACS Catal., 2025, 15, 9301–9345 CrossRef CAS.
- J. G. Buschermöhle, J. Müller-Hülstede, H. Schmies, D. Schonvogel, T. Zierdt, R. Lucka, F. Renz, P. Wagner and M. Wark, ACS Catal., 2025, 15, 4477–4488 CrossRef.
- B. Liu, P. Guo, Y. Dai, B. Liu, Z. Zhang, J. Cai, Y. Xia, Q. Pan, L. Shen, Y. Zhang, L. Zhao and Z. Wang, Chem. Eng. J., 2025, 507, 160174 CrossRef CAS.
- L. Chen, X. Wang, T. Lu, H. Pang, S. Zhang, L. Xu, G. Yang, Q. Zhou and Y. Tang, Appl. Catal., B, 2025, 366, 125007 CrossRef CAS.
- F. D. Speck, J. H. Kim, G. Bae, S. H. Joo, K. J. Mayrhofer, C. H. Choi and S. Cherevko, JACS Au, 2021, 1, 1086–1100 CrossRef CAS PubMed.
- H. T. Chung, D. A. Cullen, D. Higgins, B. T. Sneed, E. F. Holby, K. L. More and P. Zelenay, Science, 2017, 357, 479–484 CrossRef CAS PubMed.
- N. Ramaswamy, U. Tylus, Q. Jia and S. Mukerjee, J. Am. Chem. Soc., 2013, 135, 15443–15449 CrossRef CAS PubMed.
- A. Zitolo, B. Goellner, V. Armel, M.-T. Sougrati, T. Minerva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937–944 CrossRef CAS PubMed.
- B. Tang, Q. Ji, X. Zhang, R. Shi, J. Ma, Z. Zhuang, M. Sun, H. Wang, R. Liu, H. Liu, C. Wang, Z. Guo, L. Lu, P. Jiang, D. Wang and W. Yan, Angew. Chem., Int. Ed., 2025, 64, e202424135 CrossRef CAS PubMed.
- G. Na, W. Hwang, H. Shin, S. Park, J. E. Park, J. Lee, Y. Shin, H. Choi, J. Shim, K. Yeom and Y. E. Sung, Adv. Energy Mater., 2024, 14, DOI:10.1002/aenm.202400565.
- M. Kim, J. M. Yoo, C.-Y. Ahn, J.-H. Jang, Y. J. Son, H. Shin, J. Kang, Y. S. Kang, S. J. Yoo, K.-S. Lee and Y.-E. Sung, ChemCatChem, 2019, 11, 5982–5989 CrossRef CAS.
- L. Song, Z. Liang, K. Nagamori, H. Igarashi, M. B. Vukmirovic, R. R. Adzic and K. Sasaki, ACS Catal., 2020, 10, 4290–4298 CrossRef CAS.
- A. Yu and Y. Yang, Angew. Chem., 2025, 137, e202424161 CrossRef.
- C. S. A. Vasconcellos, M. L. Souza, N. A. Galiote, K. Sasaki, M. Li, N. Khan, E. A. Paredes-Salazar and F. H. B. Lima, Catalysts, 2025, 15, 821 CrossRef CAS.
- M. E. Orazem and B. Tribollet, Electrochemical Impedance Spectroscopy, John Wiley & Sons, New Jersey, 2nd edn, 2017, pp. 243–301 Search PubMed.
- U. Tröltzsch and O. Kanoun, Electrochim. Acta, 2012, 75, 347 CrossRef.
- J. Wei, D. Xia, Y. Wei, X. Zhu, J. Li and L. Gan, ACS Catal., 2022, 13, 7811–7820 CrossRef.
- W. Liu, S. Ye and L. Shi, ACS Appl. Mater. Interfaces, 2025, 17, 4895–4903 CrossRef PubMed.
- D.-H. Lim and J. Wilcox, J. Phys. Chem. C, 2012, 116, 3653–3660 CrossRef CAS.
- Y. Wang and P. B. Balbuena, J. Phys. Chem. B, 2005, 109, 14896–14907 CrossRef CAS PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods, John Wiley & Sons, New York, 1980, pp. 280–315 Search PubMed.
- K. T. Santos, K. Kumar, L. Dubau, H. Ge, S. Berthon-Fabry, C. Vasconcellos, F. H. B. Lima, T. Asset, P. Atanassov and V. A. Saveleva, et al. , J. Power Sources, 2023, 564, 232829 CrossRef CAS.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density, Springer, Dordrecht, 2004, pp. 1–338 Search PubMed.
- D. Malko, A. Kucernak and T. Lopes, Nat. Commun., 2016, 7, 13285 CrossRef CAS PubMed.
- N. Ramaswamy and S. Mukerjee, J. Phys. Chem. C, 2011, 115, 18015–18026 CrossRef CAS.
- N. M. Markovic, H. A. Gasteiger, B. N. Grgur and P. N. Ross, J. Electroanal. Chem., 1999, 467, 157–163 CrossRef CAS.
- P. Han and D. M. Bartels, J. Phys. Chem., 1996, 100, 5597–5602 CrossRef CAS.
- T. Kaskiala, Miner. Eng., 2002, 15, 853–857 CrossRef CAS.
- J. Wang and X. Guo, Chemosphere, 2020, 258, 127279 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |